








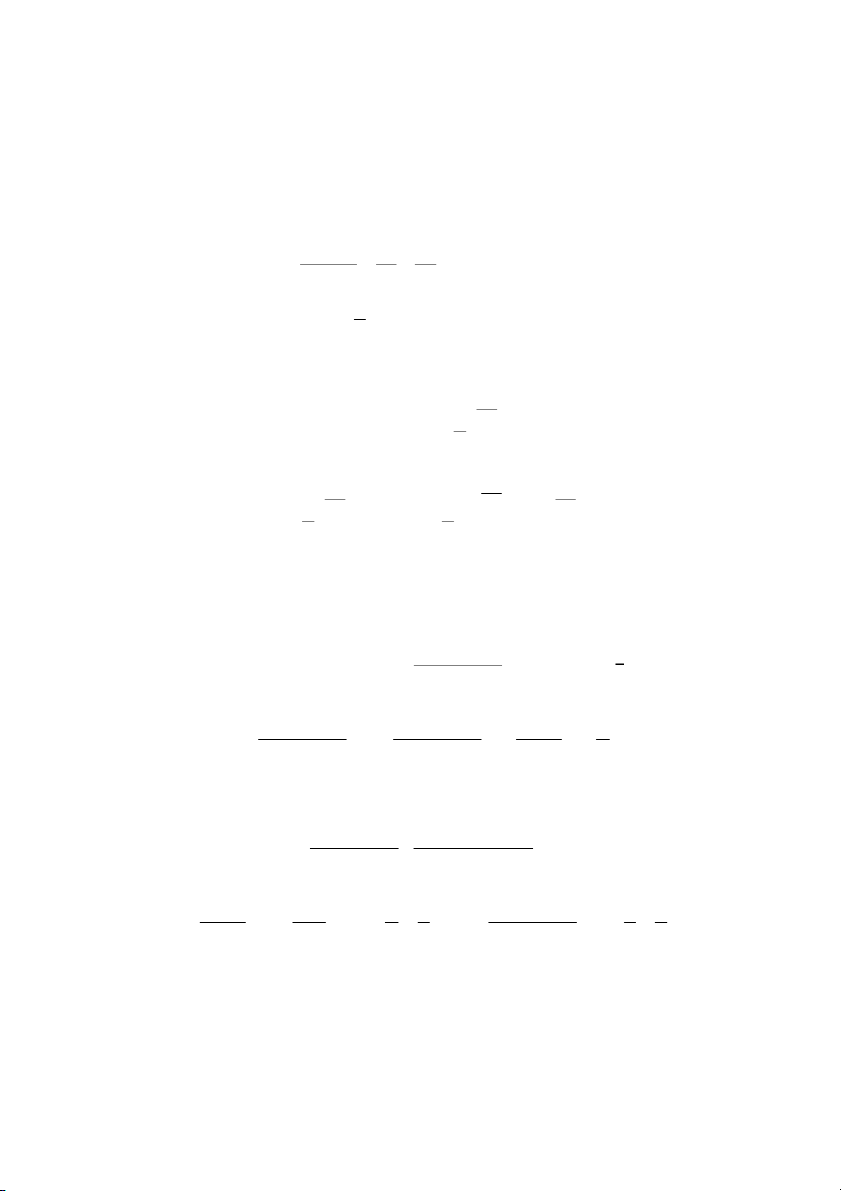


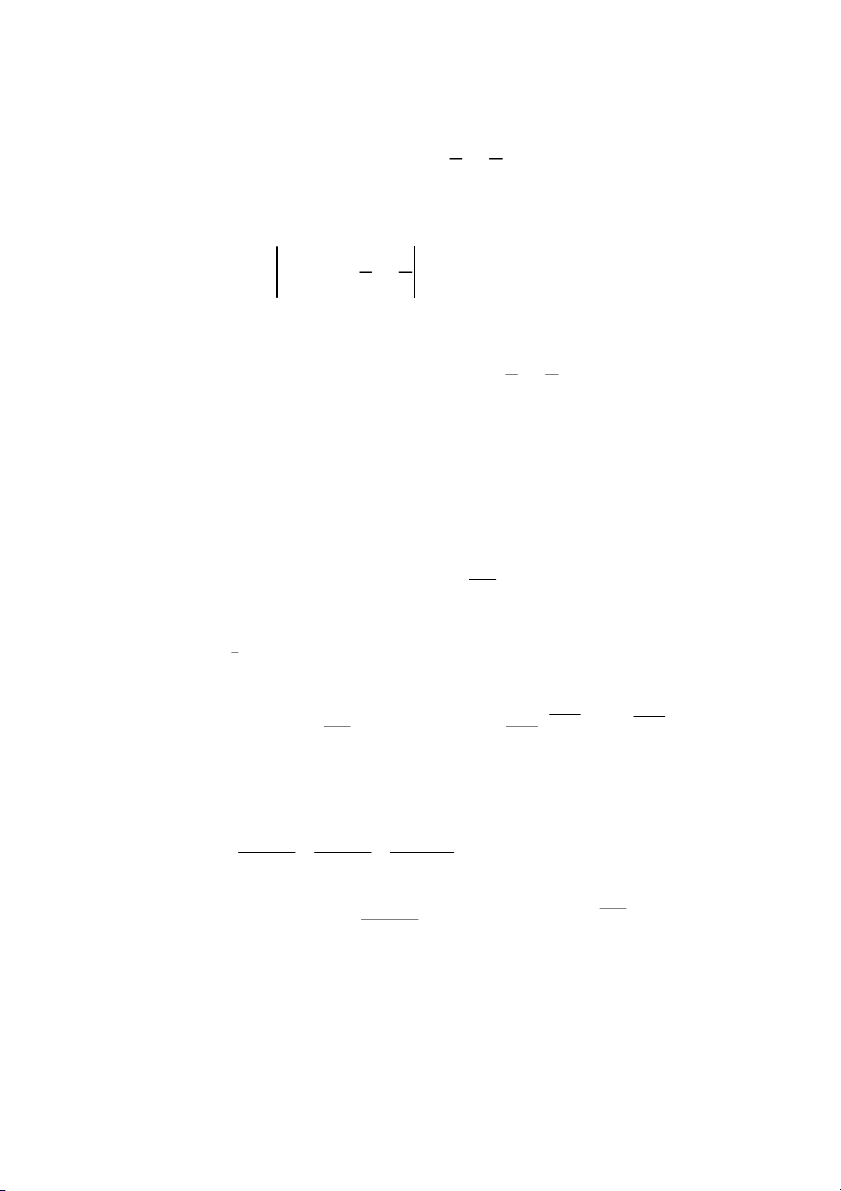

Preview text:
HÀM HAI BIẾN SỐ
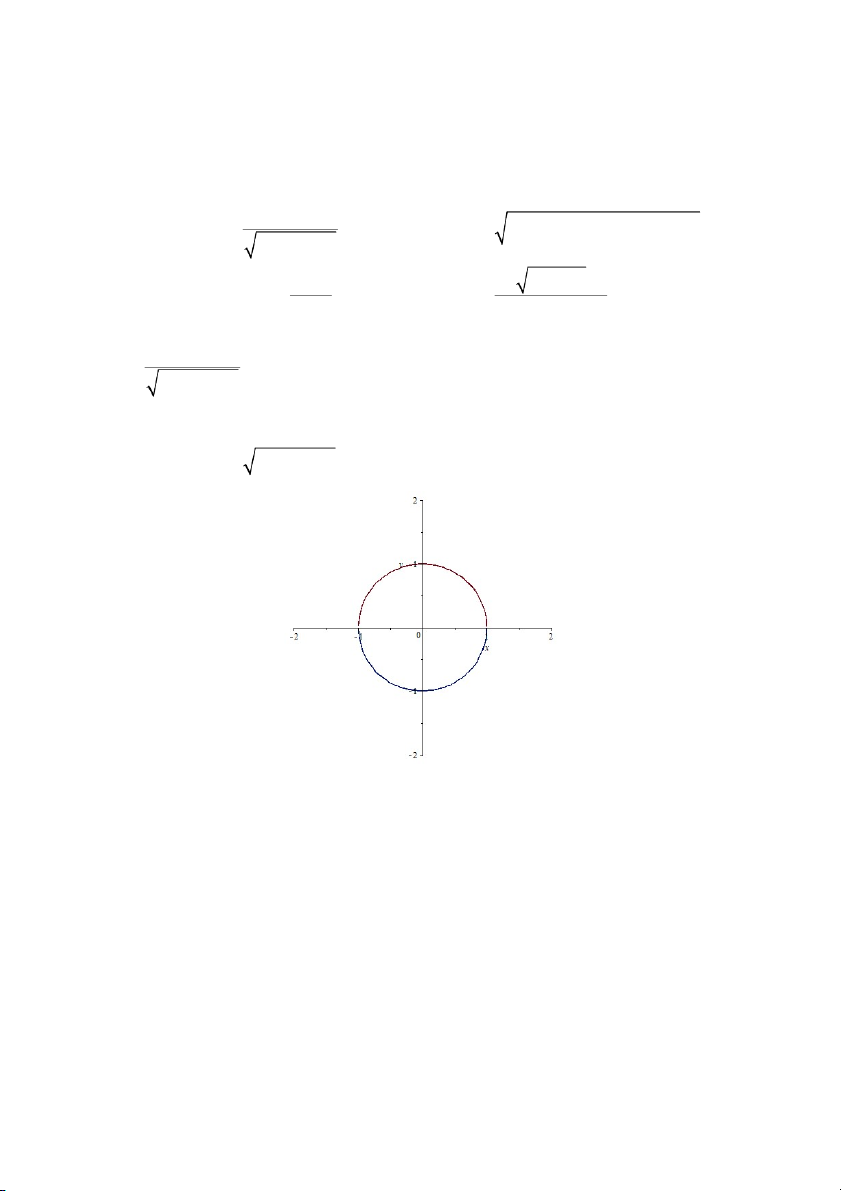
Bài tập. Tìm và biểu diễn tập xác định của các hàm số sau: 1 a. z b. z 2 2 x y 2 2 1 4 x y 2 2 x y 1 2 4 c. arcsin x y x y z d. z x y ln 2 2 1 x y 1 a) z 2 2 x y 1 2 2 x y 1 0 2 2 2 2
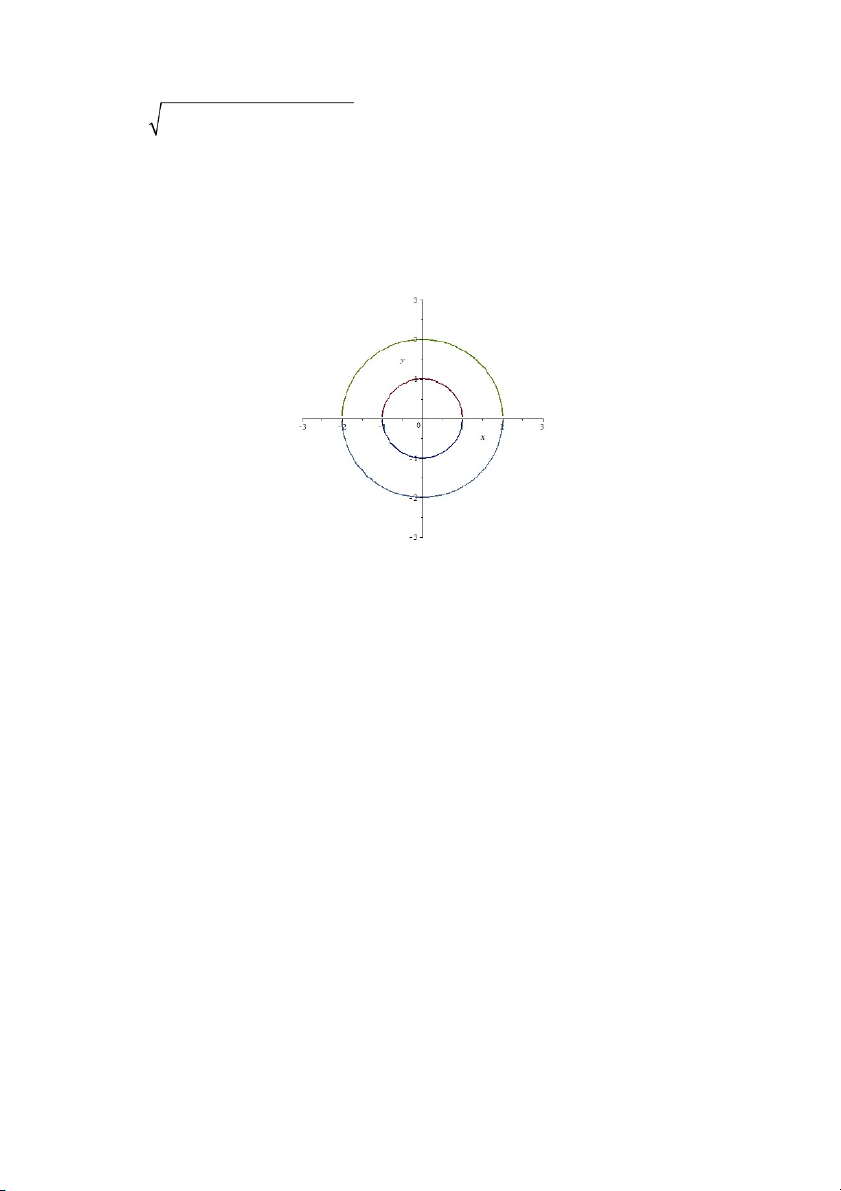
x y 1 0 x y 1 2 2 x y 1 0 b. z 2 2 x y 2 2 1 4 x y 2 2 2 2 x y 1 0 x y 1 2 2 2 2 4 x y 0 x y 4 2 2 x y 1 2 2 4 x y 0 2 2 2 2 x y 1 0 x y 1 2 2 2 2
4 x y 0 x y 4 2 4x y d. z ln 2 2 1 x y 2 y 2 2 4 0 4 x x y y x 4 2 2 2 2 2 2
1 x y 0 x y 1 x y 1 ln 1 x y 2 2 2 2 2 2 0 x y 0 x y 0 c) arcsin x y z x y 1 x y 1, x y x y
1,x y x y x y ,x y x y x y 2 2 2 2 x y x y
x 2xy y x 2xy y 4xy 0 x y x y x y x 0; y 0 4xy 0 x 0;y 0 x y x y
GIỚI HẠN VÀ LIÊN TỤC CỦA HÀM HAI BIẾN SỐ
Định nghĩa 1. Điểm �㕀Ø(�㕥Ø, �㕦Ø) hội tụ đến �㕀Ø(�㕥Ø, �㕦Ø) trong �㕅Ø và ký hiệu �㕀Ø nếu: lim �㕥 �㕦 Ø→∝ Ø = �㕥Ø và lim Ø→∝ Ø = �㕦Ø
Định nghĩa 2. Hàm �㕓(�㕥, �㕦) có giới hạn �㔿 khi (�㕥, �㕦) → (�㕥Ø, �㕦Ø) nếu:
∀�㔀 > 0, ∃�㗿 > 0: 0 < �㔌 < �㗿 → |�㕓(�㕥, �㕦) − �㔿| < �
Trong đó �㔌 = (�㕥 − �㕥Ø)Ø + (�㕦 − �㕦Ø)Ø hoặc:
∀�㕀Ø(�㕥Ø, �㕦Ø) → �㕀Ø(�㕥 �Ø, � 㕓( 㕦 � Ø) 㕥Ø→ , �lim 㕦 Ø→ Ø) = �㔿 Ký hiệu: lim
f x, y lim f x, y L x,y x , y 0 0 x 0 x y y0
Định nghĩa 3. Hàm �㕓(�㕥, �㕦) liên tục tại điểm (�㕎, �㕏) ∈ �㔷 nếu: lim f , x y f , a b x a y b
Hàm số liên tục tại mọi điểm trong miền �㔷 ∈ �㕅Ø gọi là liên tục trên �㔷.
Tính giới hạn kép khi giới hạn không bị vi phạm
Với các trường hợp này, giới hạn nhận được khi thay trực tiếp các biến số đã cho.
Bài tập 1: Tính giới hạn của hàm số 2 5x 4 y 1 5 9 2 lim x1 xy 3 2 3 5 y 2
Bài tập 2: Tính giới hạn của hàm số ln 2 2 y x e ln 0 2 e lim ln3 x 1 2 3 x xy y 2 1 0 0
Bài tập 3: Tính giới hạn của hàm số cos 2 x 2 y cos 1 2 lim x arcsin 2y 1 arcsin 1 y0 2
Một số giới hạn kép (có dạng vô định) không có giới hạn
- Thông thường, khi gặp dạng vô định 0/0, ∞/∞ mà bậc theo các biến x và y của tử
số và mẫu số bằng nhau (hay tốc độ biến thiên về 0 hay ∞ của tử số và mẫu số như
nhau) thì khả năng sẽ không tồn tại giới hạn.
- Để chứng minh hàm số không tồn tại giới hạn, ta xét hai dãy (�㕥 Ø, Ø Ø Ø Ø �㕦 ), Ø(�㕥 , Ø �㕦 ) Ø
cùng dần tiến về (�㕥 Ø Ø Ø Ø Ø, �㕦Ø) nhưn , g �()� 㕦Ø 㕥 → Ø �㔿Ø ≠ (,�㕥 �) Ø 㕦→ �㔿Ø. 2 2
Bài tập 1. Tính giới hạn của hàm số lim x y 2 2 x 0 x y y 0 Cho ,
x y 0,0 theo phương của đường thẳng y kx thì ta có: 2 2 2 2 2 x k x 1 k 1 , k f x kx , x 0 2 2 2 2 2 x k x 1 k 1 k
Vậy khi ,x y 0,0 theo những phương khác nhau thì hàm số đã cho tiến tới
những giá trị khác nhau. Do đó không tồn tại giới hạn. sin
Bài tập 2. Tính giới hạn của hàm số lim x x0 2x y y 0 Cho ,
x y 0,0 theo phương của đường thẳng y kx thì ta có: , sin x f x kx sin sin , x 0 2x kx 2 k 2 k
Vậy khi ,x y 0,0 theo những phương khác nhau thì hàm số đã cho tiến tới
những giá trị khác nhau. Do đó không tồn tại giới hạn. x 2
Bài tập 3. Tính giới hạn của hàm số lim y x0 3x y y 0 1 1
Xem xét 2 dãy điểm M 0, và N ,0 : n n n n 1 0 2. 1 n M M f n n 1 0, lim 0,0 : lim 0, lim 2 n n n n n 1 3.0 n 1 2.0 1 n N N f n n 1 1 ,0 lim 0,0 : lim ,0 lim n n n n n 1 3 3. 0 n 1 1 lim f 0, lim f ,0
, như vậy không tồn tại giới hạn. n n n n
Bài 4. Tính giới hạn của hàm số 2 x y lim x 4x 3y y
Xem xét 2 dãy điểm M n,n và N n,2n : n n 1 1 2 n n n M n n M f n n n n 1 , lim , : lim , lim lim n n n 7 n n 7 7 2 2 1 n n n N n n N f n n n n 2 1 ,2 lim , : lim ,2 lim lim n n n 10 n n 10 10 lim f ,
n n lim f n,2n , như vậy không tồn tại giới hạn. n n
Bài 5. Tính giới hạn của hàm số 2x y 2 2 1 lim x 0 3x y 1 y 1 1 1 1 1 Xem xét 2 dãy điểm M ,1 và N ,1 : n n n n n n 1 1 1 2. 3 1 1 n n n M M f n n 2 2 1 1 3 ,1 lim 0,1 : lim ,1 lim lim n n n n n n n 1 1 n 4 4 3. n n n 1 1 1 2. 3 1 1 n n n N N f n n 2 2 1 1 3 ,1 lim 0,1 : lim ,1 lim lim n n n n n n n 1 1 n 2 2 3. n n n 1 1 1 1
lim f ,1 lim f ,1 , như vậy không tồn tại giới hạn. n n n n n n
Bài 6. Tính giới hạn của hàm số ln�㕥�㕦 + 2�㕥Ø lim →! �㕥�㕦 + �㕦Ø !→!
Xem xét 2 dãy điểm M n,n và N 2n,n : n n 2 2 2 n n n n M n n M f n n n n ln 2 ln , lim , : lim , lim lim 1 2 2 n n n 2 n n n 2 2 2 n n n n N n n N f n n n n ln 2 8 ln 2 2ln 8 8 2 , lim , : lim 2 , lim lim 2 2 n n n 3 n n 3n 3 lim f , n n lim f 2 ,
n n , như vậy không tồn tại giới hạn. n n Tính giới hạn lặp
Lần lượt tính giới hạn theo từng biến, trong đó khi tính theo biến này thì xem biến
kia là hằng số và sử dụng các phương pháp tính giới hạn của hàm một biến số để
tính: vô cùng lớn, vô cùng bé tương đương, l’Hospital, …
lim f x, y lim lim f x, y lim lim f x, y x 0 x x 0 x y 0 y y 0 y x 0 x y 0 y
Bài tập 1. Tính giới hạn của hàm số 3xy 1 1 lim 2 x 0 5xy y1 xy xy 3xy 1 1 3xy 1 1 3 1 1 3 1 1 lim lim lim limlim 2 2 x 0 x 0 y 1 x 0 y 1 2 5xy 5xy 5xy 3xy 1 1 y 1 3xy 3 3 3 lim lim lim lim lim 2 x 0 y 1
5 xy 3xy1 1 x 0 y 1
5 y 3x1 1 x 0
5 3x1 1 10
Bài tập 2. Tính giới hạn của hàm số xy 2 x y 2x 2y 1 1 lim 2 x x 4xy y 1 y 1 xy xy 2 2 2 x y 2x 2y 1 1
x y 2x 2 y 1 1 x 2x 1 x lim limlim lim 2 2 2 x x y1 x 4xy y 1 x 4xy y 1 x x 4x 2 y 1 2 x 1 2 x x 4x 2 2 x 4x 2 2 2x 1 x 2x 1 x 2x 1 2 x 1 lim x lim 2 lim 1 x 2 x 4 x2 e e 2 2 x x 4x 2 x x 4x 2 1 lim1 uu e u 0
Bài tập 3. Tính giới hạn của hàm số yx x x 2 y 1 lim 2 x 1 ln x xy y y 1 yx x x2 y yx 1
x x2 y x 1 lim lim lim lim x x 2 2 x 1 x 1 y 1 x 1 ln x xy y ln x xy y ln x x 1 y 1 Ta có: x
y x ln y x ln x (x 0) ' y 1 ln x x ln x1 y x y' ln x 1 x x x 1 x x x L x x x x . L ln 2 x x 1 ln 1 x 1 lim lim lim x 2 x 1 x 1 ln x x 1 1 x 1 1 1 2 x x
Tính giới hạn kép dựa trên giới hạn của hàm 1 biến
Sử dụng các bất đẳng thức sau: 2 2 2xy x y , , x y x y x y2 2 2 , x 0, y 0 2 2 x y 1 1 , x 0, y 0 4 4 2 2 x y x y 1 x y x y 2 2 2 2 2 , x , y 4 2 x 1 xy
Bài tập 1: Tính giới hạn của hàm số lim 1 (có dạng 1) x x y 1 2 x x x lim x 1 x y 1 x y x x y y1 lim 1 lim 1 e e x x x x y 1 y 1 sin x e cosx
Bài tập 2: Tính giới hạn của hàm số lim (có dạng Ø) x 0 sin xy Ø y2 sin x sin e cos x x e cos x xy 1 lim lim .lim .lim x0 x0 x0 x0 sin xy x sin xy y y2 y2 y 2 y 2 Ta có: sin x sin e cos x L x e cosx sin lim x 1 x0 x 1 y 2 xy t 1 1 sinx e cos x 1 1 lim lim 1;lim lim 1.1. x 0 t 0 x0 sin xy sint y 2 x0 sin xy 2 2 y 2 y 2 y 2
Tính giới hạn kép nhờ định lý giới hạn kẹp và bất đẳng thức giới hạn
- Bất đẳng thức giới hạn: cho 2 hàm số �㕓(�㕥, �㕦) ≤ �㕔(�㕥, �㕦), ∀
�㕉(�㕥Ø, �㕦Ø){(�㕥Ø, �㕦Ø)} thỏa mãn điều kiện: lim �㕓(�㕥, �㕦) = � � 㕔 㕎 ( ; � li 㕥 m , �㕦) = �㕏 →! →! !→!! !→!! Thì �㕎 ≤ �㕏.
- Định lý giới hạn kẹp: cho 3 hàm số �㕓(�㕥, �㕦) ≤ �㕔(�㕥, �㕦) ≤ ℎ(�㕥, �
�㕉(�㕥Ø, �㕦Ø){(�㕥Ø, �㕦Ø)} thỏa mãn điều kiện:
lim f x,y limhx,y a; lim g x,y a x 0 x x 0 x x 0 x y y0 yy0 y y0 Thì: lim g , x y a x 0 x y 0 y 2 2 x y
Bài tập 1. Tính giới hạn của hàm số lim (có dạng ) x y x e y Nhận thấy: 2 2 2 2 0 2 2 2 x y x y , 0, 0 0 t x y x y x y , t x y x y x y t e e e 2 L t 2 L t 2 2 2 lim x y t lim lim 0 lim 0 t t t x t t e e e x y x e y y
Bài tập 2. Tính giới hạn của hàm số lim x y (có dạng ) 2 2 x x xy y y Nhận thấy: 2 2 x y x y 1 1 x xy y xy 0, x 0,y 0 0 , x 0,y 0 2 2 x xy y xy x y 1 1 1 1 lim lim lim 0 x x x x y x y y y y lim x y 0 2 2 x x xy y y x y3
Bài 3. Tính giới hạn của hàm số lim 2 2 x x 2y y Với x 0, y 0:
x 2 y 2 x y 2 x y2 2 2 2 2 x 3 y x y3 1 x y 2 2 2 x 2 y 2x y 2 Ta có: 1 x y lim x y 3 lim 2 2 x 2 x x 2 y y y
Bài 4. Tính giới hạn của hàm số x y 1 1 lim sin sin x 0 x y y 0 Nhận thấy: x 1 1 0 y sin sin x y ,x 0, y 0 x y Ta có: 1 1 lim
limx ysin sin 0 x y 0 x 0 x 0 x y y 0 y 0
Bài 5. Tính giới hạn của hàm số lim 1 x y 1 2 2 x 2 y x 0 y 0
Ta có: lim1 u 1u e u 0 2 2 2 2 x y x y lim x y x x y lim 1 x y 1 x 2
y lim 1 x y 1 2 0 2 2 2 2 2 2 2 y 0 x y e x 0 x 0 y 0 y 0 Nhận thấy: x y x y x y2 2 2 2 2 0 x y , x 0, y 0 x 2 y x y x y 2 2
lim 0 lim x y x y 0 lim 2 2 1 x y 1 x 2 y 1 x 0 x 0 x 0 x 2 y y 0 y 0 y 0
Sự liên tục của hàm nhiều biến
Định nghĩa: Hàm số �㕓(�㕥, �㕦) được gọi là liên tục tại điểm (�㕎, �㕏) ∈ �㔷 nếu:
lim�㕓(�㕥, �㕦) = f(�㕎, �㕏) →! !→!
Hàm số liên tục tại mọi điểm trong miền �㔷 ∈ �㕅Ø gọi là liên tục trên �㔷. Bài tập 1. Cho hàm số: f x y x 2y 1 , x 1
Chứng minh rằng �㕓 liên tục tại gốc tọa độ. Ta có: f 0 2.0 1 0,0 1 0 1 f x y x 2y 1 lim , lim 1 f 0,0 x 0 x 0 x 1 y 0 y 0




