lOMoARcPSD|50734573 Chương 2
Biến ngẫu nhiên và phân phối xác suất
1. Một thiết bị gồm 3 bộ phận hoạt ộng ộc lập với nhau, xác suất trong thời gian t các bộ
phận bị hỏng tương ứng là 0,15; 0,1; 0,13. Gọi 𝑋 là số bộ phận bị hỏng trong thời gian t.
a) Lập bảng phân phối xác suất của 𝑋.
b) Viết biểu thức hàm phân phối của 𝑋.
c) Tìm xác suất trong thời gian t thiết bị có không quá một bộ phận bị hỏng.
d) Tìm 𝐸(𝑋), 𝑉(𝑋), 𝑚 và 𝑚 .
2. Biến ngẫu nhiên rời rạc 𝑋 có quy luật phân phối xác suất như sau: 𝑋 𝑥 𝑥 P 𝑝 0,7
Tìm 𝑥 , 𝑥 và 𝑝 biết 𝐸(𝑋) = 2,7 và 𝑉(𝑋) = 0,21 (𝑥 > 𝑥 ).
3. Ba máy ATM 1, 2, 3 có xác suất không cho giao dịch tại cùng một thời iểm lần lượt là
0,02; 0,03; 0,05. Tại thời iểm ó, mỗi máy ược một người rút lền. Tính số máy không
cho giao dịch ln chắc nhất trong ba máy trên vào thời iểm ó, biết rằng ba máy ATM này hoạt ộng ộc lập.
4. Trong 100 000 vé xổ số phát hành có 1 giải trị giá 100 triệu ồng, 1 giải trị giá 20 triệu
ồng, 5 giải trị giá 5 triệu ồng, 15 giải trị giá 1 triệu ồng. Tìm số lền lãi kì vọng của một
người khi mua một vé xổ số, biết giá vé là 10 000 ồng.
5. Có hai hộp sản phẩm; hộp thứ nhất có 7 chính phẩm và 3 phế phẩm, hộp thứ hai có 8
chính phẩm và 2 phế phẩm. Lấy ngẫu nhiên một hộp rồi từ ó lấy ngẫu nhiên ra 3 sản phẩm.
a) Lập bảng phân phối xác suất của số chính phẩm ược lấy ra.
b) Tìm xác suất ể sai lệch giữa số chính phẩm ược lấy ra và kỳ vọng toán của nó nhỏ hơn 1.
6. Một hộp có 10 sản phẩm gồm chính phẩm và phế phẩm. Gọi 𝑋 là số phế phẩm có trong
hộp. 𝑋 có bảng phân phối xác suất như sau: 𝑋 0 1 2 P 0,6 0,3 0,1 lOMoARcPSD|50734573
Lấy ngẫu nhiên từ hộp 2 sản phẩm. Gọi 𝑌 là số phế phẩm có trong 2 sản phẩm lấy ra.
Tìm quy luật phân phối xác suất của 𝑌.
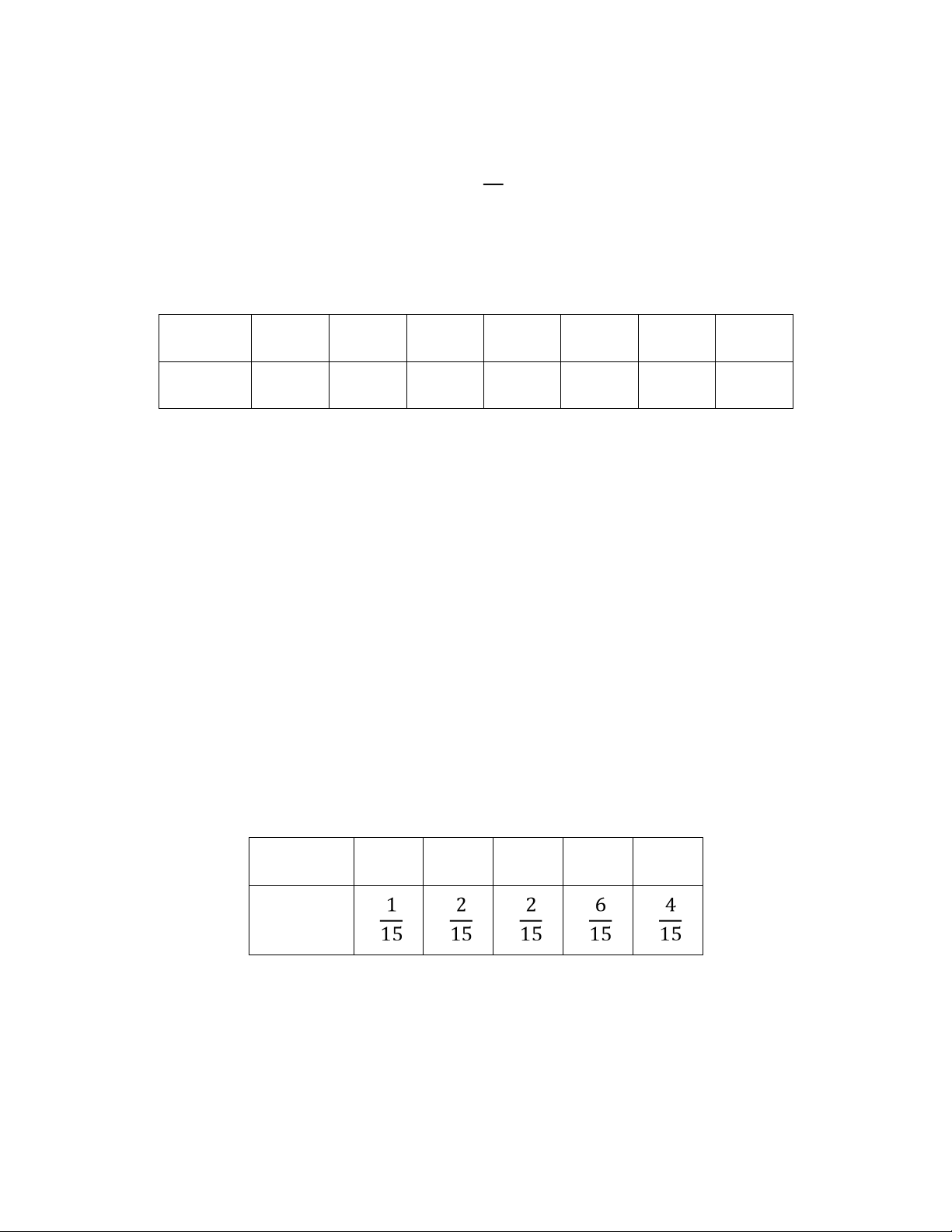
7. Lượng hàng bán ược trong ngày về một loại thực phẩm tại một cửa hàng có bảng phân phối xác suất như sau: Lượng bán (kg) 30 31 32 33 34 35 36 Xác suất 0,05 0,1 0,2 0,3 0,15 0,12 0,08
Mỗi kg thực phẩm mua vào với giá 20 ngàn ồng, bán ra với giá 25 ngàn ồng song nếu
bị ế thì cuối ngày phải bán với giá 15 ngàn ồng mới bán hết. Để lợi nhuận trung bình là
lớn nhất thì mỗi ngày cửa hàng nên ặt mua bao nhiêu kg thực phẩm.
8. Một công ty thuê một luật sư trong một vụ kiện với hai phương án trả công như sau:
Phương án 1: Trả 7 triệu ồng bất kể thắng hay thua kiện.
Phương án 2: Trả 1 triệu ồng nếu thu kiện và 15 triệu ồng nếu thắng kiện. Luật sư
ã chọn phương án 2. Vậy theo ánh giá của luật sư thì khả năng thắng kiện của công ty tối thiểu là bao nhiêu.
9. Theo thống kê, một người ở ộ tuổi 40 sẽ sống thêm một năm nữa với xác suất 0,995.
Một công ty bảo hiểm nhân thọ bán bảo hiểm một năm cho những người ở ộ tuổi ó
với giá là 1 triệu ồng. Trong trường hợp người mua bảo hiểm bị chết thì số lền bồi
thường là 100 triệu ồng. Giả thiết bỏ qua toàn bộ các chi phí khác ngoài việc chi trả
lền bảo hiểm cho khác thì lợi nhuận trung bình của công ty khi bán mỗi thẻ bảo hiểm loại này là bao nhiêu.
10. Trong một cuộc thi, người ta có hai hình thức thi như sau:
Hình thức thứ nhất: Mỗi người phải trả lời hai câu hỏi, mỗi câu trả lời úng ược 5 iểm.
Hình thức thứ hai: Nếu trả lời úng câu thứ nhất thì mới ược trả lời câu thứ hai, nếu
không thì dừng. Trả lời úng câu thứ nhất ược 5 iểm, trả lời úng câu thứ hai ược 10 iểm.
Trong cả hai hình thức thi, các câu trả lời sai ều không ược iểm. Giả sử xác suất trả lời
úng mỗi câu ều là 0,8; việc trả lời úng mỗi câu là ộc lập với nhau. Theo bạn, nên chọn
hình thức nào ể số iểm trung bình ạt ược nhiều hơn.
11. Biến ngẫu nhiên 𝑋có phân phối xác suất như sau:
𝑃(𝑋 = 𝑘) = 𝐶 𝑝 (1 − 𝑝) , (𝑘 = 0,1,2, . . . , 𝑛) Tìm 𝑚 (mốt) của 𝑋. lOMoARcPSD|50734573
12. Biến ngẫu nhiên 𝑋có phân phối xác suất như sau: 𝜆 𝑃(𝑋 = 𝑘) = 𝑒 . , (𝑘 = 0,1,2, . . . ) 𝑘!
với 𝜆 là số dương cho trước. Tìm 𝑚 (mốt) của 𝑋.
13. Theo dõi hiệu quả kinh doanh của một công ty qua nhiều năm, các chuyên gia thiết lập
bảng phân phối xác suất của lãi suất ầu tư của công ty như sau: 𝑋(%) 8 9 10 11 12 13 14 P 0,07 0,14 0,2 0,3 0,16 0,1 0,03
a) Khả năng ầu tư vào công ty ó ể ạt lãi suất ít nhất 11% là bao nhiêu?
b) Tìm mức lãi suất nhiều khả năng nhất và mức lãi suất trung bình khi ầu tư vào công ty ó.
c) Tìm mức ộ rủi ro khi ầu tư vào công ty ó.
14. Thống kê về tai nạn giao thông cho thấy tỉ lệ tai nạn xe máy (vụ/tổng số xe/năm) chia
theo mức ộ nhẹ và nặng tương ứng là 0,001 và 0,005. Một công ty bán bảo hiểm xe
máy với mức thu phí hàng năm là 30 000 ồng và số lền bảo hiểm trung bình một vụ là
1 triệu ồng ối với trường hợp nhẹ và 3 triệu ồng ối với trường hợp nặng. Hỏi lợi nhuận
trung bình hàng năm mà công ty thu ược ối với mỗi hợp ồng bảo hiểm là bao nhiêu?
Biết rằng thuế doanh thu phải nộp là 10% và tổng tất cả các chi phí khác chiếm 15% doanh thu.
15. Một cửa hàng mua vào bốn thùng hàng với giá 120 nghìn ồng/thùng. Số thùng hàng
chưa bán ược, khi hết hạn sử dụng ược nhà phân phối mua lại với số lền bằng số lền
cửa hàng ã mua vào. Gọi 𝑋 là số thùng hàng bán ược của cửa hàng, 𝑋có phân phối xác suất như sau: 𝑋 0 1 2 3 4 P
Nếu giá bán ra của mỗi thùng hàng trên như nhau, thì giá ó là bao nhiêu ể lợi nhuận kì
vọng ối với 4 thùng hàng này là 40 nghìn ồng/thùng.
16. Thống kê về mức ộ hỏng và chi phí sửa chữa của hai loại ộng cơ A và B, có bảng số liệu sau: lOMoARcPSD|50734573 Mức ộ hỏng 1 2 3
Chi phí sửa chữa (triệu A 5,5 7,2 12,5
ồng/năm) của một ộng cơ B 6,0 7,5 10,8 Tỉ lệ hỏng (%/năm) A 2 5 3 B 1 4 5
Một công ty ang sử dụng 6 ộng cơ loại A và 4 ộng cơ loại B. Tính chi phí sửa chữa trung
bình hàng năm cho cả hai loại ộng cơ trên của công ty.
17. Cơ quan dự báo khí tượng thủy văn chia thời lết thành các loại “xấu”, “bình thường”,
“tốt” với xác suất tương ứng là 0,25; 0,45; 0,3. Với —nh trạng trên thì khả năng nông
nghiệp ược mùa tương ứng là 0,2; 0,6; 0,7. Nếu như sản xuất nông nghiệp ược mùa
thì mức xuất khẩu lương thực tương ứng với —nh trạng trên là: 2,5 triệu tấn, 3,3 triệu
tấn, 3,8 triệu tấn. Hãy —m mức xuất khẩu lương thực có khả năng nhất.
18. Tuổi thọ của một loại sản phẩm ( ơn vị: năm) là biến ngẫu nhiên liên tục có hàm phân phối xác suất dạng 0 khi 𝑥 < 5 𝐹(𝑥) = 𝑘 1 − khi 𝑥 ≥ 5 𝑥
a) Tìm 𝑘? Tính xác suất ể trong 10 sản phẩm có 3 sản phẩm hỏng trước 6 năm.
b) Một công ty kinh doanh sản phẩm này khi bán ược một sản phẩm lãi 500.000
ồng. Nếu sản phẩm bị hỏng trong thời gian bảo hành thì phải bỏ ra 1.000.000 ồng
cho chi phí sửa chữa. Muốn có lền lãi trung bình là 300.000 ồng cho một sản
phẩm bán ược thì công ty phải quy ịnh thời gian bảo hành là bao nhiêu năm.
19. Thời gian (phút) xếp hàng chờ mua hàng của khách là biến ngẫu nhiên liên tục với hàm
phân phối xác suất như sau: 0 voi 𝑥 ≤ 0
𝐹( 𝑥) = 𝑎𝑥 − 3𝑥 + 2𝑥 voi 0 < 𝑥 ≤ 1 1 voi 𝑥 > 1 a) Tìm 𝑎.
b) Tìm thời gian xếp hàng trung bình. lOMoARcPSD|50734573
20. Tuổi thọ của một loại sản phẩm ( ơn vị: năm) là biến ngẫu nhiên liên tục có hàm mật ộ xác suất: 0 khi 𝑥 < 5 𝑓(𝑥) = 𝑥
a) Tìm 𝑘? Tính tuổi thọ trung bình của sản phẩm.
b) Nếu muốn tỉ lệ sản phẩm phải bảo hành là 20% thì phải quy ịnh thời gian bảo hành là bao nhiêu?
21. Tuổi thọ (œnh theo năm) của một thiết bị iện tử là biến ngẫu nhiên có hàm mật ộ xác suất như sau: 𝑓(𝑥) = 𝑘. 𝑒 với 𝑥 ≥ 0 0 với 𝑥 < 0
Xác ịnh 𝑘 và œnh xác suất ể thiết bị này sử dụng ược ít nhất 2 năm. 22. Cho hàm số
𝑘(1 + 𝑥), 𝑥 ∈ −1; 0) 𝑓(𝑥) =
𝑘(1 − 𝑥), 𝑥 ∈ [0; 1] 0, 𝑥 ∉ [−1; 1]
a) Xác ịnh 𝑘 ể 𝑓(𝑥) là hàm mật ộ xác suất của biến ngẫu nhiên 𝑋 và —m hàm phân phối xác suất.
b) Tìm kỳ vọng và phương sai của 𝑋.
23. Nhu cầu hàng năm về mặt hàng A là biến ngẫu nhiên liên tục 𝑋 có hàm mật ộ xác suất
như sau ( ơn vị: ngàn sản phẩm):
𝑘(30 − 𝑥), 𝑥 ∈ (0; 30) 𝑓(𝑥) = 0, 𝑥 ∉ (0; 30) a) Xác ịnh 𝑘 ?
b) Tìm xác suất ể nhu cầu về loại hàng ó không vượt quá 12 ngàn sản phẩm trong một năm.
c) Tìm nhu cầu trung bình hàng năm về mặt hàng A.
24. Cho biến ngẫu nhiên 𝑋 có hàm mật ộ xác suất như sau: 0; lOMoARcPSD|50734573 f x( ) k.sin , víi x x 2 0, víi x 0; 2 a) Xác ịnh k.
b) Tính xác suất ể khi thực hiện 3 phép thử ộc lập 𝑋 nhận giá trị trong khoảng ; ít nhất một lần.
25. Cho biến ngẫu nhiên 𝑋 có hàm mật ộ xác suất
𝑎𝑥 + 𝑏𝑥 , với 𝑥 ∈ (0; 1) 𝑓(𝑥) = 0, với 𝑥 ∉ (0; 1)
Biết 𝐸(𝑋) = 0,6. Tìm hàm phân phối xác suất của 𝑋; œnh 𝑃
−1 < 𝑋 < và 𝑉(𝑋).
26. Giả sử hàm mật ộ của biến ngẫu nhiên 𝑋 là:
𝑓(𝑥) = 𝐴. 𝑒 , với 𝑥 > 0 (𝜆 > 0) 0, với 𝑥 ≤ 0 a) Tìm 𝐴.
b) Tìm hàm phân phối của 𝑋.
c) Tìm kì vọng và phương sai của 𝑋.
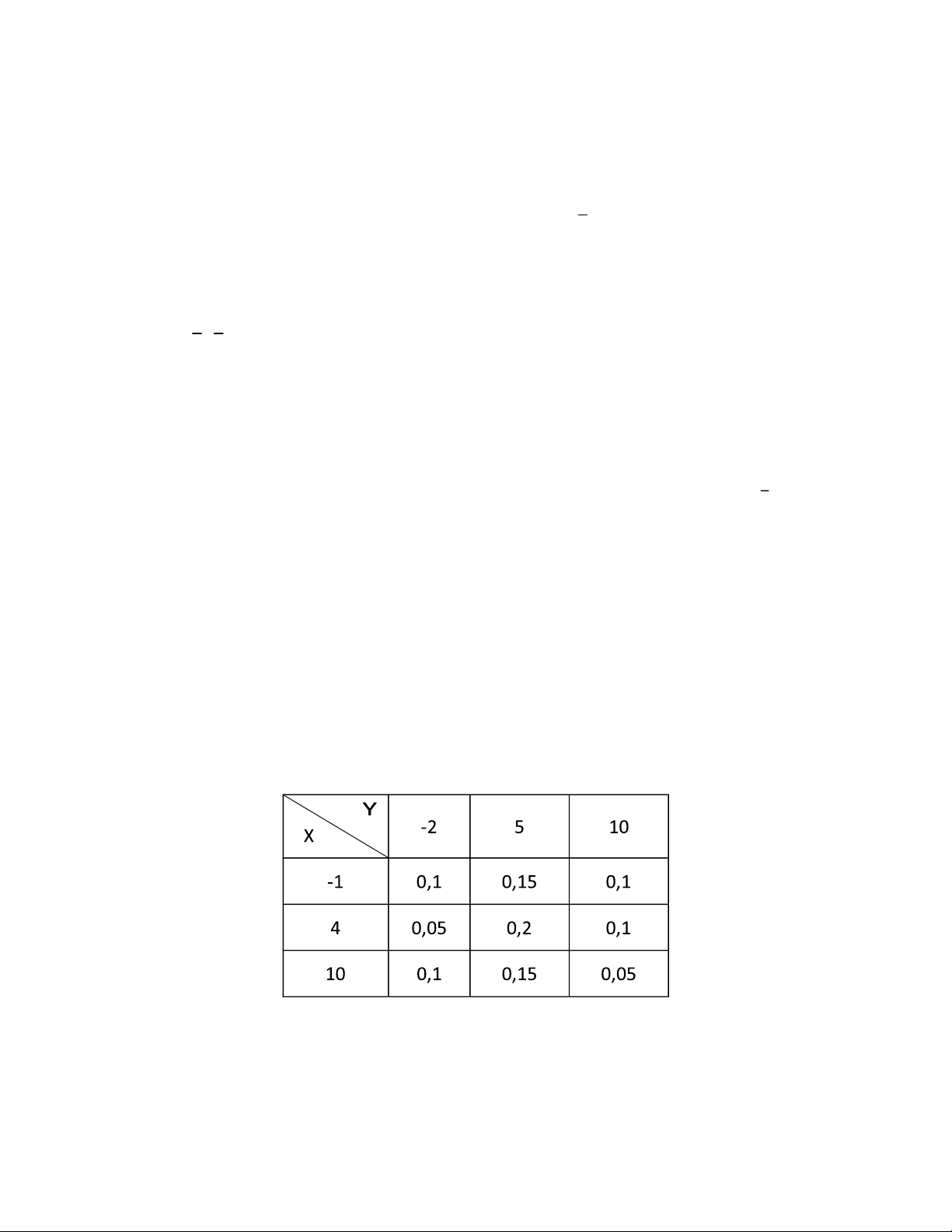
27. Thống kê về lãi cổ phần œnh cho 100 USD của 2 ngân hàng A và B trong một số năm
tương ứng là X ( ơn vị %), Y ( ơn vị %) kết quả cho trong bảng:
a) Lập bảng phân phối biên của X, của Y. Tính lãi cổ phần trung bình cho từng ngân hàng.
b) Khi Y = 5%, œnh lãi cổ phần trung bình của X.
c) X và Y có ộc lập với nhau không? Tính 𝜌 . lOMoARcPSD|50734573
d) Lập bảng phân phối của T = X + Y. Tính E(T) và V(T).
28. Chọn ngẫu nhiên 3 quả cầu từ hộp có 3 cầu ỏ, 4 cầu trắng, 5 cầu vàng. Gọi X, Y tương
ứng là số cầu ỏ, cầu vàng có trong 3 quả chọn ra.
a) Lập bảng phân phối ồng thời của X và Y
b) Tìm các phân phối biên của X và Y.
c) Tìm phân phối của số cầu ỏ biết số cầu vàng ã chọn ược là 1. d) Tính 𝜌 .
29. Một lô hàng có 3 sản phẩm loại A, 4 sản phẩm loại B, 3 sản phẩm loại C. Chọn ngẫu nhiên
2 sản phẩm từ lô hàng. Gọi X là số sản phẩm loại A, Y là số sản phẩm loại B trong 2 sản phẩm lấy ra.
a) Lập bảng phân phối xác suất ồng thời của X và Y
b) Tìm phân phối có iều kiện của Y với iều kiện X = 0
c) X, Y có ộc lập với nhau không.
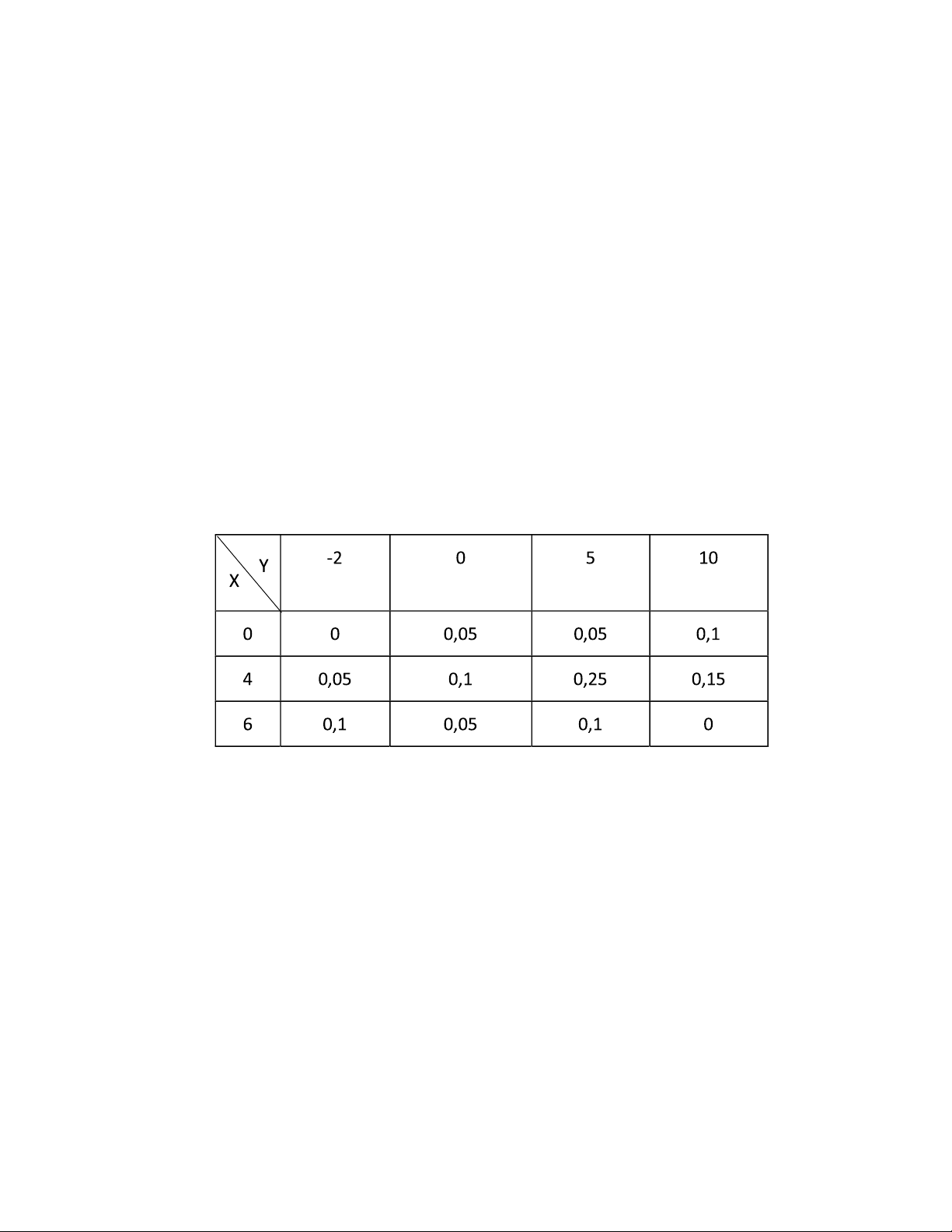
30. Có hai loại cổ phiếu A, B ang ược bán trên thị trường chứng khoán với lãi suất của chúng
tương ứng là các biến ngẫu nhiên X, Y có bảng phân phối như sau:
a) Nếu ầu tư toàn bộ vào cổ phiếu A thì lãi suất kì vọng và mức ộ rủi ro là bao nhiêu
b) Tính 𝑃(𝑌 ≥ 5|𝑋 = 4); 𝐸(𝑌|𝑋 = 4) c) Tính cov(X, Y).
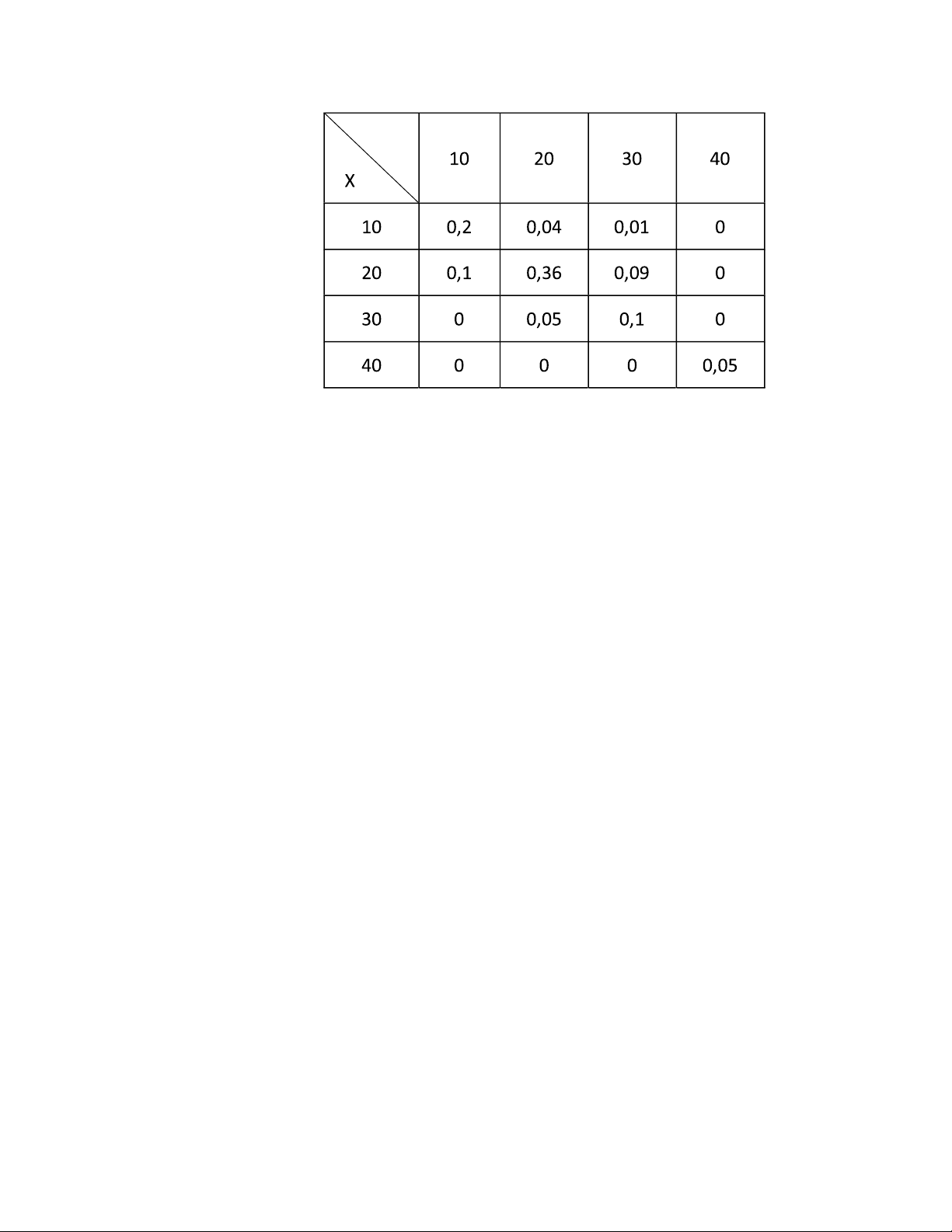
31. Điều tra thu nhập hàng năm ( ơn vị 10 triệu ồng) của các cặp vợ chồng ang làm việc.
Thu nhập của vợ, chồng tương ứng là X, Y ược cho trong bảng: lOMoARcPSD|50734573 Y
a) Tìm phân phối biên của thu nhập của chồng, của vợ; thu nhập trung bình hàng năm của họ.
b) Tìm phân phối thu nhập của vợ có chồng thu nhập 20 triệu/năm; thu nhập trung bình của họ. c) Tìm 𝜌
, từ ó cho kết luận về sự phụ thuộc giữa thu nhập của vợ chồng
d) Lập bảng phân phối xác suất của tổng thu nhập của các cặp vợ chồng. Tính trung
bình của tổng thu nhập ó. Hướng dẫn, áp số
1. b) Hàm phân phối xác suất của X: 0 nếu 𝑥 ≤ 0 ⎧
⎪ 0,66555 nếu 0 < 𝑥 ≤ 1 𝐹(𝑥) =
0,9564 nếu 1 < 𝑥 ≤ 2
⎨⎪0,99805 nếu 2 < 𝑥 ≤ 3 ⎩ 1 nếu 𝑥 > 3
4. Gọi X là lền lãi (ngàn ồng) khi mua 1 vé xổ số, lập bảng phân phối xác suất của X, œnh E(X).
6. HD: (𝑋 = 0), (𝑋 = 1), (𝑋 = 2) là các biến cố tạo nên một nhóm ầy ủ các biến cố. Tính
xs của các biến cố (𝑌 = 0), (𝑌 = 1), (𝑌 = 2) qua nhóm ầy ủ này. lOMoARcPSD|50734573
𝑃(𝑌 = 0) = 𝑃(𝑋 = 0). 𝑃(𝑌 = 0|𝑋 = 0) + 𝑃(𝑋 = 1). 𝑃(𝑌 = 0|𝑋 = 1) + 𝑃(𝑋 = 2). 𝑃( 𝑌 = 0|𝑋 = 2) 𝐶 𝐶 = 0,6 × 1 + 0,3 × + 0,1 × 𝐶 𝐶
8. HD: Luật sư lựa chọn phương án 2, như vậy theo ánh giá của luật sự thì:
E(“lợi nhuận khi lựa chọn phương án 2”) E(“lợi nhuận khi lựa chọn phương án 1”).
9. Gọi X là lợi nhuận (triệu ồng) của công ty khi bán 1 thẻ bảo hiểm, lập bảng phân
phối xác suất của X, œnh E(X).
10. Gọi X, Y lần lượt là số iểm ạt ược khi chọn hình thức thi 1 và 2 tương ứng. Lập bảng
ppxs của X, Y, œnh và so sánh E(X), E(Y).
14. Lợi nhuận trung bình hàng năm mà công ty thu ược ối với mỗi hợp ồng bảo hiểm là 6.500 ồng
17. HD: Gọi H1, H2, H3 tương ứng là các biến cố —nh trạng thời lết năm ó là “xấu”, “bình
thường” và “tốt”, { H1, H2, H3} tạo nên một nhóm ầy ủ các biến cố; A = “sản xuất
nông nghiệp ược mùa” và X = “mức xuất khẩu lương thực” (triệu tấn). Khi ó: (X =
2,5) = (H1|A); (X = 3,3) = (H2|A); (X = 3,8) = (H3|A).
18. a) 𝑘 = 25. Sử dụng công thức công thức Becnulli. 19. a) 𝑎 = 2
b) Gọi X là thời gian (phút) xếp hàng chờ mua hàng của khách, cần œnh E(X).
20. a) 𝑘 = 50. Gọi X là tuổi thọ (năm) của sản phẩm, cần œnh E(X).
b) Gọi t (năm) là thời gian bảo hành sản phẩm. Cần —m t sao cho: P(X ≤ t) = 0,2. 21. 𝑘 = 2 22. 𝑘 = 1 23. a)
b) Cần œnh 𝑃(𝑋 ≤ 12) c) Cần œnh 𝐸(𝑋) 24. a) 𝑘 = 1
25. 𝑎 = 3,6; 𝑏 = −2,4. Hàm phân phối xác suất của X: 0 với 𝑥 ≤ 0 𝐹(𝑥) = 1,8𝑥
− 0,8𝑥 với 0 < 𝑥 ≤ 1 1 với 𝑥 > 1 lOMoARcPSD|50734573
27. a) 𝐸(𝑋) = 4,05; 𝐸(𝑌) = 4,5 b) 𝐸(𝑋|𝑌 = 5%) = 4,3 c) 𝜌 = −0,089 28. 29. .
30. b) 𝑃(𝑌 ≥ 5|𝑋 = 4) = 0,7273; 𝐸(𝑌|𝑋 = 4) = 4,8182. lOMoARcPSD|50734573