Bài tập chương 2 môn Kỹ thuật phân tích mạch | Đại học Bách khoa Hà Nội

Chương 2
CÁC KHÁI NIỆM CƠ BẢN VỀ MẠCH ĐIỆN
2.1. Tính các giá trị của R trên mạch hình 2.1 4 6A R 50V 9 Hình 2.1
2.2. Cho mạch điện như hình vẽ R3 R4 A R1 R2 R a. R I 7 B
1=R2=R3=R4=2(Ω), R5=R7=1(Ω), R5 R6 R6=3(Ω),UAB=10(V). Hình 2.2a
Tính: RAB, I, IR3, UR6. (hình 2.2a)
b. R1=R7= 2(Ω), R2=R3=R6=1(Ω), R2 R R R 4=R5=3(Ω), UAB= 12(V). 1 I B A R R7 4 R5 R6
Tính: RAB, I, IR4, UR3, P. (hình 2.2b) Hình 2.2b R2 R4 R c. R 5 1=R2= R3= 1(Ω), R4=R5=1(Ω), A R1 C R6 D R9 R E B
7=R8=4, R6 =R9=3(Ω), UAE= 5(V). I R3 R7 R8
Tính: RA, IAB, UBC, UCD, IR6, IR8, PR8 (hình 2.2c) Hình 2.2c
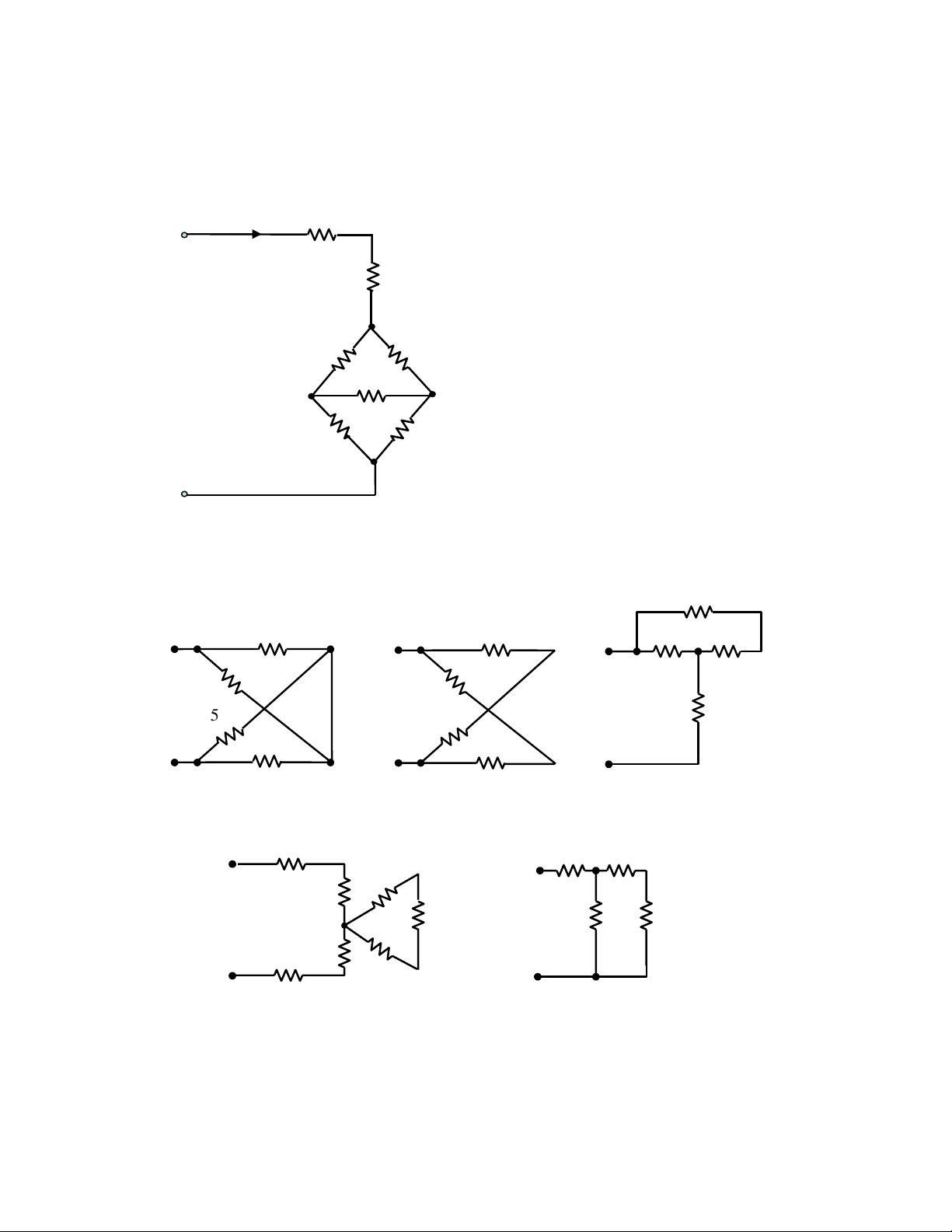
d. UAB= 10(V). Tính RAB, IAB. (Hình 2.2d) 1Ω a A IAB 2Ω b 6Ω 6Ω 2Ω c d 4Ω 4Ω e B Hình 2.2d
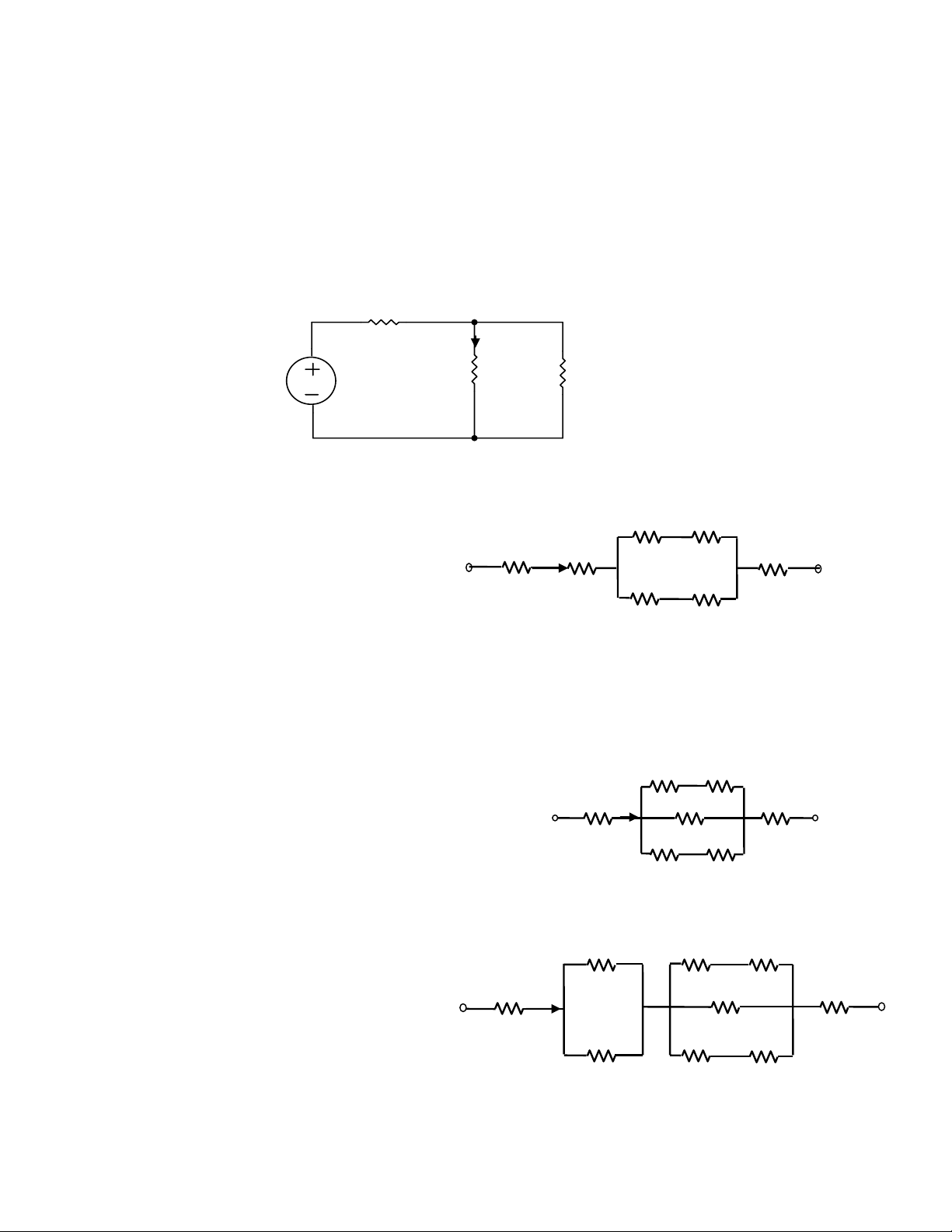
2.3. Tìm các điện trở tương đương của các mạch sau 10 A 30 A 30 A 4 6 50 50 50 12 50 B 30 B 30 B a b c e A d A 10 10 5 4 7 4 10 10 12 B 4 B 3 Hình 2.3
2.4. Tính các điện áp U1, U2, U3, U4 và E của nguồn biết điện áp hai đầu điện trở 2 là 8V 4 4 + U1 – + U3 – + 2 8V + – E U2 18 + – 4 U4 – Hình 2.4 I I 1 R1 A 2 R2
2.5. Cho mạch điện như hình 2.24. Với R1=1(Ω), I3
R2=3(Ω), R3=6(Ω),E1= 10(V), E2=4(Ω), E3=6(Ω). R3
Tính: I1, I2, I3 PR1, PR2, PR3 + E + + 1 E3 E2 - - - B Hình 2.5
2.6. Cho mạch điện như hình 2.25 R1=3(Ω), R2=4(Ω), I3 I R 1 1 A R3 I2 R3=8(Ω), E1=6(V), E2=8(V). R2 Tính: I1, I2, I3 E + + 1 E2 - - - - B Hình 2.6 2A
2.7. Tính: I1, I2, I3, I4 A I1 4Ω A 2Ω B I3 I 4 I2 4Ω 2Ω + 12V - - Hình 2.7
2.8. Tính: I1, I2, I3, 12V + - I1 2Ω A 3Ω C B I I 2 3 + 24V - 4A 6Ω A Hình 2.8 2.9. Tìm I1 và I2 32  6  I1 4  12  40  50V 15  6  30  I2 2  Hình 2.9 Rab
2.10. Dùng phép biến đổi tam giác – sao, tính dòng I trong hai trường hợp 2 Rbc Rca 5 a. Rab = Rbc = Rca = 3 I
b. Rab = Rca = 30 và Rbc = 40 57V + - 8 I Hình 2.10 2.11. Tìm dòng I 12 6 4 3A 4 12 Hình 2.11
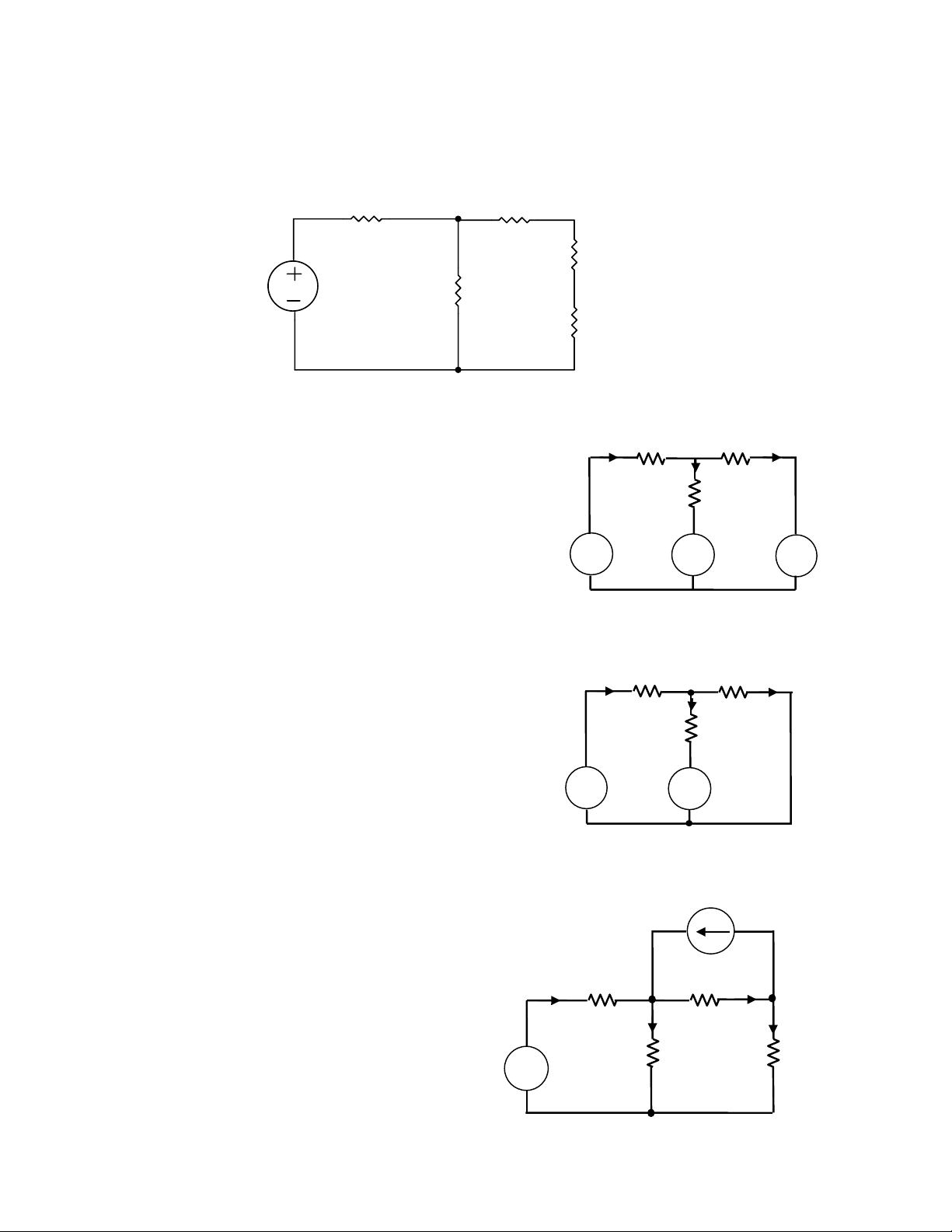
2.12. Tính dòng điện qua các nhánh 6Ω 12Ω - + 6A 36V 6Ω 3Ω Hình 2.12
2.13. Cho mạch như hình. Tìm dòng I 10 I 2 5 30V 20V Hình 2.13
2.14. Cho mạch như hình 2.14. Tìm dòng I 10 I 20 100V 35 100V Hình 2.14
2.15. Cho mạch điện như hình 2.15 I I 2 1 R1 R2 I3
E1= 10(V), E2= 6(V), E3= 2(V). + R3 + E1 - - E2 R +
1= 4(Ω), R2= 4(Ω), R3= 4(Ω). - E3 Tính I1, I2, I3 Hình 2.15
2.16. Cho mạch như hình 2.16. Tìm dòng I 40 10 20 60V I 30V 30V Hình 2.16 E3
2.17. Cho E1= 6(V), E2= 8(V), E3= 10(V). + -
R1= 2(Ω), R2= 4(Ω), R3= 6(Ω). I2 I1 R1 R2 Tính I1, I2, I3 I3 + E + 1 E2 - R3 - Hình 2.17
2.18. Cho E1= 10(V), E2= 4(V), R1= 2(Ω), R2= 4(Ω). R6 R R R 2
3= 2, R4= 4(Ω), R5= 2, R6= 2(Ω) 1 R E2 5 + - + E1
Tính dòng điện qua các nhánh - R4 R 3 Hình 2.18 R R2 R3 1
2.19. Cho E1= 8(V), E2= 4(V), R1= 1(Ω), +
R2= 2(Ω), R3= 4, R4= 4(Ω), R5= 2(Ω). E R4 + 1 R5 E2 - -
Tính dòng điện qua các nhánh Hình 2.19
2.30. Tìm dòng điện trong các nhánh như hình 2.30 I1 10 40 I2 0.4V 20 0.03A 1V I3 Hình 2.30
2.31. Tính I cho sơ đồ mạch điện như hình bên I A B 2Ω V 1 8Ω 2A 4Ω 0 Hình 2.31
2.32. Tính các giá trị trên sơ đồ mạch điện như hình bên 8V I 6Ω 1 6Ω B C + - I4 I2 I3 + 28V 2Ω V 4Ω 12Ω - Hình 2.32
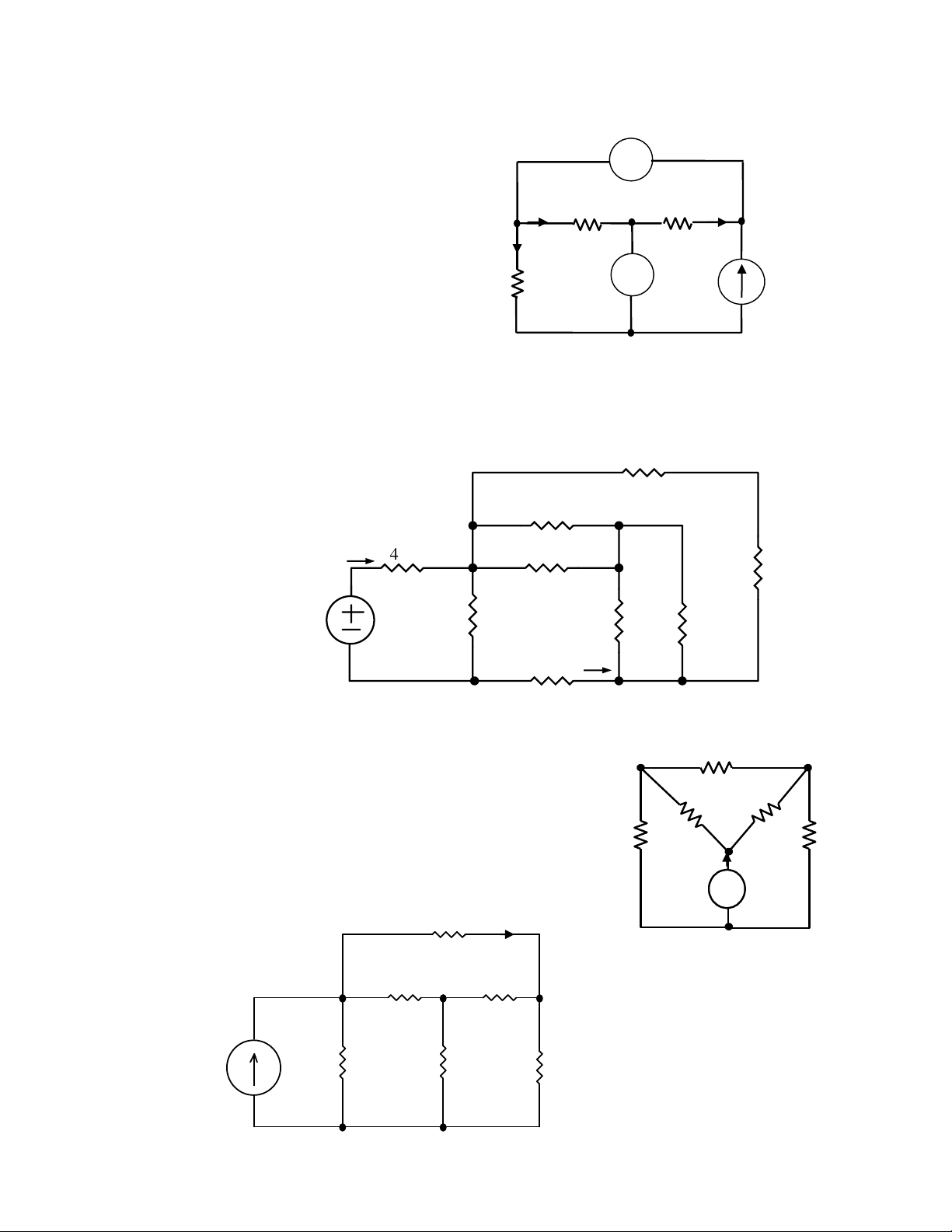
2.33. Tính các giá trị trên sơ đồ mạch điện hình bên 12V a b I4 + - I1 I2 I3 6A V 2A 2Ω 6Ω Hình 2.33
2.34. Tìm dòng và áp trên các phần tử và nghiệm lại sự cân bằng công suất trong mạch 2A 4 1 38V 5A 3
(ĐS: Tổng CS phát (38W +40W +130 W)
=Tổng CS thu (36W +64W +108 W) Hình 2.34
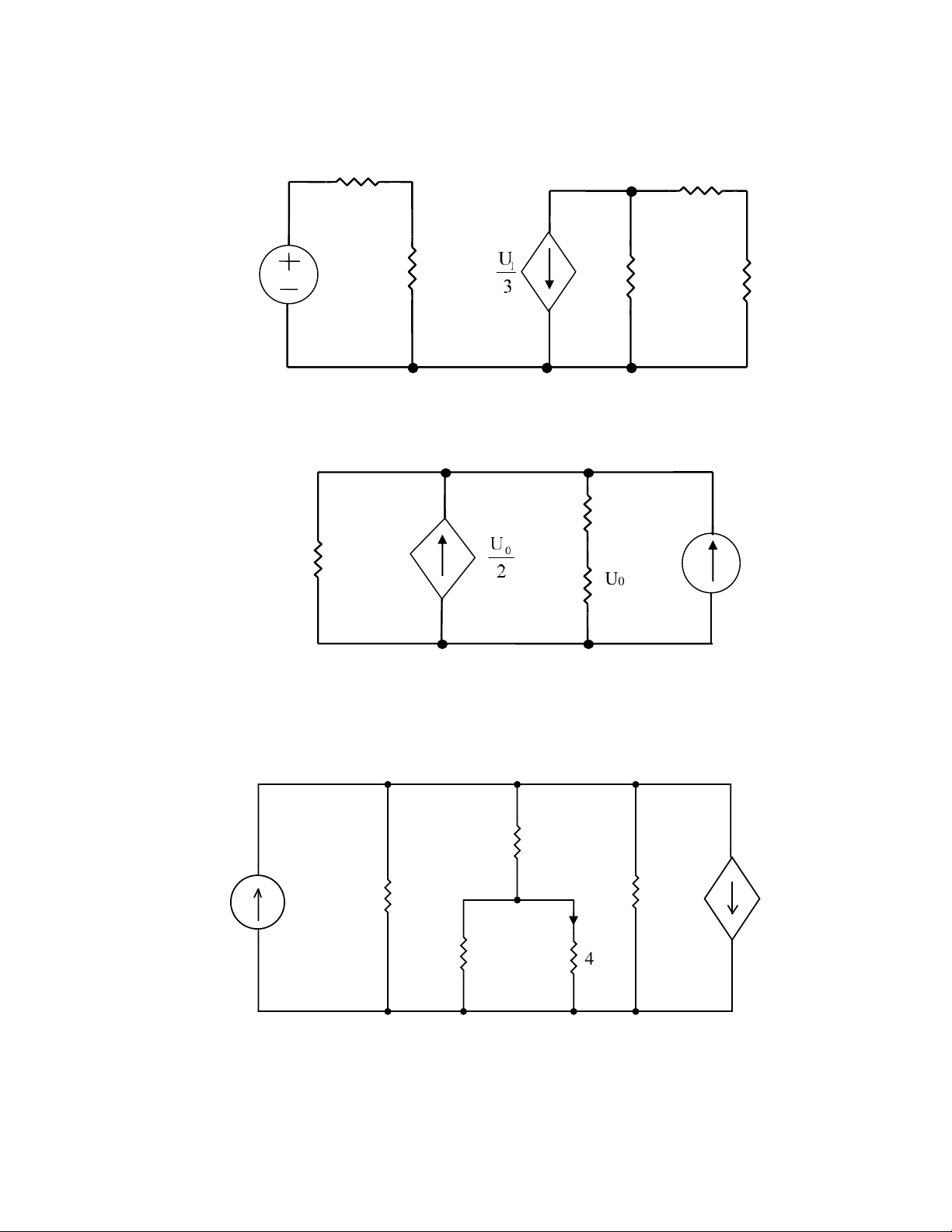
2.35. Xác định điện áp U1 và công suất tiêu tán trên điện trở 8 6 4 – u1 + 3u1 20V 5V 4 (ĐS: u Hình 2.35 1 = -2V; P = 2W) U 10 2.36 Tính hệ số k 0  E + 1000i E 1K U0 i – U Hình 2.36 (ĐS: 0  50 ) E 10
2.37 Tính i và u0 của mạch sau theo E và   i + 50 E 3K u0 i – Hình 2.37  ĐS: E 60 E i  ; u  ( 50   2) 0   2 U
2.38. Xác định tỉ số E R1 i i2 1 + E R2 i1 i2 U 0 - Hình 2.38 U 2  R2 (ĐS:  ) E (  ) 1 2 1 R
2.39. Xác định R để I = 5A I1 R 10 I 5V 5I1 25V Hình 2.39
2.40. Xác định I1 và U 10 4 + U – + 3I1 9V 3V I1 – Hình 2.40 2.41. Tìm U 6  2  + + 5 V U1 4  24  6  – U Hình 2.41 2.42. Tìm áp U0 2 6 + 4A U0 1 – Hình 2.42
2.43. Tìm điện áp U0 3 + 4 12 4Ix 6A Ix Uo 12 R1 4 Hình 2.43
2.44. Tìm điện áp U0 12V 1 1 + 2 2 1 2Ix U 0 Ix – Hình 2.44