Bài tập chương 2 Môn Trí tuệ nhân tạo | Trường Học Viện nông nghiệp Việt Nam

TRÍ TUỆ NHÂN TẠO Bài tập chương 2
1. Hãy xác định không gian trạng thái của các bài toán sau:
1a) Bài toán đong nước: Cho 2 bình có dung tích lần lượt là m và n (lit). Với nguồn
nước không hạn chế, dùng 2 bình trên để đong k lit nước. Không mất tính tổng quát có
thể giả thiết k <= min(m,n).
1b) Bài toán trò chơi sắp xếp 8 số.
1c) Bài toán Tháp Hà nội.
1d) Bài toán người đưa hàng: Người đưa hàng cần phải xác định được hành trình
ngắn nhất sao cho mỗi thành phố đi đến đúng một lần và quay trở lại thành phố xuất phát.
Giả sử thành phố xuất phát là thành phố 1, có tất cả n thành phố đánh số từ 1 đến n.
(Hướng dẫn: Mỗi trạng thái cho bởi danh sách các thành phố đã đi qua cho đến thời điểm
hiện tại, trong đó không cho phép một thành phố nào được xuất hiện nhiều hơn một lần
trừ thành phố 1 sau khi đã liệt kê tất cả các thành phố còn lại.
Các toán tử tương ứng với các hành động: đi tới thành phố 1 đi tới thành phố 2 đi tới thành phố 3).
2. Hãy biểu diễn không gian trạng thái của các bài toán trên bởi danh sách kề.
3. Thực hiện tìm kiếm theo bề rộng cho các bài toán: 1a) với m = 5, n= 4, k =3. 1b)
4. Thực hiện tìm kiếm theo chiều sâu cho các bài toán: 1a) với m = 5, n= 4, k =3 1c).
5. Thực hiện tìm kiếm leo đồi cho bài toán 1b).
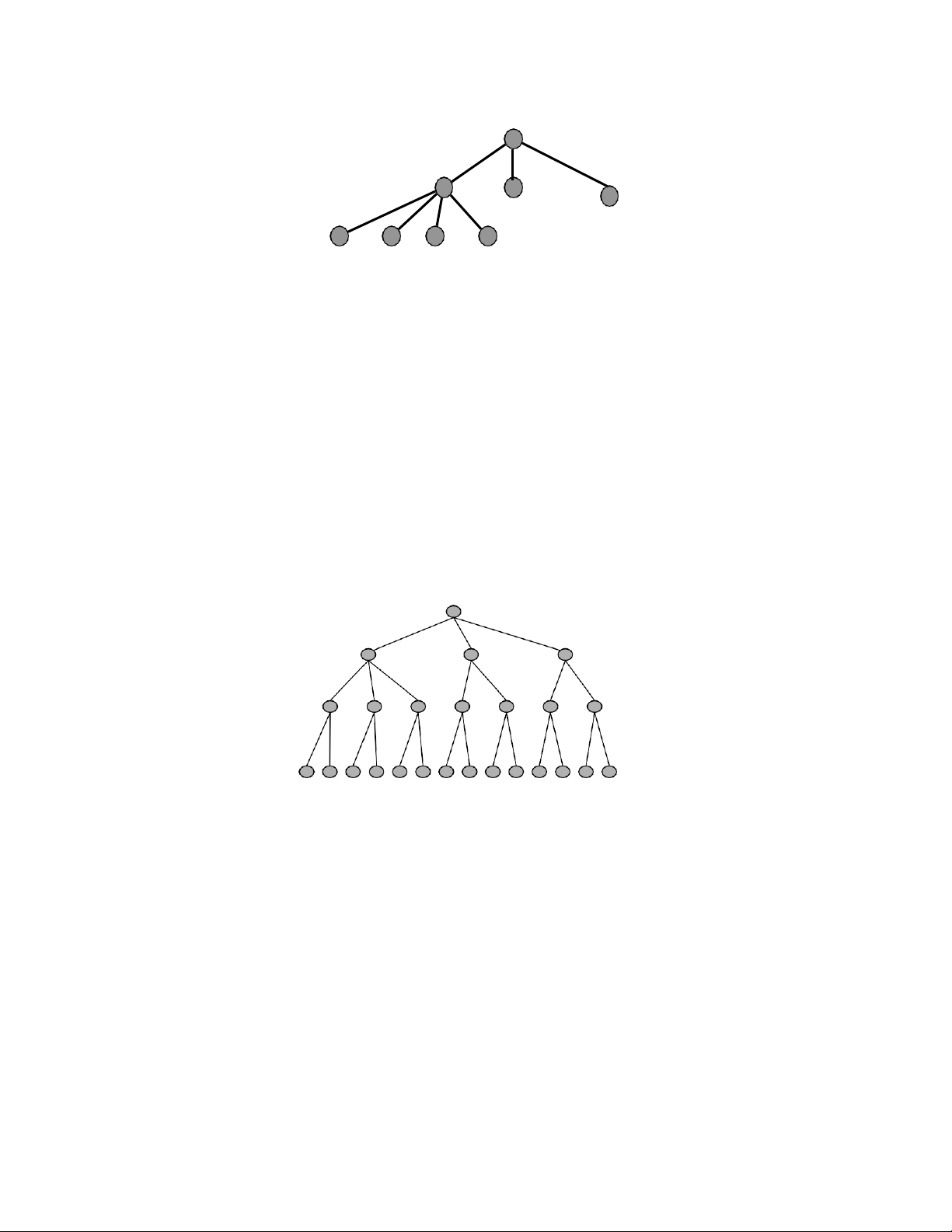
6. Cho một không gian các trạng thái mà ở đó trạng thái đầu có nhãn là số 1, trạng thái
tiếp theo trạng thái có nhãn n là các trạng thái có nhãn là 2n và 2n+1.
a) Hãy viết một phần của không gian trạng thái với các nhãn từ 1 đến 15.
b) Giả sử trạng thái đích có nhãn là 11, hãy liệt kê thứ tự mà các đỉnh sẽ được thăm
khi sử dụng các thủ tục tìm kiếm theo chiều rộng (breadth-firsth), tìm kiếm theo chiều
sâu (depth-first), tìm kiếm theo chiều sâu lặp (dept-limited search) với độ sâu 3?
7. Hình vẽ sau đây cho biết một phần của cây tìm kiếm mở rộng. Mỗi cạnh có gán chi phí
thực hiện toán tử tương ứng, các lá cho biết giá trị của hàm heuristic, h.
Nút nào (chỉ ra bằng ký tự chữ cái) sẽ được mở rộng tiếp theo nếu sử dụng một trong các
giải thuật tìm kiếm sau: a) Depth-first search? b) Breadth-first search?
c) Best First Search (Best-FS) d) A* search? h=20 A 3 5 B 19 C D 6 h=18 4 5 5 h=15 E F G H h=10 h=12 h=0 h=10
8. Trò chơi bốc bi: Có 2 đống bi có số bi lần lượt là m và n viên bi. Hai người chơi, mỗi
người đến lượt mình đi chỉ được phép bốc tối đa k viên.
a) Xây dựng không gian tìm kiếm với m=10, n=8, k=5
b) Cài đặt giải thuật minimax cho máy (người chơi thứ nhất là máy và người chơi thứ
hai là người sử dụng chương trình)?
9. Xem xét cây trò chơi cho trong hình dưới đây. Các giá trị của hàm định giá được cho
bên cạnh các nút lá. Giả sử nút gốc tương ứng với người chơi ở mức MAX, và việc tìm
kiếm luôn luôn được thực hiện trên các con từ trái sang phải.
a) Tính toán giá trị cho các nút theo giải thuật minimax. Kết quả viết cạnh các nút tương ứng trên cây.
b) Tính toán giá trị cho các nút theo giải thuật alpha-beta. Những nút nào sẽ không
được kiểm tra nếu sử dụng giải thuật alpha-beta pruning?
c) Max nên chọn đi nhánh nào nếu tất cả các giá trị đã được tính? Max A Min B C D Max E F G H I J K Min L M N O P Q R S T U V W X Y 2 3 8 5 7 6 0 1 5 2 8 4 10 2
10. Cho một phần của cây trò chơi như sau:
a. vẽ thêm các trạng thái ứng với độ sâu d =3
b. Xác định giá trị cho các nút lá trên cây (các nút ở độ sâu d=3) theo hàm đánh giá đã
xây dựng trong bài giảng sau đó gán giá trị cho các nút trong của cây theo chiến lược minimax.
c. Xác định giá trị cho các nút trên cây theo giải thuật alpha-beta. Những nút nào sẽ
không được kiểm tra nếu sử dụng giải thuật alpha-beta pruning?
11. Cài đặt giải thuật tìm kiếm leo đồi.
12. Demo ít nhất 2 giải thuật tìm kiếm trên cây trò chơi đã học (tham khảo trên website AIMA).