Bai tap chuong 2 (p2) - tai lieu quan tron - Tài liệu tham khảo | Đại học Hoa Sen
Bai tap chuong 2 (p2) - tai lieu quan tron - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả
Môn: Toán rời rạc(qe) 10 tài liệu
Trường: Đại học Hoa Sen 4.8 K tài liệu
Tác giả:
Preview text:
PHÉP TÍNH VI PHÂN CỦA HÀM NHIỀU BIẾN (tt)
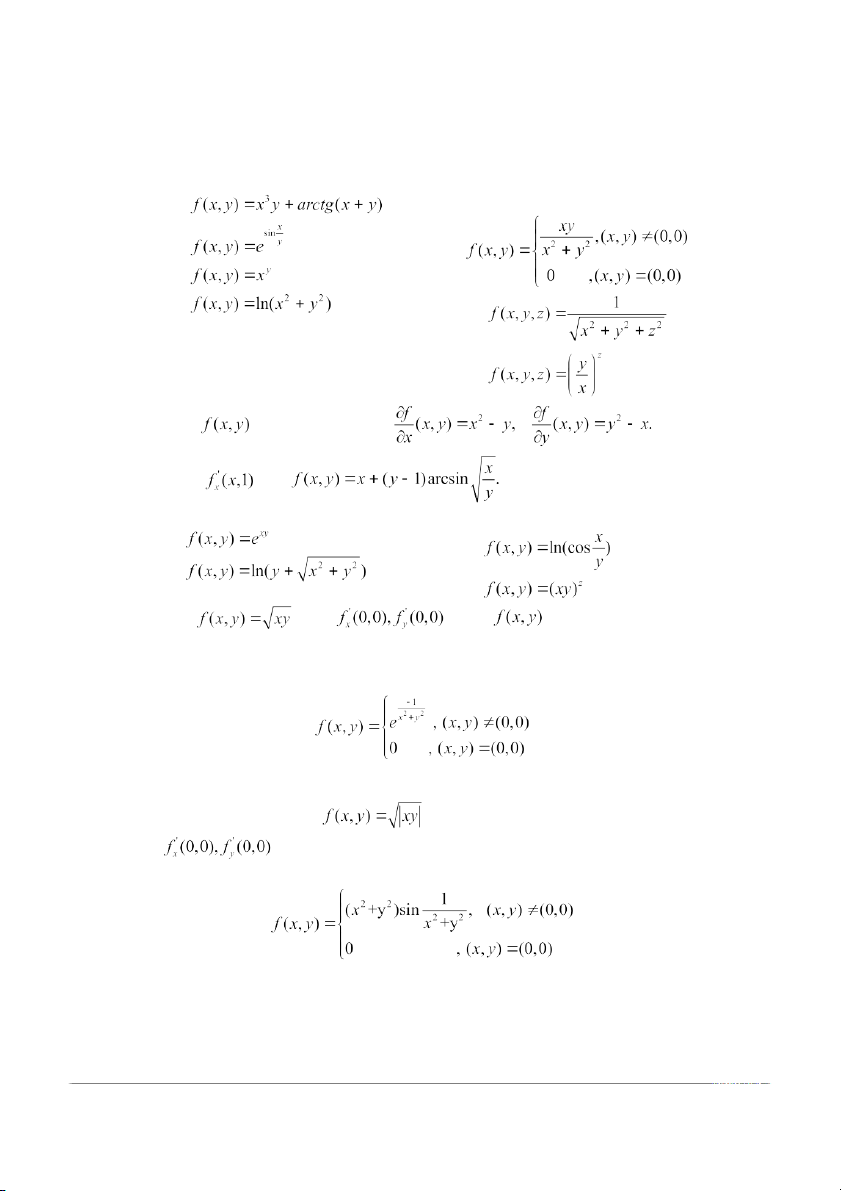
1. Tính các đạo hàm riêng của các hàm sau: a) e) b) c) d) f) g) 2. Tìm hàm, nếu biêt rằng: 3. Tìm nếu
4. Tính vi phân của các hàm sau: a) c) b) d) 5. Cho .Tính . Hàm
có khả vi tại điểm(0,0) ? tại điểm (1,1) ?
6. Khảo sát tính khả vi của hàm tại điểm (0,0). 7. Chứng minh rằng hàm
liên tục tại (0,0), có cả 2 đạo hàm riêng
nhưng không khả vi tại (0,0). 8. Chứng minh rằng có các đạo hàm riêng
trong lân cận điểm (0,0) và các đạo hàm
riêng này gián đoạn tại điểm (0,0), tuy nhiên vẫn khả vi tại (0,0).
9. Tính gần đúng các giá tri sau nhờ vi phân cấp 1 a) b) biết ln2=0,69 c) biết
10. Đạo hàm và vi phân cấp cao a) b) c) d) e) f)
11. Đạo hàm và vi phân của hàm hợp a) b) c) d) e)
12. Đạo hàm và vi phân của hàm ẩn a) b) c) d) e) f)