Bất đẳng thức Bunhiacopxki và ứng dụng - Toán rời rạc | Đại học Hoa Sen

Cho 2 bộ số thực ( ) 1 2 ; ;...; n aa a và ( ) 1 2 ; ;...; n bb b , mỗi bộ gồm n số. Khi đó ta có: ( ) ( )( ) 2 2 2 22 2 2 11 2 2 1 2 1 2 ... ... ... n n n n ab ab ab a a a b b b + ++ ≤ + ++ + ++ Dấu đẳng thức xảy ra khi và chỉ khi: 1 2 1 2 ... n n a a a bb b = == với quy ước nếu mẫu bằng 0 thì tử phải bằng 0. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán rời rạc(qe)

Trường: Đại học Hoa Sen

Thông tin:

37 trang 1 tuần trước

Tác giả:

Profile Phạm Thị Huyền
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page1
I.Bất đẳng thức Bunhiacôpxki ( BCS ) :
Cho 2 bộ số thực
()
12
; ;...;
n
aa a và
()
12
; ;...;
n
bb b , mỗi bộ gồm n số. Khi đó ta có:
()
()
(
)
2
22 222 2
11 2 2 1 2 1 2
... ... ...
nn n n
ab a b a b a a a b b b+++ ≤+++ +++
Dấu đẳng thức xảy ra khi và chỉ khi:
12
12
...
n
n
a
aa
bb b
===
với quy ước nếu mẫu bằng 0 thì tử phải bằng 0.
II. Các hệ quả :
Hệ quả 1:
Nếu
11
...
nn
ax a x C++ =(không đổi) thì
()
22
1
22
1
min ...
...
n
n
C
xx
aa
++ =
+
+
đạt được khi
1
1
...
n
n
x
x
aa
==
Hệ quả 2:
Nếu
222
1
...
n
x
xC++ = (không đổi) thì
()
22
11 1
max ... ...
nn n
ax a x C a a
+
+= ++
đạt được khi
1
1
... 0
n
n
x
x
aa
== ≥
()
22
11 1
min ... ...
nn n
ax a x C a a++ =− ++
Dấu “=” xảy ra
1
1
... 0
n
n
x
x
aa
⇔==≤
III.Bất đẳng thức Bunhiacôpxki mở rộng:
• Mở rộng bất đẳng thức Bunhiacôpxki cho 3 dãy số thực không âm
()
12
; ;...;
n
aa a ;
()
12
; ;...;
n
bb b ;
()
12
; ;...;
n
cc c ta luôn có :
()
()
(
)
(
)
2
33 333 333 3
111 222 1 2 1 2 1 2
... ... ... ...
nnn n n n
abc abc a bc a a a b b b c c c+++ ≤+++ +++ +++
Chứng minh:
Đặt
33 3 33 3 33 3
333
12 12 12
... , ... , ...
nn n
Aaa aBbb bCcc c= + ++ = + ++ = + ++
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page2
Nếu 0A = hoặc 0B = hoặc 0C = thì bất đẳng thức hiển nhiên đúng vì khi đó cả hai vế của bất đẳng thức
đều bằng 0.
Vậy ta chỉ xét trường hợp
0; 0; 0ABC>>>
Đặt
;;
iii
iii
abc
xyz
ABC
===
với 1;2;3i =
Khi đó ta có:
333
123
333
123
333
123
1
1
1
xxx
yyy
zzz
⎧
++=
⎪
++=
⎨
⎪
++=
⎩
và bất đẳng thức cần chứng minh trở thành:
111 2 22 3 33
1xyz xyz xyz++≤
Áp dụng bất đẳng thức Cauchy cho 3 số không âm:
(
)
333
;; 1;2;3
iii
xyzi=
ta có:
333
111
111
333
222
222
333
333
333
3
3
3
x
xx
xyz
xx
xyz
x
xx
xyz
⎧
++
≤
⎪
⎪
⎪
+
+
≤
⎨
⎪
⎪
++
≤
⎪
⎩
Cộng các bất đẳng thức trên lại ta được:
111 2 22 3 33
1xyz xyz xyz
+
+≤(đpcm)
Đẳng thức xảy ra
111
111
222
222
333
333
abc
ABC
xyz
abc
xyz
ABC
xyz
abc
ABC
⎧
==
⎪
==
⎧
⎪
⎪⎪
⇔==⇔ ==
⎨⎨
⎪⎪
==
⎩
⎪
==
⎪
⎩
Hay
()
:: :: 1;2;3
iii
abc ABCi==tức là:
111 2 2 2 3 3 3
:: :: ::abc abc abc
=
=
• Tổng quát : bất đẳng thức Bunhiacôpxki mở rộng cho rộng cho m dãy số thực không âm:
Cho
m dãy số thực không âm:
()
12
; ;...;
n
aa a ,
()
12
; ;...;
n
bb b , … ,
()
12
; ;...;
n
KK K
Ta có:
()
(
)
(
)( )
11 1 2 2 2 1 2 1 2 1 2
... ... ... ... ... ... ... ...
m
mm mmm m m m m
nn n n n n
ab K a b K a b K a a a b b b K K K+++ ≤++++++ +++
Dấu “=” xảy ra khi và chỉ khi:
11 1 2 2 2
: : ...: : :...: : : ...:
nn n
ab K ab K a b K==( chứng minh tương tự như trên)
I- MỘT SỐ VÍ DỤ :
Bài 1:
Cho ,,
x
yz là ba số dương thỏa 4 9 16 49xy z++ =. Chứng minh rằng:
12564
49T
xy z
=
++≥
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page3
Đẳng thức xảy ra khi nào?
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki cho sáu số 2;3;4
x
yzvà
158
;;
x
yz
ta được:
()
()()()
2
2
2
222
12584 1 5 8
49. 4 9 16 2 3 4Txyz x y z
xy z
xyz
⎡
⎤
⎛⎞
⎛⎞
⎛⎞
⎛⎞
⎡⎤
⎢
⎥
=++ ++ = + + + +
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎢⎥
⎜⎟
⎣⎦
⎢
⎥
⎝⎠
⎝⎠
⎝⎠
⎝⎠
⎣
⎦
2
2
158
2. 3. 4. 49xyz
xyz
⎛⎞
≥++ =
⎜⎟
⎜⎟
⎝⎠
12564
49T
xy z
⇒=+ + ≥
Đẳng thức xảy ra khi
1
2
158
5
234
3
4 9 16 49
2
x
xyz
y
xy z
z
⎧
=
⎪
⎧
⎪
==
⎪⎪
⇔=
⎨⎨
⎪⎪
++ =
⎩
=
⎪
⎪
⎩
Bài 2 : Cho 0; 0xy>> và
22
x
yxy+≤+.Chứng minh:
325xy+≤+
Hướng dẫn giải
Giả thiết:
22
22
111
222
xyxy x y
⎛⎞⎛⎞
+≤+⇔− +− ≤
⎜⎟⎜⎟
⎝⎠⎝⎠
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
()
11
1; 3 ; ;
22
xy
⎛⎞
−−
⎜⎟
⎝⎠
ta có:
2
22
11 11
1. 1 3. 10 5
22 22
yxy
⎡⎤
⎡⎤
⎛⎞⎛ ⎞ ⎛ ⎞⎛ ⎞
−+−≤ −+−≤
⎢⎥
⎜⎟⎜ ⎟ ⎜ ⎟⎜ ⎟
⎢⎥
⎝⎠⎝ ⎠ ⎝ ⎠⎝ ⎠
⎣⎦
⎢⎥
⎣⎦
()
2
32 5xy⇒+− ≤
32 5xy⇒+ −≤
325xy⇒+ ≤+
Đẳng thức xảy ra khi
15
210
135
210
x
y
⎧
=+
⎪
⎪
⎨
⎪
=+
⎪
⎩
Bài 3 :
Cho , , 0abc≥ ; 1abc++=.Chứng minh:
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page4
222
1111
30
ab bc ac
abc
+
++≥
++
Hướng dẫn giải
Gọi
222
1111
A
ab bc ac
abc
=+++
++
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
(
)
222
222
1111
;;;
;3 ;3 ;3
ab bc ca
abc
abc ab bc ca
⎛⎞
⎜⎟
++
⎝⎠
++
Ta có:
()
()
2
222
1333 9 9 9a b c ab bc ca A+++ ≤ + + + + +
()( )
2
100 7abc abbcca A
⎡⎤
⇒≤+++ ++
⎣⎦
(*)
Mà
()
2
11
(do 1)
33
ab bc ca a b c a b c++≤ ++ = ++=
Do đó: (*)
30.A⇒≥
Đẳng thức xảy ra khi
1
3
abc===
Bài 4 : Cho ; ; 0xyz> và thoả 1
x
yz++≤.Chứng minh :
222
222
111
82xyz
xyz
++ ++ +≥
Hướng dẫn giải
Gọi
222
222
111
Sx y z
x
yz
=+++++
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
()
1
1; 9 ; ;x
x
⎛⎞
⎜⎟
⎝⎠
Ta có:
22
22
911
181. 82.xxx
x
x
x
+≤ + + = +
(1)
Tương tự:
2
2
91
82.yy
y
y
+≤ +
` (2)
2
2
91
82.zz
z
z
+≤ +
(3)
Cộng (1),(2) và (3) theo vế ta được:
111
.82 9Sxyz
x
yz
⎛⎞
≥+++ + +
⎜⎟
⎝⎠
Hay
() ()
111
.82 81 9 80Sxyz xyz
xyz
⎛⎞
≥+++++−++
⎜⎟
⎝⎠
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page5
()
111
2.9.3. 80 162 80 82xyz
xyz
⎛⎞
≥++++−≥−=
⎜⎟
⎝⎠
Vậy
222
222
111
82xyz
xyz
++ ++ +≥
Bài 5 : Cho ba số thực dương ,,abcthoả ab bc ca abc
+
+= .Chứng minh rằng:
22 22 22
222
3
ba cb ac
ab bc ca
+++
++≥
Hướng dẫn giải
Ta có:
22 22
22 2 2
2211
2
ba ba
ab
ab a b
++
==+
(do ,abdương)
Đặt
111
;;xyz
abc
===
thì
giả thiết
,, 0 ;; 0
1
abc x yz
ab bc ca abc x y z
>>
⎧⎧
⇔
⎨⎨
++= ++=
⎩⎩
và (đpcm)
22 22 22
2223xy yz zx⇔+++++≥
Áp dụng BĐT Bunhiacôpxki ta có:
()
(
)
()
2
22 222
323
x
yxyyxyy+=++≥++
()
22
1
22
3
x
yxy⇒+≥ +
Tương tự
()
22
1
22
3
y
zyz+≥ +
()
22
1
22
3
zx zx+≥ +
Vậy
()
22 22 22
1
2223333
3
xy yz zx xyz+++++≥ ++=
Đẳng thức xảy ra khi
1
3
xyz===
Với
1
3
xyz=== thì
3abc===
Bài 6 : Chứng minh:
()
111 1abccab−+ −+ −≤ + với mọi số thực dương
;; 1abc≥
Hướng dẫn giải
Đặt
222
1;1;1axbycz−= −= −=
Với ; ; 0.xyz> Bất đẳng thức cần chứng minh trở thành:
()()()
222
1111xyz z x y
⎡
⎤
++≤ + + ++
⎣
⎦
Áp dụng BĐT Bunhiacôpxki ta có:
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page6
()() ()
(
)
22 22
11 11
x
yx y xyzx y z+≤++⇒++≤+++ (1)
()() ()()
22 22 2
11 111.1xy zxy z+++≤++++ (2)
Kết hợp (1) và (2) ta có
()()()
222
1111xyz z x y
⎡
⎤
++≤ + + ++
⎣
⎦
Vậy
()
111 1abccab−+ −+ −≤ + (đpcm)
Bài 7 : Cho ; ; 0abc> và thoả
1abc =
.Chứng minh:
()()()
333
1113
2
abc bca cab
++≥
+++
Hướng dẫn giải
Đặt
111
;;xyz
abc
===
1; 0; 0; 0xyz x y z⇒=>>>
Ta cần chứng minh bất đẳng thức sau : A=
222
3
2
xyz
yz zx xy
+
+≥
+++
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số :
()
;; ; ; ;
xyz
yz zx xy
y
zzxxy
⎛⎞
+++
⎜⎟
⎜⎟
+++
⎝⎠
Ta có:
()( )
2
x
yz yzzxxyA++ ≤ +++++
3
33
.
22 2
xyz
Axyz
++
⇒≥ ≥ =(do 1xyz = )
3
2
A⇒≥
Đẳng thức xảy ra khi 1
x
yz===
Với 1
x
yz===thì 1.abc===
Bài 8 : Cho ; ; 0abc> .Chứng minh:
()() ()() ()()
1
abc
a abac b bcba c cacb
++≤
++ + ++ + ++ +
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
(
)
(
)
;;;ab ca
Ta có:
()
()() ()()
2
ac ab a b c a ac ab a b c a+≤++⇒+≤++
()()
aacaba abca⇒+ + ≤+ + +
()()
aaa
aacab abc
aabac
⇒≤=
++ ++
++ +
(1)
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page7
Tương tự:
()()
bb
abc
bbcba
≤
++
++ +
(2)
()()
cc
abc
ccacb
≤
++
++ +
(3)
Cộng (1),(2) và (3) theo vế ta được:
()() ()() ()()
1
abc
a abac b bcba c cacb
++≤
++ + ++ + ++ +
Đẳng thức xảy ra khi
abc==.
Bài 9 : Cho ; 0ab> và thoả
22
9ab+=.Chứng minh :
32 3
32
ab
ab
−
≤
++
Hướng dẫn giải
Ta có:
22
9ab+=
()
()()
2
29
233
ab a b
ab a b a b
⇔=+−
⇔=++ +−
2
3
3
3
322
ab
ab
ab
ab a b
ab
⇔=+−
++
+
⇔=−
++
Mà theo BĐT Bunhiacôpxki thì
22
2. 3 2ab a b+≤ + =
Nên
32 3
32
ab
ab
−
≤
++
Đẳng thức xảy ra khi
22
;0
3
9
2
ab
ab ab
ab
>
⎧
⎪
⎪
+=⇔==
⎨
⎪
⎪
=
⎩
Bài 10: Cho ; ; ;abcddương tuỳ ý.Chứng minh :
111
p
qpqpq
a b c pa qb pb qc pc qa
+
++
++≥ + +
+++
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có
() ()
2
2
..
pq pq
p
qpaqb paqb
ab ab
⎛⎞
⎛⎞
+= + ≤+ +
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
Tương tự ta chứng minh được
() ()() ()
22
;
pq pq
p
qpbqcpqpcqa
bc ca
⎛⎞ ⎛⎞
+≤+ + +≤+ +
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
Cộng các vế tương ứng của ba bất đẳng thức ta có :
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page8
() ()
2
111 111
pq pq
p
aqb pbqc pcqa abc
⎡⎤
⎛⎞
+++≤+++
⎜⎟
⎢⎥
+++
⎝⎠
⎣⎦
Hay
()
111111
pq
p
aqb pbqc pcqa abc
⎡⎤
+++≤++
⎢⎥
+++
⎣⎦
Vậy
111
p
qpqpq
a b c pa qb pb qc pc qa
+
++
++≥ + +
+++
Bài 11 : Cho 4 số dương ;;;abcd.Chứng minh:
33332222
3
a b c d abcd
bcd cd a bd a abc
+++
+++≥
++ ++ + + ++
Hướng dẫn giải
Đặt
3333
abcd
P
bcd cda bd a abc
=+++
++ ++ ++ ++
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
()()()()
()
3333
;;;; ;;;
abcd
ab c d bc d a cd b a d a b c
bcd cd a bd a abc
⎛⎞
++ + + ++ ++
⎜⎟
⎜⎟
++ ++ ++ ++
⎝⎠
Ta có:
()
()()()()
2
222 2
a b c d Pabcd bcda cd ab dabc+++ ≤ +++ +++ +++ ++⎡⎤
⎣⎦
()
()
(
)
2
2
222 2 222 2
abcd Pabcd abcd
⎡⎤
⇔ +++ ≤ +++ − +++
⎣⎦
(1)
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
()
(
)
; ; ; ; 1; 1;1;1abcd ta được:
()
()
2
222 2
4abcd abcd+++ ≤ + + + (2)
Từ (1) và (2) ta được
()
(
)
2
222 2 222 2
222 2
3
3
abcd Pabcd
abcd P
+++ ≤ +++
⇔+++≤
Vậy
33332222
3
a b c d abcd
bcd cd a bda abc
+++
+++≥
++ ++ ++ ++
Bài 12 :
Cho các số dương ;;abc thỏa a + b + c = 1 . Chứng minh : 1
111
abc
ba cb ac
+
+≥
+− +− +−
Hướng dẫn giải
Đặt
111 222
abc abc
A
ba cb ac bc ca ab
=++ =++
+− +− +− + + +
Áp dụng BĐT Bunhiacôpxki ta có:
() () () ()
()()()
2
2
222
222
222
222
abc
abc a bc b ca c ab
bc ca ab
abc
abc bca cab
bc ca ab
⎡⎤
++ = + + + + +
⎢⎥
++ +
⎣⎦
⎡⎤
≤++ +++++
⎡⎤
⎣⎦
⎢⎥
+++
⎣⎦
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page9
()
()
2
3
abc
A
ab bc ca
++
⇔≥
++
Ta lại có:
()( )
2
3abc abbcca++ ≥ + +
. Suy ra
(
)
()
3
1
3
ab bc ca
A
ab bc ca
++
≥=
++
Vậy
1
111
abc
ba cb ac
++≥
+− +− +−
Dấu đẳng thức xảy ra khi
222
1
3
1
bc ca ab
abc abc
abc
+= += +
⎧
⎪
== ⇔===
⎨
⎪
++=
⎩
Bài 13 : Giả sử các số thực ;;;
x
yztthoả mãn điều kiện:
(
)
(
)
22 22
1ax y bz t
+
++= với ;ablà hai số dương cho
trước. Chứng minh:
()()
ab
xzyt
ab
+
++≤
Hướng dẫn giải
Do ; 0ab> nên từ giả thiết ta có:
()()
2222
22 22
22 22
1
1
1
xy zt
ax y bz t
baab
xzyt
babaab
++
++ +=⇔ + =
⇔+++=
Áp dụng BĐT Bunhiacôpxki ta có:
() ()
2
22
2
..
x
zxz
xz b a ba
ba
ba
⎛⎞
⎛⎞
+= + ≤+ +
⎜⎟
⎜⎟
⎝⎠
⎝⎠
(1)
Tương tự :
()()
22
2
y
t
yt ba
ba
⎛⎞
+≤+ +
⎜⎟
⎝⎠
(2)
Cộng từng vế (1) và (2) ta được:
()()()
22 22
22
x
zyt ab
xz yt ba
baba ab
⎛⎞
+
+++≤+ +++ =
⎜⎟
⎝⎠
(3)
Mặt khác
()()()()
22
2
x
zyt xzyt+++≥ + + (4)
Do đó từ (3) và (4) suy ra:
()()
ab
xzyt
ab
+
++≤
Dấu đẳng thức xảy ra
xz
ba
xy
yt
ax
ba
zt
b
xz yt
⎧
=
⎪
=
⎪
⎧
⎪⎪
⇔= ⇔
⎨⎨
==
⎪⎪
⎩
+=+
⎪
⎪
⎩
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page10
Bài 14 : Cho các số thực dương ;;;
x
yztthoả mãn 1.xyzt
=
Chứng minh:
()()()()
3333
11114
3
x yz zt ty y xz zt tx z xt ty yx t xy yz zx
+++ ≥
++ ++ ++ + +
Hướng dẫn giải
Với
;;;
x
yzt
dặt
1111
; ; ; ( ; ; ; 0)abcd abcd
xyzt
==== >và
1abcd
=
1111
;;;xyzt
abcd
⇒= = = =
Bất đẳng thức cần chứng minh tương với:
333 3
11114
11 1 1 11 1 1 11 1 1 11 1 1
3
bc cd bd ac cd ad ad bd ab ab bc ac
abc d
+++≥
⎛⎞⎛⎞⎛ ⎞⎛⎞
++ ++ ++ ++
⎜⎟⎜⎟⎜ ⎟⎜⎟
⎝⎠⎝⎠⎝ ⎠⎝⎠
3333
4
3
abcd
bcd cda dab abc
bcd adc abd abc
⇔+++≥
++ + + ++ ++
()()()()
333 3
4
3
abcd
abcd bcd a cdab dabc
⇔+++≥
++ + + ++ ++
(vì
1abcd =
)
222 2
4
3
abcd
bcd cd a d ab abc
⇔+++≥
++ + + ++ ++
Đặt
2222
abcd
S
bcd cd a dab abc
=+++
++ + + ++ ++
Áp dụng BĐT Bunhiacôpxki ta có:
()()()()( )
2
.S bcd cda dab abc abcd++ + + + + ++ + ++ ≥ +++
⎡⎤
⎣⎦
()
()
()
2
1
33
abcd
Sabcd
abcd
+++
⇒≥ = +++
+++
(1)
Áp dụng BĐT Cauchy với 2 số dương:
2 ; 2ab ab cd cd+≥ +≥
Suy ra
()
2abcd ab cd+++ ≥ +
Lại áp dụng BĐT Cauchy cho 2 số dương
;ab cd ta có:
4
222ab cd abcd abcd+≥ = =
(vì
1abcd
=
) (2)
Từ (1) và (2) suy ra
4
3
S ≥
Vậy
333 3
11114
11 1 1 11 1 1 11 1 1 11 1 1
3
bc cd bd ac cd ad ad bd ab ab bc ac
abc d
+++≥
⎛⎞⎛⎞⎛ ⎞⎛⎞
++ ++ ++ ++
⎜⎟⎜⎟⎜ ⎟⎜⎟
⎝⎠⎝⎠⎝ ⎠⎝⎠
Dấu đẳng thức xảy ra khi
11abcd x yzt====⇔==== .
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page11
4444
1234
3333
1234
1
4
xxxx
xxxx
+++
≥
+++
Bài 15 : Cho
1234
;;;
x
xxxdương thoả điều kiện
1234
1xx xx
+
++=.Chứng minh :
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
()
(
)
2
2222
1234 1 2 3 4
14
x
xxx xxxx= +++ ≤ +++
2222
1234
1
4
xxxx⇒+++≥
(1)
•
()
(
)
2
2222 3 3 3 3
1234 11 22 33 44
....
x
xxx xxxxxxxx+++ = + + +
()
()
3333
12341 234
x
xxxxxxx≤+++ +++
3333
1234
x
xxx=+++
(vì
1234
1xxxx+++=)
3333
2222
1234
1234
2222
1234
xxxx
x
xxx
xxxx
+++
⇔ ≥+++
+++
(2)
•
()
2
3333
1234
x
xxx+++
()
2222
11 2 2 33 4 4
....
x
xxxxxxx=+++
()()
22224444
12341234
x
xxxxxxx≤ +++ +++
4444 3333
1234 1234
3333 2222
1234 1234
x
xxx xxxx
x
xxx xxxx
+++ +++
⇒≥
+++ +++
(3)
Từ (1);(2) và (3) suy ra:
Bài 16 : Cho bốn số dương ; ; ;abcd.Chứng minh:
()
()
()
()
()
()
()
()
444 4
22 22 2 2 22
4
abc dabcd
aba b bcb c cdc d dad a
+++
++ + ≥
++ ++ ++ ++
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
()
()()
()
(
)
(
)
22
22 22 22 22
224ab ab abab ab ab+≤ +⇔+ +≤ +≤ + (1)
()
()
()
44
22
1
4
ab
ab
aba b
+
⇔≥+
++
Mặt khác:
()
()
44
22
ab
ab
aba b
−
=−
++
Đặt
()
()
()
()
()
()
()
()
444 4
22 22 2 2 22
abc d
N
abab bcbc cdcd dad a
=+++
++ ++ ++ ++
4444
1234
3333
1234
1
4
xxxx
xxxx
+++
≥
+++
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page12
Ta có:
()()
()
()
()()
()
()
(
)
(
)
()
()
(
)( )
()
()
44 44 44 44 4 4 4 4 44 44
22 22 2 2 22
2
ab ab bc bc cd cd da d a
N
aba b bcb c cdc d d ad a
−++ −++ −++ −++
=+++
++ ++ ++ ++
(1)
() () () ()
1111
2
4444
Nababbcbccdcddada⇔≥ ++−+ ++−+ ++−+ ++−
()()
11
2
44
N abbccdda N abcd⇔ ≥ +++++++ ⇔ ≥ +++ ( đpcm )
Bài 17 : Cho ; ;abclà các số thực dương.Chứng minh:
222
1
888
abc
abcbaccab
+
+≥
+++
(Trích đề thi Olympic Toán Quốc Tế lần thứ 42, năm 2001)
Hướng dẫn giải
Đặt
222
888
abc
A
abcbaccab
=++
+++
Áp dụng BĐT Bunhiacôpxki hai lần ta được:
()
2
2
222
444
222
444
222
222
333
.. 8 .. 8 .. 8
888
. 8 8 8
888
. . 8 . 8 . 8
abc
abc aa bc bb ac cc ab
abc bac cab
abc
a a bc b b ac c c ab
abcbaccab
A a a abc b b abc c c abc
⎡⎤
++ = + + + + +
⎢⎥
+++
⎣⎦
⎡⎤
⎡
⎤
≤++ +++++
⎢⎥
⎣
⎦
+++
⎣⎦
⎡⎤
=+++++
⎣⎦
()
()
333
.24A abca b c abc≤+++++ (1)
Mặt khác
() ()()()
3
333
3abc a b c abbcac++ = + + + + + +
Áp dụng BĐT Cauchy với hai số dương ta có:
2 ; 2 ; 2a b ab b c bc a c ac+≥ +≥ +≥
Suy ra:
()()()
8a b b c a c abc+++≥
() ()()()
3
333 333
324abc a b c abbcac a b c abc⇒++ =+++ + + +≥+++ (2)
Từ (1) và (2) suy ra:
()()()()
232
..abc A abcabc Aabc++ ≤ ++ ++ = ++
Do đó
1
A
≥
, nghĩa là
222
1
888
abc
abcbaccab
++≥
+++
Dấu đẳng thức xảy ra khi
abc==.
Bài 18 : Cho ; ;xyz
+
∈ thoả 1xy yz zt tx+ ++=.Chứng minh:
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page13
3333
1
3
xyz t
yztxztxytxyz
+++ ≥
++ ++ ++ ++
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
()
()
(
)
2
22222222
x
yyzzttx x y z t y z t x+++ ≤ +++ +++
2222
1
x
yzt⇔≤ + + + (1)
Đặt: ; ; ;
X
y z tY x z tZ x y tT x y z=++ =++ =++ =++
Không mất tính tổng quát giả sử:
x
yzt≥≥≥
2222
x
yzt⇒≥≥≥và
3333
x
yzt≥≥≥
và
y
zt xzt xyt xyz X Y Z T++≤++≤++≤++⇔ ≤ ≤ ≤
1111
X
YZT
⇒≥≥≥
Áp dụng BĐT Trê-bư-sếp cho hai dãy số sau:
3333
1111
x
yzt
X
YZT
⎧
≥≥≥
⎪
⎨
≥≥≥
⎪
⎩
()
3333
3333
11111
4
xyzt
x
yzt
XY ZT XYZT
⎛⎞
+++≥ +++ +++
⎜⎟
⎝⎠
(2)
Áp dụng BĐT Trê-bư-sếp cho hai dãy
2222
xyzt
x
yzt
≥≥≥
⎧
⎨
≥≥≥
⎩
()
()
()
3333 2222
1
4
x
yzt xyztxyzt+++ ≥ +++ +++
Mặt khác:
()()
11
33
x
yzt xyzxytxztyzt XYZT+++= +++++++++++ = +++
()()
()
3333 2222
11
.
43
x
yzt xyzt XYZT⇒+++≥ +++ +++ (3)
Từ (2) và (3) rút ra:
()
()
3333
2222
1 1111
48
xyzt
xyztXYZT
X
YZT XYZT
⎛⎞
+++≥ +++ +++ +++
⎜⎟
⎝⎠
Theo (1) ta lại có:
2222
1
x
yzt≤+++
Áp dụng BĐT Cauchy cho
;;; 0XYZT> ta có:
()
4
4
4...
1111 1
4
...
1111
.16
XYZT XYZT
XYZT XYZT
XYZT
XYZT
+++≥
+++≥
⎛⎞
⇒+++ +++≥
⎜⎟
⎝⎠
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page14
Vậy
3333
11
.1.16
48 3
xyzt
XY ZT
+++≥ =
Thay
;;;
X
YZTta được kết quả:
3333
1
3
xyz t
yztxztxytxyz
+++ ≥
++ ++ ++ ++
Dấu đẳng thức xảy ra khi
1
2
xyzt====
Bài 19 : Cho n là số tự nhiên.Chứng minh rằng:
(
)
12
... 2 1
nn
nn n
CC C n+++≤ −
Hướng dẫn giải
Chọn hai dãy
(
)
()
12
12 12
; ;...; ; ... 1
n
nnnn n
aCaCaCbb b== = ====
Áp dụng BĐT Bunhiacôpxki ta có:
(
)
()
()
2
12 12
... ... 1 1 ... 1
nn
nn n nn n
CC C CC C+++ ≤+++ +++ (1)
Theo nhị thức Newton ta có:
()
1
n
n
kknk
n
k
ab Cab
−
=
+=
∑
Cho
1ab==.Ta có:
01 1
2 ... 2 1 ...
nnnn
nn n n n
CC C C C=+++⇒−=++
Vậy từ (1) ta có:
(
)
12
... 2 1
nn
nn n
CC C n+++≤ −
Dấu đẳng thức xảy ra khi
12
... 1
n
nn n
CC Cn===⇔=
.
Bài 20 : Cho ; ; ; 0abcd> .Chứng minh :
2
23 2 3 23 23 3
abcd
bcdcdad ababc
+
++≥
++ + + ++ ++
(Trích đề dự bị Quốc Tế Toán Mỹ năm 1993)
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
2
11 1
nn n
i
ii i
ii i
i
x
x
yx
y
== =
⎛⎞
⎛⎞⎛⎞
≥
⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
⎝⎠
∑∑ ∑
với
()()( )
(
)
1234 1234
4; ; ; ; ; ; ; ; ; ; ; 2 3 ; 2 3 ; 2 3 ; 2 3n x x x x abcd y y y y b c dc d ad a ba b c== =++++++++
⇒VT
()
()
2
4
abcd
ab ac ad bc bd cd
+++
≥
++ +++
(1)
Mặt khác
()()
2
3
8
ab ac ad bc bd cd a b c d+++++ ≤ +++ (2)
Từ (1) và (2) ⇒VT
2
3
≥ ( đpcm )
Bài 21 : Cho 0; 0; 0abc>>>.Chứng minh :
444333
2
a b c abc
bc ca ab
+
+
++≥
++ +
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page15
Hướng dẫn giải
Đặt
444
222
123
;;
abc
xxx
bc ca ab
===
++ +
và
() () ()
2
22 22 2
123
;;abc ybca ycab y
+
=+=+=
Áp dụng BĐT Bunhiacôpxki ta có cho các số
123
;;
x
xxvà
123
;;
y
yyta được:
()()()
()
444
2
2
2
22 333
abc
abc bca cab a b c
bc ca ab
⎛⎞
⎡⎤
++ +++++≥++
⎜⎟
⎣⎦
++ +
⎝⎠
Nên
()
()()()
2
333
444
2
22
abc
abc
bc ca ab
abc bca cab
++
++≥
++ +
++ ++ +
Để chứng minh được bài toán ta cần chứng minh:
()
()()()
2
333 2 2
2 abc abcbcacab++ ≥ ++ ++ + (**)
(**)
332 2 332 2332 2
0ababbabcbcbccacaca⇔+−−++−−++−−≥
()()()()()()
222
0ab ab bc bc ca ca⇔− ++− ++− +≥
(***)
Bất đẳng thức (***) là đúng ⇔ (**) là đúng – Bài toán đúng.
Vậy
444333
2
abcabc
bc ca ab
++
++≥
++ +
Bài 22 : Cho 0; 1;2;...;
i
x
in>= có
12
... 1
n
xx x+++=.Cho
12
; ;...;
n
ii i
x
xxlà hoán vị của
12
; ;...;
n
x
xx.Chứng minh:
(
)
2
2
2
1
1
1
k
n
k
k
i
n
x
xn
=
⎛⎞
+
+≥
⎜⎟
⎜⎟
⎝⎠
∑
Hướng dẫn giải
Theo Bunhiacôpxki:
2
22
11 11
11 1
.
kk k
nn nn
kkk
kk kk
ii i
nx x x
xx x
== ==
⎡⎤
⎛⎞⎛⎞⎛ ⎞
+≥ + = +
⎢⎥
⎜⎟⎜⎟⎜ ⎟
⎜⎟⎜⎟⎜ ⎟
⎢⎥
⎝⎠⎝⎠⎝ ⎠
⎣⎦
∑∑ ∑∑
Mà
1
1
n
k
k
x
=
=
∑
2
22
11 1
1
11
k
kk
k
nn n
i
n
kk k
ii
i
k
n
x
nn
xx
x
== =
=
⎛⎞
⎛⎞
≥⇒ ≥ =
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑∑ ∑
∑
Vậy
(
)
2
2
2
1
1
1
k
n
k
k
i
n
x
xn
=
⎛⎞
+
+≥
⎜⎟
⎜⎟
⎝⎠
∑
BÀI TẬP :
Bài 1:
Cho
;;; 0abcd>
và thỏa
()
3
22 22
cd ab+= + .Chứng minh:
33
1
ab
cd
+
≥
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page16
Bài 2: Cho ;;; 0abcd> .Chứng minh:
11416 64
abc d abcd
+++ ≥
+
++
Bài 3: Cho ;;abclà 3 số dương và
222
1abc++≥.Chứng minh:
333
1
2
abc
bc ca ab
+
+≥
++ +
Bài 4: Cho
222
1abc++=
.Chứng minh: 13abcabacbc+++ + + ≤+
Bài 5: Cho ;;abclà các số dương.Chứng minh:
444222
222222
3
abcabc
abab bbcc caca
++
++≥
+
+++++
Bài 6: Cho 3 số ;;
x
yzthoả
()()()
4
111
3
xx yy zz−+ −+ −≤.Chứng minh: 4xyz
+
+≤
Bài 6: Cho ; ;abclà 3 số không âm.Chứng minh:
222
333
ab bc ca
abc
+++
++≥++
Bài 7: Cho 3 số dương ; ;abccó
1abc =
.Chứng minh:
22 22 22
3
2
bc ca ab
ab ac bc ba ca cb
+
+≥
+
++
Bài 8: Cho 3 số dương ;;
x
yzcó 1
x
yz++=.Chứng minh:
1
11933
2
y
xz
yz zx xy
+
+++
++≥
+++
Bài 9: Chứng minh:
()
2
abc
abc
xyz xyz
++
++≥
++
Bài 10: Cho 0xyz≥≥>.Chứng minh:
()
222
2
222
xy yz zx
x
yz
zxy
++≥++
Bài 11: Cho 1; 1ab≥≥.Chứng minh:
22 2
log log 2 log
2
ab
ab
+
⎛⎞
+≤
⎜⎟
⎝⎠
Bài 12: Cho ; ; 0abc> .Chứng minh:
()
()
2
333
111
abc abc
abc
⎛⎞
++ ++ ≥++
⎜⎟
⎝⎠
Bài 13: Cho ; ;abc∈ .Chứng minh:
() () ()
222
222
32
111
2
abbcca+− + +− + +− ≥
Bài 14: Cho ;; 0xyz> và
3
2
xyz++≤.Chứng minh:
222
222
1113
17
2
xyz
xyz
++ ++ +≥
Bài 15: Cho trước 2 số dương ;abvà 2 số dương ;cdthay đổi sao cho abcd
+
<+.Chứng minh:
()
2
22
ac
ca
cd abcd ab
−
+≥
++−−+
. Dấu “=” xảy ra khi nào?
Bài 16: Cho
12
; ;...;
n
aa alà các số thực thoả mãn
22 2
12
... 3
n
aa a
+
++ =.Chứng minh:
12
... 2
23 1
n
a
aa
n
+++ <
+
Bài 17: Cho ; ; ; ; 0abc pq> .Chứng minh:
3abc
p
bqc pcqa paqb pq
++≥
+
+++
Bài 18: Chứng minh rằng với mọi
()
1;2;...;
i
ai n∈= ta có:
() () ()
22 2
22 2
1223 1
1 1 ... 1
2
n
n
aaaa aa+− ++− +++−≥
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page17
Bài 1: Cho
A
BCΔ
thoả mãn hệ thức:
333 2
2( )
9
a b c abc
br cR cr aR ar bR R
++
++=
++ +
(1).CM
A
BCΔ
đều
Hướng dẫn giải
Để đơn giản ta đặt:
0
0
0
xbrcR
ycraR
zarbR
=+ >
=+ >
=+ >
(2)
vậy (1)
333 2
2( )
9
abc abc
xyz R
++
⇔++=
Từ (2) ta có:
()()ax by cz ab bc ca r R++= ++ +(3)
333
444 2 2 2 2 2 2
()( ) ()()()
abc y x z y x z
ax by cz a b c ab a b bc b c ca c a
x
yz x y y z z x
++ ++ =+++ + + + + +
Theo BĐTCauchy,ta có:
333
444 2222
( )( ) 2 . .2 .2 ( )
abc
ax by cz a b c ab ab bc bc ca ca a b c
xyz
++ ++ ≥+++ + + ≥ ++
Suy ra :
()
333 222
()
()
()
abc abc
x
y z ab bc ca r R
++
++ ≥
++ +
(theo 3) (4)
mặt khác ta luôn có (Cauchy):
222
a b c ab bc ca++≥ ++
nên (4):
333 2222 222
222
()
()()
a b c abc abc
x y z a b c rR rR
++ ++
++≥ =
++ + +
2
()
3( )
abc
rR
++
≥
+
(theo BĐT BCS)
Mà
9
23( )3( )
22
R
R
Rr rR R≥⇒ +≤ +=
từ đó:
333 2
2( )
9
abc abc
xyz R
++
++≥
333 2
2( )
9
a b c abc
br cR cr aR ar bR R
++
⇒++≥
++ +
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page18
dấu “=” xảy ra khi
222222
,,
abc
Rr
y
yz yx z
abbcca
x
zy zy x
⎧
⎪
==
⎪
⎪
=
⎨
⎪
⎪
===
⎪
⎩
⇔
A
BC
Δ
đều
Bài 2 : CM: 1 cos cos cos 3 sin sin sinABC ABC+≥ với A, B,C nhọn
Hướng dẫn giải
Do tgA>0,tagB>0,tgC>0 và 1
22 22 22
AB BC C A
tg tg tg tg tg tg++=
Áp dụng BCS ta có:
22 22 22
1
22 22 223
AB BC C A
tg tg tg tg tg tg++≥
(1)
Mặt khác theo BĐT Cauchy ta có:
222
3
3
22 22 22 2 2 2
AB BC C A A B C
tg tg tg tg tg tg tg tg tg++≥
(2)
1
3
2223
ABC
tg tg tg⇔≤
từ (1)và(2):
22 22 22
4
143
22 22 223 222
AB BC C A ABC
tg tg tg tg tg tg tg tg tg+++≥≥
222 222
111 111 83
222 222 222
ABC ABC ABC
tg tg tg tg tg tg tg tg tg
⎛⎞⎛⎞⎛⎞⎛⎞⎛⎞⎛⎞
⇔+ + + +− − − ≥
⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠⎝⎠⎝⎠⎝⎠
222
222 222
111 222
222 222
1.. 3..
111 111
222 222
ABC ABC
tg tg tg tg tg tg
ABC ABC
tg tg tg tg tg tg
−−−
⇔+ ≥
+++ +++
1 cos cos cos 3 sin sin sinABC ABC⇔+ ≥
Dấu “=” xảy ra khi
A
BCΔ
đều
Bài 3 : Cho a, b, c, là số đo 3 cạnh Δ .chứng minh rằng
acb
a
T
−+
=
22
+
1
2222
≥
−+
+
−+ cba
c
bac
b
Hướng dẫn giải
Áp dụng BĐT Bunhiacốpxki cho 6 số:
()()()
cbacbacbacba
cba
c
bac
b
acb
a
−+−+−+
−+−+−+
22;22;22;
22
;
22
;
22
Ta có:
()()()
[]
(
)
2
222222. cbacbacbacbacbaT ++≥−++−++−+
Sau đó dùng biến đổi tương đương chứng minh:
(a + b+ c)
2
≥ 4ab +4bc +4ca –a
2
–b
2
- c
2
Từ đó suy ra đpcm.
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page19
Bài 4 : Cho ABCΔ và đường tròn nội tiếp Δ , các tiếp tuyến của đường tròn song song với 3 cạnh của
Δ
nhỏ
và
có diện tích S
1
; S
2
; S
3
. Gọi S là diện tích
ABC
Δ
. Chứng minh:
3
321
S
SSS ≥++
Hướng dẫn giải
Giả sử S
1
= S
AMN
Ta có: AMNΔ đồng dạng ABCΔ với tỉ số đồng dạng là:
ha
rha 2
−
với r là bán kính đường tròn nội tiếp và h
a
là
đường cao kẻ từ đỉnh A.
Ta có:
2
2
1
1
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
p
a
ha
rha
S
S
(Vì S =
p
a
ha
r
praha =⇒=
2
2
1
với p là nửa chu vi)
Vậy:
p
a
S
S
−=1
1
Tương tự:
p
b
S
S
−=1
2
;
p
c
S
S
−=1
3
Do đó:
13
321
=
++
−=
++
p
cba
S
SSS
Áp dụng BĐT Bun ta có:
S =
()
()
()
321
222
2
321
111.1.1.1 SSSSSS ++++≤++
⇒
123
3
S
SSS++≥ (đpcm). Dấu “=” xảy ra khi
ABC
Δ
đều
Bài 5 : Cho ABCΔ và 1 điểm Q nào đó ở trong
Δ
. Qua Q kẻ đường thẳng song song với AB cắt AC ở M và cắt
BC ở N. Qua điểm Q kẻ đường thẳng song song với AC cắt AB ở F; cắt BC ở E. Qua E kẻ đường thẳng song
song với BC cắt AC ở P, cắt AB ở R. Kí hiệu S
1
= dt(QMP); S
2
= dt(QEN); S
3
= dt(QFR) và S =
dt(ABC).Chứng minh:
a)
()
2
123
SSSS=++ b)
123
1
3
SSS S++≥
Hướng dẫn giải
a) Ta có: QMPΔ đồng dạng
B
ACΔ (tỉ số
M
P
AC
).
Suy ra
2
1
1
S
S
M
PMP
SAC AC
S
⎛⎞
=⇒=
⎜⎟
⎝⎠
.
Tương tự
3
2
;
S
S
PC AM
AC AC
SS
==
Do đó:
123
1
SSS
MP PC AM AC
AC AC
S
++
++
===
www.MATHVN.com
www.MATHVN.com
Tröôøng THPT Chuyeân Tieàn Giang GV Ñoã Kim Sôn
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 Page20
Suy ra:
()
2
123 123
SSSSSSSS=++⇒= ++
b) Áp dụng BĐT Bunhiacôpxki ta có:
()
()
()
2
222
123 123
123
1. 1. 1. 1 1 1
1
Suy ra
3
SSSS SSS
SSS S
=++ ≤++++
++≥
Dấu “=” xảy ra khi
123
SSS== ⇔ Q là trọng tâm ABC
Δ
Bài 6 : Cho a , b , c là 3 cạnh của tam giác.Chứng minh:
abc
abc
bca cab abc
++≥++
+− +− +−
Hướng dẫn giải
Đặt
0
0
0
bca x
cab y
abc z
+−= >
⎧
⎪
+−= >
⎨
⎪
+−=>
⎩
Khi đó ta cần chứng minh:
() () ()
()
222
222
2 (1)
yz zx xy yz zx xy
xyz
yz y z zx z x xy x y xyz x y y z x z
+++ + + +
++≥ + +
⇔+++++≥ +++++
Dễ thấy
()
(1) 2VT xy yz zx≥++ (2)
Theo BĐT Bunhiacôpxki ta có:
()
()
()
()
2
6
6
(2) 2 3 (3)
xy yz zx xyz
xy yz zx xyz
VT xyz x y z
++ ++ + ≤ ++
⇒+++++≤ ++
≤++
Rõ ràng ta có
()
()()
()
22 22 22
2
3
3 (4)
xy xy xy xyz x y z
xy yz zx xyz x y z
xy yz zx xyz x y z
++≥ ++
⇒++ ≥ ++
⇒++≥ ++
Từ (1) (2) (3) (4)⇒đpcm. Dấu “=” xảy ra khi
abc
=
=
Bài 7 : Cho ∆ABC. Chứng minh : a
2
b(a – b) +b
2
c(b – a) + c
2
a(c – a) ≥ 0
( Trích đề thi vô địch toán quốc tế 1983 )
Hướng dẫn giải
Gọi A’; B’; C’ là các tiếp điểm:
www.MATHVN.com
www.MATHVN.com
| 1/37
| | Tải xuống

Có thể bạn quan tâm:

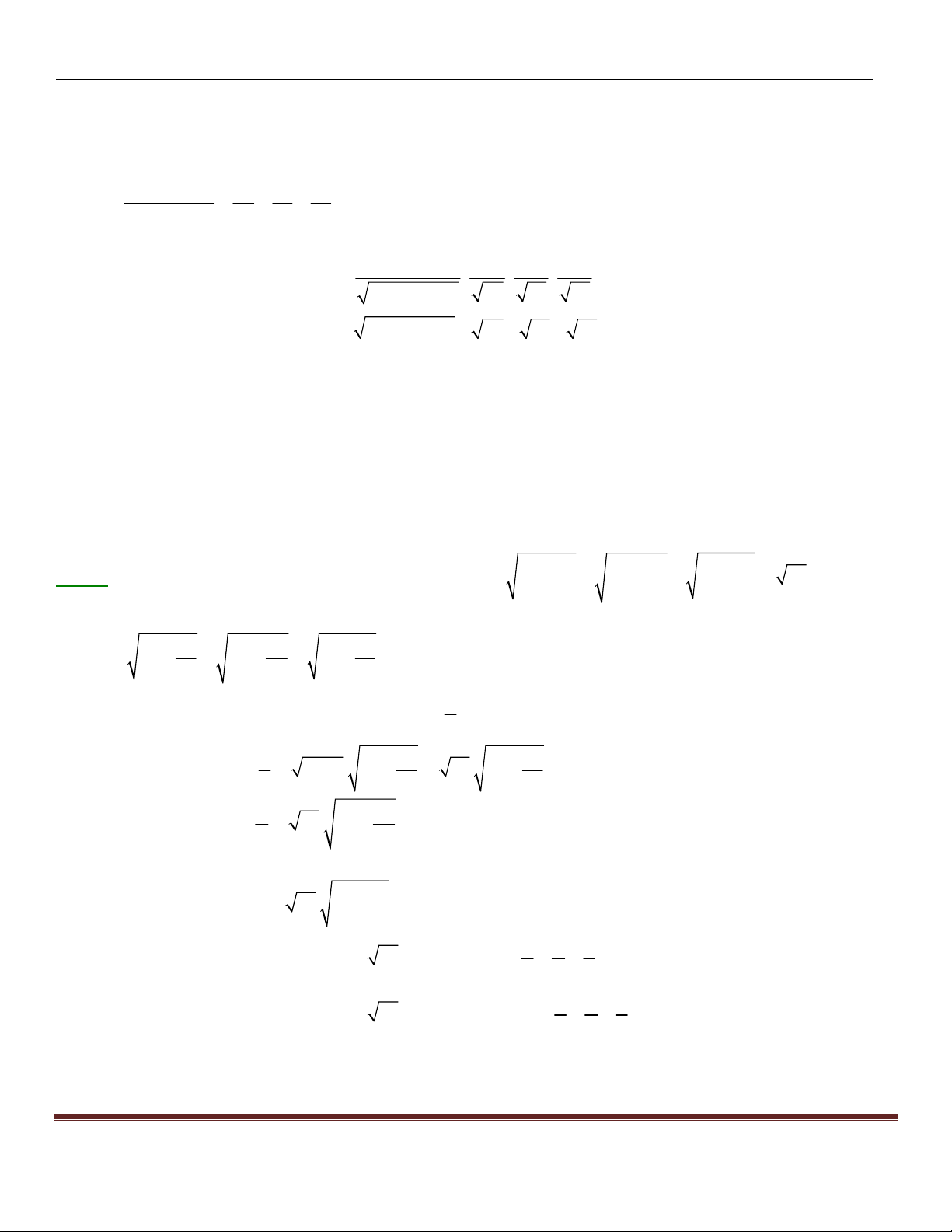
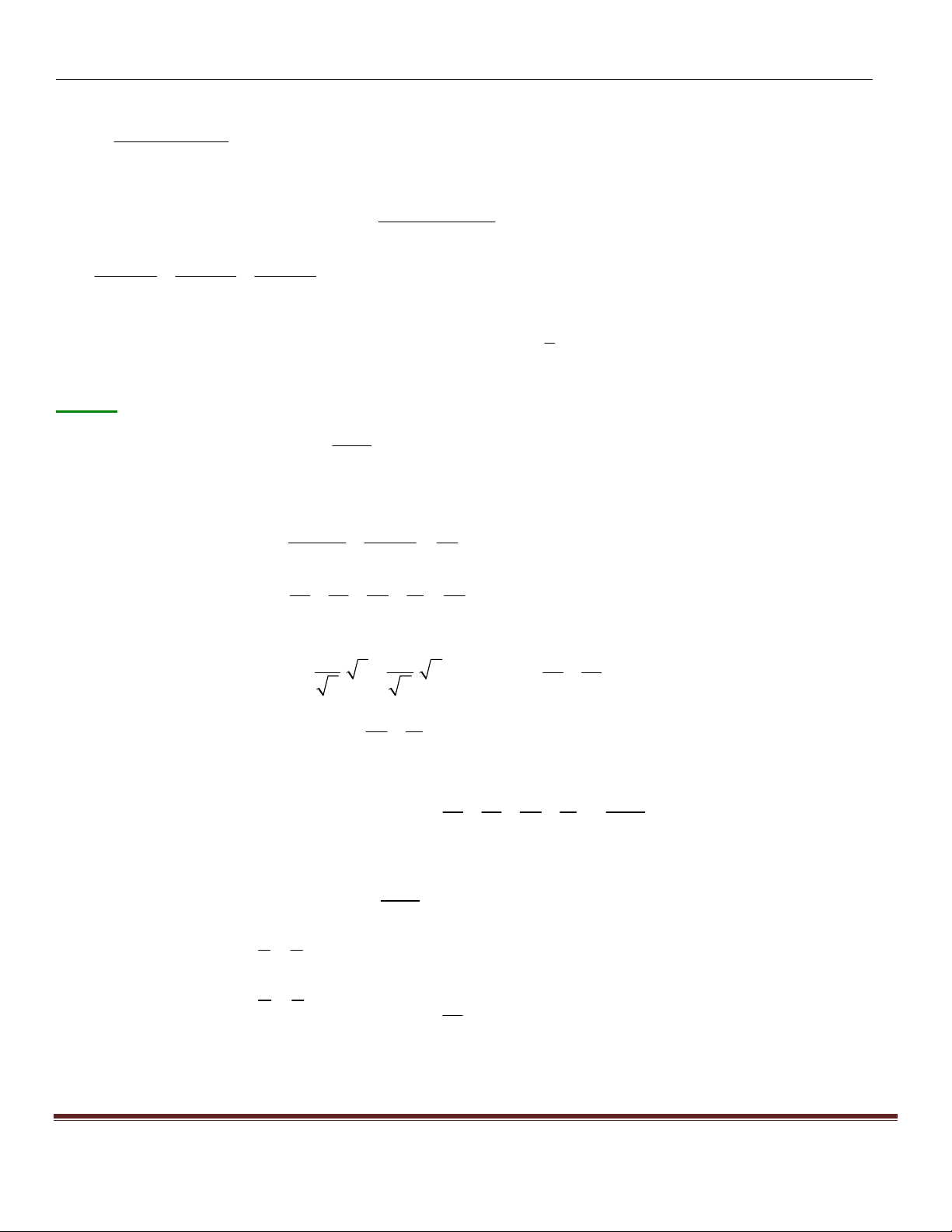
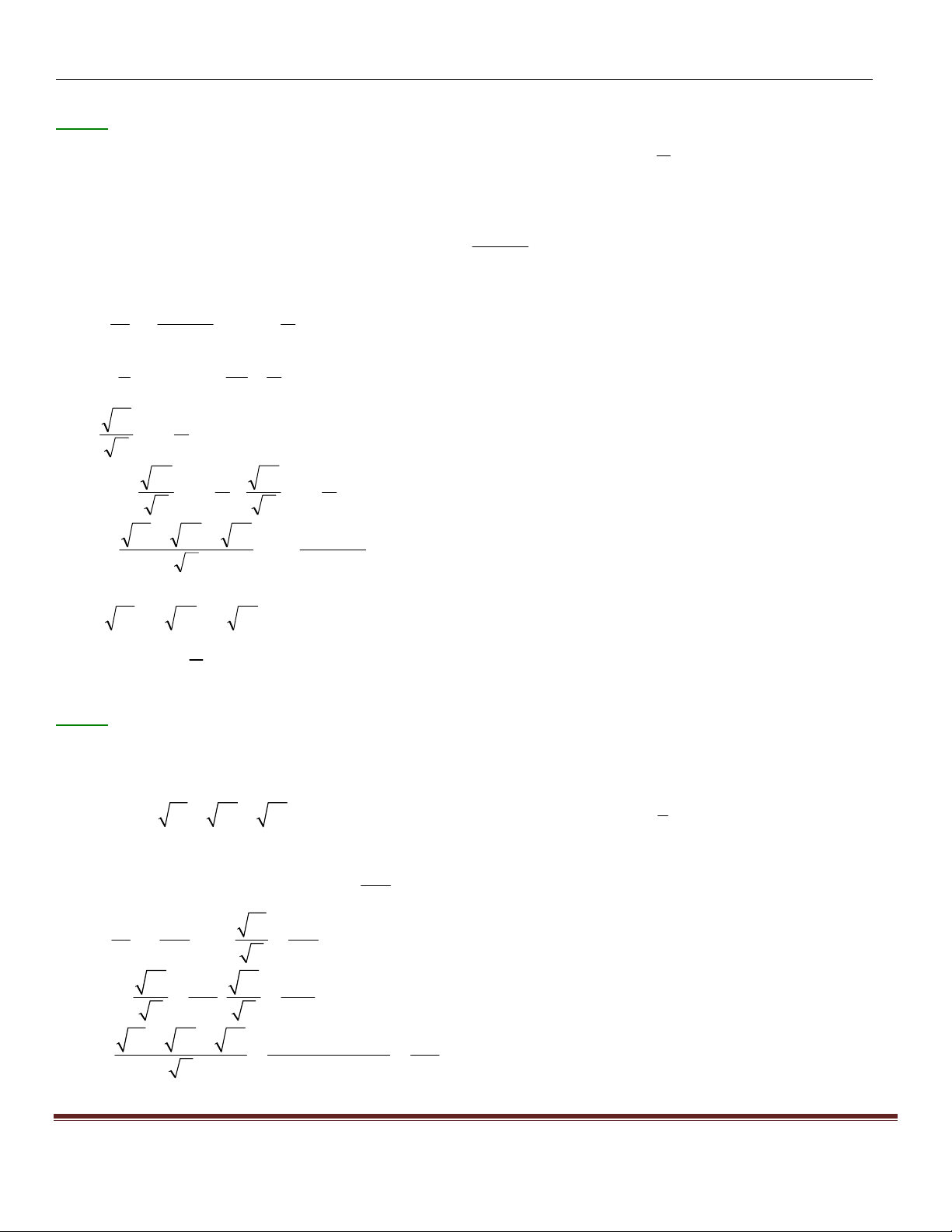
Preview text:

Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
I.Bất đẳng thức Bunhiacôpxki ( BCS ) :
Cho 2 bộ số thực (a ;a ;...;a và (b ;b ;...;b , mỗi bộ gồm n số. Khi đó ta có: 1 2 n ) 1 2 n )
(a b + a b +...+ a b ≤ a + a + + a b +b + +b n n )2 ( 2 2 2 ... n ) ( 2 2 2 ... 1 1 2 2 1 2 1 2 n )
Dấu đẳng thức xảy ra khi và chỉ khi: a a a 1 2 = = ... n =
với quy ước nếu mẫu bằng 0 thì tử phải bằng 0. b b b 1 2 n II. Các hệ quả : Hệ quả 1: C
Nếu a x + ... + a x = C (không đổi) thì min ( 2 2 x + ... + x = 1 n ) 1 1 n n 2 2 a + ... + a 1 n x x đạt được khi 1 = ... n = a a 1 n Hệ quả 2: Nếu 2 2 2
x + ... + x = C (không đổi) thì max (a x + ... + a x = C a + ... + a 1 1 n n ) 2 2 1 n 1 n x x đạt được khi 1 = ... n = ≥ 0 a a 1 n
min (a x + ... + a x = − C a + + a n n ) 2 2 ... 1 1 1 n x x Dấu “=” xảy ra 1 ⇔ = ... n = ≤ 0 a a 1 n
III.Bất đẳng thức Bunhiacôpxki mở rộng:
• Mở rộng bất đẳng thức Bunhiacôpxki cho 3 dãy số thực không âm
(a ;a ;...;a ;(b ;b ;...;b ;(c ;c ;...;c ta luôn có : 1 2 n ) 1 2 n ) 1 2 n )
(a b c + a b c +...+ a b c ≤ a + a + + a b + b + + b c + c + + c n n n )2 ( 3 3 3 ... n ) ( 3 3 3 ... n ) ( 3 3 3 ... 1 1 1 2 2 2 1 2 1 2 1 2 n ) Chứng minh: Đặt 3 3 3 3 3 3 3 3 3 3 3 3
A = a + a + ... + a , B = b + b + ... + b
, C = c + c + ... + c 1 2 n 1 2 n 1 2 n
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 1
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Nếu A = 0 hoặc B = 0 hoặc C = 0 thì bất đẳng thức hiển nhiên đúng vì khi đó cả hai vế của bất đẳng thức đều bằng 0.
Vậy ta chỉ xét trường hợp A > 0; B > 0;C > 0 a b c Đặt i x = ; i y = ; i z = với 1 i = ; 2;3 i i i A B C 3 3 3
⎧x + x + x = 1 1 2 3 ⎪ Khi đó ta có: 3 3 3
⎨y + y + y = 1 và bất đẳng thức cần chứng minh trở thành: x y z + x y z + x y z ≤ 1 1 2 3 1 1 1 2 2 2 3 3 3 ⎪ 3 3 3
z + z + z = 1 ⎩ 1 2 3 3 3 3 ⎧ x + x + x 1 1 1 x y z ≤ ⎪ 1 1 1 3 ⎪ 3 3 3 ⎪ x + x + x Áp
dụng bất đẳng thức Cauchy cho 3 số không âm: 3 3 3
x ; y ; z (i = 1;2;3 ta có: 2 2 2 ⎨x y z ≤ i i i ) 2 2 2 3 ⎪ 3 3 3 ⎪ x + x + x 3 3 3 ⎪x y z ≤ 3 3 3 3 ⎩
Cộng các bất đẳng thức trên lại ta được: x y z + x y z + x y z ≤ 1(đpcm) 1 1 1 2 2 2 3 3 3 ⎧a b c 1 1 1 = = ⎪ A B C
⎧x = y = z ⎪ 1 1 1 ⎪ ⎪a b c Đẳng thức xảy ra 2 2 2
⇔ ⎨x = y = z ⇔ ⎨ = = 2 2 2 A B C ⎪x y z ⎪ = = ⎩ 3 3 3 ⎪a b c 3 3 3 = = ⎪⎩ A B C
Hay a : b : c = A : B : C (i = 1;2;3 tức là: a : b : c = a : b : c = a : b : c i i i ) 1 1 1 2 2 2 3 3 3
• Tổng quát : bất đẳng thức Bunhiacôpxki mở rộng cho rộng cho m dãy số thực không âm:
Cho m dãy số thực không âm:
(a ;a ;...;a ,(b ;b ;...;b , … , (K ;K ;...;K 1 2 n ) 1 2 n ) 1 2 n ) Ta có:
(a b ...K + a b ...K +...+ a b ... m m m K ≤ a + a + ... m m m + a b + b + ... m + b ... m m K + K + ... m + K 1 1 1 2 2 2 n n n ) ( 1 2 n ) ( 1 2 n ) ( 1 2 n )
Dấu “=” xảy ra khi và chỉ khi:
a : b : ... : K = a : b : ... : K = a : b : ... : K ( chứng minh tương tự như trên) 1 1 1 2 2 2 n n n
I- MỘT SỐ VÍ DỤ :
Bài 1: Cho x, y, z là ba số dương thỏa 4x + 9y +16z = 49 . Chứng minh rằng: 1 25 64 T = + + ≥ 49 x y z
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 2
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Đẳng thức xảy ra khi nào?
Hướng dẫn giải 1 5 8
Áp dụng BĐT Bunhiacôpxki cho sáu số 2 x;3 y; 4 z và ; ; ta được: x y z 2 2 2 ⎡ ⎤ ⎛ ⎞ ⎡ ⎤ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞
T = ( x + y + z) + + = ⎜
⎟ ⎢( x )2 + ( y )2 + ( z )2 1 25 84 1 5 8 49. 4 9 16 2 3 4 ⎢ + ⎜ ⎟ ⎜ ⎟ + ⎥ ⎝ x y z ⎠ ⎣ ⎥ ⎜ ⎟ ⎦ ⎢⎝ x ⎜ ⎠ y ⎟ ⎝ ⎠ ⎝ z ⎠ ⎥ ⎣ ⎦ 2 ⎛ 1 5 8 ⎞ 2 ≥ ⎜ 2 x. + 3 y. + 4 z. ⎟ = 49 ⎜ x y z ⎟ ⎝ ⎠ 1 25 64 ⇒ T = + + ≥ 49 x y z ⎧ 1 x = ⎪ 2 ⎧ 1 5 8 ⎪ ⎪ = = ⎪ 5
Đẳng thức xảy ra khi ⎨2x 3y 4z ⇔ ⎨y = 3
⎪⎩4x 9y 16z 49 ⎪ + + = ⎪z = 2 ⎪⎩
Bài 2 : Cho x > 0; y > 0 và 2 2
x + y ≤ x + y .Chứng minh:
x + 3y ≤ 2 + 5
Hướng dẫn giải 2 2 ⎛ 1 ⎞ ⎛ 1 ⎞ 1 Giả thiết: 2 2
x + y ≤ x + y ⇔ x − + y − ≤ ⎜ ⎟ ⎜ ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ 2 ⎛ ⎞
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số: ( ) 1 1
1;3 ; x − ; y − ⎜ ⎟ ta có: ⎝ 2 2 ⎠ 2 2 2 ⎡ ⎛ 1 ⎞ ⎛ 1 ⎞⎤ ⎡⎛ 1 ⎞ ⎛ 1 ⎤ ⎞ 1. 1− + 3. y − ≤ 10 ⎢ ⎜ ⎟ ⎜ ⎟⎥ ⎢ x − + y − ⎜ ⎟ ⎜ ⎟ ⎥ ≤ 5 ⎣ ⎝ 2 ⎠ ⎝ 2 ⎠⎦ ⎢⎝ 2 ⎠ ⎝ 2 ⎠ ⎣ ⎥⎦
⇒ (x + y − )2 3 2 ≤ 5
⇒ x + 3y − 2 ≤ 5
⇒ x + 3y ≤ 2 + 5 ⎧ 1 5 ⎪x = + ⎪ Đẳng thức xảy ra khi 2 10 ⎨ ⎪ 1 3 5 y = + ⎪⎩ 2 10
Bài 3 : Cho a,b,c ≥ 0 ; a + b + c = 1.Chứng minh:
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 3
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn 1 1 1 1 + + + ≥ 30 2 2 2 a + b + c ab bc ac
Hướng dẫn giải 1 1 1 1 Gọi A = + + + 2 2 2 a + b + c ab bc ac
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số: ⎛ 1 1 1 1 ⎞ ⎜ ; ; ; ⎟ 2 2 2
⎝ a + b + c ab bc ca ⎠ ( 2 2 2
a + b + c ;3 ab;3 bc;3 ca ) Ta có: ( + + + )2 ≤ ( 2 2 2 1 3 3 3
a + b + c + 9ab + 9bc + 9ca) A ⇒
≤ ⎡(a + b + c)2 100
+ 7(ab + bc + ca)⎤ A ⎣ ⎦ (*) 1 1
Mà ab + bc + ca ≤ (a + b + c)2 = (do 1
a + b + c = ) 3 3
Do đó: (*) ⇒ A ≥ 30. 1
Đẳng thức xảy ra khi a = b = c = 3 1 1 1 Bài 4 : Cho ;
x y; z > 0 và thoả x + y + z ≤ 1.Chứng minh : 2 2 2 x + + y + + z + ≥ 82 2 2 2 x y z
Hướng dẫn giải 1 1 1 Gọi 2 2 2 S = x + + y + + z + 2 2 2 x y z ⎛ ⎞
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số: ( ) 1 1;9 ; ; x ⎜ ⎟ ⎝ x ⎠ 9 1 1 Ta có: 2 2 x + ≤ 1+ 81. x + = 82. x + (1) 2 2 x x x 9 1 2 y + ≤ 82. y + Tương tự: 2 y y ` (2) 9 1 2 z + ≤ 82. z + (3) 2 z z ⎛ 1 1 1 ⎞
Cộng (1),(2) và (3) theo vế ta được: S. 82 ≥ x + y + z + 9 + + ⎜ ⎟ ⎝ x y z ⎠ ⎛ ⎞ S ≥
(x + y + z) 1 1 1 . 82 81 + 9 + + − 80 ⎜ ⎟
(x + y + z) Hay ⎝ x y z ⎠
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 4
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn ⎛ ⎞ ≥
(x + y + z) 1 1 1 2.9.3. + + − 80 ≥ 162 − 80 = 82 ⎜ ⎟ ⎝ x y z ⎠ 1 1 1 Vậy 2 2 2 x + + y + + z + ≥ 82 2 2 2 x y z
Bài 5 : Cho ba số thực dương a, ,
b c thoả ab + bc + ca = abc .Chứng minh rằng: 2 2 2 2 2 2 b + 2a c + 2b a + 2c + + ≥ 3 ab bc ca
Hướng dẫn giải 2 2 2 2 b + 2a b + 2a 1 1 Ta có: = = + 2
(do a,b dương) 2 2 2 2 ab a b a b 1 1 1
Đặt x = ; y = ; z = thì a b c ⎧a, , b c > 0 ⎧ ; x y; z > 0 giả thiết ⎨ ⇔ ⎨
⎩ab + bc + ca = abc
⎩x + y + z = 1 và (đpcm) 2 2 2 2 2 2
⇔ x + 2y + y + 2z + z + 2x ≥ 3
Áp dụng BĐT Bunhiacôpxki ta có: (x + y )= (x +y +y )≥(x+y+y)2 2 2 2 2 2 3 2 3 1 2 2 ⇒ x + 2y ≥ (x + 2y) 3 1 Tương tự 2 2 y + 2z ≥ ( y + 2z) 3 1 2 2 z + 2x ≥ (z + 2x) 3 1 Vậy 2 2 2 2 2 2
x + 2y + y + 2z + z + 2x ≥
(3x + 3y + 3z) = 3 3 1
Đẳng thức xảy ra khi x = y = z = 3 1
Với x = y = z = thì a = b = c = 3 3
Bài 6 : Chứng minh: a −1 + b −1 + c −1 ≤ c (ab + )
1 với mọi số thực dương ; a ; b c ≥ 1
Hướng dẫn giải Đặt 2 2 2
a −1 = x ;b −1 = y ;c −1 = z Với ;
x y; z > 0.Bất đẳng thức cần chứng minh trở thành:
x + y + z ≤ ( 2
z + ) ⎡⎣( 2x + )( 2 1 1 y + ) 1 +1⎤⎦
Áp dụng BĐT Bunhiacôpxki ta có:
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 5
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn x + y ≤ ( 2 x + )( 2
y + ) ⇒ x + y + z ≤ ( 2 x + )( 2 1 1 1 y + ) 1 + z (1)
( 2x + )( 2y + ) + z ≤ ( 2x + )( 2y + ) 2 1 1 1 1 + 1. z +1 (2)
Kết hợp (1) và (2) ta có x + y + z ≤ ( 2
z + ) ⎡⎣( 2x + )( 2 1 1 y + ) 1 +1⎤⎦
Vậy a −1 + b −1 + c −1 ≤ c (ab + ) 1 (đpcm) Bài 7 : Cho ; a ;
b c > 0 và thoả abc = 1.Chứng minh: 1 1 1 3 + + ≥ 3 a (b + c) 3 b (c + a) 3
c (a + b) 2
Hướng dẫn giải 1 1 1
Đặt x = ; y = ; z = ⇒ xyz = 1; x > 0; y > 0; z > 0 a b c 2 2 2 x y z 3
Ta cần chứng minh bất đẳng thức sau : A= + + ≥ y + z z + x x + y 2 ⎛ x y z ⎞
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số : ( y + z; z + x; x + y );⎜ ; ; ⎟ ⎜ y z z x x y ⎟ + + + ⎝ ⎠ Ta có: ( + + )2 x y z
≤ ( y + z + z + x + x + y) A x + y + z 3 3 3 3 ⇒ A ≥
≥ . xyz = (do xyz = 1) ⇒ A ≥ 2 2 2 2
Đẳng thức xảy ra khi x = y = z = 1 Với 1
x = y = z = thì a = b = c = 1. Bài 8 : Cho ; a ;
b c > 0 .Chứng minh: a b c + + ≤ 1
a + (a + b)(a + c) b + (b + c)(b + a) c + (c + a)(c + b)
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số:
( a; b);( c; a) Ta có: ( + )2 ac ab
≤ (a + b)(c + a) ⇒ ac + ab ≤ (a + b)(c + a)
⇒ a + ac + ab ≤ a + (a + b)(c + a) a a a ⇒ ≤ = (1)
a + (a + b)(a + c)
a + ac + ab a + b + c
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 6
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn b b Tương tự: ≤ (2)
b + (b + c)(b + a) a + b + c c c ≤ (3)
c + (c + a)(c + b) a + b + c
Cộng (1),(2) và (3) theo vế ta được: a b c + + ≤ 1
a + (a + b)(a + c) b + (b + c)(b + a) c + (c + a)(c + b)
Đẳng thức xảy ra khi a = b = c . ab 3 2 − 3 Bài 9 : Cho ; a b > 0 và thoả 2 2
a + b = 9 .Chứng minh : ≤ a + b + 3 2
Hướng dẫn giải Ta có: 2 2 a + b = 9
⇔ ab = (a + b)2 2 − 9
⇔ 2ab = (a + b + 3)(a + b − 3) 2ab ⇔ = a + b − 3 a + b + 3 ab a + b 3 ⇔ = − a + b + 3 2 2
Mà theo BĐT Bunhiacôpxki thì 2 2
a + b ≤ 2. a + b = 3 2 ab 3 2 − 3 Nên ≤ a + b + 3 2 ⎧ ; a b > 0 ⎪⎪ 3 Đẳng thức xảy ra khi 2 2
⎨a + b = 9 ⇔ a = b = 2 ⎪ ⎪⎩a = b 1 1 1 p + q p + q p + q Bài 10: Cho ; a ; b ;
c d dương tuỳ ý.Chứng minh : + + ≥ + + a b c pa + qb pb + qc pc + qa
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có 2 ( + ) ⎛ ⎞ 2 p q ⎛ p q ⎞ p q = ⎜ . pa + . qb ⎟ ≤ + ⎜ ⎟ ⎜ ⎟( pa + qb) a b ⎝ ⎠ ⎝ a b ⎠
Tương tự ta chứng minh được ( )2 ⎛ p q ⎞ ⎜ ⎟( ) ( ⎛ ⎞ + ≤ + + p + q)2 p q p q pb qc ; ≤ + ⎜ ⎟( pc + qa) ⎝ b c ⎠ ⎝ c a ⎠
Cộng các vế tương ứng của ba bất đẳng thức ta có :
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 7
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn ( + )2 ⎡ 1 1 1 ⎤ + + ≤ ⎢ ⎥ ( + )⎛ 1 1 1 ⎞ p q p q + + ⎜ ⎟ ⎣ pa + qb pb + qc pc + qa ⎦ ⎝ a b c ⎠ ⎡ ⎤ Hay ( + ) 1 1 1 1 1 1 p q + + ≤ + + ⎢ ⎣ pa qb pb qc pc qa ⎥ + + + ⎦ a b c 1 1 1 p + q p + q p + q Vậy + + ≥ + + a b c pa + qb pb + qc pc + qa
Bài 11 : Cho 4 số dương ; a ; b ; c d .Chứng minh: 3 3 3 3 2 2 2 2 a b c d
a + b + c + d + + + ≥ b + c + d
c + d + a b + d + a a + b + c 3
Hướng dẫn giải 3 3 3 3 a b c d Đặt P = + + + b + c + d
c + d + a b + d + a a + b + c
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số: 3 3 3 3 ⎛ a b c d ⎞ ⎜ ; ; ; ⎟; ⎜ + + + + + +
+ + ⎟ ( a (b + c + d ); b(c + d + a); c(d + b + a); d (a + b + c) ) b c d c d a b d a a b c ⎝ ⎠ Ta có: ( + + + )2 2 2 2 2 a b c d
≤ P ⎡a (b + c + d ) + b(c + d + a) + c(d + a + b) + d (a + b + c)⎤ ⎣ ⎦ 2
⇔ ( + + + ) ≤ ⎡( + + + )2 2 2 2 2 − ( 2 2 2 2 a b c d P a b c d
a + b + c + d )⎤ ⎣ ⎦ (1)
Áp dụng BĐT Bunhiacôpxki cho 2 bộ số: (a; ; b ; c d );(1;1;1; ) 1 ta được:
(a + b + c + d )2 ≤ ( 2 2 2 2
4 a + b + c + d ) (2)
(a +b + c + d )2 2 2 2 2 ≤ 3P ( 2 2 2 2
a + b + c + d ) Từ (1) và (2) ta được 2 2 2 2
⇔ a + b + c + d ≤ 3P 3 3 3 3 2 2 2 2 a b c d
a + b + c + d Vậy + + + ≥ b + c + d
c + d + a b + d + a a + b + c 3 a b c
Bài 12 : Cho các số dương ; a ;
b c thỏa a + b + c = 1 . Chứng minh : + + ≥ 1
1+ b − a 1+ c − b 1 + a − c
Hướng dẫn giải a b c a b c Đặt A = + + = + +
1+ b − a 1+ c − b 1+ a − c
2b + c 2c + a 2a + b
Áp dụng BĐT Bunhiacôpxki ta có: 2 ( + + ) ⎡ ⎤ 2 a = ⎢ ( b c a b c
a 2b + c) +
b(2c + a) +
c (2a + b)⎥ 2b + c 2c + a 2a + b ⎣ ⎦ ⎡ a b c ⎤ ≤ + + ⎡a ⎢
⎥ ⎣ (2b + c) + b(2c + a) + c (2a + b)⎤
⎣ 2b + c 2c + a 2a + b ⎦ ⎦
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 8
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
(a +b + c)2 ⇔ A ≥
3(ab + bc + ca) Ta lại có: (
3(ab + bc + ca)
a + b + c)2 ≥ 3(ab + bc + ca) . Suy ra A ≥ ( =
ab + bc + ca) 1 3 a b c Vậy + + ≥ 1
1+ b − a 1+ c − b 1+ a − c
⎧2b + c = 2c + a = 2a + b ⎪ 1
Dấu đẳng thức xảy ra khi ⎨a = b = c
⇔ a = b = c = 3
⎪a +b + c =1 ⎩
Bài 13 : Giả sử các số thực ;
x y; z;t thoả mãn điều kiện: a ( 2 2
x + y ) + b( 2 2
z + t ) = 1 với ;
a b là hai số dương cho +
trước. Chứng minh: ( + )( + ) a b x z y t ≤ ab
Hướng dẫn giải Do ;
a b > 0 nên từ giả thiết ta có: + +
a (x + y ) + b(z + t ) 2 2 2 2 x y z t 1 2 2 2 2 = 1 ⇔ + = b a ab 2 2 2 2 x z y t 1 ⇔ + + + = b a b a ab
Áp dụng BĐT Bunhiacôpxki ta có: 2 2 2 ( + )2 ⎛ x z ⎞ ⎛ x z ⎞ x z = . b + . a ≤ ⎜ ⎟
(b + a)⎜ + ⎟ (1) ⎝ b a ⎠ ⎝ b a ⎠ 2 2 ⎛ y t ⎞ Tương tự :
( y + t)2 ≤ (b + a)⎜ + ⎟ (2) ⎝ b a ⎠
Cộng từng vế (1) và (2) ta được: 2 2 2 2 ⎛ x z y t ⎞ a + b
(x + z)2 + ( y + t)2 ≤ (b + a)⎜ + + + ⎟ = (3) ⎝ b a b a ⎠ ab
Mặt khác ( x + z)2 + ( y + t)2 ≥ 2( x + z)( y + t) (4) +
Do đó từ (3) và (4) suy ra: ( + )( + ) a b x z y t ≤ ab ⎧ x z = ⎪b a ⎪ ⎧x = y ⎪ y t ⎪
Dấu đẳng thức xảy ra ⇔ ⎨ = ⇔ ⎨ ax b a z = t = ⎪ ⎪⎩ b
⎪x + z = y + t ⎪⎩
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 9
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Bài 14 : Cho các số thực dương ;
x y; z;t thoả mãn xyzt = 1.Chứng minh: 1 1 1 1 4 + + + ≥ 3
x ( yz + zt + ty) 3
y ( xz + zt + tx) 3
z ( xt + ty + yx) 3
t ( xy + yz + zx) 3
Hướng dẫn giải 1 1 1 1 Với ;
x y; z;t dặt a = ;b = ;c = ; d = ( ; a ; b ;
c d > 0) và abcd = 1 x y z t 1 1 1 1
⇒ x = ; y = ; z = ;t = a b c d
Bất đẳng thức cần chứng minh tương với: 1 1 1 1 4 + + + ≥ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 3 + + + + + + + + 3 ⎜ ⎟ 3 ⎜ ⎟ 3 ⎜ ⎟ 3 ⎜ ⎟
a ⎝ bc cd bd ⎠ b ⎝ ac cd
ad ⎠ c ⎝ ad bd ab ⎠ d ⎝ ab bc ac ⎠ 3 3 3 3 a b c d 4 ⇔ + + + ≥ b + c + d c + d + a d + a + b a + b + c 3 bcd adc abd abc 3 3 3 3 a b c d 4 ⇔ + + + ≥ (vì abcd = 1)
a (b + c + d ) b(c + d + a) c(d + a + b) d (a + b + c) 3 2 2 2 2 a b c d 4 ⇔ + + + ≥ b + c + d c + d + a d + a + b a + b + c 3 2 2 2 2 a b c d Đặt S = + + + b + c + d c + d + a d + a + b a + b + c
Áp dụng BĐT Bunhiacôpxki ta có:
S ⎡⎣(b + c + d ) + (c + d + a) + (d + a + b) + (a + b + c)⎤ ≥
⎦ (a + b + c + d )2 .
(a + b + c + d)2 1 ⇒ S ≥ =
a + b + c + d (1)
3(a + b + c + d ) ( ) 3
Áp dụng BĐT Cauchy với 2 số dương:
a + b ≥ 2 ab; c + d ≥ 2 cd
Suy ra a + b + c + d ≥ 2( ab + cd )
Lại áp dụng BĐT Cauchy cho 2 số dương ab; cd ta có: 4 ab + cd ≥ 2
abcd = 2 abcd = 2 (vì abcd = 1) (2) 4
Từ (1) và (2) suy ra S ≥ 3 1 1 1 1 4 Vậy + + + ≥ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 1 ⎛ 1 1 1 ⎞ 3 + + + + + + + + 3 ⎜ ⎟ 3 ⎜ ⎟ 3 ⎜ ⎟ 3 ⎜ ⎟
a ⎝ bc cd bd ⎠ b ⎝ ac cd
ad ⎠ c ⎝ ad bd ab ⎠ d ⎝ ab bc ac ⎠
Dấu đẳng thức xảy ra khi a = b = c = d = 1 ⇔ x = y = z = t = 1 .
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 10
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Bài 15 : Cho x ; x ; x ; x dương thoả điều kiện x + x + x + x = 1.Chứng minh : 1 2 3 4 1 2 3 4 4 4 4 4 + + + x x x x 1 1 2 3 4 ≥ 3 3 3 3
x + x + x + x 4 1 2 3 4
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
1 = ( x + x + x + x )2 ≤ 4( 2 2 2 2
x + x + x + x 1 2 3 4 1 2 3 4 ) 1 2 2 2 2
⇒ x + x + x + x ≥ (1) 1 2 3 4 4 2 • ( 2 2 2 2
x + x + x + x ) = ( 3 3 3 3
x . x + x . x + x . x + x . x 1 2 3 4 1 1 2 2 3 3 4 4 )
≤ ( x + x + x + x )( 3 3 3 3
x + x + x + x 1 2 3 4 1 2 3 4 ) 3 3 3 3
= x + x + x + x (vì x + x + x + x = 1) 1 2 3 4 1 2 3 4 3 3 3 3
x + x + x + x 1 2 3 4 2 2 2 2 ⇔
≥ x + x + x + x (2) 2 2 2 2 1 2 3 4
x + x + x + x 1 2 3 4 •
(x + x + x + x )2 3 3 3 3 1 2 3 4 = ( 2 2 2 2
x .x + x .x + x .x + x .x 1 1 2 2 3 3 4 4 ) ≤ ( 2 2 2 2
x + x + x + x )( 4 4 4 4
x + x + x + x 1 2 3 4 1 2 3 4 ) 4 4 4 4 3 3 3 3
x + x + x + x
x + x + x + x 1 2 3 4 1 2 3 4 ⇒ ≥ (3) 3 3 3 3 2 2 2 2
x + x + x + x
x + x + x + x 1 2 3 4 1 2 3 4 Từ (1);(2) và (3) suy ra: 4 4 4 4
x + x + x + x 1 1 2 3 4 ≥ 3 3 3 3
x + x + x + x 4 1 2 3 4
Bài 16 : Cho bốn số dương ; a ; b ; c d .Chứng minh: 4 4 4 4 a b c d
a + b + c + d + + + ≥ ( a + b)( 2 2
a + b ) (b + c)( 2 2
b + c ) (c + d )( 2 2
c + d ) (d + a)( 2 2 d + a ) 4
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có:
(a + b)2 ≤ (a + b ) ⇔ (a + b )(a + b)2 2 2 2 2 ≤ ( 2 2 a + b ) ≤ ( 2 2 2 2 4 a + b ) (1) 4 4 a + b 1 ⇔ ≥ + ( a + b)( a b 2 2 a + b ) ( ) 4 4 4 a − b Mặt khác: = − ( a + b)( a b 2 2 a + b ) 4 4 4 4 a b c d Đặt N = + + + ( a + b)( 2 2
a + b ) (b + c)( 2 2
b + c ) (c + d )( 2 2
c + d ) (d + a)( 2 2 d + a )
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 11
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn Ta có: ( 4 4 a − b ) + ( 4 4 a + b ) ( 4 4 b − c ) + ( 4 4 b + c ) ( 4 4 c − d ) + ( 4 4 c + d ) ( 4 4 d − a ) + ( 4 4 d + a ) 2N = + + + ( (1) a + b)( 2 2 a + b ) (b + c)( 2 2 b + c ) (c + d)( 2 2 c + d ) (d + a)( 2 2 d + a ) 1
⇔ N ≥ (a + b) 1
+ a − b + (b + c) 1
+ b − c + (c + d ) 1 2
+ c − d + (d + a) + d − a 4 4 4 4 1
⇔ N ≥ (a + b + b + c + c + d + d + a) 1 2
⇔ N ≥ (a + b + c + d ) ( đpcm ) 4 4 a b c Bài 17 : Cho ; a ;
b c là các số thực dương.Chứng minh: + + ≥ 1 2 2 2 a + 8bc b + 8ac c + 8ab
(Trích đề thi Olympic Toán Quốc Tế lần thứ 42, năm 2001)
Hướng dẫn giải a b c Đặt A = + + 2 2 2 a + 8bc b + 8ac c + 8ab
Áp dụng BĐT Bunhiacôpxki hai lần ta được: 2 ( ⎡ ⎤
a + b + c)2 a b c 4 2 4 2 4 2 = ⎢
. a. a + 8bc +
. b. b + 8ac +
. c. c + 8ab ⎥ 4 2 4 2 4 2 ⎣ a + 8bc b + 8ac c + 8ab ⎦ ⎡ a b c ⎤ 2 2 2 ⎡ ⎢ ⎥ . a a 8bc b b 8ac c c 8ab ⎤ ≤ + + + + + + + 2 2 2 ⎣ a 8bc b 8ac c 8ab ⎣ ⎦ + + + ⎦ 3 3 3 .
A ⎡ a. a 8abc b. b 8abc c. c 8abc ⎤ = + + + + + ⎣ ⎦
≤ A (a + b + c)( 3 3 3 .
a + b + c + 24abc) (1) Mặt khác
(a + b + c)3 3 3 3
= a + b + c + 3(a + b)(b + c)(a + c)
Áp dụng BĐT Cauchy với hai số dương ta có:
a + b ≥ 2 ab; b + c ≥ 2 bc; a + c ≥ 2 ac
Suy ra: (a+b)(b+c)(a+c)≥8abc
⇒ (a + b + c)3 3 3 3
= a + b + c + (a + b)(b + c)(a + c) 3 3 3 3
≥ a + b + c + 24abc (2) Từ (1) và (2) suy ra:
(a + b + c)2 ≤ A (a + b + c)(a + b + c)3 = A (a + b + c)2 . . a b c
Do đó A ≥ 1, nghĩa là + + ≥ 1 2 2 2 a + 8bc b + 8ac c + 8ab
Dấu đẳng thức xảy ra khi a = b = c . Bài 18 : Cho ; x y; z + ∈
thoả xy + yz + zt + tx = 1.Chứng minh:
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 12
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn 3 3 3 3 x y z t 1 + + + ≥ y + z + t x + z + t x + y + t x + y + z 3
Hướng dẫn giải
Áp dụng BĐT Bunhiacôpxki ta có: ( + + + )2 ≤ ( 2 2 2 2 + + + )( 2 2 2 2 xy yz zt tx x y z t
y + z + t + x ) 2 2 2 2
⇔ 1 ≤ x + y + z + t (1)
Đặt: X = y + z + t;Y = x + z + t; Z = x + y + t;T = x + y + z
Không mất tính tổng quát giả sử: x ≥ y ≥ z ≥ t 2 2 2 2
⇒ x ≥ y ≥ z ≥ t và 3 3 3 3
x ≥ y ≥ z ≥ t
và y + z + t ≤ x + z + t ≤ x + y + t ≤ x + y + z ⇔ X ≤ Y ≤ Z ≤ 1 1 1 1 T ⇒ ≥ ≥ ≥ X Y Z T
Áp dụng BĐT Trê-bư-sếp cho hai dãy số sau: 3 3 3 3
⎧x ≥ y ≥ z ≥ t ⎪ ⎨ 1 1 1 1 ≥ ≥ ≥ ⎪⎩ X Y Z T 3 3 3 3 x y z t 1 ⎛ 1 1 1 1 ⎞ + + + ≥ + + + ⎜ ⎟( 3 3 3 3
x + y + z + t ) (2) X Y Z T 4 ⎝ X Y Z T ⎠
⎧x ≥ y ≥ z ≥ t
Áp dụng BĐT Trê-bư-sếp cho hai dãy ⎨ 2 2 2 2
⎩x ≥ y ≥ z ≥ t 1 ( 3 3 3 3
x + y + z + t ) ≥ (x + y + z + t)( 2 2 2 2
x + y + z + t ) 4 Mặt khác: 1
x + y + z + t = ( x + y + z + x + y + t + x + z + t + y + z + t) 1
= ( X + Y + Z + T ) 3 3 ⇒ ( 1 1 3 3 3 3
x + y + z + t ) ≥ ( 2 2 2 2
x + y + z + t ). ( X + Y + Z + T ) (3) 4 3 Từ (2) và (3) rút ra: 3 3 3 3 x y z t 1 ( ⎛ 1 1 1 1 2 2 2 2 ⎞ + + + ≥
x + y + z + t )( X + Y + Z + T ) + + + ⎜ ⎟ X Y Z T 48 ⎝ X Y Z T ⎠ Theo (1) ta lại có: 2 2 2 2
1 ≤ x + y + z + t
Áp dụng BĐT Cauchy cho X ;Y; Z;T > 0 ta có: 4
X + Y + Z + T ≥ 4 X .Y.Z.T 1 1 1 1 1 4 + + + ≥ 4 X Y Z T
X .Y.Z.T ( ⎛ ⎞
⇒ X + Y + Z + T ) 1 1 1 1 . + + + ≥ 16 ⎜ ⎟ ⎝ X Y Z T ⎠
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 13
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn 3 3 3 3 x y z t 1 1 Vậy + + + ≥ .1.16 = X Y Z T 48 3
Thay X ;Y; Z;T ta được kết quả: 3 3 3 3 x y z t 1 + + + ≥ y + z + t x + z + t x + y + t x + y + z 3 1
Dấu đẳng thức xảy ra khi x = y = z = t = 2
Bài 19 : Cho n là số tự nhiên.Chứng minh rằng: 1 2 C + C + ... n
+ C ≤ n(2n − n n n )1
Hướng dẫn giải Chọn hai dãy ( 1 2
a = C ; a = C ;...; n
a = C ; b = b = ... = b = 1 1 n 2 n n n ) ( 1 2 n ) 2
Áp dụng BĐT Bunhiacôpxki ta có: ( 1 2 n
C + C + + C ) ≤ ( 1 2 ... C + C + ... n + C + + + (1) n n n n n n ) (1 1 ... ) 1 n
Theo nhị thức Newton ta có: (a + b)n k k n k = ∑C a b − n k 1 =
Cho a = b = 1.Ta có: n 0 1 n n 1
2 = C + C + ... + C ⇒ 2 −1 = C + ... n + C n n n n n Vậy từ (1) ta có: 1 2 C + C + ... n
+ C ≤ n(2n − n n n )1
Dấu đẳng thức xảy ra khi 1 2 C = C = ... n = C ⇔ n = 1. n n n a b c d 2 Bài 20 : Cho ; a ; b ;
c d > 0 .Chứng minh : + + + ≥
b + 2c + 3d
c + 2d + 3a
d + 2a + 3b
a + 2b + 3c 3
(Trích đề dự bị Quốc Tế Toán Mỹ năm 1993)
Hướng dẫn giải 2 n n n ⎛ x ⎞⎛ ⎞ ⎛ ⎞
Áp dụng BĐT Bunhiacôpxki ta có: i
⎜ ∑ ⎟ ∑ x y ≥ ∑ x ⎜ i i ⎟ ⎜ i ⎟
⎝ i 1= yi ⎠⎝ i 1= ⎠ ⎝ i 1= ⎠
với n = 4;( x ; x ; x ; x = a; ; b ;
c d ; y ; y ; y ; y = b + 2c + 3d;c + 2d + 3a;d + 2a + 3 ;
b a + 2b + 3c 1 2 3 4 ) ( ) ( 1 2 3 4 ) ( )
(a + b + c + d )2 ⇒ VT ≥ (1)
4(ab + ac + ad + bc + bd + cd ) 3
Mặt khác (ab + ac + ad + bc + bd + cd ) ≤ (a + b + c + d )2 (2) 8 2
Từ (1) và (2) ⇒ VT ≥ ( đpcm ) 3 4 4 4 3 3 3 a b c a + b + c Bài 21 : Cho 0
a > ;b > 0;c > 0 .Chứng minh : + + ≥ b + c c + a a + b 2
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 14
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Hướng dẫn giải 4 4 4 a b c Đặt 2 2 2 x = ; x = ; x = và 2 a (b + c) 2 2
= y ;b c + a = y ;c a + b = y 1 ( ) 2 2 2 ( ) 2 1 2 3 b + c c + a a + b 3
Áp dụng BĐT Bunhiacôpxki ta có cho các số x ; x ; x và y ; y ; y ta được: 1 2 3 1 2 3 4 4 4 ⎛ a b c ⎞ 2 ⎜ + + ⎡
⎟ a (b + c) 2
+ b (c + a) 2
+ c (a + b) 2 ⎤ ≥ ( 3 3 3
a + b + c )2
⎝ b + c c + a a + b ⎣ ⎦ ⎠ (a +b + c a b c )2 3 3 3 4 4 4 Nên + + ≥ 2 b + c c + a a + b a (b + c) 2
+ b (c + a) 2
+ c (a + b)
Để chứng minh được bài toán ta cần chứng minh: ( + + ) 2 3 3 3 ≥ ( + ) 2 + ( + ) 2 2 a b c a b c
b c a + c (a + b) (**) (**) 3 3 2 2 3 3 2 2 3 3 2 2
⇔ a + b − a b − b a + b + c − b c − bc + c + a − c a − ca ≥ 0
⇔ (a − b)2 (a + b) + (b − c)2 (b + c) + (c − a)2 (c + a) ≥ 0 (***)
Bất đẳng thức (***) là đúng ⇔ (**) là đúng – Bài toán đúng. 4 4 4 3 3 3 a b c a + b + c Vậy + + ≥ b + c c + a a + b 2
Bài 22 : Cho x > 0;i = 1; 2;...;n có x + x + ... + x = 1.Cho x ; x ;...; x là hoán vị của x ; x ;...; x .Chứng minh: i 1 2 n 1 i 2 i n i 1 2 n 2 n ⎛ 1 ⎞ ( 2n + )2 1 ∑⎜ x + ⎟ ≥ k ⎜ ⎟ k 1 = x n ⎝ ⎠ k i
Hướng dẫn giải 2 2 2 n ⎛ 1 ⎞ ⎡ n ⎛ 1 ⎞⎤ n n ⎛ 1 ⎞ Theo Bunhiacôpxki: . n ∑⎜ x + ⎟ ≥ ⎢∑⎜ x +
⎟⎥ = ⎜ ∑ x + ∑ ⎟ k k k ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ k 1 = x ⎝ ⎠ ⎢ = x ⎣ ⎝ ⎠⎥ = = x i k 1 i k 1 k 1 ⎦ ⎝ ⎠ k k k i n n n n 2 ⎛ ⎞⎛ 1 ⎞ 1 n Mà ∑ x = 1 2 2 ∑x ⎜ ⎟⎜ ∑ ⎟ ≥ n ⇒ ∑ ≥ = n k k i n ⎜ ⎟ k 1 = ⎝ k 1= ⎠ k 1= x = x i k 1 ⎝ ⎠ k k i ∑xki k 1 = 2 n ⎛ 1 ⎞ ( 2n + )2 1 Vậy ∑⎜ x + ⎟ ≥ k ⎜ ⎟ k 1 = x n ⎝ ⎠ k i BÀI TẬP : 3 3 a b Bài 1: Cho ; a ; b ; c d > 0 và thỏa + = ( + )3 2 2 2 2 c d a b .Chứng minh: + ≥ 1 c d
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 15
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn 1 1 4 16 64 Bài 2: Cho ; a ; b ;
c d > 0 .Chứng minh: + + + ≥ a b c d
a + b + c + d 3 3 3 a b c 1 Bài 3: Cho ; a ;
b c là 3 số dương và 2 2 2
a + b + c ≥ 1.Chứng minh: + + ≥ b + c c + a a + b 2 Bài 4: Cho 2 2 2
a + b + c = 1.Chứng minh: a + b + c + ab + ac + bc ≤ 1+ 3 4 4 4 2 2 2 a b c a + b + c Bài 5: Cho ; a ;
b c là các số dương.Chứng minh: + + ≥ 2 2 2 2 2 2
a + ba + b
b + bc + c
c + ac + a 3 Bài 6: Cho 3 số ;
x y; z thoả x ( x − ) + y ( y − ) + z ( z − ) 4 1 1
1 ≤ .Chứng minh: x + y + z ≤ 4 3 a + 2b b + 2c c + 2a Bài 6: Cho a; ;
b c là 3 số không âm.Chứng minh: + +
≥ a + b + c 3 3 3 bc ca ab 3
Bài 7: Cho 3 số dương ; a ;
b c có abc = 1.Chứng minh: + + ≥ 2 2 2 2 2 2
a b + a c b c + b a c a + c b 2 1+ x 1+ y 1+ z 9 + 3 3
Bài 8: Cho 3 số dương ;
x y; z có x + y + z = 1.Chứng minh: + + ≥ y + z z + x x + y 2 ( + + )2 a b c a b c Bài 9: Chứng minh: + + ≥ x y z x + y + z 2 2 2 x y y z z x 2
Bài 10: Cho x ≥ y ≥ z > 0 .Chứng minh: + + ≥ ( 2 2 2
x + y + z ) z x y ⎛ a + b ⎞
Bài 11: Cho a ≥ 1;b ≥ 1.Chứng minh: log a + log b ≤ 2 log 2 2 2 ⎜ ⎟ ⎝ 2 ⎠ ⎛ 1 1 1 ⎞
Bài 12: Cho a; ;
b c > 0 .Chứng minh: (a + b + c ) + + ≥ ⎜
⎟ (a + b + c)2 3 3 3 ⎝ a b c ⎠ 3 2
Bài 13: Cho a; ;
b c ∈ .Chứng minh: a + (1− b)2 + b + (1− c)2 + c + (1− a)2 2 2 2 ≥ 2 3 1 1 1 3 Bài 14: Cho ;
x y; z > 0 và x + y + z ≤ .Chứng minh: 2 2 2 x + + y + + z + ≥ 17 2 2 2 2 x y z 2
Bài 15: Cho trước 2 số dương ;
a b và 2 số dương ;
c d thay đổi sao cho a + b < c + d .Chứng minh: c ( − )2 2 2 a c a + ≥
. Dấu “=” xảy ra khi nào? c + d
a + b − c − d a + b a a a
Bài 16: Cho a ; a ;...; a là các số thực thoả mãn 2 2 2
a + a + ... + a = 3.Chứng minh: 1 2 + + ... n + < 2 1 2 n 1 2 n 2 3 n +1 a b c 3
Bài 17: Cho a; ; b ;
c p;q > 0 .Chứng minh: + + ≥ pb + qc pc + qa pa + qb p + q
Bài 18: Chứng minh rằng với mọi a ∈ (i = 1;2;...;n ta có: i ) + ( n a
1− a )2 + a + (1− a )2 + ... + a + − a ≥ n (1 )2 2 2 2 1 2 2 3 1 2
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 16
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn 3 3 3 2 a b c
2(a + b + c)
Bài 1: Cho ΔABC thoả mãn hệ thức: + + = (1).CM ΔABC đều
br + cR cr + aR ar + bR 9R
Hướng dẫn giải
x = br + cR > 0
Để đơn giản ta đặt: y = cr + aR > 0 (2)
z = ar + bR > 0 3 3 3 2 a b c
2(a + b + c) vậy (1) ⇔ + + = x y z 9R Từ (2) ta có:
ax + by + cz = (ab + bc + ca)(r + R) (3) 3 3 3 a b c y x z y x z 4 4 4 2 2 2 2 2 2
(ax + by + cz)( +
+ ) = a + b + c + ab(a + b ) + bc(b + c ) + ca(c + a ) x y z x y y z z x Theo BĐTCauchy,ta có: 3 3 3 a b c 4 4 4 2 2 2 2
(ax + by + cz)( +
+ ) ≥ a + b + c + 2 . ab ab + .2 bc bc + c .2
a ca ≥ (a + b + c ) x y z 3 3 3 2 2 2 a b c
(a + b + c ) Suy ra : ( + + ) ≥ (theo 3) (4) x y z
(ab +bc + ca)(r + R)
mặt khác ta luôn có (Cauchy): 2 2 2
a + b + c ≥ ab + bc + ca 3 3 3 2 2 2 2 2 2 2 a b c
(a + b + c ) a + b + c nên (4): + + ≥ = 2 2 2 x y z
(a + b + c )(r + R) r + R 2
(a + b + c) ≥ (theo BĐT BCS) 3(r + R) R 9R
Mà R ≥ 2r ⇒ 3(r + R) ≤ 3( + R) = 2 2 3 3 3 2 a b c
2(a + b + c) 3 3 3 2 a b c
2(a + b + c) từ đó: + + ≥ ⇒ + + ≥ x y z 9R
br + cR cr + aR ar + bR 9R
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 17
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn ⎧
⎪a = b = c ⎪⎪
dấu “=” xảy ra khi ⎨R = r ⇔ ΔABC đều ⎪ y y z y x z 2 2 2 2 2 2 ⎪a = b ,b = c ,c = a ⎪⎩ x z y z y x
Bài 2 : CM: 1+ cos Acos B cosC ≥ 3 sin Asin B sin C với A, B,C nhọn
Hướng dẫn giải A B B C C A
Do tgA>0,tagB>0,tgC>0 và tg tg + tg tg + tg tg = 1 2 2 2 2 2 2 A B B C C A 1 Áp dụng BCS ta có: 2 2 2 2 2 2 tg tg + tg tg + tg tg ≥ (1) 2 2 2 2 2 2 3
Mặt khác theo BĐT Cauchy ta có: A B B C C A A B C 2 2 2 3 tg tg + tg tg + tg tg ≥ 3 tg tg tg (2) 2 2 2 2 2 2 2 2 2 A B C 1 ⇔ 3tg tg tg ≤ 2 2 2 3 từ (1)và(2): A B B C C A 4 A B C 2 2 2 2 2 2 1+ tg tg + tg tg + tg tg ≥ ≥ 4 3tg tg tg 2 2 2 2 2 2 3 2 2 2 ⎛ A ⎞⎛ B ⎞⎛ C ⎞ ⎛ A ⎞⎛ B ⎞⎛ C ⎞ A B C 2 2 2 2 2 2 ⇔ 1+ tg 1+ tg 1+ tg + 1− tg 1− tg 1− tg ≥ 8 3tg tg tg ⎜ ⎟⎜ ⎟⎜ ⎟ ⎜ ⎟⎜ ⎟⎜ ⎟ ⎝ 2 ⎠⎝ 2 ⎠⎝ 2 ⎠ ⎝ 2 ⎠⎝ 2 ⎠⎝ 2 ⎠ 2 2 2 2 A 2 B 2 C A B C 1− tg 1− tg 1− tg 2tg 2tg 2tg 2 2 2 2 2 2 ⇔ 1+ . . ≥ 3 . . 2 A 2 B 2 C 2 A 2 B 2 C 1+ tg 1+ tg 1+ tg 1+ tg 1+ tg 1+ tg 2 2 2 2 2 2
⇔ 1+ cos Acos B cosC ≥ 3 sin Asin Bsin C
Dấu “=” xảy ra khi ΔABC đều
Bài 3 : Cho a, b, c, là số đo 3 cạnh Δ .chứng minh rằng a b c T = + + ≥1 b 2 + 2c − a
2c + 2a − b 2a + 2b − c
Hướng dẫn giải
Áp dụng BĐT Bunhiacốpxki cho 6 số: a b c ; ; ; a( b
2 + 2c − a); b(2c + 2a − b); c(2a + b 2 − c) b 2 + 2c − a
2c + 2a − b 2a + b 2 − c
Ta có: T [.a(2b + 2c − a)+ b(2c + 2a − b)+ c(2a + b − c)]≥ (a + b + c)2 2
Sau đó dùng biến đổi tương đương chứng minh:
(a + b+ c)2 ≥ 4ab +4bc +4ca –a2 –b2 - c2 Từ đó suy ra đpcm.
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 18
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn Bài 4 : Cho ABC Δ
và đường tròn nội tiếp Δ , các tiếp tuyến của đường tròn song song với 3 cạnh của Δ nhỏ S
và có diện tích S1; S2; S3. Gọi S là diện tích ΔABC . Chứng minh: S + S + S ≥ 1 2 3 3
Hướng dẫn giải Giả sử S1= SAMN ha − 2r Ta có: AM Δ
N đồng dạng ABC Δ
với tỉ số đồng dạng là:
với r là bán kính đường tròn nội tiếp và h ha a là
đường cao kẻ từ đỉnh A. 2 2 S
⎛ ha − 2r ⎞ ⎛ a ⎞ Ta có: 1 = ⎜ ⎟ = 1 ⎜⎜ − ⎟⎟ S ⎝ ha ⎠ ⎝ p ⎠ 1 r a (Vì S = aha = 2 pr ⇒ = với p là nửa chu vi) 2 ha p S1 a Vậy: =1− S p S S 2 b 3 c Tương tự: =1− ; =1− S p S p S + S + S a + b + c Do đó: 1 2 3 = 3 − = 1 S p Áp dụng BĐT Bun ta có: 2 S = ( . 1 S + . 1 S + . 1 S
≤ 1 +1 +1 S + S + S 1 2 3 ) ( 2 2 2)( 1 2 3) ⇒ S
S + S + S ≥
(đpcm). Dấu “=” xảy ra khi ABC Δ đều 1 2 3 3
Bài 5 : Cho ΔABC và 1 điểm Q nào đó ở trong Δ . Qua Q kẻ đường thẳng song song với AB cắt AC ở M và cắt
BC ở N. Qua điểm Q kẻ đường thẳng song song với AC cắt AB ở F; cắt BC ở E. Qua E kẻ đường thẳng song
song với BC cắt AC ở P, cắt AB ở R. Kí hiệu S1= dt(QMP); S2 = dt(QEN); S3 = dt(QFR) và S = dt(ABC).Chứng minh: 1
a) S = ( S + S + S )2 b) S + S + S ≥ S 1 2 3 1 2 3 3
Hướng dẫn giải MP a) Ta có: QM Δ
P đồng dạng B Δ AC (tỉ số ). AC 2 S ⎛ MP ⎞ S MP Suy ra 1 1 = ⇒ = ⎜ ⎟ . S ⎝ AC ⎠ S AC S PC S AM Tương tự 2 3 = ; = S AC S AC S + S + S
MP + PC + AM AC Do đó: 1 2 3 = = = 1 S AC AC
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 19
Tröôøng THPT Chuyeân Tieàn Giang www.MATHVN.com GV Ñoã Kim Sôn
Suy ra: S = S + S + S ⇒ S = ( S + S + S )2 1 2 3 1 2 3
b) Áp dụng BĐT Bunhiacôpxki ta có:
S = (1. S +1. S +1. S )2 ≤ ( 2 2 2 1 +1 +1 S + S + S 1 2 3 )( 1 2 3) 1
Suy ra S + S + S ≥ S 1 2 3 3
Dấu “=” xảy ra khi S = S = S ⇔ Q là trọng tâm ABC Δ 1 2 3
Bài 6 : Cho a , b , c là 3 cạnh của tam giác.Chứng minh: a b c + +
≥ a + b + c
b + c − a
c + a − b
a + b − c
Hướng dẫn giải b
⎧ + c − a = x > 0 ⎪
Đặt ⎨c + a − b = y > 0
⎪a +b −c = z > 0 ⎩
Khi đó ta cần chứng minh: y + z z + x x + y y + z z + x x + y + + ≥ + + 2 x 2 y 2 z 2 2 2
⇔ yz ( y + z) + zx(z + x) + xy(x + y) ≥ 2 xyz ( x + y + y + z + x + z ) (1)
Dễ thấy VT (1) ≥ 2( xy + yz + zx) (2)
Theo BĐT Bunhiacôpxki ta có:
( x+ y + y + z + z + x)2 ≤ 6(x+ y + z)
⇒ x + y + y + z + z + x ≤ 6(x + y + z)
VT (2) ≤ 2 3xyz ( x + y + z) (3) Rõ ràng ta có 2 2 2 2 2 2
x y + x y + x y ≥ xyz ( x + y + z)
⇒ ( xy + yz + zx)2 ≥ 3xyz (x + y + z)
⇒ xy + yz + zx ≥ 3xyz (x + y + z) (4)
Từ (1) (2) (3) (4) ⇒ đpcm. Dấu “=” xảy ra khi a = b = c
Bài 7 : Cho ∆ABC. Chứng minh : a2b(a – b) +b2c(b – a) + c2a(c – a) ≥ 0
( Trích đề thi vô địch toán quốc tế 1983 )
Hướng dẫn giải
Gọi A’; B’; C’ là các tiếp điểm:
Chuyeân ñeå boài döôõng hoïc sinh gioûi K10 www.MATHVN.com Page 20