Bài tập chương 4, 5 Nhiệt động lực học và chu trình động cơ | Môn Truyền nhiệt và nhiệt động - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315
PHẦN I – NHIỆT ĐỘNG LỰC KỸ THUẬT
CHƯƠNG IV – CÁC CHU TRÌNH NHIỆT ĐỘNG
1. Các đại lượng trong chu trình nhiệt động - Công của chu trình: 𝑛 𝑛
𝑙0 = ∑(𝑙𝑖) = ∑(𝑙𝑘𝑡𝑖) 𝑖=1 𝑖=1 - Hiệu suất nhiệt:
𝜂𝑡 = 𝜂 = 𝑞𝑙01 = 𝑞1−𝑞1|𝑞2| = 1 − |𝑞𝑞21|
- Hệ số làm lạnh: 𝑞2 𝑞2 𝜀 = = |𝑙0| |𝑞1| − 𝑞2 - Hệ số bơm nhiệt: 𝑞1 𝑞1 𝜑 = = |𝑙0| |𝑞1| − 𝑞2
- Quan hệ giữa ε và φ: 𝜑 = 𝜀 + 1
2. Động cơ nhiệt và máy làm lạnh Carnot - Động
cơ nhiệt (chu trình thuận): 𝑇2 𝜂𝑐 = 1 − 𝑇1
- Máy làm lạnh (chu trình nghịch): 𝑇2 𝜀𝑐 = 𝑇1 − 𝑇2
3. Động cơ đốt trong
- Định nghĩa: Động cơ đốt trong là một loại động cơ nhiệt, tạo ra công cơ học
bằng cách đốt nhiên liệu bên trong động cơ.
a) Chu trình động cơ đốt trong cấp nhiệt đẳng tích (chu trình Otto) - Tỷ số nén: 𝑣1 𝜀 = lOMoAR cPSD| 58970315 𝑣2 - Tỷ số tăng áp: 𝑝3 𝜆 = 𝑝2 - Hiệu suất nhiệt: 1
𝜂𝑡,𝑂𝑡𝑡𝑜 = 1 − 𝜀 𝑘−1
b) Chu trình động cơ đốt trong cấp nhiệt đẳng áp (chu trình Diesel) - Tỷ số nén: 𝑣1 𝜀 = 𝑣2 - Tỷ số giãn nở sớm: 𝑣3 𝜌 = 𝑣2 - Hiệu suất nhiệt: 𝜌𝑘 − 1
𝜂𝑡,𝐷𝑖𝑒𝑠𝑒𝑙 = 1 − 𝑘 . 𝜀𝑘−1. (𝜌 − 1)
c) Chu trình động cơ đốt trong cấp nhiệt hỗn hợp (chu trình Diesel hiện nay) - Tỷ số nén: 𝑣1 𝜀 = 𝑣2 - Tỷ số tăng áp: 𝑝3 𝜆 = 𝑝2 - Tỷ số giãn nở sớm: 𝑣4 𝜌 = 𝑣3 - Hiệu suất nhiệt: 𝜆. 𝜌𝑘 − 1 lOMoAR cPSD| 58970315
𝜂𝑡 = 1 − 𝜀𝑘−1. (𝜆 − 1) + 𝑘. 𝜆. 𝜀𝑘−1. (𝜌 − 1)
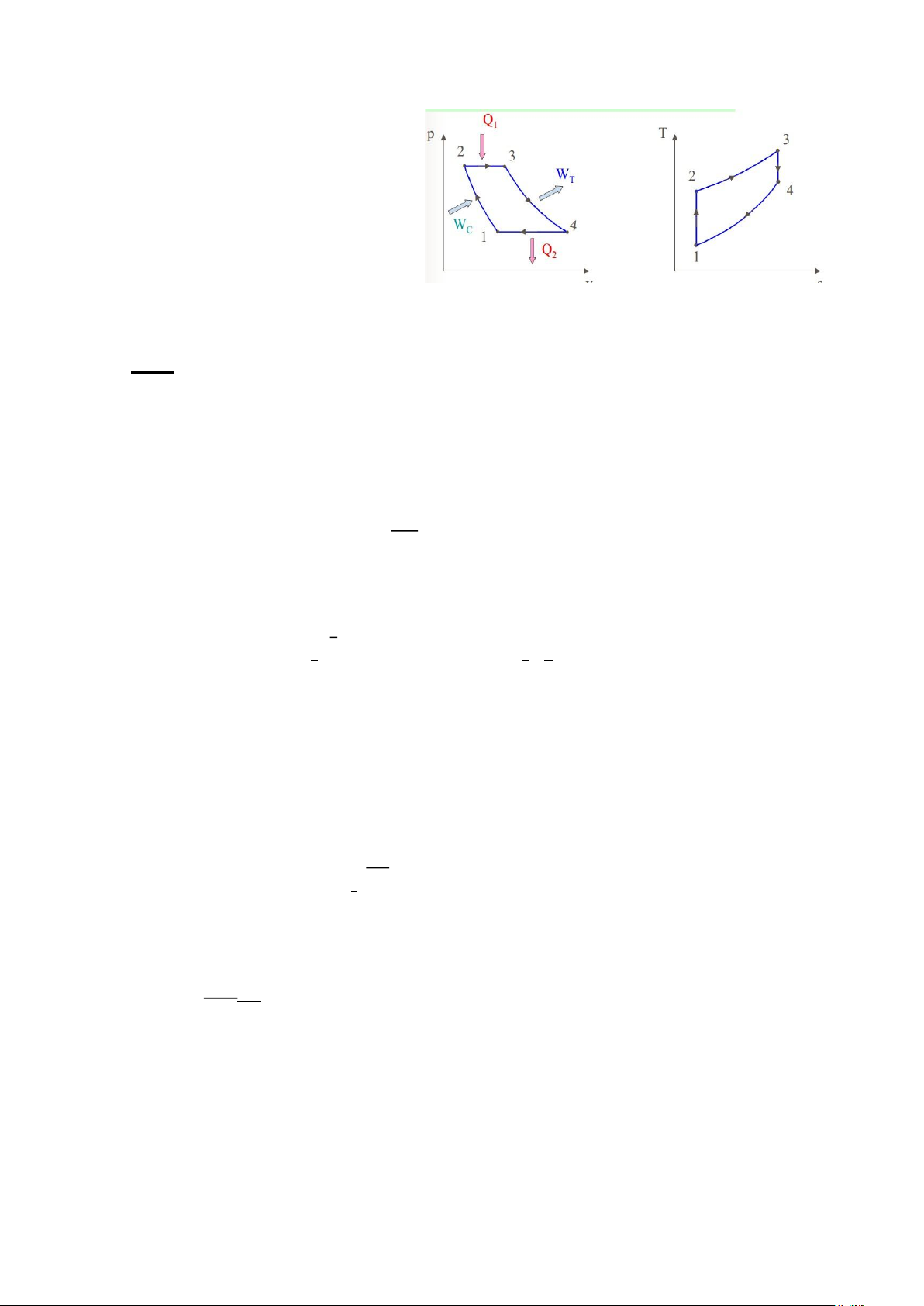
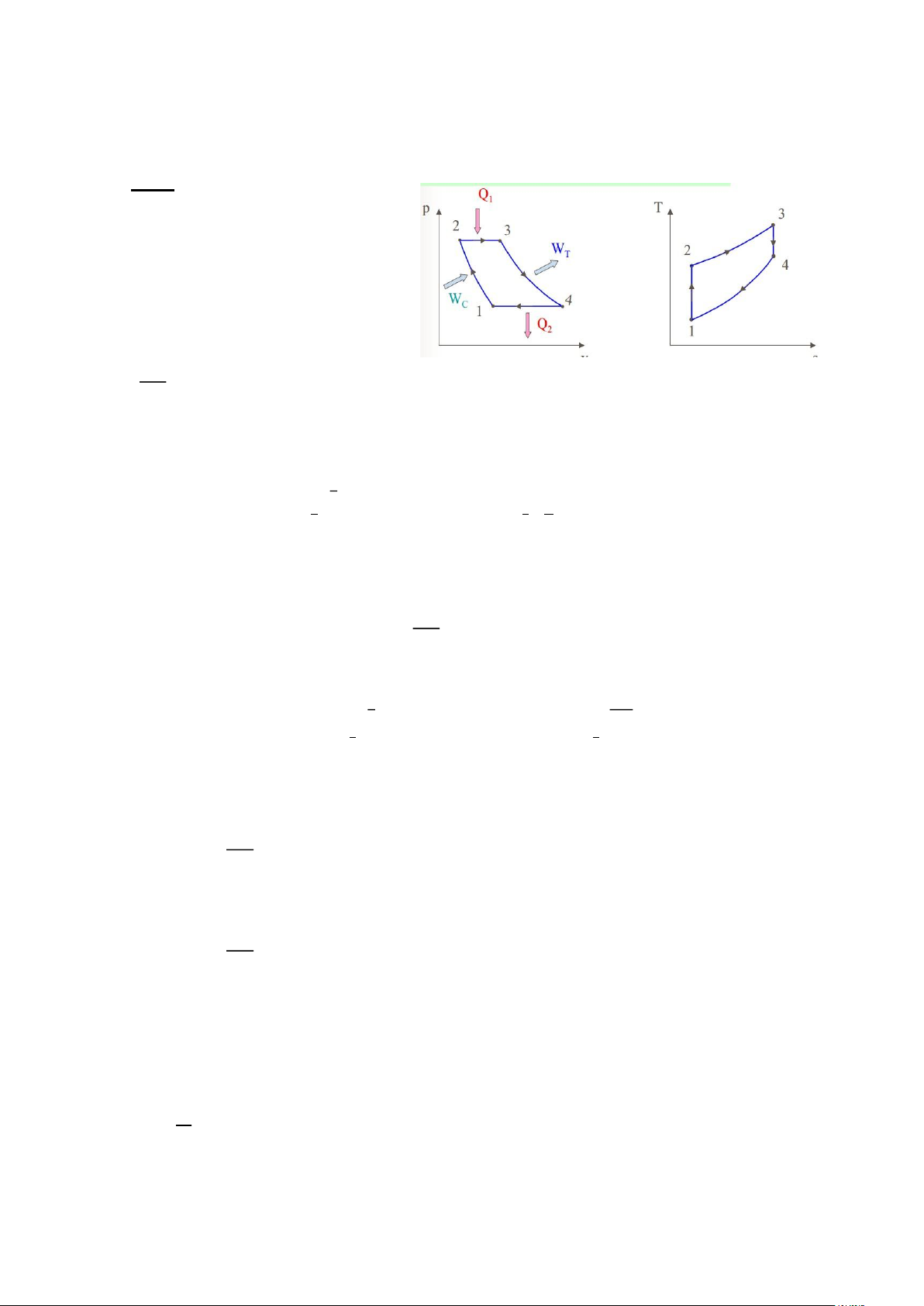
4. Chu trình động cơ turbine khí (Chu trình
Brayton) - Tỷ số tăng áp không khí trong máy nén: 𝑝2 𝛽 = 𝑝1 - Tỷ số giãn nở sớm: 𝑣3 𝜌 = 𝑣2 - Hiệu suất nhiệt: 1 𝜂𝑡 = 1 − 𝑘−1 𝛽 𝑘
- Hiệu suất nhiệt khi có bộ hồi nhiệt: 𝑇1 𝑘−1 𝜂𝑡 = 1 − ( ) . 𝛽 𝑘 𝑇3
5. Chu trình động cơ phản lực
- Tỷ số tăng áp không khí trong máy nén: 𝑝3 𝛽 = 𝑝1 - Tỷ số giãn nở sớm: 𝑣4 𝜌 = 𝑣3 - Hiệu suất nhiệt: 1 𝜂𝑡 = 1 − 𝑘−1 𝛽 𝑘
6. Chu trình động cơ tên lửa - Tỷ số tăng áp: 𝑝2 𝛽 = lOMoAR cPSD| 58970315 𝑝1 - Tỷ số giãn nở sớm: 𝑣3 𝜌 = 𝑣2 - Hiệu suất nhiệt: 𝑇3 − 𝑇4 𝜌 1 𝜂𝑡
= 𝑇3 − 𝑇2 = 𝜌 − 1 (1 − 𝛽𝑘−𝑘1 )
7. Chu trình nhà máy nhiệt điện (chu trình
Rankine) - Nhiệt lượng q1 nhận được từ lò hơi: 𝑞1 = 𝑖1 − 𝑖4 -
Nhiệt lượng q2 nhả ra bình ngưng: |𝑞2| = 𝑖2 − 𝑖3 - Hiệu suất nhiệt: 𝑙 |𝑞2| 𝑖2 − 𝑖3
(𝑖1 − 𝑖2) − (𝑖4 − 𝑖3) 𝜂𝑡 = = 1 − = 1 − = 𝑞1 𝑞1 𝑖1 − 𝑖4 𝑖1 − 𝑖4
8. Chu trình máy làm lạnh (nén hơi) lý tưởng - Hệ số làm lạnh: 𝑞2 𝑖1 − 𝑖4 𝜀 = = |𝑙0| 𝑖2 − 𝑖1 - Hệ số bơm nhiệt: 𝑞1 𝑖2 − 𝑖3 𝜑 = = |𝑙0| 𝑖2 − 𝑖1 - Năng suất nhiệt: 𝑄0 = 𝐺. 𝑞2 - Công suất máy nén: 𝑁 = 𝐺. |𝑙0| lOMoAR cPSD| 58970315 BÀI TẬP
BÀI TẬP CÓ LỜI GIẢI
CHU TRÌNH ĐỘNG CƠ ĐỐT TRONG
Bài 4.1: Một chu trình động cơ đốt trong cấp nhiệt đẳng tích, môi chất là khí 2 nguyên
tử với k =1,4 và R = 287 J/kg.K. Áp suất điểm thấp nhất chu trình 1 bar, nhiệt độ thấp
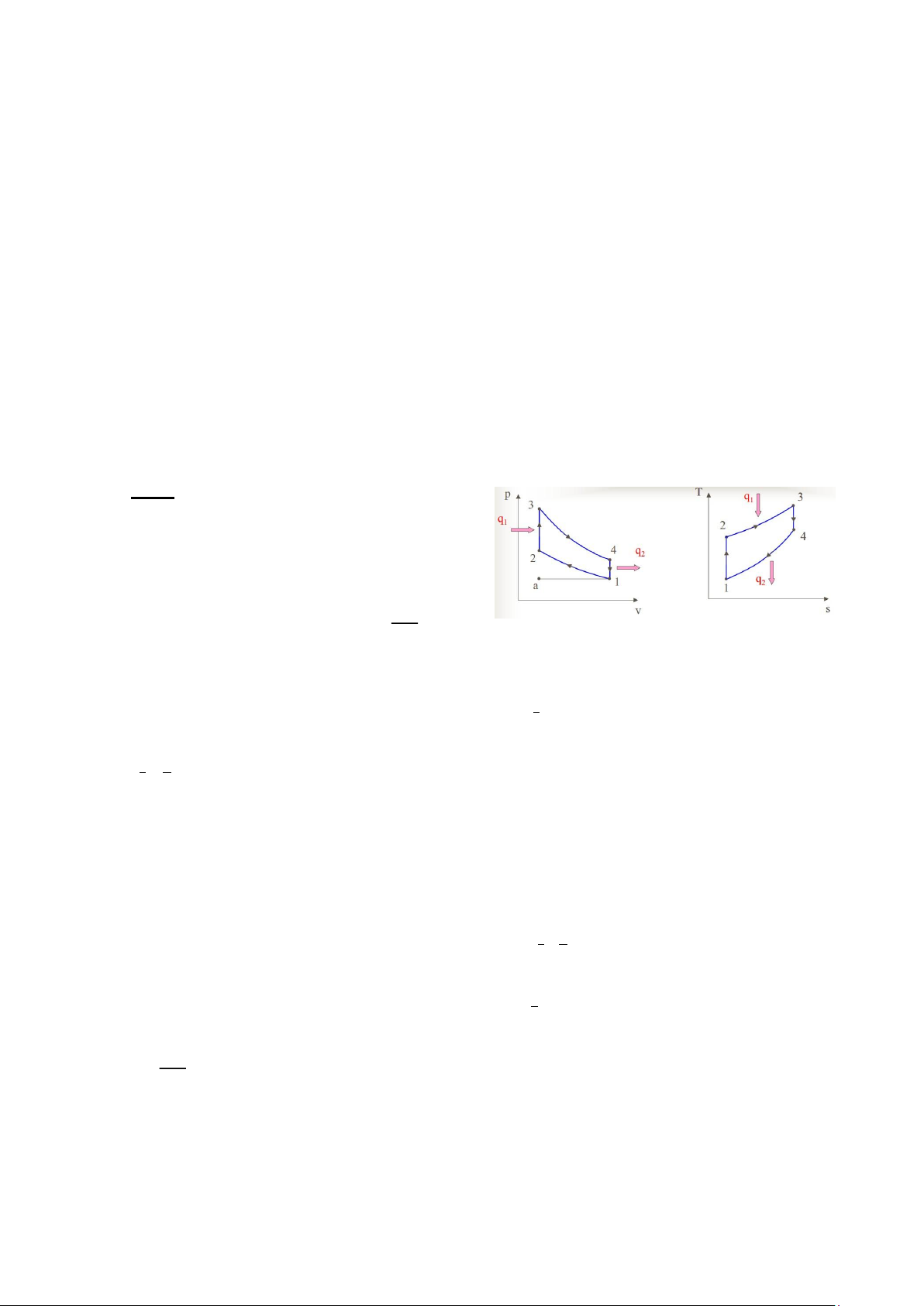
nhất 320K, tỷ số nén ε = 4, và tỷ số tăng áp λ = 4. a) Biểu diễn chu trình trên p-v và T- s.
b) Xác định thông số các điểm nút.
c) Xác định nhiệt lượng cung cấp cho chất môi giới q1 và nhiệt nhả ra môi trường q2.
d) Xác định hiệu suất nhiệt chu trình. Giải: a)
b) Thông số các trạng thái + Trạng thái 1:
p1 = 1 bar; T1 = 320 K => 𝑣1 = 𝑅 𝑝.𝑇11 = 0,915 m3/kg.
+ Trạng thái 2: v2 = v1/ε = 0,23 m3/kg; 𝑝2 = 𝑝1. (𝑣𝑣1)𝑘 = 6,96 bar; 𝑇2 = 𝑝2𝑅𝑣2 = 558 K. 2 + Trạng thái 3:
v3 = v2 = 0,23 m3/kg; p3 = λ.p2 = 27,84 bar; 𝑇3 = 𝑝𝑃32𝑇2 = 2232 K.
+ Trạng thái 4: v4 = v1 = 0,915 m3/kg; 𝑇4 = 𝑇3. (𝑣𝑣3)𝑘−1 = 1282 K; 𝑝4 = 𝑅 𝑣.𝑇44 = 4 bar. 4
c) + Nhiệt cung cấp cho môi chất lOMoAR cPSD| 58970315
𝑞1 = 𝑞23 = 𝐶𝑣. (𝑇3 − 𝑇2) = 1201 kJ/kg.
+ Nhiệt môi chất nhả ra môi trường
𝑞2 = 𝑞41 = 𝐶𝑣. (𝑇1 − 𝑇4) = −690 kJ/kg. d)
Hiệu suất nhiệt của chu trình:
𝜂𝑡 = 1 − |𝑞𝑞21| = 0,425 = 42,5%.
Bài 4.2: Một chu trình Otto lý tưởng có tỷ số nén là 10,5 đưa không khí vào ở 90 kPa
và 40 oC, và được lặp lại 2500 lần trong mỗi phút. Sử dụng các nhiệt dung riêng không
đổi ở nhiệt độ phòng, hãy xác định hiệu suất nhiệt của chu trình này và tốc độ nhận
nhiệt nếu chu trình này tạo ra công suất 90 kW. Giải:
+ Tính chất của không khí ở nhiệt độ phòng: k = 1,4; R = 0,287 kJ/kg.K =>
Cv = R/(k-1) = 0,72 kJ/kg.K và Cp = k.Cv = 1,005 kJ/kg.K.
+ Hiệu suất nhiệt của chu trình: 1 𝜂𝑡 = 1 − 𝜀 𝑘−1 = 0,61 = 61%. + Tốc độ nhận nhiệt: 𝑙 𝑃
𝑞1 = 𝜂𝑡 = 𝜂𝑡 = 148 kW.
Bài 4.3: Một chu trình động cơ đốt trong cấp nhiệt đẳng áp, môi chất là không khí với
k =1,4 và R = 287 J/kg.K. Các thông số cơ bản ở trạng thái trước khi nén là 1 bar và
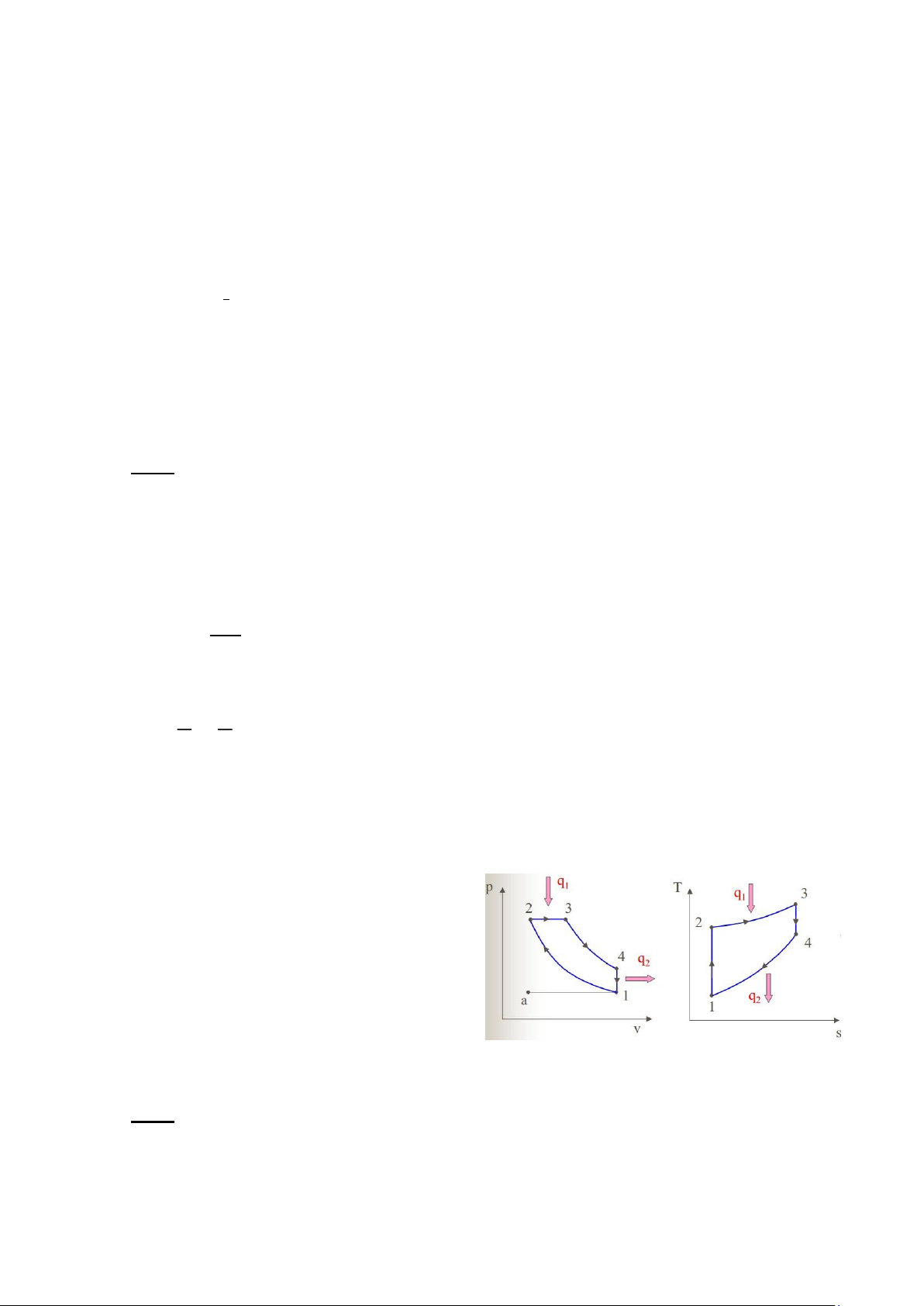
350K, tỷ số nén ε = 20, và tỷ số giãn nở sớm ρ = 2. a) Biểu diễn chu trình trên p-v và T-s.
b) Xác định thông số các điểm nút.
c) Xác định nhiệt lượng cung cấp cho
chất môi giới q1 và nhiệt nhả ra môi trường q2.
d) Xác định hiệu suất nhiệt chu trình. Giải: a)
b) Thông số các trạng thái + Trạng thái 1: lOMoAR cPSD| 58970315
p1 = 1 bar; T1 = 350 K => 𝑣1 = 𝑅 𝑝.𝑇11 = 1,0045 m3/kg. + Trạng thái 2:
v2 = v1/ε = 0,05 m3/kg; 𝑝2 = 𝑝1. (𝑣𝑣12)𝑘 = 66,29 bar; 𝑇2 = 𝑝2𝑅𝑣2 = 1155 K. + Trạng thái 3:
v3 = ρ.v2 = 0,1 m3/kg; p3 = p2 = 66,29 bar; 𝑇3 = 𝑣𝑣32𝑇2 = 2310 K. + Trạng thái 4:
v4 = v1 = 1,0045 m3/kg; 𝑝4 = 𝑝3. (𝑣𝑣34)𝑘 = 2,64 bar; 𝑇4 = 𝑝4𝑅.𝑣4 = 924 K.
c) + Nhiệt cung cấp cho môi chất
𝑞1 = 𝑞23 = 𝐶𝑝. (𝑇3 − 𝑇2) = 1160,2 kJ/kg.
+ Nhiệt môi chất nhả ra môi trường
𝑞2 = 𝑞41 = 𝐶𝑣. (𝑇1 − 𝑇4) = −411,6 kJ/kg. d)
Hiệu suất nhiệt của chu trình:
𝜂𝑡 = 1 − |𝑞𝑞21| = 0,65 = 65%.
Bài 4.4: Một chu trình lý tưởng với động cơ đốt trong cấp nhiệt hỗn hợp, môi chất là
không khí có thông số khi nạp là 1 bar và 27 oC, tỷ số nén ε = 12,7, tỷ số tăng áp λ =
1,4 và tỷ số giãn nở sớm ρ = 1,6. Cho biết Cp = 1,01 kJ/kg.K; Cv = 0,72 kJ/kg.K. a)
Biểu diễn chu trình trên p-v và T-s.
b) Xác định thông số các điểm nút.
c) Xác định nhiệt lượng cung cấp cho chất môi giới q1 và nhiệt nhả ra môi trường q2.
d) Xác định công hiệu suất nhiệt chu trình. Giải: a)
b) Thông số các trạng thái + Trạng thái 1: lOMoAR cPSD| 58970315
p1 = 1 bar; T1 = 300 K => 𝑣1 = 𝑅 𝑝.𝑇11 = 0,861 m3/kg. + Trạng thái 2: 𝑣1 𝑘
bar; 𝑝 v2 = v1/ε = 0,068 m3/kg; 𝑝2 = 𝑝1. (𝑣 ) = 35,1 𝑇2 = 2𝑅𝑣2 = 831,7 K. 2 + Trạng thái 3:
v3 = v2 = 0,068 m3/kg; p3 = λ.p2 = 49,14 bar; 𝑇3 = 𝑝3𝑅𝑣3 = 1164,3 K. + Trạng thái 4:
v4 = ρ.v3 = 0,1088 m3/kg; p4 = p3 = 49,14 bar; 𝑇4 = 𝑣𝑣43𝑇3 = 1826,9 K. + Trạng thái 5: 𝑣4 𝑘
bar; 𝑝 v5 = v1 = 0,861 m3/kg; 𝑝5 = 𝑝4. (𝑣 ) = 2,71
𝑇5 = 5𝑅.𝑣5 = 814,4 K. 5
c) + Nhiệt cung cấp cho môi chất
𝑞1 = 𝑞23 + 𝑞34 = 𝐶𝑣. (𝑇3 − 𝑇2) + 𝐶𝑝. (𝑇4 − 𝑇3) = 908,7 kJ/kg.
+ Nhiệt môi chất nhả ra môi trường
𝑞2 = 𝑞51 = 𝐶𝑣. (𝑇1 − 𝑇5) = −370,4 kJ/kg. d) + Công của chu trình:
𝑙 = 𝑞1 + 𝑞2 = 538,5 kJ/kg
Hiệu suất nhiệt của chu trình: 𝑙
𝜂𝑡 = 𝑞 1 = 0,59 = 59%.
CHU TRÌNH TURBINE KHÍ
Bài 4.5: Chu trình turbine khí cấp nhiệt đẳng áp không khí vào máy nén có áp suất 0,1 lOMoAR cPSD| 58970315
MPa, nhiệt độ 15 oC, ra khỏi máy
có áp suất 0,5 MPa, nhiệt độ điểm
cao nhất trong chu trình là 900 oC.
a) Biểu diễn chu trình trên đồ thị p-v, T-s.
b) Xác định nhiệt độ, áp suất ở các v s
điểm nút của chu trình.
c) Tính hiệu suất chu trình. Giải: a)
b) + Không khí nên: k = 1,4; R = 287 J/kg.K. + Trạng thái 1:
p1 = 1 bar; T1 = 288 K => 𝑣1 = 𝑅 𝑝.𝑇11 = 0,83 m3/kg. + Trạng thái 2: 1
p2 = 5 bar; 𝑣2 = 𝑣1. (𝑝𝑝12)𝑘 = 0,263 m3/kg; 𝑇2 = 𝑝2𝑅𝑣2 = 458 K. + Trạng thái 3:
p3 = p2 = 5 bar; 𝑇3 = 1173 K. + Trạng thái 4: 1−𝑘
p4 = p1 = 1 bar; 𝑇4 = 𝑇3. (𝑝𝑝34) 𝑘 = 741 K.
c) Hiệu suất của chu trình: 1 𝜂𝑡 = 1 − 𝑘−1 = 0,37 = 37%. 𝛽 𝑘
Bài 4.6: Cho một hệ thống turbine khí làm việc theo chu trình cấp nhiệt và nhả nhiệt
đẳng áp, nén và giãn nở đoạn nhiệt, môi chất là không khí có nhiệt dung riêng không
đổi, có các thông số: p1 = 1 bar; t1 = 17 oC, p2 = 8 bar; t3 = 600 oC.
a) Biểu diễn chu trình trên đồ thị p-v, T-s và xác định các thông số cơ bản ở các điểm nút của chu trình. lOMoAR cPSD| 58970315
b) Tính nhiệt lượng trao đổi giữa môi chất với các nguồn nhiệt.
c) Tính công và hiệu suất chu trình. Giải:
a) + Vẽ các đồ thị + Không khí
nên: k = 1,4; R = 287 J/kg.K.
+ Trạng thái 1: p1 = 1 bar; T1 = 290 K => 𝑣 v 1 = s 𝑅 .𝑇1 = 0,8323 m3/kg. 𝑝1 + Trạng thái 2: 1
p2 = 8 bar; 𝑣2 = 𝑣1. (𝑝𝑝12)𝑘 = 0,188 m3/kg; 𝑇2 = 𝑝2𝑅𝑣2 = 525 K. + Trạng thái 3:
p3 = p2 = 8 bar; 𝑇3 = 873 K; 𝑣3 = 𝑅 𝑝.𝑇33 = 0,313 m3/kg. + Trạng thái 4: 1 1−𝑘
p4 = p1 = 1 bar; 𝑣4 = 𝑣3. (𝑝𝑝34)𝑘 = 1,38 m3/kg; 𝑇4 = 𝑇3. (𝑝𝑝34) 𝑘 = 482 K.
b) + Nhiệt cung cấp cho môi chất 𝑘𝑅 𝑞1 = 𝑞23 = 𝑘
−1 . (𝑇3 − 𝑇2) = 350 kJ/kg.
+ Nhiệt môi chất nhả ra môi trường 𝑘𝑅 𝑞2 = 𝑞41 = 𝑘
−1 . (𝑇1 − 𝑇4) = −193 kJ/kg. c) + Công của chu trình:
𝑙 = 𝑞1 + 𝑞2 = 157 kJ/kg
Hiệu suất nhiệt của chu trình: 𝑙
𝜂𝑡 = 𝑞 1 = 0,45 = 45%.
CHU TRÌNH NHÀ MÁY NHIỆT ĐIỆN lOMoAR cPSD| 58970315
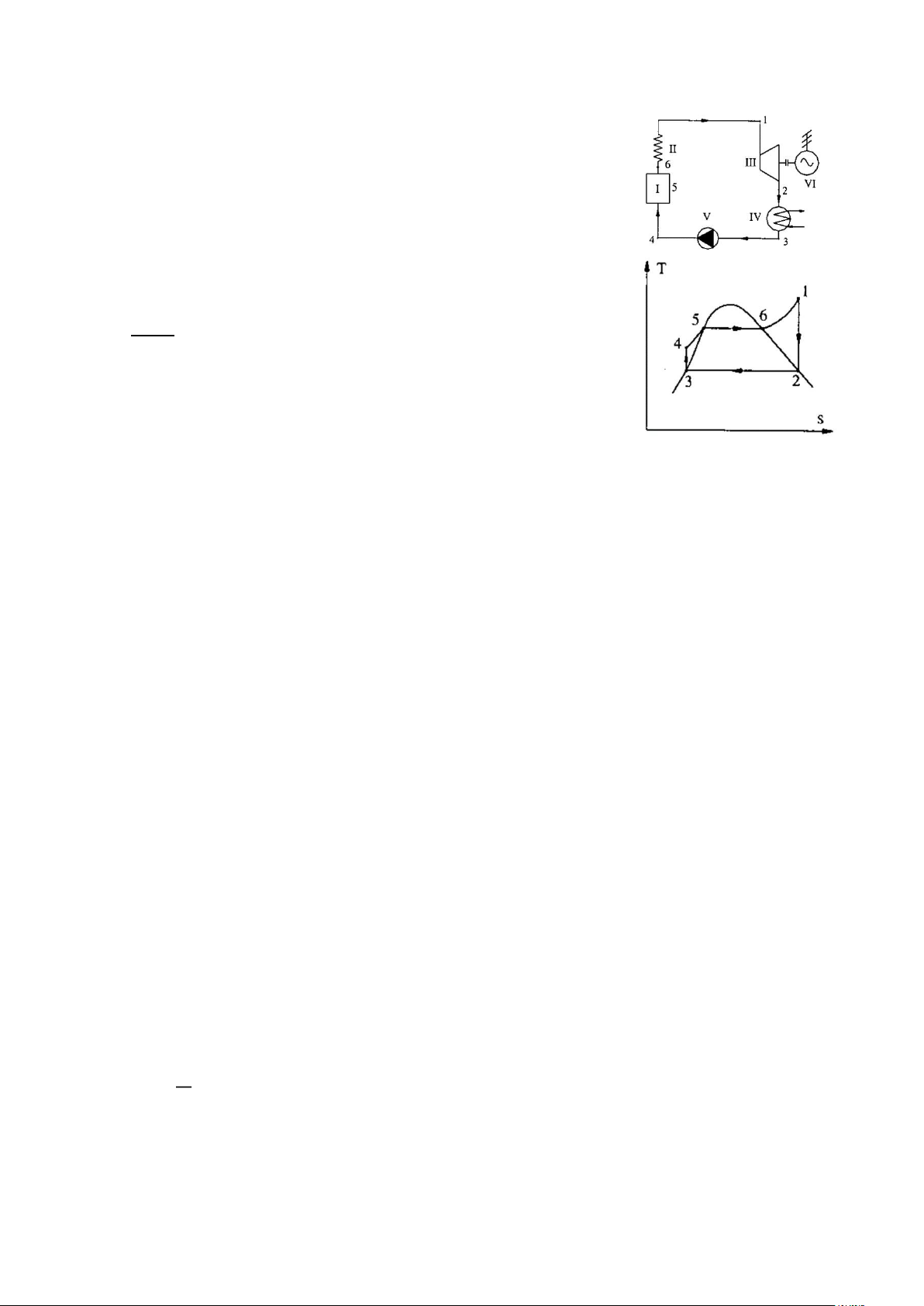
Bài 4.7: Chu trình Rankine hơi nước, hơi nước từ lò hơi vào turbine là hơi bão hòa
khô có áp suất 1 MPa, áp suất của hơi từ turbine vào bình
ngưng là 10 kPa, ra khỏi bình là nước bão hòa.
a) Biểu diễn chu trình trên đồ thị p-v, T-s, và i-s.
b) Tính entanpi của môi chất tại các điểm nút.
c) Tính công, nhiệt lượng trao đổi và hiệu suất chu trình. Giải:
a) Trạng thái (6) ≡ (1), vẽ hình
b) + Trạng thái (6) ≡ (1) hơi bão hòa khô (phụ lục 4) p1 = 1
MPa = 10 bar => i1 = 2778 kJ/kg và s1 = 6,587 kJ/kg.K.
+ Trạng thái (2): hơi ẩm (phụ lục 4) p2 = 0,1 bar và s2 = s1 = 6,587
kJ/kg.K => x = (s2 – s’)/(s” – s’) = 0,7 => i2 = i’ + x.(i” – i’) = 1866,4 kJ/kg.
+ Trạng thái (3): nước bão hòa (phụ lục 4) p3 = p2 = 0,1 bar
=> i3 = 191,9 kJ/kg và s3 = 0,6492 kJ/kg.K.
+ Trạng thái (4): nước chưa sôi (phụ lục 5) p4 = p1 = 10 bar và s4
= s3 = 0,6492 kJ/kg.K => i4 = 193,35 kJ/kg.
c) + Nhiệt nhận được từ lò hơi: q1 = i1 – i4 = 2584,65 kJ/kg.
+ Nhiệt nhả ra bình ngưng: q2
= i3 – i2 = -1674,5 kJ/kg.
+ Công chu trình thực hiện: l
= q1 + q2 = 910,15 kJ/kg. + Công của bơm:
lb = i4 – i3 = 1,45 kJ/kg.
+ Hiệu suất của chu trình: 𝑙
𝜂𝑡 = 𝑞 1 = 0,352 = 35,2%.
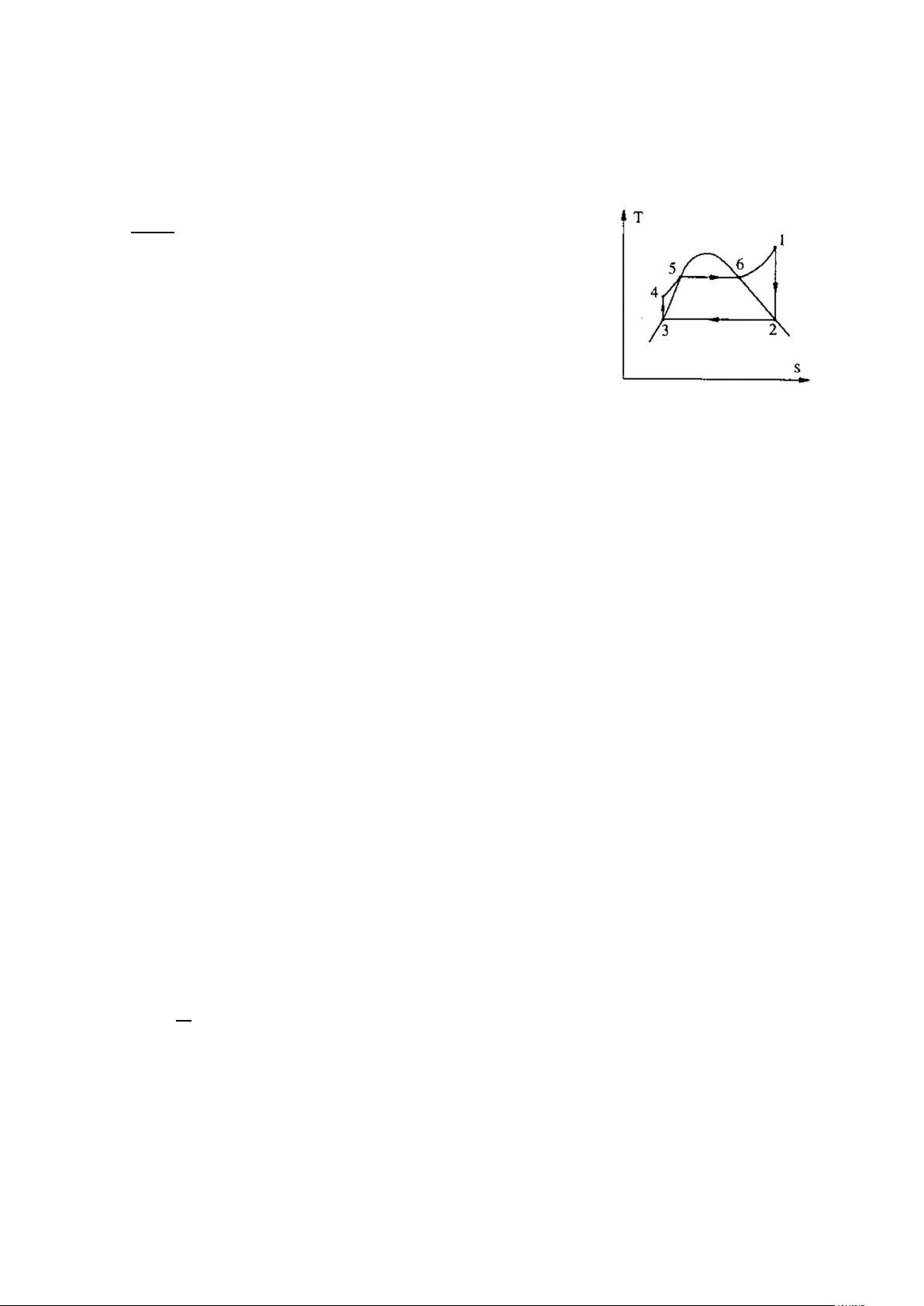
Bài 4.8: Chu trình Rankine hơi nước với thông số hơi vào turbine là 30 bar và nhiệt độ
400 oC, áp suất trong bình ngưng là 0,04 bar. lOMoAR cPSD| 58970315
a) Biểu diễn chu trình trên đồ thị p-v, T-s, và i-s.
b) Tính entanpi của môi chất tại các điểm nút.
c) Tính công, nhiệt lượng trao đổi và hiệu suất chu trình. Giải: a) b)
+ Trạng thái (1) hơi quá nhiệt (phụ lục 5) p1 = 30
bar => i1 = 3229 kJ/kg và s1 = 6,916 kJ/kg.K.
+ Trạng thái (2): hơi ẩm (phụ lục 4) p2 = 0,04 bar và s2 =
s1 = 6,916 kJ/kg.K => x = (s2 – s’)/(s” – s’) = 0,807 => i2 = i’ + x.(i” – i’) = 2084 kJ/kg.
+ Trạng thái (3): nước bão hòa (phụ lục 4) p3 = p2 = 0,04 bar
=> i3 = 121,42 kJ/kg và s3 = 0,4225 kJ/kg.K.
+ Trạng thái (4): lỏng chưa sôi (phụ lục 5) p4 = p1 = 30 bar và s4
= s3 = 0,4225 kJ/kg.K => i4 = 125,15 kJ/kg. c)
+ Nhiệt nhận được từ lò hơi: q1 = i1 – i4 = 3103,85 kJ/kg.
+ Nhiệt nhả ra bình ngưng: q2
= i3 – i2 = -1962,58 kJ/kg.
+ Công chu trình thực hiện: l
= q1 + q2 = 1141,27 kJ/kg.
+ Công của bơm: lb =
i4 – i3 = 3,73 kJ/kg.
+ Hiệu suất của chu trình: 𝑙
𝜂𝑡 = 𝑞 1 = 0,368 = 36,8%.
CHU TRÌNH MÁY LẠNH MÁY NÉN HƠI
Bài 4.9: Tủ lạnh sử dụng chất làm lạnh – 134a làm môi chất và hoạt động theo chu
trình làm lạnh nén hơi lý tưởng trong khoảng 0,14 đến 0,8 MPa. Nếu tốc độ dòng
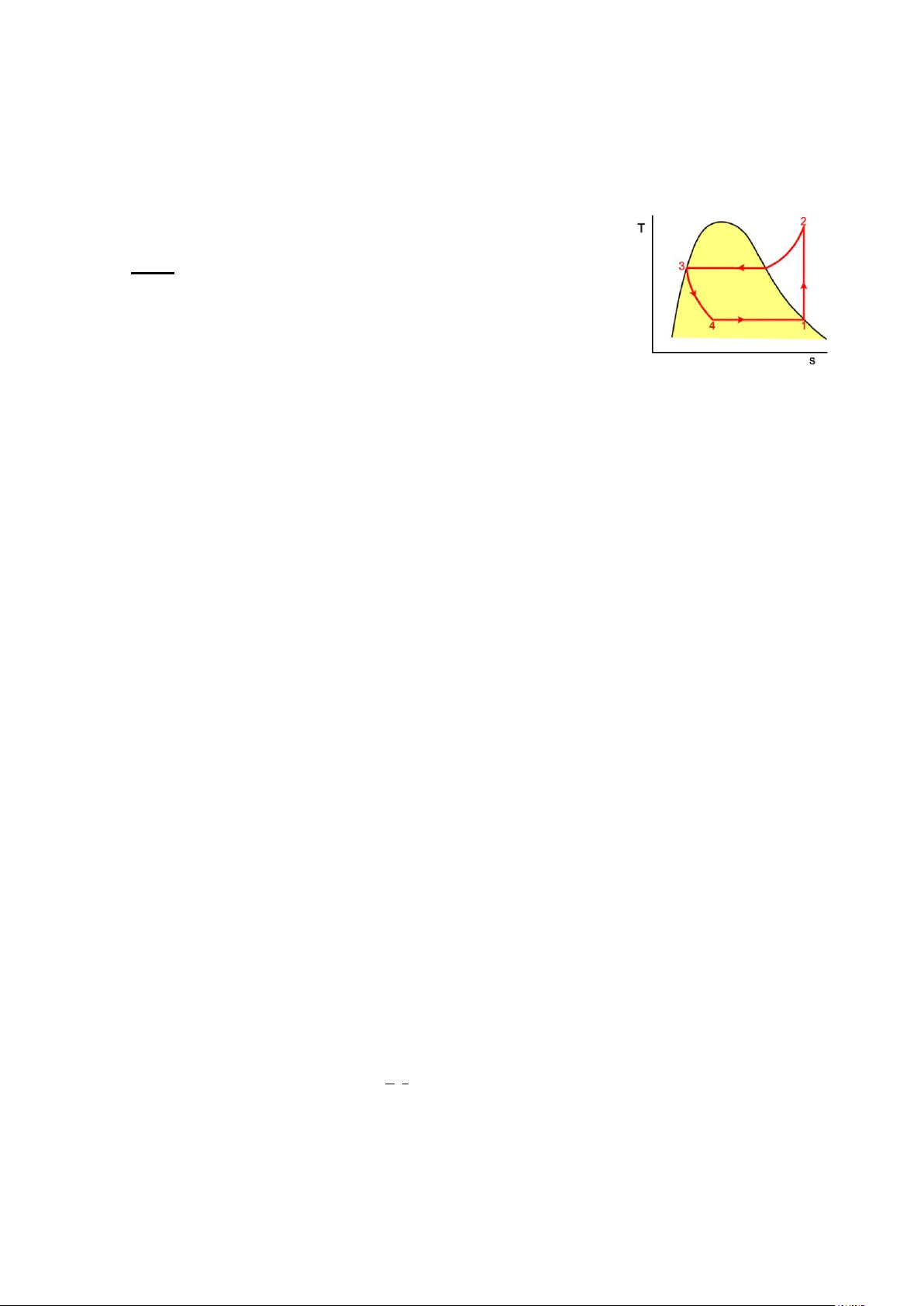
khối lượng của chất làm lạnh là 0,05 kg/s, hãy: a) Vẽ đồ thị chu trình trên đồ thị T-s. lOMoAR cPSD| 58970315
b) Xác định entanpi của các điểm nút.
c) Xác định tốc độ lấy nhiệt từ buồng lạnh và công suất đầu vào máy nén.
d) Xác định tốc độ thải nhiệt ra môi trường.
e) Tính hệ số làm lạnh của tủ lạnh. Giải: a)
b) Chu trình máy làm lạnh nén hơi lý tưởng, do đó máy nén
đẳng nhiệt, chất làm lạnh rời bình ngưng dưới dạng chất
lỏng bão hòa và đi vào máy nén dưới dạng hơi bão hòa.
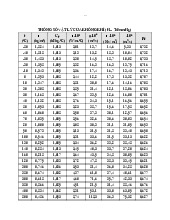
Từ bảng chất làm lạnh – 134a (A-11-A-13), entanpi của các trạng thái được xác định.
+ Trạng thái (1): hơi bão hòa (A-12) p1 = 0,14 MPa => i1 = i” =
239,19 kJ/kg và s1 = s” = 0,94467 kJ/kg.K.
+ Trạng thái (2): hơi quá nhiệt (A-13) p2 = 0,8 MPa và s2 = s1 =
0,94467 kJ/kg.K => i2 = 275,40 kJ/kg.
+ Trạng thái (3): lỏng bão hòa (A-12) p3 =
p2 = 0,8 MPa => i3 = i’ = 95,48 kJ/kg.
+ Trạng thái (4): tiết lưu p4 = p1 = 0,14
MPa => i4 = i3 = 95,48 kJ/kg.
c) + Tốc độ lấy nhiệt từ buồng lạnh:
𝑞2 = 𝐺 (𝑖1 − 𝑖4) = 0,05. (239,19 − 95,48) = 7,19 kW.
+ Công suất đầu vào máy nén:
𝑃 = 𝑙 = 𝐺 (𝑖2 − 𝑖1) = 0,05. (275,40 − 239,19) = 1,81 kW.
d) Tốc độ thải nhiệt ra môi trường:
𝑞1 = 𝐺 (𝑖3 − 𝑖2) = 0,05. (95,48 − 275,40) = −9,00 kW.
(có thể tính: 𝑞1 = −(𝑞2 + 𝑃) = −9,00 kW.
e) Hệ số làm lạnh của tủ lạnh: 𝑞2 𝑞2 𝜀 = 𝑙 = 𝑃 = 3,97. lOMoAR cPSD| 58970315
Bài 4.10: Chu trình máy lạnh sử dụng môi chất NH3, nhiệt độ ngưng tụ 35 oC, nhiệt độ
bay hơi -15 oC, hơi hút về máy nén là hơi bão hòa khô, môi chất sau thiết bị ngưng tụ là lỏng bão hòa.
a) Xác định entanpi của môi chất tại các điểm nút.
b) Xác định nhiệt ngưng tụ riêng, năng suất lạnh riêng, công nén môi chất, và hệ số làm lạnh của chu trình. Giải:
a) Từ bảng lỏng bão hòa – hơi bão hòa – hơi quá nhiệt của NH3 (NH3-1, NH3-2),
entanpi của các trạng thái được xác định. + Trạng thái (1): hơi bão hòa (NH3-1)
t1 = -15 oC => i1 = i” = 1424,6 kJ/kg và s1 = s” = 5,5397 kJ/kg.K.
+ Trạng thái (2): hơi quá nhiệt (NH3-2) t2 = 35 oC và s2 = s1 = 5,5397
kJ/kg.K => i2 = 1525.8 kJ/kg và p2 = 0,5 MPa.
+ Trạng thái (3): lỏng bão hòa (A-12) p3 =
p2 = 0,5 MPa => i3 = i’ = 199,3 kJ/kg.
+ Trạng thái (4): tiết lưu p4 =
p1 => i4 = i3 = 199,3 kJ/kg.
c) + Năng suất lạnh riêng:
𝑞2 = 𝑖1 − 𝑖4 = 1225,3 kJ/kg. + Nhiệt ngưng tụ riêng:
𝑞1 = 𝑖3 − 𝑖2 = −1326,5 kJ/kg.
+ Công nén môi chất: l
= -q1 – q2 = 101.2
e) Hệ số làm lạnh của tủ lạnh: 𝑞2 𝜀 = = 12,1. 𝑙
BÀI TẬP CÓ ĐÁP SỐ
Bài 4.11: Một chu trình Otto lý tưởng có tỷ số nén là 8,5 đưa không khí vào ở 90 kPa
và 40 oC, và được lặp lại 2500 lần trong mỗi phút. Sử dụng các nhiệt dung riêng không
đổi ở nhiệt độ phòng, hãy xác định hiệu suất nhiệt của chu trình này và tốc độ nhận
nhiệt nếu chu trình này tạo ra công suất 90 kW. lOMoAR cPSD| 58970315
Đáp số: 𝜂𝑡 = 57,5%; q1 = 157 kW.
Bài 4.12: Một chu trình Otto lý tưởng có tỷ số nén 8. Tại thời điểm bắt đầu quá trình
nén, không khí ở 95 kPa và 27 oC, và 750 kJ/kg nhiệt được truyền cho không khí trong
quá trình nhận nhiệt đẳng tích. Các nhiệt dung riêng không đổi ở nhiệt độ phòng, xác định:
a) Áp suất và nhiệt độ ở cuối quá trình nhận nhiệt.
b) Công chu trình thực hiện. c) Hiệu suất nhiệt.
Đáp số: a) T3 = 1734 K, p3 = 4,4 MPa; b) l = 423 kJ/kg; c) 𝜂𝑡 = 56,4%.
Bài 4.13: Một chu trình Diesel lý tưởng với môi chất là không khí có tỷ số nén là 16
và tỷ số giãn nở sớm là 2. Tại thời điểm bắt đầu của quá trình nén, không khí ở 95 kPa
và 27 oC. Các nhiệt dung riêng không đổi ở nhiệt độ phòng, xác định: a) Nhiệt độ sau quá trình nhận nhiệt.
b) Áp suất nhiệt của chu trình.
Đáp số: a) T3 = 1818,8 K; b) 𝜂𝑡 = 61,4%.
Bài 4.14: Một chu trình Diesel lý tưởng có tỷ số nén là 17 và tỷ số giãn nở sớm là 1,3.
Xác định nhiệt độ cực đại của không khí và tốc độ nhận nhiệt của chu trình này khi nó
tạo ra công suất 140 kW và trạng thái của không khí lúc bắt đầu nén 90 kPa và 57 oC.
Sử dụng các nhiệt dung riêng không đổi ở nhiệt độ phòng.
Bài 4.15: Một chu trình cấp nhiệt hỗn hợp lý tưởng, sử dụng môi chất là không khí, có
tỷ số nén là 14 và tỷ số giãn nở sớm là 1,2. Tỷ số tăng áp trong quá trình nhận nhiệt
đẳng tích là 1,5. Xác định áp suất và nhiệt độ khí cực đại, nhiệt lượng nhận được, và
hiệu suất nhiệt khi chu trình này hoạt động ở 80 kPa và 20 oC lúc bắt đầu nén. Đáp số:
pmax = p3 = p4 = 4,83 MPa; Tmax = T4 = 1516 K; q1 = 556,5 kJ/kg; 𝜂𝑡 = 64,6%.
Bài 4.16: Một động cơ máy bay, sử dụng turbine khí, hoạt động theo chu trình Brayton
lý tưởng với tỷ số tăng áp là 10. Nhiệt được nhận vào chu trình với tốc độ 500 kW;
không khí đi qua động cơ với tốc độ 1kg/s; và không khí lúc bắt đầu nén ở 70 kPa và
0oC. Xác định công suất do động cơ này sinh ra và hiệu suất nhiệt của nó. Cho 𝑞1 =
𝐺 . 𝑃𝑛ℎậ𝑛 𝑛ℎ𝑖ệ𝑡.
Đáp số: P = 241,2 kW; 𝜂𝑡 = 48,2%.
Bài 4.17: Một động cơ máy bay, sử dụng turbine khí, hoạt động theo chu trình Brayton
lý tưởng với tỷ số tăng áp là 15. Nhiệt được nhận vào chu trình với tốc độ 500 kW; lOMoAR cPSD| 58970315
không khí đi qua động cơ với tốc độ 1kg/s; và không khí lúc bắt đầu nén ở 70 kPa và
0oC. Xác định công suất do động cơ này sinh ra và hiệu suất nhiệt của nó. Cho 𝑞1 =
𝐺 . 𝑃𝑛ℎậ𝑛 𝑛ℎ𝑖ệ𝑡.
Đáp số: P = 269,2 kW; 𝜂𝑡 = 53,8%.
Bài 4.18: Một chu trình Brayton lý tưởng với bộ phản hồi nhiệt có tỷ số tăng áp là 10.
Không khí vào máy nén ở 300 K và turbine là 1200 K. Nếu hiệu suất của bộ hồi nhiệt
là 100%, hãy xác định liệu suất nhiệt của chu trình.
Đáp số: 𝜂𝑡 = 51,7%.
Bài 4.19: Nhà máy điện hơi nước hoạt động theo chu trình Rankine lý tưởng giữa giới
hạn áp suất 3 MPa và 50 kPa. Nhiệt độ hơi ở đầu vào turbine là 300 oC, và tốc độ dòng
hơi qua chu trình là 35 kg/s.
a) Biểu diễn chu trình trên đồ thị T-s.
b) Xác định hiệu suất nhiệt của chu trình.
c) Công suất chu trình cấp cho máy phát điện.
Đáp số: b) 𝜂𝑡 = 27,1%; c) P = 25,2 MW.
Bài 4.20: Một chu trình Rankine lý tưởng sử dụng nước làm môi chất vận hành bình
ngưng của nó ở 40 oC và lò hơi của nó 300 oC. Tính công do Turbine sinh ra, nhiệt
lượng cung cấp trong lò hơi, và hiệu suất của chu trình này khi hơi đi vào turbine là hơi bão hòa khô.
Đáp số: l = 974,5 kJ/kg; q1 = 2573,4 kJ/kg; 𝜂𝑡 = 37,5%.
Bài 4.21: Một chu trình làm lạnh nén hơi lý tưởng sử dụng chất làm lạnh – 134a làm
môi chất duy trì bình ngưng ở 800 kPa và dàn bay hơi ở -12 oC. a) Tính entanpi tại
các điểm nút của chu trình.
b) Xác định hệ số làm lạnh của máy lạnh.
Đáp số: a) i1 = 243,34 kJ/kg, i2 = 273,71 kJ/kg, i3 = 95,48 kJ/kg, i4 = i3 = 95,48 kJ/kg; b) ε = 4,87.
Bài 4.22: Xét một hệ thống làm lạnh 300 kJ/phút hoạt động theo chu trình làm lạnh
nén hơi lý tưởng với chất làm lạnh – 134a là môi chất. Môi chất làm lạnh đi vào máy
nén dưới dạng hơi bão hòa ở 140 kPa và được nén đến 800 kPa. a) Biểu diễn chu
trình trên đồ thị T-s.
b) Xác định độ khô (x) của môi chất lạnh ở cuối quá trình tiết lưu. lOMoAR cPSD| 58970315
c) Xác định hệ số làm lạnh.
d) Xác định công suất đầu vào máy nén.
Đáp số: b) x = 0,3225; c) ε = 3,97; d) P = 1,26 kW. lOMoAR cPSD| 58970315
CHƯƠNG 5: TRUYỀN NHIỆT 5.1. DẪN NHIỆT
I. TÓM TẮT LÝ THUYẾT
1. Định luật Fourier về dẫn nhiệt: t q =− gradt = n . . 0 n
Trong đo λ là hệ so dà n nhiệ t (W/mK)
2. Dẫn nhiệt ổn định qua hai vách
 Dà n nhiệ t quà và ch phà ng: Do ng nhiệ t quà và ch là q (W/m2): t − t Và ch mo t lớ p: q = w1 w2 t − t
Và ch nhiệ u lớ p: q = w1 w n( +1) n i = i i 1
tw1: nhiệ t đo bệ mà t trong cu ng (0C)
tw(n+1): nhiệ t đo bệ mà t ngoà i cu à lớ p ngoà i cu ng (0C)
 Dà n nhiệ t quà và ch tru : Do ng nhiệ t quà 1 mệ t chiệ u dà i cu à và ch tru là q1: t − t Và ch mo t lớ p: q = 1 w1 w2 1 ln d2 2 d1 t − t Và ch nhiệ u lớ p: q = w1 w n( +1) 1 12 i 1=n 1 ln ddi 1+i
di: đướ ng kí nh cu à lớ p thư i. 
Dà n nhiệ t quà và ch cà u: 2 (t − t ) lOMoAR cPSD| 58970315
Do ng nhiệ t quà và ch cà u mo t lớ p: Q = w1 w2 1 1 − d1 d2 ( ) 2 t w1 − t
Do ng nhiệ t quà và ch cà u nhiệ u lớ p: Q = w n( +1) n 1 1 1 = i di − di 1+ i 1
3. Dẫn nhiệt ổn định khi có nguồn nhiệt bên trong:
 Dà n nhiệ t cu à và ch phà ng đo ng chà t, dà y 2δ q ( ) ( v −2 x2 t + qv + qv
Phà n bo nhiệ t đo : t = t ) w + = f −2 x2 2 2 qv qv 2
Nhiệ t đo ớ tà m cu à tà m: t = + + 0 t f 2
Mà t đo do ng nhiệ t: q = q = ( − ) v t w tf
 Dà n nhiệ t quà và ch tru co nguo n nhiệ t bệ n trong:
Phà n bo nhiệ t đo : t = t + f 2q ( ) ( ) v r + = + 0 4q v r02 − r2 t w 4q v r02 − r2 qv r0 + qv r02 = t w + qv r02 Nhiệ t đo tà i tà m: t0 = +t f 2 4 4 qv r
Mà t đo do ng nhiệ t: q = (t − t )= w f 2 0
II. BÀI TẬP CÓ LỜI GIẢI lOMoAR cPSD| 58970315
Bài 5.1: Tí nh mà t đo do ng nhiệ t truyệ n quà và ch phà ng ro ng, đo ng chà t, chiệ u dà y và ch δ = 50mm,
nhiệ t đo bệ mà t trong và bệ mà t ngoà i duy trí kho ng đo i t1 = 1000C và t2 = 900C vớ i cà c trướ ng hớ p và ch
là m bà ng cà c và t liệ u sàu: à.
Và ch thệ p co hệ so dà n nhiệ t λ = 40W/mK b.
Và ch bệ to ng co λ = 1,1W/mK. c.
Gà ch diàtomit co λ = 0,11W/mK Giải t = t Mà t đo do ng nhiệ t: q = w1 w2 100 100−90 b. Và ch bệ to ng: q = à. Và ch thệ p: q = = 8000(W / m2 ) −90 = 220(W /m2 ) 100
c. Và ch gà ch diàtomit: q = −90 = 22(W /m2 )
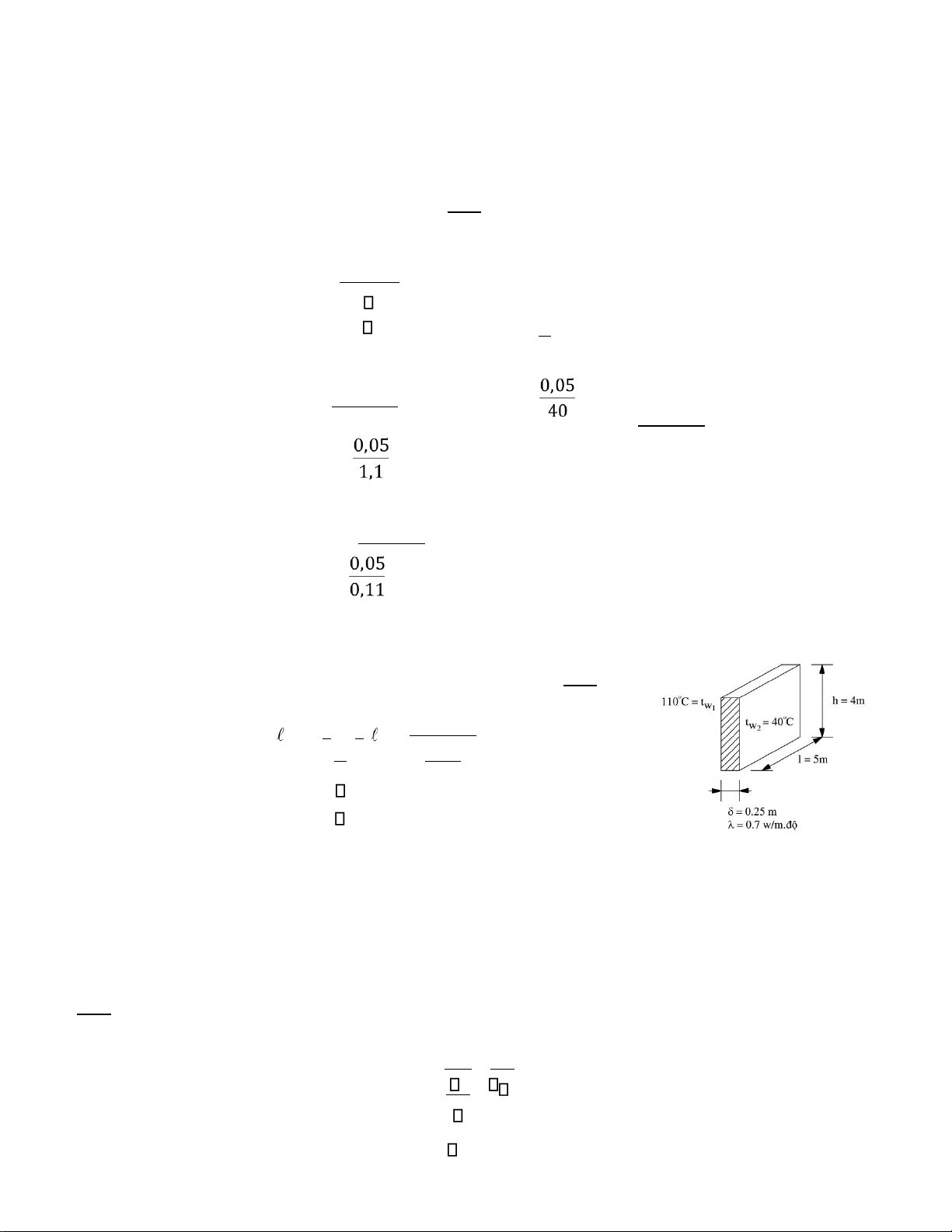
Bài 5.2: Xà c đi nh to n thà t nhiệ t Q truyệ n quà cà ch là m bà ng gà ch đo co λ = 0,70W/mK. Và ch co kí ch
thướ c: chiệ u dà i ℓ = 5m, chiệ u cào h = 4m, chiệ u dà y δ = 250mm. Nhiệ t
đo trệ n bệ mà t và ch duy trí kho ng đo i t1 = 1100C và t2 = 400C. Giải
t1 − t2 . .h = 110− 40.5.4 =3920W Tà co : Q = q.F = q. .h = 0,25 0,7
Bài 5.3: Tí nh bệ dà y lớ p cà ch nhiệ t cu à mo t và ch phà ng đệ to n thà t nhiệ t kho ng vướ t quà 450W/m2,
biệ t nhiệ t đo bệ mà t trong t1 = 4500C và bệ mà t ngoà i t2 = 500C vớ i cà c loà i và t liệ u cà ch nhiệ t sàu: à.
λ1 = 0,09 + 0,0000872.t (W/mK)
b. λ2 = 0,209 + 0,000146.t (W/mK) Giải =
Cướ ng đo do ng nhiệ t truyệ n quà và ch: q = t ( ) tb t w1 − t w2 tb