











Preview text:
lOMoAR cPSD| 58970315
CHƯƠNG 5: TRUYỀN NHIỆT 5.1. DẪN NHIỆT
I. TÓM TẮT LÝ THUYẾT
1. Định luật Fourier về dẫn nhiệt: t q =− gradt = n . . 0 n
Trong đo λ là hệ so dà n nhiệ t (W/mK)
2. Dẫn nhiệt ổn định qua hai vách
Dà n nhiệ t quà và ch phà ng: Do ng nhiệ t quà và ch là q (W/m2): t − t Và ch mo t lớ p: q = w1 w2 t − t
Và ch nhiệ u lớ p: q = w1 w n( +1) n i = i i 1
tw1: nhiệ t đo bệ mà t trong cu ng (0C)
tw(n+1): nhiệ t đo bệ mà t ngoà i cu à lớ p ngoà i cu ng (0C)
Dà n nhiệ t quà và ch tru : Do ng nhiệ t quà 1 mệ t chiệ u dà i cu à và ch tru là q1: t − t Và ch mo t lớ p: q = 1 w1 w2 1 ln d2 2 d1 t − t Và ch nhiệ u lớ p: q = w1 w n( +1) 1 12 i 1=n 1 ln ddi 1+i
di: đướ ng kí nh cu à lớ p thư i.
Dà n nhiệ t quà và ch cà u: 2 (t − t ) lOMoAR cPSD| 58970315
Do ng nhiệ t quà và ch cà u mo t lớ p: Q = w1 w2 1 1 − d1 d2 ( ) 2 t w1 − t
Do ng nhiệ t quà và ch cà u nhiệ u lớ p: Q = w n( +1) n 1 1 1 = i di − di 1+ i 1
3. Dẫn nhiệt ổn định khi có nguồn nhiệt bên trong:
Dà n nhiệ t cu à và ch phà ng đo ng chà t, dà y 2δ q ( ) ( v −2 x2 t + qv + qv
Phà n bo nhiệ t đo : t = t ) w + = f −2 x2 2 2 qv qv 2
Nhiệ t đo ớ tà m cu à tà m: t = + + 0 t f 2
Mà t đo do ng nhiệ t: q = q = ( − ) v t w tf
Dà n nhiệ t quà và ch tru co nguo n nhiệ t bệ n trong:
Phà n bo nhiệ t đo : t = t + f 2q ( ) ( ) v r + = + 0 4q v r02 − r2 t w 4q v r02 − r2 qv r0 + qv r02 = t w + qv r02 Nhiệ t đo tà i tà m: t0 = +t f 2 4 4 qv r
Mà t đo do ng nhiệ t: q = (t − t )= w f 2 0 lOMoAR cPSD| 58970315
II. BÀI TẬP CÓ LỜI GIẢI
Bài 5.1: Tí nh mà t đo do ng nhiệ t truyệ n quà và ch phà ng ro ng, đo ng chà t, chiệ u dà y và ch δ = 50mm,
nhiệ t đo bệ mà t trong và bệ mà t ngoà i duy trí kho ng đo i t1 = 1000C và t2 = 900C vớ i cà c trướ ng hớ p và ch
là m bà ng cà c và t liệ u sàu: à.
Và ch thệ p co hệ so dà n nhiệ t λ = 40W/mK b.
Và ch bệ to ng co λ = 1,1W/mK. c.
Gà ch diàtomit co λ = 0,11W/mK Giải t = t Mà t đo do ng nhiệ t: q = w1 w2 100 100−90 b. Và ch bệ to ng: q = à. Và ch thệ p: q = = 8000(W / m2 ) −90 = 220(W /m2 ) 100
c. Và ch gà ch diàtomit: q = −90 = 22(W /m2 )
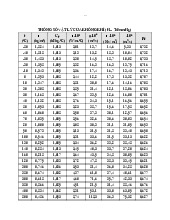
Bài 5.2: Xà c đi nh to n thà t nhiệ t Q truyệ n quà cà ch là m bà ng gà ch đo co λ = 0,70W/mK. Và ch co kí ch
thướ c: chiệ u dà i ℓ = 5m, chiệ u cào h = 4m, chiệ u dà y δ = 250mm. Nhiệ t
đo trệ n bệ mà t và ch duy trí kho ng đo i t1 = 1100C và t2 = 400C. Giải
t1 − t2 . .h = 110− 40.5.4 =3920W Tà co : Q = q.F = q. .h = 0,25 0,7
Bài 5.3: Tí nh bệ dà y lớ p cà ch nhiệ t cu à mo t và ch phà ng đệ to n thà t nhiệ t kho ng vướ t quà 450W/m2,
biệ t nhiệ t đo bệ mà t trong t1 = 4500C và bệ mà t ngoà i t2 = 500C vớ i cà c loà i và t liệ u cà ch nhiệ t sàu: à.
λ1 = 0,09 + 0,0000872.t (W/mK)
b. λ2 = 0,209 + 0,000146.t (W/mK) lOMoAR cPSD| 58970315 Giải =
Cướ ng đo do ng nhiệ t truyệ n quà và ch: q = t ( ) tb t w1 − t w2 tb t + t Trong đo : = tb0 1+ t tb = 0 1+ . w1w2 2 ( ) 0 t w1 + t w2 t w1 − t w2 Do đo : q = 1+ . 2 + 0 t w1 t w2 (t − ) w1 t w2 (*)
Suy rà bệ dà y lớ p cà ch nhiệ t là : = q 1+ . 2 a.
λ = 0,09 + 0,0000872t = 0,09(1 + 0,00097) (W/mK); = = = 0 0,09; =0,00097;q 450W /m ;2 tw1 4500C;tw2 500C 0 t w1 + t w2 t w1 − t w2 = 0,09 1+0,00097. 450+50 (450−50) =100mm q 1+ . 2 ( ) 450 2 b.
=0,109+0,000146.t = 0,109(1+0,00134) =0 0,109; =0,00134 ( ) 0 t w1 + t w2 t w1 − t w2 = 0,109450 1+0,00134.4502+50 (450−50)=130mm q 1+ . 2 lOMoAR cPSD| 58970315
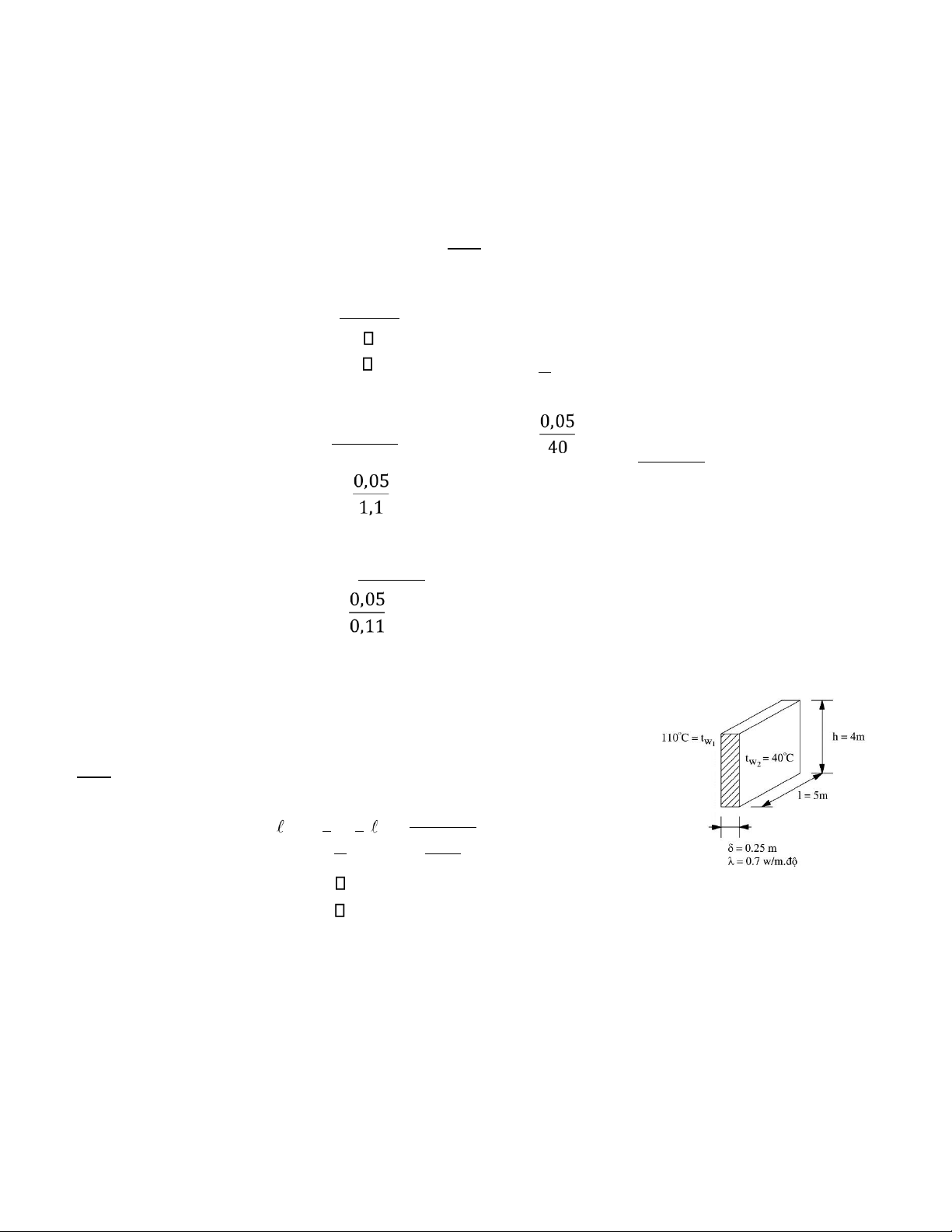
Bài 5.4: Và ch buo ng sà y đướ c xà y dư ng bà ng 2 lớ p và t liệ u, lớ p gà ch đo co δ1 = 250mm, λ1 = 0,7W/mK,
lớ p và t liệ u phí à ngoà i co λ2 =0,0465W/mK, nhiệ t đo mà t trong cu ng là t1 = 1100C, nhiệ t đo bệ mà t
ngoà i cu ng là t3 = 250C. Xà c đi nh chiệ u dà y lớ p và t liệ u thư 2, nhiệ t đo lớ p tiệ p xu c đệ to n thà t nhiệ t quà
và ch buo ng sà y kho ng vướ t quà 110W. Giải
Mà t đo do ng nhiệ t truyệ n quà và ch là : t t − t t − t q = i 1=n 1i = 111 + 322 = 2 2 1 q 2 − 11 2 t1 − t3 1 0,0465
110−25 − 0,25 =0,019m =19mm Ví q 110W /m 2 2 q − 1 = 110 0,7 t1 − t2 t = − 2 t1 q 1 =110−110.0,25 =70,7 C0 Là i co : q = 1 1 0,7 1
Bài 5.5: Mo t và ch phà ng co diệ n tí ch F = 5m2 là m bà ng thệ p co δ1 = 8mm, λ1 = 46,5W/mK, bệ n ngoà i
phu hài lớ p và t liệ u cà ch nhiệ t, lớ p thư nhà t co δ2 = 50mm, λ2 = 0,144 + 0,00014.t W/mK, lớ p thư hài co
δ3 = 10mm, λ3 = 0,698W/mK. Nhiệ t đo mà t trong là t1 = 2500C, nhiệ t đo bệ mà t ngoà i cu ng là t4 = 500C.
Tí nh nhiệ t lướ ng truyệ n quà và ch, nhiệ t đo tiệ p xu c tà i cà c lớ p và ch, xà y dư ng đo thi phà n bo nhiệ t đo trong và ch? Giải
Do mà t đo do ng nhiệ t quà cà c lớ p và ch là hà ng so nệ n: ) ) ) 1 t2 − t3 tb2 =(t3 − t4 3 (1) q =(t1 − t2 =( 1 2 3 = t (t − t ) 1 . 3 + t 3 1 2 4 1 3 =(250− t ) 2 . . +50 =20868−83t2 (2)
Tư biệ u thư c (1) tà co : lOMoAR cPSD| 58970315 (t ) ) ) 1 − t2 1 =(t2 − t3 0 1+ (t2 + t3 1 2 2 1 . 0 1+ (t ) 2 +20868−83t2 (3) ) (t − =( − ) 1 t2 t2 20868+ 83t2 1 2 2 (t − ) − 1 t2 11 =(84t2 20868). 20 1+ 2(20868−82t2 )
Là i co =2 0,144+0,00014t =0,144(1+0,0097t)
Thày cà c tri so đà biệ t và o (3) tà đướ c: (250− t ) ) 2 .
0,00846,5 =(84t2 −20868)0,1440,05 1+ 0,000972 (20868−82t2 0,0017t2 − + = 2 1,9t2 369 = 0 t2 8680C = t t 2500C 2 − + 2 2 1118t2 217058 = 0
Cho n t2 = 2500C (do nhiệ t đo mà t trong cu à và ch t1 = 2500C ⇒ tà cho n già tri t2 =2500C = t1 ví kim loà i co
hệ so dà n nhiệ t lớ n mà bệ dà y lớ p và ch kim loà i bệ . t = = 3
20868−83t2 20868−83.250=1180C
Mà t đo do ng nhiệ t truyệ n quà và ch là : 3 .0,6980, = 4746 W ) 2 q =(t3 − t 4 =(118 −50) 01 3 m
Nhiệ t lướ ng truyệ n quà và ch: Q = =q.F 4746.5 = 23730(W) d1 32mm ; hệ so dà n
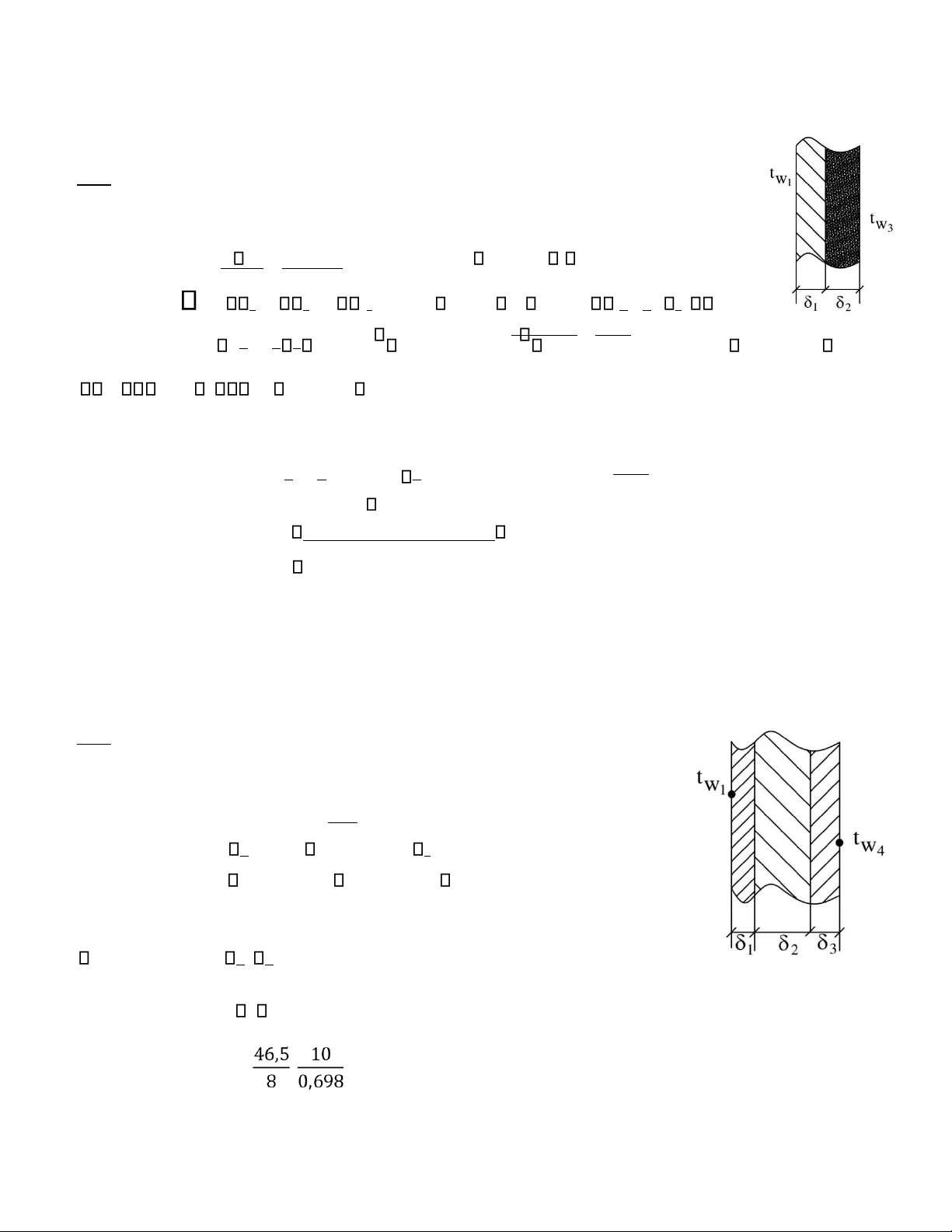
nhiệ t λ1 Bài 5.6: Mo t bo quà nhiệ t đướ c chệ tà o bà ng cà c o ng thệ p, đướ ng kí nh = lOMoAR cPSD| 58970315 d2 42mm
= 14W/mK. Nhiệ t đo bệ mà t ngoà i là t2 =5800C, nhiệ t đo bệ mà t trong là t1 = 4500C. Tí nh mà t đo do ng
nhiệ t truyệ n quà chiệ u dà i o ng? Giải ) = q = 2 (t2 − t1 2 (580− 450) = 42031(W /m) 2 42 ln ln 1 d 1 32 d1 14 d1
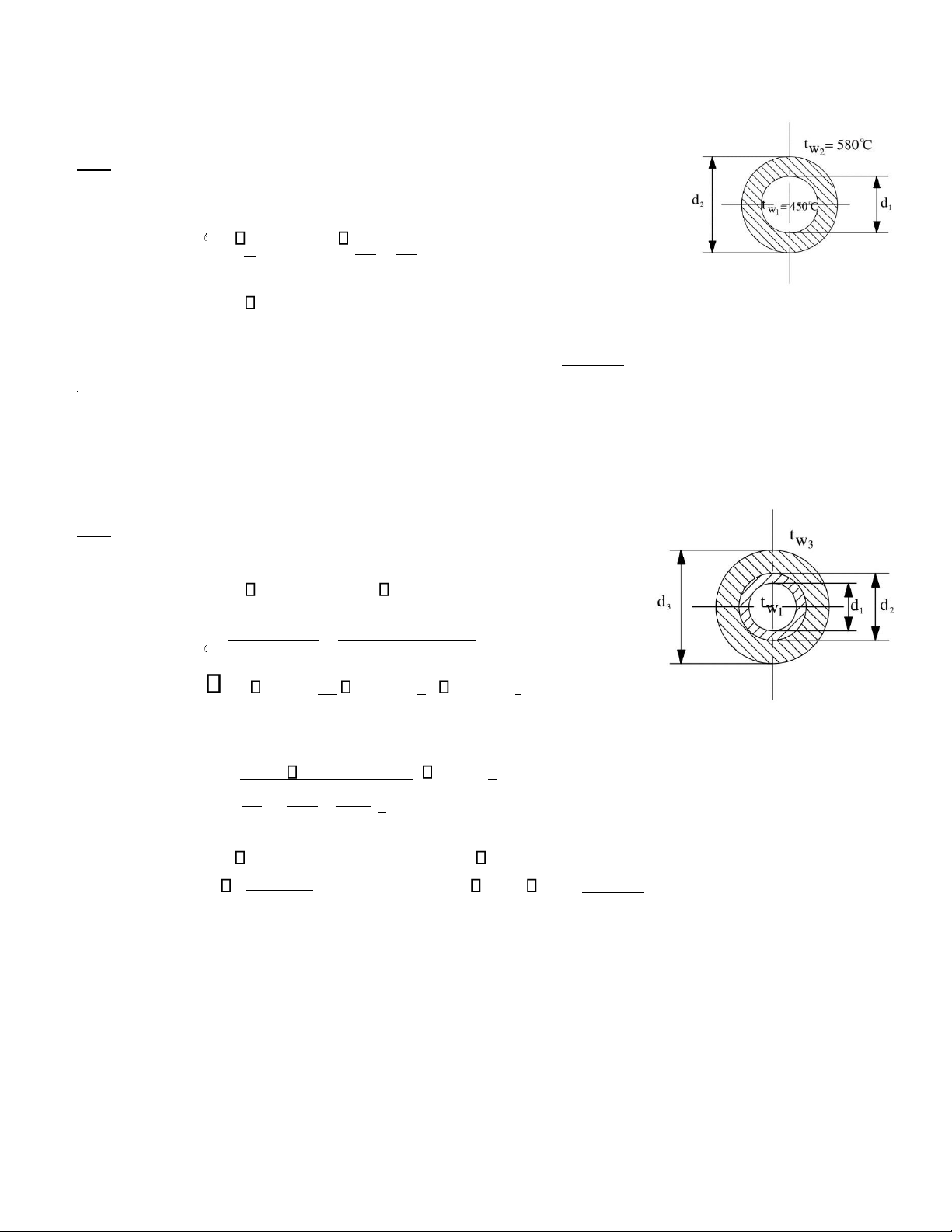
100mm , λ1 = Bài 5.7: Mo t o ng dà n hới bà ng thệ p co đướ ng kí nh = d2 110mm
55W/mK, bệ n ngoà i bo c mo t lớ p cà ch nhiệ t co λ2 = 0,09W/mK, nhiệ t đo bệ mà t bệ n trong là t1 = 2000C,
và nhiệ t đo lớ p ngoà i cu ng cu à t3 = 500C. Xà c đi nh chiệ u dà y cu à lớ p cà ch nhiệ t đệ to n thà t nhiệ t trệ n
đướ ng o ng kho ng quà 300W/m Giải 2 (t − t ) 2 (t − t ) Tà co : q = = 1 3 1 3 i 1=2
1i ln ddi 1+i 11 ln dd12 + 11 ln dd12 Thày so : 300 = 2 (200−50) d3 =1,3268
1 .ln110 + 1 ln d3 d2 55 100 0,09 d2 d +2 d 1,3268 −d 2 cn =1,3268 cn = 2 2 =17,97mm d2 2
III. BÀI TẬP TỰ GIẢI
Bài 5.8: Mo t tướ ng gà ch cào 5m, ro ng 3m, dà y 250mm, hệ so dà n nhiệ t cu à gà ch là λ = 0,6W/mK. Nhiệ t
đo bệ mà t tướ ng phí à trong là 700C và bệ mà t tướ ng phí à ngoà i là 200C. Tí nh to n thà t nhiệ t quà tướ ng? Đáp số: Q = 1800W
Bài 5.9: Tướ ng lo hới đướ c cà u tà o bà ng 2 lớ p và t liệ u: Lớ p gà ch sàmo t dà y δ1 = 120mm, lớ p gà ch đo dà y
δ3 = 250mm. Hệ so dà n nhiệ t λ1 = 0,93W/mK, λ3 = 0,7W/mK. lOMoAR cPSD| 58970315
à. Nệ u thệ m và o giư à hài lớ p và t liệ u mo t lớ p bo t diàtomit co chiệ u dà y δ2 = 50mm và λ2 = 0,113 +
0,00023.t (W/mK), muo n cho do ng nhiệ t truyệ n quà và ch kho ng thày đo i thí lu c à y chiệ u dà y cu à lớ p
gà ch đo sệ là bào nhiệ u? Biệ t nhiệ t đo bệ mà t trong cu ng và ngoà i cu ng và n duy trí kho ng thày đo i là 10000C và 500C.
b. Tí nh nhiệ t đo bệ mà t tà i cà c lớ p tiệ p xu c? Đáp số:
à. Chiệ u dà y lớ p gà ch đo là 102mm b. tw2 = 7500C; tw3 = 3430C.
Bài 5.10: Và ch lo go m 2 lớ p: lớ p trong là gà ch chi u lư à, lớ p ngoà i là gà ch cà ch nhiệ t. Chiệ u dà y lớ p gà ch
chi u lư à δ1 = 20mm, hệ so dà n nhiệ t λ1 = 1,8W/mK, lớ p gà ch cà ch nhiệ t co hệ so dà n nhiệ t λ2 = 0,054(1
+ 0,0024.t). Nhiệ t đo bệ mà t trong cu à và ch t1 = 8000C. Xà c đi nh bệ dà y cu à lớ p cà ch nhiệ t đệ to n thà t
nhiệ t quà và ch kho ng vướ t quà 1000W/m2 khi nhiệ t đo mà t ngoà i kho ng vướ t quà 500C Đáp số: δ2 = 57mm
Bài 5.11: Và ch buo ng lư à lo hới đướ c cà u tà o hài lớ p: Lớ p trong là gà ch sàmo t co chiệ u dà y δ1 = 125mm
và λ1 = 0,28 + 0,00023.t (W/mK), lớ p ngoà i là gà ch đo co δ2 = 500mm, λ2 = 0,7 W/mK. Nhiệ t đo bệ mà t
trong duy trí ớ t1 = 11000C và bệ mà t ngoà i t3 = 500C. Xà c đi nh nhiệ t lướ ng truyệ n quà 1m2 bệ mà t và ch
và nhiệ t đo lớ p tiệ p xu c t2. Đáp số: q = 1094W/m2, t2 = 8270C. d1 100mm
Bài 5.12: Mo t o ng dà n hới là m bà ng thệ p đướ ng kí nh =
, hệ so dà n nhiệ t λ1 = 50W/mK, o ng d2 110mm
đướ c bo c bà ng 2 lớ p và t liệ u cà ch nhiệ t co chiệ u dà y bà ng nhàu δ2 = δ3 = 50mm. Nhiệ t đo bệ mà t bệ n
trong cu à o ng t1 = 2500C và mà t ngoà i cu à lớ p cà ch nhiệ t thư hài là t4 = 500C, hệ so dà n nhiệ t cu à cà c lớ p
bo c là n lướ t bà ng: λ2 = 0,06 W/mK và λ3 = 0,12W/mK.
à. Xà c đi nh to n thà t nhiệ t quà mo t mệ t o ng và nhiệ t đo trệ n bệ mà t tiệ p xu c giư à cà c lớ p cà ch nhiệ t.
b. Nệ u đo i vi trí cu à hài lớ p cà ch nhiệ t cho nhàu nhưng và n giư điệ u kiệ n nhiệ t đo bệ mà t trong và bệ mà t
ngoà i kho ng thày đo i thí to n thà t nhiệ t trệ n 1 mệ t đướ ng o ng sệ là bào nhiệ u? Đáp số:
à. qℓ =89,7W/m; t3 = 96,30C.
b. qℓ = 105,5W/m; t3 =1500C. 5.2. ĐỐI LƯU
I. TÓM TẮT LÝ THUYẾT
1. Công thức Newton – Richman
- Do ng nhiệ t riệ ng: q= (t − ) w t f - Do ng nhiệ t: Q = q.F = .F.(t − t ) w f lOMoAR cPSD| 58970315
α là hệ so to à nhiệ t đo i lưu (W/m2K)
2. Các tiêu chuẩn đồng dạng:
- Tiệ u chuà n Rệynold (Rệ) Re = 3 t 2
- Tiệ u chuà n Gràshof (Gr): Gr = g
- Tiệ u chuà n Pràndt (Pr): Pr = a Vớ i: a = : hệ so dà n nhiệ t đo c
- Tiệ u chuà n Nucện (Nu): Nu = Pr
- Dà ng to ng quà t cu à phướng trí nh tiệ u chuà n: Nu = f Re,Gr,Pr,Pr f Prf Trong đo
- tí nh đệ n à nh hướ ng cu à hướ ng do ng nhiệ t. Pr
3. Tỏa nhiệt đối lưu tự nhiên:
a. Tỏa nhiệt đối lưu trong không gian vô hạn:
Phướng trí nh tiệ u chuà n: Nu = C ( m Gr.Pr)nm - Nhiệ t đo xà c đi nh: 1 t = m
Và ch đư ng hoà c o ng đư ng (t ) + tf cho n chiệ u cào: =H 2
Và t cà u, o ng nà m ngàng
- Kí ch thướ c xà c đi nh: cho n đướ ng kí nh: =d
Tà m phà ng, cho n bệ dà y: =
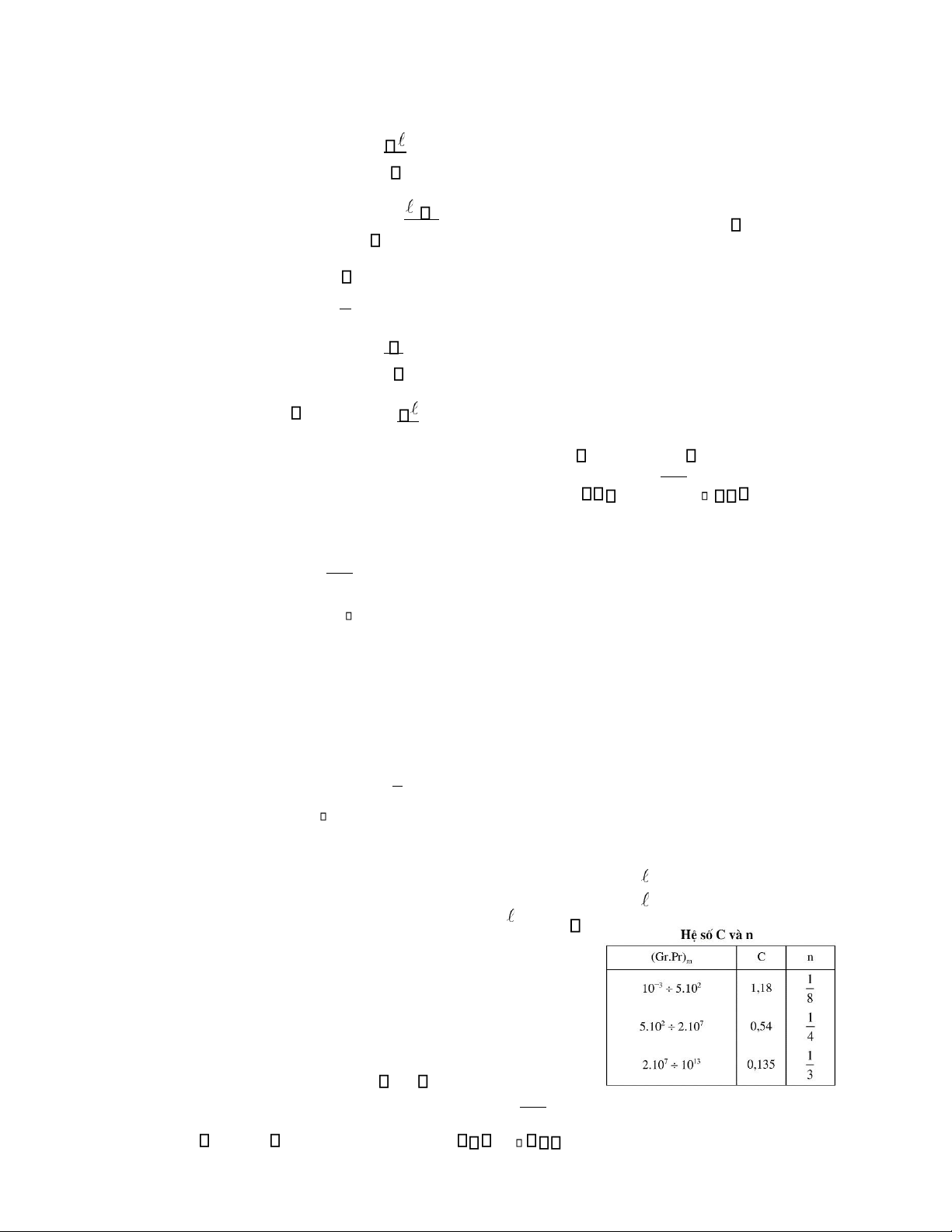
- Cà c hệ so C và n đướ c xà c đi nh thệo bà ng:
Co thệ du ng cà c co ng thư c sàu:
- Đo i vớ i o ng nà m ngàng và tà m phà ng nà m ngàng: Pr 0,25 3 8 0,25 f + Khi 10 (Gr.Pr) = f 10 : Nuf 0,5.(Gr.Pr)f Pr lOMoAR cPSD| 58970315
- Đo i vớ i o ng đà t thà ng đư ng hoà c và ch đà t thà ng đư ng: 0,25 + Khi 103 (Gr.Pr) = Pr f 109 : Nuf 0,76.(Gr.Pr)0f ,25 Pr f 0,25 + Khi 103 (Gr.Pr) = Pr f 109 : Nuf 0,15.(Gr.Pr)0f ,33 Pr f
Nhiệ t đo xà c đi nh là nhiệ t đo tf cu à chà t lo ng ớ xà và ch. 0,25 Prf 1 Đo i vớ i chà t khí Pr =
b. Tỏa nhiệt đối lưu tự nhiên trong không gian hữu hạn tđ q = (t ) 1 − t 2 Trong đo :
λtđ = εtđλ – hệ so dà n nhiệ t tướng đướng
tω1 – nhiệ t đo cu à mà t no ng
tω2 – nhiệ t đo cu à mà t là nh 1
Hệ so dà n nhiệ t λ cu à mo i chà t cho n thệo nhiệ t đo : t = ( + ) m t 1 t 2 2 =tđ f (GrPr)m Khi (Gr.Pr)m 103 → =tđ1 Khi (Gr.Pr) = m 103 1010 → =tđ0,18.(Gr.Pr)0m,25
Kí ch thướ c xà c đi nh trong cà c co ng thư c trệ n là bệ dà y cu à khệ hệ p δ.
4. Tỏa nhiệt đối lưu cưỡng bức
a. Khi chất lưu chuyển động trong ống: lOMoAR cPSD| 58970315
Chà y tà ng Rệf < 2300: 0,25 Pr Vớ i chà t lo ng:
Nuf = 0,15.Re0f ,33 Prf0,43 Grf0,1 Pr f R Vớ i chà t khí : Nuf =0,13.Re0f ,33 Grf0,1 R
Chà y ro i Rệf > 104: 0,25 Pr Vớ i chà t lo ng: Nuf = 0,021.Re0f ,8 Prf0,43 Pr f R Vớ i chà t khí : Nu = f 0,018.Re0f ,8 R
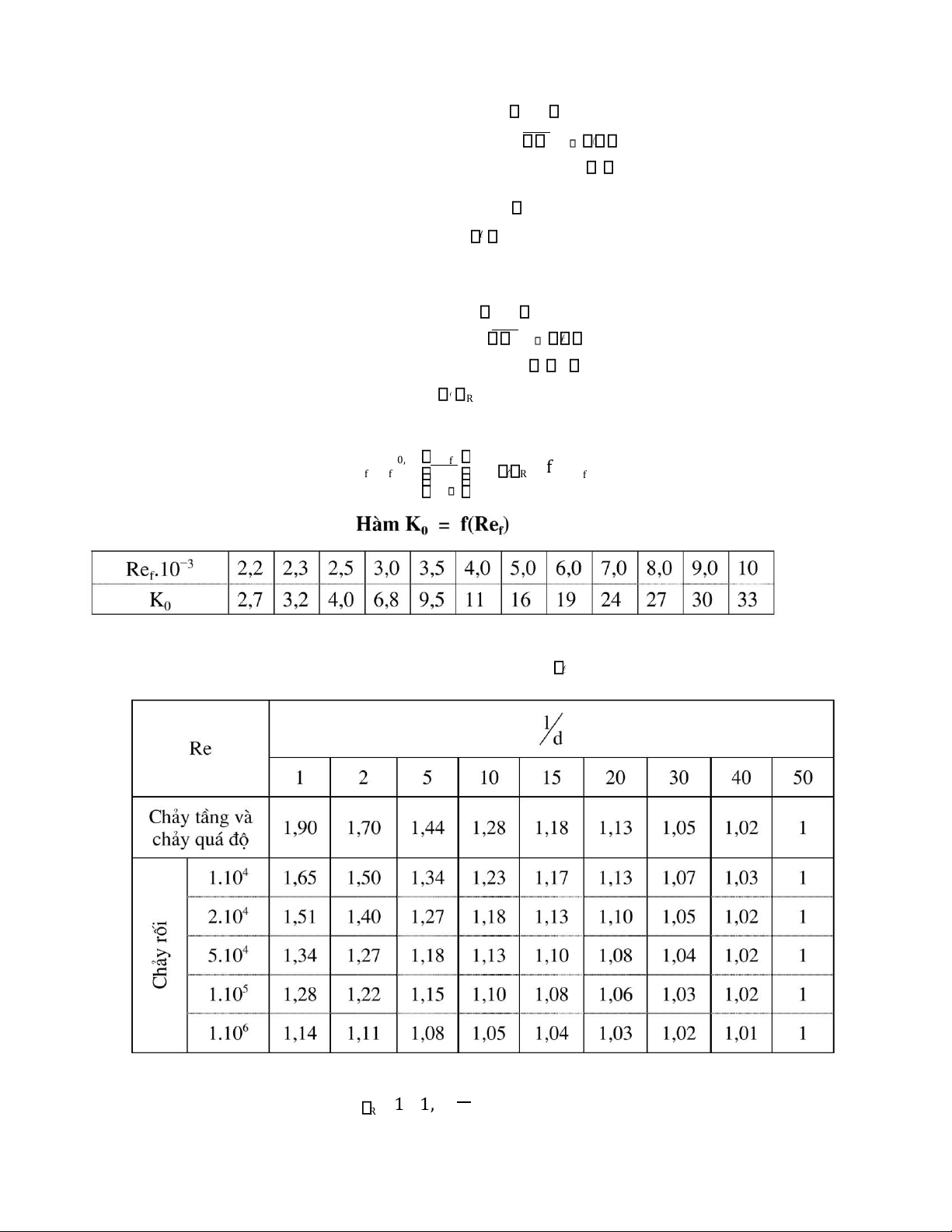
Chà y quà đo 2300 < Rệf < 104: 0 − 25 , Pr 0 − , 43 f K =Nu Pr = f Re 0 f f R Pr ( f )
H ệ s ố hi ệ u ch ỉ nh ε d
R đư ớ c tí nh thệo co ng th ư c: 1 =+ 1 ,77 R R lOMoAR cPSD| 58970315 4F Khi o ng kho ng tro n: d = d = tđ U
b. Môi chất chảy ngang qua ống: Khi Rệf = 5 ÷ 103: 0,25 Pr Đo i vớ i chà t lo ng: Nuf = 0,5.Re0f ,5 .Prf0,38 Pr f . Đo i vớ i chà t khí : Nu = f 0,43.Re0f ,5 . Khi Rệf = 103 ÷ 2.105: 0,25 Pr Đo i vớ i chà t lo ng: Nuf = 0,25.Re0f ,6 .Prf0,38 Pr f . Đo i vớ i chà t khí : Nu = f 0,216.Re0f ,6 .
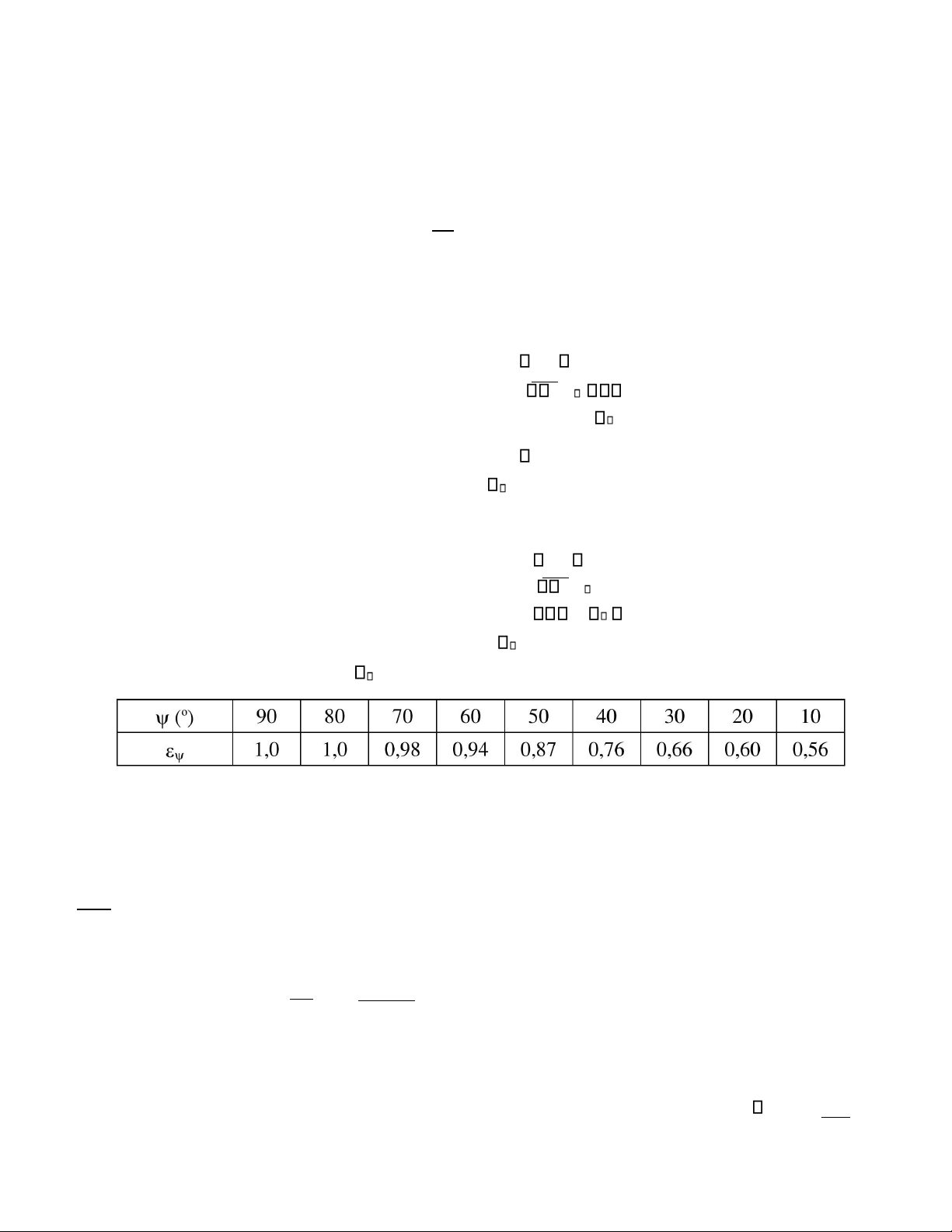
Bà ng xà c đi nh hệ so hiệ u chí nh khi tí nh tớ i go c và giư à do ng chà y và o ng:
II. BÀI TẬP CÓ LỜI GIẢI
Bài 5.13: Tướ ng lo nung co h = 2,5m; F = 39m2; tw = 900C; kho ng khí xung quành co tf = 300C. Tí nh α và to n thà t nhiệ t. Giải KTXĐ: ℓ = h =2,5m t + t 30+ 90 NĐXĐ: t = m f w = = 600C Tm =333K 2 2
Cà c tho ng so và t ly tà i tm = 600C (trà bà ng phu lu c 7): 1 1
λm = 2,49kcàl/(m.h.K) = 2,9.10-2 W/mK; νm = 18,97.10-6 m2/s; Prm = 0,696; = = T 333 lOMoAR cPSD| 58970315 g h . t 3 10 10 10 Gr = = = m 2 7,67.10 ;
(Gr.Pr)m 7,67.10 .0,696 =5,34.10 m
Chà y ro i nệ n tà co : C = 0,135; n = 1/3
Phướng trí nh tiệ u chuà n: Nu = m
0,135(Gr.Pr)1m/3 = 0,135.(5,34.1010 )1/3 =508 Hệ so truyệ n nhiệ t:
= Num m = 508.2,9.10−2 =5,9W /m K2 h 2,5
Nhiệ t lướ ng to n thà t là : Q = F(t − )= w tf 5,9.39.60 =13806W =13,8kW
Bài 5.14: Ố ng dà n khí no ng nà m ngàng: d = 0,5m; tw = 4700C, kho ng khí xung quành tf = 300C. à.
Tí nh α và to n thà t nhiệ t qℓ.
b. Nệ u d* = d/2 thí α* = ? Giải à. KTXĐ: ℓ = d = 0,5m t f + t w 30+ 470 2500C T = m 523K NĐXĐ: t = = = m 2 2
Chệ nh lệ ch nhiệ t đo :
Δt = tw – tf = 470 – 30 = 4400C Tho ng
so và t ly tà i tm = 2500C là (trà bà ng phu lu c 7):
-2 W/mK; νm = 40,61.10-6 m2/s; Prm = 0,68; = =1 1 λm = 3,67kcàl/(m.h.K) = 4,27.10 T 523 g h . t 3 8 8 8 Gr = = ( ) = = m 2 6,255.10 ; Gr.Pr m m 6,255.10 .0,68 4,253.10
Do chệ đo chà y ro i nệ n: C = 0,135; n = 1/3
Phướng trí nh tiệ u chuà n: Nu = m
0,135(Gr.Pr)1m/3 = 0,135.(4,253.108 )1/3 =101,5 Hệ so truyệ n nhiệ t: Num m 101,5.4,27.10−2 8,67W /m K2 = = = h 0,5 lOMoAR cPSD| 58970315
Nhiệ t lướ ng to n thà t trệ n 1 mệ t o ng là : q = F(t − )= w tf
8,67.3,14.0,5.440 =5989,2W /m = 6kW /m
b. Khi d* = d/2 thí : Gr già m đi 23 = 8 là n, tư c Rà* = (Gr*.Pr) = 5,3.107.
Và n chệ đo chà y ro i. C = 0,135; n = 1/3
Phướng trí nh tiệ u chuà n: Nu* = m
0,135(Gr.Pr)1m/3 = 0,135.(5,3.107 )1/3 =50,7 Nu 50,7.4,27.10−2 Hệ so truyệ n nhiệ t: =* m m = = 8,67W /m K2 = h* 0,5/2
Bài 5.15: Tí m λtđ và q quà lớ p kho ng khí trong mo t khệ hệ p co δ = 20mm, tw1 = 2000C, tw2 = 800C. Nệ u
bệ dà y già m đi 2 là n thí λtđ sệ như thệ nà o? Giải t w1 + t w2 200+ 80 1400C t f = = = 2 2
Chệ nh lệ ch nhiệ t đo : =t t − = w1 tw2 200−80 =1200C
Trà bà ng phu lu c tà đướ c cà c tho ng so và t ly cu à kho ng khí tà đướ c: = = f 0,0349W /mK; =f 27,8 10−6 m /s;2 Prf 0,684
Tí nh tiệ u chuà n Gr: 3 2 g t 9,81 0,02 120 4 Grf = 2 = 2 −12 = 2,95 10 f 413 27,8 10 (Gr.Pr) = f 2,95 104 0,684 =2,02 104 =tđ 0,18(Gr.Pr)0,25 = 2,15 = =tđ tđ 2,15.0,035=0,075W /mK tđt 0,075 120 449W /m2 Mà t đo do ng nhiệ t: q = = = 0,02
Khi bệ dà y già m 2 là n:
Grf* = Grf/23 = 0,37, tư c là Rà* = (Grf*.Pr) = 2,53.103. lOMoAR cPSD| 58970315
λtđ* = 0,18(Grf*.Pr)0,25.λ = 0,18.(2,53.103)0,25.0,035 = 0,045 W/mK = 0,6λtđ.
Bài 5.16: Nướ c chà y trong o ng co đướ ng kí nh d = 17mm, dà i 1,5m, vớ i và n to c 2m/s. Biệ t nhiệ t đo trung
bí nh cu à nướ c là 300C. Xà c đi nh hệ so to à nhiệ t. Giải
Kí ch thướ c xà c đi nh: ℓ = 17.10-3m Nhiệ t đo xà c đi nh: tf = 300C
Trà bà ng tà co cà c tho ng so và t ly cu à nướ c tướng ư ng vớ i nhiệ t đo tf tà đướ c:
λ = 0,618 W/mK; ν =0,805.10-6 m2/s; Prf = 5,42; Prw = 2,55 −3 2.17.10 Thày và o tí nh: Re = = = f −6 42236 0,805.10 0,25 0,25 Do đo : Nuf = 0,021.Ref .Prf = ( 0,8 0,43 PrPrwf 0,021.(42236)0,8 5,42)0,43 52,,5542 = 264 Nu .f f 264.0,618 9597W /m K2 Hệ so to à nhiệ t: = == 3 − 17.10
Bài 5.17: Xà c đi nh hệ so to à nhiệ t tư và ch o ng bí nh ngưng cu à tuàbin hới đệ n nướ c là m mà t. Biệ t rà ng
nhiệ t đo trung bí nh cu à và ch o ng tw = 370C, đướ ng kí nh o ng d = 16mm, nhiệ t đo cu à nướ c và o là 270C,
nhiệ t đo nướ c rà là 330C. To c đo trung bí nh cu à nướ c là 2m/s. Xà c đi nh lướ ng nhiệ t truyệ n cho nướ c là m
mà t và chiệ u dà i o ng. Hệ so to à nhiệ t α thày đo i thệ nà o nệ u to c đo cu à nướ c tà ng 2 là n khi cà c điệ u kiệ n khà c kho ng thày đo i. Giải
Kí ch thướ c xà c đi nh: ℓ = 16.10-3m t + t 33+27 t = f w1 w2 = =300C Nhiệ t đo xà c đi nh: 2 2
Trà cà c tho ng so cu à hới nướ c ớ nhiệ t đo tf tà đướ c: = 0,618W /mK;
= 0,805.10−6 m /s;2 = 995,7kg /m ;3 C = = = p 4,174kJ/kgK; Prf 5,42; Prw 4,64 . 2.16.10−3 lOMoAR cPSD| 58970315
Tư đo tà tí nh đướ c: Re = = = f −6 39752 0,805.10
Già thiệ t L/d > 50 nệ n εℓ = 1. Và y tà co : 0,25 0,25 0,8 0,43 Prf 0,021.397520,8.5,420,43 5,42 = 216 Nuf = 0,021.Ref .Prf = Prw 4,64 Nu .f 216.0,618 8343W /m K2 Do đo : = == 3 − 16.10 3,14.0,0162
Lưu lướ ng nướ c chà y quà o ng: G = f = 2. .995,7 = 0,4kg 4
Lướ ng nhiệ t truyệ n quà o ng là : Q = GC ( − )= p tf2 tf1
0,4.4,174.(33−27)=10kJ/s =10kW
Chiệ u dà i o ng đướ c tí nh tư co ng thư c: Q = . d.L(t − t ) w f Q 10.103 L = = − = 3 3,4m . d(t − ) w t f 8343.3,14.16.10 (37 −30) Thư là i kệ t quà :
L/d = 3,4/0,016 =212,5 > 50. Và y già thiệ t bàn đà u đà t rà là đu ng.
Khi to c đo do ng chà y tà ng 2 là n thí α tà ng 20,8 là n.
Bài 5.18: Nướ c chà y ngàng quà o ng thà ng co đướ ng kí nh 20mm, vớ i to c đo 0,5m/s, và nhiệ t đo trung
bí nh cu à nướ c tf =150C. Nhiệ t đo bệ mà t o ng là tw = 800C. Tí nh hệ so to à nhiệ t. Nệ u nướ c chà y xiệ n đi mo t
go c 500 thí hệ so to à nhiệ t là bào nhiệ u? Giải
Kí ch thướ c xà c đi nh: ℓ = d = 20.10-3m. Nhiệ t đo xà c đi nh: tf = 150C.
Trà cà c tho ng so cu à nướ c tà i nhiệ t đo tf tà đướ c: =58,58.10−2 W /mK; =1,156.10−6 m /s;2 Pr = = f 8,27 Prw 2,21 0,25 0,25 Tư đo tí nh đướ c: Nuf = 0,25.Ref .Prf . = lOMoAR cPSD| 58970315 0,6 0,38 PrPrwf 0,25.86500,6.8,270,38 82,,2127 =179 = Do đo = 3 20.10 −
Nu .f 179.58,58.10−2 =5243W /m K2
Khi nướ c chà y xiệ n go c =500 , trà bà ng tà đướ c: = 0,88 hệ so to à nhiệ t: = . = 0 0,88.5243 = 4614W / m K2 . 90
III. BÀI TẬP TỰ GIẢI
Bài 5.19: Nhiệ t đo mà t ngoà i tướ ng lo nung là 800C. Nhiệ t đo kho ng khí xung quành là 350C. Tí nh hệ so
to à nhiệ t tư tướ ng lo nệ u kho ng khí biệ t chiệ u cào cu à tướ ng là 2,5m. Đáp số: α = 5,3W/m2K.
Bài 5.20: Tí m hệ so dà n nhiệ t tướng đướng và mà t đo do ng nhiệ t cu à mo t khệ hệ p kho ng khí do hài tà m
phà ng tà o nệ n. Chiệ u dà y cu à khệ là δ = 25mm. Nhiệ t đo bệ mà t no ng là tw1 = 1500C, nhiệ t đo bệ mà t là nh là tw2 = 500C. Đáp số:
=tđ 0,0846W /mK; q =3384W /m2
Bài 5.21: Tí nh hệ so to à nhiệ t trung bí nh cu à dà u mà y biệ n à p chà y trong o ng co đướ ng kí nh d = 8mm,
chiệ u dà i 1m, nhiệ t đo trung bí nh cu à dà u là tf = 800C, nhiệ t đo trung bí nh cu à và ch o ng là tw = 200C, to c
đo chà y cu à dà u trong o ng là =0,6m/s . Đáp số: =215W /m K2
Bài 5.22: Co mo t tà m phà ng trớn chiệ u ro ng 1m, chiệ u dà i 1,2m. Nhiệ t đo bệ mà t và ch tw = 800C. Nhiệ t
đo do ng khí tf = 200C, to c đo do ng chà y ngàng quà tà m =6m/s . Tí nh hệ so to à nhiệ t và nhiệ t lướ ng to à rà trệ n bệ mà t tà m. Đáp số: =24W /m K;2 Q =1728W
Bài 5.23: Mo t dà y dà n bà ng đo ng co đướ ng kí nh d = 15mm, đướ c là m nguo i bà ng do ng khí chà y ngàng
quà vớ i to c đo là 1m/s. Nhiệ t đo cu à kho ng khí là tf = 200C. Tí nh hệ so to à nhiệ t tư bệ mà t dà y và o kho ng
khí và cướ ng đo do ng điệ n cho phệ p quà dà y đệ nhiệ t đo bệ mà t dà y kho ng quà 800C. Biệ t điệ n trớ suà t
cu à dà y là =0,0175 mm /m2 Đáp số: =24W /m K;2 I =827A 5.3. ĐỐI LƯU lOMoAR cPSD| 58970315
I. TÓM TẮT LÝ THUYẾT
1. Các định luật cơ bản về bức xạ nhiệt C1
a. Định luật Planck: E0 = C 2 5e T −1
b. Định luật dịch chuyển Wien: max.T = =b 2,898.10 (mK−3 )
c. Định luật Stefan – Boltzmann: 4 T
- Đo i vớ i và t đện tuyệ t đo i: E = 0 0T4 = C0 100 4 - Đo i vớ i và t xà m: E = 0T4 = C T 100 E E E
d. Định luật Kirchhoff: 1 = 2 = ... = n = E = 0 f (T) ; E = E A0 A = A1 A2 An
2. Trao đổi nhiệt giữa các vật trong môi trường trong suốt
a. Giữa hai vách phẳng song song vô hạn: 4 2 - Do ng nhiệ t riệ ng: q = C 12 0 T − T 1 2 100 100 1 =12 - Khi kho ng co mà n chà n: : đo đện cu à hệ . 1 1 + − 1 2 1 - Khi co n mà n chà n: 12 = 1 1 2 + −1+ n −1
b. Giữa hai vật bọc nhau 1 2 m C F01 T1 4 − T2 2 - Do ng nhiệ t: Q = 12 100 100 lOMoAR cPSD| 58970315 - Đo đện quy dà n: 1 qd = 1 + F 1 1 −1 1 F2 2 F Khi F1 = F2 thí = = qd12 ; Khi F1 << F2 thí 1 0 qd 1 1 F2
- Khi co đà t n mà n chà n: 1 qd,m = 1 =n FFm,i1 1m,i −1 + qd i 1
II. BÀI TẬP CÓ LỜI GIẢI
Bài 5.24: Mo t thành thệ p co nhiệ t đo là 7270C, đo đện ε = 0,7. Tí nh khà nà ng bư c xà cu à thành thệ p. Nệ u
nhiệ t đo già m đi 2 là n thí khà nà ng bư c xà già m đi mà y là n? Giải T = 727 + 273 = 1000K 4 4 T 1000 4 2 lOMoAR cPSD| 58970315
Khà nà ng bư c xà cu à thành thệ p: E = C0 = 0,7.5,67. =3,97.10 W / m 100 100
Nệ u nhiệ t đo trung bí nh cu à thệ p già m đi 2 là n thí : T = +273 = 636,5K 4 636,5 E = 0,7.5,67. = 6514,4W / m2 100 E 3,97.104 = = 6,09 là n.
Bài 5.25: Hài tà m phà ng đà t song
Khà nà ng bư c xà già m đi: E 6514,4
song, tà m thư nhà t co nhiệ t đo t1=
5270C, đo đện ε1 = 0,8, tà m thư 2 co nhiệ t đo t2 = 270C, đo đện ε2 = 0,6. Tí nh khà nà ng bư c xà cu à mo i
tà m và nhiệ t lướ ng trào đo i bà ng bư c xà giư à hài tà m phà ng? Nệ u giư à hài tà m co đà t mo t mà n chà n co
đo đện εm = 0,05 thí nhiệ t lướ ng trào đo i giư à hài tà m phà ng là bào nhiệ u? Tí nh nhiệ t đo cu à mà n chà n? Giải T1 = 527 + 273 = 800K T2 = 27 + 273 = 300K
Khà nà ng bư c xà cu à tư ng tà m: 4 4 E1 = 1C0 T1 = 0,8.5,67. 800 =18579W / m2 100 100 4 4 T2 = 0,6.5,67. 300 = 275W / m2 E = 2 2C0 100 100
Lướ ng nhiệ t trào đo i bà ng bư c xà giư à hài tà m phà ng ư ng vớ i mo t đớn vi diệ n tí ch: 1 1 == 12 0,526 = 1 1 1 1 1 − 1 − + + 1 2 0,8 0,6 4 2 q12 = 12C0 T1 − T2 =0,526.5,67. 800 4 − 300 4 =11975W /m2