



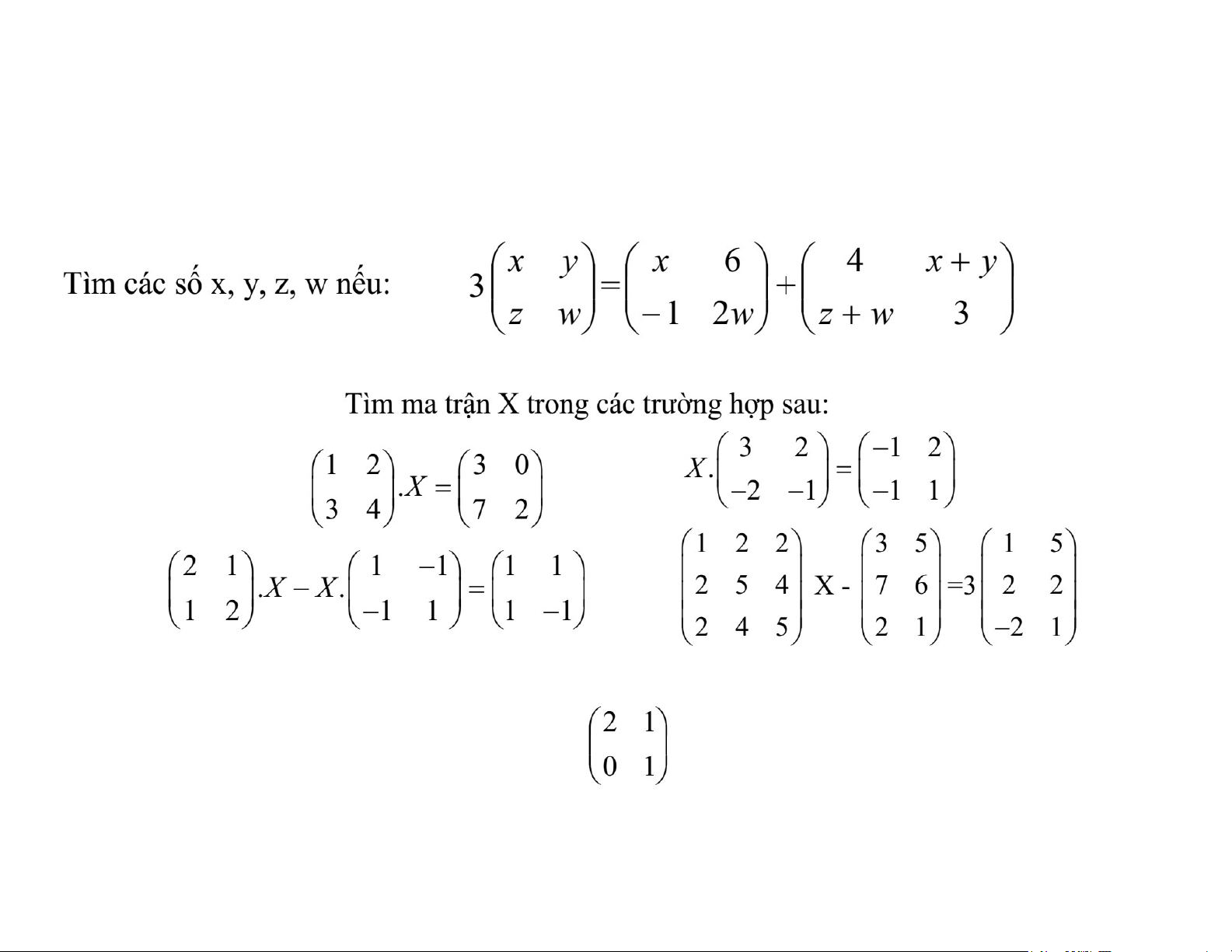




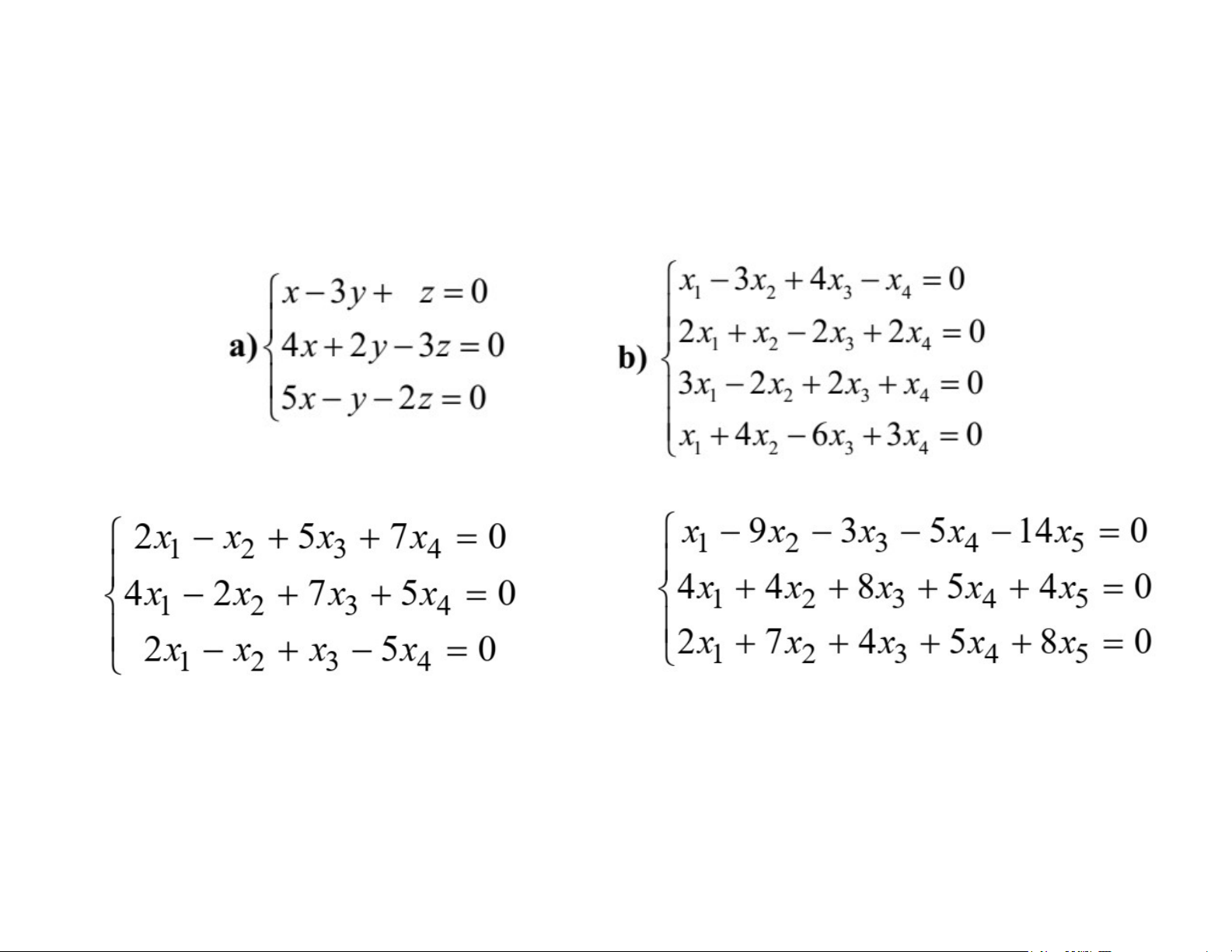
Preview text:
I. BÀI TẬP ĐỊNH THỨC 1.1: Tính các định thức 2 1 a) b) c) d) e) 3 1 0 1 1 1 x y x y 1 0 a b f) g) y x y x 1 a 0 c h) x y x y i) 1 b c 0 j) k) l) 3 3 3 2 2 2 3 3
a) 5; b) 40; c) -6; d) 20; e) a +b +c -3abc; f) a +b +c -2 ab +bc+ca ; g) -2 x +y n n+1 2
h) x x-y-zx+y+z; i) abc+abx+bcx+cax; j)- n-1 n-1 1 n!; k) x ; l) - n-1 1 n! 1 2
1.2: Chứng minh bài toán định thức b c c a a b a b c
a) b'c' c'a' a'b' 2 a' b' c' b)
b' c ' c ' a ' a ' b' a ' b' c ' c) (a, , b c 0) d) a b c a ' b' c ' a' b' c ' e)
a ' b' c ' a ' b ' c ' a ' b' c ' f) a' b' c' a b c a b c 2
1.3: Giải phương trình, bất phương trình từ định thức a) b) c) d) f) g) e) h) i) a) x 2,3,or 4; b) x ; R c) 6 x 4
; d) x 1,3 2,or 3 2; e) x 3 ,or 4 3 I . BÀI TẬP MA TRẬN 2.1: Phép tính ma trận g x 2 1 x 2x 1 g A ? x g) n n n h) i) j) k) 4 2.2: Tìm ma trận a) * * c) b) d) e) 1 0 0 1 2
Tìm ma trận giao hoán với ma trận sau: f) g) h) 0 1 0 * 1 1 3 1 2 5 2.3: Ma trận nghịch đảo
*Tìm ma trận nghịch đảo: a) b) c)
*Định m để tồn tại ma trận nghịch đảo (khả nghịch, không suy biến) và tìm ma trận nghịch đảo d) e) 6 2.4: Hạng của ma trận *Tìm hạng của ma trận: a) b)
*Định tham số m để có hạng xác định hoặc biện luận hạng theo m: c) d) e) f) g) h) 7
I I. GIẢI HỆ PHƯƠNG TRÌNH TUYẾN TÍNH 3.1: Giải hệ pttt a) b) c) d) e) 8
3.2: Giải hệ và biện luận nghiệm pttt theo tham số f) g) h) 9
IV. TÌM HỆ NGHIỆM CƠ BẢN c) d) 10




