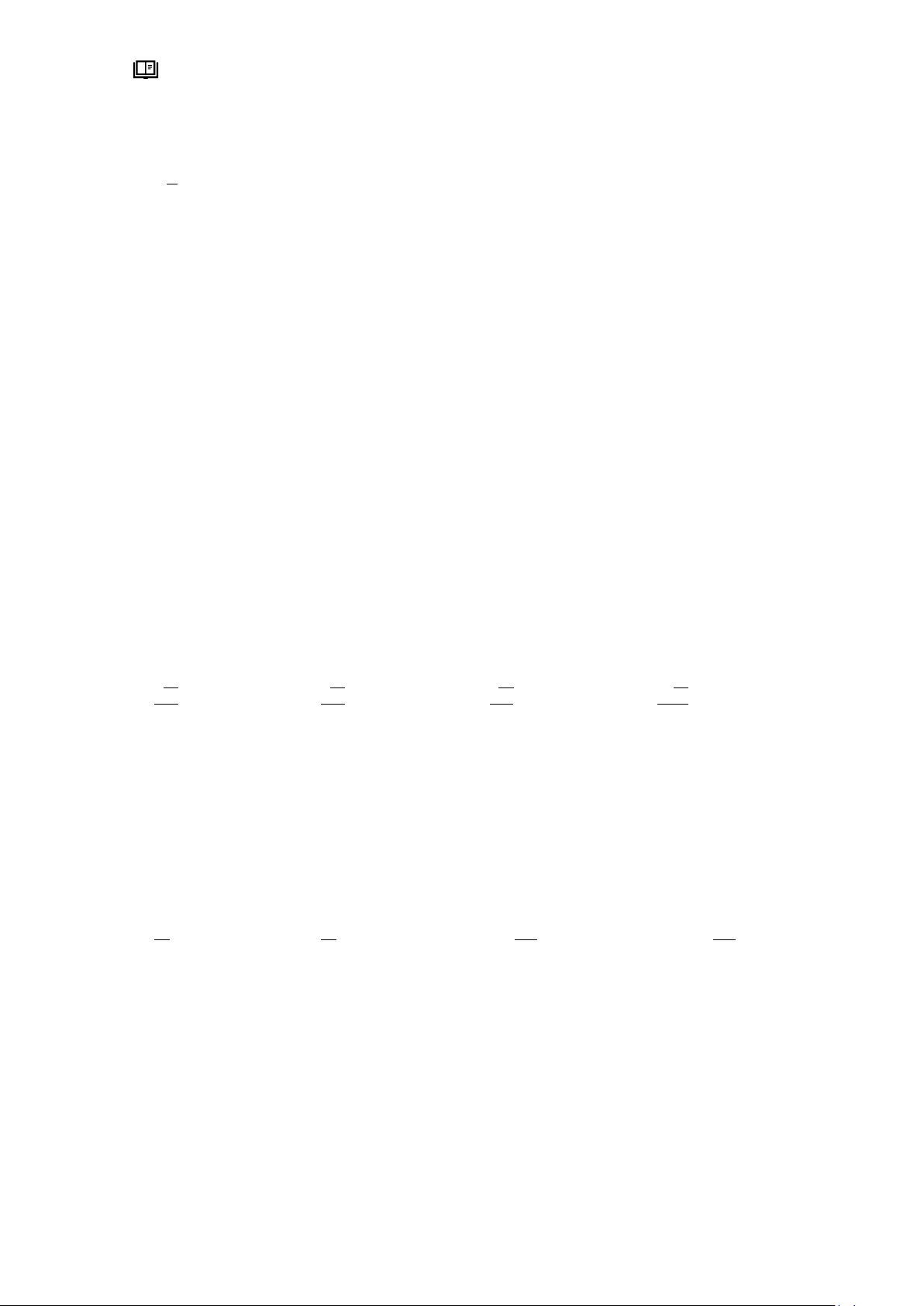
Preview text:
KHÓA NỀN TẢNG TOÁN 12
CHƯƠNG II : TỌA ĐỘ CỦA VÉC TƠ TRONG KHÔNG GIAN
BÀI TẬP VECTER (TIẾP)
Phần I: Câu hỏi trắc nghiệm một phương án
Câu 1: Trong không gian, cho bốn điểm phân biệt 𝐴, 𝐵, 𝐶, 𝐷. Đẳng thức nào sau đây là đúng? A. 𝐵𝐶 ⃗⃗⃗ + 𝐶𝐷 ⃗⃗⃗ = 𝐵𝐷 ⃗⃗⃗ B. 𝐴𝐵 ⃗⃗⃗ − 𝐵𝐶 ⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗ C. 𝐵𝐷 ⃗⃗⃗ − 𝐵𝐶 ⃗⃗⃗ = 𝐷𝐶 ⃗⃗⃗ D. 𝐴𝐷 ⃗⃗⃗ + 𝐷𝐶 ⃗⃗⃗ = 𝐶𝐴 ⃗⃗⃗ .
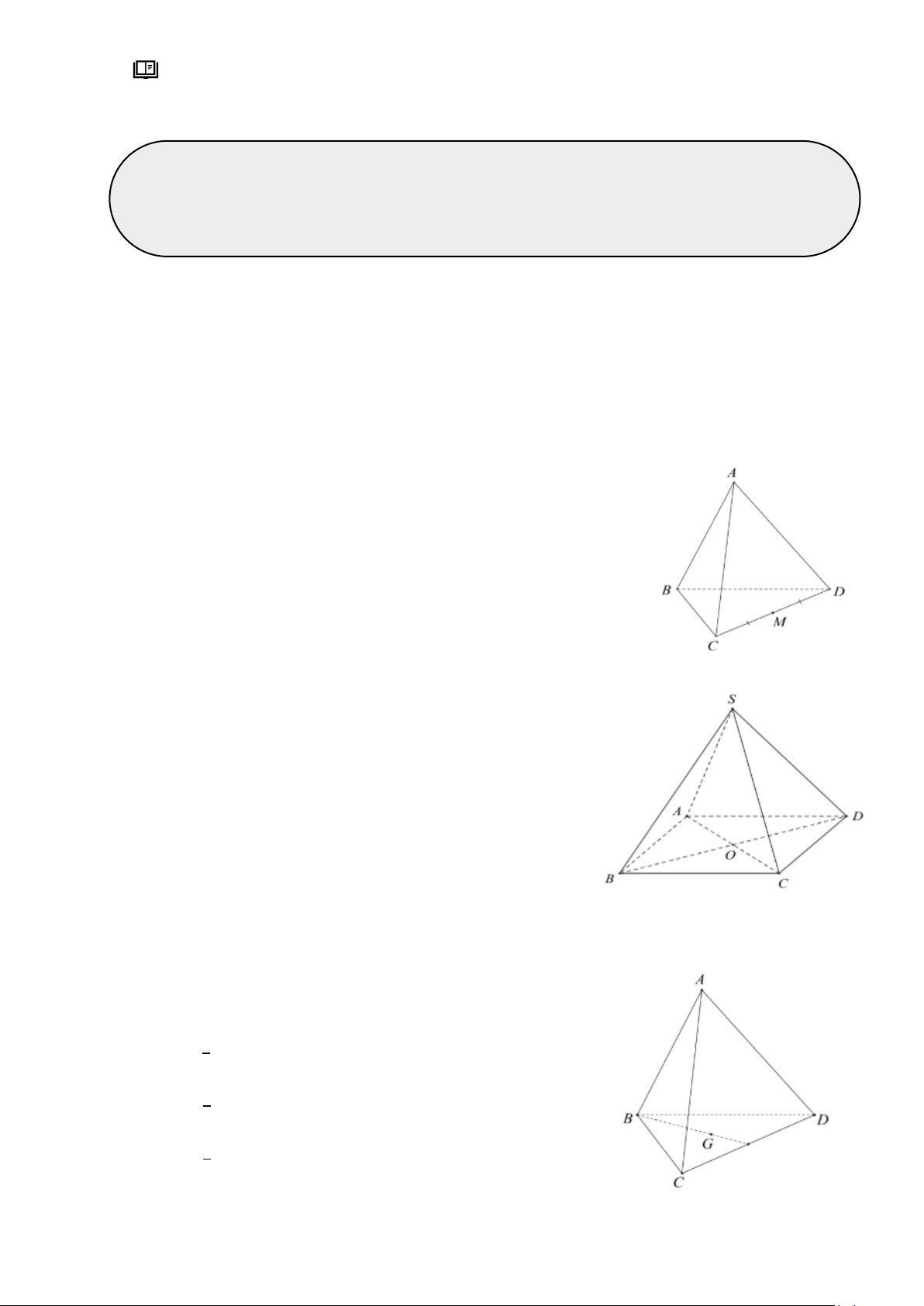
Câu 2: Cho tứ diện 𝐴𝐵𝐶𝐷, gọi 𝑀là trung điể m của 𝐶𝐷.
Khẳng định nào sau đây đúng? A. 𝑀𝐴 ⃗⃗⃗ + 𝑀𝐷 ⃗⃗⃗ = 0⃗ . B. 𝑀𝐵 ⃗⃗⃗ + 𝑀𝐶 ⃗⃗⃗ = 0⃗ . C. 𝑀𝐷 ⃗⃗⃗ + 𝑀𝐶 ⃗⃗⃗ = 0⃗ . D. 𝑀𝐴 ⃗⃗⃗ + 𝑀𝐵 ⃗⃗⃗ = 0⃗ .
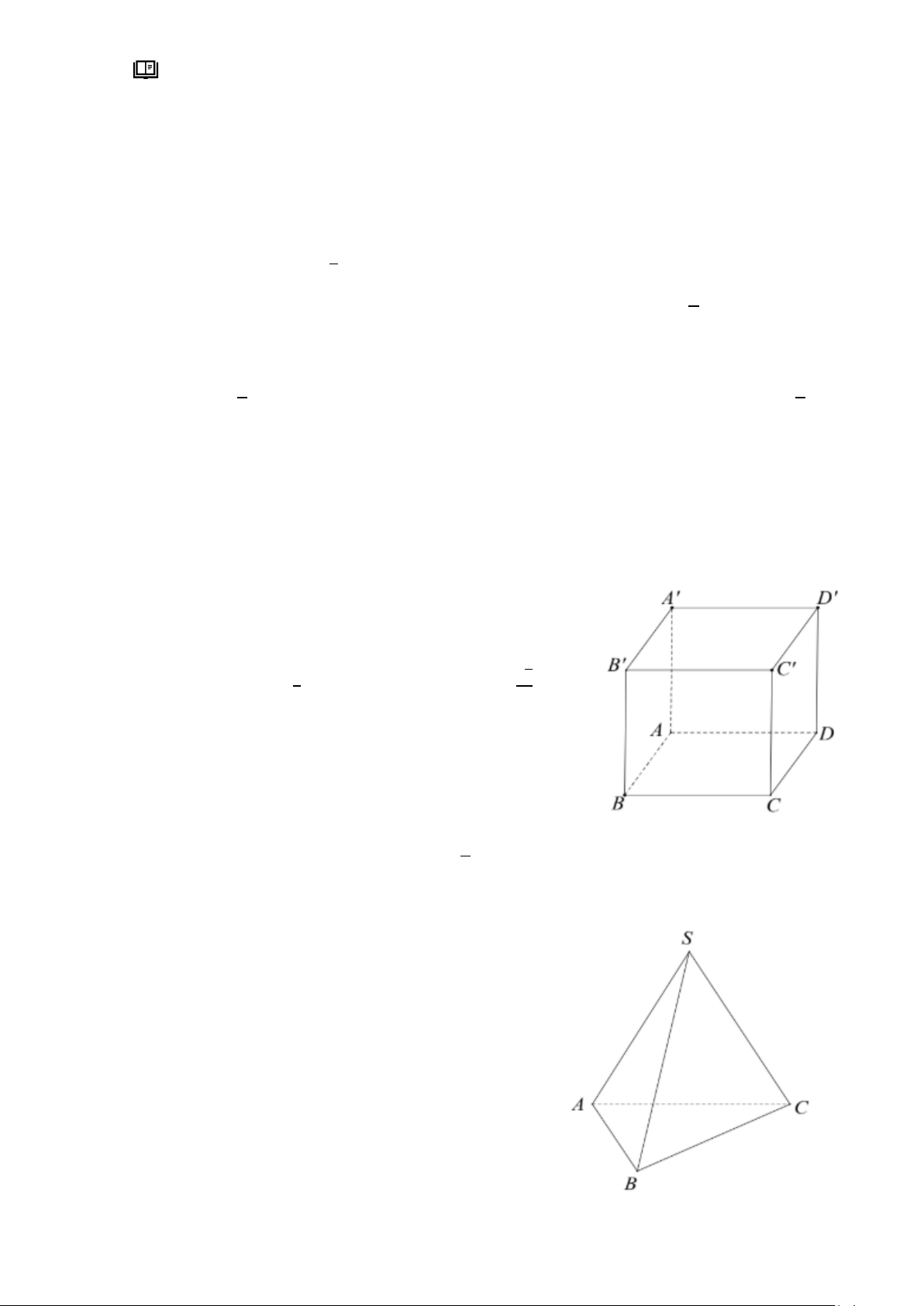
Câu 3: Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷có đáy 𝐴𝐵𝐶𝐷là hình bình hành tâm 𝑂. Chọn mệnh đề đúng. A. 𝑆𝐴 ⃗⃗⃗ + 𝑆𝐵 ⃗⃗⃗ + 𝑆𝐶 ⃗⃗ + 𝑆𝐷 ⃗⃗⃗ = 4𝑆𝑂 ⃗⃗⃗ . B. 𝑆𝐴 ⃗⃗⃗ + 𝑆𝐵 ⃗⃗⃗ + 𝑆𝐶 ⃗⃗ + 𝑆𝐷 ⃗⃗⃗ = 4𝑂𝑆 ⃗⃗⃗ . C. 𝑆𝐴 ⃗⃗⃗ + 𝑆𝐵 ⃗⃗⃗ + 𝑆𝐶 ⃗⃗ + 𝑆𝐷 ⃗⃗⃗ = 2𝑆𝑂 ⃗⃗⃗ . D. 𝑆𝐴 ⃗⃗⃗ + 𝑆𝐵 ⃗⃗⃗ + 𝑆𝐶 ⃗⃗ + 𝑆𝐷 ⃗⃗⃗ = 8𝑆𝑂 ⃗⃗⃗ .
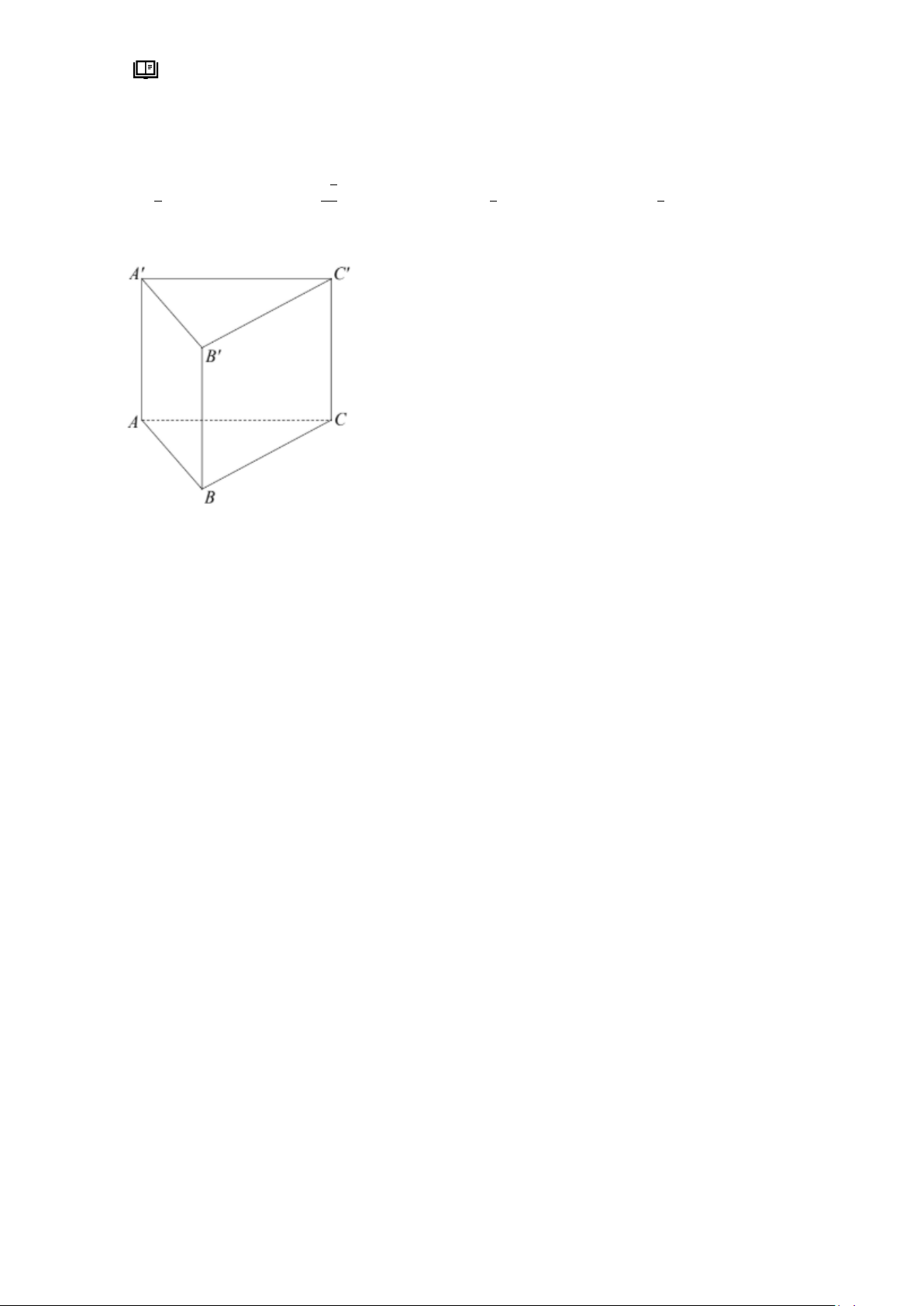
Câu 4: Cho tứ diện 𝐴𝐵𝐶𝐷, biết 𝐴𝐵 ⃗⃗⃗ = 𝑏⃗ , 𝐴𝐶 ⃗⃗⃗ = 𝑐 , 𝐴𝐷
⃗⃗⃗ = 𝑑 , 𝐺 là trọng tâm tam giác 𝐵𝐶𝐷. Tìm
hệ thức liên hệ giữa 𝐴𝐺
⃗⃗⃗ với ba vectơ 𝑏⃗ , 𝑐 , 𝑑 . A. 𝐴𝐺
⃗⃗⃗ = 𝑏⃗ + 𝑐 + 𝑑 . B. 1 𝐴𝐺
⃗⃗⃗ = (𝑏⃗ + 𝑐 + 𝑑 ). 3 C. 1 𝐴𝐺
⃗⃗⃗ = (𝑏⃗ + 𝑐 + 𝑑 ). 4 D. 1 𝐴𝐺
⃗⃗⃗ = (𝑏⃗ + 𝑐 + 𝑑 ). 2 KHÓA NỀN TẢNG TOÁN 12
Câu 5: Với hai vectơ 𝑢⃗ , 𝑣 khác vectơ–không tùy ý, tích vô hướng 𝑢⃗ ⋅ 𝑣 bằng
A. ∣ 𝑢⃗ ∣ . ∣ 𝑣 ∣⋅ cos(𝑢⃗ , 𝑣 ).
B. −∣ 𝑢⃗ ∣ . ∣ 𝑣 ∣⋅ cos(𝑢⃗ , 𝑣 ).
C. ∣ 𝑢⃗ ∣ . ∣ 𝑣 ∣⋅ sin(𝑢⃗ , 𝑣 ).
D. −∣ 𝑢⃗ ∣ . ∣ 𝑣 ∣⋅ sin(𝑢⃗ , 𝑣 ).
Câu 6: Cho hai vectơ 𝑢⃗ , 𝑣 trong không gian có độ dài lần lượt là 𝑎 và 2𝑎. Cosin của
góc giữa hai vectơ bằng 1. Tính tích vô hướng 𝑢⃗ ⋅ 𝑣 : 2 A. 𝑎2 B. 𝑎 C. 2𝑎2 D. 𝑎2√3
Câu 7: Cho 2 vectơ 𝑢⃗ , 𝑣 có ∣ 𝑢⃗ ∣= 2, ∣ 𝑣 ∣= 5 và (𝑢⃗ , 𝑣 ) = 30∘. Tính 𝑢⃗ ⋅ 𝑣 .
A. 𝑢⃗ ⋅ 𝑣 = 5√2.
B. 𝑢⃗ ⋅ 𝑣 = 5.
C. 𝑢⃗ ⋅ 𝑣 = 10.
D. 𝑢⃗ ⋅ 𝑣 = 5√3.
Câu 8: Cho hai vectơ 𝑎 và 𝑏⃗ thỏa mãn ∣ 𝑎 ∣= 3, ∣ 𝑏⃗ ∣= 2và 𝑎 ⋅ 𝑏⃗ = −3. Xác định góc 𝛼 giữa hai vectơ 𝑎 và 𝑏⃗ . A. 𝛼 = 30∘. B. 𝛼 = 45∘. C. 𝛼 = 60∘. D. 𝛼 = 120∘.
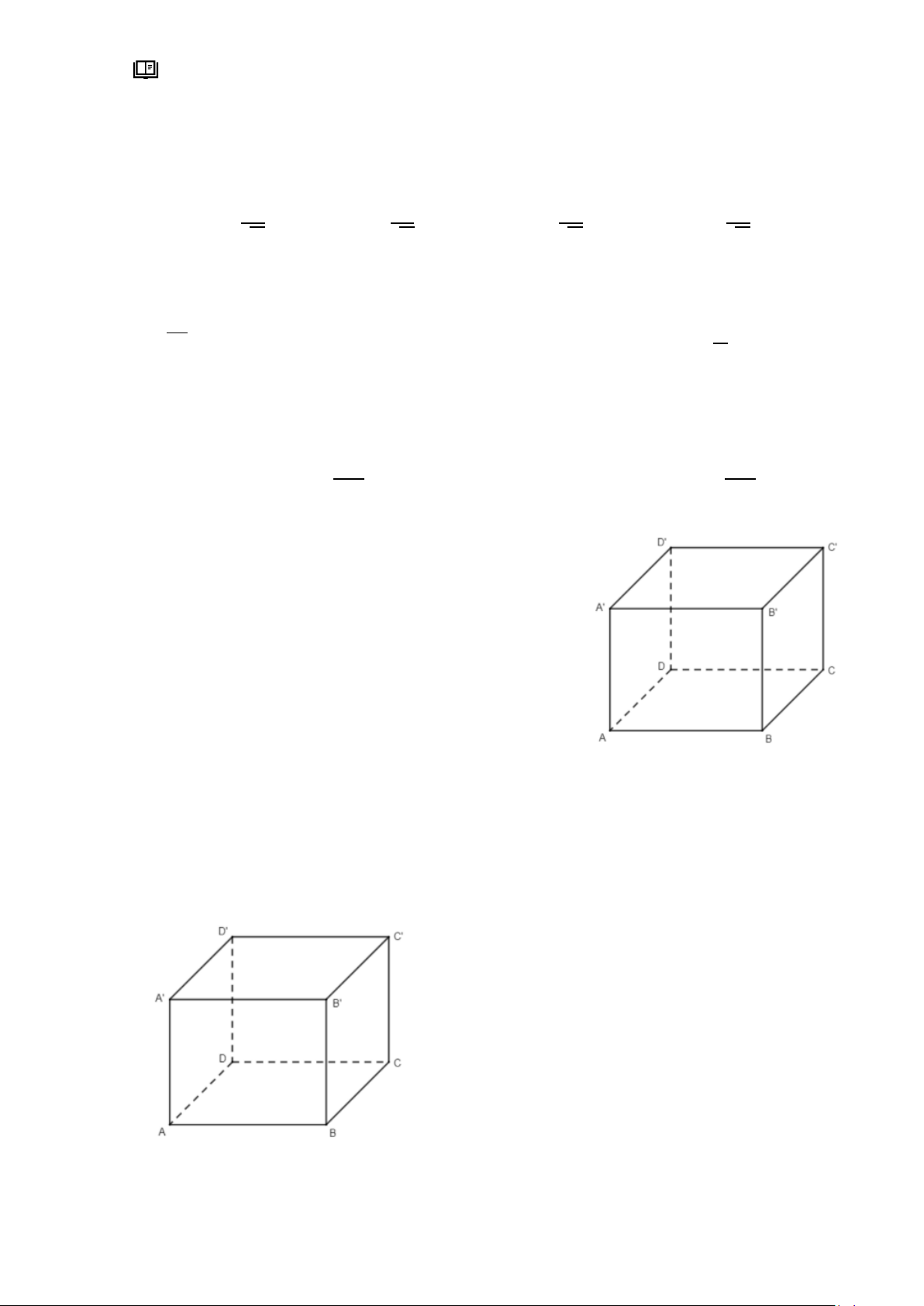
Câu 9: Cho hình lập phương 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′. Tính cos(𝐵𝐷 ‾ , 𝐴′𝐶 ‾ ′). A. cos(𝐵𝐷 ‾ , 𝐴′𝐶 ‾ ′) = 0. B. cos(𝐵𝐷 ‾ , 𝐴′𝐶 ‾ ′) = 1. C. 1 cos(𝐵𝐷 ‾ , 𝐴′𝐶 ‾ ′) = . D. cos(𝐵𝐷 ‾ , 𝐴′𝐶 ‾ ′) = √2. 2 2
Câu 10: Cho hình chóp 𝑆. 𝐴𝐵𝐶có 𝐵𝐶 = 𝑎√2, các cạnh còn lại đều bằng 𝑎.
Góc giữa hai vectơ 𝑆𝐵 ⃗⃗⃗ và 𝐴𝐶 ⃗⃗⃗ bằng: A. 60∘ B. 120∘ C. 30∘ D. 90∘ KHÓA NỀN TẢNG TOÁN 12
Câu 11: Cho hình lăng trụ tam giác đều 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′có tất cả các cạnh đều bằng 𝑎. Tính ∣ cos(𝐴 ⃗ 𝐵 ⃗⃗ ′ ⃗ , 𝐵 ⃗⃗𝐶 ⃗⃗ ′ ⃗ ) ∣. A. 3 B. √2 C. 1 D. 1 4 4 2 4
Câu 12: (MĐ102 – BGD&ĐT – 2020 Lần 1) Trong không gian 𝑂𝑥𝑦𝑧, hình chiếu vuông góc
của điểm 𝐴(1; 2; 5) trên trục 𝑂𝑥có tọa độ là: A. (0; 2; 0) B. (0; 0; 5) C. (1; 0; 0) D. (0; 2; 5)
Câu 13: (MĐ104 – BGD&ĐT – 2019) Trong không gian 𝑂𝑥𝑦𝑧, hình chiếu vuông góc của
điểm 𝑀(3; 1; −1)t rên trục 𝑂𝑦 có tọa độ là: A. (3; 0; −1) B. (0; 1; 0) C. (3; 0; 0) D. (0; 0; −1)
Câu 14:Trong không gian với hệ trục tọa độ 𝑂𝑥𝑦𝑧, hình chiếu vuông góc của 𝑀(0; 4; 3) trên trục 𝑂𝑧 là: A. 𝑀′(0; −4; 3) B. 𝑀′(0; 4; 0) C. 𝑀′(0; 4; 0) D. 𝑀′(0; 0; 0)
Câu 15: (ĐỀ MINH HỌA 2020 Lần 1) Trong không gian 𝑂𝑥𝑦𝑧, hình chiếu vuông góc của
điểm 𝑀(2; −2; 1)trên mặt phẳng (𝑂𝑥𝑦) có tọa độ là: A. (2; 0; 1) B. (2; −2; 0) C. (0; −2; 1) D. (0; 0; 1)
Câu 16: (ĐỀ MINH HỌA 2020 Lần 2) Trong không gian 𝑂𝑥𝑦𝑧, hình chiếu vuông góc của
điểm 𝑀(2; 1; −1) trên mặt phẳng (𝑂𝑧𝑥) có tọa độ là: A. (0; 1; 0) B. (2; 1; 0) C. (0; 1; −1) D. (2; 0; −1)
Câu 17: Cho 𝐴(1; 1; 1), 𝐵(2; 3; 3), tính độ dài đoạn thẳng 𝐴𝐵 A. 𝐴𝐵 = 3 B. 𝐴𝐵 = 2 C. 𝐴𝐵 = 4 D. 𝐴𝐵 = 1 KHÓA NỀN TẢNG TOÁN 12
Câu 18: Trong không gian 𝑂𝑥𝑦𝑧, cho hai điểm 𝑀(2; 1; 1)và 𝑁(2; 4; −3). Khoảng cách 𝑀𝑁bằng: A. √5 B. 5 C. 1 D. 7
Câu 19: Trong không gian với hệ tọa độ 𝑂𝑥𝑦𝑧, cho 𝑎 = (2; 1; −2) và 𝑏⃗ = (1; 0; 2).
Tìm tọa độ vectơ 𝑐 là tích có hướng của 𝑎 và 𝑏⃗ .
A. 𝑐 = (2; 6; −1).
B. 𝑐 = (4; 6; −1).
C. 𝑐 = (4; −6; −1). D. 𝑐 = (2; −6; −1).
Câu 20: Cho 𝑎 = (−2; 0; 1), 𝑏⃗ = (1; 3; −2). Trong các khẳng định sau, khẳng định nào đúng?
A. [𝑎 , 𝑏⃗ ] = (−3; −3; −6).
B. [𝑎 , 𝑏⃗ ] = (3; 3; −6).
C. [𝑎 , 𝑏⃗ ] = (1; 1; −2).
D. [𝑎 , 𝑏⃗ ] = (−1; −1; 2).
Câu 21: Trong không gian 𝑂𝑥𝑦𝑧, tọa độ một vectơ 𝑛⃗ vuông góc với cả hai vectơ
𝑎 = (1; 1; −2), 𝑏⃗ = (1; 0; 3) là: A. (2; 3; −1). B. (3; 5; −2). C. (2; −3; −1). D. (3; −5; −1).
Câu 22: Trong không gian 𝑂𝑥𝑦𝑧, cho tam giác 𝐴𝐵𝐶có 𝐴(1; 0; 0), 𝐵(0; 0; 1), 𝐶(2; 1; 1).
Khoảng cách từ điểm 𝐴đến đường thẳng 𝐵𝐶 bằng: A. √30. B. √30. C. √30. D. 2√30. 5 10 6 5
Câu 23: Trong hệ trục tọa độ 𝑂𝑥𝑦𝑧, cho bốn điểm 𝐴(1; −2; 0), 𝐵(2; 0; 3), 𝐶(−2; 1; 3) và
𝐷(0; 1; 1). Thể tích khối tứ diện 𝐴𝐵𝐶𝐷 bằng: A. 6. B. 8. C. 12. D. 4.
Câu 24: Cho hai vectơ 𝒂 ⃗ , 𝒃
⃗ có ∣ 𝑎 ∣= 5, ∣ 𝑏⃗ ∣= 12 và ∣ 𝑎 + 𝑏⃗ ∣= 13. Khi đó cosin của góc
giữa hai vectơ (𝑎 − 𝑏⃗ ) và (𝑎 + 𝑏⃗ ) bằng: A. 12 B. 5 C. - 119 D. 119 13 12 169 169
Câu 25: Cho 𝑢⃗ = 𝑎 + 3𝑏⃗ vuông góc với 𝑣 = 7𝑎 − 5𝑏⃗ và 𝑥 = 𝑎 − 4𝑏⃗ vuông góc với
𝑦 = 7𝑎 − 2𝑏⃗ . Khi đó góc giữa hai vectơ 𝑎 và 𝑏⃗ bằng
A. (𝑎 , 𝑏⃗ ) = 75∘
B. (𝑎 , 𝑏⃗ ) = 60∘
C. (𝑎 , 𝑏⃗ ) = 120∘
D. (𝑎 , 𝑏⃗ ) = 45∘ KHÓA NỀN TẢNG TOÁN 12
Câu 26: Cho hai vectơ 𝑎 , 𝑏⃗ thỏa mãn: ∣ 𝑎 ∣= 4; ∣ 𝑏⃗ ∣= 3; 𝑎 ⋅ 𝑏⃗ = 10. Xét hai vectơ
𝑦 = 𝑎 − 𝑏⃗ , 𝑥 = 𝑎 − 2𝑏⃗ . Gọi α là góc giữa hai vectơ 𝑥 , 𝑦 . Chọn khẳng định đúng. A. 2 1 3 2 cos 𝛼 = − B. cos 𝛼 = C. cos 𝛼 = D. cos 𝛼 = √15 √15 √15 √15
Câu 27: Trong không gian cho hai vectơ 𝑢⃗ , 𝑣 có (𝑢⃗ , 𝑣 ) = 120∘, ∣ 𝑢⃗ ∣= 3 và ∣ 𝑣 ∣= 8. Độ dài
của vectơ ∣ 𝑢⃗ + 𝑣 ∣ bằng: A. √19. B. 7. C. 11. D. 15. 2
Câu 28: Cho hai vectơ 𝑎 , 𝑏⃗ thỏa mãn:∣ 𝑎 ∣= 26, ∣ 𝑏⃗ ∣= 28 và ∣ 𝑎 + 𝑏⃗ ∣= 48. Độ dài vectơ 𝑎 − 𝑏⃗ bằng? A. 25 B. √616 C. 9 D. √618
Câu 29: Cho hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′với các đỉnh
𝐴(−1; 2; 3),𝐵(2; −4; 1),D(3; −1; 1), 𝐴′(0; 1; 2).
Tìm tọa độ các đỉnh còn lại của hình hộp.
Câu 30: Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷có đáy 𝐴𝐵𝐶𝐷là hình chữ nhật, 𝐴𝐵 = 1,𝐴 𝐷 = 2, 𝑆𝐴vuông
góc với mặt phẳng đáy, 𝑆𝐴 = 3. Với hệ tọa độ 𝑂𝑥𝑦𝑧được thiết lập như sau: gốc tọa độ 𝑂trùng
với điểm 𝐴, các vectơ 𝐴𝐵 ⃗⃗⃗ , 𝐴𝐷 ⃗⃗⃗ , 𝐴𝑆
⃗⃗⃗ lần lượt cùng hướng với 𝑖 , 𝑗 , 𝑘⃗ .
Tìm tọa độ điểm 𝐷, 𝐶, 𝑆, 𝐼. KHÓA NỀN TẢNG TOÁN 12
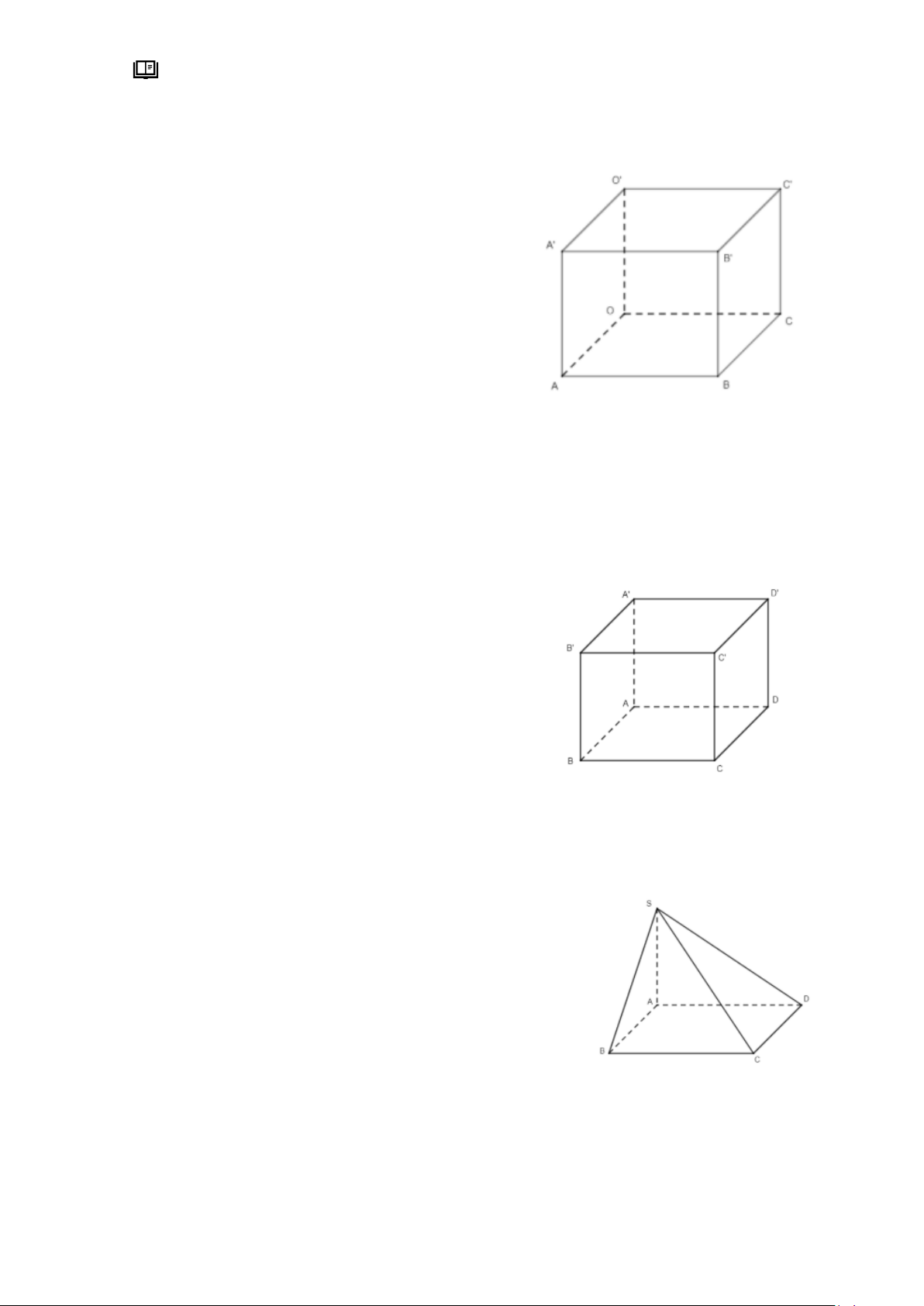
Câu 31: Cho hình hộp 𝑂𝐴𝐵𝐶. 𝑂′𝐴′𝐵′𝐶′có cạnh 𝑂𝐴 = 3,𝑂 𝐶 = 4, OO' = 3. Cho hệ trục tọa
độ 𝑂𝑥𝑦𝑧 có gốc O; các điểm A, C, O' lần lượt nằm trên các tia 𝑂𝑥, 𝑂𝑦, 𝑂𝑧. Xác định tọa độ
điểm 𝐵′. Tìm tọa độ các điểm. A. 𝐵′(3; 4; 0) B. 𝐵′(3; 4; 3) C. 𝐵′(3; 3; 4) D. 𝐵′(4; 3; 3)
Câu 32: Trong không gian với hệ tọa độ 𝑂𝑥𝑦𝑧, cho điểm 𝐴(−5; 8; 1). Tìm tọa độ của vectơ 𝑂𝐴 ⃗⃗⃗ . A. (−5; 8; 1) B. (−5; 8; 0) C. (0; 8; 1) D. (−5; 0; 1)
Câu 33: Trong không gian 𝑂𝑥𝑦𝑧, cho hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′có đỉnh A trùng
với gốc O, các vectơ 𝐴𝐵 ⃗⃗⃗ , 𝐴𝐷 ⃗⃗⃗ , 𝐴 ⃗⃗𝐴 ⃗⃗ ′
⃗ theo thứ tự cùng hướng với 𝑖 , 𝑗 , 𝑘⃗ và có 𝐴𝐵 = 4,𝐴 𝐷 =
5, 𝐴𝐴′ = 2. Tìm tọa độ vectơ 𝐴 ⃗⃗𝐶 ⃗⃗ ′ ⃗ . A. (4; 5; −2) B. (4; 2; 5) C. (5; 4; 2) D. (4; 5; 2)
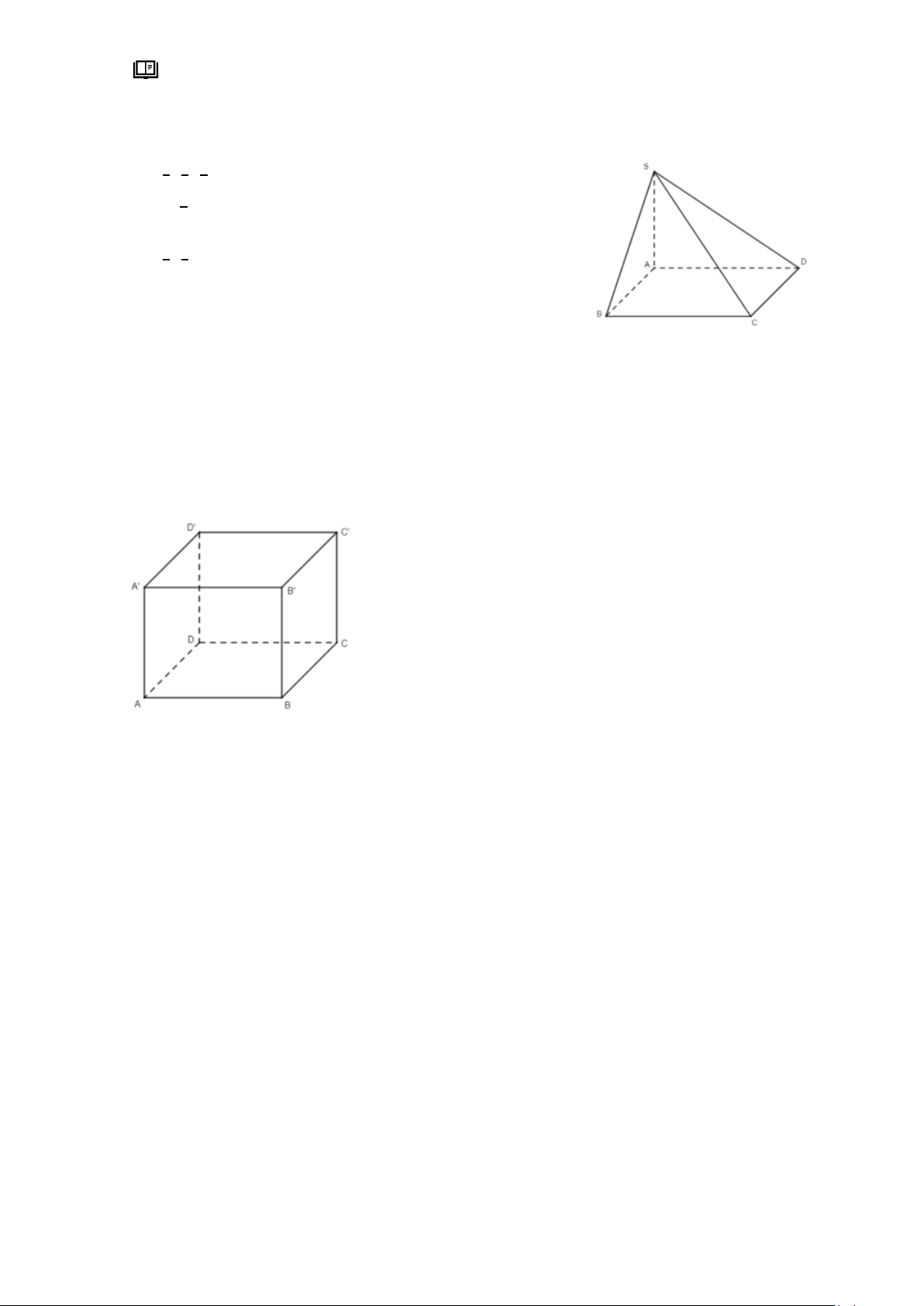
Câu 34: Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt
phẳng đáy và có độ dài bằng 3. Chọn hệ tọa độ 𝑂𝑥𝑦𝑧có gốc O trùng với điểm A, các điểm B,
D, S lần lượt nằm trên các tia 𝑂𝑥, 𝑂𝑦, 𝑂𝑧.
a) Xác định tọa độ vectơ 𝐴𝐶 ⃗⃗⃗ A. (0; 1; 1) B. (1; 0; 1) C. (1; 0; 0) D. (1; 1; 0) KHÓA NỀN TẢNG TOÁN 12
b) Xác định tọa độ vectơ 𝐴𝑀
⃗⃗⃗ , với M là trung điểm SC A. 1 1 3 ( ; ; ) 2 2 2 B. 1 (1; ; 0) 2 C. (1; 1; 1) D. 1 1 ( ; ; 0) 2 2
Câu 35: Trong không gian với hệ tọa độ 𝑂𝑥𝑦𝑧, cho hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′, biết rằng
𝐷(0; 0; 1), 𝐴(−3; 0; 0), 𝐵(0; 2; 0), 𝐴′(1; 2; 3). Tìm tọa độ điểm 𝐶′. A. (10; 4; 4) B. (−13; 4; 4) C. (13; 4; 4) D. (7; 4; 4)



