BÀI TẬP CƠ LÝ THUYẾT I
Ñaùnh giaù keát quaû hoïc taäp:
- - Điểm quá trình (trọng số 0.2) -
+ Học tập chuyên cần: 0.3
+ Bài tập đầy đủ: 0.7
- Thi giữa kỳ (trọng số 0.2)
- Thi cuối kỳ (trọng số 0.6) 1 BÀI TẬP CƠ LÝ THUYẾT I
CHƯƠNG 1: BÀI TOÁN PHẲNG MỘT VẬT Bài 1.1 N =? N =? A B Q=? để xe vượt qua bậc GIẢI
1. Vật khảo sát bánh xe
Hệ lực tác dụng lên bánh xe gồm: + Lực hoạt động P,Q + Lực liên kết N ,N A B
Hệ lực (P,Q,N ,N ) = 0 do bánh xe nằm cân bằng A B
Đây là hệ đồng quy phẳng,hệ pt cân bằng của hệ lực:
∑F = Q - N .cosα =0 N =Q/cosα x B B
∑F = -P+ N +N sinα =0 N =P-Qtgα y A B A 2 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.2
Giả sử 2 thanh đều bị nén.chọn vật khảo sát là ròng rọc,
-Hệ lực tác dụng lên ròng rọc là: + Lực hoạt động P,Q + Lực liên kết S ,S A B
Vì ròng rọc nằm cân bằng nên hệ (P,F,S ,S )=0 A B Hệ lực ực trên đồng phẳ
n đồng phẳng,ta có pt cân bằng c ng của hệ lực ∑F =Fcosβ+ β+S .cosα-S .cosα=0 A.cosα-S .cosα= x A B
∑F = -P+Fsinβ+S .sinα+S .sinα=0 (R:là bán kính nh ròng rọc) y A B ∑m (F )= )=0 - 0 > -> -F -FR+PR=0 o k 3 BÀI TẬP CƠ LÝ THUYẾT I BÀI 1.3 L=4m P’=5kN
Bức tường dày 0.5m tựa trên 2 cạnh tường A,B. Đầu C treo P = 40kN N =? , N =? A B Giải Vật khảo sát là dầm
Hệ lực tác dụng lên dầm +lực tác động là P,P’ +Phản lực liên kết N ,N A B
Vì dầm nằm cân bằng nên hệ (P,P’,N ,N )=0 A B Pt cân bằng của hệ là: ∑F = -P -P’+ N -N = 0 y = -P -P’+ N y A-NB =
∑m (F )=0 => 0 + P.BC + P’.1/2PC-N .AB = 0
B(Fk)=0 => 0 + P.BC + P’.1/2PC-NA.AB = B k A Giải r ra ta có: NA=(2P+P‘)BC/2AB 2AB = 340kN N = N – P – P’ = 295 kN B = NA – P – P’ = 295 k 4 B A BÀI TẬP CƠ LÝ THUYẾT I Bài 1.4 Xe mang vật nặng P =40kN 1
Hệ lực tác dụng lên dằm +Lực hoạt động :P,P1 +Lực liên kết:N ,N A B
Dầm nằm cân bằng nên hệ lực (P,P ,N ,N )=0 1 A B
Phương trình cân bằng của hệ lực: ∑F = - P - P + N + N = 0 (1) iy 1 A B
∑m (F )= - P. AB /2 - P .AC + N . AB=0 (2) A i 1 B
Từ (2) => - P. AB/2 - P .AB.n + N .AB=0 trong đó n= AC/AB 1 B
=> N =P/2 + n.P1 = 30+40.n = (3+4n).10 kN B
(1) => N = P + P – N = P/2+(1-n)P =30+ (1-n) 40 A 1 B 1 =(7-4n).10 kN 5 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.5
Vật khảo sát ở 2 ổ đỡ A,B
+ Lực hoạt động:P ,P ,P 1 2 3 + Lực liên kết:N ,N A B 2 vật nằm câ c n b ân ằng n bằng ên nên hệ hệ (P (P ,P , P , N ,N )=0 1,P2, P3, NA,NB)= 1 2 3 A B Hệ lực trên song song song nên nên pt pt câ cân bằ n b ng c ằng của hệ lực l c là: ∑F =0 - P -P -P +N +N =0 iy 1 2 3 A B
∑m (F )=0 - P .95-P .150 - P .265 + N .300 =0 A i 1 2 3 B =>giải ta có N =4,78 kN A
NB=(95. P +150 P +265 . P )/300 = 5,22 kN
1+150 P2+265 . P3 )/300 = 5,22 1 2 3 6 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.6
Vật khảo sát là thanh AB, giả sử thanh CD bị kéo khi đó ta có hệ lực tác động lên thanh: + Lực hoạt động:P
+ Lực liên kết: do bản lề A như 1 gối cố định : X ,Y do thanh CD chiu kéo S A A và C vật AB nằm AB nằ
m cân bằng nên hệ (P, S , X ,Y )=0 C, XA,YA)= C A A Hệ lực ực trên đồng phẳ
n đồng phẳng,ta có pt cân bằng c ng của hệ lực ∑F = X + S cos α = 0 A + SC cos α = x A C ∑F = -P+ Y +S .sinα = 0 A+S .sinα = y A C
∑m (F )=0 nên -> - P. AB – S . AC. Sin α=0
A(F )=0 nên -> - P. AB – SC. AC. Sin α= A k C Giải ra ta có:
( dấu trừ sai nên ta đổi lại ta đổi lại chiều S iều S ) C 7 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.7
A. Vật khảo sát là cầu AB
Hệ lực tác dụng lên cầu + lực hoạt động : P, Q + Lực liên kết: X ,Y ,N A A B
Cầu cân bằng nên hệ lực bằng 0
Pt cân bằng của hệ lực: ∑F jx= XA + Q = 0 XA=-Q ∑F jy= - P+ NB + YA = 0 => YA=P- NB
∑m (F ) = - P.AB/2 - Q.h + N .AB=0 N A (Fj) = - P.AB/2 - Q.h + N B=(Qh+P.a)/2a =P/2+Qh/2a A j
B.AB=0 NB=(Qh+P.a)/2a =P/2+Qh/2 Suy ra: YA=P-NB=P/2 - Qh Qh/2a 8 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.7 B.Vật khảo sát cầu AB
Hệ lực tác dung lên vật: +Lực hoạt động Q, P +Lực liên kết:X ,Y ,N A A B
Hệ lực cân băng nên Pt cân bằng: ∑ ∑Fjx=0 Q + XA – NB . sinα =0 ∑ Fjy=0 => P + YA + NB B . Cosα =0
∑m (F )=0 -Qh - P.AB/2 + N .AB . Cosα =0
A (Fj )=0 -Qh - P.AB/2 + NB.AB . Cosα =0 A j B 9 BÀI TẬP CƠ LÝ THUYẾT I Bài 1.8
Xác định phản lực ở ngàm của dầm nằm ngang có trọng lượng không đáng
kể,chịu lực như trên hình vẽ
- Vật khảo sát: cái dằm -Hệ tác dung lên dằm: +Lực hoạt động:Q,F,M
+Lực liên kết: Xₒ,Yₒ,Mₒ
- Dằm cân bằng nên hệ lực (Q,F,M,Xₒ,Yₒ,Mₒ)=0
Pt cân bằng của hệ lực : ∑Fjx=0 -Fsinα + Xₒ = 0 ∑Fjy=0 = => -Q + Fcosα Fcosα +Yₒ=0
∑m̅ₒ(Fj) = 0 -Q.3/2 + F.5.cosα – M + Mₒ=0 Giải ta có: Xₒ= F. F.sinα Xₒ=2,8 kN kN Yₒ= Q- Fcosα => Yₒ=1,67 kN Mₒ= Q.3/2- F.5.cosα cosα +M Mₒ= -5,35 kN kNm 10 Bài 1.9 BÀI TẬP CƠ LÝ THUYẾT I
Xác định phản lực ở ngàm của dầm nằm ngang trong lượng ko đáng kể. Q =1/2. 4. 4,5 = 9 kN 1=1/2. 4. 4,5 = 9 1 Q = 2.3=6 kN 2= 2.3=6 kN 2 Q = 2.3.1/2 = 3 kN 3= 2.3.1/2 = 3 3 Chọn vật vật khảo sát
sát là dầm, khi đó hệ lực
c tác dụng lên vật Xác định + Lực hoạt đ động: F, Q , Q , Q , M 1, Q2, Q3, M 1 2 3 + Lực liên kế
kết ổ ngàm: Xₒ, Yₒ, Mₒ Dầm nằm ngang cân b bằng nên ta có có hệ lực cân bằng, pt câ
cân bằng của hệ lực là: ∑Fkx= Fsinα - Xₒ=0
∑Fky=F cosα- Q -Q -Q +Yₒ=0 1-Q2-Q3+Yₒ=0 1 2 3
∑m̅A(Fk)= -Q1.2/3.AB- (AB+1/3 BO)-Q (AB+BO/2)+M +Yₒ.AO-Mₒ=0 3(AB+BO/2)+MA+Yₒ.AO-Mₒ= 3 A  Xₒ=Fsi Fsinα= 5.sin30⁰ =2,5 kN 11 BÀI TẬP CƠ LÝ THUYẾT I BÀI 1.10 Hệ v vật khảo o sá sát : cần trục ABC Hệ l lực t tác dụng lên vật: +Lực hoạ oạt độn ộng : P +Lực liên kết: XA,Y ,YA ,X ,XB Hệ l lực ( (P,X
,X ,X ,Y ) nằm cân bằng do cần trục ABC nằm cân bằng.
A ,X B,YA ) nằm cân bằng do cần trục ABC nằm cân bằng. A B A Do hệ lực c là đ đồn
ồng quy phẳng nên phương trình hệ lực này là: ∑Fkx= XA–XB=0 YA =P=9,6 kN kN ∑Fky= YA-P=0 XA=XB = 12, 12,8 KN ∑m̅A(Fk) =0
 P.2,4- XB.1,8=0 nên XB=9,6. 3.4/1,8 ,8 k kN 12 BÀI TẬP CƠ LÝ THUYẾT I BÀI 1.11 Vật khảo sat :cái chày Hệ lực tác dụng : +Lực hoạt đông: P
+ Lực liên kết: NB, NC, ND
Hệ lực trên đồn
ồng phẳng và cân bằng (do chày cân bằng)
Có PT cân bằng của hệ lực: ∑Fkx=0
=> Psinα - NC + ND = 0 ∑Fky ky=0
- Pcosα + NB =0
∑m̅A(Fk) =0 - N . AC + N . AD= 0 C . AC + ND . AD= 0 C D N B = P c o o sα = >
N = Pcosα B = Pcosα B NC- ND=Psinα ND=1/6.Psinα -5 N +35 N = 7 /6 P sinα
C +35 ND =0 NC=7ND = 7 /6 P sin C D =0 NC=7ND vậy: NB= Pcos o s α=√3/2 k kN ND=1 /6.Psinα=1/1 /12 kN 13 NC=7.ND=7/1 /12 kN BÀI TẬP CƠ LÝ L TH T UYẾT I BÀI 1.16 Chon on vật khảo s o sát là tay đòn ABC Hệ lực tác c dụng gồm:
+Lực hoạt đông: Trọng lực P + Lực ực liên kết ết: T T 1 , T2 1 , 2
Hệ lực trên đồng phẳng và cân bằng (do chày cân bằn n bằ g) ng) Có Ta P cT c c ó: âTn= P và T = P 1 = P1 và T2 = 1 b bằn 1 g của 2 hệ 2 lực: Hệ lực ( P
P, T , T ) cân bằng do đòn nằm cân bằng. Ở đây ta tìm phương
1, T2 ) cân bằng do đòn nằm cân bằng. Ở đây ta tìm phương 1 2
pháp đơn giản nhất để tính T T 1 , T2 1 , ∑m̅ => B(Fk) =0 -Ph
Ph + T . AB. Sin(BAE) – T . BC. Sin(BCF) = 0
1 . AB. Sin(BAE) – T2 . BC. Sin(BCF) = 0 1 2 v
ậ y :

S i n ( vậy: Sin( B C F) = (
T .AB. Sin(BAE)- Ph)/ (T . BC) 1.AB. Sin(BAE)- Ph)/ (T2 . BC 1 2 = ( (P .AB.sin(EAB)-P.h)/(P . BC) 1 .AB.sin(EAB)-P.h)/(P2 . BC 1 2 Thay số S số i Sin(BCF) F)= (310.0,4 ,4. si sin 135 -80.0,212)/100= 0 0,707 14 Góc (BCF)= 45o 5 hoặ oặc 135o 5 BÀI TẬP CƠ LÝ THUYẾT I BÀI 1.19 15 BÀI TẬP CƠ LÝ THUYẾT I
CHƯƠNG 2: BÀI TOÁN PHẲNG HỆ VẬT 16 BÀI TẬP CƠ LÝ THUYẾT I
CHƯƠNG 2: BÀI TOÁN PHẲNG HỆ VẬT
II.PHƯƠNG PHÁP GIẢI BT
Để hệ các vật rắn mà CB thì mỗi vật rắn thuộc hệ phải CB nên để
giải hệ vật có 2 phương pháp: 1.pp tách vật:
tách riêng từng vật một để khảo sát. Mỗi vật rắn tách ra tối đa tối đa 3
thành phần CB => thiết lập dược một hệ các PTCB
2. pp hóa rắn:
- Ban đầu coi toàn bộ hệ vật là một vật rắn
- Khảo sát CB của hệ vật rắn đó( tối đa 3 PTCB)
- Sau đó tách riêng môt số vật để k/sát tiếp => 1hệ các PTCB đủ để giải BT 17 BÀI TẬP CƠ LÝ THUYẾT I
CHƯƠNG 2: BÀI TOÁN PHẲNG HỆ VẬT
*Điều kiện CB của thanh OA: (X ,Y , N , , Q )=0 o ,Yo , N B , , Q )=0 o o B
F = X -N sinα+Q = 0 (1) kx 0 B
F =Y N cosα = 0 (2) ky 0 0 + b
mₒ(F )= N .OB - Q.O
Q.OA sinα = 0 (3) k B 18 BÀI TẬP CƠ LÝ THUYẾT I BÀI 2.1 ( tiếp) 2.Xets
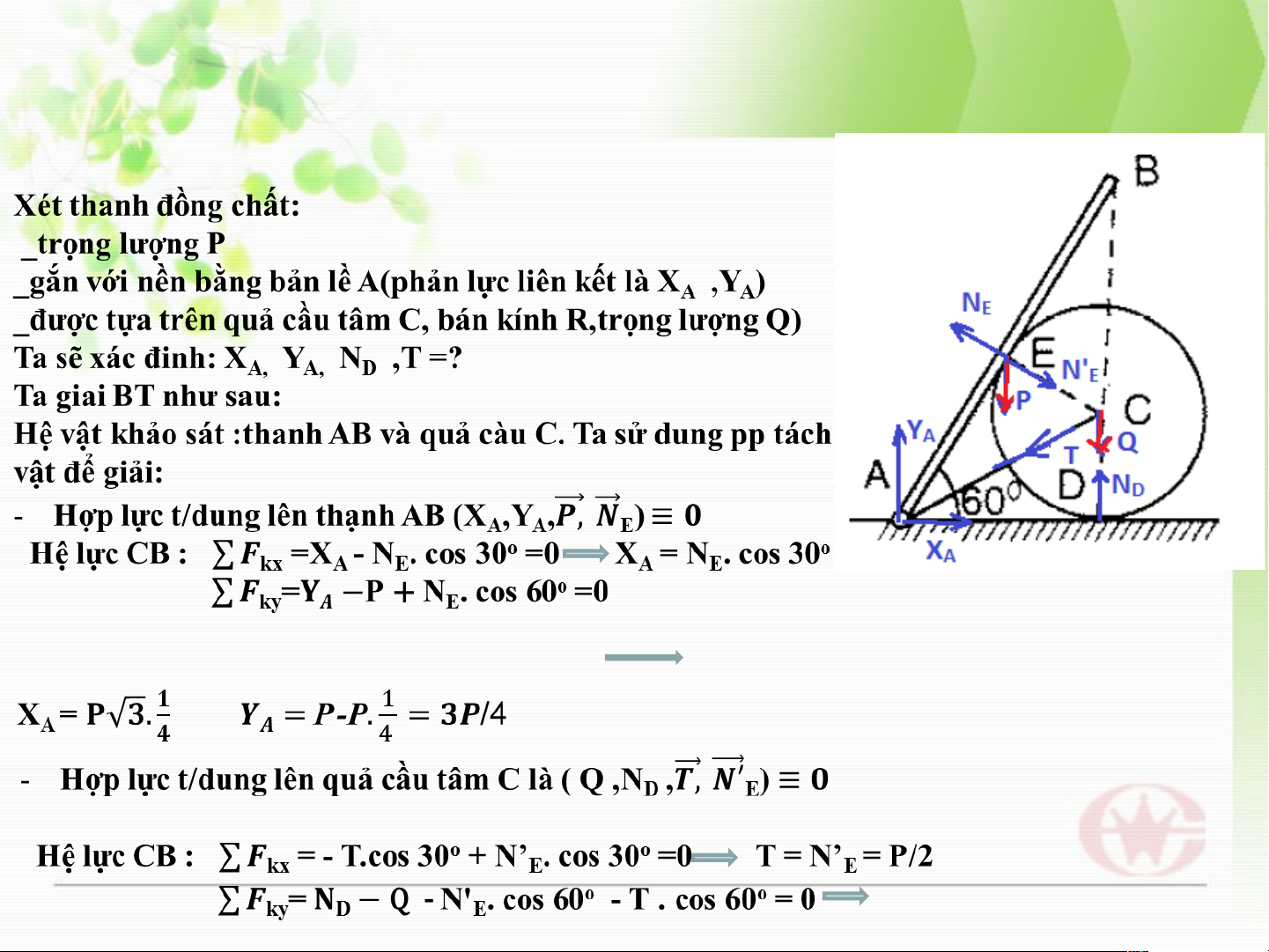
2.Xets khối trụ tâm trụ tâm C Khối trụ tâm C c m C chịu ịu t/dụng
t/dụng của hệ lực như hình như hình vẽ: (N’
’ , N , N , P )
D , P B E D
F = N’ .sinα- N =0 kx B E
F = -N’
-N’ cosα + N –P = 0 ky B D 19 BÀI TẬP CƠ LÝ THUYẾT I BÀI 2.2
m (F )= -P.AB.0,5 cos 60o + N .0,5. AB = 0 N = P cos 600 = P/2 A k E E 20 N = Q+ P/2 D