Bài tập cực trị tự do và phương trình vi phân | Bài tập giải tích

Chương 3. HÀM NHIỀU BIẾN
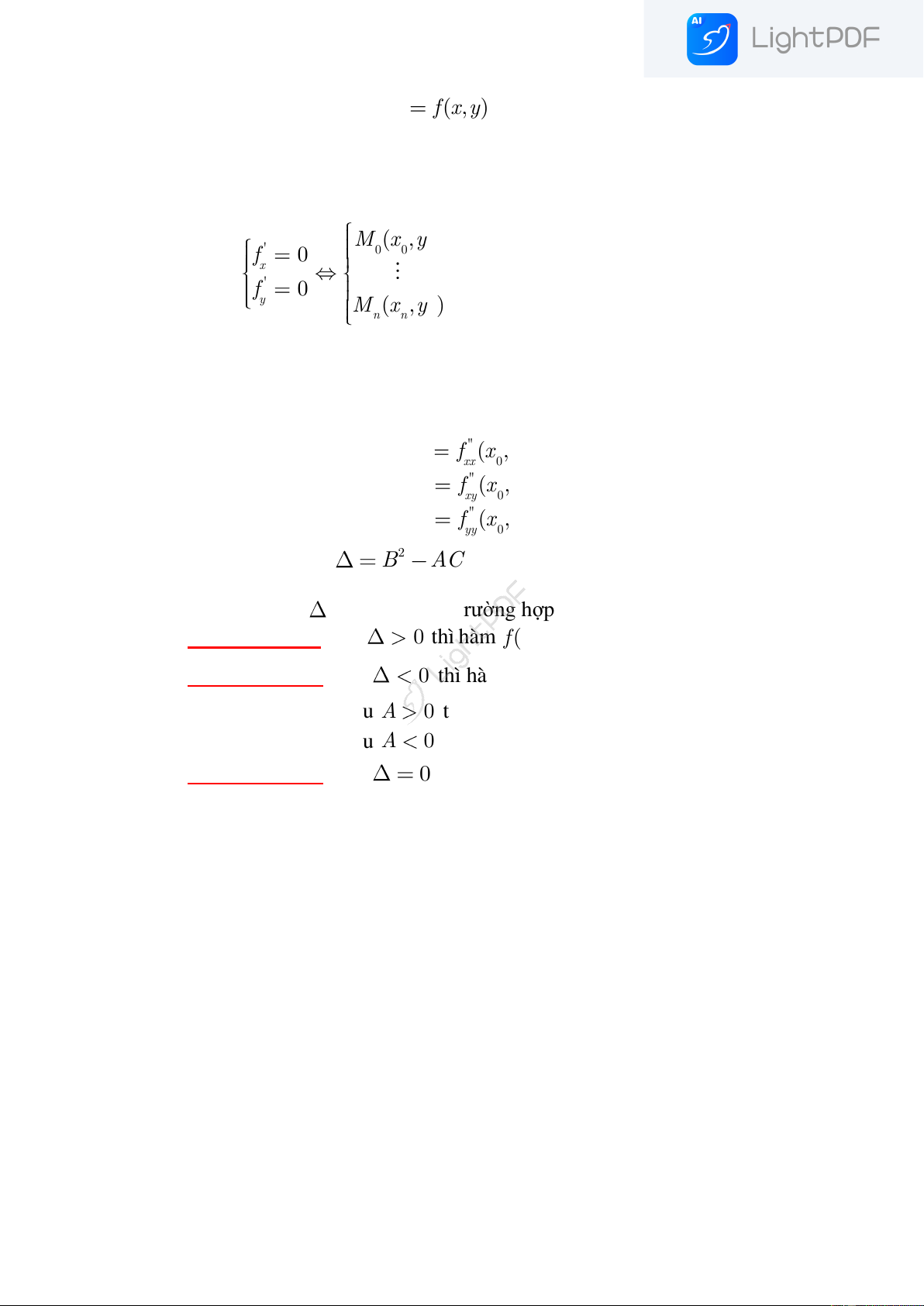
1. Bài toán. Tìm cực trị của hàm z f (x,y).
2. Các bước giải.
Bước 1. Tính các đạo hàm riêng cấp 1 là : ' f và ' f . x y
Bước 2. Giải hệ phương trình M (x ,y ) ' 0 0 0 f 0 x
(các điểm nghi ngờ đạt cực trị). ' f 0 y M (x ,y ) n n n
Bước 3. Tính các đạo hàm riêng cấp 2 là : '' '' f , f và '' f . xx xy yy
Bước 4. Xét tại điểm M (x ,y ) 0 0 0 Đặt '' A
f (x ,y ), xx 0 0 '' B
f (x ,y ), xy 0 0 '' C f (x ,y ) yy 0 0 và 2 B AC .
Bước 5. So sánh số với số 0, có 3 trường hợp sau
Trường hợp 1. Nếu
0 thì hàm f (x,y) không đạt cực trị tại M (x ,y ) 0 0 0
Trường hợp 2. Nếu
0 thì hàm f (x,y) đạt cực trị tại M (x ,y ) 0 0 0 2.1. Nếu A
0 thì hàm f (x,y) đạt cực tiểu. 2.2. Nếu A
0 thì hàm f (x,y) đạt cực đại.
Trường hợp 3. Nếu
0 thì ta chưa có kết luận gì về điểm M (x ,y ). 0 0 0
Chương 5. PHƯƠNG TRÌNH VI PHÂN
1. Phương trình vi phân tuyến tính cấp 1. Xác định ( p x) ...; f (x) ... 0.25 Tính ( p x)dx ... ( p x)dx ... 0.25 p(x )dx 0.25 Tính e ... p(x )dx 0.25 Tính e ...
Vậy nghiệm tổng quát của phương trình đã cho là p(x )dx p(x )dx 0.25 y ( f (x).e dx C ).e ... 0.25 = Đáp số 0.25
Thay điều kiện ban đầu, giải ra C
... và kết luận nghiệm riêng 0.25
(Dành riêng cho bài toán Cauchy)
2. Phương trình vi phân tuyến tính cấp 2 hệ số hằng '' ' y py qy P (x). x e n Trong đó, ,
p q là các hằng số; P (x) n a a x
a x là đa thức bậc n và n 0 1 n
là một số thực cho trước.
Bước 1. Giải phương trình thuần nhất tương ứng ' ' y py qy 0
Có phương trình đặc trưng là: 2 k pk q 0
Nghiệm tổng quát (NTQ) của phương trình thuần nhất là
Phương trình đặc trưng
NTQ của phương trình thuần nhất
Có 2 nghiệm thực phân biệt: k k . k x k x 1 2 y C e C e 1 2 1 2 Có nghiệm kép: k k k . kx kx y C e C xe 1 2 1 2
Có 2 nghiệm phức: k a ib ( cos sin ). ax y C bx C bx e 1,2 1 2
Bước 2. Tìm một nghiệm riêng *
y của phương trình không thuần nhất Số Dạng của * y
Không là nghiệm của phương trình đặc y ( n A Ax A x ). x e 0 1 n trưng: k , k . 1 2
Là một nghiệm của phương trình đặc y ( n A Ax
A x ).x. x e 0 1 n trưng: k hoặc k . 1 2
Là nghiệm kép của phương trình đặc n 2 y (A Ax
A x ).x . x e 0 1 n trưng: k k . 1 2
Bước 3. Xác định các hệ số A ,A , ,A . 0 1 n • Tính * ' (y ) và * ' (y ) . • Thay * y , * ' (y ) và * '
(y ) vào phương trình không thuần nhất Rút gọn hai vế cho x e So sánh hai đa thức Hệ phương trình Giải hệ phương
trình để tìm A ,A , ,A . 0 1 n
• Thay A ,A , ,A vừa tìm được vào biểu thức của * y . 0 1 n
Bước 4. NTQ của phương trình không thuần nhất là * Y y y