Bài Tập Cuối Kỳ Phân tích định lượng | Đại học Hoa Sen

lOMoAR cPSD| 47206521 BÀI TẬP LẦN 3
Phạm Thị Hương Thơm_22013305
3.1 Công ty điện thoại ở một thành phố muốn ước lượng thời gian trung bình của
một cuộc điện đàm đường dài vào những ngày cuối tuần. Mẫu ngẫu nhiên 20 cuộc
gọi đường dài vào những ngày cuối tuần cho thấy thời gian điện đàm trung bình là
14,8 phút, độ lệch mẫu hiệu chỉnh là 5,6 phút. Với độ tin cậy 90% , hãy ước lượng
thời gian điện đàm trung bình của dân cư thành phố đó vào những ngày cuối tuần.
Cho biết thời gian điện đàm là đại lượng ngẫu nhiên có phân phối chuẩn. Ta có:
• n = 20 (n < 30 -> tra bảng student)
• 1 – α = 0.90 -> Z = 1.729 • x = 14.8 • S = 5.6
ε=¿ Tn-1;α2 × √S n = 1.729 ×
5.6 ≈ 2.165
Khoảng ước lượng của μ là ( x−ε;x +¿ ε ) = ( 12.635 ; 16.965 ) Thời gian trung
bình của một cuộc điện đàm đường dài vào cuối tuần được ước lượng
khoảng từ 12.635 đến 16.965
3.2. Cho dữ liệu doanh thu phòng vé của hệ thống 25 rạp chiếu phim ngày cuối tuần (đơn vị: nghìn đồng). 2020 1015 1300 1132 9700 0 0 0 0 1400 1120 8350 7300 9940 0 0 1075 1270 1350 6240 7430 0 0 0 1390 4200 6750 6700 9330 0 1318 2140 1138 1080 9200 5 0 0 0 lOMoAR cPSD| 47206521
Người quản lý cho rằng doanh thu trung bình mỗi phòng vé trong hệ thống rạp là 10
triệu đồng vào ngày cuối tuần. Bạn hãy đưa ra kết luận phù hợp với mức ý nghĩa 1%. Ta có:
• n = 25 (n < 30 -> tra bảng student)
• α = 0.01 -> = 0.005 -> T24;0.005 = 2.797 • x = 10905 • S ≈ 3962.114 Ta kiểm tra giả thuyết:
H0: μ = 10000 ; H1: μ ≠ 10000 x−μ0 T =
S × √n = 3962.114
Vì |T| ≤ T24;0.005 nên ta chấp nhận H0, nghĩa là dữ liệu doanh thu vào ngày cuối tuần đáng tin.
3.3. Khảo sát năng suất lao động (tính bằng số sản phẩm làm ra trong 1 ngày) của
100 công nhân được chọn ngẫu nhiên trong xí nghiệp B, người ta có số liệu sau:
Năng suất lao động 70 – 75 75 – 80 80 – 85 85 – 90 90 – 95 95 – 100 Số công nhân 4 16 22 28 20 10
a) Hãy ước lượng năng suất lao động trung bình của công nhân toàn xí nghiệp
với độ tin cậy 90%. Ta có: • n = 100 (n ≥ 30)
• 1−α = 0.90 ->Z = 1.65 • S ≈ 6.652
ε=¿ Zα2 × √S n = 1.65 × √100
b) Cho biết năm trước năng suất trung bình của công nhân xí nghiệp là 80 sản
phẩm / ngày, các số liệu trên được khảo sát sau khi xí nghiệp đã có những lOMoAR cPSD| 47206521
cải tiến kỹ thuật trong sản xuất. Với mức ý nghĩa 1%, hãy đánh giá hiệu quả
của việc cải tiến kỹ thuật. Ta có: • n = 100 (n ≥ 30)
• α = 0.01 -> Z = 2.58 • x = 86.2 Ta kiểm tra giả thuyết: H0: µ = 80 ; H1: µ ≠ 80 => Z0 =
x−Sμ0 × 6.652 | |
Vì Z0 >Zα2 = 2.58 nên ta bác bỏ H0
Thì cần so sánh tần suất mẫu xvới μ0:
x>μ0 nên ta kết luận μ>μ0
3.4. Khi điều trị bằng thuốc A, tỉ lệ bệnh nhân khỏi bệnh là 80%. Đổi sang thuốc B
để điều trị cho 1100 người thì thấy có 920 người khỏi bệnh. Với mức ý nghĩa  =
0,02 có thể cho rằng thuốc B hiệu quả hơn thuốc A hay không? Ta có: • n = 1100 (n ≥ 30)
• α = 0.02 -> Z = 2.33 • p = Ta kiểm tra giả thuyết: H0: P = 0.8 ; H1: P ≠ 0.8 => × = Vì |Z0| Z = 2.33 nên ta bác bỏ H0
Thì cần so sánh tần suất mẫu pvới p0: lOMoAR cPSD| 47206521
p>p0 nên ta kết luận p>p0
3.5. Thời gian tự học trong ngày của một số sinh viên năm thứ nhất (được chọn ngẫu
nhiên) ở một trường đại học ghi nhận được như sau:
Thời gian tự học (giờ) 0 – 2 2 – 4 4 – 6 6 – 8 8 – 10 Số sinh viên 25 46 14 11 4
a) Với độ tin cậy 95%, hãy ước lượng tỉ lệ sinh viên của trường có thời gian tự học
trong ngày từ 4 giờ trở lên. Ta có:
• 1 - α = 0.95 -> Z = 0.68 • n = 100 (n ≥ 30) • p = = 0.68 × 2 b)
Ở mức ý nghĩa 2%, có thể cho rằng tỉ lệ sinh viên tự học trên 6 giờ / ngày là 20% được không?
• H0: p = 0.2 ; H1: p ≠ 0.2 • p = • Z = 2.33 • Z0 = -1.25
• |Z0| < Z => chấp nhận H0 c)
Phòng hỗ trợ công tác sinh viên của trường cho rằng sinh viên dành trung bình
4giờ mỗi ngày để tự học, bạn hãy nhận xét về tuyên bố này với mức ý nghĩa 5%. • n > 30 • α = 0.05 • S = 2.143
• H0: μ = 4 ; H1: μ ≠ 4 • Z = 1.96 • Z0 = -2.52 lOMoAR cPSD| 47206521
• |Z0|>Z => bác bỏ H0 d)
Muốn sai số khi ước lượng số giờ tự học trung bình không vượt quá 0,5 giờ
vớiđộ tin cậy 99% thì cần khảo sát thêm bao nhiêu sinh viên nữa? • Z = 2.58 • n = 123
3.6. Trước đây định mức tiêu thụ điện cho 1 hộ gia đình là 140 kw/tháng. Hiện nay,
do đời sống nâng cao, người ta cho rằng cần thay đổi định mức. Khảo sát 100 hộ gia
đình, người ta thu được các số liệu trong bảng sau đây: Mức tiêu thụ
100 – 120 120 – 140 140 – 160 160 - 180 180 - 200 điện (kw/tháng) Số hộ gia đình 14 25 30 20 11
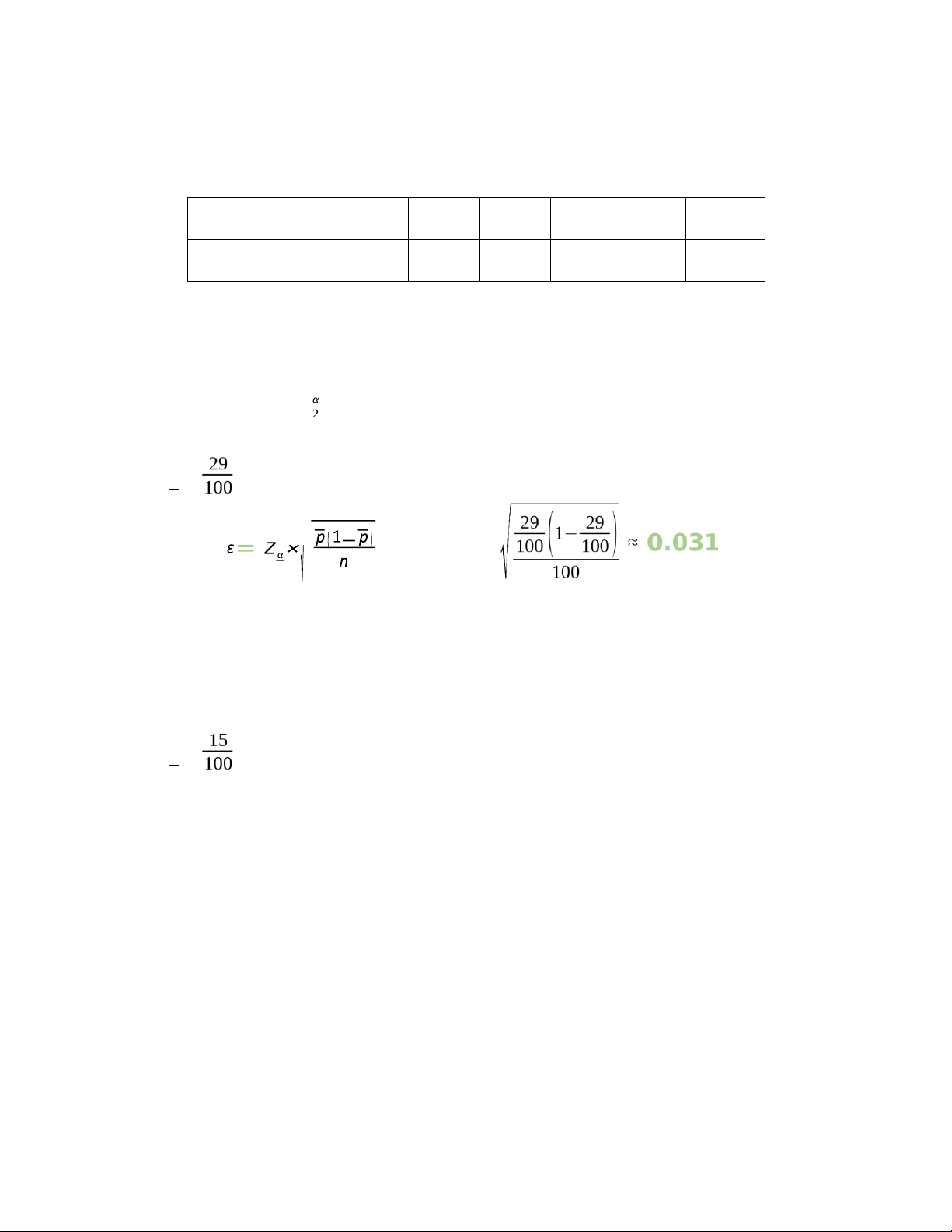
a) Hãy ước lượng tỉ lệ hộ gia đình có mức tiêu thụ điện trên 140 kw/tháng với độ tin cậy 95%. Ta có:
• 1 - α = 0.95 -> Z = 0.68 • n = 100 (n ≥ 30) • p = ε≈0.033 b)
Hãy ước lượng mức tiêu thụ điện trung bình của mỗi hộ gia đình với độ tin cậy 97%. • n = 100 • x= 147.8
• S = 24.103  σ = 0.97 • = 0.485 • Z = 2.17 • ε = 5.23
• μ (147.8 ± 5.23) lOMoAR cPSD| 47206521 c)
Với độ tin cậy 98%, muốn sai số ở câu b không vượt quá 2 kw/tháng thì
cầnkhảo sát thêm tối thiểu bao nhiêu hộ gia đình nữa? • ε≤0.02
• S = 24.103  σ = 0.98 • = 0.49 • Z = 2.33 • n ≥ 789
• Khảo sát thêm 689 hộ nữa