Bài tập giới hạn và đạo hàm chương 1 Môn Toán giải tích | Trường Học Viện nông nghiệp Việt Nam

BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023 Chương 1: Hàm một biến
Bài 1. Tính các giới hạn sau: 𝑎. lim 𝑥3−2𝑥+1 𝑏. lim 4𝑥−3𝑥+2 𝑐. lim x2−4 𝑑. lim 𝑥3−3𝑥+1 𝑒. lim 3𝑥+1 𝑥→+∞ 𝑥2−𝑥+5
𝑥→+∞ 5𝑥−1+2𝑥−2 𝑥→2 𝑥2−3𝑥+2 𝑥→+∞ 2𝑒𝑥+5 𝑥→+∞ ln(2𝑥−3)
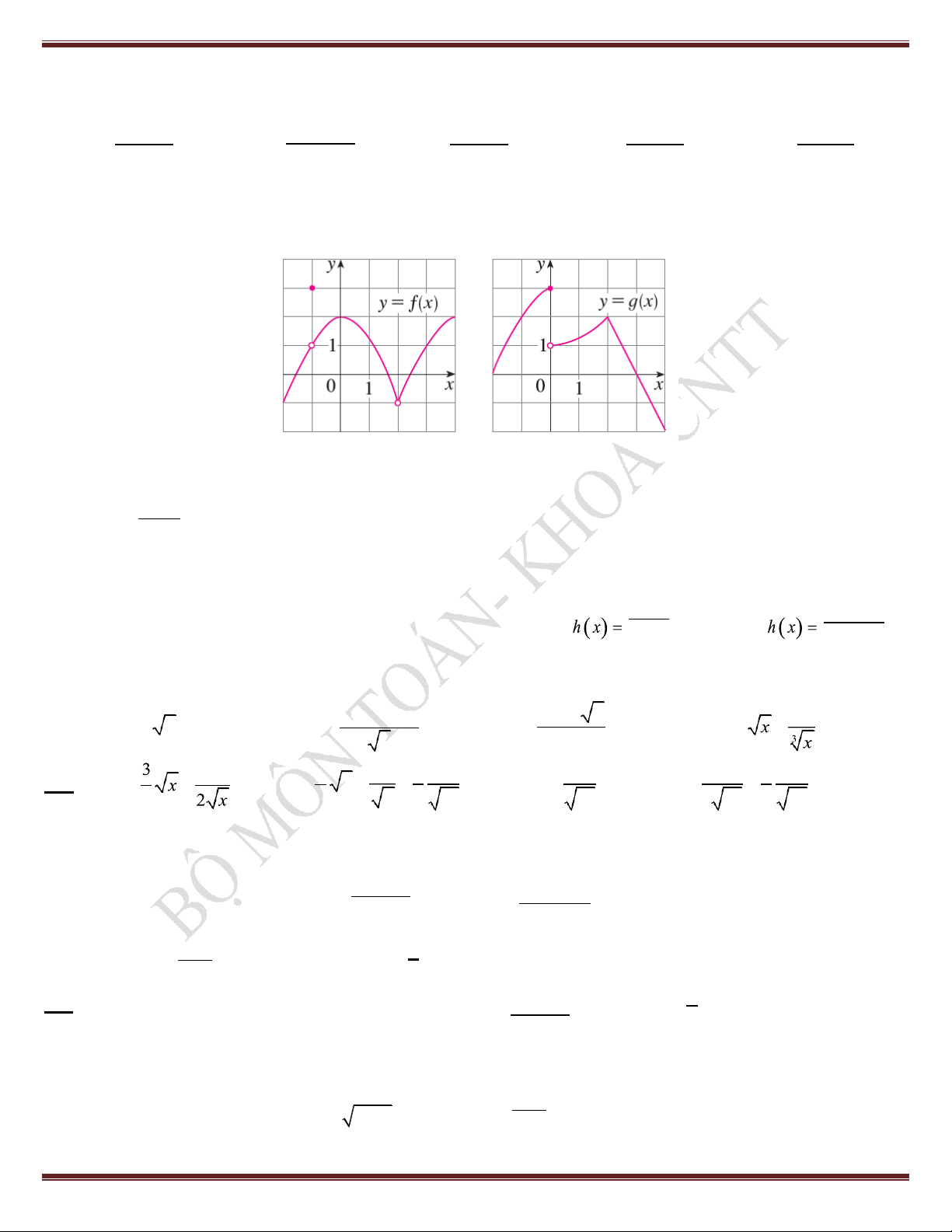
Bài 2. Cho các hàm số f  x và g  x  có đồ thị như hình vẽ (hình tròn rỗng thể hiện hàm số không xác định tại
điểm đang xét, hình tròn đặc thể hiện giá trị hàm số tại điểm đang xét). Sử dụng các đồ thị hàm số, hãy xác định các giới hạn sau.
1) lim  f  x  g x
2) lim  f x  g x
3) lim  f  x g  x x2 x0 x1
 f  x 4) lim  
5) lim x2 f  x
6) f 1  lim g  x x2  x x3  1 g  x 
Bài 3. Giả sử rằng f 2  3, g 2  4, f '2  2, g '2  7 . Hãy tìm h '2 khi: f  x g  x
1. h  x  5 f  x  4g  x
2. h  x  f  x g  x 3. 4. g  x 1 f  x
Bài 4. Tính đạo hàm của các hàm số sau: x2  4x  3  1 2 x2  2 x
1) y  x  x 1 ; 2) y  ; 3) y  ; 4) v     . x x   3 1 2 1 ĐS: 1 2 3 1 1) y '    ; 2) y '  x 
; 3) y '  1 1 ; 4) v '  1  . 2 2 x 2 x3 x3 36 x5 3 3 x5
Bài 5. Tính đạo hàm của các hàm số sau: 1
1. F x  4x  x2  100
2. g t   ln(2x 1) tại 3. x  1 y  tại
4. y  e x2 2 x x  0 4  3 t 1  x x 1   1  2 5. * y  arctan  
6. * y  x arcsin 2 
7. * y  ln arccos x
8. y  ex sin x   x   x  12t3 ĐS:
1) F ' x  1004  2x4x  x2 99 ;
2) g 't   ;
3) y '(1)  2  ln 3 ; 4) y '  2 . 4 t4 1 3
Bài 6. Tính vi phân của các hàm số sau: y  ln u 1
1) y  x2 sin 2x ; 2) 1 t2 ; 3) y  ;
4) y  1 r3 2 ; u 1 BỘ MÔN TOÁN-KHOA
CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 1
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023 3
5) * y  1 x2 .arccos x tại x  ;
6) f t   3 1 tan t tại t  0 . 2
ĐS: 1) dy  2x sin 2x  2x2 cos 2xdx ; 2) dy  2t dt ; 3) dy  2 du ; 1 t 2 u 12 6r2 x.arccos x  3    3     4) dy  y '  1  dy   1 dx ;   1 dr ; 5) 3 2 6 3  r  1 x2     1 1 1  1
6) f 't  
df 0  dt . 3 3 3
1 tan t 2 cos2 t
Bài 7. Tính y và dy tại giá trị đã cho của x và dx  x :
1) y  2x  x2, x  2, x  0.4
2) y  x; x  4; x 1 5
3) y  , x  8, x  1
4) y  ex , x  0, x  0.5 x ĐS:
1) dy  0.8; y  0.64
2) dy  0.250; y  0.236
3) dy  0.078; y  0.069 4)
𝑑𝑦 = 0.5 ; ∆𝑦 = √𝑒 − 1
Bài 8*. Tính gần đúng các biểu thức sau (áp dụng vi phân). 2. 𝐵 = cos 310 3. 𝐶 = arctan 0.02 4. 𝐷 = sin 580 5. 𝐸 = 𝑒0.03.
6. 𝐹 = ln 1.01
1. 𝐴 = 3√0.97
Bài 9: Tìm đa thức Tay-lor, đa thức Mac-lau-ranh (Maclaurin).
1. Tìm đa thức Taylor bậc 2 của hàm số 𝑓(𝑥) = 𝑥2 tại 𝑥 = 1. 2𝑥−1
2. Tìm đa thức Maclaurin bậc 4 của hàm 𝑝(𝑥) = (𝑥 + 1). ln(𝑥 + 1)
3. Tìm đa thức Taylor bậc 3 của hàm 𝑔(𝑥) = (𝑥2 + 2). 𝑒𝑥−2 tại điểm 𝑥 = 2.
4. Tìm đa thức Taylor bậc 2 của hàm số ℎ(𝑥) = 𝑥2 sin(𝑥 + 2) tại 𝑥 = −2.
Bài 10. Biết khai triển Taylor bậc 3 của hàm 𝑓(𝑥) tại điểm 𝑥 = 2 có dạng:
𝑓(𝑥) = 3 + 5(𝑥 − 2) + 4 (𝑥 − 2)3 + 𝛼(𝑥) với lim 𝛼(𝑥) = 0. 𝑥→2
1. Tính tổng: 𝑓′(2) + 𝑓′′(2) + 𝑓′′′(2).
2. Tính giá trị gần đúng của 𝑓(2,03).
Bài 11. Tìm đa thức Maclaurin bậc 2 của các hàm số sau. 1 1/. x2  3 f (x) 
2/. f (x)  arctan 2x
3/. f (x)  ln 1 2x
4/. f  x  4  x x 1
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 2
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023
Chương 2: Các phép tính tích phân hàm một biến
Bài 1. Tìm họ các nguyên hàm của các hàm số sau: x 2 4x
1) f (x)  1   ; 2) g(x)  1 ; ;
3) h(x)  3e 3 x2 1 2x     1
4) l(x)  3cos x ; 5) * k(x)  1 ; 6* m(x)  1    dx ;    x2  9 3   1 4x2   1 dx
7) sin(5x  2)dx ; 8) dx ; 9) . 2  x 1 1 2x  7 10)  dx 11)  dx 12) dx  x2  7x 10 x2  4x  5 x2  7x 10
ĐS: với C là hằng số tùy ý, x2 2 1
1) F (x)  x    C ;
2) G(x)  ln(1 2x)  C ; 6 x 2 3  2
3) H (x)  e 4x  x3/2  C ; 4) 
L(x)  9 sin 
x  C ; 4 3    3   1 1 1
5) K (x)  arcsin(2x)  C ; 6) x  3
M (x)  ln 3x   ln 9x2 1  C . 2 3 6 x  3
Bài 2. Tính nguyên hàm, tích phân xác định bằng phương pháp đổi biến số. 𝑥3 1 2 𝑎. ∫ 𝑑𝑥 𝑏. ∫ ln 𝑥 𝑑𝑥 𝑐. ∫ 𝑒𝑥 𝑑𝑥
𝑑. ∫ (2𝑥 − 3)(𝑒𝑥 −3𝑥 − 2) 𝑑𝑥 √𝑥2 + 2 𝑥3 𝑒𝑥 + 𝑒−𝑥 0 1 √2 2 𝑒 1 1 + sin ( ) − 1 1 + sin(lnx) 𝑥 √𝑥 𝑒. ∫ 𝑑𝑥 𝑓. ∫ 𝑑𝑥 𝑔. ∫ 𝑑𝑥
ℎ. ∫ (3𝑥2 − 2). (cos(𝑥3 − 2𝑥) + 𝑥) 𝑑𝑥 𝑥2 𝑥 𝑥 1 0 1
Bài 3. Tính nguyên hàm, tích phân xác định bằng phương pháp tích phân từng phần. 0 2 a. *∫ arcsin 𝑥 𝑑𝑥
b. ∫ (5𝑥 − 3)cos(3𝑥) 𝑑𝑥
c. ∫ (2𝑥 − 3)𝑒𝑥+2 𝑑𝑥
d. ∫ (4𝑥 − 1) ln(2𝑥 − 1) 𝑑𝑥 −2 1 4 x 1 ln x
e. ∫ (𝑥 + 2) ln 𝑥 𝑑𝑥
f. *∫ 𝑥 arctan 𝑥 𝑑𝑥 g.  dx h.  e x dx x 0 1
Bài 4*. Tính độ dài đường cong 𝐴𝐵 . 1.
𝑦 = ln 𝑥 từ điểm 𝑥 = 1 đến điểm 𝑥 = √3 3.
𝑟 = 2(1 + cos 𝜑) với 0 ≤ 𝜑 ≤ 𝜋 . 4.
𝑥 = 𝑡 − cos 𝑡 , 𝑦 = sin 𝑡 với 0 ≤ 𝑡 ≤ 𝜋. 2.
𝑦 = 2𝑥√𝑥 từ điểm (0,0) đến điểm có hoành độ 𝑥 = 2. 3
Bài 5*. Tính độ dài phần đường cong thuộc đồ thị hàm số:
1) y2  x3 từ điểm (1;1) đến điểm (4;8) ; 1
2) y  ln(1 x2 ) với 0  x  ; 2 1 1
3) y  arcsin x  1 x2 từ điểm x  0 đến x  ; 4) y 
x.(x  3) với 1  x  9 . 2 3 1 5) y  ln 5
x  x2 1 từ điểm x  đến x  ; 6) y  ex  e x  với 0  x  1. 2 2 1 3 125 13 13 1 10 1 ln 1  1  ĐS: 1) ; 2) ln 3  ; 3) 2  2 ; 4) 3 ; 5) 2 2 ; 6)  e   . 27 2 2  e  BỘ MÔN TOÁN-KHOA
CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 3
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023
Bài 6A: Tính các tích phân suy rộng sau. 0 +∞ +∞  1 3. 𝑅 = ∫ 𝑥. e3𝑥−1𝑑𝑥 1 ln x 1. 𝑅1 = ∫ 𝑑𝑥 3 2 −∞ 5. 𝑅5 = ∫ 𝑑𝑥 7.  dx 𝑥 +𝑥−2 −1 √2𝑥+3 2 3 x +∞ = ∫ 𝑥 1 𝑑𝑥 +∞ 1 4. 𝑅4 +∞ 2. 𝑅 3+cos = ∫ 𝑥 𝑑𝑥 √2−3𝑥 1 2𝑥+1 −∞ 6. 𝑅6 = ∫ 𝑑𝑥 𝑥.√𝑥2+3 8. ∫ 𝑑𝑥 2 𝑥2 1 𝑥2+𝑥−2 2 √2
Bài 6B: Xét sự hội tụ của các tích phân suy rộng sau. +∞ +∞ +∞ ln(1+𝑥) a/. 𝑇1 = ∫ 𝑥2+3𝑥 𝑑𝑥 𝑑𝑥 𝑥4−𝑥2+5 b/. 𝑇2 = ∫ 𝑥2+3𝑥 𝑑𝑥 𝑥3−𝑥2+5 c/. 𝑇3 = ∫ 𝑥 1 0 1
Bài 7*. Xét sự hội tụ và phân kỳ của các tích phân suy rộng sau.   x3 ln 3  2x  e x2 1)  dx ; 2*)  dx ; dx ; 3) 
2x4  3x2  5 x 1 x2 1 1   1 x2  dx x2 4)  3 5)  dx ; 6)  dx ; e x 1 1 1 x3 1 3
Chương 3: Hàm nhiều biến
Bài 1. Tính các đạo hàm riêng cấp 1, cấp 2 (của hàm 2 biến, 3 biến)
a/ z  x 5  5xy3  4x.y  x  2
b/ z  x2  xy 1 y  2
c/ z  ln x2  y2 1
d/ z  sin x.cos y  ex  e2y
e/ * u(x, y, z)  arcsin  x  2 y  3z 
f/ u(x, y, z)  x2  2 y.ln z
g/ f (x, y)   x  2 y 3
h/ g(x, y)  x.ey  y.ex  x3  2 y y
i/ z   sin xy
k/ u(x, y, z)  x.sin y  y.sin z  z.sin x x
Bài 2. Tìm vi phân toàn phần của hàm số:
a/ z  sin x2  y2 
b/ z  ln x2  xy  2 y3 
c/ f  ex. x sin y  cos y  d/ u  x  y  z
Bài 3. Cho hàm số f (x, y)  ex x2  y2
a/. Tìm vi phân toàn phần của hàm số trên tại điểm 𝑥 = 1; 𝑦 = 1
b/. Tính gần đúng giá trị biểu thức P  e0,02 0, 022 1, 012
Bài 4. Cho hàm số f (x, y)  3 x2  y2
a/. Tìm vi phân toàn phần của hàm số trên tại điểm 𝑥 = 1; 𝑦 = 0.
b/. Tính gần đúng giá trị biểu thức P  3 1, 022  0, 052
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 4
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023
Bài 5. Áp dụng vi phân toàn phần, tính gần đúng: 1, 05
a/ A  4, 052  2,932 b/ B  c/ * C  arctan 3 0, 093  0,993 0,92   d/ 𝐷 = ln(1,092 + 5.0,92)
e/ E  ln 0,99.sin 32o
(gợi ý: đổi 32o   (radian) ) 6 90
Bài 6. Tìm các điểm cực trị và giá trị cực trị nếu có của các hàm số sau:
a/ z  x2  xy  y2  x  y 1 .
b/ z  x3  6xy  2 y2  6x .
c*/ f (x, y)  x  y  x.ey
d/ f (x, y)  2x4  y4  x2  2 y2 .
e/ f (x, y)  x2 12xy  xy3
f/ f (x, y)  4(x  y)  x2  y2 Chương 4: Tích phân bội
Bài 1: Tính tích phân kép trên miền hình chữ nhật vuông (các cận là hằng số) + miền hình chữ nhật cong (một cận
xác định và một cận phụ thuộc biến (bậc nhất)) 1  x  1
a/ A   x2  3xy  4 y2  x  y dxdy trên miền D :  . 0  y  2 D 
b/ B   ex y dxdy với 𝐷 = {(𝑥; 𝑦) ∈ ℝ2||𝑥| ≤ 1; |𝑦| ≤ 2 }. D  
c/ C  sin x  cos y  dxdy trên miền giới hạn bởi các đường thẳng x  0, x  , y  0, y  . 4 2 D
d/ D   (x  2 y) dxdy với miền D :
1  x  5, x 1  y  x  2 . D
e/ E   y2dxdy trên miền D giới hạn bởi 3 đường thẳng: 𝑦 = 0 ; 𝑥 = 2 ; 𝑥 + 𝑦 = 3. D
f/ F   ydxdy với D là miền giới hạn bởi các đường 𝑦 = 1; 𝑦 = 𝑥; 𝑥 = 4. D 1 g/ G  
dxdy với D là miền hình chữ nhật có 4 đỉnh là 𝐴(0; 1) ; 𝐵(3; 1) ; 𝐶(0; 4) ; 𝐷(3; 4). x  2 y D x y
x  y  1
h*/ H   ex y dxdy , với D là miền giới hạn bởi  .
x  0; y  0 D
Bài 2. Tính tích phân kép có đổi biến số (Đổi biến đưa tích phân kép trên miền hình bình hành về miền h.c.n)
a/ A   (x  y)3.(x  y)2 dxdy với D là miền giới hạn bởi các đường thẳng: D
x  y  1, x  y  1, x  y  3 , x  y  1. ĐS: 203
b/ B   (x  y) dxdy với D là miền giới hạn bởi các đường thẳng: D
y  x 1, y  x  2 , y  2x 1, y  2x  4 . ĐS: 9 2
2x  y 1  0 
 2x  y 1  0
c/ C   xy dxdy với 
D :  x  3y  0 D
 x  3y  3  0 BỘ MÔN TOÁN-KHOA
CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 5
BÀI TẬP THAM KHẢO HỌC PHẦN TOÁN GIẢI TÍCH 9-2023
Chương 5: Phương trình vi phân
Bài 1. Giải các phương trình vi phân cấp 1 sau (PTVP có biến số phân ly):
a/ x(1 y).y  2 y
b/ x3. y 1 dx  x4 1dy  0
c/ y  1 y2
d/ dx  cos2 x. sin y  cos y  dy 1 x2 1
e/  y3 1 y ' 
f) x 1 y2 dx  y 1 x2 dy  0 1 x2 1 2x
g) 1 e2x  y2dy  exdx h) yy '  y
Bài 2. Giải các phương trình vi phân cấp 1 sau (PTVP tuyến tính cấp 1): 2 y x2
a/ y  y  ex/2 , y(0)  1
b/ y  2xy  x.e , y(0)  c/ y   x3 2 x 2 y 1 2x 1  x2
d/ y  xy  sin x.e 2 e) y '
  x 13 , y(0)  i) y ' y   x 1 2 x2 1 x2  1
f) xy ' 2 y  x2
g) y ' 2y  4x
h) xy ' y  x2 arctan x
Bài 3. Giải các phương trình vi phân cấp 2 tuyến tính với hệ số hằng (vế phải có dạng mũ 𝑒𝛼𝑥. 𝑃𝑛(𝑥))
a/ y   3y  2 y  ex
b/ y   3y  2  6x
c/ 𝑦′′ − 𝑦 = 𝑒2𝑥
d/ y   5y  6y  x.ex , y(0)   7 , y(0)  0.
e/ y   2 y  y  4e2x 144 HẾT.
BỘ MÔN TOÁN-KHOA CÔNG NGHỆ THÔNG TIN-HỌC VIỆN NÔNG NGHIỆP VIỆT NAM 6