






















































Preview text:
Downloaded by VietJack TV Official (vietjackvideos@gmail .com) BÀI TẬP CHƯƠNG 1 n
Bài toán 1: Chứng minh nhị thức Newton với các số phức: (z1 + z2)n = (Ckzn−k n 1 zk2) (1) với n k=0 nguyên dương. Bài làm • Với n = 1: 1 Ta có: z (đúng) 1 + z2 = (C01z1−0 1
z02) = C01z11 + C11z2 = z1 + z2 k=0 ⇒ (1) đúng với n = 1. i
• Giả sử (1) đúng với n = i. Ta có: (z1 + z2)i = (Ckzi−k i 1 zk2). k=0 i+1
• Ta cần chứng minh (1) đúng với n = i + 1, tức là (z1 + z2)i+1 = (Cki+1zi+1−k 1 zk2). k=0 Thật vậy:
(z1 + z2)i+1 = (z1 + z2)i(z1 + z2) i = (Ckzi−k i 1 zk2)(z1 + z2) k=0 i i = (Ckzi−k+1 (Ckzi−k i 1 zk2) + i 1 zk+1 2 ) k=0 k=0 i i+1 = C01zi+1 1 + (Ckzi−k+1 (Ck−1zi−k+1 i 1 zk2) + i 1 zk2) k=1 k=1 i = zi+1 1 + (Ck zi+1 i+1zi−k+1 1 zk2) + (Ci+1 i+1 2 ) k=1 i+1 = (Cki+1zi−k+1 1 zk2). k=0
Vậy (1) đúng với n nguyên dương.
Bài toán 2: Mô tả tập hợp các điểm z trong mặt phẳng phức ở mỗi trường hợp sau: a) |z − 1 + i| ≤ 2 b) |z| = Rez + 1 c) |z − i| + |z + i| = 4
d) |z − 2| − |z + 2| > 3 Bài làm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
a) Giả sử A(x, y) là biểu diễn hình học của số phức z = x + iy (x, y ∈ R) thỏa |z − 1 + i| ≤ 2.
Khi đó, ta có: |z − 1 + i| ≤ 2 ⇔ (x − 1)2 + (y − 1)2 ≤ 2 ⇔ (x − 1)2 + (y − 1)2 ≤ 4.
Vậy tập hợp các điểm A là hình tròn tâm I(1, −1) bán kính bằng 2.
b) Giả sử B(x, y) là biểu diễn hình học của số phức z = x + iy (x, y ∈ R) thỏa |z| = Rez + 1.
Khi đó, ta có: |z| = Rez + 1 ⇔ x2 + y2 = x + 1 ⇔ x2 + y2 = (x + 1)2 ⇔ y2 = 2x + 1.
Vậy tập hợp các điểm B là Parabol y2 = 2x + 1.
c) Giả sử C(x, y) là biểu diễn hình học của số phức z = x + iy (x, y ∈ R) thỏa |z − i| + |z + i| = 4. Khi đó, ta có: |z − i| + |z + i| = 4 ⇔ x2 + (y − 1)2 + x2 + (y + 1)2 = 4
⇔ x2 + (y − 1)2 + 2 x2 + (y − 1)2 x2 + (y + 1)2 + x2 + (y + 1)2 = 16 ⇔
x2 + (y − 1)2 x2 + (y + 1)2 = −x2 − y2 + 7
⇔ x4 + y4 + 2x2y2 + 2x2 − 2y2 + 1 = x4 + y4 + 49 + 2x2y2 − 14x2 − 14y2 x2 y2 ⇔ 16x2 + 12y2 = 48 ⇔ + = 1 3 4
Vậy tập hợp các điểm C là Elip x2 y2 + = 1. 3 4
d) Giả sử D(x, y) là biểu diễn hình học của số phức z = x + iy (x, y ∈ R) thỏa |z − 2| − |z + 2| > 3. Khi đó, ta có: |z − 2| − |z + 2| > 3 ⇔ (x − 2)2 + y2 − (x + 2)2 + y2 > 3 (x − 2)2 + y2 > (x + 2)2 + y2
⇔ (x −2)2 +y2 −2 (x−2)2 +y2 (x+2)2 +y2 +(x+2)2 +y2 > 9 x < 0
⇔ 2 (x −2)2 +y2 (x+2)2 +y2 < 2x2 +2y2 −1 x < 0 ⇔ 28x2 −36y2 > 63 x < 0 ⇔ x2 y2 > 1 − 9 7 4 4
Vậy tập hợp các điểm D là phần trong của nhánh bên trái Hyperbol x2 y2 = 1. 9 − 7 4 4
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) n n Bài toán 3: Cho z2 = z2 với z k
1; z2..., zn ∈ C. Chứng minh rằng: |Rez| ≤ |Rezk| k=1 k=1 Bài làm
Giả sử z = a + ib, (a, b ∈ R), zk = ak + ibk, (a, b ∈ R, k = 1, 2, 3, ...). n Do z2 = z2 nên ta có: k k=1 n 2iab = 2i x kyk (1) k=1 n a2 − b2 = (x2 ) (2) k − y2 k k=1 n 2 n n Từ (1) suy ra a2b2 = xkyk ≤ x2 y2
(3) (Bất đẳng thức Cauchy-Schwarz) k k k=1 k=1 k=1 1 n Ta chứng minh |a| ≤ x2 2 k k=1 1 1 n n Giả sử phản chứng | 2 2 a| > x2 . Khi đó từ (3) ta có: y2 k |b| < k k=1 k=1 n n n n (2) ⇔ a2 = b2 + (x2 ) < y2 + (x2 ) = x2 (mâu thuẫn) k − y2 k k k − y2 k k k=1 k=1 k=1 k=1 1 n n n 2 Vậy |a| ≤ x2 2 , mặc khác do x2 nên k k ≤ |xk| k=1 k=1 k=1 n n |Rez| = |a| ≤ |xk| = |Rezk| k=1 k=1
Bài toán 4: Chứng minh rằng có thể tính arg(x + iy) bằng công thức y π tan−1 + [1 − sgnx] khi x = 0 x 2 π arg(x + iy) = sgn(y) khi x = 0 và y = 0 2 không xác định khi x = 0 và y = 0
Ở đây hàm dấu sgn được định nghĩa như sau 1 khi t > 0 sgn(t) := 0 khi t = 0 −1 khi t < 0
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Bài làm z = x + iy • x = 0
⇒ z = x + iy = r(cos ϕ + i sin ϕ) x = r cos ϕ y ⇒ ⇒ tanϕ = x y = rsinϕ y ⇒ ϕ = tan−1 + kπ, (k ∈ Z) x y ϕ = tan−1 + π ⇒ x y ϕ = tan−1 x y 1 ⇒ ϕ = tan−1 + (1 − sgnx) x 2 • x = 0, y = 0 π π
r cos ϕ = 0 ⇒ cos ϕ = 0 ⇔ ϕ = ± = .sgn(y). 2 2 • x = 0, y = 0
⇒ z = 0 ⇒ Không xác định do không tồn tại arg 0.
Vậy ta có điều phải chứng minh.
Bài toán 5: Chứng minh rằng biểu thức x f (x, y) = sgn(y) cos− 1 tại các điểm liên x2 + y2
tục của nó bằng với Arg(x + iy). Bài làm
Hàm số liên tục trên {x ≤ 0, y = 0}. x
• Với y > 0 có sgn(y) = 1. Do −1 ≤ ≤ 1 có x2 + y2 x f (x, y) = cos−1 = Arg(x + iy) ∈ (0, π) x2 + y2 x
• Với y > 0 có sgn(y) = −11. Do −1 ≤ ≤ 1 có x2 + y2 x f (x, y) = −cos−1 = Arg(x + iy) ∈ (−π, 0) x2 + y2
• Với y = 0, x > 0 có sgn(y) = 0. Do x
= 1 có f (x, y) = 0 = Arg(x + iy) x2 + y2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Vậy x f (x, y) = sgn(y) cos− 1
tại các điểm liên tục của nó bằng với Arg(x + iy). x2 + y2
Bài toán 6: Chứng minh z − 1 ≤ |arg(z)| với mọi số phức z = 0 và Bài làm thích ý nghĩa |z|
hình học của bất đẳng thức này. Bài làm
Giả sử z = r (cosϕ + isinϕ) Ta có: z r(cosϕ + isinϕ) − 1 = − 1 |z| r = |(cosϕ + isinϕ) − 1| = (cosϕ − 1)2 + (sinϕ)2 =
(cosϕ)2 − 2cosϕ + 1 + (sinϕ)2 = 2 − 2cosϕ = 2 (1 − cosϕ) 1 ϕ 2 = 4. . (1 − cosϕ) = 4 sin 2 2 ϕ = 2 sin = |ϕ| = |arg (z)| , ∀z = 0 (điều cần chứng minh) 2 * Ý nghĩa hình học: y B ϕ A O 1 x
Vẽ đường tròn đơn vị (C) = {M(x, y) | x2 + y2 = 1}. Nếu điểm A(1, 0) ∈ (C) biểu diễn cho số phức z z z thì độ dài dây
1 = 1 và điểm B(cosϕ, sinϕ) ∈ (C) biểu diễn cho số phức z2 = AB = − 1 , độ |z| |z|
dài cung AB= |ϕ| = |arg (z)|. Vậy bất đẳng thức trên cho ta: AB ≤AB.
Bài toán 7: Cho a, b, c ∈ C và a + b + c = 0, |a| = |b| = |c| = 1. Chứng minh rằng a3 = b3 = c3. Bài làm
Với x ∈ C bất kì ta có z · z = |z|2.
Suy ra với các số phức a, b, c của bài toán thì |a|2 1 |b|2 1 |c|2 1 a = = , b = = , c = = . a a a b c c
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Ta có: a + b + c = 0. Suy ra a + b + c = 0 và b + c = −a. Khi đó 1 1 1 bc + ac + ab bc + a(b + c) bc − a2 0 = a + b + c = + + = = = . a b c abc abc abc Suy ra a2 = bc hay a3 = abc.
Chứng minh tương tự ta được: b3 = abc và c3 = abc. Vậy a3 = b3 = c3 (đpcm). 2πi
Bài toán 8: Cho m là số nguyên dương, l là số nguyên không chia hết cho m. Đặt ω m . m := e Chứng minh rằng:
a) 1 + ωm + ω2 + ... + ωm−1 = 0,
b) 1 + ωl + ω2l + ... + ω(m−1).l m m m m m = 0. Bài làm
Ta chứng minh kết quả sau để áp dụng chứng minh câu a và b: Với z = 1, ta có
zn − 1 = 1 + z + z2 + ... + zn−1(∗) z − 1 Chứng minh: Ta có
(z − 1)(1 + z + z2 + ... + zn−1) = z + z2 + z3 + ... + zn − 1 − z − z2 − ... − zn−1 = zn − 1.
Do z = 1 nên ta chia z − 1 cho 2 vế, ta được
zn − 1 = 1 + z + z2 + ... + zn−1. z − 1
a) 1 + ωm + ω2 + ... + ωm−1 = 0 m m 2πi Đặt 2πi z = ω m , hiển nhiên m = e z = 1 (do 0 <
< 2πi, với mọi m là số nguyên dương và e2πi = 1. m Áp dụng (∗), ta có zm − 1 e2πi − 1
1 + ωm + ω2 + ... + ωm−1 = 1 + z + z2 + ... + zm−1 = = = 0. m m z − 1 z − 1 b)
1 + ωl + ω2l + ... + ω(m−1)l m m m = 0 2πil
Đặt z = ωl = e m , hiển nhiên z = 1 (do l không chia hết cho m nên ta có thể viết l = k + m với m 2πil 2πik
k ∈ Z và 0 < k < m, nên ta có z = e m = e m = 1) và zml = (e2πi)l = 1. Áp dụng (∗), ta có zml − 1 (e2πi)l − 1
1 + ωl + ω2l + ... + ω(m−1)l = = 0. m m m
= 1 + zl + z2l + ... + z(m−1)l = z − 1 z − 1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 9: Giả sử các chuỗi ∞ z và ∞
z2 hội tụ . Chứng minh rằng nếu Rez k=1 k k=1 k n ≥ 0 thì chuỗi ∞ k=1 |zk|2 hội tụ. Bài làm Đặtz vì chuỗi ∞ hội tụ nên chuỗi ∞ hội tụ. k = ak + ibk z a k=1 k k=1 k Theo giả thiết ta có Rez hội tụ nên
k = ak > 0 và với k đủ lớn thì ak < 1 ( do chuỗi ∞ a lim k=1 k x→∞ ak = 0
) Từ đây suy ra 0 < a2 < a do đó chuỗi ∞ a hội tụ. k k k=1 k Với z thì . Vì chuỗi ∞ hội tụ nên chuỗi ∞ k = ak + ibk z2 = (a2 ) + i2a z2 (a2 ) hội tụ. k k − b2 k kbk k=1 k k=1 k − b2 k Mà chuỗi ∞
a2 hội tụ nên suy ra chuỗi ∞ b2 hội tụ. k=1 k k=1 k Với z thì k = ak + ibk |zk|2 = (a2 + b2) k k Do chuỗi ∞ a2 và chuỗi ∞ b2 hội tụ nên chuỗi ∞ (a2 + b2) hội tụ. k=1 k k=1 k k=1 |zk|2 = ∞ k=1 k k Bài toán 10 √ : Cho dãy điểm {z và n = n + i
2n}. Tính khoảng cách cầu của các điểm zn ∞ trong n→∞ C . Chứng minh rằng ∞ zn −→ ∞ Bài làm Ta có 1 1 1 d(z n→∞ n, ∞) = = = . Vì d(zn, ∞) n→∞ −→ 0 nên zn −→ ∞. 1 + |z √ n + 1 n|2 1 + |n + i 2n|2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 2
Bài toán 1:Trong C cho các tập hợp được mô tả bởi các bất phương trình sau: π A : |z − 1 + i| ≤ 2, B : |Argz| < , C : 0 < |z − 1| < 2, 6 D : −1 < Imz ≤ 2, E : |z| ≥ 1, F : (Rez)2 > 2.
a) Tập hợp nào trong các tập hợp đã cho là tập hợp mở?
b) Tập hợp nào trong các tập hợp đã cho là miền?
c) Tập hợp nào trong các tập hợp đã cho là tập hợp bị chặn?
d) Mô tả biên của các tập hợp đã cho.
e) Tập hợp nào trong các tập hợp đã cho là tập hợp compact? Bài làm
a) Tập hợp B,C,F là tập hợp mở trong C π • B : |Argz| < 6 Với mỗi π −π z thuộc B, ta gọi là khoảng cách từ tới và 0 r1, r2 z0 Argz = Argz = 6 6 Đặt r = min{r1, r2}
Vậy quả cầu mở tâm z , bán kính tùy ý nên B mở. 0 r nằm trong B. Do z0 • C : 0 < |z − 1| < 2
Với mỗi z thuộc C, ta lấy 0
r sao cho r = |z0 − 1| thì 0 < r < 2
Vậy quả cầu mở tâm z , bán kính 0 r nằm trong C và C mở • F : (Rez)2 > 2 √ √
Với mỗi z thuộc F, ta gọi là khoảng cách từ tới 0 r1, r2 z0 Rez = 2 và Rez = − 2 Đặt r = min{r1, r2}
Vậy quả cầu mở tâm z , bán kính tùy ý nên F mở. 0 r nằm trong F. Do z0
b) Tập B,C là tập mở liên thông trong C
c) Tập hợp A,C là tập hợp bị chặn trong C • A : |z − 1 + i| ≤ 2 √
Ta có: |z − 1 + i| ≤ 2 ⇔ |z − (1 − i)| ≤ 2 ⇔ ||z| − |1 − i|| ≤ |z − (1 − i)| ≤ 2 ⇒ |z| ≤ 2 + 2 √ √
Vậy với mọi z thuộc A tồn tại M = 2 + 2 thì |z| ≤ 2 + 2 và A bị chặn. • C : 0 < |z − 1| < 2
Ta có: |z − 1| < 2 ⇔ |z| − |1| < |z − 1| < 2 ⇒ |z| < 3
Vậy với mọi z thuộc C thì |z| < 3 và C bị chặn.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
d) Biên của các tập hợp là π ∂A : |z − 1 + i| = 2; ∂B : |Argz| = ∂C : {|z − 1| = 2} ∪ {1} 6
∂D : {Imz = −1} ∪ {Imz = 2}; ∂E : |z| = 1;
∂F : {Rez = −2} ∪ {Rez = 2}.
e) Tập hợp A là tập compact. • A : |z − 1 + i| ≤ 2
Ta thấy A là quả cầu đóng tâm z0 = 1 − i, bán kính r = 2 mà A bị chặn (chứng minh ở câu c) nên A là tập compact. Bài toán 2: Cho tập 1 1 1 A =
1, , , ..., , ... . Tìm tất cả các điểm biên của A trong C. 2 3 n Bài làm
• Lấy x ∈ A tùy ý. Ta chứng minh x ∈ ∂A Khi đó x có dạng 1 1 r 1 x =
với n ∈ N. Với mọi r > 0, ta có: 1 ∈ B( , r)∩ A và 1 + i ∈ B( , r) ∩ (C\ A). n n n n 2 n Ta chứng minh 0 ∈ ∂A. Thật vậy, với mọi 1
r > 0, ta có 1 ∈ B(0, r) ∩ A với n ∈ Nvà n > mà 0 ∈ B(0, r) ∩ (C \ A). n r Do đó A ∪ {0} ⊂ ∂A.
Ta chứng minh ∂A ⊂ A ∪ {0}.
Đặt B = A ∪ {0} và d(x, A) = inf{|x − x0|, x0 ∈ A}
. Ta chứng minh B = A, qua 2 bước sau:
• Chứng minh B là tập đóng hay C \ B là tập mở
Lấy tuỳ ý x = a + bi ∈ C \ B TH1: b
b = 0, dễ thấy |b| ≥ d(x, A). Khi đó, ta xét z ∈ B(x, ) 2 Ta có, b |x − z| <
nên z /∈ B. Suy ra z ∈ C \ B 2 Vậy b B(z, ) ∈ C \ B 2 TH2: b = 0 -TH2.1: |a| a < 0 chọn = thì B(x, ) ⊂ C \ B 2 -TH2.2: 1 1 1
a > 0. Khi đó, tồn tại n . Chọn 0 ∈ Nsao cho 1 < a < = min{a − , − a} n0 + 1 n0 n0 + 1 n0 Dẫn đến B(x, ) ⊂ C \ B
Vậy, với mọi x ∈ C \ B, tồn tại sao cho B(x, ) ⊂ C \ B hay C \ B mở • Chứng minh B = A
A ⊂ B (hiển nhiên do A ⊂ B mà B đóng) Ta có dãy 1 xn = ⊂ A. x n
n → 0 nên 0 ∈ A. Suy ra B ⊂ A Do đó, B = A Ta có, ˚ A = ∅ nên ∂A = A \ ˚ A = A = B
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 3: Cho Z là điểm thuộc A. Chứng minh rằng: Nếu z không là điểm trong là 0 A thì z0 điểm biên của A. Bài làm
Xét không gian topo X, tập A ⊂ X, A = ∅.
Giả sử z0 ∈ A và không là điểm trong của A. ◦ ◦
Suy ra z0 ∈ A ⇒ z0 ∈ X \ A. Mà z0 ∈ A nên ta được: z 0 ∈ A A ⊂ ¯ A mà . ◦ ◦ z 0 ∈ X \ A X \ A = X \ A z Suy ra 0 ∈ A . z0 ∈ X \ A
Do đó z0 ∈ A ∩ X \ A = ∂A. Vậy z0 ∈ ∂A.
Bài toán 4: Chứng minh rằng biên của một tập compact trong C là tập compact trong C Bài làm
Giả sử A là tập compact trong C, nghĩa là A là tập đóng và bị chặn trong C. A bị chặn trong C nên δA bị chặn trong C.
Ta chứng minh δA là tập đóng.
Mà ta có δA ⊂ δA , vậy ta cần chứng minh δA ⊂ δA. Lấy z0 ∈ δA(1).
Khi đó với mọi ε > 0 có B (z0, ε) ∩ ∂A = ∅, B (z0, r) ∩ (C\∂A) = ∅. Suy ra có (z n→∞ . n) ⊂ δA, zn −→ z0
Dẫn đến ∀ε > 0, ∃n0, ∀n ≥ n0 ⇒ zn ∈ B (z0, ε). Đặc biệt zn ∈ B (z , ε ) ⊂ B (z 0
0, ε) nên ∃ε > 0 : B (zn0 0, ε).
Suy ra B (zn , ε ) ∩ A = ∅, B (z , ε ) ∩ (C\A) = ∅ vì z ∈ δA. 0 n0 n0
Do đó B (z0, ε) ∩ A = ∅, B (z0, ε) ∩ (C\A) = ∅. Vậy z0 ∈ δA (2) .
Từ (1) và (2) suy ra δA ⊂ δA, do đó δA là tập đóng.
Vậy δA là tập đóng và bị chặn trong C, tức là δA là tập compact trong C.
Kết luận: Biên của một tập compact trong C là tập compact trong C.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 5: Cho K ⊂ C . Chứng minh nếu và chỉ nếu . ∞ K compact trong C∞ K đóng trong C∞ Bài làm
(⇒) Giả sử K compact trong C . ∞
Với mọi dãy {zn}n∈N⊂ K, zn → a.
Do K compact nên tồn tại {zn } → a ∈ K. k k∈N, znk
Do tính duy nhất của giới hạn nên a = a ∈ K. Suy ra K đóng trong C . ∞
(⇔) Giả sử K đóng trong C . ∞ Xét metric (C . ∞, δ) với δ(z, w) = d[¯ π(z), ¯ π(w)], ∀z, w ∈ C∞ ∀z ∈ C , do ∞
δ(0, z) ≤ 1 nên z ∈ B(0, 1). Suy ra C bị chặn. ∞
Dẫn đến K bị chặn, mà K đóng nên theo định lý Bolzano-Weierstrass, ∀{zn}n∈N⊂ K, tồn tại dãy con {z hội tụ. n } k k∈N Vậy K compact. Bài toán 6: Cho {F
là tập compact. Chứng minh
n} là dãy giảm các tập con đóng trong C và F1 ∞ rằng Fn = ∅. n=1 Bài làm
Thật vậy, với mỗi n ta lấy điểm z . n ∈ Fn Ta có (z . Do là tập compact nên . n) ⊂ F1 F1
(zn) có dãy con (zn ) hội tụ về z k 0 ∈ F1
Với mọi m ∈ Ncố định thì z với mọi n ∈ F ⊂ F ⊂ F k > m (do {F k nk nm m
n} là dãy giảm các tập con đóng trong C). Mà F đóng nên . m zn −→ z k 0 ∈ Fm ∞ Vì z với mọi nên . 0 ∈ Fm m ∈ Fm z0 ∈ Fm n=1 ∞ Vậy {F là tập compact thì
n} là dãy giảm các tập con đóng trong C và F1 Fn = ∅. n=1
Bài toán 7: Nếu S và T là miền thì S ∩ T có là miền không? Bài làm
Ta có S và T là các miền nên S và T là các tập mở, khác rỗng và liên thông.
i): S ∩ T = ∅.Khi đó S ∩ T không phải là miền.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) ii: S ∩ T = ∅.
Ta có nhận xét rằng giao của hai tập mở, liên thông đường có thể là tập liên thông đường, cũng có thể
là tập không liên thông đường.
◦ Giao của hai tập mở, liên thông đường có thể là tập liên thông đường. Ví dụ nếu S và T là hai tập
lồi thì S ∩ T cũng là tập lồi nên liên thông đường.
Trong trường hợp giao của hai tập mở là liên thông đường thì S ∩ T là tập mở khác rỗng trong C, liên
thông đường nên theo định lý 2.5.10 S ∩ T cũng là tập liên thông.
Do đó ta có S ∩ T là tập mở khác rỗng trong C và liên thông nên S ∩ T là miền.
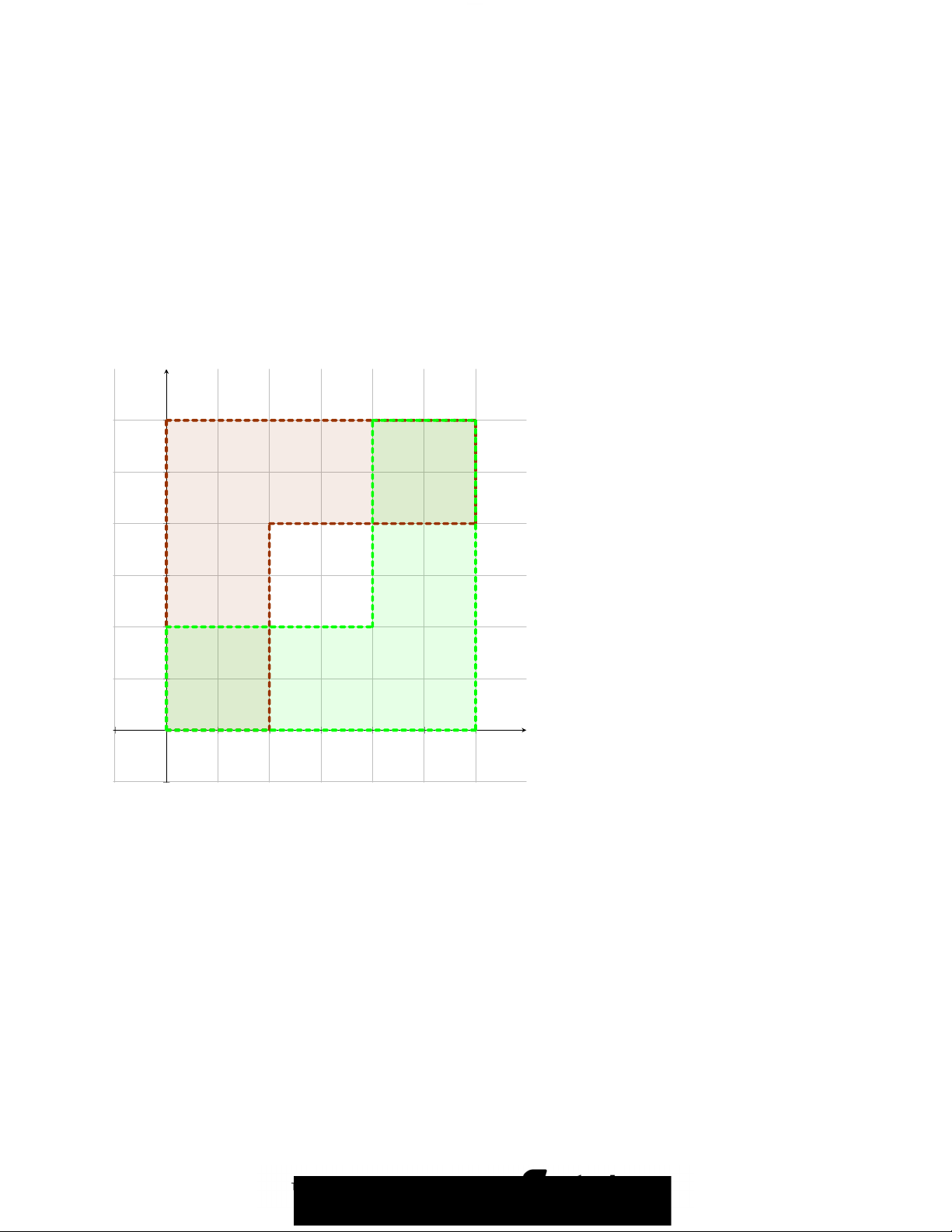
◦ Mặt khác S ∩ T cũng có thể là tập không liên thông đường như ví dụ dưới đây. y 3 2.5 S 2 1.5 T 1 0.5 −0.5 O 0.5 1 1.5 2 2.5 3 x −0.5 0 < x < 1 1 ≤ x < 3 S = z = x + iy (x, y) ∈ R2 : ∨ 0 < y < 3 2 < y < 3 0 < x ≤ 2 2 < x < 3 T = z = x + iy (x, y) ∈ R2 : ∨ 0 < y < 1 0 < y < 3 0 < x < 1 2 < x < 3 S ∩ T = z = x + iy (x, y) ∈ R2 : ∨ 0 < y < 1 2 < y < 3
Ta có S ∩ T không liên thông đường do (0, 5; 0, 5) và (2, 5; 2, 5) đều thuộc S ∩ T nhưng không tồn tại
đường nối hai điểm trên nằm trong S ∩ T.
Trong trường hợp giao của hai tập mở không liên thông đường, giả sử S ∩ T là tập liên thông thì theo
định lý 2.5.10 S ∩ T là tập mở khác rỗng trong C và liên thông nên S ∩ T liên thông đường (vô lý).
Vậy S ∩ T không là tập liên thông do đó cũng không là miền.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) KẾT LUẬN:
• TH: S ∩ T = ∅ thì S ∩ T không là miền.
• TH: S ∩ T = ∅. S ∩ T là tập liên thông đường thì S ∩ T là miền và ngược lại S ∩ T không là tập liên
thông đường thì cũng không là miền.
Bài toán 8:Chứng minh nếu A liên thông trong C và B ⊂ C sao cho A ⊂ B ⊂ A thì B liên thông. Bài làm
Giả sử A liên thông và B thỏa: A ⊂ B ⊂ A Khi đó ∃V mở không giao nhau trong 1, V2 B sao cho B = V1 ∪ V2 Vì A ⊂ B ⇒ A ∩ V là mở trong 1; A ∩ V2 A.
Suy ra A = (A ∩ V1) ∪ (A ∩ V2) Vì A liên thông nên:
A ∩ V1 = ∅ ∧ A ∩ V2 = A
A ∩ V2 = ∅ ∧ A ∩ V1 = A
Không mất tính tổng quát, giả sử: A ∩ V1 = ∅ và A ∩ V2 = A.
A ∩ V1 = ∅ ⇒ ∃x ∈ B ⊂ A và > 0 sao cho B(x, ) ∩ A = ∅. Mâu thuẫn x ∈ A.
Vậy B là tập liên thông.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 3
Bài toán 1: Tìm tất cả các hàm f : C → C thoả mãn ∀z ∈ C: f(z) + zf(−z) = 1 + z (1) Bài làm
Lần lượt thế z = i và z = −i vào (1) ta có f (i) + i.f (−i) = 1 + i ⇔ f(i), f(−i) ∈ R.
f (−i) + (−i)f (i) = 1 − i
Thay z bởi −z vào (1) ta có hệ sau
f (z) + z · f (−z) = 1 + z
f (z) + z(1 − z + z · f (z)) = 1 + z ⇔
f (−z) + (−z)f (z) = 1 − z
f (−z) = 1 − z + z.f (z)
f (z) + z − z2 + z2f (z) = 1 + z
⇔ f(−z) = 1−z +z.f(z) 1 + z2)f (z) = 1 + z2
⇔ f(−z) = 1−z +z.f(z)
⇔f(z) = f(−z) = 1, ∀z ∈ C \ {−i, i}. a + bi, z = i,
Như vậy, ta tìm được hàm f(z) =
1 − b + (a − 1)i, z = −i,
thoả mãn yêu cầu đề bài. 1, z ∈ C \ {i, −i} Bài toán 2: Cho hàm số 1 w = z
a) Tìm ảnh của các đường x = C, | z |= R, | z = 1 |= 1 qua w.
b) Tìm ảnh của {z : 0 ≤| z |≤ 1} qua w.
c) Tìm tạo ảnh của các đường u = C, v = C qua w. Bài làm a) Với 1 x −y x = C, ta có w = = + i = u(x, y) + v(x, y). z x2 + y2 x2 + y2 x −y u = , v = x2 + y2 x2 + y2
Tại C = 0 ⇒ x = 0 ⇒ ảnh là đường thẳng x = 0, trừ góc tọa độ. 2 Tại 1 u 1 ! C = 0 ⇒ u2 + v2 = = ⇔ u − + v2 = x2 + y2 C 2C 4C2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) 1
⇒ ảnh là đường tròn tâm 1 ,0 , R = 2C 2 | C | Với 1 1
| z |= R ⇒ x2 + y2 = 1 ⇒ u2 + v2 = = x2 + y2 R2
⇒ ảnh là đường tròn tâm O bán kính là 1 . R Với x 1
| z − 1 |= 1 ⇒ (x − 1)2 + y2 = 1 ⇒ x2 + y2 = 2x ⇒ u = = x2 + y2 2 1
⇒ ảnh là đường thẳng u = 2 b) Ta có 1 0 < x2 + y2 ≤ 1 ⇒ ≥ 1 ⇒ u2 + v2 ≥ 1 x2 + y2 c) Với u = C
Nếu C = 0 ⇒ x = 0 tạo ảnh là trục ảo trừ gốc O. 2 2 Nếu x 1 1 C = 0 ⇒ = C ⇔ x − + y2 =
. Tạo ảnh là đường tròn tâm 1, 0 , bán x2 + y2 2C 2C 2 kính 1 . 2 | C | Với v = C
Nếu C = 0 ⇒ y = 0 tạo ảnh là trục thực trừ gốc tọa độ. 2 2 Nếu y 1 1 −1 C = 0 ⇒ x2 + y2 + = 0 ⇔ x2 + y + =
. Tạo ảnh là đường tròn tâm 0, C 2C 2C 2C bán kính 1 . 2 | C |
Bài toán 3: Cho hàm ω = f(z) = ez
a) Tìm miền xác định và miền giá trị của hàm số. b) Chứng minh 1 f (−z) = . f (z)
c) Tìm ảnh của đường thẳng nằm ngang π Imz = . 4 d) Tìm ảnh của dải π 0 ≤ Imz ≤ qua ω. 4 Bài làm
Ta có f(z) = ez = ex+yi = exeiy = ex(cosy + isiny), với (x, y) ∈ R2.
a) Do x, y xác định trong R nên tập xác định của hàm f(z) là C. Tìm tập đích của f(z) :
Vì ex > 0, cosy ∈ [−1, 1], siny ∈ [−1, 1], ∀(x, y) ∈ R2 và siny, cosy không đồng thời bằng 0 với mọi số
thực y nên f(C) ⊂ C\{0}. Ta sẽ chứng minh C\{0} ⊂ f(C). Thật vậy: Lấy z ∈ C\{0} tùy ý. Suy ra
z = x + iy với (x, y) ∈ R2\{(0, 0)}. Khi đó x = ln x2 + y2 = 0 và x y z = x + iy = x2 + y2. + i . x2 + y2 x2 + y2 Vì
x2 + y2 = 0 nên ta có thể chọn x = ln x2 + y2. Vì x và y ∈ [−1, 1] nên ta có x2 + y2 x2 + y2
thể chọn y ∈ [0, 2π] sao cho
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) x y y = arccos = arcsin . Suy ra, x2 + y2 x2 + y2 x y x2 + y2 = ex ; = cosy ; = siny x2 + y2 x2 + y2
⇒ z = ex . (cosy + isiny ) = f(x + iy ), với x , y ∈ R ⇒ ∃z ∈ C : z = f(z).
Vậy tập đích là f(C) = C\{0}.
b) Lấy z ∈ C tùy ý. Khi đó, z = x + iy với x, y ∈ R. Ta có:
f (−z).f(z) = e−x.(cos(−y) + isin(−y))ex.(cosy + isiny)
= e−x.ex.(cos(−y) + isin(−y)).(cosy + isiny)
= (cosy − isiny)(cosy + isiny)
= cos2y + isiny.cosy − isiny.cosy − i2sin2y = cos2y + sin2y = 1. Suy ra 1 f (−z) = . f (z) c) Với mọi π π
z nằm trên đường thẳng (d) : Imz =
, z có dạng z = x + i , với x ∈ R. f(d) là ảnh cần 4 4
tìm. Lấy z nằm trên đường thẳng (d) tùy ý. Ta có: √ √ π π 2 2 f (z) = ex.(cos + isin ) = ex + i ex, z ∈ d. 4 4 2 2
Do ex > 0 nên f(z) là điểm nằm trên tia Rez = Imz > 0. Lấy z tùy ý nằm trên tia Rez = Imz > 0. √
Suy ra, z = a + ia với a > 0. Đặt x − ln 2a. x tồn tại do a > 0. Khi đó, √ √ 2 2 z = a + ia = ex + i ex. 2 2 Vậy ảnh của π
(d) là tia {z ∈ C : Rez = Imz > 0} = {z ∈ C : Argz = }. 4
d) Xét họ các đường thẳng π
(dm) : Imz = m với m ∈ M = [0, ]. Lấy m ∈ M tùy ý. Suy ra, mọi zin(d 4 m)
đều có dạng z = x + im, x ∈ R. Nếu m = 0, z = x ∈ R. Suy ra, f(z) = ex, ∀z ∈ (dm) là toàn bộ tia Rez > 0 Imz = 0. Nếu m = 0, ta có:
f (z) = ex.(cosm + isinm) = excosm + iexsinm.
Chú ý rằng ex > 0, suy ra, f(z) nằm trên tia (d ) m Rez = t > 0 Imz = t.tanm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Lấy t
z = (t, t.tanm) ∈ (d ) tùy ý. Khi đó, đặt x = ln(
), ta được z = excosm + iexsinm = m cosm
f (x + ix.tanm) và x + i.tanx ∈ C. Vậy ảnh của (dm) qua ω là tia (d ) m Rez = t > 0 Imz = t.tanm Kết hợp với ảnh của π d và là họ các tia 0
tan0 = 0, ảnh của dải 0 ≤ Imz ≤ 4 Rez = t > 0 π π , m ∈ 0, .
hay là tập S = {z ∈ C : 0 ≤ Argz ≤ } 4 4 Imz = t.tanm
Bài toán 4: Ánh xạ Joukowski là ánh xạ được xác định bởi 1 1 ω = J(z) = z + 2 z Chứng minh: (a) 1 J(z) = J z
(b) J biến đường tròn |z| = 1 lên đoạn [−1, 1] (c) v2
J biến đường tròn |z| = r (r > 0, r = 1) lên elip u2 + = 1 có tiêu 1 1 2 1 1 2 r + r − 2 r 2 r điểm ±1 Bài làm (a) 1 J (z) = J z - Trường hợp 1: 1 1 1 z ∈ C \ {0}. Khi đó J = + z = J(z) z 2 z - Trường hợp 2: 1 1 1 1 1 z = ∞. Khi đó J(∞) = ∞ + = ∞ và J = J(0) = 0 + = ∞ 2 ∞ ∞ 2 0 Suy ra 1 J(z) = J . z - Trường hợp 3: 1 1 1 1 1 z = 0 ta có J(0) = 0 + = ∞ và J = J(∞) = ∞ + = ∞ 2 0 0 2 ∞ Suy ra 1 J(z) = J z Vậy 1 J (z) = J z
(b) J biến đường tròn |z| = 1 lên đoạn [−1, 1]
Giả sử z = reiφ,r = |z| ta có 1 1 1 1 ω = u + iv = reiφ + =
r(cos φ + i sin φ) + (cos φ − i sin φ) 2 reiφ 2 r 1 1 1 1 = r + cos φ + i r − ) φ. 2 r 2 r
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) 1 1 u = r + cos φ −1 ≤ u ≤ 1 Suy ra 2 r . Với r = 1 ta có 1 1 v = r − sin φ v = 0 2 r
Vậy J biến đường tròn |z| = 1 lên đoạn [−1, 1]. (c) v2
J biến đường tròn |z| = r (r > 0, r = 1) lên elip u2 + = 1 có tiêu 1 1 2 1 1 2 r + r − 2 r 2 r điểm ±1 Từ (b) ta có 1 1 u = r + cos φ 2 r 1 1 v = r − sin φ 2 r . Suy ra u2 v2 + = 1 1 1 2 1 1 2 r + r − 2 r 2 r
Vậy J biến đường tròn |z| = r(r > 0, r = 1) lên elip u2 v2 + = 1 1 1 2 1 1 2 r + r − 2 r 2 r 2 2 có tiêu điểm 1 1 1 c = ± 12 r + − r − = ±1 r 2 r π Bài toán 5: Cho i π
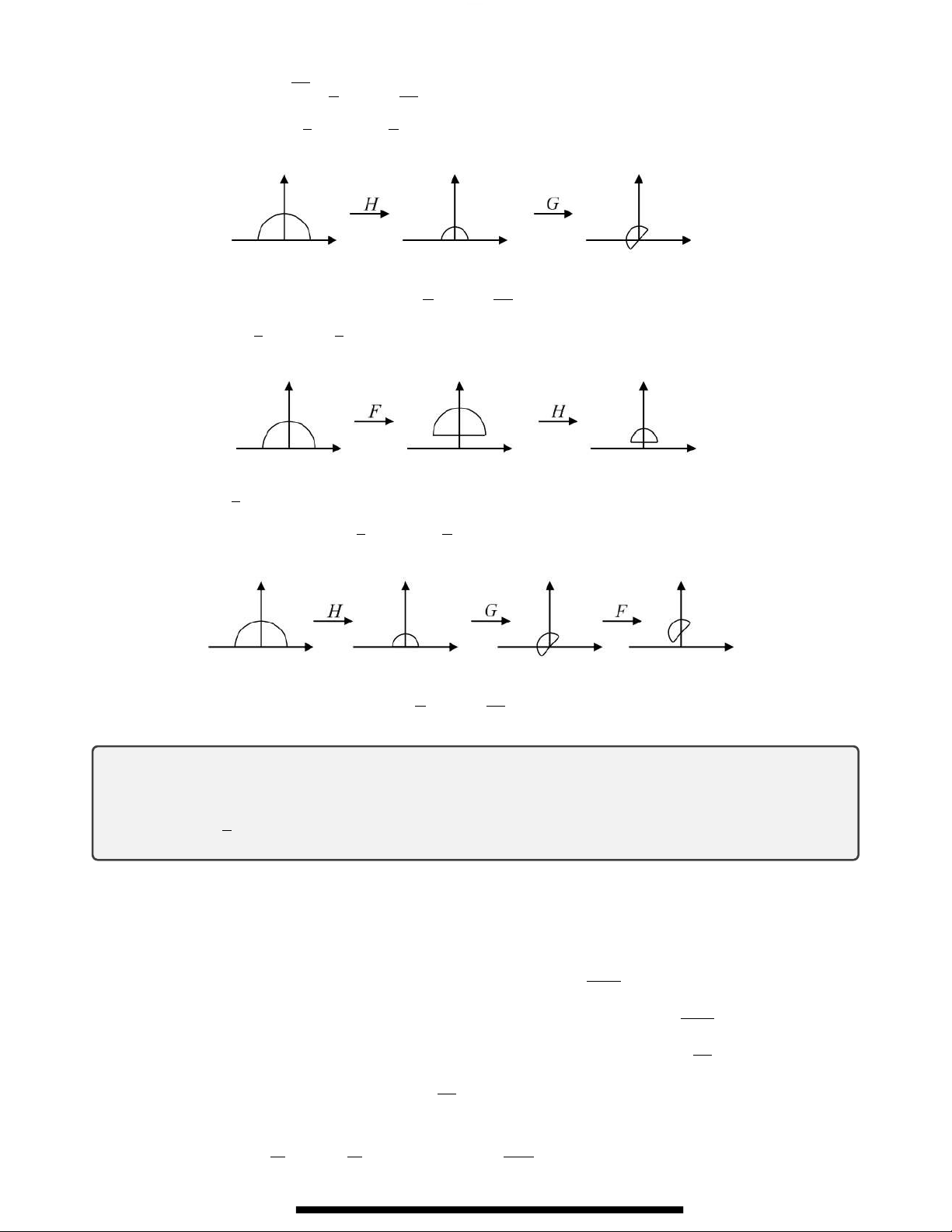
F (z) = z + i, G(z) = e 4 z và H(z) = . Tìm ảnh của nửa đĩa 2
{z : |z| ≤ 2, Imz ≥ 0} qua hàm hợp: (a) G(F (z)). (b) G(H(z)). (c) H(F (z)). (d) F (G(H(z))). Bài làm 3π a) i π
G(F (z)) = reiβ + e 4 với β = ϕ + . 4
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) 3π i π 5π G(F (A)) = w = reiβ + e 4 : ≤ β ≤ , 0 ≤ r ≤ 2 . 4 4 b) r π
G(H(z)) = r eiβ với r = , β = ϕ + 2 4 π 5π
G(H(A)) = w ∈ C : w = r eiβ : 0 ≤ r ≤ 1, ≤ β ≤ . 4 4 c) i r H(F (z)) = r eiϕ + với r = 2 2 i H(F (A)) = w =
+ r eiϕ : 0 ≤ ϕ ≤ π, 0 ≤ r ≤ 1 . 2 d) r π
F (G(H(z))) = r eiβ + i với r = , β = ϕ + 2 4 π 5π
F (G(H(A))) = w = i + r eiβ : 0 ≤ r ≤ 1, ≤ β ≤ . 4 4
Bài toán 6: Tìm một miền đơn diệp của hàm sau: a) f(z) = e3iz b) 4 f (z) = z + z Bài làm a) Ta có với z1 = z2 2kπi
f (z1) = f (z2) ⇔ e3iz1 = e3iz2 ⇔ 3i (z1 − z2) = 2kπ ⇔ z1 − z2 = , k ∈ Z 3
Miền D muốn đơn diệp nếu chứa điểm 2kπi
z thì không được chứa điểm 1 z2 = z1 + , k ∈ Z 3
Vậy chọn miền đơn diệp là một dài song song với trục ảo có bể rộng không quá 2π . 3 Chọn 2π D =
x + iy : −∞ < x < +∞, 0 < y ≤ . 3 b) Ta có: với z thì 1z2 4 4 4 f (z1) = f (z2) ←→ z1 + = z −→ (z = 0 −→ z z 2 + 1 − z2)(1 − 1z2 = 4 1 z2 z1z2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Vậy D muốn đơn diệp thì không được chứa đồng thời 2 điểm z mà 1, z2 z1z2 = 4.
Chọn D=(z ∈ C : |z| ≤ 2).
Bài toán 7: Chứng minh rằng định nghĩa lim f(z) = ∞ tương đương với định nghĩa: Giới hạn z→z0 của f(z) khi z → z là 0
∞ nếu lim d(f(z), ∞) = 0 (với d(z, w) là khoảng cách cầu của z và w). z→z0 Bài làm • Chiều thuận
Với mọi > 0, ta xét 2 TH: - Nếu ≥ 1, khi đó
+ Do lim f (z) = ∞ nên tồn tại δ > 0 : ∀z ∈ C, |z − z0| < δ ⇒ |f(z)| > 0. z→z0
+ Chọn δ = min{1, δ }, ta có 1 < 1 ≤ . 1 + |f(z)|2 - Nếu < 1, khi đó 1
+ Do lim f (z) = ∞ nên tồn tại δ > 0 : ∀z ∈ C, |z − z0| < δ ⇒ |f(z)| > − 1. z→z 2 0 1
+ Chọn δ = δ , thì ∀z ∈ C, |z − z0| < δ , ta có 1 < < . 1 + |f(z)|2 2 1 1 + − 1 2 Vậy 1 lim = 0. z→z0 1 + |f (z)|2 • Chiều nghịch Với mọi M > 0 1 1 1 + Do lim
= 0 nên tồn tại δ > 0 : ∀z ∈ C, |z − z . 0| < δ ⇒ < √ z→z0 1 + |f (z)|2 1 + |f(z)|2 1 + M 2
+ Chọn δ = δ , thì ∀z ∈ C, |z − z0| < δ , ta có 1 1 < √
⇒ |f(z)|2 > M2 ⇒ |f(z)| > M (do |f(z)| > 0, M > 0) 1 + |f(z)|2 1 + M 2 Vậy lim f(z) = ∞ z→z0
Bài toán 8: Xét sự tồn tại của giới hạn 1 z z lim − z→0 2i z z Bài làm Đặt z = a + bi a → 0
Theo định lý ta có z → 0 ⇔ . b → 0
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Khi đó 1 z z 1 z2 − (z)2 1 4abi 2ab − = = = . 2i z z 2i z.z 2i a2 + b2 a2 + b2 Suy ra 1 z z 2ab lim − = lim . z→0 2i z z (a,b)→(0,0) a2 + b2 Xét 2ab f (a, b) = . a2 + b2 2 Xét 1 1 1 1 (a, b) = , → (0, 0). Khi đó f , = n2 → 1. n n n n 1 1 + n2 n2 4 Xét 1 2 1 2 4 (a, b) = , → (0, 0). Khi đó f , = n2 → . n n n n 1 4 5 + n2 n2 Vậy 2ab 1 z z f (a, b) =
không tồn tại giới hạn hay lim − không tồn tại. a2 + b2 z→0 2i z z
Bài toán 9: Tìm A để hàm số f(x) liên tục tại z = 0. Rez z , khi z = 0 , khi z = 0 (a) f(x) = z (b) f(x) = |z| A , khi z = 0 A , khi z = 0 Re z Imz (z)2 , khi z = 0 , khi z = 0 (c) f(x) = |z|2 (d) f(x) = |z| A , khi z = 0 A , khi z = 0 Bài làm Rez , khi z = 0 (a) f(x) = z A , khi z = 0 Đặt z = x + yi. Với mọi x x2 xy z = 0, ta có f (z) = = − i = u(x, y) + v(x, y). x + yi x2 + y2 x2 + y2
Nhận thấy giới hạn của u(x, y), v(x, y) khi (x, y) → (0, 0) không tồn tại. Thật vậy, xét các dãy 1 1 1 1 (xn, yn) = 0, , (x , y ) = , 0 và (x , ). n n n n n”, yn”) = ( n n Ta có:
lim u(xn, yn) = 0 = 1 = lim u(x , y ). n n n→ ∞ n→ ∞ 1
lim v(xn, yn) = 0 = − = lim v(xn”, yn”). n→ ∞ 2 n→ ∞
Do đó, giới hạn không tồn tại nên không có số A ∈ C để f(z) liên tục tại z = 0. z , khi z = 0 (b) f(x) = |z| A , khi z = 0 Đặt z = x + yi. Với mọi x + yi x y z = 0, ta có f (z) = = + i = u(x, y) + v(x, y). x2 + y2 x2 + y2 x2 + y2
Nhận thấy giới hạn của u(x, y), v(x, y) khi (x, y) → (0, 0) không tồn tại. Thật vậy, xét các dãy 1 1 (xn, yn) = 0, , (x , y ) = , 0 . n n n n
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Ta có:
lim u(xn, yn) = 0 = 1 = lim u(x , y ). n n n→ ∞ n→ ∞
lim v(xn, yn) = 1 = 0 = lim v(x , y ). n n n→ ∞ n→ ∞
Do đó, giới hạn không tồn tại nên không có số A ∈ C để f(z) liên tục tại z = 0. Re (z)2 , khi z = 0 (c) f(x) = |z|2 Đặt z = x + yi. A , khi z = 0 Với mọi z = 0, ta có Re[(x + yi)2] Re(x2 − y2 + 2xyi) f (z) = = x2 + y2 x2 + y2 x2 − y2 x2 y2 = = − i x2 + y2 x2 + y2 x2 + y2 = u(x, y) + v(x, y).
Theo chứng minh câu a) thì giới hạn của u(x, y), v(x, y) khi (x, y) → (0, 0) không tồn tại nên
không có số A ∈ C để f(z) liên tục tại z = 0. z Imz , khi z = 0 (d) f(x) = |z| A , khi z = 0 Với mọi zImz z = 0, ta có 0 ≤ |f(z)| =
≤ Imz. Mặt khác, lim 0 = lim Imz = 0, nên theo hệ quả |z| z→0 z→0
nguyên lý kẹp, lim f(z) = 0. z→0
Do đó, f(z) liên tục tại z = 0 khi và chỉ khi A = 0.
Bài toán 10: Cho f(z) = u(x, y) + iv(x, y). Giả sử rằng tồn tại f (z). Chứng minh rằng
f (z) = uxx + ivxx = −uyy − ivyy Bài làm Do tồn tại f (z + h) − f(z)
f (z) nên hàm f khả vi phức tại z = x + iy. Ta có f (z) = lim . Giới hạn h→0 h
này tồn tại không phụ thuộc vào cách tiến đến 0 của h = h . Chọn 1 + ih2 h = h1(h2 = 0), ta có u(x + h u(x, y) + iv(x, y) f (z) = lim 1, y) + iv(x + h1, y) − h1→0 h h u(x + h v(x + h = lim 1, y) − u(x, y) + i lim 1, y) − v(x, y) h1→0 h h1→0 h
Khi đó f (z) = ux(x, y) + ivx(x, y).
Tượng tự, chọn h = ih2(h1 = 0), ta có
f (z) = −iuy(x, y) + vy(x, y). Ta cũng có f (z + h) − f (z)
f cũng khả vi phức tại z = x + iy. Ta có f (z) = lim . Bằng cách chứng h→0 h
minh tương tự như trên, ta có
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
• Với f (z) = ux(x, y) + ivx(x, y) thì f (z) = uxx(x, y) + ivxx(x, y).
• Với f (z) = −iuy(x, y) + vy(x, y. thì f (z) = −uyy(x, y) − ivyy(x, y).
Vậy f (z) = uxx(x, y) + ivxx(x, y) = −uyy(x, y) − ivyy(x,y).
Bài toán 11: Chứng minh rằng
a) Nếu f (z) chỉnh hình trong miền D và hoặc Ref (z) hoặc Imf (z) là hàm hằng trên D thì f (z) là hàm hằng trên D;
b) Nếu f (z) và f (z) là hàm chỉnh hình trong một miền D thì f là hàm hằng trên D;
c) Nếu f (z) chỉnh hình trong D và |f(z)| là hàm hằng trong D thì f là hàm hằng trên D;
d) Nếu f (z) và |f(z)| là hàm chỉnh hình trong một miền D thì f là hàm hằng trên D. Bài làm
a) Nếu f(z) chỉnh hình trong miền D và hoặc Ref(z) hoặc Imf(z) là hàm hằng trên D thì f(z) là hàm hằng trên D ∂u ∂v =
Do f(z) chỉnh hình trong miền D nên ∂x ∂y ∂u ∂v = − ∂y ∂x ∂u ∂v
• Giả sử Ref = const, khi đó ∂u = = 0. Suy ra ∂v = = 0 ∂x ∂y ∂y ∂x Khi đó ∂u ∂v f (z) = + i
= 0. Dẫn đến f (z) là hàm hằng trên D. ∂x ∂x ∂v ∂u
• Giả sử Imf = const, khi đó ∂v = = 0. Suy ra ∂u = = 0 ∂x ∂y ∂y ∂x Khi đó ∂u ∂v f (z) = + i
= 0. Dẫn đến f (z) là hàm hằng trên D. ∂x ∂x
b) Nếu f(z) và f(z) là hàm chỉnh hình trong một miền D thì f là hàm hằng trên D
Gọi f(z) = u(x, y) + iv(x, y), f(z) = u(x, y) − iv(x, y) u .v .u = |f (z)|2 Ta có: x y − vx y 2 u ( ) )u = .v .u ) = x −vy − (−vx y −(ux y − vx y −|f (z)|2 = |f(z) | 2
⇒ |f (z)|2 + |f(z) | = 0 ⇒ f (z) = f(z) = 0. Suy ra: f là hàm hằng.
c) Nếu f(z) chỉnh hình trong D và |f(z)| là hàm hằng trong D thì f là hàm hằng trên D;
• Nếu f(z) = 0 thì |f(z)| = 0 và đương nhiên f là hàm hằng trên D.
• Nếu f(z) = 0 với mọi z ∈ D
Ta có f(z)f(z) = |f(z)|2 = c2 > 0 Suy ra c2 f (z) = f(z)
Do f(z) chỉnh hình trong D và f(z) = 0 với mọi z ∈ D nên f(z) chỉnh hình trên D.
Theo câu b) suy ra f(z) là hàm hằng trên D.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
d) Nếu f(z) và |f(z)| là hàm chỉnh hình trong một miền D thì f là hàm hằng trên D.
Giả sử f(x, y) = u(x, y) + iv(x, y), khi đó ta có |f(x, y)| = u2(x, y) + v2(x, y). √ Do u2 + v2 ∂(0)
|f(z)| là hàm chỉnh hình trong D nên ∂ = = 0. x y √ Suy ra ∂ u2 + v2 ∂(0) |f(z)| = + i
= 0 nên |f(z)| là hàm hằng trong D. x y
Do f(z) chỉnh hình trong D mà |f(z)| là hàm hằng trong D nên theo câu c), f là hàm hằng trên D.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 4
Bài toán 1: Chứng minh rằng hàm zn F (z) =
hội tụ về 0 khi |z| < 3 và hội tụ về 1 khi zn − 3n |z| > 3. Bài làm
Lấy |z| < 3 tùy ý. Ta có: z n zn F (z) = = 3 zn − 3n z n 1 − 3 n Vì z |z| < 3 nên khi n → ∞,
→ 0. Mặc khác z = 1 nên suy ra, F (z) → 0 khi n → ∞. 3 3
Lấy |z| > 3 tùy ý. Ta có: z n zn 1 F (z) = = 3 = zn − 3n z 1 − ( )n 1 3 z n − 1 3 n Vì z |z| > 3 nên khi n → ∞, → ∞. 3
Suy ra, F (z) → 1 khi n → ∞. Bài toán 2: Cho nz 3 Fn(z) = + , n = 1, 2, .... n + 1 n
Chứng minh Fn(z) hội tụ đều về F (z) = z trên mọi đĩa đóng |z| ≤ R. Bài làm
Định nghĩa: Xét dãy hàm fn : X → C. Dãy {fn} được gọi là hội tụ đều trên A ⊂ X đến hàm f : A → n
C, ký hiệu fn −→ f, nếu
∀ε > 0.∃N ∈ N: ∀z ∈ A ⇒ |fn(z) − f(z)| < ε . Có nz 3 3 z |Fn(z) − F (z)| = + − z = − , n = 1, 2, .... n + 1 n n n + 1 Mà z z z R R − = ≤ ≤ = . n + 1 n + 1 n n n Vậy 3 z 3 R 3 + R |Fn(z) − F (z)| ≤ + − ≤ + =
, n = 1, 2, ... với mọi z ∈ C, |z| ≤ R. n n + 1 n n n
Khi n −→ +∞ thì 3 + R −→ 0 nên theo định nghĩa về sự hội tụ đều thì F n
n(z) sẽ hội tụ đều về F (z) = z
trên mọi đĩa đóng |z| ≤ R. ∞ Bài toán 3: Cho chuỗi hàm
(zn − zn+1). Tìm tập hợp T các điểm mà chuỗi hội tụ và tính n=0
tổng của chuỗi. Chứng minh rằng trên T chuỗi không hội tụ đều.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Bài làm n−1 Xét Sn(x) = zk − zk+1 = 1 − zn. k=0 1 khi Kiểm tra |z| < 1 lim S và n(z) =
lim Sn(z) không tồn tại trong các trường hợp còn lại. n→∞ 0 khi z = 1 n→∞
Do đó T = {z ∈ C : |z| < 1 và z = 1}. 1 khi Tổng chuỗi bằng |z| < 1 S(z) = lim S . n(z) = n→∞ 0 khi z = 1
Vì S(z) không liên tục trên đoạn [0, 1] nên chuỗi không hội tụ đều trên T . ∞
Bài toán 4: Giả sử chuỗi
fk (∗) hội tụ đều trên A, z0 ∈ ∂A và có các giới hạn hữu hạn k=1 ∞ lim f hội tụ và nếu
k(z) = Ck, z ∈ A, k = 1, 2, .... Chứng minh chuỗi Ck
f là tổng của chuỗi (∗) z→z0 k=1 ∞ thì lim f(z) = Cn z→z0 n=1 Bài làm ∞ Do
f nên theo tiêu chuẩn Cauchy ta có: n n=1
∀ > 0, ∃N( ), |fn+1(z) + ... + fn+p(z)| < với ∀n > N( ), ∀p ≥ 1
Cho z → z ,0 z ∈ A ta có |Cn+1 + ... + Cn+p| < ε với ∀n > N(ε), ∀p ≥ 1 ∞
Do đó theo tiêu chuẩn Cauchy ta suy ra C hội tụ. n n=1 ∞ Đặt C = C , khi đó với mọi n z ∈ A ta có: n=1 ∞ ∞
|f(z) − C| ≤ |f(z) − Sn(z)| + Sn(z) − Ck + Ck − C k=1 k=1 ∞ ∞ Vì chuỗi
f hội tụ đều và chuỗi hội tụ nên với k Ck
ε > 0 ta tìm được N (ε) sao cho: k=1 k=1 ε n ε |f(z) − S và với mọi n(z)| < C n > N (ε), ∀z ∈ A 3 k − C < 3 k=1 n
Cố định n > N (ε). Theo giả thiết ta có lim Sn(z) = Ck z→z0 k=1 Do đó ta tìm được ε δ = δ(ε) > 0 sao cho |S với n(z) − n C ∀z ∈ A, |z − z k=1 k| < 3 0| < δ ∞ ∞
Vậy với |z − z0| < δ ta có |f(z) − C| ≤ |f(z) − Sn(z)| + Sn(z) − Ck + Ck − C < ε. k=1 k=1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 5: Tìm bán kính hội tụ của các chuỗi sau: ∞ ∞ ∞ ∞ a) zn ; b) zn ; c) n nnzn; d) zn; n=1 n + 1 n=1 (n + 1)! n=1 n=1 3n ∞ ∞ ∞ e) n! 1 − i zn; f) (−i)nzn; g) zn. n=1 nn n=1 n=1 2n Bài làm ∞ a) zn . n=1 n + 1 Vì zn |z| n = √ và |z| √
→ |z| khi n → +∞ nên theo dấu hiệu hội tụ Cauchy thì chuỗi hội n + 1 n n + 1 n n + 1
tụ tuyệt đối tại mọi z thỏa |z| < 1. ∞ b) zn . n=1 (n + 1)! Vì zn |z| n = và |z|
→ |z| khi n → +∞ nên theo dấu hiệu hội tụ Cauchy thì (n + 1)! n (n + 1)! n (n + 1)!
chuỗi hội tụ tuyệt đối tại mọi z thỏa |z| < 1. ∞ c) nnzn. n=1
Vì n |nnzn| = |n||z| và |n||z| → +∞ khi n → +∞ nên chuỗi trên phân kỳ với mọi z khác 0.
Nếu z = 0 thì |n||z| → 0 nên theo dấu hiệu Cauchy thì chuỗi hội tụ tuyệt đối tại z = 0 ∞ d) n zn. n=1 3n √ √ Vì n |z|. n n n |z| n zn = và |z|. n →
khi n → +∞ nên theo dấu hiệu hội tụ Cauchy thì chuỗi hội tụ 3n 3 3 3
tuyệt đối tại mọi z thỏa |z| < 3. ∞ e) n! zn. n=1 nn Vì (n + 1)!zn+1 nn z.nn 1 1 |z| . = = z. và z. → khi n → +∞.Do đó theo (n + 1)n+1 n!zn (n + 1)n 1 1 e (1 + )n (1 + )n n n
dấu hiệu D’Alambert thì chuỗi hội tụ tuyệt đối với mọi |z| < e. ∞ f) (−i)nzn. n=1
Vì n |(−i)nzn| = |z| và |z| → |z| khi n → +∞ nên theo dấu hiệu hội tụ Cauchy thì chuỗi hội tụ tuyệt
đối tại mọi z thỏa |z| < 1. ∞ g) 1 − izn. n=1 2n √ √ n n Vì 1 − i 2.|z| 2.|z| |z| n zn = và →
khi n → +∞ nên theo dấu hiệu hội tụ Cauchy thì chuỗi hội 2n 2 2 2
tụ tuyệt đối tại mọi z thỏa |z| < 2.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) ∞
Bài toán 6: Bán kính hội tụ của chuỗi
cnzn bằng R (0 < R < ∞). Xác định bán kính hội tụ n=1 của chuỗi: ∞ ∞ ∞ (a) c nkc nzn . (c) nzn. (b) (2n − 1)cnzn. n=1 n=1 n! n=1 ∞ ∞ ∞ (d) c c4 zn. (e) nk+1c nzn . n nz2n. (f) n=1 n=1 n=1 nn Bài làm ∞ (a)
nk+1cnzn có bán kính hội tụ là n=1 b nkc n k c R n n n 1 = lim = lim = lim · lim = R. n→∞ bn+1 n→∞ (n + 1)kcn+1 n→∞ n + 1 n→∞ cn+1 ∞ (b)
cnzn có bán kính hội tụ là n=1 n! b (n + 1)!c c R n n n 2 = lim = lim = lim (n + 1) = +∞. n→∞ bn+1 n→∞ n!cn+1 n→∞ cn+1 ∞ (c)
(2n − 1)cnzn có bán kính hội tụ là n=1 1 n 1 − b (2n − 1)c 2 c R R n n n 3 = lim = lim = lim n · lim = n→∞ bn+1 n→∞ (2n+1 − 1)cn+1 n→∞ 1 n→∞ c 2 2 − n+1 2 ∞ (d)
c4 zn có bán kính hội tụ là n n=1 b c4 c 4 R n n n 4 = lim = lim = lim = R4. n→∞ bn+1 n→∞ c4 n→∞ c n+1 n+1 ∞ ∞ ∞ (e) cnz2n(1). Đặt ω = z2 ⇒ cnz2n = cnωn(2). n=1 n=1 n=1
Giả sử chuỗi (2) có bán kính hội tụ là R ⇒ chuỗi (2) hội tụ trên {ω : |ω| < R} ⇒ chuỗi (1) hội tụ trên √
{z : |z|2 < R} ⇒ chuỗi (1) hội tụ trên {z : |z| < R}. ∞ √ Vậy, chuỗi
cnz2n có bán kính hội tụ R. n=1 ∞ (f)
cnzn có bán kính hội tụ là n=1 nn lim sup n 1 1 R n→∞ 5 = = = = +∞. lim sup n |b c n n| lim sup |c n n n| n→∞ lim sup n→∞ n→∞ nn
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 7: Tìm tập hợp các điểm mà các chuỗi sau hội tụ chuẩn tắc. ∞ ∞ a) (z − 1)n b) (z + 2)2n (−1)n · n=1 n22n n=1 n Bài làm ∞ ∞ a) (z − 1)n 1 = · (z − 1)n n=1 n22n n=1 n22n Ta có: cn = 0, ∀n Mặt khác: |c (n + 1)2 · 2n+1 2(n + 1)α R = lim n| = lim = lim = 2 n→∞ |cn+1| n→∞ n2.2n n→∞ n2 ∞ Suy ra chuỗi
(z − 1)n hội tụ chuẩn tắc trên {z ∈ C : |z − 1| < 2}. n=1 n22n ∞ b) (z + 2)2n (−1)n · (1) n=1 n ∞ Đặt Zn
Z = (z + 2)2, suy ra chuỗi (1) viết lại được như sau: (−1)n · n=1 n Ta có: cn = 0, ∀n Mặt khác: |c n + 1 1 lim n| = lim = lim 1 + = 1. n→ ∞|cn+1| n→ ∞ n n→ ∞ n ∞ Do đó chuỗi Zn (−1)n ·
hội tụ chuẩn tắc trên {Z ∈ C : |Z| < 1}. n=1 n ∞ Suy ra chuỗi zn (−1)n ·
hội tụ chuẩn tắc trên {z ∈ C : |(z + 2)2| < 1} hay {z ∈ C : |z + 2| < 1}. n=1 n
Bài toán 8: Tính tổng các chuỗi sau trong miền: {z ∈ C : |z| < 1} ∞ a) nzn n=1 ∞ b) n2zn n=1 Bài làm a. Ta có |c n R = n| = = 1. |cn+1| n + 1
Do đó chuỗi hội tụ chuẩn tắc trên {z ∈ C : |z| < 1} và theo định lý 4.2.8 ta có: ∞ ∞ ∞ 1 z nzn = z nzn−1 = z zn = z = 1 − z 1 − z2 n=1 n=1 n=1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
b. Ta có n2 = (n + 1)(n + 2) − 3(n + 1) + 1 Khi đó ∞ ∞ ∞ ∞ n2zn = (n + 1)(n + 2)zn − 3 (n + 1)zn + zn n=1 n=1 n=1 n=1 ∞ ∞ ∞ = (n + 2)zn+1 − 3 zn+1 + zn n=1 n=1 n=1 ∞ ∞ ∞ = zn+2 − 3 zn+1 + zn n=1 n=1 n=1 Ta có ∞ 1 zn = −1 + = A 1 − z n=1 ∞ 1 C =
zn+2 = −(1 + z + z2) + 1 − z n=1 2 → C = −2 + (1 − z)3 ∞ 1 B = zn+1 = −1 − z + 1 − z n=1 1 → B = −1 + (1 − z)2 ∞ vậy 1 2 3 1 2 3 n2zn = A + C − 3B = −1 + − 2 + + 3 − = + − 1 − z (1 − z)3 (1 − z)2 1 − z (1 − z)3 (1 − z)2 n=1 ∞
Bài toán 9: Giả sử chuỗi
fk (∗) hội tụ đều trên A, z0 ∈ ∂A và có các giới hạn hữu hạn k=1 ∞ lim f , hội tụ và nếu k(z) = Ck
k = 1, 2, . . . chứng minh chuỗi Ck
f là tổng của chuỗi (∗) z→z0,z∈A k=1 ∞ thì lim f (z) = C . k z→z0,z∈A k=1 Bài làm ∞ Chuỗi f hội tụ đều về k f (z) trên A, tức k=1
∀ε > 0, ∃N > 0 : ∀m > n > N suy ra |fn+1(z) + . . . + fm(z)| < ε, ∀z ∈ A. Ta có z , 0 ∈ ∂A và lim fk(z) = Ck k = 1, 2, . . . z→z0,z∈A Suy ra lim (f .
n+1(z) + fn+2(z) + . . . + fm(z)) = Cn+1 + . . . + Cm z→z0,z∈A
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Suy ra với z đủ gần với z và 0 z ∈ A ta có
|Cn+1 + . . . + Cm| = |−fn+1(z) − . . . − fm(z) + Cn+1 + . . . + Cm + fn+1(z) + . . . + fm(z)|
≤ |fn+1(z) + . . . + fm(z) − Cn+1 − . . . − Cm| + |fn+1(z) + . . . + fm(z)| ≤ ε + ε = 2ε. ∞ Vậy chuỗi C hội tụ. k k=1 ∀ε > 0, ∃N Với
1 > 0 : ∀n > N1 ⇒ |Sn(z) − f (z)| < ε. S là tổng riêng thứ n n của Q, ta có
∀ε > 0, ∃N2 > 0 : ∀n > N2 ⇒ |Sn(z) − f (z)| < ε. Đặt N = max {N ,
1, N2} và với z đủ gần zo z ∈ A thì
∀ε > 0, no > N : |f(z) − Q| = |f(z) − Sn (z) + S (z) − S o no n + Sn − Q|
≤ |f(z) − Sn (z)| + |S (z) − S o no n| + |Sn − Q| ≤ ε + ε + ε = 3ε. ⇒ lim f(z) = Q . z→zo,z∈A ∞ Kết luận ⇒ lim f(z) = C . k z→zo,z∈A n=1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 5
Bài toán 1: Chứng minh rằng các đa thức p(z) = anzn + an−1zn−1 + ... + a0, an = 0 (1) được viết
dưới dạng p(z) = a (z − z0)d1 (z − z2)d2 ... (z − z0)dr thì: a. n = d ; 1 + d2 + ... + dr
b. an−1 = −an (d1z1 + d2z2 + ... + drzr) c. a0 = an (−1)n zd1 1 zd2 2 ...zdr r Bài làm a. Ta có:
p(z) = an(z − z1)d1(z − z2)d2...(z − zr)dr = an.A.B.C
= anzd1+d2+...+dr − an(d1z1zd1+d2+...+dr−1 + d2z2zd1+d2+...+dr−1 + ... + drzrzd1+d2+...+dr−1) + ... + an(−1)d1+d2+...+drzd1 1 zd2 2 ...zdr (2) r A = zd1 zd1−1z z( ( − C1 1 + ... + C d1−1 −z1)d1−1 + Cd1 −z1)d1 d1 d1 d1 Trong đó B = zd2 − C1 zd2−1z z( ( d 2 + ... + C d2−1 d −z2)d2−1 + Cd2 d −z2)d2 2 2 2 C = zdr − C1 zdr−1z z( ( d r + ... + C dr−1 −zr)dr−1 + Cdr −zr)dr r dr dr
So sánh (1) và (2) ta suy ra: n = d1 + d2 + ... + dr
an−1 = −an(d1z1 + d2z2 + ... + drzr) a0 = an(−1)n(zd1 1 zd2 2 ...zdr ) r b, c
Nếu p(z) = anzn+an−1zn−1+...+a0, an = 0 được viết dưới dạng: p(z) = a (z − z0)d1 (z − z2)d2 ... (z − z0)dr
thì ta cần phải chứng minh
an−1 = −an (d1z1 + d2z2 + ... + drzr) và a0 = an (−1)n zd1 1 zd2 2 ...zdr r Ta có n = d
(chứng minh trên) và áp dụng cách khai triển của công thức Pascal: 1 + d2 + ... + dr
(a − b)n = an − n.(an−1.b) + ... + (−1)nbn, ta có: p(z) = ad zd1zd2...zdr − (d 1 +d2 +...+dr
1z1 + d2z2 + ... + drzr) zd1+d2+...+dr−1 + ... + (−1)d1+d2+...+dr .zd1 1 zd2 2 ...zdr r = ad zd1+d2+...+dr − (d 1 +d2+...+dr
1z1 + d2z2 + ... + drzr) zd1+d2+...+dr−1 + ... + (−1)d1+d2+...+dr .zd1 1 zd2 2 ...zdr r Hay an−1 = −ad (d 1 +d2+...+dr
1z1 + d2z2 + ... + drzr) = −an (d1z1 + d2z2 + ... + drzr) và a0 = ad (−1)d1+d2+...+drzd1 = a 1 +d2+...+dr 1 zd2 2 ...zdr r n(−1)nzd1 1 zd2 2 ...zdr r
Bài toán 2: Nếu p(z) = anzn + an−1zn−1 + ... + a0, an = 0 thì ta gọi đa thức ngược của nó là:
p∗(z) = an + an−1z + ... + a0zn. Chứng minh rằng a) 1 p∗(z) = znp z
b) Nếu p(z) có không điểm tại z ( 0
= 0) thì p*(z) có không điểm tại 1 z0
c) Với |z| = 1 ta có |p(z)| = |p∗(z)|
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Bài làm n n−1 a) Ta có 1 1
p∗(z) = an + an−1z + ... + a0zn = zn an + a + ... + a z n−1 z 0 1 n 1 n−1 1 = zn an + a + ... + a , ∀z = 0 z n−1 z 0 = znp z b) Từ câu a ta có: p*(z) = 1 zn . p( ) z Suy ra: p*( 1 ) = ( 1 )n . p(z )n . p(z
là không điểm của p(z), z z 0) = ( 1 0) (với z0 0 = 0) 0 z0 z0
Do z là không điểm của p(z) nên p( ) = 0 hay 0 z0 p(z0) = 0
Vì thế p*( 1 )= ( 1 )n . p(z z 0) = 0 (đpcm) 0 z0
Vậy nếu p(z) có không điểm tại z ( 0
= 0) thì p*(z) có không điểm tại 1 z0 c) Ta có: 1 zz = |z|2 = 1 ⇒ z = z Lại có: 1 p∗(z) = zn.p z Suy ra 1 1 |p∗(z)| = |zn| . p = p = |p (z)| (dpcm) z z
Bài toán 3: Chứng minh rắng nếu đa thức p(z) có một không điểm cấp d tại z thì với mọi 0 z đủ
gần với z , tồn tại các hằng số dương sao cho 0 c1, c2
c1|z − z0|d ≤ |p(z)| ≤ c2|z − z0|d Bài làm
Vì p(z) có một không điểm cấp d tại z nên o
p(z) = (z − z0)dg(z) với g(z) là một đa thức, g(zo) = 0. Khi
đó |p(z)| = |(z − z0)|d|g(z)|, g(z0) = 0 với z ∈ B(z0, r) với r đủ nhỏ sao cho B(z0, r) không chứa điểm nào khác z của 0
g(z) (do g liên tục, g(z0) = 0)), g liên tục trên B(z0, r) nên tồn tại các hằng số dương c thỏa mãn: 1, c2 c với 1 ≤ |g(z)| ≤ c2 z ∈ B(z0, r)
c1|z − z0|d ≤ |p(z)| ≤ c2|z − z0|d với z ∈ B(z0, r)
Vậy ta có điều phải chứng minh.
Bài toán 4: Chứng minh rằng nếu hàm hữu tỷ Rm,n(z) có bậc của tử là m và bậc của mẩu là n
thì với mọi z với |z| đủ lớn tồn tại các hằng số dương c sao cho 1, c2
c1|z|m−n ≤ |Rm,n(z)| ≤ c2|z|m−n Bài làm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Viết Rm,n(z) = zm−ng(z). Chọn M đủ lớn để g không có không điểm và cực điểm trên
A = {z ∈ C : |z| ≥ M}. Lây M đủ lớn cho |z| ≥ M, thì trên tập đó không chứa những không điểm và
cực điểm tại modul của những không điểm và cực điểm hữu hạn.
Khi đó tồn tại các hằng số dương c sao cho 1, c2 c với 1 ≤ |g(z)| ≤ c2 z ∈ A
Suy ra c1|z|m−n ≤ |Rm,n(z)| ≤ c2|z|m−n với z ∈ A
Bài toán 5: Tìm ánh xạ phân tuyến tính biến 0, 1, ∞ lần lượt thành: a) 0, i, ∞ b) 0, 1, 2 c) −i, ∞, 1 d) -1, ∞, 1 Bài làm Ta có: z1 − z3 z 0 − ω 0 − z z − 1 : 1 − z = : = z2 − z3 z2 − z 1 − ω 1 − z z a) 0, i, ∞ Ta có: z z ω ω
000 1 − z3 : 1 − z = 1 − ω3 : 1 − ω z2 − z3 z2 − z ω2 − ω3 ω2 − ω z − 1 1 ω − i ⇔ = . z 1 − i ω ω − i z − 1 ⇔ = .(1 − i) ω z i (z − 1)(1 − i) ⇔ 1 − = ω z i z − (z − 1)(1 − i) ⇔ = ω z iz iz ⇔ ω = = z − (z − 1)(1 − i) i(z + 1) + 1 Vậy iz ω = 1 + i(z + 1) b) 0, 1, 2 Ta có: z z ω ω
000 1 − z3 : 1 − z = 1 − ω3 : 1 − ω z2 − z3 z2 − z ω2 − ω3 ω2 − ω 1 − z 0 − 2 0 − ω ⇔ = : −z 1 − 2 1 − ω z − 1 1 − ω ω − 1 ⇔ = 2. = 2. z −ω ω 1 z − 1 ⇔ 1 − = ω 2z 1 2z − z − 1 z − 1 ⇔ = = ω 2z 2z 2z ⇔ ω = z − 1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Vậy 2z ω = z − 1 c) −i, ∞, 1 Ta có: z z ω ω
000 1 − z3 : 1 − z = 1 − ω3 : 1 − ω z2 − z3 z2 − z ω2 − ω3 ω2 − ω z − 1 −i − 1 −i − ω 1 − ω ω − 1 ⇔ = : = = z ∞ − 1 ∞ − ω −i − ω ω + i
⇔ (z − 1)(ω + i) = z(ω − 1)
⇔ zω + zi − ω − i = zω − z ⇔ i(z − 1) − ω = −z ⇔ ω = z + i(z − 1) Vậy ω = z + i(z − 1) d) −1, ∞, 1. Ta có: z z ω ω
000 1 − z3 : 1 − z = 1 − ω3 : 1 − ω z2 − z3 z2 − z ω2 − ω3 ω2 − ω z − 1 −1− −1 − ω −ω ω ⇔ = : = = z ∞ − 1 ∞ − ω −1 − ω ω + 1 ⇔ (z − 1)(ω + 1) = zω ⇔ zω + z − ω − 1 = zω ⇔ ω = z − 1 Vậy ω = z − 1
Bài toán 6: Tìm ảnh qua phép đối xứng qua đường tròn |z| = 1 của các đường sau: a) 1 |z| = ; b) |z − 2| = 2; c) Imz = 1; d) x2 − y2 = 1. 4 Bài làm a) (C): 1 |z| = 4
Gọi z∗ = (x∗, y∗) là ảnh của z = (x, y) ∈ C qua phép đối xứng đường tròn (C1) : |z| = 1 là đường tròn
tâm z bán kính R. Tương đương 0
|z − z0|.|z∗ − z0| = R2 và z = k.z∗, k ∈ Z, k = 0 Tương đương, 1
x = k.x∗, y = k.y∗, (x∗)2 + (y∗)2 = k Mà 1 1 z = (x, y) ∈ (C) nên x2 + y2 = suy ra (x∗)2 + (y∗)2 = 4 16k2 Vậy 1 16k2 = k suy ra k =
Do đó (x∗)2 + (y∗)2 = 16 hay ảnh của (C) qua phép đối xứng đường tròn 16
(C1) là đường tròn (C2) : |z| = 4 b) (C):|z − 2| = 2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Gọi z∗ = (x∗, y∗) là ảnh của z = (x, y) ∈ (C) qua phép đối xứng đường tròn (C1) : |z| = 1 là đường tròn
tâm z bán kính R. Tương đương 0
|z − z0|.|z∗ − z0| = R2 và z = k.z∗, k ∈ Z, k = 0. Tương đương, 1
x = k.x∗, y = k.y∗, (x∗)2 + (y∗)2 = k Mà 4x z = (x, y) ∈ (C) nên
x2 + y2 = 4x suy ra (x∗)2 + (y∗)2 = k2 Vậy 4x 1 1 = suy ra x∗ =
Do đó ảnh của (C) qua phép đối xứng đường tròn (C k2 k 4 1) đường thẳng 1 (d) : Rez = 4 c) (C): Imz = 1
Gọi z∗ = (x∗, y∗) là ảnh của z = (x, y) ∈ (d) qua phép đối xứng đường tròn (C1) : |z| = 1 là đường tròn
tâm z bán kính R. Tương đương 0
|z − z0|.|z∗ − z0| = R2 và z = k.z∗, k ∈ Z, k = 0 Tương đương, 1
x = k.x∗, y = k.y∗, (x∗)2 + (y∗)2 = k Mà 1
z = (x, y) ∈ (d) nên y = 1 suy ra y∗ = k Vậy 1 1
(x∗)2 + (y∗)2 = y∗ Do đó (x∗)2 + (y∗ − )2 =
hay ảnh của (d) qua phép đối xứng đường tròn (C 2 4 1) là đường tròn 1 1 (C) : |z − .i| = 2 4 d) (C): x2 − y2 = 1
Gọi z∗ = (x∗, y∗) là ảnh của z = (x, y) ∈ (H) qua phép đối xứng đường tròn (C1) : |z| = 1 là đường tròn
tâm z bán kính R. Tương đương 0
|z − z0|.|z∗ − z0| = R2 và z = k.z∗, k ∈ Z, k = 0 Tương đương, 1
x = k.x∗, y = k.y∗, (x∗)2 + (y∗)2 = k Mà 1
z = (x, y) ∈ (H) nên x2 − y2 = 1 suy ra (x∗)2 − (y∗)2 = k2
Vậy ((x∗)2 + (y∗)2)2 − ((x∗)2 − (y∗)2) = 0.
Do đó ảnh của (H) qua phép đối xứng đường tròn (C1) là đường Lemniscat Bài toán 7: Cho z là . Chứng 1, z2, z3
3 điểm phân biệt cùng nằm trên đường tròn C trong C∞
minh rằng z và z∗ đối xứng qua C nếu và chỉ nếu (z∗, z1, z2, z3) = (z, z1, z2, z3). Bài làm
Trước hết ta giả sử C là đường tròn {z ∈ C : |z| = R}. Ta có
(z∗, z1, z2, z3) = (z, z1, z2, z3)
⇔ (z∗, z1, z2, z3) = (z, z1, z2, z3) R2 R2 R2 R2 ⇔ (z∗, z
(hàm phân tuyến tính bảo toàn tỉ số kép) 1, z2, z3) = , , , z z1 z2 z3 R2 ⇔ (z∗, z ( do 1, z2, z3) = , z z z 1, z2, z3
1, z2, z3 ∈ {z ∈ C : |z| = R})
⇔ z∗.z = R2 ⇔ z∗, z đối xứng nhau qua C.
Với đường tròn C bất kỳ trong C luôn tồn tại ánh xạ phân tuyến tính ∞
f biến nó thành đường tròn
{z ∈ C : |z| = R}. Gọi w, w∗, w lần lượt là ảnh của qua 1, w2, w3 z, z∗, z1, z2, z3
f . Vì f bảo toàn tỉ số
kép và bảo toàn tính đối xứng nên z∗, z đối xứng nhau qua C ⇔ w∗, w đối xứng nhau qua C .
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
⇔ (w∗, w1, w2, w3) = (w, w1, w2, w3)
⇔ (z∗, z1, z2, z3) = (z, z1, z2, z3).
Vậy ta có điều phải chứng minh.
Bài toán 8: Chứng minh rằng 4 điểm phân biệt ω
cùng nằm trên đường tròn trong 1, ω2, ω3, ω4 C nếu và chỉ nếu ∞
(ω1, ω2, ω3, ω4) là số thực Bài làm
Nhận xét: Với đường tròn C bất kỳ trong C , luôn tồn tại hàm phân tuyến tính ∞ f biến nó thành đường thẳng thực.
Giả sử f(ω1) = z1, f(ω2) = 1, f(ω3) = 0, f(ω4) = ∞. Vì hàm phân tuyến tính bảo toàn tỉ số kép nên ω
nằm trên cùng đường tròn trong 1, ω2, ω3, ω4
C∞ ⇔ z1, 1, 0, ∞ thẳng hàng. z z ⇔ (ω 1 − 0 1 − ∞
1, ω2, ω3, ω4) = (z1, 1, 0, ∞) = : = z 1 − 0 1 − ∞ 1 ∈ R.
Bài toán 9: Tìm đạo hàm của nhánh chính của z1+i tại z = i Bài làm
Ta có nhánh chính của z1+i là e(1+i)Log(z). Đặt f(z) = e(1+i)Log(z).
Ta tính được đạo hàm của f(z), z ∈ C như sau 1 + i f (z) = .e(1+i)Log(z) z
Vậy, đạo hàm cuả nhánh chính của z1+i tại z = i là 1 + i f (i) =
.e(1+i)Log(z) = (1 − i)e(1+i)Log(z). i
Bài toán 10: Chứng minh rằng 1 1 1 sec−1z = −ilog + 2 . − 1 z z2
Sử dụng các giá trị chính xác định tập giá trị của sec−1x khi x > 1 và khi x < −1 Bài làm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Đặt 1 2
w = sec−1z. w là nghiệm của phương trình z = secw và z > 0. Ta có: z = secw = = cosw eiw + e−iw ⇔ z.e2iw − 2eiw + z = 0.
Xem eiw là biến, z là tham số, ta được √ √ 1 + 1 − z2 1 1 − z2 1 1 eiw = = + = + − 1 z z z z z2 1 1 1 1 1 1 ⇒ 2 2 w = −ilog + hay sec−1z = + . − 1 −ilog − 1 z z2 z z2
Với x ∈ R, x > 1 hoặc x < −1, thì |x| > 1. 1 Ta có: 1 1 |x| > 1 ⇒ − 1 < 0. Suy ra
1 − 1 2 = −i. 1 − là phần nằm bên dưới trục thực. Mặc x2 x2 x21 khác, 1 nằm trong đoạn 1 2
[−1, 1] khi |x| > 1 nên 1 + − 1 nằm ở nửa dải x x x2 −1 ≤ Rez ≤ 1; Imz < 0 2 2
và là một phần của đường tròn đơn vị vì 1 1 1 − + = 1. x2 x 1 Suy ra 1 1 2 log + = i.θ với − 1 −π < θ < 0. x x2 1 Do đó, 1 1 sec−1x = −ilog + 2 = − 1 −θ ∈ (0, π). x x2
Bài toán 11: Xác định hàm ngược của hàm ω = q (z) := 2ez + e2z.
Sử dụng công thức tìm tất cả các giá trị cùa z sao cho q(z) = 3 Bài làm √ √
Ta có e2z + 2ez − ω = 0 ⇔ (ez + 1)2 = ω + 1 ⇔ ez = −1 ± ω + 1 ⇔ z = ln −1 ± ω + 1 . √
Vậy hàm ngược của q (z) là z = ln −1 ± ω + 1 . √ z = 2kπi
Với w = q (z) = 3, ta có z = ln −1 ± 4 ⇔ (k ∈ Z). z = ln 3 + (2k + 1) πi
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 6
Bài toán 1: Chứng minh rằng elip x2 y2 +
= 1 là một đường cong khả vi liên tục và đưa ra một a2 b2 tham số hóa. Bài làm x = a sin t
Phương trình tham số của eclip x2 y2 + = 1 là t ∈ [0, 2π] a2 b2 y = b cos t
Ta có sin t, cos t(t ∈ [o, 2π]) là hàm số sơ cấp
=⇒ sin t, cos t liên tục và khả vi y2
=⇒ f(t) = x(t) + iy(t) (x(t) = a sin t, y(t) = b cos t, t ∈ [0, 2π] khả vi liên tục nên elip x2 + = 1 là a2 b2
một đường cong khả vi liên tục.
Bài toán 2: Tính tích phân 6 2 +
+ 1 − 3 (z − i)2 dz với C là đường tròn |z − i| = (z − i)2 z − i C
4 quay một vòng ngược chiều quay kim đồng hồ. Bài làm y 1 x O
Dễ thấy chiều quay ngược kim đồng hồ là chiều dương. Với z = i + 4eit, t ∈ [0; 2π] ta có z = 4ieit. Ta có 2π 6 2 6 2 I = + + 1 − 3 (z − i)2 dz = + + 1 − 3 4eit 2 .4ieitdt (z − i)2 z − i (4eit)2 4eit C 0 2π 3i 3 2π =
e−it + 2i + 4ieit − 192ie3it dt = − e−it + 2it + 4eit − 64e3it = 4πi 2 2 0 0
Vậy tích phân đã cho bằng 4πi.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Bài toán 3: Tính
z dz trong đó C là biên hình D = {1 ≤| z | 2,Imz ≥ 0}. C | z | Bài làm C 1 = {| z |= 2, I mz > 0}, C Ta có: z z z z z 2 = {= 2 ≤ Rez ≤ −1, z = 0}, dz = dz+ dz+ dz+ dz với C | z | C | z | | z | | z | | z | 1 C2 C3 C4
C3 = {| z |= 1, I mz > 0},
C4 = {1 ≤ Rez ≤ 2, Imz = 0}. Mà ta lại có: z z 1 π 1 dz = dz = [2eit2ieit]dt = 2i (e0 − e2iπ) = 0. C | z | 2 2 2i 1 C1 0 z −1 x dz = dx = −1. C | z | | x | 2 −2 z 1 π 1 dz = −
[eit2ieit]dt = −i (e0 − e2iπ) = 0. C | z | 2 4i 3 0 z 2 x dz = dx = 1. C | z | | x | 4 1 Vậy z dz = 0. C | z | 2−i Bài toán 4: Tính I =
(3xy + iy2)2dz dọc theo đường thẳng nối hai điểm z = i và z = 2 − i i Bài làm
Giả sử z = x + iy ⇒ dz = dx + idy Khi đó: 2−i I = (3xy + iy2)2(dx + idy) i 2−i =
(9x2y2 − y4 + 6ixy3)(dx + idy) i 2−i 2−i =
(9x2y2 − y4)dx − 6xy3dy + i (9x2y2 − y4)dy + 6xy3dx i i I1 I2
Đường thẳng đi từ z = i đến z = 2 −i tương ứng với đường thẳng đi từ điểm A(0, 1) đến điểm B(2, −1).
Khi đó trên đoạn AB, ta có: y = −x + 1, 0 ≤ x ≤ 2. Suy ra dy = −dx
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Từ đó dẫn đến: 2 I1 =
[9x2(−x + 1)2 − (−x + 1)4]dx − 6x(−x + 1)3(−dx) 0 2 =
(8x4 − 14x3 + 3x2 + 4x − 1)dx − (6x4 − 18x3 + 18x2 − 6x)dx 0 2 =
(2x4 + 4x3 − 15x2 + 10x − 1)dx 0 2x5 15x3 2 34 = + x4 − + 5x2 − x = 5 3 5 0 2 I2 =
[9x2(−x + 1)2 − (−x + 1)4](−dx) + 6x(−x + 1)3dx 0 2 =
(−8x4 + 14x3 − 3x2 − 4x + 1)dx + (−6x4 + 18x3 − 18x2 + 6x)dx 0 2 =
(−14x4 + 32x3 − 21x2 + 2x + 1)dx 0 14x5 2 58 = − + 8x4 − 7x3 + x2 + x = − 5 5 0 Suy ra 34 58 I = − i. 5 5 Bài toán 5: Tính π π
log zdz với γ : |z| = 1, − ≤ arg (z) ≤ . γ 2 2 Bài làm
Ta có log z := ln z + iArg(z), −π ≤ Arg(z) ≤ π.
Ta chứng minh hàm log z định nghĩa ở trên Bài làm tích trên miền D = {z = reiϕ, r > 0, −π < ϕ < π}.
Với mọi z = reiϕ ∈ D, ta kiểm tra phương trình Cauchy-Riemann cho tọa độ cực. Ta có log z = ln reiϕ + iArg reiϕ = ln r + iϕ = u (r, ϕ) + iv (r, ϕ) .
Hàm u (r, ϕ) = ln r khả vi trên (0, +∞), hàm v (r, ϕ) = ϕ khả vi trên (−ϕ, ϕ) và ∂u 1 ∂v ∂v ∂v = , = 0, = 0, = 1 ∂r r ∂ϕ ∂r ∂ϕ
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) ∂u 1 ∂v ∂v 1 ∂v ⇒ = , = − . ∂r r ∂ϕ ∂r r ∂ϕ
Điều này dẫn đến hàm log z thỏa điều kiện Cauchy-Riemann cho tọa độ cực với mọi z ∈ D, từ đó khả
vi trên D và Bài làm tích trên D.
Ta thấy γ ⊂ D. Với cách định nghĩa log z, ta có π π
∀z = eiArg(z) ∈ γ ⇒ log z = ln |z| + iArg(z) = iArg(z), − ≤ Arg(z) ≤ . 2 2 Do đó log zdz = iArg(z)d eiArg(z) γ γ π 2 = iArg(z)ieiArg(z)d (Arg(z)) π − 2 π 2 = − Arg(z)eiArg(z)d (iArg(z)) π − 2 π − 2 = teitdt π 2 π π − − 2 2 = t cos tdt + i t sin tdt π π 2 2 = 0 − 2i = −2i. Vậy log zdz = −2i. γ
Bài toán 6: Giả sử (C) là đường cong đóng đơn giới hạn một miền D có diện tích S. Chứng minh rằng: a) xdz = iS b) ydz = −S c) ¯ zdz = 2iS C C C Bài làm a) xdz = iS C Ta có xdz = xd(x + iy) = xdx + i. xdy. C C C C i) Tính xdx: C
Áp dụng công thức Green: P(x, y)=x, Q(x, y)=0, ta có: ∂Q ∂P xdx = P dx + Qdy = − dxdy = 0dxdy = 0. ∂x ∂y C C D D ii) Tính xdy: C
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Áp dụng công thức Green: P(x, y)=0, Q(x, y)=x, ta có: ∂Q ∂P xdy = P dx + Qdy = − dxdy = (1 − 0)dxdy = S. ∂x ∂y C C D D Suy ra xdz = 0 + iS = iS. C b) ydz = −S C Ta có ydz = yd(x + iy) = ydx + i. ydy. C C C C i) Tính ydx: C
Áp dụng công thức Green: P (x, y) = y, Q(x, y) = 0, ta có: ∂Q ∂P ydx = P dx + Qdy = − dxdy = (0 − 1)dxdy = −S. ∂x ∂y C C D D ii) Tính ydy: C
Áp dụng công thức Green: P (x, y) = 0, Q(x, y) = y, ta có: ∂Q ∂P ydy = P dx + Qdy = − dxdy = 0dxdy = 0. ∂x ∂y C C D D Suy ra ydz = −S + i.0 = −S. C c) ¯ zdz = 2iS C Ta có: zdz = (x − iy)dz = xdz − i. ydz = iS − i.(−S) = 2iS. C C C C
Bài toán 7: Trong miền hình sao dς
C− với tâm 1. Chứng minh rằng = log r + iϕ với γ là ς γ
đường cong lấy tích phân từ 1 đến z = reiϕ. Bài làm Đặt z1 = 1, z2 = 2, z3 = 3.
Xét ∂z = [z1, z2] + [z2, z3] + [z3, z1], khi đó tham số hóa của
[z1, z2] : z = t, t ∈ [1, 2].
[z2, z3] : z = t, t ∈ [2, 3].
[z3, z1] : z = 6 − t, t ∈ [3, 5] 2 3 5 3 3 Ta có dς dt dt d(6 − t) dt dt = + − = − = 0. ς t t 6 − t t t ∂z 1 2 3 1 1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Theo định lý 6.3.4 (Tiêu chuẩn khả tích của miền hình sao), 1 khả tích trong C−. Theo định lý 6.3.1, ς
dς = log z − log 1 = log(reiϕ) − log1 = log(reiϕ) = log(r) + iϕ. ς γ
Bài toán 8: Cho 0 < R = a. Chứng minh rằng dz 2πR ≤ . |z|=R z2 − a2 |R2 − |a|2| Bài làm
Mệnh đề đánh giá cơ bản tích phân đường: f (z)dz ≤ l(γ)|f| với γ |f|γ = max f(z). γ z∈γ Với lúc này, hàm 1 f (z) =
và đường cong γ là B(O, R) có l(γ) = 2πR. z2 − a2
Hơn nữa, ta có |z2 − a2| ≥ ||z|2 − |a|2| = |R2 − |a|2|, ∀z ∈ γ. Suy ra, 1 1 1 2πR ≤ , |f| và l(γ)|f| . |z2 − a2| |R2 − |a|2| γ = |R2 − |a|2| γ = |R2 − |a|2|
Áp dụng mệnh đề đánh giá cơ bản tích phân đường, ta có điều phải chứng minh. Bài toán 9: Chứng minh 1 a) eπ π e z dz ≤
với γ : |z| = 1, 0 ≤ Argz ≤ ; γ 2 2 √ b)
ez2dz ≤ 5e3 với γ : Rez = 2Imz, z ∈ [0; 2 + i]; γ √ c)
1 dz ≤ 4 2 với γ : Rez + Imz = 1,z ∈ [1;i]. γ ¯ z4 Bài làm
a) Với z = x + iy (x, y ∈ R), ta có: 1 x − iy 1 1 x Re
e z = e x2 + y2 , e z = e z = e x2 + y2 = ex ≤ e|z| = e(|z| = 1) Hơn nữa đường cong π π
γ được tham số hóa bởi z(t) = cos(t) + i sin(t), t ∈ [0, ] nên l(γ) = . 2 2 1 1 Do đó, eπ e z dz ≤ max z . z∈|γ| e l(γ) = γ 2 x 3 b) Với (x+i )2 x2+ix2
z = x + iy (x, y ∈ R), ta có: x = 2y, x ∈ [0, 2] nên ez2 = e 2 = e4 . 3 Khi đó x2 ez2dz = eRez2 = e4 ≤ e3.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) √ √
Hơn nữa đường được lấy tích phân có độ dài l(γ) = 5, do đó ez2dz ≤ 5e3. γ √
c) Đường được lấy tích phân có độ dài l(γ) = 2.
Với z = x+ iy (x, y ∈ R), trên γ : Rez +Imz = 1, z ∈ [1; i], ta có 1 đạt giá trị lớn nhất với mọi z ∈ |γ| ¯ z4 √ khi 1 1 1 1 1
|¯z| đạt giá trị nhỏ nhất, tức là z = +i . Do đó, dz ≤ max l(γ) = l(γ) = 4 2. 2 2 z∈|γ| 4 γ ¯ z4 ¯ z4 1 + i 2
Bài toán 10: Tính các tích phân sau với đường cong đã chỉ ra: a)
(3z2 − 5z + i)dz dọc theo đoạn thẳng nối từ z = i đến z = 1; Γ b)
ezdz dọc theo nữa đường tròn |z| = 1 từ z = 1 đến z = −1; Γ c)
1 dz với mọi đường cong nằm trong nửa mặt phẳng phải nối từ z = −3i đến z = 3i; Γ z d)
1 dz với mọi đường cong đóng không qua 0, ±π,±2π,...; Γ sin2 z Hình 1 e)
sin2 z cos zdz dọc theo đường cong như trong hình 1. Γ f)
ez cos zdz dọc theo đường cong như trong hình 1. Γ 1 g)
z 2 dz dọc theo đường cong như trong hình 1. Γ h)
(log z)2 dz dọc theo đoạn thẳng nối từ z = 1 đến z = i; Γ i) 1
dz dọc theo đoạn thẳng nối từ z = 1 đến z = 1 + i; Γ 1 + z2 Bài làm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) a) Ta có 5
z3 − z2 + iz là nguyên hàm của 3z2 − 5z + i nên : 2 5 1 5 5
3z2 − 5z + i dz = z3 − z2 + iz
= 13 − · 12 + i − i3 − · i2 + i2 = −3 + 2i. Γ 2 2 2 i −1 b) Ta có 1
ez là nguyên hàm của ez nên: ezdz = ez = − e. Γ e 1
c) Tại mọi điểm của Γ, hàm 1 là đạo hàm của nhánh chính hàm log z. Nên: z dz 3i π π = log(z)
= log(3i) − log(−3i) = ln 3 + i − ln 3 − i = iπ. z 2 2 −3i Γ d)
1 dz với mọi đường cong đóng không qua 0,±π,±2π,.... Γ sin2 z Ta có: 1
liên tục trên C trừ các điểm 0, ±π, ±2π, ... và có nguyên hàm là − cot z. Do đó với sin2 z
mọi đường cong đóng không qua 0, ±π, ±2π, ... ta có: 1 dz = 0 Γ sin2 z . e) Ta có: 1 F (z) =
sin3 z là nguyên hàm của f (z) = sin2 z cos z nên tích phân đã cho không phụ 3
thuộc vào dạng đường đi. Do đó: 1 i 1 i i 3 I = sin2 z cos zdz = sin3 z = sin3 i = − e . Γ 3 3 24 e π u = cos z du = − sin z f) Đặt ⇒ dv = ez v = ez
Sử dụng tích phân từng phần ta được: i I = ez cos z +
ez sin zdz = ei cos i − eπ + I1. π Γ Ta có: I1 = ez sin zdz Γ
Sử dụng tích phân từng phần ta được: i I1 = ez sin z − I. π Thay vào I, ta có: 2I = ei(cos i + sin i) + eπ ei eπ ⇔ I = (cosh 1 + i sinh 1) + 2 2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) 1 3
g) Tại mỗi điểm của hàm log z
Γ hàm z 2 là đạo hàm của nhánh chính của 2 e 2 . Do đó: 3 1 3 3π 3 √ √ 3 2 i log z 2 i ln(π) 2 2 2 I = z 2 dz = e 2 = e 4 − e 2 = − + i − π 2 . Γ 3 3 3 2 2 π
h) Ta có z log2 z − 2z log z + 2zlà nguyên hàm của (log z)2 nên i π2
(log z)2 dz = z log2 z − 2z log z + 2z = π − 2 + i 2 − . Γ 4 1
i) Ta có arctan z là nguyên hàm của 1 nên 1 + z2 1 1+i dz = arctan z = arctan(1 + i) − arctan(i). Γ 1 + z2 1 Ta có i i − (1 + i)2 i i 1 arctan(1 + i) = log = log(−1 − 2i) = ln 5 + i arctan 2 . 2 i − (1 + i) 2 2 2 Do đó 1 i 1 π dz = ln 5 + i arctan 2 − . Γ 1 + z2 2 2 4
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 7
Bài toán 1: Chứng minh nếu f (z) liên tục tại z = 0 thì 2π lim f reiϕ dϕ = 2πf (0) . r→0 0 Bài Làm
Theo giả thiết f (z) liên tục tại z = 0 ta có lim f (z) = f (0) z→0 nên 2π 2π f reiϕ dϕ − 2πf (0) = f reiϕ − f (0) dϕ ≤
sup |f (z) − f (0)| 2π → 0 |z|=r 0 0
khi r → 0. Vậy ta có điều phải chứng minh.
Bài toán 2: Dùng định lí về giá trị trung bình tính 2π 1 e(eit)dt. 2π 0 Bài Làm
Áp dụng công thức giá trị trung bình cho hàm số f(z) = ez, f ∈ O(C) với zo = 0 và r = 1. Khi đó: 2π 1 e(eit)dt = f (0) = e0 = 1 2π 0 Bài toán 3: Tính 3 1 1 I = −
dz, với C : |z| = 5; C : |z − 2i| = . C z + i z − 2i 2 Bài Làm
Với C : |z| = 5. Ký hiệu G là miền bao bởi c C.
• Rõ ràng z = −i và z = 2i đều nẳm trong Gc.
Và bao hai điểm z = −i và z = 2i lần lượt bởi các đường tròn C1 : |z + i| = 1 và C2 : |z − 2i| = 1, khi đó: 3 1 3 1 3 1 I = − dz = − dz + − dz C z + i z − 2i C z + i z − 2i z + i z − 2i 1 C2 dz dz dz dz = 3 − + 3 − C z + i z − 2i z + i z − 2i 1 C1 C2 C2
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) dz dz • z = −i nằm trong C nên theo hệ quả 5 ta có: 1, z = 2i nằm ngoài C1 = 2πi và = C1 z + i C1 z − 2i 0. dz dz • z = 2i nằm trong C nên theo hệ quả 5 ta có: 2, z = −i nằm ngoài C2 = 0 và = C2 z + i C2 z − 2i 2πi.
Vậy I = 3.2πi − 2πi = 4πi. 1
• Với C : |z − 2i| = . Ký hiệu G là miền bao bởi C. 2 c
Rõ ràng z = −i nằm ngoài G . c, z = 2i nằm trong Gc Bao điểm 1 z = 2i bởi đường tròn C , khi đó: 1 : |z − 2i| = 4 3 1 3 1 dz I = − dz = − dz = − = −2π C z + i z − 2i C z + i z − 2i z − 2i 1 C1 2−i Bài toán 4: Tính I =
3xy + iy2 2 dz trong các trường hợp sau: i
a. Dọc theo đường thẳng nối hai điểm z = i và z = 2 − i.
b. Dọc theo đường cong x = 2t − 2 và y = 1 + t − t2. Bài làm
a. Giả sử z = x + iy ⇒ dz = dx + idy, khi đó 2−i 2−i I = 3xy + iy2 2 dz = 3xy + iy2 2 (dx + idy) i i 2−i 2−i = 9x2y2 − y4dx − 6xy3dy + i 6xy3dx + 9x2y2 − y4dy i i
Đường thẳng đi từ z = i và z = 2 − i tương ứng với đường thẳng đi từ điểm A (0, 1) đến điểm
B (2, −1), khi đó trên AB ta có: y = −x + 1 với 0 ≤ x ≤ 2. Suy ra: 2 I =
9x2 (−x + 1)2 − (−x + 1)4 dx − 6x (−x + 1)3 (−dx) 0 2 + i
6x (−x + 1)3 dx + 9x2 (−x + 1)2 − (−x + 1)4 (−dx) 0 2 2 =
2x4 − 4x3 − 15x2 + 10x − 1 dx − i
2x4 − 4x3 − 15x2 + 10x − 1 dx 0 0 2 2 2 2 = x5 − x4 − 5x3 + 5x2 − x − i x5 − x4 − 5x3 + 5x2 − x 5 5 0 0 126 126 = − + i 5 5
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
b. Tại điểm z = i ⇒ t = 1 và z = 2 − i ⇒ t = 2
Ta có z = x + iy = 2t − 2 + i (1 + t − t2) ⇒ dz = [2 + i (1 − 2i)] dt Khi đó: 2 I =
3 (2t − 2) 1 + t − t2 + i 1 + t − t2 2 (2 + i (1 − 2t)) dt 1 2 =
−14t3 + 27t2 + t − 13 + i 12t4 − 30t3 + 10t2 + 14t − 4 dt 1 2 7 1 12 15 10 = − t4 + 9t3 + t2 − 13t + i t5 − t4 + t3 + 7t2 − 4t 2 2 5 2 3 1 52 37 67 = 20 + i − −7 + i = 27 + i 15 30 30
Bài toán 5*: Chứng minh rằng 1
ezt dz = sin t, nếu t > 0;C : |z| = 3. 2πi C z2 + 1 Bài Làm Đặt ezt ezt I = dz = dz. C z2 + 1 C (z − i)(z + i)
Nhận thấy z = i và z = −i đều nằm trong C. Bao hai điểm z = i và z = −i lần lượt bởi các đường tròn 1 1 C và . Khi đó ta có: 1 : |z − i| = C 2 2 : |z + i| = 2 ezt ezt ezt I = dz = dz + dz = I . 1 + I2 C (z − i)(z + i) C (z − i)(z + i) (z − i)(z + i) 1 C2 ezt Tính ezt I z+i 1 = dz = dz. C (z − i)(z + i) z − i 1 C1 Đặt ezt f (z) = , z z + i 0 = i.
Rõ ràng f(z) Bài làm tích trong và trên C nên áp dụng công thức tích phân Cauchy ta có: 1 ezt eit I1 = 2πi.f(i) = 2πi. = 2πi. = πeit. z + i 2i z=i ezt Tính ezt I z−i 2 = dz = I1 + I2 = dz. C (z − i)(z + i) z + i 2 C2 Đặt ezt g(z) = , z z − i 0 = −i.
Rõ ràng g(z) Bài làm tích trong và trên C nên áp dụng công thức tích phân Cauchy ta có: 2 ezt e−it I2 = 2πig(−i) = 2πi = 2πi. = −πe−it. z − i −2i z=−i
Vậy I = πeit − πe−it = π (eit − e−it) = π2i sin t. Suy ra 1 ezt dz = sint. 2πi C z2 + 1
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Bài toán 6 Giả sử α là chu tuyến giới hạn một miền có diện tích bằng S hãy chứng minh rằng: a. xdz = iS, γ b. ydz = −S γ Bài làm
Đặt D là miền mà có chu tuyến là γ, theo định nghĩa tích phân đường loại II thì: 1 S = xdy = − ydx = xdy − ydx = dxdy ( γ là đóng kín). γ γ 2 D a) Ta có xdz = x(dx + idy) γ γ = xdx + i xdy γ γ = xdx + i xdy γ γ = xdx + 0dy + i xdy γ γ Trong (1) ta có : ∂0 ∂x = 0 =
, theo định lý 4 mệnh đề tương đương thì xdx = 0. Suy ra ∂x ∂y α xdz = iS γ b) Tương tự ydz = ydx + i ydy = −S. γ γ γ
Bài toán 7. Chứng minh rằng : 1 2n (2n)! z−1 z + dz = 2πi. . |z|=1 z (n!)2 Bài làm Đặt (z2 + 1)2n (z2 + 1)2n I = dz = dz |z|=1 z2n+1 |z|=1 (z − 0)2n+1
Chọn f(z) = (z2 + 1)2n, theo công thức tích phân Cauchuy với đạo hàm ta có: (2n)! (z2 + 1)2n f 2n(0) = . dz 2πi |z|=1 (z − 0)2n+1 Mặt khác: 2n f (z) = .z4n−2k.Ck2 ( n ∗) k=0
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Rõ ràng lấy đạo hàm cấp thứ 2n tại z = 0 thì các hạng tử có bật khác 2n sẽ bằng 0, do đó trong (∗) ta có k = n và: (2n!)2 f 2n(0) = (n!)2 Từ đó suy ra 2πi (2n)! I = .f 2n(0) = 2πi (dpcm). (2n!) (2!)2
Bài toán 8. Cho P là đa thức có bậc lớn hơn 1 và các không điểm của P nằm bên trong đường tròn |z| = r. Chứng minh : dx = 0 |z|=r p(z) Bài làm Giả sử p(z) = (z − a
là ngiệm không kề trùng nhau với mỗi , chọn sao
1)(z − a2).....(z − an) , các ai ai εi
cho các đường cong: γi = ai + εieit, t ∈ [0; 2π] ,i = 1, n là một đôi một không giao nhau
khi đó đặt: λ = (|z| = r) ∪ γ−1 ∪ γ−2 ∪ .......γ−n ta có : dx = 0 λ p(z) n 1 i=1 suy ra : dz dx dx z = n với mỗi k, ta có : = − ai dz = 2π n = |Z|=r P (z) k=1 γK P (Z) γK P (Z) γK z − a i=1 k 1 ak − ai do đó: dx 1 = 2πi( n n )(∗) γK P (Z) k=1 i=1 ak − ai
với n=2 ,biểu thức (*) sẽ : 1 1 2πi + = 0 a2 − a1 a1 − a2
dễ dàng quy nạp được với k = n, thì(∗) = 0 Vậy dx = 0 |z|=r p(z) Bài toán 9. Tính z3 − 2z dz. |z|=2 (z − 1)2 Bài làm
Đặt f(z) = z3 − 2z thì f chỉnh hình trong miền |z| ≤ 2
Áp dụng định lý Cauchy cho tích phân với đạo hàm:
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
z3 − 2z dz = 2πi.f (1) = 2πi |z|=2 (z − 1)2 Bài toán 10. Tính cos z dz z2 |z|=4 − π2 Bài làm
Vì π, −π ∈ (|z| < 4) nên áp dụng định lý Cauchy cho miền đa liên ta được: cos z dz = 0 z2 − π2 (|z|=4)∪γ−∪γ− 1 2 cos z cos z cos z ⇒ dz = dz + dz z2 z2 z2 |z|=4 − π2 − π2 − π2 γ− γ− 1 2 Trong đó γ là đường tròn tâm 1, γ2
π, −π có bán kính nắm trong miền |z| < 4.
Tiếp tục áp dụng định lý Cauchy cho tích phân với đạo hàm ta được: cos z cos (−π) cos (π) dz = 2πi. + 2πi. = 0 z2 |z|=4 − π2 −2π −2π
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) BÀI TẬP CHƯƠNG 8
Bài toán 1. Có tồn tại một hàm f(z), không đồng nhất bằng 0, chỉnh hình trên đĩa mở D : |z| < 1
và triệt tiêu tại vô hạn điểm trong D? Bài làm. Xét hàm số 1 f (z) = sin
, z ∈ D. Vì f khả vi trên D nên f(z) chỉnh hình trên D. Rõ ràng f(0) = 1 + z 1
sin 1 = 0 nên f (z) = 0 trên D. Ngoài ra f (z) = 0 tại vô hạn điểm zk =
− 1, k ∈ N∗ trong D. Thật kπ
vậy, với mọi k ∈ N∗ ,ta có 1 1 1 0 < < 1 ⇔ −1 < − < 0 ⇔ 0 < 1 − < 1. kπ kπ kπ Suy ra 1 |zk| = | − 1| < 1 nên z kπ k ∈ D = {z : |z| < 1}.
Hơn nữa, ta có f(zk) = sin kπ = 0, ∀k ∈ N∗.
Vậy tồn tại hàm f(z), không đồng nhất bằng 0, chỉnh hình trên đĩa mở D : |z| < 1 và triệt tiêu tại vô hạn điểm trong D. Bài toán 2.
a. Tìm dãy điểm đôi một khác nhau {zn} ⊂ C và hai hàm chỉnh hình khác nhau f(z) và g(z)
trên C sao cho f(zn) = g(zn) với mọi n.
b. Tìm hàm f(z) chỉnh hình trên C∗ = C\{0} và dãy điểm đôi một khác nhau {zn} sao cho
zn → 0, f(z) = 0 với mọi n nhưng f (z) = 0. Bài làm.
a. Tìm dãy điểm đôi một khác nhau {zn} ⊂ C và hai hàm chỉnh hình khác nhau f(z) và g(z) trên
C sao cho f (zn) = g(zn) với mọi n.
Xét hai hàm f(z) và g(z) như sau f (z) = sin z, g(z) = 0.
Rõ ràng, đây là hai hàm chỉnh hình khác nhau trên C.
Xét dãy điểm đôi một khác nhau {zn} trong C với zn = n.π, ∀n ∈ N.
Khi đó với mọi n ∈ N, ta có
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) f (zn) = sin nπ = 0 = g(zn).
b. Tìm hàm f(z) chỉnh hình trên C∗ = C\{0} và dãy điểm đôi một khác nhau {zn} sao cho zn → 0,
f (z) = 0 với mọi n nhưng f (z) = 0. Xét hàm 1 f (z) = sin . z
Dễ dàng thấy rằng f(z) là hàm chỉnh hình trên C∗.
Xét dãy {zn} trong C∗ với 1 zn = . nπ Ta có 1 lim zn = lim = 0 n→∞ n→∞ nπ 1 f (z = sin nπ = 0 ( n) = sin ∀n ∈ N). 1 nπ Tuy nhiên rõ ràng f(z) = 0.
Bài toán 3. Cho f là hàm chỉnh hình trong miền G và có một điểm c ∈ G sao cho tại c hàm |f|
đạt cực tiểu địa phương, nghĩa là |f(c)| = inf |f(z)| với U là một lân cận nào đó của c trong G. z∈U
Khi đó hoặc f(c) = 0 hoặc f là hàm hằng. Bài làm.
Định nghĩa 2.5.1. Một hàm f : X → C được gọi là hàm hằng địa phương trong X nếu với mọi x ∈ X
có một lân cận U ⊂ X nào đó (của x) sao cho f| là hàm hằng. U
Định lý 2.5.2. Với mọi không gian mêtric X, các mệnh đề sau là tương đương:
i) Mọi hàm hằng địa phương (trong X) là hàm hằng.
ii) Tập con khác rỗng của X mà vừa đóng vừa mở chỉ là X (hay X liên thông).
Định lý 8.3.1 (Định lý ánh xạ mở ). Cho D là tập mở khác rỗng trong C. Nếu f chỉnh hình và không
hằng địa phương trong D thì nó là ánh xạ mở từ D vào C.
Giả sử f là hàm chỉnh hình trong miền G và có một điểm c ∈ G sao cho |f(c)| = inf |f(z)| (0) z∈U
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
với U là một lân cận nào đó của c trong G.
Ta xét trường hợp f(c) = 0. Suy ra |f(c)| > 0. Khi đó, từ (), ta có
|f(z)| ≥ |f(c)| > 0, ∀z ∈ U.
Đặt H = {z ∈ G : f(z) = 0}. Xét hàm g : G → C với f (z), nếu z ∈ H g(z) = 1 . , nếu z ∈ G \ H f (z)
Do f chỉnh hình trên G nên ta suy ra f chỉnh hình trên H ⊂ G và 1 chỉnh hình trên G \ H (f = 0). f
Suy ra g chỉnh hình trên H ∪ (G \ H) = G. Rõ ràng 1
H ∩ U = ∅ (vì |f(z)| > 0, ∀z ∈ U) nên U ⊂ G \ H. Suy ra g(z) = , ∀z ∈ U. Khi đó, với f (z) mọi z ∈ U ta có 1 1 |f(z)| ≥ |f(c)| > 0 ⇒ ≤ ⇒ |g(z)| ≤ |g(c)| . f (z) f (c) Suy ra 1
g (U) ⊂ {w ∈ C : |w| ≤ |g(c)|} = B. Do |g(c)| =
> 0 nên B là quả cầu đóng tâm O bán f (c)
kính r = |g(c)|. Suy ra g(U) ⊂ B không là một lân cận của g(c). Kết hợp với U là một lân cận của c,
ta suy ra g không là ánh xạ mở.
Lúc này, do g chỉnh hình và G là tập mở khác rỗng trong C (do G là miền và c ∈ G) nên áp dụng Định
lý ánh xạ mở, ta được g là hàm hằng địa phương trên G. Hơn nữa, vì G liên thông (G là miền) nên
ta suy ra g là hàm hằng trên G (Định lý 2.5.2).
• Nếu g = const = 0 trên G thì theo định nghĩa hàm g, ta có g(z) = f(z) = 0 nếu z ∈ H. Suy ra 1 H = ∅. Do đó, const = g =
trên G \ H = G hay f = const trên G. f 1
• Nếu g = 0 trên G, cũng theo định nghĩa hàm g, ta có g(z) = = 0 nếu z ∈ G \ H. Suy ra f (z)
G \ H = ∅. Do đó, 0 = g = f trên H = G hay f = 0 trên G.
Tóm lại f = const trên G. Hơn nữa, ta đang xét trường hợp f(c) = 0 nên ngược lại, nếu f không là
hàm hằng trên G thì f(c) = 0.
Vậy hoặc f(c) = 0 hoặc f là hàm hằng trên G.
Bài toán 4. Cho đa thức P = zn + a . Chứng minh rằng:
n−1zn−1 + · · · + a1z + a0 max |P (z)| ≥ 1. |z|=1 Bài làm.
Định lý (Bất đẳng thức Cauchy đối với đạo hàm). Giả sử f là một hàm chỉnh hình trên miền D và
z0 ∈ D, R > 0 sao cho B(z0, R) D. Khi đó M · n! |f(n)(z)| ≤ , n ∈ N Rn
trong đó M = max{|f(z)| : |z − z0| = R}.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Ta nhận xét thấy P là hàm đa thức nên chỉnh hình trên toàn bộ C. Với z0 = 0 ∈ C, R = 1 > 0
thì B(z0, R) là quả cầu mở tâm 0 bán kính R = 1 nên bị chặn trong C và rõ ràng B(z0, R) ⊂ C. Suy ra B(z0, R)
C. Khi đó, áp dụng Bất đẳng thức Cauchy đối với đạo hàm bậc n cho hàm P , ta có M · n! |P (n)(z)| ≤ = M · n! (0) Rn trong đó M = max |P (z)|. |z|=1
Mặt khác, ta có đạo hàm bậc n của P là P (n) = n!. Suy ra |P (n)(z)| = |n!| = n!.
Kết hợp với (), ta được
n! = |P (n)(z)| ≤ M · n! = max |P (z)| · n!. |z|=1 Suy ra max |P (z)| ≥ 1. |z|=1
Bài toán 5. Cho f : E → G là song ánh chỉnh hình và Gr := f(B(0, r)) là ảnh của B(0, r), r ∈
(0, 1) qua f . Chứng minh rằng:
a. Nếu G là tập lồi thì Gr, r ∈ (0, 1) cũng là tập lồi
b. Nếu G là tập hình sao tâm f(0) thì Gr, r ∈ (0, 1) cũng là tập hình sao. Bài làm.
a. Với mỗi r ∈ (0, 1), lấy y, z ∈ G , do sao cho r
f song ánh nên tồn tại duy nhất x1, x2, x1 = x2
f (x1) = y, f (x2) = z. Ta chứng minh t = λy + (1 − λ)z ∈ Gr, λ ∈ (0, 1). Do G tập lồi nên
t ∈ G. Hơn nữa, vì f song ánh nên tồn tại duy nhất c ∈ E sao cho f(c) = t. Vì f chỉnh hình nên
c ∈ B(0, r). Do đó t ∈ G . Vậy là tập lồi. r Gr
b. Ta xét với mỗi r ∈ (0, 1) lấy x ∈ G , do r
f là song ánh nên tồn tại duy nhất a sao cho f (a) = x.
Do G là tập hình sao tâm f(0) nên ta có u = λx + (1 − λ)f(0) ∈ G với λ ∈ (0, 1). Vì f song ánh
nên tồn tại duy nhất a ∈ E sao cho f(a) = u. Vì f chỉnh hình nên a ∈ B(0, r) hay u ∈ G . Vậy r
ta có điều phải chứng minh.
Bài toán 6. Chứng minh rằng nếu dãy hàm f chỉnh hình và đơn ánh trong tập mở liên thông n
G, hội tụ compact về f trong G thì f hoặc đơn ánh hoặc là hàm hằng. Bài làm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Lấy tùy ý a ∈ G. Khi đó G = G \ {a} là một tập mở liên thông mà với mọi z ∈ G = G \ {a} có
gn(z) = fn(z) − fn(a) = 0. Theo định lý Hurwitz ta có lim gn(z) = f(z) − f(a) hoặc là hàm hằng 0 n→∞
hoặc không có không điểm trên G . Vậy f(z) ≡ f(a) hoặc f(z) = f(a) khi z = a. Vì a là bất kỳ ta suy ra kết luận.
Bài toán 7. Cho f là hàm chỉnh hình trên tập mở liên thông G và f không là hàm hằng 0. Giả
sử c ∈ G và f(c) = 0. Khi đó tồn tại R > 0 sao cho B(c, R) ⊂ G và f(z) = 0 với mọi z thỏa 0 < |z − c| < R. Bài làm
Mệnh đề: Cho f là hàm chỉnh hình trên tập mở liên thông G, f không là hàm hằng 0 và c ∈ G. Hai
mệnh đề sau tương đương
i) f có bội n < ∞ tại c;
ii) f(z) = f(c) + (z − c)nF (z) với F là hàm chỉnh hình tại c và thỏa F (c) = 0.
Đặc biệt v(f, c) = 1 ⇔ f (c) = 0.
Theo Mệnh đề trên f(z) = (z − c)nF (z) với F là hàm chỉnh hình tại c và thỏa F (c) = 0. Khi đó tồn tại
R > 0 sao cho B(c, R) ⊂ G sao cho F (z) = 0 với mọi z thỏa |z − c| < R và ta có điều phải chứng minh.
Bài toán 8.Giả sử D là tập mở khác rỗng trong C và f : D → C là hàm chỉnh hình. a. Giả sử z trong
0 ∈ D và f (zo) = 0. Chứng minh rằng tồn tại một lân cận B của zo D sao
cho f| : B → C là ánh xạ 1 − 1. B
b. Chứng minh rằng f là song chỉnh hình địa phương tại c ∈ D nếu và chỉ nếu f (c) = 0 (tức là f bảo giác tại c ). Bài làm
Định lý 5.19: Giả sử D là tập mở khác rỗng trong C. Nếu f : D → C là ánh xạ chỉnh hình 1 − 1 thì
D := f (D) là tập mở khác rỗng trong C và f (z) = 0 với mọi z ∈ D (tức là f bảo giác trên D ). Đồng
thời ánh xạ f : D → D là ánh xạ song chỉnh hình và ánh xạ ngược f−1 thỏa măn 1 f −1 (w) = với mọi w ∈ D . f (f −1(w))
Định lý 2.23: Cho D là tập mở khác rỗng trong C. Các khẳng định sau về một hàm khả vi thực
f : D → C là tương đương.
i) f chinh hình và f khác 0 trên D;
ii) f bảo toàn độ lớn và hướng quay của góc trên D.
Chú thích: Nếu f (z0) = 0 tính bảo toàn độ lớn của góc không còn đúng. Chẳng hạn xét hàm
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
w = f (z) = z2. Ta có f (0) = 0. Qua phép biến hình này, tia arg z = 0 có ảnh là arg w = 0, tia π arg z =
ảnh là arg w = π. Như vậy độ lớn của góc giữa hai tia Ox và Oy không được bảo toàn qua 2 phép biến hình.
a. Vì f cũng là hàm chỉnh hình tại z và sao cho 0
|f (z0)| > 0 nên tồn tại đĩa mở B tâm tại zo |f (z |f (z) − f (z 0)| với mọi tùy ý thuộc B. Gọi nằm 0)| ≤ z ∈ B. Lấy z Γ là đọan nối z 2 1, z2 1, z2 trong B. Ta có |f (z1) − f (z2)| = f (z)dz Γ = f (z [f (z Γ 0) dz − Γ 0) − f (z)] dz f (z f (z ≥ |f (z 0) 0) 0) (z2 − z1)| − |z |z 2 2 − z1| = 2 2 − z1| .
b. (⇒) Lấy tùy ý zo ∈ D, ta có f bảo giác trên D. (theo định lý 2.23).
(⇐)f (c) = 0 nên theo câu a) tồn tại một lân cận U của c trong D sao cho f| : U → C là ánh xạ U
1 − 1. Khi đó theo định lý 5.19 (định lý về tiêu chuẩn song chỉnh hình) có f| : U → f(U) song U chỉnh hình. Bài toán 9. Giả sử f là hàm chỉnh hình trên 1, f2, ..., fn
D, liên tục trên D. Chứng minh hàm
g(z) = |f1(z)| + |f2(z)| + ... + |fn(z)| hoặc là hàm hằng hoặc đạt cực đại trên biên ∂D. Bài làm
Đầu tiên, ta chứng minh hàm g(z) = |f1(z)| + |f2(z)| + ... + |fn(z)| là hàm hằng.
Ta chứng minh bằng phản chứng, giả sử rằng tại điểm z0 ∈ D (z0 = ∞) mođun của hàm f1(z)
khác hàm hằng đạt cực đại của nó. Tức là trong lận cận nào đó U(z , hàm thỏa 0, ), > 0 của z0 f1 |f1(z)| ≤ |f1(z0)|.
Trước tiên ta cần chứng minh rằng |f1(z)| ≡ |f1(z0)| trong lân cận U(z0, 0). Giả sử B(z0, ) ⊂ D với bán kính <
và tâm là . Theo định lý giá trị trung bình ta có 0 z0 2π 1 f1(z0) = f 2π 1(z0 + eit)dt 0
Từ đó ta có bất đẳng thức giá trị trung bình 2π 1 |f1(z0)| ≤ |f 2π 1(z0 + eit)|dt 0 suy ra 2π 1 0 ≤ |[f 2π 1(z0 + eit)| − |f1(z0)|]dt. 0
Ta thấy biểu thức dưới dấu tích phân trong bất đẳng thức trên là không dương. Do đó chỉ có thể xảy ra trường hợp
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) |f1(z0 + eit)| ≡ |f1(z0)|, tức là |f nên
1(z)| ≡ |f1(z0)| trên B(z0, ). Do 0 < < 0
|f1(z)| ≡ |f1(z0)| trong lân cận U(z0, 0). Nếu
f1(z0) = 0 thì |f1(z)| ≡ 0 và do đó f1(z) ≡ 0 trong lân cận U(z0, 0). Ngược lại, nếu f1(z0) = 0 thì
f1(z) = 0 và do đó f1(z) ≡ 0 trong lân cận U(z0, 0). Trong lân cận này, ta xét
F1(z) = lnf1(z) = ln|f1(z)| + iargf1(z) = u + iv. Do |f chỉnh hình trên
1(z)| ≡ |f1(z0)| với z ∈ U (z0, 0) nên u ≡ const (u = ln|f1(z)| = |f1(z0)|). Do f1 D
nên theo điều kiện Cauchy - Riemann ta có ∂u ∂v = ≡ 0 ∂x ∂y ∂u ∂v = − ≡ 0. ∂y ∂x
suy ra u ≡ const trong U(z0, ). Do đó hàm F1(z) = lnf1(z) ≡ const và từ đó f1(z) ≡ const trong lân
cận của điểm z . Như vậy . Điều này vô lý. 0
f1(z) ≡ const trong lân cận của điểm z0
Tiếp theo, ta xét trường hợp miền ∞ ∈ D và hàm f1(z) có modun cực đại tại ∞. Trong trường hợp này ta xét hàm 1
F1(z) = f ( ). Hàm này chỉnh hình trong miền D∗ thu được từ ánh xạ D qua ánh xạ w 1 w = . Hàm F z
1(w) có cực đại tại w = 0 và điểm này là điểm trong của D∗. Theo chứng minh trên ta
có F1(w) = const trong D∗. Do đó f1(z) ≡ const trong miền D.
Chứng minh tương tự với các hàm f còn lại chỉnh hình trên 2, ..., fn
D, liên tục trên D ta có f2(z) =
const, ..., fn(z) = const. Từ đây ta suy ra g(z) = |f1(z)| + |f2(z)| + ... + |fn(z)| ≡ const trong miền D.
Trong phần này, ta sẽ chứng minh hàm g(z) = |f1(z)| + |f2(z)| + ... + |fn(z)| đạt cực đại trên biên ∂D.
Thật vậy, trong Bài làm tích thực ta có hàm |f1(z)| (liên tục trong miền D nhận giá trị cực đại của
nó tại điểm z nào đó của miền 0
D.Tương tự như vậy, các hàm |f2(z)|, ..., |fn(z)|(liên tục trong miền D
nhận giá trị cực đại của nó tại điểm z nào đó của miền 0
D. Theo nguyên lý mođun cực đại, điểm z0
không thể nằm trong D. Do đó điểm z chỉ có thể nằm trên biên 0 ∂D của miền D.
Vậy hàm g(z) = |f1(z)| + |f2(z)| + ... + |fn(z)| đạt cực đại trên biên ∂D.
Bài toán 10.Cho M > 1, giả sử f là hàm chỉnh hình trong B(0, 1) sao cho f(0) = 1 và |f(z)| < M với mọi 1
z ∈ B(0, 1). Chứng minh |f(z) − 1| ≤ M|z| với mọi z ∈ B 0, . M Bài làm Đặt 1 g =
, do g là hàm hằng trong B(0, 1) nên g chỉnh hình trong B(0, 1). M Xét f w = f.g =
, do f và g là các hàm chỉnh hình trong B(0, 1) nên w là hàm chỉnh hình trong M f (0) 1 B(0, 1). Ta có w(0) = =
, |w| < 1 (do M > 1). Ta đặt: M M
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) 1 f (z) 1 w − − f (z) − 1 h(z) = M = M M = M. 1 1 f (z) M 2 1 − .w − f(z) 1 − . M M M
Hàm h thỏa mãn các giả thiết của bổ đề Schwarz nên ta có: |f(z) − 1| M. ≤ |z|. |M2 − f(z)| Suy ra |M2 − f(z)| M 2 1 |f(z) − 1| ≤ .|z| ≤
.|z| ≤ M|z| với mọi z ∈ B 0, . M M M
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)

