Bài tập Hệ phương trình đối xứng loại II
Bộ câu hỏi ôn tập học phần "Toán cao cấp" bao gồm câu hỏi tự luận giúp sinh viên củng cố kiến thức và đạt điểm cao trong bài thi kết thúc học phần.
Môn: Toán cao cấp (52.IE.001.2) 2 tài liệu
Trường: Học viện Ngoại giao 0.9 K tài liệu
Tác giả:
Preview text:
lOMoARcPSD|35973522
HỆ PHƯƠNG TRÌNH ĐỐI XỨNG LOẠI II. (Một số bài tập)
Loại 2 có cách giải chủ yếu dựa vào các phép biến đổi cơ bản như trừ theo vế các phương trình rồi
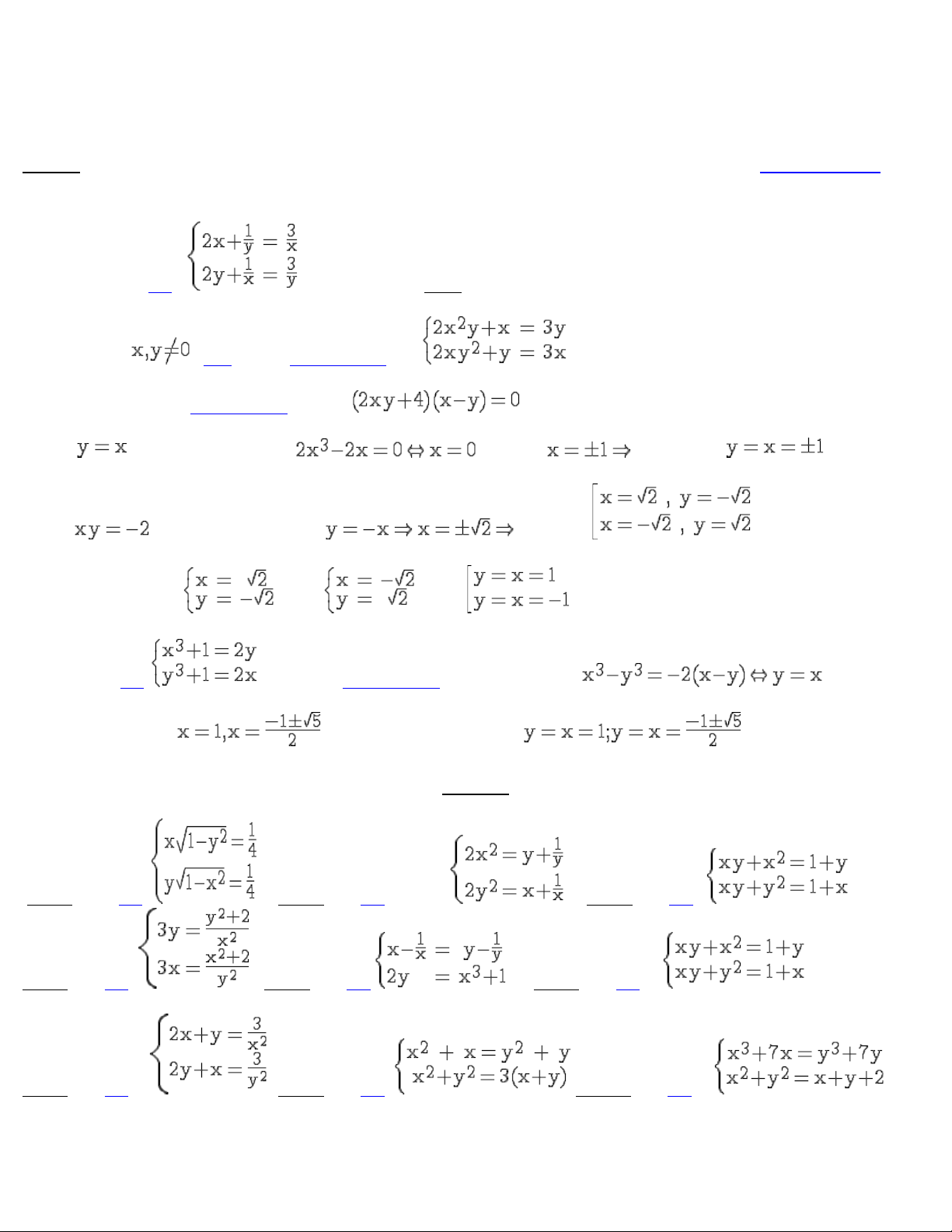
nhóm và phân tích thành nhân tử. Ví dụ 1: Giải hpt: Giải: Với điều kiện
. Hpt đã cho tương đương với (*)
Trừ vế với vế của hai phương trình ta được a) Với
thế trở lại (*) ta được (loại) và hai nghiệm . b) Với
, thế trở lại (*) ta được 2 nghiệm Vậy hệ có nghiệm: ; ; Ví dụ 2:Giải hpt
Trừ hai phương trình cho nhau ta được . Thế vào hệ ta được . Hệ có ba nghiệm . Bài tập Bài 2 Giải hpt: Bài 3Giải hpt sau : Bài 4Giải hpt : Bài 5Giải hpt: Bài 6Giải hpt Bài 7Giải hpt:a) Bài 8Giải hpt : Bài 9Giải hpt: Bài 10Giải hpt :
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Bài 11Giải hpt: Bài 12Giải hpt : Bài 13Giải hpt : Bài 14Giải hpt : Bài 15Giải hệ : Bài 16Giải hpt Bài 17Giải hpt Bài 18Giải : Bài 19Giải hpt Bài 20Giải hpt Bài 21Giải hpt Bài 22Giải hpt Bài 23Giải hpt . Bài 24Giải hpt Bài 25Giải hpt
Bài 26Giải hpt sau: Bài 27Giải hpt b) Bài 28 Giải hpt:
Bài 29 Bài 17Giải hpt:
Giải và biện luận hệ phương trình theo yêu cầu bài toán
Bài 1 Tìm m để hpt có nghiệm: Bài 2Cho hệ:
a) Giải hệ với m=1. b) Với những giá trị nào của m thì hệ đã cho có nghiệm?
Bài 3Chứng minh hệ: có ba nghiệm.
Bài 4 Tìm a để hệ :
Có duy nhất một nghiệm thỏa mãn: và .
Bài 5 Tìm a để hệ có nghiệm duy nhất:
Bài 6 Xác định tham số a để hpt sau có nghiệm duy nhất:
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522
Bài 7 Tìm để hệ sau có nghiệm duy nhất Bài 8 Tìm để hpt có nghiệm duy nhất Bài 9 Cho hpt: (*) 1) Giải hệ (*) khi
2) Tìm sao cho hệ (*) có nghiệm duy nhất
Bài 10Tìm m để hpt có nghiệm duy nhất. Bài 11.Cho hệ:
.Tìm m hpt đã cho có nghiệm duy nhất.
Bài 12 Tìm m để hpt có nghiệm: Bài 13 Cho hệ:
a) Giải hệ với m=1. b) Với những giá trị nào của m thì hệ đã cho có nghiệm?
Bài 14 Chứng minh hệ: có ba nghiệm.
Bài 15 Tìm a để hệ :
Có duy nhất một nghiệm thỏa mãn: và .
Bài Biện luận số nghiệm của hệ:
Bài 16 Tìm a để hệ có nghiệm duy nhất:
Bài 18 Xác định tham số a để hệ sau có nghiệm duy nhất :
Bài 19Xác định các giá trị âm của a để hpt :
có nghiệm duy nhất .Bài 20 Biện luận số nghiệm của hệ:
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)