. TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC:
CẠNH – CẠNH – CẠNH (C.C.C)
I. KIẾN THỨC CƠ BẢN
 Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì
hai tam giác đó bằng nhau. A
AB  A' B ' 
AC  A'C '  A  BC  A
 'B 'C ' .c .cc B C  A'
BC  B 'C ' II. BÀI TẬP B' C'
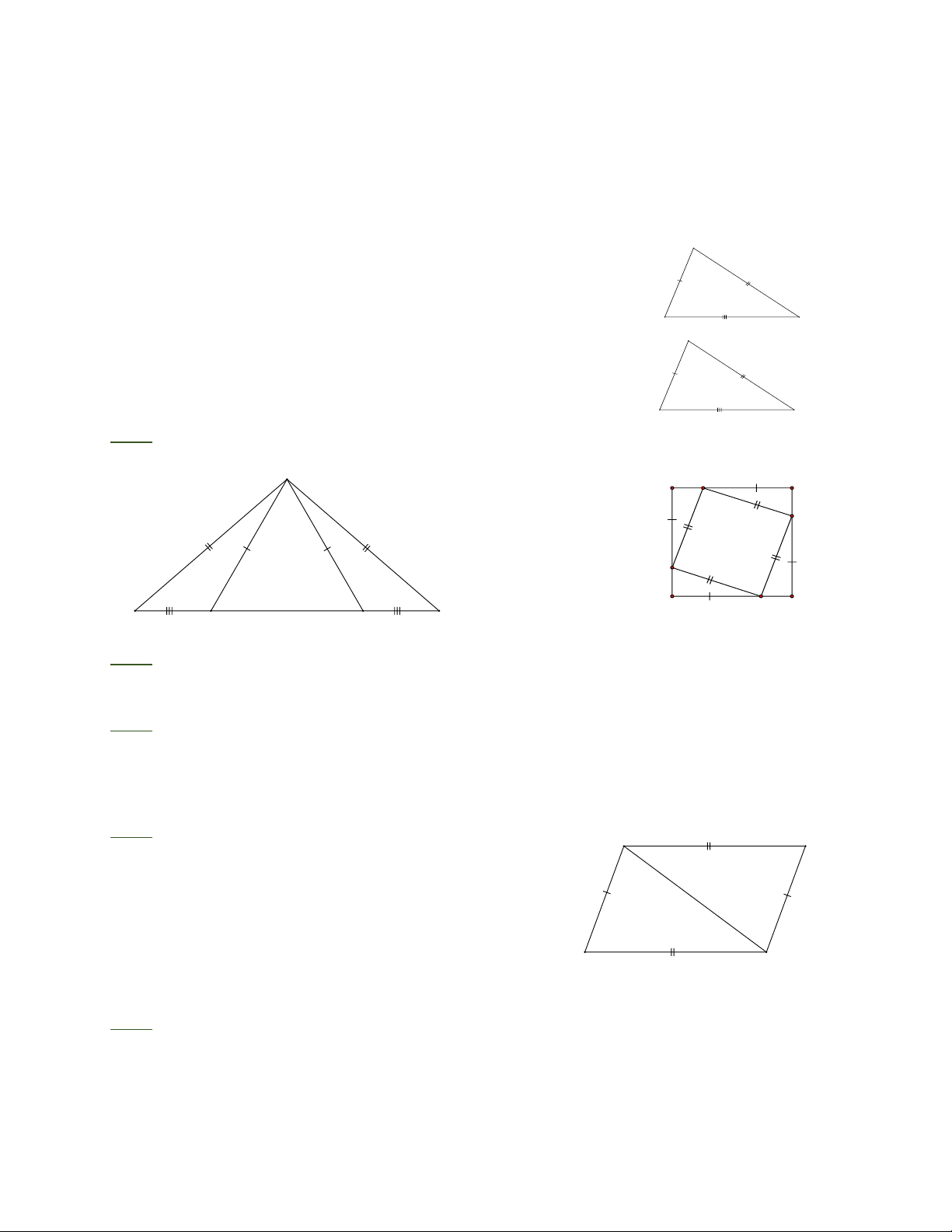
Bài 1: Tìm các tam giác bằng nhau trên hình dưới đây. A M R N S Q P O T B E C D
Bài 2: Cho hình vuông MNOP như hình vẽ, tìm trong hình những tam giác nào bằng nhau.
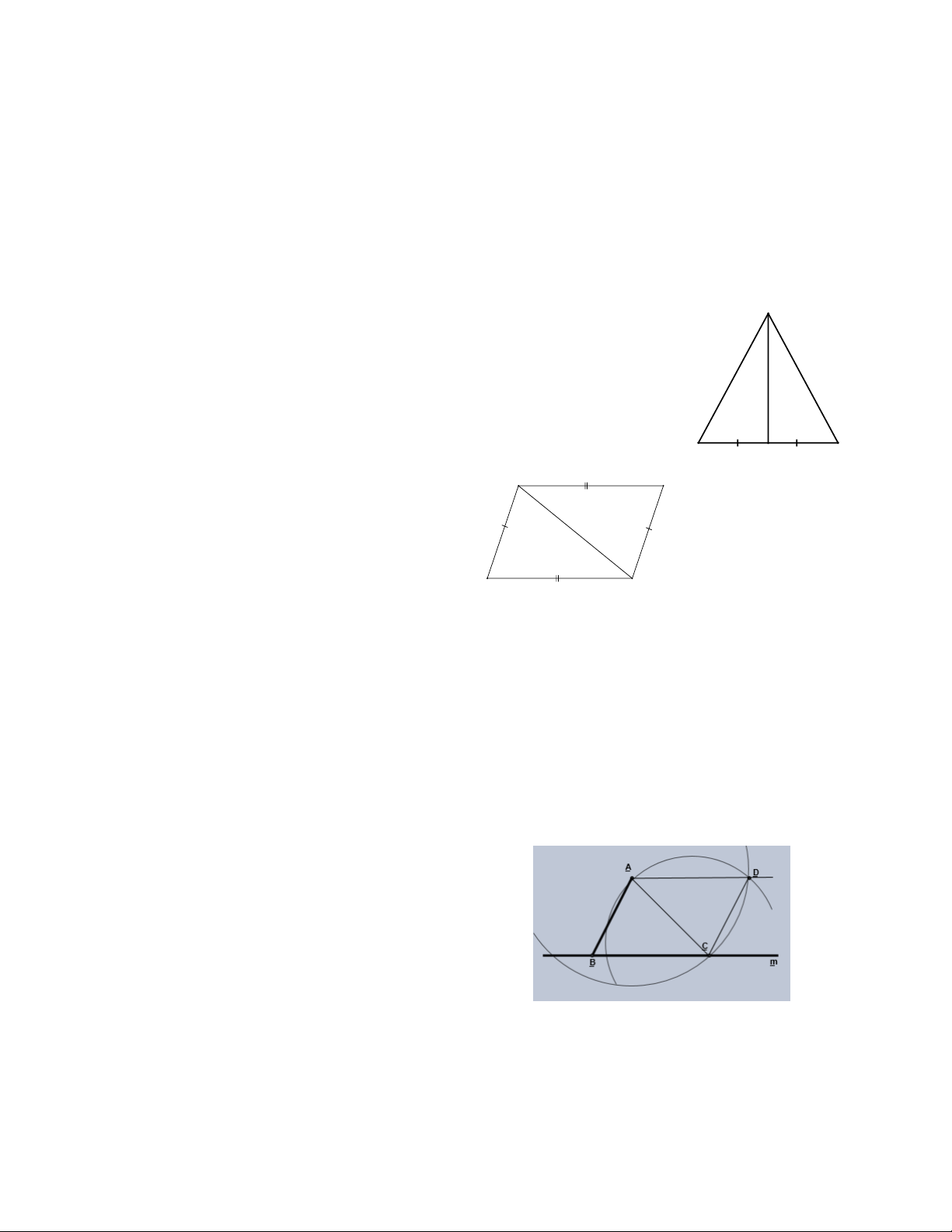
Bài 3: a). Vẽ tam giác ABC có BC = 2cm , A B = A C = 3cm .
b). Gọi E là trung điểm của cạnh BC ở ABC 
trong câu a). Chứng minh rằng AE là tia
phân giác của góc BA C . Bài 4: Cho hình vẽ A B a) Chứng minh DACB= DCAD · ·
b) Chứng minh BAC = DCA và suy ra A B / / DC . D C
c) Chứng minh A D/ / BC .
Bài 5: ( Bài toán dựng đường song song bằng thước thẳng và compa )
Cho điểm A nằm ngoài đường thẳng m .
Để vẽ đường thẳng qua A và song song với m , người ta vẽ như sau : Trang 1
- Lấy hai điểm B , C tùy ý trên đường thẳng m.
- Vẽ đường tròn tâm C, bán kính AB và đường tròn tâm A, bán kính BC.
- Gọi D là giao điểm của hai đường tròn
( D và B thuộc hai nửa mặt phẳng đối nhau bờ là AC).
Em hãy chứng minh A D // m .( Vẽ lại hình vào bài làm)
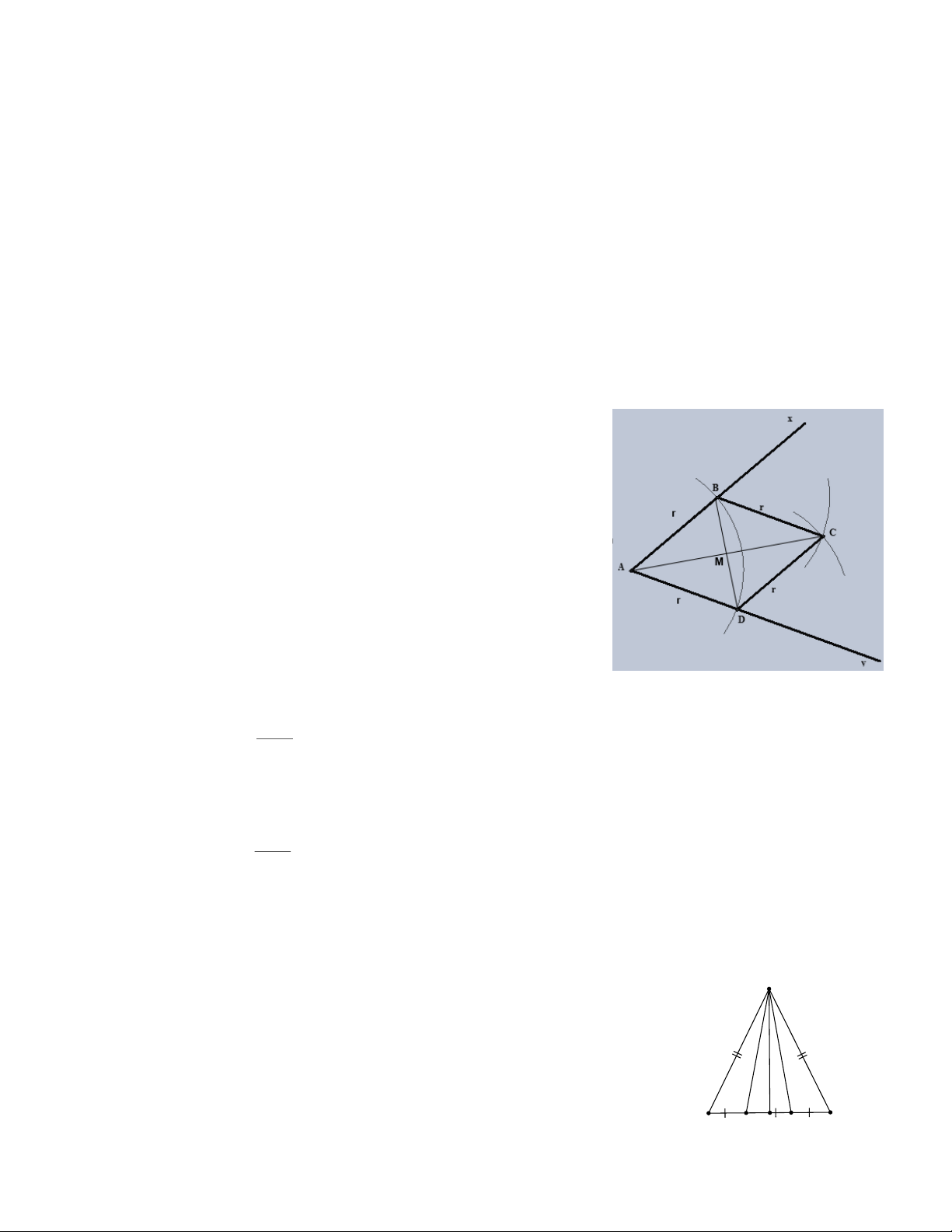
Bài 6: ( Bài toán vẽ tia phân giác bằng thước thẳng và compa).(Vẽ lại hình vào bài làm)
Cho góc xA y . Lấy A làm tâm, vẽ dường tròn bán kính r cắt Ax tại B., cắt Ay tại D.
Lần lượt lấy B và D làm tâm vẽ hai đường tròn cùng có bán kính bằng r , hai đường tròn
này cắt nhau tại C ( C khác A ). Chứng minh :
a) AC là tia phân giác của góc xA y .
b) BD là tia phân giác của góc A B C . c) AD // BC. d) AC  DB. Bài 7:
Cho tam giác ABC có A B = A C ; D; E thuộc cạnh
B C sao cho BD = DE = EC Biết A D = A E · ·
a. Chứng minh EA B = DA C ·
b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của DAE . · c. Giả sử 0
DAE = 60 . Tính các góc còn lại của tam giác DA E . HẾT Trang 2 HDG
Bài 1: HS chỉ ra các 3 cặp cạnh tương ứng của hai tam giác bằng nhau từ đó kết luận được A  BC  A
 ED (c.c.c), A  BD  A  EC (c.c.c).
Bài 2: Do MNOP là hình vuông nên MN = NO = OP = P Q RN = SO = TP = QM từ đó suy ra MR = NS = OT = P Q
Kết quả: MQR  NRS  OSI  PT ( Q c.c.c) A
Bài 3: a) HS tự vẽ hình (nêu cách vẽ) 3 3 b) B  AE  C
 AE (c.c.c)  BAE  CAE (hai góc tương ứng)
 AE là tia phân giác của góc BAC . B E C Bài 4: 2 A B a) Xét ΔACB và ΔCAD có : AB=CD ü ïïïï
AD=BC ý Þ ΔACB= ΔCAD (c - c - c) ïï D C AC chungïïþ b) Vì D = D ( ) · · A CB CA D cmt
Þ BA C = DCA (cặp góc tương ứng) mà hai góc này ở vị trí so
le trong nên AB//CD · ·
c) Vì ΔACB= ΔCAD Þ DAC = BCA (cặp góc tương ứng ) mà hai góc này ở vị trí so le trong nên D A / /BC
Bài 5: (HS vẽ hình)
* Chứng minh AD//m
Nối A với D , D với C và A với C .
Xét D A BC và C  DA có AB  D
C (bằng bán kính đường tròn tâm C ) BC  D
A (bằng bán kính đường tròn tâm A ) AC là cạnh chung  A  BC  C
 DA (c c c) Trang 3
 BCA  DAC (cặp góc tương ứng ) mà hai góc này ở vị trí so le trong
nên AD//BC  AD//m (vì B,C  m ) Bài 6:
a) Nối A với C . Chứng minh được ΔABC  ΔADC (c  c  ) c
 BAC DAC (cặp góc tương ứng ) mà AC là tia nằm trong BAD
 AC là tia phân giác của BAD  AC là tia phân giác của góc xAy ( Vì B Ax ; D Ay )
b) BD là tia phân giác của góc ABC .
Nối B với D . Chứng minh được ΔABD  ΔCBD (c  c  ) c
 ABD CBD (cặp góc tương ứng ) mà BD là tia nằm trong
ABC  BD là tia phân giác của ABC
c) Vì ΔABC  ΔADC (c  c  ) c
 BCA  DAC (cặp góc tương ứng ) mà hai góc này ở vị trí so le trong  D A / /BC .
d) Gọi M là trung điểm của BD
* Chứng minh được ΔABM  ΔADM (c  c  c) 0 180 0  AMB  AMD   90 2
*Chứng minh được ΔCBM  ΔCDM (c  c  ) c 0 180 0  CMB CMD   90 2 * Cộng góc ta được 0 AMC 180  ,
A M ,C thẳng hàng  AC  D B tại M . A Bài 7:
a) DA BE = DA CD(c.c.c) · · Þ EA B = DA C
b) DA DM = DA EM (c.c.c) B C D M E Trang 4 · · Þ ·
DA M = EA M Þ A M là phân giác của DAE .
c) DA DB = DA EC (c.c.c) · · · ·
Þ A DB = A EC Þ A DE = A ED (180° 30°): 2 75° = - = Trang 5