
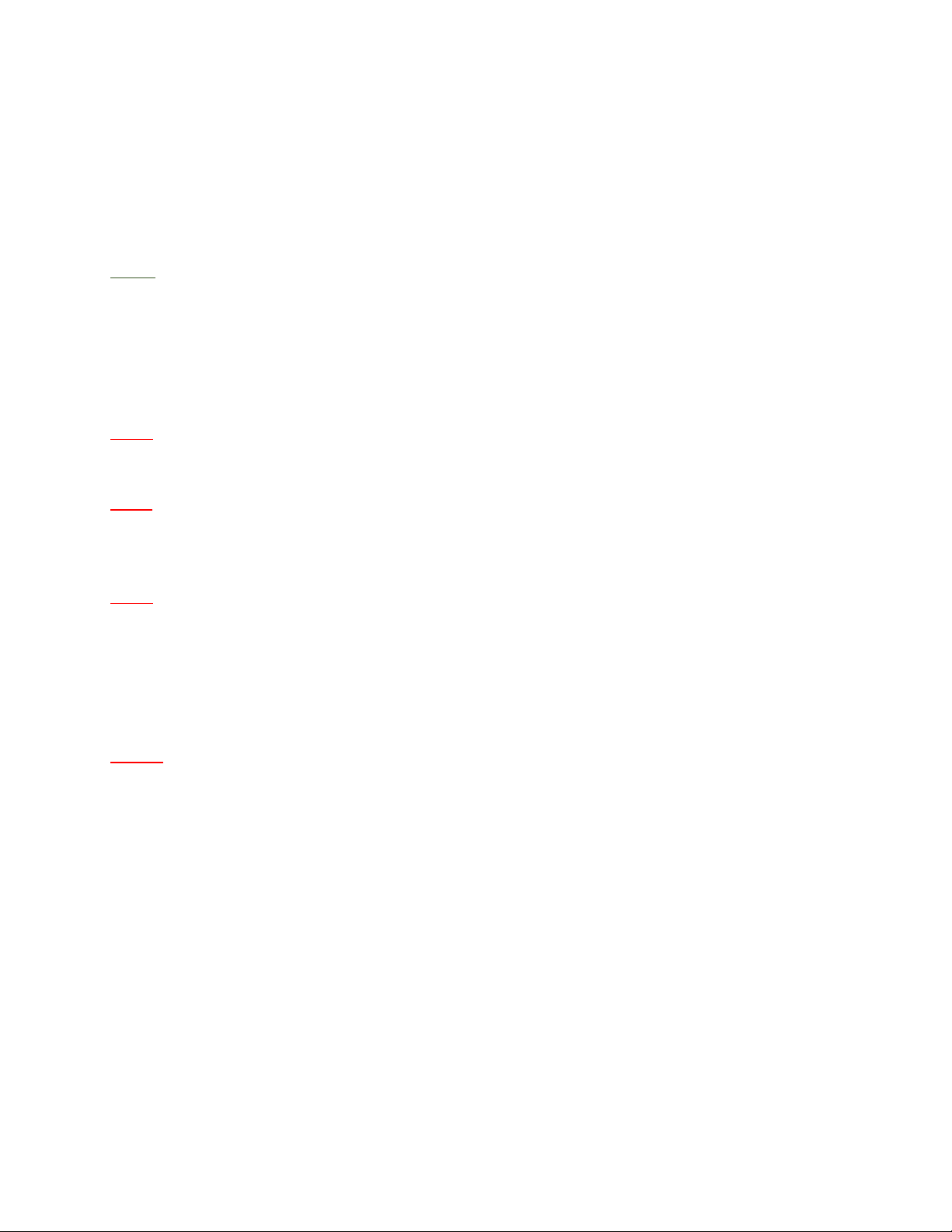


Preview text:
TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
I. KIẾN THỨC CƠ BẢN A
Định lí 1. Ba đường trung trực của một tam giác cùng đi qua một
điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Trên hình bên, điểm O là giao điểm các đường trung trực của O DAB . C
Ta có OA = OB = O .
C Điểm O là tâm đường tròn ngoại tiếp DAB . C B C
Định lí 2. Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường
trung tuyến ứng với cạnh đáy. II. BÀI TẬP
Bài 1: Chứng minh rằng trong tam giác vuông, tâm đường tròn ngoại tiếp tam giác là
trung điểm của cạnh huyền.
Bài 2: Cho tam giác MNP cân tại .
M Trên cạnh MN lấy điểm K, trên cạnh MP lấy điểm
D sao cho MK = D .
P Đường trung trực của MP cắt đường trung trực của DK tại . O · ·
a) Chứng minh MKO = PD . O
b) Chứng minh O thuộc đường trung trực của . MN ·
c) Chứng minh MO là tia phân giác của NM . P
Bài 3: Cho tam giác ABC cân tại A, 0
A 90 . Các đường trung trực của AB và của AC cắt
nhau tại O và cắt BC tại D và E. Chứng minh rằng:
a) OA là đường trung trực của BC; b) BD = CE; c) ODE là tam giác cân;
Bài 4: Cho DABC nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối
của tia OB lấy điểm D sao cho OB = O . D
a) Chứng minh O thuộc đường trung trực của AD và . CD
b) Chứng minh các tam giác ABD, CBD vuông. · · c) Biết ABC = 70 .
° Hãy tính số đo góc AD . C µ
Bài 5: Cho DABC vuông tại A, C = 30 .
° Kẻ đường trung trực của đoạn thẳng AC, cắt
AC tại H và cắt BC tại .
D Nối A và . D
a) Chứng minh D ABD đều. Trang 1 µ
b) Kẻ phân giác góc B cắt AD tại K, cắt DH kéo dài tại I. Chứng minh I là tâm đường
trong đi qua ba đỉnh của tam giác AD . C
c) Gọi E, F là hình chiếu vuông góc của I xuống các đường thẳng BC, B . A Chứng minh
IE = IF = I . K ·
d) Tính số đo góc DAI. µ
Bài 6: Cho tam giác ABC có A > 90 .
° Trên cạnh BC lấy các điểm D và E sao cho
BD = BA, CE = CA . Gọi I là giao điểm các tia phân giác trong của tam giác AB . C
a) Chứng minh BI, CI là đường trung trực của AB, A . C
b) Chứng minh rằng IA = ID = I . E
Bài tập tự luyện
Bài 7: Tam giác ABC cân tại A có AB = 14cm. Đường trung trực của AB cắt cạnh AC ở E.
Biết chu vi tam giác BEC bằng 24cm. Tính độ dài BC.
Bài 8: Cho tam giác ABC có 0
B 90 . Gọi d là đường trung trực của BC, O là giao điểm của
AB và d. Trên tia đối của tia CO lấy điểm E sao cho CE = BA. Chứng minh rằng d là đường trung trực của AE.
Bài 9: Cho tam giác ABC cân ở A, đường phân giác AK. Các đường trung trực của AB
và AC cắt nhau tại . O
a) Chứng minh rằng ba điểm A, K, O thẳng hàng.b) Kéo dài CO cắt AB ở D, kéo dài
BO cắt AC ở .
E Chứng minh rằng AK và các đường trung trực của AD và AE đồng quy.
Bài 10: Cho tam giác ABC vuông tại .
A Kẻ AH vuông góc với BC, H B . C Tia phân
giác của góc HAB cắt BC tại D, tia phân giác của góc HAC cắt BC tại . E Chứng minh
rằng điểm cách đều ba cạnh của ABC chính là điểm cách đều ba đỉnh của A D . E Hết Trang 2 HDG Bài 1:
Gọi O là tâm đường tròn ngoại tiếp tam giác AB . C B
Do đó, OA = OB = O . C µ ¶ µ ¶
Suy ra: B = A , C = A . 2 1 O ìï ¶ ¶ 2 ïO = 180° - 2A ï 1 2 2 Þ í ï ¶ µ. ïO = 180° - 2A 2 1 1 ïî 1 · ¶ ¶ µ Þ A C
BOC = O + O = 360° - 2A = 180°. 1 2
Þ B, O, C thẳng hàng, mà OB = OC
Þ O là trung điểm của . BC Bài 2: M
a) Từ giả thiết suy ra OK = OD, OM = O . P · · D
DMKO = DPDO (c.c.c) Þ MKO = PD . O · ·
b) Từ kết quả câu a), suy ra OKN = OD . M K O
Có MN = MP, MK = PD Þ NK = M . D
Chứng minh DOKN = DODM (c.g.c) Þ ON = OM N P
Þ O thuộc đường trung trực của . MN
c) Xét DMNP có O là giao điểm các đường trung trực của MN và . MP
Þ MO là đường trung trực của . NP ·
Mà DMNP cân tại M nên MO đồng thời là tia phân giác của góc NM . P Bài 3:
a) O là giao điểm các đường trung trực của ABC OB OC ABC
cân tại A AB AC
Vậy AO là đường trung trực của BC
b) Gọi H là trung điểm của AB, K là trung điểm của AC. H BD K
CE (g.c.g) BD CE c) H BD K
CE HDB KEC ODE OED ODE cân tại O Trang 3 Bài 4:
a) Ta có OA = OB = OC nên OA = OD = OC
Þ O là giao điểm hai đường trung trực của AB và AC. ¶ ·
b) Ta có : OA = OB Þ B = BA . O 2 A ¶ ·
OA = OD Þ D = DA . O 1 Xét D BAD có: D 1 2 ¶ · · ¶
B + BAO + DAO + D = 180° 2 2 O 2 · · 1
Þ 2(BAO+ DAO)= 180° B C · Þ BAD = 90°.
Vậy tam giác ABD vuông tại . A
Tương tự, ta chứng minh được tam giác BCD vuông tại C. ¶ ¶
c) Ta có: B + D = 90 ; ° ¶ ¶ B + D = 90° 2 1 1 2 ¶ ¶ ¶ ¶
Suy ra B + B + D + D = 180°. 1 2 2 1 · · Þ ABC + ADC = ° 180 · · Þ ADC = 18 ° 0 - ABC = 11 ° 0 . Bài 5: B µ µ
a) C = 30° Þ B = 60 . ° D · µ K E
Ta có: DA = DC Þ DAC = C = 30° · 30°
Þ BAD = 60° Þ DABD đều. A H C
b) D ABD đều Þ BK là đường trung trực của AD Þ F IA = I . D I
Mà I Î DH Þ IA = I . C
Vậy IA = IC = I . D
Þ I là tâm đường tròn đi qua ba đỉnh của tam giác AD . C µ
c) I thuộc phân giác của góc B Þ IE = IF. ·
DH là đường trung trực của AC Þ DH là phân giác của ADC Þ IK = I . E
Vậy IE = IF = I . K ·
d) IK = IF Þ AI là tia phân giác của DAF. · · · DAF
BAD = 60° Þ DAF = 120° · Þ DAI = = 60°. 2 Trang 4 Bài 6:
a) Vì DABC đều và O là giao điểm ba đường trung trực nên A µ
AO là tia phân giác của . A · M · BAC Þ MAO = = 30°. 2 P O ·
b) Tương tự câu a), OCP = 30 . ° B N C
Có DMAO = DOPC (c.g.c).
c) Có: DMAO = DOPC Þ OM = OP ( ) 1 .
Chứng minh tương tự câu b), DMAO = DNBO (c.g.c)
Þ OM = ON (2). Từ ( ) 1 và ( )
2 suy ra O là giao điểm ba đường trung trực của tam giác MN . P Trang 5




