






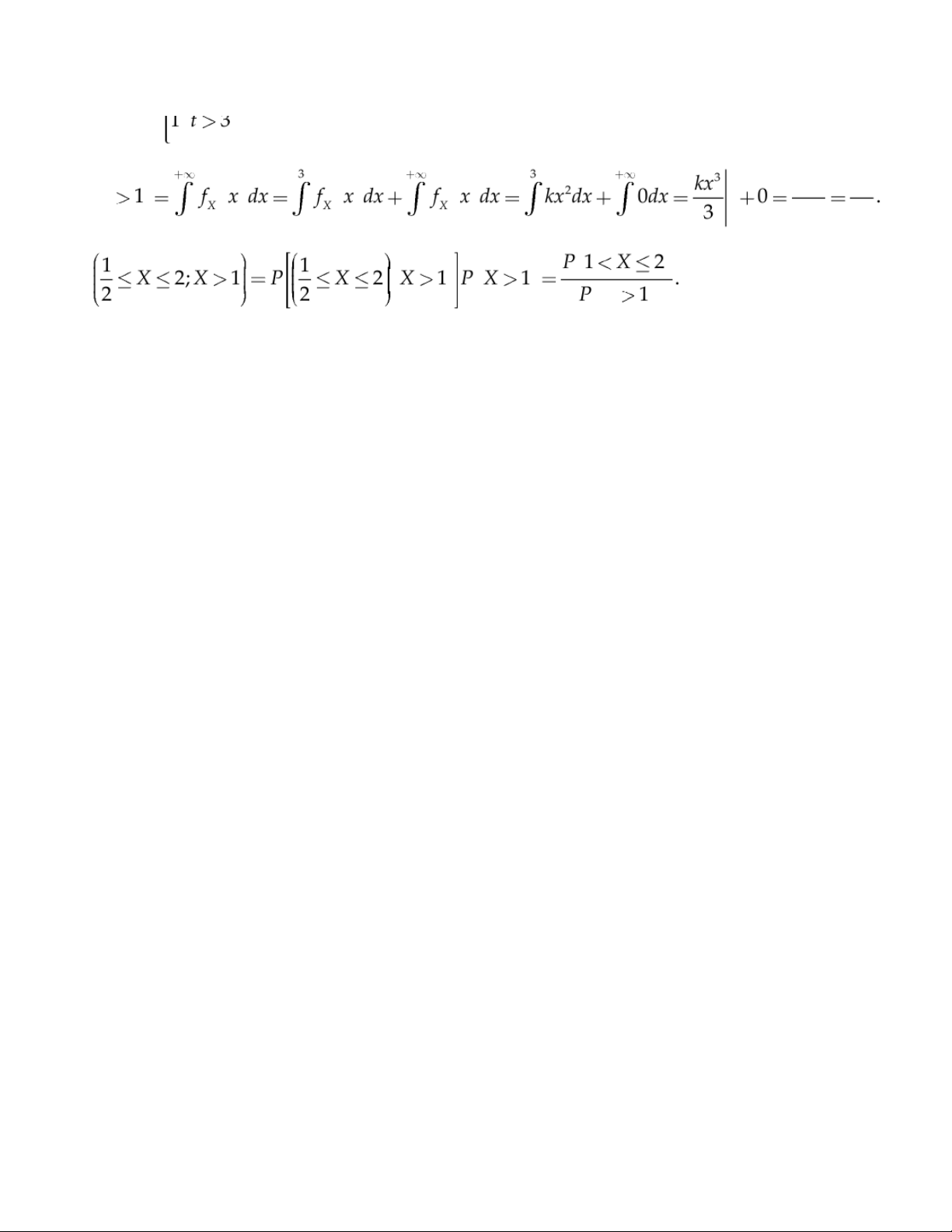





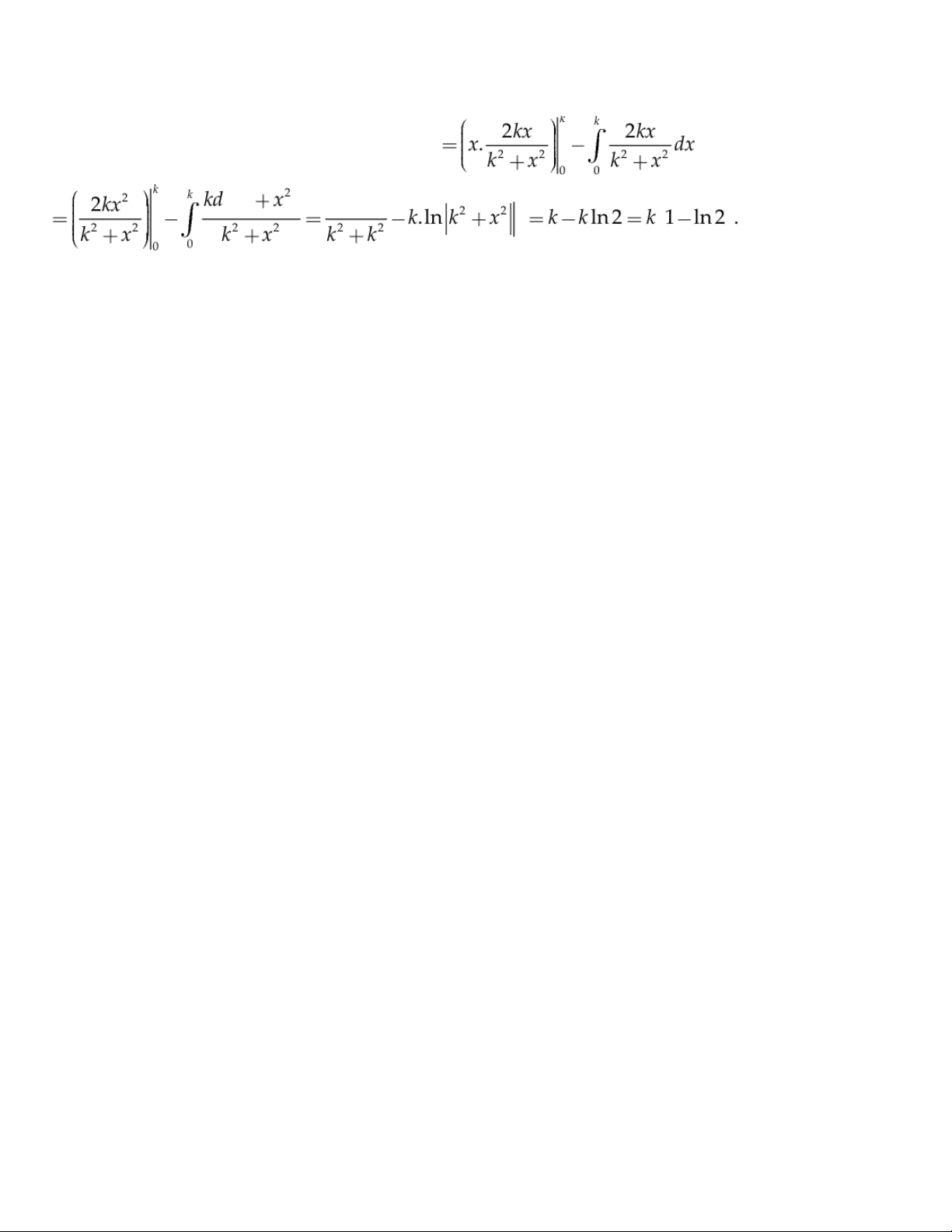






Preview text:
21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
MỘT SỐ BÀI TẬP XÁC SUẤT THỐNG KÊ “NGHI” KIỂM TRA SẮP TỚI Ở FTU
(Các bài thuộc phạm vi chương 1, 2 Giáo trình “Xác suất thống kê” hiện hành)
Tác giả: Khuyết danh :D
Bài 1: Biết rằng một người có nhóm máu AB có thể nhận máu của bất kì người nào. Nếu người
đó có nhóm máu A ,B ho c
ặ O thì chỉ có thể nhận được máu của người cùng nhóm máu với
mình hoặc người có nhóm máu O. Biết tỉ lệ người có nhóm máu O A
, , B và AB tương ứng là 33,7%, 37,5%, 20, 9%,7,9%. a) L y ng ấ
ẫu nhiên một người c n ti ầ
ếp máu và một người cho máu. Tính xác suất người cần tiếp
máu có nhóm máu A và sự truy
ền máu được thực hiện? b) L y ng ấ
ẫu nhiên một người tiếp máu và một người cho máu. Tính xác suất để sự truyền máu được thực hiện?
Hướng dẫn giải: Gọi B , , ,
lần lượt là biến cố: “Chọn được người c n ti ầ ếp máu có nhóm máu O A B BB ABB O A, B , , AB ”. Gọi C C , C , , C
lần lượt là biến cố: “Chọn được người cho máu có nhóm máu O A, B , , AB ”. O A B AB
a) Biến cố “Chọn được người c n ti ầ
ếp máu có nhóm máu A và người cho máu có nhóm máu A “ là B C . A A
Biến cố “Chọn được người cần tiếp máu có nhóm máu A và người cho máu có nhóm máu O “ là BA OC .
Biến cố “Chọn được người cần tiếp máu có nhóm máu A và sự truy c th ền máu đượ ực hiện” là BA A C
Vì hai biến cố B ,C độc lập nên: P B C A A A A
Vì hai biến cố B ,C độc lập nên: P B C A O A A
Vì hai biến cố BA AC và BA OC xung khắc nên P B C A A
b) Biến cố sự truyền máu được thực hiện là: D Ta có: P B AB 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Vì hai biến cố B ,C độc lập nên: P B C O O O O Vì hai biến cố B , độ ập nên: P B C A A C c l A A Vì hai biến cố T ,
độc lập nên: P T C A O C A O Vì hai biến cố B ,
độc lập nên: P B C B B C B B 1 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu Vì hai biến cố B ,
độc lập nên: P B C B O C B O
Xác suất để sự truyền máu được thực hiện là: P D
Bài 2: Một lô hàng có 6 s n ph ả m. M ẩ ỗi l n ki ầ
ểm tra chất lượng lấy ngẫu nhiên 2 s n ph ả m. Sau ẩ khi kiểm tra xong l i tr ạ
ả vào lô hàng. Tính xác suất để sau 3 l n ki ầ
ểm tra lô hàng thì tất c s ả n ả
phẩm đều được kiểm tra?
Hướng dẫn giải:
Gọi A là biến cố: “Lần thứ k lấy được 2 s n ph ả ẩm chưa được ki n c ểm tra”, khi đó biế ố: “Sau k 3 l n ki ầ
ểm tra lô hàng thì tất c
ả các sản phẩm đều được kiểm tra là A 3 .
Theo công thức nhân xác suất P A | A P A | . A A 1 3 1 2 CC 22 2 C 2 1 Ta có: P A 1 C C C 5 15 6 6 6 Do đó: P A 2 1 2 5 15 75
Bài 3: Trong một trận không chiến giữa máy bay ta và máy bay địch, máy bay ta bắn trước với
xác suất trúng là 0,6. Nếu bị ch b trượt, máy bay đị n tr ắ v
ả ới xác suất trúng là 0,5 u còn nế
không bị trúng đạn, máy bay a bắ
n trả với xác suất trúng là 0,4.
a) Tính xác suất để máy bay đị ch bị rơi.
b) Tính xác suất để máy bay ta bị rơi.
Hướng dẫn giải:
Gọi A1 là biến cố: “Máy bay ta bắn trúng ở l n th ầ
ứ nhất”, A2 là biến cố: “Máy bay ta bắn trúng ở lần thứ hai”.
Từ giả thiết ta có: P A 1
a) Biến cố : “ Máy bay địch bị rơi” là: A
.A Vì hai biến cố . . là xung 3 A1 và A A A 1 2 3 khắc nên P A 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
b) Biến cố : “ Máy bay ta bị rơi” là: A . A. 1 2
Theo công thức nhân xác suất thì: P A. 1 A 2 2 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Bài 4: Có hai cái hộp, hộp thứ nhất có 3 bi trắn và 4 bi đén, hộp thứ hai có 4 bi trắng và 6 bi đen.
a) Từ mỗi hộp lấy ra ngẫu nhiên một viên bi, tính xác suất để l ng ?
ấy được hai viên bi trắ b) Sau khi l y ng ấ
ẫu nhiên từ mỗi hộp ra một viên bi, các viên bi còn lại trong hai hộp được dồn
hết và một hộp thứ ba. Từ hộp thứ ba lấy ngẫu nhiên ra một viên bi. Tính xác suất để viên bi lấ y
ra từ hộp thứ ba là bi đen ?
Hướng dẫn giải:
a) Gọi A là biến cố: ‘’Lấy được viên bi đen từ hộp thứ ba’’.
Gọi A1 là biến cố: ‘’Lấy được bi tr ng t ắ
ừ hộp thứ nhất’’. A2 là biến cố: ‘’Lấy được bi trắng từ hộp thứ hai’’ Khi đó hệ A , , , là một hệ đầy đủ n c các biế ố. Ta th y ấ , là hai biến cố 1 A2 A 1 A 2 1 A 2 1 A2 A A A1 A 2 độc lập, do đó: 3 6 18 P A 1 A 2 7 10 70 1 10 Ngoài ra ta có C P A| A 1 A 2 C 15 15 3 6 18 Tương tự P A A 1 2 7 10 70 C1 9 P A| A 1 A 2 C 15 15 4 4 16 P A 1 A 2 7 10 70 C1 9 P A| A 1 A 2 C 15 15 4 6 24 P A A 1 2 7 10 70 C1 8 P A|A A C 1 2 15 15 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Theo công thức xác suất đầy đủ ta đượ c: P A Thay vào ta có: P A 12 10 18 9 16 9 27 8 103 70 15 70 15 70 15 70 15 175 3 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu Bài 5: Cho biến ng c
ẫu nhiên liên tụ X
có hàm mật độ xác suất f x X a) Tìm hằng số k?
b)Tìm hàm phân bố xác suấ t F x ? K c) Tính P X d) Tính P
Hướng dẫn giải: a) Ta có 3 3 0 Theo tính chấ k1
t của hàm mật độ xác suất thì do đó 1 hay 9 b) t t Nếu t thì F t X Nếu t thì t t 0 t t 0 3 t X F t 27 0 Nếu t thì t t 3 0 3 0 3 X F t 0 0 Vậy X F t 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu 3 k 26 26 c) P X 3 27 1 1 3 1 3 1 d) P X 4 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu 2 2 2 7 7 Xét k P 1 Do đó: 3 27 1 1 1 7 7 P 26 26 27
Bài 6: Thời gian phục vụ khách hàng tại một điểm dịch vụ là biến ngẫu nhiên liên tục X có hàm mật độ xác suấ t f x
với X được tính bằng phút/khách hàng. K
a) Tìm xác suất để thời gian phục vụ ột khách hàng nào đó nằ m m trong khoảng từ 0,4 n đế 1 phút?
b) Tìm thời gian trung bình để phục vụ ột khách hàng? m
Hướng dẫn giải: 1 1 1 a) Ta có P 0,4 0 ,4 0 ,4 0 ,4
b) Từ hàm mật độ của X , ta suy ra biến ngẫu nhiên X có phân bố mũ với tham số λ Theo 1 1
tính chất của phân bố mũ, ta có E X λ 5
Vì X là thời gian phục vụ khách hàng nên thời gian trung bình phục vụ một khách hàng là kì
vọng của X , do đó thời gian trung bình phục vụ một khách hàng là E X
Bài 7: Tuổi thọ X của người là một biến ngẫu nhiên liên tục có hàm mật độ xác suất f x trong đó λ
Biết xác suất người sống quá 60 tuổi bằng 0,5. a) Tìm λ?
b) Một người năm nay 60 tuổi, tìm xác suất để người này sống quá 70 tuổi? c) Gọi A
Tính các xác suất P B A | P; B C | ?
Hướng dẫn giải: a 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu a Với mọi ta có bb P X a a a ln 2 a) Theo đề bài P X nên e 60 5 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu P X ln 2 b) Ta có: P X P X P X
c) Ta có: P B| A P X P B C | Bài 8: Cho biến ng c
ẫu nhiên liên tụ X với hàm mật độ xác suất fX x a) Tìm k?
b) Tính kì vọng E X ?
Hướng dẫn giải: a) Ta có: 0 a a 0 Do đó k 2
Theo tính chất của hàm mật độ xác suất thì do đó k hay k 2 b) Ta có: E X 0 0 a a Xét 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu a V y ậ E X 6 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu Bài 9: Cho biến ng c
ẫu nhiên liên tụ X với hàm phân bố xác suất F x X
a) Tìm hàm mật độ xác suấ t f x ? K b) Tính xác suất P
c) Tính kì vọng E X ?
Hướng dẫn giải: k2 a) Ta có: k 2
Do đó hàm mật độ xác suấ t f x ủ X K c a là fK x b) Ta có P . c) E X 0 k 0 2 k 2k k 0 Đặt 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Theo công thức tích phân từng phần: E X k 2 2 k 2 . k k 0 7 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Bài 10: Trong một hòm có 10 tấm thẻ trong đó có 4 tấm thẻ ghi số 1, 3 t m th ấ ẻ ghi số 2,2 tấm
thẻ ghi số 3 và 1 tấm thẻ ghi số 4. Chọn ngẫu nhiên hai tấm thẻ.
a) Gọi X là tổng số ghi trên hai tấm thẻ. L p b ậ
ảng phân bố xác suất của X và hàm phân bố xác suất của F x ? K
b) Với mỗi số trên thẻ chọn được thưởng 20$. Gọi Y là tổng số tiền được thưởng. Tính E Y ?
Hướng dẫn giải:
a) Số cách chọn được hai tấm thẻ bất kì trong 10 t m
ấ là C210 . Số cách chọn hai t m th ấ ẻ trong đó
có một thẻ ghi số 1 và một thẻ số 2 là C1. C
1 . Vậy xác suất chọn được một thẻ số 1 và một thẻ 4 3 1 1 .4 số 2 là C4 C 3 C 2 15 10
b) X nhận các giá trị 2; 3; 4; 5;6;7. 2 6 X
là biến cố: ‘’Chọn được hai thẻ số 1 ’’, do đó C P X C 45 10 1 1 .12 X
là biến cố: ‘’Chọn được một thẻ số 1 và một thẻ số 2 ’’, do đó C C P X C 45 10 X
trong đó A là biến cố: ‘’Chọn được một thẻ số 1 và một thẻ số 3 ’’, còn A là
biến cố: ‘’Chọn được hai thẻ số 2 ’’. 1 1 2 .8 3 Ta có C C C P A C 45 45 10 C 10
Vì hai biến cố A và B xung khắc nên P X 8 3 11 45 45 45 X
trong đó C là biến cố: ‘’Chọn được một thẻ số 1 và một thẻ số 4 ’’, còn D là
biến cố: ‘’Chọn được một thẻ số 2 và một thẻ số 3 ’’. 1 1 1 1 .4 6 . Ta có C C C C P C C 45 45 10 C 10
Vì hai biến cố C và D xung khắc nên P X 4 6 2 45 45 9 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu X
trong đó E là biến cố: ‘’Chọn được một thẻ số 2 và một thẻ số 4 ’’, còn F là
biến cố: ‘’Chọn được hai thẻ số 3 ’’. 1 1 2 .3 1 Ta có C C C P E C 45 45 10 C 10
Vì hai biến cố E và F xung khắc nên P X 3 1 4 45 45 45 8 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu 1 1 .2 X
là biến cố: ‘’Chọn được một thẻ số 3 và một thẻ số 4 ’’, do đó C C P X C 45 10 Bảng phân bố xác suấ t của X X 2 3 4 5 6 7 P 6 12 11 10 4 2 45 45 45 45 45 45 Hàm phân bố xác suấ t F x K khi x i x 2 2 khi hi 3 hi 11 F x hay F x 45 11 10 5 hi 45 45 11 10 4 6 hi 45 45 45 khi x hi x
c) Kì vọng của X là E X 6 12 11 10 4 2 45 45 45 45 45 45 Ta th y ấ Y nên E Y Bài 11: Một x th
ạ ủ đem 5 viên đạn bắn kiểm tra trước ngay thi bắn. Xạ thủ bắn từng viên vào
bia với xca suất trúng vòng 10 là 0, 85. Nếu b n
ắ 3 viên liên tiếp trúng vòng 10 thì thôi không
bắn nữa. Gọi Y là số đạn x th ạ ủ này đã bắn.
a) Lập hàm phân bố xác suất của Y? b) Tính E Y ?
c) Xét trường hợp 3 viên liên tiếp trúng vòng 10 thì ngừng b n. G ắ
ọi Z là số đạn còn thừa. Tìm
quy luật phân bố xác suất của Z? 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
Hướng dẫn giải: Ta th y ấ Y nhận 3 giá trị là 3; 4; 5.
Gọi A là biến cố: ‘’Xạ thủ bắn trúng vòng 10 ở l n b ầ n th ắ
ứ k ’’. Khi đó P A k k Ta có: Y . 3
Vì ba biến cố A , A, A độc lập nên 1 2 3 P Y 9 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu Y . 3 4A
Vì bốn biến cố A , A, , A A độc lập nên 1 2 3 4 P Y Ta có: P X 625.
Bảng xác suất của Y: Y 3 4 5 P 0, 614125 0, 09211875 0, 29375625 khi x 5 khi3
Hàm phân bố xác suất F x hay X 5 khi x khi x 5 khi3 F x khi X 375 4 khi x
b) Kì vọng của Y: E Y c) Ta có Z
Vì Y nhận các giá trị 3; 4; 5
nên Z nhận giá trị 2;1; 0. P Z 5625 ; P Z 1875 ; P Z 25.
Bảng xác suất của Z: Z 2 1 0 P 0, 614125 0, 09211875 0, 29375625
Bài 12: Cho biến ngẫu nhiên X có kì vọng E X và độ lệch chu n ẩ σ . Hãy tính xác suất P X
trong các trường hợp sau:
a) X có phân bố mũ. 21:59, 27/01/2026
Bài Tập Xác Suất Thống Kê Ở FTU: Kiểm Tra Sắp Tới Những Tình Huống Khác Nhau - Studocu
b) X có phân phối Poisson với tham số λ
Hướng dẫn giải: 1 1 a) Gi s
ả ử X có phân phối mũ có tham số λ khi đó μ λλ Hàm mật độ xác suấ t của X: f x 10




