1/Một người tiêu thụ có thu nhập I = 1200đ dùng để mua 2 sản phẩm X và Y với
Px = 100đ/sp; Py = 300đ/sp. Mức thoả mãn được thể hiện qua hàm số: TUx =
-1/3X2 +10X; TUy = -1/2Y2 + 20Y. Lợi ích biên của 2 sản phẩm là
MUx = -2/3X + 10; MUy = -Y + 20 Bài 2
Giả sử lợi ích của người tiêu dùng A là X và Y , cho hàm sau TU = X2+2Y.
Tính lợi ích cận biện của việc tiêu dùng hàng hóa X và Y? MUx=TU’x=2X MUy=TU’y=2 Bài 3:
Một người dành một khoản thu nhập I = 600 ngàn đồng, chi tiêu hết cho 2
loại sản phẩm X và Y với PX = 10 ngàn đồng/sp; PY = 30ngàn đồng/sp, hàm
tổng lợi ích ( hữu dụng ) của người này phụ thuộc vào số lượng X và Y tiêu
dùng TU(x,y) = 2xy. Tại phương án tiêu dùng tối ưu, số lượng x và y người này mua là: Bài giải Ta có: X+3Y=60 (1)
MUx/Px=MUy/Py => 2Y/1=2X/3 => X-3Y=0 (2) (1),(2) => x=30, y=10 Bài 4
a/ Tìm sự kết hợp tối đa hóa hữu dụng, biết I=9,Px=1,Py=2
b/ Tính tổng hữu dụng tối đa Bài giải a/Ta có: MUx/Px=MUy/Py X.Px+Y.Py=I
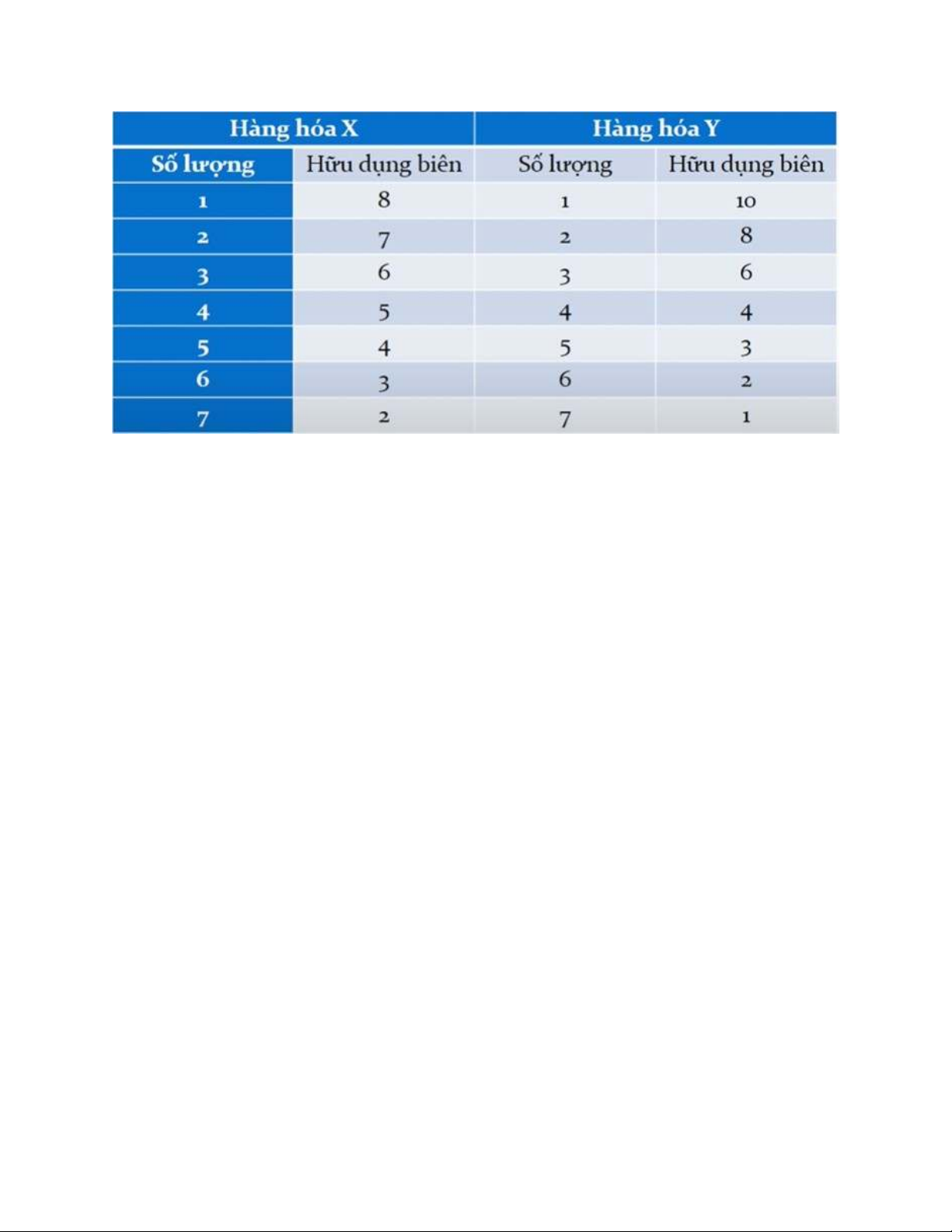
Từ đó tại X=5, Y=2 thỏa điều kiện Do 4/1=8/2 và 5.1+2.2=9
b/ TUmax=MUx+MUy=8+7+6+5+4+10+8=48 Bài 5:
Cho TU(x,y)=X2+Y2 , đường ngân sách X+4Y=2 a/ Tìm x và y b/ Tìm TUmax Bài giải a/Ta có : X+4Y=2 (1)
MUx/Px=MUy/Py => 2X/1=2Y/4 => 4X-Y=0 (2) (1),(2) => x=2/17, y=8/17
b/ TUmax = (2/17)2+(8/17)2 = 4/17