Bài tập lớn Đề tài Giải thuật Di truyền | Môn Nhập môn về trí tuệ nhân tạo - Đại học Hải Phòng

lOMoAR cPSD| 58707906
TRƯỜNG ĐẠI HỌC HẢI PHÒNG
Khoa Công nghệ thông tin
BÀI TẬP LỚN TRÍ TUỆ NHÂN TẠO
Đề tài: Giải thuật di truyền SVTH : GVHD: Năm 2024 lOMoAR cPSD| 58707906 MỤC LỤC Giới thiệu I.
Giải thuật di truyền (GA) và ứng dụng giải một số bài toán……
II. Một số bài toán liên quan đến giải thuật di truyền (GA)……….
III. Ứng dụng python……………………………………….. IV.
KẾT LUẬN…………………………………………….. lOMoAR cPSD| 58707906 Giới thiệu
- Genetic Algorithms (GAs) - Giải thuật di truyền là một kỹ thuật khoa
học máy tính nhằm giải quyết các bài toán tối ưu tổ hợp. GAs dựa trên
quá trình thích nghi tiến hóa của các quần thể sinh học dựa trên học
thuyết của Darwin. Nó vận dụng các nguyên lý: di truyền, đột biến, chọn
lọc tự nhiên và trao đổi chéo. GAs dùng một số thuật ngữ của ngành di
truyền học như: nhiễm sắc thể, quần thể (Population), Gene... Nhiễm sắc
thể được tạo thành từ các Gene (được biểu diễn của một chuỗi tuyến
tính). Mỗi Gene mang một số đặc trưng và có vị trí nhất định trong nhiễm
sắc thể. Mỗi nhiễm sắc thể sẽ biểu diễn một lời giải của bài toán. Trong
bài viết này tôi sẽ giải thích các khái niệm song song với việc lập trình ở một bài toán cụ thể.
GAs được sử dụng cho những bài toán khó, và đã được ứng dụng thành
công cho một số bài toán như: lập kế hoạch, hệ thống điều khiển, bài
toán người đi du lịch,… I.
Giải thuật di truyền (GA) và ứng dụng giải một số bài toán
- Giải thuật di truyền (GA) cũng như các mạng neuron, các thuật toán di truyền
cũng dựa trên 1 ẩn dụ sinh học: Các thuật toán này xem việc học như là sự
khó khăn trong 1 quần thể gồm những lời giải người mua việc đang tiến hóa
của bài toán. Một hàm ‘thích nghi’ (fitness function) sẽ đánh giá mỗi lời giải
để quyết định liệu nó mang đóng góp cho thế hệ những lời giải kế tiếp hay
không. Sau đó, phê chuẩn những phép toán na ná có biến đổi gene trong sinh
sản hữu tính, giải thuật sẽ tạo ra một quần thể những lời giải người mua việc mới
1. Giải thuật di truyền là như thế nào ? lOMoAR cPSD| 58707906
- Trình bày giải thuật di truyền tổng quát. Tùy theo từng bài toán mà nhà – ngoại
hình giải thuật sẽ phải mô tả yếu tố hơn về:
- Phương pháp biểu diễn một cá thể trong quần thể những lời giải người tìm
việc của bài toán, hay nói khác hơn là hình thức trình diễn 1 lời giải tiềm năng
của bài toán. Không phải lời giải của mọi bài toán đều với thể được mã hóa 1
bí quyết dễ dàng và khi không dưới dạng biểu diễn mức bit như trong bài toán
thỏa mãn CNF dưới đây.
- Độ lớn của quần thể là số lượng ứng viên với trong quần thể. Thông thường
những ứng viên của quần thể ban đầu được sắm 1 phương pháp ngẫu nhiên.
Độ to của quần thể là ko đổi qua những thế hệ, vì vậy, sẽ mang một công đoạn
tậu lọc và dòng bỏ một số lời giải người chọn việc sở hữu độ thích nghi thấp.
- Điều kiện ngừng của vòng lặp: mang thể là chương trình đạt tới một số lần lặp
một mực nào đó, hay đạt đến trung bình độ phải chăng nào đó của quần thể,…
- Hàm đánh giá (fitness function): Dùng để đánh giá một ứng cử viên mang
thấp hay không. Một ứng cử viên càng phải chăng tức là độ thích ứng của nó
càng cao và tiến tới trở thành lời giải đúng của bài toán. Việc ngoại hình 1
hàm kiểm tra phải chăng là siêu quan yếu trong thuật toán di truyền. Một
hàm kiểm tra không chính xác mang thể làm mất đi các người mua việc rẻ trong quần thể.
- Chọn lựa bao nhiêu phần trăm lời giải tốt để giữ lại? Hay mua bao nhiêu lời
giải ứng viên để kết hợp sở hữu nhau và sinh ra lời giải con. Phương pháp tạo
thành viên mới từ thành viên hiện có, còn gọi là toán tử di truyền (genetic operators): lOMoAR cPSD| 58707906
- Các toán tử di truyền phổ biến là Lai ghép (cross-over): Toán tử lai ghép lấy
hai lời giải người tậu việc và chia từng lời giải ra thành hai phần, sau đó bàn
thảo các phần có nhau để tạo ra ứng viên mới.
- Đột biến (mutation): Đột biến lấy 1 người sắm việc đơn lẻ và thay đổi 1
phương pháp tự nhiên một khía cạnh nào đó của nó. Độ thích nghi(fitness)
2. ví dụ minh họa giải thuật và toán tử di truyèn
- Trong ví dụ minh họa bằng hình 9.18, ta thấy tại thế hệ thiết bị n ta với một
lời giải mang độ thích nghi siêu tốt (2), và vì vậy, nó ko được dùng trong quá
trình tái sản xuất. Thay vào đó, lời giải với độ thích ứng cao nhất (13) sẽ được
nhân đôi và đưa vào quá trình tái sản xuất.
Hoặc ít phổ biến hơn là các toán tử di truyền: •
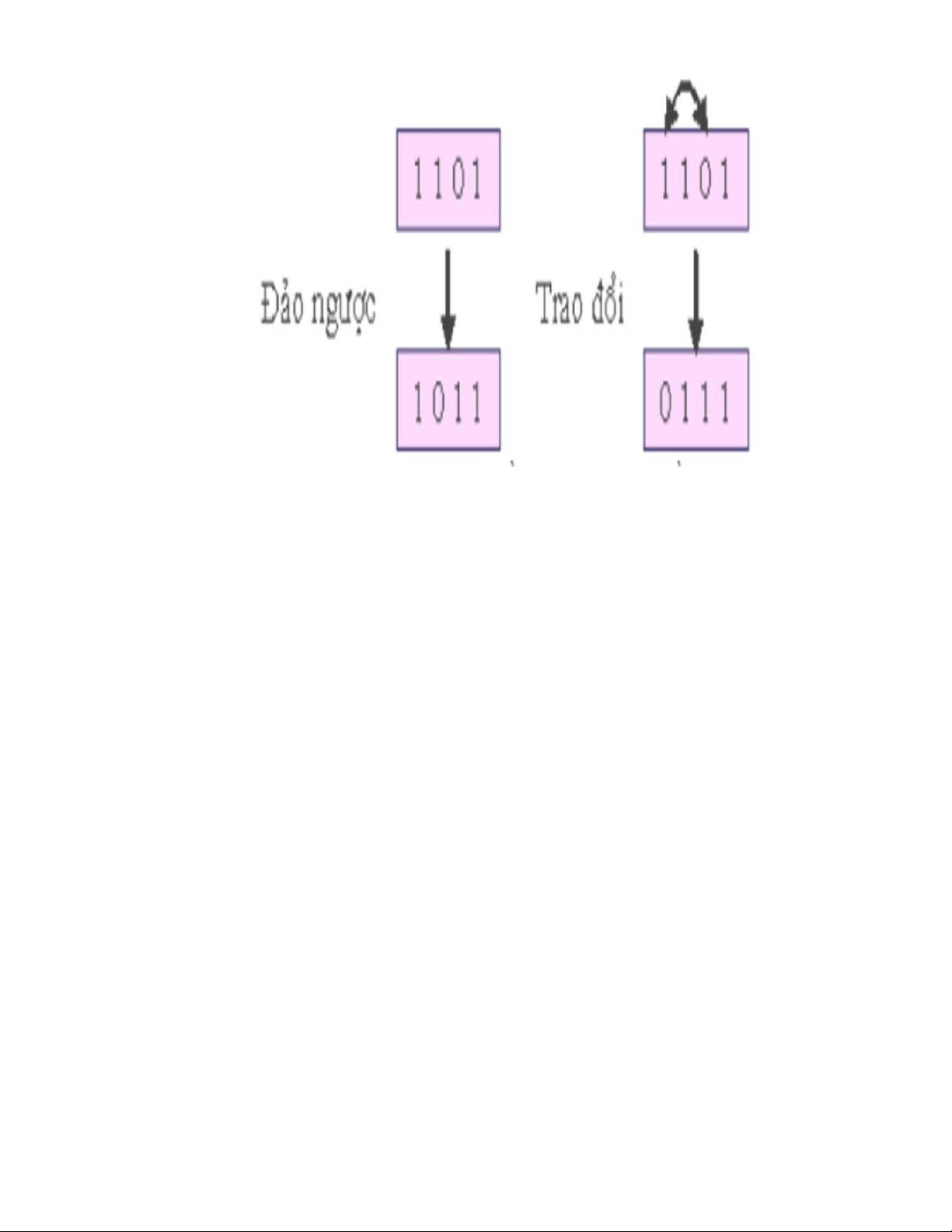
Đảo ngược (inversion): Đảo ngược thứ tự các bit trong chiếc lời giải. •
Trao đổi (Exchange): Trao đổi hai bit bất kỳ trong dòng lời giải sở hữu nhau. lOMoAR cPSD| 58707906
- Một toán tử di truyền tốt đóng 1 vai trò quan trọng trong thuật toán di truyền.
Toán tử di truyền buộc phải bảo toàn các mối quan hệ cốt yếu trong quần thể;
ví dụ, sự với mặt và sự độc nhất của mọi những thành phố trong hành trình
của người bán hàng trong bài toán người đi bán hàng.
II. Một số bài toán liên quan đến giải thuật di truyền (GA) Bài toán thỏa CNF
Bài toán thỏa mãn dạng chuẩn hội (Conjunctive normal form – CNF) là 1 bài toán
đơn giản: Một biểu thức của các mệnh đề (clause) ở dạng chuẩn hội hay CNF lúc nó
là 1 dãy những biến mệnh đề được kết nối mang nhau bởi toán tử quan hệ and (∧).
Mỗi mệnh đề sở hữu dạng là 1 tuyển (disjunction), gồm các toán tử quan hệ or (∨)
trên các biến mệnh đề (literal).
Ví dụ : Nếu ta sở hữu 6 biến mệnh đề a, b, c, d, e và f, thì biểu thức sau đây là 1 CNF:
Thỏa mãn CNF với nghĩa rằng chúng ta bắt buộc tìm ra một phép gán true hoặc false
(1 hoặc 0) cho mỗi biến mệnh đề a, b, c, d, e, f sao cho biểu thức CNF có giá trị là TRUE.
Một phương pháp trình diễn trùng hợp cho lời giải của bài toán này là một dãy sáu
bit, mỗi bit theo đồ vật tự a, b, c, d, e, f trình diễn true (1) hoặc false (0) cho mỗi
biến mệnh đề. Như vậy cái bit:
1 0 1 0 một 0 cho biết a, c, và e là true và b, d, và f là false, và do đấy lúc thay
những giá trị này vào biểu thức (1-3), thì cho giá trị false.
Chúng ta muốn rằng những toán tử di truyền sinh ra những thế hệ lời giải sao cho
biểu thức CNF mang trị true, vì thế mỗi toán tử buộc phải sinh ra 1 dòng 6-bit của
phép gán true cho biểu thức. Cách biểu diễn lời giải dưới dạng 1 dòng các bit như
trên sở hữu lại cho ta vô cùng 1 điều vô cùng thuận tiện là bất kỳ toán tử di truyền
nào (lai ghép, đột biến, đảo ngược, hay trao đổi) đều tạo ra 1 chiếc bit mới là một
lời giải khả dĩ hợp lệ.
Việc tậu lựa một hàm thích ứng cho quần thể những chuỗi bit này không bắt buộc
hoàn toàn dễ dàng. Thoạt nhìn chuỗi bit, ta khó có thể xác định 1 hàm thích ứng để
đánh giá được chất lượng của nó như thế nào, tức thị khó đoán được độ rẻ của nó so
với đáp án đúng. Đáp án đúng ở đây chính là chuỗi bit sao cho biểu thức CNF với giá trị true.
Tuy nhiên sở hữu 1 số bí quyết khác. Nếu ta để ý đến biểu thức CNF (1-3), thì ta
thấy rằng nó được tạo thành từ hội của 5 mệnh đề. Do ấy chúng ta với thể thiết lập
một hệ phân hạng cho phép chúng ta gần hạng những lời giải (mẫu bit) tiềm năng
trong khoảng giá trị từ 0 đến 5, tùy thuộc vào căn số đề mà loại đấy thỏa mãn. Do
ấy mẫu: 1 một 0 0 1 0 sở hữu độ thích nghi là 1
0 1 0 0 một 0 với độ thích nghi là 2
0 1 0 0 1 1 với độ thích ứng là 3
1 0 một 0 một một mang độ thích ứng là 5, và nó chính là 1 lời giải. lOMoAR cPSD| 58707906
Bài toán người đi bán hàng TSP
- Bài toán người bán hàng (traveling salesperson problem – TSP) là một bài
toán cổ điển đối mang AI và khoa học máy tính
- Phát biểu của bài toán TSP: Một người bán hàng có nhiệm vụ lép thăm N
thành thị như là 1 phần của lịch trình bán hàng. Đường đi giữa mỗi cặp thị
thành với 1 chi phí (ví dụ như độ dài đoạn đường, giá vé máy bay). Hãy tìm
ra đường đi có chi phí tốt nhất cho người bán hàng để bắt đầu lên đường tại 1
thành phố, thăm mọi các thị thành khác chỉ đúng 1 lần rồi quay lại thành thị xuất phát.
- Như chúng đã giới thiệu ở chương III, hầu hết ko gian trạng thái của nó đòi
hỏi cần phê duyệt N! trạng thái để mang thể tậu ra lời giải tối ưu, trong ấy N
là số thành thị nên đi qua. Khi N hơi to thì bài toán sẽ bị bùng nổ tổ hợp, bởi
vậy người ta đặt vấn đề là mang buộc phải thiết hay ko cho việc chạy một máy
trạm làm cho việc đắt tiền trong nhiều giờ để cho 1 lời giải thông minh hay
chỉ cần chạy 1 PC rẻ tiền trong vài phút để sở hữu được những kết quả “đủ
tốt”. Giải thuật di truyền chính là một giải pháp cho lựa chọn đồ vật hai.
- Ở bài toán này, tiêu dùng chiếc bit để trình diễn cho lời giải của bài toán không
-phải là một bí quyết hay. Chẳng hạn, ta với chín tỉnh thành cần kẹ thăm 1, 2,
…9, ta xem mỗi thành thị như một loại 4 bit 0001, 0010,… 1001.
Khi đấy 1 lời giải khả dĩ sẽ có hình thức như sau:
0001 0010 0011 0100 0101 0110 0111 1000 1001.
- Với cách trình diễn như vậy, việc ngoại hình những toán tử di truyền sẽ trở
thành rất khó khăn. Toán tử lai ghép một mực là không được, vì chuỗi mới
được tạo từ hai cha mẹ khác nhau hầu như sẽ không biểu diễn một đường đi
trong đấy ghẹ thăm mỗi tỉnh thành đúng một lần. Trong thực tế, với lai ghép,
một số đô thị có thể bị xóa bỏ trong khi những thị thành khác được xẹp thăm
nhiều hơn 1 lần, và do đó đấy ko buộc phải là một lời giải hợp lệ. Còn toán tử
đột biến thì thế nào? Giả sử bit trái nhất của tỉnh thành trang bị sáu, 0110,
được đột biến thành 1? 1110, hay là 14, thì nó không còn là một thị thành hợp lệ.
- Một phương pháp tiếp cận khác là sẽ bỏ qua trình diễn dạng loại bit và đặt cho
mỗi thành phố một tên theo bảng chữ chiếc hoặc số, thí dụ 1, 2, …9; xem
đường đi qua những thành thị là 1 sự sắp vật dụng tự của chín ký số này, và
sau ấy sắm toán tử di truyền ưng ý để tạo ra những đường đi mới. Ở đây ta
thấy phép trao đổi (exchange) trùng hợp hai thị thành trong đường đi với thể
sử dụng được, còn phép toán lai ghép (crossover) thì không. Việc trao đổi các
đoạn của 1 đường đi với các đoạn khác của cộng đường đi đó, hoặc bất cứ
toán tử nào sắp xếp lại những chữ mẫu của đường đi ấy (mà không xóa bỏ,
thêm, hay nhân đôi bất cứ thành thị nào) đều có thể sử dụng được. Tuy nhiên,
những phương pháp này gây cạnh tranh cho việc đưa vào thế hệ con cháu
những thành phần “tốt hơn” của những chiếc trong những đường đi qua của
những thành thị của hai bố mẹ khác nhau. lOMoAR cPSD| 58707906
- Nhiều nhà nghiên cứu đã đưa ra các toán tử lai ghép với khả năng khắc phục
các vấn đề này, trong đó với toán tử lai ghép với đồ vật tự (order crossover)
do Davis đưa ra vào năm 1985. Lai ghép mang đồ vật tự xây dựng con cháu
bằng phương pháp chọn một dãy con các thành thị trong đường đi của một
mẫu cha mẹ. Nó cũng bảo toàn đồ vật tự khá những đô thị từ cha mẹ kia. Đầu
tiên, sắm hai điểm cắt, diễn tả bởi dấu “|”, điểm cắt này được chen vào 1 cách
khi không vào cộng một vị trí của mỗi cái cha mẹ.
- Những điểm cắt này là ngẫu nhiên, nhưng một lúc được chọn, thì những vị trí
như nhau sẽ được dùng cho cả hai cha mẹ. Ví dụ, sở hữu hai cái cho má p1 và
p2, với những điểm cắt sau thành thị vật dụng ba và vật dụng bảy:
p1 = (1 9 2 | 4 6 5 7 | 8 3) p2 = (4 5 9 | 1 8 7 6 | 2 3)
Hai chiếc con c1 và c2 sẽ được sinh ra theo bí quyết sau. Đầu tiên, các đoạn
giữa hai điểm cắt sẽ được chép vào những chiếc con:
c1 = (x x x | 4 6 5 7 | x x) c2 = (x x x | 1 8 7 6 | x x)
- Bước kế tiếp là khởi đầu từ điểm cắt đồ vật hai của một trong hai mẫu cha mẹ,
giả dụ ta đang muốn hoàn tất mẫu c1, thì ta sẽ khởi đầu từ điểm cắt trang bị
hai của dòng p2, ta chép các đô thị từ điểm cắt này theo vật dụng tự vào các
chỗ còn trống của c1, bỏ qua những thành phố mà c1 đã mang (các ký số được
in đậm và nghiêng trong lược đồ bên dưới). Khi tới cuối cái p2, thì quay lại
đầu loại p2 tiếp tục chép sang c1 cho tới khi c1 đủ.
- Với giải thuật lai ghép này, những đường đi của thế hệ con sẽ được bảo đảm
là những đường đi hợp lệ, đi qua mỗi tỉnh thành một lần duy nhất.
Tóm lại, trong lai ghép trang bị tự, những mảnh của 1 đường đi được truyền
từ 1 cha mẹ, p1, sang một con, c1, trong khi gần xếp của những đô thị còn lại
của con c1 được thừa kế từ ba má kia, p2. Điều này ủng hộ cho trực quan hiển
nhiên là thiết bị tự của các thành phố đóng vai trò quan yếu trong việc tạo ra
đường đi có mức giá phải chăng nhất, và do vậy việc truyền lại những đoạn
thông tin sở hữu vật dụng tự này từ những bố mẹ với độ thích ứng cao sang
con chiếc là 1 điều vô cùng quan trọng.
- Ngoài toán tử lai ghép vật dụng tự trên, còn sở hữu vô cùng đa dạng toán tử
lai ghép và đột biến khác được đưa ra để giải quyết bài toán này. Bảng 9.5 liệt
kê các toán tử lai ghép,
Danh sách những toán tử đột biến cho bài toán TSP.
Đánh giá giải thuật
- Các thí dụ vừa nêu trên làm cho vượt trội các vấn đề có tính duy nhất của thuật
toán di truyền về biểu diễn tri thức, tậu toán tử di truyền, và ngoại hình hàm
thích nghi. Biểu diễn được tậu phải tương trợ cho những toán tử di truyền.
Một điểm dáng để ý nữa là những toán tử di truyền phải được kiểu dáng sao lOMoAR cPSD| 58707906
cho bảo lưu được những mảnh thông tin có ý nghĩa trong lời giải tiềm năng từ
thế hệ này sang những thế hệ tiếp theo.
- Một sức mạnh quan yếu của thuật toán di truyền là bản chất đồng thời trong
tìm kiếm của nó. Các thuật toán này thực hành 1 dạng mạnh của leo núi (hill
climbing) trong đấy duy trì phổ biến lời giải (trong quần thể những lời giải),
chiếc bỏ những lời giải ko với triển vọng, và tăng chất lượng của những lời
giải tốt. Hình 9.19 phỏng theo Holland (1986), cho thấy nhiều lời giải tụ họp
về các điểm hợp lý trong không gian tậu kiếm.
- Trong hình này, trục hoành trình diễn các điểm với thể có trong ko gian lời
giải, trong khi trục tung phản ảnh chất lượng của các lời giải đó. Các điểm
chấm nằm trên cung là những thành viên của quần diễn đạt tại. Khởi đầu, các
lời giải được rải trong không gian những lời giải sở hữu thể có. Sau 1 vài thế
hệ, chúng có thiên hướng cụm lại kế bên các vùng có chất lượng lời giải cao hơn.
Các thuật toán di truyền được xem là leo núi song song
- (theo Holland 1986) Tuy nhiên, với sức mạnh như vậy, giải thuật genetic cũng
không thể áp dụng cho toàn bộ các bài toán sở hữu thể có. Vì như ta thấy qua
hai ví dụ trên, lời giải của bài toán buộc phải được trình diễn dưới một dạng
mẫu phù hợp cho các toán tử di truyền hoạt động. Trong thực tế mang phổ
biến bài toán ko thể khiến được điều này. Vì vậy, khi nghiên cứu về giải thuật
này, mang siêu rộng rãi câu hỏi đã được đưa ra nhằm hiểu rõ hơn nữa về thực
chất hoạt động của nó: •
Liệu chúng ta sở hữu thể đưa ra những đặc điểm về những loại bài toán
màgiải thuật di truyền (GA) với thể thực hành tốt • Các chiếc bài toán nào thì ko ưa thích với GA. •
Dựa vào đâu để ta với thể nói là GA thực hành phải chăng hay ko thấp
đối mang 1 loại bài toán nào đó? •
Liệu sở hữu những qui luật nào thể hiện hành vi của GA ở mức vĩ mô?
Hay cụ thể hơn, là liệu với bất kỳ sự phán đoán nào về sự đổi thay của độ
thích ứng của những nhóm con trong quần thể theo thời gian? •
Có phương pháp nào để diễn tả những hiệu ứng khác nhau của các toán
tử di truyền như lai ghép, đột biến, đảo ngược, v.v… •
Trong các trường hợp nào (bài toán nào, toán tử di truyền nào) thì GA
sẽ thực hiện thấp hơn những phương pháp nghiên cứu của TTNT truyền
thống. Những câu hỏi này (và còn rộng rãi hơn nữa) vẫn đã và đang được
những nhà kỹ thuật như Holland, Mitchell, Golderg,… nghiên cứu. III. Ứng dụng python lOMoAR cPSD| 58707906
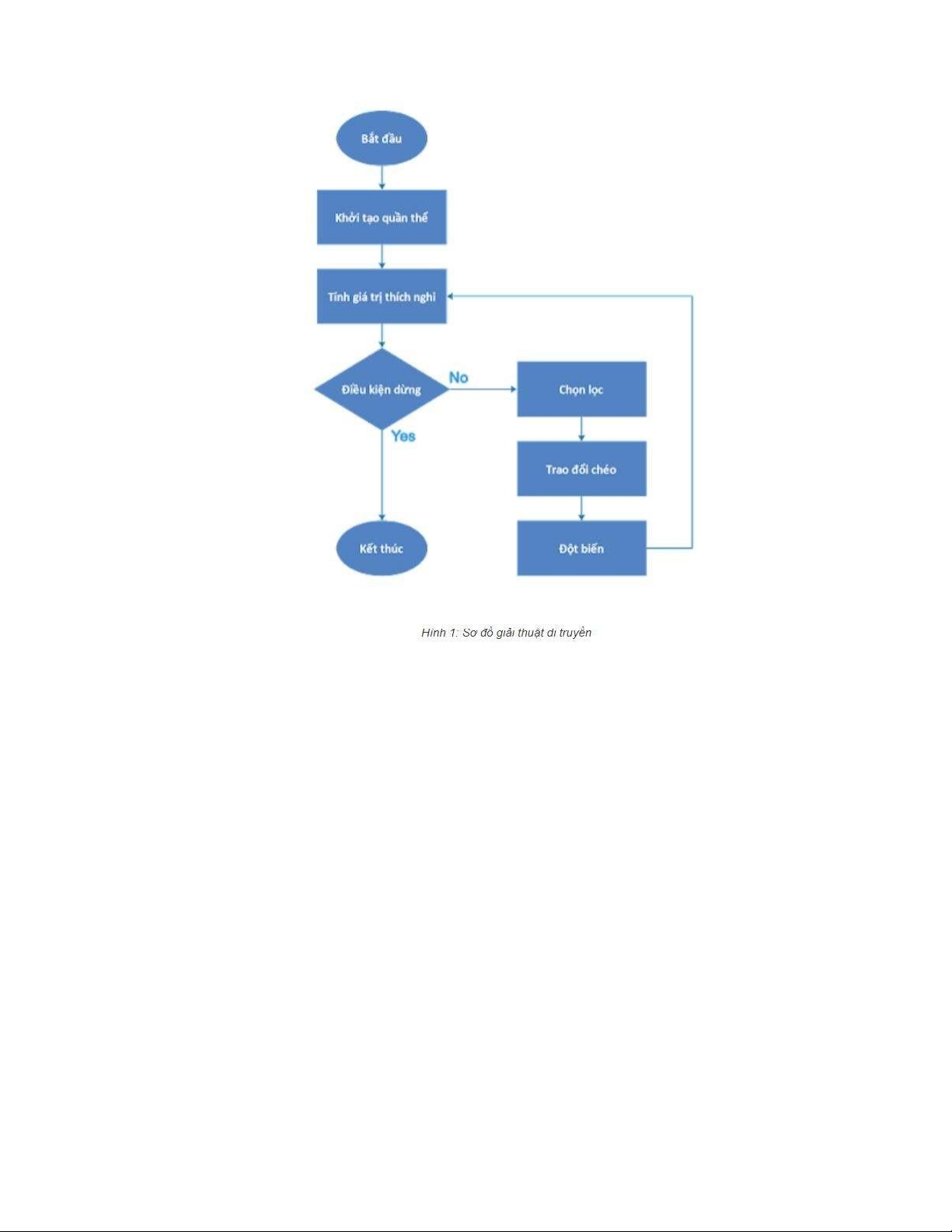
1. Sơ đồ thuật toán
Giải thuật sẽ được thực hiện qua các bước sau: •
Khởi tạo quần thể: Sinh ra ngẫu nhiên một quần thể gồm n cá thể (trong đó
n là lời giải cho bài toán). •
Tính giá trị thích nghi: Ước lượng độ thích nghi của mỗi cá thể. •
Điều kiện dừng: Kiểm tra điều kiện để kết thúc giải thuật. •
Chọn lọc: Chọn hai cá thể bố mẹ từ quần thể cũ theo độ thích nghi của chúng
(cá thể có độ thích nghi càng cao thì càng có nhiều khả năng được chọn). •
Trao đổi chéo: Với một xác suất được chọn, trao đổi chéo hai cá thể bố mẹ
để tạo ra một cá thể mới. •
Đột biến: Với một xác suất đột biến được chọn, biến đổi cá thể mới. •
Chọn kết quá: Nếu thỏa mãn điều kiện dừng thì giải thuật kết thúc và chọn
được lời giải tốt nhất trong quần thể hiện tại.
Ta có thể thấy rằng, khi Điều kiện dừng chưa được thỏa mán, quần thể mới sẽ liên
tục được tạo ra bằng cách lặp lại 3 bước Chọn lọc, Trao đổi chéo và Đột biến.
GAs có 2 điều kiện dừng cơ bản: lOMoAR cPSD| 58707906
1. Dựa trên cấu trúc nhiễm sắc thể, kiểm soát số gene được hội tụ, nếu số gene
được hội tụ tại một điểm hoặc vượt quá điểm đó thì giải thuật kết thúc.
2. Dựa trên ý nghĩa đặc biệt của nhiễm sắc thể, đo sự thay đổi của giải thuật sau
mỗi thế hệ, nếu thay đổi này nhỏ hơn một hằng số xác định thì giải thuật kết thúc.
3. Bài toán: Guessing Password - Đoán mật khẩu
Nào chúng ta bắt đầu ứng dụng giải thuật di truyền vào giải quyết bài toán đoán mật khẩu.
Về bài toán, sử dụng những ký tự trong bảng chữ cái để tái tạo lại mật khẩu. Cụ thể,
ở bài này chúng ta sẽ bắt đầu với những ký tự: a-z, A-Z, !. để tái tạo nên mật khẩu: "Hello World!".
Các bước giải bài toán: •
Khởi tạo quần thể: Sinh ra ngẫu nhiên một đoạn dài 11 ký tự (dài bằng với mục tiêu "Hello World". •
Tính giá trị thích nghi: Đếm số ký tự trùng giữa đoạn tạo ra và "Hello World". •
Điều kiện dừng: Kiểm tra xem số ký tự trùng bằng 11 hay không. •
Chọn lọc: Chọn hai cá thể bố mẹ từ quần thể cũ theo độ thích nghi của chúng
(cá thể có độ thích nghi càng cao thì càng có nhiều khả năng được chọn). •
Trao đổi chéo (Không thực hiện ở bài toán này): Với một xác suất được
chọn, trao đổi chéo hai cá thể bố mẹ để tạo ra một cá thể mới. •
Đột biến: Với một xác suất đột biến được chọn, biến đổi cá thể mới. Chọn
kết quá: Khi số ký tự trùng bằng 11 thì dừng giải thuật. Chromosomes và Gene
Trong sinh học, nói một cách khái quát, trong một Chromosomes (nhiễm sắc thể) sẽ
có thể chứa rất nhiều loại gene khác nhau.
Ở bài toán của chúng ta, tất cả những trình tự đoạn 11 ký tự ( độ dài bằng với "Hello
World") được gọi là Chromosomes. Và mỗi loại ký tự sẽ đại diện cho 1 loại Gene khác nhau. geneSet = "
abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ" target = "Hello World"
Đầu tiên chúng ta khai báo biến geneSet chứa các ký tự trong bảng chữ cái, mỗi ký
tự đại diện cho một loại Gene. Cù ng với đó, khai báo biến target là đoạn ký tự mục tiêu "Hello World". lOMoAR cPSD| 58707906
Bước 1: Khởi tạo quần thể import random
def initialize_chromosomes(length): chromosomes = [] while
len(chromosomes) < length: sampleSize = min(length - len(chromosomes), len(geneSet))
chromosomes.extend(random.sample(geneSet, sampleSize))
return ''.join(chromosomes)
Sử dụng random.sample để tạo ngẫu nhiên từ geneSet theo độ dài cho trước.
Chúng ta có thể có test bằng initialize_chromosomes(11). Kết quả sẽ có dạng: 'yTtumWSgfkM'
Chú ý: Vòng While sinh ra nhằm xử lý vấn đề nếu độ dài của Chromosomes dài hơn
số lượng loại Gene ban đầu
Bước 2: Tính giá trị thích nghi
Chúng ta thấy rằng, Chromosomes có khả năng là những trường hợp như: • Sekmo xosmd • Seklo Wocle • Fello Wosld • Gello World • Hello World
Có thể nhận ra ngay đoạn cuối cùng là đoạn chính xác. Nhưng làm sao chúng ta có
thể "đo" được độ tối ưu của Chromosomes này?
Hàm lỗi (error function/ cost function/loss function) là một hàm số giúp đo độ tối
ưu của một Chromosome. Ở hàm này, chúng ta đang hướng tới giá trị càng nhỏ càng tốt.
Với bài toán Đoán mật khẩu, để đo độ tối ưu, chúng ta đếm số kí tự sai khác trên
cùng vị trí giữa Chromosome và đoạn kí tự mục tiêu "Hello World". Vì vậy, hàm lỗi
ở đây sẽ tối ưu ở số kí tự sai khác bằng 0.
Dùng quy luật trên để tính sai khác cho các trường hợp Chromosomes trên: • Sekmo xosmd(6) • Seklo Wocle(4) • Fello Wosld(2) • Gello World(1) • Hello World(0) lOMoAR cPSD| 58707906
def error_function(chromosome):
return len(target) - sum(1 for expected, actual \
in zip(target, chromosome) \ if expected == actual)
Hàm error_function sẽ tính số ký tự sai khác ở cùng một vị trí giữa Chromosome và
"Hello World". Có thể test hàm trên như sau: error_function("Hello World") sẽ cho kết quả bằng 0.
Bước 3: Điều kiện điểm dừng
Kiểm tra điều kiện điểm dừng là error_function có bằng 0 hay không. Bước 4: Tiến hóa
Trong bước này, chúng ta sẽ gộp chung cả 3 kỹ thuật: chọn lọc, trao đổi chéo và
đột biến. Mục tiêu của bước này là tạo ra thế hệ mới tối ưu hơn thế hệ cũ. Độ tối
ưu sẽ được đo theo hàm lỗi. Chúng ta có thể mường tượng ra rằng, đây là một vòng
lặp, mỗi vòng lặp sẽ thực hiện 3 kỹ thuật trên, sau đó check điều kiện dừng. Nếu
không đáp ứng được thì vòng lặp sẽ tiếp tục cho đến khi đáp ứng được thì thôi.
Ở bài toán này, chúng ta sẽ chỉ sử dụng chọn lọc và đột biến. Phần về trao đổi chéo
tôi sẽ có một bài riêng vì nó có chút phức tạp hơn.
def mutate(parent): index = random.randrange(0, len(parent)) childGenes = list(parent)
newGene, alternate = random.sample(geneSet, 2)
childGenes[index] = alternate \ if
newGene == childGenes[index] \
else newGene return ''.join(childGenes)
index sẽ là một số được chọn ngẫu nhiên tức là đột biến sẽ xảy ra một cách ngẫu
nhiên trên Chromosome. newGene và alternate cũng sẽ được ngẫu nhiên tạo ra từ geneSet.
Vì sao lại phải tạo ra tận 2 đột biến? Câu trả lời là đột biến có thể vô nghĩa tại 1 điểm
nên cần 1 đột biến khác thay thế. Hàm hỗ trợ
Xây dựng hàm display giúp hiển thị sự thay đổi qua từng thế hệ và thời gian chạy tương ứng lOMoAR cPSD| 58707906 import datetime
def display(guess): timeDiff = datetime.datetime.now() - startTime fitness = error_function(guess)
print("{0}\t{1}\t{2}".format(guess, fitness, str(timeDiff))) Main
Sau đây sẽ là phần chạy main cho giải thuật GAs: random.seed ( 1 )
startTime = datetime.datetime.now ()
bestParent = initialize_chromosomes ( len ( target ))
bestFitness = error_function ( bestParent ) display ( bestParent ) while True:
child = mutate ( bestParent )
childFitness = error_function ( child )
if bestFitness <= childFitness : continue display ( child )
if childFitness == 0 : break hJYVdpgEBDO 11 0:00:00 HJYVdpgEBDO 10 0:00:00 HJYVdpgEBDd 9 0:00:00.001003
bestFitness = childFitness bestParent = child HJYVopgEBDd 8 0:00:00.001003 HJYVopgErDd 7 0:00:00.004010 HJYVopgErld 6 0:00:00.005012 HJlVopgErld 5 0:00:00.008021 HJlVo gErld 4 0:00:00.008021 HelVo gErld 3 0:00:00.009036 lOMoAR cPSD| 58707906
HelVo gorld 2 0:00:00.010026 Hello gorld 1 0:00:00.017045 Hello World 0 0:00:00.020052
Khởi tạo quần thể với Chromosome đầu tiên bestParent . Tính hàm lỗi cho
Chromosome này cho chúng ta kết quả là 11,
cho thấy chưa có vị trí nào
giữa Chromosome khởi tạo và "Hello World" trùng nhau.
Chúng ta sẽ thấy rằng, việc chọn lọc đã diễn ra ở điều kiện vòng lặp, tức là cứ mỗi
khi hàm lỗi giảm là sẽ giữ lại bestParent t hay thế cho Chromosome cũ kém tối ưu hơn. IV. KẾT LUẬN
Chúng ta đã cùng nhau xây dựng một giải thuật di truyền và hiểu các bước diễn ra bên trong giải thuật.
Giải thuật trên gần như là dạng đơn giản nhất. Nếu có bài tiếp theo, tôi sẽ giới thiệu
thêm về một số vấn đề bên trong và xử lý những bài toán phổ biến và có đôi chút phức tạp hơn.
Xin cảm ơn vì đã đọc đến đây :D. Nguồn tham khảo:
1. https://github.com/handcraftsman/GeneticAlgorithmsWithPython