Bài tập lớn đề tài Mã Đi Tuần | Môn Nhập môn về trí tuệ nhân tạo - Đại học Hải Phòng

lOMoAR cPSD| 58707906
TRƯỜNG ĐẠI HỌC HẢI PHÒNG
Khoa Công nghệ thông tin
BÀI TẬP LỚN TRÍ TUỆ NHÂN TẠO
Đề tài: Mã đi tuần
SVTH : Nguyễn Vũ Xuân Kiên Trần Việt Dương Nguyễn Huy Toàn
GVHD : Đào Việt Anh Năm 2024 lOMoAR cPSD| 58707906 MỤC LỤC Giới thiệu
I. Cài đặt môi trường code Game với C++, IDE visual studio (2012 - 2019)…….
II. Tổng quan trò chơi……………………………………………………………..
1. Đối với Quân Xe…………………………………………………………………
2. Đối với quân tượng……………………………………………………………….
3. Đối với quân mã………………………………………………………………….
4 Đối với vua……………………………………………………………………….
5 Đối với Tốt………………………………………………………………………
6 Với Hậu…………………………………………………………………………… 7 Hàm tìm với tham số n
:…………………………………………………………..III. Các hàm Đánh cờ
và Undo……………………………………………………..
IV: cây trò chơi, chiến lược Minimax, cắt tỉa Alpha-Beta…………………………
1 Lý Thuyết…………………………………………………………………………
2 Ứng dụng trong cờ vua:…………………………………………………………... Giới thiệu
Trong cờ vua có các quân cờ chính và cách đi như sau :
· Xe di chuyển theo các đường thẳng dọc theo cột hay hàng tới ô còn trống mà
không có quân nào cản trên đường đi hay tới ô bị quân đối phương chiếm giữ (ăn
quân) nhưng không thể vượt qua quân đang đứng ở ô đó. · Tượng di chuyển theo
đường chéo tới ô có cùng màu với nguyên lý tương tự như Xe tới ô còn trống hay
ô bị quân đối phương chiếm giữ (ăn quân).
· Hậu có nước đi là tổ hợp đơn giản của chuyển động của Xe và Tượng. Trong một
nước đi nó có thể di chuyển theo đường chéo hoặc đường thẳng dọc theo cột hay
hàng, với nguyên lý đi và ăn quân giống như Tượng và Xe.
· Mã có thể di chuyển tới ô còn trống hay ô bị quân đối phương chiếm giữ (ăn
quân) theo dạng hình chữ L (hình chữ nhật 3×2 hay 2×3) lOMoAR cPSD| 58707906
· Tốt có thể di chuyển thẳng về phía trước chỉ một ô một lần tới ô còn trống (đi mà
không ăn quân), nhưng khi di chuyển quân để ăn quân đối phương thì đi chéo.
Nó có thể di chuyển 1 hoặc 2 ô nếu nó đi từ vị trí xuất phát ban đầu tới ô chưa bị
chiếm giữ, nhưng không thể nhảy qua một quân khác để tới ô đó.
Tốt còn một đặc điểm nữa là khi nó di chuyển đến hàng cuối cùng thì người chơi
có quyền phong cấp cho nó thành bất kỳ quân nặng hay nhẹ nào (Hậu, Xe, Tượng,
Mã).(trong game mặc định là Hậu) · Vua là quân quan trọng nhất, nếu mất Vua thì
người chơi thua cuộc. Mỗi lần đi nó có thể ăn quân hoặc di chuyển sang các ô bao
quanh ô mà nó hiện tại đang chiếm giữ, nhưng không thể tới ô mà quân của mình đang chiếm giữ.
I.Cài đặt môi trường code Game với C++, IDE visual studio (2012 - 2019)
Sơ bộ: ngôn ngữ: visual C++ và thư viện đồ họa SFML Tham khảo:
II. Tổng quan trò chơi •
Mặc định bên người chơi là quân trắng đi trước, thao tác là click chuột vào
quân minh, hiện ra các nước đk đi rồi click vào các nước đó=> quân cờ sẽ di
chuyển đến vị trí mới •
Đã có: các chức năng di chuyển, ăn các quân, phong hậu cho tốt •
Hạn chế: chưa có chức năng nhập thành,chiếu bí, hàm đánh giá đơn giản,
thiếu chiến thuật, mức độ sơ cấp
Lớp quản lý toàn bộ trò chơi: class GameManager { public:
QuanCo f[33]; //mang lưu các quân cờ
Vector2f positiveMove[32];//vi tri cac nuoc co the di chuyen
int positiveCount;// so nuoc co the di chuyen
stack posS;//lưu vị trí các nước đã đi
stack nS;//lưu index của các quân đã đi ,tương ứng với vị trí bên trên
void move(int n,Vector2f oldPos,Vector2f newPos);//đánh cờ
void Undo();//quay lại nước trước
void Create();// khởi tạo mảng quân cờ và các giá trị cần thiết
void Play(); // mọi thao tác trong game xử lý tại đây
void PositiveXe(int n,int x,int y,int grid[9][9]);//tim cac nuoc co the di Xe
void PositiveTuong(int n,int x,int y,int grid[9][9]); void PositiveMa(int lOMoAR cPSD| 58707906
n,int x,int y,int grid[9][9]); void PositiveVua(int n,int x,int y,int
grid[9][9]); void PositiveTot(int n,int x,int y,int grid[9][9]);
void IncreasePositive(int i,int j);//tang thêm 1 nước có thể đi ở vị tri i,j
void PositiveMoving(int n);//tim cac nuoc co the di ung voi index n //AI
int CostMove();//tính điểm nước đi( hàm đánh giá) //int Minimax(int
depth,bool luot);// Chien luoc Minimax int Alpha_Beta(int depth,bool
luot,int alpha,int beta);//cat tia alpha beta Vector2f getNextMove(bool
luot);// tra ve nuoc di tot nhat theo chien luoc }; int main() { GameManager gm; gm.Play(); }
Vẽ bàn cờ, hiển thị các quân •
bàn cờ: mỗi ô cờ có kích thước size=56, viền xung quanh :28 tổng cạnh bàn
cờ= 28+56*8+28=504. Sử dụng vectơ offset=(28,28) điều chỉnh khi chọn, di chuyển •
sử dụng mảng Quan cờ: f[32]: lưu trữ 32 quân trong bàn cờ.. mỗi quân có 1
hình ảnh Sprite(kích thước size*size) ,1 index: trị số sử dụng, 1 cost: giá trị
sử dụng trong hàm đánh giá lOMoAR cPSD| 58707906 •
bảng giá trị index tương ứng trên bàn cờ lúc xuất phat: mặc định: f[0],f[7] là
xe đen ứng với index=-1 ,f[1],f[6] là mã đen(index=-2), tương tự như vậy với các quân còn lại
void GameManager::Create()//gan gia tri can thiet vao danh sach Quan co {
positiveCount=0;//so nuoc co the di ban dau duong nhien =0(chua chon gi ca)
int k=0; for(int i=0;i<8;i++){ for(int j=0;j<8;j++) {
int n = board[i][j]; if (!n) continue;
int x = abs(n)-1; int y = n>0?1:0;
f[k].index=n; f[k].s.setTextureRect(
IntRect(size*x,size*y,size,size) );
f[k].s.setPosition(size*j+offset.x,size*i+offset.y); //cost int v=0,g; g=abs(f[k].index); if(g==1) v=50; else if(g==2|| g==3) v=30; else if(g==4) v=90; else if(g==5) v=900; else if(g==6) v=10; f[k].cost=f[k].index/g*v; k++; } } }
Xây dựng các hàm tính các nước được phép đi •
Vì hàm này tìm các ô có thể đi nên để kiểm tra dễ dàng ta sử dụng 1 mảng ô
cờ grid[8][8] lưu trữ index của bàn cờ (ô nào ko có quân grid=0,, có grid= index của quân cờ) •
Ví dụ: nếu grid[x][y] => vị trí tương ứng quân cờ:
Vector2f(xsize+offsetX,ysize+ offsetY)
Hàm tăng số vị trí các nước có thể đi: lOMoAR cPSD| 58707906
void GameManager::IncreasePositive(int i,int j) {
positiveMove[positiveCount]=Vector2f(i*size,j*size)+offset; positiveCount++; }
1. Đối với Quân Xe
xuất phát từ vị trí ô cờ ứng với quân xe đang chọn, duyệt theo 4 hướng
ngang,dọc :nếu ko gặp vật cản(index=0) đánh dấu ô có thể đi, nếu gặp vật
cản(index !=0) thì dừng lại, nếu vật cản đó là quân đối phương, đánh dấu ô
đó có thể đi ð Các nước đi phải nằm trong phạm vi bàn cờ
void GameManager::PositiveXe(int x,int y,int grid[9][9])//tu vi tri (x,y) xet ra { for(int i=x+1;i<8;i++) { if(grid[i][y]!=0) {
if(grid[i][y]*grid[x][y]<0) IncreasePositive(i,y); break; } IncreasePositive(i,y); } for(int i=x-1;i>=0;i--) { if(grid[i][y]!=0) {
if(grid[i][y]*grid[x][y]<0) IncreasePositive(i,y); break; } IncreasePositive(i,y); } for(int j=y+1;j<8;j++) { if(grid[x][j]!=0) {
if(grid[x][j]*grid[x][y]<0) IncreasePositive(x,j); break; } IncreasePositive(x,j); } for(int j=y-1;j>=0;j--) { if(grid[x][j]!=0) { lOMoAR cPSD| 58707906
if(grid[x][j]*grid[x][y]<0) IncreasePositive(x,j); break; } IncreasePositive(x,j); } }
2. Đối với quân tượng
Tương tự xe nhưng theo 4 hướng chéo: lOMoAR cPSD| 58707906
void GameManager::PositiveTuong(int x,int y,int grid[9][9])//tu vi tri (x,y) xet ra
for(int i=x+1,j=y+1;(i<8&&j<8);i++,j++) { if(grid[i][j]!=0) {
if(grid[i][j]*grid[x][y]<0) IncreasePositive(i,j); break; } IncreasePositive(i,j); }
for(int i=x+1,j=y-1;(i<8&&j>=0);i++,j--) { if(grid[i][j]!=0) {
if(grid[i][j]*grid[x][y]<0) IncreasePositive(i,j); break; } IncreasePositive(i,j); }
for(int i=x-1,j=y+1;(i>=0&&j<8);i--,j++) { { lOMoAR cPSD| 58707906 if(grid[i][j]!=0) {
if(grid[i][j]*grid[x][y]<0) IncreasePositive(i,j); break; } IncreasePositive(i,j); }
for(int i=x-1,j=y-1;(i>=0 && j>=0);i--,j--) { if(grid[i][j]!=0) {
if(grid[i][j]*grid[x][y]<0) IncreasePositive(i,j); break; } IncreasePositive(i,j); } }
3. Đối với quân mã
Ứng với vị trí x,y nó đang đứng có 8 vị trí nó có thể di chuyển nếu các nước
này nằm trong bàn cờ và không có quân nào hoặc quân đối thủ:
void GameManager::PositiveMa(int x,int y,int grid[9][9])//xet 8 vi tri co the di {
if((grid[x+2][y+1]==0||grid[x][y]*grid[x+2][y+1]<0) && x+2<8 && y+1<8) IncreasePositive(x+2,y+1);
if((grid[x+2][y-1]==0||grid[x][y]*grid[x+2][y-1]<0) && y-1>=0 && x+2<8) IncreasePositive(x+2,y-1);
if((grid[x-2][y+1]==0||grid[x][y]*grid[x-2][y+1]<0) && x-2>=0 && y+1<8) IncreasePositive(x-2,y+1);
if((grid[x-2][y-1]==0||grid[x][y]*grid[x-2][y-1]<0) && x-2>=0 && y-1>=0) IncreasePositive(x-2,y-1);
if((grid[x+1][y+2]==0||grid[x][y]*grid[x+1][y+2]<0) && x+1<8 && y+2<8) IncreasePositive(x+1,y+2);
if((grid[x-1][y+2]==0||grid[x][y]*grid[x-1][y+2]<0) && x-1>=0 && y+2<8) IncreasePositive(x-1,y+2);
if((grid[x+1][y-2]==0||grid[x][y]*grid[x+1][y-2]<0) && y-2>=0&& x+1<8) IncreasePositive(x+1,y-2);
if((grid[x-1][y-2]==0||grid[x][y]*grid[x-1][y-2]<0) && x-1>=0 && y-2>=0) IncreasePositive(x-1,y- 2); } lOMoAR cPSD| 58707906 4 Đối với vua
Xét 8 vị trí xung quanh nó:
void GameManager::PositiveVua(int x,int y,int grid[9][9])//xet 8 vi tri co the di {
if((grid[x+1][y]==0||grid[x][y]*grid[x+1][y]<0) && x+1<8) IncreasePositive(x+1,y);
if((grid[x-1][y]==0||grid[x][y]*grid[x-1][y]<0) && x-1>=0) IncreasePositive(x-1,y);
if((grid[x+1][y+1]==0||grid[x][y]*grid[x+1][y+1]<0) && x+1<8 && y+1<8) IncreasePositive(x+1,y+1);
if((grid[x-1][y+1]==0||grid[x][y]*grid[x-1][y+1]<0) && x-1>=0 && y+1<8) IncreasePositive(x-1,y+1);
if((grid[x][y+1]==0||grid[x][y]*grid[x][y+1]<0) && y+1<8) IncreasePositive(x,y+1);
if((grid[x-1][y-1]==0||grid[x][y]*grid[x-1][y-1]<0) && x-1>=0 && y-1>=0) IncreasePositive(x-1,y-1);
if((grid[x+1][y-1]==0||grid[x][y]*grid[x+1][y-1]<0) && y-1>=0 && x+1<8) IncreasePositive(x+1,y-1);
if((grid[x][y-1]==0||grid[x][y]*grid[x][y-1]<0) && y-1>=0) IncreasePositive(x,y-1); } 5 Đối với Tốt
• Lúc xuất phát có thể đi thẳng 2 ô với điều kiện ô đầu ko có quân nào
• ngoài ra đi thẳng 1 ô, ăn chéo 1 ô void
GameManager::PositiveTot(int x,int y,int grid[9][9]) {
int k=grid[x][y]/abs(grid[x][y]);// 1 hoac -1
if((y==1 || y==6) &&grid[x][y-k]==0 && grid[x][y-2*k]==0 && y-2*k>=0
&& y-2*k<8) IncreasePositive(x,y-2*k);
if(grid[x][y-k]==0 && y-k>=0 && y-k<8) IncreasePositive(x,y-k);
if(grid[x+1][y-k]*grid[x][y]<0 && y-k>=0 && y-k<8 && x+1<8) IncreasePositive(x+1,y-k);
if(grid[x-1][y-k]*grid[x][y]<0 && y-k>=0 && y-k<8 && x-1>=0) IncreasePositive(x-1,y-k); } lOMoAR cPSD| 58707906 6 Với Hậu
Tổ hợp đơn giản của Xe và Tượng
7 Hàm tìm với tham số n :
void GameManager::PositiveMoving(int n) {
Vector2f pos=f[n].s.getPosition()-offset; int x=pos.x/size; int y=pos.y/size;
int grid[9][9];//mang luoi(8x8) luu lai cac vi tri ban co:
Vector2i vtri; for(int i=0;i<8;i++) for(int j=0;j<8;j++)
grid[i][j]=0;// neu khong co quan co nao o O nay thi =0 for(int j=0;j<32;j++) {
vtri=Vector2i( f[j].s.getPosition()-offset);
grid[vtri.x/size][vtri.y/size]=f[j].index;// neu co = index cua quan co }
if(abs(f[n].index)==1) PositiveXe(x,y,grid);//xe else
if(abs(f[n].index)==2) PositiveMa(x,y,grid);//ma else
if(abs(f[n].index)==3) PositiveTuong(x,y,grid);//tuong else
if(abs(f[n].index)==4)//hau: hop lai cac nuoc cua ca xe va tuong { PositiveXe(x,y,grid); PositiveTuong(x,y,grid); }
else if(abs(f[n].index)==5) PositiveVua(x,y,grid);//vua
else PositiveTot(x,y,grid); //tot }
III Các hàm Đánh cờ và Undo
Để dễ dàng em chia làm 3 bước: đi có ăn( quân bị ăn biến mất) và đi có phong hậu
đi ko ăn: khi ta ăn phải di chuyển con bị ăn vào sau mh vậy lúc undo phải làm sao
void GameManager::move(int n,Vector2f oldPos,Vector2f newPos) {
posS.push(oldPos); posS.push(newPos);
nS.push(n); for(int i=0;i<32;i++){//đoạn này ko thể undo if lOMoAR cPSD| 58707906
(f[i].s.getPosition()==newPos)
f[i].s.setPosition(-100,-100); } void GameManager::Undo() { int n= nS.top(); nS.pop();
Vector2f p=posS.top(); //kiem tra xem co = (-100,-100) => day la con bi an posS.pop();
f[n].s.setPosition(posS.top()); posS.pop(); }
đi có ăn: giải pháp: thêm 1 lần di chuyển con bị ăn vào sau mh: lưu vào
stack: lúc undo ta undo liên tiếp 2 lần Câu hỏi: lúc phong hậu cho tốt,, undo
: hậu vừa phong ko quay lại làm tốt: làm sao
void GameManager::move(int n,Vector2f oldPos,Vector2f newPos) { posS.push(oldPos); posS.push(newPos); nS.push(n);
int y=int((newPos-offset).y/size);//kiem tra xem co phong hau hay khong for(int i=0;i<32;i++){
if (f[i].s.getPosition()==newPos) {
f[i].s.setPosition(-100,-100);//di chuyen con bị ăn ra khỏi mh
posS.push(newPos); posS.push(Vector2f(-100,-100)); nS.push(i); } }
f[n].s.setPosition(newPos);//di chuyen em an vao vi tri moi } void GameManager::Undo() { int n= nS.top(); nS.pop();
Vector2f p=posS.top();//kiem tra xem co = (-100,-100) => day la con bi an posS.pop();
f[n].s.setPosition(posS.top()); posS.pop();
if(p==Vector2f(-100,-100)) Undo();// luc nay moi dy chuyen con an } lOMoAR cPSD| 58707906
giải pháp: khi phong hậu cho tôt ta push vào stack nS 1 con số nào đấy, để
khi undo ta biết đk phải biến ngược lại hậu thành tốt
void GameManager::move(int n,Vector2f oldPos,Vector2f newPos) { posS.push(oldPos); posS.push(newPos); nS.push(n);
int y=int((newPos-offset).y/size);//kiem tra xem co phong hau hay khong //phong hau cho tot
if(y==0 && f[n].index==6){
nS.push(100);//de ty undo xoa phong hau di f[n].index=4; f[n].cost=90;
f[n].s.setTextureRect(IntRect( 3*size,size,size,size)); }
if(y==7 && f[n].index==-6){ nS.push(-100); f[n].index=-4; f[n].cost=- 90;
f[n].s.setTextureRect(IntRect( 3*size,0,size,size)); lOMoAR cPSD| 58707906
if(p==Vector2f(-100,-100)) Undo();// luc nay moi dy chuyen con an }
Vậy là xong phần giao diện chơi game,,xong phần này có thể tạo môi trường cho 2
người chơi với nhau chỉ cần sửa hàm Play() bên trên 1 chút
IV Phần AI: cây trò chơi, chiến lược Minimax, cắt tỉa Alpha-Beta lOMoAR cPSD| 58707906 1 Lý Thuyết •
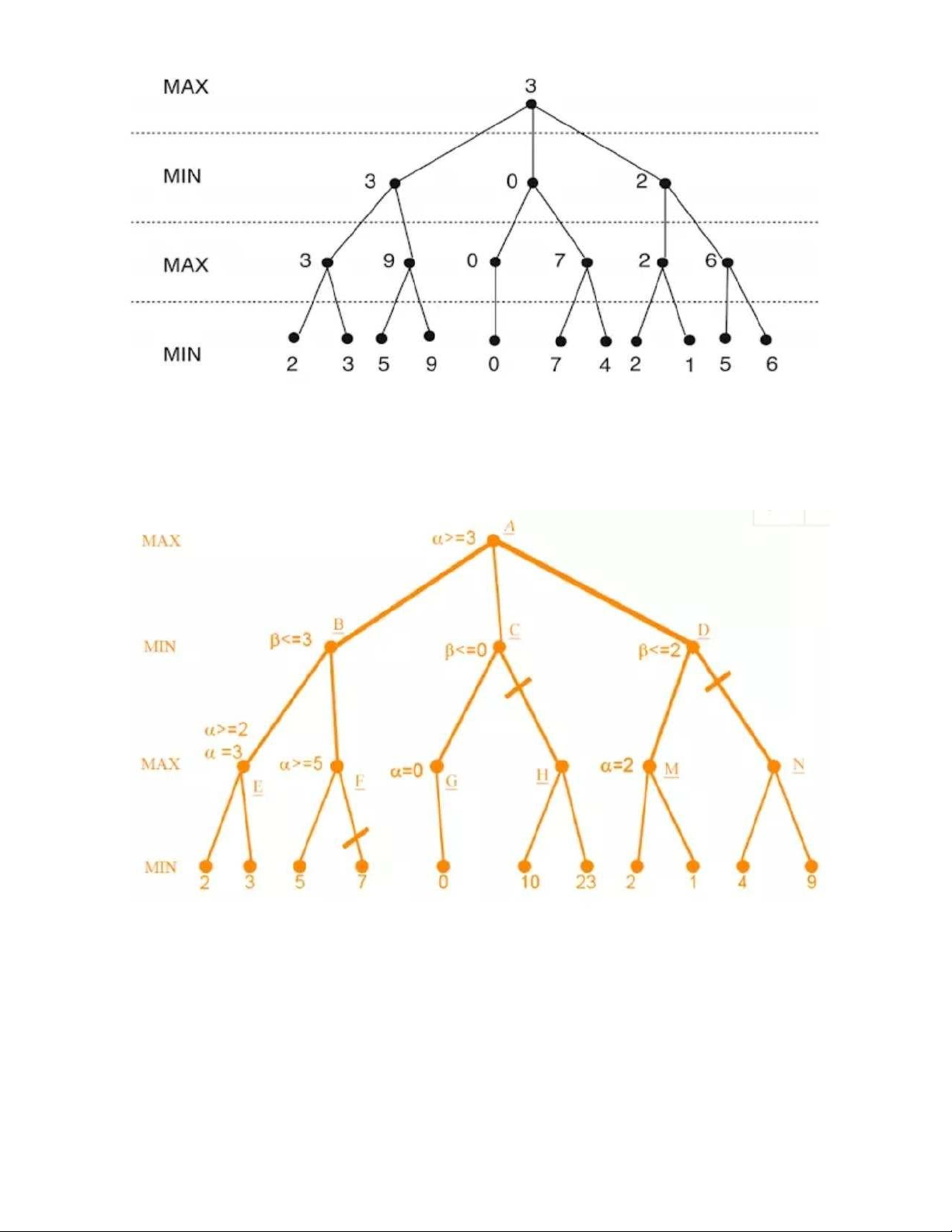
Cây trò chơi:lượt quân trắng mỗi đỉnh ứng với 1 trạng thái có thể đi của quân trắng o Chiến lược Minimax:
Lượt quân trắng : tìm trong số các nước đi có thể của nó nước đi nào là tốt nhất,,
tương tự với quân đen ð Làm sao để tính đk
Ta đi đến mức thấp nhất của cây + hàm đánh giá tính điểm sau đó xác định điểm
của các nhánh trên: với quân trắng(max trong các nước đi),đen thì ngược lại
ð Đương nhiên dùng duyệt theo chiều sâu để tìm Thực tế để làm như vậy mà đi
đến nước cuôi cùng thì máy tính không thể xử lý nôi => giải pháp: Giới hạn độ sâu
Từ a-> b-> e(hết =-3) chuyển sang f => k…. đúng theo DFS
Tầng min chọn đỉnh bé nhất trong số các đỉnh con, max ngược lại lOMoAR cPSD| 58707906 •
Cắt tỉa Alpha Beta Ở chiến thuật minimax dù đã giảm độ cao của cây nhưng
không gian vẫn quá lớn, ở phương pháp này ta cắt đi không xét đến những
nhánh không cần thiết để giảm không gian TT
Alpha = giá trị tại các nút max, Beta ………….. min
Ví dụ:đi từ A-> E: (alpha=3) lên lại B(gán tạm Beta=3(thực chất<=3) ) xét đến F(có
nhánh con =5) (alpha=5(thực chất >=5)) Lúc này (Beta<=alpha) khỏi phait xet tiếp
nut F làm gì Tương tự như vậy tại A ta cắt bơt đk tạiC và D 2 Ứng dụng trong cờ vua: lOMoAR cPSD| 58707906 •
Hàm đánh giá: đơn giản đặt giá trị cho môi quân cờ, quân nào bị an mất thì ko tính điểm nó nữa int meM Ga
anager :: CostMove () // don gian con nao bi chet thi khong tinh diem cua con da y { int s = 0 ; or
f ( int i = 0 ;i < 32 ;i ++ ) { if ( f[i s.
]. getPosition () == Vector2f ( - 100 , - 100 ))
continue ; //neu no da bi out- > ko tinh die m s += f[i].cost ; } return s ; } •
Cắt tỉa Alpha Beta: trả về giá trị điểm cho trạng thái gốc muốn xét
int GameManager::Alpha_Beta(int depth,bool luot,int alpha,int beta) { if(depth==0){ return CostMove(); }
Vector2f positiveMovetemp[32];//luu lai vi tri cac nuoc co the di
if(luot==true){ int bestMove=-10000;//gia cua bestMove
ban dau for(int j=16;j<32;j++)//cac quan cua nguoi choi {
if(f[j].s.getPosition()==Vector2f(-100,-100)) continue; PositiveMoving(j);
int coun=positiveCount;//ta khong the dung PositiveCount vi no thay
doi lien tuc khi ta de quy positiveCount=0; for (int i = 0; i < coun; i++)
positiveMovetemp[i]=positiveMove[i]; for(int i=0;i {
move(j,f[j].s.getPosition(),positiveMovetemp[i]);
bestMove=max(bestMove,Alpha_Beta(depth1,!luot,alpha,beta)); //undo Undo(); alpha=max(alpha,bestMove);
if(beta<=alpha) return bestMove; } } lOMoAR cPSD| 58707906 return bestMove; } else {
int bestMove=10000;//gia cua bestMove ban dau
for(int j=0;j<16;j++)//quan cua may {
if(f[j].s.getPosition()==Vector2f(-100,-100)) continue; PositiveMoving(j);
int coun=positiveCount;//ta khong the dung PositiveCount vi no thay
doi lien tuc khi ta de quy positiveCount=0; for (int i = 0; i < coun; i++)
positiveMovetemp[i]=positiveMove[i]; for(int i=0;i {
move(j,f[j].s.getPosition(),positiveMovetemp[i]);
bestMove=min(bestMove,Alpha_Beta(depth-1,!luot,alpha,beta)); //undo Undo(); beta=min(beta,bestMove);
if(beta<=alpha) return bestMove; } } return bestMove; } } •
hàm duyệt các nước đi của máy: sau đó dùng Alpha Beta tính điểm cho các
nước đó, chọn ra nước tốt nhất để đi:
Vector2f GameManager::getNextMove(bool luot) {
Vector2f oldPos,newPos,oldPostemp,newPostemp;// ta can tim vi tri co
minimax nho nhat de ung voi may( quan den) int
minimaxtemp=10000,minimax=10000; int count1,n;
Vector2f positiveMovetemp[32]; lOMoAR cPSD| 58707906 for(int i=0;i<16;i++) {
if(f[i].s.getPosition()==Vector2f(-100,-100)) continue; ////// PositiveMoving(i);
count1=positiveCount;//khong the dung PositiveCount vi no thay doi lien tuc khi ta de quy positiveCount=0; ///set///
for (int k = 0; k < count1; k++) positiveMovetemp[k]=positiveMove[k];
//set oldPos va newPos tam thoi
oldPostemp=f[i].s.getPosition();
//newPostemp=positiveMove[0]; for(int j=0;j {
move(i,oldPostemp,positiveMovetemp[j]); int alpha=-9999,beta=9999;
int temp=Alpha_Beta(3,!luot,alpha,beta); if(minimaxtemp>temp){
newPostemp=positiveMovetemp[j]; minimaxtemp=temp; } Undo(); lOMoAR cPSD| 58707906 } if(minimax>minimaxtemp){ minimax=minimaxtemp; oldPos=oldPostemp; newPos=newPostemp; n=i; } } //lay cac thong tin nuoc di
posS.push(oldPos);//luu tam o trong stack ty ra ngoai xoa di nS.push(n); return newPos; } •
Trong hàm main phần xử lý computerMove: else //computer moving {
newPos= getNextMove(LuotChoi);
int c=nS.top(); nS.pop();//lay dk thong tin roi xoa di
oldPos=posS.top(); posS.pop();//vi ham move tu nhet trong stack roi move(c,oldPos,newPos); LuotChoi=!LuotChoi; //reset click=0; } Full Code: #include #include #include #include