Bài tập lớn môn Đại số tuyến tính đề tài "Vẽ quỹ đạo của vật theo phương trình chuyển động"

lOMoARcPSD| 36782889 Bài tập 5:
Vẽ quỹ đạo của vật theo phương trình chuyển động 1. Yêu cầu
Sử dụng Matlab để giải bài toán sau:
“Một khí cầu bay lên từ mặt đất với vận tốc không đổi 0. Gió truyền cho khí cầu thành phần
vận tốc theo phương ngang = , y là độ cao. Cho trước các giá trị 0, a.
a. Xác định phương trình chuyển động của vật
b. Xác định phương trình quỹ đạo của vật.
c. Vẽ quỹ đạo của vật trong khoảng thời gian từ t=0 đến t=5s. 2 . Điều kiện
1) Sinh viên cần có kiến thức về lập trình cơ bản trong MATLAB.
2) Tìm hiểu các lệnh Matlab liên quan symbolic và đồ họa. 3 . Nhiệm vụ
Xây dựng chương trình Matlab:
1) Nhập các giá trị ban dầu (những đại lượng đề cho).
2) Thiết lập các phương trình tương ứng. Sử dụng các lệnh symbolic để giải hệ phương trình. 3) Vẽ hình.
Chú ý: Sinh viên có thể dùng các cách tiếp cận khác
TÓM TẮT BÀI BÁO CÁO
Báo cáo tìm hiểu về chuyên sâu về chủ đề chuyển động của vật bao gồm những khái niệm cơ
bản, khái niệm chuyên sâu hơn cũng như các công thức ứng với từng đề mục trong bài. Ngoài
ra, báo cáo còn đưa ra những tìm hiểu sơ bộ về ứng dụng công cụ Matlab để hỗ trợ việc tính
toán, minh hoạ cho chủ đề chuyển động. Hơn thế nữa, những câu lệnh và chức năng cụ thể
của từng thuật toán được giải thích cặn kẽ để ta hiểu hơn về mối liên hệ giữa cơ sở lý thuyết
và ứng dụng trong việc lập trình. 1 lOMoARcPSD| 36782889
LỜI CẢM ƠN
Chúng em xin gửi lời cảm ơn chân thành đến cô Lê Như Ngọc, Trường ĐH Bách Khoa
TPHCM đã tạo điều kiện thuận lợi cho chúng em học tập và hoàn thành đề tài BTL vật lý. Đặc
biệt, chúng em xin bày tỏ lòng biết ơn sâu sắc đến cô đã truyền đạt kiến thức và hướng dẫn
chúng em trong quá trình làm bài.
Em đã cố gắng vận dụng những kiến thức đã học được trong học kỳ qua để hoàn thành bài
tiểu luận. Nhưng do kiến thức hạn chế và không có nhiều kinh nghiệm về Matlab nên khó
tránh khỏi những thiếu sót trong quá trình nghiên cứu và trình bày. Rất kính mong sự góp ý
của quý thầy cô để bài tiểu luận của em được hoàn thiện hơn.
Một lần nữa, em xin trân trọng cảm ơn sự quan tâm giúp đỡ của cô Ngọc đã giúp đỡ em
trong quá trình thực hiện bài tiểu luận này. Xin trân trọng cảm ơn! MỤC LỤC
CHƯƠNG 1. MỞ ĐẦU ...................................................................................................... . 5 1.1
Đề tài ...................................................................................................... ..................... 5 1.2
Yêu cầu ...................................................................................................... ................. 5
Điều kiện ...................................................................................................... ............... 5 1.4
Nhiệm vụ ...................................................................................................... ............... 5 1.5
Lý do chọn đề tài ...................................................................................................... ... 5 1.6
Phương pháp nghiên cứu ...................................................
.......................................... 6
CHƯƠNG 2. CƠ SỞ LÝ THUYẾT ...................................................
Khái niệm chuyển động: ...................................................
.......................................... 7 2.2
Khái niệm phương trình chuyển động: ...................................................
..................... 7 Khái niệm quỹ đạo và phương trình quỹ đạo:
................................................... .......... 7
2.4 Vecto vận tốc ...................................................................................................... lOMoARcPSD| 36782889
......... 8 2.5 Phân tích chuyển động bài toán: ...................................................
............................... 9 2.6
Hướng dẫn giải bài ...................................................
................................................. 10 CHƯƠNG 3. MATLAB
...................................................
.................................................. 12 3.1
Giới thiệu về MATLAB ...................................................
......................................... 12 3.2
Giới thiệu một số hàm thường dùng trong MATLAB . .............................................. 13 3.3
Lưu đồ thuật toán ...................................................................................................... 14
3.4 Bài code ......................................................................................................
.............. 15 CHƯƠNG 4. KẾT LUẬN ...................................................
.............................................. 20
DANH MỤC HÌNH ẢNH
Hình 2.5.2.1.Minh hoạ chuyển động khinh khí cầu ................................................... ............. 10 Hình 3.1.1.1.Lưu đồ thuật toán
...................................................
............................................ 14 Hình 3.4.1.1.Dòng code từ 1-16
...................................................
.......................................... 16 Hình 3.4.1.2.Phương trình chuyển động và phương trình quỹ
đạo . ........................................ 17 Hình 3.4.2.1.Dòng code từ 17-42
...................................................
........................................ 18 Hình 3.4.2.2.Phương trình chuyển động và quỹ đạo ví dụ minh
họa . ..................................... 19
Hình 3.4.2.3.Hình vẽ quỹ đạo của khí cầu ...................................................
........................... 19
CHƯƠNG 1. MỞ ĐẦU 1.1 Đề tài
VẼ QUỸ ĐẠO CỦA VẬT THEO PHƯƠNG TRÌNH CHUYỂN ĐỘNG 1.2 Yêu cầu
SỬ DỤNG MATLAB ĐỂ GIẢI BÀI TOÁN SAU
“Một khí cầu bay lên từ mặt đất với vận tốc không đổi 0 . Gió truyền cho khí cầu thành phần
vận tốc theo phương ngang = , y là độ cao.Cho trước các giá trị 0, a”
a. Xác định phương trình chuyển động của vật
b. Xác định phương trình quỹ đạo của vật
c. Vẽ quỹ đạo của vật trong khoảng thời gian từ t=0 đến t=5s lOMoARcPSD| 36782889 1.3 Điều kiện
1.3.1 Sinh viên cần có kiến thức về lập trình cơ bản trong MATLAB 1.3.2
Tìm hiểu các lệnh MATLAB liên quan symbolic và đồ họa 1.4 Nhiệm vụ
Xây dựng chương trình MATLAB
1.4.1 Nhập các giá trị ban đầu (những đại lượng đề cho) 1.4.2 Thiết lập
các phương trình tương ứng. Sử dụng các lệnh symbolic để giải hệ
phương trình 1.4.3 Vẽ hình
1.5 Lý do chọn đề tài
Bộ môn vật lý 1 đại cương là một bộ môn đầy lý thú và hết sức quan trọng, mang đầy tính
thiết thực đối với sinh viên các trường khối khoa học kỹ thuật – công nghệ ứng dụng nói
chung và sinh viên trường đại học Bách Khoa- ĐHQG TPHCM nói riêng. Do đó để học tốt
được môn học này ta phải dành nhiều gian để học hỏi, nghiên cứu, tìm tòi, sáng tạo và đặc biệt
quan trọng hơn cả là ta phải mô hình hóa, trực quan hóa các bài toán, vấn đề, hiện tượng liên
quan trực tiếp và gián tiếp đến cuộc sống diễn ra hằng ngày của chúng ta. Và để giúp sinh viên
hiểu rõ và nắm kĩ được vai trò của việc mô hình hóa bài toán đó một cách logic và đầy đủ thì
chúng em đã chọn đề tài vẽ quỹ đạo của vật thông qua phương trình chuyển động.
Thông qua đề tài này,sinh viên sẽ hiểu rõ được bản chất của chuyển động là gì cũng như
ứng dụng đầy quan trọng của phương trình chuyển động và phương trình quỹ đạo vào
trong các sự vật, hiện tượng trong cuộc sống.
1.6 Phương pháp nghiên cứu
VIệc ứng dụng công cụ tin học trong quá trình giải thích các cơ sở dữ liệu của vật lý, các bài
toán về sự vật, hiện tượng cũng như mô phỏng quá trình đã trở nên tiện lợi và đạt hiệu quả cao
đồng thời cũng rút ngắn được thời gian. Như ta đã biết, phần mềm ứng dụng matlab là một
công cụ hỗ trợ đắc lực để giúp chúng ta giải quyết các vấn đề đó một cách có hệ thống đồng
thời cũng biểu diễn cho ta mô hình đồ thị trực quan và sinh động. Vì thế việc tìm hiểu và ứng
dụng công cụ matlab vào thực hành môn vật lý 1 đại cương rất quan trọng và có tính cấp thiết
cao. Thông qua đề tài mà chúng em đã chọn, ta sẽ nghiên cứu cách viết và chạy một chương
trình matlab giúp chúng ta thông qua dữ kiện của bài toán, biến đổi điều kiện và áp dụng quy
tắc toán học rồi từ đó tìm ra được phương trình chuyển động và phương trình quỹ đạo. Để trực
quan hóa phương trình chuyển động và phương trình quỹ đạo, ta vẫn sẽ vận dụng tính năng vẽ
hình của phần mềm matlab giúp ta quan sát được quỹ đạo của vật trong khoảng thời gian cụ
thể nào đó một cách chi tiết. lOMoARcPSD| 36782889
CHƯƠNG 2. CƠ SỞ LÝ THUYẾT
2.1 Khái niệm chuyển động: 2.1.1 Chuyển động của một vật là sự
thay đổi liên tục vị trí của vật đó theo thời gian.
2.1.2 Hệ vật được quy ước là đứng yên dùng để xác định vị trí của các
vật khác chuyển động đối với nó được gọi là hệ quy chiếu. Người ta
thường gắn điểm gốc của một hệ trục tọa độ vào hệ quy chiếu, và hệ trục
tọa độ này cũng được gọi là hệ quy chiếu.
2.2 Khái niệm phương trình chuyển động:
2.2.1 Trong hệ trục tọa độ Descartes, chất điểm M được xác định bởi các thành phần x,y,z của vectơ
vị ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ (x,y,z) (⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
gọi là trí ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗=
bán kính vectơ được vẽ từ gốc của hệ tọa độ đến vị trí của chất điểm M).
2.2.2 Phương trình chuyển động là các hàm số biểu thị sự thay đổi của
các tọa độ của chất điểm M theo từng thời điểm cụ thể.
2.2.3 Khi chất điểm M chuyển động, vectơ vị ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ sẽ thay đổi theo thời trí gian: = 1() (2.2)
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ = {= 2() = 3()
Các phương trình (2.2) gọi là phương trình chuyển động của chất điểm M.
2.3 Khái niệm quỹ đạo và phương trình quỹ đạo:
2.3.1 Khái niệm quỹ đạo: 2.3.1.1 Qũy đạo là đường mà chất điểm M vạch nên trong không
gian trong suốt quá trình chuyển động.
2.3.1.2 Qũy đạo còn được hiểu là tập hợp tất cả các vị trí mà chất điểm đi qua trong quá trình chuyển động. 2.3.2
Khái niệm phương trình quỹ đạo: lOMoARcPSD| 36782889
2.3.2.1 Phương trình quỹ đạo là phương trình biểu diễn mối liên hệ giữa các tọa độ không gian của chất điểm 2.4 Vecto vận tốc
Vectơ vận tốc là đạo hàm của vectơ vị trí theo thời gian, có gốc đặt tại điểm chuyển
động, phương tiếp tuyến với quỹ đạo tại điểm đó, chiều là chiều chuyển động và có độ lớn là = lim
→0 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ =
2.4.1 Vectơ vận tốc trung bình
Vectơ vận tốc trung bình của chất điểm trong khoảng thời gian từ t1 đến t2 bằng thương số của
vectơ độ dời 12 và khoảng thời gian ∆t = t2 – t1 1
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 2
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ =
Vecto vận tốc trung bình có phương và chiều trùng với vecto độ dời 12
Trong chuyển động thẳng, khi chọn trục Ox trùng với đường thẳng quỹ đạo, vectơ vận tốc trung bình có độ lớn: = 2 − 1 = 2 − 1
2.4.2 Vectơ vận tốc tức thời
Vecto vận tốc tức thời: là đại lượng đặc trưng cho chuyển động về sự nhanh, chậm và về phương, chiều. Đặc điểm:
Gốc: tại vật chuyển động;
Hướng: là hướng của chuyển động lOMoARcPSD| 36782889
Độ dài: tỉ lệ với độ lớn của vận tốc tức thời theo một tỉ lệ xích nào đó.
Độ lớn của vận tốc tức thời: v = △s. △t
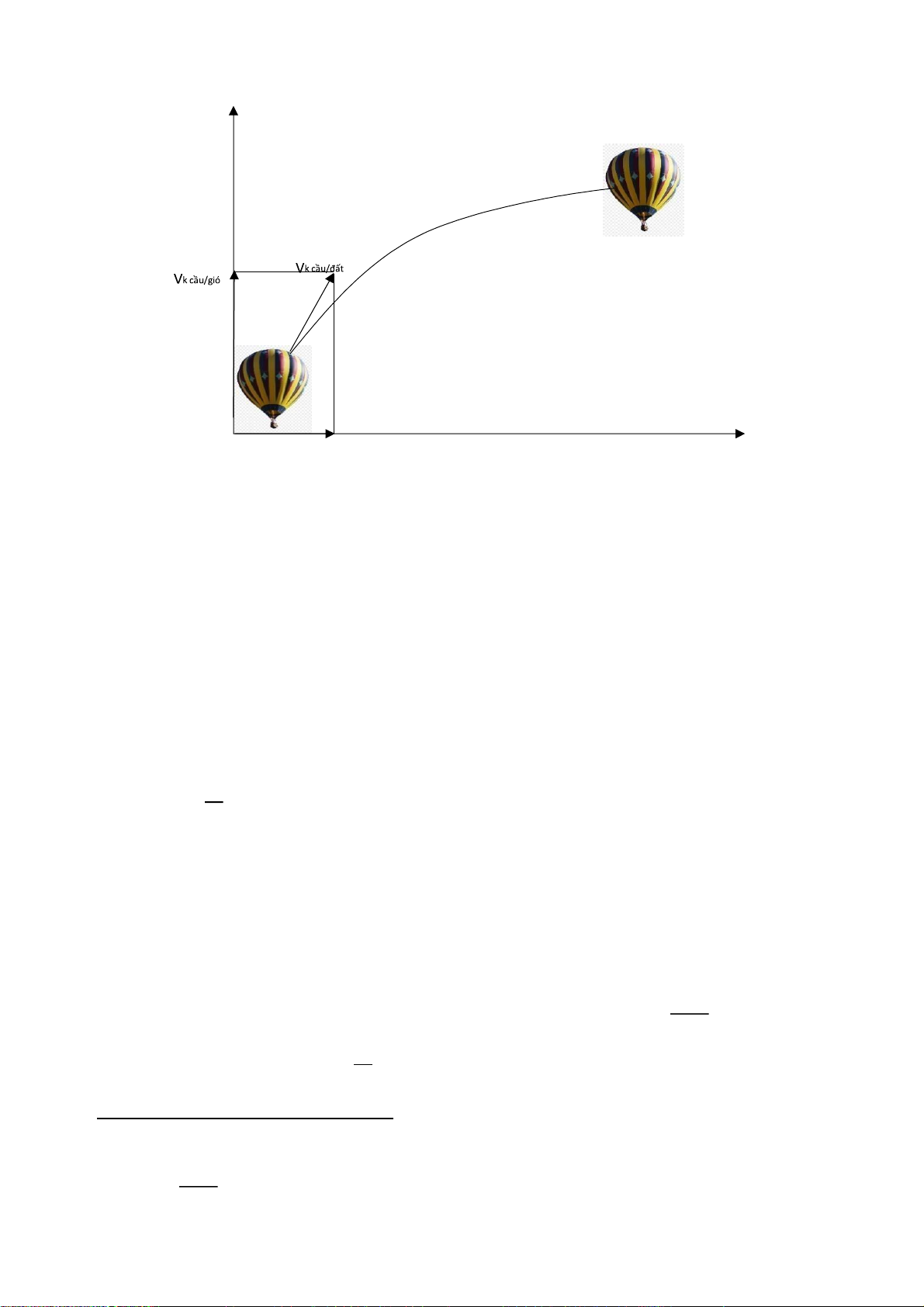
2.5 Phân tích chuyển động bài toán: Y O X
2.5.1 Khinh khí cầu chuyển động theo phương Oy là chuyển động thẳng đều
2.5.1.1 Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng có vận tốc không
thay đổi theo thời gian.
2.5.1.2 Một số công thức: = const = ⅆ
; ∫0 ⅆ = ∫0 ⅆ ⇒ = 0 +
2.5.2 Khinh khí cầu chuyển động theo phương Ox là chuyển động thẳng
biến đổi đều
2.5.2.1 Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo là đường thẳng và có độ
lớn vận tốc tức thời tăng đều hoặc giảm đều theo thời gian.
2.5.2.2 Một số công thức: = = ∫0 ⅆ hay = + 0
(với 0 là vận tốc đầu lúc t=0) s = + lOMoARcPSD| 36782889 0 0 2 − 2 0 = 2 ( −
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 0 ) y Vgió/đất x
Hình 2.5.2.1.Minh hoạ chuyển động khinh khí cầu
2.6 Hướng dẫn giải bài
A/ xác định phương trình chuyển động của vật
Ban đầu khí cầu bay lên theo phương thẳng đứng Theo trục oy ta có = → = → →y= = 0 0 ∫0 =∫0 0 0 Theo trục Ox ta có == → = → → x=02 ∫0 = →∫0 =∫0 0 2 ∫0 Vâỵ
phương trình chuyên động của vật là y=0 ; x=02 2 lOMoARcPSD| 36782889 B/ t= 0 → x=2 02 → x= 2 0 x= 2
Vậy phương trình quỹ đao của vật là : x=2 0 Một số phương trình: Phương trình vận tốc: Theo Oy: = 0 Theo Ox: =
Phương trình chuyển động: Theo Oy: y=0 Theo Ox: x=02 2
Phương trình quỹ đạo: x=2 20
CHƯƠNG 3. MATLAB
3.1 Giới thiệu về MATLAB 3.1.1
Tổng quan về MATLAB -
MATLAB là viết tắt của "matrix laboratory", là ngôn ngữ lập trình cao cấp thế hệ
thứ 4 của Mathworks. MATLAB cung cấp môi trường tương tác để thực hiện tính toán và lập trình, .... -
MATLAB là ngôn ngữ lập trình do MathWorks phát triển, cho phép người dùng
xây dựng ma trận, vẽ đồ thị hàm số hay biểu đồ dữ liệu, thực hiện các phép toán, tạo các giao
diện người dùng, liên kết các chương trình máy tính được viết trên nhiều ngôn ngữ khác nhau, lOMoARcPSD| 36782889
bao gồm cả C, C++, Java, và FORTRAN, phân tích dữ liệu, phát triển các thuật toán, tạo ra
các mô hình và ứng dụng. -
MATLAB được tích hợp nhiều lệnh và các hàm toán học, giúp người dùng thực
hiện tínhtoán các con số, vẽ đồ thị và thực hiện các phương pháp số.
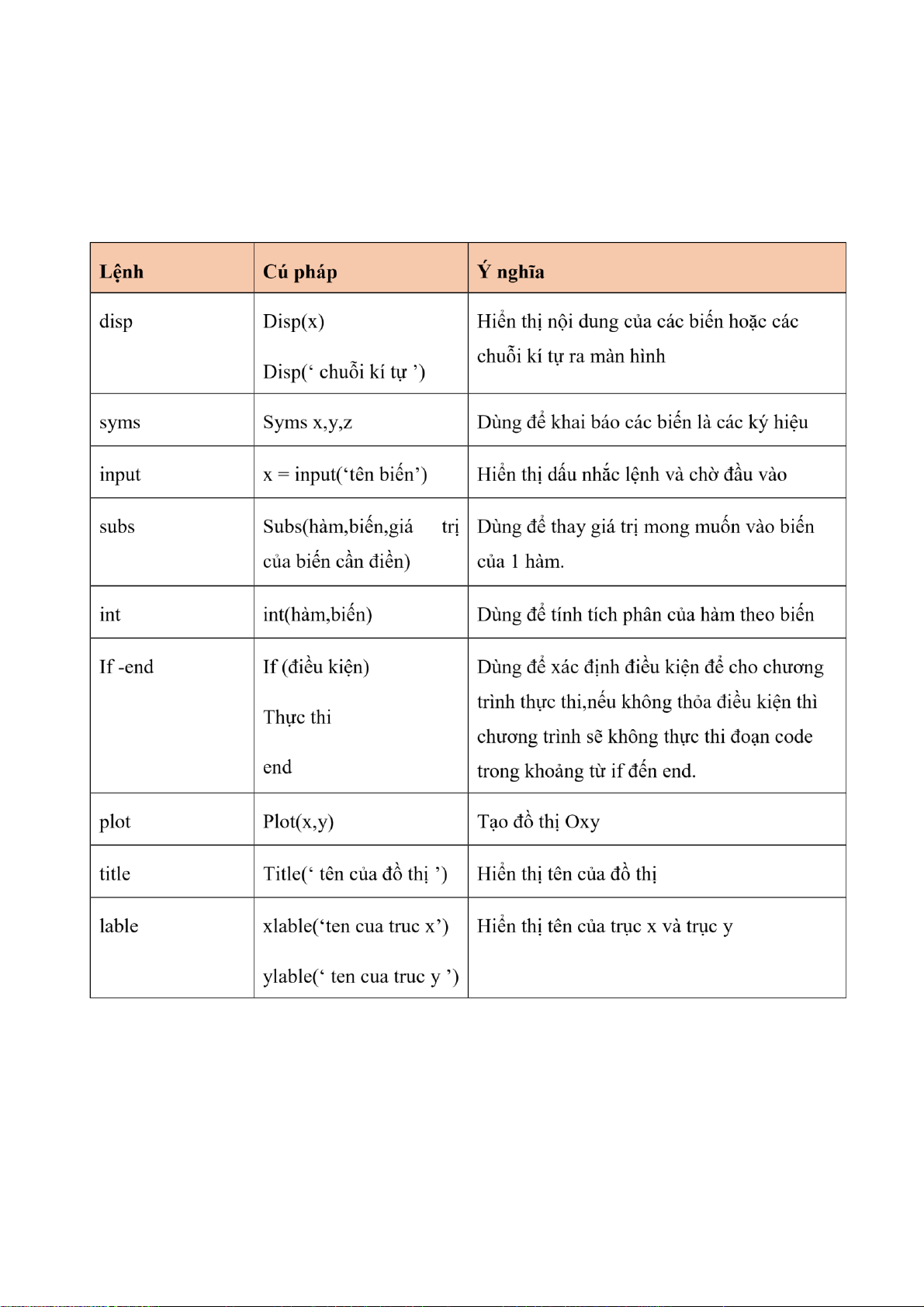
3.2 Giới thiệu một số hàm thường dùng trong MATLAB lOMoARcPSD| 36782889
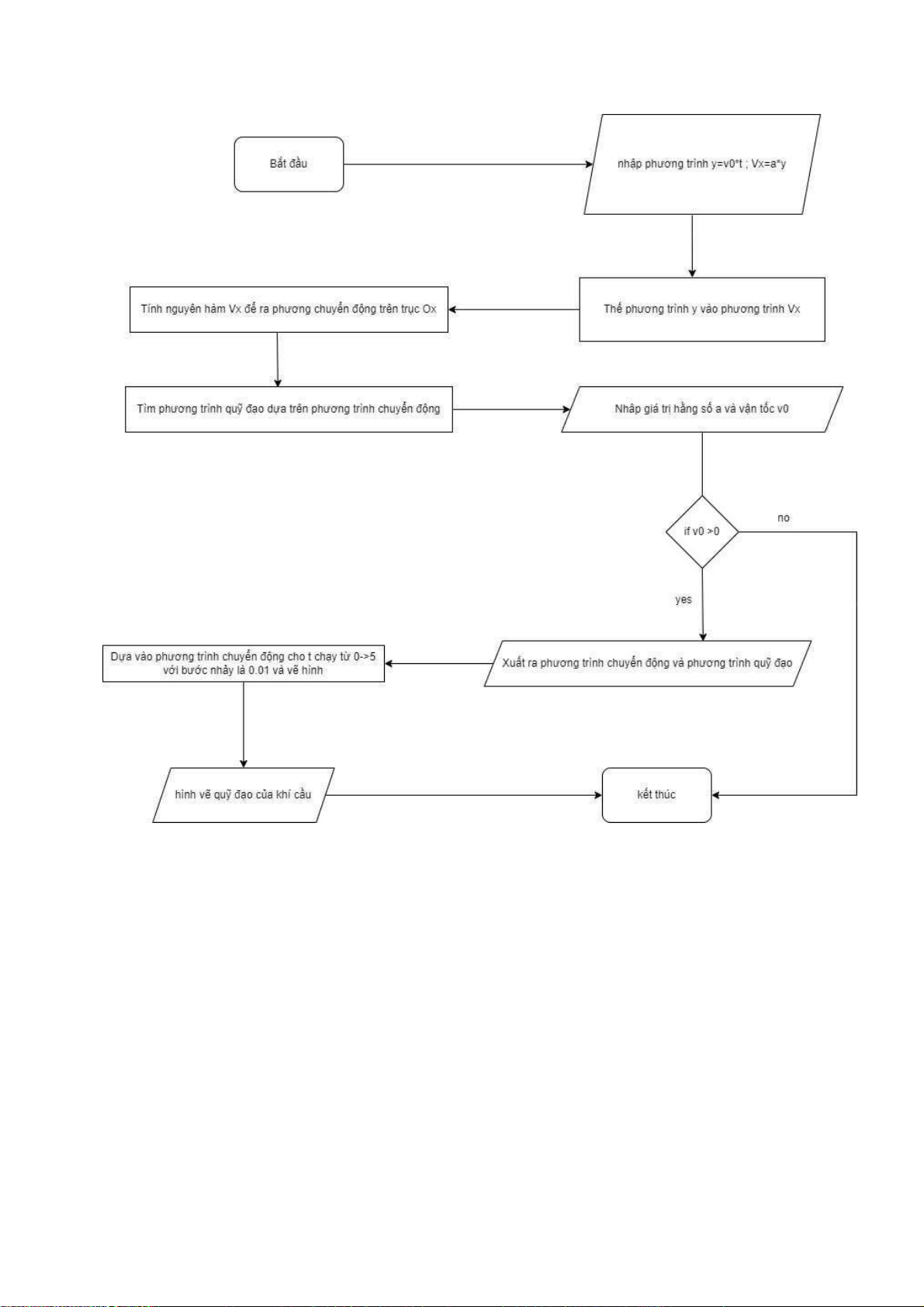
3.3 Lưu đồ thuật toán
Hình 3.1.1.1.Lưu đồ thuật toán 3.4 Bài code 1. %bien doi cong thuc 2. syms a v0 x y t ; 3. y=v0*t; 4. Vx=a*y; 5. disp(' ');
6. disp('phuong trinh Vx sau khi bien doi:');disp('Vx=');
7. %chen y=v0*t vao bien y cua phuong trinh Vx=a*y 8. disp(subs(Vx,y,y)); 9. disp(' ');
10.%nguyen ham phuong trinh Vx de tim phuong trinh chuyen dong tren truc x 11. x=int(Vx,t); lOMoARcPSD| 36782889
12.disp('cong thuc phuong trinh chuyen dong:'); 13.disp('x=');disp(x); 14.disp('y=');disp(y);
15.disp('cong thuc phuong trinh quy dao:');
16. disp('x/(y^2)=');disp(x/(y^2)); 17.%Vi du the so
18.a=input('nhap hang so a la: ');
19.v0=input('nhap van toc v0: '); 20.if v0>0 21. y=v0*t; 22.Vx=a*y; 23.x=int(Vx,t); 24.disp('x=');disp(x); 25.disp('y=');disp(y);
26. disp('x/(y^2)=');disp(int(Vx,t)/(y^2)); 27.%ve hinh
28.%cho bien t chay tu 0 den 5 voi buoc la 0.01 29. t=[0:0.01:5];
30. % tinh do cao cua khinh khi cau 31. y=v0*t;
32. % tinh do dat cua khinh khi cau 33. x=a*v0*t.^2/2;
34.%do thi ve quy dao cua khinh khi cau 35.plot(x,y,'red'); 36.hold on; 37.% ten cua do thi
38.title('quy dao cua khi cau trong khoang thoi gian 0 den 5 giay');
39.% chu thich truc hoanh do thi 40.xlabel('do dat(m)');
41.% chu thich truc tung do thi 42.ylabel('do cao(m)'); 43.hold off 44.end
3.4.1 Dùng matlab tìm phương trình chuyển động và phương trình quỹ đạo:
- Đoạn code từ dòng 1 – 16 ta khai báo các biến trong chương trình, nhập vào các công
thức có từ dữ kiện của đề bài. Đầu tiên ta dùng hàm subs(Vx,y,v0*t) đối với phương
trình vận tốc theo trục Ox, ta thay biến y trong phương trình Vx thành v0*t từ đó ta có phương trình Vx=a*v0*t lOMoARcPSD| 36782889
- Sau khi đã có phương trình vận tốc trên trục Ox theo biến t, ta dùng hàm int(Vx,t) để
tính nguyên hàm của phương trình Vx theo biến t rồi từ đó ta có được phương trình chuyển
động của trục Ox theo biến thời gian t là x= 1 2 2 0
- Để tìm được phương trình quỹ đạo ta lấy phương trình chuyển động trên trục Ox mà ta
đã tìm được trước đó là x đem chia cho bình phương của phương trình chuyển động
trên trục Oy là y^2. Từ đó chương trình sẽ tự tính toán và rút gọn biến t cho ta được phương 2 trình: = 2 ∗ 0
Hình 3.4.1.1.Dòng code từ 1-16
- Kết quả in ra màn hình của đoạn code từ dòng 1-16 gồm phương trình Vx sau khi biến
đối, lần lượt là phương trình chuyển động theo trục Ox và phương trình chuyển động
trục Oy, phương trình quỹ đạo: lOMoARcPSD| 36782889
Hình 3.4.1.2.Phương trình chuyển động và phương trình quỹ đạo
3.4.2 Nhập hằng số a và vận tốc v0 và vẽ hình:
- Đoạn code từ dòng 17 – 44 là đoạn chương trình dùng để nhập hằng số a và vận tốc v0
rồi ta dùng hàm plot để vẽ hình. Đầu tiên ta sử dụng lệnh input để cho người dùng nhập
dữ liệu, tiếp đến ta lặp lại tương tự đoạn code dòng 1-16 vì chương trình chạy từ trên
xuống dưới nên để chương trình tự hiểu giá trị từ dữ kiện mà ta nhập vào thế vào đâu
thì ta phải cho các phương trình tính toán ở dưới lệnh input để từ đó matlab hiểu và thi
hành lệnh. Phần mềm matlab sẽ tự tính toán và chạy ra được phương trình chuyển động
và phương trình quỹ đạo sau khi đã thay số. Sau đó ta dùng lệnh disp() để xuất ra các
kết quả mà ta mong muốn lên màn hình. Tuy nhiên theo dữ kiện đề bài thì khí cầu xuất
phát từ vị trí là mặt đất nên v0 không thể nào là số âm được, vì thế ta phải thêm lệnh và để chương trình hiểu là chỉ khi v0 lớn
hơn 0 thì chương trình mới tiếp tục thực thi lệnh code từ đoạn 21 đến đoạn 43, còn nếu
v0<=0 thì chương trình sẽ dừng lại.
- Đoạn code từ dòng 27 – 43 gồm các lệnh để vẽ quỹ đạo đường đi của khí cầu trên đồ
thị Oxy. Đầu tiên ta phải quy định biến thời gian t chạy từ đâu cho đến đâu thông qua
lệnh t=[thời điểm đầu : bước nhảy : thời điểm cuối]. Tiếp theo ta nhập phương trình
chuyển động trục Ox và phương trình chuyển động trục Oy mà ta đã tìm được trước đó
để matlab hiểu là biến thời gian t sẽ được tính vào các phương trình nào rồi từ đó cho
ra tọa độ từng thời điểm của khí cầu từ đó vẽ nên được quỹ đạo của khí cầu. Để xuất ra
quỹ đạo của khí cầu trên đồ thị Oxy ta dùng lệnh plot(x,y), ở giữa hold on và hold off lOMoARcPSD| 36782889
ta dùng lệnh title để đặt tên chú thích cho đồ thị Oxy, dùng lệnh xlable để đặt tên chú
thích cho trục Ox, lệnh ylable đặt tên chú thích cho trục Oy để cho đồ thị được chi tiết và chỉnh chu hơn.
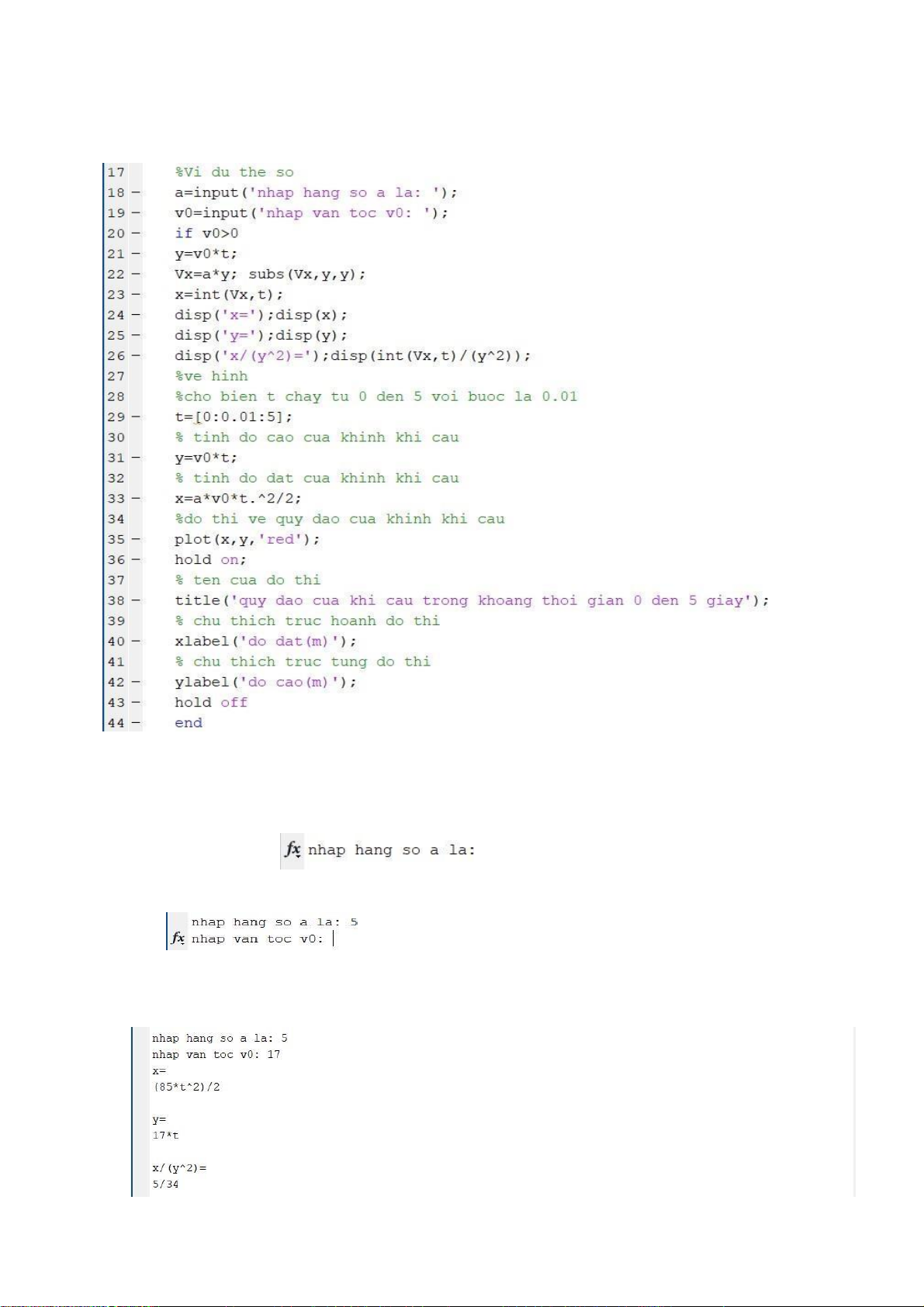
Hình 3.4.2.1.Dòng code từ 17-42
- Sau khi chạy chương trình, trên màn hình output sẽ xuất hiện như thế này yêu cầu ta nhập hằng số a
rồi ta nhập giá trị ví dụ a=5 bên cạnh
và bấm enter thì chương trình sẽ cho ra tiếp yêu cầu ta nhập giá trị vận tốc v0
sau đó ta nhập giá trị v0 ví dụ v0=17 thì chương trình sẽ
tự động xuất ra màn hình output các phương trình chuyển động và phương trình quỹ
đạo sau khi đã thế số, tính toán và rút gọn .
Hình 3.4.2.2.Phương trình chuyển động và quỹ đạo ví dụ minh họa lOMoARcPSD| 36782889
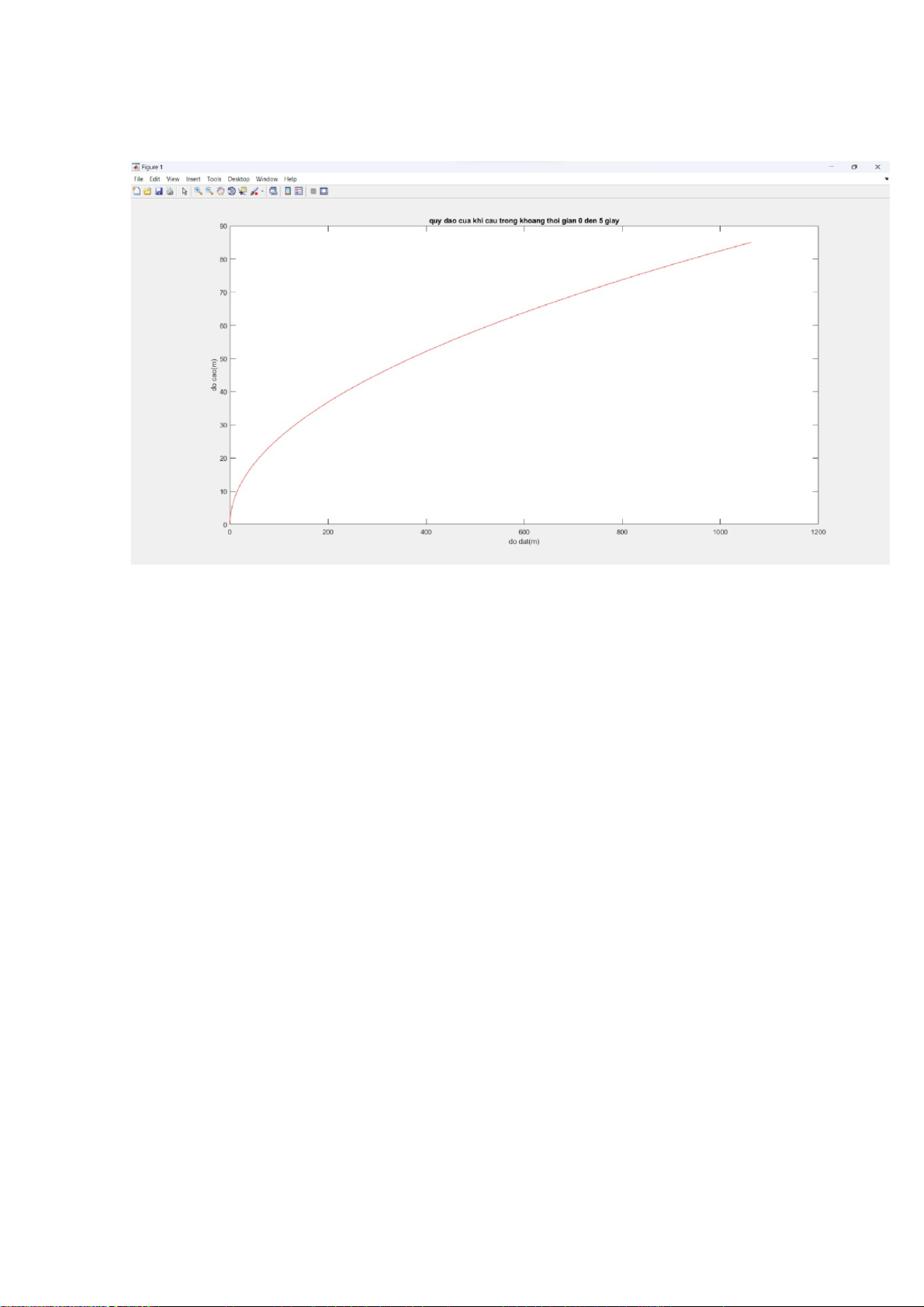
- Sau khi đã xuất ra màn hình các phương trình chuyển động và phương trình quỹ đạo đã
thế số và rút gọn như ta mong muốn, chương trình sẽ xuất ra tiếp một đồ thị như hình
3.4.2.3 biểu diễn quỹ đạo của khí cầu là một đường parabol đi qua trục tọa độ.
Hình 3.4.2.3.Hình vẽ quỹ đạo của khí cầu lOMoARcPSD| 36782889
CHƯƠNG 4. KẾT LUẬN
Chúng ta vừa tìm hiểu xong về chuyển động của khinh khí cầu, bài toàn về chuyển động của
khinh khí cầu khá phức tạp đã được giải quyết với một phần giúp đỡ khá lớn của matlab, nó có
rất nhiều lệnh và hàm toán học nhằm hỗ trợ đắc lực cho bạn trong việc tính toán, vẽ các hình vẽ
biểu đồ. Ta có thể dễ dàng sử dụng matlab để mô phỏng hay tính toán chuyển động của vật khi
nắm được các thông số liên quan đến chuyển động như vận tốc ban đầu góc ném, gia tốc Lập
trình trong Matlab có thể giải quyết những bài toán trong nhiều lĩnh vực khoa học kỹ thuật đáp
ứng được các yêu cầu của người lập trình. Nhưng nó vẫn còn khuyết điểm đó là thiết kế một
đoạn code rất rườm và mất rất nhiều thời gian công sức, còn mô phỏng trong phạm vi chủ đề
được chỉ định, chưa sáng tạo sang các chủ đề tính toán kĩ thuật khác. lOMoARcPSD| 36782889
TÀI LIỆU THAM KHOẢ
[1] Vật lí đại cương A1 – Nguyễn Thị Bé Bảy và CS, Giáo trình trường ĐHBK
TP.HCM [2] Phạm Thị Ngọc Yến, Lê Hữu Tình, “Cơ sở Matlab và ứng dụng”, NXB
Khoa học & Kỹ thuật.
[3] Bài tập vật lí phần Cơ học – Nguyễn Thị Bé Bảy