Báo cáo bài tập lớn môn Đại số tuyến tính đề tài "Nêu cơ sở lý thuyết của phân tích thành phần chính (PCA) và ứng dụng trong giảm chiều dữ liệu"

lOMoARcPSD| 36991220 Mục lục:
Lời mở ầu .................................................................................................. 4
Phần I.TỔNG QUAN PCA.............................................................................5
Chương 1: Mở ầu :.................................................................................... .5
1.Sơ lược về PCA (Principle component analyst):.............................5
2. Yêu cầu ..........................................................................................5
3. Điều kiện.........................................................................................5
4. Nhiệm vụ ........................................................................................5
Chương 2 Cơ sở lí thuyết của PCA trong giảm chiều dữ liệu........................6
1.Khái niệm cơ bản:.............................................................................6
2. Áp dụng lí thuyết ể phân tích ề tài:...............................................6
3. Thuật toán PCA……….....................................................................7
4.Giới thiệu về PCA và một số ứng dụng của PCA..............................10
Phần II.ỨNG DỤNG........................................................................................12
Chương 3: Chương 3: Các bước thực hiện và giải thuật PCA (Principal Component
Analysis) trong giảm chiều dữ liệu..................................................................12
1.Hình thành.........................................................................................12
2.Giải thuật...........................................................................................12
Chương 4: Ứng dụng và Giải thuật một số bài……………………………........14
1.Vì sao phải giảm chiều dữ liệu: ...........................................................14
2 Các ví dụ về giảm chiều dữ liệu: .........................................................14
Chương 5: Kết luận..........................................................................................18
Tài liệu tham khảo............................................................................................19
Một số thuật ngữ liên quan...............................................................................19
Nhận xét giảng viên..........................................................................................19
Lời mở ầu
Đại số tuyến tính là môn học có tầm quan trọng ối với sinh viên ĐH Bách Khoa
TPHCM nói riêng và sinh viên các ngành khối khoa học kỹ thuật – công nghệ nói lOMoARcPSD| 36991220
chung. Do ó, việc dành cho môn học này một khối lượng thời gian nhất ịnh và thực
hành là iều tất yếu ể giúp cho sinh viên có ược cơ sở vững chắc về các môn KHTN
và làm tiền ề ể học tốt các môn khác trong chương trình ào tạo.
Trong suốt quá trình thực hiện bài tập lớn nói trên, nhóm chúng em ã nhận ược
rất nhiều sự quan tâm và ủng hộ, giúp ỡ tận tình của thầy cô, anh chị và bạn bè.
Ngoài ra, nhóm cũng xin gửi lời tri ân chân thành ến Thầy Đặng Văn Vinh, là giảng
viên và cũng là người hướng dẫn nhóm em trong ề tài này. Nhờ có thầy hết lòng
chỉ bảo mà nhóm ã hoàn thành tiểu luận úng tiến ộ và giải quyết tốt những vướng
mắc gặp phải. Sự hướng dẫn của thầy ã là chìa khóa cho mọi hành ộng của nhóm
và phát huy tối a ược mối quan hệ hỗ trợ giữa thầy và trò trong môi trường giáo dục.
Sau khi thực hiện ề tài, nhóm em ã có cái nhìn sâu sắc hơn về sự gắn kết giữa
lý thuyết và thực tế. Cũng góp phần cũng cố kiến thức nền tảng về chuyên ề Phân
tích thành phần chính. Bên cạnh ó cũng giúp chúng em phát huy khả năng làm việc
nhóm, xử lí thông tin và dữ liệu, nâng cao hiểu biết về sử dụng công nghệ thông tin
trong học tập và công việc sau này.
Lời cuối, xin một lần nữa gửi lời biết ơn sâu sắc ến các cá nhân, các thầy cô ã
dành thời gian chỉ dẫn cho nhóm. Đây chính là niềm tin, nguồn ộng lực to lớn ể
nhóm có thể ạt ược kết quả này.
Phần I.TỔNG QUAN PCA Chương 1: Mở ầu
1.Sơ lược về PCA (Principle component analyst):
PCA ược phát triển vào ầu thế kỷ 20 bởi nhà thống kê người Anh Karl Pearson và nhà toán
học người Pháp Henri Hotelling. Pearson ã phát triển PCA như một phương pháp giảm kích
thước của tập dữ liệu trong khi vẫn giữ lại những ặc tính quan trọng của nó. Trong khi ó, Hotelling
ã phát triển PCA như một công cụ ể phân tích mối tương quan giữa các biến trong tập dữ liệu.
Tuy nhiên, ý tưởng của PCA ã ược sử dụng từ trước ó trong các lĩnh vực khác như toán học
và vật lý. Ví dụ, các nhà khoa học ã sử dụng phương pháp này ể giảm kích thước của các bản ồ
thế giới và các tấm hình ảnh. lOMoAR cPSD| 36991220
Từ ó, PCA ã ược sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ khoa học dữ liệu, thống
kê, máy học ến các ứng dụng thực tiễn như xử lý ảnh và nhận dạng khuôn mặt.
Hiện nay, PCA vẫn ược sử dụng phổ biến trong các lĩnh vực khác nhau và ã trở thành một
trong những công cụ quan trọng nhất trong xử lý và phân tích dữ liệu. 2. Yêu cầu ề tài:
1/ Nêu cơ sở lý thuyết của phân tích thành phần chính (PCA: principle component analysis).
2/ Ứng dụng của phân tích PCA ể giảm chiều dữ liệu. 3. Điều kiện:
• Sinh viên cần có kiến thức về bộ môn Đại số tuyến tính nói chung và hiểu biết cơ bản về phép
phân tích thành phần chính trong machine learning nói riêng.
• Tìm hiểu các ứng dụng phân tích thành phần chính PCA thực tiễn. 1.4- Nhiệm vụ:
• Tìm hiểu về cơ sở lý thuyết nền tảng của thuật toán PCA. 8 • Không nhất thiết phải dùng matlab
ể minh họa, nhưng phải có ít nhất 1 ví dụ thực tế.
Chương 2: Cơ sở lí thuyết & giới thiệu 1.Khái niệm cơ bản:
Phương pháp phân tích thành phần chính ( PCA ) là phương pháp biến ổi từ một không gian
nhiều chiều thành một không gian mới ít chiều, cụ thể là giảm chiều dữ liệu từ D về K < D là chỉ
giữ lại K là phần tử quan trọng nhất. Tuy nhiên, việc làm này chắc chắn chưa phải tốt nhất vì
chúng ta chưa biết xác ịnh thành phần nào là quan trọng hơn. Hoặc trong trường hợp xấu nhất,
lượng thông tin mà mỗi thành phần mang là như nhau, bỏ i thành phần nào cũng dẫn ến việc mất
một lượng thông tin lớn. Tuy nhiên, nếu chúng ta có thể biểu diễn các vector dữ liệu ban ầu trong
một hệ cơ sở mới cái mà có tầm quan trọng giữa các thành phần là khác nhau rõ rệt, thì chúng ta
có thể bỏ qua những thành phần ít quan trọng nhất. Mục tiêu của chúng ta là tìm ra K chiều mà có
thể ảm bảo rằng các dữ liệu khi ược biểu diễn, không bị tr 甃 ng lắp không bị mất mát thông tin (
tách biệt nhau hoàn toàn )
2. Áp dụng lí thuyết ể phân tích ề tài:
PCA là phương pháp biến ổi giúp giảm số lượng lớn các biến có tương quan với nhau thành
tập ít các biến sao cho các biến mới tạo ra là tổ hợp tuyến tính của những biến cũ không có
tương quan lẫn nhau. Ví dụ, chúng ta có 1000 biến ban ầu có tương quan tuyến tính với nhau, khi lOMoAR cPSD| 36991220
ó chúng ta sử dụng phương pháp PCA xoay chiều không gian cũ thành chiều không gian mới mà
ở ó chỉ còn 10 biến không có tương quan tuyến tính mà vẫn dữ ược nhiều nhất lượng thông tin từ
nhóm biến ban ầu. Hay nói cách khác, PCA chính là phương pháp i tìm 1 hệ cơ sở mới sao cho
thông tin dữ liệu chủ yếu tập trung ở 1 vài tọa ộ 1 cách trực quan, phần còn lại chỉ mang một
lượng nhỏ thông tin ( ể ơn giản trong tính toán, PCA sẽ tìm 1 hệ trực chuẩn làm cơ sở mới ).
PCA (Principal Component Analysis) là một phương pháp phân tích a biến ược sử dụng rộng rãi
trong xử lý dữ liệu và giảm chiều dữ liệu. Phương pháp này có những ưu iểm và nhược iểm như sau: Ưu iểm: -
Giảm chiều dữ liệu: PCA có thể giảm số chiều của dữ liệu bằng cách chọn một số thành
phần chính có ộ giải thích phương sai cao nhất. Việc giảm chiều này giúp cho việc xử lý và hiển
thị dữ liệu trở nên dễ dàng và nhanh chóng hơn. -
Loại bỏ tương quan giữa các biến: PCA có thể loại bỏ sự tương quan giữa các biến và tạo
ra các biến không tương quan mới (thành phần chính), giúp cho việc phân tích và mô hình hóa dữ
liệu trở nên dễ dàng hơn. -
Giảm nhiễu: PCA có thể giảm nhiễu trong dữ liệu bằng cách loại bỏ các thành phần chính có giá trị riêng thấp. -
Tính toán ơn giản: PCA ược tính toán dễ dàng và nhanh chóng bằng các phương pháp tính
toán ma trận hiệp phương sai và vector riêng. Nhược iểm: -
Đôi khi khó hiểu: PCA có thể khó hiểu với người mới học vì nó liên quan ến các khái niệm ại
số tuyến tính như ma trận và vector riêng. -
Cần chọn số thành phần chính: Việc lựa chọn số lượng thành phần chính là một vấn ề quan
trọng trong PCA. Việc chọn số lượng này có thể ảnh hưởng ến kết quả cuối cùng và cần phải ược thực hiện cẩn thận. -
Không phù hợp với dữ liệu phi tuyến: PCA chỉ phù hợp với dữ liệu tuyến tính. Nếu dữ liệu là
phi tuyến, PCA có thể không cho kết quả tốt. 3. Thuật toán PCA => Ý tưởng:
Giả sử ta có tập dữ liệu gồm các iểm dữ liệu thuộc 𝑅2, và ây là tập dữ liệu sau khi ược chuẩn hóa. lOMoARcPSD| 36991220
Hình 2: Dữ liệu sau khi ược chuẩn hóa. Trục tung và trục hoành là trục thể hiện thuộc tính của dữ liệu.
Một cách trực quan, khi nhìn vào tập dữ liệu, ta thấy ược thông tin về mối quan hệ giữa hai
thuộc tính ược thể hiện qua phương sai của tập dữ liệu (hay hiệu phương sai của hai thuộc tính).
Nói cách khác, nếu một iểm dữ liệu có thuộc tính 1 lớn thì thuộc tính 2 cũng sẽ lớn, và ngược lại
(hiệu phương sai dương). Vì lẽ ó, nên khi ta mang những iểm dữ liệu trên vào không gian thấp
chiều hơn (trong trường hợp này là ( R) thì ta muốn ý nghĩa về phương sai trên vẫn ược bảo toàn.
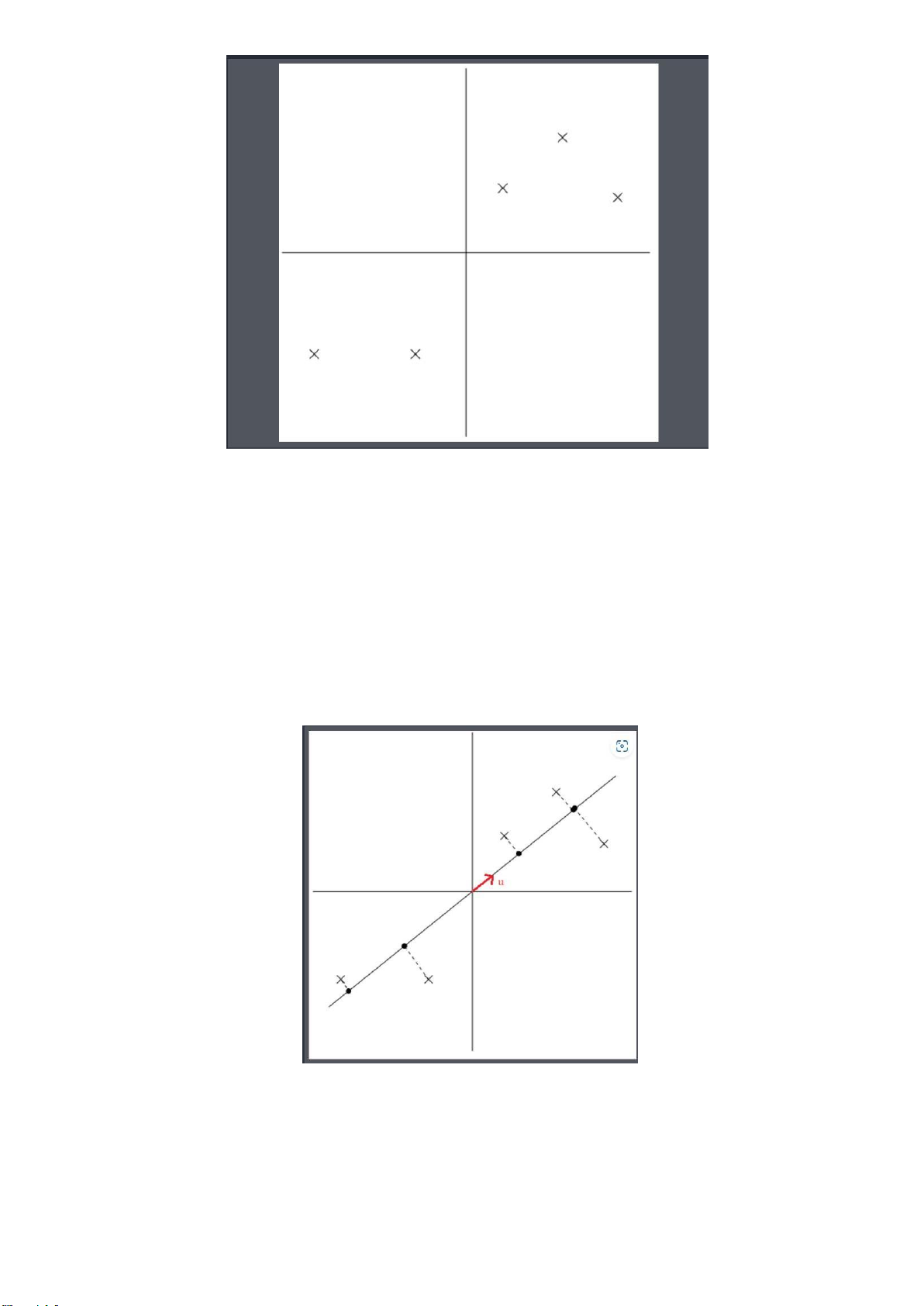
Cụ thể hơn, ta muốn tìm những vector ơn vị u sao cho, khi ta chiếu những iểm dữ liệu lên ường
thẳng có u là vector chỉ hướng thì phương sai của những iểm dữ liệu mới ược tối a.
Để hiểu rõ hơn về cách chọn vector u, ta sẽ xem qua hai trường hợp mà ở ó một trường hợp
vector u ược chọn tốt còn trường hợp còn lại thì không.
Hình 3: Các iểm dữ liệu ược chiếu lên ường thẳng cóu là vector chỉ hướng tốt
Ta thấy những iểm dữ liệu mới (chấm en) ược chiếu lên ường thẳng có u là vector chỉ hướng
vẫn cách nhau khá xa, hay có phương sai lớn. Những iểm dữ liệu mới (chấm en) thể hiện khá tốt
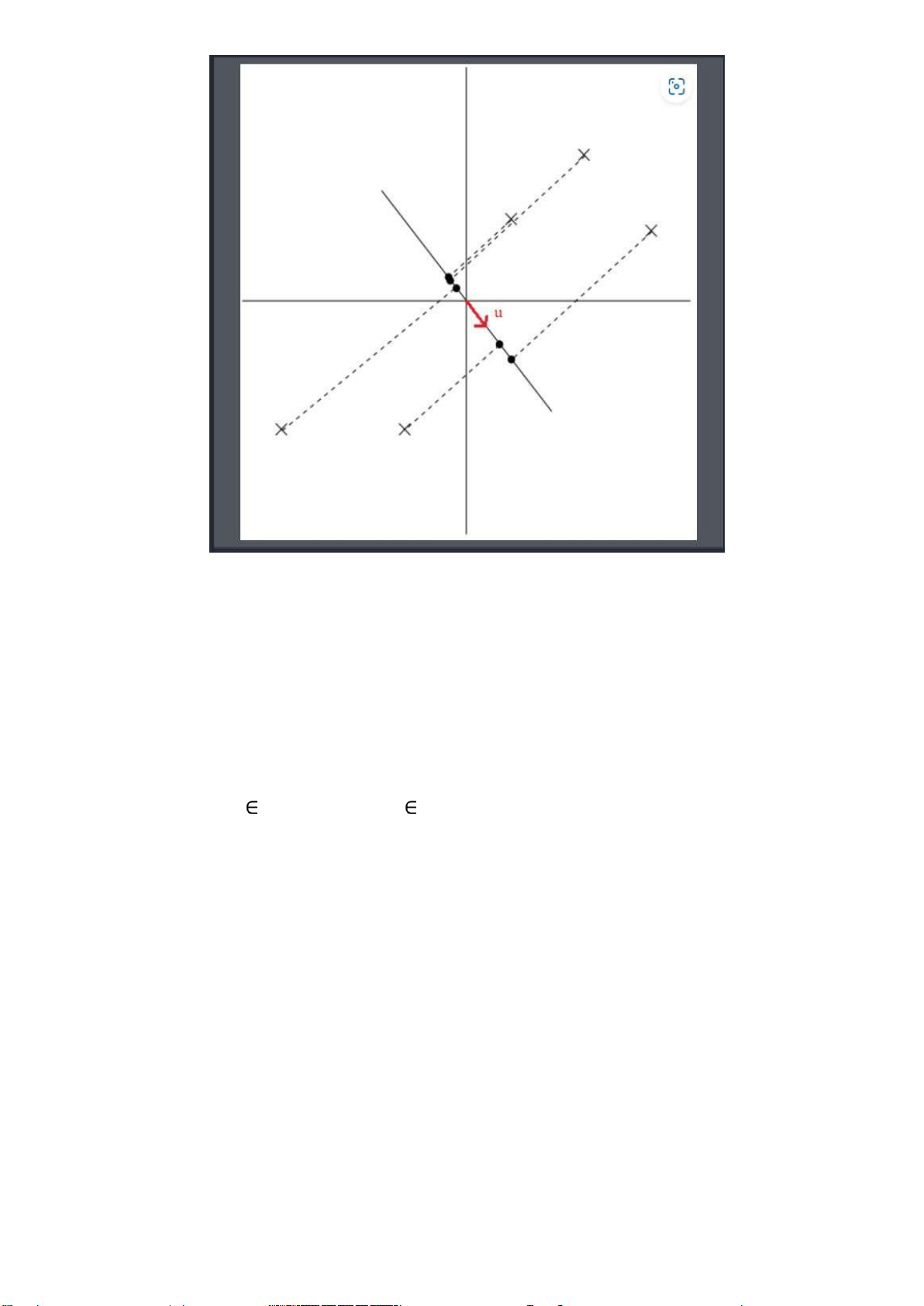
những iểm dữ liệu ban ầu (dấu x). Ngược lại với cách chọn trên, ta có cách chọn vector u không ược tốt. lOMoARcPSD| 36991220
Hình 4: Các iểm dữ liệu ược chiếu lên ường thẳng có u là vector chỉ hướng không tốt.
Trong trường hợp này, những iểm dữ liệu mới (chấm en) rất gần nhau, hay có phương sai nhỏ,
ây không phải là cách thể hiện tốt cho những iểm dữ liệu ban ầu (dấu x).
Tóm lại, ý tưởng của PCA là tìm ra những vector u sao cho, khi ta chiếu những iểm dữ liệu ban
ầu lên các ường thẳng có u là vector chỉ hướng thì những iểm dữ liệu mới sẽ có phướng sai lớn.
Sau khi tìm ược k vector u lần lượt là 𝑢1, 𝑢2, …. 𝑢𝑘 thì ta sẽ chiếu iểm dữ liệu lên k ường thẳng
có 𝑢1, 𝑢2, …. 𝑢𝑘 lần lượt là vector chỉ hướng, sẽ có ược iểm dữ liệu trong tọa ộ mới thuộc 𝑅𝑘
(việc làm này sẽ ược cụ thể hơn trong phần trình bày bằng toán học).
𝑋 (𝑖) 𝑅 (𝑑) → 𝑋 (𝑖)′ 𝑅 (𝑘)
Qua ó ta rút ra ược những nhận xét:
+ Phương sai của tập dữ liệu mới sẽ úng bằng trung bình cộng của bình phương khoảng cách
của những iểm dữ liệu mới ến gốc tọa ộ bởi vì tập dữ liệu ã ược chuẩn hóa cho giá trị trung bình là 0.
+ Những vector là 𝑢1, 𝑢2, …. 𝑢𝑘 ộc lập tuyến tính với nhau vì mục ích của PCA là “nén” các
iểm dữ liệu vào một chiều không gian nhỏ hơn nên nếu có một vector là tổ hợp tuyến tính của
những vector u còn lại thì tọa ộ ược thể hiện bằng vector xem như bị “thừa”.
+ K < D . Dễ hiểu vì ta ang muốn giảm chiều của dữ liệu.
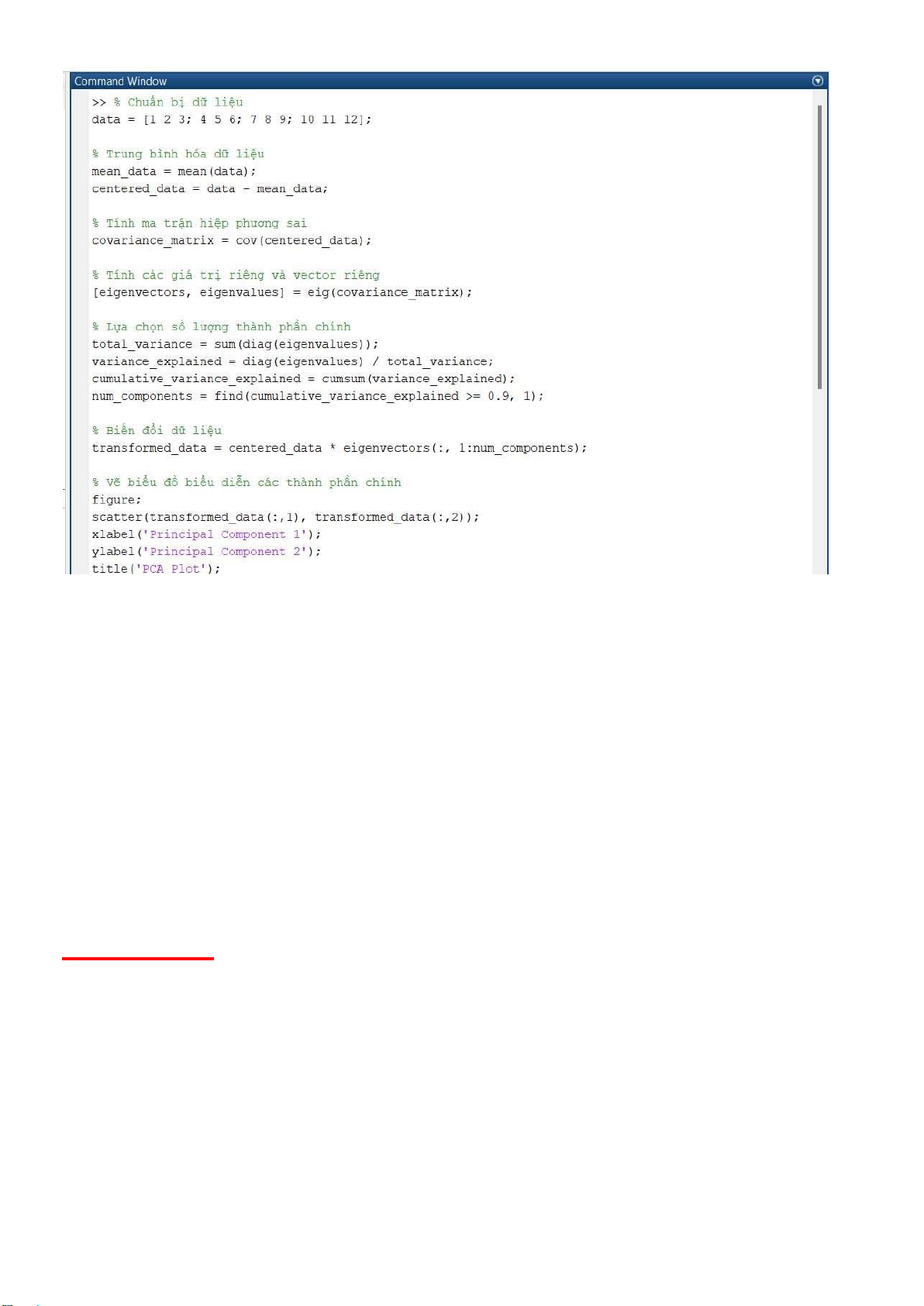
Để thực hiện PCA, ta cần thực hiện các bước sau: -
Chuẩn bị dữ liệu: chuẩn bị ma trận dữ liệu, với mỗi hàng tương ứng với một quan sát, và
mỗi cột tương ứng với một biến. lOMoAR cPSD| 36991220 -
Trung bình hóa dữ liệu: tính toán giá trị trung bình của mỗi biến và trừ giá trị trung bình này
từ mỗi giá trị trong cột tương ứng. -
Tính ma trận hiệp phương sai (covariance matrix): tính toán ma trận hiệp phương sai của
dữ liệu ã ược trung bình hóa. Ma trận hiệp phương sai có kích thước bằng số biến, với mỗi phần
tử tại vị trí (i,j) tương ứng với hiệp phương sai giữa biến i và j. -
Tính các giá trị riêng và vector riêng: tính toán các giá trị riêng và vector riêng của ma trận
hiệp phương sai. Các vector riêng sẽ là các thành phần chính của dữ liệu. -
Lựa chọn số lượng thành phần chính: chọn số lượng thành phần chính dựa trên tỷ lệ
phương sai giải thích của từng thành phần chính. Thông thường, ta chọn số lượng thành phần
chính sao cho tổng phương sai giải thích của các thành phần chính ược chọn ạt tới một mức ộ
nào ó (ví dụ như 90% hoặc 95%). -
Biến ổi dữ liệu: biến ổi dữ liệu ban ầu sang không gian mới ược tạo ra từ các thành phần
chính bằng cách nhân ma trận dữ liệu với ma trận các thành phần chính ược chọn.
4.Giới thiệu về PCA và một số ứng dụng của PCA
PCA có nhiều ứng dụng, ở chỉ giới thiệu một vài ứng dụng.
Đầu tiên, PCA d 甃 ng ể nén dữ liệu qua việc thể hiện iểm dữ liệu 𝑥(𝑖)bằng iểm dữ liệu 𝑦(𝑖)
trong không gian mới thấp chiều hơn. Nếu ta giảm chiều dữ liệu về k=2 hoặc k=3, ta có thể vẽ các
iểm dữ liệu mới 𝑦(𝑖) trong không gian 𝑅(2) hoặc 𝑅(3).Từ ó, qua hình vẽ ta có thể ưa ra nhận xét
về cấu trúc của dữ liệu, như những iểm dữ liệu tương ồng thường ở gần nhau thành cụm.
Tiếp ến, PCA d 甃 ng ể tiền xử lý dữ liệu. Ta có thể giảm chiều cho các iểm dữ liệu 𝑥(𝑖) trước khi
cho vào thuật toán học có giám sát. Ngoài tác dụng ể giảm thời gian tính toán, việc giảm chiều dữ
liệu còn giảm ộ phức tạp của các hàm giả thiết tránh việc overfitting thường xảy ra trong các thuật toán học có giám sát.
PCA còn ược xem như thuật toán giảm nhiễu cho dữ liệu.
Ngoài ra còn ứng dụng trong Hồi quy tuyến tính, Nhận dạng khuôn mặt,.......
Sau ây là một số ví dụ trực quan giúp ta dễ tiếp cận hơn với phương pháp này: lOMoARcPSD| 36991220
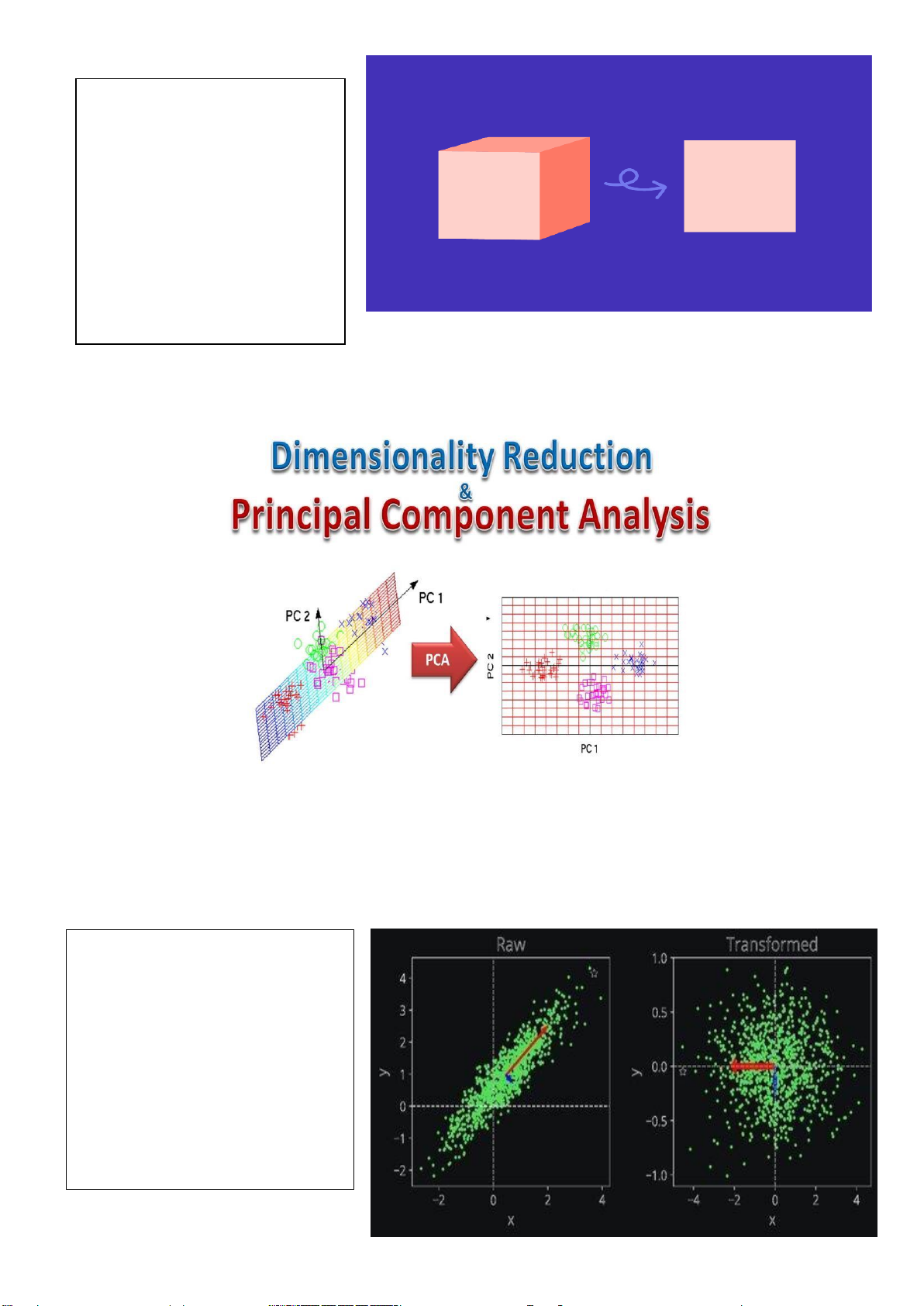
Từ một khối lập phương 3
chiều, sau khi ược giảm chỉ
còn 1 chiều trông như một hình vuông.
Hình 1. Khối lập phương sau khi ược giảm chiều dữ liệu.
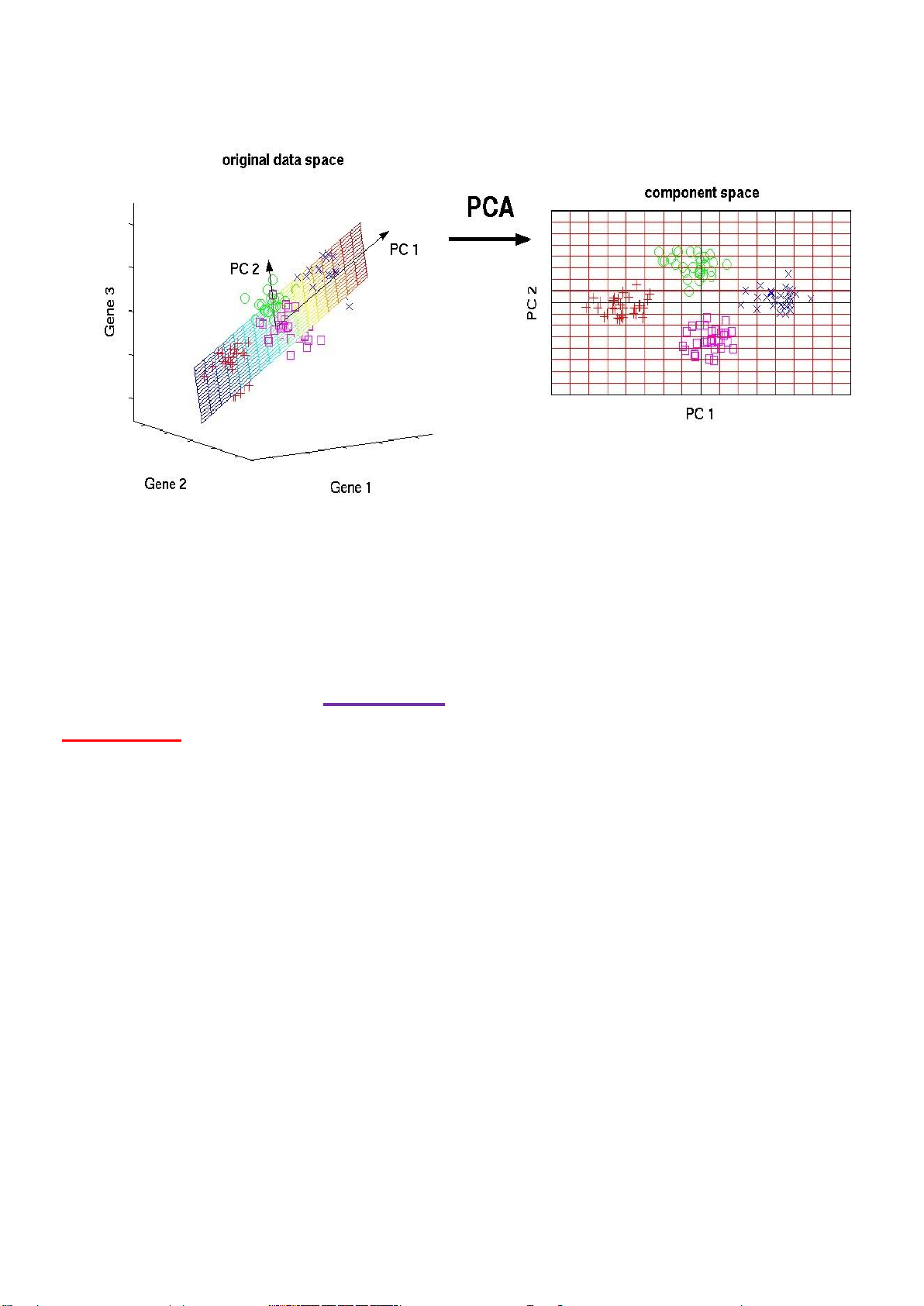
Hình 2. Ứng dụng PCA trong giảm chiều dữ liệu
Qua hình ảnh trên ta có thể thấy dữ liệu từ a chiều với vector PC2, PC1 trong không gian 4
chiều ã ược chuyển thành dạng ồ thị 2 chiều, từ ó trong việc ọc giúp ta dễ phân tích dữ liệu hơn
tuy nhiên cũng làm giảm bớt lượng thông tin từ ồ thị gốc.
Việc ổi chiều dữ liệu giúp ta có
góc nhìn khác và thông tin hình ảnh em lại lOMoARcPSD| 36991220
Hình.. ổi chiều dữ liệu Phần II.Ứng Dụng
Chương 3: Các bước thực hiện và giải thuật PCA (Principal Component
Analysis) trong giảm chiều dữ liệu. 1.Hình thành:
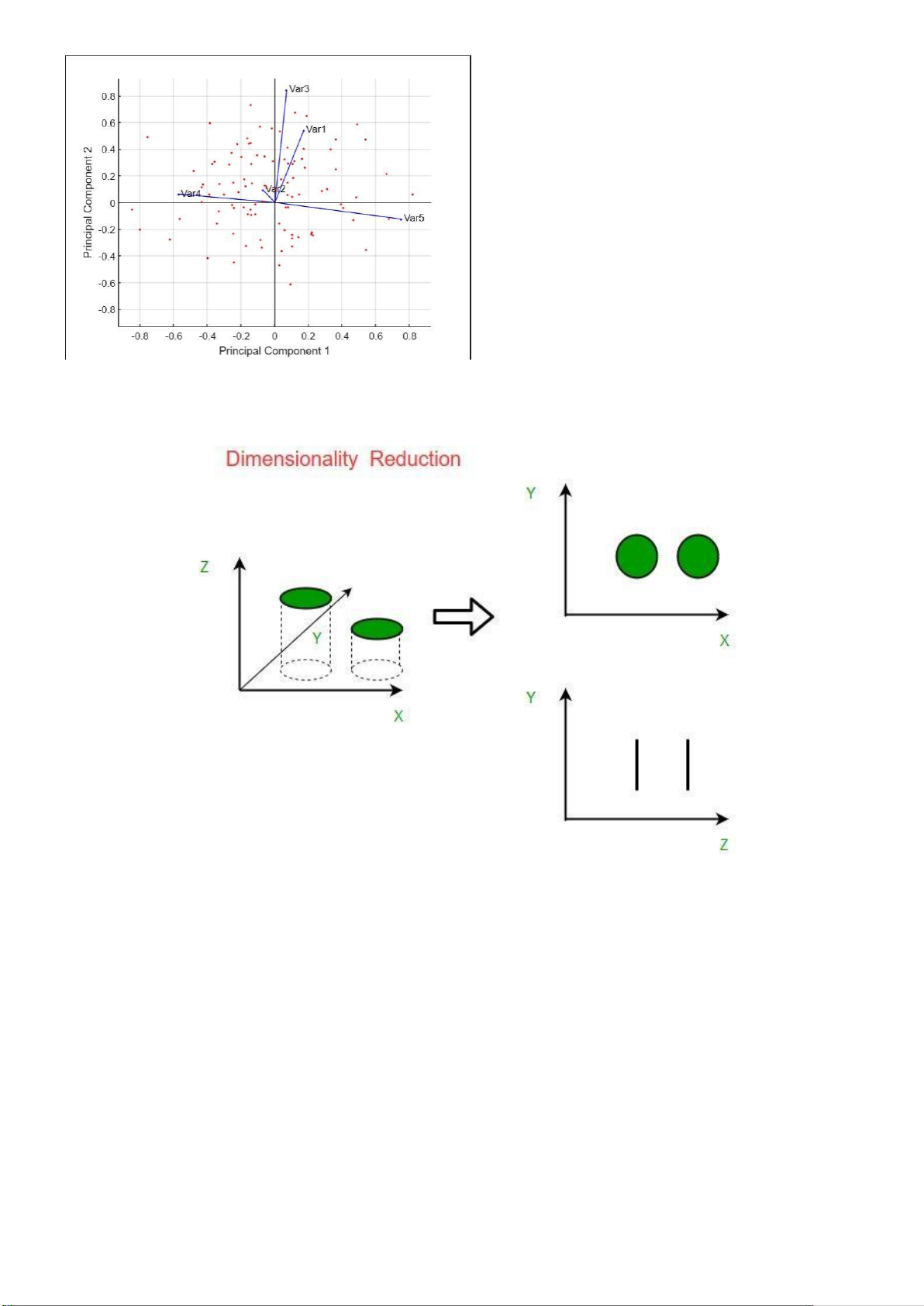
Dimensionality Reduction (giảm chiều dữ liệu), là một trong những kỹ thuật quan trọng trong
Machine Learning. Các feature vectors trong các bài toán thực tế có thể có số chiều rất lớn, tới vài
nghìn. Ngoài ra, số lượng các iểm dữ liệu cũng thường rất lớn. Nếu thực hiện lưu trữ và tính toán
trực tiếp trên dữ liệu có số chiều cao này thì sẽ gặp khó khăn cả về việc lưu trữ và tốc ộ tính toán.
Vì vậy, giảm số chiều dữ liệu là một bước quan trọng trong nhiều bài toán. Đây cũng ược coi là
một phương pháp nén dữ liệu. Dimensionality Reduction, nói một cách ơn giản, là việc i tìm một
hàm số, hàm số này lấy ầu vào là một iểm dữ liệu ban ầu 𝑥 ∈ 𝑅 𝐷 với D rất lớn, và tạo ra 1 iểm dữ
liệu mới 𝑧 ∈ 𝑅 𝐾 có số chiều K < D. Phương pháp ơn giản nhất trong các thuật toán
Dimensionality Reduction dựa trên một mô hình tuyến tính, có tên là Principal
Component Analysis (PCA), tức Phân tích thành phần chính. Phương pháp này dựa trên quan sát
rằng dữ liệu thường không phân bố ngẫu nhiên trong không gian mà thường phân bố gần các
ường/mặt ặc biệt nào ó.
Mấu chốt là ta sẽ phân tích dữ liệu và sau ó tìm ra các thành phần chính của dữ liệu ể giữ lại các
thành phần ó. Ví dụ dữ liệu của chính ta có N features thì sau khi áp dụng PCA sẽ còn K features
chính mà thôi (KViệc làm như trên sẽ giúp cho chúng ta: lOMoARcPSD| 36991220 •
Giảm chiều dữ liệu mà vẫn giữ ược ặc trưng chính, chỉ mất i “chút ít” ặc trưng. •
Tiết kiệm thời gian, chi phí tính toán •
Dễ dàng visualize dữ liệu hơn ể giúp ta có cái nhìn trực quan hơn.
2 Giải thuật giảm chiều dữ liệu:
Để làm ược việc này, thuật toán PCA cần thực hiện qua các bước: •
Chuẩn bị dữ liệu cần giảm chiều là X với kích thước (n_sample, n_feature), tương ứng
mỗi hàng là 1 mẫu dữ liệu có n_feature thuộc tính •
Trừ mỗi iểm dữ liệu cho vector kỳ vọng: 𝑋𝑘 = 𝑋𝑘 - 𝑋𝑚𝑒𝑎𝑛
với k = 1....n_sample và 𝑋𝑚𝑒𝑎𝑛 là vector trung bình của tất cả các iểm dữ liệu 1 𝑇 ∗ 𝑋 •
Tính ma trận hiệu phương sai : S = ∗ 𝑋
𝑛− 𝑠𝑎𝑚𝑝𝑙𝑒 •
Tìm trị riêng, vector riêng của ma trận S •
Lấy k trị riêng có giá trị lớn nhất, tạo ma trận U với các hàng là các vector riêng ứng với k trị riêng ã chọn •
Ánh xạ không gian ban ầu sang không gian k chiều: 𝑋𝑛𝑒𝑤= X * U. •
Note: Nếu không hiểu phép nhân ở Step 6 bạn có thể lấy từng mẫu dữ liệu nhân với từng
vector riêng, khi ó mỗi mẫu dữ liệu ban ầu sẽ ược nhân với k vector nên sẽ có k chiều.
Dưới ây là một ví dụ về cách thực hiện PCA trong matlab: lOMoARcPSD| 36991220
Chương 4: Ứng dụng của PCA giảm chiều dữ liệu thực tế.
1.Vì sao phải giảm chiều dữ liệu:
 Như mọi người ã biết, trong các bài toán học máy thì dữ liệu có kích thước rất lớn. Máy tính
có thể hiểu và thực thi các thuật toán trên dữ liệu này, tuy nhiên ối với con người ể "nhìn" dữ liệu
nhiều chiều thật sự là rất khó. Vì vậy bài toán giảm chiều dữ liệu ra ời giúp ưa ra cái nhìn mới cho
con người về dữ liệu nhiều chiều. Ngoài ể trực quan dữ liệu, các phương pháp giảm chiều dữ liệu
còn giúp ưa dữ liệu về một không gian mới giúp khai phá các thuộc tính ẩn mà trong chiều dữ liệu
ban ầu không thể hiện rõ, hoặc ơn giản là giảm kích thước dữ liệu ể tăng tốc ộ thực thi cho máy tính.
2 Các ví dụ về giảm chiều dữ liệu: lOMoARcPSD| 36991220
Ta sẽ tìm hiểu về khái niệm giảm chiều dữ liệu qua ví dụ. Ta có tập dữ liệu { 𝑥(1) , 𝑥(2), . .
𝑥(𝑛)} mỗi iểm dữ liệu 𝑥(𝑖)∈ 𝑅(𝑑) thể hiện cho một khách hàng. Một khách hàng i có những thuộc
tính: tuổi, nghề nghiệp, thu nhập, tổng giá trị sản phẩm ã mua,… tương ứng với 𝑥1𝑖 , 𝑥2𝑖 ,
𝑥3𝑖 , … . 𝑥𝑑𝑖 . Trong các thuộc tính trên có những thuộc tính có thể phụ thuộc lẫn nhau. Ta có thể
dùng suy luận ể nhận xét rằng, một người có thu nhập cao sẽ chi ra nhiều tiên ể mua sản phẩm
của công ty, nói cách khác mối quan hệ của thuộc tính “thu nhập” và “tổng giá trị sản phẩm ã
mua” có thể biểu diễn bằng hàm y=ax+b. Do ó, ta chỉ cần một vector d−1 chiều ể biểu diễn 𝑥(2) ∈𝑅(𝑑) .
Những thuật toán giảm chiều dữ liệu sẽ giúp thực hiện việc suy luận mối quan hệ của các
thuộc tính một cách tự ộng và tối ưu nhất từ ó có thể giảm chiều dữ liệu cho tập dữ liệu ban ầu.
Tiếp theo ta có ví dụ giảm chiều dữ liệu khác:
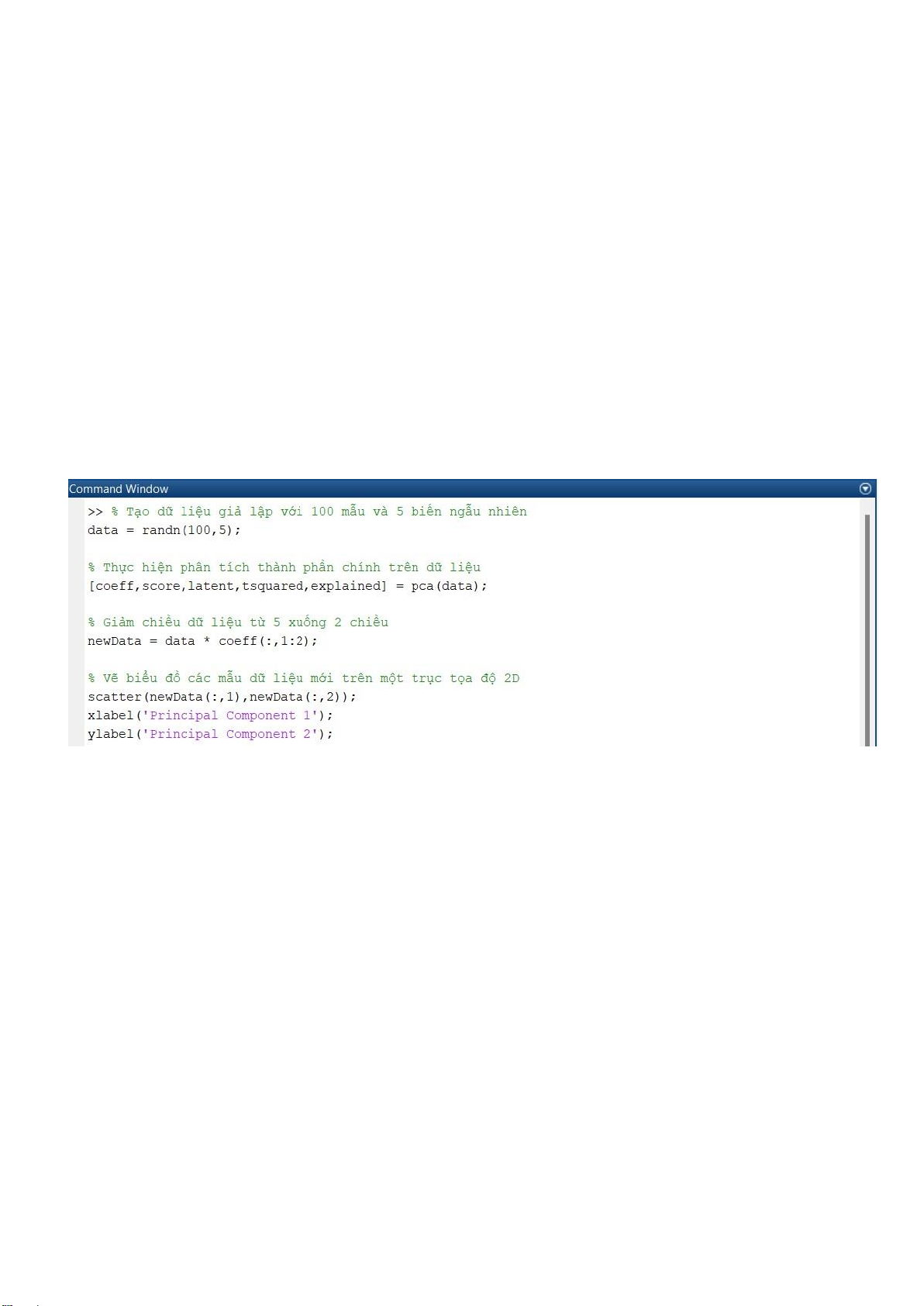
Trong ví dụ này, chúng ta tạo ra một ma trận ngẫu nhiên 100x5 (100 mẫu và 5 biến), sau ó
thực hiện PCA ể giảm chiều dữ liệu từ 5 xuống 2 chiều bằng cách sử dụng hai thành phần chính
ầu tiên. Cuối cùng, chúng ta vẽ biểu ồ các mẫu dữ liệu mới trên một trục tọa ộ 2D.
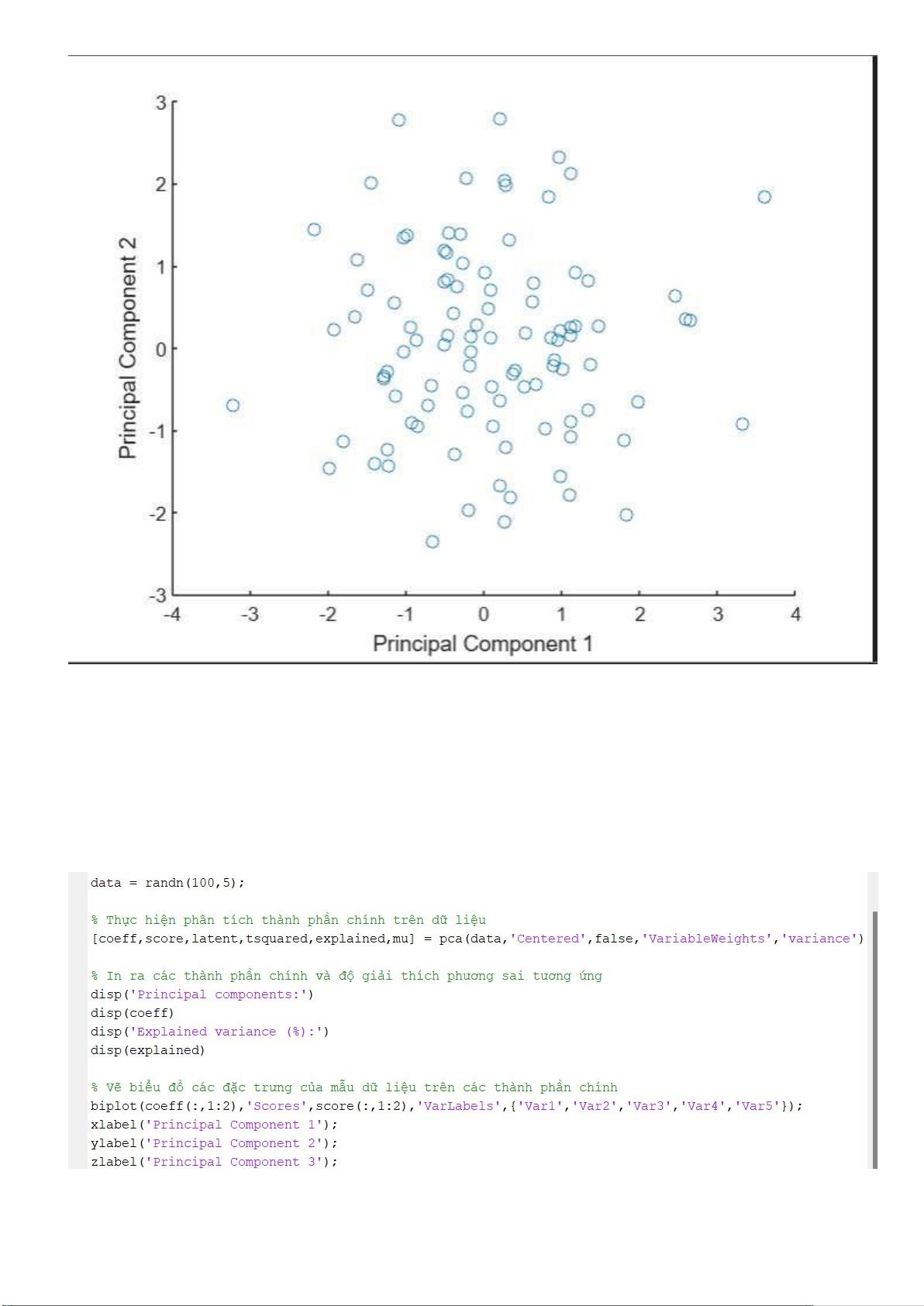
Và ồ thị sau khi ược giảm chiều: lOMoARcPSD| 36991220
Tương tự như ví dụ trên: chúng ta tạo ra một ma trận ngẫu nhiên 100x5 (100 mẫu và 5 biến), sau
ó thực hiện PCA trên dữ liệu. Tùy chọn 'Centered',false ược sử dụng ể không tạo ra một ma trận
dữ liệu trung bình và 'VariableWeights','variance' ược sử dụng ể xác ịnh trọng số của các biến
dựa trên phương sai của chúng.
Sau ó, chúng ta in ra các thành phần chính và ộ giải thích phương sai tương ứng. Cuối cùng, chúng ta
vẽ biểu ồ các ặc trưng của mẫu dữ liệu trên các thành phần chính bằng cách sử dụng hàm biplot. lOMoARcPSD| 36991220
Ngoài ra nó còn ứng dụng với hình học không gian:
Hình Giảm chiều dữ liệu trong ồ thị Ví
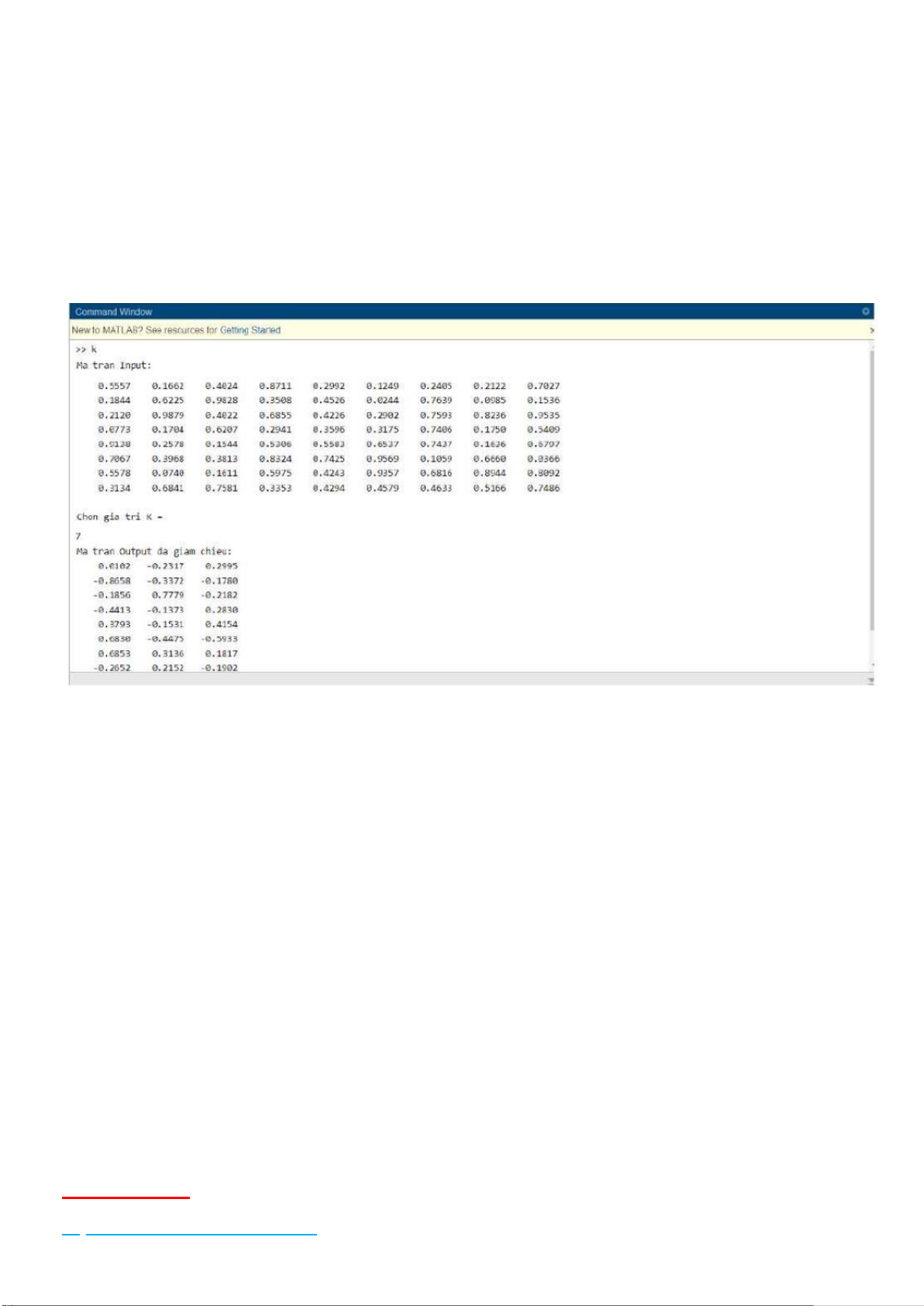
dụ giảm chiều ma trận : Ta có ma trận 109 sau:
0.5557 0.1662 0.4024 0.8711 0.2992 0.1249 0.2405 0.2122 0.7027
0.1844 0.6225 0.9828 0.3508 0.4526 0.0244 0.7639 0.0985 0.1536
0.2120 0.9879 0.4022 0.6855 0.4226 0.2902 0.7593 0.8236 0.9535
0.0773 0.1704 0.6207 0.2941 0.3596 0.3175 0.7406 0.1750 0.5409
0.9138 0.2578 0.1544 0.5306 0.5583 0.6537 0.7437 0.1636 0.6797
0.7067 0.3968 0.3813 0.8324 0.7425 0.9569 0.1059 0.6660 0.0366
0.5578 0.0740 0.1611 0.5975 0.4243 0.9357 0.6816 0.8944 0.8092
0.3134 0.6841 0.7581 0.3353 0.4294 0.4579 0.4633 0.5166 0.7486 lOMoARcPSD| 36991220
Sau khi xử lí giảm xuống 3 chiều ta ược: 0.0102 -0.2317 0.2995 -0.8658 -0.3372 -0.1780 -0.1856 0.7779 -0.2182 -0.4413 -0.1373 0.2830 0.3793 -0.1531 0.4154 0.6830 -0.4475 -0.5933 0.6853 0.3136 0.1817 -0.2652 0.2152 -0.1902
Hình 5.3: Kết quả sau khi giảm chiều
Chương 5: Kết luận.
1. Kết luận chung về PCA: lOMoARcPSD| 36991220 •
PCA (Principal Component Analysis) là một phương pháp ược sử dụng ể giảm chiều dữ
liệu trong các bài toán phân tích a biến. Phương pháp này hoạt ộng bằng cách tìm các
thành phần chính của dữ liệu, ó là các hướng trong không gian dữ liệu có phương sai lớn
nhất. Sau ó, dữ liệu ược biểu diễn trong không gian mới ược tạo ra từ các thành phần
chính, với số chiều dữ liệu giảm xuống. •
PCA ược ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm xử lý ảnh, nhận dạng giọng nói,
và phân tích dữ liệu trong khoa học dữ liệu. PCA có thể giúp giảm kích thước của dữ liệu,
cải thiện hiệu suất và giảm ộ phức tạp tính toán trong các bài toán lớn.
Tuy nhiên, khi sử dụng PCA, cần lưu ý rằng việc giảm chiều dữ liệu có thể dẫn ến mất mát thông
tin và hiệu quả của phương pháp còn phụ thuộc vào sự lựa chọn số lượng thành phần chính. Nếu
số lượng thành phần chính ược chọn quá thấp, thì sẽ có mất mát thông tin, và nếu số lượng
thành phần chính ược chọn quá cao, thì sẽ có nhiễu và không giảm ược kích thước dữ liệu.
Tóm lại, PCA là một phương pháp hữu ích ể giảm chiều dữ liệu, tuy nhiên cần phải ược sử dụng
úng cách và với sự lựa chọn số lượng thành phần chính phù hợp ể ảm bảo tính hiệu quả và chính xác của phương pháp.
2. Những kiến thức nhận lại.
Qua ề tài này nhóm chúng em nhận ược những thứ áng quí: -
Những kiến thức về PCA (principle component analysis)
- Ứng dụng vào giảm chiều dữ liệu nói riêng và các ứng dụng khác nói chung -
Khả năng làm việc nhóm hiệu quả.
Nhờ ề tài về ứng dụng phân tích thành phần chính PCA ể giảm chiều dữ liệu, nhóm của
chúng em ã có cái nhìn sâu sắc hơn về sự liên kết giữa lý thuyết và thực tế trong bộ môn Đại số
tuyến tính. Trong quá trình thực hiện ề tài, chúng em ã học ược nhiều kiến thức bổ ích và sâu sắc
về phương pháp giảm chiều dữ liệu và phân tích thành phần chính.
Ban ầu, khi ược giao làm bài tập lớn cùng nhau, chúng em gặp nhiều khó khăn. Tuy nhiên,
chúng em ã học ược cách phân chia nhiệm vụ cho nhau, ồng thời xây dựng tinh thần và trách
nhiệm trong ội nhóm. Chúng em cố gắng và nỗ lực ể hoàn thành trách nhiệm của mình. Một lần
nữa, chúng tôi muốn bày tỏ lòng biết ơn ến các giáo viên ã cung cấp cho chúng tôi cơ hội ể làm
việc và phát triển c 甃 ng nhau, giúp ỡ nhau ể tiến bộ trong hành trình học tập. HẾT Tài liệu tham khảo:
[1] Bộ môn Toán ứng dụng – Khoa Khoa học Ứng dụng: Giáo trình Đại số tuyến
tính (Tài liệu lưu hành nội bộ), trường ĐH Bách Khoa – ĐH Quốc gia TPHCM, 2020. lOMoARcPSD| 36991220
[2]:https://machinelearningcoban.com/2017/06/15/pca/#241-d-liu-mt-chiu
[3]:https://en.wikipedia.org/wiki/Principal_component_analysis#PCA_and_informatio n_t heory [4] Builtin : LINK.
[5]: https://tuanvanle.wordpress.com/2013/12/25/phuong-phap-phan-tich-thanhphan-
chinh-principal-component-analysis-pca/
[6]: Ưu iểm của phương pháp PCA Nhược iểm của PCA - Tài liệu text (123docz.net)
[7]: [Solved] PCA (Principle Component Analysis) is a dimensionality reduction
technique that projects - Studocu
[8]: https://machinelearningcoban.com/2017/06/15/pca/ Một
số thuật ngữ liên quan:
PCA (Principal component analyst): Phân tích thành phần chính.
Dimensionality reduction: Giảm chiều dữ liệu. Matrix : ma trận. Data: dữ liệu
Random: Số ngẫu nhiên Features: tính năng.
Nhận xét của giảng viên:
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................
......................................................................................................................................