Bài tập lớn - Phân tích phương pháp Bellman môn Hệ thống điện | Trường Đại học Bách Khoa Hà Nội

ĐẠI HỌC BÁCH KHOA HÀ NỘI TRƯỜNG KINH TẾ ****** ****** BÀI TẬP LỚN
HỌC PHẦN: KINH TẾ VẬN HÀNH HỆ THỐNG ĐIỆN
Giảng viên hướng dẫn: TS Phan Diệu Hương
Nhóm sinh viên thực hiện: Nhóm 3 Phạm Thanh Hương 20222921 Hà Duy Hiếu 20222918 Phùng Minh Quang 20222952 Đặng Anh Khôi 20222928 Lê Hoàng Vinh 20222901 Phạm Thuỳ Linh 20222935 Dương Thu Thảo 20222957 Mã Thị Thu Hương 20222920 Lê Thị Quỳnh Anh 20222906 Nguyễn Trà My 20222940
Hà Nội, tháng 11 năm 2024 MỤC LỤC 1.
ĐẶT VẤN ĐỀ, KHÁI QUÁT VỀ PHƯƠNG PHÁP BELLMAN VÀ CƠ SỞ LÝ THUYẾT 3
1.1. Đặt vấn đề 3
1.2. Khái quát về phương pháp Bellman 3
1.3. Cơ sở lý thuyết 3
2. BÀI TOÁN QUY HOẠCH TUYẾN ĐƯỜNG ĐI 4
3. ÁP DỤNG QUY HOẠCH ĐỘNG BELLMAN VÀO PHÂN PHỐI TỐI ƯU 9 PHỤ TẢI 9 2
1. ĐẶT VẤN ĐỀ, KHÁI QUÁT VỀ PHƯƠNG PHÁP BELLMAN VÀ CƠ SỞ LÝ THUYẾT
1.1. Đặt vấn đề
Quy hoạch động là một phương pháp thường được
áp dụng để giải quyết bài toán phân phối tối ưu phụ tải giữa
các tổ máy trong nhà máy nhiệt điện cũng như trong hệ thống điện.
Mô hình động là một phương pháp toán học giải
quyết vấn đề lựa chọn tối ưu bằng cách phân chia vấn đề tối
ưu bằng cách phân chia vấn đề cần giải quyết thành các giai
đoạn nhỏ dễ giải quyết hơn. Mô hình động giải quyết một
cách điển hình vấn đề tối ưu hóa theo giai
đoạn, từ đó giải quyết vấn đề tối ưu hóa toàn bộ. Việc tính toán trong các giai đoạn khác nhau
được liên kết thông qua mối quan hệ lặp trong cách thức đạt được các lời giải tối ưu có thể
đến khi toán bộ vấn đề được giải quyết ở giai đoạn cuối cùng. Mô hình động được coi là một
chương trinh đa giai đoạn, được ứng dụng trong các vấn đề ra quyết định theo thời gian.
Quy hoạch động Bellman rất thuận tiện cho việc phân phối các phụ tải nhưng để áp
dụng vào thực tế thì chịu ảnh hưởng của rất nhiều các yếu tố khác, không đơn giản như
những bài toán con, đòi hỏi phải phân tích công phu, nhận biết thế nào là thích hợp và nhiều
thời gian suy nghĩ mới có thể thực hiện được.
1.2. Khái quát về phương pháp Bellman
Phương pháp Bellman thường được áp dụng để giải bài toán phân phối tối ưu
phụ tải giữa các tổ máy trong nhà máy điện cũng như mô hình hệ thống điện với điều
kiện như sau: Nhà máy nhiệt điện gồm nhiều tổ máy. Phụ tải của nhà máy luôn thay
đổi. Số tổ máy cần hoạt động, công suất từng tổ máy sao cho chi phí sản xuất là nhỏ nhất.
1.3. Cơ sở lý thuyết
Cơ sở lý thuyết mô hình động là nguyên tắc tối ưu hoá của Bellman được phát biểu
như sau: “Một quỹ đạo tối ưu có đặc điểm là dù bất kỳ tình trạng và quyết định ban đầu như
thế nào, những quyết định còn lại phải tạo thành quỹ tạo tối ưu, với việc xem trạng thái đó
là kết quả từ quyết định đầu tiên.”
Vấn đề của bài toán quy hoạch động là tìm quỹ đạo tối ưu chứ không chỉ tìm một bộ phận tối ưu. 3
Cần chú ý: nếu lời giải có (n) bước trong đó có bước thứ (k) thì lời giải tổng thể có
thể rất khác với lời giải tối ưu ở bước thứ (k). Thủ tục trong quy hoạch động Bellman có thể
lặp xuôi hay lặp ngược.
2. BÀI TOÁN QUY HOẠCH TUYẾN ĐƯỜNG ĐI
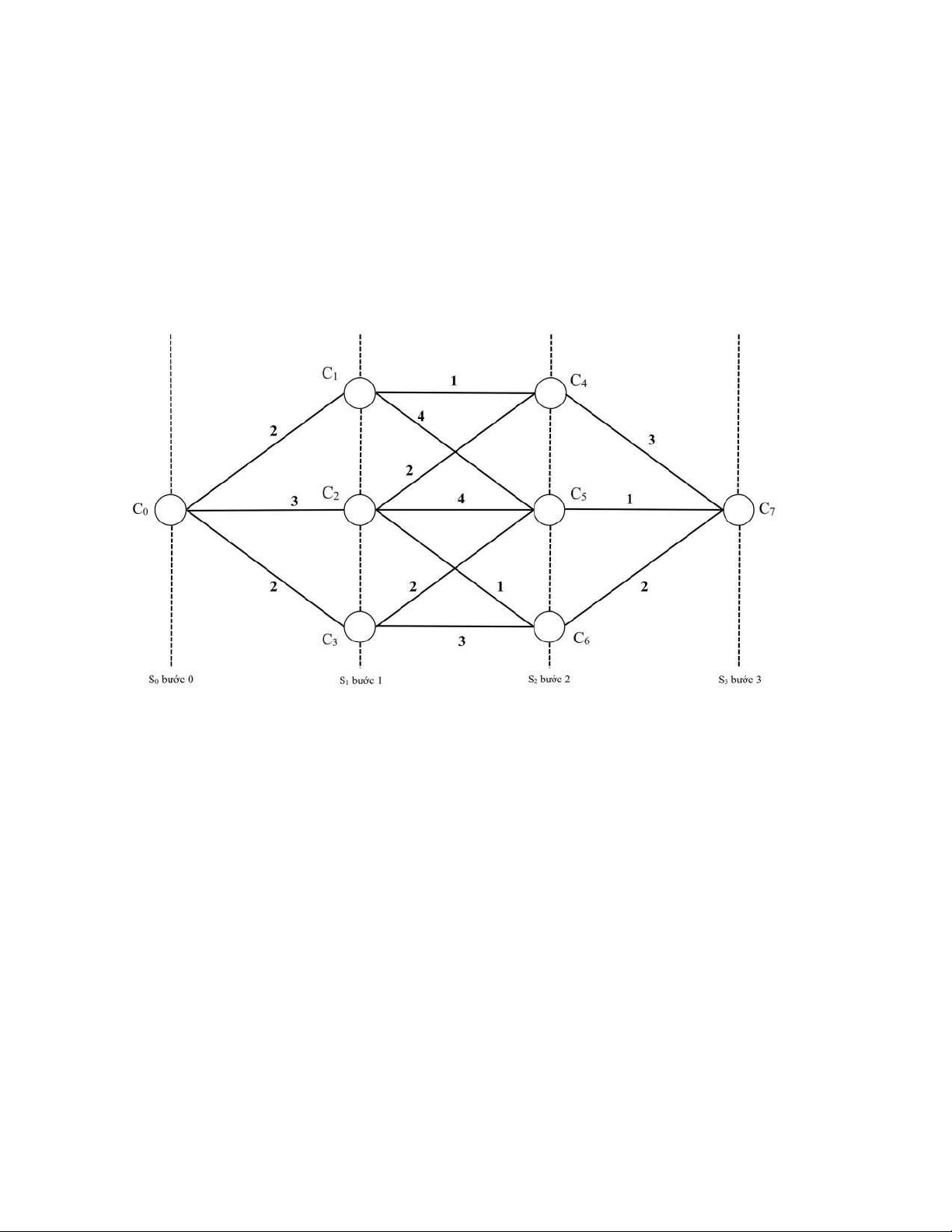
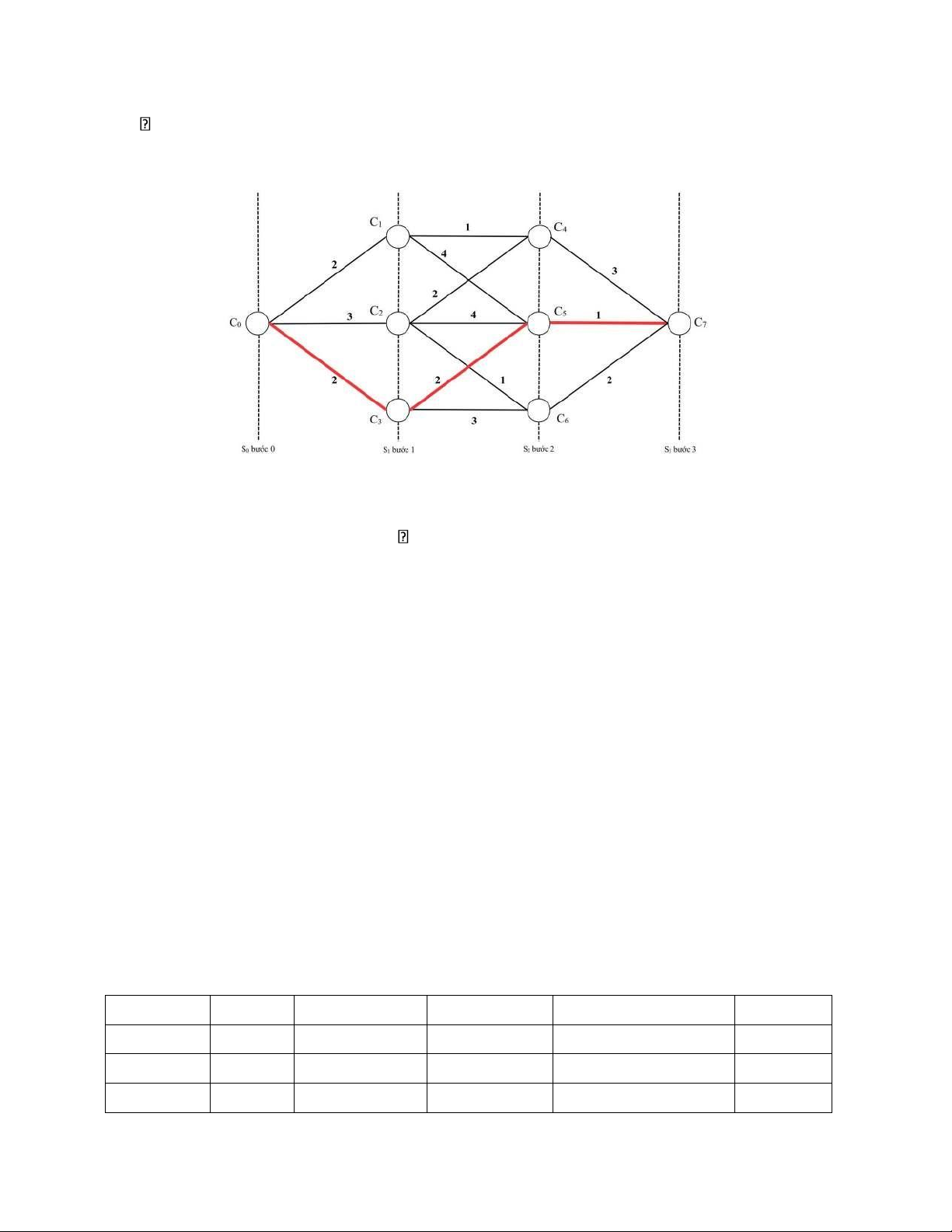
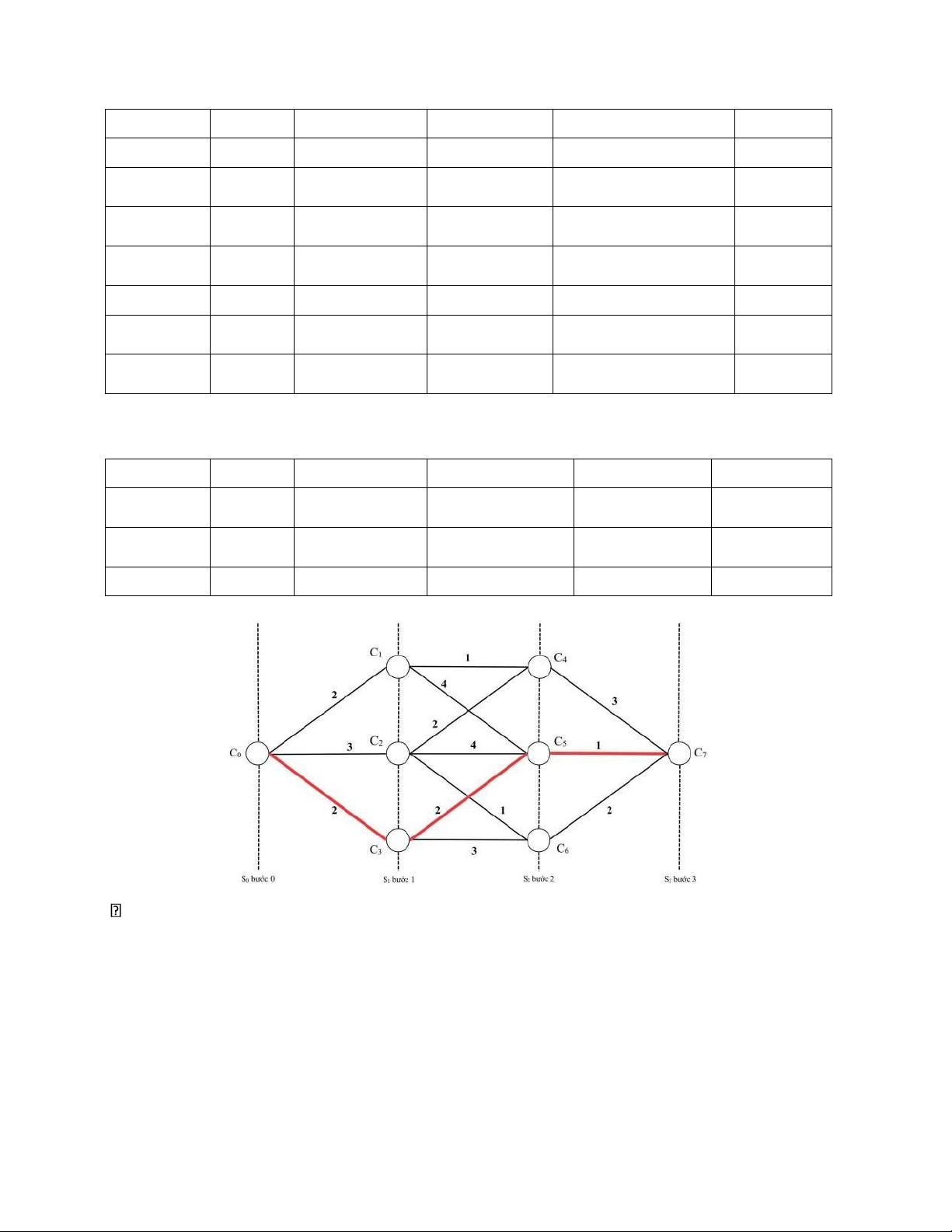
2.1. Bài toán: Có mạng giao thông được cho như hình dưới đây, hãy quyết định
tuyến đường để đi từ thành phố C0 đến thành phố C7.
Một cung đường (hay đoạn) nối giữa hai điểm bất kỳ (hay các thành phố) thể hiện con
đường giữa các thành phố.
Chi phí của việc đi lại giữa hai thành phố bất kì được chỉ ra dọc theo con đường trên
hình. Có 4 giai đoan dừng từ C0 đến C7.
- Điểm dừng đầu tiên là điểm xuất phát C0.
- Điểm dừng thứ hai là tại 1 trong 3 thành phố C1, C2 hay C3.
- Điểm dừng thứ ba là tại 1 trong 3 thành phố C4, C5 hay C6. - Điểm dừng cuối cùng là tại C7.
Yêu cầu bài toán đặt ra: Tìm con đường đi từ thành phố C0 đến C7 sao cho chi phí đi
lại là ít nhất. (Đơn vị chi phí: $)
2.2. Giải bài toán.
Nếu đi từ C0 đến C7 thì tổng chi phí đi lại sẽ tăng dần qua từng bước cho tới khi tiến tới
điểm cuối cùng. Có thể thấy rằng, tổng chi phí để đến được một bước (giai đoạn) hiện tại 4
nào đó sẽ bằng tổng chi phí để đến bước ngay trước bước hiện tại cộng với chi phí chuyển
từ bước ngay trước bước hiện tại đó sang bước hiện tại. Ví dụ:
Tổng chi phí tại bước n =
Tổng chi phí đi từ bước 1 + Chi phí chuyển từ bước
đến bước (n – 1) (n – 1) sang bước n.
Mối quan hệ lặp lại đó được thể hiện như sau: f *
ij(n) = Cij + fi (n – 1)
Trong đó: fij(n) : Tổng chi phí của việc chuyển tới trạng thái (j) ở bước hiện tại (n)
từ trạng thái (i) của bước trước (n – 1).
Cij : Chi phí chuyển từ trạng thái (i) của bước thứ (n – 1) (bước trước)
sang trạng thái (j) của bước thứ (n) (bước hiện tại).
f *i(n – 1) : Tổng chi phí nhỏ nhất tới trạng thái (i) của bước (n – 1).
- Các bước: các điểm dừng (4 điểm dừng).
- Các trạng thái: các thành phố ở mỗi điểm dừng.
Như vậy nếu đi từ C0 đến C7, dòng tiền sẽ được tích lũy dần theo hướng từ C0 đến C7.
Thủ tục lặp lại như vậy gọi là thủ tục lặp lại xuôi: f * *
j (n) = min S1{ fij(n) = Cij + fj (n – 1) }
Các bước tính toán cụ thể từng giai đoạn được thể hiện trong các bảng sau:
Bước 1 (n = 1) 5 Trạng Trạng Chi phí Tổng chi phí Tổng chi phí Tổng chi thái thái chuyển từ Si nhỏ nhất đến tới trạng thái phí nhỏ
trước đó hiện tại S bước trước hiện tại: f nhất đến j ij(n) Si S f *(n – 1) * trạng thái j C i = C (n – ij ij + fi 1) hiện tại: f *j(n) C0 C1 2 0 2 2 C0 C2 3 0 3 3 C0 C3 2 0 2 2
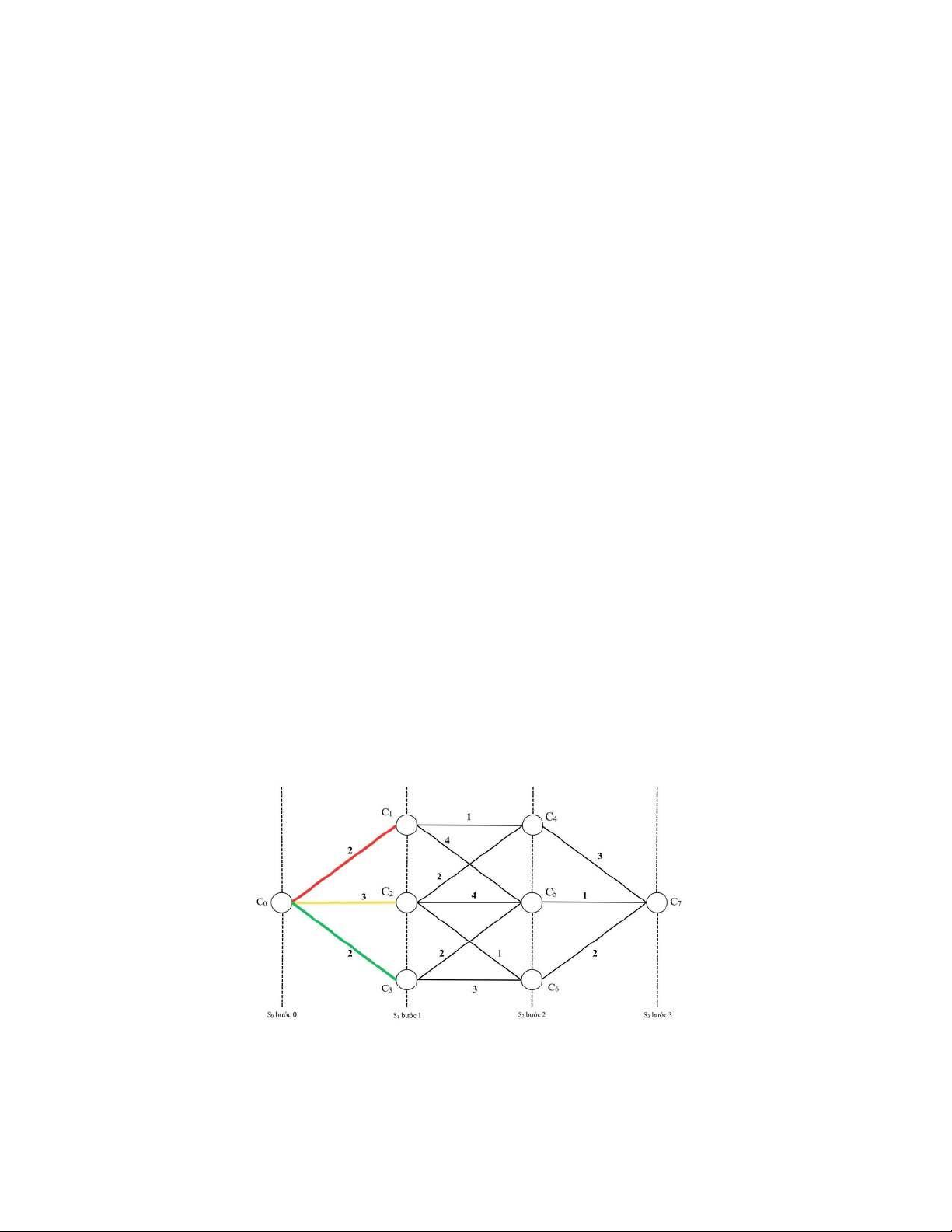
- Chi phí di chuyển từ C0 đến C1 là 2$, tổng chi phí nhỏ nhất đến trạng thái hiện tại là 2$.
- Chi phí di chuyển từ C0 đến C2 là 3$, tổng chi phí nhỏ nhất đến trạng thái hiện tại là 3$.
- Chi phí di chuyển từ C0 đến C3 là 3$, tổng chi phí nhỏ nhất đến trạng thái hiện tại là 2$.
Bước 2 (n = 2) S * * * i Sj Cij fi (n – 1)
fij(n) = Cij + fi (n – fj (n) 1) C1 C4 1 2 3 3 C1 C5 4 2 6 C2 C4 2 3 5 C2 C5 4 3 7 C2 C6 1 3 4 4 C3 C5 2 2 4 4 6 C3 C6 3 2 5
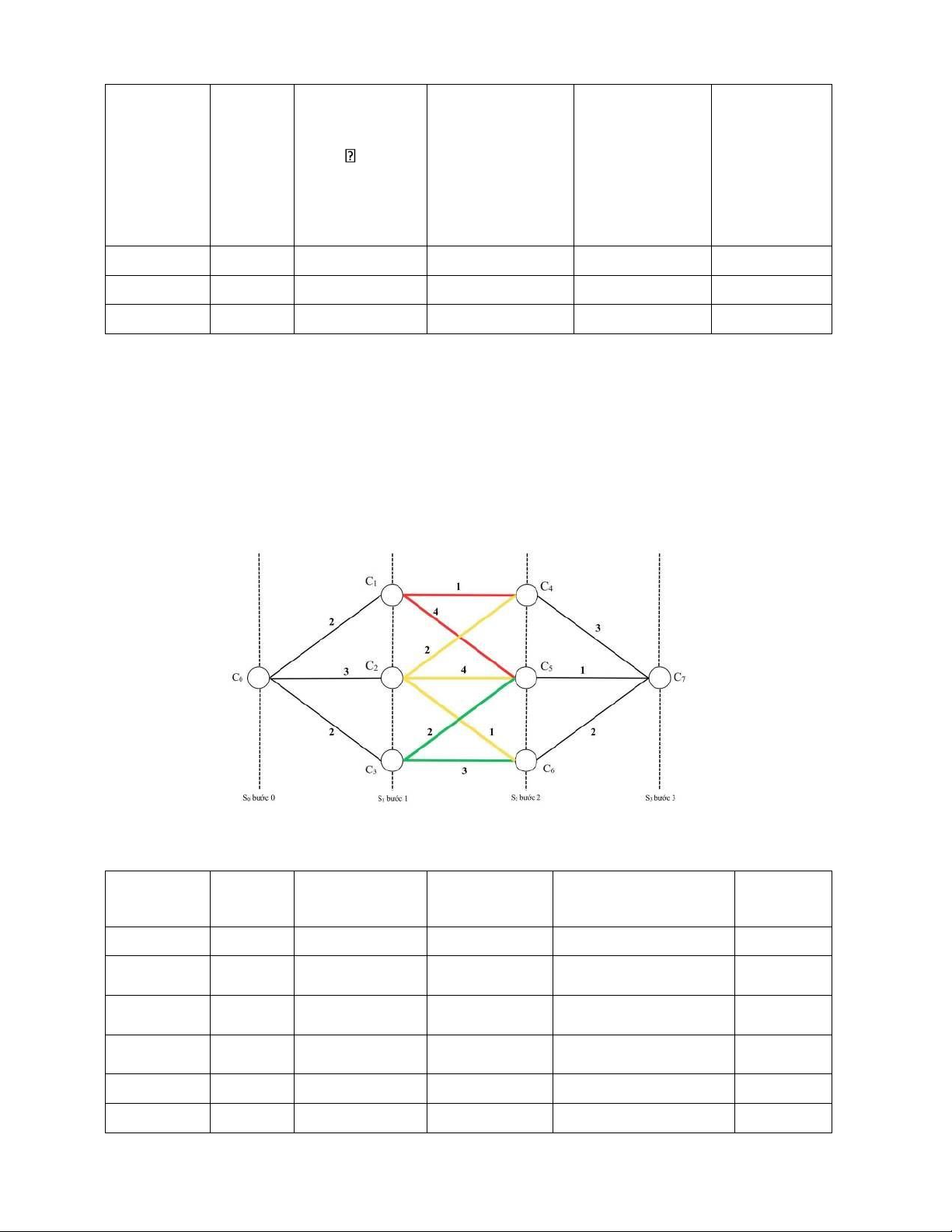
- Có 2 cách để di chuyển từ C1: đến C4 hoặc C5.
+ Chi phí từ C1 đến C4 là 1$, tổng chi phí tới trạng thái hiện tại là 3$.
+ Chi phí từ C1 đến C5 là 4$, tổng chi phí đến trạng thái hiện tại là 6$.
Khi đi từ C1 đến thành phố tiếp theo, tổng chi phí nhỏ nhất tới hiện tại: min{3; 6} = 3$.
- Có 3 cách để di chuyển từ C2: đến C4, C5 hoặc C6.
+ Chi phí từ C2 đến C4 là 2$, tổng chi phí đến hiện tại là 5$.
+ Chi phí từ C2 đến C5 là 4$, tổng chi phí đến hiện tại là 7$. +
Chi phí từ C2 đến C6 là 1$, tổng chi phí đến hiện tại là 4$.
Khi đi từ C2 đến thành phố tiếp theo, tổng chi phí nhỏ nhất tới hiện tại: min{5; 7; 4} = 4$.
- Có 2 cách để di chuyển từ C3: đến C5 hoặc C6.
+ Chi phí từ C3 đến C5 là 2$, tổng chi phí đến hiện tại là 4$.
+ Chi phí từ C3 đến C6 là 3$, tổng chi phí đến hiện tại là 5$.
Khi đi từ C3 đến thành phố tiếp theo, tổng chi phí nhỏ nhất tới hiện tại: min{4; 5} = 4$.
Bước 3 (n = 3) S * * * i Sj Cij fi (n – 1)
fij(n) = Cij + fi (n – fj (n) 1) C4 C7 3 3 6 C5 C7 1 4 5 5 C6 C7 2 4 6
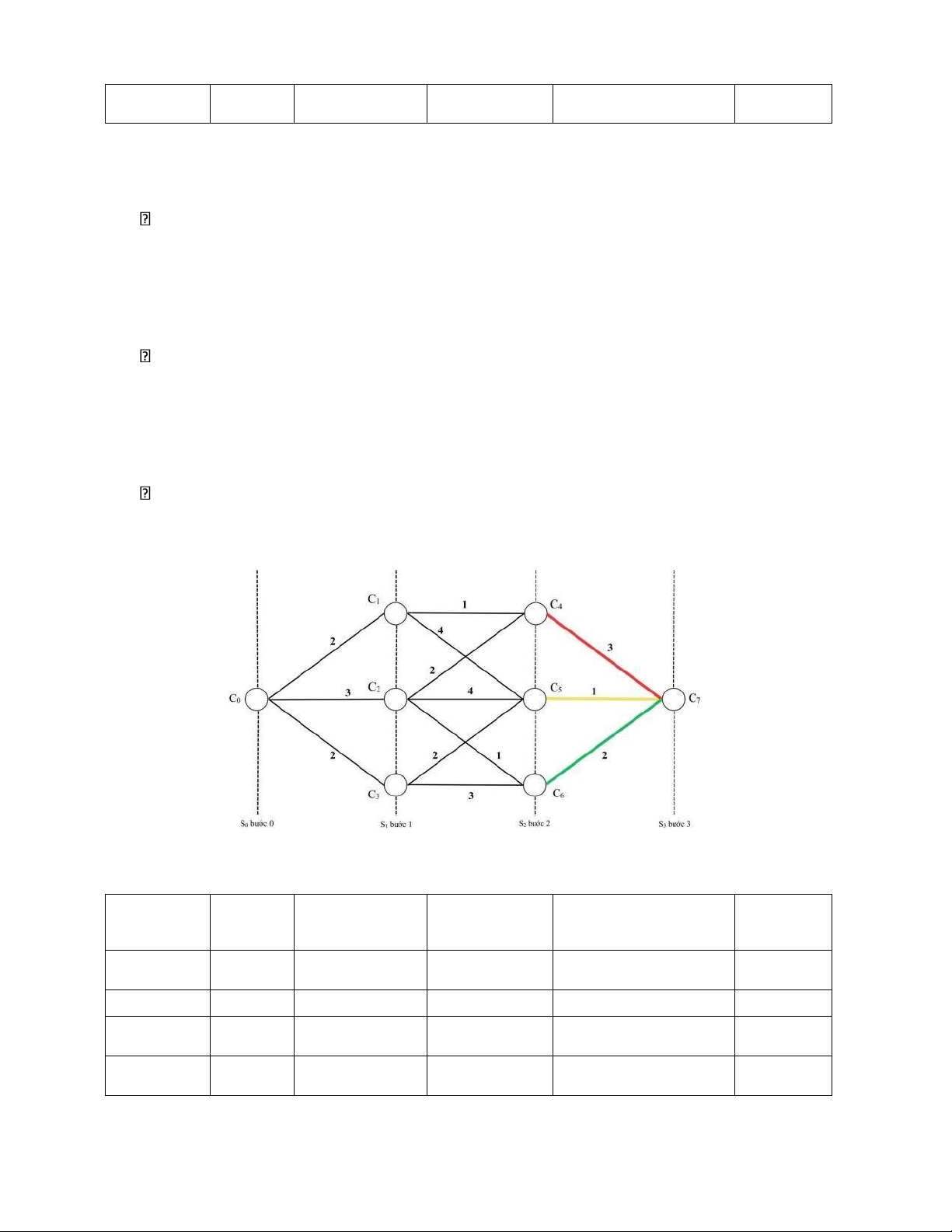
- Chi phí di chuyển từ C4 đến C7 là 3$, tổng chi phí đến hiện tại là 6$. -
Chi phí di chuyển từ C5 đến C7 là 1$, tổng chi phí đến hiện tại là 5$. 7
- Chi phí di chuyển từ C6 đến C7 là 2$, tổng chi phí đến hiện tại là 6$.
Khi đi từ các thành phố đến thành phố C7, tổng chi phí nhỏ nhất tới hiện tại: min{6; 5; 6} = 5$.
Vậy đường đi tối ưu: C7, C5, C3, C0 C0, C3, C5, C7 với tổng chi phí nhỏ nhất là 5$.
Nếu đi từ điểm cuối C7 về điểm xuất phát C0 thì tổng chi phí đi lại sẽ được tích lũy hướng từ
C7 về C0, thủ tục lặp lại như vậy gọi là lặp ngược.
Tổng chi phí của thủ tục lặp ngược: f * *
j (n) = min Si { fij(n) = Cij + fj (n + 1) } Trong đó:
f *j(n) : Tổng chi phí đi tới trạng thái (j) của bước hiện tại (n) từ trạng thái (i) của bước (n + 1) (bước trước).
Cij : Chi phí chuyển từ trạng thái (i) (bước trước n + 1) tới trạng thái (j) của bước hiện tại (n).
f *j(n + 1) : Tổng chi phí nhỏ nhất tới được trạng thái (i) của bước (n + 1) nghĩa là bước trước.
Bước 2 (n = 2) S * j Si Cij fi (n + 1) fij fj(n) C4 C7 3 0 3 3 C5 C7 1 0 1 1 C6 C7 2 0 2 2 8
Bước 1 (n = 1) S * j Si Cij fi (n + 1) fij fj(n) C1 C4 1 3 4 4 C1 C5 4 1 5 C2 C4 2 3 5 C2 C5 4 1 5 C2 C6 1 2 3 3 C3 C5 2 1 3 C3 C6 3 2 5
Bước 0 (n = 0) S * j Si Cij fi (n + 1) fij fj(n) C0 C1 2 4 6 C0 C2 3 3 6 C0 C3 2 3 5 5
Vậy đường đi tối ưu trong thủ tục lặp ngược: C0, C3, C5, C7 với chi phí là 5$.
3. ÁP DỤNG QUY HOẠCH ĐỘNG BELLMAN VÀO PHÂN PHỐI TỐI ƯU PHỤ TẢI
Phương pháp quy hoạch động bellman được áp dụng trong việc phân phối tối ưu
phụ tải trong nhà máy và hệ thống cả ở ngắn hạn và trung hạn. Việc áp dụng được trình bày qua bài toán sau: 9
Bài toán: Cần phân phối phụ tải (P) cho (n) tổ máy đang vận hành của nhà máy. Đặc
tính năng lượng của các tổ máy là Qi(Pi) đã cho.
• Bài toán được phát biểu dưới dạng công thức toán như sau: • Hàm mục tiêu: n
∑Qi (Pi)→Min i=1 n • Hàm ràng buộc: ∑ Pi=P i=1 Pmin i ≤ Pi≤ Pmaxi
• Công thức lặp Bellman được áp dụng trong phân phối tối ưu ở bước thứ (i):
f n( P)=min{f n−1(P−Pn)+Qn (Pn)} Trong đó:
f n( P): Tổng tiêu hao năng lượng toàn nhà máy ở bước thứ (n) ứng với phụ tải (P)
f n−1(P−Pn): Tổng tiêu hao năng lượng toàn nhà máy ở bước (n-1) ứng với phụ tải (P−Pn)
Qn (Pn): Tiêu hao năng lượng của tổ máy thứ (n) ở bước (n) ứng với phụ tải (Pn)
Kết quả ở bước thứ (n) sẽ là kết quả tối ưu từ (n) bước lặp.
- Bước quyết định đầu tiên (bước 1):
+ Chỉ xét một tổ máy chạy với phạm vi công suất
+ Xét tiêu hao năng lượng với phạm vi đã cho -
Bước tiếp theo (bước 2):
+ Đưa thêm một tổ máy bất kỳ vào.
+ Tính toán các tiêu hao năng lượng tương ứng với các nấc công suất có thể của cả
hai tổ máy cung cấp được.
+ Chọn sự phối hợp tối ưu ở từng nấc công suất (tiêu hao năng lượng nhỏ nhất).
( Cần tìm tiêu hao năng lượng tối ưu cho các khả năng phối hợp cung cấp công suất
đẳng trị của 2 tuabin). 10 - Các bước tiếp theo
+ Lần lượt đưa các tổ máy vào vận hành
+ Tìm tiêu hao năng lượng tối ưu cho các nấc công suất đẳng trị của các tổ máy
- Bước lặp được thực hiện liên tiếp cho đến tổ máy cuối cùng
+ Phối hợp tối ưu của các tổ máy ở bước cuối cùng là kết quả phân phối tối ưu công
suất cho tổ máy cuối cùng và các tiêu hao năng lượng nhỏ nhất đối với từng nấc công suất của nhà máy
+ Phụ tải tối ưu phân cho các tổ máy khác được tìm bằng cách đi ngược lại quá trình tính toán trên
Ví dụ: Áp dụng phương pháp quy hoạch động Bellman để phân phối tối ưu phụ tải cho 3 tổ
máy sau. Biết 3 tổ máy chạy song song và các tiêu hao năng lượng được cho ở bảng: Tổ máy Công suất (MW) 0 2 4 6 B1 (t/h) 2 3 4 5 B2 (t/h) 1 2 3 6 B3 (t/h) 1 3 4 5
Bước 1: Xác định tiêu hao năng lượng của tổ máy 1 ở các nấc công suất khác nhau:
f1( P) ¿Q1(P1)
Phạm vi phụ tải: (0, 2, 4, 6 MW). Các tiêu hao năng lượng tương ứng: 2, 3, 4, 5 (t/h)
Bước 2: Đưa tổ máy 2 vào vận hành, xác định hàm f2( P) theo công thức:
f2( P)=min{f 1(P−P2)+Q2(P2)}
Hàm xác định trong khoảng phụ tải (0-12MW), với các tiêu hao năng lượng ở từng nấc công suất đẳng trị: •
P = 0 MW, f2(0 )=min{f1(0−P2)+Q2 (P2)}
Vì P1, P2 không thể nhỏ hơn 0MW nên chỉ có một trường hợp (P1, P2 = 0) và tiêu hao năng
lượng tương ứng: f2(0) = 2+1 = 3 (t/h): •
P = 2 MW, f2(2)=min{f 1(2−P2)+Q2(P2)}
Các phối hợp công suất có thể giữa 2 tổ máy để cung cấp 2MW:
(P1 = 0MW; P2 = 2MW) và (P1 = 2MW; P2 = 0MW) Tiêu
hao năng lượng tương ứng với công suất đẳng trị: 11
f2(2)=f1 (0)+Q2 (2)=2+2=4 (t/h) f2(2)=f1 (2)+Q2(0 )=3+1=4 (t/h) f2(2)=4(t/h)
Áp dụng tính tương tự ứng với: •
P = 4MW, f2( 4)=min{f 1(4−P2)+Q2(P2)}=5(t/h) •
P = 6MW, f2(6 )=min{f1(6−P2)+Q2 (P2)}=6 (t/h) •
P = 8MW, f2(8 )=min{f1(8−P2)+Q2(P2)}=7 (t/h) •
P = 10MW, f2(10)=min{f1(10−P2)+Q2(P2)}=8 (t/h) •
P = 12MW, f2(12)=min{f1 (12−P2)+Q2 (P2)}=11 (t/h)
Bước 3: Đưa tổ máy thứ 3 vào vận hành, xác định hàm f3( P) theo công thức:
f3( P)=min{f2(P−P3)+Q3(P3)}
Hàm xác định trong khoảng phụ tải (0 - 18MW), với các tiêu hao năng lượng ở từng nấc công suất đẳng trị:
P = 0 MW f3(0 )=min{f2(0−P3)+Q3 (P3)}
Vì P1, P2, P3 không thể nhỏ hơn 0MW nên chỉ có một trường hợp (P1, P2, P3 = 0) và tiêu
hao năng lượng tương ứng: f3(0 )=2+1+1=4 (t/h)
Áp dụng tính tương tự ứng với: •
P = 2 MW, f3(2)=min{f2(−2P3)+Q3(P3)}=5(t/h) •
P = 4 MW, f3( 4)=min{f2(4−P3)+Q3(P3)}=6(t/h) •
P = 6 MW, f3(6 )=min{f2(6−P3)+Q3(P3)}=7(t/h) •
P = 8 MW, f3(8 )=min{f2(8−P3)+Q3(P3)}=8(t/h) •
P = 10 MW, f3(10 )=min{f2(10−P3)+Q3 (P3)}=9(t/h) •
P = 12 MW, f3(12)=min{f 2(12−P3)+Q3(P3)}=11(t/h) •
P = 14 MW, f3(14 )=min{f2 (14−P3)+Q3(P3)}=12(t/h) •
P = 16 MW, f3(16 )=min{f2(16−P3)+Q3 (P3)}=13(t/h) •
P = 18 MW, f3(18 )=min{f2(18−P3)+Q3 (P3)}=16(t/h) Kết quả tính toán
được ghi lại trong bảng sau: 12 P ∑ P1 f1( P) P2 f2( P) P3 f3( P) 0 0 2 0 3 0 4 2 2 3 0,2 4 0 5 4 4 4 0,2,4 5 0 6 6 6 5 2,4 6 0 7 8 4 7 0 8 10 6 8 0 9 12 11 2,4,6 11 14 4,6 12 16 6 13 18 6 16
sXây dựng bảng tính toán mới để tìm ra kết quả tương ứng với từng bước ở trên đảm bảo
thuận lợi hơn mà không bỏ sót các trường hợp Bước 1: (Tổ máy 1 và 2) P1 0 2 4 6 P2 B2 B1 2 3 4 5 0 1 3 4 5 6 2 2 4 5 6 7 4 3 5 6 7 8 6 6 8 9 10 11
Bước 2: (Tổ máy 1,2 và 3) P1,2 0 2 4 6 8 10 12 P 3 B3 B1,2 3 4 5 6 7 8 11 0 1 4 5 6 7 8 9 12 2 3 6 7 8 9 10 11 14 4 4 7 8 9 10 11 12 15 6 5 8 9 10 11 12 13 16
Bảng phân phối tối ưu phụ tải cho 3 tổ máy trong nhà máy nhiệt điện P1,2,3 (MW) 0 2 4 6 8 10 12 14 16 18 B1,2,3 (t/h) 4 5 6 7 8 9 11 12 13 16 P 3 0 0 0 0 0 0 2,4,4… 4,6,6 6 6 P2 0 2,0 0,2,4 0,2,4 4,6 4 4,4,2… 4,4,2 4,4 6 13 P1 0 0,2 4,2,0 6,4,2 4,2 6 6,4,6… 6,4,6 4,6 6,6 14