













Preview text:
lOMoARcPSD|46958826 lOMoARcPSD|46958826
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC BÁCH KHOA TPHCM BÁO CÁO
BÀI TẬP LỚN VẬT LÝ 1 ĐỀ TÀI 5:
VẼ QUỸ ĐẠO CỦA VẬT THEO PHƯƠNG TRÌNH CHUYỂN ĐỘNG GVHD: LÊ NHƯ NGỌC NHÓM: 5 LỚP: DT05
Thành phố Hồ Chí Minh-2021 1 lOMoARcPSD|46958826
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC BÁCH KHOA TPHCM BÁO CÁO
BÀI TẬP LỚN VẬT LÝ 1 ĐỀ TÀI 5:
VẼ QUỸ ĐẠO CỦA VẬT THEO PHƯƠNG TRÌNH CHUYỂN ĐỘNG GVHD: LÊ NHƯ NGỌC NHÓM:5 LỚP: DT05
Thành phố Hồ Chí Minh-2021 2 lOMoARcPSD|46958826
Danh sách thành viên: Họ và tên MSSV Ghi chú
(hoàn thành công việc) Trần Quang Huy 2013336 100% Võ Bạch Thiên Hương 1913664 100% Lê Đào Quang Huy 2011259 100% Vũ Văn Huy 1913580 100% Võ Chiêu Hùng 2013376 100% Bài tập 5: 3 lOMoARcPSD|46958826
Vẽ quỹ đạo của vật theo phương trình chuyển động 1. Yêu cầu
Sử dụng Matlab để giải bài toán sau:
“Một khí cầu bay lên từ mặt đất với vận tốc không đổi v0. Gió truyền cho khí cầu thành
phần vận tốc theo phương ngang v ay x
, y là độ cao. Cho trước các giá trị v0, a.
Xác định phương trình chuyển động của vật
Xác định phương trình quỹ đạo của vật.
Vẽ quỹ đạo của vật trong khoảng thời gian từ t=0 đến t=5s. 2. Điều kiện
1) Sinh viên cần có kiến thức về lập trình cơ bản trong MATLAB.
2) Tìm hiểu các lệnh Matlab liên quan symbolic và đồ họa. 3. Nhiệm vụ
Xây dựng chương trình Matlab:
1) Nhập các giá trị ban dầu (những đại lượng đề cho).
2) Thiết lập các phương trình tương ứng. Sử dụng các lệnh symbolic để giải hệ phương trình. 3) Vẽ hình.
Chú ý: Sinh viên có thể dùng các cách tiếp cận khác. LỜI CẢM ƠN
Trong suốt quá trình thực hiện tiểu luận nói trên, nhóm chúng tôi đã nhận được rất nhiều
sự quan tâm và ủng hộ, giúp đỡ tận tình của thầy cô, anh chị em và bè bạn. 4 lOMoARcPSD|46958826
Ngoài ra, nhóm cũng xin gửi lời tri ân chân thành nhất đến cô Lê Như Ngọc, là giảng viên
hướng dẫn cho đề tài matlab này. Nhờ có cô hết lòng chỉ bảo mà nhóm đã hoàn thành tiểu
luận đúng tiến độ và giải quyết tốt những vướng mắc gặp phải. Sự hướng dẫn của cô đã là
kim chỉ nam cho mọi hành động của nhóm và phát huy tối đa được mối quan hệ hỗ trợ
giữa thầy và trò trong môi trường giáo dục.
Lời cuối, xin một lần nữa gửi lời biết ơn sâu sắc đến các cá nhân, các thầy cô đã dành thời
gian chỉ dẫn cho nhóm. Đây chính là niềm tin, nguồn động lực to lớn để nhóm có thể đạt được kết quả này.
TÓM TẮT BÀI BÁO CÁO
Báo cáo tìm hiểu về chuyên sâu về chủ đề chuyển động ném xiên bao gồm những khái
niệm cơ bản (gia tốc, bán kính cong,…) khái niệm chuyên sâu hơn (quỹ đạo, tầm xa, độ
cao,…) cũng như các công thức ứng với từng đề mục trong bài. Ngoài ra, báo cáo còn đưa
ra những tìm hiểu sơ bộ về ứng dụng công cụ Matlab để hỗ trợ việc tính toán, minh hoạ 5 lOMoARcPSD|46958826
cho chủ đề ném xiên. Hơn thế nữa, những câu lệnh và chức năng cụ thể của từng thuật
toán được giải thích cặn kẽ để ta hiểu hơn về mối liên hệ giữa cơ sở lý thuyết và ứng dụng trong việc lập trình. MỤC LỤC LỜ
I CẢM ƠN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 TÓM
TẮT BÀI BÁO CÁO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 DANH
MỤC HÌNH ẢNH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
C HƯƠNG I: GIỚI THIỆU CHUNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 6 lOMoARcPSD|46958826
1.1. Lý do chọn đề tài.................................................................................................... 10
1.2. Phương pháp nghiên cứu........................................................................................ 10
1.3. Nội dung và nhiệm vụ nghiên cứu......................................................................... 10
1.3.1. Nội dung......................................................................................................... 10
1.3.2. Nhiệm vụ......................................................................................................... 10
1.4. Cấu trúc của Báo cáo tổng kết................................................................................ 11
1.5. Hình thứcbài báo cáo............................................................................................. 11 CHƯ
ƠNG II: CƠ SỞ LÝ THUYẾT . ............................................................................ 12
2.1. Vecto vận tốc.......................................................................................................... 12
2.1.1. Vectơ vận tốc trung bình................................................................................. 12
2.1.2. Vectơ vận tốc tức thời...................................................................................... 12
2.2. Vecto gia tốc........................................................................................................... 13
2.2.1. Khái niệm về gia tốc....................................................................................... 13
2.2.2. Bán kính cong và độ cong tại một điểm của quĩ đạo:...................................... 13
2.2.3. Gia tốc pháp tuyến.......................................................................................... 15
2.2.4. Gia tốc tiếp tuyến............................................................................................ 16
2.2.5. Gia tốc toàn phần............................................................................................ 16
2.2.6. Gia tốc trọng trường........................................................................................ 17
2.3. Chuyển động ném xiên.......................................................................................... 18 CHƯ
ƠNG III: MATHLAB . ........................................................................................... 22
3.1. Tổng quan về matlab.............................................................................................. 22
3.2. Giải bài toán bằng tay............................................................................................ 22
3.3. Lưu đồ giải thuật matlab........................................................................................ 23 7 lOMoARcPSD|46958826
3.4. Các lệnh Matlab sử dụng.......................................................................................24
3.5. Đoạn code hoàn chỉnh............................................................................................27
3.6. Giải thích code và chạy thử kết quả.......................................................................28
3.6.1. Giải thích code................................................................................................28
3.6.2. Chạy thử kết quả với một vài giá trị đầu vào..................................................30
CHƯƠNG IV: KẾT LUẬN............................................................................................33
TÀI LIỆU THAM KHẢO..............................................................................................34 DANH MỤC HÌNH ẢNH
Hình 2. 1 Bán kính cong tại điểm M bất kì trên quỹ đạo chuyển động của vật.........14
Hình 2. 2 Gia tốc toàn phần tại điểm M bất kì trên quỹ đạo của vật..........................17
Hình 2. 3 Quỹ đạo chuyển động ném xiên lên của vật.................................................18 8 lOMoARcPSD|46958826
CHƯƠNG I: GIỚI THIỆU CHUNG
1.1. Lý do chọn đề tài
Vật lý đại cương 1 là môn học đại cương có tầm quan trọng đối với sinh viên ĐH Bách
Khoa TPHCM nói riêng và sinh viên các ngành khối khoa học kỹ thuật – công nghệ nói
chung. Do đó, việc dành cho môn học này một khối lượng thời gian nhất định và thực
hành là điều tất yếu để giúp cho sinh viên có được cơ sở vững chắc về các môn KHTN và
làm tiền đề để học tốt các môn khác trong chương trình đào tạo. 9 lOMoARcPSD|46958826
1.2. Phương pháp nghiên cứu
Việc ứng dụng tin học trong quá trình giải thích các cơ sở dữ liệu của vật lý, giải các bài
toán vật lý đã làm cho thời gian bỏ ra được rút ngắn lại và mang hiệu quả cao hơn. Như ta
đã biết, phần mềm ứng dụng Matlab đã giải quyết được các vấn đề đó. Vì thế việc tìm
hiểu matlab và ứng dụng matlab trong việc thực hành môn học vật lý đại cương 1 rất quan
trọng và có tính cấp thiết cao.
1.3. Nội dung và nhiệm vụ nghiên cứu 1.3.1. Nội dung
Sử dụng matlab để giải bài toán “Vẽ quỹ đạo của vật theo phương trình chuyển động”.
Xác định phương trình quỹ đạo và chuyển động của vật, vẽ quỹ đạo của vật trong khoảng
thời gian từ t=0 đến t=5s. 1.3.2. Nhiệm vụ
Xây dựng chương trình Matlab:
- Nhập các giá trị ban dầu (những đại lượng đề cho).
- Thiết lập các phương trình tương ứng. Sử dụng các lệnh symbolic để giải hệ phương trình. - Vẽ hình.
1.4. Cấu trúc của Báo cáo tổng kết -Bìa. -Phụ bìa. -Mục lục. -Danh mục bảng. -Danh mục hình. -Tóm tắt bài viết. 10 lOMoARcPSD|46958826
-Nội dung báo cáo tổng kết (Phần mở đầu, phần nội dung, phần kết luận).
1.5. Hình thứcbài báo cáo
Báo cáo tổng kết phải được trình bày ngắn gọn, rõ ràng, mạch lạc, sạch sẽ, không tẩy xóa,
không có lỗi chính tả, lỗi đánh máy... Văn bản phải được đánh máy vi tính trên hệ soạn
thảo Microsoft Word, sử dụng Bảng mã Unicode và kiểu chữ Times New Roman Cỡ chữ (size): 13
-Khoảng cách dòng (line spacing): 1,5
- Khoảng cách các đoạn (paragraph spacing): before: 6pt, after: 0pt.
- Lề trên (top): 2.5cm, lề dưới (bottom): 2.5cm, lề trái (left): 3.0cm, lề phải (right): 2.0cm
- Từ 10 đến 20 trang đối với bài tiểu luận, số trang này chỉ tính cho phần nội dung.
CHƯƠNG II: CƠ SỞ LÝ THUYẾT 2.1. Vecto vận tốc
Vectơ vận tốc là đạo hàm của vectơ vị tristheo thời gian, có gốc đặt tại điểm chuyển
động, phương tiếp tuyến với quỹ đạo tại điểm đó, chiều là chiều chuyển động và có độ lớn là .
2.1.1. Vectơ vận tốc trung bình
Giả sử ở thời điểm , chất điểm ở tại P có vectơ vị trí . Tại thời điểm , chất điểm ở tại
Q và có vectơ vị trí . Vậy trong khoảng thời gian , vectơ vị trí đã thay đổi một lượng .
Người ta định nghĩa vectơ vận tốc trung bình trong khoảng thời gian là: 11 lOMoARcPSD|46958826
2.1.2. Vectơ vận tốc tức thời
Để đặc trưng một cách đầy đủ về phương, chiều và tốc độ chuyển động của chất điểm,
người ta đưa ra đại lượng vật lý vectơ vận tốc tức thời (hay vectơ vận tốc) được định nghĩa như sau:
Vectơ vận tốc tức thời là giới hạn của vectơ vận tốc trung bình khi .
Trong hệ tọa độ Descartes 2.2. Vecto gia tốc
2.2.1. Khái niệm về gia tốc
Trong quá trình chuyển động, vận tốc của chất điểm có thể thay đổi cả về độ lớn cũng
như về phương và chiều. Để đặc trưng cho sự thay đổi của vận tốc theo thời gian , người
ta đưa thêm vào một đại lượng vật lý mới gọi là gia tốc.
Giả sử sau một khoảng thời gian , vận tốc của chất điểm thay đổi một lượng là thì theo
định nghĩa gia tốc trung bình trong khoảng thời gian là :
Khi tiến đến giới hạn, cho ta được biểu thức của gia tốc tức thời tại một điểm trên quĩ đạo :
Kết hợp lại ta có thể biểu diễn gia tốc : 12 lOMoARcPSD|46958826
2.2.2. Bán kính cong và độ cong tại một điểm của quĩ đạo:
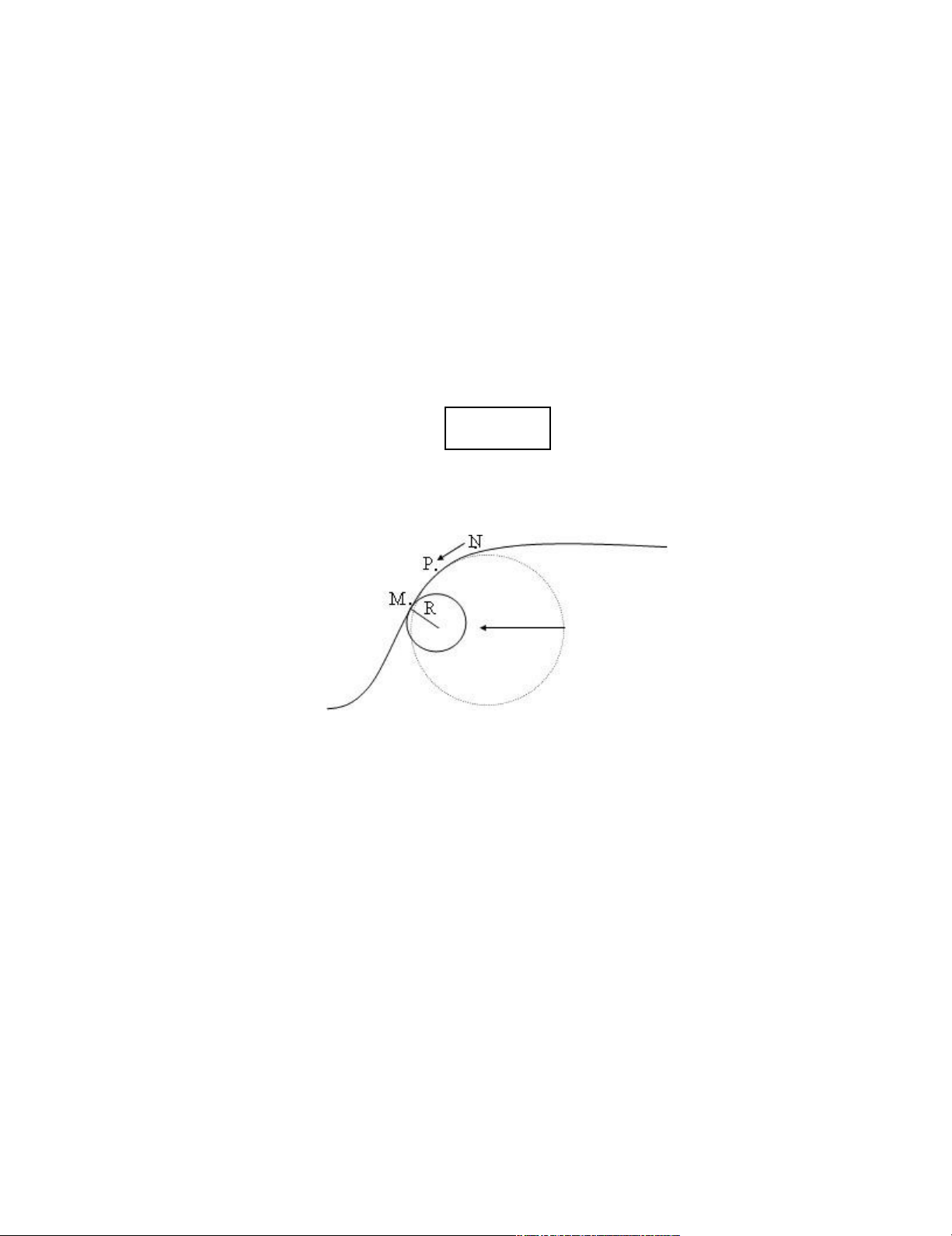
Ta xét hai điểm M và N ở gần nhau trên quĩ đạo của chất điểm. Lấy một điểm P bất kỳ
nằm giữa M và N, qua ba điểm M, N và P không thẳng hàng đó ta vẽ một đường tròn.
Cho điểm N tiến lại gần M và qua ba điểm mới ta lại vẽ được một đường tròn mới. Khi N
tiến tới giới hạn ở M thì các đường tròn trên cũng sẽ tiến tới một đường tròn giới hạn gọi
là đường tròn mật tiếp với quĩ đạo tại điểm M. Bán kính R của đường tròn mật tiếp được
gọi là bán kính cong của quĩ đạo tại điểm M. Giá trị nghịch đảo của R là K được gọi là độ
cong của quĩ đạo tại điểm M. K=1/R
Cần lưu ý rằng tại các điểm khác nhau thì quĩ đạo có thể có các bán kính cong và độ cong khác nhau.
Hình 2. 1 Bán kính cong tại điểm M bất kì trên quỹ đạo chuyển động của vật
Khi R = const, quỹ đạo chuyển động là tròn. Trong chuyển động tròn, thay quãng đường s
trong các công thức bằng góc quay j của bán kính R = OM, ta cũng thu được các công thức tương ứng: - Vận tốc góc:
s là quãng đường đi được trong khoảng thời gian t tương ứng với góc quay : Người ta định nghĩa:
được gọi là vận tốc của chất điểm và có đơn vị là rad/s. 13 lOMoARcPSD|46958826 Ta có:
đặc trưng cho chiều quay và độ nhanh chậm của chuyển động tròn. - Gia tốc góc: Ta có: Người ta định nghĩa:
được gọi là gia tốc góc của chất điểm và có đơn vị là rad/s2.
Nếu b =const, chuyển động là tròn, biến đổi đều (b>0 nhanh dần đều, b<0 chậm dần
đều), và cũng có các công thức ( coi to= 0): , .
Nếu , các công thức này trở thành: , .
Trường hợp riêng khi R = ¥ , quĩ đạo chuyển động là thẳng. Trong chuyển động thẳng, an = 0, a = at.
Nếu at= const, chuyển động thẳng biến đổi đều. Nếu t0= 0, ta có các biểu thức: Nếu s0=0 thì =s= và
Nếu a>0, chuyển động nhanh dần đều.
Nếu a<0, chuyển động thẳng chậm dần đều.
2.2.3. Gia tốc pháp tuyến
Gia tốc pháp tuyến là đại lượng đặc trưng cho sự thay đổi về phương của vecto vận tốc. Gia tốc tiếp tuyến có: 14 lOMoARcPSD|46958826
Phương vuông góc với tiếp tuyến quỹ đạo
Chiều hướng về phía lõm của quỹ đạo
Công thức gia tốc pháp tuyến: Trong đó:
- v là tốc độ tức thời (m/s).
- R là độ dài bán kính cong (m).
- Nếu xét trường hợp đơn giản là chuyển động tròn đều (tốc độ không đổi) trên quỹ đạo là
đường tròn thì cả v và R là không đổi và gia tốc hướng tâm là không đổi.
2.2.4. Gia tốc tiếp tuyến
Gia tốc tiếp tuyến đặc trưng cho sự thay đổi độ lớn của vecto vận tốc. Gia tốc tiếp tuyến có:
Phương trùng với phương của tiếp tuyến
Cùng chiều với chuyển động nhanh dần và ngược chiều với chuyển động chậm dần
Công thức gia tốc tiếp tuyến: Trong đó:
- v là tốc độ tức thời (m/s).
- t là thời gian tức thời(s).
Mối quan hệ giữa gia tốc tiếp tuyến và gia tốc pháp tuyến.
Một vật chuyển động trên quỹ đạo hình cong gia tốc bao gồm 2 thành phần: Gia tốc tiếp
tuyến và gia tốc pháp tuyến .
2.2.5. Gia tốc toàn phần
Gia tốc toàn phần là tổng của gia tốc tiếp tuyến và gia tốc pháp tuyến. 15 lOMoARcPSD|46958826
Hình 2. 2 Gia tốc toàn phần tại điểm M bất kì trên quỹ đạo của vật
Công thức gia tốc toàn phần: Trong đó: gia tốc toàn phần. : gia tốc tiếp tuyến. gia tốc pháp tuyến.
2.2.6. Gia tốc trọng trường
Gia tốc trọng trường là gia tốc do lực hấp dẫn tác dụng lên một vật. Bỏ qua ma sát do sức
cản không khí, theo nguyên lý tương đương mọi vật nhỏ chịu gia tốc trong một trường
hấp dẫn là như nhau đối với tâm của khối lượng. Điều này là đúng bất kể các vật có khối
lượng khác nhau và thành phần của chúng như thế nào.
Tại các điểm khác nhau trên Trái Đất, các vật rơi với một gia tốc nằm trong khoảng 9,78
và 9,83 m/s2 phụ thuộc vào độ cao (và còn do Trái Đất không là khối cầu hoàn hảo cũng
như vật chất phân bố không đều bên trong), với giá trị tiêu chuẩn chính xác bằng 9,80665
m/s2. Các vật có mật độ nhỏ không chịu cùng gia tốc như các vật nặng hơn do lực đẩy nổi
và sức cản không khí tác động vào.ng 9,78 và 9,83 m/s2 phụ thuộc vào độ cao (và còn do
Trái Đất không là khối cầu hoàn hảo cũng như vật chất phân bố không đều bên trong), với
giá trị tiêu chuẩn chính xác bằng 9,80665 m/s2. Các vật có mật độ nhỏ không chịu cùng
gia tốc như các vật nặng hơn do lực đẩy nổi và sức cản không khí tác động vào. 16 lOMoARcPSD|46958826
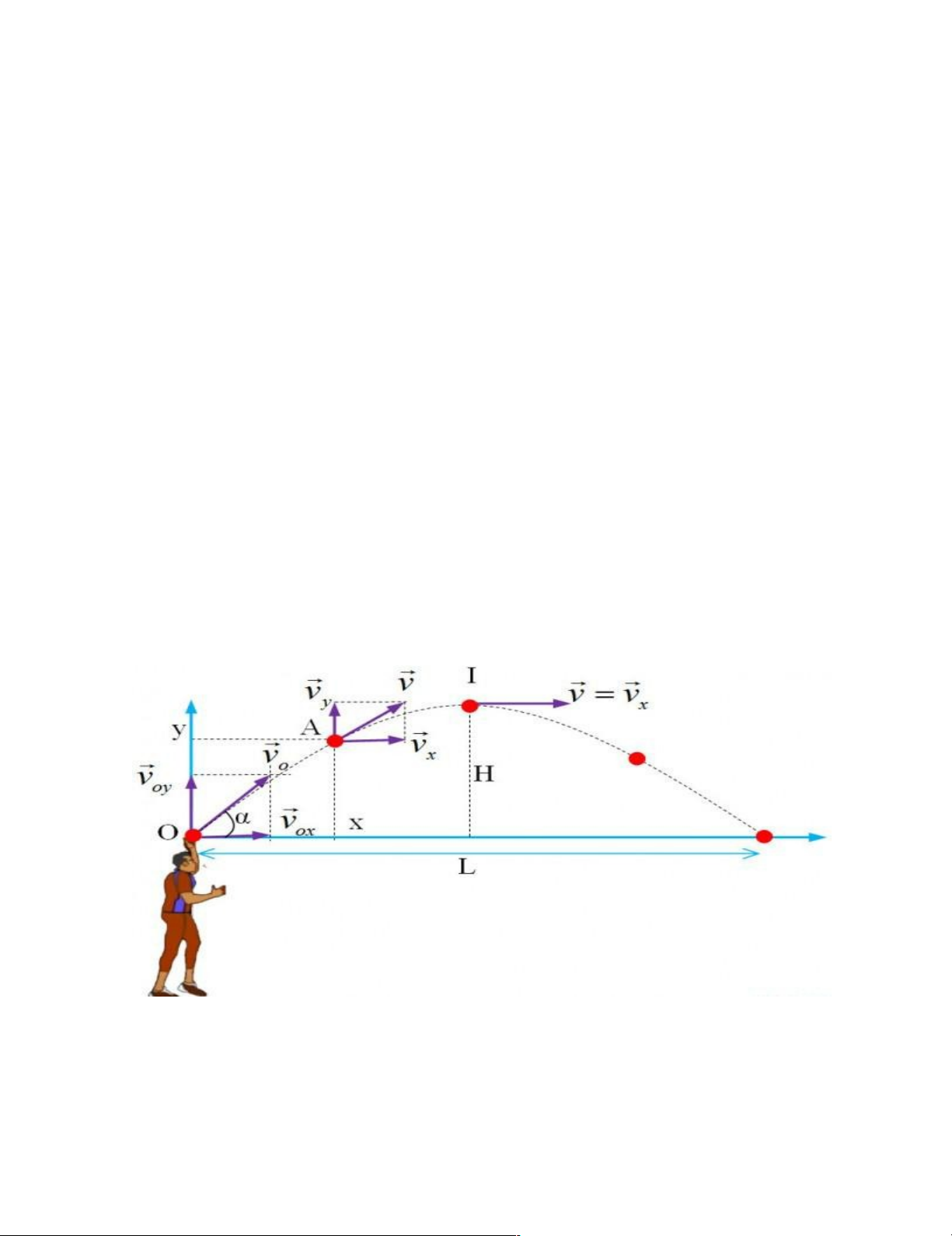
2.3. Chuyển động ném xiên
Chuyển động ném xiên là chuyển động của một vật được ném lên với vận tốc ban đầu
hợp với phương ngang một góc α (gọi là góc ném).Vật ném xiên chỉ chịu tác dụng của trọng lực. Những lưu ý quan trọng
- Theo phương ngang vật không chịu tác dụng của lực => chuyển động của vật là chuyển động thẳng đều.
- Theo phương thẳng đứng:
+ Giai đoạn 1: vật chuyển động đi lên đến độ cao cực đại (tại đó ) chịu tác dụng của trọng
lực hướng xuống => vật chuyển động thẳng chậm dần đều với gia tốc –g.
+ Giai đoạn 2: vật chuyển động đi xuống lúc này chuyển động của vật tương đương với chuyển động ném ngang.
- Độ lớn của lực không đổi => thới gian vật chuyển động đi lên đến độ cao cực đại đúng
bằng hời gian vật đi xuống ngang với vị trí ném2.2.2. Quỹ đạo chuyển động ném xiên
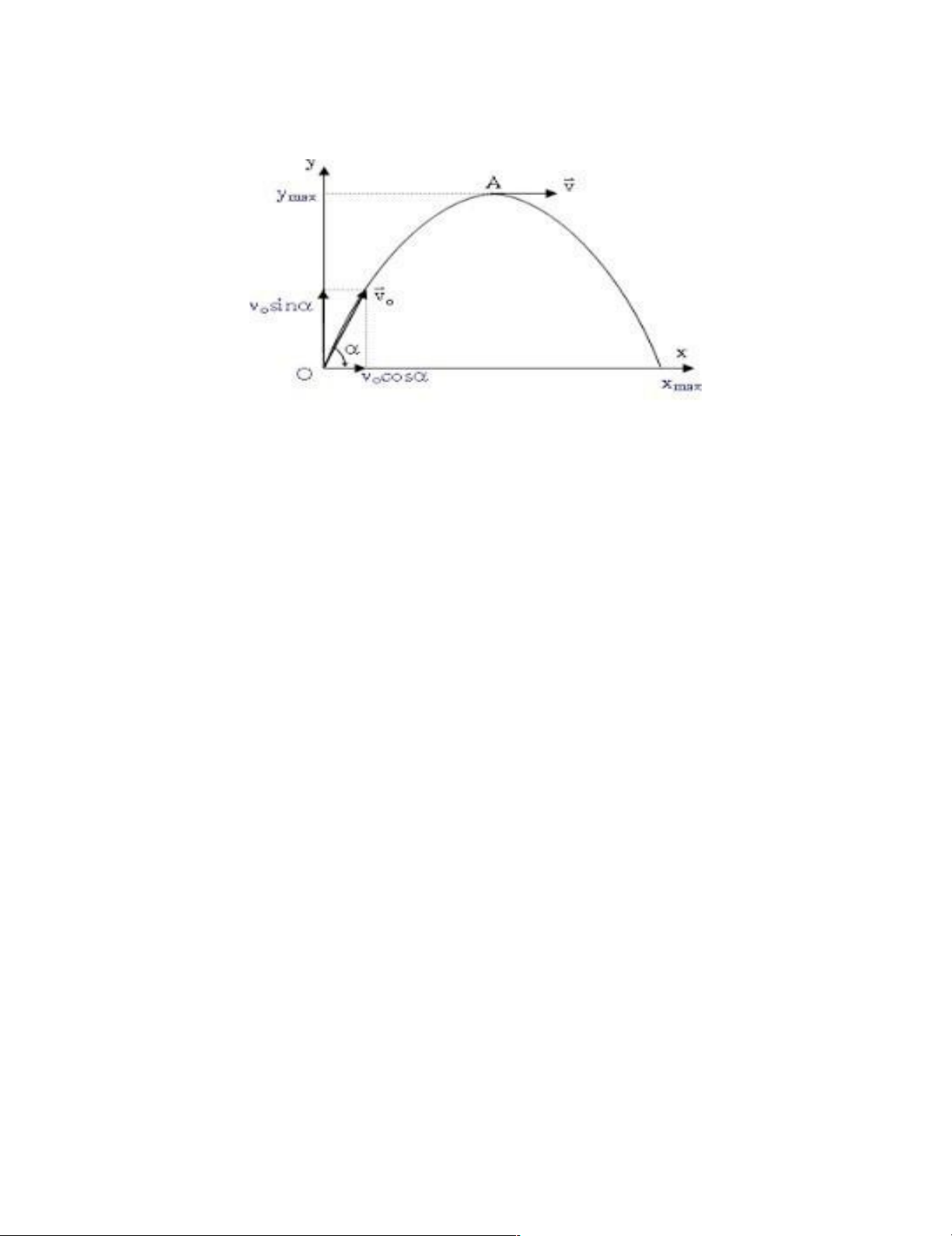
Hình 2. 3 Quỹ đạo chuyển động ném xiên lên của vật
Chọn hệ quy chiếu Oxy như hình vẽ, bỏ qua mọi lực cản của không khí khi đó vật
ném chỉ chịu tác dụng của trọng lực. Chọn gốc thời gian t0 là lúc bắt đầu ném ta có: 17 lOMoARcPSD|46958826 Tại thời điểm t0=0
Theo phương Ox vật không chịu tác dụng của lực nào => ax=0 => vật chuyển động thẳng
đều theo phương Oy vật chịu tác dụng của trọng lực.khi chưa đạt đến điểm có độ cao cực
đại=> = -g => vật chuyển động thẳng chậm dần đều
Sau khoảng thời gian Δt=t –=t vật chuyển động đến vị trí A Tọa độ của điểm A thay vào =>
Phương trình có dạng đồ thị của hàm số là một đường parabol có đỉnh ở trên => Quỹ đạo
của chuyển động ném xiên là đường parabol. Chuyển động Parabol:
Chuyển động của viên đạn là một ví dụ cụ thể cho chuyển động với gia tốc không đổi trong không gian hai chiều.
Giả sử viên đạn được bắn ra với vận tốc đầu , chuyển động của viên đạn sẽ là chuyển
động cong vì ngoài việc tiếp tục chuyển động theo quán tính, nó còn chịu tác dụng của
trọng trường với gia tốc hướng thẳng đứng xuống dưới.
Vectơ vị trí được xác định bởi: 18 lOMoARcPSD|46958826
Ta chọn một hệ trục tạo độ như hình 1 với gốc O là điểm mà viên đạn bắt đầu chuyển động ()
Chuyển động của viên đạn có thể được phân tích thành hai chuyển động hình chiếu trên Ox và Oy.
- Chuyển động hình chiếu trên Ox
Vì chuyển động hình chiếu trên Ox là chuyển động thẳng đều với (1)
- Chuyển động hình chiếu trên Oy
Vì chuyển động trên Oy là chuyển động thẳng thay đổi đều. Với: (2) Và (3)
Từ (1) và (3) ta suy ra phương trình quỹ đạo của viên đạn:
Vậy viên đạn có quỹ đạo là một parabol. 19 lOMoARcPSD|46958826
- Khi viên đạn đạt đến độ cao cực đại, và Vậy:
- Khi viên đạn chạm đất khi , lúc đó tầm xa của viên đạn sẽ là: CHƯƠNG III: MATHLAB
3.1. Tổng quan về matlab
MATLAB (Matrix Laboratory) là một phần mềm khoa học được thiết kế để cung cấp việc
tính toán số và hiển thị đồ họa bằng ngôn ngữ lập trình cấp cao. MATLAB cung cấp các
tính năng tương tác tuyệt vời cho phép người sử dụng thao tác dữ liệu linh hoạt dưới dạng
mảng ma trận để tính toán và quan sát. Các dữ liệu vào của MATLAB có thể được nhập
từ "Command line" hoặc từ "mfiles", trong đó tập lệnh được cho trước bởi MATLAB.
MATLAB cung cấp cho người dùng các toolbox tiêu chuẩn tùy chọn. Người dùng cũng
có thể tạo ra các hộp công cụ riêng của mình gồm các "mfiles" được viết cho các ứng dụng cụ thể.
3.2. Giải bài toán bằng tay . 20

