
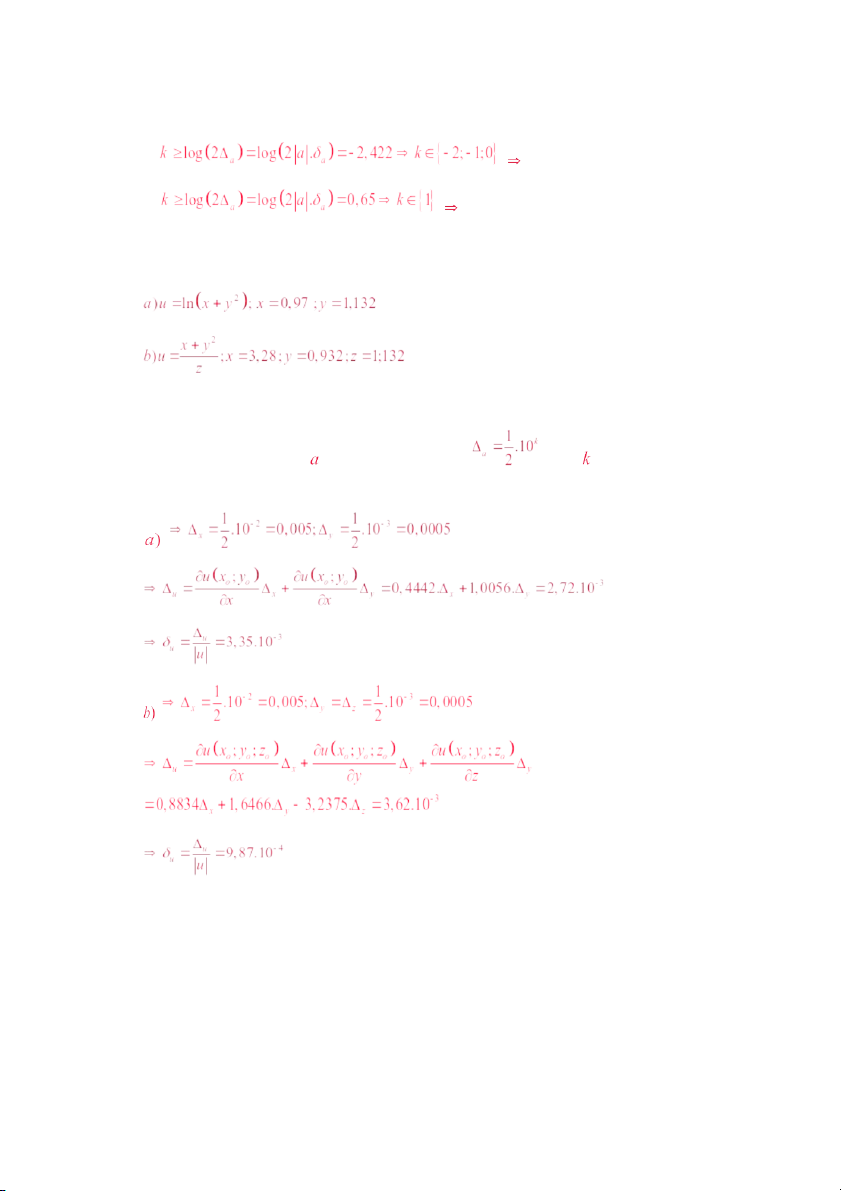

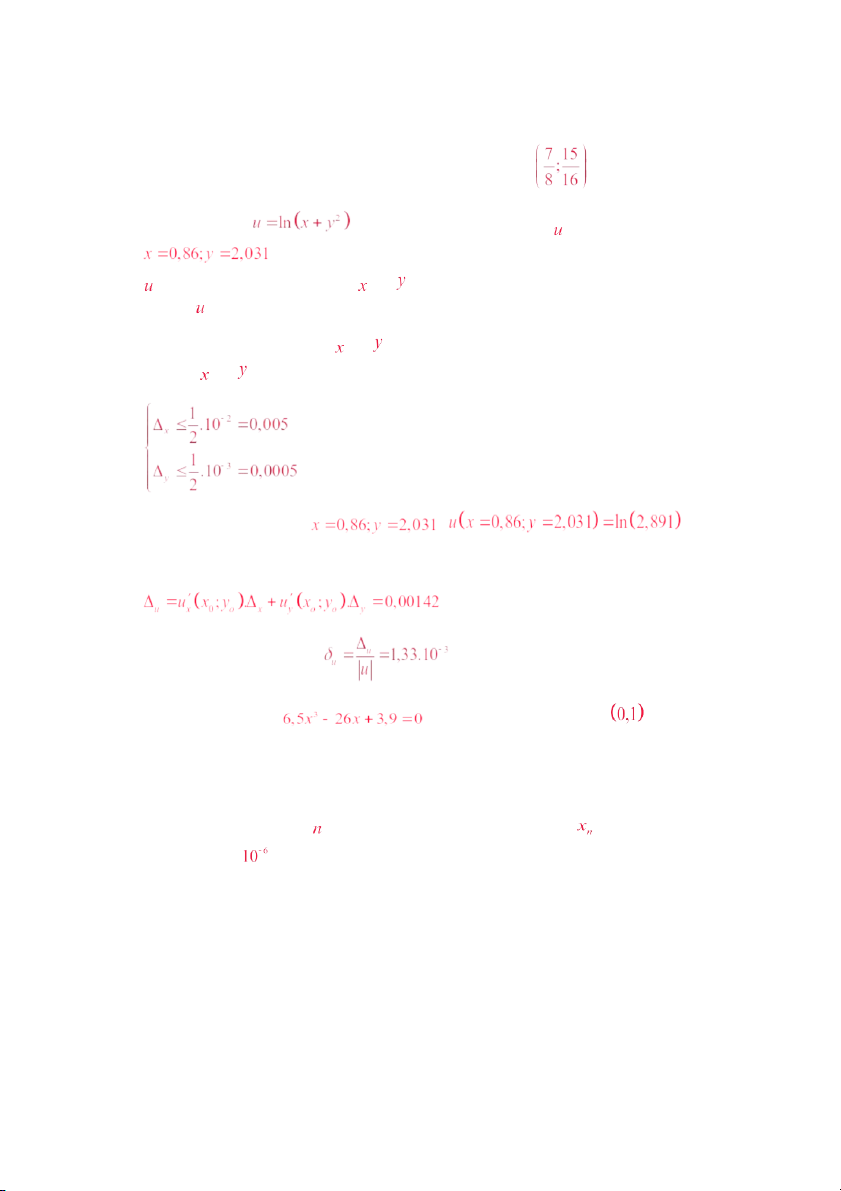
























Preview text:
Luyện tập Phương pháp tính
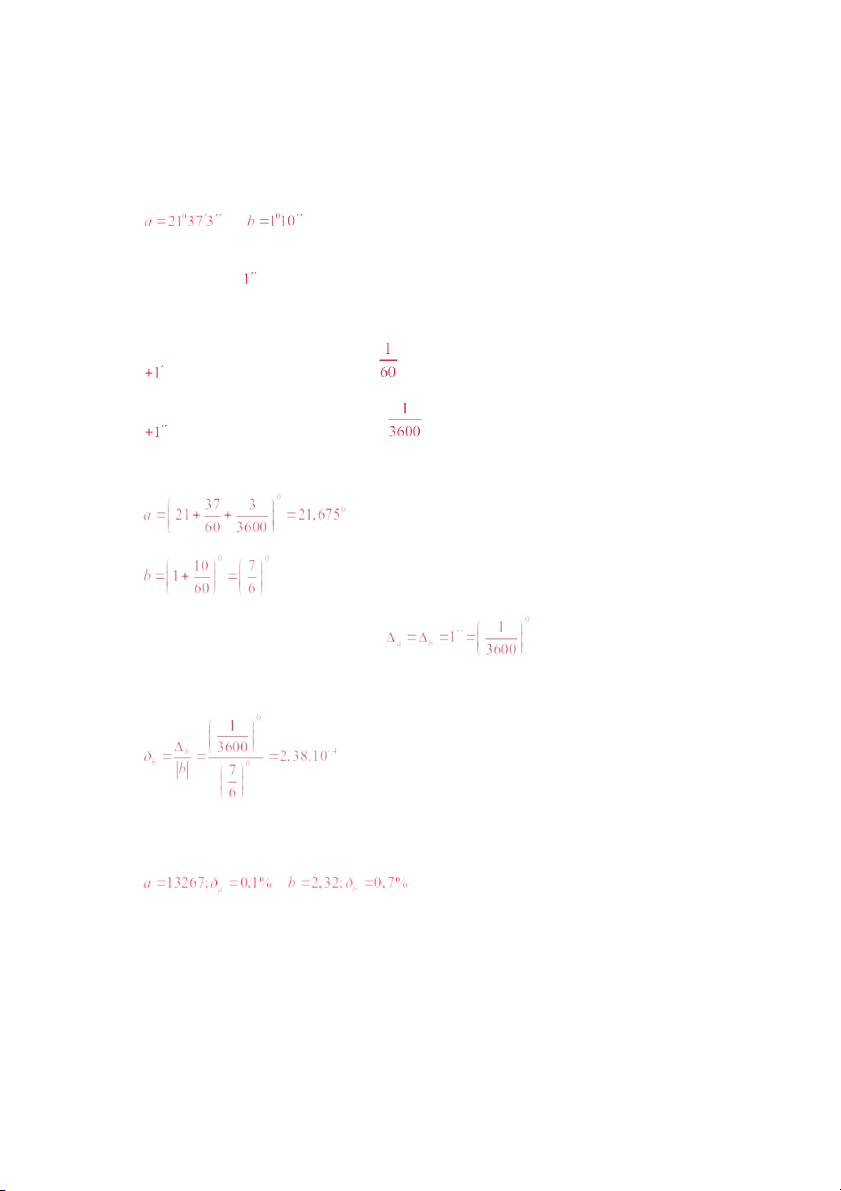
1. Khi đo một số góc ta thu được các giá trị sau : và
Hãy tính sai số tương đối của các phép xấp xỉ đó , biết rằng sai số tuyệt đối trong các phép đo là .
Ta cần đổi hết về đơn vị độ với tiêu chuẩn như sau :
: 1 phút góc : tương đương với độ
: 1 phút giây : tương đương với độ Khi đó :
Sai số tuyệt đối trong mỗi phép đo :
Khi đó sai số tương đối của các phép xấp xỉ :
2. Hãy xác định sai số tuyệt đối của các số xấp xỉ sau đây , cho biết sai số tương đối của chúng : ;
3. Xác định số các chữ số đáng tin trong các số với sai số tuyệt đối như sau :
Khai triển thập phân của số đã cho có dạng :
Chữ số trong khai triển được gọi là chữ số đáng tin khi và chỉ khi :
Như vậy số chữ số đáng tin : 3
Khai triển thập phân của số đã cho có dạng :
Chữ số trong khai triển được gọi là chữ số đáng tin khi và chỉ khi :
4. Hãy xác định những chữ số đáng tin trong các số với sai số tương đối như sau : Áp dụng công thức : a) có 3 chữ số đáng tin b) có 1 chữ số đáng tin
5. Xác định giá trị của hàm số dưới đây cùng với sai số tuyệt đối và sai số tương
đối ứng với những giá trị của đối số cho mọi chữ số có nghĩa đều đáng tin.
Do mọi chữ số có nghĩa đều đáng tin nên :
Sai số tuyệt đối của 1 số được xác định bằng : , với chữ số cuối
cùng , hàng bên phải trong khai triển thập phân 6. Cho phương trình
. Hãy tìm một khoảng phân ly nghiệm
của phương trình thỏa mãn điều kiện Xét hàm số : Xét hàm số trên đoạn , ta có : Nên ta chọn
là khoảng phân ly nghiệm ban đầu
Sử dụng phương pháp chia đôi :
Khoảng phân ly đầu với 2 đầu mút : 0 0 1 1 1 1 2 1 3 1 4
Vậy ta chọn khoảng phân li thỏa mãn yêu cầu bài toán là : 7. Cho hàm số :
. Hãy xác định giá trị hàm số tại
, sai số tuyệt đối giới hạn , sai số tương đối giới hạn của hàm số
biết mọi chữ số có nghĩa của và đều đáng tin . Viết giá trị tìm được của hàm số theo quy ước
Do mọi chữ số có nghĩa của và đều đáng tin nên ta có các sai số tuyệt đối giới hạn của và sẽ là :
Giá trị hàm số đã cho tại :
Sai số tuyệt đối giới hạn của hàm số đã cho là :
Sai số tương đối giới hạn : 8. Cho phương trình
và khoảng phân ly nghiệm
a) Kiểm tra điều kiện hội tụ của phương pháp lặp đối với phương trình trên
b) Tìm nghiệm đúng bằng phương pháp lặp 3 lần
c) Cần tính tới số lần lặp bằng bao nhiêu để nghiệm gần đúng có sai số tuyệt đối không quá . a) Xét phương trình trên đoạn
Đưa phương trình về các phương án sau đây : Phương án 1 : Phương án 2 : Phương án 3 :
Nếu dùng phương án 1 : Chọn hàm lặp Như vậy :
liên tục và khả vi trên
Thỏa mãn điều kiện hội tụ
Nếu dùng phương án 2 : Chọn hàm lặp : Hàm
bị gián đoạn trong khoảng
nên điều kiện hội tụ không thỏa mãn !
Nếu dùng phương án 3 : Chọn hàm lặp :
, dẫn đến không thỏa mãn điều kiện hội tụ
Như vậy ta chọn hàm lặp là hàm : với dãy lặp là : ; hệ số co : b) Do
nên ta lấy xấp xỉ đầu : n 1 0 0,15 2 0,15 3 0,1508581 c)
sử dụng công thức Sai số tiền nghiệm :
Giải bất phương trình : 9. Cho phương trình
và khoảng phân ly nghiệm
Kiểm tra điều kiện hội tụ của phương pháp dây cung đối với khoảng trên
Xuất phát từ khoảng trên , tìm nghiệm gần đúng bằng phương pháp dây
cung . Đánh giá sai số của
Xuất phát từ khoảng trên , tìm nghiệm gần đúng với sai số tuyệt đối không quá
bằng phương pháp tiếp tuyến . Xét hàm số : trên có : khả vi tới cấp 2 Chọn xấp xỉ đầu là thỏa mãn : Chọn :
Như vậy phương trình đã cho thỏa mãn điều kiện hội tụ của phương pháp dây cung
Xây dựng dãy lặp dây cung :
Bảng thao tác: với dãy hàm số : 0 1 2
c) Kiểm tra điều kiện hội tụ của phương pháp Newton : Xét hàm số : trên có : khả vi tới cấp 2 Chọn xấp xỉ đầu là thỏa mãn : Chọn :
Như vậy phương trình đã cho thỏa mãn điều kiện hội tụ của phương pháp Newton
Xây dựng dãy lặp Newton : Bảng thao tác : 0 1 2 3 4
Chọn nghiệm gần đúng là : 10. Cho phương trình Chứng minh rằng
là một khoảng phân ly nghiệm
Kiểm tra điều kiện hội tụ của phương pháp tiếp tuyến đối với khoảng trên
Tính theo phương pháp tiếp tuyến đến lần lặp thứ 3 là . Đánh giá sai số của
theo công thức hai phép lặp liên tiếp . Hãy viết nghiệm gần đúng chỉ gồm
những chữ số đáng tin . Xét hàm số : trên :
liên tục và khả vi trên Nên khoảng đã cho
là một khoảng phân ly nghiệm b) Xét trên
liên tục và khả vi đến cấp 2 không đổi dấu trên Chọn xấp xỉ đầu : sao cho
Phương pháp đã cho thỏa mãn điều kiện hội tụ của phương pháp Newton
c) Xây dựng công thức lặp :
Chọn xấp xỉ đầu là :
Đánh giá sai số qua 2 lần lặp liên tiếp : Bảng thao tác: n 0 1 2 3 Ta thu được : Sai số : 11. Cho phương trình
xác định trên khoảng :
a) Kiểm tra điều kiện hội tụ của phương pháp tiếp tuyến đối với khoảng trên
b) Tính đến và đánh giá sai số của theo công thức hai phép lặp liên tiếp
c) Để có nghiệm xấp xỉ với 4 chữ số đáng tin sau dấu phẩy , cần ít nhất bao nhiêu phép lặp Xét hàm số trên khoảng
liên tục và khả vi đến cấp 2 cùng dấu trên
Chọn giá trị xấp xỉ đầu : sao cho ở đây ta chọn
làm giá trị xấp xỉ đầu . Như vậy phương trình đã cho thỏa
mãn điều kiện hội tụ của phương pháp Newton
b) Sai số qua hai phép lặp liên tiếp : Trong đó : Bảng thao tác : n 0 1 2 0,78366 3 0,78366 Sai số :
c) Để có 4 chữ số đáng tin sau dấu phẩy : Điều kiện dừng : Tiếp túc quy trình : n 3 0,76023 4 0,76023 0,75955 0,00068
Như vậy cần phải thực hiện ít nhất lần lặp
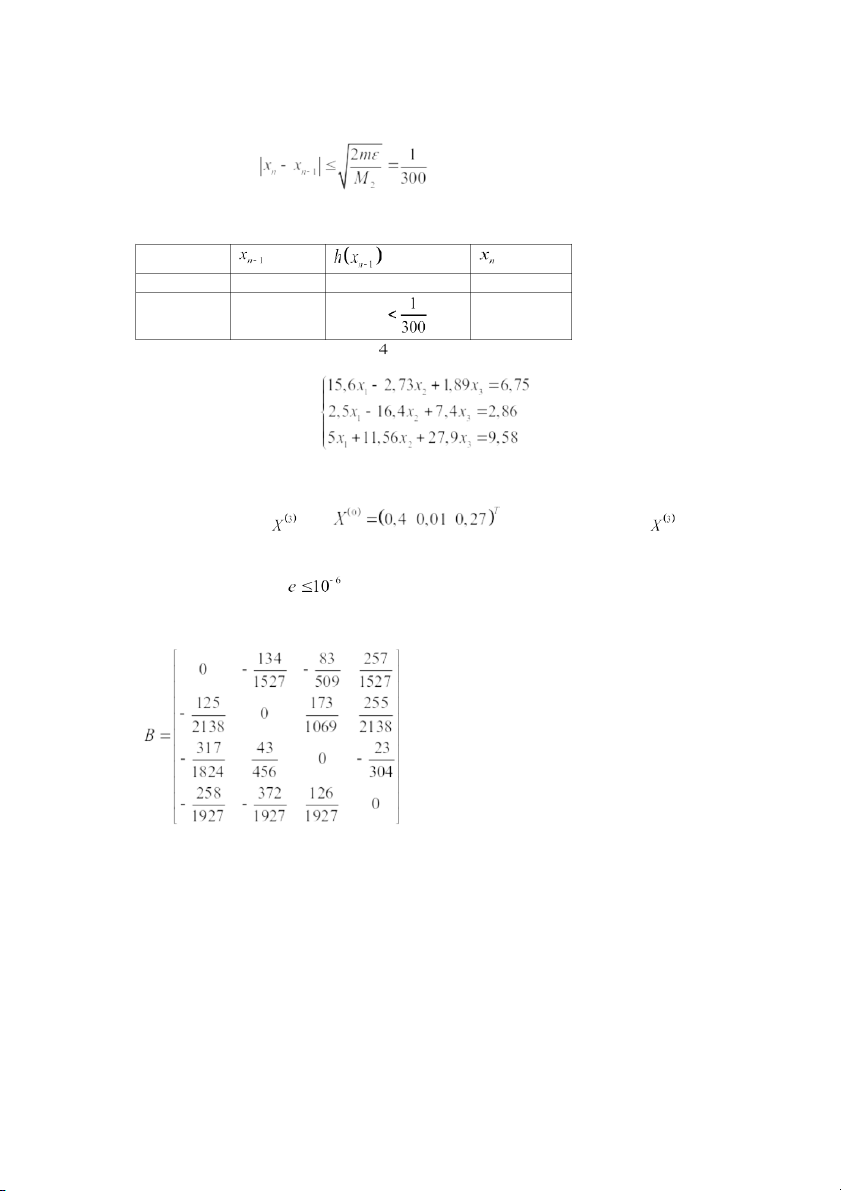
12. Cho hệ phương trình :
a) Kiểm tra điều kiện hội tụ của phương pháp lặp đơn b) Tính đến xấp xỉ biết . Đánh giá sai số của
bằng công thức 2 xấp xỉ liên tiếp
c) Để đạt được sai số
cần tính đến xấp xỉ thứ bao nhiêu là ít nhất
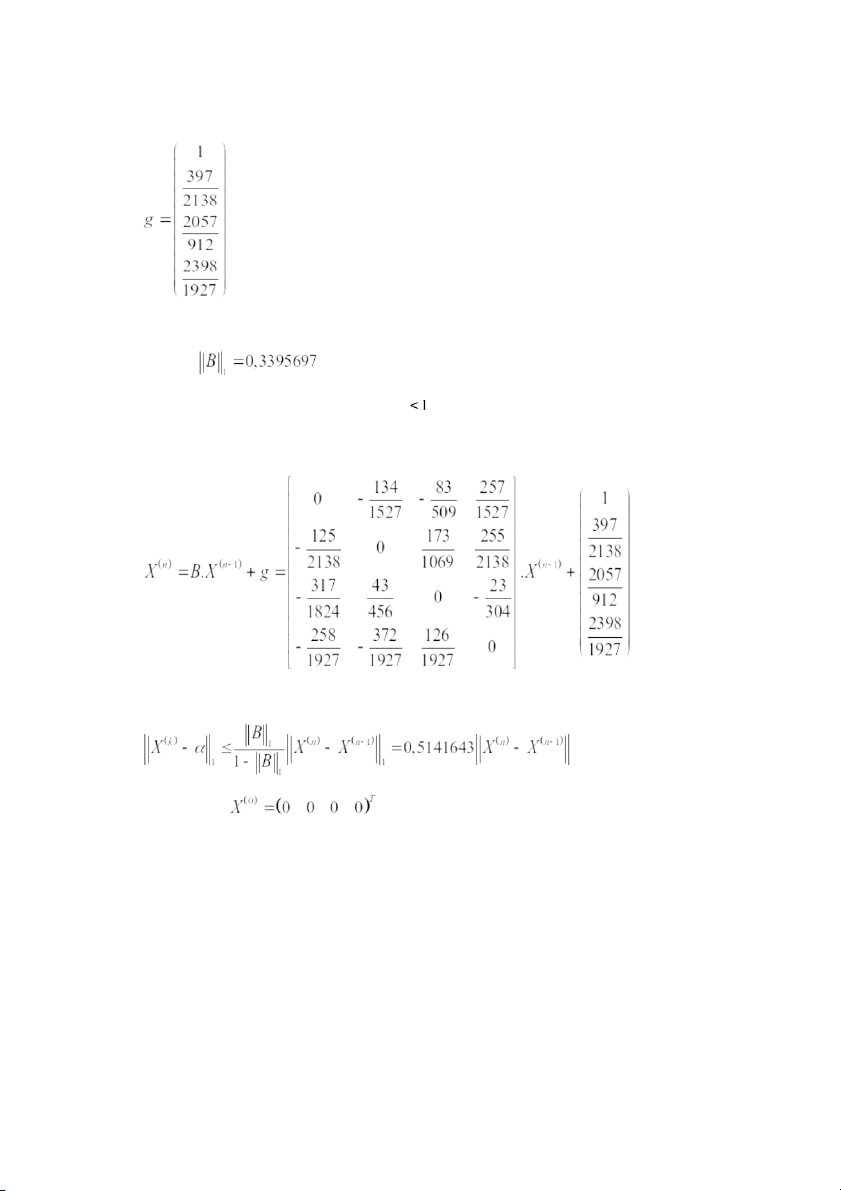
a) Từ hệ ta đi xây dựng ma trận lặp : Vector lặp : Xây dựng dãy lặp : Ta có :
Đồng thời có ít nhất 1 chuẩn cho giá trị
và ma trận hệ số đã cho là ma trận
đường chéo trội hàng nên thỏa mãn điều kiện hội tụ của phương pháp lặp đơn . Ta có dãy lặp :
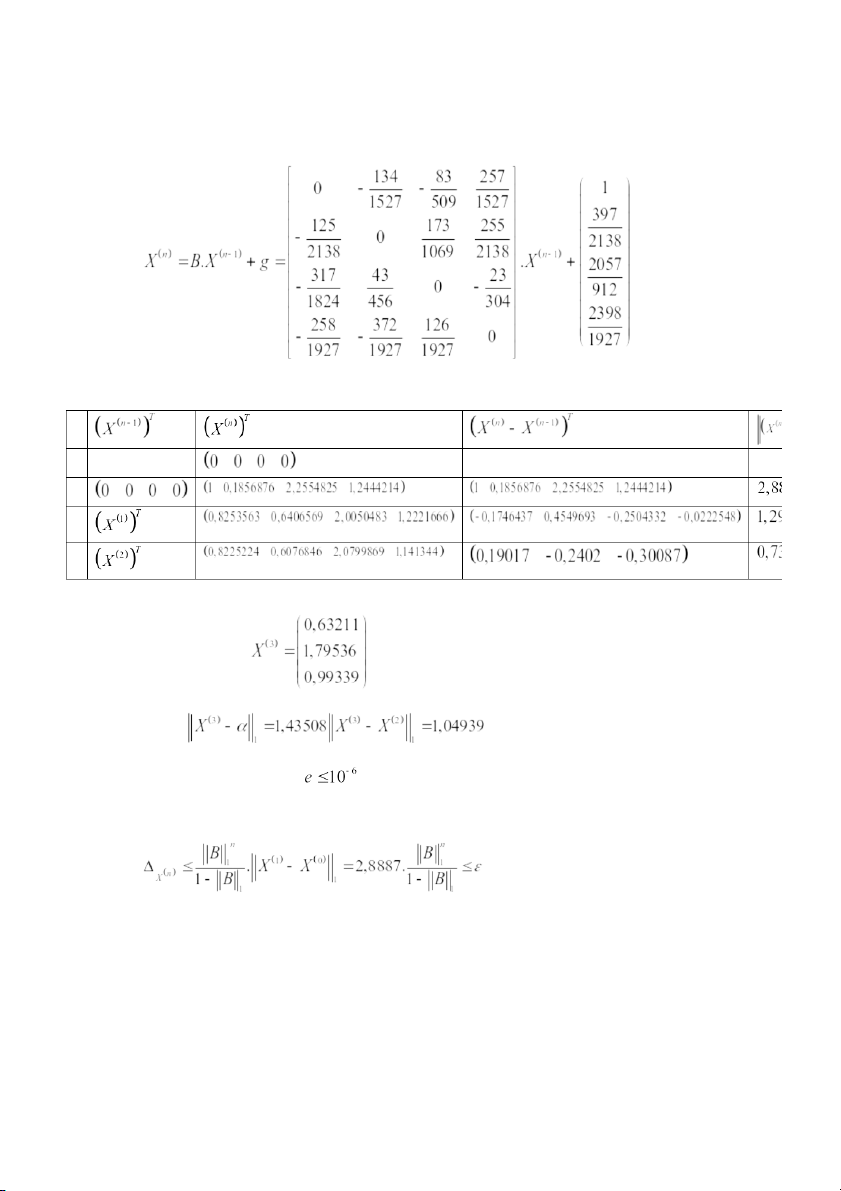
b) Sai số qua công thức hai xấp xỉ liên tiếp : Xấp xỉ đầu : Dãy lặp : n 0 1 2 3 Như vậy vector Sai số
c) Để đạt được sai số là
theo công thức sai số dựa trên 2 xấp xỉ đầu : Như vậy cần ít nhất lần !
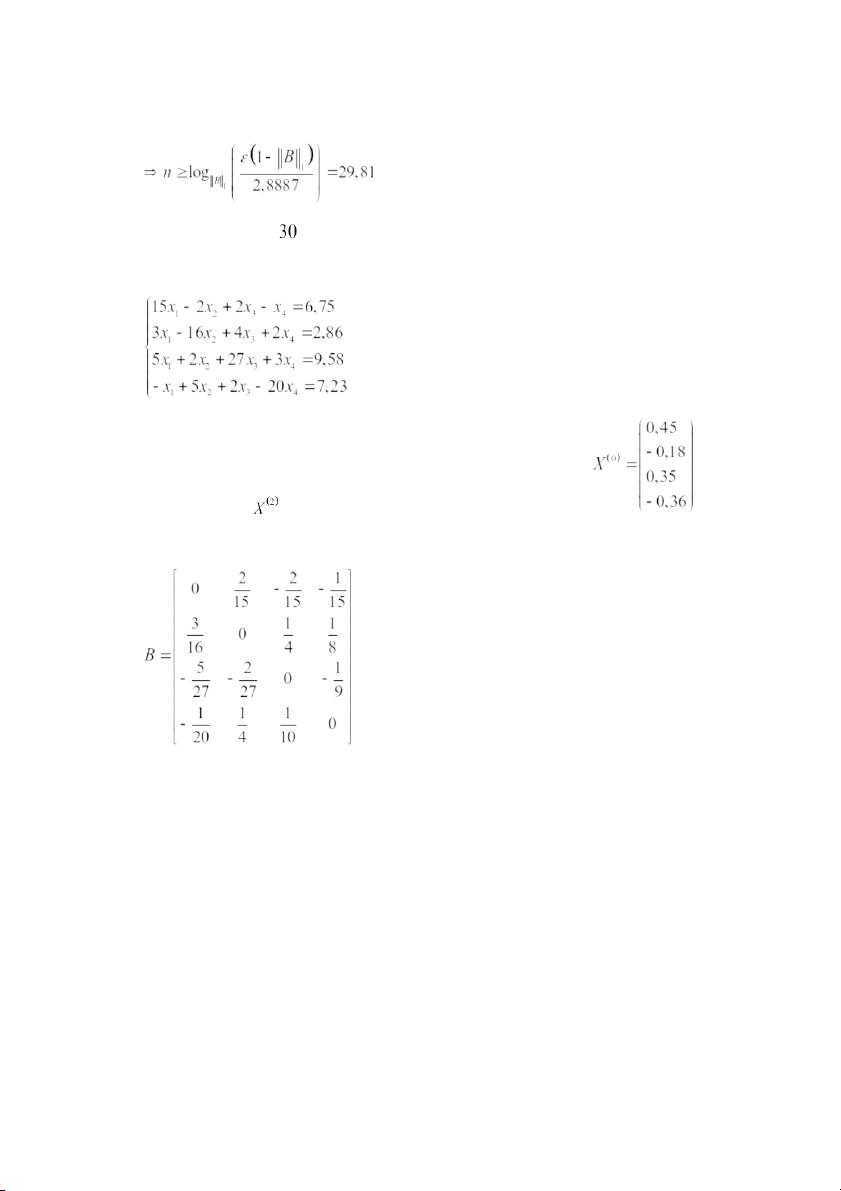
13. Cho hệ phương trình : Tính đến xấp xỉ
bằng phương pháp lặp Seidel với xấp xỉ đầu :
Xác định ma trận lặp và vector lặp : Vector lặp :
Do ma trận hệ số đã cho là ma trận có đường chéo trội đồng thời
Dãy vector đã cho thỏa mãn điều kiện hội tụ của phương pháp lặp Seidel Xây dựng dãy lặp : vector xấp xỉ đầu : Bảng : m 0 0,45 -0,18 0,35 -0,36 1 2 14. Cho bảng giá trị 0 1 2 4 2 0 64 630
a) Xây dựng đa thức nội suy Lagrange
b) Dùng sơ đồ Hoocne tính giá trị đa thức vừa nhận được tại Có tất cả :
nút nên đa thức Lagrange
của chúng ta được xây dựng như sau : b) Đa thức nội suy : Sơ đồ Hoocne : 15. Cho hàm số được cho dưới bảng : 2 2,2 2,3 2,5 0,30103 0,34242 0,36173 0,39794 Tính gần đúng :
bằng đa thức nội suy Lagrange .Đánh giá sai số của giá
trị gần đúng vừa nhận được Có tất cả :
nút nội suy nên đa thức Lagrange được xác định như sau: Sai số : 15. Cho bảng số –4 –3 0 2 5 6 1015 371 –1 –29 259 875
1. Xây dựng đa thức nội suy Newton lùi xuất phát từ nút
2. Tính giá trị đa thức nhận được tại .
Do có nút nên ta sẽ xây dựng đa thức nội suy bậc 5
Khi đó đa thức Newton lùi xuất phát từ nút là :
Trong đó các tỉ hiệu được tính: Trong đó: : tỉ hiệu cấp
Từ đây ta viết được đa thức Newton nội suy lùi xuất phát từ nút :
b) Khi đó giá trị đa thức tại là :
16. Cho bảng giá trị của hàm số . 100 150 200 250 300 0,1736 0,2588 0,3420 0,4226 0,5 1. Tính gần đúng
bằng đa thức nội suy Newton tiến, xuất phát từ nút .
2. Đánh giá sai số của giá trị gần đúng nhận được.
Do có nút nên ta sẽ xây dựng đa thức nội suy Newton tiến bậc 4
Khi đó đa thức nội suy Newton tiến xuất phát từ nút là :
Trong đó các tỉ hiệu được tính: Trong đó: : tỉ hiệu cấp
Khi đó đa thức nội suy Newton tiến xuất phát từ nút sẽ là :
Khi đó ta tính gần đúng
qua đa thức mới tìm được: b) trong đó : Với
Ngoài ra ta để ý thêm dữ liệu bài toán cho ở dạng các nút nội suy cách đều nên ta
có thể sử dụng phương pháp sai phân hữu hạn để giải bài toán trên như sau
a) Các nút nội suy cách đều với bước nhảy
Lúc này ta có được công thức Newton tiến xuất phát từ nút dưới dạng sai phân hữu hạn : Với
Bảng sai phân đường chéo của công thức Newton tiến:
Khi đó ta tính gần đúng : Với
17. Tìm hàm thực nghiệm dạng từ bảng số: 0,48 1,05 1,85 2,37 4,23 5,13 0,185 2,574 8,536 15,478 51,984 79,123 Hàm thực nghiệm :
Hệ phương trình điểm dừng : Trong đó :
18. Tìm hàm thực nghiệm dạng
bằng phương pháp bình phương tối thiểu từ bảng số: 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 0,2049 0,4839 0,800
1,1429 1,5072 1,8895 2,2876 2,6995 3,1240 Lấy logarit cơ số 10: Đặt , , Khi đó:
Hệ phương trình điểm dừng: Trong đó : 19. Cho tích phân
1. Tính gần đúng tích phân trên bằng phương pháp hình thang (tổng quát) với phép chia đoạn thành 10 đoạn bằng nhau
2. Đánh giá sai số của giá trị gần đúng tìm được. 3. Cần chia
thành ít nhất bao nhiêu đoạn bằng nhau để khi dùng công thức
Simpson (tổng quát) tính tích phân trên thì giá trị gần đúng tìm được có 4 chữ số
đáng tin phần thập phân. Chia đoạn
thành 10 đoạn bằng nhau với bước chia:
Áp dụng công thức hình thang tổng quát cho tích phân : với ta có : Trong đó: b) Với Khi đó: Khi đó sai số sẽ là :
c) Để có 4 chữ số đáng tin phần thập phân:
Mặt khác ta lại có công thức sai số của công thức Simson suy rộng: Trong đó Trong đó: Từ bất phương trình :
20. Tính gần đúng tích phân sau bằng phương pháp Simpson với số đoạn chia là 10 và đánh giá sai số. Chia đoạn ra làm
đoạn bằng nhau với bước chia:
Sử dụng công thức Simson mở rộng ta được : Ta lại có : 0,5 0,4524 0,4098 0,3717 0,3378 0,3076 0,2808 0,257 0,2358 0,2169 0,2 Sai số : Trong đó : Với:
Từ đây ta có được sai số:
20. Dùng phương pháp Euler tìm nghiệm của: trên đoạn với bước đi .
Từ phương trình vi phân đã cho ta biến đổi về dạng : Chia đoạn
làm 6 đoạn bằng nhau với bước chia: Với
Xây dựng công thức Euler:
Từ đây ta có bảng biểu diễn: 0 4 1 1 4,2 2 4,4 3 4,6 11,71534 4 4,8 11,98931 5 5 12,24299 6 5,2 12,47794
21. Dùng phương pháp Runge–Kutta cấp 4 tìm nghiệm gần đúng của: tại điểm , lấy bước đi
Biến đổi phương trình đã cho: Từ đây ta có: Ta có:
Xây dựng công thức R-K cấp 4: Trong đó: Ta cần tính Trong đó :




