Bài tập môn Cơ học (có lời giải)

Bộ câu hỏi ôn tập học phần "Cơ học" bao gồm câu hỏi tự luận (có đáp án) giúp sinh viên củng cố kiến thức và đạt điểm cao trong bài thi kết thúc học phần.

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Cơ học

Trường: Học viện kỹ thuật quân sự

Thông tin:

79 trang 6 tháng trước

Tác giả:

Profile Ngọc Diệp




!"ω#ϕ
$" $

%
!"ω#ϕ
%
$"%$
&'()*+,-!
$ϕ
.ϕ
%
%/π0 /12!345
6$ϕ
.ϕ
%
"%/# $π5
$ϕ
.ϕ
%
"%/# $
2
π
5
($ϕ
.ϕ
%
7'6/8


9:;06<,()*27
-=7>12-6(?3)@
AB07C/D6<+8E7062B-27
12!8
$Fϕ
ϕ
%
#%/πA2" $7

!"ω#ϕ
$
!"ω#ϕ
%
#%/π$
!"ω#ϕ
%
$0

%
!"ω#ϕ
%
$
FG7
21
a
y
a
x
=

x
a
a
y
1
2
=
H.
≤
!"
ω
#
ϕ
$
≤
 4.
≤

≤

HB-I$24J6(?6K
x
a
a
y
1
2
=
 AL .
≤

≤


6$92M-I$

!"
ω
#
ϕ
$
!"
ω
#
ϕ
%
#%/
π
#
π
$.
!"
ω
#
ϕ
%
$
FG7N4J6(?6K
x
a
a
y
1
2
−=
AL .
≤

≤

$F
ϕ

ϕ
%
#"%/# $
2
π
(?(2N6>
1
a
y
a
x
2
2
2
2
1
2
=+
26(?+41O-AP071LA2Q;
48
($=/D-" $A2"%$8R3</2!3!
" $A2"%$
11
1
sin.sincos.cos
ϕωϕω
tt
a
x
−=
 "S$
22
2
tt
a
y
ϕωϕω
sin.sincos.cos
−=
 "T$
UV"S$AL!
ϕ
%
A2"T$AL.!
ϕ
WA<ALA<
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
)sin(.sincoscos
121
2
2
1
t
a
y
a
x
ϕϕωϕϕ
−=−
"X$
9V"S$AL!
ϕ
%
A2"T$AL.!
ϕ
WA<ALA<
)sin(cossinsin
121
2
2
1
t
a
y
a
x
ϕϕωϕϕ
−=−
"Y$
Z-"X$A2"Y$WA<ALA<
)(sin)cos(
12
2
12
21
2
2
2
2
1
2
aa
xy2
a
y
a
x
ϕϕϕϕ
−=−−+
"[$
"[$6(?+41O-8
 !"!#$%#$#%&!'
ϕ
(
)
ϕ
*
%&+,-./012#3
RPPG\]<\ZALAB3A
T^/_+W1G\
ZKA\]ALAB3A
%
S^/_+8
FAB36PP4+A]Z0Z]7`

a)C+]Z6;!8F!bOAB36cP>
0'45.4++!5+6
4+45.6
=v
F,
./, sm539
vv
vv2
v
1
v
1
2
v
s
v
s
ss
tt
ss
v
21
21
2121
=
+
=
+
=
+
+
=
+
+
=
A(
F!3,
./,
sm539v =
R+>R+J/=X^+
PP5/PPd
%^^  +  6e I  
+  a- PP "f .%$8 Z< PP
ALAB3SY/_+8
fQ $ U+  -=  c
L 2  a- N PP` Z< ;
+ALAB3A
%
 ^0g/_+5
6$U+-=ALAB 3Q
6;647a-,PP`

$R3a-NPPZ++GRLZ-=6;+
PPG]LZ

12
v
AB
v
MB
=
" $
hD('1:2!3!]ZR7
,
sinsin
αβ
ABMB
=
 AL
a
h
=
β
sin
"%$
FG" $A2"%$N
]
R
Z

β
α
if E
f
.
%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
8330
v
v
a
h
2
1
,.sin ==
α

α
XY
^
S^ja
α
 %S
^
S^j8
775+0''89:;<0
α
=>:;?<.
'
'
30
123
30
56
00
≤≤
α
3@+
'
'
30
123
30
56
00
<<
α
5+0''
5?++8<AB3
C/'+?DE5+'+<F?<.+G0'
2
1
v
v
a
h
.sin >
α
3
:0
MD
v
v
AD
h
a
v
v
a
h
MD
1
AD
ADMD
2
1
2
1
.....
sin
.sin
sinsin
=
>=→=
β
α
αβ
8
21
v
MD
v
AD
>
1-05++!8'F95++!5+'F#3
6$7a-,PPALAB3Qk2;1N2+
<+l121NcPPL"+a-NPP2/P-=+,1C-O
+$0AAB0c-I$@LA2AB3+-=7)
2
1
v
v
a
h
.sin =
α
HALm
α
!"
α
$
≤
 4
12
2
1
v
a
h
v1
v
v
a
h
.. ≥
≤
h
hkm9sm52
a
hv
v
1
2
//,
min
===
8
9N20+-=cLRi0ALRi
⊥
]R8
RAB,=G/OI6KS^^8fQ!61V
ABLa0<
$nOI614"cLJ>$ALAB3X_!5
6$nOI3"c-J>$ALAB3X_!5
$nOI>48

n/OI0ABK4/OIcAB3/OI8U</O
I 3(LALAB3A
^
+2ABL=C
-6B+
htg
2
1
tv
2
0
=+ ..
8
om(-27/<)=
g
vgh2v
t
0
2
0
−+
=
8
n/OI14403(La>40-(6>
2ALAB36IA
^
.X_!0A
^
X_!5aA
^
^A27/<)=
$g0T!5 6$[0S!5 $[0g!8
RAB,=Gf#c-J>EEj"Ep12V
f#$8oq1N7AB>,r14GEpc-J>
ALAB3A
^
8
$fQAB3A
^
-=6;64ABa-K`
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
6$FO/=@ABL1Na-c+`
$U</P7AB>AB>1L6;64`

oIL1P>M(
$ F+ AB  G E<  a-  12
g
H2
t =
l
6;+AB%GEj<s0(7
gH2
H
2
hH
2
gt
t
h
vtg
2
1
tvh
0
2
0
+
=+=→−=
..
6$n=@AB+L/a-,
Oc)C+!A2!jAB,
"f#$."!#!j$8
( ) ( )
).(
...
tgH2H2
H
2
hH
tvhHtg
2
1
tvgt
2
1
hHx
0
2
0
2
−
+
=
−+=
−−−+=
$ hD ( P > )  A0 0 !    J 6< t 
sa2vv
2
0
2
..=−
ALAB3KM6;A^0.0!

!0</P
7!M=KAB 0AB%14<M12
H4
hH
g2
v
h
22
)(
max
+
==
8
F=M(ABG u0Yr8FO
$vC+2AB,^0 VIA2^0 V3+
8
6$F+I<AB< IA2 38


hD(P>A)C+AB,!+/G1N6eI
,=
2
gt
2
1
s =
!b7P>)cA+AB,
+7/GA'O=12
g
h2
t =
8-(P>2!b=1+
,VQ62B-2
$vC+2AB,^0 !I
m04901089
2
1
tg
2
1
s
22
1
,,.,. ===
8
Ft+AB
( )
s2
89
6192
g
h2
t ===
,
,.
8
vC+AB,^0 !3q0,Oc)C+,
%.^0  0u!I
( ) ( ) ( )
m9110289
2
1
61910tg
2
1
hs
22
2
,,.,.,, =−−=−−=
8
f
E
Ej
s
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
6$FM4
F+AB, I
s450
89
12
g
s2
t
3
3
,
,
.
===
8
F+AB< 3
s050
89
6182
2ttt
4
,
,
,.
=−=−=
H"(I$J<
6
FG6]0Z0o4Add+W+=6AB8HB
>c-J>]R)VAdd"f .S$0AB>c(V
ZR0AB>6c(VoR8fQAB2LRL40<6Q)!`


vC+A23AB> !
%w0
0AB>!
%

%w!
^
AMB
0
%
!
^
AMB
0AB>6!
S
%w!
^
AMB
0
S
!
^
AMC
8
UB0+<RAB12
3
3
32
2
2
1
1
1
a
s2
tt
a
s2
g
R4
a
s2
t ======
HB06ABqLR1N8
 =rABc-J>GT^ALAB3A
^
6;647La
$FL
τ
 V!AL+,-ABM(`
6$h
τ
 V!AL+,-ABM(`
9 ^_!
%
8


hD(P>O+</62X
g
vgh2v
t
0
2
0
−+
=
A2P>+M(
g
h2
t =

 AB   !L0  -= r AB 3 (L AL AB 3 A
^
= C
-
( )
gh2vggh2v
g
vgh2v
g
h2
0
2
0
0
2
0
+−=+→=
−+
−
ττ

]

Z

o
R
f
.
S
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
Z-A<-,
( )
( )
(
)
( )
τ
ττ
ττ
ggh22
ggh22g
v0gh2v2gh2vg2g
000
2
−
−
=→=++−
$AB!L0-(AL
τ
 !7
(
)
( )
( )
sm712
110401022
110401022110
v
0
/,
...
....
=
−
−
=
HBAB,rJ>3(L8
6$AB0-(AL
τ
. !7
(
)
( )
( )
sm78
110401022
110401022110
v
0
/,
...
....
−=
+
+−
=
HBAB,rJ>1448
RABJt<)C+]ZYV8
HB3AB/)]6;X_!/)Z6; X_!8F(2)C
+]Z8

(
Fc'x03AB
( )
2
AB
sm
3
5
6
515
t
vv
t
v
a
/=
−
=
−
=
∆
∆
=
8
FG77O)C+]ZcP>
2
A
at
2
1
tvAB +=
F!3,]ZY^8
*
9:;0AB36J6<t7P>
a606;
2
vv
v
BA
+
=
04]Z7(2
( )
m606
2
155
t
2
vv
tvAB
BA
=
+
=
+
== ...
Rc1D@";4+J$ 0X/8
FD+I0c1D(I0D+!
c1DB(I8HB31Lc1D@76;
X^/_+8
Z<;'!3334+6;8FO
$s3c1D8
6$F+c1D<)C+@8

HB36c1D12
h
km
25
2
50
v
/
/
==
8
F+c1D< 0X/212
*(JDB ===== 63h0602551vst ,,/,/
8
s3c1D
( )
(
)
( )
2
sm1290
s6081
sm6350
81
hkm50
2t
v
a
/,
.,
/,/
,
/
/
max
====
B
8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
K+!L!8E!HM!/0<L+!N/$!$D !'AO
%+6+G
sa2vv
2
0
2
..=−
(
)
2
2
2
0
2
sm1290
km51
hkm50
s2
vv
a /,
,
/
==
−
=
8
1PQ'D0E!.5($R<#
Rc1D6eI(I4+J
)La+)!>ALI>8Z<;c
>)La+)!<+
τ
YV8fQ>!b
)La+)!61V`
-(+,-[8


sm112(2y0

12+I)La+
)!8-(-Jt07
o(2>
22
1
a
2
1
at
2
1
l τ==

o(2". $
2
1n
at
2
1
l)1n(
−
=−
o(2I
2
n
at
2
1
nl =
8
FG 7 !  +    >   ) L a + ) !
1nn(ttt
1nnn
−−τ=−=∆
−
$8
HL[07
∆
[
 0 g!8
Rd,rc-;ALAB3A
^
 X_!8FO
3--<A23<-<d!1Nr V8


HB3ABc->!/r !A

u0g_!8
s7
α
@AB3ABA2-J>=C
y
x
v
v
tg =
α
8&c
Ab648
FG703--<A23<-<AB1N2O12@2
-I<3
A

A

A
^
α
α
8!
α

8!
α
A
A
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
( )
( )
222
2
n
2
t
2
222
y
2
x
x
n
sm452889agga
sm28
8915
1589
vv
vg
ga
/,,,cos
/,
,
.,
.
sin
=−=−==
=
+
=
+
==
α
α
U+r)=67ALAB3A
^
 ^_!c-,-ALa
-J;7
α
T^
^
8s=!D)=67,rGa8fQ
$1L2)=677,8
6$FI)=678
$F+G1Nr67L1N678


',@1,62a0I1:;07
AB6W/1B-c-
J>A2c-8
oc-J>12J6<tAL
36;0AB36I6;A
^
A
^
8!
α
8oc-12
JALAB3/Pt6;A
A
^
8!
α
8
$MA2+AB\14)<AB36Ic
-J>A
^

( )
m12
g2
v
g2
v
y
22
0
2
y0
,
sin.
max
===
α
$F+6AB
( )
s31
g
v2
g
v
2t
0
y0
,
sin.
. ===
α
6$oP>IABr4
m10
g
2v
g
v2
vtvL
2
00
0x
====
αα
α
sin.sin
.cos
FG\-f%X+rd14-O4ALAB
3A
^
 X_!c-,-ALa-J;7
α
S^
^
8&'
$F+d5
6$n=GV-<yd5
$HB3d1N8

FG\-A4d144,
(
)
(
)
m872
892
3015
g2
v
g2
v
h
2
0
2
0
2
y0
,
,.
sin.
sin
====
α
z
f
α
A
^
9
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
+d
(
)
(
)
( )
s153
89
782252
89
57
g
hH2
g
v
t
y0
,
,
,
,
,
=
+
+=
+
+=
FI
(
)
m411533015tvL
0
0
=== ,.cos..cos
α
HB31N
(
)
(
)
(
)
( )
( )
sm7263015323vvv
sm32378225892hHg2v
2
02
2
x
2
y
y
/,cos.,
/,,.,.
=+=+=
=+=+=
C!+?+'%0+8%&HSA3
TNUAV'/9+V&<+Q/W3
X'A !/8U0'
2
0
2
y
0x
tg
2
1
tvHtg
2
1
tvHy
tvtvx
..sin..
.cos
−+=−+=
=
=
α
α
Y<5++!+$+?+'=Z3
Y<"<!<?[/,K+9+Q$!!'</0
%+- !K3
Y</LB<\$97-
tgvv
constvv
0y
0x
.sin
cos
−=
=
=
α
α

!#]$(JD^%#_($(<^#*J$2<`D3
FG\-fS^0+rd3ALAB
3A
^
 ^_!c-,-ALa-J;7
α
S^
^
8F
$F+dLa/GNr`
6$n=GV-<yd`
$E)*d`

F(q---362 . T8
omzALz;V-8
$ABc2
)(..sin..
)(.cos
2tg
2
1
tvHtg
2
1
tvHy
1tvtvx
2
0
2
y
0x
−−=−−=
=
=
α
α
+0=-^
0t5t5300t10
2
1
t301030
220
=−−↔=−− ...sin.
om(,+d%!8
6$I{A'OV-640,O8
m317m31023010tvx
0
0
,.cos..cos ≈===
α
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
$6<()*A40I-)*
2"-)@A2C/D6<+$
nD+-" $A2"%$6;NG-" $W
A2"%$
(
)
m310x0
15
x
3
x
30
v2
xg
tgxH
v
x
g
2
1
v
x
vHtg
2
1
tvHy2
v
x
t1
2
2
2
0
2
2
00
0
2
0
0
≤≤−−=
−−=
−−=−−=→
=→
/9+
α
α
αα
αα
α
cos
.
.
coscos
.sin...sin.)(
cos
)(
2\;0)*A412-618
fQ-=rABc-,-ALa-J;7
α
6;64ALAB36IL0IAB12M8

hD(P>OIAB,r4C1B-,62 . S
g
v
g
2v
L
2
0
2
0
≤=
α
sin.
HB!b,IM6;
g
v
L
2
0
=
max
/!%
α
 0
α
TX
^
8
n|1}Kf2U12 %0Y[r8fQ<t>K&4c6
 /M"qAB3 6 IA274$0/|14!b126
4`
o6<"f2U$u0[%[_!
%
5"&4c6$u0g ^_!
%
8


FG P > I 
g
2v
L
2
0
α
sin.
=
 B 0 AL 1M } /P t " A
^
/Pt$A27r/Pt"r/7r6;TX
^
$I9!b\
1'AL3m+8E77',/\1}2
-3&cr6
( )
m56126712
8109
7279
L
g
g
L
HN
XP
HN
XP
,,.
,
,
===
FAB37
$F))7"F)Ad)
7%T+$8
6$/+A2/-NWW5
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
$RaF~))F"RaF~))F
Ad%[24$5
($AVF)4)*dAL/6;gg
-N8


hD(P>OAB37
T
2
π
ω
=
A21:/•-=tN3
AL12V"!$!b,
$HB37M))
( )
srad10267
3600
24
2
5
/.,
.
.
−
==
π
ω
6$o/•)/-N12 8n+)<Ad12 %<4AB
37/+A2/-N12 T0X8 ^
.X
(_!5 0[T8 ^
.S
(_!
$ol-(P>4AL/•/7AB37
a~)12%0[8 ^
.Y
(_!5
($oA7/)12gg-N12 0 u8 ^
.S
(_!
AB3(2)4af2U8
Z<;Axf2U12
α
%
^
8


Fc62 . gAB37M)712
ω
[0%Y8 ^
.X
(_!8Z/O)*f2U"c$12
α
cos
R
r
=
8
FG77AB3(2f2U12
A
ω
8
ω
8w8!
α
F!3A2,ATS^_!8
Y0<%0++8"Ba7- !'A!'!
b<H"Gc+L/9+7- !'AO%+6+G/9+
DM-!'
ϕ
!'.5D$/L
ω
!'/LH0+/$
+!L
β
!'+!L5!Bde!<A&DL%&%
Kf3
z
ω
α
w
f62 .
u
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522

 RAP1~ ! / 6eI ) ,  -N ,AB 3[^^
Ad_-N8FO37AP1~A2!3Ad2AP1~C),-N
<AP1~12(I8


HB37AP1~
ω
[^^Ad_-N[^^8%
π
_Y^"(_!$!+
τ

-NY^!8
R2
ω

β
8
τ


( )
2
srad221
3600
1400
60
601400
/,
/
====
π
π
τ
ω
β
8
s7),!+
τ
 -N12
( )
rad70060221
2
1
2
1
22
πτβϕ
=== .,..
EAB0!3Ad), -N12
/f]RZ
*
===
π
π
π
ϕ
2
700
8
R6c)B(I0!-NAB37=GS^^
Ad_-N3 g^Ad_-N8F36cA2!3Ad26cC)
,-N8

Fc'xA3771P372
( )
2
0
srad210
60
602300602180
/,
/./.
−=
−
=
−
=
π
π
τ
ω
ω
β
8
s7),(MA23)MAL)A..!
J6<tN
(
)
(
)
1/f#
240
2102
602300602180
2
22
2
0
2
=
−
−
=
−
=
,.
/./.
ππ
β
ωω
ϕ
8
fa(MA2P>AB376
1/f#
2401
2
300180
2
0
=
+
=
+
= ..
τ
ω
ω
ϕ
R6c76/Ow ^1NI>40!7))
7AL376;S0 T(_!
%
8fQ0!V>
$HB37A2AB3(24A26`
6$s3-- <03 <- < A2 32-I4
A26`
$s7@32-IA26/O6c">ALq4
A26`

$hV>0AB37A2AB3(24A2612
(
)
( )
sm314010143Rv
srad1431143t
/,,.,.
/,.,.
===
=
=
=
ω
β
ω
s3<-<7'/PtA23--<
1N2
α
f


Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
(
)
( )
222
n
2
t
sm986010143Ra
sm314010143Ra
/,,.,.
/,,.,.
===
===
ω
β
od32-I6;
(
)
2
2
n
2
t
sm031aaa /,=+=
8
$s7@32-IA26/O12
α
=C
031
3140
a
a
t
,
,
sin ==
α

α
 [
^
TYj8
o/)6c6/OX^12^0 V8F
$HB3(2A2AB37A265
6$s3--<@6/O8


HB3(2A2AB374A26
( )
( )
srad862
50
431
R
v
sm431
10
502
T
R2
v
/,
,
,
/,
,
,.
===
====
ω
π
π
f/f<A4A'+!5+
f45 !H0++G
6$s3--<{3LV@6/O
(
)
2222
n
sm9862508622Rra //,.,/. ====
ωω
8
R226eIA2+d06/O /0(2Y^^0
ALAB3XT/_+822<)C+7S^V8FAB3(20
3--<03<-<032-IA23722K3
)C+78o2212(I8


ow / ^^^0A
^
XT/_ X_!0!Y^^0S^!8
hD(P>AJA2d6<t!b
O,1,I<8
(
)
(
)
( )
2
22
0
t
2
t0
sm
3
1
30
30156002
t
tvs2
ata
2
1
tvs /
.
=
−
=
−
=
+=
8
HB3I3+Ad
( ) ( )
hkm90sm2530
3
1
15tavv
t0
//. ==+=+=
8
s3--<{3LVI
( )
2
22
2
n
sm6250
1000
25
R
v
Ra /,====
ω
od32-I12
( )
2
22
2
n
2
t
sm7080
8
5
3
1
aaa
/,
=
+
=+=
s372I
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
( )
24
t
srad1033
1000
31
R
a
/.,
/
−
≈==
β
HB341c4DP6;A%0%8 ^
g
_!8FOAB
37A23--<41c<c)*712Add6
/O^0X8 ^
.g
8


€1cA%0%8 ^
g
_!%0%8 ^
Y
_!5w^0X8 ^
.g
^0X8 ^
. ^
8
HB37A23LV{3--<1I1,
ω
A_wT0T8 ^
Y
(_!5

ω
%
wu0Yg8 ^
%%
_!
%
R+3•)!P7(dL=8U<+•
cLGA'O]!A'OZ"]Z
⊥
AL(d!P0 .T$!+

 ^-N!bLA'OoZ/=! %^8U<+•
A-O,(d!+
%
 %0X-N!bLNA'OZ8
oAB33AL(dL12/Pt8FO
$Z1!P5
6$HB3A3AL(dL5
$HB3(dL3AL6+!P5
($s7
γ
8


FG]<o<+
 ^-N0]<Z<+
%
 %0X-N0Zo7(2!Zo %^8
V12 62  t ,-AB38F  W
+    q AL (d L AL AB 3
→
u
A2
!AL(dL"(+•$ALAB3
→
v
8
ot,-O123AL
6+!PALAB3
→→→
+=
uvV
8
F+,->62>AL .T0+
,->>AL .T68
FcAb07-!
!8
51A8
51"A8!
γ
$8
%
5A8!
γ
5
( )
sm20
600
120
t
s
u
1
/,
===
8
'
,
cos.cos..
5336
5
4
512
10
t
t
tvtvl
0
2
1
21
=→===→==
γγγ
( )
sm330
3
1
53
20u
v
v
u
5
3
/,
/
,
sin
sin
====→==
γ
γ
8
o(d!P
m2006010330tvl
1
=
=
=
)..(,.
8

]

Z

o
R
f .T
γ
A

H

]

Z

o
γ
A
H
!

1
f
.
T6
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
U+•)!PcLAP7AL6+!PAL
AB3[0%/_8UL=CA-OP(d/= X^8
F
$HB3(dL3AL6+!P5
6$ F+  I   ) , !P8 o 6<    !P 6;
^0X/8

Z(d!P1^0X/X^^8! X^0H[0%/_%_!8
FGAb
( )
sm6002
500
150
v
l
s
u
l
s
v
u
/,..
===→=
8
F+<!!P
( )
s250
2
500
v
l
v
AB
V
AC
t =====
8
-!3$^0Y^_!56$%X^!8
R66GA'O]LA'OZ8]Z;cLFVPA2
/=S^^/8&'+6<
$nP775
6$o77tcLUZe5
$o77tcLFVP8
o6<AB376;A
%^_!0AB363AL/P/OA
%
Y^^/_8

]ZS^^/07A
%^_![%/_0A
%
Y^^/_8
$F+66M<-G]<Z
( )
1B#
30h50
600
300
v
l
t
2
====
,
8
6$FM62 .%Y063LA'OZ07-=6<A-O
7
α
!AL-]Z8F7
( )
hkm59672600vvV
22
2
1
2
2
/=−=−=
8
F+66G]<Z12
( )
B
230h5030
596
300
V
s
t ,, ====
8
$s7PGFV!P8F+6
I(q12
( )
B
826h4460
72600
300
vv
s
t
12
,, ==
+
=
+
=
8
f .XP=68
$o6<O78
6$x@W'A28
$h!AB368

]

Z

o
f62
.
%[

A

H
!

1

Z
]
A
%
A
α
f62 .%g
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


$UA2W'=6212(I
8
6$sW'AL+6<+-
8
$Z012AqL8HB3yABG1N
B/8W'AB32(33AB21L"3
6<!37+J$8FGW'07!!3AB
S
‚
‚
%
8
f .YW'AB38fC6<
4yz]0]Z0Zo0oE8


z]AB-+^W(IAL
3/1L8
W']Z6<AB!8
W'Zo6ABB(I8
W'oEAB<-B(IAL31L
/Zo8HB(G1328

A

z
]
Z
o
E
f
.
Y
f
.
X
A

 
S
%
z
f .Xj
A

S
%
z
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


%. 8Rc7/31,%^^^^/0B(I(L(
1M6;Y^^^U0AB36Ic6; X_!8fQ
$s3c5
6$h61Vc(G15
$+cC,/G1NC</c(GJ8


$s3c,Oc'1BiiUcƒ
„_.Y^^^_%^^^^.^0S_!
%
8
6$F+/G1NC</(G1
( )
3DRZ
Z$])
(R)Z
!
/

==
∆
=∆= t
$vC+/G1NC</(G1
!A
^
8#8
%
_%888S[X8
%.%8 R  y a TuU 6' /…- @  a -J J
>"%.T$89M r-J74 ya 12 T[U8
fQ1MQI Va y`f!3 ! @
yA2ar-/^0%8


9MV ^[0gU51Mu0gU
n3y3I1M„
f
L3(L01M!
4ayL144"f%.T$0d/3Vy14
41M!1L3(L"f%.T6$8
FGAb201M(q"„
f
$A2V„
U
y-=7
'Q
„
f

(
)
N8949147202PNk2PFF
2ms1ms
,.,..
=
−
=
−
×
=
−
+
„
U

(
)
N810749147202PNk2PFF
2ms1ms
,.,..
=
+
=
+
×
=
+
+
%.S8fQ-=(1M6;64142>47
(IA2!+S^V7, 8o6<1M!
26;X†m1,28


sm„121M(1428&rc-01MV3
20c'1BU%06; „.‡
!

F712/31,A2
2
t
s2
a =
123I8
„
f
„
U
„
!
„
!%

f%
.
T

f%
.
T
6
f%.T
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
FG7!
2
ms
t
ms2
mg5mafF
..
% +=+=
8
F!3! 0S^!0 X0Y XY^^/,„
≈
g%^^U8
1C"G%0++L+ !!"%&<=(R$J\#3
%.T8R+(<cALAB3/Pt89NI+/r
cA-OL0!7+}cA-O!8F=+,-02c
,-ALa-J;7
α
8fQ+,-2+-=a14
c1M1L`Z<;m1,c120!3!@6cA2a
+12/8


H<-'1BiiUcƒ1M(A2c8F2-I1M
t,-<c - J >A2 ;  6; ^ . /P 7 
c-J>0c-./P73
c-4
F+,-/rcA-OL"%. j$ 1MrAP7c 14a
+12
P - F.
N
0
P
F.
N
sin
sin
=
=
−
+
H2
msms
FF0FF
=
=
−
α
α
cos.cos.
R201M!(14c
„
!
/U/".„!
α
$
(
)
α
α
sincos FPkF
−
=
αα
sin
cos
k
kP
F
+
=
F+,-}cA-O!"%. j6$
Z;-VOM0O,1M!a14c+,-
212
„
!
/Uj/"#„!
α
$
H21M„jIa142c
αα
sin
cos
'
k
kP
F
−
=
wk2„j
‚„8UAB+,-}cA-O!+-=(q
1M1L8
%.X8RAB7/31,X/,a4a-J4,-AL
a-J;7
α
S^
^
8f!3!@ABA2a-J46;
/^0%8F3AB4a-J48


U
„
„
!
Uj
„j
„j
!
α
f%
.
j
f%
.
j6
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
F-VO1M(A2ABWS1MJ
>0 U AP 7 AL a 4 A2 „
!
; 4 a
48
'1BiiUcƒAB
a
m
F
N
P
ms
.
=++
o< -  2 c - AP 7 AL a
-J4"-z$A2-!!ALa-J
4"-z$,
=−
=+−
maFP
0NP
ms
α
α
sin
cos

−
=
=
m
FP
a
PN
ms
α
α
sin
cos
R2„
!
/8U4
( )
αα
α
α
α
α
cossin
cossincossin
kg
m
kmgmg
m
kPP
a −=
−
=
−
=
8
F
α
S^
^
0/^0%0u0gO,S0%T_!
%
8
[7-e!\'$+!L !/e<bO+e
7UA/0L+ !/3
%.Y8RAB,34a-J4,-ALa-J;
7
α
TX
^
8n,,)C+!SY0T0AB,AB3A%_!8&
'!3!@ABA2a-J48

-(P>3AB62%.X7
(
)
α
α
cossin kga
−
=


α
α
α
α
coscos
sin
g
a
tg
g
ag
k −=
−
=
8
hD(/<>iA3)A..!73AB,2
12
S
2
v
S
2
0v
S
2
vv
a
222
2
0
2
.
.
.
=
−
=
−
=
8
α
α
cos.gS2
v
tgk
2
−=
FP!3C
α
TX
^
0A%_!0!SY0T^0SYT,/
≈
^0%8
%.[8R!,(VG,a4a62!-I76Pk
38h,(V6eI,4a62/(2-I6Pk6;
%X†(2(V8&'!3!/@!,(VA2a628

‡
!
f62%.[
„
!
α
U
z

f62%.X
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
sm12m1,=(V0
12m1,-I6Pk8FcI
620(2-I6Pk6;%X†(2(V

%X†8
&rc-!,(V0(V'(1M
A2‡
!
8
R3(V6eI,-=7
‡
!
‡
!
%X†8
R20‡
!
/8U/8"[X†$8
FG7%X†/8"[X†$
330
3
1
75
25
k ,≈==
8
%.g8 $RPP/31,4+6;0!3!
@6PPA2a+12^0 8FO1M/rPP+,-
$ˆP5
6$ˆP(IAL36;%_!
%
5
%$olVQ4+,-PPA2
$94(37(3T†56$&3(378
f!3!6;^0 !3+8

Ft,-1M(14PPW1M/r
F
PP0m1M
→
P
0-=
1M--<
N
a+A21M!a+
ms
f
8
'1BiiUcƒPP12
→
→
+
→
+
→
+
→
=
a
m
ms
fNPF
om(12c8o<-214-
,
$ nc4+;
kmgmafmaFmafF
msms
+
=
+
=
=
−
F!3  ^^^/5/^0 5u0g_!
%
5A2
$n0^
„ug^U8
6$n(IAL3%_!
%
„%ug^U8
%$ nc4+(3
$ˆP14(3
α
α
α
α
sincossinsin
mgkmgmaPfmaFmaPfF
msms
+
+
=
+
+
=
=
−
−
F70!
α
^0^T12(3(3
!
α

010401
2
,, ≈−
(
)
N137204089100018910001001000F
=
+
+
×
=
,.,..,..,
6$ˆP3(3„"/!
α
.!
α
$8
α
α
α
α
sincossinsin
mgkmgmaPfmaFmaPfF
msms
−
+
=
−
+
=
=
+
−
F!3
(
)
N588,041000.9,8.0,8.10,1.1000.901000F
=
−
+
×
=

„
U
‡
!
„j
Uj
‡p
!
α
f62%
.
g
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
%.u8R!,(V,Ae)dm7/31,/P/0I
6AB7/31,
A2
%
"
‚
%
$8&'3ABA2!>~
(V8o!/P/8
-(6;!3
%
%
 /8


E!,(V/PC0dm/P/31,0/P!4!,(V
1P~AL1M~(VF5AB!bALq38H
‚
%
4
!1M/r1L
%
12
3(Ld
%
6'
/r1448
om(GAB,-AL
yAB"Ab$8'1BiiUcƒGABr4-

=−
=−
amPTm
amTPm
222
111
:
:
oA<cA<-4,
(
)
ammPP
2121
+
=
−

2
21
21
21
21
sm273g
mm
mm
mm
PP
a
/,=
+
−
=
+
−
=
&c-'1BiiUcƒAB
7
.F
8
g
mm
mm2
g
mm
mm
mgmamPT
21
21
21
21
1111
+
=
+
−
−=−= .
FG7O,
N
55
6
T
,
=
%. ^8 R 2 0 ! /  -0   AL  3 /P t
γ
^0X_!
%
8 %V!/6eI0+e2A22
B(IL/(GJ8F426)C+!3!
6;/^0^ 8F
$HB31L25
6$F+26/G1N2-L/2(GJ5
$s32B(I5
($vC+2622C,8


%
%
F
F
f62%.u
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
FIc
s AL3
^0X_!
%
+
 %!8
s%B(IAL3
%
/8^0^ 8u0g^0^ug_!
%
(L(=1M!+
∆
8
o7AbW'AB3Ic+48
$HB31LI
(
)
(
)
hkm621sm61250tav
11
/,/.,
max
=
=
=
=
6$FIB(I+
( )
s261
0980
6
a
v
t
2
,
,
max
===∆
Ft+I"/G1N-<1N(G1$
(
)
s27326112ttt
12
,,
=
+
=
∆
+
=
8
$s3I/B(I12
%
^0^ug_!
%
8
($vC+IC,6;‰(OŠ,r
( )
m62192736
2
1
tv
2
1
s
2
,,...
max
===
%. 8R6=y],a4a-J;8Z=],3AL
6=yZ/6;!,(VAe)dm3'"Ab%.X$8
n31,dmA2(V/P/8
$FO1M~(V<
]
%^^5
Z
S^^0!3!@6=]A2
a-J;/^0%X8
6$U<tA'O]A2Z1M~(V!b6;64`&c!3
!A‹l8


&rAB7/31,
0
%
,3AL4%.X8o1M
(A2ABC,\k4Ab8
‡
!
F
F
%
U
%

f%.X
A

A



%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
o7  A< -  ' 1B ii Ucƒ   AB 2 r 4 -
N",\6;l47(‰#Š64$
=−
=−
)(:
)(:
2amfTm
1amTPm
2ms2
111
F70
22ms
PkNkf
..
=
=
8
oA<cA<-" $A2"%$4,
(
)
ammfP
21ms1
+
=
−

g
mm
mkm
mm
gmkgm
mm
fP
a
21
21
21
21
21
ms1
+
−
=
+
−
=
+
−
=
..
FG-" $!
(
)
g
mm
mmk1
g
mm
kmm
mgmamPT
21
21
21
21
1111
+
+
=
+
−
−=−= .
%+-?/GMgHQ'e\'$6+/!+f !<
(
/0
<
*
!MgHQ'76+3h'$MgHQ'7UA/0/+Nb
<
(
e<b%0/0<
*
8%eH9+!'0+3F$?Q!#/0Q
%#?/GMgHQ'G!%&
(
)
(
)
( )
N47189
3020
30202501
g
mm
mmk1
T
BA
BA
,,
,,
,.,,
=×
+
+
=
+
+
=
"F!3/^0%X5
]
%^^^0%/5
Z
S^^^0S/$
%. %8fAB7/31,
/0
%
%/,3AL6;!,(V
A2,a4a62;8Eq!,(V/Ae)dm0
I(V6A2
%
A2I/6A2AB>67/31,
S
S/"%.
Y$8o!/P/8FO1M~!,(V8


Fm1M
S
122-I1M(c-A212
ABALq38F7
321
3
mmm
gm
a
++
=
&r4AB
7
( )
N94
321
8931
mmm
gmm
amT
321
31
11
,
,..
=
++
=
++
==
&r4AB
S
7
(
)
agmTamTgm
32323
−
=
=
−
S
F
%
%
U
%

F
%
F
U
S
f%
.
Y
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522

( )
N71489
321
321
g
mmm
mmm
mmm
gm
gmT
321
321
321
3
32
,,.
).(
)(
=
++
+
=
++
+
=
++
−=
8
%. S8\a-J4,-ALa-J;7
α

S^
^
A2
β
TX
^
"%.[$07edm/31,/P/8Eq!,
(VAe)dm0I(V3ALAB]A2Za4a-J48
n31,AB]A2Z6; /8ZQ)=1M!8F3
A21M~(V8

F 62  20  1 r     AB c -   a
48E!,(V3AB/P6'C4AB!bALq
38om(Ab"%.$8o1M(
A2ABC,\48
'1BiiUcƒ,<14-AB
(
)
( )
=−
=−
2amPTm
1amTPm
222
111
β
α
sin:
sin:
oA<cA<-4,
(
)
ammPP
2121
+
=
−
β
α
sinsin
 g
mm
mm
mm
PP
a
21
21
21
21
+
−
=
+
−
=
β
α
β
α
sinsinsinsin
FG-" $!
21
21
21
21
1111
mm
gmm
g
mm
mm
mgmamPT
+
+
=
+
−
−=−=
)sin(sin..
sinsin
.sinsin
αβ
β
α
αα
F'I62C"
6;
]
0
%
6;
Z
$A26
>3A21M~(V,
2
sm021a /,−=
5
N
9
5
T
,
=
8
n<)=2>Q;0,AL(CmAL
371L6; 0^%_!
%
8
ia%0+e$!!!'&/;DWL
f / > %,  e3 F $  %0+  0' !   T +G H  
'A8+G+D/9++G.T5++?+e3C'+e$7+
<L+<A7-6N//'$!c%\'
Ea+b?+!L7S+GH.T3
QL+ S5++?+ed HU  5 N
7<!D3@+N7<!D$MHU/0<j+/7UA
F
α
U
U
%
%
F


β
f%
.
[
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
/0+G'A !/c/+NT+GH !UA3@+
N<!D$k0+G !M<!DUA/0+G'A !/$
H7+?DEla+G'A !/3C5
!.+?+"<+G'AHm?+!L !/%,Q<
%A?++?+++G'A/0+?++%0+3C\+e7!+H+
<0+?+B/05"<0'?++5++?+!+"3C!
+G0'%&1D!+.0<+G%0+/0BB+G
++N<)M!DM0'/m?+HM!eDMn<!DD<A
,K0"M/!+fM/0M?#b%&+<
!91K/0DD0"M/!+fM$M+o/0M
?#b+?+/0+?+%0+9P0+3
%. T8R22WI0 ^0A2X03AL
c>M46;@1d38Z<;/'(1M6;
X^^U1dC 8ZQ)!8FOC1d+,-
$226eI601M/rI/PtA2! ^VAB
322L _!5
6$2214(374X†ALAB3/Pt8

C1dVc'1BfN„/8
FG7',!32W
./. mN105
cm
1
N500
x
F
k
4
===

$ 9M ~  1d  > 
7 A d 1M /r =   I
8FG'1BiiUcƒ
7F
"
#
%
$0AL
t
v
a =
8h
C1d>
(
)
cm3m103
10
10
5
110510
t
k
vmm
k
T
x
2
4
3
211
1
==
+
=
+
==
−
.
.
.
..
.
)(
9M~1d>F
%

%

C1d>
cm1m101
10
10
5
1105
t
k
vm
k
T
x
2
4
3
22
1
=====
−
.
.
.
..
.
6$n2I14(38o1M1d-=V6;AL2
-Im1M/r38o
(
)
α
α
sin.
sin.
gmT
gmmT
22
211
=
+
=
F70(37412X†0>12!
α
^0^X8
C1d
(
)
(
)
cm714m1470
10
5
0508910510
k
gmm
k
T
x
4
3
211
1
,,
.
,.,..
sin
==
+
=
+
==
α
cm94m0490
10
5
05089105
k
gm
k
T
x
4
3
22
2
,,
.
,.,..sin
=====
α
„
F

F
F
%
F
%
f62%. T
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
%. X8RAB7/31,%^^0,cKI!,(V(2T^5
AB)a-J;ALAB3/Pt!!,(VAa
78s=!D/7(VAL-J>7
α
SY
^
8FAB37
ABA21M~(V8


HBAAdd76/Ow18!
α
8
9M(14ABWm1M
→
P
A21M~
→
T
"Ab$8Ft,-1M
21221MLVVdAB
→
+
→
=
→
TPF
ht
 " $
FG%.
N452
36
8920mgP
T
0
,
cos
,.,
cos
cos
====
αα
„

8
α
88
α
8 R2„

8w
ω
%
818!
α
8
ω
%
8
2
ht
mltgmgF
ωαα
.sin. ==
8
E7
s/rad6,5
cosl
g
=
α
=ω
%. Y8&'3 AB
%.g8ZQ)!0/31,
dmA2(V8-(+,-

%
8

1
α
F
f62%
.
X
%
%
F
F
F
f%
.
g
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
oN:;!>~(Vm6;06;F8FGAb%.g0
<r4AB
07
.F
" $
U<r4AB
%
07
%F.
%

%
%
8 "%$
hD(Odm3'A2dm;0)C+

-1I)C+AB
%
0G7/rc
%
%
"S$
UVA<" $AL%WA<cA<AL"%$!
21
21
21
mm4
gmm22
a2a
+
−
==
)(
8
U<

%

( )
2
21
sm923
5
g2
a2a /,===
8
!'+, !!
(
/01(#!<Mg !HQ'

21
21
21
21
11111
mm4
gmm3
mm4
gmm22
mgmamPT
+
=
+
−
−=−=
)(
%. [8vdm]/31,/P/0+1W!,(V0
I6A2)=aR
0I/6A2dmZ/31,/P
/8vZ1Ae!,(V/8fI(V3AL)=aR
%
A2R
S
8wdm
]AL26mAB,cA21M/<1d"%.u$8
&'3)=aR
S
A2!3\F41M/<0<R
%
≠
R
S
0R
‚R
%
#
R
S
8

om(AB%.u8FG3)
A+dA23'3)3AB
321
aaa2
+
=
"Œ$
Edm7/31,A21M!Kt76Q)47
(
)
1T2TT2T
211
=
=
;
&rc-AB0-'1BiiUcƒ
(
)
2TgMaM
1111
−
=
%
R
F
F
F
%
F
%
R
%
R
S
S

F
f%.u
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
(
)
3gMTaM
2222
−
=
(
)
4gMTaM
3233
−
=
FM-r-6<t
( ) ( ) ( )
(
)
2
1121
2212211
M2
aMgM2M
agM2MaM2aM322
−
−
=→−=+→+ .
( ) ( ) ( )
(
)
3
1131
3313311
M2
aMgM2M
agMMaM2aM422
−
−
=→−=+→+ .
F
%
0
S
A2"Œ$
(
)
(
)
3
1131
2
1121
1
M2
aMgM2M
M2
aMgM2M
a2
−
−
+
−
−
=
UV=A<-AL%8R
%
R
S

( ) ( )
gMM4MMMMaMM4MMMM
aMMgMM2gMMaMMgMM2gMMaMM4
3232211323121
12132211313231132
−+=++
−
−
+
−
−
=
(
)
323121
323121
1
MM4MMMM
gMM4MMMM
a
++
−
+
=
hD(/<)=2A26>
S
,
( )
(
)
( )( ) ( )
( )
g
MM4MMMM
MM4MMMM3
MM4MMMMM2
gMM4MMMMMgMM4MMMMM2M
M2
MM4MMMM
gMM4MMMM
MgM2M
a
323121
323121
3231213
323121132312131
3
323121
323121
131
3
.
++
−−
=
++
−+−++−
=
++
−
+
−−
=
FG"%$
323121
321
1111
MM4MMMM
gMMM8
aMgMT
++
=−=
h!3\1M/<
323121
321
1
MM4MMMM
gMMM16
T2T
++
==
%. g8R<c/31,%^/7/P!4a
-J;8F4c7ad/31,%/"%. ^$0!3!
@dA2c12^0%X89I>+(14d1M6;%U01I
>%.6;%^U89M7-;A2L(mcc8&'
$9M!@dA2c5
6$s3dA2c+,-48


9M!\M@dA2c"‡
!
$

/^0%X8%8u0gT0uU8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
.
C5 - \
„%U8 E7 „•‡
!
d  /P , 4 c8
F+,-2dA2c,-2AB(ALq
38F7
2
sm090
2
20
2
m
M
F
a /,=
+
=
+
=
sm‡
!
121M!@cA2d"%. ^$8&r4c7
N81
m
M
MF
aMf
ms
,. =
+
==
)C5-!+
„j%^U
F+,-2„j‚"‡
!
$

8fd,4c
1M!@cA2
dN6;1M!1L‡
!
/T0uU8
sm
123d0
%
123c8
U<r4d07
„j.‡
!

"S$
U<r4c7
„
!
R
%
"T$
FG"S$A2"T$!
2
ms
1
s/m5,7
m
f'F
a =
−
=
2
ms
2
s/m25,0
M
f
a ==
%. u8U+/r/Nym1,ALAB3/Pt6;!,
(V(218n=GI(VLa6;"%. $
$F!3!@/NyA2a"(V,6A2mV/N
y$5
6$U<(V6A2I/Ny1L1M!7t/P`


$sm
→
F
121M/ry0
α
7,-6K(V/rA2a8H/Ny
4
„!
α
.‡
!
^ " $
‡
!
R
„
‡
!
f%
.
^
„


1
]
U
‡
!
α
f%. 
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
FG" $!
l
hl
.Ff
22
ms
−
=
9MrAP714a+
l
h
FPsinFPN −=α−=

E7!3!
Fh
Pl
hlF
N
f
k
22
ms
−
−
==
6$hMta1M
→
F
12ta-1MU@yA2
a!2/P12t1L1M28E71M!A‹@'l8
%.%^8H<-A46/P/O0
</<1M=/P/O8o6<1M=/P/O|1ALAB3A4
0!3|112/0/31,A46;8


9M=/P/O14A4‡
./A0/12!3\18
Fc'1BU>
dt
dv
mkv =−

dt
m
k
v
dv
−=
" $
FO-VA<" $,
t
m
k
Cev
−
=
"%$
o12;!3O-V89N^5AA
K
G"%$!oA
8
"%$K2
t
m
k
o
evv
−
=
"S$
sm12)C+2A4,c-7
t
m
k
o
ev
dt
dx
v
−
==
"T$
h
Be
k
mv
x
t
m
k
o
+
−
=
−
"X$
Z12;!3O-V8FG/^0^0!
k
mv
B
o
=

FZA2"X$,
−=
− t
m
k
o
e1
k
mv
x
%.% 8H<-AB</<1M=/P
/O06<;1M=|1ALAB3AB8


9Mt,-a14AB„{/A
Fc'1BU>
dt
dv
mkvmg =−
8
−−=−=
k
mg
v
m
k
v
m
k
g
dt
dv
" $
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
a
k
mg
vu −=
8" $K2
dt
m
k
u
du
u
m
k
dt
du
−=→−=
"%$
9O-VA<"%$
t
m
k
t
m
k
Ce
k
mg
v
k
mg
vCeu
−−
+=→−==
"o12;!3O-V$8
F+^0A^
k
mg
C −=
−=
−
t
m
k
e1
k
mg
v
vC+2AB,<+"-$
−+=
−==
−−
1e
k
gm
t
k
mg
dte1
k
mg
dtvx
t
m
k
2
2
t
0
t
m
kt
0
...
8
%.%%8FO1M}63!N14IKd!N
6606<;I7/31, ^0+
d12
∆
^0^^ V0AB3A4KId12AgYX_!8


s36A4d!N
t
v
t
0v
t
v
a
∆
=
∆
−
=
∆
∆
=
8
9M}63!N14A4
N8650
t
mv
amF =
∆
== .
%.%S8Rc/31,%^ALAB36IAXT/_8
&'1M6(14c0<c(G1!+$ -NT^
V56$ ^V5$ V8


92M62%.%%KV121MC8FA‹7P>
t
vm
amF
∆
∆
== ||.
F!3%^%^8 ^
S
/5AXT/_ X_!5
sm15v0v /||
=
−
=
∆
A2
/=+>"tcA'V$!b7,/<)=48
%.%T8RA4/31, ^ALAB3A
^
%^^_!B-A2
yA24!VA2y18Z<+A4
y6;T8 ^
.T
V8&'1M=6y14A4A2
41A48


s36A4/4A2y
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
t
v
0
t
v0
t
v
a
00
=
−
−
=
∆
∆
=
||
||
||
8
9M=6y14A4
( )
N5000
10
4
2001010
t
mv
amF
4
3
0
====
−
−
.
..
||.
4VA4
( )
cm4m104104200
2
1
tv
2
1
t
v
2
v
a2
v
l
24
0
0
2
0
2
0
======
−−
....
||
8
%.%X8 R -V D 7 /3 1,   T0XY8 ^
.%S
   AL AB 3 A
Y^_!A2WA226AL74
α
Y^
^
8FO1,1M
A-VD14268

hD('1BiiUcƒ(%,1M-VD(142
612
(
)
(
)
sN107426060210564v2mvmPtF
24026
..,cos....,cos....
−−
===∆=∆=∆
α
%.%Y8Rc/31, XB(IAL371L
6;^0Tu_!
%
8Z<AB36Ic12A
^
%[/_8fQ$9MC(14
c56$h61Vc(G18

89MC(14c
(
)
N735049,0.10.15maF
3
===
o7,
68F+c(G112
a
v
t0atvv
o
o
=→=−=
( )
s3,15
49,0
6,3/27
t ≈=
%.%[8Fa-J>mzALz;0zJ
>8
R,rG7"%0^$"A'r$c-J
>144ALAV3 ^_!8FO6<4Pc1,
3AL3z/=+G1Nr14<1N3NA'O6
I8o/31, /8


9Nr
11
prLL
×==
9NABK1r
122
prprLL
×−=×==
 "
12
pp
−
=
$
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
644c1,
vmr2LLL
12
×−=−=∆
&rA1L
(
)
s/m.kg402.10.1.2x.v.m.2L
2
===∆
%.%g88o/31,,r14Gz4a0ALAB
36IA
^
cL47
α
ALa-J8&'Pc
1,  3 AL z +  AB 3     ;
8

Rc1,
g2
cos.sinmv
L
g2
sinv
.cosv.my.v.mL
23
o
22
o
omaxx
αα
α
α
=
==
%8S 8o/31,,r14Gz4aALAB3
IA
^
cL47
α
ALa-J8&'+A23
ALz8
$Pc1M(145
6$Pc1,8
ZQ)!>=/P/O8


8U1M12m1M0cm1M
t.cosmgvmgxM
oo/p
α
=
=
"12c-AB$
68Rc1,
prL
×=
( )
xy
zyx
yvxvm
vvv
zyx
kji
mL −==→
( )
αααα
cosvgt
2
1
tsinvgtsinv.t.cosvmL
o
2
ooo
−−−=
2
o
t.cos.v.g.m.
2
1
L
α
=
%.S^8 F4a-J;Ž"%. %$7 /31,
6A2 !,(V/P(C0I/(V,/r) 1yQzAL
AB3/Pt8FO!>~(Vc/=@A2z6<;
/
^
0AB312
ω
^
8
z
f%
.
%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


Z=2c1,7
2
2
o
ooo
r
r
rmvmvr
ωω
=→=
9M~F!,(V
3
4
o
2
o
2
r
r
mrmT
ωω
==
%.S 8R+/31,X^/>3(I
AL36;T0u_!
%
8fQ+7=<2A2m1,6/<
+7`
- !3 U+ 7 =  ‰Š  -I m 1,8 Fm 1, 6 /<
6; TXU

'1BiiUcƒ-(+
(
)
gamNamgmN
nnn
−=→=+
N,m
n
12/31,+A2-=1M2!2(14+"AL1L
6;m1,+$
F3(I0
a
L304
(
)
mgagmN
<
−
=
HB+=…A2m1,6/<+
(
)
agmN'P
−
=
=
(
)
(
)
N2459,48,9.50'P
≈
−
=
%.S%8F+c6<1d0KI1d7c6
AB/31,1I1,6; /0%/A2S/8FO1M~1d
$9N>456$9NM(8


89M~1d1I1,
F

u0gU0
F
%

%
 u0YU 0
F
S

S
%u0TU
689M~1d+,-M(
0TgmgmT
=→=+
fF
F
%
F
S
^
%.SS8R,cKI(V-14-O48
9NI (I !7A2 L/
(G1B(I8fQ)401M~(V-
t<2`o=+4!`


F+,->+=‰aŠ5
F+,->.6+
F+,->6.‰…Š8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
'1BiiUcƒ-(/>+
(
)
gamTamgmT
−=→=+
n(I14-O40
a
L14(7
(
)
agmTT
1
+
=
=
" $
n
mgTT
2
=
=
nB(I14-O40
a
L3(7
(
)
agmTT
3
−
=
=
HB41M~(V-c>M=(I
'1BiiUcƒ-(+
(
)
gamNamgmN
nnn
−=→=+
N,m
n
12/31,+A2-=1M2!2(14+"AL1L
6;m1,+$
s3-" $0m1,+c>M4!b=(I0
+c>M!b=•a•0•6+•0A2•…•8
%.ST8F4x;)0+aAB7/31,
/)X^8f!3!@ABA2x6;/^0%X8fQ
$9M!-=71L6;64AB,@4x<x)
ALAB3 %Ad_-N5
6$HLAB372AB6eI,/Qx`


o1M(A2AB6W1MAB0-=1Mx147"M3
ALm1M$A21M!8'1BUcƒ
rfm4rmmaF
222
htms
πω
===
8/P,
rfm4F
22
ms
π
≥
( )
N789,05,0.
60
12
.14,3.1.4F
2
2
ms
=
≥
68E
kmgkNF
ms
=
≤
04AB6eI,/Qxc" $07
r
kg
kmgrm
2
≥→≥
ωω
HB6eI,/
( )
srad22
50
89250
/,
,
,.,
≈=
ω
%.SX8&'1Mr-PA2<6KA2-
Ad21</31,-P6;[X/06/OAd21
6;%^^0A2AB36Ad211P1P/PtA26;
SY^/_8


'1BiiUcƒ-(-P
amNgm
=+
" $
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
N
12-=1M2<(14-P"6;A2,AL1Mr
-P14<$8
FAd210c-LV0" $,A<2
−=→=+ g
R
v
mN
R
v
mNmg
22
1
(
)
( )
N301589
200
100
75N
2
1
=
−=
,
FM-Ad21
+=→=+− g
R
v
mN
R
v
mNmg
2
2
2
2
(
)
( )
N448589
200
100
75N
2
2
=
+= ,
%.SY8R6-=1M6ALAB3u^^/_8s=<-P7'
,!M~m1,14X1I8F6/OQAd1,267
,8


f,-1M(A2-Pc-LV12„

8'1BiiUcƒ
R
mv
F
2
ht
=
F6")<-)O$-P'(m1MA2
1MLV
amFgm
ht
=+
Fc62
g4
R
v
g5|
m
F
g|
2
ht
≤→≤+
(
)
( )
m1600
8,9.4
250
g4
v
R
2
2
≈=≥→
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522



S. 8F6\7a60/31,1I
1,6;
0
%
0
S
8&'/3V678
-(+,-
%

S
5
%8


omAb8F
"^5
2a3
/
$5
%
"._%5^$5
S
"_%5^$8E7
=
i
i
i
ii
G
m
rm
r
2
a
mmm
mm
mmm
xmxmxm
x
321
23
321
332211
G
.
++
−
=
++
+
+
=

( )
321
1
321
332211
G
mmm2
am3
mmm
ymymym
y
++
=
++
++
=
.
HL
%

S
0
%
4
a3
y0x
GG
==
,
5>s;O@
+-V>AL7\a/31,%8
S.%8F4xdW6/Ow7/r1ydQ6/O5
V1y/r;Vx6;w_%8&'A'O/3V
x48


z

%
S
s
G
r
f62S
.
%
1
r
2
r
z
z
z
%
w
w_%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522

o7xd6I12WxdQ"-I6'/r$06
/O07/3V;z
%
01e-AL-Ixd1!/1L6'/r"-I,P
6;($07mV;z
8f41227mVA2
NVzx6I8
&r)<73;Vxd8smAcA'O/3V
x/r1y0xC/r1yA2-Ix6'/r1I1,12
,,,
bac
8F7
2Rb0c
/,
==
8
F7
bmamcM
21
+=
.
(
)
brarR0R
2222
....
ρπππρπρ
+−=
" 7
ρ
12 B  /3 1, 
x$8
( ) ( )
b
b
rR2
Rr
b
b
b
rR
r
b
rR
r
a
22
2
22
2
22
2
...
−
−=
−
−=
−
−=
HB0/3VxC6'/r;VzA-O3(AL1y/r

( )
22
2
rR2
Rr
bx
−
==

S.S8o76!N/31, ^7/P!4+
8F46!N7e/}6/31,X8s=!D/}6=
c-+8H47/31, ^^/A27AB3Id12X^^_!8
&'AB36!N!/6e06<;
$9NI6!N>45
6$FL/6e06!NALAB3 g/_c6e5
$FL/6e06!NALAB3 g/_,6e8


sm/31,!NA2A41I1,12RA20AB36!NLA2
!/6e0A46e/Qd1I1,12A0AjA2A
^
8&rA46e,
6I8
Fc'1B6=21,
(
)
)'('
0
vvmMvvmM
−
+
=
+
(
)
(
)
0
mvvmMvmM
+
+
=
+
'
0
v
m
M
m
vv
+
+=
'
$Z!N>4A^0A
^
X^^"_!$
( )
sm313500
100
10
15
100
0v
3
/,.
.
'
≈
+
+=
Z!N,6eALAB3S0S "_!$8
6$Z!Nc6eAg"/_$X"_!$0A
^
.X^^"_!$
(
)
sm6913135v
/,,'
=
−
=
Z!Nq6eALAB3 0Yu"_!$8
$Z!N,6eAX"_!$0A
^
X^^"_!$
(
)
sm3183135v
/,,'
=
+
=
Z!N,6eALAB3g0S "_!$8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
S.T8RcKI/P!ALAB3A
_!4a
+;"S.S$8F26c7/31,R ^/8R)=I/3
1,%/6c,1ALAB3;A
%
[_!8
h/a-c0)=I;B-8fQ!7cc
20ALAB36;64`


Fc'1B6=21,

(
)
vmMmvMv
21
+
=
−
( )
sm330
2
10
72110
m
M
mvMv
v
21
/,
..
−≈
+
−
=
+
−
=
"o(AB3126Ic$
HB0cALAB3^0SS"_!$,AL6I
c8
S.X8R/}6/P76-B3B0=(L7
α
TX
^
!ALa-J;8H47/31, ^/A27AB36IA
^
%^^_!867/31,RX^^/8fQAB3B!N<6Q)
!`


smAB3B!N12A8E6Q)!46=21,c
-
0mvMv
0
=
+
α
cos
( )
sm822
500
4510
M
mv
v
0
0
/,
cos.
cos
−≈−=−=
α
S.Y8R=?1NI>40!7-/Oa-O!ALAB3
/PtS^^_!3AL=?8FyV01,/O-6;
µ
u^8
n31,t6I=?6;R
^
%[^8fQ
$h61V=?LAB3AT^_!5
6$ n /3 1, t   =? 12 u^  AB3  = ?12 6
4`
ZQ)!>=/P/OA21MNF8


&r  +  0 /3 1, d 1  = ? 12 R0 AB 3 12 A8 h 
/=+Q(=?-74/31,(R0AB312A#(A0
-I/O-7AB312"A.$8
Fc'1B6=21,
(
)
).()(. uvdMdvvdMMvM
−
+
+
−
=
fS
.
S
A
%
A
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
0
u
dM
dv
M
=
−
.
.
=
=
M
M
v
0
0
M
dM
u
dv
M
dM
u
dv
tM
M
M
M
u
v
0
00
µ
−
==
lnln
HB3=?+Vc6>
−
==
tM
M
u
M
M
uv
0
00
µ
lnln
"Œ$
$F+AB3=?AB3AT^_!8FG6>"Œ$!
µµ
0
0
0
M
u
v
1t
tM
M
u
v
−−=
−
=
expexp
( )
s3750
90
270
300
40
1t
,.exp
≈
−−=
6$HB3=?//31,dRu^
( )
sm330
90
270
300
M
M
vv
0
0
/ln.ln
≈==
S.[8FPc1,F3AL)478&cF
12Ia0W76/OwYT^^/07/31,4
6
ρ
X0X_
S
8


RPc1,)=IaW)+/O12
( )
( )
smkg1027
3600
24
10465500
15
16
T
R
15
16
RR
3
4
T5
4
T
2
MR
5
2
IL
233
5
6252
232
/..,
.
.,.
.
....
≈==
=
==
πρπ
π
ρ
ππ
ω
S.g8RxdW/31,^0S/076/Ow^0T0)
ALAB37
ω
X^^Ad_-N8F(14xPcC5x)B
(IA2!+
∆
%^V(G18FPcC78


3AL))3'ALPc1M/Pt0AB3
76<tc+AL37
t
I
M
0
ω
ω
β
−
==
( )
( )
mN190
20
2
60
21500
4030
t
2
mR
t
I
t
L
M
2
0
2
0
.,
.
.
.,.,
−≈−=−=
−
=
∆
=
π
ωωω
S.u8Ra0W/31, ^^/06/Ow^0X)
)78F(141MC„%TS0TU0<-<ALa
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
A2AP7AL)8h+
∆
S 0TV0(G18FOAB37
1N6eI(1MC8

n(1MC„14a0Pc1MC1
)
I
M
t
=
−
=
0
ω
ω
β

( )
( )
srad300
50100
43142432
mR
Ft2
2mR
FRt
I
Mt
2
0
/
,.
,.,.
/
≈
−
−=
−=−=−=
ωω
S. ^8Ry7/31,X^/0+/O 0)ALAB3g^^
Ad_-N8F(A21MC<-<ALaA2AP7AL
)8h%-NS[V0(G18F
$RPcC56$9MC<-<8


F7
( )
( )
mN
t
mR
t
I
t
L
M .67,6
157
60
2.800
.5,0.50
2
2
0
−≈−=−=
∆
−
=
∆
∆
=
π
ωωω
( )
N
t
mR
R
M
F
34,13
5,0
67,6
−=−=−==
ω
S. 8RW(21^0X^7)M()
;)I8RA4/31,^0^ /6c
-;ALAB3AT^^_!L4A2I/A2eA2
8FAB37!/A4B-A28Z<;Pc
)O3AL)6;X/
%
8


-('1B6=2Pc1,{A4
(
)
ωω
2
mlIImvl +== '
( )
srad40
500105
50400010
mlI
mvl
22
/,
,.,
,..,
≈
+
=
+
=
ω
S. %8RxdW/31,
^^/)ALAB37
ω
 ^
Ad_-N8R+/31,
%
Y^/>Kr-x8fQAB37x/
+A2>KVx8o+8

-('1B6=2Pc1,+{x
2211
ω
ω
II
=
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
1
1
21
1
2
1
2
2
2
1
1
2
1
2
m
m2m
Rm50
RmRm50
I
I
ωωωω
+
=
+
==
.,
.,
2210
100
602100
2
=
+
=
.
.
ω
"Ad_-N$
S. S8&'Pc)OW(2/31,3
AL!V
$F)@A2AL7
α
275
6$F!!ALA2(5
$FAP7ALA2@(8


$F!!+,-2AL+,-))@A2
AP7AL 8F  +,-0   4 0
/=G7<)-!31I/Pt12!1I
α
sin.
1
rr
=
α
22
1
2
rdmrdm sin.. =
=
dmrdmr
2
1
22
..sin
α
αα
222
1
ml
12
1
II sinsin. ==
6$&r)qAL0m40/=G7
<)1P6;/P04Pc)O3AL)q
AL126;^8hD('1:fc.hcc
22
0
mdmdI
=+=
$hD('1:fc.hcc
22
12
1
mdmlI
+=
S. T8Rx6;W"/31,4-g0u ^
S
/_
S
$76(26T8 ^
.
S
06/OwX8 ^
.%
8x6'/r1yd6/Ow_%S.T8F
Pc)OxC6'/r3ALAP7ALxA2)Vz
x8


sm i
^
12 Pc ) O  x  6' /rAL )
∆
 ) V A2
AP7ALx5i
A2i
%
12Pc)O-I6'/r3AL)
)V-I6'/rA2AP7ALx8F
2
2
...
2
4222
0
bRRRbMR
I
πρπρ
===
FM
32
bR
8
R
4
R
b
2
R
2
m
II
4
2
2
2
21
πρ
π
ρ
==
==
.
.
..
Fc'1:hcc{fc0Pc)O-I6'/rAL
)
∆
12
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
32
bR3
2
R
4
R
b
32
bR
II
4
2
24
21
πρπ
ρ
πρ
=
+== .''
RPc)Oi
/
xC6'/r3AL
∆
12
( )
24
4334
44
210k
mkg1022
16
05010410985
16
bR5
32
bR3
2
2
bR
IIII
..,
,....,.
.''
−
−
≈==
−=−−=
ππρ
πρπρ
S. X8FPc)OF3AL)7<16/O
F12wYT^^/A2/31,46F6;-X0X8 ^
.
S
/8
S
8


F7I4Pc)OF3AL)712
( ) ( )
237
5
63
5
232
mkg109910461055
15
8
15
R8
RR
3
4
5
2
mR
5
2
I
..,.,..,.
..
≈=
===
π
πρπ
ρ
S. Y8F(14  6c6/O w  ^0X A27 Pc ) O i
%^/8
%
01M<-<ALA26„
 ^^U8F
$s36c5
6$HB3(24A26!/(1M ^V6<;
1NI6c>48


s376c12
(
)
2
/5,2
20
5,0.100
srad
I
RF
I
M
t
====
β
HB34A26c! ^!12
(
)
(
)
sm512501052RtRv /,,..,
=
=
=
=
β
ω
S. [8R6c6/OwX^)(L(Pc1MR
ug^U8fQ-=y-(14A261M6;64
6c)B(IAL37
β
.%0X(_!
%
8Z<!3!/^0%X0Pc
)O6c3AL)iX^/8
%
"S8X$8


sm1M2y-(14A26c12„89M!VCc!b
7-<-<AL6cA27t1L6;%/„"(-$8
F7
I
kFR2M
I
MM
ms
−
=
−
=
β
(
)
( )
N4420
502502
5250980
kR2
IM
F =
−
−
=
−
=
,.,.
,.
β
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
S. g8R\7/31,,a4a-J;"
S.Y$8RPc)O\3AL76;i8U+/r\
6;1M8fQ
$ s7
α
@ 1M
→
F
A2a -J ;  -=6; 6 4   \
73A-O1M/r5
6$9M
→
F
-=71L6;64\/P,`o!3!
@\A2a-J6;/8


$R3\73A-O1M/r0\-=)c/
WW8n7
(
)
0rFrRF
>
−
−
α
α
α
α
sin.sincoscos
0
Fr
FR
>
−
α
cos
R
r
>
α
cos
6$F7-
( )
+=−
=−−
==−
βα
α
βγα
2
ms
mRIFrFR
0FNmg
mRmFF
cos
sin
cos
( )
+
+
=
+
−
−=
−=
22
ms
mRI
mRrI
F
mRI
rRF
mRFF
FmgN
αα
α
α
coscos
cos
sin
\/P,I7
≤
≥
kNF
0N
ms
( )
−≤
+
−
≤
α
α
α
sin
cos
sin
Fmgk
mRI
mRrI
F
mg
F
2
(
)
( )
)sin(sincos
2
ααα
kRrmRkI
mRIkmg
F
+++
+
≤
S8 u.F4y/31, /0+!,(V/PC
7/31,A2+/OQ/P/8IM((V,e4
3'"S.[$8(L(m1,8F3A2
!>~(Vc8
F
F
t
F
n
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


F AG ) AG 8 sm F 12 !> ~ (V8 F< 1B-  -  1M A2
Pc1M07
ββ
γ
2
mRITR
m
T
mg
==
=
−
Ra/0G314@AB3(2A2AB3707
RRv
β
γ
ω
=
=
F7-
=
=
==
=−
γ
γ
γβ
γ
mT
mgm2
mmRT
mTmg
( )
( )
===
===
N94
2
891
2
mg
T
sm94
2
89
2
g
2
,
,.
/,
,
γ
S.%^8fAB7/31,1I1,6;
A2
%
"
‚
%
$0,3AL
6;!,(VAe)dm"/31,dm6;$"S.g$8F
$s3AB5
6$h>~F
A2F
%
(Vc8odm12xd5!/P
/8-(6;!3
%/0
%
 /5 /8

F<1B--1MA2Pc1M
1111
mTgm
γ
=
−
2222
mgmT
γ
=
−
( )
R
2
mR
IRTT
3
2
21
γ
β
.==−
F

Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522

E?
γ
γ
γ
γ
=
=
=
321
07-
( )
( )
( )
( )
( ) ( )
+−−=
+=
−=
=−
+=
−=
γγ
γ
γ
γ
γ
γ
2121
22
11
21
22
11
mmgmm
2
m
gmT
gmT
2
m
TT
gmT
gmT
( )
( )
( ) ( )
(
)
( )
( )
++
−
=
++
+
=
++
+
=
−=++
+=
−=
mm2m2
gmm2
mm2m2
gmm4m
T
mm2m2
gmm4m
T
gmm2mm2m2
gmT
gmT
21
21
21
12
2
21
21
1
2121
22
11
γ
γ
γ
γ
S.% 8RWaW/31,R%0XT/A2ABa
/31,^0X/,3AL6;!,(VAe)dm"S.u$8ZQ
)/31,(V0dmA2/eAL8F3ABaA2
!>~(V8


smF12!>~(V0G-1MA2Pc1M07!
=
=−
+==
=−
γ
γ
γ
β
γ
M
2
3
T
mTmg
R
MR
2
MR
ITR
mTmg
2
2
( )
( )
≈==
≈
+
=
+
=
=
+=
N33414154251M
2
3
T
sm141
5425150
8950
M
2
3
m
mg
M
2
3
T
M
2
3
mmg
2
,,.,.,
/,
,.,,
,.,
γ
γ
γ
γ
S.%%8RAB]/31,,4a-J4A212)6
c76/Ow"S. ^$8RPc)O
6 c 3 AL  ) 6; i8 n3 1,  (V
/P/8F376c`
%
%
F
%
F
F
F
„
!
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


smF12!>~(V07-
==+−
=
βγαα
β
mRmkmgmgT
ITR
sinsin
ααββ
cossin kmgmgmR
R
I
−=−

(
)
2
mR
I
kmgR
−
−
=
α
α
β
cossin

HL/12!3!a-J4
#U<
α
tgk
>
0KV6;
0
=
β
8
#U<
0
=
k

2
mR
I
mgR
−
=
α
β
sin
8
S.%S8R7(21 ));)
I89NI0KA'O;0!7,="S. $8
F371N6eI=A21N)A'OJ>8

RPc1M(m1MV))/47!AL
-J>12
(
)
α
sin.2/
lFM
=
HB
l2
g3
4
l
mml
12
1
2
mgl
I
M
2
2
α
α
β
sin
.
sin
=
+
==
#FA'O6I = 90
0
:
(
)
2
/7,14
1
.
2
8,9.3
2
3
sm
l
g
===
β
#FA'O)A'OJ> = 0:
0
=
β
.
S.%T8RxdW6/Ow
/31,7))
;AP7ALxA2Vxw_%8x6eI)GA'
O>ALA'OVxALAB3I6;^8&'Pc
1,x3AL)/x)A'O-8


RPc)Ox3AL)12
4
3
22
1
2
2
2
mRR
mmRI =
+=
-('1B6=2~1,
(
)
I
L
I
I
ImgR
2
2
2
1
2
2
2
===
ω
ω
gRmR
gRm
mgRIL
2
3
4
6
2
32
===
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
S.%X8R7t1,6;
→
K
A2Pc1,
→
L
3
ALz8& 'Pc1,3ALzj6<
→
'OO

→
0
r
8
F+,-2Pc1,/P-z`

RPc1,3ALzj12

(
)
∧+=∧=
i
iiOOOi
i
iiiOO
vmrrvmrL
'''
∧+∧=
i
ii0
i
iiOi
vmrvmr
∧+∧=
i
ii0
i
iiOi
vmrvmr
KrL
0O
∧+=
RPc1,/P-A2z
00
0'
=⇔=∧⇔= KKrLL
OO
S.%Y8o>;Pc1,
→
L
3ALz
e1AL)<n76K
→
L

→
L
^
#
→
0
r
•
→
P
07
→
L
^
12Pc
1,3AL/3V0
→
0
r
12Ar6/O/3V3ALz
n0
→
P
12t1,8


FM62S.%X0z6;mVs0A2zj6;zn07
PrLL
OO
∧+=
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


T. 8fQ6-=7P!6;6406<;67
/31,   S^^^/0/614  / -= -N8 ZQ)!> = 
/P/O8


R3 6 14 0  6 -= 3 P  e P =  m 1M ] 

∆
8FG7!P!6

t
hmg
t
A
∆
∆
=
∆
FS^^^/0 / ^^^0
∆
-NY^!A2A26>4
O,Tu^/‘8
T.%8FOPI</r1dC%^06<;1M/r|1AL
C1dA231dC -=I1MS^U8


f!32W1d6;
m
N
3000
cm
1
N
30
k
/
/
=
=
oP1M/r
 ]
( )
2
xk
dxxkdxF
2
x
0
x
0
)(
...
∆
==
∆∆
0
HL/S^^^U_5
∆
%^^0%]Y^’8
T.S8RPP/31,0/e3(37AB3
/PtAXT/_84(312T†8fQPP-=7P!6
4714,(34qALAB3XT/_8


H/e3(30PP7AB3/Pt4-=7/
‡
!
!
α
8
c14(31M/r„
/
PP-=6;
„
/
‡
!
#8!
α
%88!
α
oP!PP/14(3ALAB3A,OcP>
kW811150408910002
).v.mg.2 ( . v F
t
SF
t
A
P
k
k
,.,.,..
sin
.
≈=
====
 " $
T.T8RPP/31,%01c14(374T†8f!3!12^0^g8
F
$oPM6KPP4)C+(2S/5
6$oP!PP06<;+ < )C+4T
-N8


9M/r-=V6;AL2-I8!
α
m1MA21M
!
mgkmgmgkmgfmgF
msk
.sin.cos.sin.sin.
+
≈
+
=
+
=
α
α
α
α
8
oP/r4)C+(2S/
(
)
(
)
(
)
J100673000080040892000SkmgSFA
6
k
.,.,,.,..sin.. =+=+==
α
8
oP!
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
kW429W10942
60
4
10067
t
A
P
4
6
,.,
.
.,
====
T.X8R22/31,X^4+;ALAB
3/Pt6;SY/_8oP!I12%%^0g/‘8F!3!@
2A2+8


n4+;01M/rII-=V6;
AL1M!
mgkfF
msk
.
=
=
8
oP!I7'cP>
vmgkvF
t
SF
t
A
P
k
k
...
.
====
0450
10891050
108220
mgv
P
k
3
3
,
.,..
.,
===
T.Y8U++'P!6;<6'Ab
T.T8
F<6'W2/…-0/…-aA28R2…-,eAL
d03d7cmABv8FmAB,m!7V6;AL1M
!A2@d;8&'P!<!3Ad)
12Y^Ad_-N0(2d/GV1 0m1,
AB6;vTu^U8Fm1,d/P/8


sm‡
!
12M!@2/…-A28F7/V
6;
lQrf
ms
..
=
8
‡
!

r
Ql
oP!
( )
[ ]
Qnl2rn2
r
lQ
. v fP
ms
ππ
=== ...
.
012!3Ad)
 V8
W10083114902P
3
.,.... ==
π
T.[8RP! X/‘-1+(V]Z"
T.X$8Z/O-1%X0 AB 3 )-1 %^ Ad_-N89M~
4](V1L-P1M~(LZ8F1M~76<
;(V!!AL8


oP!-1
„8A“"F
]
.F
Z
$8”8%
π
88
1
v
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
FG/F
]
%F
Z
!F
]
%8F
Z

n
r
P
.
.
π
8
F!3
( )
N9556
2250
1015
T2T
3
BA
===
.,.
.
π
T.g8R<c/31,%^^^^/B(I(L(
1M!6;Y^^^U8h+c(G18HB36Ic12
XT/_8FO
$oP1M!5
6$vC+2cC,/G1N71M!(L/c
(GJ8


EMc'1:~0P=1M!12=~cG
'6IA^0(70P271LO6;~6Ic
J102521520000
2
1
vm
2
1
EA
622
Kms
.,...|| ===∆=
8
vC+2c(,/G1NCc</c(GJ
( )
m375
6000
10252
f
A
S
6
ms
ms
===
.,
T.u8FOPI<22/31,g8 ^
X
/
$F~3GA
SY/_<A
%
XT/_3
6$EG1<AB36I12[%/_8


F!b-('1:~6<4~AB6;P(
1M(A2AB(7
$oP12c~AB3GA
SY/_ ^_!<A
%
XT/_ X_!
J10510108
2
1
15108
2
1
vm
2
1
vm
2
1
EA
72525
2
1
2
2K
......... =−=−=∆=
6$oP12c=AB3GA
^
[%/_%^_!<A^_!
J106120108
2
1
0vm
2
1
vm
2
1
EA
825
2
0
2
K
.,..... −=−=−=∆=
oP212P="PV$8
T. ^8R/}-/31,RTX^/=c-;8
-7/31,X/0AB3IdATX^_!8n6e06-BA-O
!!TX8F1MC6(14-8


smH12AB3B1q/}-8EMA2'1B6=21,-
(-7
0
v
m
V
M
=+
.
.
 v
M
m
V
.−=
F
]
F
Z
1
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
9MC/}-!P12=~/}-
2
VM
2
1
SF
.. =
.<
FG7
( )
N12500
4504502
4505
Ms2
vm
S2
VM
F
22
222
==
==
.,.
.
..
.
.
.
.<
T. 8RA4/31, ^/6 ALAB3A ^^_!a-
6=y(2A2e!VA26=y!T8F
$9M=66=y14A45
6$HB3A4!//Q6=y\(2(%8


$FA‹!D('1:A~7,-
( )
N1250
0402
10010
s2
mv
F
2
mv
2
0m
sF
2
2
0
c
2
0
2
c
−=−=−=→−=
−−
,.
.
.
.
6$H47/=~4!VA26=yTL(G18U<6=y\
(2%!/4)6=y0A4A‹d<-ALAB3
Aj•A8Fc'1:A~
]j
dF
2
mv
2
mv
c
2
0
2
−
=−
'
0
! Aj
(
)
22
0
c
100
10
02012502
v
m
dF2
+
−
=+
,.
≈
[ _!8
T. %8R c 4 G \  (3 -J Eo 7"T.Y$ A2
(GJ1!/C,;oZ8o]Z!5]o 5!3!
@cA2a+4EoA2oZ6;8
FO!3!A23c4+EoA2Zo8


.F\a-J4c7<~‘
8oO<~2C(q
eP]
A2]
%
1M!4+EoA2oZ8E7‘
]
#
]
%
07P1M!4EoA2oZ12
]
/8"8!
α
$8Eo/815
]
%
/"!.1$8
R
H
A
α
!
1
]
Z
o
E
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
FG7!
(
)
kmgslskmgkmglmgh
=
−
+
=
/
h
8
.VO1MA2-('1BU>0,-
!
α
."‡
!
$
Eo
8
Eo
0 " $
./8
oZ
 "%$
FG" $!
!
α
./8"8!
α
$8
Eo

( )
Z>
−
+
=
+
−
+
=−=
s
l
1
hl
gh
hl
l
s
h
hl
h
gkga
22
2222
CD
..cossin
αα
odG"%$
0g
s
h
kga
CB
<−=−= .
-!3
g
s
h
kga
s
l
1
lh
gh
a
s
h
k
CB
22
DC
.;; −=−=
−
+
==
8
T. S8R AB /31,  , /P ! G \  a I3(L
"T.[$8fQG/=
∆
2"OG\aI$AB6eI/QaI8
o6/OaIwu^8

F)AB,4aI0AB'(1Mm1M
ABA2-=1Mw
aI8Ft,-1M22-I2-I
--<7Ad1MLVdAB02-I<-
<-V,(IAB8
&r2-I--<
R
vm
mg
R
vm
PR
R
vm
amRP
22
nn
2
htnn
.
cos
..
. −=−===−
α
Ra/0c'1B6=2~=<~AB6;~
~AB8

∆

2
1
A
%
8
∆
−=
∆
−
∆−
=
∆
−=
R
h3
1mg
R
hmg2
R
hR
mg
R
hmg2
mgR
n
α
cos
HB \ 7 ,m126 4 a I< 7 d -14 a I1M
"6;-=1Mw
aI$0>12w
≥
^8hM+/QaI6eI=/
w
^8f
0
R
h3
1mgR
n
=
∆
−=

.cm30
3
R
h ==∆

w

∆
w

fT.`
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
T. T8RAB/31, /,4a-J4,-ALa
;7
α
!!
α
^0 8h/,<a-J40ABd
<-4a-J;1 ^L(G18f!3
!!3)/^0^X8FAB3ABK3a-J
4893m+ ^_!
%
8

E(1M!‡
!
./0AB,4a-JZoAL
3./88smA12AB3ABK3a-J40c'1:
~7
( )
sm16310100502kgl2v
mv
2
1
lkmgmv
2
1
0lf
22
ms
/,..,.
..
≈==→
=
−=
T. X8FG\-%^0+rd/31,X^c
-4ALa-J;0ALAB36IA
^
 g_!8nL
ad7AB3A%T_!8FOP1M=/P/O14d8


om3O<~;a8F+I4d7~
mghmv
2
1
W
2
0t
+=
F+da77~
2
t
mv
2
1
W ='
wk2~1N!d6;~6Id4
P!1M0(7
WWAAWW
CC
−
=
+
=
''
( )
( )
J5320890501824
2
050
mghvv
2
m
A
22
2
0
2
C
,.,.,
,
)(
−=−−=
−−=
T. Y8RAB/31, ^/,G\a-J4%^
38nLV(3AB7AB3 X_!8FOP!8

oP!6K1M!6;6<4~AB
( )
J8352089101510
2
1
mghmv
2
1
WWA
22
C
−=−=−=−= .,...
9D!
T. [8I!,(Vz]0(21S^7cABa"T.g$8fQ
-]-=ABAB36r6;64AB7
)da-JJ>8


α
!
1
f
o
Z
]
9
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
F]AB,~
2
A
mv
2
1
8h7AB6eId
14-O48F<~AB~(I0~"(7AB3$AB=(I
"T.g$8
R3ABda-JJ>0AB3A
Z
AB
Z-=1L12!,(V1P6'~"F
≥
^$8
H Z AB'  (  m 1M
→→
= mgP
A2 1M ~
→
T
" L c
-J>$1MLVdAB04
Tmg
l
mv
F
2
B
ht
+==
8
HBAB3QZAB7)d
A
Z

gl
8 " $
Ra/0c'1B6=2~
"
∆
‘
$
]Z
."
∆
‘
$
]Z
0
!
gl4vv
2
B
2
A
+=
8
HB AB 3Q  I  AB] 7)d a -J
J>
sm83gl5vgl4vv
A
2
B
2
A
/,,)()(
minminmin
==
+=
T. g8R1em1,,/r/Q-J>7
α
u^
^
0!71e,=8o>;!>~(Vc6;S/
1e)A'OV6;8


n)A'OV6;0,-1M@!>~(VA2m1M1e
1MLV28
F
A
z
A
v
B
v
]
Z
1
F

Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
l
mv
amPT
2
ht
==− .

mg
l
mv
T
2
+=
-('1B6=2~7
mglmv
2
1
2
=
FG7!!>~F
P3mg3mg
l
mgl2
T ==+=
T. u8 R)= I /3 1,  ^0 / , e K I  …(2 1 
0%[/31,/P/8f)a-JJ>)I
/8F)=I7AB3A
^
T0 S_!8
$F !M- <~A2~)=Ic7
α
,-6K
A2-J>8om3O<~A'O-)=I8
6$&'1M(F)=I14c7
α
8FFA'O
-A2)=I8


om3O<~A'O-])=I8n)=IKo0
,-AL-J>7
α

$<~A2~)=I12
‘

o
18" .!
α
$5
‘

2
mv
2
1
Fc'1B6=2~7
‘
#‘
"‘
$
^
#"‘
$
^
8
f
( ) ( )
2
0
2
mv
2
1
l2mgmv
2
1
1mgl +=+− ..cos
α
(
)
2
0
v1gl2v ++=
α
cos.
5  ‘

2
mv
2
1

)cos(
α
++ 1mglmv
2
1
2
0
6$1MLVAB,)<'6Km1MA21MF
ααα
α
cos)cos(cos
cos
mg1mg2
l
mv
mg
l
mv
T
mgT
l
mv
F
2
0
2
2
ht
+++=+=→
−==
z
v
]
Z
o
F
α
o
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
F
+α+ g2cosg3
l
v
m
2
0
F-0
α
^
( )
N246895
271
134
10g5
l
v
mT
2
2
0
,,.
,
,
., =
+=
+=
F0
α
 g^
^
0
( )
N363089
271
134
10g
l
v
mT
2
2
0
,,.
,
,
., =
−=
−=
8
o=A'O0AB/r~8
T.%^8AB3A4+(q1eD87126
cKI!,(V"T.u$8nA44A26076'e7A26
,V14278FAB31N7!e-4A268
Z</31,A4120/31,612R8


V1262A8R3=70-('1B6=2
1,A2'1B6=2~8 sm AA2H1I1,12AB3L/
4A26A2AB36!/74A28
'1B6=21,
A"R#$H8 " $
'1B6=2~
"#R$
2
V
2
"#R$8

gh2V =
"%$
FG" $A2"%$!A
gh2
m
Mm
V
m
Mm
..
+
=
+
8
0R0!bO,AB3AA48
T.% 8R3|/31,R7MA2m4c,B6;
N/31,8|,eKI>(21m1,
/P/"T. ^$8n73|04c630N6'6B(L-
!4c8fQAB36B6rN-=6;643|7
),=Ad)cz8


smA0H1I1,12AB3NA2AB33|8
-('1B6=21,7
R8H8A
Fc/<)=62T. [03|7d)
czAB3H7-2-==C/
gl5V ≥

α
A
R
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
m
gl5M
m
VM
v ≥=
.
T.%%8Rd6/31,/P!4+C7
(AbT. 8fd6,=/P7AB36IG%w0/O
L6Q/P/8fQ
$2d6+/Q+C`
6$1L2d6!b,!/+/Q+C`

$&c62B-T. S0T. gd6+/Q+C/1Mrd614C
6;/P8FG/4!
8!
α

R
mv
2
0
" $
-('1B6=2~)]Z"Z12d6++
C$7f

R
3
5
"T.Sj$8
6$HB3d6Z,!G" $
A
^
3
Rg2
8h/++C06c-61\o8HB
3;Ko"A
$
A
^
!
α
0AB3J>"A
$
A
^
!
α
.8-('
1B6=2~)]o0!
f
%

R
27
50
8
T.%S8R)=I/31,%/0ALAB3S_!0A4
VAL)=I>/31,S/qAL)=I>
ALAB3 _!8FAB3)=I!A<
$H12222W8
6$H12/P2W"$8


A

R

H
1
z
A
%
A
%
#
]
Z
o
f
f
%
fT
.
%%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
$H2W
H  @ AB V c '1B 6= 2 1, A26= 2 
~8F7-6=2
22112211
vmvmvmvm
+
=
+
''
" $
2
22
2
11
2
22
2
11
vm
2
1
vm
2
1
vm
2
1
vm
2
1
+=+ ''
"%$
o=!314)<
AA<014)<
%
!A<d
1-4
(
)
(
)
''
222111
vvmvvm
−
=
−
"S$
(
)
(
)
2
2
2
21
2
1
2
11
vvmvvm '' −=−
"T$
E!A0ABtAB3471"T$A<A<AL"S$
,
2211
vvvv
+
=
+
''
"X$
UVA<"X$AL
%
WA<cA<AL"S$,
(
)
(
)
22111112
vm2vvmvvm
=
−
+
+
''
(
)
21
12122
1
mm
vmmvm2
v
+
−
+
=→ '
"Y$
92M"atAd\!3 A2%$N
(
)
21
21211
2
mm
vmmvm2
v
+
−
+
='
"[$
-(AL
%/0
%
S/0A
S_!0A
%
 _!A2"Y$A2"[$O,
Aj
^0Y_!5Aj
%
%0Y_!8
6$H
hA0AB!b7qAB3A Aj
Aj
%
A8
H2Vc'1B6=21,
22112211
vmvmvmvm
+
=
+
''
 
(
)
221121
vmvmvmm
+
=
+
21
2211
mm
vmvm
v
+
+
=
F'/31,A2AB3C,Aj
Aj
%
A 0g_!8
T.%T8f)=I,cKI!,(V!!(26;8fI/
!,(V,6A2!)=I<-NALA2V
Nq;4+;"T. %$8n31,)=I1I
1,6;%^^A2 ^^8v=I>,V14T0XA2=38
fQ!A0)=I,V1464<
$H12222W56$H128


%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
F622!bAB(='1B6=2~1e
62T. g0T.%^A262AA4V62T.%S8
UL/)=I A2)=I%77AB312
gh2v
1
=
hA0)=I7AB312A
j5A
%
jA2N!b14
A2
%
>6;
g2
v
h
2
1
1
'
=
5
g2
v
h
2
2
2
'
=
8
$ U< A  @  AB 12 2 W0 - ( P >  62 T.%S AL
%^^%
%
5A
%
^
11
v
3
1
v ='
5
12
v
3
4
v ='
8FG7,
( )
cm5054
9
1
h
9
1
g2
v
9
1
g2
v
h
2
1
2
1
1
,,.
'
=====
5
( )
cm8h
9
16
g2
v
9
16
g2
v
h
2
1
2
2
2
==== .
'
8
6$U<A@AB12 Aj
Aj
%
%A
_S8
( )
cm2h
9
4
g2
v
9
4
g2
v
hh
2
1
2
1
21
===== ..
'
8
T.%X8RAB/31,
LAA2AB>>
40/31,
%
8oA124VA2222W8fQ!3-I~
~6IAB>CAB>!A`
-(+,-$

%
56$
u
%
8


-(P>A2W7,62%.%SAL
0v0v
21
=
≠
;

O,AB3)=I>%!A
21
11
2
mm
vm2
v
+
='
FG7!|!3-I~~2AB CAB%
2
21
21
2
21
2
1
1
2
2
11
2
22
d
d
mm
mm4
mm
m4
m
m
vm
vm
W
W
1
2
)()(
'
'
+
=
+
===
η
8
n

%

η
 ^^†8
n
u
%

η
SY†
T.%Y8RxWa%^U01~/P,4a-J;
ALAB3AT_!8F~x8


xW7Pc)O
2
Rm
2
1
I .=
"ALw126/Ox$8
nx1~/P,4!2;07/
ω
R
v
=
8
~x6W~'<A2~)
‘

222222222
mv
4
3
Rm
4
1
mv
2
1
Rm
2
1
2
1
mv
2
1
I
2
1
mv
2
1
=+=
+=+
ωωω
....
T.%[8FOPI<12AP1~A2d+/O 0
/31,X^^/0>4)LAB3 %^Ad_-N8


RPc)OAP1~A2d
2
R
m
I
.
=
8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
HB3)AP1~12 %^Ad_-N" %^8%
π
($_"Y^V$T
π
"(_!$8
oP12AP1~)O6;~~")$AP1~
]
∆
‘

( ) ( )
kJ10J1000041500
8
1
dm
4
1
2
1
I
2
1
2
2222
====
πωω
.......
T.%g8R)=IaW7/31, /01~/P,ALAB3
A
 ^_!<B-A22+W6BALAB3A
%
g_!8FO1,=
A78


h A  ~  AB =8  =  a 2= (L (
v.
∆
‘
8nOIN:;)=IAG7~'<AG7
~)8~))=Ia0W01~/P,
‘
)

222222
vm
5
1
Rm
5
1
mR
5
2
2
1
I
2
1
...... ==
=
ωωω
E7ƒ
ƒ
)
#ƒ


2
2
2
mv
10
7
2
mv
mv
5
1
=+
8
HB01,=(A
(
)
( )
( )
J2251081
10
7
vvm
10
7
WQ
22
2
1
2
2d
,.. =−−=−−=∆−=
T.%u8R W7X0 KA'OJ>6't
38&'
$HB3(2\/75
6$H'OR4!/RAB37N6;
AB3AB=M(GA'OR8

$A'OJ>07<~ƒ
2
mgh
8ntLa<~
26<2~)KA'O‘

2
1
i
ω
%
07i12Pc
)O3AL)3i
3
mh
2
0
ω
12AB371N
8
-('1B6=2~
2
mgh
I
2
1
2
=
ω
..
mgh
3
mh
2
2
=
ω
.
h
g3
=
ω
FG7!AB3(2\1NA
ω

2125103gh3 ,.. ==
_!8
6$sm12R/KA'OJ>8-(P>O
AB3ABM(07AB3R/
M
v
gx2
8
Fc/I62
ω

gx2
gx2
h
g3
x =.

h
3
2
 ^_SS0SS8
T.S^8FG\a-J4^0X0+ABW
7(/1~/P,4a-J478FAB3(2
ABK3a-J4<
$HB7()=Ia5
6$HB12xd5
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
$HB12A2d8
"s=!DAB36IAB6;/P$8


s= !D ; 7  AB a 1~ /P ,0 /P AB 3 I G \  a
-J478RPc)OAB7A<6;i/88w
%
0
7/12;!3-A2AB8nAB1~/P,ALAB
3(2AAB7~)
‘
)

2222
kmv
2
1
kmR
2
1
I
2
1
==
ωω
.
8
~2-IAB
‘
‘
)
#‘


( )
222
mv1k
2
1
mv
2
1
kmv
2
1
+=+
8
Fc'1B6=2~0~ABKVa-J46;
=<~AB
( )
mghmv1k
2
1
2
=+
1k
gh2
v
+
=
8
-(/<)=t)2AL^0X0AB7(
$)=Ia/%_X8
( )
sm652
7
508910
7
gh10
152
gh2
v /,
,.,.
/
===
+
=
6$xa/ _%8
( )
sm562
3
50894
3
gh4
121
gh2
v /,
,.,.
/
===
+
=
$)=Ia/ 8
( )
sm2125089gh
11
gh2
v /,,., ===
+
=
T.S 8o76;P"a$06;"y$q,=G
\a-J48oN7q6/OwYA2q/31,
^0X/8Ra,)r!38fQ
$HB3'<K3a-J47//P`
6$RPc)Oy5
$h61V1~/P,LVa-J4`o6<
\a-J4^0X074
α
S^
^
0/31,4P
-
%Y^^/_
S
A2-
%
 S^^/_
S
8

$EMA2/<)=62T.S^0AB2a"!3Pc)O
Q$AB3(2NVa421L8E706220
7/<1B;0/3a6;P!b1~/36;8
6$UC6<0Pc)O/3PA2,'
6;P>>i

2
RR
mI
2
mR
2
1
2
2
2
+
=,
07w
126/O
8
H/31,6;4
ρ
9
π
w
%

ρ
%
9
π
"w
%
.
2
1
R
$07912
(20
ρ
A2
ρ
%
12/31,4PA28
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
ρ
%
2
1
R
"
ρ
%
.
ρ
$w
%

(
)
2
2
12
2
1
R
R
ρ
ρρ
−
=
FG7O,
=
+
=
2
RR
mI
2
1
2
2
2
2
12
mR
2
2
.
ρ
ρ
ρ
−
0"
2
12
2
2
k
ρ
ρ
ρ
−
=
$8
HB3P/1~LV(3"c62T.S^$
3
gh4
121
gh2
v
Al
=
+
=
/
8
HB3/1~LV(3
Al
12
2
2
12
Pb
v
3
gh4
4
gh4
1
2
2
gh2
1k
gh2
v =<
−
=
+
−
=
+
=
ρρ
ρ
ρ
ρρ
.
"A
21
ρ
ρ
<
$
$EMA2/<)=AAB3AB1~/P,62T.S^
( )
mghmv1k
2
1
2
=+
F2c+A<-2,
(
)
(
)
(
)
α
sin'.''.
vmgvmv1kmghvmv1k
=
+
=
+
1
k
g
va
+
==
α
sin
'
(
)
(
)
( )
(
)
αα
2
g
1kh2
1kg
1kgh2
a
v
t
sin
.
/sin
/
+
=
+
+
==
F70^0X0
α
S^
^
0
-(/3P0/ _%
(
)
( )
s780
3089
121502
t
02
,
sin.,
/.,.
=
+
=
-(/30
2
12
2
2
k
ρ
ρ
ρ
−
=

113
100
11300
2
2600113002
=
−
.
.

(
)
( )
s880
3089
1113100502
t
02
,
sin.,
/.,.
=
+
=
T.S%8R+W4<sP-/A2I)=0y)=7
/31, ^/8n=Gy)=L)12^0[X8s<)ALAB3
ω
Ad_!8fQP(+MA2AB3<<+71
/=Gy)=<)\d12^0%^06<Pc)O
+A2<3AL)12i
^
%0X/8
%
8

RPc)O+A2)=1N6IA21N!
(
)
( )
22
2
202
22
2
101
kgm3032010252dm2II
kgm751375010252dm2II
,,..,..
,,..,..
=+=+=
=+=+=
n))7~A2Pc1,12
111
IL
ω
=
‘
 

( ) ( )
J27527513
2
1
I
2
1
22
11
==
πω
.,.
8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
EPc1,,6=24AB37)!/+
1=C6>
( )
srad3382
33
7513
I
I
ILLI
1
2
1
2111222
/,.
,
,
ππωωωω
======
Fc'1:A~0+CI3P6;
]
∆
‘
‘
%
.‘

2
11
2
22
I
2
1
I
2
1
ωω
−
( ) ( ) ( )
J87127513
2
1
33833
2
1
22
=−=
ππ
.,.,.,.
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


X. 8F1MNRaF+14AB7/31, ;4aF
06<;/31,RaF+R 0u[8 ^
S^
/A2/=6Ga
<VRaF+12 Tu8 ^
Y
/8


-(P>'1BAAB-(‹
( )
( )
N
r
mM
GF
6
2
9
303
11
2
10.9,5
10.149
10.97,1.10
10.67,6
−
−
−
≈==
X.%8n=@FA2RaF~12SgT^^^/8n31,F
12X0uY8 ^
%[
A2RaF~12[0SX8 ^
%X
8&'A'O71MN
RaF~A2F14V6;8


sm/=G71MNRaF~A2FV6;
<VF12"k2•1$8F7
22
)( xl
mM
G
x
mM
GFF
ME
ME
−
==
(
)
( )
( )
km
MM
l
x
x
M
M
xl
xMxlM
EM
E
M
ME
345600
10.96,5/10.35,71
384000
/1
2725
2
2
≈
+
=
+
=
=−
=−
X.S8R)=I/31,
a I
  W    J  4
-/r(28F7(210 /3
1,
%
8F1MN14)=I8


o2@(Q0/71MN714/31,
12
( ) ( )
2
21
2
1
...
xall
dxmm
G
xal
dmm
GdF
−+
=
−+
−=
9MNt14)=I12
( )
)(
11
.
0
1
.
2121
21
0
2
21
ala
mGm
alal
mGm
l
xall
mGm
xal
dx
l
mGm
dFF
l
+
=
+
−=
−+
=
−+
−==
X.T8f)=I7q6/O/31,41I1,6;-
A2-
%
,a
P+1Q7/31,412-
^
8fQ/2
 
z
]
#.
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
$f)=IN5
6$f)=I}8
o6</OLP+1Q1L!AL/OL)=IA2
-
‚-
%
8


&r)=I>
#9M-(‹@)=I12
2
21
3
2
3
1
22
21
1
3
4
.
3
4
..
r
kRR
r
G
r
mm
GF
ρ
ρ
π
ρ
π
ρ
===
"AL
9
16
62
GR
k
π
=
$
#E/OLP+1L)=I4//P7
)=I>01M-(‹P+14)=>c-/
M41‹8U<6L-I1Q0-Id1!b(1M
-(‹q1L,AL1M-(‹(-IV8KV0
-I12-I1Q6'<6K)=I>8FMK4l7
2
01
2
r
kF
ρ
ρ
=
#U<m„
12(0t,-1M(14)=I 6;
( )
02
2
1
21
ρρ
ρ
−=−=
r
kFFF
s3(14)=I 12
(
)
2
02
3
1
2
021
1
4
3
.
r
K
Rr
k
m
F
a
ρ
ρ
πρ
ρ
ρ
ρ
−
=
−
==
"AL
3
4
3
GR
K
π
=
$
#FM0<mLA-O)=I12(01Mt,-
(14)=I%12
( )
01
2
2
'
ρρ
ρ
−=
r
kF
2
01
'
r
Ka
ρ
ρ
−
=
s33@N
2
021
0
2
'
r
Kaaa
ρ
ρ
ρ
−
+
=+=
$f)=I1I
2
020'
21
0021
ρ
ρ
ρρρρ
+
<⇔>−+⇔>+ aa
6$f)=I
2
020'
21
0021
ρ
ρ
ρρρρ
+
>⇔<−+⇔<+ aa
X.X8F)=I6;6/Ow+/r1yI8Ra
1y<-NALa)=IA2)V78n31,)=I
L//r1y6;R8F4-yV)=IA21y0+a
d6Q/31,V)=I("X.%$8F1M-(‹2
)=I"C/r1y$(14d68


9M-(‹)=IC/r1yN6;1M-(‹V6K
)=I/r1yA2-I6'/r8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
9M-(‹)=I/r1y14d6
2
1
d
Mm
GF =
9M-(‹-I6'/r14d6
( )
2
3
22
3
2
2
22
3
4
.
2
8
2
23
4
..
.
'
Rd
Mm
GR
R
d
m
G
R
d
R
m
G
r
mM
GF
−
=
−
=
−
==
π
ρ
π
ρ
HB01M-(‹)=IC/r1y14d6
( )
2
22
22
21
22
287
)2(2
11
Rd
RdRd
GMm
Rdd
GMmFFF
−
+−
=
−
−=−=
X.Y8FAB3(2F))RaF+06<;/31,
Ra F+ 12 R  %8 ^
S^
/ A2 /=   6 @ F  A2 Ra F+ ( 
0X8 ^
g
/8


9MLVF)RaF+O121M-
(‹
hthd
FF
=
( ) ( )
skmsm
d
GM
v
d
v
M
d
MM
G
S
E
SE
/30/10.3
10.5,1
10.2.10.67,6
4
11
3011
2
2
=≈==
=
−
X.[8FAB3(2AVF6<;)*A
12d8HK6 ^^^/8oA\'=K1M
NFA2K401M=/P/O/P/8o6/O
FwYS[^/8


9B-1BM62X.YAV)F0
7
( ) ( )
skmsm
hR
GM
d
MG
v
EE
./34,7/10.344,7
10.37,610
10.96,5.10.67,6.
3
66
2411
=≈
+
=
+
==
−
X.g8 f 2  )  ) Ra F+ AL  )*   I N 12
@Add6/O1I1,6;w
 X^8 ^
Y
/0"F$A2w
%
 ^g8 ^
Y
/
"h/$8F|!3AB3(2278

hD(1B-1BA2O62X.Y07
2
2
1
1
;
d
GM
v
d
GM
v
SS
==
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
85,0
10.150
10.108
.
6
6
1
22
12
1
≈===
d
d
GM
d
d
GM
v
v
S
S
X.u8n31,RaF~ Q/31,Fg 1I0+/ORa
F~6;S_ +/OF8fQ+4aaY^^14
RaF~!ba648


Fc'1BAAB-(‹
2
E
E
R
mM
GP =
( )
P
k
k
R
mM
G
k
k
Rk
mMk
G
R
mM
GP
E
E
E
E
M
M
2
2
1
22
2
1
2
2
1
2
' ====
( )
( )
NP 100600.
11/3
81/1
'
2
≈=
X. ^876;AP<"AP<$/e-m
4a+-714A‰3'Š">4aA!
/P3ALa$8R3AB-=A2
a-JOGFV!PALAB376;AB3F
))78
fCOAB3(2A2A78Z</F)
)   7 12 F  %S + XY -N T V8 Z /O O  F  12 w 
YS[g/8


sm/=GA<VF12(0AB3(2A12
E
E
GM
d
v
d
T
d
GM
v
3
2
2
π
π
===
( )
( ) ( )
kmm
GMT
d
E
4212610.126,42
4
10.96,5.10.67,6.86164
4
6
3
2
2411
2
3
2
2
=≈==
−
ππ
HB0AB3(2A2A12
( )
sm
T
GM
d
GM
v
EE
/10.07,3
86164
10.96,5.10.67,6.22
3
3
2411
3
≈===
−
ππ
(
)
kmRdh 35748637842126
=
−
=
−
=
X. 8FAB3Al-ii3ALRaF~"x12AB341D
-7G6aRaF~I-=777/Q!>NRaF~$8


s3m+46aRaF~
2
M
M
M
R
M
Gg =
HB3Al-,OcP>
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
( )
( )
sm
R
GM
Rgv
M
M
MMM
/10.38,2
10.37,6.11/3
10.35,7.10.67,6.22
2
3
6
2211
≈===
−
X. %8U+41D0AVI4F,14
X^^/8
$F3m+K75
6$=-7ALAB36;64c-AP7AL6
/OF)*7)F12+d8n7/
)A)F6;64`
96/OF6;YX^^/03m+46aF
6;u0g_!
%
8ZQ)!>=/P/O8


$s3m+,OcP>
( )
2
22
0
2
2
2
/45,8
5006500
6500
.8,9. sm
hR
R
g
R
M
G
r
R
r
M
Gg ≈
+
=
+
=
==
6$)*A12+d01M-(‹N6;1MLV
hthd
FF
=
( ) ( )
skmsm
hR
Rg
v
hR
R
R
GM
hR
GM
v
r
v
m
r
mM
G
EEE
/69,7/10.69,7
10.7000
10.6500.8,9
.
3
3
622
0
2
2
2
2
=≈=
+
=
+
=
+
==
o/•)A12
( )
( )
'3515720
10.5,6.8,9
10.7
22
2
122
183
2
0
3
hs
Rg
hR
v
r
T
≈≈=
+
==
ππ
π
X. S8RmAB4a'!>NRaF+8H64"RaF+K
‰(LVŠ$1M74AL1MNF062"RaF+K4‰\
IŠ$1M7G6L1MNF8HAB064mAB-=a
62077N/P`F!`


nPN0ARaF+N=F1‹AB46aF8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
Y. 8HB-=7AB364/OL7c-
=%1I8

/OLABc-=%1I0I7
5,01
2
2
0
==−= k
c
v
l
l
(
)
222
k1cv −=
( )
sm1062501103k1cv
8282
/.,,.. ≈−=−=
Y.%8Rxd6/OwJALAB3Ac-!
!ALax8fQ)<eALF0x7(`

xd/JALAB3Ac-!!ALa
x!b6'r2c1-8nOLc-6'1/
/OLc-AP7,@48sm-+64x
)<eAL712
222
''
Ryx
=+
Ra/
';1'
2
2
yy
c
v
xx
=−=
HB0-+64)<eALF
22
2
2
2
1
Ry
c
v
x
=+
−
V12-+c1-8
Y.S8o77WW3"W6$3AL
AbY. 893O+121NWW]j)3(WW]8fQ3AL
+)!>4!AL7WW]/WW\+7
<2`HA'O/0=WW8


H'O/WW(O3!MW+!
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
Y.T8f4•PAlALAB36;^0uX1IAB3
!8fQ/=+cWW+)!>4F>AL
/=‰+!3ŠV4•P8

hD(P>A+
( )
s
c
v
t
t 2,3
95,01
1
1
'
2
2
2
≈
−
=
−
∆
=∆
Y.X8n31,
α
~464<~AB37G^<^0u
1IAB3!8

U<~AB30/31,l~14
( )
2
0
/1 cv
m
m
−
=
( )
( )
kg
cv
mmmm
27
2
27
2
00
10.6,8
1
9,01
1
.10.67,1.41
/1
1
−
−
≈
−
−
=
−
−
=−=∆
Y.Y8n31,41c6;1I/31,\78F
~41c48

 ~ c1c 6;~1, 2-I1N  A2 1N
>4
(
)
( )
J
cmcmmcmW
141631
2
0
2
00
2
10.2,810.9.10.1,9
2.
−−
≈=
=−=∆=
Y.[8n-VV
u%
–
%SX
~1,=-7/=%^^
RcH8Ft/31,/-V /18
]
]j
fY
.
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522

U~1,=-7\1BAL/3
2
mcE ∆=
( )
kmolkg2140
10
9
1002561061200
c
NE
c
E
m
16
2613
2
0
2
/,
.
.,..,.
.
≈===∆
−
Y.g8FAB34•P<~1,2-I4•P76;
^1I~1,\78


U~1,2-I4•P6;/1I~1,\
2
0
2
2
2
0
1
ckm
c
v
cm
W =
−
=
−==−
2
22
22
2
k
1
1cv
k
1
c
v
1
( )
sm109852
10
1
1103
k
1
1cv
8
2
8
2
/.,. ≈−=−=
Y.u8$Ry-NRaF+6>~1,6;Y0X8 ^
%
/‘8U<6>
RaF+12 /P t+ /3 1,  7 =D126
4`
6$s=O!M</31,RaF+1/Pt8


$hMt/31,-A2!Mt~1,
2
mcE ∆=∆
( )
s10793
10631056
1091097150
P
mc
P
E
t
18
621
16302
.,
.,..,
...,.,
≈=
∆
=
∆
=
11
10.2,1≈ t
"~$
6$RaF+AG~1,AGB~1,G6428U<-I~
1,BA26;-I0~1,RaF+/Pt04/31,Ra
F+/Pt8
Y. ^8&'‰+!3Š
τ
4•P
µ
7~1,‘ ^
u
cH"
)<-dO$5+!34•P\12
τ
^
%0%8 ^
.Y
!0/3
1,4•P
µ
12%^Y0[
c
"
c
12/31,41c$8


‰F+!3Š4•P)<-dO,'
cP>
( )
s1012
10910197206
1022106110
mc
W
mc
cm
m
m
c
v
1
5
1631
6199
2
0
0
2
2
v0v
2
2
0
−
−
−−
≈====
−
= .,
...,.,
.,..,.
τ
τ
ττ
τ
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522


[. 8FAB3=(d/Ooz
%
3(‹6<;>D+/3
1,/O=)<(36;^0X /8n31,4/O
6;[0X/_
S
8+/O36;%8o/O121Q1:K8


sm/31,/O=)<(3A'+12
µ
8
F7
Sv
t
Sl
t
V
t
m
ρ
ρ
ρ
µ
====
..
( )
sm120
2
102
57
1
1800
510
S
v
2
2
/,
.
.,
.
,
≈
==
−
π
ρ
µ
[.%871y+/O( 8+/O6
E^0X8F!M-AB3MLK6A2M
L8-(6;!3+,-^0%8


smh
A2h
%
12<(6A21y5A
A2A
%
12AB3=L
!aLA2=)=1y8n70c-Zc1
2
2
2
1
2 vghv =+
Ra/0(O14(d=
2211
SvSv
=
gh2vv
S
S
v
2
1
2
1
2
2
1
2
2
+=
=
gh2
d
D
1v
4
4
2
1
=
+
( ) ( )
)(
//
Dddogh2
D
d
dD
gh2
dD1
gh2
v
2
2
44
1

=≈
+
=
n^0%0AB3ML12
( )
sm1092720892
50
010
v
4
2
1
/.,,.,.
,
,
−
≈
=
[.S8F4627a6L02671yQ;6

A2ML
%
8RML6,@/Pt8
fQL3a621y96;64"c-;
$`s=62+,-
$
%XA2
%
 Y5
6$
 YA2
%
%X8


HB3L/)1y
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
20
gh2v =
h//Q1y0-IDLABrALAB
36I6;A
^
8
F+G//Q1y</12
g
h
t
1
2
=
FIL12
21
1
20
hh2
g
h2
gh2tvL === .
$
%X0
%
 Y
(
)
cmL 4016.252 ==
6$
 Y0
%
%X
(
)
cmL 4025.162 ==
[.T8U+a6L72J>4a62;8
F4267(q1yQ8o1yq;4+J>8s=!D
<(6!AL<(1y!>L6
/Pt8
$o>;AB3L4a626;8
6$o>;3L3q4a62
/=G1y<>L6-=6;/=G1y/<
a628
$R3L--=1yA'O2`


&r1yKA'Oa62/=
A2aL12
%
8
HB3L//Q1y12
20
2ghv =
$hD('1B6=2~1,-IL!//Q6
121
2
0
2
mghmghmghmv
2
1
mv
2
1
+=+=
gH2hhg2v
21
=+=
)(
HLf12>L!ALa628
wk2;AB3La62/P-A2A'O1y8
6$FG/<)=62[.S07
(
)
hHh2hh2L
21
−==
(
)
''' hHh2L −=
LA2q
'
L
L
=
)'(')( hHhhHh
−
=
−
0hhhhH
22
=−−−
)'()'(
0hhHhh
=
−
−
−
)')('(
E
''' hHhhayhhHhh
−
=
+
=
≠
$hD(6J>oP!
(
)
HhHh2L ≤−=
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
E‰Š=/A2\/
hHh
−
=

2
H
h =
8
[.X8s@IL6'1yQ8R>LKI
  I f S^8 fQL = ) 1y AL AB 3 6; 6 4 
+,-!
$sIL>45
6$sI,V14
$sIAL3 0%_!
%
144W3(L8
($sIc-;AL3 0%_!
%
8


HB 3 L =  /Q I -  A2 - ! r- 14  I8 n I
AL3L144a3(L!b-!-r-
14I8F7
ahghP
S
ma
ghPv
2
1
P
00
2
0
ρρρρ
++=++=+
(
)
hag2v +=
"(Lc-m1M$
ŒU<I>4a,V14
^
(
)
sm42230892gh2v /,,.,. ≈==
ŒU<IAL3 0%_!
%
L144
(
)
(
)
(
)
sm5723021892hag2v /,,,,. ≈+=+=
A2/3L3(L
(
)
(
)
(
)
sm2723021892hag2v /,,,,. ≈−=−=
ŒU<IAL3 0%_!
%
c-0-!-\
42I4/P7(12tAB3L=!AL
/I8
(
)
sm422gh2v /,≈=
[.Y8R60(Oh>IL8671y
(Oh
8fQ
$h61VLK6=<`
6$ML-+<2/K1y8ZQ)L
L8


hD(6>AB3L>LCOK62[.%07
( )
2
1
SS1
gh2
v
/
+
=
( ) ( )
dt
SS1
g2
h
dh
SS1
gh2
dt
dh
2
1
2
1
// +
−=
+
−=
( )
( )
( )
t
SS1
g2
hh2dt
SS1
g2
h
dh
2
1
0
t
0
2
1
h
h
0
//'
'
+
−=−
+
−=
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
( )
2
2
1
0
t
SS1
g2
h2
4
1
h
+
−=
/
F+L6=<12
( )
g
SSh ]/1[2
2
10
+
=
τ
ŒU<
1
SS

7
g
h2
S
S
0
1
=
τ
2
1
0
t
2
g
S
S
hh
−= .
[.[8F V+7,^0%1OLA268fQK6-=7
1y+/O6;64>L6/PtA276;
"/G1y$8


>L6/Pt01,LtA2-=6;1,L=

21
dVdV
=
dtgh2SvSdtdtk .. ==
( )
25
3
m10524
1892
1020
gh2
k
S
−
−
≈== .,
.,.
.,
( )
m1067
105244S4
d
3
5
−
−
≈== .,
.,.
ππ
[.g8U+('3(mc>ILALAB
3Ag0S_!"[.%$8fQ>L(V1438


-('1BZc1
( )
00
2
00
2
hhgPv
2
1
ghPv
2
1
P ++=++=+
ρρρρ
( )
m543
892
338
g2
v
h
22
,
,.
,
≈==
[.u8 U+  t /P /O)  3 ]Z "[.S$8 o>y -N 7 X 1O
/P/O=)38EO<(-I]6;%
%
0-IQZA2
-I366;^0X
%
8F>L
∆
368Z</31,
4/P/O6; 0S%/_
S
8


Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
U+t/P/O)3]Z"[.S$8o>y-N7 X1O/P
/O=)38EO<(-I]6;%
%
0-IQZA2
-I366;^0X
%
8F>L
∆
368Z</31,4
/P/O6; 0S%/_
S
8
sm
ρ
0
ρ
%
1I1,12/31,4/P/OA2L5h
0h
%
12(O
<(3"h
‚h
%
$0H12O/O,t)3 V8
-('1BZc1
2211
2
212211
2
11
''
2
1
2
1
ghghvPghghvP
ρρρρρρ
+++=+++
0hghg
S
V
S
V
2
1
21
2
2
2
2
1
2
1
=∆+∆−
−
ρρρ
( )
−
−
=∆
2
1
2
212
2
1
S
1
S
1
g2
V
h
ρρ
ρ

( )
( ) ( )
mm570m1075
104
1
10250
1
8932110002
0150321
4
44
2
,.,
..,,.,
,.,
=≈
−
−
=
−
−−
[. ^8F46a-<-JA2;+a67/r
 1y Q K  -O 3  " [.T$8 E O  1y 6;  A2 6; h
^^^
%
8R1y/r!601y//rKX^8Z>LL
f ^^8F36!/K1y8ZQ)!@
A268n31,6Q/P/8Z<(O<(6
h
^0X
%
8


&1M(146/K1y12
( )
ghS2gh2gh2S
dt
SdtvSdtv
dt
vdmvdm
dt
dp
F
21
2
2
2
12211
ρρ
ρρ
=−=
−
=
−
==
..
( )
22
6
11
sm10961
150
50891010002
HS
Sgh2
HS
ghS2
M
F
/.,
.,
,.,...
−
−
=====
ρ
ρ
γ
[. 8R62J>))7"•$AL
AB37
ω
8Z>I1Q8
$&'(a1Q68
6$s=!D-!V66;-
^
0-!1Q14/
68n31,41Q12
^
8
$s=!D1Q612L8F-!
∆
-L14a64
6!6/6)ALAB37
ω
 %0Y(_!A2/6
>48Z/O612w^0X8

$n6)0y-VD6a1Q/31,
'(t,-1M
#1M)O1V
ω
%
8
#m1M8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
Ra1Q6'4A2;V6;/7J7ALt,-1M8
4,'6K7

g
r
mg
rm
tg
22
ωω
α
==
F17
dr
g
r
dz
dr
dz
tg
2
ω
α
=
=
g
r
zz
2
22
0
ω
+=
HB0(a1Q12-6P1Pd)•8

6$-!46>AL6/O12
22
22
0
22
0
r
P
g
r
zggzP
ρωω
ρρ
+=
+==
$o1Q2a7(2(Q
zdrrdV ..2
π
=

+==
R
dr
g
r
zrdVV
0
22
0
2
.2
ω
π
+=
+=
2
2
0
24
2
2
0
4
0
4
R
g
zR
R
r
g
rzV
ω
π
πω
π
n6/P)0-!612
+===
g
R
zg
R
V
gghP
4
22
0
2
1
ω
ρ
π
ρρ
HB0-!L14a64!6/6)A2/
6>412
( )
24
22
2222
0
22
012
/10
4
5,0.6,12.1000
442
mN
R
g
R
zg
g
R
zgPPP
≈=
=
+−
+=−=∆
ρωω
ρ
ω
ρ
[. %8R3(‹7u^
^
7L="[.X$8&'1M
(2314Ly3<<(312A27(O
6;hT
%
011,L=)312v%T1O_-N8


F7
( )
12
vv
dt
dm
dt
pd
F
−==
E
S
Q
vv ==
21
0
Q
dt
dm
ρ
=
A2
21
vv
⊥
4
( )
N
S
Q
F 564,0
10
.
4
60
10.24
.1000
.22
4
2
3
2
≈
==
−
−
ρ
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
Hc1M,-AL-7TX
^
A2LA-O1k3
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)
lOMoARcPSD|35973522
| 1/79
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

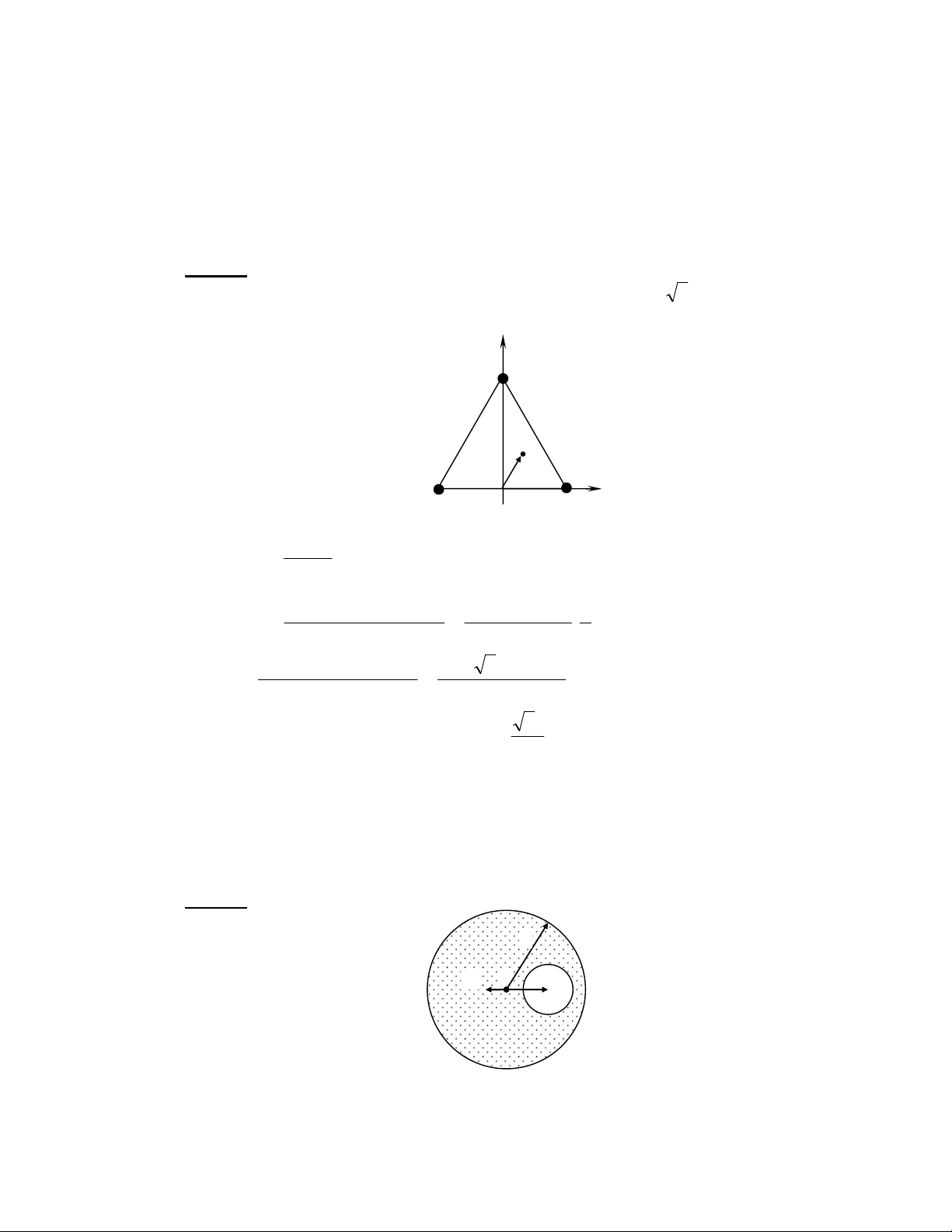
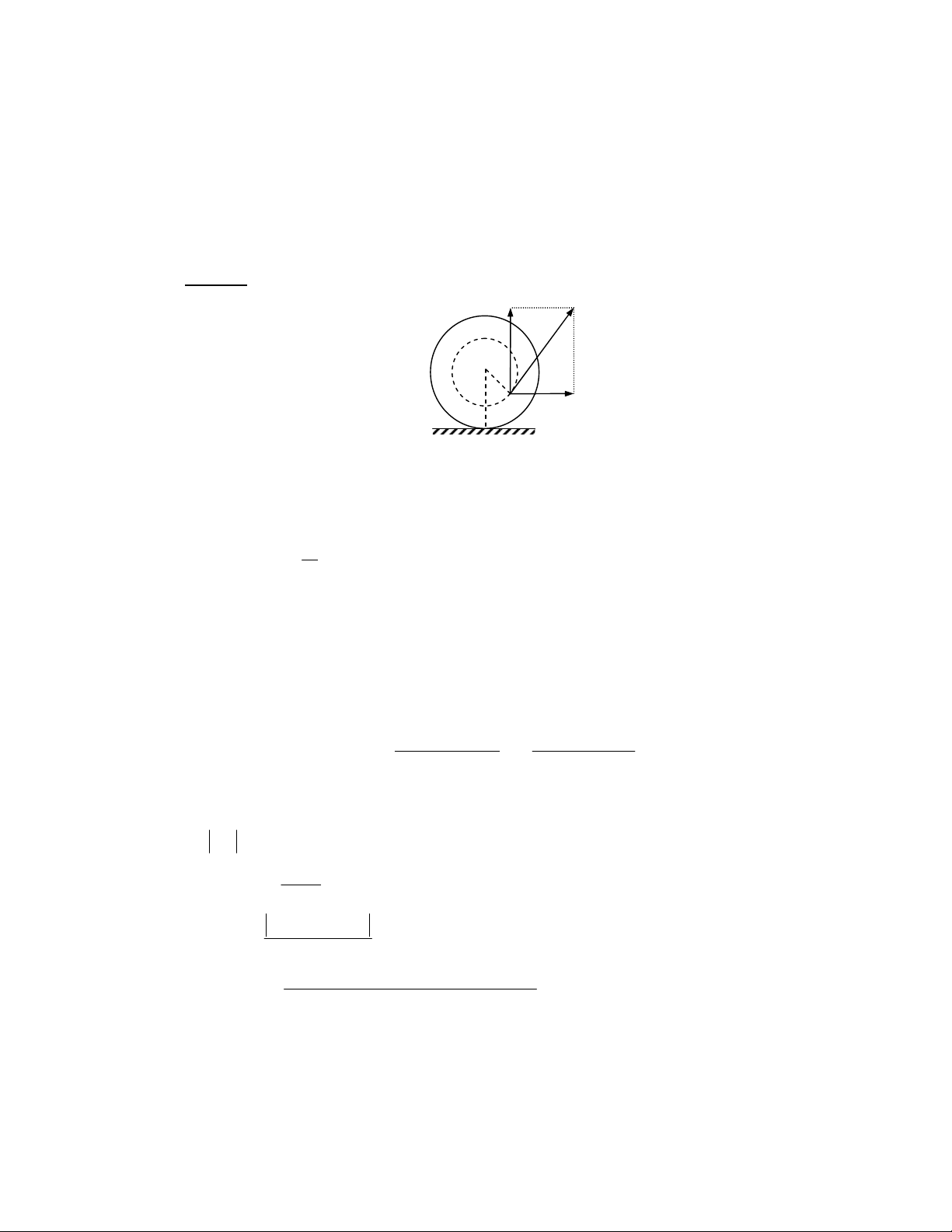
lOMoARcPSD|35973522 !"ω # ϕ $ " $ % !"ω # ϕ%$ "%$ & ' ( ) * + ,- ! $ ϕ . ϕ% %/π0 / 12 !3 4 5 6$ ϕ . ϕ% "%/ # $π5 π $ ϕ . ϕ% "%/ # $ 5 2 ($ ϕ . ϕ% 7 ' 6 / 8 9 : ; 0 6 < , ( ) * 2 7 - = 7 > 12 - 6 ( ? 3 ) @ AB 0 7 C / D 6 < + 8 E 70 62 B- 2 7 12 ! 8 $ F ϕ ϕ% # %/π A2 " $ 7 !"ω # ϕ $ !"ω # ϕ% # %/π$ !"ω # ϕ%$0 % !"ω # ϕ%$ FG 7 x y a = y 2 = x a a a 1 2 1 H . ≤ !"ω # ϕ $ ≤ 4 . ≤ ≤ HB - I $ 2 4 J 6 ( ? 6K a y 2 = x AL . ≤ ≤ a1 6$ 92 M - I $ !"ω # ϕ $
!"ω # ϕ% # %/π#π$ . !"ω # ϕ%$ FG 7 N 4 J 6 ( ? 6K a y 2 = − x AL . ≤ ≤ a1 π $ F ϕ ϕ% # "%/ # $ (? (2 N 6 > 2 x 2 y2 + = 1 a 2 a 2 1 2 2 6 ( ? + 41O- A P 0 7 1L A2 Q ; 4 8 ($ = / D - " $ A2 "%$8 R 3 < / 2 !3 ! " $ A2 "%$
x = cosωt.cosϕ − sinωt.sinϕ "S$ 1 1 a1
y = cosωt.cosϕ − sinωt.sinϕ "T$ 2 2 a 2 U V "S$ AL !ϕ% A2 "T$ AL . !ϕ W A< AL A<
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 x y cosϕ −
cosϕ = sinωt.sin(ϕ − ϕ ) "X$ 2 1 2 1 a a 1 2 9
V "S$ AL ! ϕ% A2 "T$ AL . ! ϕ W A< AL A< x y sinϕ −
sinϕ = cosωt sin(ϕ − ϕ ) "Y$ 2 1 2 1 a a 1 2 Z - "X$ A2 "Y$ W A< AL A< 2 2 x y 2xy + −
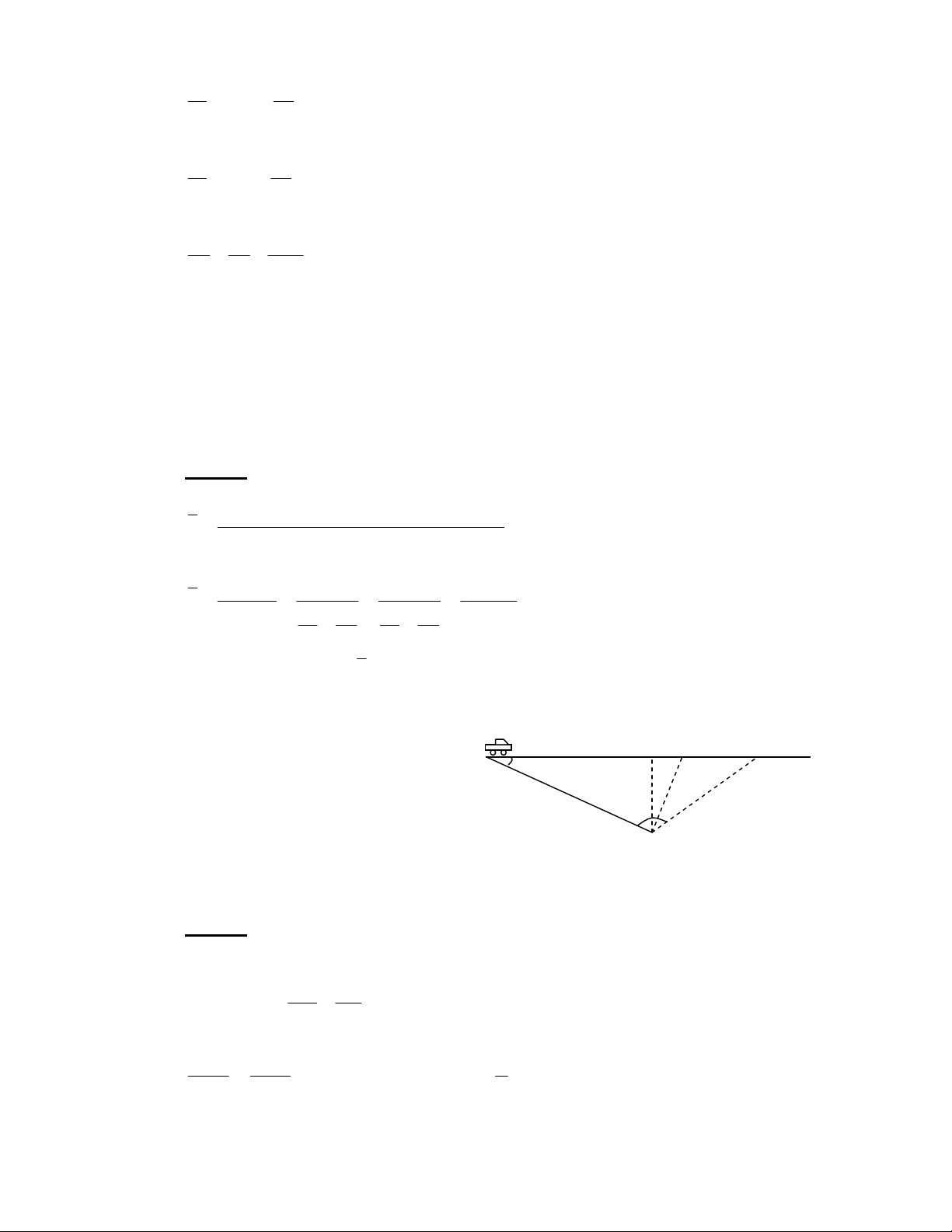
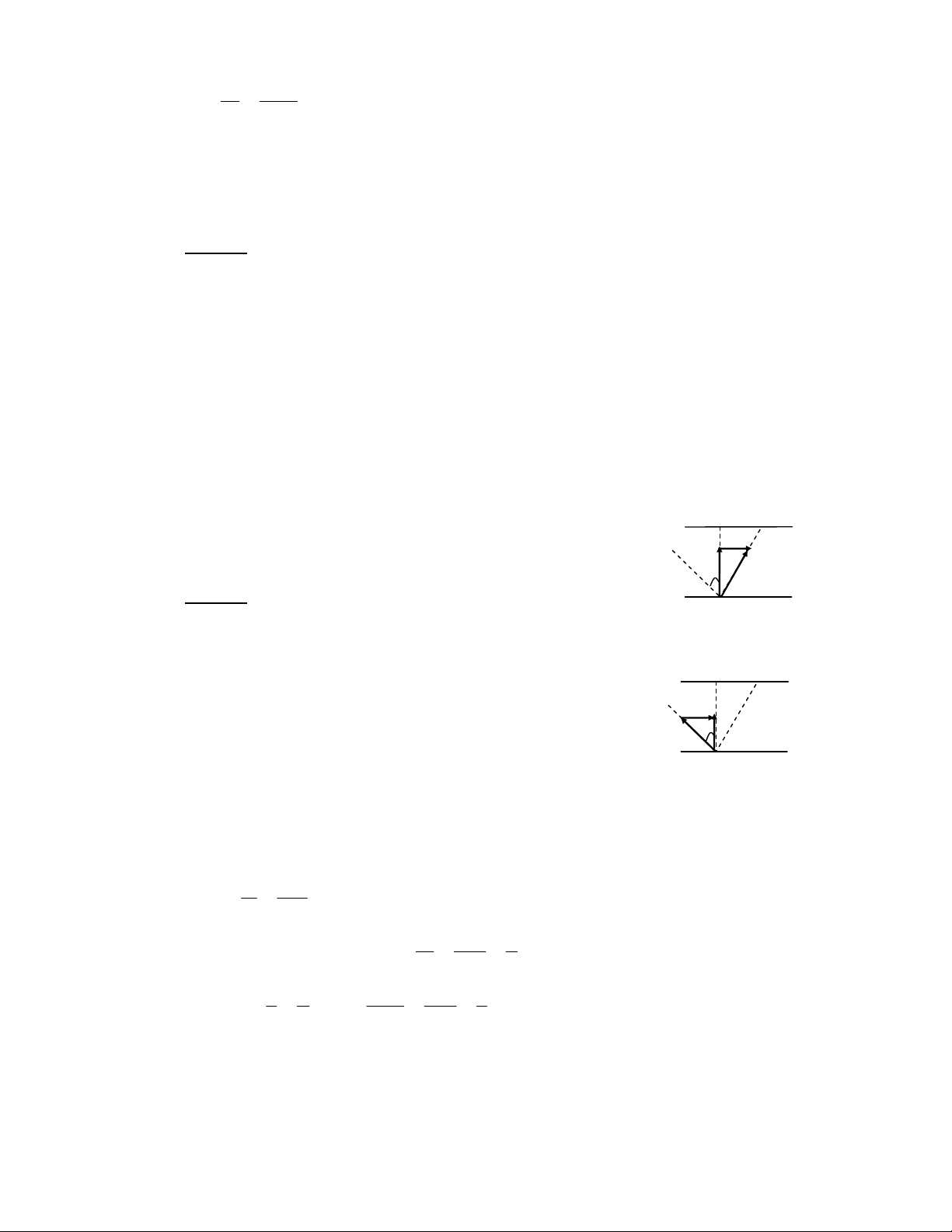
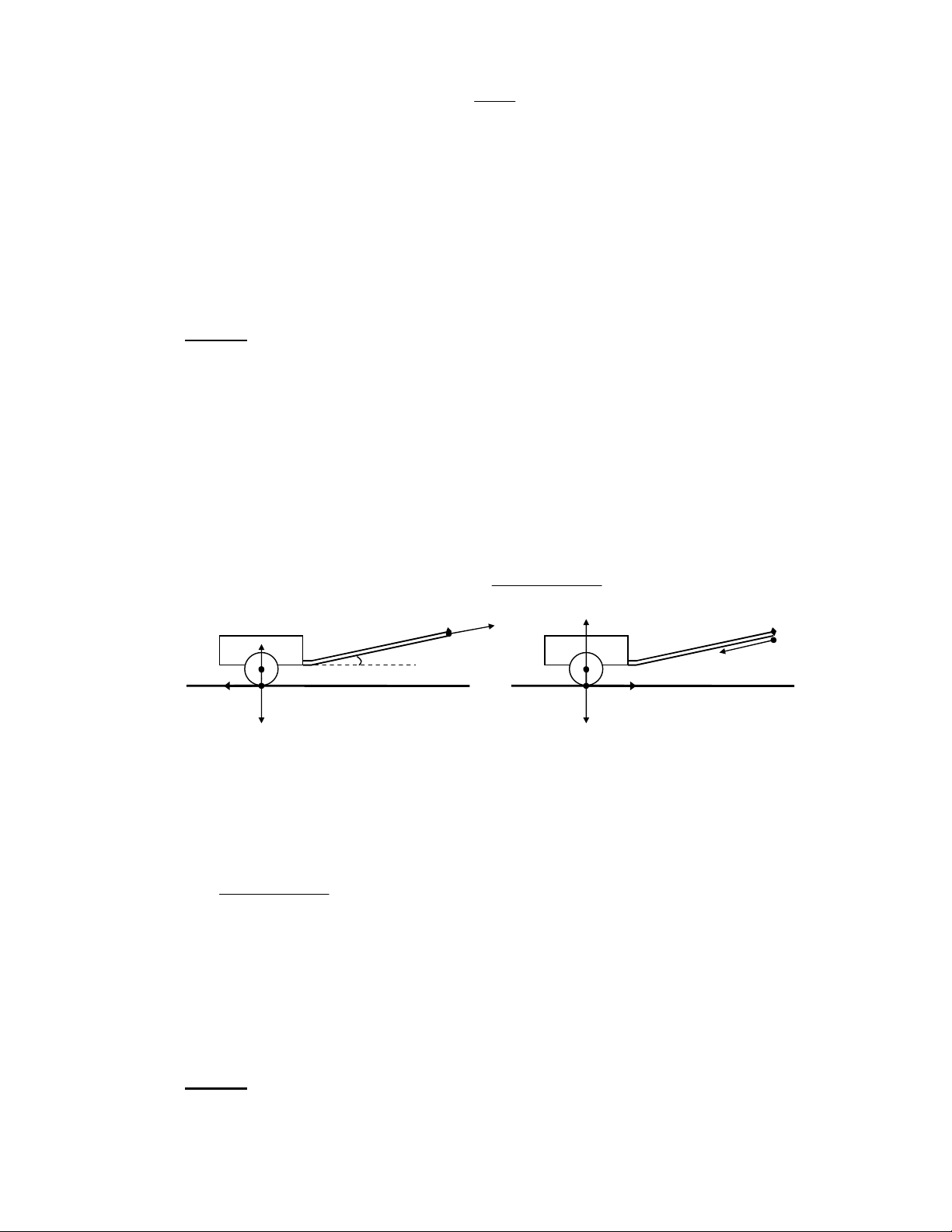
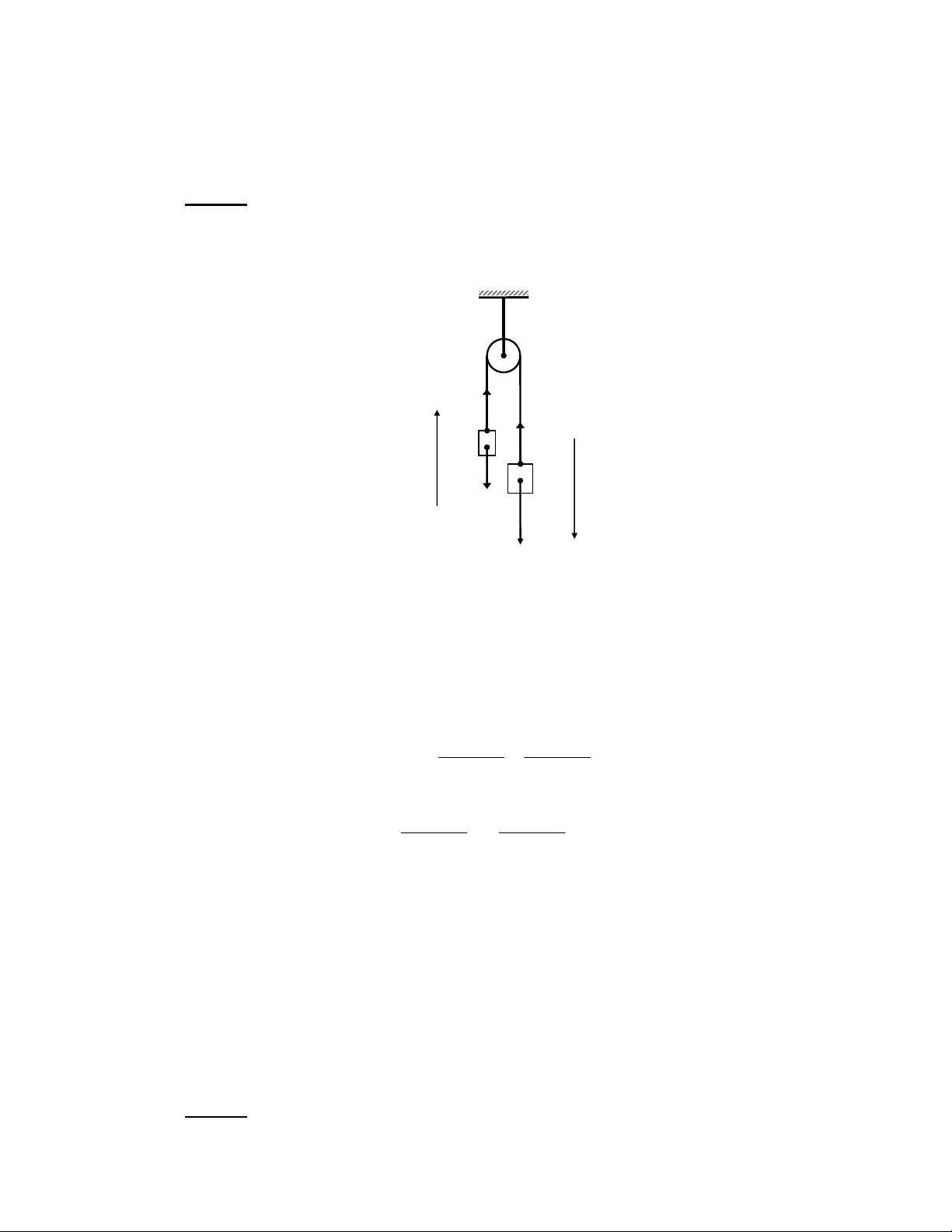
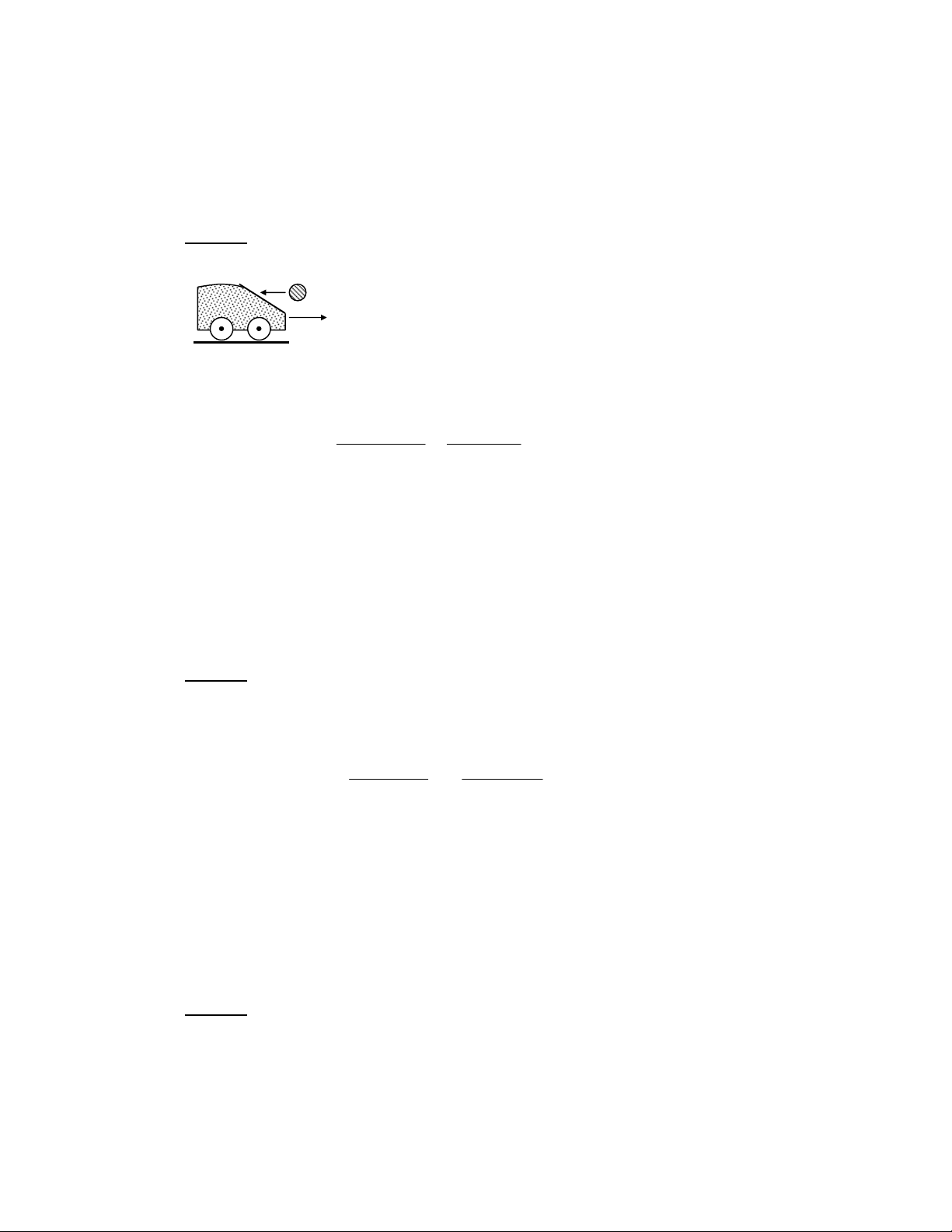
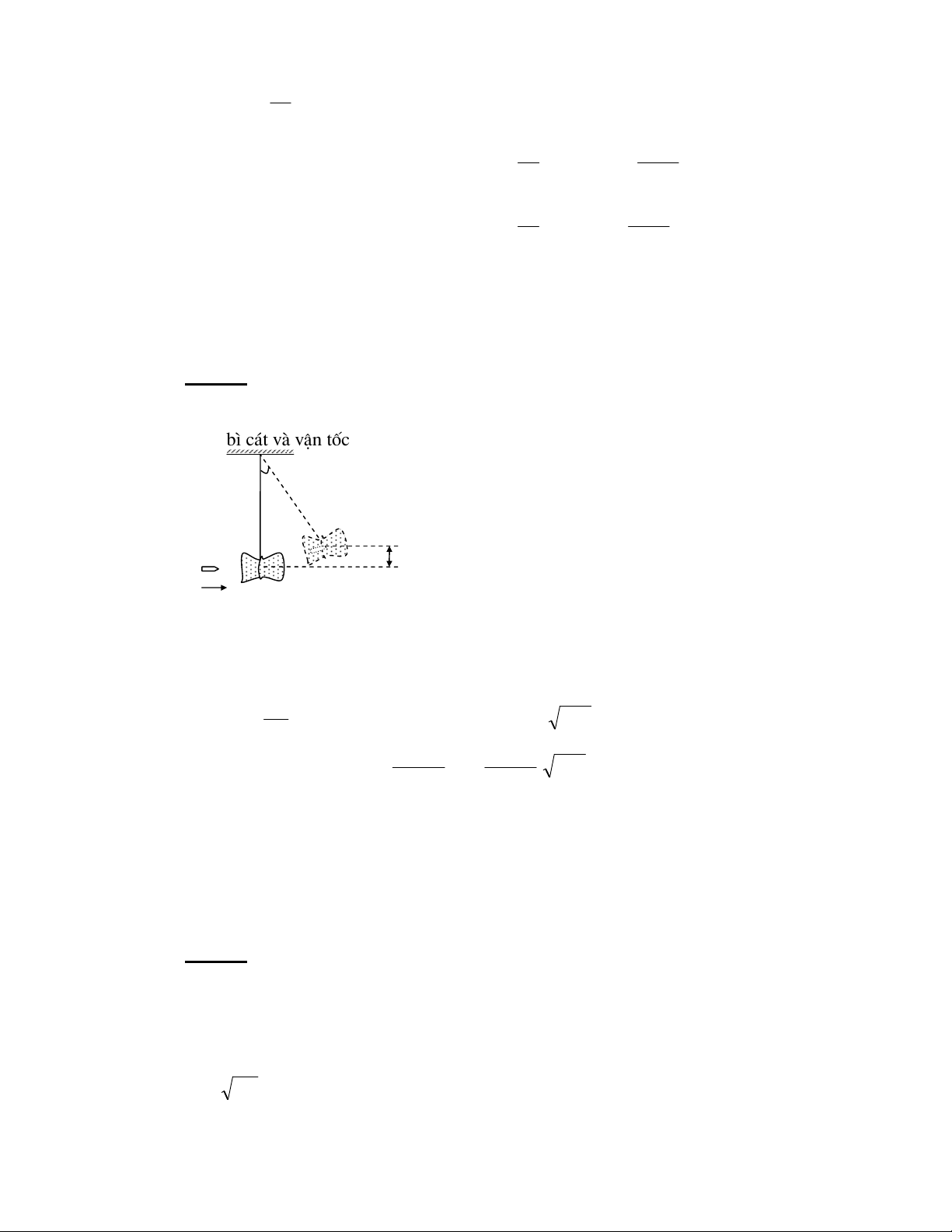
cos( ϕ − ϕ ) = sin2 (ϕ − ϕ ) "[$ 2 2 2 1 2 1 a a a a 1 2 1 2 "[$ 6 ( ? + 41O-8 ! " !#$ %#$ # %& !' ϕ() ϕ* %& + , - . /0 12#3 R P P G \ ] < \ Z AL AB 3 A T^/ _ + W 1 G \ Z K A \ ] AL AB 3 A% S^/ _ +8 F AB 3 6 P P 4 + A ]Z0 Z] 7` a ) C + ]Z 6; !8 F !b O AB 3 6 c P > 6 . 4 5 4+ v = 6 5+ +! 4+ . 4 5 0' F , s + s s + s 2 2v v v 1 2 = = = = = 9,5 m 3 / s. t + t s s 1 1 v + v ( A 1 2 + + v v v v 1 2 1 2 F !3 , v = 9,5 m 3 / s. R + > R + J / = X^ + P P5 / P P d f i E Z %^^ + 6e I + a- P P "f .%$8 Z < P P β ] AL AB 3 SY/ _ +8 fQ $ U + - = c α L 2 a- N P P` Z < ; R + AL AB 3 A% ^0g / _ +5 f .% 6$ U + - = AL AB 3 Q 6; 6 4 7 a- , P P` $ R 3 a- N P P Z + + G R L Z - = 6; + P P G ] L Z MB AB = " $ v v 2 1 hD ( ' 1: 2 !3 ! ]ZR 7 MB AB h = , AL sin β = "%$ sin β sinα a FG " $ A2 "%$ N
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 h v1 sinα = . = 0 8 , 33 α XY^S^j a α %S^S^j8 a v2 7 7 5+ 0' ' 8 9 :; <0 α = >:; ? <. 5603 ' 0 ≤ α ≤ 12303 ' 0 3 @ + 5603 ' 0 < α < 12303 ' 0 5+ 0' ' 5 ?+ + 8 h v C / ' +? DE 5+ ' + < F ? <. +G 0' 1 sinα > . 3 a v2 MD AD 1 h v a v :0 = → AD = sinα . M . D 1 > . . A . D 1 = M . D 8 sin β sinα sin β a v h v 2 2 AD MD > 1 - 0 5+ +! 8 ' F 9 5+ +! 5+ ' F#3 v v 1 2 6$ 7 a- , P P AL AB 3 Q k 2 ; 1N 2 + < + l 12 1N c P P L " + a- N P P 2 / P - = + , 1C - O + $0 A AB 0 c - I $ @ L A2 AB 3 + - = 7 ) h v1 sinα = . a v2 H AL m h v h α ! "α$ ≤ 4 1 . ≤ 1 v ≥ v . 2 1 a v a 2 h hv v 1 = = 2 5
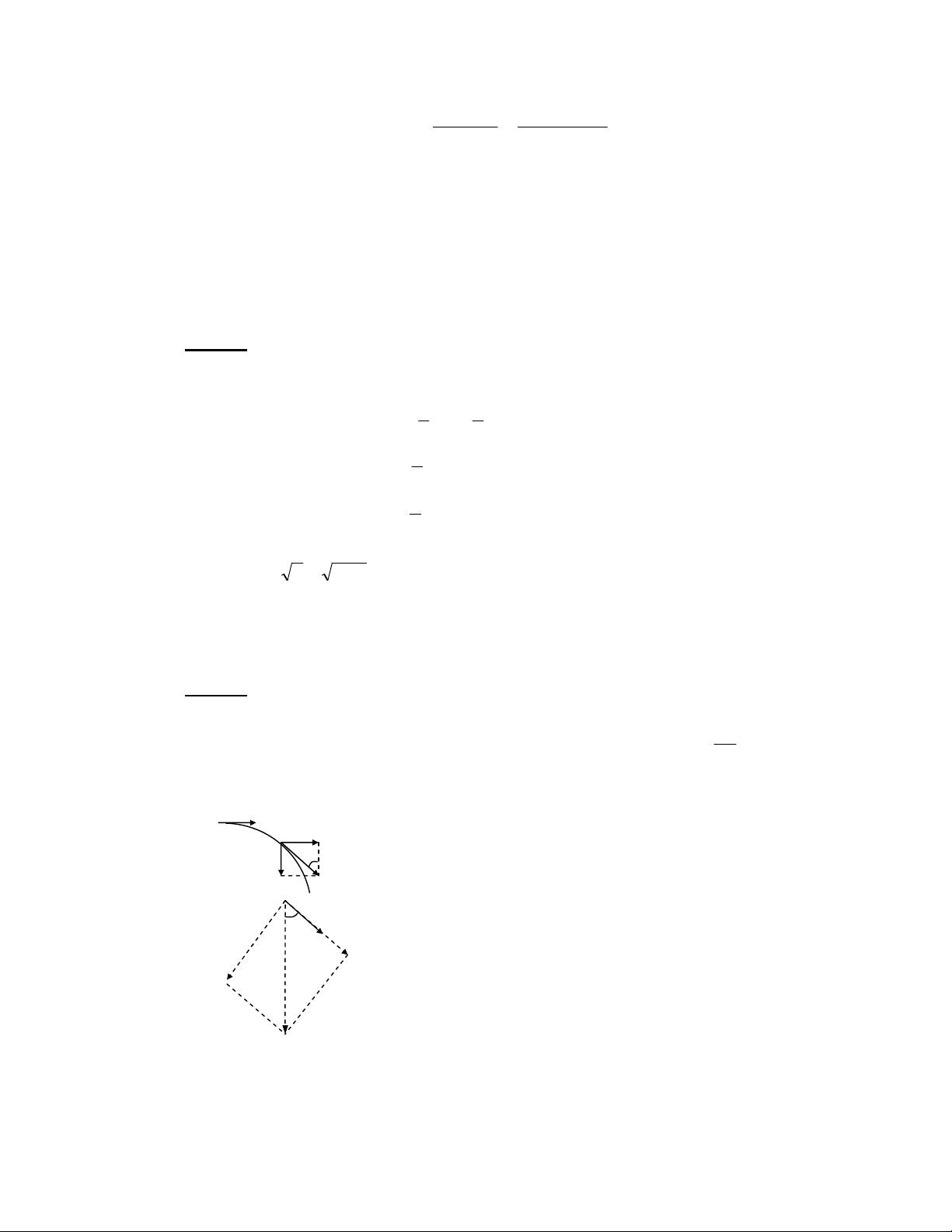
, m / s = 9km / h 8 2 min a 9N 2 0 + - = c L Ri0 AL Ri ⊥ ]R8 R AB , = G / O I 6 K S^^ 8 fQ ! 6 1V AB L a 0 < $ n O I 6 14 " c L J > $ AL AB 3 X _!5 6$ n O I 3 " c - J > $ AL AB 3 X _!5 $ n O I > 4 8 n / O I 0 AB K 4 / O I c AB 3 / O I 8 U< / O I 3 ( L AL AB 3 A^ + 2 AB L = C - 6B + 1 v t . + g t 2 . = h 8 0 2 v 2 + 2gh − v o m ( - 2 7 /< ) = t 0 0 = 8 g n / O I 14 4 0 3 ( L a > 4 0 - ( 6 > 2 AL AB 3 6 I A^ .X _!0 A^ X _!5 a A^ ^ A2 7 /< ) = $ g0T! 5 6$ [0S! 5 $ [0g!8 R AB , = G f # c - J > EEj "Ep 12 V f # $8 oq 1N 7 AB > , r 14 G Ep c - J > AL AB 3 A^8 $ fQ AB 3 A^ - = 6; 6 4 AB a- K `
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 6$ FO / = @ AB L 1N a- c + ` $ U< / P 7 AB > AB > 1L 6; 6 4 ` oI L 1 P > M ( $ F + AB G E < a- 12 2H t = l g 6; + AB % G Ej < s0 ( 7 E f 1 + 2 h gt H h h = v t . − g t . → v = + = 2gH 0 s 2 0 t 2 2H 6$ n = @ AB + L / a- , O c ) C + ! A2 !j AB , "f # $ . "! # !j$8 Ej x = (H + h) 1 2 1
− gt − v .t − g.t 2 = + − 0 (H h) v .t 2 2 0 H + h =
( 2H − 2gH .t ) 2H $ hD ( P > ) A0 0 ! J 6 < t v2 − v 2 = 2 a . s . AL AB 3 K M 6; A ^0 . 0 ! ! 0 < / P 0 7 !M = K AB 0 AB % 14 < M 12 v2 ( H + h 2 ) h = = 8 max 2g 4H F = M ( AB G u0Y r 8 FO $ v C + 2 AB , ^0 V I A2 ^0 V 3 + 8 6$ F + I < AB < I A2 3 8 hD ( P > A ) C + AB , ! + / G 1N 6e I , = 1 2 s = gt !b 7 P > ) c A + AB , 2 + 7 / G A' O = 12 2h t = 8 - ( P > 2 !b = 1+ g , V Q 62 B- 2 $ v C + 2 AB , ^0 ! I 1 2 1 s = g t . = 9 8 , 0 . 12 , = 0 0 , 49m 8 1 2 2 Ft + AB 2h 2.19 6 , t = = = 2(s)8 g 9 8 , v C + AB , ^0 ! 3 q 0 , O c ) C + , %.^0 0u ! I 1 s = h − g − , = , − . , . − , = , 8 2 (t 0 )2 1 1 19 6 9 8 (2 0 ) 1 2 1 ( 9 m) 2 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 6$ F M 4 s 2 F + AB , I 2.1 t 3 = = = 0 4 , s 5 8 3 g 9 8 , F + AB < 3 2.18 6 , t = t − t = 2 − = 0 0 , s 5 4 6 (I$J< H" 9 8 , FG 6 ]0 Z0 o 4 Ad d + W + = 6 AB 8 HB > c - J > ]R ) V Ad d "f .S$0 AB > c (V ZR0 AB > 6 c (V oR8 fQ AB 2 L R L 4 0 < 6Q ) ! ` ] Z o R f .S v C + A2 3 AB > ! %w0 0 AB > !% ^ ^ ^ ^ %w ! AMB 0 % ! AMB 0 AB > 6 !S %w ! AMB 0 S ! AMC 8 U B 0 + < R AB 12 s 2 4R s 2 s 2 1 2 3 t = = = = t = t = 1 2 3 a g a a 1 2 3 HB 0 6 AB q L R 1N 8 = r AB c - J > G T^ AL AB 3 A^ 6; 6 4 7 L a $ F L τ V ! AL + ,- AB M ( ` 6$ h τ V ! AL + ,- AB M ( ` 9 ^ _!%8 hD ( P > O + < / 62 X v 2 + 2gh − v 2h t 0 0 = A2 P > + M ( t = g g AB !L 0 - = r AB 3 ( L AL AB 3 A^ = C - 2 2h v + 2gh − v 0 0 − = τ → v 2 + g 2 h = gτ − + 0 (v 2gh 0 ) g g
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Z - A< - , ( 2 g 2 2gh − g gτ ) − 2gτ (v + 2gh + = → = 0 ) τ ( τ ) 2v 2gh 0 v 0 0 2( 2gh − gτ ) $ AB !L 0 - ( AL τ ! 7 10. (
1 2 2.10.40 −10. ) 1 v = = , / 0 2( 2 1 . 0 4 . 0 −10. ) 12 7(m s) 1 HB AB , r J > 3 ( L 8 6$ AB 0 - ( AL τ . ! 7 −10. ( 1 2 2 1
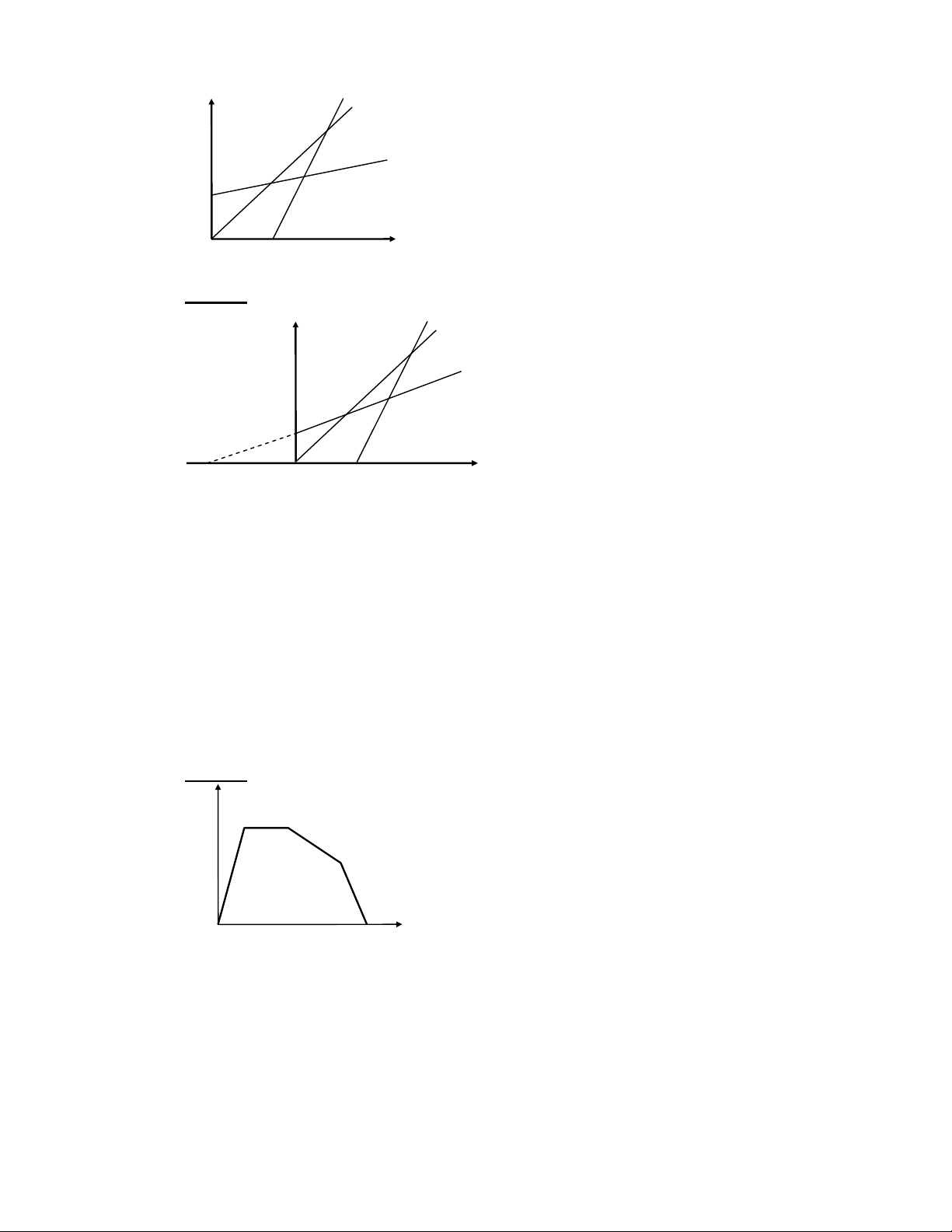
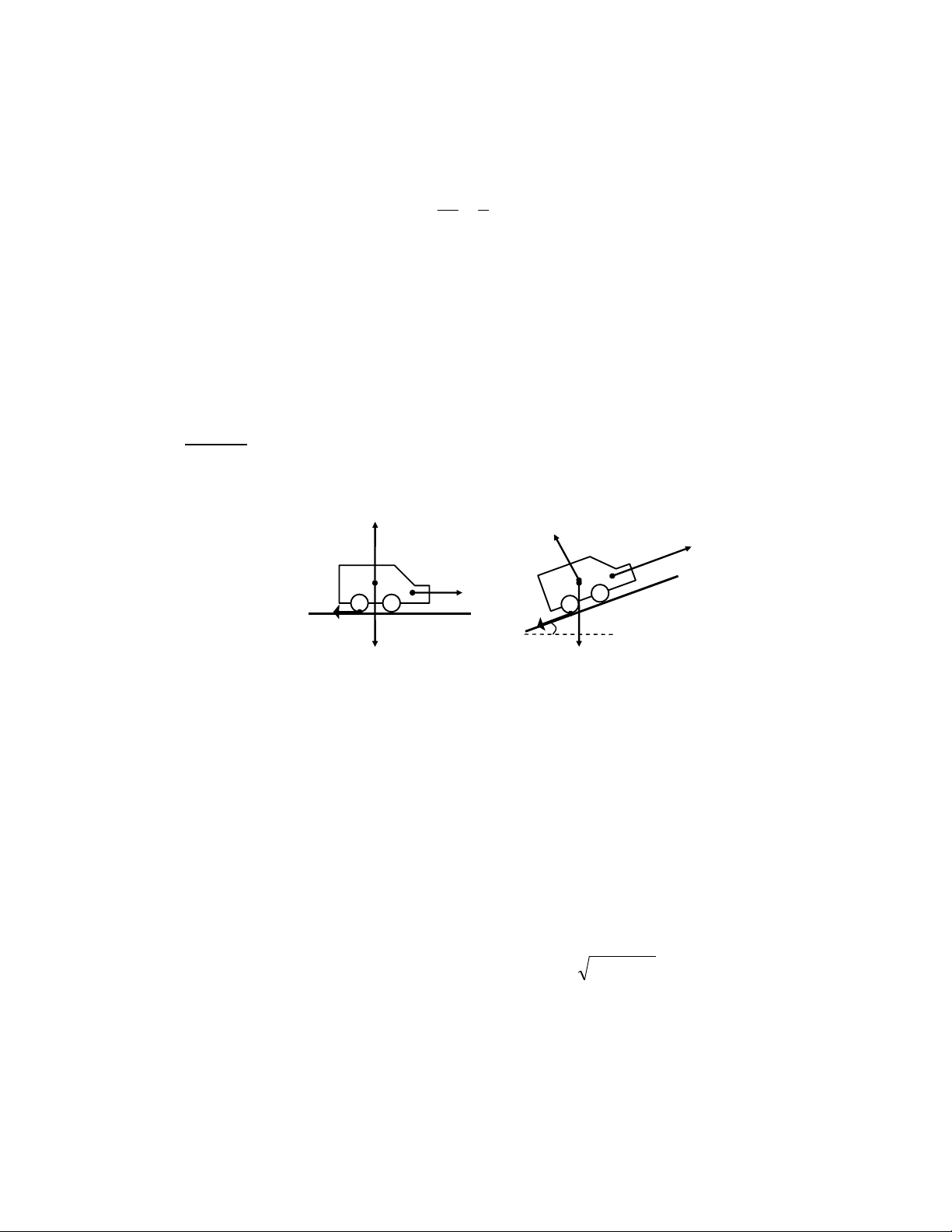
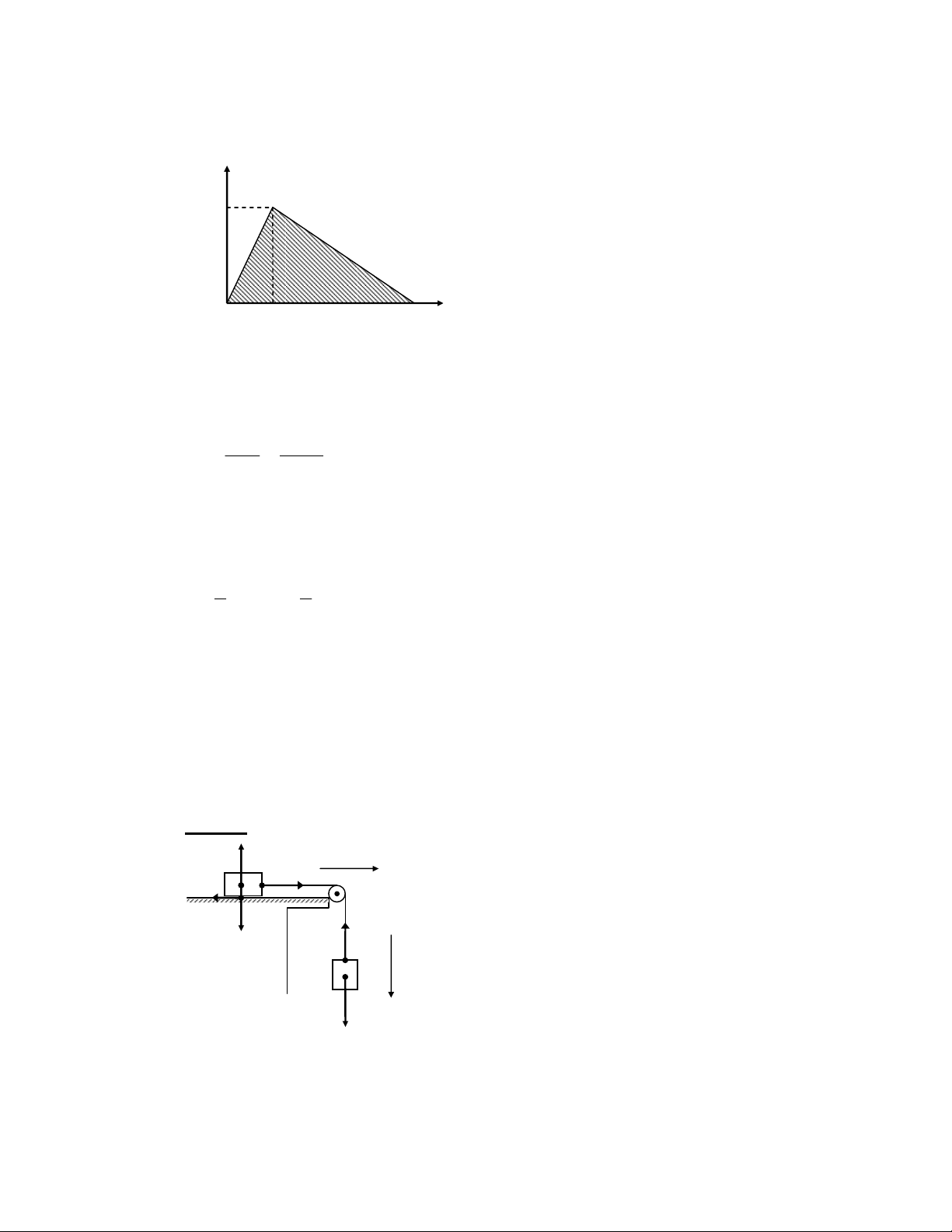
. 0.40 +10. ) 1 v = = − , / 0 2( 2.10 4 . 0 +10. ) 8 7(m s) 1 HB AB , r J > 14 4 8 R AB J t < ) C + ]Z Y V 8 HB 3 AB / ) ] 6; X _! / ) Z 6; X _!8 F (2 ) C + ]Z8 ( ∆ − − F c ' x 0 3 AB v v v 15 5 5 B A a = = = = ( 2 m / s )8 t ∆ t 6 3 FG 7 7 O ) C + ]Z c P > 1 2 AB = v t + at A 2 F !3 , ]Z Y^ 8 * 9 : ; 0 AB 3 6 J 6 < t 7 P > + a 6 0 6; v v v A B = 0 4 ]Z 7 (2 2 v + v 5 +15 AB = v t A B . = t . = 6 . = 6 ( 0 m) 2 2 R c 1D @ " ; 4 + J $ 0X/ 8 F D + I 0 c 1D (I 0 D + ! c 1D B (I 8 HB 3 1L c 1D @ 7 6; X^/ _ +8 Z < ; ' !3 3 3 4 + 6; 8 FO $ s 3 c 1D 8 6$ F + c 1D < ) C + @ 8 HB 3 6
c 1D 12 v = 50 / 2 = 25km / h 8 F + c 1D < 0X/ 2 12 t = s / v = 15 , / 25 = 0 0 , 6h = 3 6 , B = *(JD 8 v 50km / h max (50 / 3 6 , ) s 3 c 1D m / s a = = = = 0 1 , 29( 2 m / s )8 (t / 2) 18 , B 1 8 , 6 . s 0
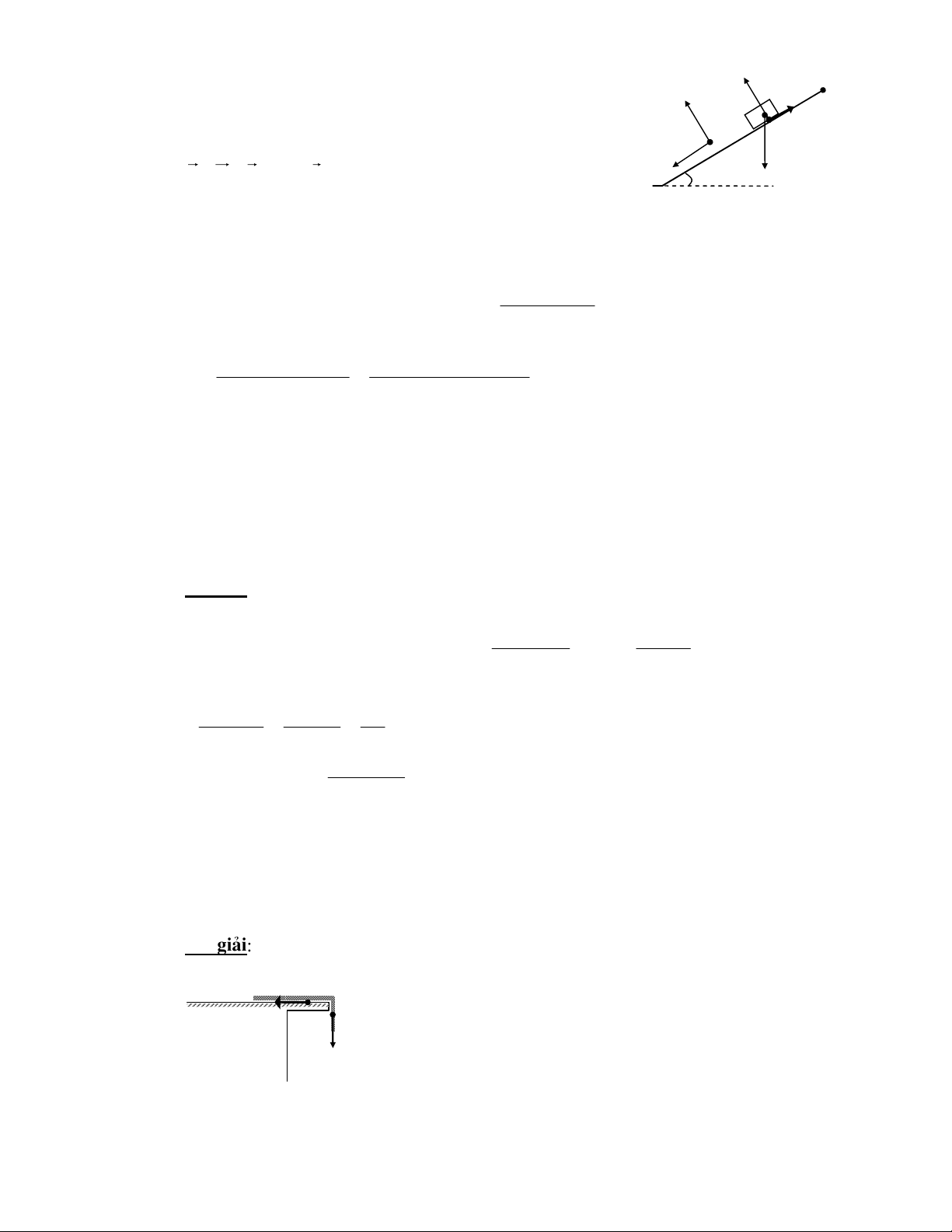
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 K +! L ! 8 E! HM! /0 ! N /$ !$ D ! ' A O 2 2 v − v 50km / h 0 ( )2 %+ 6+ G v2 − v 2 = 2 a . s . 2 a = = = 0 1 , 29m / s 8 0 s 2 1 5 , km 1P Q' D 0 E! . 5 ($R <# R c 1D 6e I (I 4 + J ) L a + ) ! > AL I > 8 Z < ; c > ) L a + ) ! < + τ Y V 8 fQ > !b ) L a + ) ! 6 1V ` - ( + ,- [8 sm 1 12 (2 y 0 12 + I ) L a + ) ! 8 - ( - J t 0 7 o (2 > 1 1 2 2 l = at = aτ 1 2 2 o (2 " . $ 1 2 (n − ) 1 l = at n 1 2 − o (2 I 1 2 nl = at 8 n 2 FG 7 ! + > ) L a + ) ! t ∆ = t − t = ( τ n − n − 1 $8 n n n 1 − HL [ 0 7 ∆ [ 0 g!8 R d , r c - ; AL AB 3 A^ X _!8 FO 3 - - < A2 3 <- < d ! 1N r V 8 HB 3 AB c - > ! / r ! A u0g _!8 s7 v α @ AB 3 AB A2 - J > = C x tgα = 8 &c v y Ab 64 8 A^ A α A A α A 8! α 8 !α FG 70 3 - - < A2 3 <- < AB 1N 2 O 12 @ 2 - I < 3
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 g v . 9 8 , 1 . 5 x a = g sinα = = = 8 2 , m / s n ( 2 ) 2 2 2 2 v + v 15 + 9 8 , x y 2 2 2 2 a = g cosα = g − a = 9 8 , − 8 2 , = 5 4 , m / s t n ( 2 ) U + r ) = 67 AL AB 3 A^ ^ _! c - ,- AL a - J ; 7 α T^^8 s = !D ) = 67 , r G a 8 fQ $ 1L 2 ) = 67 7 , 8 6$ FI ) = 67 8 $ F + G 1N r 67 L 1N 67 8 ' , @ 1 , 62 a 0 I 1 : ; 0 7 AB 6 W / 1B- c - J > A2 c - 8 o c - J > 12 J 6 < t AL 3 6; 0 AB 3 6 I 6; A^ A^8! α8 o c - 12 J AL AB 3 / P t 6; A A^8 !α8 $ M A2 + AB \ 1 4 ) < AB 3 6 I c - J > A^ v 2 α 0 y v2 2 .sin y 0 = = = 2, max ( 1 m) 2g 2g v . sinα $ F + 6 AB 0 y 2 v t = 2 0 . = = 1, ( 3 s) g g 6$ oP > I AB r 4 2v sinα v2 .sin 2α L = v t = v 0 0 cosα . = = 10m x 0 g g FG \ - f %X + r d 14 - O 4 AL AB 3 A^ X _! c - ,- AL a - J ; 7 α S^^8 & ' $ F + d 5 6$ n = G V - < y d 5 $ HB 3 d 1N 8 A^ f α z 9 FG \ - A 4 d 14 4 , v 2 α 0 y ( 2 2 v sin .sin 0 ) (15 300 ) h = = = = 2 8 , 7m 2g 2g 2.9 8 ,
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 + d v0 ( 2 H + h) 7 5 , ( 2 25 + 2 7 , 8) t y = + = + = 31 , ( 5 s) g g 9 8 , 9 8 , FI L = v cosα t
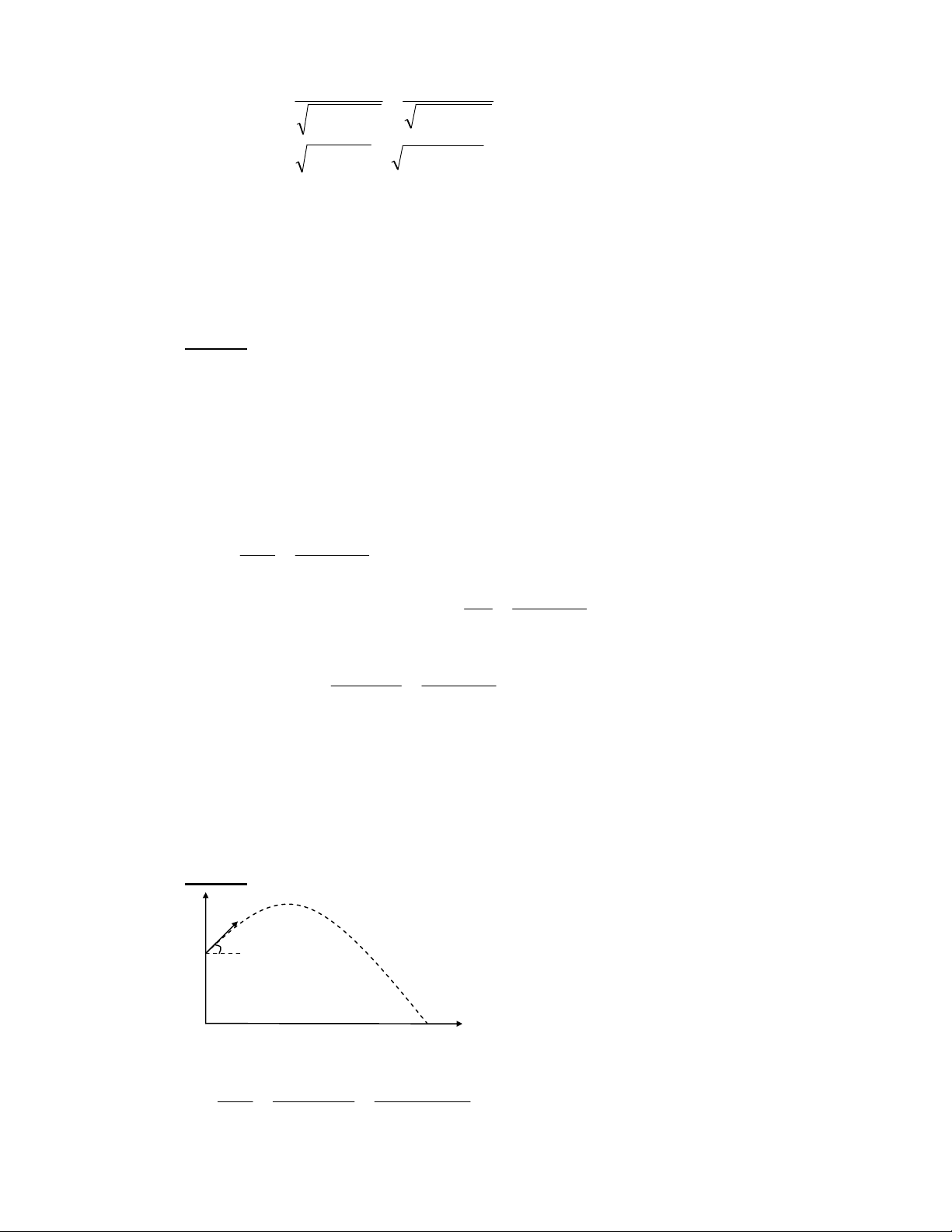
. = 15.cos 300.31 , 5 = 4 0 ( 1 m) HB 3 1N v = g 2 + = . , . + , = , / y (H h) 2 9 8 (25 2 78) 23 ( 3 m s) 2 v = v 2 + v 2 = 23 32 , + .cos = , / y x (15 300 ) 26 7(m s) C! +?+ ' %0+ 8 %& HS A3 T N U A V ' /9+ V &< + Q /W3 X ' A ! / 8 U 0' x = v t = v cosα t . x 0 1 1 2 2 y = H + v t − g t .
= H + v .sinα t. − g t. y 0 2 2 Y < 5+ +! +$ +?+ ' = Z3 Y < "< ! < ? [ /, K + 9+ Q $ ! !' < /0 %+ - ! K 3 Y < / L B < \ $ 9 7 - v = v cosα = const x 0 v = v sinα − g t . y 0
!# ]$(JD ^ %# _($(< ^ # *J$2<`D3 FG \ - f S^ 0 + r d 3 AL AB 3 A^ ^ _! c - ,- AL a - J ; 7 α S^^8 F $ F + d L a / G N r ` 6$ n = G V - < y d ` $ E ) * d ` F (q - - - 3 62 . T8 o m z AL z ; V -8 $ AB c 2
x = v t = v cosα .t (1) x 0 1 2 1 y = H − v t −
g.t = H − v .sinα .t − g.t 2 ( 2 ) y 2 0 2 + 0 = - ^ 0 1 30 −10.sin 30 t . − 1 . 0 t2 . = 0 ↔ 30 − 5t − 5t2 = 0 2 o m ( , + d %!8 6$ I { A' O V - 6 4 0 , O 8 x = v cosα t . = 10.cos 300 2 . = 10 m 3 ≈ 17, m 3 0
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 $ 6 < ( ) * A 4 0 I - ) * 2 "- ) @ A2 C / D 6 < + $ n D + - " $ A2 "%$ 6; N G - " $ W A2 "%$ x
(1) → t = v cosα 0 2 1 2 x 1 x
( 2 ) → y = H − v .sinα t . − g t .
= H − v .sinα . − g 0 2 0 v cosα 2 v cosα 0 0 g x 2 .
= H − x t.gα − 2v 2 2 cos α 0 x x 2 = 30 − − ( /9+ 0 ≤ x ≤10 m 3 ) 3 15 2 \ ; 0 ) * A 4 12 - 6 18 fQ - = r AB c - ,- AL a - J ; 7 α 6; 6 4 AL AB 3 6 I L 0 I AB 12 M 8 hD ( P > O I AB , r 4 C 1B- , 62 . S v2 .sin 2α v2 L 0 0 = ≤ g g v 2 HB !b , I M 6; L 0 = / ! %α 0 α TX^8 max g n| 1 } K f2 U 12 %0Y[ r 8 fQ < t > K & 4 c 6 / M " q AB 3 6 I A2 7 4 $0 /| 1 4 !b 12 6 4 ` o 6 < "f2 U $ u0[%[ _!%5 "& 4 c 6 $ u0g ^ _!%8 v2 .sin 2α FG P > I L 0 = B 0 AL 1M } / P t " A^ g / P t $ A2 7 r / P t " r / 7 r 6; TX^$ I 9 !b \ 1 ' AL 3 m + 8 E 7 7 ' , /\ 1 } 2 - 3 & c r 6 g 9 7 , 27 L HN = L = 1 . 2 6 , 7 = 12 5 , XP HN ( 6 m) g 9 8 , 10 XP F AB 3 7 $ F ) ) 7 "F ) Ad ) 7 %T +$8 6$ / + A2 / - N W W5
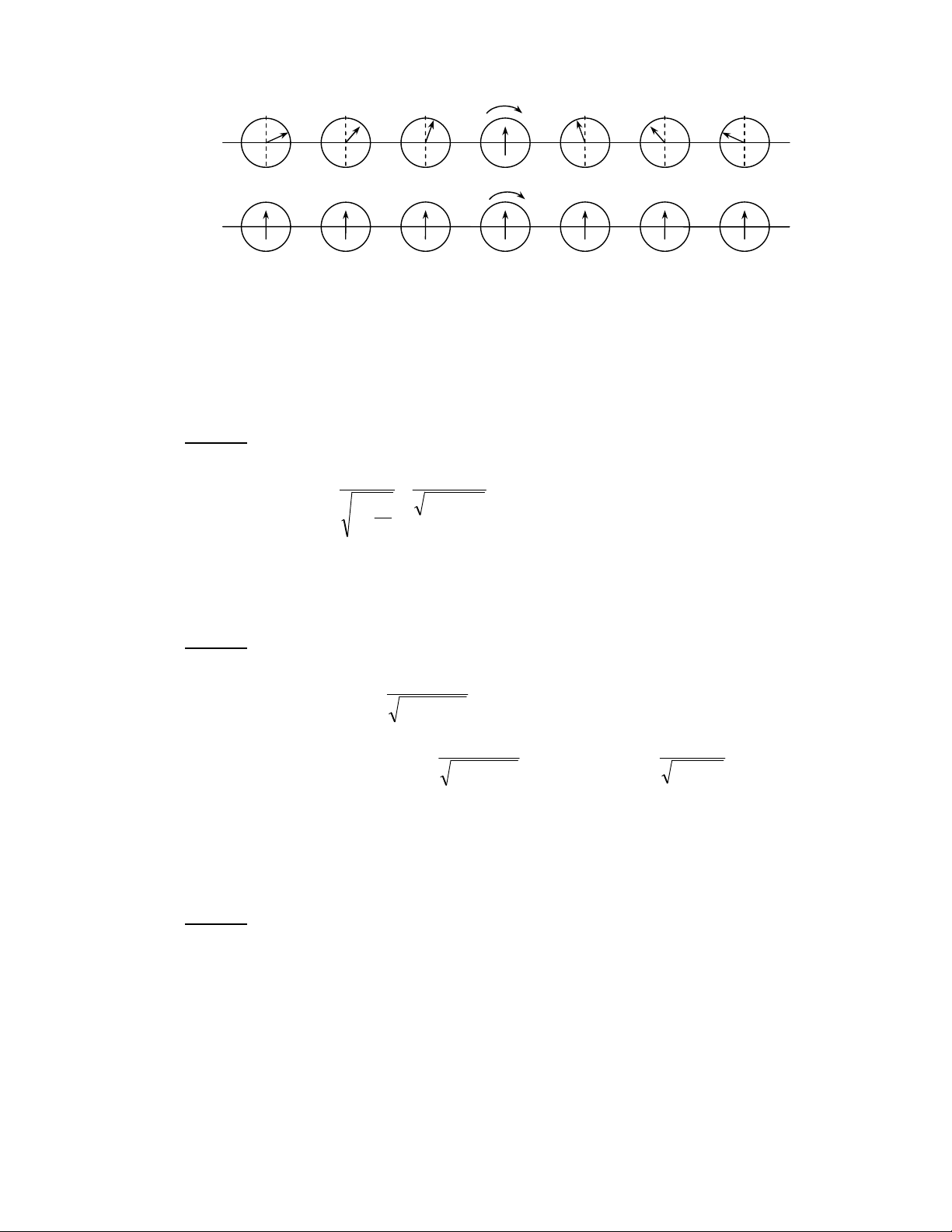
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 $ Ra F ~ ) ) F "Ra F ~ ) ) F Ad %[ 2 4 $5 ($ A V F ) 4 ) * d AL / 6; gg - N 8 hD ( P > O AB 3 7 2π ω = A2 1 : /• - = t N 3 T AL 12 V "!$ !b , π $ HB 3 7 M ) ) 2. ω = = 7 2
, 6.10−5 (rad / s) 24.3600 6$ o /• ) / - N 12 8 n + ) < Ad 12 % < 4 AB 3 7 / + A2 /
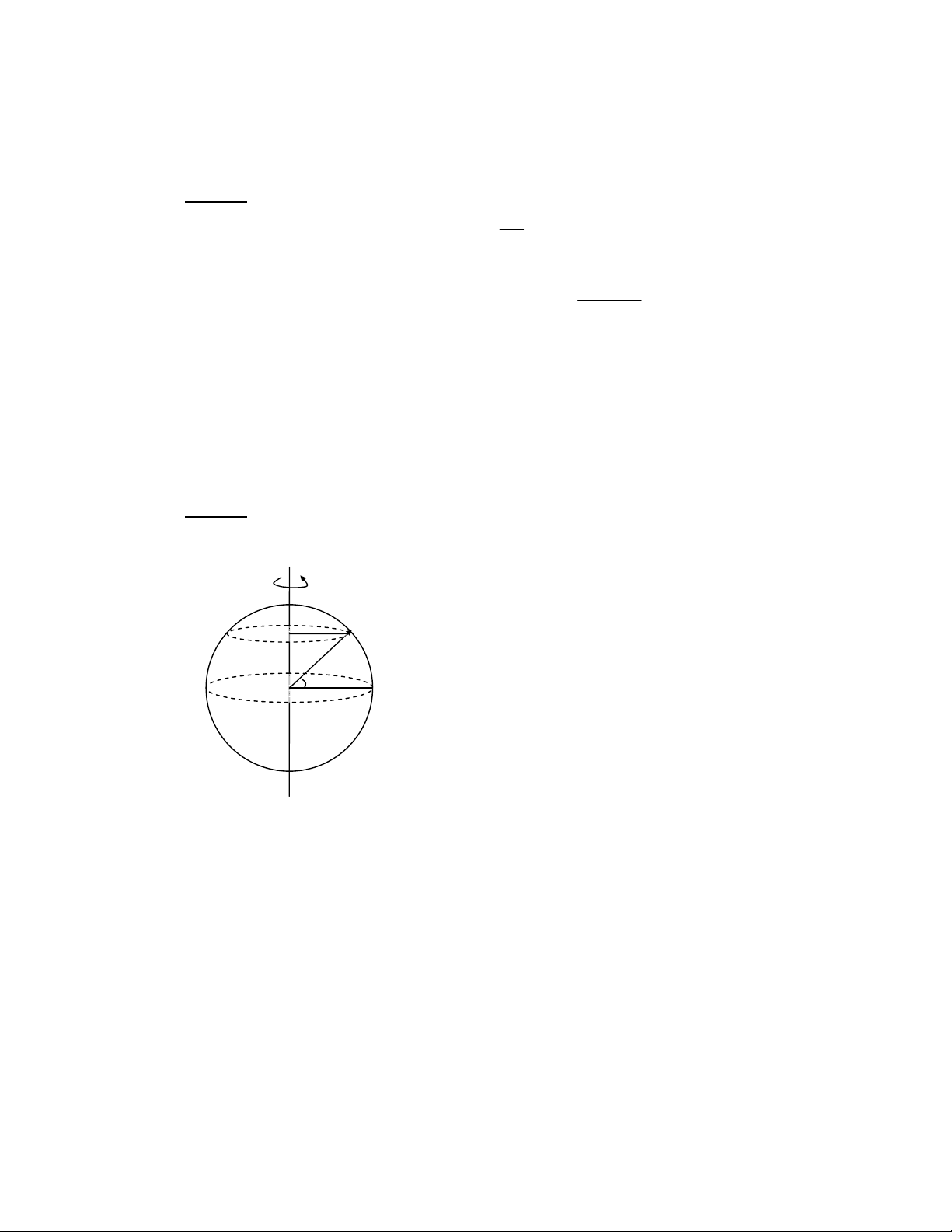
- N 12 T0X 8 ^.X (_!5 0[T 8 ^.S (_! $ ol - ( P > 4 AL /• / 7 AB 3 7 a ~ ) 12 %0[ 8 ^.Y (_! 5 ($ o A 7 / ) 12 gg- N 12 0 u 8 ^.S (_! AB 3 (2 ) 4 a f2 U 8 Z < ; Ax f2 U 12 α % ^8 F c 62 . g AB 3 7 M ) 7 12 ω [0%Y8 ^.X (_!8 Z /O ) * f2 U " c $ 12 ω w z α f 62 . u r = R cosα 8 FG 7 7 AB 3 (2 f2 U 12 A ω8 ω8w8 !α F !3 A2 , A TS^ _!8 Y 0< %0+ + 8 " B a 7 - ! ' A !' ! b < H" G c +L /9+ 7 - ! ' A O %+ 6+ G /9+ DM - !' ϕ !' . 5 D$ / L ω !' / L H0+ /$ +! L β !' +! L 5 ! B d e ! & DL %& % K f 3
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 R AP 1~ ! / 6e I ) , - N , AB 3 [^^ Ad _- N 8 FO 3 7 AP 1~ A2 !3 Ad 2 AP 1~ C ) , - N < AP 1~ 12 (I 8 HB 3 7 AP 1~ ω [^^Ad _- N [^^8%π_Y^ " (_!$ ! + τ - N Y^!8 ω π π R2 1400 / 60 1400 ω β8 τ β = = = = 1 2 , 2( 2 rad / s )8 τ 60 3600 s7 ) , ! + τ - N 12 1 2 1 ϕ = β τ . = .1 2 , 2 6 . 02 = 700π (rad) 2 2 E AB 0 !3 Ad ) , - N 12 ϕ 70 π 0 = = = ]RZ /f 8 *π π 2 R 6 c ) B (I 0 ! - N AB 3 7 = G S^^ Ad _- N 3 g^ Ad _- N 8 F 3 6 c A2 !3 Ad 2 6 c C ) , - N 8 F c ' x A 3 7 7 1 P 3 7 2 ω − ω 180 2
. π / 60 − 300.2π / 60 0 β = = = −0 2 , 1 ( 2 rad / s )8 τ 60 s7 ) , (M A2 3 ) M AL ) A. .! J 6 < t N 2 2 ω − ω . π / − . π / 0 (180 2 60)2 (300 2 60)2 ϕ = = = 240 1/f # 8 2β − 2.0 2 , 1 f a (M A2 P > AB 3 7 6 ω + ω 180 + 300 0 ϕ = .τ = .1 = 240 1/f # 2 2 R 6 c 7 6 /O w ^ 1N I > 4 0 ! 7 ) ) 7 AL 3 7 6; S0 T (_!%8 fQ 0 ! V > $ HB 3 7 A2 AB 3 (2 4 A2 6 ` 6$ s 3 - - < 0 3 <- < A2 3 2 - I 4 A2 6 ` $ s7 @ 3 2 - I A2 6 /O 6 c "> AL q 4 A2 6 ` $ h V > 0 AB 3 7 A2 AB 3 (2 4 A2 6 12 ω = β t. = 31 , 4.1 = 31 , 4 (rad / s) v = ω R . = 31 , 4 0 . 1 , = 0 3 , 14 (m / s) s 3 <- < 7 ' / P t A2 3 - - < α 1N 2 f
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 a = β R . = 31 , 4.0 1 , = 0 3 , 14 ( 2 m / s t ) 2 2 a = ω R . = 31 , 4 .0 1 , = 0 9 , 86 m / s n ( 2 ) od 3 2 - I 6; 2 2 a = a + a = 1 0 , 3 m / s 8 t n ( 2 ) $ s7 @ 3 2 - I A2 6 /O 12 α = C a 0 3 , 14 t sinα = = α [^TYj8 a 1 0 , 3 o / ) 6 c 6 /O X^ 12 ^0 V 8 F $ HB 3 (2 A2 AB 3 7 A2 6 5 6$ s 3 - - < @ 6 /O 8 HB 3 (2 A2 AB 3 7 4 A2 6 +G H0+ ! 4 5 f 2 R π 2π 0 . 5 , v = = = = 31 4 , (m / s) 5+ +! ' 4A f T 0 1 , v 31 4 , ω = = = 62 8 , (rad / s) R 0 5 , 6$ s 3 - - < { 3 L V @ 6 /O 2 2 2 a = ω r = ω R . / 2 = 62 8 , .0 5
, / 2 = 986 m / s 8 n ( 2 ) R 2 2 6e I A2 + d 0 6 /O / 0 (2 Y^^ 0 AL AB 3 XT / _ +8 2 2 < ) C + 7 S^ V 8 F AB 3 (2 0 3 - - < 0 3 <- < 0 3 2 - I A2 3 7 2 2 K 3 ) C + 78 o 2 2 12 (I 8 o w / ^^^ 0 A^ XT/ _ X _!0 ! Y^^ 0 S^!8 hD ( P > A J A2 d 6 < t !b O , 1 , I < 8 1 2 s − v t 2 600 −15 3 . 0 1 2 ( 0 ) ( ) s = v t + a t a = = = m / s 8 0 t t ( 2 ) 2 2 2 t 30 3 HB 3 I 3 + Ad 1
v = v + a t = 15 + .30 = 25 / = / 8 0 t (m s) 90 (km h) 3 s 3 - - < { 3 L V I 2 2 v 25 2 a = ω R = = = 0 6 , 25 m / s n ( 2 ) R 1000 od 3 2 - I 12 2 2 2 2 1 5 a = a + a = + = 0 7 , 08 m / s t n ( 2 ) 3 8 s 3 7 2 I
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 a 1 / 3 t −4 β = = ≈ 3 3 , 1 . 0 ( 2 rad / s ) R 1000 HB 3 41c 4 D P 6; A %0%8 ^g _!8 FO AB 3 7 A2 3 - - < 41c < c ) * 7 12 Ad d 6 /O ^0X8 ^.g 8 €1c A %0%8 ^g _! %0%8 ^Y _!5 w ^0X8 ^.g ^0X8 ^. ^ 8 HB 3 7 A2 3 L V { 3 - - < 1I 1 , ω A_w T0T 8 ^ Y (_!5 ω%w u0Yg 8 ^%% _!% R + 3 • ) !P 7 (d L = 8 U< + • c L G A' O ] ! A' O Z "]Z ⊥ AL (d !P 0 .T$ ! + ^ - N !b L A' O o Z / = ! %^ 8 U< + • A - O , (d ! + % %0X - N !b L N A' O Z8 o AB 3 3 AL (d L 12 / P t 8 FO $ Z 1 !P 5 6$ HB 3 A 3 AL (d L 5 Z o $ HB 3 (d L 3 AL 6+ !P 5 ! ($ s7 γ8 R A H γ FG ] < o < + ] ^ - N 0 ] < Z < + f .T % %0X - N 0 Zo 7 (2 ! Zo %^ 8 V 12 62 t ,- AB 3 8 F W Z o → + q AL (d L AL AB 3 u A2 1 → ! AL (d L "( + • $ AL AB 3 v 8 H A γ o t ,- O 12 3 AL → → → 6+ !P AL AB 3 ] V = v+ u 8 F + ,- > 62 > AL .T 0 + f .T6 ,- > > AL .T68 F c Ab0 7 - ! ! 8 5 1 A8 5 1 "A8 ! γ$8 %5 A8! γ 5 s 120 u = = = 0 2 , (m / s)8 t 600 1 t 10 4
l = v.t = v.cos γ .t → cos 1 γ = = = → γ = 3605 ' 3 1 2 t 12,5 5 2 3 u u 0 2 , 1 sinγ = = → v = = = = 0 3 , 3 (m / s)8 5 v sinγ 3 / 5 3 o (d !P l = v t . = 0 3
, 3.(10.60 ) = 200 m 8 1
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 U + • ) !P c L A P 7 AL 6+ !P AL AB 3 [0%/ _ 8 U L = C A - O P (d / = X^ 8 F $ HB 3 (d L 3 AL 6+ !P 5 6$ F + I ) , !P 8 o 6 < !P 6; ^0X/ 8 Z (d !P 1 ^0X/ X^^ 8 ! X^ 0 H [0%/ _ % _!8 FG Ab Z o u s s 150 ! = → u = v . = .2 = 0 6 , 0 (m / s) 8 v l l 500 A 1 F + < ! !P H AC AB l 500 t = = = = = 250 (s)8 ] V v v 2 - !3 $ ^0Y^ _! 5 6$ %X^!8 f 62 .%[ R 6 6 G A' O ] L A' O Z8 ]Z ; c L FV P A2 / = S^^/ 8 & ' + 6 < $ n P 7 75 6$ o7 7 t c L U Ze 5 $ o7 7 t c L FV P 8 o 6 < AB 3 7 6; A %^ _!0 AB 3 6 3 AL / P / O A% Y^^/ _ 8
]Z S^^/ 0 7 A %^ _! [%/ _ 0 A% Y^^/ _ 8 $ F + 6 6 M <- G ] < Z l 300 t = = = 0 5 , (h) = 30 1 B # 8 v 600 2 6$ F M 62 .%Y0 6 3 L A' O Z0 7 - = 6 < A - O 7 α ! AL - ]Z8 F 7 V = v 2 − v 2 = 6002 − 722 = 596 / 8 2 1 (km h) ] Z F + 6 6 G ] < Z 12 α A s 300 t = = = 0 5 , 03 (h) = 30 2 , B 8 A% V 596 $ s 7 P G FV ! P 8 F + 6 f 62 .%g I (q 12 s 300 t = = = 0 4 , 46 (h) = 26 8 , B 8 v + v 600 + 72 2 1 f .X P = 6 8 $ o 6 < O 78 6$ x @ W ' A2 8 $ h ! AB 3 6 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 A % S z f .X A % S z f .Xj $ U A2 W ' = 6 2 12 (I 8 6$ s W ' AL + 6 < + - 8 $ Z 0 12 A q L 8 HB 3 y AB G 1N B / 8 W ' AB 3 2 (3 3 AB 2 1L " 3 6 < !3 7 + J $8 FG W '0 7 ! ! 3 AB S ‚ ‚ %8 f .Y W ' AB 3 8 fC 6 < 4 y z]0 ]Z0 Zo0 oE8 A ] Z o E z f .Y z] AB - + ^ W (I AL 3 / 1L 8 W ' ]Z 6 < AB ! 8 W ' Zo 6 AB B (I 8 W ' oE AB <- B (I AL 3 1L / Zo8 HB (G 1 3 2 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 %. 8 R c 7 / 3 1 , %^^^^/ 0 B (I ( L ( 1M 6; Y^^^U0 AB 3 6 I c 6; X _!8 fQ $ s 3 c5 6$ h 6 1V c (G 1 5 $ + c C , / G 1N C < / c (G J 8 $ s 3 c , O c ' 1 B ii Ucƒ „_ .Y^^^_%^^^^ . ^0S _!%8 6$ F + / G 1N C < / (G 1 ∆/ Z ) (R = ∆t = = = RZ (D)3 ! ) Z$] $ v C + / G 1N C < / (G 1 ! A^8 # 8 %_% 8 8 8 S[X 8 %.%8 R y a TuU 6' /…- @ a - J J f %.T > " %.T$8 9M r- J 7 4 y a 12 T[U8 fQ 1M Q I V a y` f !3 ! @ y A2 a r- / ^0%8 9M V ^[0gU 5 1M u0gU „U „f „ „ ! !% f %.T f %.T6 n 3 y 3 I 1M „f L 3 ( L 0 1M ! 4 a y L 14 4 "f %.T $0 d / 3 V y 14 4 1M ! 1 L 3 ( L "f %.T6$8 FG Ab 2 0 1M (q "„f $ A2 V „U y - = 7 ' Q „f F + F − P = 2 × k N . − P = 2 0 . 2 , 1 . 47 − 49 = 9, m 1 s ms2 ( 8 N) „U F + F + P = 2 × k N . + P = 2.0 2 , 1 . 47 + 49 = 107, m 1 s ms2 ( 8 N) %.S8 fQ - = ( 1M 6; 6 4 14 2 > 4 7 (I A2 ! + S^ V 7 , 8 o 6 < 1M ! 2 6; X† m 1 , 2 8 sm „ 12 1M ( 14 2 8 &r c - 0 1M V 3 2 0 c ' 1 B U %0 6; „ . ‡ ! F 7 12 / 3 1 , A2 s 2 a = 12 3 I 8 2 t
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 FG 7 ! 2 s . m . F = f + ma = 5%mg + 8 ms 2 t F !3 ! 0 S^!0 X0Y XY^^/ , „ ≈ g%^^U8 1C " G %0+ + L+ ! ! " %& < = (R$J \ #3 %.T8 R + ( < c AL AB 3 / P t 8 9N I + /r c A - O L 0 ! 7 + } c A - O ! 8 F = + ,-0 2 c ,- AL a - J ; 7 α8 fQ + ,- 2 + - = a 14 c 1M 1L ` Z < ; m 1 , c 12 0 !3 ! @ 6 c A2 a + 12 /8 H < - ' 1 B ii Ucƒ 1M ( A2 c8 F 2 - I 1M t ,- < c - J > A2 ; 6; ^ . / P 7 c - J > 0 c - ./ P 7 3 c - 4 F + ,- /r c A - O L " %. j $ 1M r A P 7 c 14 a + 12 N + F.sin − P = 0 N = P - F.sin H2 F.cosα − F = 0 F.cosα = F ms ms R20 1M ! ( 14 c „ ! /U /" . „! α$ kP
Fcosα = k(P − F sinα )
F = cosα + k sinα U Uj „ α „j „ ! „j ! f %. j f %. j6 F + ,- } c A - O ! " %. j6$ Z; - V O M0 O , 1M ! a 14 c + ,- 2 12 „ ! /Uj /" # „! α$ H2 1M „j I a 14 2 c kP '
F = cosα − k sinα wk 2 „j ‚ „8 U AB + ,- } c A - O ! + - = (q 1M 1L 8 %.X8 R AB 7 / 3 1 , X/ , a 4 a - J 4 ,- AL a - J ; 7 α S^^8 f !3 ! @ AB A2 a - J 4 6; / ^0%8 F 3 AB 4 a - J 4 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 F - V O 1M ( A2 AB W S 1M J U > 0 U A P 7 AL a 4 A2 „ ! ; 4 a „ 4 8 ! z ' 1 B ii Ucƒ AB P + N + F α ms = m a . o < - 2 c - A P 7 AL a - J 4 "- z $ A2 - ! ! AL a - J f 62 %.X 4 "- z $ , N = P cosα − P cosα + N = 0 P sinα − F P sinα − F = ma a = ms ms m R2 „ ! /8U 4
P sinα − kP cosα
mg sinα − kmg cosα a = =
= g(sinα − k cosα )8 m m F α S^^0 / ^0%0 u0g O , S0%T _!%8 [ 7 - e ! \'$ +! L ! / e O +e 7 U A /0 L+ ! / 3 %.Y8 R AB , 3 4 a - J 4 ,- AL a - J ; 7 α TX^8 n , , ) C + ! SY0T 0 AB , AB 3 A % _!8 & ' !3 ! @ AB A2 a - J 4 8 - ( P > 3 AB 62 %.X 7 g sinα − a a
a = g(sinα − k cosα ) k = = tgα − 8 g cosα g cosα hD ( / < > i A 3 ) A. .! 7 3 AB , 2 v2 − v 2 2 2 2 − 12 v 0 v a 0 = = = 8 2 S . 2 S . 2 S . v2
k = tgα − 2.gScosα F P !3 C α TX^0 A % _!0 ! SY0T ^0SYT , / ≈ ^0%8 %.[8 R !, (V G , a 4 a 62 ! - I 7 6 P k 3 8 h, (V 6e I , 4 a 62 / (2 - I 6 P k 6; %X† (2 (V 8 & ' !3 ! / @ !, (V A2 a 62 8 ‡ ! f 62 %.[
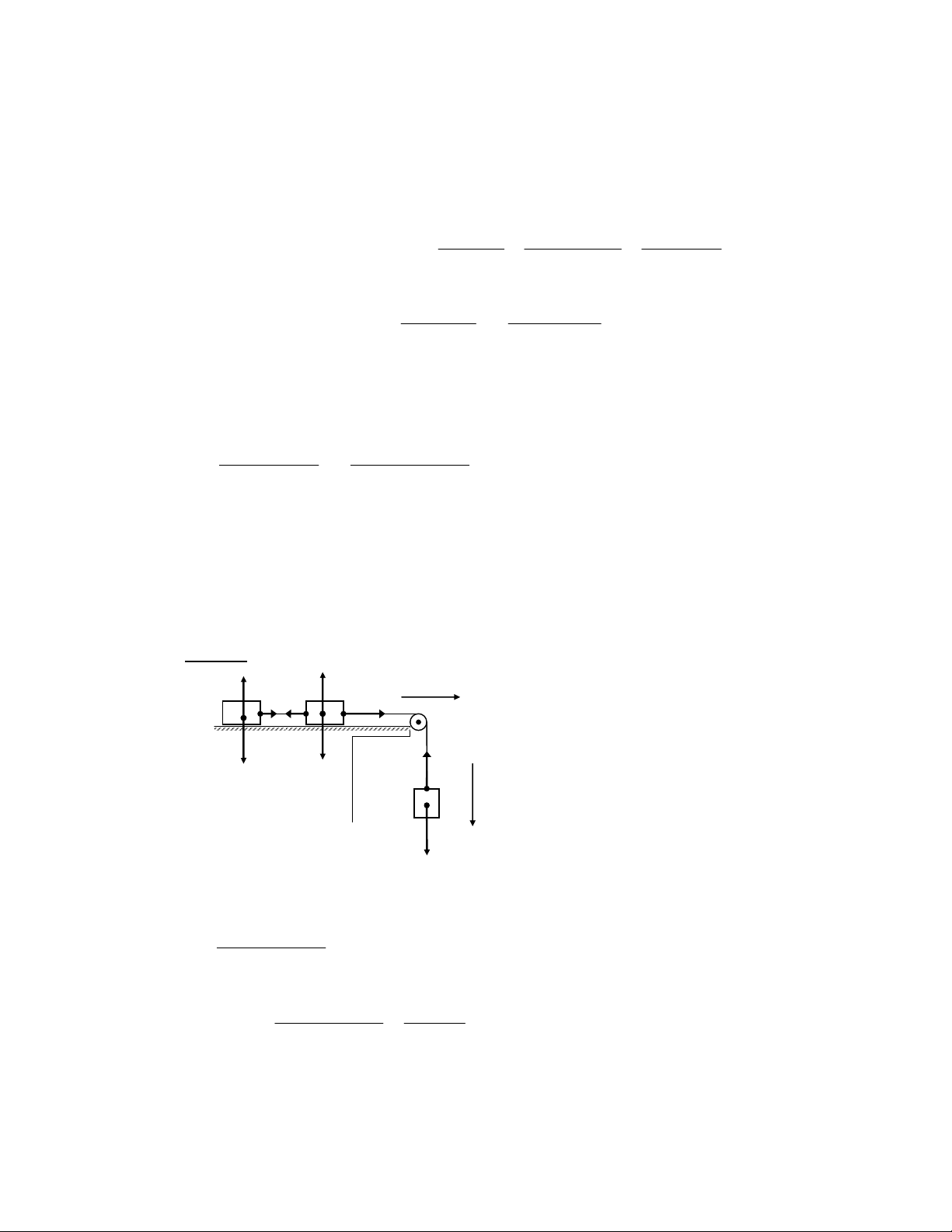
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 sm 12 m 1 , = (V 0 12 m 1 , - I 6 P k 8 F c I 62 0 (2 - I 6 P k 6; %X† (2 (V %X† 8 &r c - !, (V 0 (V ' ( 1M A2 ‡ !8 R 3 (V 6e I , - = 7 ‡ ! ‡ ! %X† 8 R20 ‡ ! / 8U /8"[X† $8 FG 7 %X† /8"[X† $ 25 1 k = = ≈ 0 3 , 3 8 75 3 %.g8 $ R P P / 3 1 , 4 + 6; 0 !3 ! @ 6 P P A2 a + 12 ^0 8 FO 1M /r P P + ,- $ ˆ P 5 6$ ˆ P (I AL 3 6; % _!%5 %$ ol V Q 4 + ,- P P A2 $ 94 (3 7 (3 T†5 6$ & 3 (3 78 f !3 ! 6; ^0 ! 3 + 8 → Ft ,- 1M ( 14 P P W 1M /r F P P0 m 1M P 0 - = 1M - - < N a + A2 1M ! a + f 8 ms U Uj „j „ ‡p ! ‡ α ! f 62 %.g → → → → → ' 1 B ii Ucƒ P P 12 F + P + N + f = m a ms o m ( 12 c8 o < - 2 14 - , $ n c 4 + ; F − f = ma F = ma + f = ma + kmg ms ms F !3 ^^^/ 5 / ^0 5 u0g _!%5 A2 $ n 0 ^ „ ug^U8 6$ n (I AL 3 % _!% „ %ug^U8 %$ n c 4 + (3 $ ˆ P 14 (3 F − f − P sinα = ma F = ma + f
+ P sinα = ma + kmg cosα + mg sinα ms ms F 70 ! α ^0^T 12 (3 (3 !α 1 − 0 0 , 42 ≈ 1 0 , F = 1000 × 0 + 0 1 , .1000.9 8 , .1 + 1000.9 8 , .0 0 , 4 = 1372(N) 6$ ˆ P 3 (3 „ "/ !α . ! α$8 F − f + P sinα = ma F = ma + f
− P sinα = ma + kmg cosα − mg sinα ms ms F !3 F = 1000 × 0 + 0,1.1000. , 9 8.1−1000.9,8. , 0 04 = 58 ( 8 N)
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 %.u8 R !, (V , Ae ) d m 7 / 3 1 , / P / 0 I 6 AB 7 / 3 1 , A2 % " ‚ %$8 & ' 3 AB A2 !> ~ (V 8 o ! / P / 8 - ( 6; !3 % % / 8 E !, (V / P C 0 d m / P / 3 1 , 0 / P ! 4 !, (V 1 P ~ AL 1M ~ (V F5 AB !b AL q 3 8 H ‚ % 4 ! 1M /r 1L % 12 3 ( L d % 6' /r 14 4 8 F F % % f 62 %.u o m ( G AB ,- AL y AB " Ab$8 ' 1 B ii Ucƒ G AB r 4 - m : P − T = m a 1 1 1 m : T − P = m a 2 2 2 o A< c A< - 4 , P − P m − m P − P = + 1 2 1 2 2 a = = g = 3 2 , 7m / s 1 2 (m m 1 2 )a m + m m + m 1 2 1 2 &c - ' 1 B ii Ucƒ AB 7 . F 8 m − m 2m m T = P − m a = m g − m 1 2 . g 1 2 = g 1 1 1 1 m + m m + m 1 2 1 2 FG 7 O , T = 6 5 , 5N %. ^8 R 2 0 ! / - 0 AL 3 / P t γ ^0X _!%8 % V ! / 6e I 0 + e 2 A2 2 B (I L / (G J 8 F 4 2 6 ) C + !3 ! 6; / ^0^ 8 F $ HB 3 1L 2 5 6$ F + 2 6 / G 1N 2 - L / 2 (G J 5 $ s 3 2 B (I 5 ($ v C + 2 6 2 2 C , 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 FI c s AL 3 ^0X _!% + %!8 s % B (I AL 3 % /8 ^0^ 8u0g ^0^ug _!% ( L ( = 1M ! + ∆ 8 A A % o7 Ab W ' AB 3 I c + 4 8 $ HB 3 1L I v = a t = 0 5 , 1 . 2 = / = , / max 1 1 ( 6 m s) 21 6(km h) 6$ FI B (I + v 6 t max ∆ = = = 61 2 , (s) a 0 0 , 98 2 Ft + I "/ G 1N - < 1N (G 1 $ t = t + t ∆ = 12 + 61 2 , = 73 2 , 8 2 1 (s) $ s 3 I / B (I 12 % ^0^ug _!%8 ($ v C + I C , 6; ‰( O Š , r 1 1 s = v t . = 6 . .73 2 , = 219, max 2 ( 6 m) 2 2 %. 8 R 6= y ] , a 4 a - J ; 8 Z= ] , 3 AL 6= y Z / 6; !, (V Ae ) d m 3 ' " Ab %.X$8 n 3 1 , d m A2 (V / P / 8 $ FO 1M ~ (V < ] %^^ 5 Z S^^ 0 !3 ! @ 6= ] A2 a - J ; / ^0%X8 6$ U< t A' O ] A2 Z 1M ~ (V !b 6; 6 4 ` &c !3 ! A‹ l8 U% F ‡ ! % F f %.X &r AB 7 / 3 1 , 0 % , 3 AL 4 %.X8 o 1M ( A2 AB C , \ k 4 Ab8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 o7 A < - ' 1 B ii Ucƒ AB 2 r 4 - N " , \ 6; l 4 7 ( ‰#Š 64 $ m : P − T = m a (1) 1 1 1 m : T − f = m a ( 2 ) 2 ms 2 F 70 f = k N . = k P . 8 ms 2 2 o A< c A< - " $ A2 "%$ 4 , P − f m g − k m . g m − k m . P − f = + a 1 ms 1 2 1 2 = = = g 1 ms (m m 1 2 )a m + m m + m m + m 1 2 1 2 1 2 FG - " $ ! m − km + 1 2 (1 k)m m
T = P − m a = m g − m . g 1 2 = g 1 1 1 1 m + m m + m 1 2 1 2 %+ - ? /G M g HQ' e \'$ 6+ /!+ f ! <( /0 <* ! M g HQ' 7 6+3 h '$ M g HQ' 7 U A /0 /+N b <( e 8 %e H 9+ !' 0 +3 F $ ? Q !# /0 Q %# ? /G M g HQ' G ! %& (1+ k)m m + , , . , A B (1 0 25)0 2 0 3 T = g = × 9 8 , = 1 4 , 7(N) m + m 0 2 , + 0 3 , A B "F !3 / ^0%X5 ] %^^ ^0% / 5 Z S^^ ^0S / $ %. %8 f AB 7 / 3 1 , / 0 % %/ , 3 AL 6; !, (V A2 , a 4 a 62 ; 8 Eq !, (V / Ae ) d m 0 I (V 6 A2 % A2 I / 6 A2 AB > 6 7 / 3 1 , S S/ " %. Y$8 o ! / P / 8 FO 1M ~ !, (V 8 U U % F F% F % % S S f %.Y F m 1M S 12 2 - I 1M ( c - A2 12 AB AL q 3 8 F 7 m g 3 a = m + m + m 1 2 3 &r 4 AB 7 m m g 1.3 9 . 8 , T = m a 1 3 = = = 4, 1 1 ( 9 N) m + m + m 1 + 2 + 3 1 2 3 &r 4 AB S 7 m g − T = m a T = m − 3 2 3 2 3 (g a)
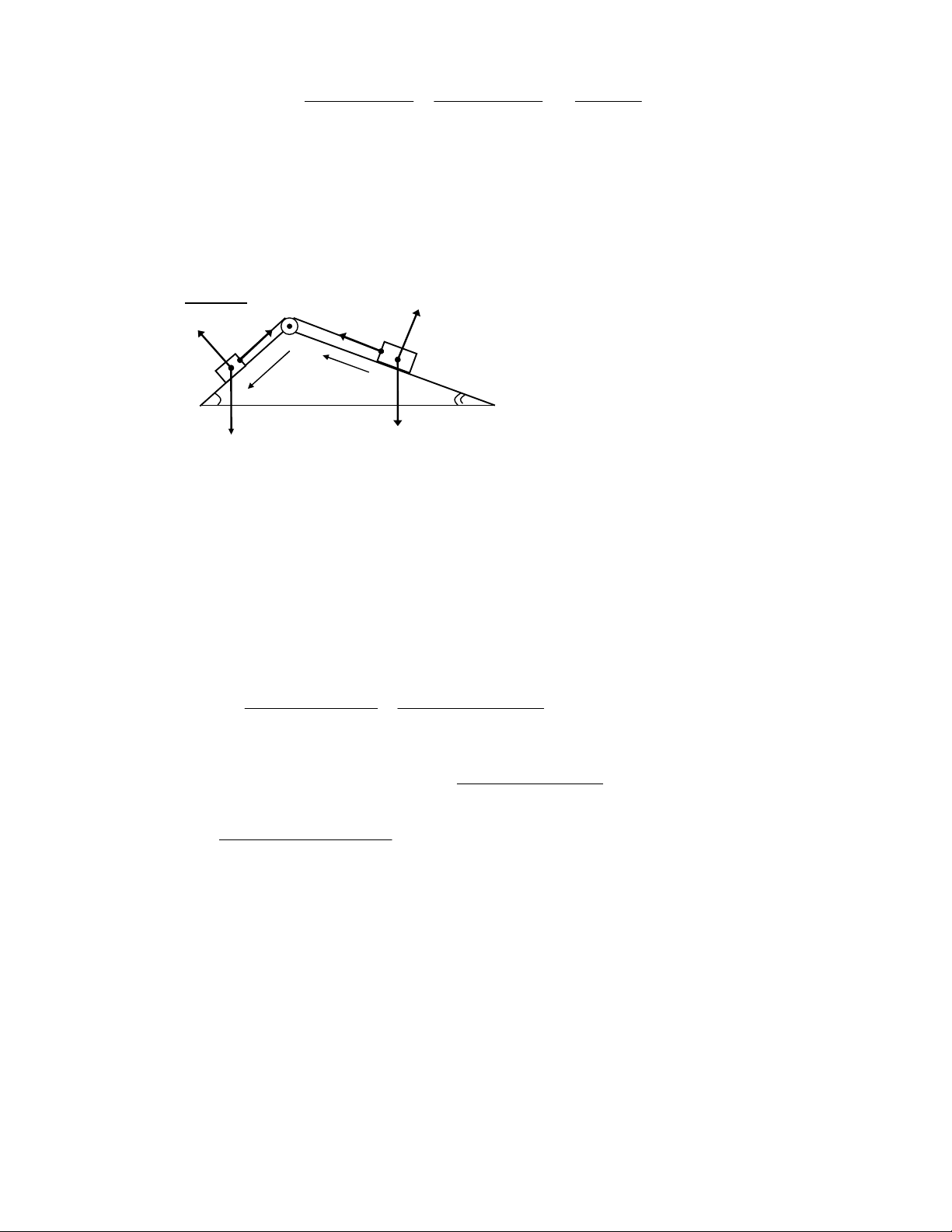
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 m g ( m + m m ) (1 + 2 ) 3 . T = m g 3 1 2 3 − = g = 9 . 8 , = 14 7 , 8 2 3 (N) m + m + m m + m + m 1 + 2 + 3 1 2 3 1 2 3 %. S8 \ a - J 4 ,- AL a - J ; 7 α S^^ A2 β TX^ " %.[$0 7 e d m / 3 1 , / P / 8 Eq !, (V Ae ) d m 0 I (V 3 AL AB ] A2 Z a 4 a - J 4 8 n 3 1 , AB ] A2 Z 6; / 8 ZQ ) = 1M ! 8 F 3 A2 1M ~ (V 8 U U F F % β α % f %.[ F 62 2 0 1 r AB c - a 4 8 E !, (V 3 AB / P 6' C 4 AB !b AL q 3 8 o m ( Ab " %.$8 o 1M ( A2 AB C , \ 4 8 ' 1 B ii Ucƒ , < 14 - AB m : P sinα − T = m a 1 1 1 ( ) 1 m : T − P sin β = m a 2 2 2 (2) o A< c A< - 4 ,
P sinα − P sin β = + 1 2 (m m 1 2 )a
P sinα − P sin β
m sinα − m sin β a 1 2 1 2 = = g m + m m + m 1 2 1 2 FG - " $ !
m sinα − m sin β 1 2
T = P sinα − m a = m g sinα − m . g 1 1 1 1 m + m 1 2 m m . g
. (sin β + sinα ) 1 2 = m + m 1 2 F ' I 62 C " 6; ]0 % 6; Z$ A2 6 > 3 A2 1M ~ (V , 2 a = 1 − 0
, 2m / s 5 T = 5 9 , N 8 n< ) = 2 > Q ; 0 , AL ( C m AL 3 7 1L 6; 0^% _!%8 i a %0+ e $ ! ! !' & / ; DW L f / > %, e 3 F $ %0+ 0' ! T +G H ' A 8 +G + D /9+ +G . T 5+ +?+ e 3 C ' +e $ 7+ < L + - 6 N / / '$ ! c % \' E a + b ? +! L 7 S +G H . T 3 Q L+ S 5+ +?+ e d HU 5 N 7 <! D 3 @ + N 7 <! D $ M HU /0 7 U A
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 /0 +G ' A ! / c /+N T +G H ! U A3 @ + N <! D $ k 0 +G ! M <! D U A /0 +G ' A ! / $ H 7 +? DE l a +G ' A ! / 3 C 5 ! . +? + "< +G ' A Hm ? +! L ! / %, Q< % A ?+ +? + + +G ' A /0 +?+ + %0+ 3 C\ +e 7 !+ H + <0 +? + B /0 5 "< 0' ?+ + 5+ +?+ !+ " 3 C! +G 0' %& 1D! + . 0< +G %0+ /0 B B +G + +N< ) M ! DM 0' /m ?+ HM! e DM n< ! D D , K 0 " M /!+ f M /0 M ? # b %& + < ! 9 1 K /0 D D 0 " M /!+ f M $ M +o /0 M ? # b +? + /0 +?+ %0+ 9 P 0+ 3 %. T8 R 2 2 W I 0 ^ 0 A2 X 0 3 AL c > M 4 6; @ 1d 3 8 Z < ; / ' ( 1M 6; X^^U 1d C 8 ZQ ) ! 8 FO C 1d + ,- $ 2 2 6e I 6 0 1M /r I / P t A2 ! ^ V AB 3 2 2 L _!5 6$ 2 2 14 (3 7 4 X† AL AB 3 / P t 8 C 1d V c ' 1 B fN „ / 8 FG 7 ' , !3 2 W F 500N k = = 5.104 = N / m. F F x c 1 m % % F F „ $ 9M ~ 1d > 7 A d 1M /r = I 8 FG ' 1 B ii Ucƒ 7 F v " # %$ 0 AL a = 8 h t C 1d > f 62 %. T T ( m + m )v + . . 1 1 2 (10 5) 103 1 x = = = = 3.10−2 m = c 3 m 1 k k t . 5 1 . 04 1 . 0 9M ~ 1d > F% % C 1d > T m v 5 1 . 03.1 x 2 2 = = = = 1 1 . 0−2 m = c 1 m 1 k k t . 5 1 . 04 1 . 0 6$ n 2 I 14 (3 8 o 1M 1d - = V 6; AL 2 - I m 1M /r 3 8 o T = + 1 (m m 1 2 )g.sinα T = m g.sinα 2 2 F 70 (3 7 4 12 X†0 > 12 ! α ^0^X8 C 1d T + sinα + . . , . , 1 (m m 1 2 )g (10 5) 103 9 8 0 05 x = = = = 0 1 , 47m = 14 7 , cm 1 k k 5.104 T m g sinα 5 1 . 03 9 . 8 , 0 . 0 , 5 x 2 2 = = = = 0 0 , 49m = 4 9 , cm 2 k k 5.104
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 %. X8 R AB 7 / 3 1 , %^^ 0 , c K I !, (V (2 T^ 5 AB ) a - J ; AL AB 3 / P t ! !, (V A a 7 8 s = !D / 7 (V AL - J > 7 α SY^8 F AB 3 7 AB A2 1M ~ (V 8 α 1 F f 62 %. X HB A Ad d 7 6 /O w 18! α8 → → 9M ( 14 AB W m 1M P A2 1M ~ T " Ab$8 Ft ,- 1M 2 12 2 1M L V V d AB → → → F = P + T " $ ht FG %. P mg 0 2 , 9 . 8 , T = = = = 2 4 , 5N cosα cosα cos 360 „ 8 α 8 8 α8 R2 „ 8wω% 818! α8ω%8 2 F = mg t
. gα = ml sinα ω . 8 ht E 7 g ω = = , 5 6rad / s l cos α %. Y8 & ' 3 AB %.g8 ZQ ) ! 0 / 3 1 , d m A2 (V 8 - ( + ,- %8 F F F % % f %.g
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 o N : ; !> ~ (V m 6; 0 6; F8 FG Ab %.g0 < r 4 AB 0 7 . F " $ U< r 4 AB %0 7 %F . % % %8 "%$ hD ( O d m 3 ' A2 d m ; 0 ) C + - 1I ) C + AB %0 G 7 /r c % % "S$ U V A< " $ AL % W A< c A< AL "%$ ! 2( 2m − m g ) 1 2 a = 2a = 8 1 2 4m + m 1 2 U< 2g a = 2a = = 3 9 , 2 m / s 8 1 ( 2 2 ) % 5 !' + , ! !( /0 1(# ! < M g ! HQ' 2( 2m − m g ) m 3 m g 1 2 1 2 T = P − m a = m g − m = 1 1 1 1 1 4m + m 4m + m 1 2 1 2 %. [8 v d m ] / 3 1 , / P / 0 + 1 W !, (V 0 I 6 A2 ) = a R 0 I / 6 A2 d m Z / 3 1 , / P / 8 v Z 1 Ae !, (V / 8 f I (V 3 AL ) = a R% A2 RS8 wd m ] AL 2 6 m AB , c A2 1M /< 1d " %.u$8 & ' 3 ) = a RS A2 !3
\ F 4 1M /<0 < R% ≠ RS0 R ‚ R% # RS8 F F F R F% R F S % S R% % f %.u o m ( AB %.u8 FG 3 ) A + d A2 3 ' 3 ) 3 AB 2a = a + a "Œ$ 1 2 3 E d m 7 / 3 1 , A2 1M ! K t 7 6Q ) 4 7 T = 2T ; T = 2T 1 1 2 ( ) 1 &r c - AB 0 - ' 1 B ii Ucƒ M a = M g − T 1 1 1 1 (2)
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 M a = T − M g 2 2 2 2 (3) M a = T − M g 3 3 2 3 (4) F M - r- 6 < t (M − 2M g − M a 1 2 )
(2)+ 2 (.3) → M a + 2M a = M − 2M g → a = 1 1 2 2 ( 1 2 ) 1 1 2 2M 2 (M − 2M g − M a 1 3 )
(2)+ 2 (.4) → M a + 2M a = M − M g → a = 1 1 3 3 ( 1 3 ) 1 1 3 2M3 F %0 S A2 "Œ$ (M − 2M g − M a M − 2M g − M a 1 2 ) 1 1 ( 1 3 ) 1 1 2a = + 1 2M 2M 2 3 U V = A< - AL %8R%RS
4M M a = M M g − 2M M g − M M a + M M g − 2M M g − M M a 2 3 1 1 3 2 3 1 3 1 1 2 2 3 1 2 1 (M M + M M + 4M M = + − 1 2 1 3 2 3 )a 1 (M M M M 4M M 1 2 2 3 2 3 )g (M M + M M − 4M M g 1 2 1 3 2 3 ) a = 1 M M + M M + 4M M 1 2 1 3 2 3 hD ( /< ) = 2 A2 6 > S , (M M + M M − 4M M 1 2 1 3 2 3 ) (M − 2M − 1 3 ) g g M1 M M + M M + 4M M a 1 2 1 3 2 3 = 3 2M3 (M − 2M + + − + − 1 3 )(M M M M 4M M 1 2 1 3 2 3 )g M1(M M M M 4M M 1 2 1 3 2 3 )g = 2M + + 3 (M M M M 4M M 1 2 1 3 2 3 ) M 3 M − M M − 4M M 1 2 1 3 2 3 = g . M M + M M + 4M M 1 2 1 3 2 3 FG "%$ 8M M M g 1 2 3 T = M g − M a = 1 1 1 1 M M + M M + 4M M 1 2 1 3 2 3 h !3 \ 1M /< 16M M M g 1 2 3 T = 2T = 1 M M + M M + 4M M 1 2 1 3 2 3 %. g8 R < c / 3 1 , %^/ 7 / P ! 4 a - J ; 8 F 4 c 7 a d / 3 1 , %/ " %. ^$0 !3 ! @ d A2 c 12 ^0%X8 9I > + ( 14 d 1M 6; %U0 1I > % . 6; %^U8 9M 7 - ; A2 L (m c c8 & ' $ 9M ! @ d A2 c5 6$ s 3 d A2 c + ,- 4 8 9M ! \ M @ d A2 c "‡ !$ / ^0%X8%8u0g T0uU8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 „ ‡ ! R ‡ ! f %. ^ . C 5 - \ „ %U8 E 7 „ • ‡ ! d / P , 4 c8 F + ,- 2 d A2 c ,- 2 AB ( AL q 3 8 F 7 F 2 2 a = = = 0 0 , 9m / s M + m 20 + 2 sm ‡ ! 12 1M ! @ c A2 d " %. ^$8 &r 4 c 7 MF f = M a . = = 1 8 , N ms M + m ) C 5 - !+ „j %^U F + ,- 2 „j ‚ "‡ !$ 8 fd , 4 c 1M ! @ c A2 d N 6; 1M ! 1L ‡ ! / T0uU8 sm 12 3 d 0 % 12 3 c8 U< r 4 d 0 7 „j . ‡ ! "S$ U< r 4 c 7 „ ! R % "T$ FG "S$ A2 "T$ ! ' F −f ms 2 a = = 7 5 , m / s 1 m f ms 2 a = = , 0 25m / s 2 M %. u8 U + /r / N y m 1 , AL AB 3 / P t 6; !, (V (2 18 n = G I (V L a 6; " %. $ $ F !3 ! @ / N y A2 a "(V , 6 A2 m V / N y$5 6$ U< (V 6 A2 I / N y 1L 1M ! 7 t / P ` → $ sm F 12 1M /r y0 α 7 ,- 6K (V /r A2 a 8 H / N y 4 „ !α . ‡ ! ^ " $ ] „ U 1 α ‡ ! f %.
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 2 FG " $ ! l − h f = . F ms l 9M r A P 7 14 a + h N = P − F sin α = P − F l 2 2 E 7 !3 ! f F l − h k ms = = N Pl − Fh → 6$ hM t a 1M F 12 t a - 1M U @ y A2 a !2 / P 12 t 1L 1M 2 8 E 7 1M ! A‹ @ ' l8 %.%^8 H < - A 4 6 / P / O0 < / < 1M = / P / O8 o 6 < 1M = / P / O | 1 AL AB 3 A 4 0 !3 | 1 12 /0 / 3 1 , A 4 6; 8 9M = / P / O 14 A 4 ‡ ./A0 / 12 !3 \ 1 8 F c ' 1 B U > dv − kv = m dt dv k = − dt " $ v m FO - V A< " $ , k − t m v = Ce "%$ o 12 ; !3 O - V 8 9N ^ 5 A AK G "%$ ! o A 8 k "%$ K 2 − t m v = v e "S$ o sm 12 ) C + 2 A 4 , c - 7 k − t dx m v = = v e "T$ o dt k h − mv − t x o = e m + B "X$ k Z 12 ; !3 O - V 8 FG / ^ 0 ^0 ! mv B o = k k F Z A2 "X$ , − t mv x = o 1 − m e k %.% 8 H < - AB < / < 1M = / P / O0 6 < ; 1M = | 1 AL AB 3 AB 8 9M t ,- a 14 AB „ { /A F c ' 1 B U > dv mg − kv = m 8 dt dv k k mg = g − v = − v − " $ dt m m k
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 a mg u = v − 8 " $ K 2 k du k du k = − u → = − dt "%$ dt m u m 9 O - V A< "%$ k k − t − t mg mg m m u = Ce = v − → v = + Ce "o 12 ; !3 O - V $8 k k F + ^0 A ^ mg C = − k k − t mg v = 1 − m e k v C + 2 AB , < + "- $ t t k 2 k − t − mg mg m g t x = v d . t = 1 − e m d . t = t . + e m −1 8 k k k 2 0 0 %.%%8 FO 1M } 6 3 !N 14 I K d !N 6 6 0 6 < ; I 7 / 3 1 , ^ 0 + d 12 ∆ ^0^^ V 0 AB 3 A 4 K I d 12 A gYX _!8 s 3 6 A 4 d !N v ∆ v − 0 v a = = = 8 t ∆ t ∆ t ∆ 9M } 6 3 !N 14 A 4 mv F = m a . = = 8650N t ∆ %.%S8 R c / 3 1 , %^ AL AB 3 6 I A XT/ _ 8 & ' 1M 6 ( 14 c0 < c (G 1 ! + $ - N T^ V 5 6$ ^ V 5 $ V 8 92 M 62 %.%% K V 12 1M C 8 F A‹ 7 P > m v ∆ F = m.| a = | t ∆ F !3 %^ %^8 ^S/ 5 A XT/ _ X _!5 v ∆ |
= 0 − v |= 15m / s A2 / = + > " t c A' V $ !b 7 , /< ) = 4 8 %.%T8 R A 4 / 3 1 , ^ AL AB 3 A^ %^^ _! B- A2 y A2 4 !V A2 y 18 Z < + A 4 y 6; T8 ^.T V 8 & ' 1M = 6 y 14 A 4 A2 4 1 A 4 8 s 3 6 A 4 / 4 A2 y
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 | v ∆ | | 0 − v | v | a 0 0 = | = = 8 t ∆ t − 0 t 9M = 6 y 14 A 4 mv 10 1 . 0 3 − 2 . 00 F = m.| a 0 = | = = 5000(N) t 4.10−4 4 V A 4 v 2 v 2 1 1 l 0 0 = = = v t = 2 . 00.4 1 . 0−4 = 4 1 . 0−2 = 8 0 (m) 4cm 2 | a | v0 2 2 2 t %.%X8 R - V D 7 / 3 1 , T0XY8 ^.%S AL AB 3 A Y^ _! A 2 W A2 2 6 AL 7 4 α Y^^8 FO 1 , 1M A - V D 14 2 6 8 hD ( ' 1 B ii Ucƒ ( % , 1M - V D ( 14 2 6 12 F. t ∆ = P ∆ = m. v ∆ = m(2 v . .cosα ) = 4 5 , 6.10 2 − 6.2 6
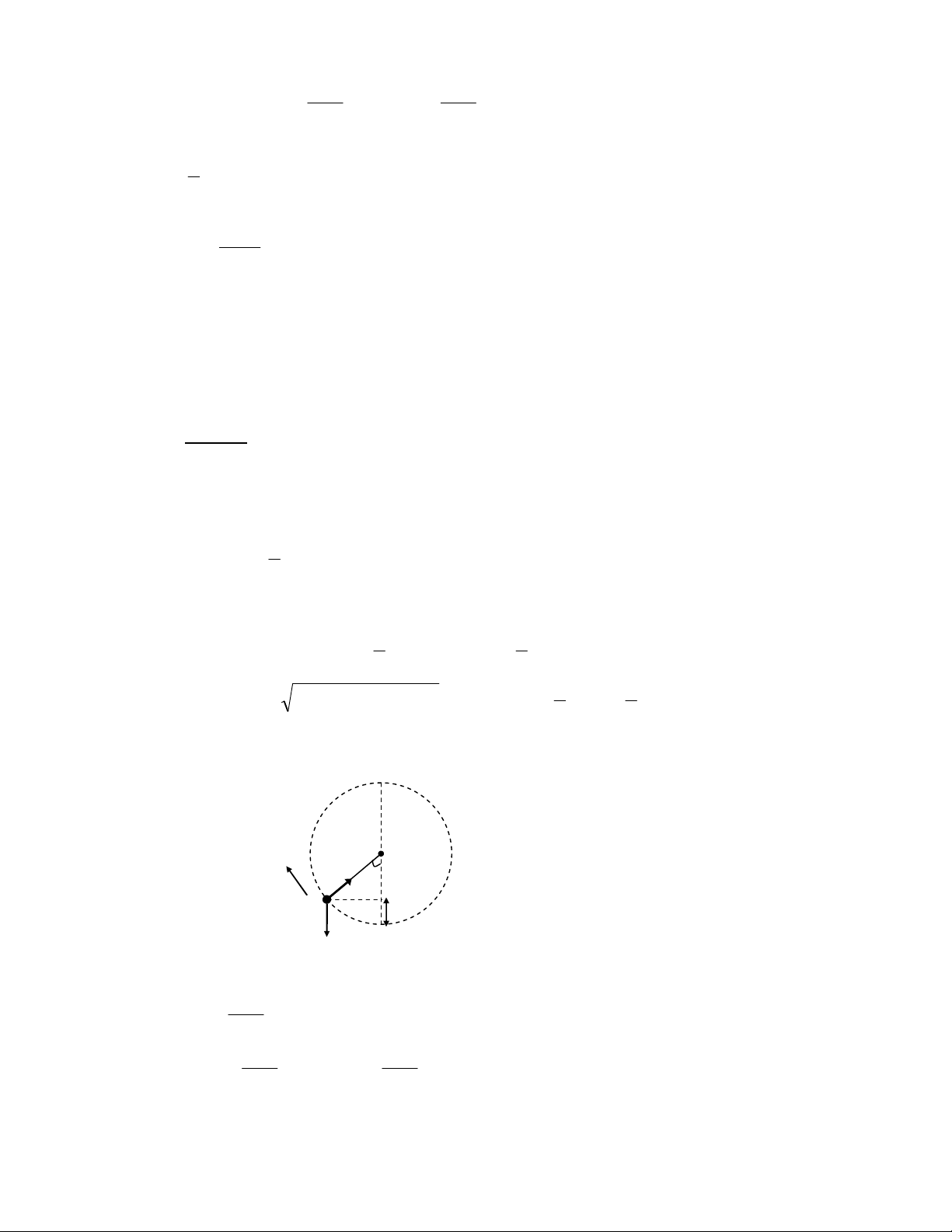
. 0.cos 600 = 2 7 , 4.10 2 − 4 (N s.) %.%Y8 R c / 3 1 , X B (I AL 3 7 1L 6; ^0Tu _!%8 Z < AB 3 6 I c 12 A^ %[/ _ 8 fQ $ 9M C ( 14 c5 6$ h 6 1V c (G 1 8 8 9M C ( 14 c F = ma = 15 1 . 03 , 0 . 49 = 735 ( 0 N) o7 , 68 F + c (G 1 12 v v = v − at = 0 → t o = o a 27 / , 3 6 t = ≈ 15 ( 3 , s) , 0 49 %.%[8 F a - J > m z AL z ; 0 z J > 8 R , r G 7 "%0 ^$ " A' r $ c - J > 14 4 AL AV 3 ^ _!8 FO 6 < 4 P c 1 , 3 AL 3 z / = + G 1N r 14 < 1N 3 N A' O 6 I 8 o / 3 1 , / 8 9N r L = L = r × p 1 1 9N AB K 1 r L = L = r × p = −r × p " p = −p $ 2 2 1 2 1
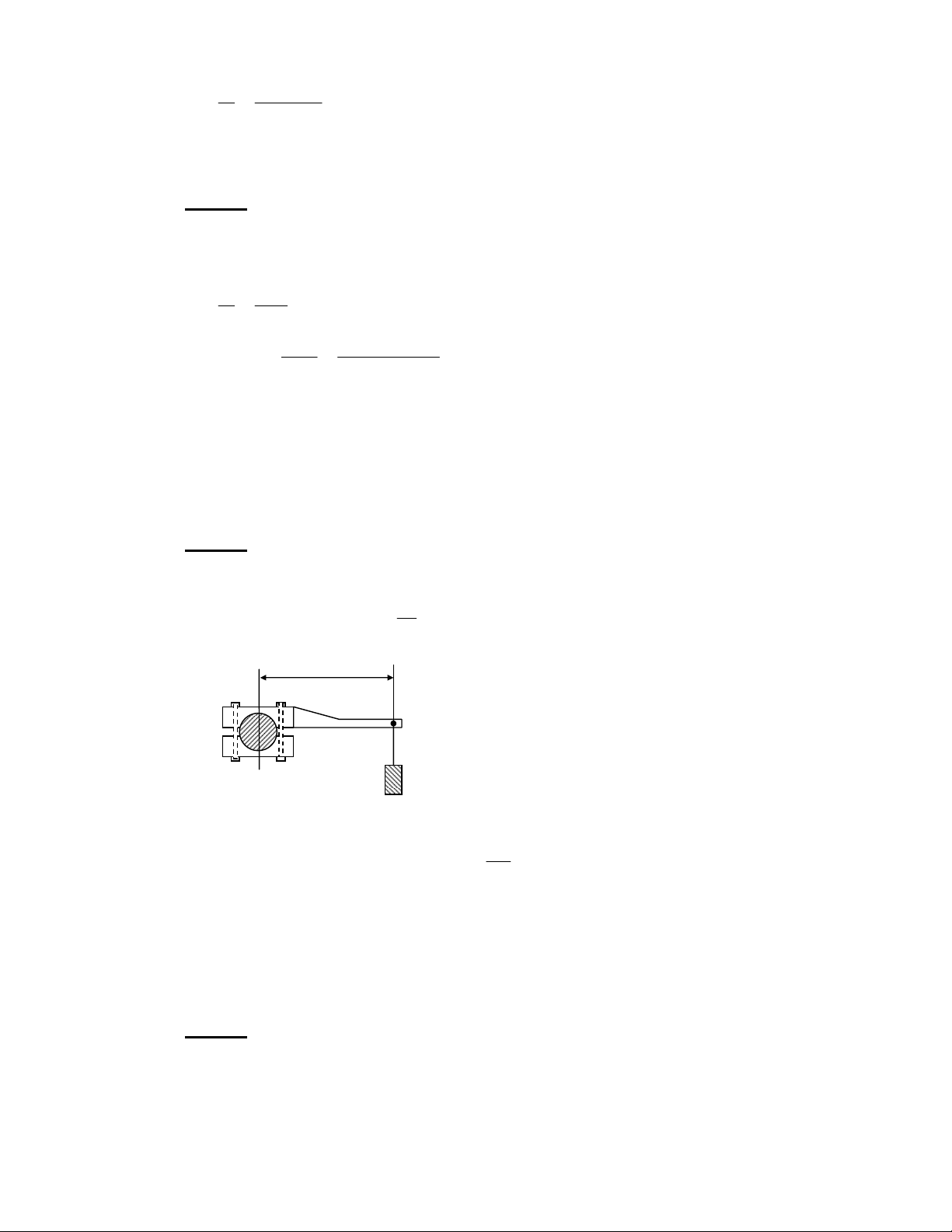
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 6 4 4 c 1 , L ∆ = L − L = 2 − r × v m 2 1 &r A 1L L ∆ = 2 x . v . m . = 2.1 1 . 0 2 . 40(kg m . 2 = / s) %.%g8 8 o / 3 1 , , r 14 G z 4 a 0 AL AB 3 6 I A^ c L 4 7 α AL a - J 8 & ' P c 1 , 3 AL z + AB 3 ; 8 R c 1 , v2 sin 2 α L = v . m y . = v . m cosα. o x max o 2g mv3 sin2 α.cosα L o = 2g %8S 8 o / 3 1 , , r 14 G z 4 a AL AB 3 I A^ c L 4 7 α AL a - J 8 & ' + A2 3 AL z8 $ P c 1M ( 14 5 6$ P c 1 , 8 ZQ ) !> = / P / O8 8 U 1M 12 m 1M 0 c m 1M M = mgx = mgv cosα t . " 12 c - AB $ p / o o 68 R c 1 , L = r × p i j k → L = m x y z = m (xv − yv y x ) v v v x y z 1 L = m v cosα t . − − − o (.v sinα gt o ) v sin αt gt 2 v cosα o 2 o 1 2 L = v . g . m . .cosα t . o 2 %.S^8 F 4 a - J ; Ž " %. %$ 7 / 3 1 , 6 A2 !, (V / P (C 0 I / (V , /r ) 1y Q z AL AB 3 / P t 8 FO !> ~ (V c / = @ A2 z 6 < ; / ^0 AB 3 12 ω^8 z f %. %
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Z= 2 c 1 , 7 2 ro mvr = mv r → ω = ω o o o 2 r 9M ~ F !, (V 4 r 2 2 o T = mω r = mωo 3 r %.S 8 R + / 3 1 , X^/ > 3 (I AL 3 6; T0u _!%8 fQ + 7 = < 2 A2 m 1 , 6 / < + 7 ` - !3 U + 7 = ‰ Š - I m 1 , 8 F m 1 , 6 / < 6; TXU ' 1 B ii Ucƒ - ( + N + m g = m a → N = m − n n n (a g) m , N 12 / 3 1 , + A2 - = 1M 2 !2 ( 14 + "AL 1L n 6; m 1 , + $ F 3 (I 0 a L 3 0 4 N = m(g − a) < mg HB + = … A2 m 1 , 6 / < + P'= N = m(g − a) P'= 50 ( . 8 , 9 − 9 , 4 ) ≈ 24 ( 5 N) %.S%8 F + c 6 < 1d 0 K I 1d 7 c 6 AB / 3 1 , 1I 1 , 6; / 0 %/ A2 S/ 8 FO 1M ~ 1d $ 9N > 4 5 6$ 9N M ( 8 8 9M ~ 1d 1I 1 , F u0gU 0 F% % u0YU 0 FS S %u0TU 68 9M ~ 1d + ,- M ( T + g m = g m → T = 0 f F F% FS ^ %.SS8 R , c K I (V - 14 - O 4 8 9N I (I ! 7 A2 L / (G 1 B (I 8 fQ ) 4 0 1M ~ (V - t < 2 ` o= + 4 ! ` F + ,- > + = ‰ a Š 5 F + ,- > . 6 + F + ,- > 6 . ‰ …Š 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 ' 1 B ii Ucƒ - ( / > + T + g m = a m → T = m(a − g) n (I 14 - O 4 0 a L 14 ( 7 T = T = m + " $ 1 (g a) n T = T = mg 2 n B (I 14 - O 4 0 a L 3 ( 7 T = T = m − 3 (g a) HB 4 1M ~ (V - c > M = (I ' 1 B ii Ucƒ - ( + N + m g = m a → N = m − n n n (a g) m , N 12 / 3 1 , + A2 - = 1M 2 !2 ( 14 + "AL 1L n 6; m 1 , + $ s 3 - " $0 m 1 , + c > M 4 !b = (I 0 + c > M !b = • a •0 •6 + •0 A2 • … •8 %.ST8 F 4 x ; ) 0 + a A B 7 / 3 1 , / ) X^ 8 f !3 ! @ AB A2 x 6; / ^0%X8 fQ $ 9M ! - = 7 1L 6; 6 4 AB , @ 4 x < x ) AL AB 3 % Ad _- N 5 6$ HL AB 3 7 2 AB 6e I , / Q x ` o 1M ( A2 AB 6 W 1M AB 0 - = 1M x 14 7 " M 3 AL m 1M $ A2 1M ! 8 ' 1 B Ucƒ F = ma = m 2 ω r = 4m 2 π f 2r ms ht 8 / P , F ≥ 4m 2 π f 2r ms 2 2 12 F ≥ 4 1 . . 1 , 3 4 . . 5 , 0 = 7 , 0 89 ms (N) 60 68 E F ≤ kN = kmg 0 4 AB 6e I , / Q x c " $0 7 ms kg m 2 ω r ≥ kmg → ω ≥ r HB 6e I , / 0 2 , 5.9 8 , ω = ≈ 2 2 , (rad / s) 0 5 , %.SX8 & ' 1M r - P A2 < 6 K A2 - Ad 2 1 < / 3 1 , - P 6; [X/ 0 6 /O Ad 2 1 6; %^^ 0 A2 AB 3 6 Ad 2 1 1 P 1 P / P t A2 6; SY^/ _ 8 ' 1 B ii Ucƒ - ( - P g m + N = a m " $
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 N 12 - = 1M 2 < ( 14 - P "6; A2 , AL 1M r - P 14 <$8 F Ad 2 1 0 c - L V 0 " $ , A < 2 v2 v2 mg + N = m → N = m − g 1 R R (100)2 N = 75 − 9 8 , = 301 1 ( 5 N) 200 F M - Ad 2 1 v2 v2 − mg + N = m → N = m + g 2 R 2 R (100)2 N = 75 + 9 8 , = 448 2 ( 5 N) 200 %.SY8 R 6 - = 1M 6 AL AB 3 u^^/ _ 8 s = < - P 7 ' , !M ~ m 1 , 14 X 1I 8 F 6 /O Q Ad 1 , 2 6 7 , 8 f,- 1M ( A2 - P c - L V 12 „ 8 ' 1 B ii Ucƒ mv2 F = ht R F 6 " ) < - ) O $ - P ' ( m 1M A2 1M L V g m + F = a m ht F c 62 F v2 | g ht + |≤ g 5 → ≤ 4g m R v2 (250)2 → R ≥ = ≈ 160 ( 0 m) 4g 4 8 , 9 .
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 S. 8 F 6 \ 7 a 6 0 / 3 1 , 1I 1 , 6; 0 %0 S8 & ' / 3 V 6 78 - ( + ,- % S 5 % 8 o m Ab8 F "^5 a 3 / 2 $5 %". _%5 ^$5 S" _%5 ^$8 E 7 s r % G z S m r i i r = i G mi i m x + m x + m x m − m a x 1 1 2 2 3 3 3 2 = = . G m + m + m m + m + m 2 1 2 3 1 2 3 m y + m y + m y m 3 a . 1 1 2 2 3 3 1 y = = G m + m + m 2 m + m + m 1 2 3 ( 1 2 3 ) HL a 3 % S 0 % x = 0,y = 5 > s ; O @ G G 4 + - V > AL 7 \ a / 3 1 , % 8 S.%8 F 4 x d W 6 /O w 7 / r 1y d Q 6 /O 5 V 1y / r ; V x 6; w_%8 & ' A' O / 3 V x 4 8 w z z w_% z% r r 1 2 f 62 S.%
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 o7 x d 6 I 12 W x d Q "- I 6' / r $0 6 /O 0 7 / 3 V ; z%0 1e- AL - I x d 1 ! / 1L 6' / r "- I , P 6; ( $0 7 m V ; z 8 f 4 12 2 7 m V A2 N V z x 6 I 8 &r ) < 7 3 ; V x d 8 sm Ac A' O / 3 V x / r 1y0 x C / r 1y A2 - I x 6' / r
1I 1 , 12 c,a,b,8 F 7
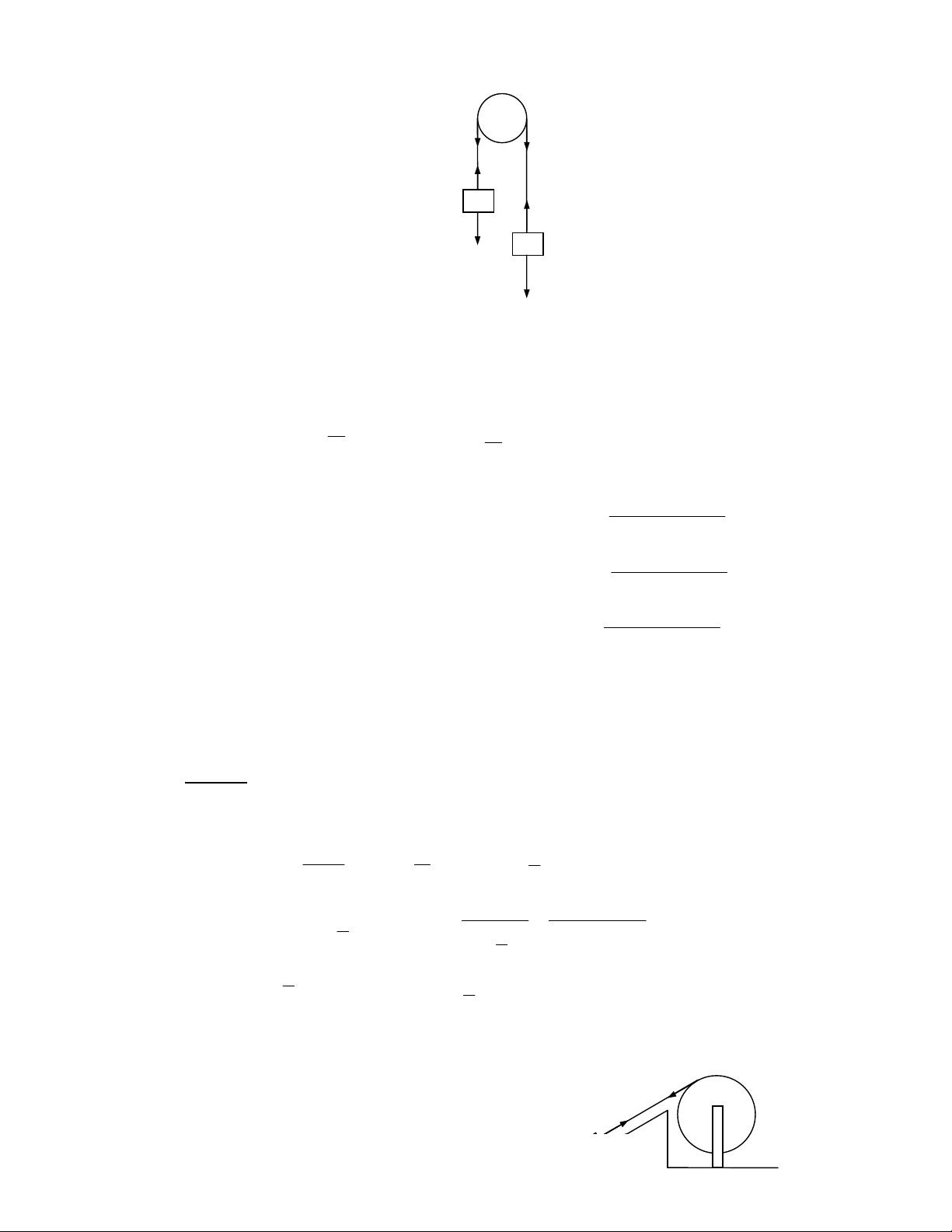
c = 0, b = R / 2 8 F 7 M c . = m a + m b 1 2 ρ. R 2 π 0 . = ρ ( R 2 π − r 2 π )a . + ρ r 2 π b . " 7 ρ 12 B / 3 1 , x $8 r 2 r 2 b Rr 2 b a = − b = − . . = − . R 2 − r 2 (R2 2 − ) b r b 2(R 2 − r 2 ) b HB 0 / 3 V x C 6' / r ; V z A - O 3 ( AL 1y / r 2 Rr x = b = 2( 2 2 R − r ) S.S8 o7 6 !N / 3 1 , ^ 7 / P ! 4 + 8 F 4 6 !N 7 e / } 6 / 3 1 , X 8 s = !D / } 6 = c - + 8 H 4 7 / 3 1 , ^^/ A2 7 AB 3 I d 12 X^^ _!8 & ' AB 3 6 !N ! / 6e 0 6 < ; $ 9N I 6 !N > 4 5 6$ F L / 6e 0 6 !N AL AB 3 g/ _ c 6e 5 $ F L / 6e 0 6 !N AL AB 3 g/ _ , 6e 8 sm / 3 1 , !N A2 A 4 1I 1 , 12 R A2 0 AB 3 6 !N L A2 ! / 6e 0 A 4 6e / Q d
1I 1 , 12 A0 Aj A2 A^8 &r A 4 6e , 6 I 8 F c ' 1 B 6= 2 1 , (M + m)v = M ' v + ( m ' v −v ) 0
(M + m)v' = (M + m)v + mv0 m v' = v + v0 M + m $ Z !N > 4 A ^0 A^ X^^ " _!$ 100 v' = 0 + .500 ≈ 3 3 , ( 1 m / s) 15.103 + 100 Z !N , 6e AL AB 3 S0S " _!$8 6$ Z !N c
6e A g"/ _ $ X " _!$0 A^ .X^^ " _!$ v' = 5 − 3 3 , 1 = 1 6 , 9(m / s) Z !N q 6e AL AB 3 0Yu " _!$8 $ Z !N , 6e A X " _!$0 A^ X^^ " _!$ v' = 5 + 3 3 , 1 = 8 3 , ( 1 m / s) Z !N , 6e AL AB 3 g0S " _!$8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 S.T8 R c K I / P ! AL AB 3 A _! 4 a + ; " S.S$8 F 2 6 c 7 / 3 1 , R ^/ 8 R ) = I / 3 1 , %/ 6 c , 1 AL AB 3 ; A% [ _!8 h / a- c0 ) = I ; B- 8 fQ ! 7 c c 2 0 AL AB 3 6; 6 4 ` F c ' 1 B 6= 2 1 , A% A f S.S Mv − mv = + 1 2 (M m)v Mv − mv 10.1 − 2 7 . v 1 2 = = ≈ 0 − 3 , ( 3 m / s) M + m 10 + 2 "o ( AB 3 12 6 I c$ HB 0 c AL AB 3 ^0SS " _!$ , AL 6 I c8 S.X8 R / } 6 / P 7 6 - B 3 B 0 = ( L 7 α TX^ ! AL a - J ; 8 H 4 7 / 3 1 , ^/ A2 7 AB 3 6 I A^ %^^ _!8 6 7 / 3 1 , R X^^/ 8 fQ AB 3 B !N < 6Q ) ! ` sm AB 3 B !N 12 A8 E 6Q ) ! 4 6= 2 1 , c - Mv + mv cosα = 0 0 mv cosα 10.cos 450 v 0 = − = − ≈ −2 8 , 2(m / s) M 500 S.Y8 R = ? 1N I > 4 0 ! 7 - / O a - O ! AL AB 3 / P t S^^ _! 3 AL = ? 8 F y V 0 1 , / O - 6; µ u^ 8 n 3 1 , t 6 I = ? 6; R^ %[^ 8 fQ $ h 6 1V = ? L AB 3 A T^ _!5 6$ n / 3 1 , t = ? 12 u^ AB 3 = ? 12 6 4 ` ZQ ) !> = / P / O A2 1M N F 8 &r + 0 / 3 1 , d 1 = ? 12 R0 AB 3 12 A8 h / = + Q ( = ? - 7 4 / 3 1 , (R0 AB 3 12 A#(A0 - I / O - 7 AB 3 12 "A. $8 F c ' 1 B 6= 2 1 ,
M.v = (M − dM)( v + dv ) + dM.( v − u )
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 M d . v − dM u . = 0 v M dv dM dv dM = = 0 M0 u M u M v M M 0 0 = ln = ln u M M − t µ 0 HB 3 = ? + V c 6 > M M v = u 0 ln = u 0 ln "Œ$ M M − t µ 0 $ F + AB 3 = ? AB 3 A T^ _!8 FG 6 > "Œ$ ! v M v M 0 0 exp = t = 1 − exp − u M − µt u µ 0 40 270 t = 1 − exp − . ≈ 0 3 , 7 ( 5 s) 300 90 6$ HB 3 = ? / / 3 1 , d R u^ M 270 v = v 0 ln = 300.ln ≈ 33 / 0 ( 0 m s) M 90 S.[8 F P c 1 , F 3 AL ) 4 78 &c F 12 I a 0 W 7 6 /O w YT^^/ 0 7 / 3 1 , 4 6 ρ X0X _ S8 RP c 1 , ) = I a W ) + /O 12 2 π π π 2 2 4 4 L = Iω = MR . = .ρ . R 3 R 2 . 5 T T 5 3 5 16 2 π ρR 5 16 2 π 5500 (.6 4 , .106 ) = = . ≈ 7 2 , 1 . 033 (kg m2 . / s) 15 T 15 24.3600 S.g8 R x d W / 3 1 , ^0S/ 0 7 6 /O w ^0T 0 ) AL AB 3 7 ω X^^ Ad _- N 8 F ( 14 x P c C 5 x ) B (I A2 ! + ∆ %^ V (G 1 8 F P c C 78 3 AL ) ) 3 ' AL P c 1M / P t 0 AB 3 7 6 < t c + AL 3 7 M ω − ω0 β = = I t . π 2 1500 2 , . , . L ∆ I(ω − ω ω 0 ) 2 0 3 0 4 mR 0 60 M = = = − = − ≈ 0 − 1 , ( 9 N m . ) t t 2t 2 2 . 0 S.u8 R a 0 W / 3 1 , ^^/ 0 6 /O w ^0X ) ) 78 F ( 14 1M C „ %TS0TU0 <- < AL a
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 A2 A P 7 AL ) 8 h + ∆ S 0T V 0 (G 1 8 FO AB 3 7 1N 6e I ( 1M C 8 n ( 1M C „ 14 a 0 P c 1M C 1 ) ω − ω M β = 0 = t I Mt FRt 2Ft ω = ω − = − = − 0 I mR 2 / 2 mR 2 ( . − 243 4 , ).31 4 , = − ≈ 300(rad / s) 100 0 . 5 , S. ^8 R y 7 / 3 1 , X^/ 0 + /O 0 ) AL AB 3 g^^ Ad _- N 8 F ( A2 1M C <- < AL a A2 A P 7 AL ) 8 h % - N S[ V 0 (G 1 8 F $ RP c C 5 6$ 9M C <- < 8 F 7 π 2 800.2 2 50. 5 , 0 . ∆L I (ω − ω ω 0 ) mR M 60 = = = − = − ≈ − 6 , 6 7(N m . ) ∆t t ∆ t 157 M mRω 6 , 6 7 F = = − = − = 1 − 3 3 , 4(N ) R t 5 , 0 S. 8 R W (2 1 ^0X^ 7 ) M ( ) ; ) I 8 R A 4 / 3 1 , ^0^ / 6 c - ; AL AB 3 A T^^ _! L 4 A2 I / A2 e A2 8 F AB 3 7 ! / A 4 B- A2 8 Z < ; P c ) O 3 AL ) 6; X/ %8 - ( ' 1 B 6= 2 P c 1 , { A 4 mvl = I' ω = ( 2 I + ml )ω mvl 0 0
, 1.400.0 5 , ω = = ≈ 0 4 , (rad / s) I + ml2 5 + 0 0 , 1.0 52 , S. %8 R x d W / 3 1 , ^^/ ) AL AB 3 7 ω ^ Ad _- N 8 R + / 3 1 , % Y^/ > K r- x 8 fQ AB 3 7 x / + A2 > K V x 8 o + 8 - ( ' 1 B 6= 2 P c 1 , + { x I ω = I ω 1 1 2 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 2 I 0 5 , m . R + m R m + 2m 1 1 2 1 2 ω = ω = ω = ω 2 1 1 1 2 I 0 5 , m . R m 2 1 1 100 + 2 6 . 0 ω = 1 . 0 = 22 "Ad _- N $ 2 100 S. S8 & ' P c ) O W (2 / 3 1 , 3 AL ! V $ F ) @ A2 AL 7 α 2 75 6$ F ! ! AL A2 (5 $ F A P 7 AL A2 @ (8 $ F ! ! + ,- 2 AL + ,- ) ) @ A2 A P 7 AL 8 F + ,-0 4 0 / = G 7 < ) - !3 1I / P t 12 ! 1I r = r .sinα 1 2 2 2 dm r . = dm r . sin α 1 r 2dm = 2 sin α . r 2 d . m 1 1 2 I = I .sin α 2 2 = ml sin α 1 12 6$ &r ) q AL 0 m 4 0 / = G 7 < ) 1 P 6; / P 0 4 P c ) O 3 AL ) q AL 12 6; ^8 hD ( ' 1: f c .h c c 2 2
I = 0 + md = md $ hD ( ' 1: f c .h c c 1 2 2 I = ml + md 12 S. T8 R x 6; W "/ 3 1 , 4 - g0u ^S/ _ S$ 7 6 (2 6 T8 ^. S 0 6 /O w X8 ^.% 8 x 6' / r 1y d 6 /O w_% S.T8 F P c ) O x C 6' / r 3 AL A P 7 AL x A2 ) V z x 8 sm i^ 12 P c ) O x 6' / r AL ) ∆ ) V A2 A P 7 AL x 5 i A2 i% 12 P c ) O - I 6' / r 3 AL ) ) V - I 6' / r A2 A P 7 AL x 8 F 2 MR ρ. . 2 b R π . 2 4 R π b ρ R I = = = 0 2 2 2 π R 2 . 2 ρ b . . R 2 . 4 πρ F M m R bR 4 I = I = = = 1 2 2 2 8 32 F c ' 1: h c c { f c 0 P c ) O - I 6' / r AL ) ∆ 12
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 πρbR 4 R 2 π R 3πρbR 4 I' = I' = + b ρ . = 1 2 32 4 2 32 RP c ) O i/ x C 6' / r 3 AL ∆ 12 4 4 πρbR 3πρbR
I = I − I' −I' = − 2. k 0 1 2 2 32 4 3 −3 4 5πρbR 5π .8 9
, .10 .4.10 .0 0 , 5 −4 = = ≈ 2 2 , 1 . 0 ( 2 kg m . ) 16 16 S. X8 F P c ) O F 3 AL ) 7 < 1 6 /O F 12 w YT^^/ A2 / 3 1 , 4 6 F 6; - X0X8 ^. S/ 8 S8 F 7 I 4 P c ) O F 3 AL ) 7 12 5 2 2 4π 8πρR 2 3 2 I = mR = ρ. R R . = 5 5 3 15 8π 3 = .5 5 , .10 (.6 4 , .10 )5 6 37 ≈ 9 9 , 1 . 0 ( 2 kg m . ) 15 S. Y8 F ( 14 6 c 6 /O w ^0X A2 7 P c ) O i %^/ 8 %0 1M <- < AL A2 6 „ ^^U8 F $ s 3 6 c5 6$ HB 3 (2 4 A2 6 ! / ( 1M ^ V 6 < ; 1N I 6 c > 4 8 s 3 7 6 c 12 M F R 100 5 , 0 . t β = = = = ( 2 5 , 2 rad / s ) I I 20 HB 3 4 A2 6 c ! ^! 12 v = R ω = (βt)R = 2 5 , 1 . 0.0 5 , = 12, ( 5 m / s) S. [8 R 6 c 6 /O w X^ ) ( L ( P c 1M R ug^U 8 fQ - = y - ( 14 A2 6 1M 6; 6 4 6 c ) B (I AL 3 7 β .%0X (_!%8 Z < !3 ! / ^0%X0 P c ) O 6 c 3 AL ) i X^/ 8 % " S8X$8 sm 1M 2 y - ( 14 A2 6 c 12 „8 9M ! V C c !b 7 - <- < AL 6 c A2 7 t 1L 6; %/„ "( - $8 F 7 M − M M − 2kFR ms β = = I I M − Iβ 980 − 50 ( . − 2 5 , ) F = = = 4420(N) 2kR 2 0 . 2 , 5 0 . 5 ,
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 S. g8 R \ 7 / 3 1 , , a 4 a - J ; " S.Y$8 RP c ) O \ 3 AL 7 6; i8 U + /r \ 6; 1M 8 fQ → $ s7 α @ 1M F A2 a - J ; - = 6; 6 4 \ 7 3 A - O 1M /r 5 → 6$ 9M F - = 7 1L 6; 6 4 \ / P , ` o !3 ! @ \ A2 a - J 6; /8 Fn F Ft $ R 3 \ 7 3 A - O 1M /r 0 \ - = ) c / W W8 n 7
Fcosα (R − r cosα ) − F sinα r . sinα > 0 FR cosα − Fr > 0 r cosα > R 6$ F 7 - F cosα − F = γ m = mRβ ms
mg − N − F sinα = 0 FR cosα − Fr = (I + 2 mR )β N = mg − F sinα ( F R cosα − r) I cosα + mRr F = Fcosα − mR = F ms I + 2 mR I + 2 mR \ / P , I 7 N ≥ 0 F ≤ kN ms mg F ≤ sinα I cosα − mRr F ≤ k(mg − F sinα ) I + mR 2 kmg( 2 I + mR )
F ≤ I(cosα + ksinα)+ mR(r + kRsinα) S8 u. F 4 y / 3 1 , / 0 + !, (V / P C 7 / 3 1 , A2 + /O Q / P / 8 I M ( (V , e 4 3 ' " S.[$8 ( L ( m 1 , 8 F 3 A2 !> ~ (V c 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 F F AG ) AG 8 sm F 12 !> ~ (V 8 F < 1B- - 1M A2 P c 1M 0 7 mg − T = γ m TR = β 2 I = mR β Ra / 0 G 3 1 4 @ AB 3 (2 A2 AB 3 7 0 7 v = R ω γ = βR F 7 - mg − T = γ m 2 γ m = mg T = mRβ = γ m T = γ m g 9 8 , γ = = = 4 9 , (m / s2 ) 2 2 mg 1 9 . 8 , T = = = 4, ( 9 N) 2 2 S.%^8 f AB 7 / 3 1 , 1I 1 , 6; A2 % " ‚ %$0 , 3 AL 6; !, (V Ae ) d m "/ 3 1 , d m 6; $ " S.g$8 F $ s 3 AB 5 6$ h> ~ F A2 F% (V c 8 o d m 12 x d 5 ! / P / 8 - ( 6; !3 %/ 0 % / 5 / 8 F < 1B- - 1M A2 P c 1M m g − T = m γ 1 1 1 1 T − m g = m γ 2 2 2 2 2 ( γ T − T = β = . 1 2 ) mR R I 3 2 R
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 F% % F % E? γ = γ = γ = γ 0 7 - 1 2 3 T = m g T m g 1 1 ( − γ ) = 1 1 ( − γ ) T = m g T m g 2 2 ( + γ ) = 2 2 ( + γ ) m T − T = γ m 1 2 γ = (m − m g m m 1 2 ) − ( + 1 2 )γ 2 2 m1(4m + m 2 )g T = 1 2m 2m m T = m γ 1 1 (g − ) + + 1 2 m2(4m + m 1 )g T = m γ 2 2 (g + ) T = 2 2m + 2m + m (2m + 2m + m γ 1 2 ) = 2(m − m 1 2 )g 1 2 2(m − m 1 2 )g γ = 2m + 2m + m 1 2 S.% 8 R W a W / 3 1 , R %0XT/ A2 AB a / 3 1 , ^0X/ , 3 AL 6; !, (V Ae ) d m " S.u$8 ZQ ) / 3 1 , (V 0 d m A2 / e AL 8 F 3 AB a A2 !> ~ (V 8 sm F 12 !> ~ (V 0 G - 1M A2 P c 1M 0 7 ! mg − T = γ m mg − T = γ m MR 2 2 γ 3 TR = β I = + MR T = Mγ 2 R 2 mg 0 5 , 9 . 8 , 3 γ = = ≈ 11 , 4(m / s2 ) mg = m + M γ 3 0 5 , + , . , 2 m + 1 5 2 54 M 2 3 T = Mγ 3 T = Mγ = 1 5 , 2 . 5 , 4.11 , 4 ≈ 4 3 , ( 3 N) 2 2 S.%%8 R AB ] / 3 1 , , 4 a - J 4 A2 12 ) 6 c 7 6 /O w " S. ^$8 RP c ) O 6 c 3 AL ) 6; i8 n 3 1 , F (V / P / 8 F 3 7 6 c` F „ !
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 sm F 12 !> ~ (V 0 7 - TR = β I
T − mg sinα + kmg sinα = γ m = mRβ
I β − mRβ = mg sinα − kmgcosα R
mgR(sinα − k cosα ) β = 2 I − mR HL / 12 !3 ! a - J 4 # U< k > tgα 0 K V 6; β = 0 8 sinα # U< mgR k = 0 β = 8 2 I − mR S.%S8 R 7 (2 1 ) ) ; ) I 8 9N I 0 K A' O ; 0 ! 7 , = " S. $8 F 3 7 1N 6e I = A2 1N ) A' O J > 8 RP c 1M ( m 1M V ) ) / 4 7 ! AL - J > 12
M = F (l / 2).sinα sinα sinα HB M mgl g 3 β = = = I 1 2 l2 2l 2. ml + m 12 4 # F A' O 6 I 3g 3. 8 , 9 = 900: β = = = 14 7 , ( 2 m / s ) 2l 2.1 # F A' O ) A' O J > = 0: β = 0 . S.%T8 R x d W 6 /O w / 3 1 , 7 ) ) ; A P 7 AL x A2 V x w_%8 x 6e I ) G A' O > AL A' O V x AL AB 3 I 6; ^8 & ' P c 1 , x 3 AL ) / x ) A' O - 8 RP c ) O x 3 AL ) 12 2 1 R mR 2 3 2 I = mR + m = 2 2 4 - ( ' 1 B 6= 2 ~ 1 , 1 (Iω)2 2 L2 mgR = Iω = = 2 2I 2I 6m2gR3 3 L = 2mgRI = = mR gR 4 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 → → S.%X8 R 7 t 1 , 6; K A2 P c 1 , L 3 → → AL z8 & ' P c 1 , 3 AL zj 6 < OO' r 8 0 F + ,- 2 P c 1 , / P - z` RP c 1 , 3 AL zj 12 L = r ∧ m v = r r m v O' O' i i i ( + Oi OO' ) ∧ i i i i = r ∧ m v + r ∧ m v Oi i i 0 i i i i = r ∧ m v + r ∧ m v Oi i i 0 i i i i = L + r ∧ K O 0 RP c 1 , / P - A2 z L = L ⇔ r ∧ K = 0 ⇔ K = 0 O' O 0 → S.%Y8 o > ; P c 1 , L 3 AL z → → → → → e 1 AL ) < n 7 6K L L ^ # r • P 0 7 L 0 ^ 12 P c → 1 , 3 AL / 3 V 0 r 12 Ar 6 /O / 3 V 3 AL z 0 → n0 P 12 t 1 , 8 F M 62 S.%X0 z 6; m V s0 A2 zj 6; z n0 7
L = L + r ∧ P O O
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 T. 8 fQ 6 - = 7 P ! 6; 6 4 0 6 < ; 6 7 / 3 1 , S^^^/ 0 / 6 14 / - = - N 8 ZQ ) !> = / P / O8 R 3 6 14 0 6 - = 3 P e P = m 1M ] ∆ 8 FG 7 ! P ! 6 A mg h ∆ = t ∆ t ∆ F S^^^/ 0 / ^^^ 0 ∆ - N Y^! A2 A2 6 > 4 O , Tu^/‘8 T.%8 FO P I < /r 1d C %^ 0 6 < ; 1M /r | 1 AL C 1d A2 3 1d C - = I 1M S^U8 f !3 2 W 1d 6; k = 30N / c 1 m = 3000N / m oP 1M /r x ∆ ∆x 2 ] ( ∆ ) F d . x = (k x . ) k x d . x = 0 2 0 0 HL / S^^^U_ 5 ∆ %^ ^0% ] Y^’8 T.S8 R P P / 3 1 , 0 / e 3 (3 7 AB 3 / P t A XT/ _ 8 4 (3 12 T†8 fQ P P - = 7 P ! 6 4 7 14 , (3 4 q AL AB 3 XT/ _ 8 H / e 3 (3 0 P P 7 AB 3 / P t 4 - = 7 / ‡ ! ! α8 c 14 (3 1M /r „/ P P - = 6; „/ ‡ ! # 8! α %8 8! α oP ! P P / 14 (3 AL AB 3 A , O c P > A F S . P k = = = F . v = ( . 2 mg.sin ).v t t k " $ = 2 1 . 000.9 8 , 0 . 0 , 4 1 . 5 ≈ 11 8 , kW T.T8 R P P / 3 1 , % 0 1c 14 (3 7 4 T†8 f !3 ! 12 ^0^g8 F $ oP M 6K P P 4 ) C + (2 S/ 5 6$ oP ! P P0 6 < ; + < ) C + 4 T - N 8 9M /r - = V 6; AL 2 - I 8! α m 1M A2 1M ! F = mg.sinα + f = mg.sinα + k m
. g cosα ≈ mg.sinα + k m . g 8 k ms oP /r 4 ) C + (2 S/ A = F S . = mg ( . sinα + k)S . = 2000.9 8 , ( . 0 0 , 4 + 0 0 , 8) 3 . 000 = 7 0 , 6 1 . 06 8 k (J) oP !
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 A 7 0 , 6.106 P = = = 2 9 , 4.104 W = 29 4 , kW t 4.60 T.X8 R 2 2 / 3 1 , X^ 4 + ; AL AB 3 / P t 6; SY/ _ 8 oP ! I 12 %%^0g/‘8 F !3 ! @ 2 A2 + 8 n 4 + ; 0 1M /r I I - = V 6; AL 1M ! F = f = k m . g 8 k ms oP ! I 7 ' c P > A F S . P k = = = F v . = k m . g v . t t k P 220 8 , 1 . 03 k = = = 0 0 , 45 mgv 50.103.9 8 , .10 T.Y8 U + + ' P ! 6; < 6' Ab T.T8 F < 6' W 2 /…-0 /…- a A2 8 R 2 …- , e AL d 0 3 d 7 c m AB v8 F m AB , m ! 7 V 6; AL 1M ! A2 @ d ; 8 & ' P ! < !3 Ad ) 12 Y^ Ad _- N 0 (2 d / G V 1 0 m 1 , AB 6; v Tu^U8 F m 1 , d / P / 8 sm ‡ ! 12 M ! @ 2 /…- A2 8 F 7 / V 6; Ql f r . = Q l . 8 ‡ ms ! r 1 v oP ! Q l. P = f . v = . π . . = π 0 12 !3 Ad ) ms ([2 n)r] 2 Qnl r V 8 P = 2.π 4
. 90.1.1 = 3 0 , 8 103 . W T.[8 R P ! X/‘ - 1 + (V ]Z " T.X$8 Z /O - 1 %X 0 AB 3 ) - 1 %^ Ad _- N 8 9M ~ 4 ] (V 1L - P 1M ~ ( L Z8 F 1M ~ 7 6 < ; (V ! ! AL 8 oP ! - 1
„8A “"F] . FZ$8 ” 8%π8 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 FG / F P ] %FZ ! F] %8FZ 8 π r . n . 3 F !3 15.10 T = 2T = = 955 A B ( 6 N) π 0 . 2 , 5 2 . F] 1 FZ T.g8 R < c / 3 1 , %^^^^/ B (I ( L ( 1M ! 6; Y^^^U8 h + c (G 1 8 HB 3 6 I c 12 XT/ _ 8 FO $ oP 1M ! 5 6$ v C + 2 c C , / G 1N 7 1M ! ( L / c (G J 8 EM c ' 1: ~ 0 P = 1M ! 12 = ~ c G ' 6 I A ^0 ( 70 P 2 7 1L O 6; ~ 6 I c 1 2 1 A | = E ∆ |= m v . = 2 . 0000 1 . 52 = 2 2 , 5.106 J 8 ms K 2 2 v C + 2 c ( , / G 1N C c < / c (G J A 2 2 , 5.106 S ms = = = 37 ( 5 m) f 6000 ms T.u8 FO P I < 2 2 / 3 1 , g8 ^X/ $ F~ 3 G A SY/ _ < A% XT/ _ 3 6$ EG 1 < AB 3 6 I 12 [%/ _ 8 F !b - ( ' 1: ~ 6 < 4 ~ AB 6; P ( 1M ( A2 AB ( 7 $ oP 12 c ~ AB 3 G A SY/ _ ^ _! < A% XT/ _ X _! 1 2 1 2 1 5 2 1 A = E ∆ = m v . − m v . = 8 . 1 . 0 1 . 5 − 8
. .105.102 = 5.107 J K 2 2 2 1 2 2 6$ oP 12 c = AB 3 G A^ [%/ _ %^ _! < A ^ _! 1 2 1 2 1 A = E ∆ = m v . − m v . = 0 − .8 1 . 05 2 . 02 = −1 6 , 1 . 08 J K 2 2 0 2 oP 2 12 P = " P V $8 T. ^8 R / } - / 3 1 , R TX^/ = c - ; 8 - 7 / 3 1 , X/ 0 AB 3 I d A TX^ _!8 n 6e 0 6 - B A - O ! ! TX 8 F 1M C 6 ( 14 - 8 sm H 12 AB 3 B 1q / } - 8 EM A2 ' 1 B 6= 2 1 , - ( - 7 m M V . + m v . = 0 V = − v . M
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 R A H 9M C / } - ! P 12 = ~ / } - 1 2 F S . = M V . .< 2 FG 7 M V 2 . m2 v2 . F = = .< 2 S . 2 s . M . 52 4 . 502 = = 1250 ( 0 N) 2 0 . 4 , 5.450 T. 8 R A 4 / 3 1 , ^/ 6 AL AB 3 A ^^ _! a- 6= y (2 A2 e !V A2 6= y ! T 8 F $ 9M = 6 6= y 14 A 4 5 6$ HB 3 A 4 ! / / Q 6= y \ (2 ( % 8 $ F A‹ !D ( ' 1: A ~ 7 , - 2 − m 02 . mv2 − mv2 10 1 . 00 Fc s 0 . = − → F 0 c = − = − = −125 ( 0 N) 2 2 s 2 2.0 0 , 4 6$ H 4 7 / = ~ 4 !V A2 6= y T L (G 1 8 U< 6= y \ (2 % ! / 4 ) 6= y0 A 4 A‹ d <- AL AB 3 Aj • A8 F c ' 1: A ~ 2 2 − ]j mv' mv0 − = Fc d 0 2 2 2F d 2 −1250 0 . 0 , 2 c 2 ( ) ! Aj 2 + v = +100 ≈ [ _!8 0 m 10 T. %8 R c 4 G \ (3 - J Eo 7 " T.Y$ A2 (G J 1 ! / C , ; oZ8 o ]Z !5 ]o 5 !3 ! @ c A2 a + 4 Eo A2 oZ 6; 8 FO !3 ! A2 3 c 4 + Eo A2 Zo8 E o α ] Z ! 1 . F \ a - J 4 c 7 < ~ ‘ 8 o O < ~ 2 C (q e P ] A2 ]% 1M ! 4 + Eo A2 oZ8 E 7 ‘ ] # ]%0 7 P 1M ! 4 Eo A2 oZ 12 ] /8" 8 !α$ 8 Eo / 81 5 ]% / "! . 1$8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 FG 7 ! h
mgh = kmgl + kmg(s − l) = kmgs / 8 s . V O 1M A2 - ( ' 1 B U > 0 , - ! α . "‡ !$Eo 8 Eo 0 " $ . / 8 oZ "%$ FG " $ ! ! α . /8" 8 !α$ 8 Eo h h l a = g sinα cosα . . CD ( − k ) = g − l2 + 2 s h l2 + h 2 gh l = 1− > Z l2 + 2 s h od G "%$ h a = −kg = − .g < 0 CB s - !3 h gh l h k = ; a = 1 − ; a = −kg = − .g 8 s DC 2 s CB 2 s h + l T. S8 R AB / 3 1 , , / P ! G \ a I 3 ( L " T.[$8 fQ G / = ∆ 2 " O G \ a I $ AB 6e I / Q a I 8 o 6 /O a I w u^ 8 w ∆ w f T.` F ) AB , 4 a I 0 AB ' ( 1M m 1M AB A2 - = 1M w a I 8 Ft ,- 1M 2 2 - I 2 - I - - < 7 A d 1M L V d AB 0 2 - I <- <- V , (I AB 8 &r 2 - I - - < m v2 . m v2 . m v2 . P − R = m a . = R = P − = mg cosα − n n ht R n n R R Ra / 0 c ' 1 B 6= 2 ~ = < ~ AB 6; ~ ~ AB 8 1 ∆ A%8 2 2m ∆ g h R − ∆h 2mg∆h ∆ 3 h R = mg cosα − = mg − = mg 1− n R R R R HB \ 7 , m 12 6 4 a I < 7 d - 14 a I 1M "6; - = 1M w
a I $0 > 12 w ≥ ^8 hM + / Q a I 6e I = / w ^8 f 3 h ∆ R R = mg 1− = 0 h ∆ = = 30cm. n R 3
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 T. T8 R AB / 3 1 , / , 4 a - J 4 ,- AL a ; 7 α ! ! α ^0 8 h / , < a - J 4 0 AB d <- 4 a - J ; 1 ^ L (G 1 8 f !3 ! ! 3 ) / ^0^X8 F AB 3 AB K 3 a - J 4 8 9 3 m + ^ _!%8 ] 9 Z α f o ! 1 E ( 1M ! ‡ ! ./ 0 AB , 4 a - J Zo AL 3 ./8 8 sm A 12 AB 3 AB K 3 a - J 4 0 c ' 1: ~ 7 1 2 1 f l. = 0 − mv kmg l . = mv2 ms 2 2 → v = 2kgl = 2.0 0 , 5.10 1 . 0 ≈ 31 , ( 6 m / s) T. X8 FG \ - %^ 0 + r d / 3 1 , X^ c - 4 AL a - J ; 0 AL AB 3 6 I A^ g _!8 n L a d 7 AB 3 A %T _!8 FO P 1M = / P / O 14 d 8 o m 3 O < ~ ; a 8 F + I 4 d 7 ~ 1 W = mv 2 + mgh t 2 0 F + d a 7 7 ~ 1 2 W ' = mv t 2 wk 2 ~ 1N ! d 6; ~ 6 I d 4 P ! 1M 0 ( 7 W' = W + A A = W' −W C C m A =
( v2 − v2 ) − mgh C 2 0 0 0 , 5 =
(242 −182 )− 0 0,5 9. 8, 2.0 = −3, ( 5 J) 2 T. Y8 R AB / 3 1 , ^/ , G \ a - J 4 %^ 3 8 n L V (3 AB 7 AB 3 X _!8 FO P ! 8 oP ! 6K 1M ! 6; 6 < 4 ~ AB 1 2 1 A = W − W = mv − mgh = .10 1 . 52 −10 9 . 8 , 2 . 0 = −83 C D! 9 ( 5 J) 2 2 T. [8 I !, (V z]0 (2 1 S^ 7 c AB a " T.g$8 fQ - ] - = AB AB 3 6r 6; 6 4 AB 7 ) d a - J J > 8
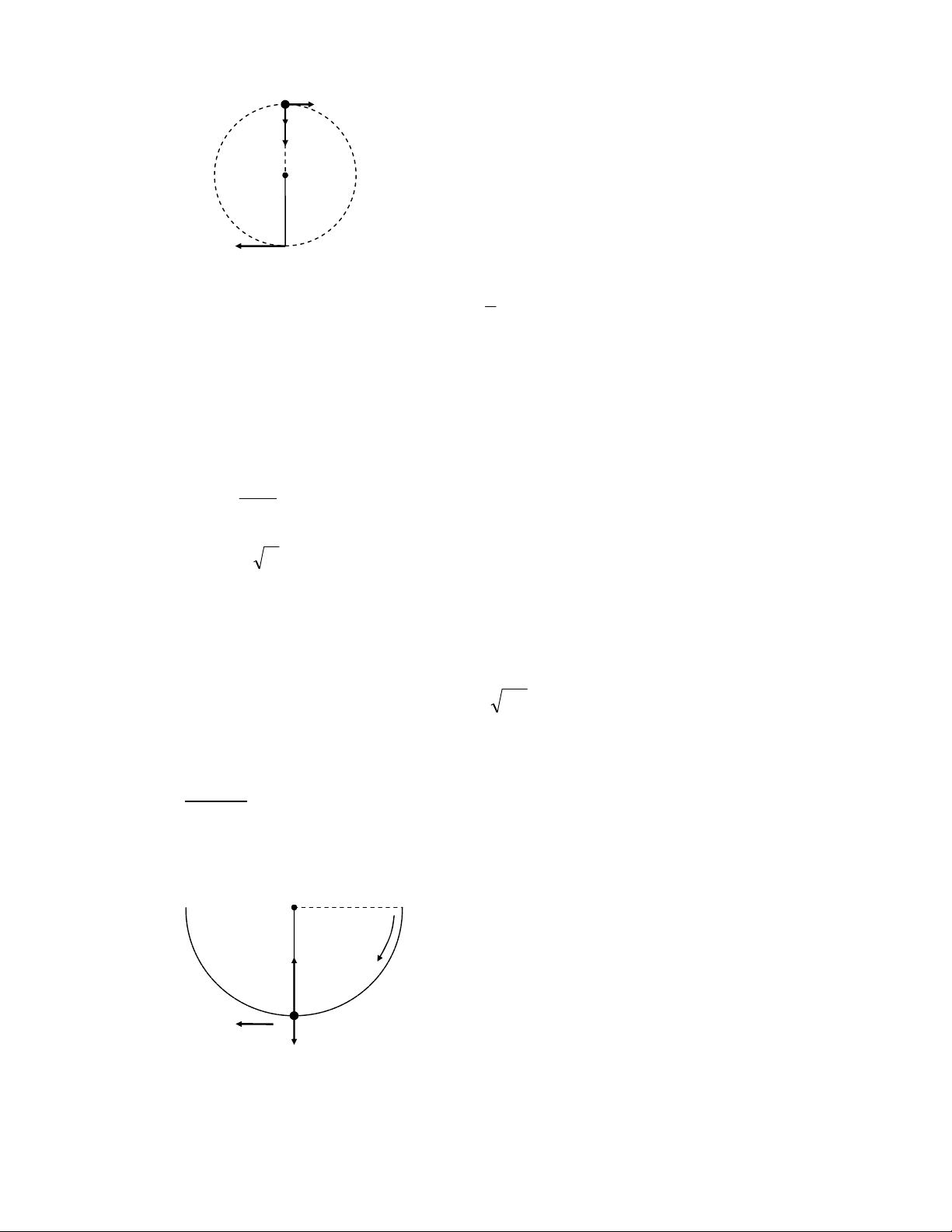
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Z vB F z 1 v ] A F ] AB , ~ 1 2 mv 8 h 7 AB 6e I d A 2 14 - O 4 8 F < ~ AB ~ (I 0 ~ "( 7 AB 3 $ AB = (I " T.g$8 R 3 AB d a - J J > 0 AB 3 AZ AB Z - = 1L 12 !, (V 1 P 6' ~ "F ≥ ^$8 → → → H Z AB ' ( m 1M P = mg A2 1M ~ T " L c - J > $ 1M L V d AB 0 4 mv2 F B = = mg + T 8 ht l HB AB 3 Q Z AB 7 ) d AZ gl 8 " $ Ra / 0 c ' 1 B 6= 2 ~ "∆‘ $]Z . "∆‘ $]Z 0 ! v 2 = v 2 + 4gl 8 A B HB AB 3 Q I AB ] 7 ) d a - J J > ( v 2 ) = ( v 2 ) + 4gl , v = g 5 l = 3 8 , m / s A min B min A min T. g8 R 1e m 1 , , /r / Q - J > 7 α u^^0 ! 7 1e , = 8 o > ; !> ~ (V c 6; S / 1e ) A' O V 6; 8 F A n ) A' O V 6; 0 ,- 1M @ !> ~ (V A2 m 1M 1e 1M L V 2 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 mv2 mv2 T − P = m a . = T = + mg ht l l - ( ' 1 B 6= 2 ~ 7 1 mv2 = mgl 2 FG 7 ! !> ~ F 2mgl T = + mg = m 3 g = P 3 l T. u8 R ) = I / 3 1 , ^0 / , e K I … (2 1 0%[ / 3 1 , / P / 8 f ) a - J J > ) I / 8 F ) = I 7 AB 3 A^ T0 S _!8 $ F !M - < ~ A2 ~ ) = I c 7 α ,- 6K A2 - J > 8 o m 3 O < ~ A' O - ) = I 8 6$ & ' 1M ( F ) = I 14 c 7 α8 F F A' O - A2 ) = I 8 o m 3 O < ~ A' O - ] ) = I 8 n ) = I K o0 ,- AL - J > 7 α $ < ~ A2 ~ ) = I 12 ‘ o 1 8 " . !α$ 5 ‘ 1 2 mv 2 F c ' 1 B 6= 2 ~ 7 ‘ # ‘ "‘ $^ # "‘ $^8 f mg ( l 1 − cosα ) 1 1 2 + mv = mg ( . 2 l . ) 2 + mv0 2 2 1 1 v = 2gl ( . 1+ cosα ) 2 + v 5 ‘ 2 mv mv2 + mg ( l 1 + cosα ) 0 2 2 0 Z z F v α o o ] 6$ 1M L V AB , ) < ' 6K m 1M A2 1M F mv2 F = = T − mg cosα ht l mv2 mv2 → T = + mg cosα 0 = + 2m (
g 1+ cosα ) + mg cosα l l
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 F v m 0 + g 3 cos α + 2g l 2 v2 4 1 , 3 F - 0 α ^ T = m 0 + g 5 = 0 1 , . + 5 9 . 8 , = 6 2 , ( 4 N) l 1 2 , 7 2 v2 4 1 , 3 F 0 α g^^0 T = m 0 − g = 0 1 , . − 9 . 8 , = 0 3 , 6 ( 3 N)8 l 1 2 , 7 o= A' O0 AB /r ~ 8 T.%^8 AB 3 A 4 + (q 1e D 8 7 12 6 c K I !, (V " T.u$8 n A 4 4 A2 6 0 7 6' e 7 A2 6 , V 14 2 78 F AB 3 1N 7 !e- 4 A2 6 8 Z < / 3 1 , A 4 12 0 / 3 1 , 6 12 R8 V 12 62 A 8 R 3 = 70 - ( ' 1 B 6= 2 1 , A2 ' 1 B 6= 2 ~ 8 sm A A2 H 1I 1 , 12 AB 3 L / 4 A2 6 A2 AB 3 6 ! / 7 4 A2 8 α R A ' 1 B 6= 2 1 , A "R # $ H8 " $ ' 1 B 6= 2 ~ " # R$ V2 " # R$ 8 V = 2gh "%$ 2 + + FG " $ A2 "%$ ! A m M m M V . = . 2gh 8 m m 0 R0 !b O , AB 3 A A 4 8 T.% 8 R 3 | / 3 1 , R 7 M A2 m 4 c , B 6; N / 3 1 , 8 | , e K I > (2 1 m 1 , / P / " T. ^$8 n 7 3 | 0 4 c 63 0 N 6' 6B ( L - ! 4 c8 fQ AB 3 6B 6r N - = 6; 6 4 3 | 7 ) , = Ad ) c z8 sm A0 H 1I 1 , 12 AB 3 N A2 AB 3 3 | 8 - ( ' 1 B 6= 2 1 , 7 R8H 8A F c /< ) = 62 T. [ 0 3 | 7 d ) c z AB 3 H 7 - 2 - = = C / V ≥ g 5 l
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 M V . M g 5 l v = ≥ m m z 1 R A H T.%%8 R d 6 / 3 1 , / P ! 4 + C 7 ( Ab T. 8 fd 6 , = / P 7 AB 3 6 I G %w0 /O L 6 Q / P / 8 fQ $ 2 d 6 + / Q + C ` 6$ 1L 2 d 6 !b , ! / + / Q + C ` $ &c 62 B- T. S0 T. g d 6 + / Q + C / 1M r d 6 14 C 6; / P 8 FG / 4 ! ] o Z f f % 8 ! mv2 α 0 " $ f T.%% R - ( ' 1 B 6= 2 ~ ) ]Z "Z 12 d 6 + + C $ 7 f 5 R " T.Sj$8 3 6$ HB 3 d 6 Z , ! G " $ A 2Rg ^ 8 h / + + C 0 6 c - 6 1 \ o8 HB 3 3 ; K o "A $ A^ !α0 AB 3 J > "A $ A^! α . 8 - ( ' 1 B 6= 2 ~ ) ]o0 ! f 50 % R 8 27 T.%S8 R ) = I / 3 1 , %/ 0 AL AB 3 S _!0 A 4 V AL ) = I > / 3 1 , S/ q AL ) = I > AL AB 3 _!8 F AB 3 ) = I ! A < $ H 12 2 2 2 W 8 6$ H 12 / P 2 W " $8 A % A% #
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 $ H 2 W H @ AB V c ' 1 B 6= 2 1 , A2 6= 2 ~ 8 F 7 - 6= 2
m v ' +m v ' = m v + m v " $ 1 1 2 2 1 1 2 2 1 1 1 1 2 2 2 2 m v ' + m v ' = m v + m v "%$ 1 1 2 2 1 1 2 2 2 2 2 2 o = !3 1 4 ) < A A<0 1 4 ) < % ! A< d 1 - 4 m v −v = m v − v "S$ 1 ( ' 1 1 ) 2 ( ' 2 2 ) m v ' −v = m v − v ' "T$ 1 ( 2 2 1 1 ) 1 ( 2 2 2 2 ) E ! A 0 AB t AB 3 4 7 1 "T$ A< A< AL "S$ , v ' +v = v ' +v "X$ 1 1 2 2 U V A< "X$ AL % W A< c A< AL "S$ ,
m v ' +v + m v ' −v = 2m v 2 ( 1 1 ) 1 ( 1 1 ) 2 2 2m v + m − m v 2 2 ( 1 2 ) 1 → v ' = "Y$ 1 m + m 1 2 92 M " a t A d \ !3 A2 %$ N 2m v + m − m v 1 1 ( 2 1 ) 2 v ' = "[$ 2 m + m 1 2 - ( AL %/ 0 % S/ 0 A S _!0 A% _! A2 "Y$ A2 "[$ O , Aj ^0Y _! 5 Aj% %0Y _! 8 6$ H h A 0 AB !b 7 q AB 3 A Aj Aj% A8 H 2 V c ' 1 B 6= 2 1 ,
m v ' +m v ' = m v + m v (m + m v = m v + m v 1 2 ) 1 1 2 2 1 1 2 2 1 1 2 2 m v + m v 1 1 2 2 v = m + m 1 2 F ' / 3 1 , A2 AB 3 C , Aj Aj% A 0g _!8 T.%T8 f ) = I , c K I !, (V ! ! (2 6; 8 f I / !, (V , 6 A2 ! ) = I <- N AL A2 V N q ; 4 + ; " T. %$8 n 3 1 , ) = I 1I 1 , 6; %^^ A2 ^^ 8 v = I > , V 14 T0X A2 = 3 8 fQ ! A 0 ) = I , V 14 6 4 < $ H 12 2 2 2 W 5 6$ H 12 8 %
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 F 62 2 !b AB ( = ' 1 B 6= 2 ~ 1e 62 T. g0 T.%^ A2 62 A A 4 V 62 T.%S8 U L / ) = I A2 ) = I % 7 7 AB 3 12 v = 2gh 1 h A 0 ) = I 7 AB 3 12 A j5 A%j A2 N !b 14 A2 % 2 2 > 6; v ' v ' h 1 = 5 h 2 = 8 1 2g 2 2g $ U< A @ AB 12 2 W 0 - ( P > 62 T.%S AL 1 4 %^^ % %5 A% ^ v ' = v 5 v ' = v 8 FG 7 , 1 1 3 2 1 3 v 2 ' 1 v 2 1 1 v 2 ' 16 v 2 16 h 1 1 = = = h = 4 . 5 , = 0, 5 h 2 1 = = . = h = 8 2 ( 8 cm) 1 ( 5 cm) 2g 9 2g 9 9 2g 9 2g 9 6$ U< A @ AB 12 Aj Aj% %A _S8 v 2 ' 4 v 2 4 h = h 1 1 = = . = h . = 8 1 2 ( 2 cm) 2g 9 2g 9 T.%X8 R AB / 3 1 , L A A2 AB > > 4 0 / 3 1 , %8 o A 12 4 V A2 2 2 2 W 8 fQ !3 - I ~ ~ 6 I AB > C AB > ! A ` - ( + ,- $ %5 6$ u %8 - ( P > A 2 W 7 ,
62 %.%S AL v ≠ 0;v = 0 1 2 O , AB 3 ) = I > % ! A 2m v 1 1 v ' = 2 m + m 1 2 FG 7 ! | !3 - I ~ ~ 2 AB C AB % 2 2 W'd m v ' m 4m 4m m 2 2 2 2 1 1 2 η = = = = 8 2 2 2 W m v m ( m + m ) ( m + m ) d1 1 1 1 1 2 1 2 n % η ^^†8 n u % η SY† T.%Y8 R x W a %^U0 1~ / P , 4 a - J ; AL AB 3 A T _!8 F ~ x 8 x W 7 P c ) O 1 2 I = m R . "AL w 12 6 /O x $8 2 n x 1~ / P , 4 !2 ; 0 7 / v = Rω 8 ~ x 6 W ~ ' < A2 ~ ) ‘ 1 1 1 1 1 1 1 3 2 2 2 2 2 2 2 2 2 mv + I ω . = mv + m R . ω . = mv + m R . ω = mv 2 2 2 2 2 2 4 4 T.%[8 FO P I < 12 AP 1~ A2 d + /O 0 / 3 1 , X^^/ 0 > 4 ) L AB 3 %^ Ad _- N 8 RP c ) O AP 1~ A2 d 2 I = m R . 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 HB 3 ) AP 1~ 12 %^Ad _- N " %^8%π ( $ _"Y^ V $ Tπ " (_!$8 oP 12 AP 1~ ) O 6; ~ ~ ") $ AP 1~ ] 1 2 1 1 2 2 1 ∆‘ I ω . = . m d . ω .
= .500.12 (.4π )2 = 1000 ( 0 J) = 10kJ 2 2 4 8 T.%g8 R ) = I a W 7 / 3 1 , / 0 1~ / P , AL AB 3 A ^ _! < B- A2 2 + W 6B AL AB 3 A% g _!8 FO 1 , = A 78 h A ~ AB = 8 = a 2 = ( L ( v .∆‘ 8 n O I N : ; ) = I AG 7 ~ ' < AG 7 ~ ) 8 ~ ) ) = I a 0 W 0 1~ / P , ‘ 1 1 2 1 1 2 2 2 2 2 2 ) I.ω = m . R .ω = m R . .ω = m v . 2 2 5 5 5 2 E 7 ƒ ƒ 1 mv 7 2 ) # ƒ 2 mv + = mv 8 5 2 10 HB 0 1 , = ( A 7 Q = − W ∆ = − m − = − . . − = , d (v 2 2 2 1 ) 7 v 1 (82 102 ) 25 2(J) 10 10 T.%u8 R W 7 X 0 K A' O J > 6' t 3 8 & ' $ HB 3 (2 \ / 7 5 6$ H' O R 4 ! / R AB 3 7 N 6; AB 3 AB = M ( G A' O R8 $ A' O J > 0 7 < ~ ƒ mgh 8 n t L a < ~ 2 2 6 < 2 ~ ) K A' O ‘ 1 iω%0 7 i 12 P c 2 ) O 3 AL ) 3 i mh 2 0 ω 12 AB 3 7 1N 3 8 - ( ' 1 B 6= 2 ~ 1 mh 2 g 3 2 mgh I . ω . = 2 ω . = mgh ω = 2 2 3 h FG 7 ! AB 3 (2 \ 1N A ω g
3 h = 3.10.5 = 12 2 , _!8 6$ sm 12 R / K A' O J > 8 - ( P > O AB 3 AB M ( 0 7 AB 3 R / v 2gx 8 M F c / I 62 g 3 2 ω 2gx x. = 2gx h ^_S S0SS 8 h 3 T.S^8 FG \ a - J 4 ^0X 0 + AB W 7 ( / 1~ / P , 4 a - J 4 78 F AB 3 (2 AB K 3 a - J 4 < $ HB 7 ( ) = I a 5 6$ HB 12 x d 5
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 $ HB 12 A2 d 8 "s = !D AB 3 6 I AB 6; / P $8 s = !D ; 7 AB a 1~ / P , 0 / P AB 3 I G \ a - J 4 7 8 RP c ) O AB 7 A < 6; i /8 8w%0 7 / 12 ; !3 - A2 AB 8 n AB 1~ / P , AL AB 3 (2 A AB 7 ~ ) ‘ 1 1 1 2 2 2 2 ) I ω . = kmR ω = kmv 8 2 2 2 ~ 2 - I AB ‘ ‘ 1 1 1 2 2 ) # ‘ kmv + mv = (k + ) 2 1 mv 8 2 2 2 F c ' 1 B 6= 2 ~ 0 ~ AB K V a - J 4 6; = < ~ AB 1 ( 2gh k + ) 1 mv2 = mgh v = 8 2 k +1 - ( /< ) = t ) 2 AL ^0X 0 AB 7 ( $ ) = I a / %_X8 g 2 h 10gh 10 9 . 8 , 0 . 5 , v = = = = 2 6 , ( 5 m / s) 2 / 5 +1 7 7 6$ x a / _%8 2gh 4gh 4.9 8 , .0 5 , v = = = = 2 5 , ( 6 m / s) 1 / 2 +1 3 3 $ ) = I a / 8 2gh v = = gh = 9 8 , 0 . 5 , = 2 2 , ( 1 m / s) 1+1 T.S 8 o7 6; P " a $0 6; " y $ q , = G \ a - J 4 8 o N 7 q 6 /O w Y A2 q / 3 1 , ^0X/ 8 Ra , ) r ! 3 8 fQ $ HB 3 ' < K 3 a - J 4 7 / / P ` 6$ RP c ) O y 5 $ h 6 1V 1~ / P , L V a - J 4 ` o 6 < \ a - J 4 ^0X 0 7 4 α S^^0 / 3 1 , 4 P - %Y^^/ _ S A2 -% S^^/ _ S8 $ EM A2 /< ) = 62 T.S^ 0 AB 2 a " !3 P c ) O Q$ AB 3 (2 N V a 4 2 1L 8 E 70 62 2 0 7 /< 1 B ; 0 / 3 a 6; P !b 1~ / 3 6; 8 6$ U C 6 < 0 P c ) O / 3 P A2 , ' 2 2 2 + 6; P > > i mR R R1 ,I = m 0 7 w 12 6 /O 2 2 2 8 H / 3 1 , 6; 4 ρ 9πw% ρ%9π "w% . 2 R $0 7 9 12 1 (2 0 ρ A2 ρ% 12 / 3 1 , 4 P A2 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 (ρ − ρ R 2 1 ) 2 ρ 2 % R "ρ R = 1 %.ρ $w% 1 ρ2 R 2 + 2 ρ − ρ ρ − ρ FG 7 O , R 2 2 I = m 1 = 2 1 2 m . R 0 " 2 1 k = $8 2 2 2ρ 2ρ 2 2 HB 3 P / 1~ L V (3 " c 62 T.S^$ 2gh 4gh v = = 8 Al 1/ 2 +1 3 HB 3 / 1~ L V (3 2gh 2gh 4ρ g . h 4gh 2 v = = = < = v "A ρ < ρ $ Pb Al k +1 2ρ − ρ ρ ρ 1 2 2 1 4 − 3 2 1 +1 2ρ2 $ EM A2 /< ) = A AB 3 AB 1~ / P , 62 T.S^ 1 (k + )1mv2 = mgh 2 F 2 c + A< - 2 , (k + ) 1 mv. ' v = mg ' h (k + ) 1 mv. ' v = mg(v sinα ) g sinα a = v' = k +1 v (2gh)/ (k + ) 1 2h ( . k + ) 1 t = = = a g sinα / (k + ) 2 1 g sin α F 70 ^0X 0 α S^^0 - ( / 3 P 0 / _% 2.0 5 , ( . 1/ 2 + ) 1 t = = 0 7 , ( 8 s) 9 8 2 , .sin 300 ρ − ρ - ( / 3 0 2 2 1 . 1300 − 2600 100 2 1 k = = 2ρ 2 1 . 1300 113 2 2.0 5 , ( . 100 / 113 + ) 1 t = = 0 8 , ( 8 s) 9 8 2 , .sin 300 T.S%8 R + W 4 < s P- / A2 I ) = 0 y ) = 7 / 3 1 , ^/ 8 n = G y ) = L ) 12 ^0[X 8 s < ) AL AB 3 ω Ad _!8 fQ P ( + M A2 AB 3 < < + 7 1 / = G y ) = < ) \ d 12 ^0%^ 0 6 < P c ) O + A2 < 3 AL ) 12 i^ %0X/ 8 %8 RP c ) O + A2 ) = 1N 6 I A2 1N ! 2 2 I = I + 2 m . d . = 2 5 , + 2 1 . 0.0 7 , 5 = 13 7 , 5 kgm 1 0 1 ( 2 ) 2 2 I = I + 2 m . d . = 2 5 , + 2 1 . 0.0 2 , = 3 3 , 0 kgm 2 0 2 ( 2 ) n ) ) 7 ~ A2 P c 1 , 12 L = I ω 1 1 1 ‘ 1 2 1 2 I ω = 1 . 3 7 , 5. π = 8 1 1 (2 ) 27 ( 5 J) 2 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 E P c 1 , , 6= 2 4 AB 3 7 ) ! / + 1 = C 6 > I 13 7 , 5 I ω = L = L = I 1 ω ω = ω = .2π = 8 3 , 3π / 2 2 2 1 1 1 2 1 (rad s) I 3 3 , 2 F c ' 1: A ~ 0 + C I 3 P 6; ] 1 1 ∆‘ ‘ 2 2 % . ‘ I ω − I ω 2 2 1 1 2 2 1 = 3 . 3 , ( . 8, π )2 1 33 − .13 7 , 5 ( . 2π )2 = 87 ( 1 J) 2 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 X. 8 F 1M N Ra F + 14 AB 7 / 3 1 , ; 4 a F 0 6 < ; / 3 1 , Ra F + R 0u[8 ^S^/ A2 / = 6 G a < V Ra F + 12 Tu8 ^Y/ 8 - ( P > ' 1 B A AB - (‹ mM −3 30 − 10 . 9 , 1 7.10 F = G 11 −6 = 6 , 6 7.10 ≈ 9 , 5 .10 (N ) r 2 (149 1.0 )2 9 X.%8 n = @ F A2 Ra F ~ 12 SgT^^^/ 8 n 3 1 , F 12 X0uY8 ^%[ A2 Ra F ~ 12 [0SX8 ^%X 8 & ' A' O 7 1M N Ra F ~ A2 F 14 V 6; 8 sm / = G 7 1M N Ra F ~ A2 F V 6; < V F 12 " k 2 • 1$8 F 7 M m M m F = F G E = G M E M 2 2 x (l − x) M 2 2 − = E (l x) M x M M l − x M = x M E l 384000 x = = ≈ 345600(km) 1+ M / M 25 27 M E 1+ 7 3 , 5 1 . 0 /( 9 , 5 6.10 ) X.S8 R ) = I / 3 1 , a # . I W J 4 - /r (2 8 F 7 (2 10 z ] / 3 1 , %8 F 1M N 14 ) = I 8 o 2 @ ( Q0 / 7 1M N 7 14 / 3 1 , 12 m .dm m .m .dx 1 1 2 dF = −G = G
(l + a − x)2
l(l + a − x)2 9M N t 14 ) = I 12 l Gm m l dx Gm m 1 1 2 1 2 F = dF = − = . 2 l
l + a − x l
l + a − x 0 ( ) 0 Gm m 1 1 Gm m 1 2 = . 1 2 − = l a l + a a(l + a) X.T8 f ) = I 7 q 6 /O / 3 1 , 4 1I 1 , 6; - A2 -% , a P + 1Q 7 / 3 1 , 4 12 -^8 fQ / 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 $ f ) = I N 5 6$ f ) = I } 8 o 6 < /O L P + 1Q 1L ! AL /O L ) = I A2 - ‚ -%8 &r ) = I > # 9M - (‹ @ ) = I 12 m m G 4π 4π ρ ρ 16 2 6 π GR 1 2 3 3 1 2 F = G = .ρ . R .ρ R = k "AL k = $ 1 2 2 1 2 2 r r 3 3 r 9 # E /O L P + 1L ) = I 4 / / P 7 ) = I > 0 1M - (‹ P + 14 ) = > c - / M 4 1‹ 8 U< 6L - I 1Q 0 - I d 1 !b ( 1M - (‹ q 1L , AL 1M - (‹ ( - I V 8 K V 0 - I 12 - I 1Q 6' < 6K ) = I > 8 F M K 4 l 7 ρ ρ 1 0 F = k 2 2 r # U< m „ 12 ( 0 t ,- 1M ( 14 ) = I 6; ρ1
F = F − F = k ρ − ρ 1 2 ( 2 2 0 ) r s 3 ( 14 ) = I 12 F kρ ρ − ρ 3 ρ − ρ 4 3 G π R 1 ( 2 0 ) 2 0 a = = . = K "AL K = $ 2 3 2 m r 4πρ R r 3 1 1 # F M0 < m L A - O ) = I 12 ( 0 1M t ,- ( 14 ) = I % 12 ρ2 F ' = k (ρ − ρ 2 1 0 ) r ρ − ρ 1 0 a' = K 2 r s 3 3 @ N ρ + ρ − 2ρ 1 2 0
a = a + a' = K 0 2 r $ f ) = I 1 I ρ + ρ
a + a' > 0 ⇔ ρ + ρ − 2ρ > 0 1 2 ⇔ ρ < 1 2 0 0 2 6$ f ) = I ρ + ρ
a + a'< 0 ⇔ ρ + ρ − 2ρ < 0 1 2 ⇔ ρ > 1 2 0 0 2 X.X8 F ) = I 6; 6 /O w + / r 1y I 8 Ra 1y <- N AL a ) = I A2 ) V 78 n 3 1 , ) = I L / / r 1y 6; R8 F 4 - y V ) = I A2 1y0 + a d 6 Q / 3 1 , V ) = I ( " X.%$8 F 1M - (‹ 2 ) = I " C / r 1y$ ( 14 d 6 8 9M - (‹ ) = I C / r 1y N 6; 1M - (‹ V 6K ) = I / r 1y A2 - I 6' / r 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 9M - (‹ ) = I / r 1y 14 d 6 Mm F = G 1 2 d 9M - (‹ - I 6' / r 14 d 6 3 4π R . m ρ. M ' m 3 2 m 4π Mm 3 F = G = . G = G .ρ R = G 2 2 2 2 r R R 3 ( 2 2d − R)2 d − 8 d − 2 2 HB 0 1M - (‹ ) = I C / r 1y 14 d 6 2 2 1 1
7d − 8dR + 2R
F = F − F = GMm − = GMm 1 2 2 2 d 2(2d − R) 2(2d − R)2 X.Y8 F AB 3 (2 F ) ) Ra F + 0 6 < ; / 3 1 , Ra F + 12 R %8 ^S^/ A2 / = 6 @ F A2 Ra F + ( 0X8 ^g/ 8 9M L V F ) Ra F + O 12 1M - (‹ F = F hd ht M M v2 G E S = M d 2 E d GM 6 , 6 7.10 1 − .12 1 . 030 v S = = ≈ 3 1
. 04 (m / s) = 30(km / s) d 5 , 1 .1011 X.[8 F AB 3 (2 A V F 6 < ; ) * A 12 d 8 H K 6 ^^^/ 8 o A \ ' = K 1M N F A2 K 4 0 1M = / P / O / P / 8 o 6 /O F w YS[^/ 8 9B- 1 B M 62 X.Y A V ) F 0 7 G M . GM 6 , 6 7.10−11 9 , 5 . 6.1024 v E E = = = ≈ 7 3
, 44.103(m / s) = 7 3 , 4(km / s . ) d R + h 106 + 3 , 6 7.106 X.g8 f 2 ) ) Ra F + AL ) * I N 12 @ Ad d 6 /O 1I 1 , 6; w X^8 ^Y/ 0 "F $ A2 w% ^g8 ^Y/ "h / $8 F | !3 AB 3 (2 2 78 hD ( 1B- 1 B A2 O 62 X.Y0 7 GM GM v S = ; v S = 1 2 d d 1 2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 v GM d d 108 1 . 06 1 = S . 2 2 = = ≈ 8 , 0 5 v d GM d 150 1 . 06 2 1 S 1 X.u8 n 3 1 , Ra F ~ Q / 3 1 , F g 1I 0 + /O Ra F ~ 6; S_ + /O F 8 fQ + 4 a a Y^^ 14 Ra F ~ !b a 6 4 8 F c ' 1 B A AB - (‹ M m E P = G 2 RE M m k M m k M m k P' = G M = G 1 E 1 = G E 1 = P R2 2 2 2 2 M (k R 2 E ) k R k 2 E 2 1/ 81 P' = 6 . 00 ≈ 100(N ) (3/1 ) 1 2 X. ^8 7 6; AP < "AP < $ / e- m 4 a + - 7 14 A ‰ 3 ' Š " > 4 a A ! / P 3 AL a $8 R 3 AB - = A 2 a - J O G FV ! P AL AB 3 7 6; AB 3 F ) ) 78 fC O AB 3 (2 A2 A 78 Z < / F ) ) 7 12 F %S + XY - N T V 8 Z /O O F 12 w YS[g/ 8 sm / = G A < V F 12 (0 AB 3 (2 A 12 GM 2 d π d 3 E v = T = = 2π d v GM E T 2GM (86164)2 6 , 6 . 7.10 1 − .1 9 , 5 6 1 . 024 d E 3 = = ≈ 42 1 , 26 1 . 06 3 (m) = 42126(km) 4 2 π 4 2 π HB 0 AB 3 (2 A2 A 12 GM 2π GM 2 6 , 6 . 7.10 1 − π . 1 9 , 5 6 1 . 024 v E E 3 = = = ≈ , 3 07 1 . 03 3 (m / s) d T 86164
h = d − R = 42126 − 6378 = 3574 ( 8 km) X. 8 F AB 3 Al - ii 3 AL Ra F ~ " x 12 AB 3 4 1D - 7 G 6 a Ra F ~ I - = 7 7 7 / Q !> N Ra F ~ $8 s 3 m + 4 6 a Ra F ~ M M g = G M 2 RM HB 3 Al - , O c P >
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 G 2 M 2 6 , 6 . 7.10−11 7 . 3 , 5.1022 v = 2g R M = = ≈ 3 , 2 8.103 / M M M (m s) R 3 /11 3 , 6 . 7 1 . 06 M ( ) X. %8 U + 4 1D 0 A V I 4 F , 14 X^^/ 8$F 3 m + K 75 6$ = - 7 A L AB 3 6; 6 4 c - A P 7 AL 6 /O F ) * 7 ) F 12 + d 8 n 7 / ) A ) F 6; 6 4 ` 9 6 /O F 6; YX^^/ 0 3 m + 4 6 a F 6; u0g _!%8 ZQ ) !> = / P / O8 $ s 3 m + , O c P > 2 2 2 M R M R 6500 g = G = .G = g = 8 , 9 . ≈ , 8 45 m / s 2 2 0 ( 2 ) r r R R + h 6500 + 500 6$ ) * A 12 + d 0 1M - (‹ N 6; 1M L V F = F hd ht M m v2 GM GM R2 G E = m v E E = = . r 2 r R + h R2 R + h g R2 8 , 9 6 . 500 . 2 106 v 0 = = ≈ 7 6
, 9.103(m / s) = 7 6 , 9(km / s) R + h 7000.103 o /• ) A 12 2 r π (R + h)3 7 . 3 1018 T = = 2π = 2π
≈ 5720(s) ≈ 1h3 ' 5 2 v g R 8 , 9 . 5 , 6 2 1 . 012 0 X. S8 Rm AB 4 a ' !> N Ra F + 8 H 6 4 "Ra F + K ‰( L V Š$ 1M 7 4 AL 1M N F 0 6 2 "Ra F + K 4 ‰ \ I Š$ 1M 7 G 6L 1M N F 8 H AB 0 6 4 m AB - = a 6 2 0 7 7 N / P ` F ! ` n P N 0 A Ra F + N = F 1‹ AB 4 6 a F 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Y. 8 HB - = 7 AB 3 6 4 /O L 7 c - = % 1I 8 /O L AB c - = % 1I 0 I 7 2 l v = 1 − = k = 5 , 0 2 l c 0 2 2 v = c ( 2 1 − k )
v = c 1− k2 = 3.108. 1 − 0 52 , ≈ 2 6 , .108 (m / s) Y.%8 R x d 6 /O w J AL AB 3 A c - ! ! AL a x 8 fQ ) < e AL F 0 x 7 ( ` x d / J AL AB 3 A c - ! ! AL a x !b 6' r 2 c1 -8 nO L c - 6' 1 / /O L c - A P 7 , @ 4 8 sm - + 6 4 x ) < e AL 7 12 2 2 2
x' + y' = R 2 Ra / v x = x' 1 − ; y = y' 2 c HB 0 - + 6 4 ) < e AL F 2 x 2 2 + y = R 2 v 1 − 2 c V 12 - + c1 -8 Y.S8 o7 7 W W 3 " W 6 $ 3 AL Ab Y. 8 9 3 O + 12 1N W W ]j ) 3 ( W W ]8 fQ 3 AL + ) ! > 4 ! AL 7 W W ] / W W \ + 7 < 2 ` H A' O / 0 = W W8 H' O / W W ( O 3 !M W + !
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 ]j ] f Y. Y.T8 f 4•P Al AL AB 3 6; ^0uX 1I AB 3 ! 8 fQ / = + c W W + ) ! > 4 F > AL / = ‰ + !3 Š V 4•P 8 hD ( P > A + t ∆ 1 ∆t' = = ≈ , 3 ( 2 s) v2 1 − 9 , 0 52 1− c2 Y.X8 n 3 1 , α ~ 4 6 4 < ~ AB 3 7 G ^ < ^0u 1I AB 3 ! 8 U< ~ AB 3 0 / 3 1 , l ~ 14 m0 m = 1− (v / c)2 1 − 1 m
∆ = m − m = m 27 −1 = 4 , 1 . 67 1 . 0 . −1 0 0 1 − (v / c)2 2 1 − 9 , 0 −27 ≈ , 8 6 1 . 0 (kg) Y.Y8 n 3 1 , 41c 6; 1I / 3 1 , \ 78 F ~ 41c 4 8 ~ c1c 6; ~ 1 , 2 - I 1N A2 1N > 4 W = m ∆ c2 . = (2m − m = 0 0 )c2 m c2 0 −31 16 1 − 4 = 1 , 9 1 . 0 .9 1 . 0 ≈ , 8 2 1 . 0 (J ) Y.[8 n - V V u%–%SX ~ 1 , = - 7 / = %^^ RcH8 F t / 3 1 , / - V / 1 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 U~ 1 , = - 7 \ 1 B AL / 3 2 E = m ∆ c E E N . 200 1 . 6 , .10 1 − 3.6 0 , 25.1026 m 0 ∆ = = = ≈ 0 2 , 1 ( 4 kg / kmol) c2 c2 9 1 . 016 Y.g8 F AB 3 4•P < ~ 1 , 2 - I 4•P 7 6; ^ 1I ~ 1 , \ 78 U~ 1 , 2 - I 4•P 6; / 1I ~ 1 , \ 2 m c 0 2 W = = km c 0 2 v 1 − 2 c 2 v 1 1 1− = 2 v = 2 c 1− 2 2 2 c k k 1 8 1 v = c 1 − = 3 1 . 0 1 − ≈ 2 9 , 85 1 . 08 (m / s) k 2 102 Y.u8 $ Ry - N Ra F + 6> ~ 1 , 6; Y0X8 ^% /‘ 8 U< 6> Ra F + 12 / P t + / 3 1 , 7 = D 12 6 4 ` 6$ s = O ! M < / 3 1 , Ra F + 1 / P t 8 $ hM t / 3 1 , - A2 !M t ~ 1 , 2 ∆E = m ∆ c E ∆ m ∆ c2 0 5 , 1 . 9 , 7 1 . 030.9 1 . 016 t = = = ≈ 3 7 , 9.1018 (s) P P 6 5 , 1 . 021 3 . 6 , 1 . 06 11 t ≈ , 1 2.10 " ~ $ 6$ Ra F + AG ~ 1 , AG B ~ 1 , G 64 2 8 U< - I ~ 1 , B A2 6; - I 0 ~ 1 , Ra F + / P t 0 4 / 3 1 , Ra F + / P t 8 Y. ^8 & ' ‰ + !3 Š τ 4•P µ 7 ~ 1 , ‘ ^ucH " ) < - d O $5 + !3 4•P \ 12 τ^ %0%8 ^.Y!0 / 3 1 , 4•P µ 12 %^Y0[ c " c 12 / 3 1 , 41c $8 ‰F + !3 Š 4•P ) < - d O , ' c P > τ m τ m c2 Wτ 109.1 6 , 1 . 0 1 − 9 2 . 2 , .10 6 − 0 v 0 v 0 τ = = = τ = = ≈ 2 1 , 1 . 0−5 2 0 (s) 2 m mc mc2 206 7 , 9 . 1 , .10−31 9 . .1016 v 1 − c2
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 [. 8 F AB 3 = (d / O oz% 3 (‹ 6 < ; > D + / 3 1 , / O = ) < ( 3 6; ^0X / 8 n 3 1 , 4 / O 6; [0X/ _ S8 + /O 3 6; % 8 o / O 12 1Q 1: K 8 sm / 3 1 , / O = ) < ( 3 A' + 12 µ8 F 7 m ρ V . ρ S . l µ = = = = S ρ v t t t µ 0 5 , 1 1 v = = . ≈ 0 1 , 2(m / s) ρS 1800 2 2.10−2 7 5 , .π 2 [.%8 7 1y + /O ( 8 + /O 6 E ^0X 8 F !M - AB 3 M L K 6 A2 M L 8 - ( 6; !3 + ,- ^0% 8 sm h A2 h% 12 < ( 6 A2 1y 5 A A2 A% 12 AB 3 = L ! a L A2 = ) = 1y 8 n 70 c - Zc 1 2 2
v + 2gh = v 1 2 Ra / 0 ( O 1 4 (d = v S = v S 1 1 2 2 2 2 S v 1 = v2 = v2 + 2gh 2 S 1 1 2 2 D4 v 1+ = 2gh 1 d4 2gh 2gh d2 v = ≈ = 2gh ( do d D ) 1 1 + (D / d)4 (D / d)4 D2 n ^0% 0 AB 3 M L 12 2 0 0 , 1 v = 2 9 . 8 , 0 . 2 , ≈ 7 9 , 2 1 . 0−4 / 1 (m s) 0 5 , [.S8 F 4 62 7 a 6 L 0 2 6 7 1y Q ; 6 A2 M L %8 RM L 6 , @ / P t 8 fQ L 3 a 62 1y 9 6; 6 4 " c - ; $` s = 62 + ,- $ %X A2 % Y 5 6$ Y A2 % %X 8 HB 3 L / ) 1y
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 v = 2gh 0 2 h / / Q 1y0 - I D L AB r AL AB 3 6 I 6; A^8 F + G / / Q 1y < / 12 2h t 1 = g FI L 12 2h1 L = v t = 2gh . = 2 h h 0 2 1 2 g $ %X 0 % Y
L = 2 25.16 = 40(cm) 6$ Y 0 % %X L = 2 16 2 . 5 = 40(cm) [.T8 U + a 6 L 7 2 J > 4 a 62 ; 8 F 4 2 6 7 (q 1y Q8 o 1y q ; 4 + J > 8 s = !D < ( 6 ! AL < ( 1y ! > L 6 / P t 8 $ o > ; AB 3 L 4 a 62 6; 8 6$ o > ; 3 L 3 q 4 a 62 / = G 1y < > L 6 - = 6; / = G 1y / < a 62 8 $ R 3 L - - = 1y A' O 2 ` &r 1y K A' O a 62 / = A2 a L 12 %8 HB 3 L /
/ Q 1y 12 v = 2gh 0 2 $ hD ( ' 1 B 6= 2 ~ 1 , - I L ! / / Q 6 1 1 2 2 mv = mv + mgh = mgh + mgh 0 1 2 1 2 2 v = 2g( h + h ) = 2gH 1 2 HL f 12 > L ! AL a 62 8 wk 2 ; AB 3 L a 62 / P - A2 A' O 1y8 6$ FG /< ) = 62 [.S0 7 L = 2 h h = 2 h − 1 2 (H h) ' L = 2 ' h (H − ' h ) L A2 q L = ' L
h( H − h ) = ' h ( H − ' h )
H( h − h' ) − ( h 2 − h 2 ' ) = 0
( h − h' )( H − h − h' ) = 0 E h ≠ ' h H = h + ' h hay h = H − ' h $ hD ( 6 J > oP! L = 2 h(H − h) ≤ H
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 E ‰ Š = / A2 \ / H
h = H − h h = 8 2 [.X8 s @ I L 6' 1y Q8 R> L K I I f S^ 8 fQ L = ) 1y AL AB 3 6; 6 4 + ,- ! $ sI L > 4 5 6$ sI , V 14 $ sI AL 3 0% _!% 14 4 W 3 ( L 8 ($ sI c - ; AL 3 0% _!%8 HB 3 L = / Q I - A2 - ! r- 14 I 8 n I AL 3 L 14 4 a 3 ( L !b - ! - r- 14 I 8 F 7 1 2 ma P + ρv = P + ρgh + = P + ρgh + ρah 0 2 0 S 0 v = 2(g + a)h " ( L c - m 1M $ Œ U< I > 4 a , V 14 ^ v = 2gh = 2.9 8 , 0 . 3 , ≈ 2 4 , ( 2 m / s) Œ U< I AL 3 0% _!% L 14 4 v = ( 2 g + a)h = 2 ( . 9 8 , +1 2 , )0 3 , ≈ 2 5 , 7(m / s) A2 / 3 L 3 ( L v = ( 2 g − a)h = 2 ( . 9 8 , −1 2 , )0 3 , ≈ 2 2 , 7(m / s) Œ U< I AL 3 0% _!% c - 0 - ! - \ 4 2 I 4 / P 7 ( 12 t AB 3 L = ! AL / I 8 v = 2gh ≈ 2 4 , 2(m / s) [.Y8 R 6 0 ( O h > I L 8 6 7 1y ( O h 8 fQ $ h 6 1V L K 6 = < ` 6$ M L - + < 2 / K 1y8 ZQ ) L L 8 hD ( 6 > AB 3 L > L C O K 62 [.%0 7 2gh v = 1+(S/ S )2 1 dh 2gh dh 2g = − = − dt dt 1+ (S / S + / 1 )2 h 1 (S S )2 1 h dh t ' 2g = − dt 2 − = − 2 ( h h0 ) 2g t h' 1 + / + / h 0 (S S1) 1 (S S )2 1 0
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 2 1 2g h = 2 h − t 0 4 1 + (S / S )2 1 F + L 6 = < 12 2h 1 [ + 0 (S / S1)2] τ = g Œ U< S S 7 1 S 2h0 τ = S g 1 2 S g 1 h = h − t . 0 S 2 [.[8 F V + 7 , ^0% 1O L A2 6 8 fQ K 6 - = 7 1y + /O 6; 6 4 > L 6 / P t A2 7 6; "/ G 1y$8 > L 6 / P t 0 1 , L t A2 - = 6; 1 , L = dV = dV 1 2 k d . t = vSdt = S 2gh d . t 3 k 0 2 , .10− −5 S = = ≈ 4 5 , 2 1 . 0 ( 2 m ) 2gh 2 9 . 8 , .1 S 4 4 4 . 5 , 2 1 . 0−5 d = = ≈ 7 6 , .10−3 (m) π π [.g8 U + (' 3 (m c > I L AL AB 3 A g0S _! " [.%$8 fQ > L (V 14 3 8 - ( ' 1 B Zc 1 1 1 2 2 P + v ρ = P + g ρ h + ρv = P + g ρ h + h 0 0 0 ( 0 ) 2 2 v2 8 3 , 32 h = = ≈ 3 5 , ( 4 m) 2g 2.9 8 , [.u8 U + t / P / O ) 3 ]Z " [.S$8 o> y - N 7 X 1O / P / O = ) 3 8 E O < ( - I ] 6; % %0 - I Q Z A2 - I 3 6 6; ^0X %8 F > L ∆ 3 6 8 Z < / 3 1 , 4 / P / O 6; 0S%/ _ S8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 U + t / P / O ) 3 ]Z " [.S$8 o> y - N 7 X 1O / P / O = ) 3 8 E O < ( - I ] 6; % %0 - I Q Z A2 - I 3 6 6; ^0X %8 F > L ∆ 3 6 8 Z < / 3 1 , 4 / P / O 6; 0S%/ _ S8 sm ρ 0 ρ% 1I 1 , 12 / 3 1 , 4 / P / O A2 L 5 h 0 h% 12 ( O < ( 3 "h ‚ h%$0 H 12 O / O , t ) 3 V 8 - ( ' 1 B Zc 1 1 1 2 2 P +
ρ v + ρ gh + ρ gh = P +
ρ v + ρ gh' +ρ gh' 1 1 1 1 2 2 1 2 1 1 2 2 2 2 1 V2 V2 ρ − − ρ g h ∆ + ρ g h ∆ = 0 2 1 S2 S2 1 2 1 2 2 ρ V 1 1 ∆h = 1 − 2(ρ − ρ g S S 2 1 ) 2 2 2 1 1 3 , 2.0 0 , 152 1 1 = − ≈ 5 7 , .10−4 (m) = 0 5 , 7(mm) 2(1000 − 1 3 , 2).9 8 , 0 2 , 5 1 . 0−4 4 1 . 0−4 [. ^8 F 4 6 a - < - J A2 ; + a 6 7 / r 1y Q K - O 3 " [.T$8 E O 1y 6; A2 6; h ^^^ %8 R 1y / r ! 6 0 1y / / r K X^ 8 Z > L L f ^^ 8 F 3 6 ! / K 1y8 ZQ ) ! @ A2 6 8 n 3 1 , 6 Q / P / 8 Z < ( O < ( 6 h ^0X %8 & 1M ( 14 6 / K 1y 12 dp dm v . − dm v . v2 ρ Sdt − v2 ρ Sdt F 1 1 2 2 1 2 = = = dt dt dt = ρ ( S 2gh − 2gh = ρ 1 2 ) 2 ghS 6 F 2ρghS S 2 gh 2.1000.10− 9 . 8 , 0 . 5 , −2 γ = = = = = 1 9 , 6 1 . 0 ( 2 m / s ) M ρHS S H 0 5 , 1 . 1 1 [. 8 R 6 2 J > ) ) 7 " •$ AL AB 3 7 ω8 Z > I 1Q 8 $ & ' ( a 1Q 6 8 6$ s = !D - ! V 6 6; -^0 - ! 1Q 14 / 6 8 n 3 1 , 4 1Q 12 ^8 $ s = !D 1Q 6 12 L 8 F - ! ∆- L 14 a 64 6 ! 6 / 6 ) AL AB 3 7 ω %0Y (_! A2 / 6 > 4 8 Z /O 6 12 w ^0X 8 $ n 6 ) 0 y - V D 6 a 1Q / 3 1 , ' ( t ,- 1M # 1M ) O 1 V ω%8 # m 1M 8
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Ra 1Q 6' 4 A2 ; V 6; / 7 J 7 AL t ,- 1M 8 4 , ' 6K 7 m 2 ω r 2 ω r tgα = = mg g 2 F 1 7 dz ω r tgα = dz = dr dr g 2 ω r2 z = z + 0 2g HB 0 ( a 1Q 12 - 6P1P d ) •8 6$ - ! 4 6 > AL 6 /O 12 2 2 2 2 ω r ρω r P = g ρ z = g ρ z + = P + 0 2 0 g 2 $ o 1Q 2 a 7 (2 ( Q R 2 ω r2 dV = 2 r π d . r.z
V = dV = 2 r π . z + dr 0 2g 0 R 2 2 πω ω V = 2 z π r + 4 r = 2 R π z + 2 R 0 0 4g 4g 0 n 6 / P ) 0 - ! 6 12 V 2 ω R2 P = g ρ h = ρg = g ρ z + 1 R2 0 π 4g HB 0 - ! L 14 a 64 ! 6 / 6 ) A2 / 6 > 4 12 2 2 2 2 2 2 ω R ω R ρω R
∆P = P − P = ρg z + − g ρ z + = 2 1 0 0 2g 4g 4 2 2 1000.1 , 2 6 5 , 0 . 4 = ≈ 10 ( 2 N / m ) 4 [. %8 R 3 (‹ 7 u^^ 7 L = " [.X$8 & ' 1M ( 2 3 14 L y 3 < < ( 3 12 A2 7 ( O 6; h T %0 1 1 , L = ) 3 12 v %T 1O _- N 8 F 7 dp dm F = = (v − v 2 1 ) dt dt E Q dm v = v = 0 = Q ρ A2 v ⊥ v 4 1 2 S dt 1 2 2 24 1 . 0 3 − 1000. Q2 ρ 60 F = 2 = 2. ≈ 5 , 0 6 ( 4 N ) S 4.10−4
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522 Hc 1M ,- AL - 7 TX^ A2 L A - O 1k 3
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)