Bài Tập Môn Truyền nhiệt và nhiệt động | Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
8. BÀI TẬP ĐỘNG HỌC VÀ ĐỘNG LỰC HỌC
I. Tóm tắt lý thuyết
1. Đông học: Xác định vận tốc (vận tốc góc) của điểm (của vật) và gia tốc (gia tốc
góc) của điểm (của vật) tại thời điểm cụ thể. -
Vật được khảo sát trong phần động học này gồm: vật chuyển động tịnh tiến,
vật quay quanh trục cố định và vật chuyển động song phẳng. -
Ba phương pháp khảo sát chuyển động của điểm: Phương pháp véctơ, phương
pháp tọa độ đề các và phương pháp tọa độ tự nhiên. Chú ý 2 phương pháp cuối.
2. Động lực học: Xác định vận tốc (vận tốc góc) của điểm (của vật) và gia tốc (gia
tốc góc) của điểm (của vật) theo quãng đường vật đi được. - Định lý động năng:
+ Động năng của vật chuyển động tịnh tiến, vật quay quanh trục cố định và vật
chuyển động song phẳng.
+ Công nguyên tố hoặc công hữu hạn của lực.
+ Áp dụng định lý động năng dạng hữu hạn hoặc dạng vi phân.
- Áp dụng nguyên lý d’Alembert tìm lực (PLLK) nếu yêu cầu. II. Ví dụ
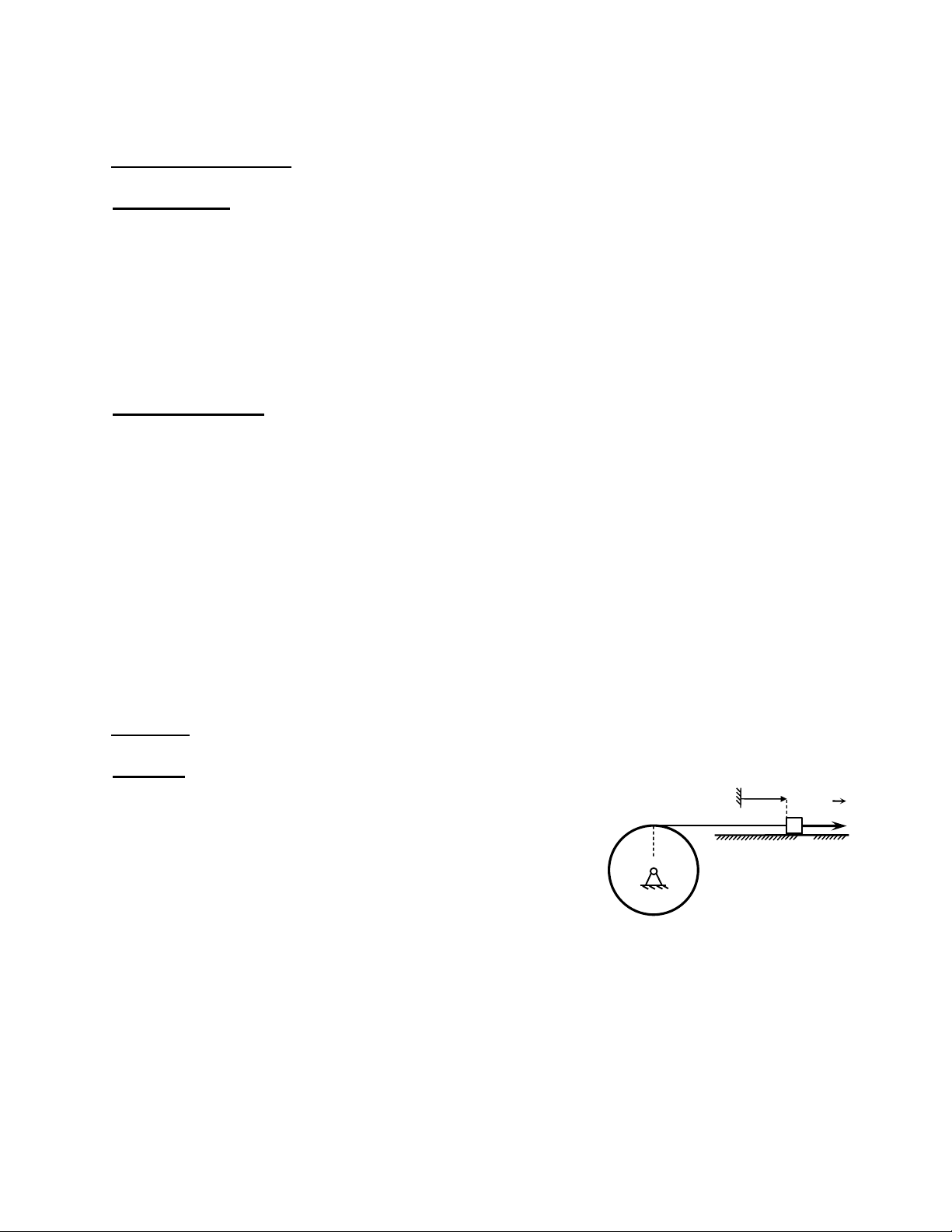
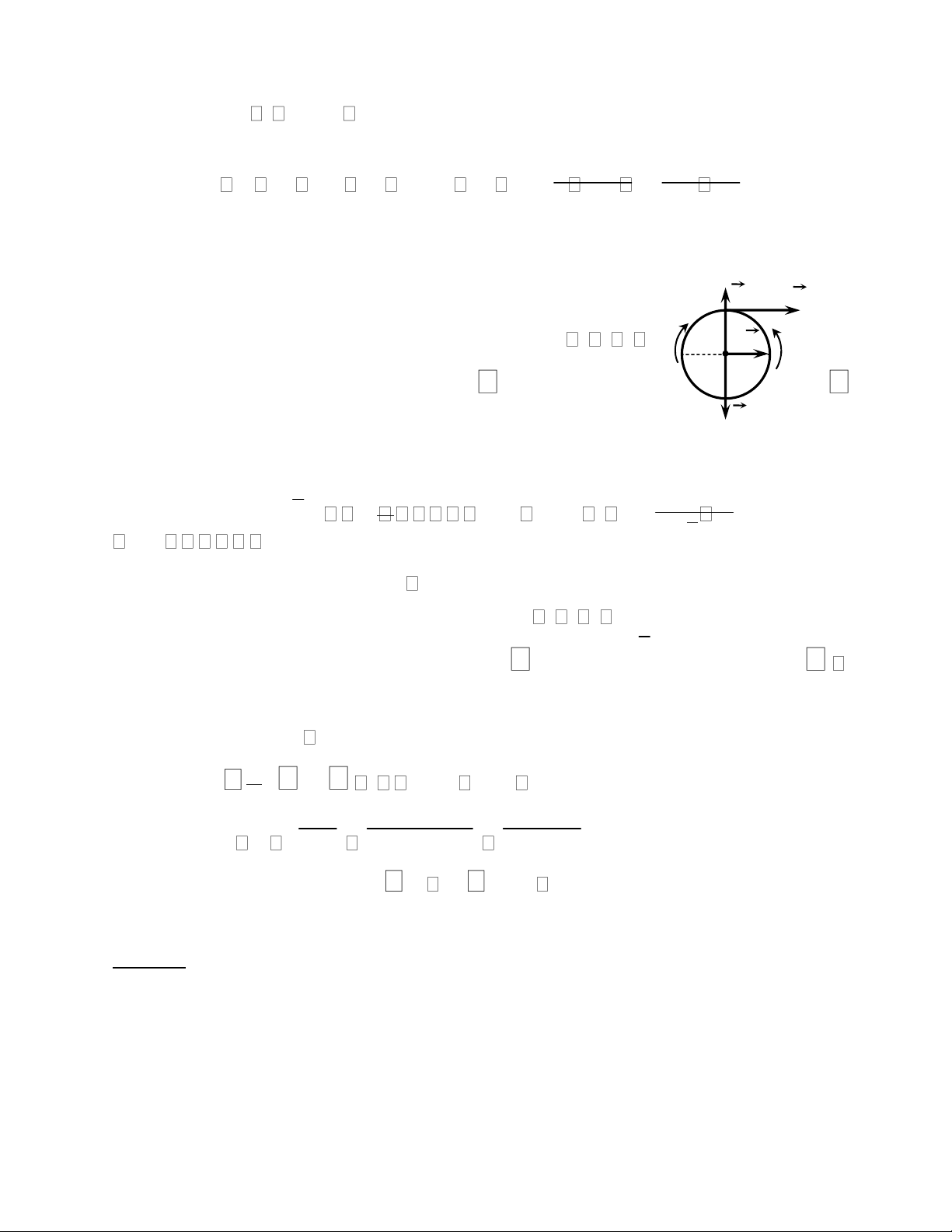
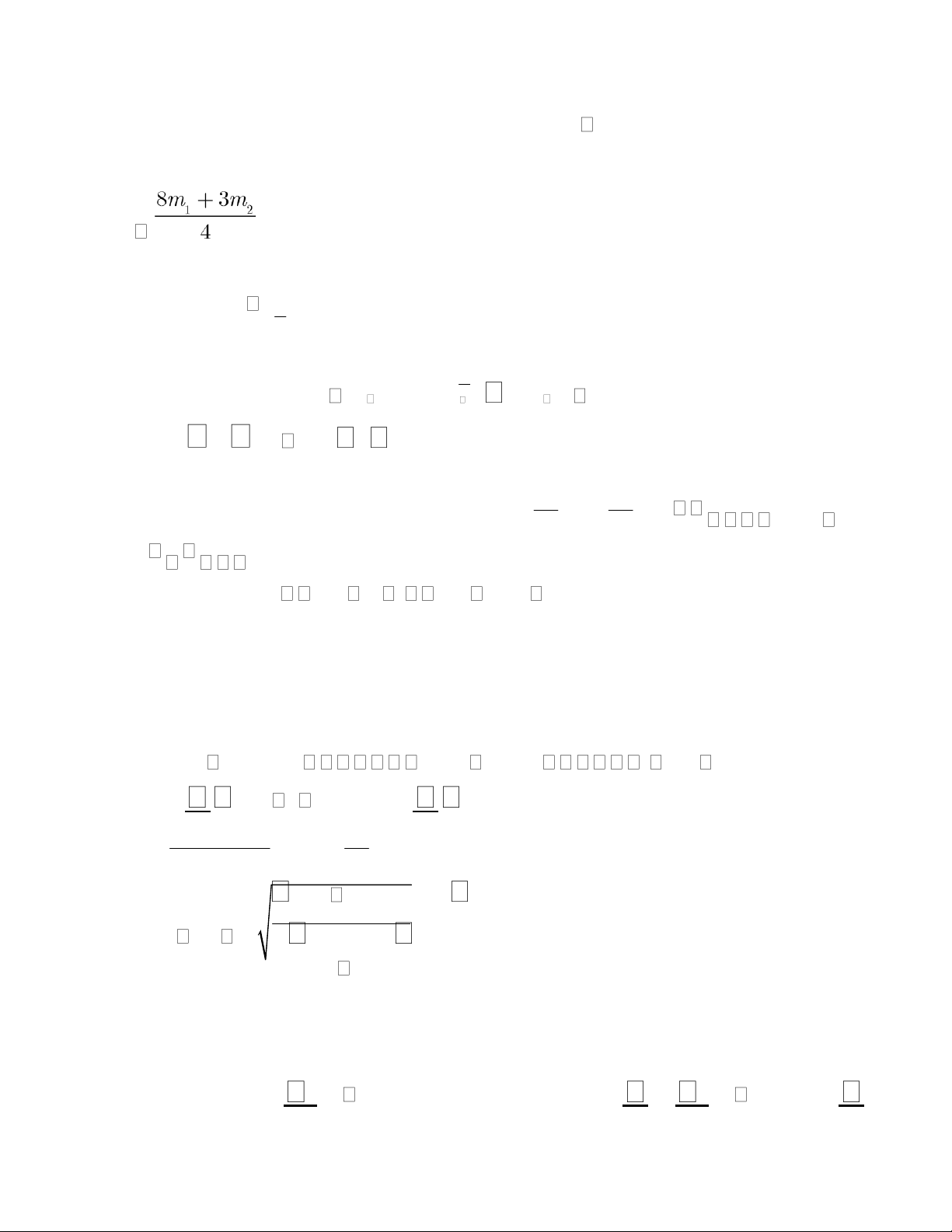
Ví dụ 1. Cho cơ hệ chuyển động trong mặt phẳng thẳng
đứng gồm vành tròn đồng chất tâm O bán kính r quay s A
quanh trục cố định Oz (trục Oz vuông góc với mặt B F
phẳng hình vẽ) nối với vật rắn A bằng một sợi dây nhẹ,
không giãn. Bỏ qua sự trượt tương đối giữa dây và vành O tròn. 1.
Động học: Nếu cho biết phương trình chuyển động của vật A là: s = 2t2(cm).
Tại thời điểm khảo sát t = 1s, hãy xác định vận tốc góc và gia tốc góc của vành tròn. 2.
Động lực học: Cho biết vành tròn đồng chất tâm O bán kính r, khối lượng m1
còn vật rắn A có khối lượng m2. Vật A chuyển động không ma sát trên đường nằm
ngang nhờ lực kéo F có phương ngang, độ lớn không đổi. Biết nhánh dây nằm ngang
luôn căng, bỏ qua ma sát ở ổ trục O và gia tốc trọng trường là g. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
a. Xác định vận tốc của vật A theo quãng đường dịch chuyển s của nó. Biết rằng ban
đầu cơ hệ đứng yên. Tính gia tốc của vật A.
b. Áp dụng nguyên lý dAlembert xác định sức căng của dây. Lời giải: 1. Động học
Do bỏ qua sự trượt tương đối giữa dây và vành tròn nên ta có mối quan hệ vận tốc như sau: s A v A B v B v B v A
PhưChiềơng ngangu từ trái O sang ph ải ω ε vB vA s 4t cm/s
Mặt khác, vành tròn tâm O quay quanh trục cố định qua O và vuông góc với mặt
phẳng hình vẽ nên ta có rad/s B vB 4t
có chiều quay cùng chiều kim
đồng hồ. v r r r t 1s r4 rad/s 4 2
rad/s có chiều quay cùng chiều kim đồng hồ. r 2. Động lực học
a. Xác định vận tốc, gia tốc của vật A lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
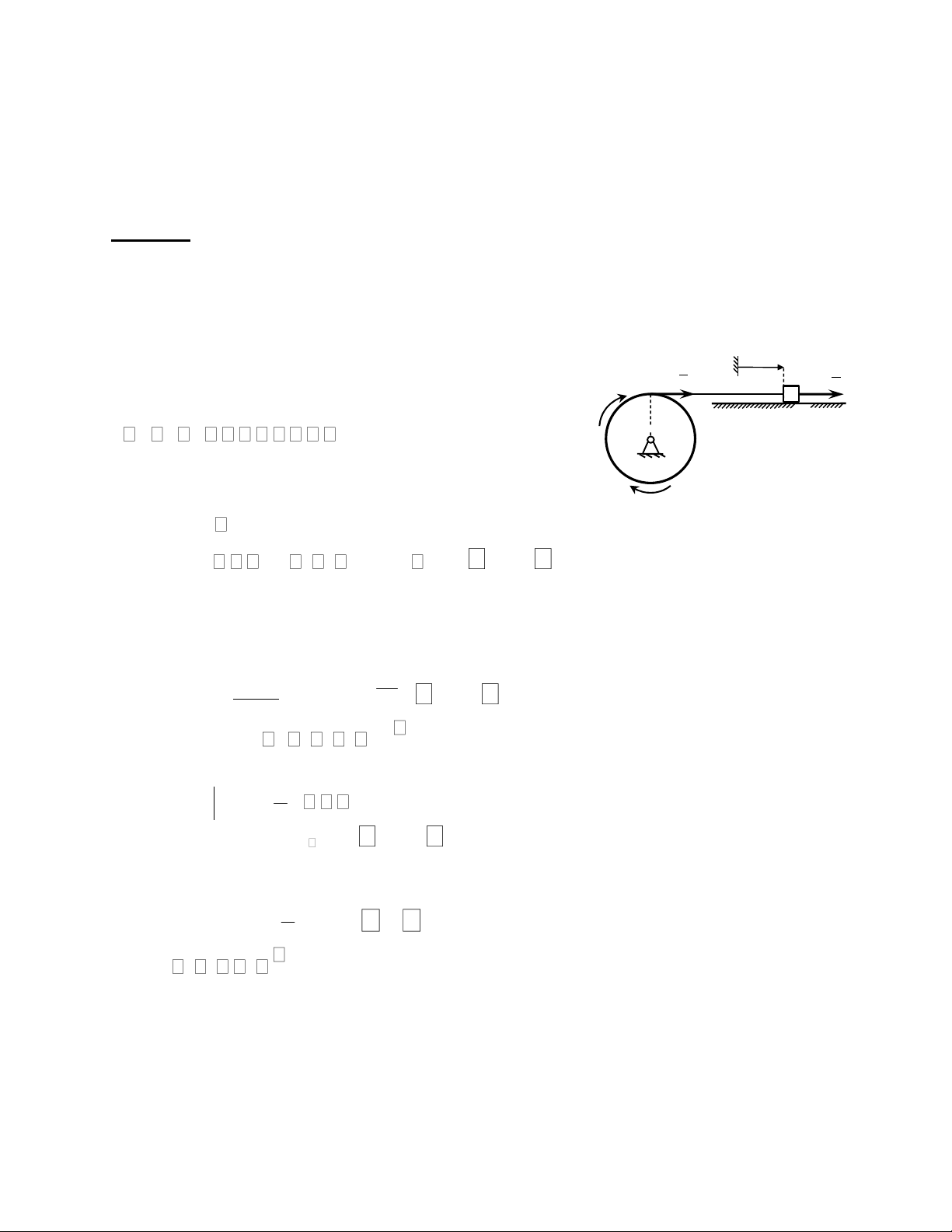
- Động năng của cơ hệ ω s A v A B v B F T TA TO O 1 2 ε T A 2m v2 A 1 2 1mr2 vA 2 TO 2Joz 21 r 21mv1 A2 1 2 1m v1 A2 21 m1 m v2 A2 T m v2 A 2 2
- Để tìm vận tốc của vật A theo quãng đường dịch chuyển của nó, ta áp dụng định lý động
năng dạng hữu hạn như sau: T1 T0 Ak"0" "1" (1) T
trong đó: “0” là thời điểm ban đầu cơ hệ đứng yên nên 0 0
“1” là thời điểm mà vật A đi được một quãng đường s nên T1 m1 m v2 A2
- Tổng công hữu hạn của cơ hệ trong khoảng thời gian từ thời điểm “0” đến thời điểm “1”
Lực sinh công: F . Ta có "0" "1" Ak"0" "1" A F Fs
Thay các đại lượng trên vào biểu thức của định lý động năng (1) ta được lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ 12
2 Fs v 2 A m12 Fsm2 vA m 12 Fsm2 cm/s m1 m v2 A v
Lấy vi phân theo thời gian t hai vế của biểu thức 2 A ta suy ra 2F 2F F 2v v dtA A
sdt 2v a dtA A v dtA aA m1 m2 m1 m2 m1 m2
b. Xác định sức căng của dây (Áp dụng nguyên lý d’Alembert) - Cách 1: + VKS: Vật nặng A N F qt a A T A F x
+ Hệ lực tác dụng lên vật nặng A gồm P N FT2, , , P 2
+ Lực quán tính của vật nặng A. Do vật A chuyển động tịnh tiến với gia tốc a A
PhưChiềơng ngangu từ trái sang ph ải F
aA m1 m2 m a qt 2 A
Suy ra ta có lực quán tính của vật A là F
+ Áp dụng nguyên lý dAlembert ta có hệ lực P N FT F2, , , , qt 0
Chiếu hệ lực lên trục x ta được lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ F T F qt 0
T F F qt F m a2 A F m1m F 2 m2 m1m F 1 m2 - Cách 2: + VKS: Vành tròn tâm O Y O T ε qt X O M O P X Y T , , , O
+ Hệ lực tác dụng lên vành tròn tâm O gồm: 1 O O P
+ Lực quán tính của vành tròn. Do vành tròn quay quanh trục cố 1
định qua O và vuông góc với mặt phẳng cố định nên lực quán
tính của vành tròn là MOqt Joz
MOqt m r1 2 m r1 2 arA mmrF1 1 m2
+ Áp dụng nguyên lý dAlembert ta có hệ lực P X Y T M qt 1, O, O, , O 0. Ta có m qt O Fk 0T r. MO 0 MOqt m rF1 m F1 T r r m 1 m2 m1 m2
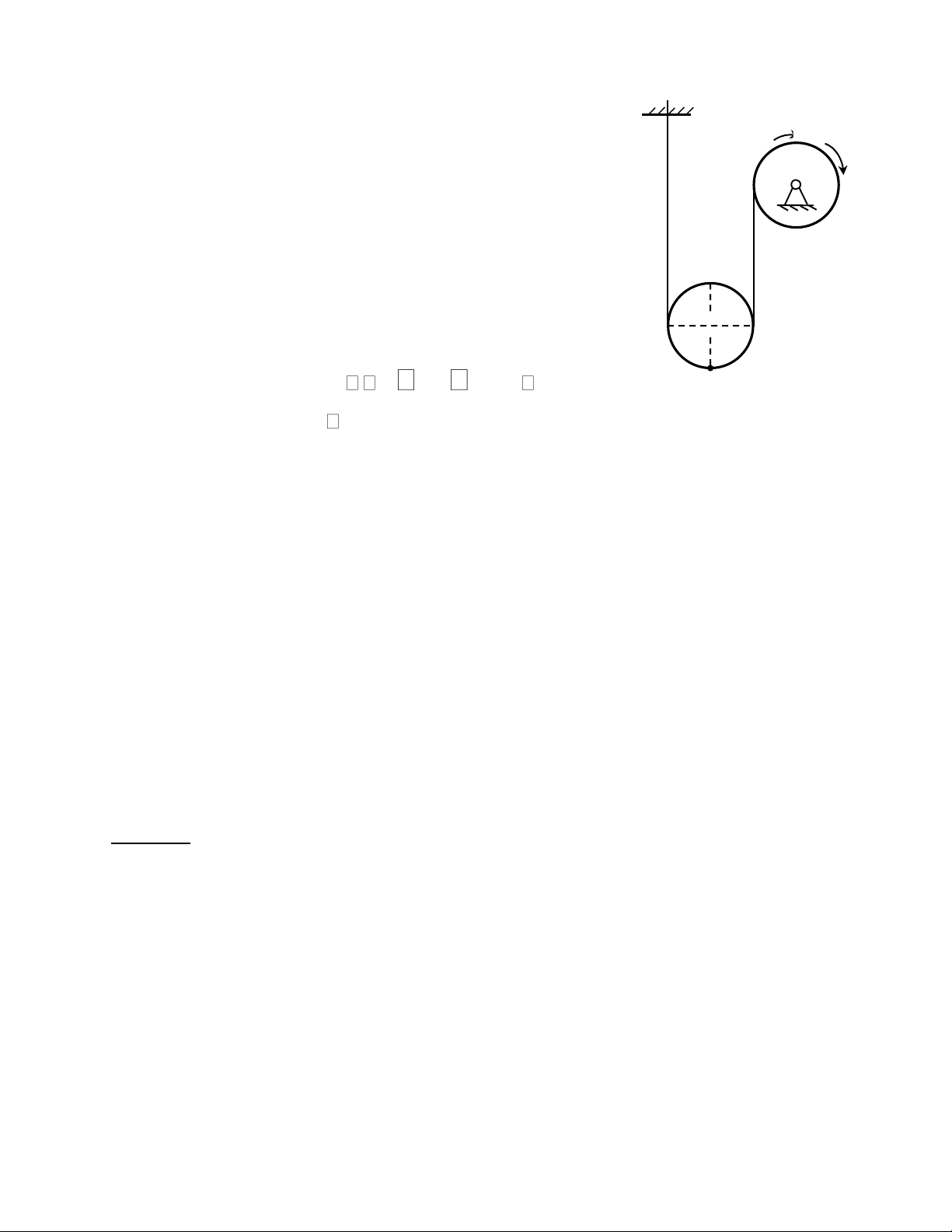
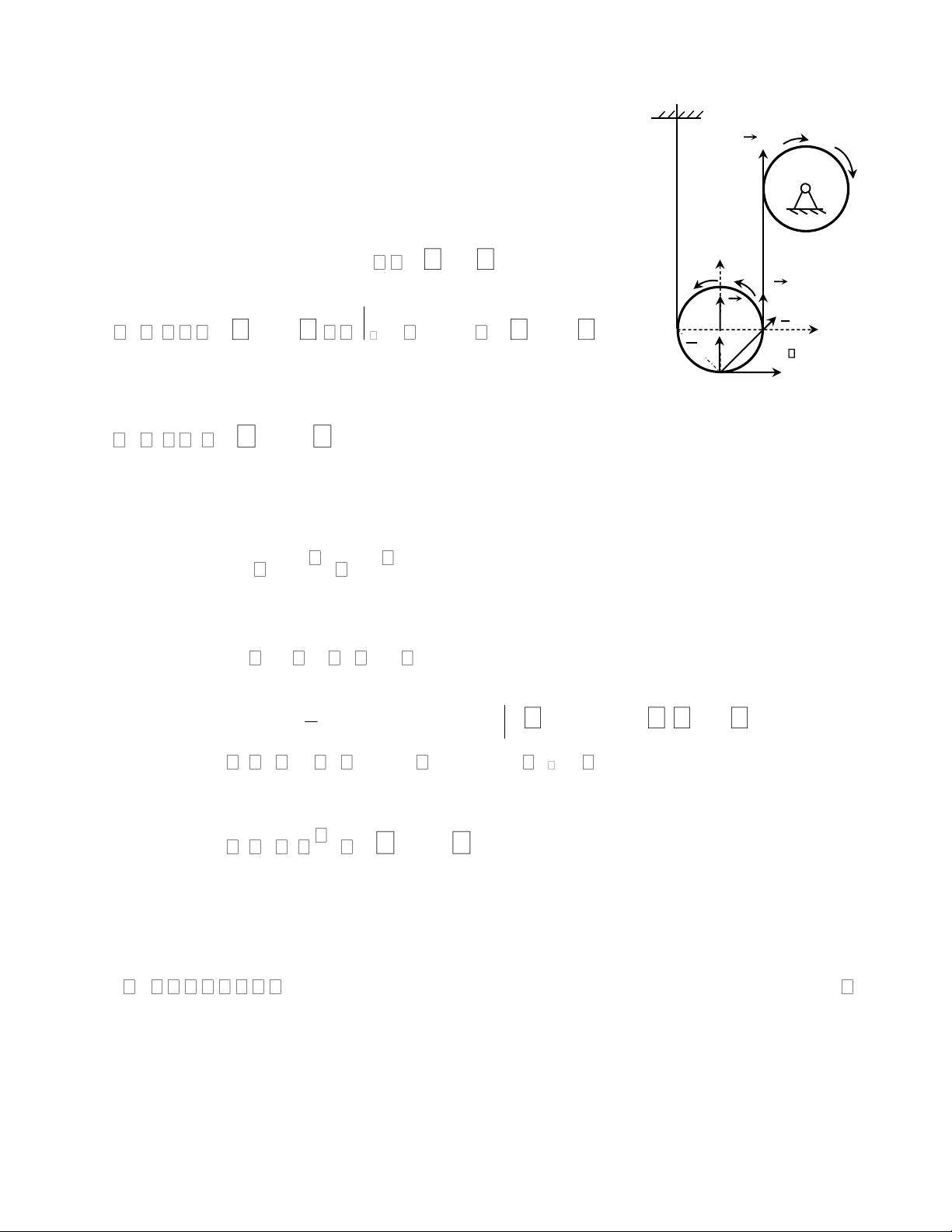
Ví dụ 2. Cho một hệ cơ học chuyển động trong mặt phẳng lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
thẳng đứng gồm ròng rọc cố định tâm O và ròng rọc động ω M 1
tâm C được mô tả như hình vẽ. Giả thiết trong quá trình O
chuyển động các nhánh dây ở hai bên mỗi ròng rọc luôn
thẳng đứng và không bị trượt so với ròng rọc (vận tốc điểm
trên dây và trên ròng rọc chỗ tiếp xúc bằng nhau). Các ròng
rọc có cùng bán kính R.
1. Động học: Giả sử ròng rọc cố định tâm O có phương C
trình chuyển động quay là t2 rad và R 40cm. A
Tại thời điểm khảo sát t 0.5s, hãy xác định:
a. Vận tốc góc, gia tốc góc của ròng rọc cố định tâm O và ròng rọc động tâm C.
b. Vận tốc và gia tốc của điểm A trên ròng rọc động (CA thẳng đứng như hình vẽ).
2. Động lực học: Cho biết ròng rọc cố định là vành tròn đồng chất tâm O khối lượng
m1 còn ròng rọc động là đĩa tròn đồng chất tâm C khối lượng m2. Ròng rọc động tâm
C được kéo lên nhờ ngẫu lực có mômen không đổi M tác dụng vào ròng rọc cố định
tâm O. Biết rằng ban đầu cơ hệ đứng yên, gia tốc trọng trường là g, bỏ qua trọng
lượng của dây và ma sát ở ổ trục của ròng rọc cố định. a.
Xác định vận tốc của tâm C theo quãng đường dịch chuyển x của nó. Tìm gia tốc tâm C. b.
Áp dụng nguyên lý dAlembert tính sức căng của nhánh dây vắt qua ròng rọc cố định O. Lời giải: 1. Động học lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
a. Vận tốc góc và gia tốc góc của ròng rọc cố định O và ω 1 ròng rọc động C. v ε B 1 O -
Ròng rọc cố định O quay quanh trục cố định qua O B
và vuông góc với mặt phẳng hình vẽ có phương trình
chuyển động của góc quay là t2 rad . Suy ra y ε 2 ω 2 v D C a C v A x 1 2t rad/s 1 t 0,5s 2.0,5 1 rad/s P n a  D AC a 
có chiều quay cùng chiều kim đồng hồ. AC A 1 2 rad/s2
có chiều quay cùng chiều kim đồng hồ. -
Ròng rọc động C chuyển động song phẳng có điểm P (điểm tiếp xúc giữa ròng rọc
động C và nhánh dây treo vào sàn cố định) là tâm vận tốc tức thời, suy ra: vD PD. 2 2R 2
Do bỏ qua sự trượt tương đối giữa dây và các ròng rọc nên ta có mối liên hệ vận tốc
vB vD R 1 2R 2 1 2 2 1 t rad/s 2t 0,5s 0,5 rad/s 2 2 1 rad/s2
b. Vận tốc và gia tốc của điểm A trên ròng rọc động (CA thẳng đứng như hình vẽ). v A
PhChiưềơng vuu phụ ông gthuộc theo chióc với APều quay 2 lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
vA AP. 2 2 .0,5R 2.40.0,5 20 2 cm/s
Chọn C làm điểm cực ta có:
a A a C a AC a ACn (a) Ta có a C
PhChiưềơng u hưthớẳng lng ênđứ ng aC R. 2 40.1 40 cm/s2 a AC Phương vuông góc AC 2
Chiều phụ thuộc theo chiều quay aAC AC. 2 40.1 40 cm/s2 a n AC
PhưChin ềơng AC u tAC.ừ A v ề2 C 40.0,52 10 cm/s2 a AC 2
Chiếu cả 2 vế của (a) lên trục x và y ta được lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ aaAxAx aaCAC aACn40 cm/s40 2 10 50 cm/s2 a 2 2 A aAx aAy 10 41 cm/s2 2. Động lực học ω 1
a. Xác định vận tốc của tâm C theo quãng đường dịch M
chuyển x của nó. Tìm gia tốc tâm C. O
- Động năng của cơ hệ y ω 2 T TO TC C v C x 1 P 2 1 2 2
TO Joz 1 m R1 1 2 2 P 2 1 2 1mv2 1 1. m R2 vC 2 TC 2JCz 2 2 2 C 2 2 2 R
21mv2 C2 43mv2 C2 Từ mối quan vC hệ
vận tốc ở phần động học có: 1 2 2 2 R 2
T 21mR2 12 43mv2 C2 21mR12 2vRC 43mv2 C2
8m1 4 3m2 vC2 1
- Để tìm vận tốc của vật A theo quãng đường dịch chuyển của nó, ta áp dụng định lý động
năng dạng hữu hạn như sau: T1 T0 Ak"0" "1" (1) lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ T
trong đó: “0” là thời điểm ban đầu cơ hệ đứng yên nên 0 0
“1” là thời điểm mà tâm C của ròng rọc động đi lên một quãng đường x với T1 vC2
- Tổng công hữu hạn của cơ hệ trong khoảng thời gian từ thời điểm “0” đến thời điểm “1” P M Lực sinh công: 2, . Ta có "0" "1" "0" "1" Ak"0" "1" A P 2 A M 2x 2MR m g x 2 Px2 M Px2 M R
Thay các đại lượng trên vào biểu thức của định lý động năng (1) ta được
8m1 4 3m2 vC2 2MR m g x2 vC2 4 2R m
M8 1 m gR x23m2 2M m gR x2 vC 2 R m8 1 3m2 v
Lấy vi phân theo thời gian t hai vế của biểu thức 2 C ta suy ra 4 2 M m gR2 4 2 M m gR2 lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ 2v v dtC C xdt 2v a dtC C v dtC R m 8 1 3m 2 R m 8 1 3m2 2 2 M m gR2 aC R m 8 1 3m2
b. Tính sức căng của nhánh dây vắt qua ròng rọc cố định O. ε Y O 1 M
+ VKS: ròng rọc cố định O M O qt O X O P X Y T M ,
+ Hệ lực tác dụng lên ròng rọc cố định O gồm: 1 T P 1 , , , O O
+ Lực quán tính của ròng rọc cố định O. Do ròng rọc cố định quay quanh trục cố
định qua O và vuông góc với mặt phẳng cố định nên M J
lực quán tính của ròng rọc O là qt O oz 1 qt 2 2 2aC 2 2 M m gR 2 4m1 2M m gR 2
MO mR1 1 mR1 2mR1 R R m 8 1 3m2 8m1 3m2
+ Áp dụng nguyên lý dAlembert ta có hệ lực P X Y T M M1, O, O, , , qt O 0. Ta có m qt O Fk 0 T R. MO M 0 M M 1 4m 2M m gR lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ T R Oqt R M 1 1 3m22 mR m2 38M 1 43m gRm12 8m III. Bài tập
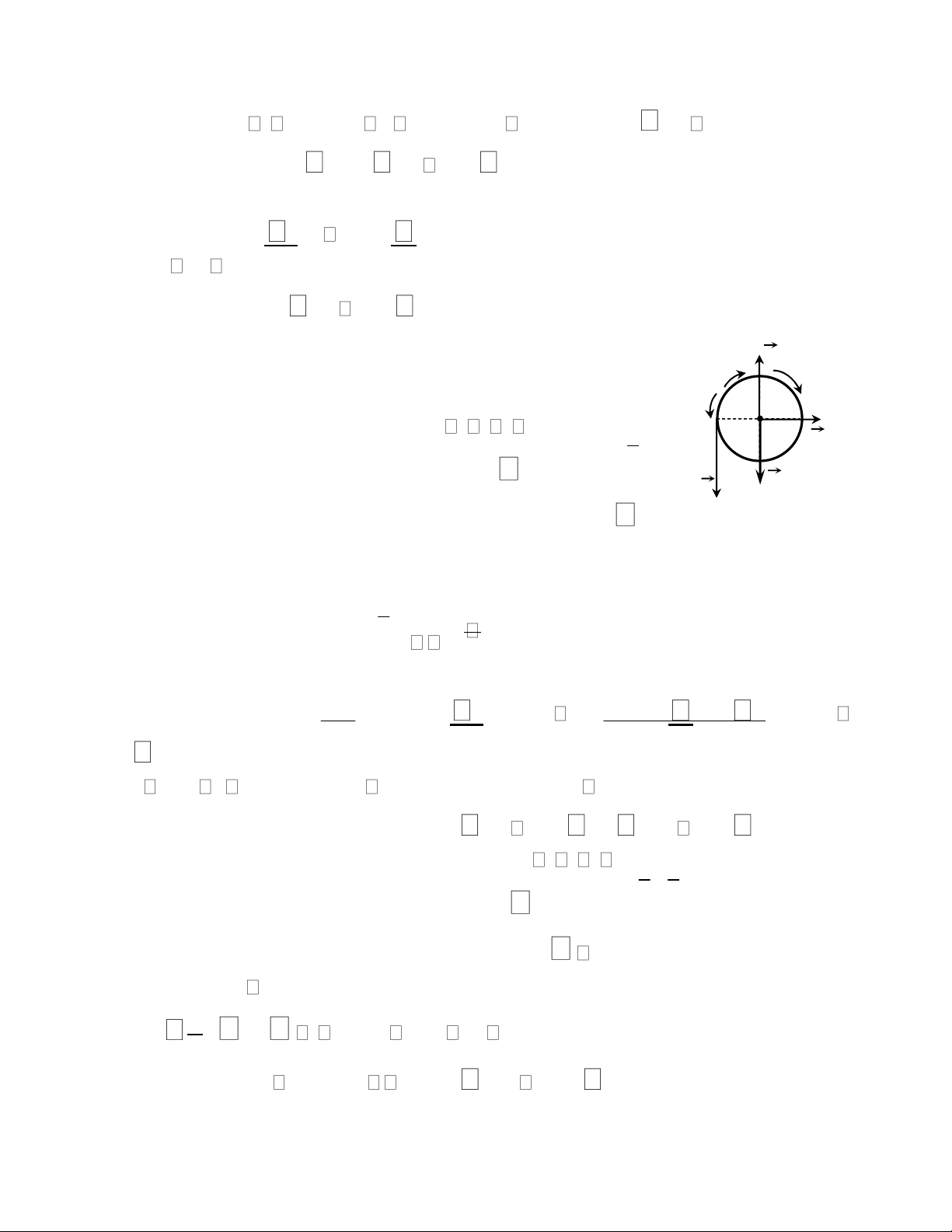
Bài 1: Đĩa tròn đồng chất tâm C có bán kính R = 40cm x O
chuyển động lăn không trượt trên đường thẳng nằm ngang. M
Một điểm A thuộc đĩa tròn với CA = 20cm. A 1.
Động học: Biết quy luật chuyển động của tâm C là: C x
= 2t2(cm). Tại thời điểm khảo sát t = 1s, CA tạo với phương
thẳng đứng góc = 60o, hãy xác định vận tốc của tâm C
và vận tốc của điểm A thuộc đĩa tròn. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ ộ ế 2.
Đ ng lực học: Cho bi t đĩa tròn đồng chất tâm C có bán kính R, khối lượng
m chịu tác dụng của ngẫu lực có mômen M không đổi. Xác định vận tốc góc của
đĩa tròn theo quãng đường dịch chuyển x của tâm C. Biết rằng ban đầu đĩa tròn
đứng yên. Tính gia tốc góc của đĩa tròn.
ĐS: 1. Động học: vC = 4 (cm/s), vA = 2 (cm/s) 2. Động lực học:
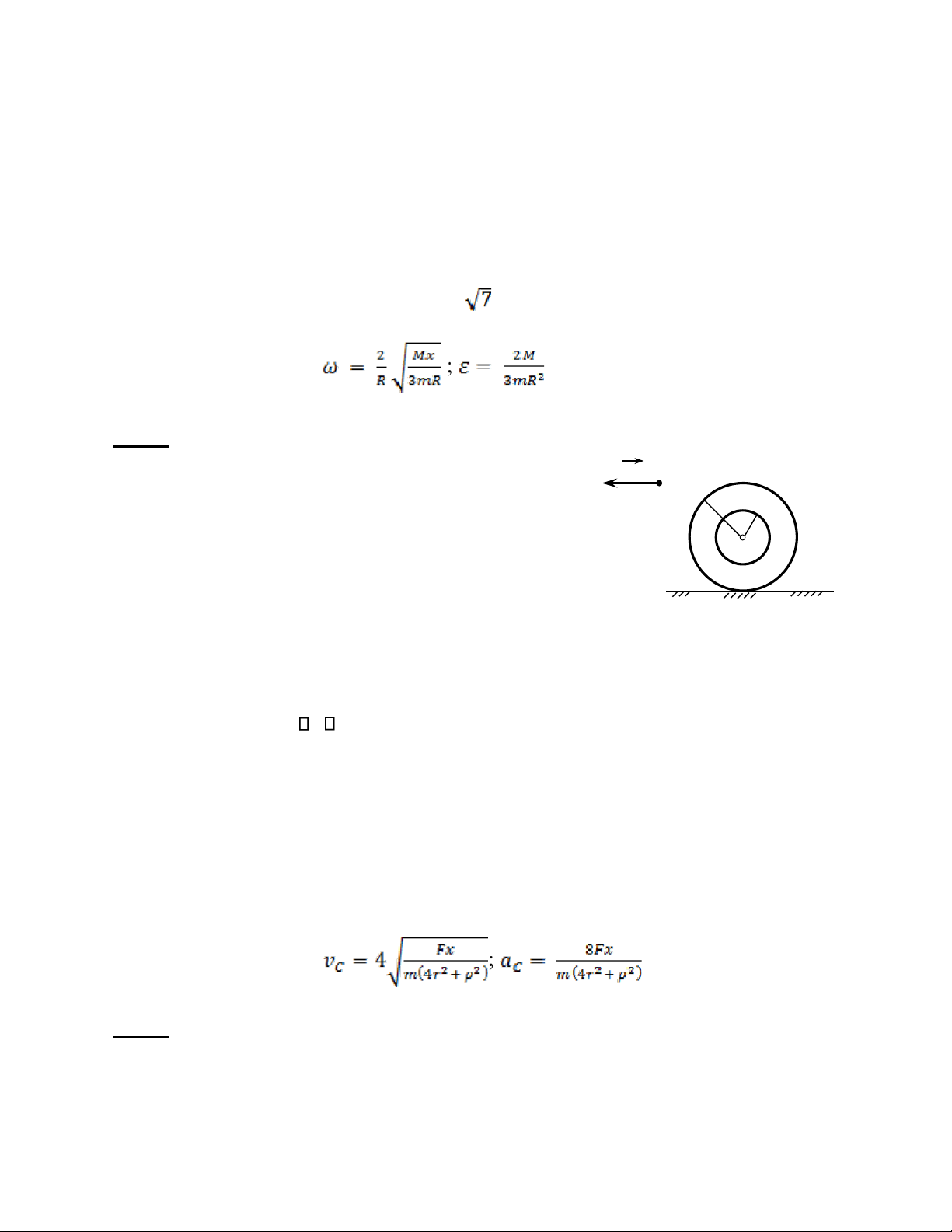
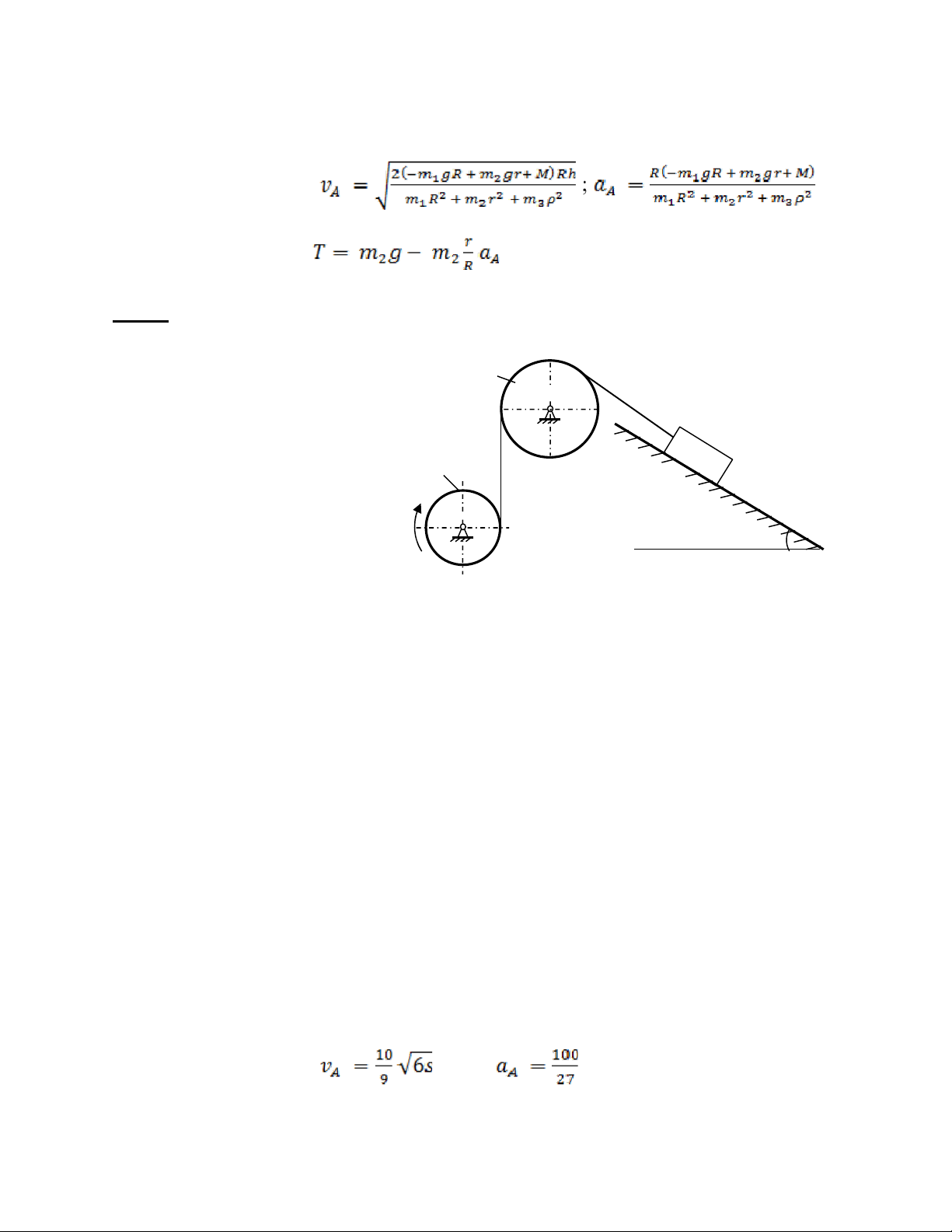
Bài 2: Cho một con lăn hai tầng tâm C, tầng trong có bán kính r, tầng ngoài có bán
kính 2r lăn không trượt trên đường nằm ngang như F hình vẽ. 2 r 1.
Động học: Biết quy luật chuyển động của tâm C r
là: x = 2t3(cm) chuyển động từ phải sang trái. Tại thời C
điểm khảo sát t = 1s, hãy xác định vận tốc góc và gia tốc góc của con lăn. 2.
Động lực học: Cho biết con lăn tâm C này có khối lượng m, bán kính quán
tính quán tính của con lăn với trục qua C và vuông góc với mặt phẳng hình vẽ là ρ
(momen quán tính JZc m 2). Tầng ngoài của con lăn được quấn bởi một sợi dây nhẹ
không giãn, đầu kia của sợi dây được kéo bởi lực F không đổi có phương nằm
ngang làm cho con lăn chuyển động lăn không trượt trên mặt nằm ngang. Xác định
vận tốc của tâm C theo quãng đường dịch chuyển x của nó. Biết rằng ban đầu con
lăn đứng yên và bỏ qua ma sát lăn. Tính gia tốc của tâm C.
ĐS: 1. Động học: ω = 3/r (rad/s), ε = 6/r (rad/s2) 2. Động lực học:
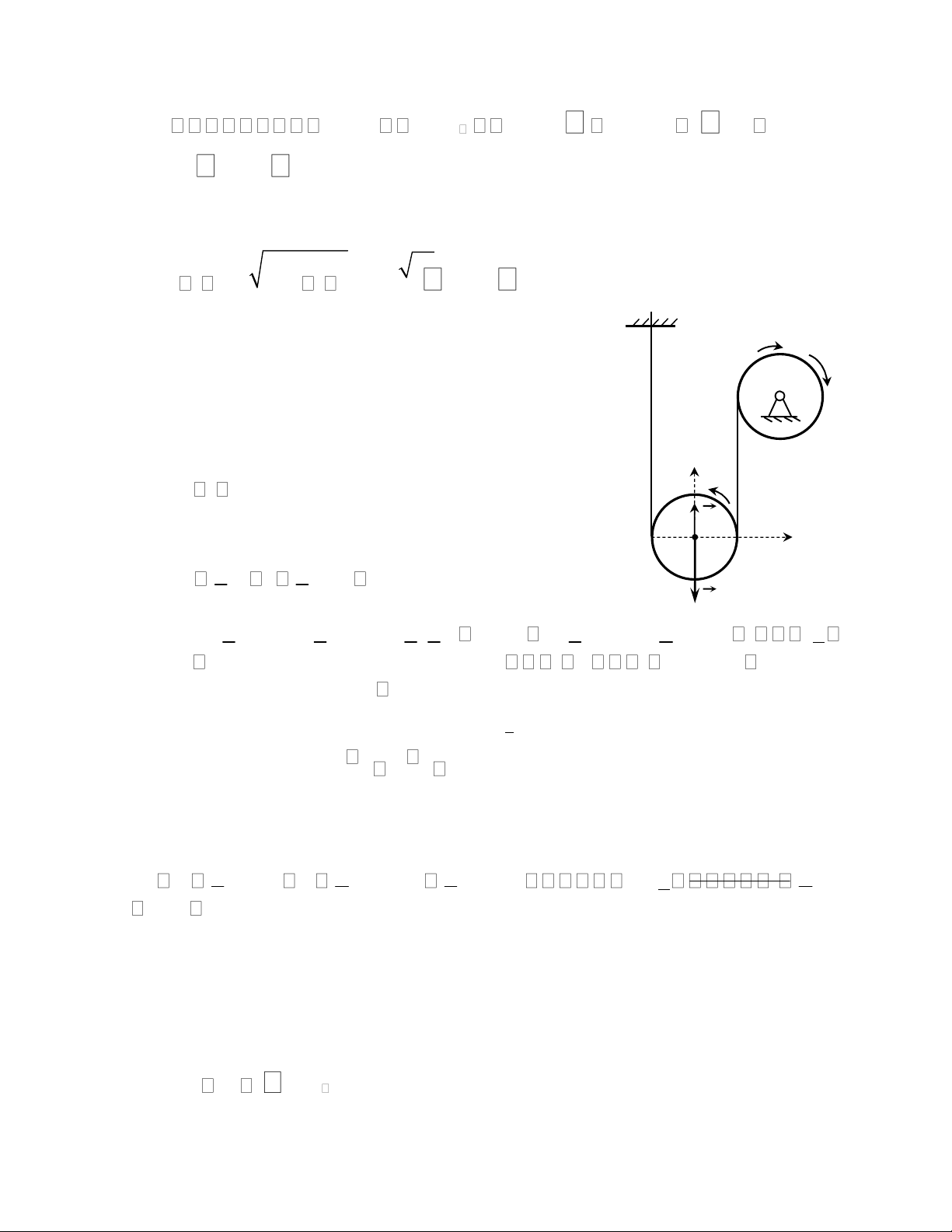
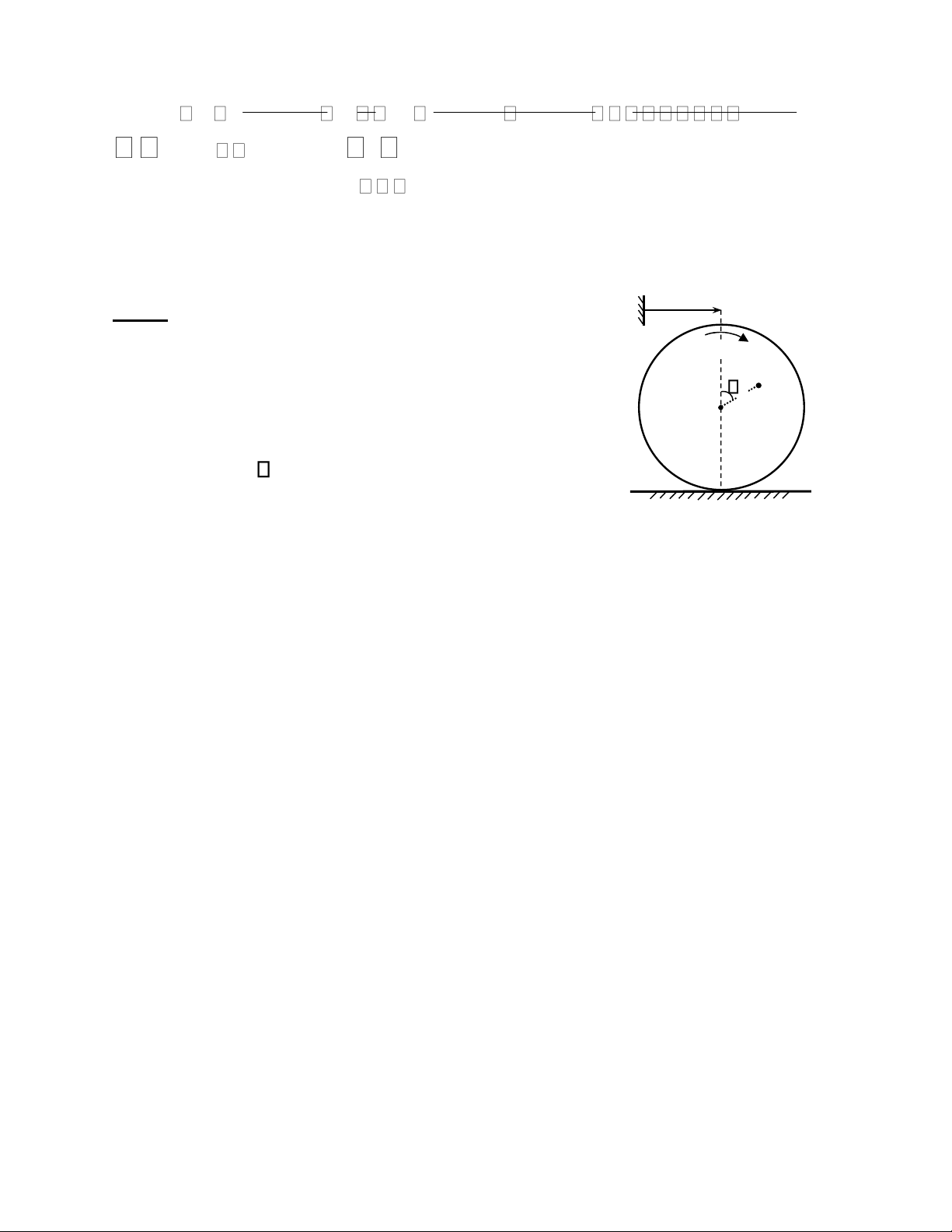
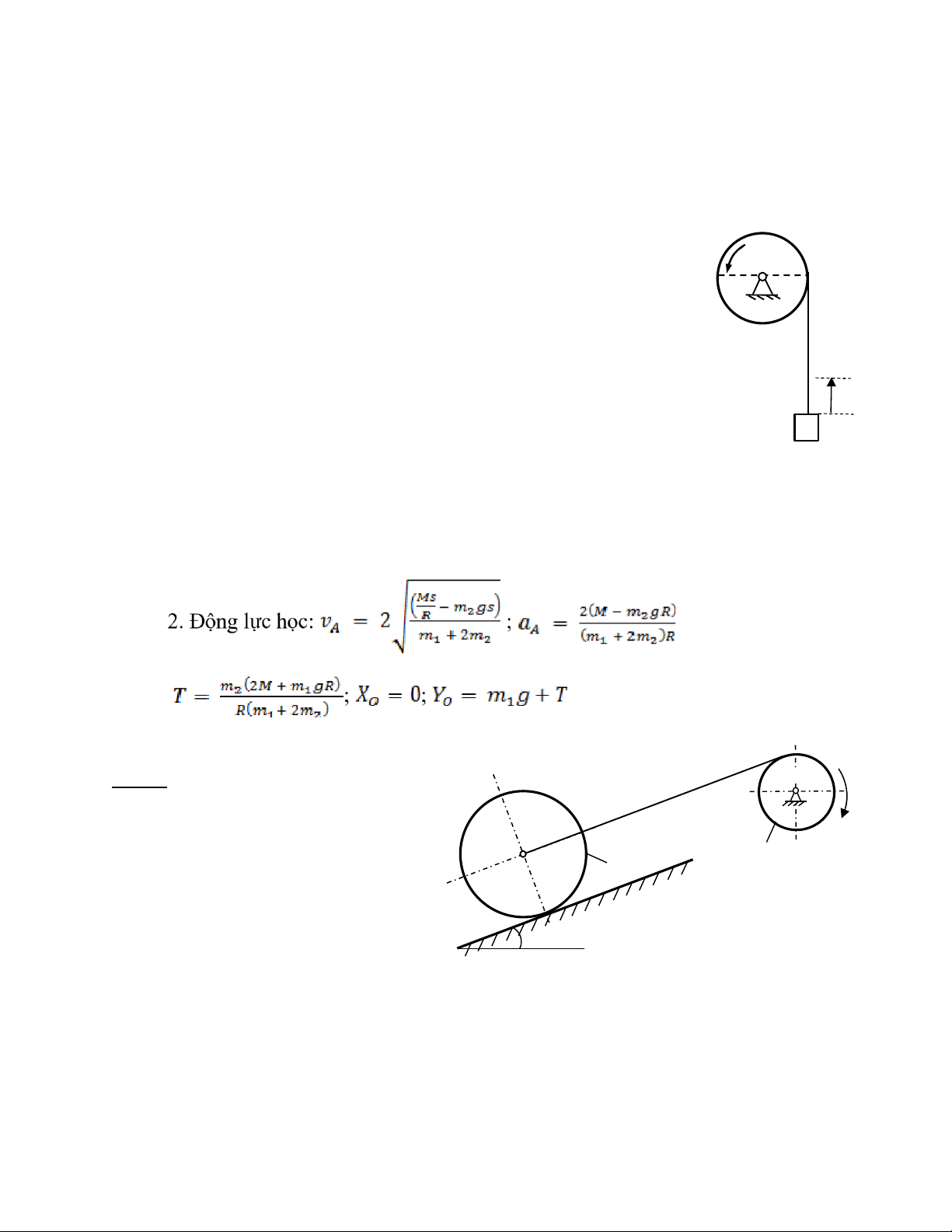
Bài 3: Cho cơ hệ chuyển động trong mặt phẳng thẳng đứng gồm một ròng rọc cố
định tâm O bán kính R quay quanh trục cố định qua O và vuông góc với mặt phẳng lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ ộ ế
chuyển động nối với vật nặng A bằng dây mềm, không giãn. Bỏ qua sự trượt tương
đối giữa dây và ròng rọc. 1.
Đ ng học: Nếu cho bi t phương trình chuyển động của vật A M
là: s = 3t2(cm). Tại thời điểm khảo sát t = 1s, hãy xác định vận tốc O
góc và gia tốc góc của ròng rọc. 2.
Động lực học: Cho biết ròng rọc tâm O bán kính R, khối lượng
m1 là một đĩa tròn đồng chất còn vật rắn A có khối lượng m2. Vật A
chuyển động đi lên nhờ ngẫu lực có mômen không đổi M tác dụng s
vào ròng rọc như hình vẽ. Bỏ qua trọng lượng của dây, ma sát ở ổ A
trục O và cho gia tốc trọng trường là g. Xác định vận tốc, gia tốc của
vật A theo quãng đường dịch chuyển s của nó. Biết rằng ban đầu cơ hệ đứng yên.
Từ đó hãy tính sức căng của dây và phản lực ở ổ trục O của ròng rọc.
ĐS: 1. Động học: ω = 6/R(rad/s), ε = 6/R(rad/s2) ;
Bài 4: Cho cơ hệ như hình vẽ gồm O M
con lăn 1 bán kính r1 và tang tời 2 bán kính r C 2
2 được nối với nhau bằng
dây mềm không giãn. Cho biết dây 1
được quấn quanh tang tời 2 và buộc
vào tâm C của con lăn 1 có phương 30 O
luôn song song với phương
nghiêng. Bỏ qua sự trượt giữa dây và tời. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ ộ ế 1.
Động học: Giả sử rằng phương trình chuyển động quay của tang tời 2 có dạng
là φ = t2 + 4t(rad). Tại thời điểm khảo sát t = 0.5s, hãy xác định vận tốc, gia tốc của tâm C của con lăn 1. 2.
Đ ng lực học: Cho bi t con lăn 1 là trụ tròn đồng chất có khối lượng m1 còn
tang tời 2 là đĩa tròn đồng chất có khối lượng m2. Để kéo con lăn 1 đi lên người ta
tác dụng vào tang tời 2 một ngẫu lực có mômen không đổi M. Biết rằng ban đầu cơ
hệ đứng yên, bỏ qua trọng lượng của dây, ma sát ở gối đỡ O và cho gia tốc trọng trường là g.
a. Xác định vận tốc của tâm C theo quãng đường dịch chuyển s của nó. Tính gia tốc của tâm C.
b. Tính lực căng của dây và phản lực gối đỡ O.
ĐS: 1. Động học: vC = 5r2, aC = 2r2 2. Động lực học:
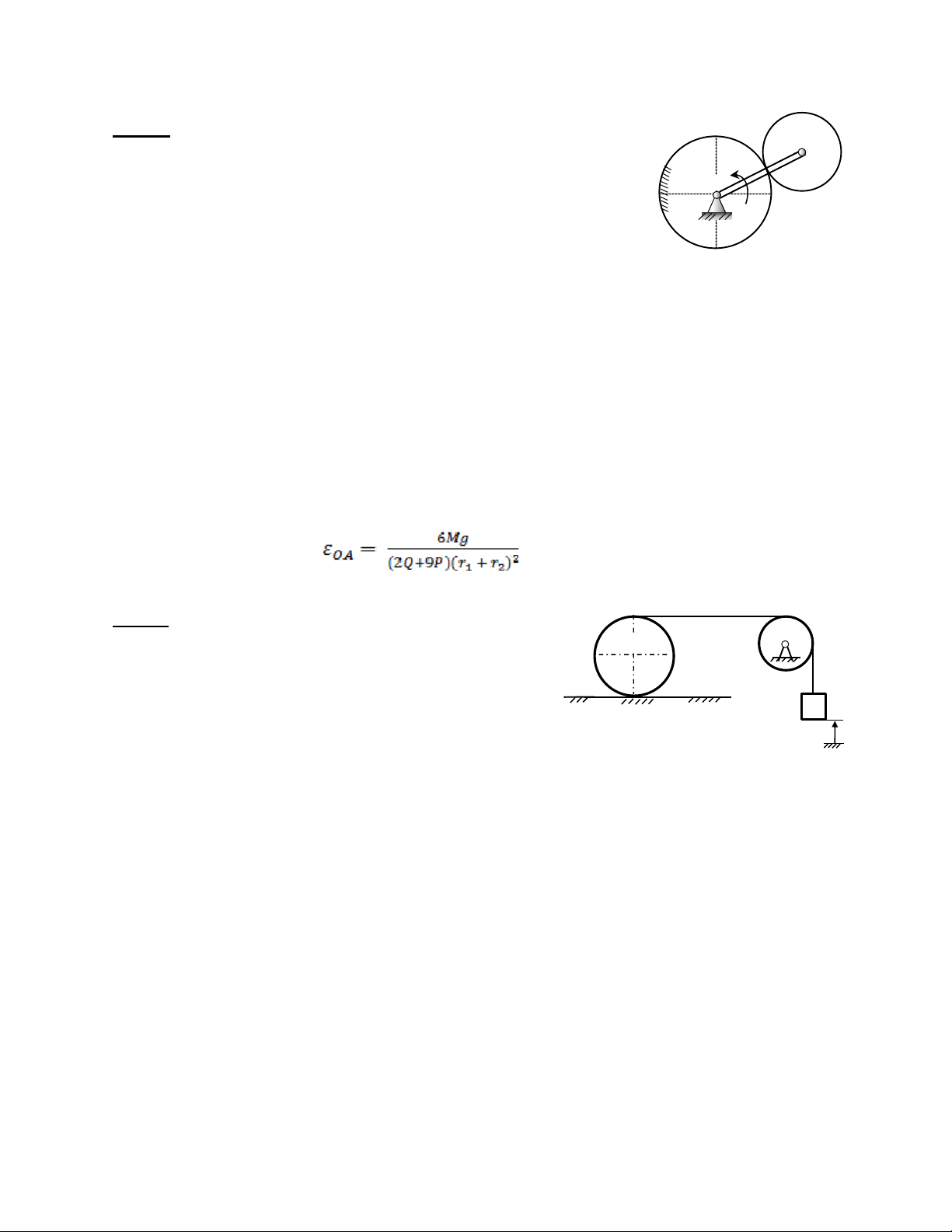
Bài 5: Hai vật A và B được buộc vào hai dây quấn vào hai tang
của tời bán kính vành trong là r, vành ngoài là R. Cho biết dây M
không giãn và bỏ qua sự trượt giữa dây và tời. 1.
Động học: Nếu cho biết vật A chuyển động đi lên theo C
quy luật x = 2t3(cm). Tại thời điểm khảo sát t = 1s, hãy xác định
vận tốc, gia tốc của vật B. 2.
Động lực học: Cho biết vật A khối lượng m1, vật B khối A
lượng m2 còn tời có khối lượng m3 và bán kính quán tính đối
với trục quay qua tâm C là ρ. Vật A được kéo lên nhờ ngẫu lực B
có mômen M không đổi tác dụng vào tời. Biết rằng ban đầu cơ hệ đứng yên, bỏ qua
trọng lượng của dây, các loại ma sát và cho gia tốc trọng trường là g. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ ộ ế
a. Xác định vận tốc của vật A tại thời điểm vật A được kéo lên một đoạn h. Tính gia tốc của vật A.
b. Tính sức căng của nhánh dây buộc vào vật B. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
ĐS: 1. Động học: vB = 6r/R, aB = 12r/R 2. Động lực học: ;
Bài 6: Cho cơ hệ như hình vẽ gồm vật nặng A được buộc vào sợi dây mềm vắt qua
ròng rọc cố định 1 và được quấn vào tang tời 2. Cho biết dây không giãn (phương
của nhánh dây buộc vào vật A 1
luôn song song với phương O nghiêng còn phương nhánh 2 A C 30 o
M dây nối ròng rọc cố định 1 và tang tời 2 luôn thẳng
đứng), bỏ qua sự trượt giữa dây và tời và ròng rọc 1 là đĩa tròn đồng chất có bán
kính r1 = 0.15m, tang tời 2 là trụ tròn đồng chất có bán kính r2 = 0.1m. 1.
Động học: Giả sử phương trình chuyển động quay của tang tời 2 là φ = t2 +
t(rad). Tại thời điểm khảo sát t = 1s, hãy xác định vận tốc, gia tốc của vật A. 2.
Động lực học: Cho biết vật nặng A có khối lượng m = 100kg, ròng rọc cố định
1 có khối lượng m1 = 20kg còn tang tời 2 có khối lượng m2 = 50kg. Vật nặng A được
kéo lên nhờ ngẫu lực có mômen không đổi M = 100Nm tác dụng vào tang tời 2. Biết
rằng ban đầu cơ hệ đứng yên, bỏ qua trọng lượng của dây và cho gia tốc trọng trường là g = 10m/s2. a.
Xác định vận tốc của vật A theo quãng đường dịch chuyển s(m) của
nó. Tính gia tốc của vật A. b.
Tính phản lực gối đỡ của ròng rọc cố định 1 và tang tời 2. ĐS: 1.
Động học: vA = 0.3(m/s), aA = 0.2(m/s2) 2. Động lực học: (m/s); (m/s2); lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ ; (N); (N); (N)
Bài 7: Cho cơ cấu gồm đĩa tròn tâm O1,
bán kính R1 = 10cm, đĩa tròn tâm O2, bán M
kính R2 = 15cm và thanh truyền O1O2 liên A
kết bản lề tại tâm của hai đĩa. Khi cơ cấu 2 R 2
chuyển động, các đĩa tròn chuyển động lăn O 2 R
không trượt trên đường nằm ngang còn 1 2 O 1 thanh O
1O2 chuyển động tịnh tiến.
1. Động học: Giả sử rằng tại thời điểm khảo sát đĩa tròn tâm O2 chuyển động với
vận tốc góc ω2 = 2rad/s, gia tốc góc ε2 = 3rad/s2, hãy xác định: a. Vận tốc tâm các
đĩa và vận tốc góc của đĩa tròn tâm O1.
b. Vận tốc và gia tốc của điểm A thuộc đĩa tròn tâm O1. Biết rằng tại thời điểm khảo
sát O1A có phương thẳng đứng.
2. Động lực học: Cho biết đĩa tròn tâm O1 khối lượng m1, đĩa tròn tâm O2 khối lượng
m2 và cả hai đĩa tròn đều đồng chất còn thanh O1O2 là thanh thẳng đồng chất khối
lượng m3. Cơ cấu chuyển động được là nhờ tác dụng vào đĩa tròn tâm O2 một ngẫu
lực có mômen không đổi M như hình vẽ. Biết rằng ban đầu cơ hệ đứng yên, bỏ qua
ma sát ở các ổ trục O1, O2 và cho gia tốc trọng trường là g. Xác định vận tốc của tâm
O2 theo quãng đường dịch chuyển s của nó. Tính gia tốc của tâm O2. ĐS: 1. Động
học: a. ω1 = 3(rad/s); ε1 = 4.5(rad/s2)
b. vA = 60(cm/s), aA = 90(cm/s2) (aA có phương thẳng đứng) 2. Động lực học: lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ
Bài 8: Cho một cơ cấu hành tinh đặt trong mặt phẳng nằm A
ngang. Tay quay OA quay quanh trục cố định qua O làm cho 1 M
bánh 2 là một đĩa tròn bán kính r2 lăn không trượt trên bánh 1 O 2
cố định là đĩa tròn bán kính r1. 1.
Động học: Giả sử phương trình chuyển động của tay
quay OA là: φ = t2 + 4t(rad). Tại thời điểm khảo sát t = 0.5s, hãy xác định vận tốc
góc, gia tốc góc của bánh 2. 2.
Động lực học: Cho biết bánh 2 là đĩa tròn đồng chất trọng lượng P còn tay
quay OA là thanh thẳng đồng chất trọng lượng Q. Cơ cấu chuyển động từ trạng thái
đứng yên nhờ một ngẫu lực có mômen không đổi M tác dụng vào tay quay OA. Bỏ
qua các lực cản và cho gia tốc trọng trường là g. Xác định gia tốc góc của tay quay OA.
ĐS: 1. Động học: a. ω2 = 5(r1 + r2)/r2(rad/s); ε2 = 2(r1 + r2)/r2 (rad/s2) 2. Động lực học:
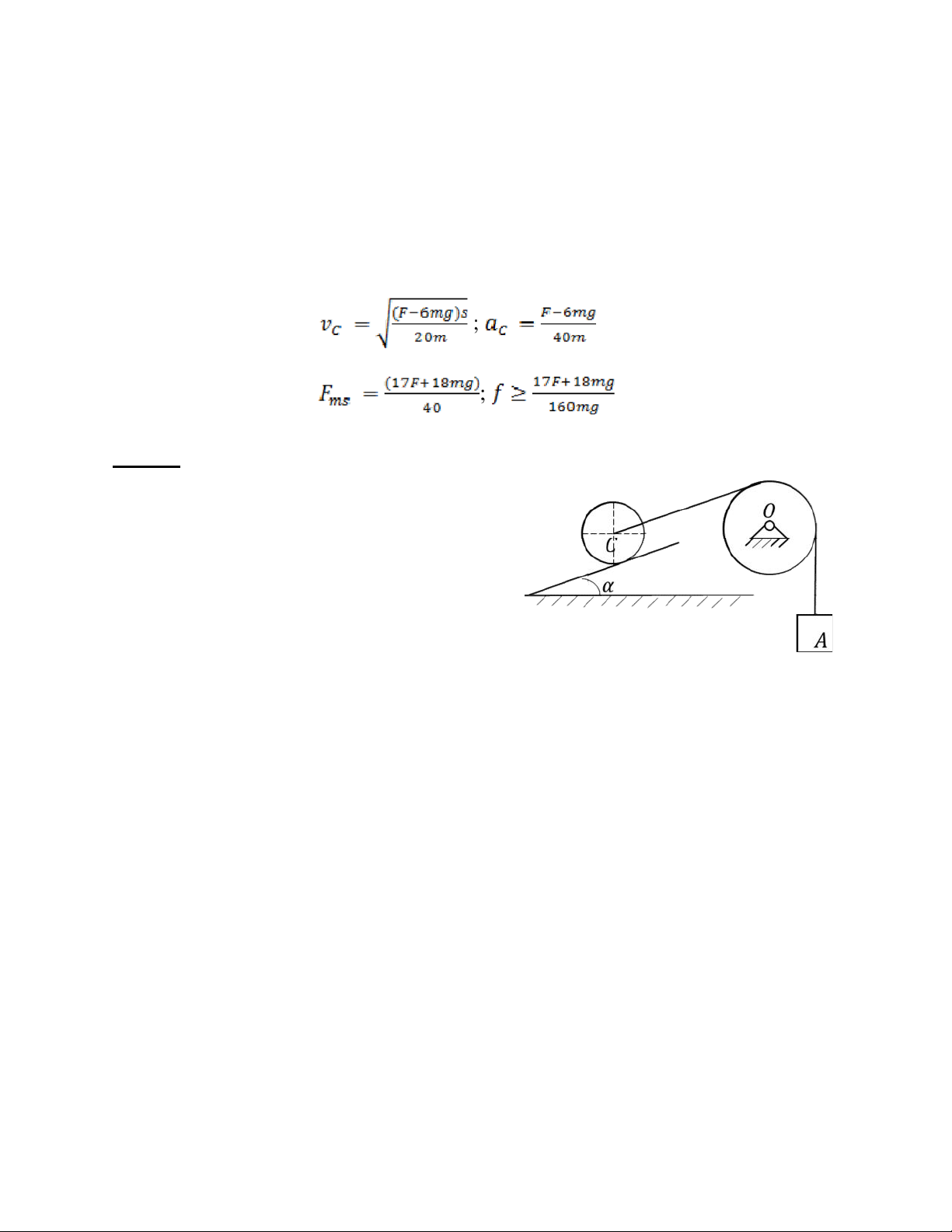
Bài 9: Cho cơ hệ như hình vẽ gồm con lăn tâm C
bán kính R, ròng rọc cố định tâm O bán kính r và C O
vật nặng A. Các vật thuộc cơ hệ được nối với nhau
bằng một sợi dây mềm, không giãn vắt qua ròng A
rọc cố định, một đầu sợi dây được quấn vào vành s
con lăn còn đầu kia treo vật nặng A. Cho biết
phương nhánh dây quấn quấn vào con lăn C luôn có phương ngang còn phương
nhánh dây buộc vào vật nặng A thì luôn thẳng đứng. Bỏ qua sự trượt giữa dây và ròng rọc. 1.
Động học: Nếu cho biết phương trình chuyển động của vật A là: s = 2t2(cm).
Tại thời điểm khảo sát t = 1s, hãy xác định vận tốc góc và gia tốc góc của con lăn C. 2.
Động lực học: Cho biết con lăn C là trụ tròn đồng chất có khối lượng 4m còn
ròng rọc cố định O là đĩa tròn đồng chất khối lượng m và vật nặng A khối lượng 3m.
Để kéo vật nặng A đi lên người ta tác dụng vào tâm C của con lăn một lực nằm ngang
F không đổi như hình vẽ. Biết rằng ban đầu cơ hệ đứng yên, bỏ qua trọng lượng của
dây, ma sát ở ổ trục O và cho gia tốc trọng trường là g. lOMoAR cPSD| 58970315
Biên soạn: Trịnh Thị Thanh Huệ a.
Xác định vận tốc của tâm C theo quãng đường dịch chuyển s của nó. Tính gia tốc của tâm C. b.
Tính lực ma sát trượt do mặt đường tác dụng lên con lăn và tìm điều kiện của
hệ số ma sát trượt f để con lăn lăn không trượt trên mặt ngang.
ĐS: 1. Động học: a. ωC = 2/R(rad/s); εC = 2/R(rad/s2) 2. Động lực học: ;
Bài 10: Cho cơ hệ gồm vật A được buộc vào dây không giãn vắt qua ròng rọc cố
định O bán kính r2 quấn vào con lăn hình trụ
tròn C bán kính r3. Biết dây không giãn và bỏ
qua sự trượt giữa dây và ròng rọc, bỏ wua ma sát tại ổ trục quay O. 1.
Động học: Giả sử vật A chuyển động
xuống theo quy luật x = 0.5t2(cm). Tại thời
điểm khảo sát t = 1s, hãy xác định vận tốc góc,
gia tốc góc của con lăn C. 2.
Động lực học: Cho biết vật A khối lượng m1, ròng rọc cố định O là trụ
tròn thành mỏng khối lượng m2, bán kính r2 còn con lăn C là trụ tròn đặc khối
lượng m3, bán kính r3. Khi vật A được hạ xuống làm cho ròng rọc O chuyển
động và con lăn C lăn không trượt trên mặt phẳng nghiêng hợp với phương
ngang một góc α. Bỏ qua trọng lượng của dây, các loại ma sát và cho gia tốc
trọng trường là g.
a. Xác định vận tốc của vật A tại thời điểm vật A được hạ xuống một đoạn h. Biết
rằng tại thời điểm ban đầu cơ hệ đứng yên. Tính gia tốc của vật A. b. Tính sức căng
của 2 nhánh dây vắt qua ròng rọc cố định.
ĐS: 1. Động học: ωC = 1/r3(rad/s), ε = 1/r3(rad/s2) 2. Động lực học: ; ;