









Preview text:
BÀI TẬP XÁC SUẤT THỐNG KÊ
HỌC KỲ I NĂM HỌC 2022 - 2023 1 CHƯƠNG 1
A. BÀI TẬP TỰ LUẬN
1. Một công ty cần tuyển 4 nhân viên. Có 8 người gồm 5 nam (trong đó có An) và 3 nữ xin dự tuyển
và mỗi người đều có cơ hôi trúng tuyển như nhau. Tính xác suất để trong 4 người được tuyển: a. Có duy nhất một nam b. Có ít nhất một nữ c. Có không quá 2 nam
d. Có 3 nam biết An không được tuyển.
2. Trong một hộp có 100 tấm thẻ như nhau được ghi số từ 1 đến 100. Rút ngẫu nhiên hai thẻ từ hộp. Tính xác suất:
a. Rút được hai thẻ mà tổng của chúng là một số lẻ
b. Rút được hai thẻ mà tích của chúng là một số lẻ
c. Rút được hai thẻ trong đó có ít nhất một thẻ được ghi số chia hết cho 5
3. Một bộ bài tiến lên có 52 lá. Rút ngẫu nhiên 6 lá. Tính xác suất để trong 6 lá rút được: a. Có 4 lá đen b. Có 2 lá đen, 1 lá rô c. Có hai lá át
d. Có 4 lá nốt biết có hai lá đen được rút.
4. Trong kho có 10 đôi giày khác màu nhau. Chọn ngẫu nhiên 10 chiếc giày từ kho. Tính xác suất:
a. Có đúng 2 chiếc ghép được thành một đôi giày hoàn chỉnh.
b. Không có đôi giày hoàn chỉnh nào được chọn.
5. Sản phẩm của nhà máy sản xuất ra được đóng thành từng kiện, mỗi kiện chứa 14 sản phẩm trong
đó có 8 sản phẩm loại A và 6 sản phẩm loại B. Khách hàng chọn cách kiểm tra như sau: Từ mỗi
kiện lấy ngẫu nhiên ra 4 sản phẩm, nếu thấy số sản phẩm loại A nhiều hơn số sản phẩm loại B thì
chấp nhận mua kiện hàng đó, ngược lại thì loại bỏ. Tính xác suất để một kiện hàng bị loại bỏ.
6. Một người có bốn viên đạn. Người này bắn độc lập các viên đạn vào một mục tiêu, xác suất bắn
trúng mục tiêu của mỗi viên đều bằng nhau và bằng 0,7.
a. Tính xác suất để trong bốn viên đạn mà người đó bắn ra có 2 viên bắn trúng mục tiêu.
b. Tính xác suất để trong bốn viên đạn mà người đó bắn ra có 3 viên bắn trúng mục tiêu.
7. Một người có ba viên đạn bắn độc lập vào một mục tiêu, xác suất bắn trúng mục tiêu của mỗi viên
đều bằng nhau và bằng 0,6. Người đó bắn theo nguyên tắc: Nếu bắn trúng mục tiêu hay bắn hết
đạn thì dừng lại không bắn nữa.
a. Tính xác suất để cho người xạ thủ bắn ra một viên
b. Tính xác suất để cho người xạ thủ bắn ra hai viên
c. Tính xác suất để cho người xạ thủ bắn ra cả ba viên
8. Trong một cuộc điều tra cho thấy tại một thành phố có 20,7% dân số dùng loại sản phẩm X, 50%
dùng loại sản phẩm Y và trong số những người dùng sản phẩm Y có 36,5% dùng sản phẩm X.
Phỏng vấn ngẫu nhiên một người dân trong thành phố đó, tính xác suất để người ấy:
a. Dùng cả sản phẩm X và Y
b. Không dùng sản phẩm X, cũng không dùng sản phẩm Y.
9. Có 100 tấm bìa hình vuông như nhau được đánh số từ 1 đến 100. Lấy ngẫu nhiên 3 tấm bìa. Tính xác suất:
a. Lấy được ba tấm bìa có chứa số không chia hết cho 5.
b. Lấy được hai tấm bìa có chứa số chia hết cho 9 biết cả ba tấm bìa đều chứa số chia hết cho 3.
c. Lấy được một tấm bìa chứa số chia hết cho 5 biết cả ba tấm bìa đều chứa số chia hết cho 2.
10. Một lô hàng có rất nhều bóng đèn trong đó có 8% bóng đèn xấu. Một người đến mua hàng với quy
định: Chọn ngẫu nhiên 10 bóng đèn để kiểm tra và nếu có nhiều hơn một bóng đèn xấu thì không
nhận lô hàng. Tính xác suất để lô hàng được nhận?
11. Nhà trường muốn chọn 3 học sinh từ một tổ gồm 7 nam sinh và 6 nữ sinh để dự lễ mitting do
thành phố tổ chức. Lần đầu chọn ngẫu nhiên 2 học sinh, sau đó chọn tiếp một học sinh nữa.
a. Tính xác suất để học sinh được chọn lần sau là nam sinh? 2
b. Biết học sinh được chọn lần sau là nam sinh. Tính xác suất để hai học sinh được chọn lần đầu là nam sinh?
12. Dây chuyền lắp ráp nhận được các chi tiết do 2 máy sản xuất. Trung bình máy thứ nhất cung cấp
60% chi tiết, máy thứ hai cung cấp 40% chi tiết. Khoảng 90% chi tiết do máy thứ nhất sản xuất là
đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai cung cấp là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây
chuyền này một sản phẩm.
a. Tính xác suất để sản phẩm lấy ra là sản phẩm đạt chuẩn?
b. Nếu sản phẩm lấy ra là sản phẩm đạt chuẩn. Tìm xác suất để sản phẩm này do máy thứ nhất sản xuất?
13. Trên đường tròn bán kính R (có một điểm A cố định) ta chọn ngẫu nhiên một điểm B. Tính xác
suất để cung AB không vượt quá R.
14. Cho P( A) = 0,2; P(B) = 0,8; P ( AB) = 0,1 . Tính:
P ( A + B); P ( A.B ); P ( A + B ); P ( A.B ); P ( A + B ), P ( A / B ); P (A / B )
15. Hai sinh viên A và B cùng tham gia một trò chơi như sau: cả hai luân phiên lấy mỗi người một
viên bi từ một hộp gồm có 4 bi đen và 2 bi trắng (bi được rút ra không được trả lại vào hộp).
Người nào lấy được bi trắng trước thì thắng cuộc. Giả sử A được phép lấy trước. Tính xác suất để B thắng cuộc?
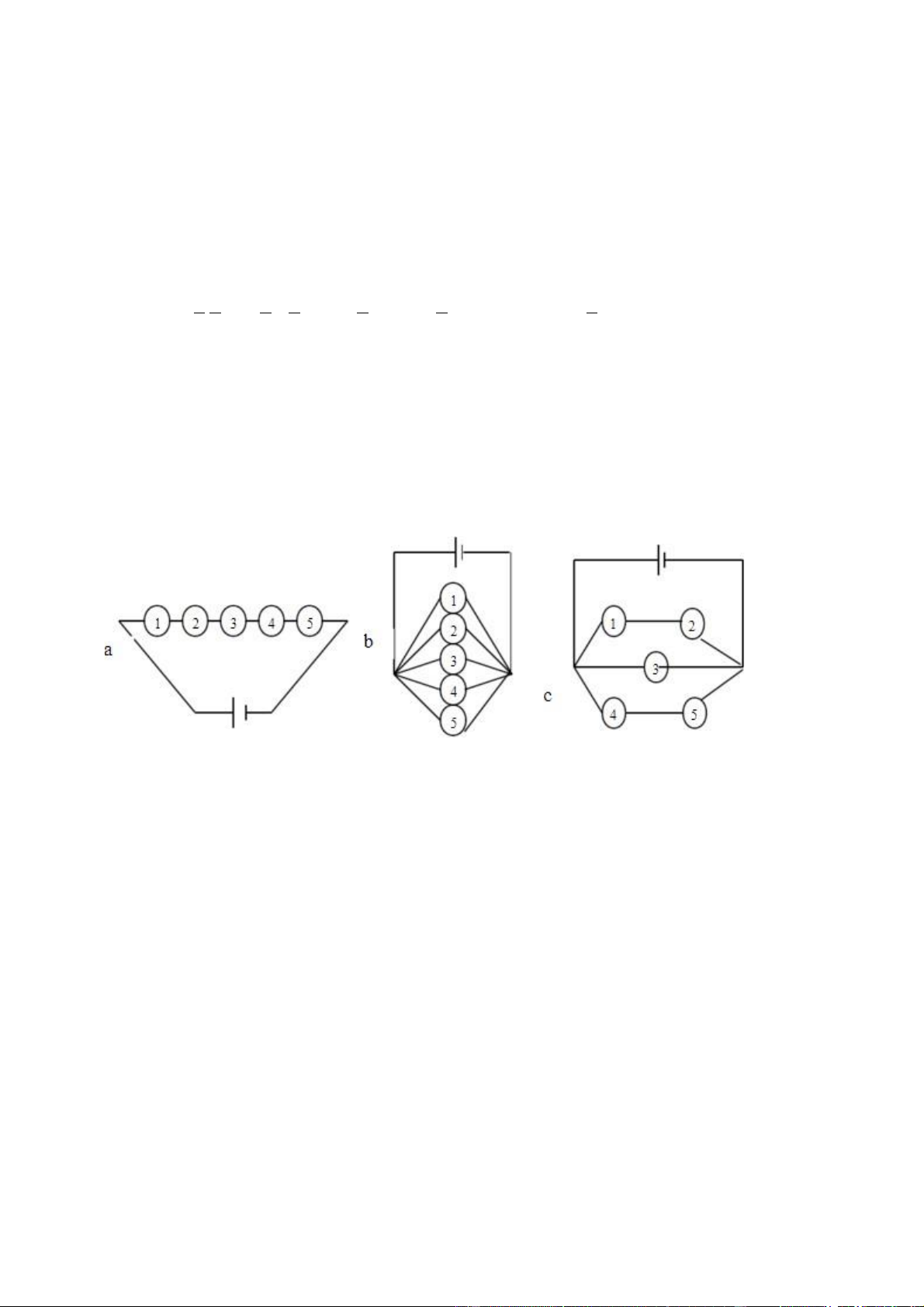
16. Có 5 linh kiện điện tử, xác suất để mỗi linh kiện hỏng trong 1 thời điểm bất kỳ lần lượt là: 0,01;
0,02; 0,02; 0,01; 0,04. Giả sử 5 linh kiện này được lắp vào một mạch điện theo sơ đồ. Trong mỗi
trường hợp sau đây hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
B. BÀI TẬP TRẮC NGHIỆM
1. GIẢI TÍCH TỔ HỢP
1. Có 8 quyển sách khác nhau và 10 quyển vở khác nhau. Hỏi có bao nhiêu cách chọn được một quyển
sách hoặc một quyển vở? A) 80 B) 18 C) 18! D) 8! 10!
2. Có 10 quyển sách khác nhau và 12 quyển vở khác nhau. Hỏi có bao nhiêu cách chọn một quyển sách và một quyển vở? A) 120 B) 22 C) 22! D) 10! 12!
3. Một người có 7 cái áo trong đó có 3 cái áo trắng và 5 cái cà vạt trong đó có 2 cái cà vạt màu vàng. Hỏi
người đó có bao nhiêu cách chọn áo và cà vạt nếu đã chọn áo trắng thì không chọn cà vạt vàng? A) 35 B) 29 C) 17 D) 12
4. Một hộp có 6 quả cầu xanh đánh số thứ tự từ 1 đến 6, 5 quả cầu đỏ đánh số thứ tự từ 1 đến 5, 4 quả
cầu vàng đánh số thứ tự từ 1 đến 4. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số? A) 64 B) 120 C) 15 D) 12
5. Từ các số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số chẵn có 3 chữ số? A) 126 B) 147 C) 168 D) 196
6. Từ các số 0, 1, 3, 5 ,7, 9 có thể lập bao nhiêu số tự nhiên có 5 chữ số khác nhau? 3 A) 120 B) 600 C) 720 D) 270
7. Có bao nhiêu số có 9 chữ số được thành lập từ các chữ số 1, 2, 3, 4, 5, trong đó có 5 chữ số 5 đứng kề
nhau và các chữ số còn lại xuất hiện đúng 1 lần? A) 24 B) 96 C) 120 D) 144
8. Có bao nhiêu số tự nhiên có 4 chữ số mà các chữ số của nó đều chẵn? A) 120 B) 96 C) 500 D) 625
9. Từ các chữ số 1, 2, 3, 4, 5 có thể thành lập được bao nhiêu số có 3 chữ số khác nhau nằm trong khoảng (300;500)? A) 36 B) 24 C) 60 D) 10
10. Có bao nhiêu số tự nhiên gồm 5 chữ số, biết rằng hai chữ số đứng kề nhau phải khác nhau? B) A 5 A 10 A) 95 C) 9 A4 D) 5 9 9
11. Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1, 3, 5, 7, 9. Trong các số đó có bao
nhiêu số bắt đầu bởi số 7? A) 24 B) 120 C) 256 D) 16
12. Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5. Trong các số đó có bao
nhiêu số không bắt đầu bằng 123? A) 6 B) 54 C) 118 D) 120
13. Từ các số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số gồm 5 chữ số khác nhau và phải có mặt chữ số 1? A) 360 B) 1200 C) 2520 D) 1560
14. Có bao nhiêu số tự nhiên có 5 chữ số sao cho chữ số đứng sau lớn hơn chữ số đứng trước? A) 126 B) 252 C) 1260 D) 1680
15. Có bao nhiêu số tự nhiên gồm 3 chữ số khác nhau và khác 0, biết rằng tổng của 3 chữ số này bằng 8? A) 8 B) 10 C) 12 D) 16
16. Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau trong đó có đúng 3 chữ số chẵn và 3 chữ số lẻ? A) 68400 B) 72000 C) 64800 D) 720000
17. Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số gồm 3 chữ số được lập từ 3 chữ số trên? A) 63 B) 36 C) A 36 D) C 3 6
18. Từ các chữ số từ 1, 2, 3, 4, 5, lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau sao cho chữ số 5 phải đứng chính giữa? A) 24 B) 120 C) 5 D) 25
19. Mỗi vé số gồm có 6 chữ số. Hỏi khi phát hành mỗi đợt sẽ phát hành được bao nhiêu vé số khác nhau? A) 6! B) 106 C) 610 D) 10!
20. Có 6 người ngồi chờ đi xe bus nhưng chỉ còn có 3 ghế trống. Hỏi có bao nhiêu cách chọn 3 người được ngồi ghế? A) 20 B) 120 C) 18 D) 200
21. Một lớp có 40 học sinh, phải chọn ra 3 học sinh để quét lớp. Hỏi có bao nhiêu cách chọn? A) 9880 B) 59280 C) 64000 D) 120
22. Có bao nhiêu cách phân phối 15 tặng phẩm cho 3 người, sao cho một người có 2 tặng phẩm, một
người có 3 tặng phẩm và người còn lại có 10 tặng phẩm? A) 6 C 2 C 3 B) A2 A3
C) 6 C 2 C 3 C10
D) A2 A3 A10 15 13 15 10 15 15 15 15 15 15
23. Lớp học có 40 đoàn viên gồm 20 nam và 20 nữ. Số cách chọn 4 bạn tham gia tập huấn văn nghệ sao
cho có ít nhất 1 nữ là: A) A4 − A4 B) A2
C) C 2 C 2 + 20C 3 D) C 4 − C 4 40 20 20 20 20 20 40 20
24. Một lớp có 30 học sinh, trong đó có 20 nam. Có bao nhiêu cách chọn một ban cán sự lớp gồm 4 học
sinh sao cho ban cán sự đó có nhiều nhất 2 nam? A) 210 B) 2004 C) 2400 D) 11160 4
25. Một chi đoàn có 15 đoàn viên nam và 10 đoàn viên nữ. Hỏi có bao nhiêu cách chọn một tổ công tác
gồm 5 người, trong đó có đúng 2 nữ? A) 1134 B) 3450 C) 20475 D) 53130
26. Một đoàn tàu có 10 toa, có bao nhiêu cách sắp xếp 4 hành khách lên 4 toa khác nhau? A) C 4 B) A 4 4 C) A D) 4! 10 4 10
27. Một giải bóng đá gồm có 14 đội, mỗi đội phải đá với đội khác hai trận: sân nhà và sân khách. Hỏi
phải tổ chức bao nhiêu trận đấu tất cả? 2 A) A B) C 2 C) 28 D) 14 14 14
28. Người ta dùng 5 cột cờ để báo hiệu trên biển. Biết rằng có tất cả 7 màu cờ khác nhau. Hỏi có bao
nhiêu tín hiệu khác nhau nếu hai cột kế nhau không được cùng màu. A) 2520 B) 9072 C) 150 D) 7!
2. BIẾN CỐ, PHÂN LOẠI VÀ BIỂU DIỄN BIẾN CỐ 1.
Một xí nghiệp có 3 ôtô hoạt động độc lập. Gọi Ai là biến cố ôtô thứ i bị hỏng trong ngày (i = 1, 2, 3), A là
biến cố trong một ngày có đúng 1 ôtô bị hỏng. Chọn biểu diễn đúng nhất của A.
A) A = A A .A + A .A .A + A .A .A
B) A = A + A + A 1 2 3 1 2 3 1 2 3 1 2 3
C) A = A + A + A D) A = A A A 1 2 3 1 2 3 2.
Ba người, mỗi người bắn một phát súng vào bia. Gọi Ai là biến cố người thứ i bắn trúng. A là biến cố
người thứ nhất bắn trúng còn người thứ hai bắn trật. Hãy chọn kết luận đúng nhất trong các kết luận sau:
A) A = ( A + A + A )( A + A + A ) B) A = A A A 1 2 3 1 2 3 1 2 3
C) A = A + A + A
D) A = A .A .A + A .A .A 1 2 3 1 2 3 1 2 3 3.
Có 3 sinh viên thi môn xác suất thống kê. Gọi Ai là biến cố sinh viên thứ i thi đỗ ( i = 1, 2, 3); B là
biến cố có sinh viên thi hỏng. Hãy chọn đáp án đúng nhất trong các đáp án sau:
A) A B = A A A + A A A + A A A 1 1 2 3 1 2 3 1 2 3
B) A B = A A A + A A A + A A A + A A A 1 1 2 3 1 2 3 1 2 3 1 2 3
C) A B = A A A + A A A + A A A 1 1 2 3 1 2 3 1 2 3
D) A B = A A A + A A A + A A A 1 1 2 3 1 2 3 1 2 3 4.
Giả sử A là biến cố ít nhất một trong ba dụng cụ được kiểm tra bị hư hỏng, B là biến cố cả ba dụng
cụ điều tốt. Khi đó, AB là biến cố gì?
A) Biến cố không thể
B) Biến cố đối lập của A C) Biến cố chắc chắn
D) Biến cố đối lập của B 5.
Gieo con xúc xắc 6 mặt, gọi Ai là biến có xuất hiện mặt có i chấm (i=1,6 ), A là biến cố “xuất hiện
mặt có số chấm chẵn”, B là biến cố “xuất hiện mặt có số chấm là bội của 3”. Hãy chọn kết luận đúng
trong các kết luận sau:
A) B = A3 + A6
B) A6 = A.B
C) A3 = B\A
D) Cả 3 kết luận điều đúng 6.
Cho 3 biến cố A, B, C. Chọn biểu thức biểu diễn biến cố đúng nhất.
A) A và B xảy ra nhưng C không xảy ra: A + B + C
B) Có một và chỉ một trong các biến cố đó xảy ra: ABC
C) Chỉ có 2 trong các biến cố đó xảy ra: ABC + ABC + ABC
D) Cả 3 biến cố cùng xảy ra: A + B + C 7.
Cho A và B là hai biến cố xung khắc, hãy chọn hệ thức đúng nhất:
A) A + AB + A + B = A
B) AB + AB + AB = AB
C) A + AB + A + B =
D) A + B = AB 8.
Có 3 sinh viên A, B, C cùng thi môn Xác suất thống kê. Gọi biến cố Ai là “có i sinh viên thi đậu” (i = 0, 1,
2, 3); C là biến cố sinh viên C thi đỗ. Biến cố A C là: 0 5 A) Sinh viên C thi hỏng
B) Chỉ sinh viên C thi hỏng
C) Có hai sinh viên thi đậu
D) Cả ba sinh viên thi hỏng 9. Hãy chọn câu đúng:
A) A và B đối lập thì A và B là hai biến cố độc lập nhau
B) A và B xung khắc thì A và B là hai biến cố đối lập nhau
C) A và B đối lập thì A và B là hai biến cố xung khắc
D) A và B đối lập thì A và B là hai biến cố không xung khắc
10. Hai xạ thủ cùng bắn vào một bia. Mỗi người bắn 1 viên. Gọi A, B tương ứng là hai biến cố người thứ
nhất và người thứ hai bắn trúng bia. A + B là biến cố:
A) Cả 2 xạ thủ cùng bắn trúng bia B) Bia trúng đạn
C) Có ít nhất 1 xạ thủ bắn trúng bia D) Bia không trúng đạn
3. ĐỊNH NGHĨA XÁC SUẤT 1.
Xếp ngẫu nhiên 10 khách đi tàu lên 3 toa tàu hỏa. Xác suất toa đầu có 3 khách là ( 27 ).C 3 (27 ).A3 27 27 10 10 A) B) C) D) 310 310 39 310 2.
Gieo ngẫu nhiên một điểm trong vòng tròn bán kính R. Xác suất để điểm đó rơi vào hình vuông nội tiếp hình tròn là 2 1 A) C) D) B) 2 R 3.
Đâm một mũi kim một cách ngẫu nhiên vào hình vuông cạnh a, trong đó có hình tròn nội tiếp bán kính
a . Hãy tìm xác suất để mũi kim rơi vào hình tròn. 2 3 A) B) C) D) 4 2 3 4 4.
Có 5 khách hàng cùng vào một cửa hàng có 3 quầy giống nhau. Tìm xác suất để 3 khách hàng cùng vào một quầy? C 3 C3.3.22 4C 3 C 3 C 2 5 A) 5 B) C) 5 D) 5 5 35 35 35 35
5. Một đoàn tàu có 4 toa đỗ ở sân ga. Có 4 hành khách từ sân ga lên tàu, mỗi người độc lập với nhau
chọn ngẫu nhiên một toa. Tìm xác suất để 1 toa có 3 người, một toa có 1 người và 2 toa không có người. 3 3 3 1 A) B) C) D) 16 64 32 2 6.
Một tập hợp 10 quả cầu gồm: 2 quả màu đỏ, 3 quả vàng và 5 quả xanh. Chọn ngẫu nhiên ra 4 quả.
Xác suất chọn được 2 quả màu xanh là A) 0,2894 B) 0,1984 C) 0,476 D) 0,0476 7.
Có 3 lô sản phẩm, mỗi lô có 10 sản phẩm. Lô thứ i có i phế phẩm. Lấy ngẫu nhiên ở mỗi lô 1 sản phẩm.
Tính xác suất: “có đúng hai sản phẩm tốt”? A) 0,398 B) 0,504 C) 0,216 D) 0,602 8.
Mỗi vé xổ số ký hiệu bởi 1 số có 5 chữ số. Tìm xác suất để 1 người mua 1 vé được “vé có 5 chữ số đều chẵn”? 5! 5! 55 55 A) 105 B) 510 C) D) 510 105 9.
Gieo một con xúc xắc cân đối và đồng chất 2 lần. Tính xác suất của biến cố: “Tích 2 mặt xuất hiện
của xúc xắc là số lẻ”. 1 1 1 1 A) B) C) D) 2 4 6 8
10. Có 9 tấm thẻ đánh số từ 1 đến 9. Chọn ngẫu nhiên ra 2 tấm thẻ. Tính xác suất để tích của hai số trên
hai tấm thẻ là một số chẵn. 6 13 5 1 5 A) 18 B) C) D) 9 6 18
11. Gieo ngẫu nhiên 1 con xúc xắc 2 lần. Tính xác suất của biến cố tổng số chấm xuất hiện trên mặt con xúc xắc hai lần là 8. A) 0,083 B) 0,139 C) 0,833 D) 0,5
12. Từ 1 bộ bài 52 lá lấy ra 3 lá. Tính xác suất để có 2 lá “át”. C C 2 1 C C 2 1 A 2 A 1 A 2 A 1 A) 4 48 B) 4 50 C) 4 48 D) 4 50 C 3 52 C 3 52 C 3 52 C 3 52
13. Ba chữ số cuối cùng của một số điện thoại bắt đầu bằng 1 2 3 bị xóa nhòa trong sổ. Tính xác suất
3 chữ số bị xóa là 3 chữ số khác nhau và khác 3 chữ số đầu. A) 0,035 B) 0,21 C) 0,343 D) 0,0014
14. Một người có 15 đôi giày, trong lúc vội vã lấy tùy ý 4 chiếc. Tính xác suất người này lấy được 2 đôi. 1 1 2 4 A) B) C) D) 261 3132 15 15
4. CÁC CÔNG THỨC TÍNH XÁC SUẤT 1 1 1 1.
Cho A và B là hai biến cố sao cho P( A) = , P(B) = , P( AB) = . Chọn câu đúng nhất: 2 3 6 5 5
A) P( A + B) =
B) P( A + B) = 6 6 1 1 C) P( AB) =
D) P( A + B) = 3 6 2.
Cho P(A) = 0,2; P(B) = 0,4; P(A/B) = 0,1. Giá trị của P(B/A) là bao nhiêu? A) 0,05 B) 0,2 C) 0,8 D) 0,17 3.
Giả sử P(A) = 0,9; P(B) = 0,8 và P(AB) = 0,75; Tìm P( A.B )? A) 0,95 B) 0,02 C) 0,3 D) 0,05 1 1 1 4.
Cho A và B là 2 biến cố sao cho P( A) = , P(B) = , P( AB) = . Hãy chọn kết quả đúng nhất của 2 3 6
biểu thức P( A + B) . 5 1 2 1 A) B) C) D) 6 3 3 6 5.
Với A1, A2 là 2 biến cố bất kỳ, hãy chọn đáp án đúng trong các câu sau:
A) P(A1 + A2) = P(A1) + P(A2)
B) P(A1 + A2) P(A1A2)
C) P(A1A2) = P(A1).P(A2)
D) P(A1 + A2) > P(A1) + P(A2) 6.
Có 3 hộp, mỗi hộp đựng 5 bi. Trong đó hộp thứ nhất có 1 bi trắng, 4 bi đen; hộp thứ hai có 2 bi
trắng, 3 bi đen; hộp thứ ba có 3 bi trắng, 2 bi đen. Lấy ngẫu nhiên từ mỗi hộp 1 bi. Tính xác suất để
được 2 bi đen và 1 bi trắng? A) 0,155 B) 0,1034 C) 0,464 D) 0,1667 7.
Có 2 hộp đựng bi. Hộp 1 đựng 3 bi trắng và 3 bi đỏ, hộp 2 đựng 6 bi trắng và 4 bi đỏ. Lấy ngẫu
nhiên 4 bi từ hộp 1 bỏ sang hộp 2, rồi sau đó lấy ngẫu nhiên 1 bi từ hộp 2 ra. Tính xác suất để bi lấy từ hộp 2 là trắng. A) 0,05 B) 0,57 C) 0,08 D) 0,67 8.
Một cầu thủ lần lượt ném 3 quả bóng vào rổ một cách độc lập với các xác suất tương ứng là 0,7;
0,8; 0,9. Biết rằng có 2 quả bóng vào rổ. Xác suất để quả bóng thứ nhất vào rổ là: A) 0,5437 B) 0,5473 C) 0,4753 D) 0,4573 9.
Bắn liên tiếp vào một mục tiêu cho đến khi viên đạn đầu tiên trúng mục tiêu hoặc hết đạn thì ngưng.
Xác suất bắn trúng mục tiêu của mỗi lần bắn là 0,6. Nếu người đó có 4 viên đạn. Tính xác suất để
bắn đến viên đạn thứ 4. A) 0,0256 B) 0,0384 C) 0,064 D) 0,936 7
10. Một người bắn liên tiếp vào một mục tiêu cho đến khi có một phát đạn trúng mục tiêu thì ngưng
bắn. Biết rằng, xác suất trúng mục tiêu của mỗi lần bắn là như nhau và bằng 0,6. Tính xác suất sao
cho bắn đến phát thứ 4 thì ngưng bắn: A) 0,0384 B) 0,064 C) 0,72 D) 0,6
11. Xác suất để một thiết bị bị hư trong một ngày làm việc là 0,01. Tìm xác suất để trong vòng 5 ngày
máy làm việc tốt. A) 0,95 B) 0,99 C) 0,05 D) 0,01
12. Một thủ kho có một chùm chìa khoá gồm 9 chiếc có bề ngoài giống hệt nhau, trong đó chỉ có 2 chiếc mở
được cửa kho. Anh ta thử ngẫu nhiên từng chìa (chìa nào không trùng thì bỏ ra). Tìm xác suất để anh ta mở
được cửa ở lần thứ 3. 2 1 2 3 A) B) C) D) 9 6 6 6
13. Có 3 hộp, mỗi hộp đựng 5 bi. Trong đó hộp thứ nhất có 1 bi trắng, 4 bi đen; hộp thứ hai có 2
bi trắng, 3 bi đen; hộp thứ ba có 3 bi trắng, 2 bi đen. Chọn ngẫu nhiên một hộp từ đó lấy ngẫu
nhiên ra 3 bi. Tính xác suất được cả 3 bi đen? A) 0,1667 B) 0,2667 C) 0,3667 D) 0,4667
14. Một hộp có 3 quả bóng màu vàng và 5 quả màu đỏ. Chọn ngẫu nhiên 1 quả bóng và xem màu, sau
đó trả lại vào hộp cùng 2 quả bóng khác nữa cùng màu. Lại tiếp tục lấy ngẫu nhiên ra 1 quả bóng,
tính xác suất để quả bóng lấy lần 2 có màu đỏ? 7 5 3 7 A) B) C) D) 16 8 16 9
15. Tín hiệu thông tin được phát đi 3 lần độc lập nhau. Xác suất thu được của mỗi lần là 0,4. Tìm xác
suất để nguồn thu nhận được thông tin đó? A) 0,4 B) 0,216 C) 0,848 D) 0,784
16. Một cuộc thi có 3 vòng thi. Vòng 1 lấy 90% thí sinh, vòng 2 lấy 80% thí sinh của vòng 1 và vòng 3
lấy 60% thí sinh của vòng 2. Khi đó, xác suất để thí sinh đó bị loại ở vòng 2 nếu biết rằng thí sinh đó bị loại là A) 0,18 B) 0,3169 C) 0,568 D) 0,108
17. Hai đấu thủ A và B thi đấu cờ. Xác suất thắng của người A trong một ván cờ là 0,6 (không có hòa).
Trận đấu có 5 ván, người nào thắng một số ván lớn hơn là người thắng cuộc. Tính xác suất để người B thắng cuộc? A) 0,3072 B) 0,2304 C) 0,4 D) 0,31744
18. Để sản xuất một loại sản phẩm có thể dùng một trong hai máy. Tỷ lệ phế phẩm đối với máy thứ nhất là 1 2
0,04 và đối với máy thứ hai là 0,03; trong một kho gồm sản phẩm của máy thứ nhất và sản phẩm 3 3
của máy thứ hai, người ta lấy ra một sản phẩm, tính xác suất để sản phẩm đó là phế phẩm? 0,1 A) 0,07 3 B) 0,07 C) 0,1 D) 3
19. Một công ty bán bảo hiểm cho người bị tai nạn chia khách hàng của mình ra thành 3 nhóm: người ít
bị rủi ro, người bị rủi ro trung bình, người thường xuyên bị rủi ro với tỷ lệ tương ứng là 60%, 30%,
10%. Xác suất bị rủi ro của các nhóm lần lượt là 0,01; 0,05; 0,1. Hãy cho biết tỷ lệ người bị tai nạn trong năm? A) 0,16 B) 0,031 C) 0,05.10−3 D) 0,969
20. Một phân xưởng có 60 công nhân, trong đó có 40 nữ và 20 nam. Tỷ lệ công nhân nữ tốt nghiệp
trung học phổ thông là 15%; còn tỷ lệ này đối với nam là 20%. Gặp ngẫu nhiên một công nhân của
phân xưởng. Tìm xác suất để gặp người công nhân tốt nghiệp phổ thông trung học. A) 0,167 B) 0,175 C) 0,35 D) 0,6 2
21. Một sinh viên đi học bằng hai cách đi xe bus hoặc xe đạp. Biết rằng sinh viên đó đi xe bus trong các 3
trường hợp, còn lại đi xe đạp. Nếu đi xe bus thì 70% trường hợp sinh viên đó về đến nhà trước 18h, còn đi 8
xe đạp thì 75% trường hợp sinh viên đó về đến nhà trước 18h. Tìm xác suất để sinh viên đó đi xe đạp biết
rằng sinh viên đó về sau 18h. A) 0,083 B) 0,298 C) 0,893 D) 0,116
22. Một nhà máy sản xuất bóng đèn, máy A sản xuât 25%, máy B sản xuất 35%, máy C sản xuất 40% số
bóng đèn. Tỷ lệ sản phẩm của mỗi máy trên số sản phẩm do máy đó sản xuất lần lượt là 3%, 2%, 1%.
Một người mua một bóng đèn do nhà máy sản xuất. Tính xác suất để sản phẩm này là sản phẩm tốt? A) 0,9815 B) 0,9412 C) 0,9997 D) 0,504
23. Biết rằng P1=0,04 là xác suất để mỗi sản phẩm được sản xuất ra từ dây chuyền 1 là phế phẩm.
Tương tự, đối với dây chuyền 2, 3, 4 thì xác suất đó lần lượt là 0,03; 0,05; 0,058. Số lượng sản
phẩm của dây chuyền 1, 2, 3, 4 lần lượt là 8, 12, 10, 5 sản phẩm. Lấy ngẫu nhiên ra 1 sản phẩm.
Tính xác suất để nhận được sản phẩm tốt? A) 0,042 B) 0,958 C) 0,999 D) 0,822
24. Thành phố H có 45% nam và 55% nữ, trong đó có 4% nam và 2% nữ bị loạn sắc. Chọn ngẫu nhiên
một người từ thành phố H, nếu người được chọn qua kiểm tra thấy loạn sắc, tính xác suất để người đó là nam. A) 0,62 B) 0,018 C) 0,06 D) 0,04 5
25. Tỷ số xe tải và xe con đi qua đường có trạm bơm dầu là
. Xác suất để 1 xe tải qua đường được 2
nhận dầu là 0.1, còn xác suất để 1 xe con qua đường được nhận dầu là 0.2, có một xe vào trạm để
nhận dầu. Tìm xác suất để đó là xe tải? 1 1 9 5 A) B) C) D) 2 4 10 9
26. Một nhà máy sản xuất bóng đèn, máy A sản xuất 25%, máy B sản xuất 35%, máy C sản xuất 40%
số bóng đèn. Tỷ lệ sản phẩm của mỗi máy trên số sản phẩm do máy đó sản xuất lần lượt là 3%, 2%,
1%. Một người mua một bóng đèn do nhà máy sản xuất, biết rằng sản phẩm này là xấu. Tính xác
suất để sản phẩm này do nhà máy C sản xuất? A) 0,35 B) 0,22 C) 0,0035 D) 0,541
27. Một người say rượu bước 8 bước, mỗi bước anh ta tiến lên phía trước 1m hoặc lùi lại phía sau 1m
với xác suất như nhau. Tìm xác suất để anh ta “trở lại điểm xuất phát”. A) 0,003 B) 0,27 C) 0,063 D) 0,25
28. Trong một lớp học có 6 bóng đèn, mỗi bóng có xác suất bị cháy là 0,25. Lớp học đủ ánh sáng nếu
có ít nhất 4 bóng đèn sáng. Tính xác suất để lớp học không đủ ánh sáng. A) 0,169 B) 0,196 C) 0,619 D) 0,75
29. Tỷ lệ người có nhóm máu O trong một nước là 30%. Chọn ngẫu nhiên 5 người từ nước này. Chọn một
câu đúng trong các câu sau đây:
A) Xác suất không chọn được người nào có nhóm máu O là 0,168
B) Xác suất cả 5 người có nhóm máu O là 0,024
C) Xác suất chọn được 2 người có nhóm máu O là 0,0309
D) Xác suất không chọn được người nào có nhóm máu O là 0,0168
30. Một máy bay được lệnh đi công kích mục tiêu đã ném 10 quả bom (ném mỗi lần 1 quả, các lần ném
độc lập nhau). Xác suất trúng đích của mỗi quả bom trong các lần ném đều bằng nhau và bằng 0,3.
Tìm xác suất để có 1 quả bom trúng đích. A) 0,012 B) 0,121 C) 0,3 D) 0,03
31. Tung một đồng xu 6 lần. Tìm xác suất để số lần được mặt sấp nhiều hơn số lần được mặt ngửa. 1 11 21 31 A) B) 32 C) 32 D) 32 32
32. Ở một cơ quan A có 3 chiếc máy tính. Khả năng xảy ra sự cố của mỗi máy tính tương đương bằng
0,1; 0,1; 0,15; Tìm xác suất sao cho cả 3 máy tính đều hoạt động được? A) 0,6885 B) 0,3115 C) 0,9985 D) 0,0015 9
33. Một máy bay có 5 động cơ, trong đó có 3 động cơ ở cạnh phải và 2 động cơ ở cạnh trái. Mỗi động
cơ ở cạnh phải có xác suất bị hỏng là 0,1. Còn mỗi động cơ ở cạnh trái có xác suất bị hỏng là 0,05.
Các động cơ hoạt động độc lập. Tìm xác suất để cả 5 động cơ bị hỏng? A) (0,1)3 (0,5)2 B) 0,05 C) 0,6 D) (0,1)3 + (0,5)2
34. Hai xạ thủ cùng bắn vào một mục tiêu, mỗi người bắn một viên đạn. Xác suất bắn trúng mục tiêu
của hai xạ thủ lần lượt là 0,7 và 0,8. Tính xác suất để mục tiêu bị trúng đạn. A) 0,56 B) 0,14 C) 0,24 D) 0,94
35. Một phòng điều trị có 3 bệnh nhân bệnh nặng với xác suất cần cấp cứu trong vòng một giờ của các
bệnh nhân tương ứng là: 0,7; 0,8; 0,9. Khi đó, xác suất để trong vòng một giờ có 2 bệnh nhân cần
cấp cứu là bao nhiêu? A) 0,056 B) 0,126 C) 0,216 D) 0,398
BÀI TẬP ĐLNN VÀ THỐNG KÊ A. TỰ LUẬN
1. Một sọt cam có 11 trái tốt và 4 trái hư. Lấy ngẫu nhiên ra bốn trái.
Gọi X là số trái tốt được lấy ra.
a. Hãy lập bảng phân phối xác suất của X
b. Tính xác suất lấy được nhiều nhất 3 trái tốt
c. Tính trung bình và phương sai của số trái tốt được lấy ra.
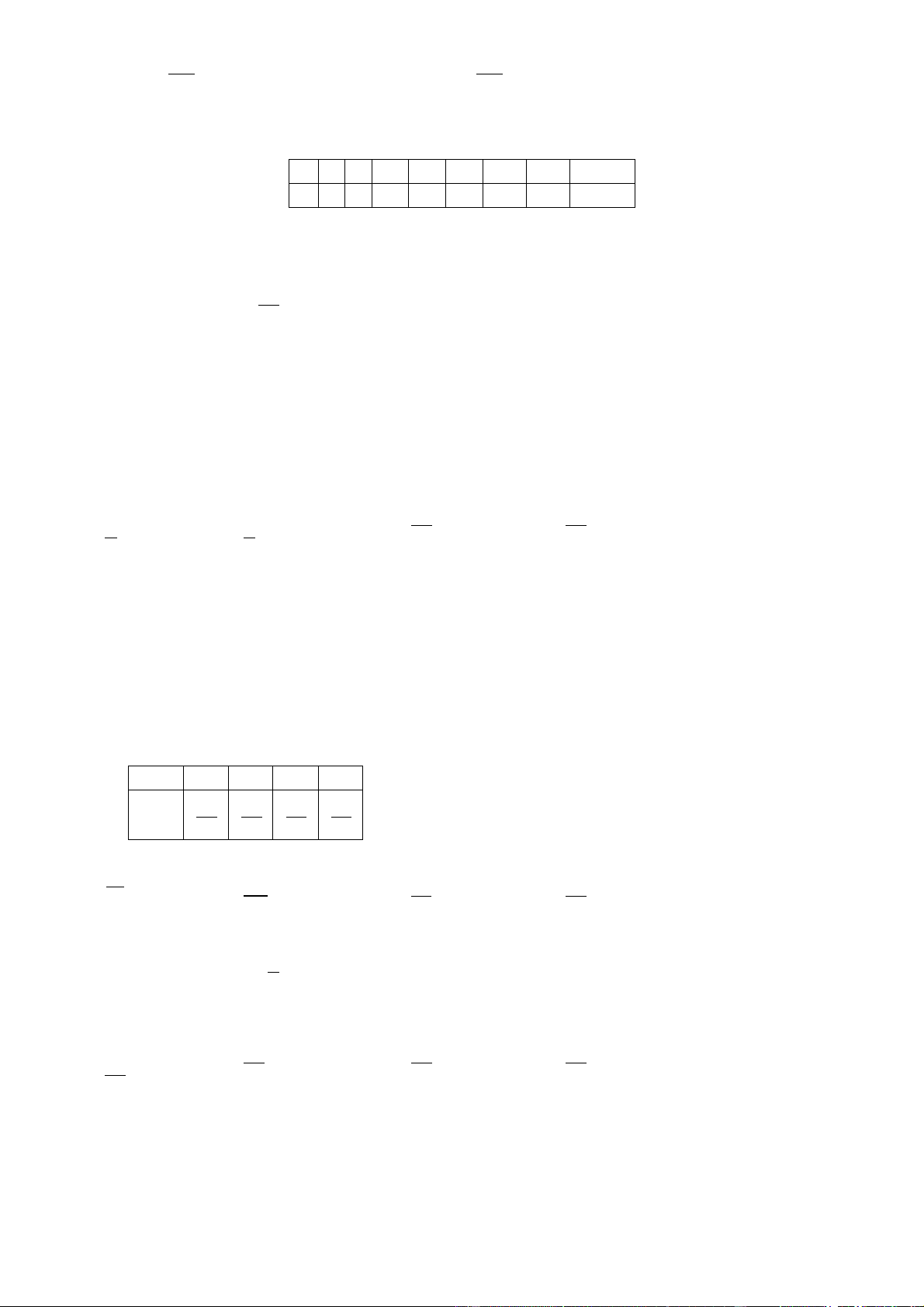
2. Cho X là đại lượng ngẫu nhiên rời rạc có bảng phân phối xác suất X -1 2 3 7 P 0.1 a 0.4 0.25 a. Hãy tìm giá trị a
b. Tính P ( X 3)
c. Tính E ( X ), E (3X + 4), E (2 X − 3), E ( X 2 )
d. Tính Var ( X ),Var (2 X ),Var (3X + 3)
3. Cho X và Y là hai đại lượng ngẫu nhiên rời rạc độc lập có bảng phân phối xác suất X -3 0 1 4 Y -1 0 2 P 0.2 0.1 0.35 0.35 P 0.4 0.4 0.2
a. Tính P (3X + Y −2)
b. Tính E ( X ), E (Y ), E (2 X + 3Y ), E (3Y − 4Y + 2)
c. Tính Var ( X ),Var (Y ),Var (2 X + 3Y ),Var (3X − 4Y + 5) 4.
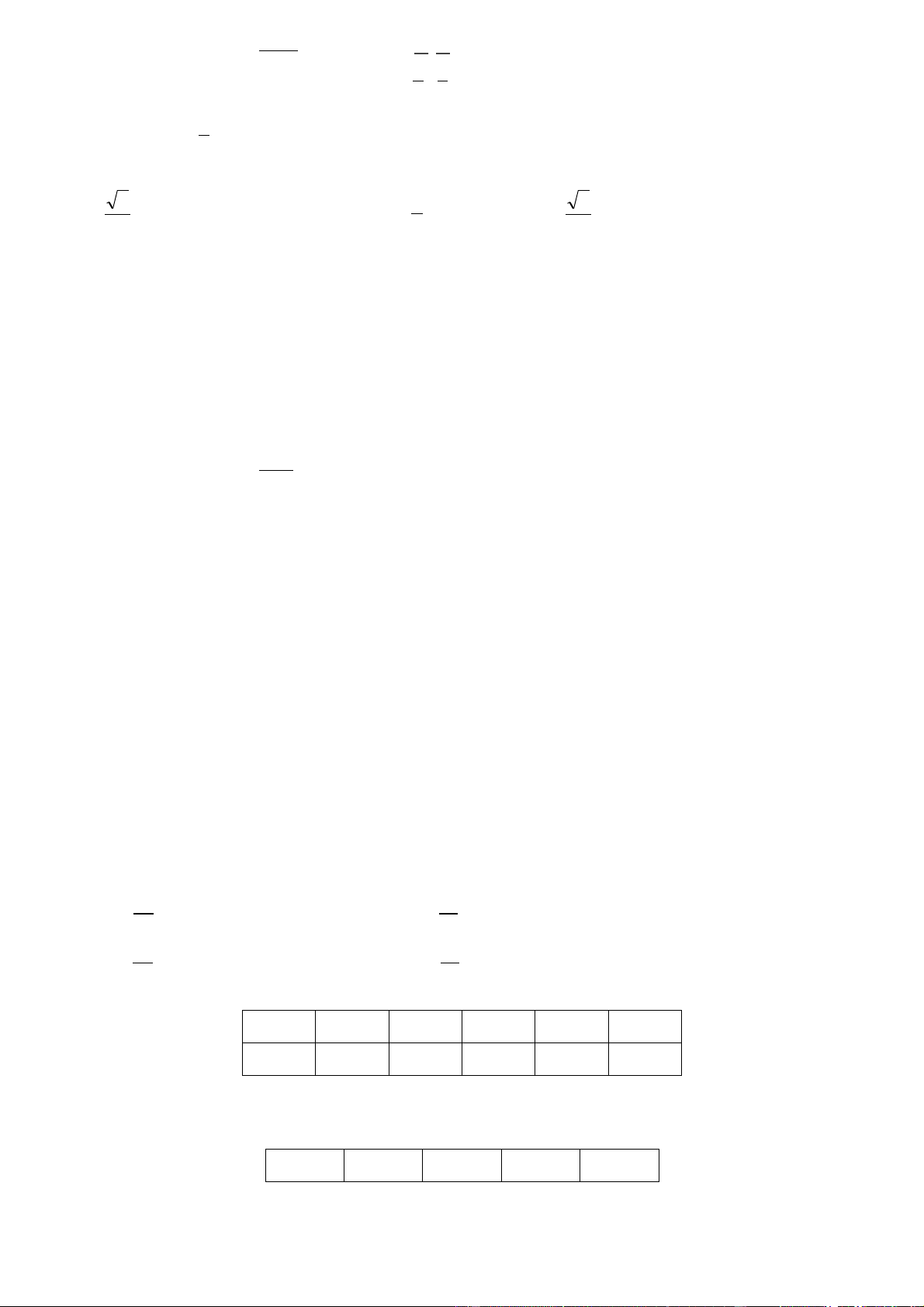
Để khảo sát về thu nhập của công nhân trong công ty, người ta điều tra 100 người và được kết quả như sau Thu nhập Số (triệu người
đồng/ tháng) 4 13 6 15 8 14 10 17 12 19 14 16 16 6
Những người có thu nhập lớn hơn hoặc bằng 12 triệu đồng được xem là những người có thu nhập cao.
a. Hãy ước lượng mức thu nhập trung bình của công nhân với mức ý nghĩa 5% 10
b. Hãy ước lượng tỷ lệ những người có thu nhập cao với độ tin cậy 99%?
c. Nếu muốn độ chính xác của việc ước lượng tỷ lệ những người có thu nhập cao là 0.086 với
mức ý nghĩa 5% thì cần phải điều tra bao nhiêu người?
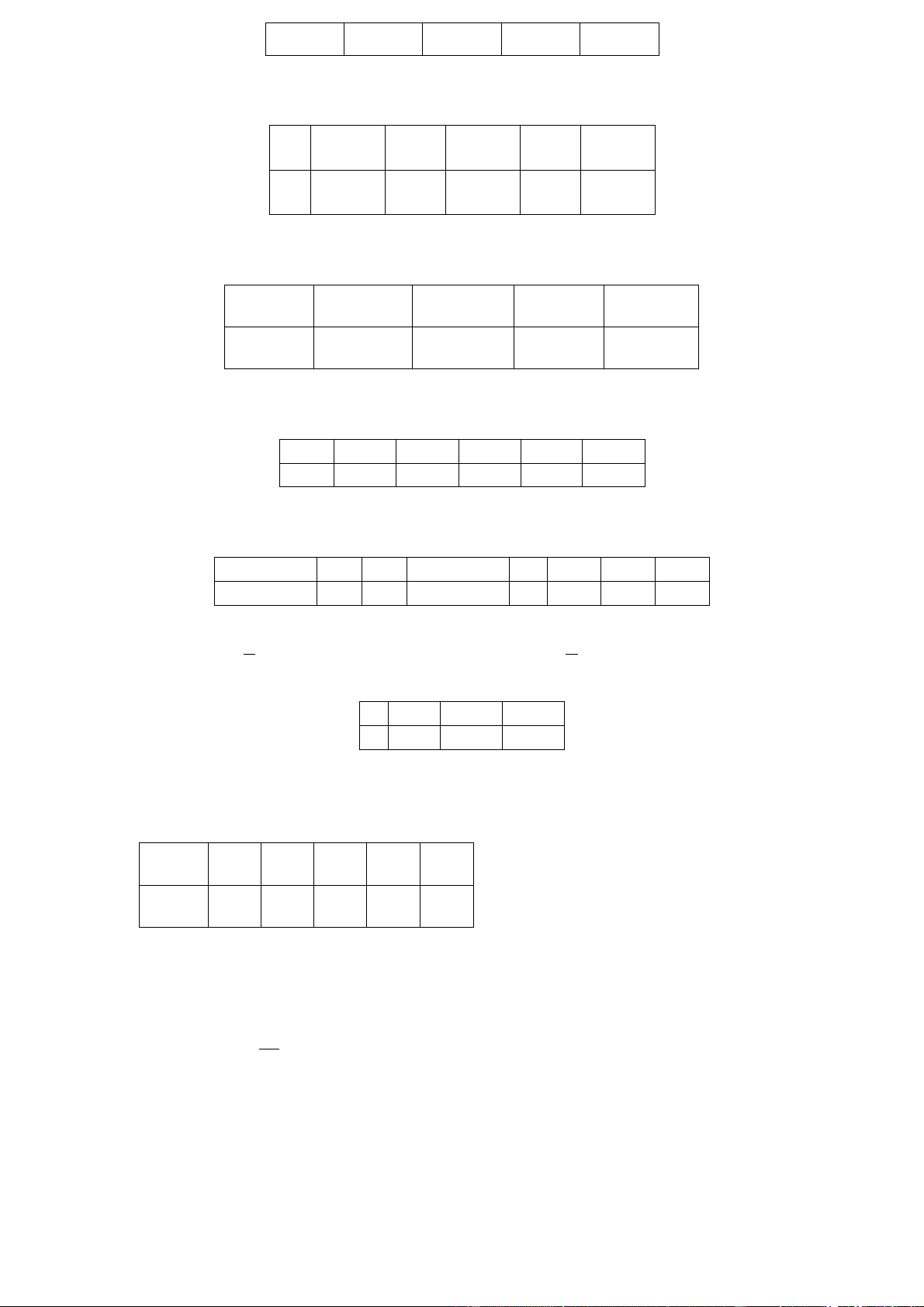
5. Ở một nhà máy vải, người ta kiểm tra số lỗi trên một số tấm vải và được kết quả sau: Số khuyết 0 1 2 3 4 5 6 tật Số tấm vải 8 20 12 40 30 25 15
Những tấm vải có không quá một lỗi được xem là những tấm vải loại I
a. Hãy ước lượng số lỗi trung bình trên tấm vải với độ tin cậy 95%?
b. Nếu muốn độ chính xác của ước lượng số lỗi trung bình trên tấm vải là 0.25 thì độ tin
cậy của ước lượng là bao nhiêu?
c. Hãy ước lượng tỷ lệ những tấm vải lợi I với mức ý nghĩa 4%?
d. Có một báo cáo nói rằng tỷ lệ vải đạt loại I thấp hơn 20%. Với mức ý nghĩa 1%, hãy cho
biết báo cáo này đúng hay sai?
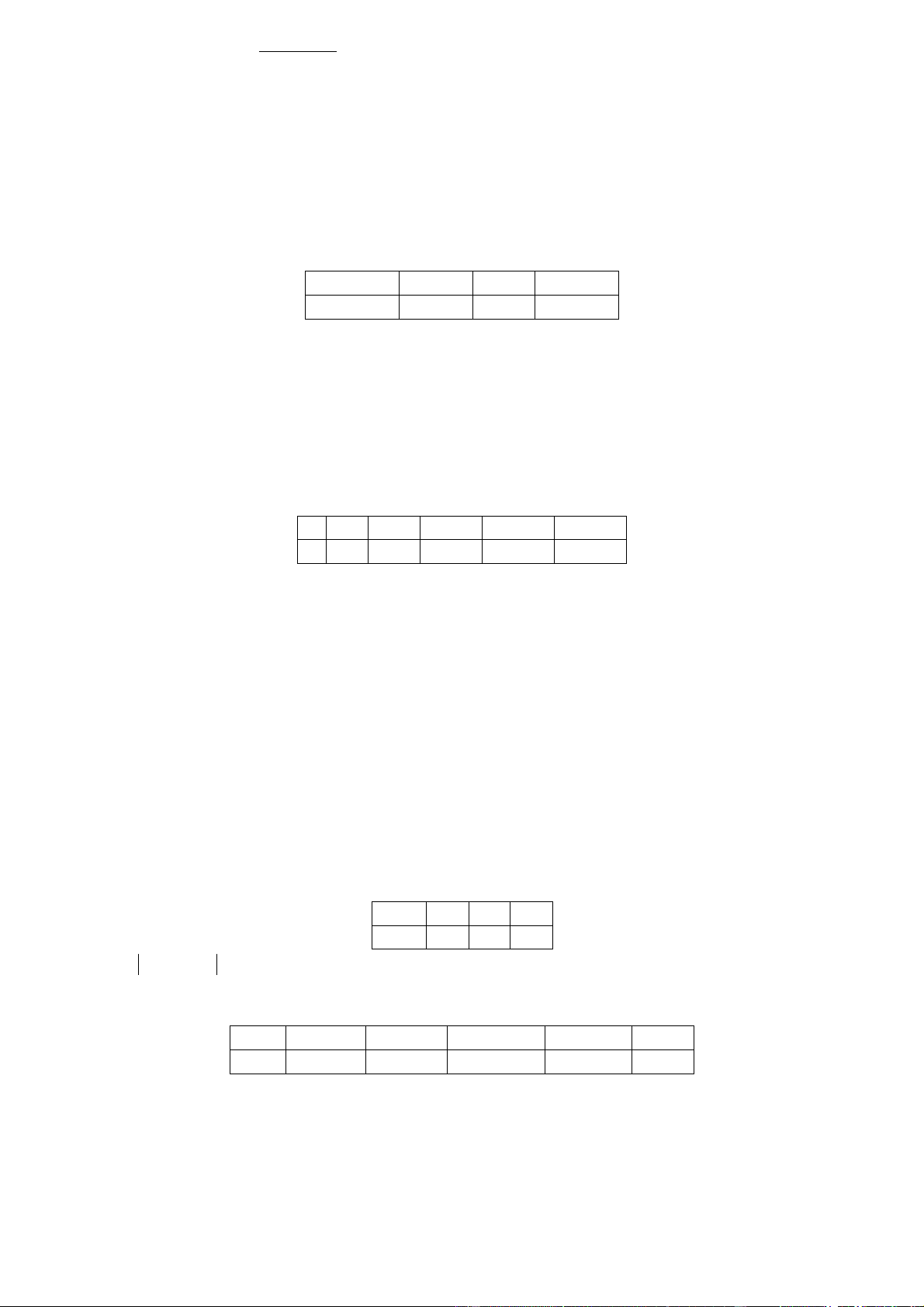
6. Để khảo sát trọng lượng của một loại vật nuôi trong nông trại người ta quan sát một mẫu và có kết quả như sau: Trọng lượng 28-32 32-36 36-40 40-44 44-48 48-52 52-56 (Kg) Số con 10 10 15 30 10 10 15
Những con có trọng lượng từ 44kg trở lên được gọi là những con đạt tiêu chuẩn
a. Hãy ước lượng trọng lượng trung bình của vật nuôi đạt chuẩn trên với độ tin cậy 95%?
b. Hãy ước lượng tỷ lệ những con đạt tiêu chuẩn với mức ý nghĩa 1%?
c. Có người cho rằng trọng lượng trung bình của loại vật nuôi là 43Kg. Khẳng định này có quá
sự thật hay không với độ tin cậy 95%?
7. Tỷ lệ hộ dân thích xem dân ca ở một vùng nông thôn là 80%. Trong một cuộc điều tra, người ta
thăm dò ngẫu nhiên 80 hộ dân thì thấy có 60 hộ thích xem dân ca. Có thể cho rằng tỷ lệ người
thích xem dân ca của vùng đã giảm xuống với mức ý nghĩa 1% hay không?
8. Một hãng sản xuất thép muốn xác định xem có sự khác nhau về năng suất sản xuất của ca ngày và
ca tối hay không. Lấy một mẫu 100 công nhân ca ngày sản xuất được x = 74.3, s = 16 ; Lấy một x
mẫu khác của 100 công nhân ca tối sản xuất được y = 69.7, s = 18 . Hãy xét xem có sự khác nhau y
về năng suất của hai ca hay không với mức ý nghĩa 1%?
9. Để nâng cao năng suất sản xuất của nhà máy người ta sử dụng một phương pháp mới. Số sản phẩm
trước và sau khi sử dụng phương pháp mới của 10 công nhân trong ngày được cho dưới bảng sau: Công 1 2 3 4 5 6 7 8 9 10 nhân Trước 58 58 56 38 70 38 42 75 60 67 Sau 60 55 63 40 67 43 37 72 56 72
Với độ tin cậy 95%, hãy đánh giá xem phương pháp mới này có hiệu quả hay không
10. Điều tra về thu nhập của 400 công nhân ở Hà Nội và Thành phố Hồ Chí Minh, người ta thu được kết quả sau: Thu nhập 30 – <30 >60 60 Thành phố Hà Nội 36 50 38
Hồ Chí Minh 69 105 102
Với độ tin cậy 95%, có thể kết luận thu nhập của công nhân phụ thuộc vào thành phố mà họ làm việc hay không? 11
11. Điều tra ngẫu nhiên 1000 người sống ở thành phố A cho thấy tỷ lệ thất nghiệp là 8%, 1200 người ở
thành phố B có tỷ lệ thất nghiệp là 8.2%. Có thể khẳng định tỷ lệ thất nghiệp của thành phố B cao
hơn thành phố A hay không với độ tin cậy 95%?
12. Một công ty kiểm tra mức độ ưa thích của nam và nữ đối với loại sản phẩm mới. Phỏng vấn ngẫu
nhiên 425 khách nam thì có 240 người thích, phỏng vấn ngẫu nhiên 370 khách nữ thì có 196 người
thích. Có một báo cáo cho rằng tỷ lệ ưa thích sản phẩm này của nam cao hơn nữ. Báo cáo này
đúng hay sai? (Với mức ý nghĩa 2%).
13. Gạo đủ tiêu chuẩn xuất khẩu là gạo có tỷ lệ hạt nguyên, hạt vỡ, tấm là: 90%, 6%, 4%. Kiểm tra
1000 hạt gạo của một lô gạo được kết quả như sau: Hạt
Hạt vỡ Tấm nguyên 880 60 60
Với độ tin cậy 95%, có thể kết luận lô gạo đó đủ tiêu chuẩn xuất khẩu hay không?
B. TRẮC NGHIỆM
1. ĐLNN VÀ LUẬT PHÂN PHỐI XÁC SUẤT 1.
Hãy chọn câu đúng trong các câu sau:
A) Biến ngẫu nhiên luôn nhận giá trị dương.
B) Biến ngẫu nhiên rời rạc chỉ nhận một số hữu hạn các giá trị.
C) Kỳ vọng của tổng hai biến ngẫu nhiên luôn luôn bằng tổng các kỳ vọng của nó.
D) Kỳ vọng của biến ngẫu nhiên rời rạc là giá trị có xác suất cao nhất. 2.
Chọn câu đúng nhất trong các câu sau đây:
A) E(CX) = CE(X) B) E(C) = 0 C) E(CX) = C2(EX) D) E(X2) = (EX)2 3.
Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau: X 0 1 2 3 P 0,216 0,432 0,288 0,064
Khi đó, hàm phân phối xác suất của X là 0 x 0 0, 216 x 0 0, 216 0 x 1 0,648 0 x 1 A) F(x) = F(x) = 0,648 1 x 2 B) 0,936 2 x 3 0,936 2 x 3 1 x 3 1 x 3 0 x 0 0,216 x = 0 C) 0,216 0 x 1 F (x) = D) F (x) = 0,648 0 x 1 0,648 1 x 2 0,936 2 x 3 0,936 2 x 3 4.
Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau: 2x
khi x [−1; 2] f (x) = 3 0
khi x [−1; 2]
Hàm phân phối xác suất F (x) = P(X x) của X là 0 khi x −1 0 khi x −1 2 − 2 A) F (x)
khi − 1 x 2 B) F (x) +
khi − 1 x 2 = 1 1 = 3 3 1 khi 2 x 1 khi 2 x 12 0 khi x −1 0 khi x −1 x 2 x 2
C) F (x) = khi − 1 x 2
D) F (x) = khi − 1 x 2 3 3 1 khi 2 x 1 khi 2 x 5.
Cho biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau: X 0 1 2 3 4 5 6 7
P 0 k 2k 2k 3k 4k2 5k2 k2 + k Giá trị của k là A) k = 1 / 10 B) k = -1 C) k = 1 D) k = 0 6.
Biến ngẫu nhiên X có hàm mật độ xác suất: k khi x [1;3] f (x) = x 2 0 khi x [1;3]
Hãy tìm hằng số k? A) 2/3 B) 3/2 C)1/2 D)1/3 7.
Cho đại lượng ngẫu nhiên liên tục có hàm mật độ xác suất:
c(3x − x 2 ) khi x [0;3] f (x) = 0 khi x [0;3]
Hãy tìm hằng số c? 2 9 20 27 A) B) C) 27 D) 20 9 2 8.
Cho hàm mật độ của biến ngẫu nhiên X có dạng như sau: 0 khi x −1 ax + a
khi − 1 x 0 f (x) = − ax + a
khi 0 x 1 0 khi x 1 Giá trị của a là A) 0 B) -1 C) 1 D) 2 9.
Ta có bảng phân phối xác suất sau: X 0 1 2 3 2 15 20 5 P(X) 42 42 42 42
Hãy tính P(1 X 3) . Chọn đáp án đúng nhất. 25 40 40 5 A) B) C) D) 42 42 42 42
10. Cho đại lượng ngẫu nhiên liên tục có hàm mật độ xác suất như sau: 2
(3x − x 2 ) f (x) = 9 khi x [0;3] 0 khi x [0;3]
Hãy tìm P(1 < X < 2). 11 12 13 14 A) 27 B) 27 C) 27 D) 27
11. Biến ngẫu nhiên X có hàm mật độ xác suất 13 cos x
khi x − , 2 2 2 f (x) = 0
khi x − , 2 2
Tìm P 0 X
. Chọn đáp án đúng nhất. 4 2 1 2 A) B) 0 C) D) 4 2 2
12. Biến ngẫu nhiên X có hàm mật độ như sau: 0 khi x 0 f (x) = 2x
khi 0 x 1 0 khi x 1
Tìm xác suất để X rơi vào khoảng (0,5; 0,75)? A) 0,3125 B) 1 C) 0 D) 0,5
13. Biến ngẫu nhiên X được cho bởi hàm phân phối: 0 khi x 1 x −1 F (x) =
khi 1 x 3 2 1 khi x 3
Tìm xác suất để biến ngẫu nhiên X nằm trong khoảng (2,5; 3,5). A) 1 B) 0,5 C) 0,75 D) 0,25
14. Cho đại lượng ngẫu nhiên X có hàm phân phối như sau: 0 khi x 0 1 / 8
khi 0 x 1
F (x) = 4 / 8
khi 1 x 2
7 / 8 khi 2 x 3 1 khi x 3
P( 0 X 2,1) có giá trị là: A) 0,5 B) 0,625 C) 0,875 D) 0,125
15. Tuổi thọ của một loại kiến là một đại lượng ngẫu nhiên X (tính theo tháng) với hàm mật độ p(x):
ax 2 (4 − x) x [0; 4] p(x) = 0 x [0; 4]
Hãy tìm a và tính xác suất để loại kiến đó chết trước 2 tháng. 3 3 A) a = ; p = 5/16 B) a = ; p = 5/16 64 12 3 3 C) a = ; p = 11/16 D) a = ; p = 11/16 64 12
16. Cho biến ngẫu nhiên X có bảng phân phối xác suất: X -1 0 2 4 5 P 0,15 0,1 0,45 0,05 0,25
Giá trị của P[(−1 X 2) ( X = 5)] là? A) 0,9 B) 0,8 C) 0,7 D) 0,6
17. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X 1 2 3 4 14 P 0,15 0,25 0,4 0,2
Giá trị kỳ vọng của X là A) 2,6 B) 2,8 C) 2,65 D) 1,97
18. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau: X -2 -1 0 1 2 P 0,09 0,3 0,37 0,2 0,04
Khi đó, E(X) có giá trị là A) 0,28 B) – 0,2 C) 0,76 D) 1,02
19. Cho X có bảng phân phối xác suất như sau: X -6,4 -3,7 -0,1 2,6 P 0,06 0,14 0,24 0,56
Hãy cho biết giá trị của E(X + 2). A) 0,53 B) 2,53 C) 1,53 D) 3,53
20. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau: X 0 1 2 3 4
P(X) 0,071 0,354 0,424 0,141 0,010
Hãy cho biết giá trị của E(3X - 2)? A) 4,995 B) 1,665 C) 2,995 D) 3,995
21. Cho 2 biến X, Y độc lập và có bảng phân phối xác suất là X 0 1 Y 2 0 -2 P 1/2 ½ P 1/6 2/3 1/6
Hãy cho biết giá trị của E(X+Y): 1 3 A) 0 B) C) 1 D) 2 2
22. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau: X 2 3 4 P 0,64 0,256 0,104
Tìm kỳ vọng và phương sai của X.
A) E(X) = 0,768; Var(X) = 1,7141
B) E(X) = 2,464; Var(X) = 0,4567
C) E(X) = 1,696; Var(X) = 1,3476
D) E(X) = 0,416; Var(X) = 1,4909
23. Cho bảng phân phối xác suất như sau: X 2 3 4 6 7 P(X) 0,1 0,2 0,3 0,2 0,2
Chọn câu trả lời đúng nhất. A) E(X) = 4,6 B) E(X2) = 24 C) Var(X) = 2,84 D) Cả a, b, c đúng
24. Cho hàm mật độ của biến ngẫu nhiên X như sau: x2
khi x [−1;2] f (x) = 3
0 khi x [−1;2]
E(4X + 3) có giá trị bằng bao nhiêu? A) 8 B) 9 C)10 D) 11
25. Tìm kỳ vọng của biến ngẫu nhiên X có hàm mật độ xác suất như sau: 15
4x(9 − x2 ) x [0; 3] f (x) = 81 0 x [0; 3] A) 8/5 B)5/8 C)4/27 D)27/4
26. Giả sử X là biến ngẫu nhiên sau cho: E(X)=2, E( X 2 ) = 5 . Tính Var(X)? A) – 1 B) 1 C) 3 D) - 3
27. Cho hai biến ngẫu nhiên X và Y độc lập. Tính Var(Z) với Z = 2X + 3Y.
A) Var(Z) = 2Var(X) + 3Var(Y)
B) Var(Z) = 4Var(X) + 9Var(Y)
C) Var(Z) = 4Var(X) + 6Var(Y)
D) Var(Z) = (Var(X))2 + (Var(Y))2
28. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất: X -1 0 1 P(X) 0,2 0,3 0,5
Khi đó, độ lệch chuẩn có giá trị là bao nhiêu? A) 0,61 B) 0,78 C) 0,16 D) 0,87
29. Cho hàm mật độ của biến ngẫu nhiên X như sau: 2(x −1) khi x [1;2] f (x) = 0 khi x [1;2]
Tìm phương sai của biến ngẫu nhiên X. A) 0,4 B) 2,5 C) 1 D) 0,05
30. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau: X 1 2 3 4 5
P 0,8 0,16 0,032 0,0064 0,0016
Tìm kỳ vọng và phương sai của X.
A) E(X) = 1,2496; Var(X) = 0,3089
B) E(X) = 1,2496; Var(X) = 1,2305
C) E(X) = 0,096; Var(X) = 1,8612
D) E(X) = 0,808; Var(X) = 0,1871
31. Thời gian phục vụ mỗi khách hàng (tính bằng phút) tại một cửa hàng mậu dịch là biến ngẫu nhiên X
tuân theo quy luật lũy thừa với hàm mật độ xác suất như sau: 5e−5 x khi x 0 f (x) = 0 khi x 0
Tìm xác suất để thời gian phục vụ một khách hàng nào đó sẽ nằm trong khoảng từ 0,4 đến 1 phút. A) 0,013 B) 0 C) 0,13 D) 0,5
32. Đại lượng ngẫu nhiên rời rạc X chỉ nhận hai giá trị x1 và x2 (x2>x1). Xác suất X nhận giá trị x1 là 0,6,
tìm các giá trị x1, x2 mà X có thể nhận nếu như biết E(X)= 1,4 và Var(X)= 0,24 A) x1=1, x2=2 B) x1=2, x2=1
C) x1=0,4; x2=0,6
D) x1=0,6; x2=0,4
33. Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X 1 4 8 P(X) 0,3 0,1 0,6
Tìm P( X − E( X ) 4) . Chọn đáp án đúng nhất. A) 5,5 B) 6 C) 4 D) 2
34. Cho ĐLNN X có bảng phân phối xác suất như sau: X 0 1 2 3 4 P(X) 0,071 0,354 0,424 0,141 0,01 Giá trị Mod(X) là A) 0,424 B) 0,01 C) 4 D) 2
35. Hai biến ngẫu nhiên X, Y độc lập. Cho biết Var(X) = 4, Var(Y) = 5. Hãy tính Var(Z) với Z = - 3X +
Y. Var(Z) có giá trị là: A) -7 B) 9 C) 17 D) 41 16
36. Gọi X là số cây Át trong 3 cây bài lấy ra từ bộ bài 52 cây. Hãy tìm Var(X). A) 0,231 B) 0,226 C) 0,213 D) 0,05
37. Năng suất của 3 loại máy cùng sản xuất một loại sản phẩm là đại lượng ngẫu nhiên X1, X2, X3 có
luật phân phối xác suất như sau: X1 1 2 3 4 X2 2 4 5 P 0,1 0,2 0,5 0,2 P 0,4 0,3 0,3 X3 2 3 4 5 P 0,1 0,4 0,4 0,1
Giả sử bạn cần mua 1 trong 3 loại máy này với giả thiết giá của 3 loại máy này là như nhau thì bạn sẽ mua loại máy nào? A) 1 hoặc 2 B) 2 hoặc 3 C) 1 D) 3
38. Một cửa hàng điện máy bán một chiếc tivi thì lời 500.000 đồng nhưng nếu chiếc tivi phải bảo hành thì
lỗ 700.000 đồng. Tính xác suất tivi phải bảo hành của cửa hàng để mức lời trung bình khi bán một chiếc
tivi là 365.000 đồng? A) 10% B) 12% C) 15% D) 23%
39. Theo thống kê trung bình cứ 1000 người đi xe máy thì có 25 người bị tai nạn trong một năm. Một
công ty bảo hiểm bán bảo hiểm loại này cho 20.000 người trong một năm với giá 98 ngàn đồng và
mức chi trả khi bị tai nạn là 3 triệu đồng. Hỏi trong một năm lợi nhuận trung bình thu được của
công ty về loại bảo hiểm này là bao nhiêu triệu đồng? A) 445 B) 450 C) 455 D) 460
40. Nhân viên tiếp thị của công ty Tiềm Năng thực hiện đợt khảo sát thị trường cho sản phẩm mới của công ty.
Trong 236 người được hỏi ngẫu nhiên có 194 người trả lời không thích sản phẩm mới này. Giả sử trong số
những người thích sản phẩm, một nửa là có nhu cầu mua sản phẩm, với quy mô thị trường có 5.698.325
người dân thì kỳ vọng có bao nhiêu người có nhu cầu mua sản phẩm này? A) 1.014.109 B) 507.055 C) 4.684.216 D) 2.342.108
41. Xác suất để một máy sản xuất ra phế phẩm là 0,02. Một ngày máy sản xuất được 250 sản phẩm.
Tìm số phế phẩm trung bình và số phế phẩm tin chắc của máy đó trong một ngày.
A) E(X) = 5; Mod(X) = 4 hoặc Mod(X) = 5
B) E(X) = 5; Mod(X) = 4,75
C) E(X) = 4,75; Mod(X) = 4,02 hoặc Mod(X) = 5,73
D) E(X) = 4,75; Mod(X) = 4,5
42. Trong hội thi, một công nhân nào đó dự thi sẽ sản xuất 2 sản phẩm. Mỗi sản phẩm loại I sẽ được thưởng
10.000 đồng, nhưng mỗi sản phẩm không phải loại I sẽ bị phạt 5.000 đồng. Giả sử xác suất để công nhân
đó sản xuất được sản phẩm loại I là 0,4. Tìm số tiền trung bình mà công nhân dự thi đó có thể có. A) 7.000 B) 1.000 C) 2.000 D) 14.000
43. Xác suất để máy thứ nhất sản xuất được sản phẩm loại I là 0,3. Đối với máy thứ hai xác suất này là 0,4.
Cho máy thứ nhất sản xuất 20 sản phẩm và máy thứ hai sản xuất 30 sản phẩm rồi mang bán với giá 8
đồng một sản phẩm loại I và 5 đồng một sản phẩm không phải loại I. Tìm số tiền thu được trung bình.
A) 304 đồng B) 364 đồng C) 284 đồng D) 386 đồng
44. Hai xạ thủ độc lập với nhau cùng bắn vào một tấm bia. Mỗi người bắn một viên. Xác suất bắn trúng
của xạ thủ thứ nhất là 0,7; của xạ thủ thứ hai là 0,8. Gọi X là số viên đạn trúng bia. Tính kỳ vọng của X. A) 1,75 B) 1,5 C) 1,54 D) 1,6
45. Theo thống kê về tai nạn giao thông của xe máy thì tỷ lệ tai nạn trong một năm tính trên đầu xe máy
theo mức độ nhẹ và nặng tương ứng là 0,001 và 0,005. Công ty Bảo Việt đề nghị tất cả các chủ xe 17
phải mua bảo hiểm xe máy một năm là 30.000 đồng và số tiền bảo hiểm trung bình một vụ là 1 triệu
đồng đối với trường hợp nhẹ và 3 triệu đồng đối với trường hợp nặng. Hỏi chi phí trung bình hàng
năm mà công ty đó phải trả cho mỗi người mua bảo hiểm là bao nhiêu?
A) 14.000 đồng B) 16.000 đồng C) 8.000 đồng D) 22.000 đồng
2. PHÂN PHỐI XÁC SUẤT CỦA MỘT SỐ BIẾN NGẪU NHIÊN THÔNG DỤNG 1.
Theo thống kê, tỷ lệ trẻ em dưới 5 tuổi thừa cân năm 2004 là 1,7%, trong một trường mầm non có
120 cháu, hỏi số trẻ thừa cân trung bình trong 120 trẻ là bao nhiêu? A) 2 B) 20 C) 17 D) 12 2.
Tại bệnh viện A trung bình 3 giờ có 8 ca mổ. Hỏi số ca mổ chắc chắn nhất sẽ xảy ra tại bệnh viện A
trong 10 giờ là bao nhiêu? A) 25 B) 26 C) 27 D) 28 3.
Xác suất có bệnh của những người chờ khám bệnh tại một bệnh viện là 72%. Khám lần lượt 61 người
này, hỏi khả năng cao nhất có bao nhiêu người bị bệnh? A) 41 người B) 42 người C) 43 người D) 44 người 4.
Xác suất để trong khi vận chuyển mỗi chai rượu bị vỡ là 0,001. Người ta tiến hành vận chuyển 2000
chai rượu đến cửa hàng. Tìm số chai vỡ có khả năng nhiều nhất khi vận chuyển. A) 1 chai B) 2 chai C) 1 hoặc 2 chai D) từ 1 đến 3 chai 5.
Cho X, Y, Z là các đại lượng ngẫu nhiên độc lập. X ~ B(6; 0,4); Y ~ H(10; 6; 3); Z ~ N(5; 0,25); T = 2X + 3Y
– Z + 5. Hãy tìm kỳ vọng của T? A) 15,2 B) 10,2 C) 8,2 D) 12,8 6.
Tỷ lệ cử tri ủng hộ ứng cử viên A trong một cuộc bầu cử là 60%. Người ta hỏi ý kiến 20 cử tri được
chọn một cách ngẫu nhiên. Gọi X là số người bỏ phiếu cho A trong 20 người đó. Tìm giá trị trung bình, độ lệch chuẩn, Mod(X).
A) E(X) = 12; D(X) = 4,8; Mod(X) = 12
B) E(X) = 12; D(X) = 2,191; Mod(X) = 12
C) E(X) = 5; D(X) = 2,191; Mod(X) = 5
D) E(X) = 5; D(X) = 4,8; Mod(X) = 5 7.
Một thùng bia có 24 chai trong đó để lẫn 3 chai quá hạn sử dụng. Chọn ngẫu nhiên từ thùng đó ra 4
chai bia. Xác suất chọn phải ít nhất 1 chai bia quá hạn sử dụng là: A) 0,4123 B) 0,5868 C) 0,4386 D) 0,5632 8.
Trong phòng có 12 người, trong đó có 4 người không thích xem bóng đá. Chọn ngẫu nhiên ra 5
người. Gọi X là số người không thích xem bóng đá trong 5 người chọn ra. Hãy cho biết xác suất
chọn được 3 người không thích xem bóng đá. A) 0,75 B) 0,1875 C) 0,141 D) 0,333 9.
Một lô hàng có 1% phế phẩm. Tìm xác suất để khi chọn ra 500 sản phẩm thì tất cả đều là sản phẩm tốt. e−500 − e500 A) e−5 B) C) e 500 D) 500! 500!
10. Gieo 1000 hạt thóc, biết tỷ lệ không nảy mầm là 0,005. Tìm xác suất để có 20 hạt không nảy mầm.
Hãy chọn đáp án đúng nhất. e−5 .520 e−0.005 .0.00520 e5 .520 A) B) e−5 .520 C) 20! 20! 20! D) 20
11. Một lô hàng thịt đông lạnh đóng gói nhập khẩu với tỷ lệ bị nhiễm khuẩn là 1,6%. Kiểm tra lần lượt
ngẫu nhiên 2000 gói thịt từ lô hàng này. Tính xác suất có đúng 36 gói thịt bị nhiễm khuẩn. A) 0,1522 B) 0,2522 C) 0,0922 D) 0,0522
12. Hàng ngày ở phòng cấp cứu trung bình có 5 ca tới cấp cứu. Tính xác suất để có 10 ca cấp cứu. e−5 510 e−5 e−10 e5 A) 10! B) 10! C) 5! D) 10! 18
13. Một xưởng in cứ in 5000 cuốn sách lại bị lỗi 1 cuốn. Tìm xác suất để trong 1800 cuốn sách mới in
không có quá 2 cuốn bị lỗi. A) 0,045 B) 0,296 C) 0,949 D) 0,994
14. Một máy tính gồm 1000 linh kiện A. Xác suất hỏng của linh kiện này là 0,001. Máy tính ngưng
hoạt động khi số linh kiện hỏng nhiều hơn 1. Tìm xác suất để có hơn 1 linh kiện A hỏng. A) 0,386 B) 0,736 C) 0,264 D) 0,632
15. Ở một tổng đài điện thoại, các cuộc gọi điện thoại gọi đến xuất hiện ngẫu nhiên, độc lập với nhau
và tốc độ trung bình 2 cuộc gọi trong một phút. Tìm xác suất để có ít nhất một cuộc gọi điện thoại
trong khoảng thời gian 10 giây? A) 0,7181 B) 0,2835 C) 0,1371 D) 0,8628
16. Cho ĐLNN X có phân phối chuẩn với trung bình là 2100 và độ lệch chuẩn là 200. Khi đó, P(X >
2400) có giá trị bằng bao nhiêu? A) 0,0668 B) 0,668 C) 0,866 D) 0,0866
17. Trọng lượng của 1 loại sản phẩm là ĐLNN X có phân phối chuẩn với = 8,6 kg, 2 = 0,36 . Lấy 1
sản phẩm bất kỳ, hãy chọn xác suất để sản phẩm ấy có trọng lượng từ 8 kg đến 9,8 kg. A) 0,8185 B) 0,1359 C) 0,952 D) 0,8581
18. Biến ngẫu nhiên X ~ N(10; 4). Tìm P(8 X 12) A) 0 B) 0,6826 C) 0,383 D) 0,6915
19. Thời gian X (tháng) từ lúc vay đến lúc trả tiền của một khách hàng tại ngân hàng A là biến ngẫu
nhiên có phân phối N(18; 16). Tính tỷ lệ khách hàng trả tiền cho ngân hàng A trong khoảng 12 đến 16 tháng? A) 24,17% B) 9,63% C) 25,17% D) 10,63%
20. Chiều cao của nam giới đã trưởng thành là biến ngẫu nhiên X (cm) có phân phối N(165; 25). Tỷ lệ nam
giới đã trưởng thành cao từ 1,65m đến 1,75m là: A) 1,6% B) 42,75% C) 45,96% D) 47,72%
21. Chiều cao của nam giới khi trưởng thành ở một vùng dân cư là biến ngẫu nhiên phân phối chuẩn
với kỳ vọng = 160 cm và độ lệch chuẩn = 6 cm . Một thành viên bị coi là lùn nếu có chiều cao nhỏ
hơn 155 cm. Tìm tỷ lệ thanh niên lùn ở vùng đó. A) 20,33% B) 79,67% C) 29,67% D) 70,33%
22. Trọng lượng sản phẩm của một loại sản phẩm do một nhà máy sản xuất là đại lượng ngẫu nhiên X.
Biết X ~ N(25; 0,25). Tỷ lệ sản phẩm có trọng lượng từ 24,5 trở lên là: A) 85,672% B) 84,134% C) 78,672% D) 95,44%
23. Thời gian cần thiết để một sinh viên đi từ ký túc xá đến lớp học là một đại lượng ngẫu nhiên có
phân phối chuẩn với trung bình là 60 phút, độ lệch chuẩn là 15 phút. Sinh viên xuất phát từ ký túc xá
trước giờ học 72 phút. Tính xác suất để sinh viên đó bị trễ học. A) 0,7881 B) 0,2881 C) 0,001 D) 0,2119
24. Các vòng bi do một máy tự động sản xuất ra được coi là đạt tiêu chuẩn nếu đường kính cúa nó sai
lệch so với đường kính thiết kế không quá 0,7 mm. Biết rằng độ sai lệch này là biến ngẫu nhiên
phân phối chuẩn với = 0 và = 0,4 mm. Tìm tỷ lệ vòng bi đạt tiêu chuẩn của máy đó. A) 21,57 % B) 43,14 % C) 45,99 % D) 91,98 % 19




