Bài tập nâng cao Toán lớp 6: Rút gọn phân số

Bài tập nâng cao Toán lớp 6: Rút gọn phân số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

91 46 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 6

Môn: Toán 6

Thông tin:

5 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Bài tập nâng cao Toán lớp 6: Rút gọn phân số
A. Lý thuyết cần nhớ về rút gọn phân số
+ Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số đó cho cùng một ước
chung (khác 1 và - 1) của cả tử số và mẫu số.
+ Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là 1 và -1.
+ Cách rút gọn một phân số về phân số tối giản: ta chia cả tử số và mẫu số của phân
số đó cho ước chung lớn nhất của cả tử số và mẫu số.
B. Bài tập vận dụng về rút gọn phân số
I. Bài tập trắc nghiệm
Câu 1: Rút gọn phân số
400
700
về phân số tối giản ta được:
A.
4
7
B.
40
70
C.
200
350
D.
2
3,5
Câu 2: Rút gọn phân số
8
200
−
về dạng phân số tối giản ta được
A.
8
200−
B.
4
100
−
C.
D.
Câu 3: Rút gọn phân số
( )
2 .3 6.5
9.6
−+
về phân số tối giản ta được phân số có tử số là:
A.6 B. 4 C. 1 D. 31
Câu 4: Rút gọn phân số
( ) ( )
9 .5. 21
6.81
−−
về phân số tối giản ta được phân số có mẫu số
là:
A. 9 B. 8 C. 15 D. -15
Câu 5: Rút gọn phân số
14 5 7
12 3 3
9 .25 .8
18 .625 .24
ta được phân số
a
b
. Tỉnh tổng
ab+
A. 14 B. 34 C. 8 D. 28
II. Bài tập tự luận
Bài 1: Tìm số nguyên
x
, biết
1,
10 3
17 4
x
x
+
=
+
2,
40 6
77 7
x
x
+
=
−
Bài 2: Rút gọn các phân số sau:
1,
1.3.5.7....49
26.27.28.29....50
2,
121212
424242
3,
187187187
221221221
4,
2.3.5 4.9.25 6.9.35 10.21.40
2.3.7 4.9.35 6.9.49 10.21.56
+ + +
+++
5,
50 14 28
13 51 30
2 .3 .7
3 .2 .7
6,
1 2 3 ... 8 9
11 12 13 ... 18 19
+ + + + +
+ + + + +
Bài 3: Cho phân số
( )
1
A Z, 2
2
n
nn
n
−
=
−
. Tìm n để A là phân số tối giản
Bài 4: Tìm số nguyên
n
sao cho:
1,
7
1
n
n
+
−
là số nguyên
2,
32
45
n
n
+
−
là số tự nhiên
Bài 5: Tìm các số tự nhiên
,ab
biết rằng:
1,
36
45
a
b
=
, biết BCNN(
,ab
)=300
2,
21
35
a
b
=
, biết UCLN(
,ab
)=30
3,
15
35
a
b
=
, biết UCLN(
,ab
).BCNN(
)=3549
C. Lời giải bài tập về rút gọn phân số
I. Bài tập trắc nghiệm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
A
C
B
B
D
II. Bài tập tự luận
Bài 1:
1,
( ) ( )
10 3
4. 10 3. 17 40 4 51 3 4 3 51 40 9
17 4
x
x x x x x x x
x
+
= + = + + = + − = − =
+
2,
( ) ( )
40 6
7. 40 6. 77 280 7 462 6 7 6 462 280
77 7
13 182 14
x
x x x x x x
x
xx
+
= + = − + = − + = −
−
= =
Bài 2:
1,
( ) ( ) ( )
( )
25
25
1.3.5.7....49 1.3.5...49 2.4.6....50
.
26.27.28.29....50 26.27.28...50 2.4.6...50
1.2.3......49.50 1.2.3...49.50 1
2
26.27.28....50. 1. 2.2 . 2.3 ... 2.25
26.27.28...50. 1.2.3...25.2
=
= = =


2,
2
121212 12.10101 12 2 .3 2
424242 42.10101 42 2.3.7 7
= = = =
3,
187187187 187.1001001 187 11
221221221 221.1001001 221 13
= = =
4,
( )
( )
2.3.5 4.9.25 6.9.35 10.21.40 2.3.5 2.2.3.3.5.5 2.3.3.3.5.7 2.5.3.7.5.8
2.3.7 4.9.35 6.9.49 10.21.56 2.3.7 2.2.3.3.7.5 2.3.3.3.7.7 2.5.3.7.7.8
2.3.5. 1 2.3.5 3.3.7 7.5.8
2.3.5
2.3.7. 1 2.3.5 3.3.7 7.5.8 2.3.
+ + + + + +
=
+ + + + + +
+++
==
+++
5
77
=
5,
50 14 28 50 13 1 28 50 13 28
13 51 30 13 50 1 28 2 13 50 28 2
2 .3 .7 2 .3 .7 2 .3 .3.7 3 3
3 .2 .7 3 .2 .7 3 .2 .2.7 .7 2.49 98
+
++
= = = =
6,
( )
( )
1 9 .10:2
1 2 3 ... 8 9 50 1
11 12 13 ... 18 19 11 19 .10:2 150 3
+
+ + + + +
= = =
+ + + + + +
Bài 3:
Để
1
A
2
n
n
−
=
−
là phân số tối giản thì UCLN(n – 1, n - 2) = 1
Gọi UCLN(n – 1, n - 2) = d thì n – 1 d và n – 2 d
(n - 1) – (n - 2) d
1 d
d = 1 với mọi n
Vậy với mọi n nguyên thì
1
A
2
n
n
−
=
−
là phân số tối giản
Bài 4:
1, Ta có
( )
7 1 8 1 8 8
1 1 8 1; 2; 4; 8
1 1 1 1 1
n n n
nU
n n n n n
+ − + −
= = + = + − =
− − − − −
Ta có bảng:
1n−
-8
-4
-2
-1
1
2
4
8
n
-7
-3
-1
0
2
3
5
9
Vậy để
7
1
n
n
+
−
nhận giá trị là số nguyên khi và chỉ khi
7; 3; 1;0;2;3;5;9n − − −
2, Ta có
32
45
n
n
+
−
là số tự nhiên
( ) ( ) ( ) ( )
3 2 4 5 4. 3 2 4 5n n n n + − + −
( ) ( )
12 8 4 5 3. 4 5 23 4 5 4 5 23 1; 23n n n n n U + − − + − − =
Ta có bảng:
45n−
-23
-1
1
23
4n
-18
4
6
28
n
9
2
−
(loại)
1
(tm)
3
2
(loại)
7
(tm)
Vậy để
32
45
n
n
+
−
nhận giá trị là số tự nhiên khi và chỉ khi
1;7n
Bài 5:
1, Ta có
36 4
4 , 5
45 5
a
a k b k
b
= = = =
BCNN(
,ab
) = 300. Mà
( ) ( )
4;5 1 300: 4.5 15k= = =
Vậy
4.15 60; 5.15 75ab= = = =
.
2, Ta có
21 3
35 5
a
b
==
UCLN(
,ab
) = 30 nghĩa là ta đã chia cho 30 để rút gọn phân số
a
b
thành phân số tối
giản
3
5
Vậy
3.30 60; 5.30 150ab= = = =
.
c, Ta có
15 3
3 ; 7
35 7
a
a k b k
b
= = = =
UCLN(
,ab
).BCNN(
,ab
)=3549 và
( )
3;7 1=
UCLN(
).
3 .7 3549kk=
UCLN(
,ab
)=
2
169
k
mà
k
, UCLN(
)
0
13k =
.
Với
39
13
91
a
k
b
= =
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Bài tập nâng cao Toán lớp 6: Rút gọn phân số
A. Lý thuyết cần nhớ về rút gọn phân số
+ Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số đó cho cùng một ước
chung (khác 1 và - 1) của cả tử số và mẫu số.
+ Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là 1 và -1.
+ Cách rút gọn một phân số về phân số tối giản: ta chia cả tử số và mẫu số của phân
số đó cho ước chung lớn nhất của cả tử số và mẫu số.
B. Bài tập vận dụng về rút gọn phân số
I. Bài tập trắc nghiệm 400
Câu 1: Rút gọn phân số
về phân số tối giản ta được: 700 4 40 200 2 A. B. C. D. 7 70 350 3,5 −8
Câu 2: Rút gọn phân số
về dạng phân số tối giản ta được 200 8 −4 −1 1 A. C. D. 200 − B. 100 25 25 ( 2 − ).3 + 6.5
Câu 3: Rút gọn phân số
về phân số tối giản ta được phân số có tử số là: 9.6 A.6 B. 4 C. 1 D. 31 ( 9 − ).5.(− ) 21
Câu 4: Rút gọn phân số
về phân số tối giản ta được phân số có mẫu số 6.81 là: A. 9 B. 8 C. 15 D. -15 14 5 7 9 .25 .8 a
Câu 5: Rút gọn phân số
ta được phân số . Tỉnh tổng a + b 12 3 3 18 .625 .24 b A. 14 B. 34 C. 8 D. 28
II. Bài tập tự luận
Bài 1: Tìm số nguyên x , biết 10 + x 3 40 + x 6 1, = 2, = 17 + x 4 77 − x 7
Bài 2: Rút gọn các phân số sau: 1.3.5.7....49 121212 187187187 1, 2, 3, 26.27.28.29....50 424242 221221221
2.3.5 + 4.9.25 + 6.9.35 +10.21.40 50 14 28 1+ 2 + 3 + ... + 8 + 9 4, 2 .3 .7 5, 6,
2.3.7 + 4.9.35 + 6.9.49 +10.21.56 13 51 30 3 .2 .7 11+12 +13 + ... +18 +19 n −1
Bài 3: Cho phân số A = (nZ,n  2) n −
. Tìm n để A là phân số tối giản 2
Bài 4: Tìm số nguyên n sao cho: n + 7 3n + 2 1, là số nguyên 2, là số tự nhiên n −1 4n − 5
Bài 5: Tìm các số tự nhiên a,b biết rằng: a 36 a 21 1, =
, biết BCNN( a,b )=300 2, =
, biết UCLN( a,b )=30 b 45 b 35 a 15 3, =
, biết UCLN( a,b ).BCNN( a,b )=3549 b 35
C. Lời giải bài tập về rút gọn phân số
I. Bài tập trắc nghiệm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 A C B B D
II. Bài tập tự luận Bài 1: 10 + x 3 1,
=  4.(10 + x) = 3.(17 + x)  40 + 4x = 51+ 3x  4x − 3x = 51− 40  x = 9 17 + x 4 40 + x 6
=  7.(40 + x) = 6.(77 − x)  280 + 7x = 462 − 6x  7x + 6x = 462 − 280 2, 77 − x 7
13x =182  x =14 Bài 2: 1.3.5.7....49 1.3.5...49 2.4.6....50 = . 26.27.28.29....50 26.27.28...50 2.4.6...50 1, 1.2.3......49.50 1.2.3...49.50 1 = = = 26.27.28....50. 1.
 (2.2).(2.3)...(2.25) 26.27.28...50.  ( 25 1.2.3...25.2 ) 25 2 2 121212 12.10101 12 2 .3 2 2, = = = = 424242 42.10101 42 2.3.7 7 187187187 187.1001001 187 11 3, = = = 221221221 221.1001001 221 13
2.3.5 + 4.9.25 + 6.9.35 +10.21.40
2.3.5 + 2.2.3.3.5.5 + 2.3.3.3.5.7 + 2.5.3.7.5.8 =
2.3.7 + 4.9.35 + 6.9.49 +10.21.56
2.3.7 + 2.2.3.3.7.5 + 2.3.3.3.7.7 + 2.5.3.7.7.8 4,
2.3.5.(1+ 2.3.5 + 3.3.7 + 7.5.8) 2.3.5 = = 5 =
2.3.7.(1+ 2.3.5 + 3.3.7 + 7.5.8) 2.3.7 7 50 14 28 50 13 1 + 28 50 13 28 2 .3 .7 2 .3 .7 2 .3 .3.7 3 3 5, = = = = 13 51 30 13 50 1 + 28+2 13 50 28 2 3 .2 .7 3 .2 .7 3 .2 .2.7 .7 2.49 98 1+ 2 + 3 + ... + 8 + 9 (1+9).10:2 50 1 6, = = = 11+12 +13 + ... +18 +19 (11+19).10:2 150 3 Bài 3: n −1
Để A = n − là phân số tối giản thì UCLN(n – 1, n - 2) = 1 2
Gọi UCLN(n – 1, n - 2) = d thì n – 1 d và n – 2 d
 (n - 1) – (n - 2) d 1 d  d = 1 với mọi n n −1
Vậy với mọi n nguyên thì A = n − là phân số tối giản 2 Bài 4: n + 7 n −1+ 8 n −1 8 8 1, Ta có = = + =1+
  n −1U (8) =  1  ; 2  ; 4  ;  8 n −1 n −1 n −1 n −1 n −1 Ta có bảng: n −1 -8 -4 -2 -1 1 2 4 8 n -7 -3 -1 0 2 3 5 9 n + 7 Vậy để
nhận giá trị là số nguyên khi và chỉ khi n  7 − ; 3 − ; 1 − ;0;2;3;5;  9 n −1 3n + 2 2, Ta có
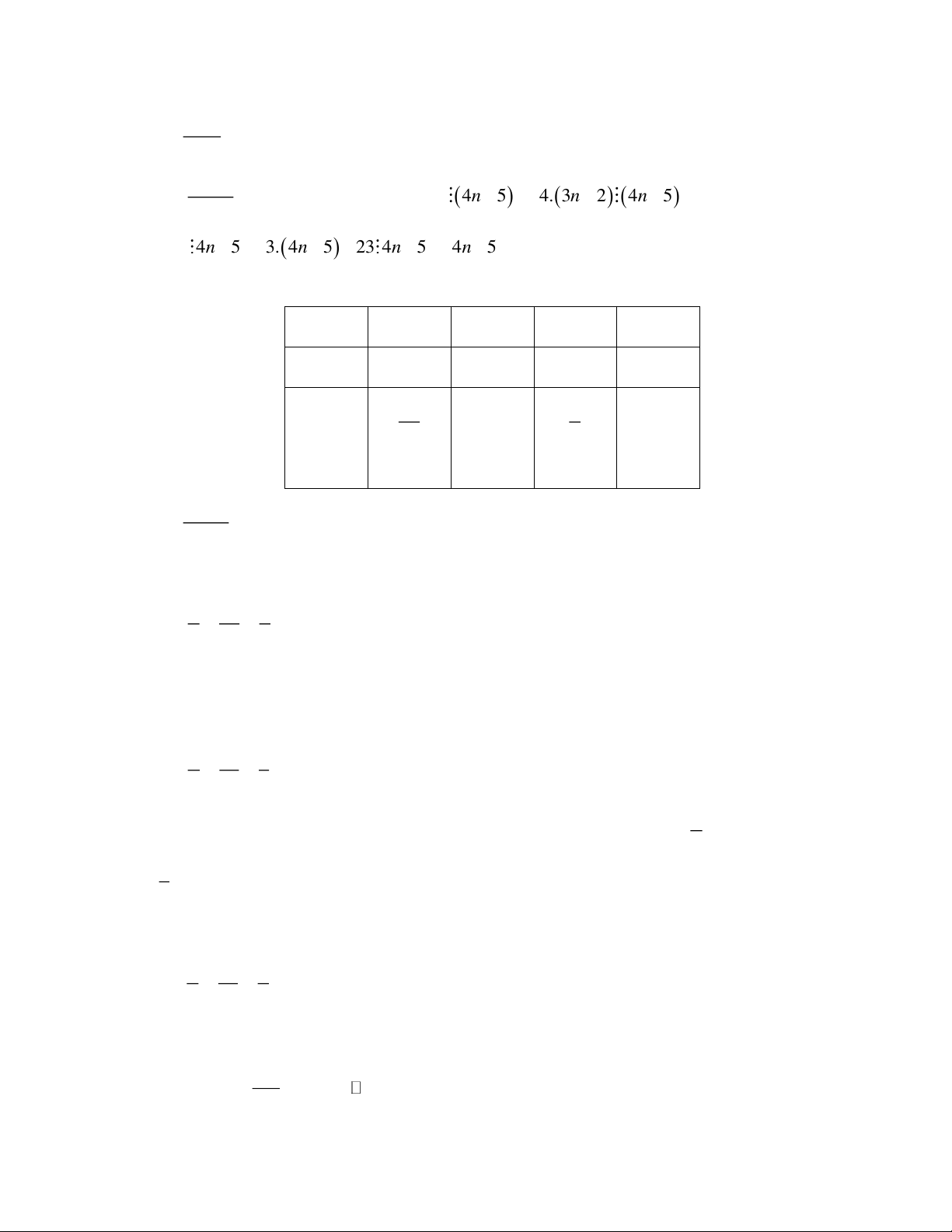
là số tự nhiên  (3n + 2) (4n − 5)  4.(3n + 2) (4n − 5) 4n − 5
12n + 8 4n − 5  3.(4n −5) + 23 4n −5  4n −5U (23) =  1  ; 2   3 Ta có bảng: 4n − 5 -23 -1 1 23 4n -18 4 6 28 n −9 3 1 7 2 2 (tm) (tm) (loại) (loại) 3n + 2 Vậy để
nhận giá trị là số tự nhiên khi và chỉ khi n 1;  7 4n − 5 Bài 5: a 36 4 1, Ta có =
=  a = 4k,b = 5k b 45 5
BCNN( a,b ) = 300. Mà (4;5) =1 k = 300 : (4.5) =15
Vậy a = 4.15 = 60;b = 5.15 = 75 . a 21 3 2, Ta có = = b 35 5 a
UCLN( a,b ) = 30 nghĩa là ta đã chia cho 30 để rút gọn phân số thành phân số tối b 3 giản 5
Vậy a = 3.30 = 60;b = 5.30 =150 . a 15 3 c, Ta có =
=  a = 3k;b = 7k b 35 7
UCLN( a,b ).BCNN( a,b )=3549 và (3;7) =1 UCLN( a,b ). 3k.7k = 3549  169 UCLN( a,b )=
mà k  , UCLN( a,b )  0  k =13. 2 k a 39 Với k = 13  = b 91