Danh sách các câu hỏi và bài tập nhập môn Thuật toán
Câu hỏi phương pháp: 1. T
rình bày phương pháp Chia để trị
trong thiết kế thuật toán. Gồm 3 bước:
B1: Chia : - khi nào chia? khi dữ liệu đầu vào l  ớn - Chia tới khi nào dừng?
 chia đến ko chia được nữa hoặc mảng có 1 phần tử hoặc đã tìm được nghiệm - Chia cái gì?
 chia dữ liệu đầu vào ( đang học là chia mảng a
tức là chia độ dài của mảng)
- Vì sao phải chia? chia để dữ liệu đầu vào nhỏ hơn 
+ giống cách giải bài toán lớn
+ khác dữ liệu đầu vào của bài toán
B2: Trị: Giải bài toán nhỏ đã được chia( bài toán dễ giải hơn bài toán lớn ban đầu)
B3: Tổng hợp: Kết hợp các lời giải của bài toán nhỏ (các phần tử) thành lời giải của bài toán lớn 2. T
rình bày phương pháp Quy hoạch động
trong thiết kế thuật toán.
B1: Tìm, xác định(phân rã ) bài toán con cơ sỡ (đã có lời giải)
B2: Xây dựng , tìm hàm, CT quy hoạch cho bài toán (để giải bài bán lớn từ
bài toán con đã có lời giải)
B3: Lập bảng để quy hoạch dựa vào thông tin của bảng để trả lời nghiệm bài toán 3. T
rình bày phương pháp Tham lam
trong thiết kế thuật toán.
S= và C là tập đề cử( p. tử được chọn xây dựng nghiệm)
Xây dựng nghiệm dần từng bước
B1: Tại thời điểm xây dựng nghiệm trong trường hợp đề cử c phần tử ‘Tốt
nhất’. Đưa phần tử x ra hỏi tập đề cử C = C\{x}
B2: Nếu x thỏa điều kiện bài toán S= S {x}
B3: Lặp lại B1: cho đến khi tập S là tập nghiệm hoặc C=
Bài tập minh hoạ cho phương pháp: 1. Cho
1 ví dụ minh hoạ thiết kế thuật toán bằng phương pháp Chia để trị
bao gồm: bài toán, áp dụng phương pháp, thuật toán giải.
2. Cho dãy số a = (5, 8, 1, 4, 9, 7, 4, 2, 5, 6). Hãy trình bày các bước áp
dụng thuật toán sắp xếp trộn để sắp dãy a theo thứ tự tăng. Cho biết
phương pháp Chia để trị áp dụng cho thuật toán này ở những điểm nào?
Thuật toán sắp xếp trộn
Sắp xếp mảng a có n phần tử theo thứ tự tăng.
• Cách chia: chia đôi cho đến khi mảng con còn phần tử.
• Giải các bài toán con: mảng có 1 phần tử thì đã được sǎp.
• Kết hợp lời giải các bài toán con: trộn 2 mảng được sắp thành 1 mảng được sắp.
3. Cho dãy số a = (5, 8, 1, 4, 9, 7, 4, 2, 5, 6). Hãy trình bày các bước áp dụng
thuật toán Quick Sort để sắp dãy a theo thứ tự tăng. Cho biết phương
pháp Chia để trị áp dụng cho thuật toán này ở những điểm nào? Thuật toán QuickSort • Cách chia:
Chọn phần tử mẫu x là phần tử bất kỳ trong mảng cần sắp (thường chọn
phần tử đầu, cuối, giữa)
Chia đôi mảng cần sắp: bên trái là những phần tử <=X, bên phải là những phần tử >=x
Lặp lại cho đến khi mảng cần sắp chỉ còn 1 phần tử. Minh hoạ
• Ban đầu cần sắp a[o..9] = (5, 8, 1, 4, 9, 7, 4, 2, 5, 6)
• Phần tử mẫu x = a[o] = 5
• Đi từ trái qua phải khi gặp phần tử lớn hơn hoặc bằng x thì dừng
• Đi từ phải qua trái khi gặp phần tử nhỏ hơn hoặc bằng x thì dừng 5, 8, 1, 4, 9, 7, 4, 2, 5, 6
Đổi hai phần tử này rồi đi tiếp 5, 8, 1, 4, 9, 7, 4, 2, 5, 6
• Đổi 8 và 2 rồi đi tiếp: 5, 2, 1, 4, 9, 7, 4, 8, 5, 6 • Đổi 4 và 9: 5, 2, 1, 4, 4, 7, 9, 8, 5, 6
Mảng được chia thành 2 phần a[o..4] gồm các phần tử <=5 và a[5..9] gồm các phần tử >=5.
Tương tự sắp mảng a[o..4]= (5, 2, 1, 4, 4 ): • x = a[0] = 5
• Chia mảng alo..4] thành 2 phần: a[o.3] và a[4..4] 4, 2, 1, 4, 5
• Mảng con a[4..4] có 1 phần tử nên đã sắp
Sắp alo.3] = (4, 2, 1, 4) với x = 4, chia 2 phần: a[o..2] và a[3.3]
• Sắp alo..2] = (4, 2, 1) với x = 4, đổi 4 với 1, chia 2 phần a[ô.1]=(1,2) và a 2.2]=(4)
Sắp a[o.1] = (1, 2), x = 1, chia 2 phần a[o.o] =(1) và a[1]=(2)
Såp mång a[5..9] = (7, 9, 8, 5, 6) • X = 7,
đổi 7 với 6: 6, 9, 8, 5, 7
đổi 9 với 5: 6, 5, 8, 9, 7
• Chia thành 2 mảng con (6, 5) và (8, 9, 7)
Sắp (6, 5) với x = 5 đổi 6 với 5 thành (5, 6) chia 2 mảng con (5) và (6) sắp xong
Sắp (8, 9, 7) x = 8, đổi 8 với 7: (7, 9, 8) chia 2 mảng (7) và (9,8)
Sắp (9, 8), x = 9, đổi 9 với 8 thành: (8, 9) chia 2 mảng con (8), (9) đã sắp.
Kết quả (1, 2, 4, 4, 5, 5, 6, 7, 8, 9)
4. Cho dãy số đã sắp tăng a = (1, 5, 9, 14, 19, 27, 34, 42, 55, 66). Hãy trình
bày các bước áp dụng thuật toán tìm nhị phân để tìm số 55 có trong dãy
a không?. Cho biết phương pháp Chia để trị áp dụng cho thuật toán này ở những điểm nào? Thuật toán tìm nhị phân
• Tìm số x trong mảng a có n số được sắp tăng.
• Cách chia: chia đôi mảng a thành 3 mảng con a[o..m- 1], a[m], a[m+1..n-1] • Giải bài toán con:
• tìm x trong từng mảng con. • Kết hợp lời giải:
• Nếu a[m] = x thì dừng, ngược lại thì
• Sử dụng tính chất mảng được sắp nên mỗi bước chỉ tìm x ở một trong hai
mảng con a[o..m-1] hoặc a[m+1..n-1] tùy thuộc vào a[m]>x hay a[m]Minh hoạ
Mảng ban đầu alo..9] = (1, 5, 9, 14, 19, 27, 34, 42, 55, 66)
• Chia mảng thành 3 phần a[o..3], a[4], a[5..9] a[4]=19 < 55 nên tìm 55 trong a[59]
• Chia a[5..9] thành 3 phần a[5..6], a[7], a[8..9]
a[7] = 42<55 nên tìm 55 trong a[8.9]
• Chia a[8..9] thành 3 phần a[], a[8], a[g]
a[8]=55 nên có 55 trong mảng tại vị trí 8.
5. Cho dãy a = (2, -15, 6, 2, 9, -4, 7, 3, -5, 2), trình bày các bước tìm đoạn
con có tổng lớn nhất của dãy a bằng thuật toán chia để trị. Cho biết
phương pháp chia để trị áp dụng cho thuật toán này ở những điểm nào? (Tương tự bài 6)
6. Cho dãy a = (2, -15, 6, 2, -9, -4, 7, 3, -5, 2), trình bày các bước tìm đoạn
con có tổng nhỏ nhất của dãy a bằng thuật toán chia để trị. Cho biết
phương pháp chia để trị áp dụng cho thuật toán này ở những điểm nào? Thuật toán chia để trị
• Chia mảng thành 2 mảng con gần bằng nhau về số phần tử (chia đôi).
• Chia cho đến khi mảng có 1 phần tử thì dừng.
• Nếu mảng có 1 phần tử thì mảng con cần tìm là chính phần tử đó.
• Kết hợp các lời giải: nếu mảng a[l..r] được chia thành 2 mảng con a[l..m]
và a[m+1..r]. Hai mảng con này đã tìm được đoạn con có tổng nhỏ nhất là
s1, s2 thì đoạn con có tổng nhỏ nhất của a[l..m] là min(s1, s2, s3) với s3 là
đoạn con có tổng nhỏ nhất có giao với hai đoạn con al..m] và a[m+1..r], tức
là đoạn đó phải chứa a[m] và a[m+1] • Để tìm s3: S3 = a[m], s = 0
Duyệt i từ m đến 1 S = s+a[i] nếu s < s3 thì s3 = s • S = s3
Duyệt i từ m+1 đến r: S = s+a[i] nếu s < s3 thì s3 = s Minh hoạ
a = (2, -15, 6, 2, -9, -4, 7, 3, -5, 2) Chia thành 2 mảng con:
a1 = (2, -15, 6, 2, 5) và a2 = (-9, -4, 7, 3, -5, 2) Chia tiếp:
ai thành a3=(2, -15), a4=(6, 2, 5) a2 thành a5=(-9, -4, 7), a6 = (3, -5, 2)
Chia tiếp a3 thành a7 = (2), a8 = (-15).
Đoạn con có tổng nhỏ nhất của a7 là 2, a8 là -15, đoạn con có tổng nhỏ nhất
có giao với a7 và a8 là -13. Vậy đoạn con có tổng nhỏ nhất của a3 là -15 (là a[i])
• Chiaa4=(6, 2, 5) thành a9=(6) và a10=(2,5)
Tương tự ao chia thành au=(2), a12=(5) đoạn con có tổng nhỏ nhất là 2 (a[3])
• Đoạn con có tổng nhỏ nhất của a4 là min(6, 2, 8)=2 (a[3]).
Vậy đoạn con có tổng nhỏ nhất của a1 = (2, -15, 6, 2, 5) là = min(-15, 2, -9) = -15 (a[1]) Tương tự:
Đoạn con có tổng nhỏ nhất của a5=(-9, -4, 7) là -13 (a[4.5]) Đoạn con có
tổng nhỏ nhất của a6 = (3, -5, 2) là -5 (a[8])
Vậy đoạn con có tổng nhỏ nhất của a2 = (-9, -4, 7, 3, -5, 2) là min(-13, -5, -6) = -13 (a[4.5])
Đoạn con có tổng nhỏ nhất của a = (2, -15, 6, 2, -9, -4, 7, 3, 5, 2) là min(-15, -13, -20) = -20 (a[1..5]) -
7. Trình bày thuật toán tìm nhị phân dùng để tìm một phần tử trong mảng
đã sắp xếp. Cho biết phương pháp Chia để trị áp dụng cho thuật toán
này ở những điểm nào? Thuật toán tìm nhị phân
• Tìm số x trong mảng a có n số được sắp tăng.
• Cách chia: chia đôi mảng a thành 3 mảng con a[o..m- 1], a[m], a[m+1..n-1] • Giải bài toán con:
• tìm x trong từng mảng con. • Kết hợp lời giải:
• Nếu a[m] = x thì dừng, ngược lại thì
• Sử dụng tính chất mảng được sắp nên mỗi bước chỉ tìm x ở một trong hai
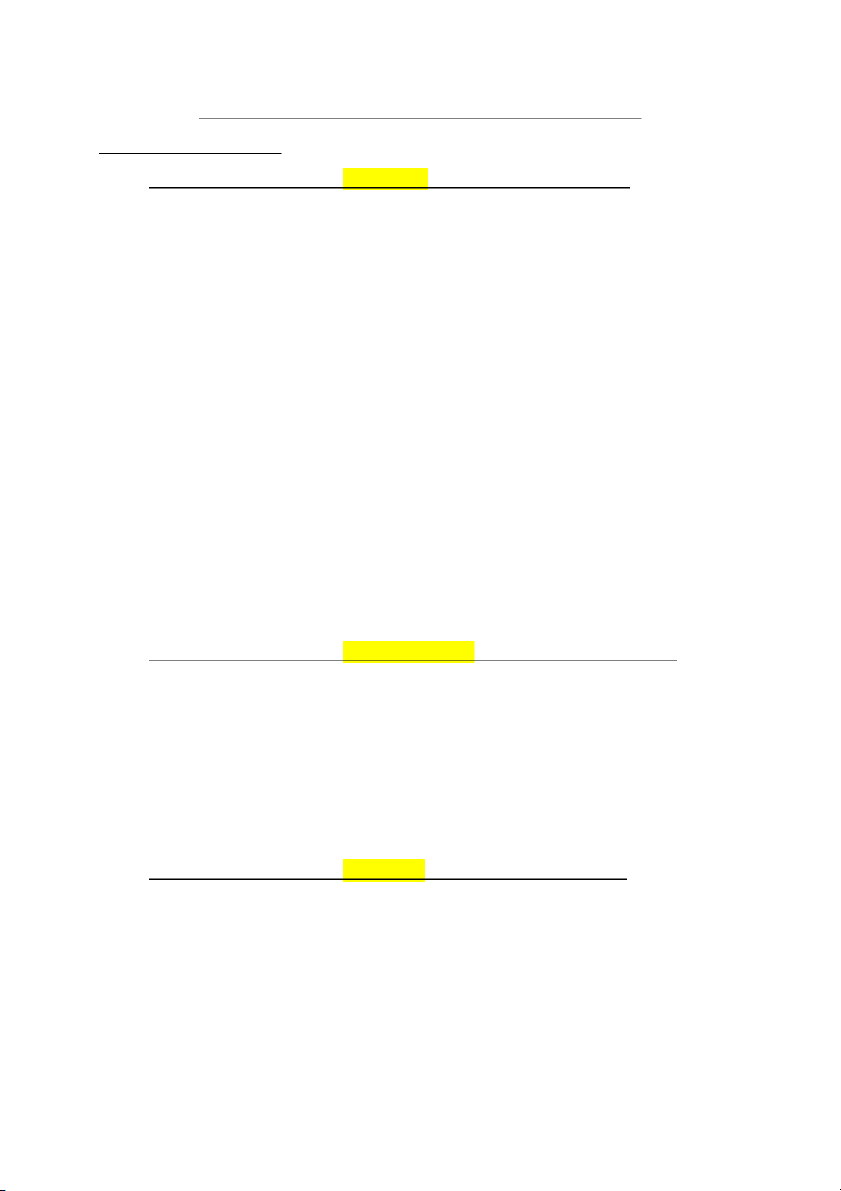
mảng con a[o..m-1] hoặc a[m+1..n-1] tùy thuộc vào a[m]>x hay a[m]8. Trình bày thuật toán tìm số lớn nhất trong một mảng bằng phương pháp Chia để trị.
9. Cho trước một dãy số nguyên a có n phần tử và một phần tử có giá trị là
x, hãy mô tả thuật toán chia để trị để đếm số lần phần tử x xuất hiện
trong dãy a (có thể x không xuất hiện trong dãy a). Hãy mô tả thuật
toán chia để trị để tính số lần xuất hiện của phần tử x = 2 trong dãy số a
= 2, 15, 6, 2, 9, 4, 7, 3, 5, 2 Thuật toán chia để trị • Cách chia:
Chia đôi mảng cho đến khi mảng có 1 phần tử
• Giải bài toán con: nếu phần tử của mảng bằng x thì trả về 1 ngược lại là o.
Tổng hợp lời giải các bài toán con: tính tổng kết quả các bài toán con. Minh hoạ
Tìm x = 2, trong a = 2, 15, 6, 2, 9, 4, 7, 3, 5, 2 1 = 0, r = 9, m = 4 demMang(a, o, 4, x) demMang(a, o, 2, x) demMang(a, 0, 1, x) demMang(a, o, 0, x) = 1 demMang(a, 1, 1, x) = 0 demMang(a, 2, 2, x) = 0 demMang(a, 3, 4, x) demMang(a, 3, 3, x) =1 demMang(a, 4, 4, x) =0
demMang(a, 5, 9, x) = 1 (làm tương tự trên) Vậy demMang(a, o, 9, x) = 3. 10.Cho
1 ví dụ minh hoạ thiết kế thuật toán bằng phương pháp Quy hoạch
động bao gồm: bài toán, áp dụng phương pháp, thuật toán giải.
11.Trình bày thuật toán quy hoạch động tìm số Fibonaci thứ n. Cho biết
phương pháp quy hoạch động áp dụng cho thuật toán này ở những điểm nào? Ví dụ 1. Fibo(n)
• Cách chia: chia thành n bài toán con Fibo(1).. Fibo(n).
• Tổ chức dữ liệu: dùng 1 mảng F[] có n phần tử lưu các số fibonacii từ 1 đến n. Công thức hồi quy: F[0] = F[1] =
F[i] = F[i-1] + F[i-2] với i>1.
Giải các bài toán con: tính F[o], F[i],..,F[n-1]
• Lời giải bài toán là giá trị trong F[n-1] int fibo(int n) { int F[n], i; F[0]= F[1] = 1; = for (i =2; i < n; i++) =
F[i] =F[i-1] +F[i-2]; return F[n-1]; }
12. Trình bày thuật toán quy hoạch động tính C k
n . Cho biết phương pháp
quy hoạch động áp dụng cho thuật toán này ở những điểm nào? Ví dụ 2. Cnk
• Cách chia: chia thành 2 bài toán con Cn-1 k và Cn-1 k-1
• Tổ chức dữ liệu: dùng mảng hai chiều C[n+1][k+1] để lưu kết quả các bài toán con. Công thức hồi quy: Cn 0= 1, Ck k=1
Cnk = Cn-1 k+Cn-1 k-1với k>o, n>k
Giải các bài toán con: từ C0 0, C1 0, ……Cnk
• Kết quả bài toán lưu trong C[n][k]
13. Trình bày thuật toán quy hoạch động tìm dãy con tăng dài nhất của
một dãy cho trước. Cho biết phương pháp quy hoạch động áp dụng cho
thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành n bài toán con: Với i = 1..n, tìm dãy con giảm dài nhất từ 1 đến i chứa a.
Dùng mảng s[] n số lưu kết quả các bài toán con.
Mảng s được tính như sau: s[i]=1. • Vớii=2..n:
s[i] = max{ s[j] : với ai>aj, j>i}+1.
s[i] = 1 nếu không có ajTổng hợp lời giải bài toán: max{ s[i]: i=1..n}
• Để lưu dãy con giảm dài nhất tìm được dùng mảng truoc[]: truoc[i] = jo,
với j0 là giá trị lớn nhất các s[j] hoặc j=i
14. Trình bày thuật toán quy hoạch động tìm dãy con giảm dài nhất của
một dãy cho trước. Cho biết phương pháp quy hoạch động áp dụng cho
thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành n bài toán con: Với i = 1..n, tìm dãy con giảm dài nhất từ 1 đến i chứa a.
Dùng mảng s[] n số lưu kết quả các bài toán con.
Mảng s được tính như sau: s[i]=1. • Vớii=2..n:
s[i] = max{ s[j] : với ais[i] = 1 nếu không có aj>ai.
Tổng hợp lời giải bài toán: max{ s[i]: i=1..n}
• Để lưu dãy con giảm dài nhất tìm được dùng mảng truoc[]: truoc[i] = jo,
với j, là giá trị lớn nhất các s[j] hoặc j=i
15. Cho dãy a = (2, 15, 6, 2, 9, 4, 7, 3, 5, 2), trình bày các bước tìm dãy con
tăng dài nhất của dãy a bằng thuật toán quy hoạch động. Cho biết
phương pháp quy hoạch động áp dụng cho thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành n bài toán con: Với i = 1..n, tìm dãy con tăng dài nhất từ 1 đến 1 chứa a
Dùng mảng s[1..n] lưu kết quả các bài toán con.
Mảng s được tính như sau: s[1]=1. • Vớii=2..n:
s[i] = max{ s[j] : với ai>aj, js[i] = 1 nếu không có ajTổng hợp lời giải bài toán: max{ s[i]: i=1..n}
• Để lưu dãy con tăng dài nhất tìm được dùng mảng truoc[]: truoc[i] = jo, với
s[j] là giá trị lớn nhất các s[j] mà a[j] < a[i], j=1..i-1 hoặc j=i nếu không có a[j]với i=1:
khởi tạo s[1] = 1, truoc[1] = 1 • i = 2:
• s[2] = s[i] + 1 = 2 vì a[i] < a[2], truoc[2]=1 • i = 3:
s[3] = s[i] + 1 = 2 vì a[i] < a[3], truoc|3]=1 i = 4:
s[4] = 1 vì không có j nào mà a[j]i = 5:
s[5] = max{ s[4], s[3], s[i] } + 1, vì a[4]= max { 1, 2, 1} + 1 = 3 (s[3]=2), nên truoc[5] = 3.
• Tương tự cho i= 6, 7, 8, 9, 10.
Kết quả đoạn con tăng dài nhất là max{s[i]: i = 1..10}=3 (chọn s[9], cũng có thể chọn s[7] và s[5])
Dãy con tăng: dựa vào mảng truoc[] bắt đầu từ vị trí 9
a[9] = 5, a[truoc[9]] = a[6] = 4, a[truoc[4]] = a[4] =2 Dừng vì truoc[4]=4.
Vậy dãy con tăng dài nhất tìm được là (2, 4, 5).
16. Cho dãy a = (2, -15, 6, 2, 9, -4, 7, 3, -5, 2), trình bày các bước tìm đoạn
con có tổng lớn nhất của dãy a bằng thuật toán quy hoạch động. Cho
biết phương pháp quy hoạch động áp dụng cho thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành n bài toán con: Với i = 1..n, tìm đoạn con có tổng lớn nhất từ 1 đến 1 chứa a
Dùng mảng s[1..n] lưu kết quả các bài toán con.
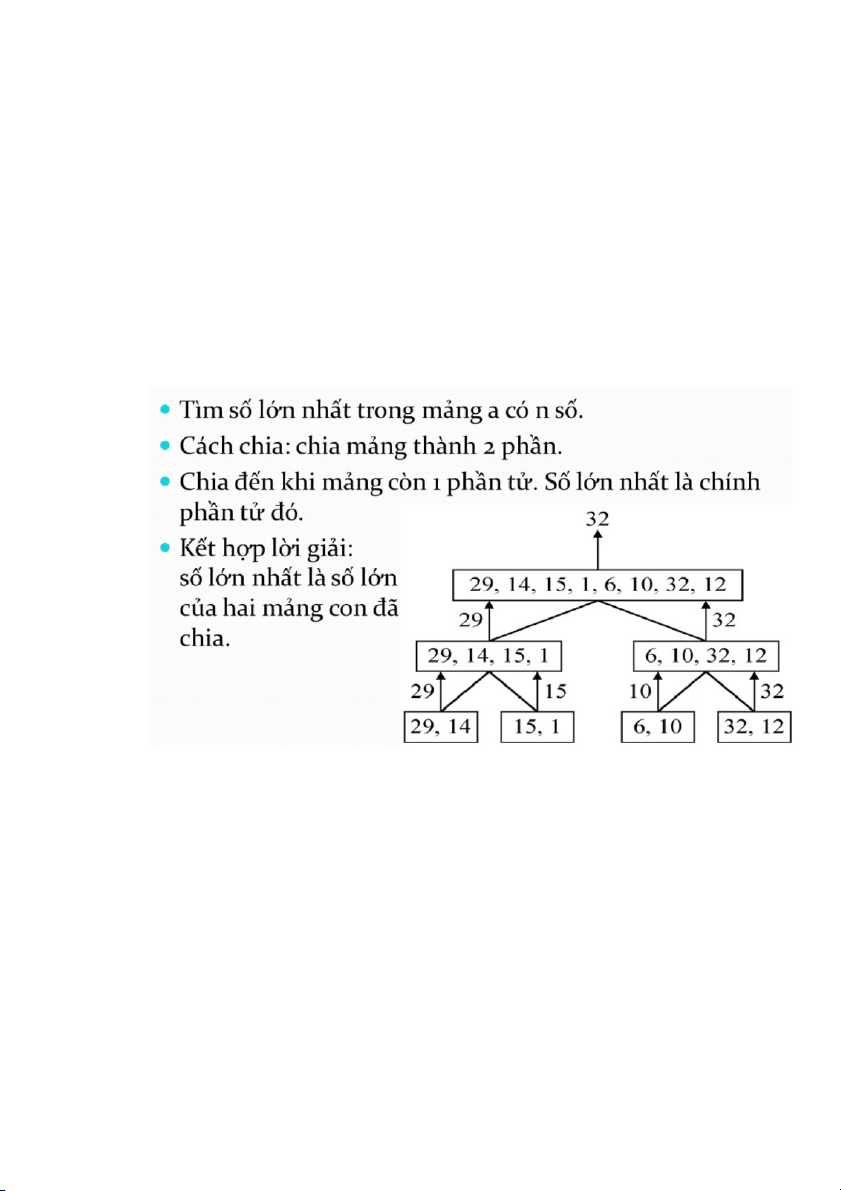
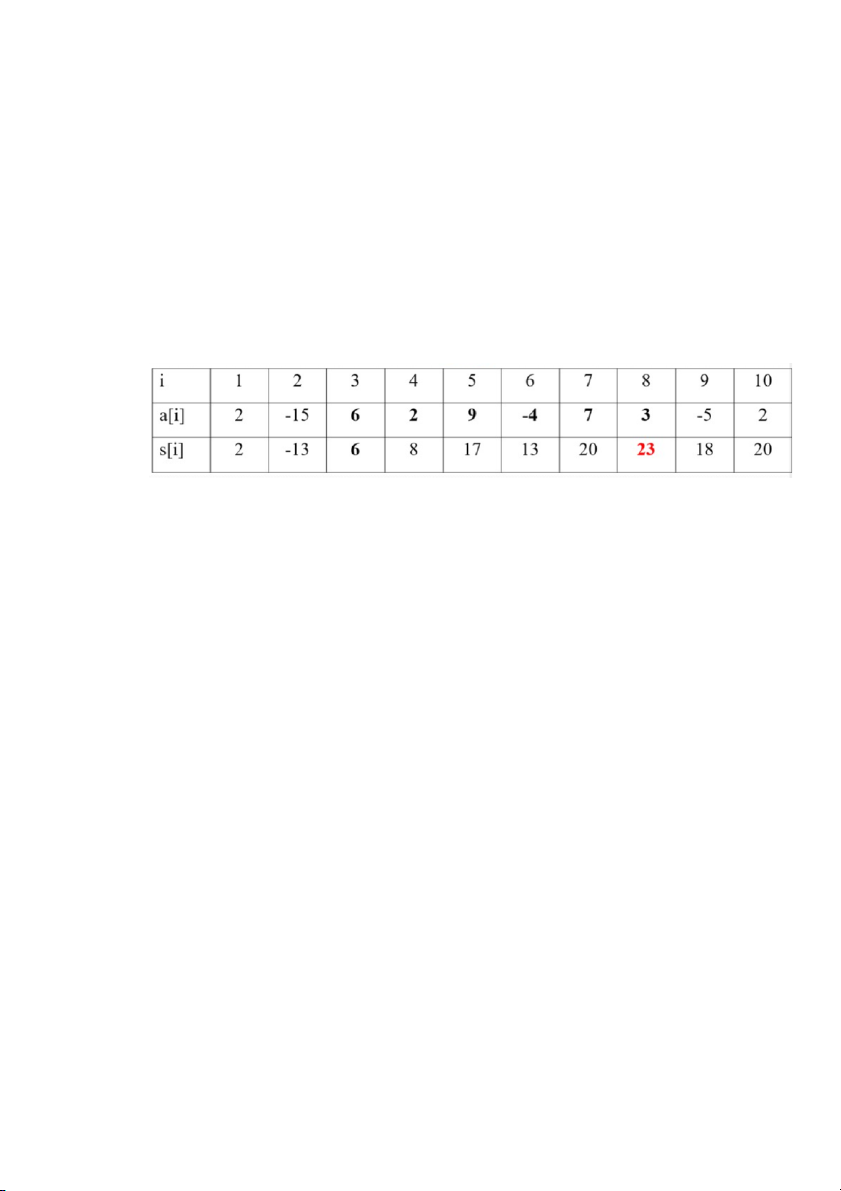
• Mảng s được tính như sau: s[i]=a[i]. • Với i=2..n:
s[i] = s[i-1] + a[i] nếu s[i-1]>o. s[i] = a[i] nếu s[i-1]<0.
Tổng hợp lời giải bài toán: max{ s[i]: i=1..n} Cách tính mảng s: i=1: s[1] = a[1] =2
• i=2: do s[i]>o nên s[2] = s[1] + a[2] = -13
• i=3: do s[2] < o nên s[3] = a[3] = 6
Tương tự cho i= 4,.., 10 như trong bảng.
• Kết quả tổng của đoạn con có tổng lớn nhất là 23 (s[8])
Tìm đoạn con có tổng lớn nhất:
Từ vị trí của s có giá trị lớn nhất (vị trí 8) duyệt ngược lại đến khi s[i]=a[i] thì dừng (i=3).
Đoạn con tìm được là đoạn a[3.8].
17. Cho dãy a = (2, -15, 6, 2, -9, -4, 7, 3, -5, 2), trình bày các bước tìm đoạn
con có tổng nhỏ nhất của dãy a bằng thuật toán quy hoạch động. Cho
biết phương pháp quy hoạch động áp dụng cho thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành n bài toán con: Với i = 1..n, tìm đoạn con có tổng nhỏ nhất từ 1 đến i chứa a
Dùng mảng s[1..n] lưu kết quả các bài toán con.
• Mảng s được tính như sau: s[i]=a[i]. • Với i=2..n:
s[i] = s[i-1] + a[i] nếu s[i-1]s[i] = a[i] nếu s[i-1]>0.
Tổng hợp lời giải bài toán: min{ s[i]:=1..n} Cách tính mảng s: • Cách tính mảng s: i=1: s[1] = a[1] = 2
• i=2: do s[i]>o nên s[2] = a[2] = -15
i=3: do s[2] < o nên s[3] = s[2] + a[3] = -9
Tương tự cho i = 4,.., 10 như trong bảng.
• Kết quả tổng của đoạn con có tổng nhỏ nhất là -20 (s[6])
Tìm đoạn con có tổng nhỏ nhất:
• + Từ vị trí của s có giá trị lớn nhất (vị trí 6) duyệt ngược lại đến khi
s[i]=a[i] thì dừng (i=2). Đoạn con tìm được là đoạn a[2..6].
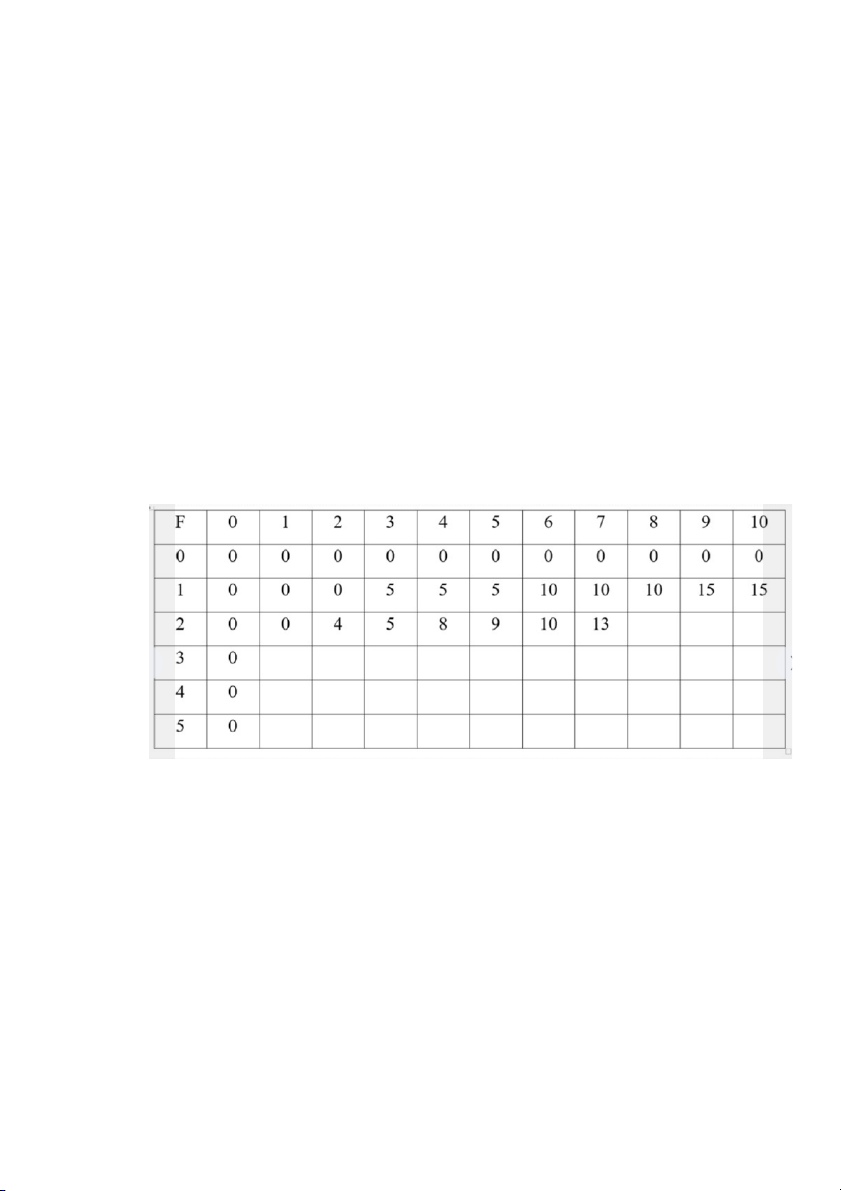
18. Cho 1 cái túi có thể chứa trọng lượng tối đa W=10 và 5 loại đồ vật có
trọng lượng tương ứng p = (3, 2, 1, 4, 2), giá trị tương ứng là v = (5, 4, 2,
7, 3), mỗi vật có số lượng là 10. Cần tìm cách chọn các đồ vật đưa vào túi
sao cho tổng trọng lượng các đồ vật không vượt quá W và tổng giá trị các
đồ vật trong túi là lớn nhất. Hãy trình bày các bước dùng phương pháp
quy hoạch động giải bài toán trên. Cho biết phương pháp quy hoạch động
áp dụng cho thuật toán này ở những điểm nào? Quy hoạch động
• Chia thành 50 bài toán con, với mỗi j=1..10, i= 1.5 bài toán tương ứng là
tìm giá trị lớn nhất của túi có trọng lượng được chọn i vật 1..i, mỗi vật tối đa số lượng 10.
• Lưu các bài toán con: dùng mảng 2 chiều F[6,n] (thêm cột o, dòng o cho dễ tính)
• Với mỗi j=1.10, i = 1.5 F[i,w] là giá trị lớn nhất của túi cho một bài toán
con tương ứng. Cột o gán bằng o với ý nghĩa túi có trọng lượng o thì không
chứa được vật nào. Dòng o gán bằng o.
Công thức tính F[i,j] = max{F[i-1,j-k*p[i]: k=o..min(10, j/p[i])} với i=1..p, j=1..W.
• Kết quả bài toán là F[p, w]
• Cách tính mảng F như sau:
Với i = 1, chỉ được phép chọn vật 1 có trọng lượng 3 giá tri 5.
• +W=1:F[i,1] = o vì đồ vật số 1 có trọng lượng là 3 hơn trọng lượng của túi. +W=2 :F[1,2]= o (tương tự)
+w=3 : F[13] = 5 vì chọn được 1 vật 1.
• +w=4:F[14]= 5 vì cũng chỉ chọn đủ 1 vật 1 mà không đủ 2 vật 1. +w=5 :F[1,5]= 5 (tương tự)
+w= 6 :F[1,6] = 10 vì chọn được 2 vật 1
Tương tự cho F[1,7], F[1,8], F[1,9], F[1,1o] (xem bảng).
Với i = 2, được phép chọn 2 vật 1 và 2.
+w= 1: F[2,1] = F[1,1] = o vì túi không đủ chọn vật 2. • +W= 2: • Có 2 phương án:
Chọn 1 vật 2 giá trị 4 trọng lượng túi còn lại là o có giá trị lớn nhất là F[z, o] vậy kết quả là F[1,o]+4
Không chọn vật 2 nào thì kết quả là F[1,2] = o.
• Vậy F[2,2] = max{ F[1, o]+4, F[1,2]} = max{4, o} = 4 (chọn 1 vật 2) • +W = 3: • Có 2 phương án:
• Chọn 1 vật 2, giá trị: F[i,1]+4 = 4
• Không chọn vật 2, giá trị: F[1,3]=5
• Vậy F[2,3] = max{ F[i,1] + 4, F[13]} = max{4, 5} = 5 • + W = 4: • Có 3 phương án:
Chọn 1 vật 2, giá trị: F[1,2]+4 = 4
Chọn 2 vật 2, giá trị: F[1,o]+8 = 8
• Không chọn vật 2, giá trị: F[1,4]=5
• Vậy F[2,4] = max{4, 8, 5} = 8. • + W = 5: Có 3 phương án:
Chọn 1 vật 2, giá trị: F[1,3]+4 = 9
Chọn 2 vật 2, giá trị: F[i,1]+8 = 8
Không chọn vật 2, giá trị: F[1,5] = 5
Vậy F[2,5] = max{9, 8, 5} = 9. • + W = 6: • Có 4 phương án:
Chọn 1 vật 2, giá trị: F[1,4]+4 = 9
Chọn 2 vật 2, giá trị: F[1,2]+8=8
Không chọn vật 2, giá trị: F[1,6] = 10
Vậy F[2,6] = max{9, 8, 10} = 9.
Tương tự cho các trường hợp còn lại.
19. Cho dãy số nguyên dương a1, .., an. Cần tìm dãy con có tổng lớn nhất
thỏa tính chất: không chứa 2 số liên tiếp trong dãy. Ví dụ cho dãy 30, 50,
40, 20, 60 thì dãy con 30, 40, 60 là dãy cần tìm. Mô tả thuật toán Quy
hoạch động giải bài toán trên. Quy hoạch động
• Chia bài toán thành n bài toán con, bài toán con thứ i (i=1..,n): tìm tổng lớn
nhất của đoạn con của dãy từ 1 đến i không chứa 2 số liên tiếp của dãy và chứa a
Dùng mảng s lưu kết quả n bài toán con. Công thức tính: s[1] = a[1], s[2] = a[2] Với i=3..n:
s[i]= max(a[i], s[j]+a[i]:j=1..i-2}
• Nghiệm của bài toán là max{s[i]:=n..n} Thuật toán int tong(int a[], int n) { int s[n];
s[0] = a[0]; s[1] = a[1]; for(i= 2; i < n; i++) { max = s[0];
for(j=1;jif (max < s[j]) max = s[j]; if (max > 0) s[i] = max + a[i]; else s[i] = a[i]; }