

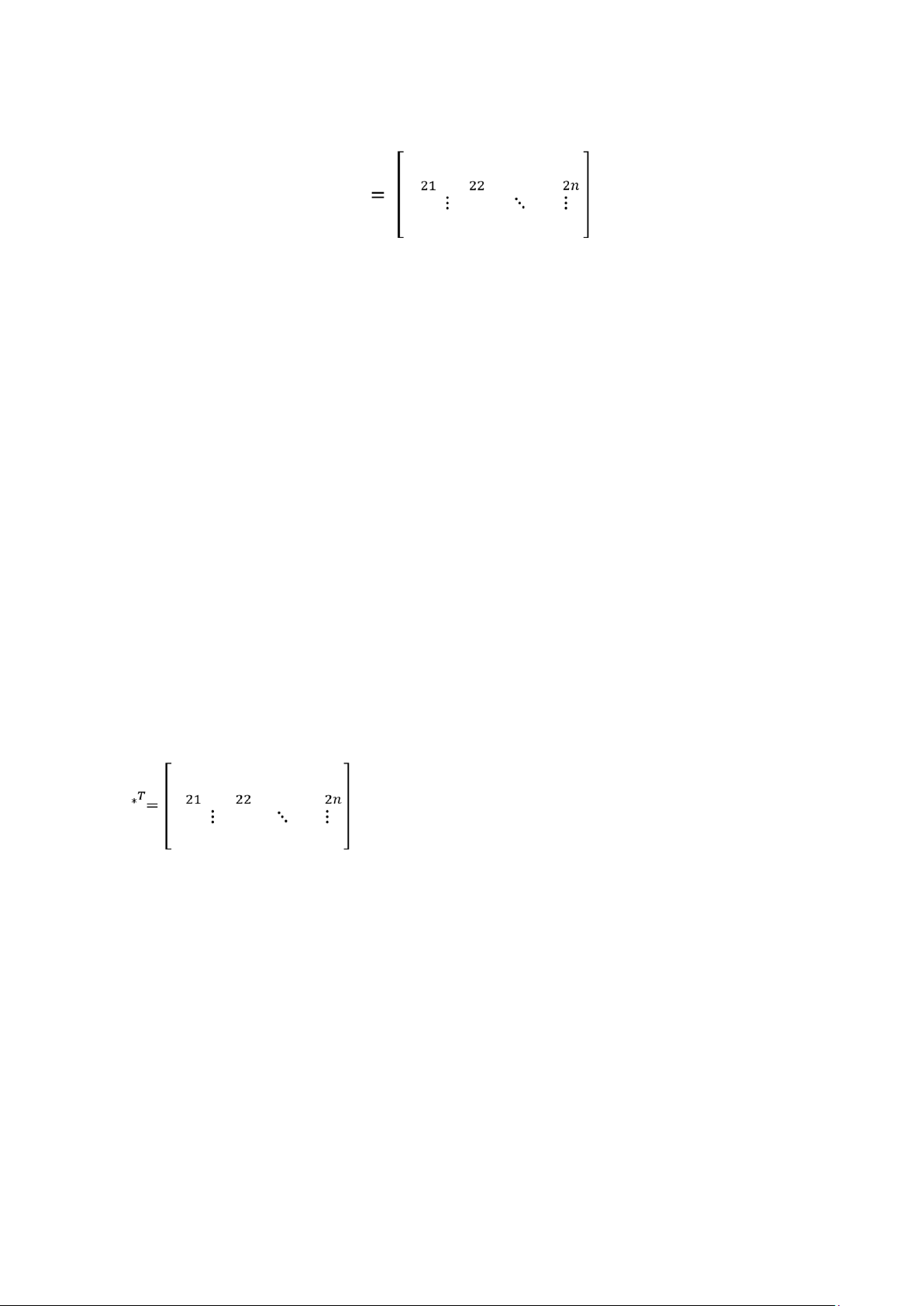
Preview text:
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
TRƯỜNG ĐIỆN – ĐIỆN TỬ --□&□-- BÀI TẬP NHÓM
MÔN: LÝ THUYẾT MẬT MÃ
Giảng viên hướng dẫn: PGS. TS. Đỗ Trọng Tuấn Nhóm thực hiện: Nhóm 01
1. Trịnh Đức Chung MSSV: 20203338 2. Trần Trọng Quyền MSSV: 20203759 3. Nguyễn Quốc Tuấn MSSV: 20203778 Hà Nội, 5/2023 MỤC LỤC
CƠ SỞ TOÁN HỌC .......................................................................... 4
1. SỐ HỌC CÁC SỐ NGUYÊN: ................................................... 4
2. SỐ HỌC MÔ-ĐUN: ................................................................... 5
Toán tử modulo ............................................................................ 5
Tập hợp các thặng dư ℤ𝑛 ............................................................. 5
Đồng dư ....................................................................................... 6
Lớp thặng dư ................................................................................ 6
Biểu đồ tròn ................................................................................. 7
Phép toán trong ℤ𝒏 ...................................................................... 8
Bảng cộng và nhân .................................................................... 12
Một số tập hợp khác cho phép cộng và phép nhân ................... 12
Hai tập hợp khác ........................................................................ 13
3. ĐỒNG DƯ TUYẾN TÍNH: ..................................................... 13
4. MA TRẬN: ............................................................................... 13
4.1. Định nghĩa .......................................................................... 13
4.2. Một số phép toán về ma trận .............................................. 14
MỘT SỐ HỆ MẬT CỔ ĐIỂN ........................................................ 15
1. Additive Cipher: ....................................................................... 15
2. Multiplicative Cipher: .............................................................. 16
3. Affine Cipher: ........................................................................... 18
4. Substitution Cipher:.................................................................. 20
5. Vigenere Cipher: ....................................................................... 21
6. Hill Cipher: ............................................................................... 22
HỆ MẬT HIỆN ĐẠI ....................................................................... 25
I.DES ............................................................................................ 25
1.Lịch sử hình thành hệ mật DES ................................................ 25
2.Mô hình hệ mật DES ................................................................. 26
3. Nguyên lý tạo khóa vòng ......................................................... 27
4. Quá trình mã hóa DES ............................................................. 29
5. Quá trình giải mã DES ............................................................. 31
II.AES .............................................................................................. 38
1.Lịch sử hình thành hệ mật AES ................................................ 38
2. Xây dựng thuật toán ................................................................. 38
3. Các dạng tấn công vào AES và phương pháp phòng chống .... 44
III.RC4 ............................................................................................. 45
1.Khái niệm .................................................................................. 45
2.Cấu tạo hệ mật ........................................................................... 46
3.Mã hóa và giải mã ..................................................................... 46 CƠ SỞ TOÁN HỌC
1. SỐ HỌC CÁC SỐ NGUYÊN:
- Z là tập hợp các số nguyên : Z = { …,-2,-1,0,1,2,…}
- Z* là tập hợp các số nguyên không âm : Z*= {0,1,2,…}
- Tập hợp Z là đóng kín đối với các phép cộng, trừ và nhân nhưng không đóng kín đối với phép chia
- Cho hai số nguyên bất kì a và b, b >1 a = q*n +r , 0 ≤ r ≤ b Trong đó: q: thương r: số dư - Phép chia hết: Cho biểu thức a = q*n +r
+ Nếu r = 0 => a chia hết cho n, kí hiệu n | a
+ Nếu r ≠ 0 => a không chia hết cho n, kí hiệu n a Một số tính chất: + Nếu a | 1 thì a = ±1
+ Nếu a | b và b | a thì a = ±b
+ Nếu a | b và b | c thì a | c
+ Nếu a | b và a | c thì a | (m*b + n*c)
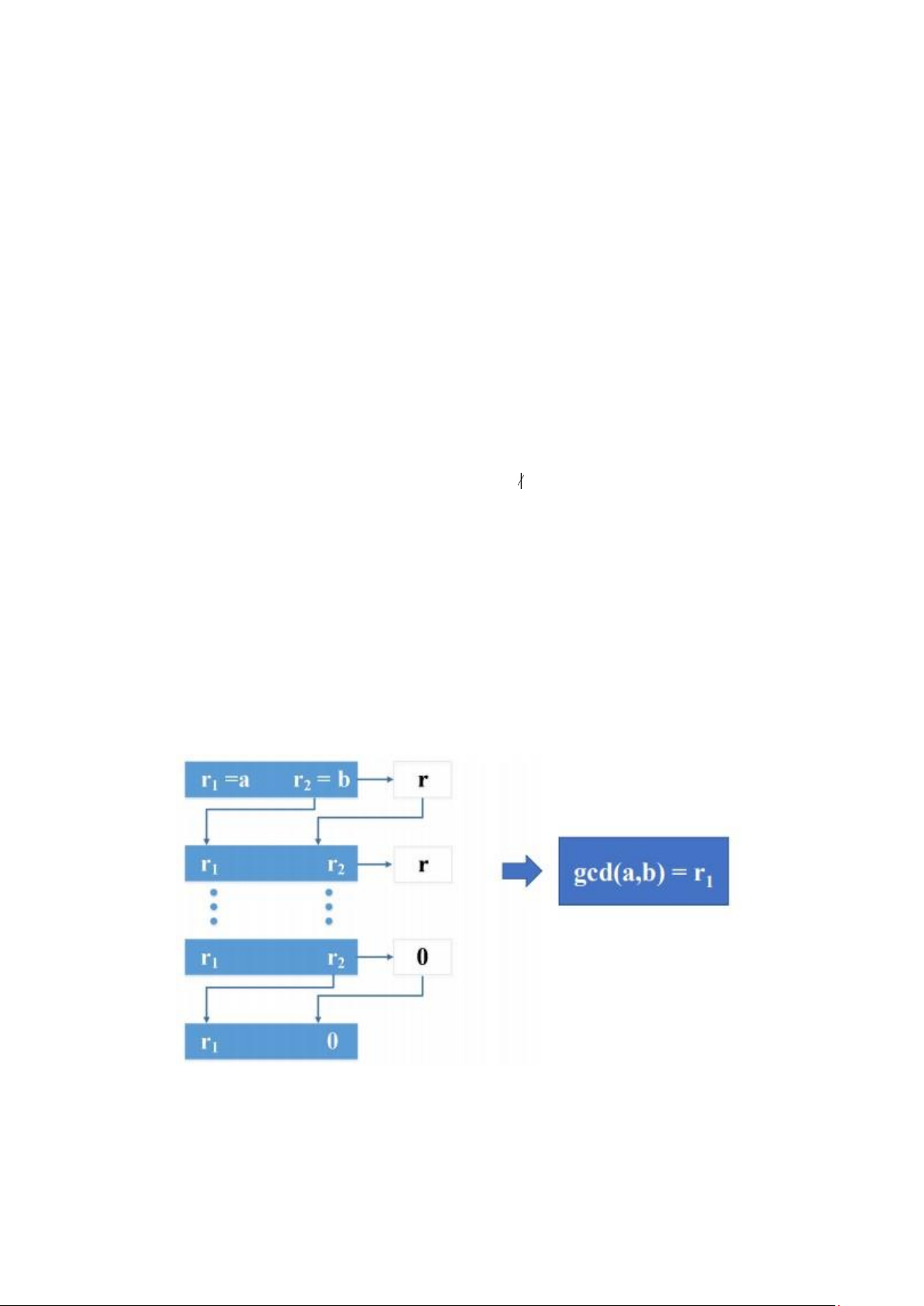
- Ước số chung lớn nhất: d = gcd(a,b)
Ta sử dụng thuật toán Euclide để tìm gcd(a,b) - Số nguyên tố :
+ Một số nguyên a>1 được gọi là số nguyên tố , nếu a không có ước số nào ngoài
1 và chính nó, và được gọi là hợp số nếu không phải là số nguyên tố. + Hai số a và
b được gọi là nguyên tố với nhau nếu gcd(a, b) = 1 + Một số nguyên n>1 bất kì
đều có thể viết dưới dạng:
N = p p1a1 * 2a2 *...* pkak
Trong đó p1, p2,...,pk là các số nguyên tố khác nhau, a1, a2,...,ak là các số mũ nguyên dương. 2. SỐ HỌC MÔ-ĐUN:
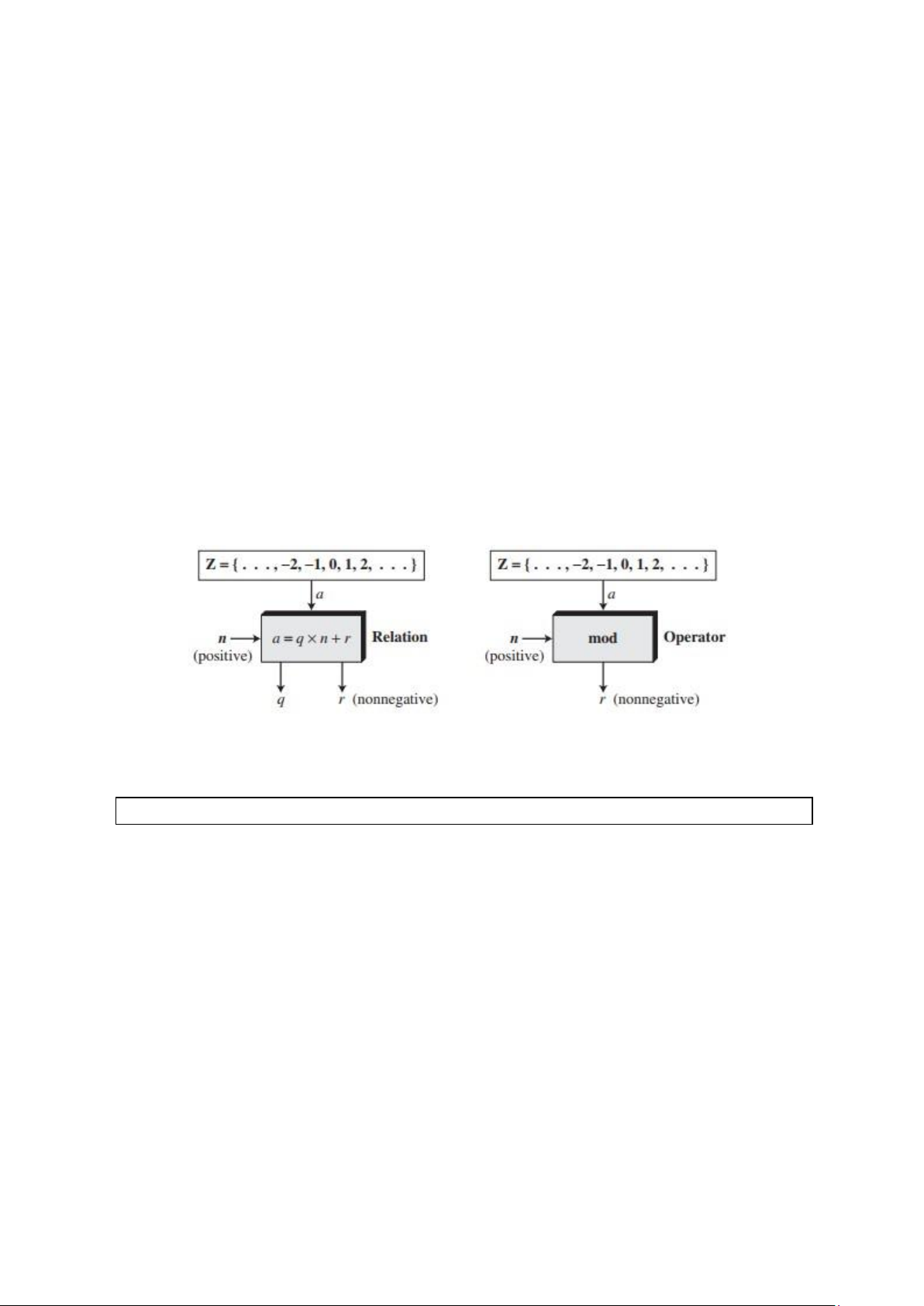
Mối quan hệ của phép chia (𝑎 = 𝑞 × 𝑛 + 𝑟) gồm hai đầu vào (𝑎 và 𝑛) và hai đầu ra
(𝑞 và 𝑟). Trong số học mô-đun, ta chỉ quan tâm đến một đầu ra duy nhất, đó chính là
số dư 𝑟, mà không cần quan tâm đến thương 𝑞. Như vậy ta có thể thay đổi mối quan
hệ trên thành một toán tử hai ngôi với hai đầu vào là 𝑎 và 𝑛, và một đầu ra là 𝑟. Toán tử modulo
Toán tử hai ngôi được nhắc đến ở trên được gọi là toán tử modulo và được ký hiệu
là mod. Đầu vào thứ hai (𝑛) được gọi là mô-đun (tiếng Anh: modulus). Đầu ra 𝑟 được
gọi là thặng dư (tiếng Anh: residue).
Toán tử modulo (mod) lấy một số nguyên (𝑎) từ tập ℤ và mô-đun (𝑛) là một số
nguyên dương. Toán tử cho kết quả một thặng dư không âm (𝑟). Ta nói
𝒂 𝐦𝐨𝐝 𝒏 = 𝒓 Một số ví dụ: a. 27 mod 5 = 2 b. 36 mod 12 = 0 c. −18 mod 14 = 10 d. −7 mod 10 = 3
Tập hợp các thặng dư ℤ𝒏
Kết quả của phép toán modulo với mô-đun 𝑛 luôn là một số nguyên từ 0 đến 𝑛 − 1.
Nói cách khác, kết quả của 𝑎 mod 𝑛 luôn luôn là một số nguyên không âm nhỏ hơn
𝑛. Ta có thể nói rằng phép toán modulo tạo ra một tập hợp, mà trong số học mô-đun
được gọi là tập hợp các thặng dư nhỏ nhất trong modulo 𝒏, hay được viết là ℤ𝒏.
Mặc dù chỉ có duy nhất một tập hợp các số nguyên (ℤ), nhưng ta có vô số tập hợp
các thặng dư (ℤ𝑛) ứng với mỗi giá trị của 𝑛 khác nhau.
Ví dụ một số tập hợp thặng dư: ℤ 𝑛 = ሼ
0, 1 , 2 , 3 , … , ( 𝑛 − 1 ) ሽ ℤ ℤ ℤ 2 = ሼ 0, 1 ሽ 6 = ሼ 0, 1 , 2 , 3 , 4 , 5 ሽ 11 = ሼ
0, 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ሽ Đồng dư
Trong mật mã, ta thường dùng khái niệm đồng dư (đồng dư thức) thay vì đẳng thức.
Ánh xạ từ ℤ tới ℤ𝑛 không phải là tương ứng một đối một (one-to-one), tức là nhiều
phần tử trong ℤ có thể ánh xạ tới cùng một phần tử trong ℤ𝑛. Vô số phần tử của tập
ℤ có thể ánh xạ tới một phần tử trong tập ℤ𝑛. Ví dụ, kết quả của 2 mod 10 = 2,
12 mod 10 = 2, 22 mod 10 = 2, v.v…. Trong số học mô-đun, số nguyên như 2, 12
và 22 được gọi là đồng dư theo mod 10. Để chỉ ra hai số nguyên đồng dư, ta sử
dụng toán tử đồng dư (≡). và thêm cụm từ (mod 𝑛) vào bên phải đồng dư thức. ℤ = ሼ
… − 𝟖 … 𝟐 … 𝟏𝟐 … 𝟐𝟐 … ሽ 10 mod 10 mod 10 mod 10 mod ℤ 10 = ሼ 0 … 2 … 9 ሽ
− 8 ≡ 2 ≡ 12 ≡ 22 ( mod 10 )
a. Toán tử đồng dư khá giống toán tử bằng, nhưng cũng có một vài điểm khác
biệt. Thứ nhất, toán tử bằng ánh xạ một phần tử trong tập ℤ tới chính nó; trong
khi đó toán tử đồng dư ánh xạ các phần tử từ tập ℤ sang một phần tử ở tập ℤ𝑛.
Thứ hai, toán tử bằng tương ứng một tới một; còn toán tử đồng dư thì tương
ứng nhiều tới một (nhiều phần tử tương ứng với một phần tử).
b. Cụm từ (mod 𝑛) được thêm vào bên phải của toán tử đồng dư chỉ là dấu hiệu
của tập đích (ℤ𝑛). Ta cần phải thêm cụm từ này để chỉ ra mô-đun nào được
dùng trong ánh xạ. Ký hiệu mod được sử dụng ở đây không được dùng với
nghĩa là toán tử hai ngôi. Nói cách khác, ký hiệu mod trong 12 mod 10 là một
toán tử; cụm từ (mod 10) trong 2 ≡ 12 (mod 10) có nghĩa tập đích là ℤ10. Lớp thặng dư
Một lớp thặng dư [𝑎] hay [𝑎]𝑛 là tập hợp các số nguyên đồng dư theo modulo 𝑛. Nói
cách khác, nó là tập hợp tất cả các số nguyên sao cho 𝑥 ≡ 𝑎 (mod 𝑛).
Ví dụ, nếu 𝑛 = 5, ta có tất cả năm tập hợp [0], [1], [2], [3] và [4] như dưới đây:
[0] = ሼ… , −15, −10, −5, 0, 5, 10, 15, … ሽ
[1] = ሼ… , −14, −9, −4, 1, 6, 11, 16, … ሽ
[2] = ሼ… , −13, −8, −3, 2, 7, 12, 17, … ሽ
[3] = ሼ… , −12, −7, −5, 3, 8, 13, 18, … ሽ
[4] = ሼ… , −11, −6, −1, 4, 9, 14, 19, … ሽ
Các số nguyên trong tập hợp [0] khi thực hiện phép toán modulo cho 5 thì đều cho
kết quả là 0. Các số nguyên trong tập [1] thì cho kết quả 1 khi thực hiện phép toán
modulo cho 5,v.v…. Trong mỗi tập hợp sẽ có một phần tử được gọi là thặng dư nhỏ
nhất (không âm). Trong tập [0], phần tử này là 0; trong tập [1], phần tử này là 1;
v.v…. Tập hợp tất cả các thặng dư nhỏ nhất chính là tập ℤ5 = ሼ0, 1, 2, 3, 4ሽ. Nói
cách khác, tập hợp ℤ𝒏 là tập các thặng dư nhỏ nhất trong modulo 𝑛. Biểu đồ tròn
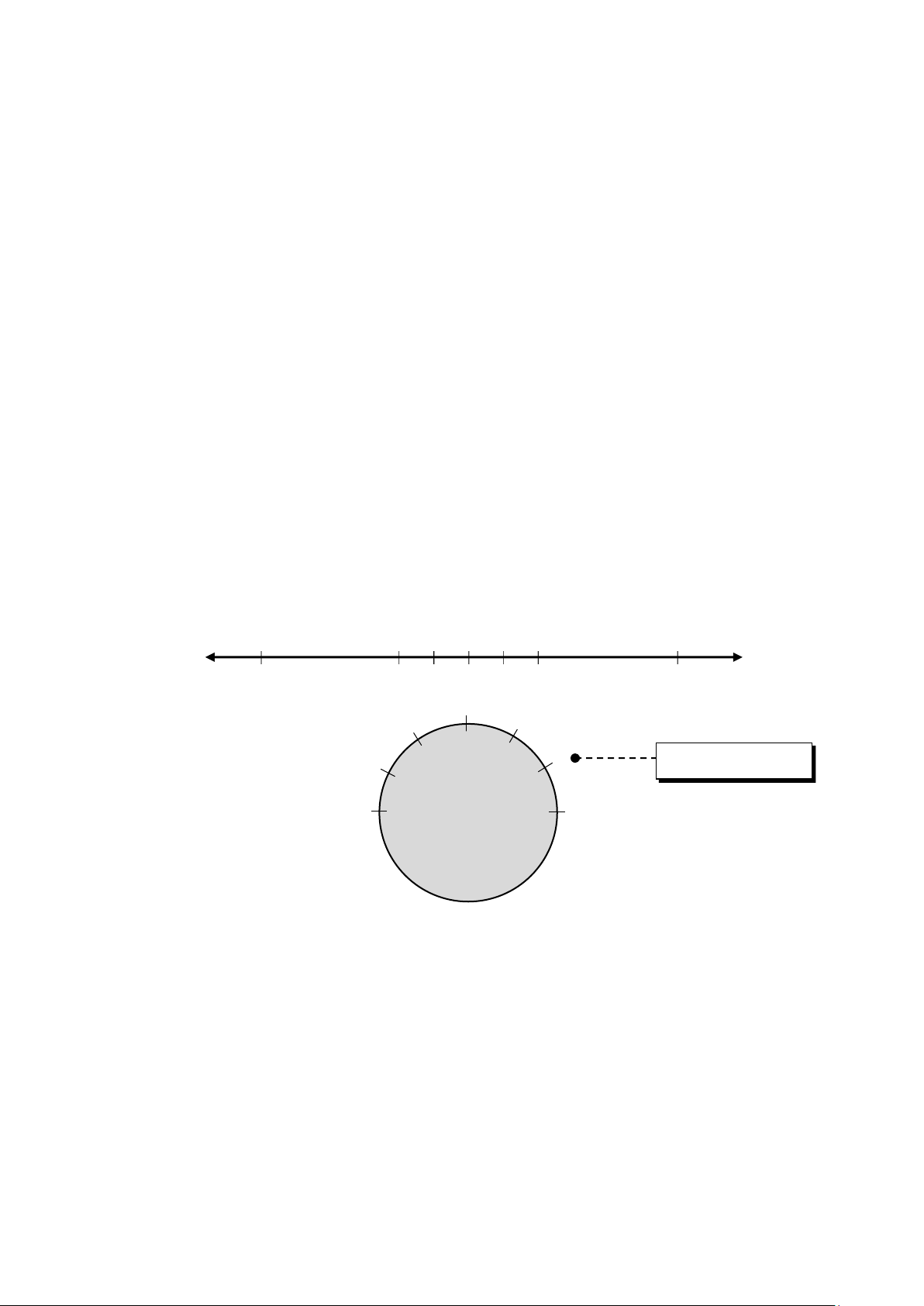
Khái niệm đồng dư có thể được hiểu rõ hơn bằng việc sử dụng một biểu đồ tròn.
Giống việc sử dụng một trục số để biểu diễn các số nguyên trong tập ℤ, ta có thể sử
dụng một đường tròn để biểu diễn các số nguyên trong tập ℤ𝑛. ℤ − ( 𝑛 − 1 ) 1 0 1 2 2 ( 𝑛 − 1 ) 0 ( 𝑛 − 1 ) 1 ( 𝑛 − 2 ) 2 𝑎 ≡ 2 ( mod 𝑛 ) ℤ 𝑛
Các số nguyên từ 0 đến 𝑛 − 1 cách đều nhau trên đường tròn. Tất cả các số nguyên
đồng dư trong modulo 𝑛 nằm cùng một điểm trên đường tròn. Các số nguyên dương
và nguyên âm từ tập ℤ được biểu diễn trên đường tròn một cách đối xứng.
Ta thường sử dụng số học đồng dư trong cuộc sống hàng ngày của chúng ta; ví dụ
như chúng ta sử dụng đồng hồ để tính thời gian. Hệ thống đồng hồ mà ta sử dụng thể
hiện một đồng dư trong modulo 12. Tuy nhiên, thay vì là 0, ta sử dụng số 12. Cho
nên, hệ thống đồng hồ bắt đầu từ 0 (hay 12) cho tới 11. Bởi vì một ngày kéo dài 24
giờ, cho nên kim giờ sẽ được quay hai vòng, vòng đầu tiên cho buổi sáng và vòng thứ hai cho buổi chiều.
Phép toán trong ℤ𝒏
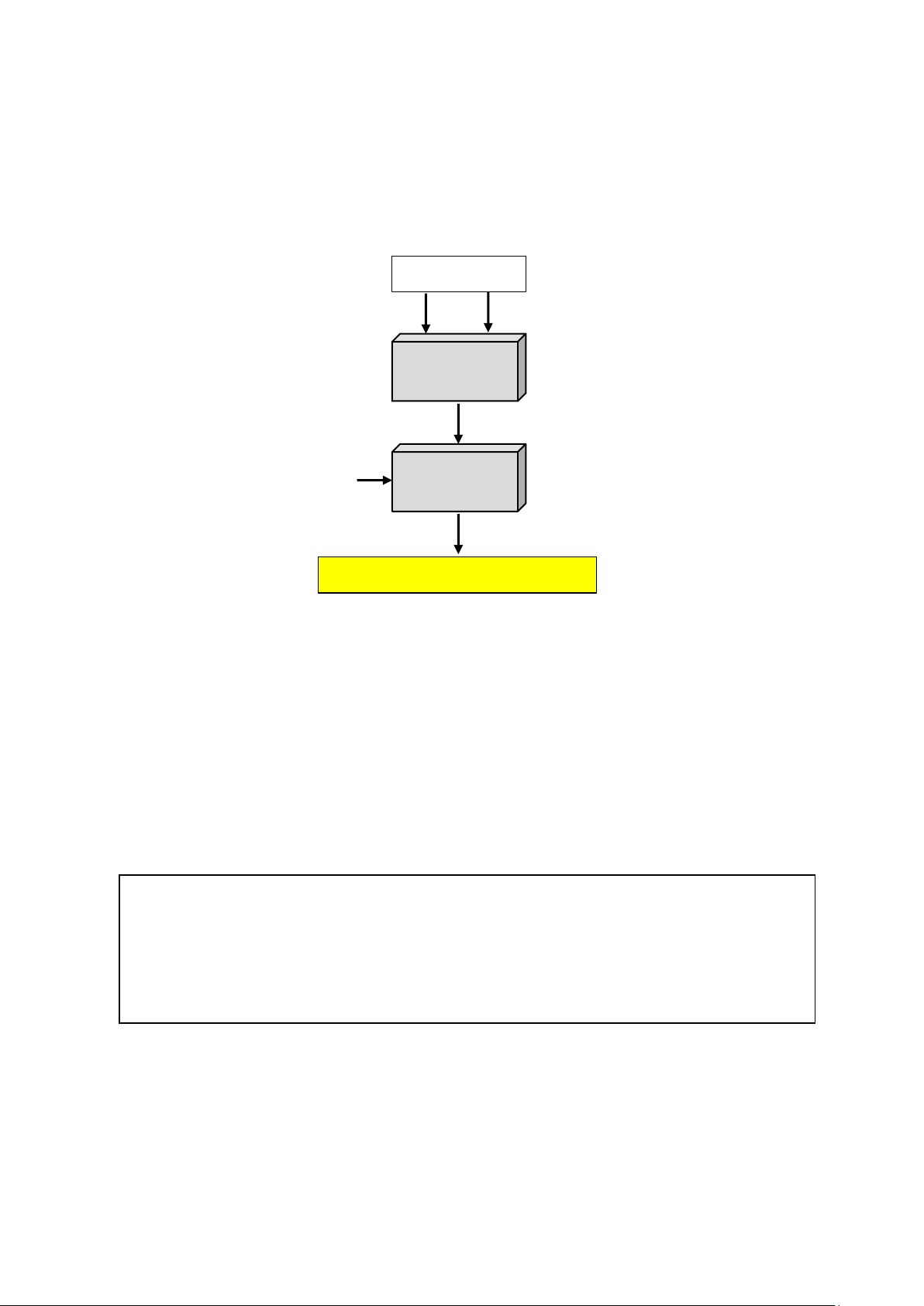
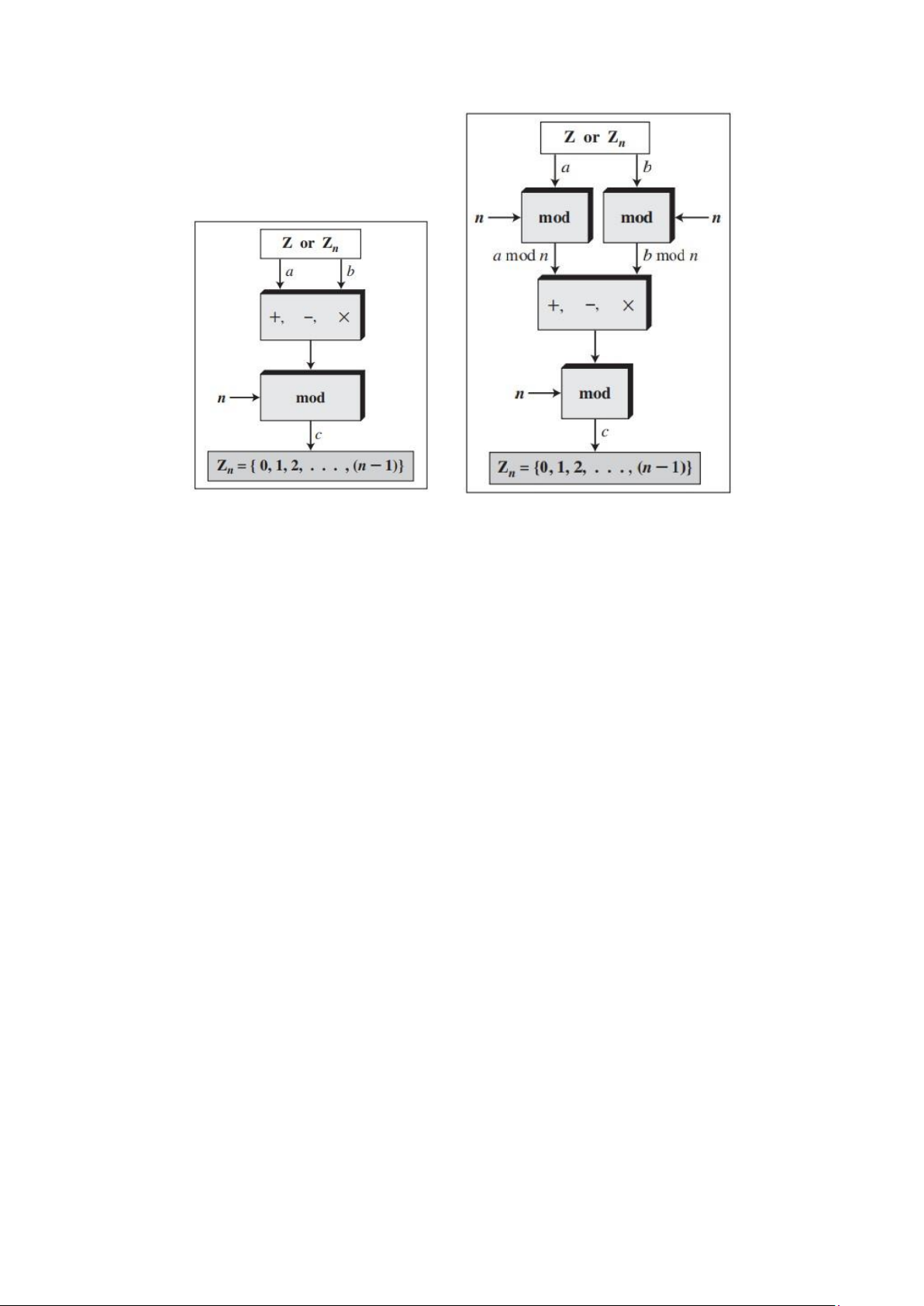
Ba phép toán hai ngôi (phép cộng, phép trừ và phép nhân) đối với tập ℤ cũng có thể
định nghĩa trong tập ℤ𝑛. Kết quả của toán tử trong ℤ𝑛 sẽ cần được ánh xạ tới tập ℤ𝑛
bằng việc sử dụng toán tử mod. ℤ ho ặ c ℤ 𝑛 𝑎 𝑏 + ,− ,× 𝑛 + ,− ,× 𝑐 ℤ 𝑛 = ሼ
0, 1 , 2 , 3 , … , ( 𝑛 − 1 ) ሽ
Thực ra, có hai loại toán tử đã được sử dụng ở đây. Loại thứ nhất đó là một trong các
toán tử hai ngôi (+, −,×); và thứ hai là toán tử mod. Ta cần sử dụng dấu ngoặc đơn
để thể hiện thứ tự ưu tiên của các phép toán. Đầu vào (𝑎 và 𝑏) có thể là các phần tử
trong tập ℤ hoặc tập ℤ𝑛. Tính chất
Ta đã từng đề cập tới việc hai đầu vào của phép toán hai ngôi trong số học mô-đun
có thể nằm trong tập ℤ hoặc ℤ𝑛. Tính chất sau đây cho phép chúng ta ánh xạ hai đầu
vào tới tập ℤ𝑛 (nếu chúng tới từ tập ℤ) trước khi thực hiện ba phép toán hai ngôi
Tính chất thứ nhất:
(𝑎 + 𝑏) mod 𝑛 = [(𝑎 mod 𝑛) + (𝑏 mod 𝑛)] mod 𝑛
Tính chất thứ hai:
(𝑎 − 𝑏) mod 𝑛 = [(𝑎 mod 𝑛) − (𝑏 mod 𝑛)] mod 𝑛
Tính chất thứ ba:
(𝑎 × 𝑏) mod 𝑛 = [(𝑎 mod 𝑛) × (𝑏 mod 𝑛)] mod 𝑛 (+, −,×).
Quá trình trước và sau khi áp dụng những tính chất trên.
Mặc dù quá trình xử lý sẽ dài hơn nếu ta sử dụng các tính chất trên, nhưng trong mật
mã ta sẽ phải xử lý với những con số rất lớn. Ví dụ, nếu ta nhân hai số nguyên lớn
với một số nguyên lớn khác, ta sẽ được môt số nguyên quá lớn để lưu trữ trong máy
tính. Áp dụng các tính chất trên, trước tiên làm cho hai toán hạng nhỏ đi, sau đó mới thực hiện phép nhân. Ví dụ:
1. (1,723,345 + 2,124,945) mod 11 = (8 + 9) mod 11 = 6
2. (1,723,345 − 2,124,945) mod 16 = (8 − 9) mod 11 = 10
3. (1,723,345 × 2,124,945) mod 16 = (8 × 9) mod 11 = 6
Trong số học, ta thường cần tìm số dư lũy thừa của 10 khi chia cho một số nguyên.
Ví dụ, ta cần tính 10 mod 3, 102 mod 3, 103 mod 3, v.v… Hay ta cần tính 10 mod 7,
102 mod 7, 103 mod 7, v.v… Tính chất thứ ba của toán tử mod ở trên sẽ làm công
việc trở nên dễ dàng hơn.
10𝑛 mod 𝑥 = (10 mod 𝑥)𝑛
Áp dụng tính chất thứ ba 𝑛 lần. Nghịch đảo
Khi ta làm việc trong số học mô-đun, ta thường cần tìm nghịch đảo của một số trong
phép tính. Ta thường cần tìm nghịch đảo cộng (liên quan tới phép cộng) hoặc nghịch
đảo nhân (liên quan đến phép nhân).
Nghịch đảo cộng
Trong tập ℤ𝑛, hai số 𝑎 và 𝑏 là nghịch đảo cộng của nhau nếu 𝑎 + 𝑏 ≡ 0 (mod 𝑛)
Trong ℤ𝑛, nghịch đảo cộng của 𝑎 có thể được tính bằng 𝑏 = 𝑛 − 𝑎. Ví dụ, nghịch đảo
cộng của 4 trong ℤ𝑛 là 10 − 4 = 6.
Trong số học mô-đun, mỗi số nguyên đều có một nghịch đảo cộng. Tổng của
một số nguyên và nghịch đảo cộng của nó đồng dư với 0 trong modulo 𝒏.
Lưu ý rằng trong số học mô-đun, mỗi một số sẽ có một nghịch đảo cộng và phần tử
nghịch đảo đó là duy nhất; mỗi số có một và chỉ một nghịch đảo cộng. Tuy nhiên,
nghịch đảo cộng của một số có thể là chính nó.
Nghịch đảo nhân
Trong 𝑍𝑛, hai số 𝑎 và 𝑏 là nghịch đảo nhân của nhau nếu 𝑎 × 𝑏
Ví dụ, nếu xét mô-đun 10, nghịch đảo nhân của 3 là 7. Nói cách khác, ta có (3 × 7) mod 10 = 1.
Trong số học mô-đun, một số nguyên có thể có hoặc không có nghịch đảo nhân.
Nếu tồn tại nghịch đảo nhân, tích của số nguyên và nghịch đảo nhân của nó
đồng dư với 1 trong modulo 𝒏.
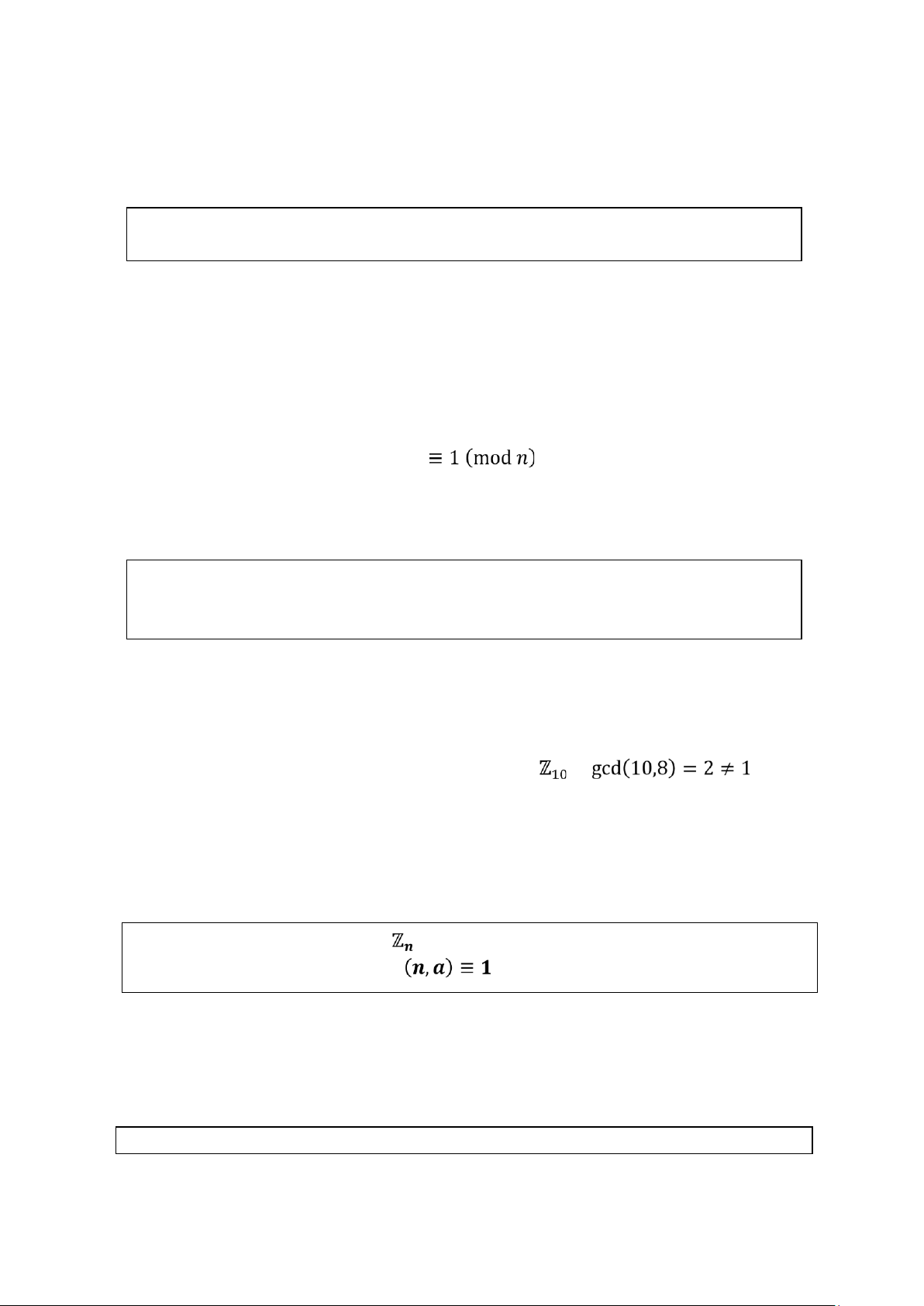
Người ta chứng minh được rằng 𝑎 có nghịch đảo nhân trong ℤ𝑛 (hay nói 𝑎 khả nghịch)
khi và chỉ khi gcd(𝑛, 𝑎) = 1. Khi đó, 𝑎 và 𝑛 được gọi là hai số nguyên tố cùng nhau. Ví dụ:
1. Không tồn tại nghịch đảo nhân của 8 trong vì . Hay
nói cách khác, ta không thể tìm được bất kỳ số nguyên nào từ 0 đến 9 mà khi
nhân với 8 cho kết quả đồng dư với 1 trong modulo 10.
2. Trong ℤ10 có ba cặp nghịch đảo nhân là (1, 1), (3,7), (9,9). Các số
0, 2, 4, 6, 8 không có nghịch đảo nhân (1 × 1) mod 10 = 1 (3 × 7) mod 10 = 1 (9 × 9) mod 10 = 1
Số nguyên 𝒂 trong tập tồn tại nghịch đảo nhân khi và chỉ khi 𝐠𝐜𝐝 (𝐦𝐨𝐝 𝒏)
Thuật toán Euclid mở rộng có thể tìm nghịch đảo nhân 𝑏 trong ℤ𝑛 khi đã biết 𝑛 và 𝑏
và tồn tại nghịch đảo nhân (khả nghịch). Để chứng tỏ điều đó, ta sẽ thay số nguyên
đầu tiên 𝑎 bằng 𝑛. Bằng thuật toán Euclid, ta có thể tìm được 𝑠 và 𝑡 trong phương
trình 𝑠 × 𝑛 + 𝑏 × 𝑡 = gcd(𝑛, 𝑏). Tuy nhiên, nếu tồn tại nghịch đảo nhân của 𝑏,
(𝒔 × 𝒏) + (𝒃 × 𝒕) = 𝟏
gcd(𝑛, 𝑏) phải bằng 1. Do đó, phương trình sẽ là
Sử dụng toán tử modulo vào cả hai vế của phương trình. Hay nói cách khác, ta ánh
xạ cả hai vế tới tập ℤ𝑛. Ta sẽ có
(𝑠 × 𝑛 + 𝑏 × 𝑡) mod 𝑛 = 1 mod 𝑛
[(𝑠 × 𝑛) mod 𝑛] + [(𝑏 × 𝑡) mod 𝑛] = 1 mod 𝑛
0 + [(𝑏 × 𝑡) mod 𝑛] = 1 (𝑏 × 𝑡) mod 𝑛 = 1
→ 𝑡 là phần tử nghịch đảo nhân của 𝑏 trong ℤ𝑛
Lưu ý, biểu thức [(𝑠 × 𝑛) mod 𝑛] ở dòng thứ ba bằng 0 vì nếu ta chia (𝑠 × 𝑛) cho 𝑛,
thương tìm được là 𝑠 và số dư là 0.
Thuật toán Euclid mở rộng tìm được nghịch đảo nhân của 𝒃 trong ℤ𝒏 khi biết
𝒏, 𝒃 và 𝐠𝐜𝐝(𝒏, 𝒃) = 𝟏.
Nghịch đảo nhân của 𝒃 là giá trị của 𝒕 sau khi ánh xạ tới ℤ𝒏.
a. Cách tìm nghịch đảo nhân b. Mô tả thuật toán
Ví dụ tìm nghịch đảo nhân của 11 trong ℤ26: 𝑞 𝑟1 𝑟2 𝑟 𝑡1 𝑡2 𝑡 2 26 11 4 0 1 −2 2 11 4 3 1 −2 5 1 4 3 1 −2 5 −7 3 3 1 0 5 −7 26 1 0 −7 26
Ta có gcd(26,11) = 1, cho nên tồn tại nghịch đảo nhân của 11. Thuật toán Euclid
mở rộng tìm được 𝑡1 = −7. Nghịch đảo nhân cần tìm là (−7) mod 26 = 19. Như
vậy, 11 và 19 là nghịch đảo nhân của nhau trong ℤ26. Thật vậy, (11 × 19) mod 26 = 209 mod 26 = 1. Bảng cộng và nhân
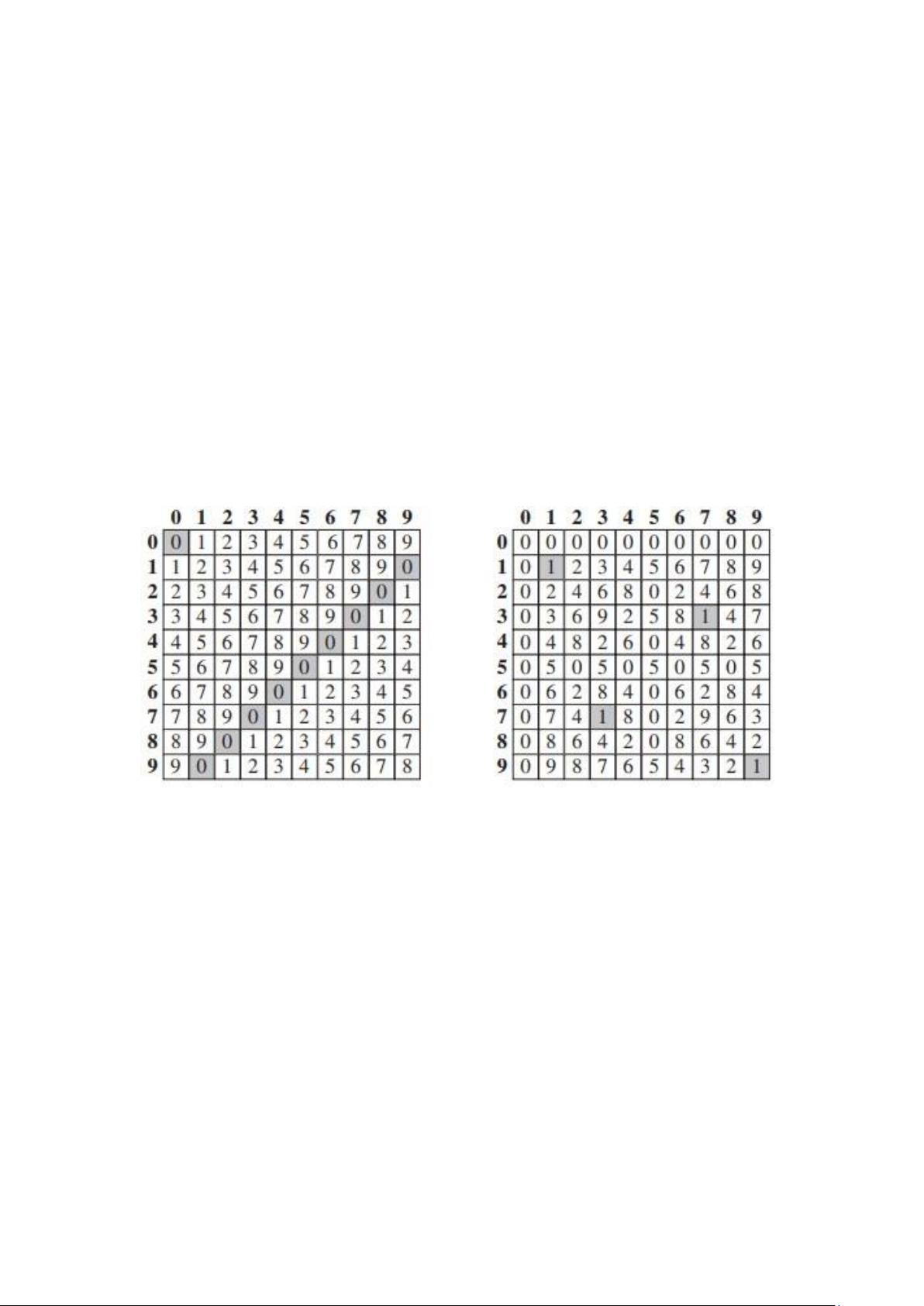
Trong bảng cộng, mỗi số nguyên đều có một phần tử nghịch đảo cộng. Các cặp phần
tử nghịch đảo được tìm thấy khi kết quả của phép cộng bằng 0. Chúng ta có các cặp
(0, 0), (1, 9), (2, 8), (3, 7), (4, 6), và (5, 5). Trong bảng nhân, ta có ba cặp nghịch đảo
nhân của nhau là (1, 1), (3, 7), và (9, 9). Các cặp này được tìm thấy trong bảng khi
phép nhân cho kết quả bằng 1. Cả hai bảng đều đối xứng qua đường chéo hướng từ
góc trên bên trái xuống góc dưới bên phải, điều này thể hiện tính giao hoán của phép
nhân và phép cộng (𝑎 + 𝑏 = 𝑏 + 𝑎 𝑣à 𝑎 × 𝑏 = 𝑏 × 𝑎). Bảng cộng cũng cho thấy mỗi
hoàng hoặc cột là một hoán vị của một hàng hoặc cột khác. Điều này không đúng trong bảng nhân. Bảng cộng trong ℤ10 Bảng nhân trong ℤ10
Một số tập hợp khác cho phép cộng và phép nhân
Trong mật mã ta thường làm việc với các phần tử nghịch đảo. Nếu người gửi sử dụng
một số nguyên (làm khóa cho mã hóa), người nhận sẽ phải sử dụng phần tử nghịch
đảo của số nguyên đó (làm khóa giải mã). Nếu phép toán (trong thuật toán mã
hóa/giải mã) là phép cộng, tập ℤ𝑛 có thể được sử dụng làm tập hợp các khóa khả thi
vì mỗi số nguyên trong tập hợp này đều có một phần tử nghịch đảo cộng tương ứng.
Mặt khác, nếu phép toán (trong thuật toán mã hóa/giải mã) là phép nhân, ℤ𝑛 không
thể là tập khóa khả thi vì chỉ một số phần tử trong tập hợp này tồn tại phần tử nghịch
đảo nhân. Ta cần một tập hợp khác để biểu diễn. Tập hợp mới là tập con của ℤ𝑛, chỉ
bao gồm các số nguyên khả nghịch trong ℤ𝑛. Tập hợp này được gọi là ℤ𝑛∗. Hình 2.17
chỉ ra một vài trường hợp của hai tập hợp. Lưu ý rằng ℤ𝑛∗ có thể tạo thành từ bảng
nhân, ví dụ như trong hình 2.16.
Mỗi phần tử của ℤ𝑛 đều có nghịch đảo cộng, nhưng chỉ một số phần tử mới tồn tại
nghịch đảo nhân. Mỗi phần tử của ℤ𝑛∗ lại đều có nghịch đảo nhân, nhưng chỉ một vài
phần tử là có nghịch đảo cộng (trong ℤ𝑛∗).
Ta cần sử dụng ℤ𝒏 khi cần đến nghịch đảo cộng; cần sử dụng ℤ𝒏∗ khi cần đến
nghịch đảo nhân. Hai tập hợp khác
Mật mã thường dùng hai tập khác là ℤ𝑝 và ℤ𝑝∗. Phần mô-đun trong hai tập là một số
nguyên tố. Số nguyên tố là số chỉ có hai ước là 1 và chính nó.
Tập ℤ𝑝 giống với tập ℤ𝑛, trừ việc 𝑛 là một số nguyên tố. ℤ𝑝 chứa tất cả các số nguyên
từ 0 đến p-1. Mỗi phần tử trong ℤ𝑝 đều có nghịch đảo cộng và mỗi phần tử khác 0
đều có nghịch đảo nhân.
Tương tự, tập ℤ𝑝∗ cũng giống tập ℤ𝑛∗ với 𝑛 là một số nguyên tố. ℤ𝑝∗ chứa tất cả các
số nguyên từ 1 đến p-1. Mỗi phần tử trong ℤ𝑝∗ đều tồn tại cả nghịch đảo cộng và
nghịch đảo nhân. ℤ𝑝∗ là một trường hợp rất tốt trong việc chọn một tập hợp có cả
nghịch đảo cộng và nghịch đảo nhân.
3. ĐỒNG DƯ TUYẾN TÍNH:
Phương trình đồng dư tuyến tính là phương trình có dạng
ax ≡ b (mod n) trong đó a, b, n là các số
nguyên, n > 0 và x là ẩn số. Cách giải:
- Tính gcd(a, n) = d, nếu d b thì phương trình vô nghiệm, nếu d | b thì phương trình
có d nghiệm. Các bước tìm nghiệm: + Chia cả 2 vế cho d
+ Nhân cả 2 vế với nghịch đảo của a/d, ta được nghiệm x0
+ Các nghiệm còn lại x = x0 + k(n/d) với k = 0,1,...,(d-1) 4. MA TRẬN: 4.1. Định nghĩa
Ma trận A kích thư–ớc m*n (m hàng, n cột) với 𝑎𝑖𝑗 là một phần tử hàng i, cột j 𝑎11 𝑎12 𝑎1𝑛 𝑎 𝑎 ⋯ 𝑎 𝐴𝑚∗𝑛
𝑎𝑚1 𝑎𝑚2 ⋯ 𝑎𝑚𝑛
4.2. Một số phép toán về ma trận Cho ma trận A,B,C
4.2.1. Cộng ma trận
C = A + B ó 𝑐𝑖𝑗 = 𝑎𝑖𝑗 + 𝑏𝑖𝑗
4.2.2. Nhân ma trận
C = A × B ó 𝑐𝑖𝑘 = ∑ 𝑎𝑖𝑗×𝑏𝑗𝑘= 𝑎𝑖1×𝑏1𝑗+𝑎𝑖2×𝑏2𝑗+…+𝑎𝑖𝑚×𝑏𝑚𝑗
(Điều kiện: số cột ma trận A = số hàng ma trận B)
4.2.3. Nhân ma trận với một số
C = tA ó 𝑐𝑖𝑗 = t × 𝑎𝑖𝑗 (t ∈ R) 4.2.4.
Ma trận phụ đại số chuyển vị Cho 𝐴𝑛×𝑛
Gọi 𝐷𝑖𝑗 là định thức con của ma trận A khi bỏ đi i hàng, j cột (det(A) ≠0) 𝐴11 𝐴12 𝐴1𝑛 𝑇 ⋯ 𝐴 𝐴 𝐴
𝑖+𝑗𝐷𝑖𝑗 𝐴 với 𝐴𝑖𝑗=(−1)
𝐴𝑛1 𝐴𝑛2 ⋯ 𝐴𝑛𝑛 4.2.5. Định thức
Cho ma trận vuông A kích thước
n*n +) n=1: det (A) = 𝑎11 +) n>1:
det(A) = ∑𝑖=1…𝑛(−1)𝑖+𝑗×𝐴𝑖𝑗×det (𝐴𝑖𝑗)
Trong đó 𝐴𝑖𝑗 là ma trận A bỏ đi i hàng, j cột
• Ma trận nghịch đảo i)
Nghịch đảo cộng:
Ma trận B gọi là nghịch đảo cộng của ma trận A ó
A+B=O Trong đó O là ma trận không ii) Nghịch đảo nhân:
Ma trận nghịch đảo nhân của A, kí hiệu 𝐴−1: A*𝐴−1=I (I: ma trận đơn vị)
Cách tính: 𝐴−1= (det(𝐴))−1*𝐴∗𝑇
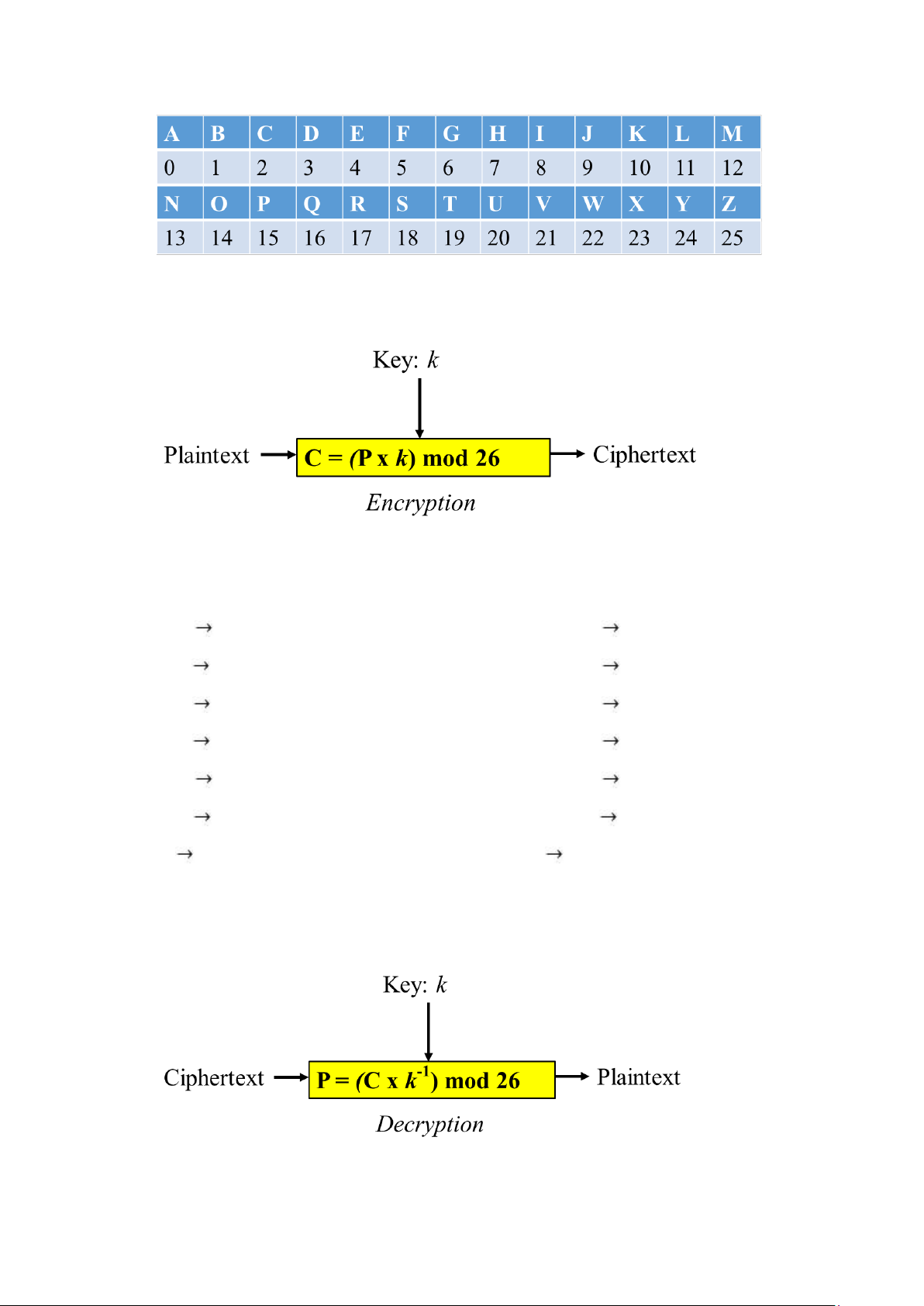
MỘT SỐ HỆ MẬT CỔ ĐIỂN 1. Additive Cipher:
Mật mã cộng (Additive cipher) còn được gọi là mật mã Caesar (Caesar cipher), là
một dạng mật mã thay thế dùng một bảng chữ cái, trong đó mỗi chữ cái được ánh xạ
tới một số, sau đó được mã hóa thông qua phép cộng module.
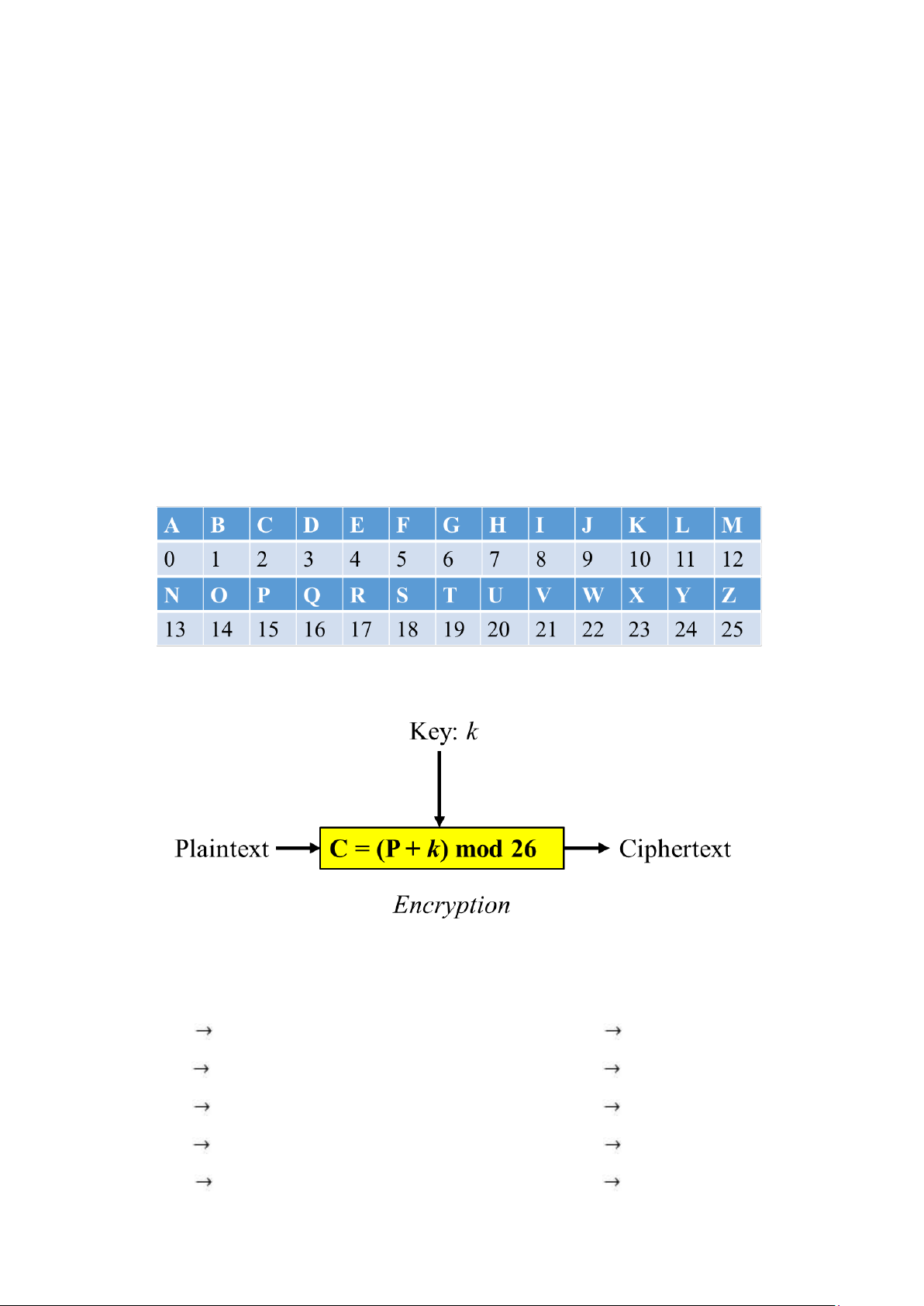
Để thực hiện mật mã hóa Caesar, trước tiên ta cần ánh xạ các kí tự trong bảng chữ
cái (La tinh) thành các số tương ứng 0..25
Sau đó, ta thực hiện quá trình mã hóa theo sơ đồ sau:
Ở đây, khóa k là một số nguyên có giá trị thuộc tập Z26 = {0,1,2,…,25}
VD: Mã hóa bản tin P = “VIETNAM” bằng mật mã cộng với khóa k = 5 V 21
=> Encryption: (21 + 05) mod 26 = 00 A I 08
=> Encryption: (08 + 05) mod 26 = 13 N E 04
=> Encryption: (04 + 05) mod 26 = 09 J T 19
=> Encryption: (19 + 05) mod 26 = 24 Y N 13
=> Encryption: (13 + 05) mod 26 = 18 S A 00
=> Encryption: (00 + 05) mod 26 = 05 F M 12
=> Encryption: (12 + 05) mod 26 = 17 R => C = “ANJYSFR”
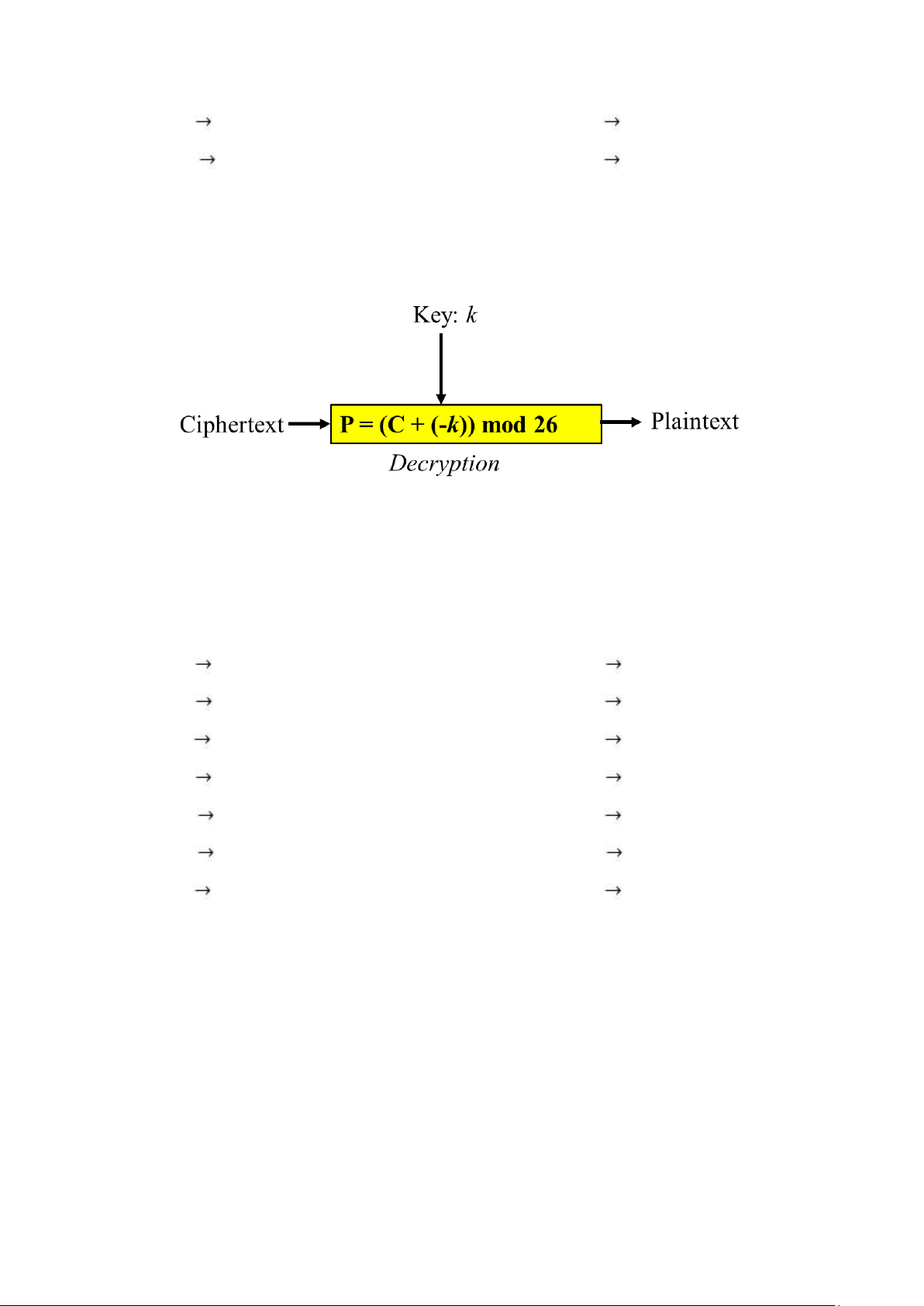
Để giải mã, ta thực hiện theo sơ đồ sau:
Trong công thức này, -k là phần tử nghịch đảo cộng của k trong tập Z26: (k
+ (-k)) mod 26 = 0
VD: Giả sử thu được ciphertext như ví dụ ở trên, biết khóa k = 5. Tìm plaintext? k = 5 => -k = 21 A 00
=> Decryption: (00 + 21) mod 26 = 21 V N 13
=> Decryption: (13 + 21) mod 26 = 08 I J 09
=> Decryption: (09 + 21) mod 26 = 04 E Y 24
=> Decryption: (24 + 21) mod 26 = 19 T S 18
=> Decryption: (18 + 21) mod 26 = 13 N F 05
=> Decryption: (05 + 21) mod 26 = 00 A R 17
=> Decryption: (17 + 21) mod 26 = 12 M => P = “VIETNAM” 2. Multiplicative Cipher:
Mật mã nhân (Multiplicative cipher) là một dạng mật mã thay thế dùng một bảng
chữ cái, trong đó mỗi chữ cái được ánh xạ tới một số, sau đó được mã hóa thông qua phép nhân module.
Để thực hiện mật mã hóa Caesar, trước tiên ta cần ánh xạ các kí tự trong bảng
chữ cái (La tinh) thành các số tương ứng 0..25
Sau đó, ta thực hiện quá trình mã hóa theo sơ đồ sau:
Ở đây, khóa k là một số nguyên có giá trị thuộc tập Z26 = {0,1,2,…,25}
VD: Mã hóa bản tin P = “VIETNAM” bằng mật mã nhân với khóa k = 5 V 21
=> Encryption: (21 x 05) mod 26 = 01 B I 08
=> Encryption: (08 x 05) mod 26 = 14 O E 04
=> Encryption: (04 x 05) mod 26 = 20 U T 19
=> Encryption: (19 x 05) mod 26 = 17 R N 13
=> Encryption: (13 x 05) mod 26 = 13 N A 00
=> Encryption: (00 x 05) mod 26 = 00 A M
12 => Encryption: (12 x 05) mod 26 = 08 I => C = “BOURNAI”
Để giải mã, ta thực hiện theo sơ đồ sau:
Trong công thức này, k -1 là phần tử nghịch đảo nhân của k trong tập Z26
k -1.k mod 26 = 1
VD: Giả sử thu được ciphertext như ví dụ ở trên, biết khóa k = 5. Tìm plaintext? k = 5 => k -1 = 21 B 01
=> Decryption: (01 x 21) mod 26 = 21 V O 14
=> Decryption: (14 x 21) mod 26 = 08 I U 20
=> Decryption: (20 x 21) mod 26 = 04 E R 17
=> Decryption: (17 x 21) mod 26 = 19 T N 13
=> Decryption: (13 x 21) mod 26 = 13 N A 00
=> Decryption: (00 x 21) mod 26 = 00 A I 08
=> Decryption: (08 x 21) mod 26 = 12 M => P = “VIETNAM” 3. Affine Cipher:
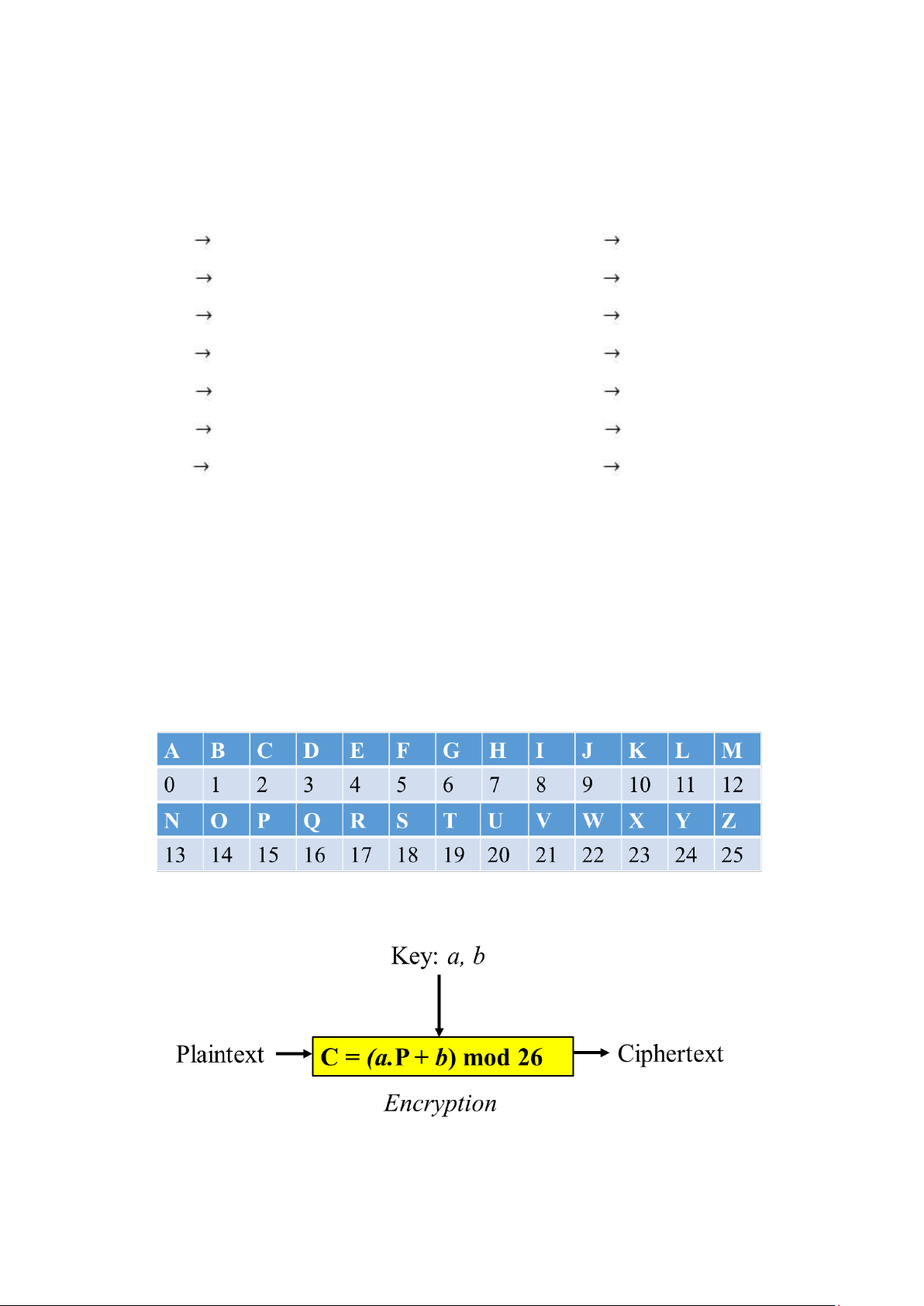
Mật mã Affine là một dạng mật mã thay thế dùng một bảng chữ cái, trong đó mỗi
chữ cái được ánh xạ tới một số, sau đó được mã hóa thông qua một hàm bậc nhất có dạng: y = ax + b
Để thực hiện mật mã hóa Affine, trước tiên ta cần ánh xạ các kí tự trong bảng
chữ cái (La tinh) thành các số tương ứng 0..25
Sau đó, thực hiện quá trình mã hóa theo sơ đồ sau:
Trong công thức này, 2 khóa a và b là 2 số nguyên thuộc tập Z26, trong đó a
và 26 là hai số nguyên tố cùng nhau (gcd(a, 26) = 1)
VD: Mã hóa bản tin P = “VIETNAM” bằng mật mã Affine với khóa a = 17 và b = 5 V 21
=> Encryption: (17.21 + 05) mod 26 = 24 Y I 08
=> Encryption: (17.08 + 05) mod 26 = 11 L E 04
=> Encryption: (17.04 + 05) mod 26 = 21 V T 19
=> Encryption: (17.19 + 05) mod 26 = 16 Q N 13
=> Encryption: (17.13 + 05) mod 26 = 18 S A 00
=> Encryption: (17.00 + 05) mod 26 = 05 F M 12
=> Encryption: (17.12 + 05) mod 26 = 01 B => C = “YLVQSFB”
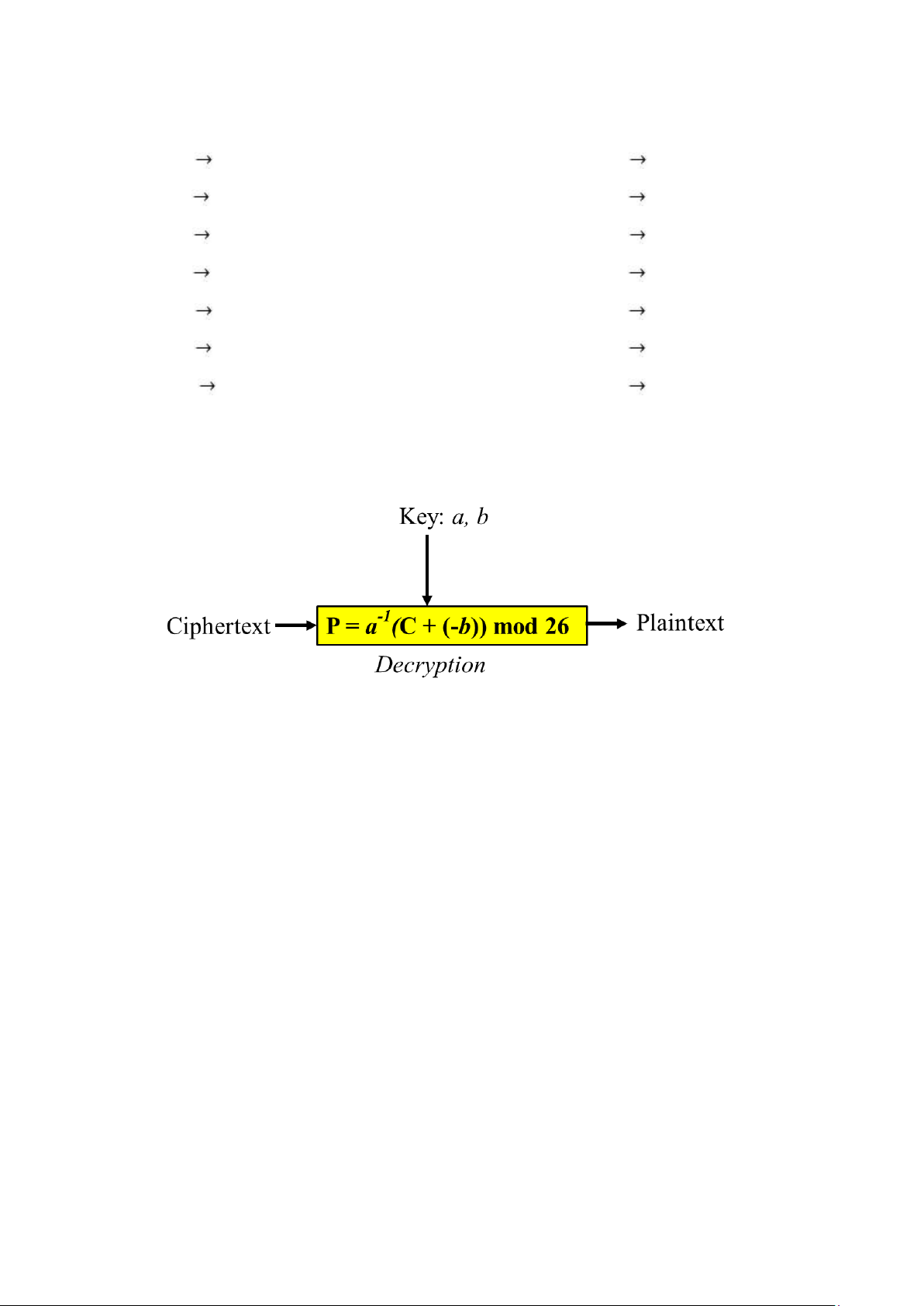
Để giải mã, ta thực hiện theo sơ đồ sau:
Ở đây, a-1 là phần tử nghịch đảo nhân của a và –b là phần tử nghịch đảo cộng
của b trong tập Z26: a.a-1 mod 26 = 1 và (b + (-b)) mod 26 = 0
Mật mã cộng là một trường hợp đặc biệt của mật mã Affine với a = 1
Mật mã nhân là một trường hợp đặc biệt của mật mã Affine với b = 0
VD: Giả sử thu được ciphertext như ví dụ ở trên, biết khóa a = 17 và b = 5. Tìm plaintext?
a = 17 => a-1 = 23
b = 05 => -b = 21 Y 24
=> Decryption: 23(24 + 21) mod 26 = 21 V L 11
=> Decryption: 23(11 + 21) mod 26 = 08 I V 21
=> Decryption: 23(21 + 21) mod 26 = 04 E Q 16
=> Decryption: 23(16 + 21) mod 26 = 19 T S 18
=> Decryption: 23(18 + 21) mod 26 = 13 N F 05
=> Decryption: 23(05 + 21) mod 26 = 00 A B 01
=> Decryption: 23(01 + 21) mod 26 = 12 M => P = “VIETNAM” 4. Substitution Cipher:
Do mật mã cộng, mật mã nhân và mật mã Affine có không gian khóa nhỏ nên chúng
rất dễ bị tấn công và kẻ tấn công có thể dễ dàng giải mã tìm ra nội dung bản tin rõ
bằng cách vét cạn hết khóa trong không gian khóa.
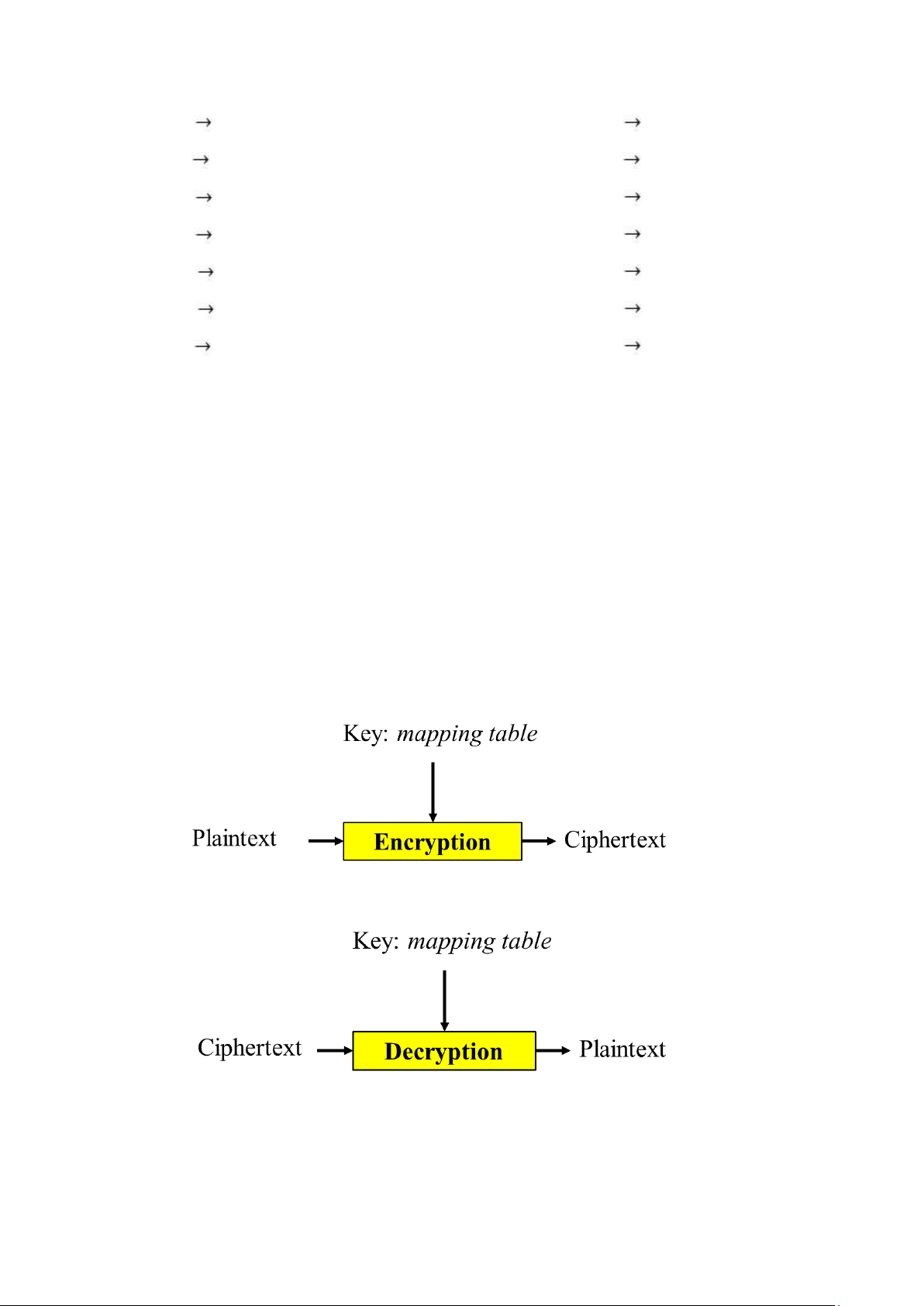
Có một giải pháp tốt hơn đó là tạo một ánh xạ giữa mỗi kí tự trong bản tin rõ với
một kí tự tương ứng trong bản tin mã hóa. Trước tiên, người gửi tin và người nhận
tin thống nhất một bảng thể hiện ánh xạ cho mỗi kí tự trong bảng chữ cái (nói theo
cách khác là đảo vị trí của các kí tự trong bảng chữ cái). Bảng này chính là chìa khóa
để mã hóa và giải mã tin.
Sơ đồ thực hiện mã hóa và giải mã như sau:
Để hiểu rõ hơn về Substitution Cipher. Ta xét ví dụ sau đây: Cho bảng: