Bài tập ôn cuối kì của môn Toán rời rạc | Trường Đại học Kinh Tế Quốc Dân

Bài 1. Cho số nguyên 𝑛 ≥ 2. Xét đồ thị đơn vô hướng 𝐻 có: 𝑛
• Tập đỉnh 𝑉 = {1,2, … , 𝑛},
• Hai đỉnh 𝑖 ≠ 𝑗được nối với nhau nếu và chỉ nếu 𝑖 + 𝑗 là hợp số.
1. Với 𝑛 = 8, hãy xác định bậc của từng đỉnh và số cạnh của 𝐻 . 8
2. So sánh số cạnh của 𝐻 với số cạnh của đồ thị (đồ thị tổng là số nguyên tố). 8 𝐺8
Bài 2. Cho số nguyên 𝑛 ≥ 2. Xét đồ thị 𝐷 với: 𝑛 • 𝑉 = {1,2, … , 𝑛},
• Hai đỉnh 𝑖, 𝑗 kề nhau nếu |𝑖 − 𝑗| là số nguyên tố. 1. Vẽ đồ thị 𝐷 . 10
2. Xác định số thành phần liên thông của 𝐷 . 10
Bài 3. Với 𝑛 ≥ 2, xét đồ thị 𝐺 đơn vô hướng có tập đỉnh ứng với các số tự nhiên từ 𝑛 1 đến
𝑛, hai số được nối với nhau nếu tổng của chúng là số nguyên tố.
1. Chứng minh rằng 𝐺 là đồ thị hai phía. 𝑛
2. Chỉ ra một phân hoạch hai phía cụ thể.
Bài 4. Với đồ thị 𝐺 như trong Bài 3. Hãy: 𝑛
1. Chứng minh rằng bậc của mỗi đỉnh bị chặn trên bởi số lượng số nguyên tố nhỏ hơn 𝑛 + 1.
2. Với 𝑛 = 20, xác định (hoặc ước lượng) đỉnh có bậc lớn nhất.
Bài 5. Xét đồ thị 𝐺 như trong Bài 3. 𝑛
1. Chứng minh rằng 𝐺 không chứa chu trình lẻ. 𝑛
2. Chứng minh rằng với 𝑛đủ lớn, 𝐺 có chứa chu trình độ dài 4. 𝑛
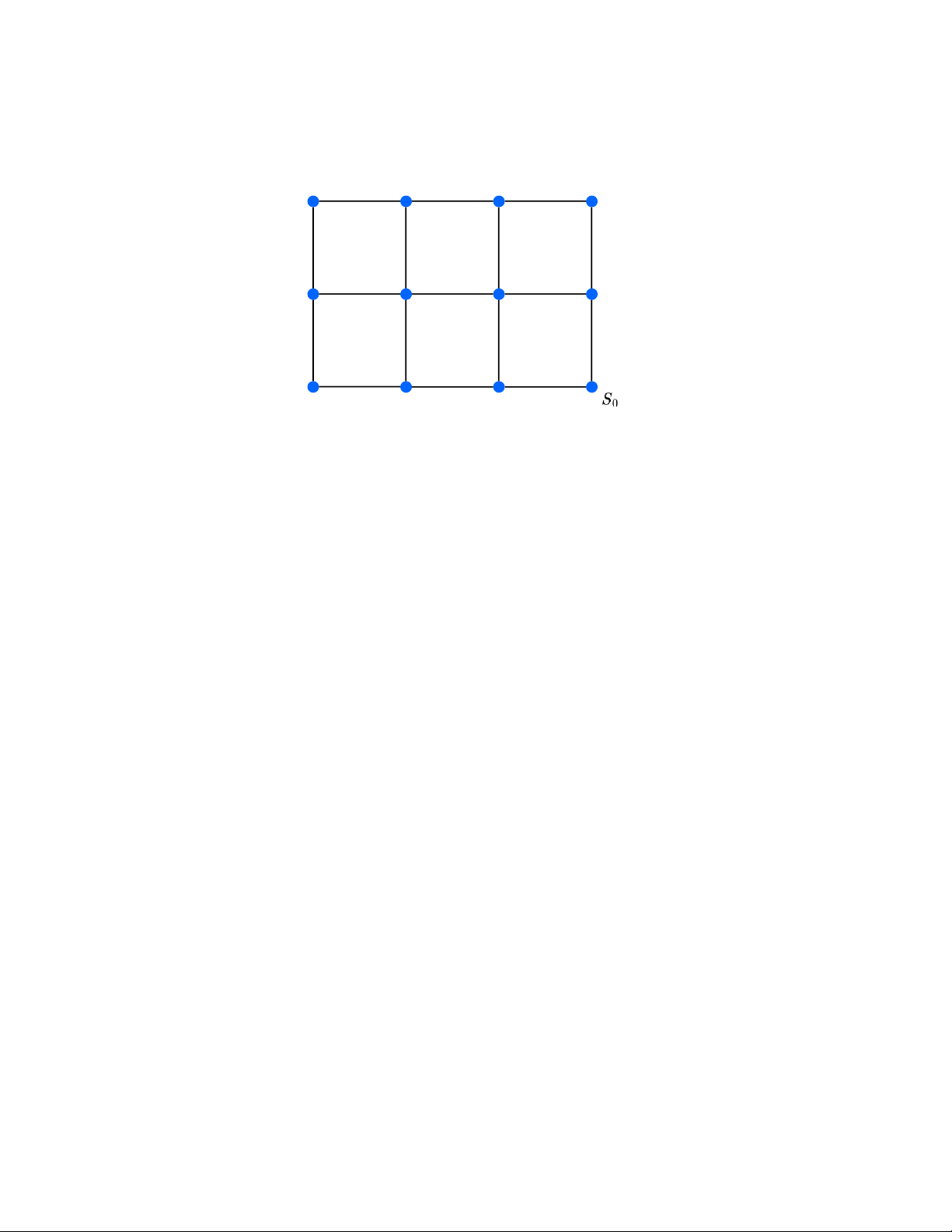
Bài 6. Cho một mạng lưới điểm mục tiêu gồm 12 điểm được sắp thành hình chữ nhật 3 × 4,
các điểm kề nhau được nối bởi các đoạn thẳng đơn vị (ngang và dọc) như sau:
Nam muốn di chuyển từ vị trí vị trí 𝑆 . 0
a) Chứng minh rằng Nam không thể đi qua tất cả các đoạn thẳng đơn vị, mỗi đoạn đúng
một lần, rồi quay lại 𝑆.
b) Xác định số đỉnh có bậc lẻ trong mạng lưới này.
c) Chứng minh rằng cần xóa ít nhất 2 đoạn thẳng đơn vị để tồn tại một chu trình Euler. Gợi ý:
• Đếm bậc các đỉnh biên và đỉnh trong.
• Áp dụng định lý Euler: đồ thị có chu trình Euler ⇔ liên thông và mọi đỉnh đều có bậc chẵn.
• Mỗi đoạn xóa làm thay đổi bậc của đúng hai đỉnh.
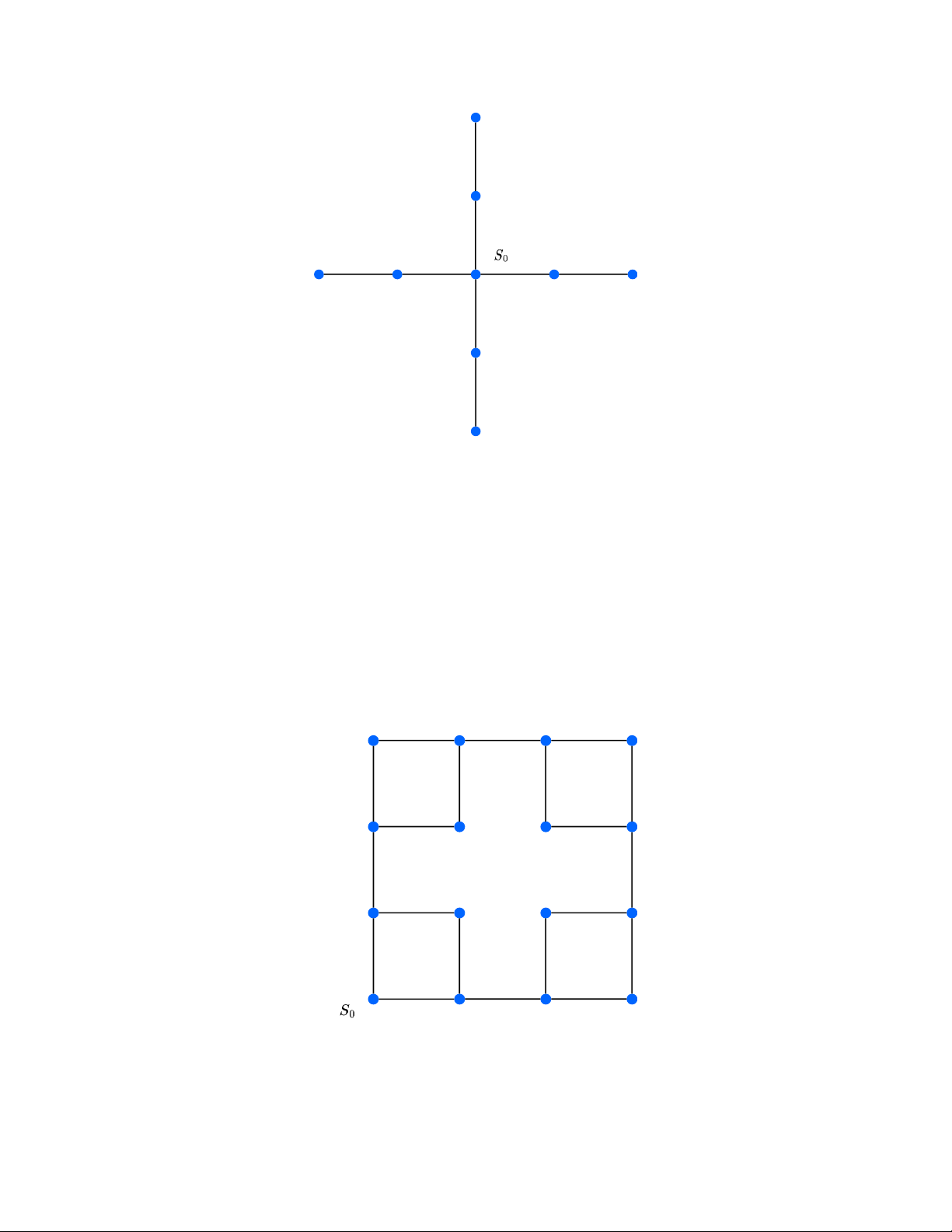
Bài 7. Cho một mạng lưới các điểm mục tiêu gồm 13 điểm tạo thành hình chữ thập. Các
điểm kề nhau được nối bởi đoạn thẳng đơn vị. Mạng có thể được trực quan như sau:
Nam xuất phát từ điểm trung tâm.
a) Chứng minh rằng Nam có thể đi qua tất cả các đoạn thẳng đơn vị đúng một lần nhưng
không thể quay lại điểm xuất phát.
b) Xác định chính xác các đỉnh có bậc lẻ.
c) Nêu điều kiện cần để biến đường đi hiện tại thành chu trình Euler.
Bài 8. Cho mạng lưới các điểm mục tiêu 4 × 4 như sau:
Nam xuất phát từ điểm mục tiêu ở góc dưới bên trái.
a) Chứng minh rằng đồ thị vẫn liên thông.
b) Xác định số đỉnh bậc lẻ.
c) Kết luận về khả năng tồn tại chu trình Euler và giải thích.
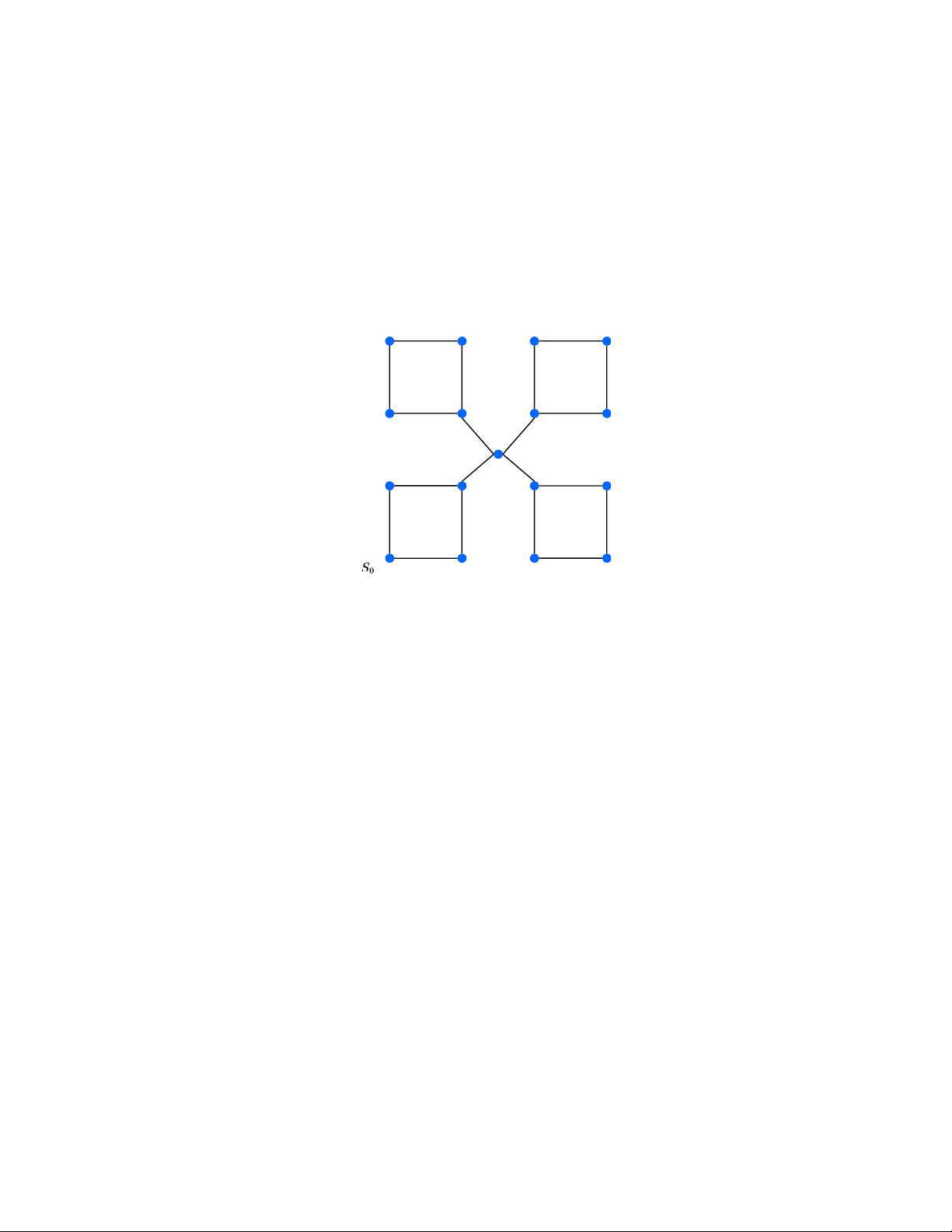
Bài 9. Cho một mạng lưới gồm 16 điểm mục tiêu như hình bên dưới. Bạn Nam xuất phát
tại một góc ngoài để duyệt qua các điểm mục tiêu này.
a) Chứng minh rằng mạng lưới có ít nhất 4 đỉnh bậc lẻ.
b) Suy ra rằng không tồn tại chu trình Euler.
c) Chứng minh rằng cần xóa ít nhất 2 đoạn thẳng đơn vị để tồn tại một đường đi Euler.
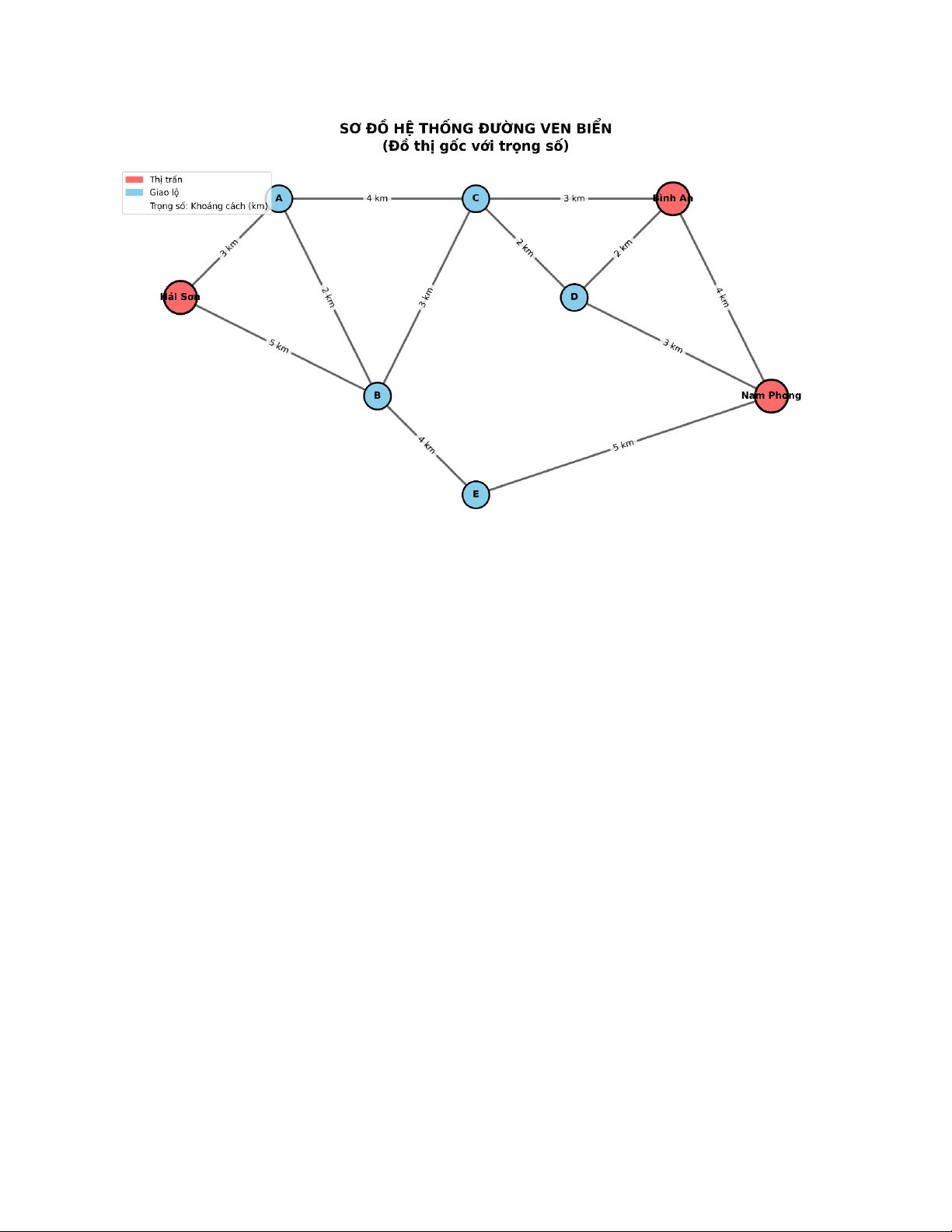
Bài 10. Sơ đồ dưới đây mô tả hệ thống các con đường ven biển nối giữa ba thị trấn Hải
Sơn, Bình An và Nam Phong. Các giao lộ được biểu diễn bởi các đỉnh 𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹, và
các cạnh mang trọng số là độ dài đoạn đường (km).
Một cuộc đua xe đạp bắt đầu tại thị trấn Hải Sơn và kết thúc tại Nam Phong.
a) Áp dụng thuật toán Dijkstra, hãy tìm đường đi ngắn nhất từ giao lộ 𝐵đến thị trấn Nam Phong.
b) Khoảng cách ngắn nhất từ Hải Sơn đến Nam Phong là bao nhiêu? Giải thích vì sao kết
quả này không phụ thuộc vào việc chọn lộ trình trung gian.
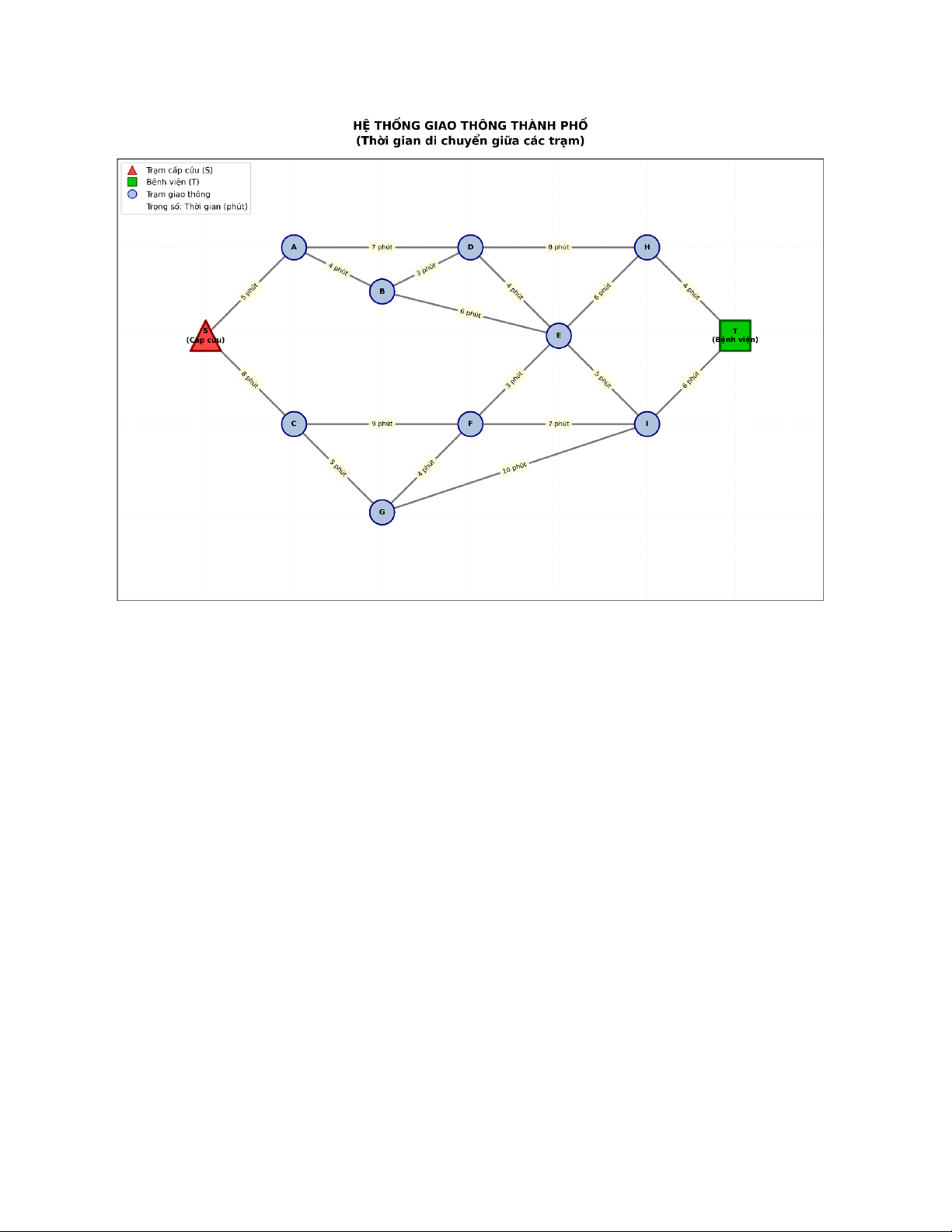
Bài 11. Một thành phố có các trạm giao thông được ký hiệu bởi
𝑆, 𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹, 𝐺, 𝐻, 𝐼, 𝑇
Trọng số trên mỗi cạnh biểu diễn thời gian di chuyển (phút) giữa các trạm.
Một xe cấp cứu xuất phát từ trạm 𝑆 và cần đến bệnh viện đặt tại trạm 𝑇.
a) Sử dụng thuật toán Dijkstra, hãy tìm đường đi có thời gian ngắn nhất từ 𝑆 đến 𝑇.
b) Nếu một đoạn đường bị ùn tắc và thời gian tăng thêm 10 phút, thuật toán Dijkstra có
còn áp dụng được không? Giải thích.
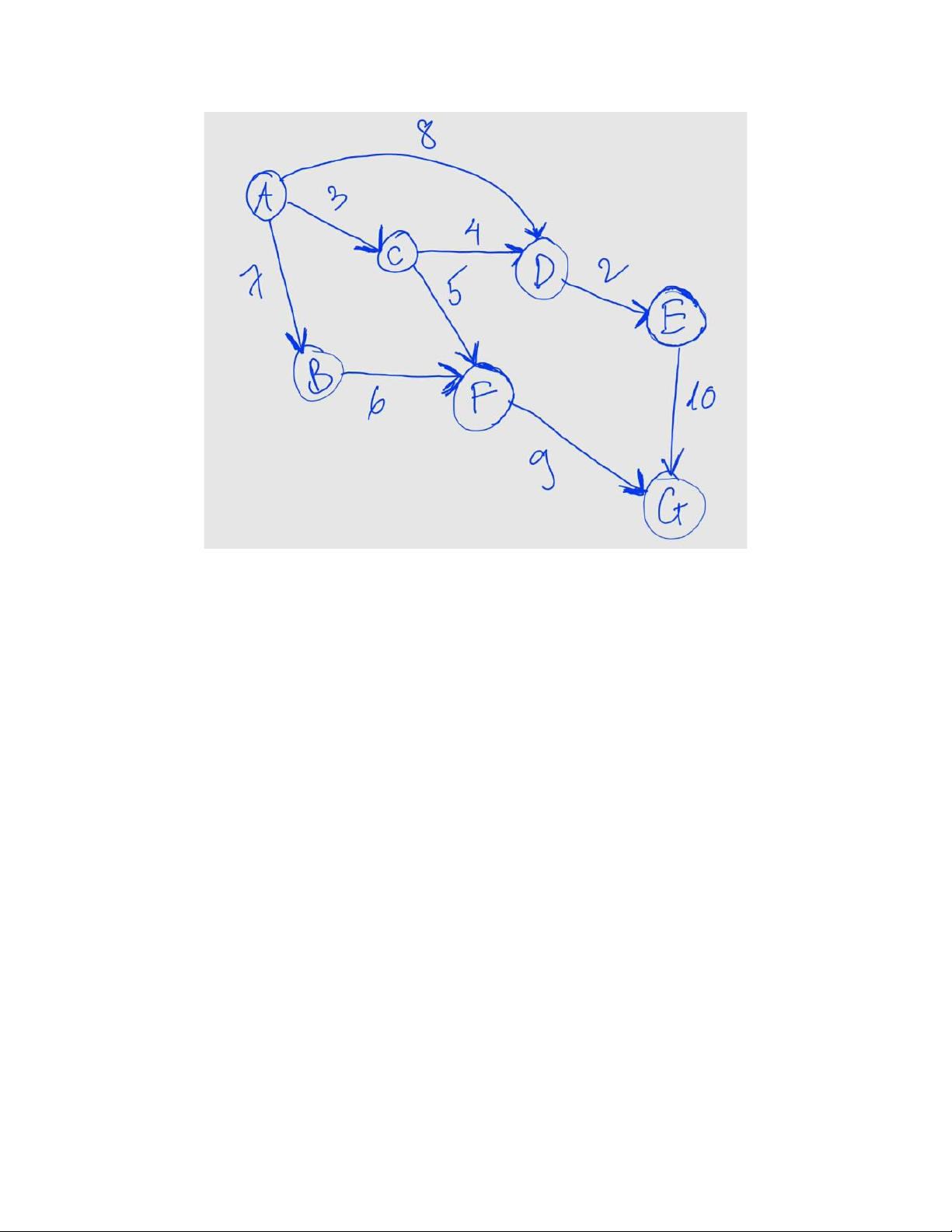
Bài 12. Cho một đồ thị có trọng số dương, biểu diễn mạng lưới đường nối giữa các thị trấn
𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹, 𝐺.
Một giải chạy đường dài cho phép vận động viên xuất phát từ một trong hai thị trấn 𝐴
hoặc 𝐵 và kết thúc tại thị trấn 𝐺.
a) Trình bày cách sử dụng Dijkstra để tìm đường đi ngắn nhất từ tập đỉnh {𝐴, 𝐵} đến 𝐺.
b) Thực hiện thuật toán và xác định điểm xuất phát nào cho quãng đường ngắn hơn.
c) Giải thích ý nghĩa thực tiễn của kết quả.
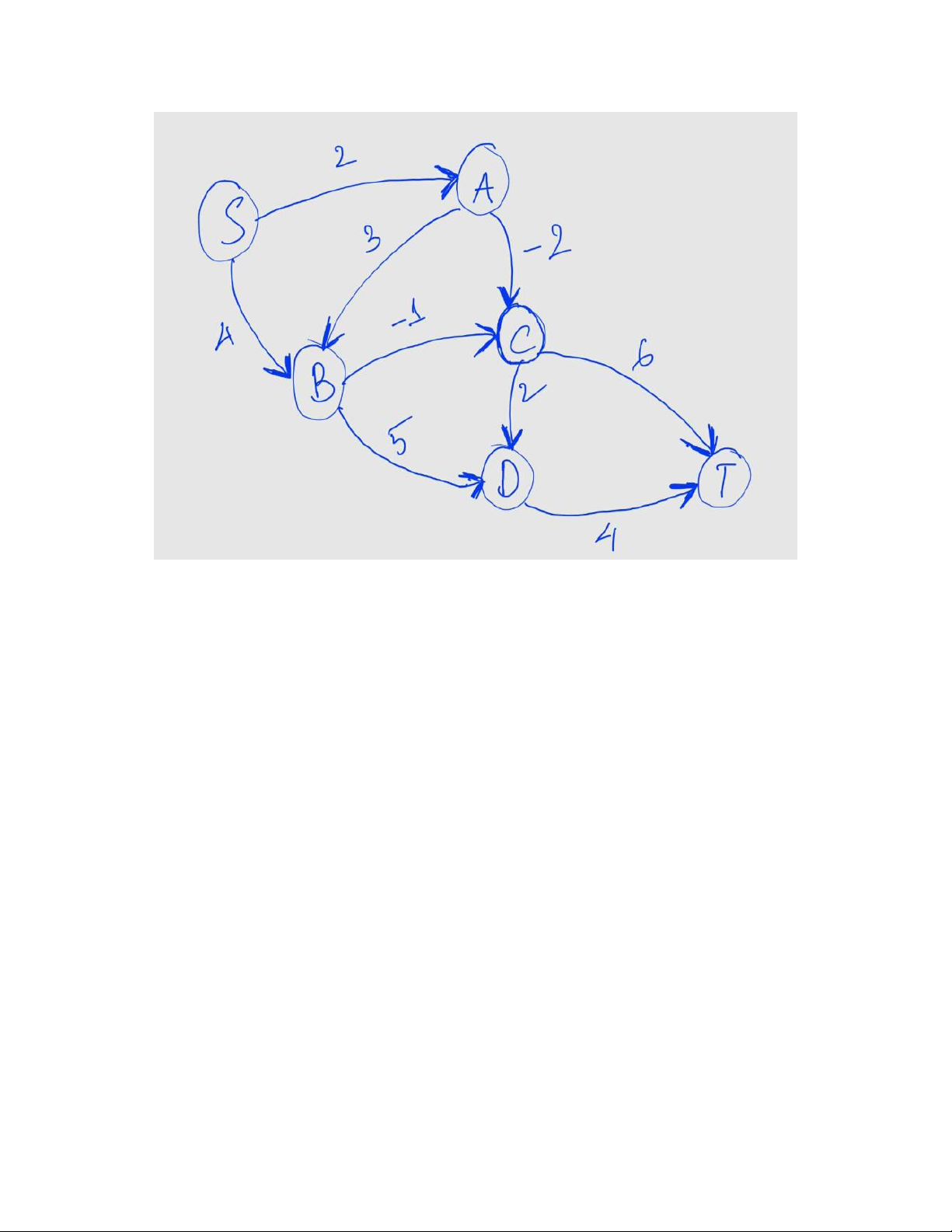
Bài 13. Một đồ thị biểu diễn mạng lưới giao thông giữa các điểm 𝑆, 𝐴, 𝐵, 𝐶, 𝐷, 𝑇. Một số
cạnh có trọng số âm do chính sách hoàn phí nhiên liệu.
a) Giải thích vì sao thuật toán Dijkstra không áp dụng được cho đồ thị này.
b) Sử dụng thuật toán Bellman–Ford để tìm đường đi ngắn nhất từ 𝑆 đến 𝑇.
c) Nêu ưu và nhược điểm của Bellman–Ford so với Dijkstra trong bối cảnh bài toán này.
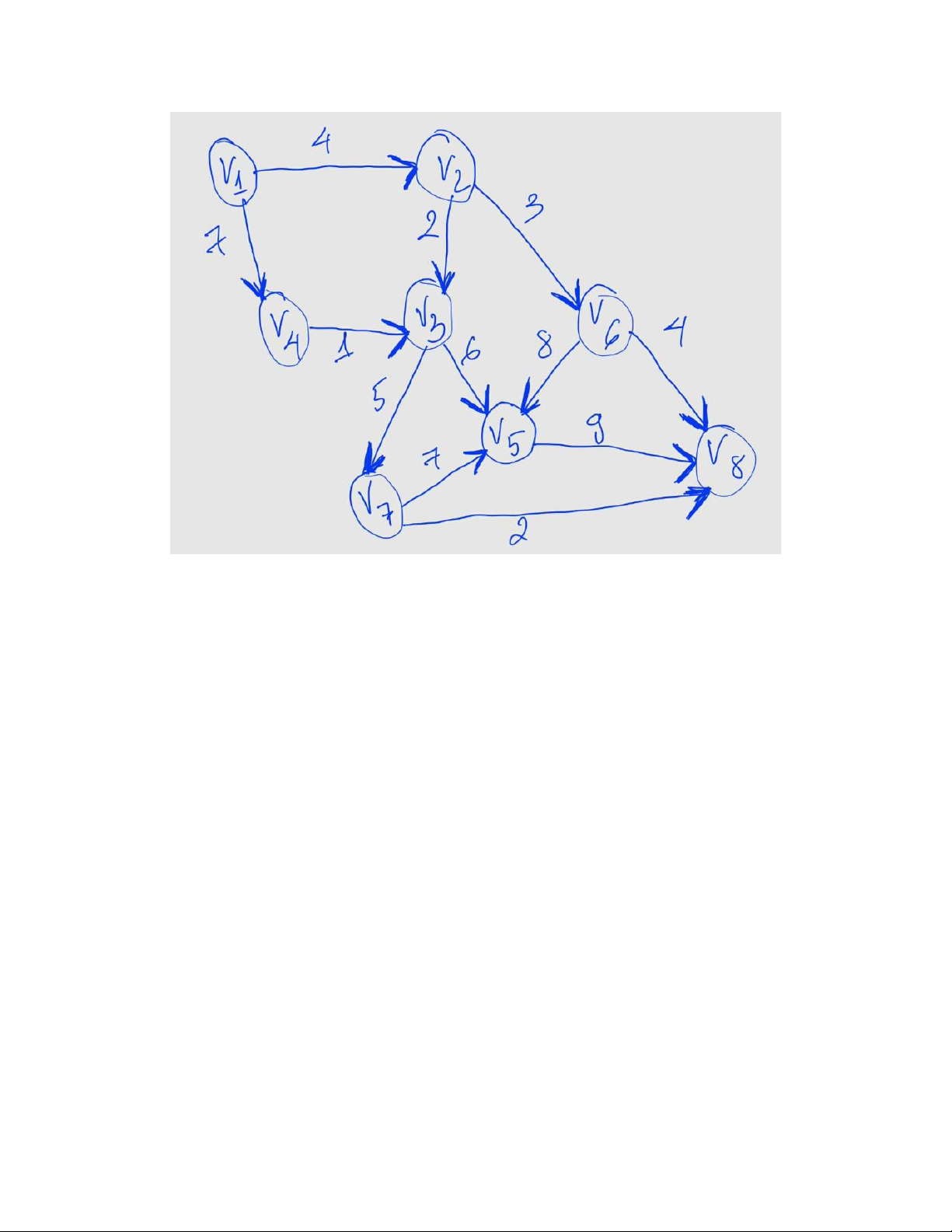
Bài 14. Một đồ thị có trọng số biểu diễn các tuyến đường nối giữa các trạm kiểm soát 𝑉
. Trọng số biểu diễn độ dài đường, tất cả đều dương. 1, 𝑉2, … , 𝑉8
Một vận động viên muốn đi từ 𝑉 đến . 1 𝑉8
a) Áp dụng thuật toán Dijkstra để tìm đường đi ngắn nhất từ 𝑉 đến . 1 𝑉8
b) Nếu vận động viên buộc phải đi qua trạm 𝑉 , khoảng cách ngắn nhất thay đổi như thế 5 nào?
c) Trình bày cách chỉnh sửa thuật toán để xử lý ràng buộc “phải đi qua một đỉnh cho trước”.
Bài 15. Cho đồ thị 𝐺 gồm 6 đỉnh được sắp thành hình chữ nhật 2 × 3, các đỉnh kề nhau
theo cạnh ngang hoặc dọc đều được nối bằng cạnh.
a) Thực hiện BFS và DFS bắt đầu từ đỉnh 1 (đánh số các đỉnh theo hàng từ trái sang phải,
từ trên xuống dưới) để tìm hai cây bao trùm khác nhau của 𝐺.
b) Chỉ ra hai cây bao trùm không thể thu được bằng BFS hay DFS (bắt đầu từ đỉnh 1).
c) Chứng minh rằng mọi cây bao trùm của 𝐺 đều có đúng 5 cạnh.
Bài 16. Cho đồ thị 𝐺 gồm 5 đỉnh {1,2,3,4,5} tạo thành một chu trình, đồng thời có thêm cạnh nối 1 với 3.
a) Dùng BFS và DFS bắt đầu từ đỉnh 1 để xác định hai cây bao trùm khác nhau.
b) Liệt kê tất cả các cây bao trùm khác nhau của đồ thị 𝐺.
c) Chứng minh rằng số cây bao trùm của 𝐺 lớn hơn số cây bao trùm của chu trình 5 đỉnh.
Bài 17. Cho đồ thị 𝐺 gồm 7 đỉnh với cấu trúc như sau: đỉnh 1 nối với 2, 3; đỉnh 2 nối với 4, 5; đỉnh 3 nối với 6, 7.
a) Thực hiện BFS và DFS bắt đầu từ đỉnh 1. Vẽ hai cây bao trùm tương ứng.
b) So sánh chiều cao của cây BFS và cây DFS thu được.
c) Chứng minh rằng cây BFS luôn có chiều cao nhỏ hơn hoặc bằng cây DFS (bắt đầu từ cùng một đỉnh).
Bài 18. Cho đồ thị 𝐺 gồm 4 đỉnh {1, 2, 3, 4} với các cạnh:
{(1,2), (2,3), (3,4), (4,1), (1,3)}.
a) Dùng BFS và DFS bắt đầu từ đỉnh 1 để tìm hai cây bao trùm khác nhau.
b) Liệt kê tất cả các cây bao trùm khác nhau của đồ thị 𝐺.
c) Giải thích vì sao mỗi cây bao trùm phải chứa đúng 3 cạnh.
Bài 19. Cho số nguyên 𝑛 ≥ 2. Gọi 𝑇 là cây đầy đủ bậc 3 (full ternary tree) có chiều cao 𝑛 𝑛, trong đó: • gốc có bậc 3,
• mọi đỉnh trong (không phải lá) đều có đúng 3 con,
• mọi lá đều ở mức 𝑛.
a) Chứng minh rằng số lá của 𝑇 bằng 𝑛 3𝑛.
b) Chứng minh rằng số đỉnh trong của 𝑇 bằng 3𝑛−1. 𝑛 2
c) Suy ra công thức tổng số đỉnh của 𝑇 . 𝑛
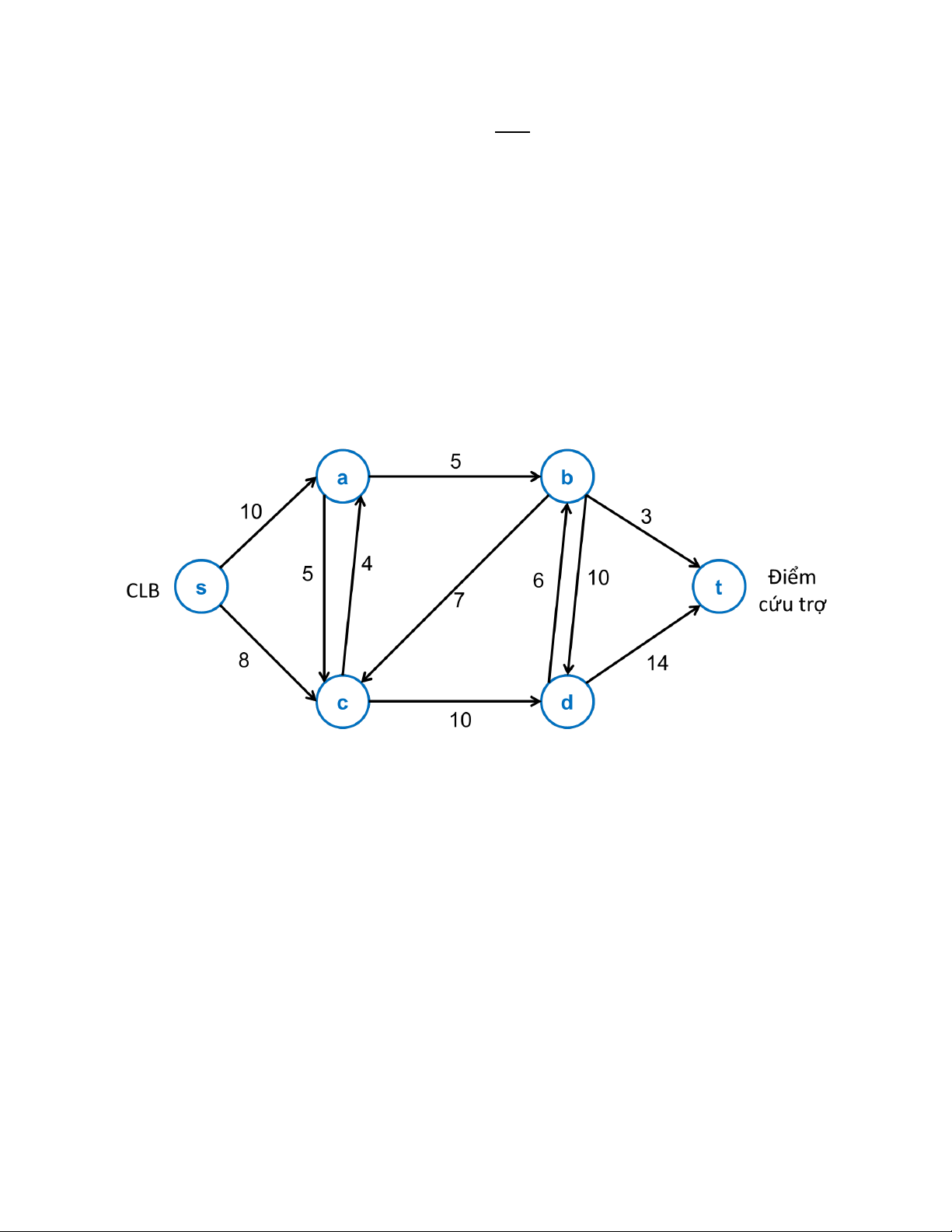
Bài 20. Cũng trong mùa mưa bão, ngoài việc quyên góp tiền, CLB cũng tổ chức vận chuyển
hàng cứu trợ tới điểm cứu trợ cần thiết. Giả sử các điểm mà hàng vận chuyển sẽ có thể đi
qua được (s, a, b, c, d, t) minh họa qua hình bên dưới. Trong đó trọng số trên các cạnh đại
diện cho lượng hàng hóa tối đa có thể vận chuyển qua đường đi đó. Tính lượng hàng hóa
tối đa có thể vận chuyển từ điểm bắt đầu là CLB (đỉnh s) đến điểm cứu trợ (đỉnh t). (Sinh
viên ghi cụ thể mỗi đường tăng luồng để đạt được kết quả cuối cùng).