Bài tập ôn tập - Hàng không dân dụng | Học viện Hàng Không Việt Nam
Bài tập ôn tập - Hàng không dân dụng | Học viện Hàng Không Việt Nam được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Hàng không dân dụng 181 tài liệu
Trường: Học viện Hàng Không Việt Nam 556 tài liệu
Tác giả:
Preview text:
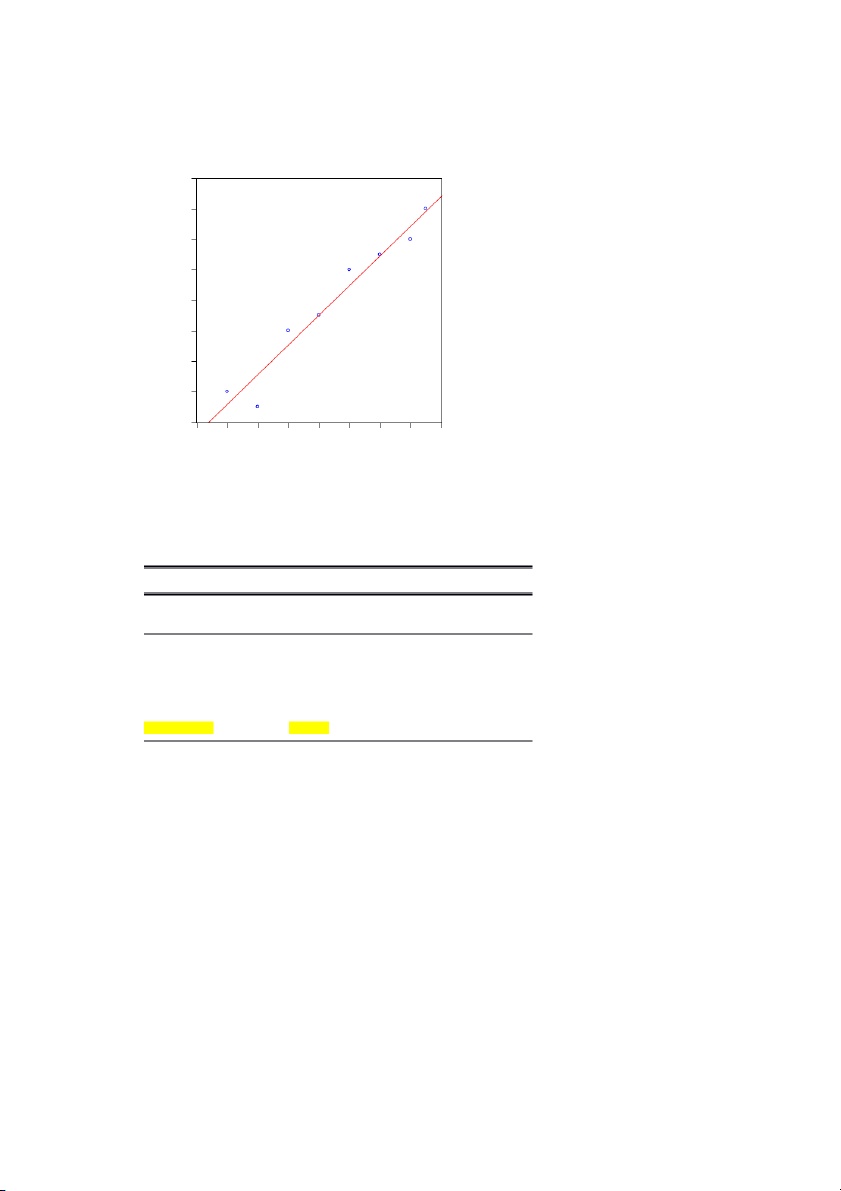
Vẽ đồ thị 140 130 120 110 Y 100 90 80 70 60 60 80 100 120 140 160 180 200 220 X Dependent Variable: Y Method: Least Squares Date: 02/23/23 Time: 14:43 Sample: 1 8 Included observations: 8 Variable Coefficient Std. Error t-Statistic Prob. C 26.92090 7.149846 3.765243 0.0093 X 0.487086 0.046092 10.56768 0.0000 R-squared 0.949012 Mean dependent var 99.37500 Adjusted R-squared 0.940515 S.D. dependent var 23.51861 S.E. of regression 5.736103 Akaike info criterion 6.543755 Sum squared resid 197.4173 Schwarz criterion 6.563616 Log likelihood -24.17502 Hannan-Quinn criter. 6.409805 F-statistic 111.6759 Durbin-Watson stat 2.895100 Prob(F-statistic) 0.000042
b. viết hàm hồi quy Yi = 26,921 + 0,487Xi
Ý nghĩa: trong điều kiện các yếu tố khác không đổi
Beta1 = 26,920: khi không có thu nhập thì chi tiêu tối thiểu là 26,921USD/ tuần
Beta2 = 0,487: khi thu nhập tăng 1USD/ tuần thì chi tiêu sẽ tăng 0,487USD/ tuần
c. tìm hệ số xác định và kiểm định sự phù hợp của hàm hồi quy với mức ý nghĩa 5% R^2 = 0,949 Giả thiết H0: R^2 = 0 Đối thiết H1: R^2 > 0
Cách 1: với mức ý nghĩa 5% => F(0,05; 1; 6) = 5,987
Vì F0 = 111,676 > 5,987 nên ta bác bỏ H0, chứng tỏ hàm hồi quy phù hợp với mức ý
nghĩa 5%. Cụ thể hơn với R^2 = 0,949, hàm hồi quy có mức độ phù hợp cao, biếm thu
nhập giải thích được 94,9% sự thay đổi của chi tiêu
Cách 2: vì probF = 0.000042 < 0,05 nên ta bác bỏ H0, chứng tỏ hàm hồi quy phù hợp với
mức ý nghĩa 5%. Cụ thể hơn với R^2 = 0,949, hàm hồi quy có mức độ phù hợp cao, biếm
thu nhập giải thích được 94,9% sự thay đổi của chi tiêu
d. với mức ý nghĩa 5%, khi thu nhập tăng thêm 1USD/ tuần thì chi tiêu thay đổi như thế nào
Coefficient Confidence Intervals Date: 02/23/23 Time: 14:59 Sample: 1 8 Included observations: 8 95% CI Variable Coefficient Low High C 26.92090 9.425862 44.41595 X 0.487086 0.374303 0.599870
với mức ý nghĩa 5%. Khi thu nhập tăng thêm 1USD/ tuần thì chi tiêu từ tăng thêm
0,374USD/ tuần đến 0,5999USD/ tuần
e. có ý kiến cho rằng, khi thu nhập giảm bớt 1USD/ tuần thì chi tiêu giảm bớt
0,5USD/ tuần với mức ý nghĩa 5%, hãy cho biết ý kiến trên là đúng hay sai Wald Test: Equation: Untitled Test Statistic Value df Probability t-statistic -0.280170 6 0.7888 F-statistic 0.078496 (1, 6) 0.7888 Chi-square 0.078496 1 0.7793 Null Hypothesis: C(2)=0.5 Null Hypothesis Summary: Normalized Restriction (= 0) Value Std. Err. -0.5 + C(2) -0.012914 0.046092
Restrictions are linear in coefficients. cách 1: giả thiết H0: beta2 = 0,5
đối thiết H1: beta2 khác 0,5
với mức ý nghĩa 5% => t(0,025; 6) = 2,447
vì t = -0.280170 thuộc (-2,447; 2,447) thì không đủ cơ sở bác bỏ H0. Chứng tỏ ý kiến
trên là đúng với mức ý nghĩa 5% cách 2:
vì probT = 0,7888 > 0,05 thì không đủ cơ sở bác bỏ H0. Chứng tỏ ý kiến trên là đúng với mức ý nghĩa 5%