Bài tập ôn tập môn Đại số tuyến tính | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Mục lục I
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH . . . . . . . . . . . . . . . . . . . 1 II
MA TRẬN – ĐỊNH THỨC . . . . . . . . . . . . . . . . . . . . . . . . . 2 III KHÔNG GIAN VECTOR
. . . . . . . . . . . . . . . . . . . . . . . . . 2 IV
ÁNH XẠ TUYẾN TÍNH . . . . . . . . . . . . . . . . . . . . . . . . . . 2 V
KHÔNG GIAN TÍCH TRONG . . . . . . . . . . . . . . . . . . . . . . . 3 VI
CHÉO HÓA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
VII DẠNG TOÀN PHƯƠNG . . . . . . . . . . . . . . . . . . . . . . . . . . 4 I
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Bài 1.1 (Hệ Phương Trình Tuyến Tính) Cho hệ phương trình thuần nhất với hai tham
số k, m, các ẩn x1, x2, x3, x4: −x1 + x2 + x3 − x4 = 0,  2x1 + mx2 + 3x4 = 0, 5x1 − x2 + kx3 + 6x4 = 0. (a1) Giải khi k = 1, m = 2.
(b) Biện luận theo k, m số chiều của không gian nghiệm của hệ phương trình trên.
(a2) Sử dụng Gauss-Jordan để giải hệ khi k = 2, m = 1.
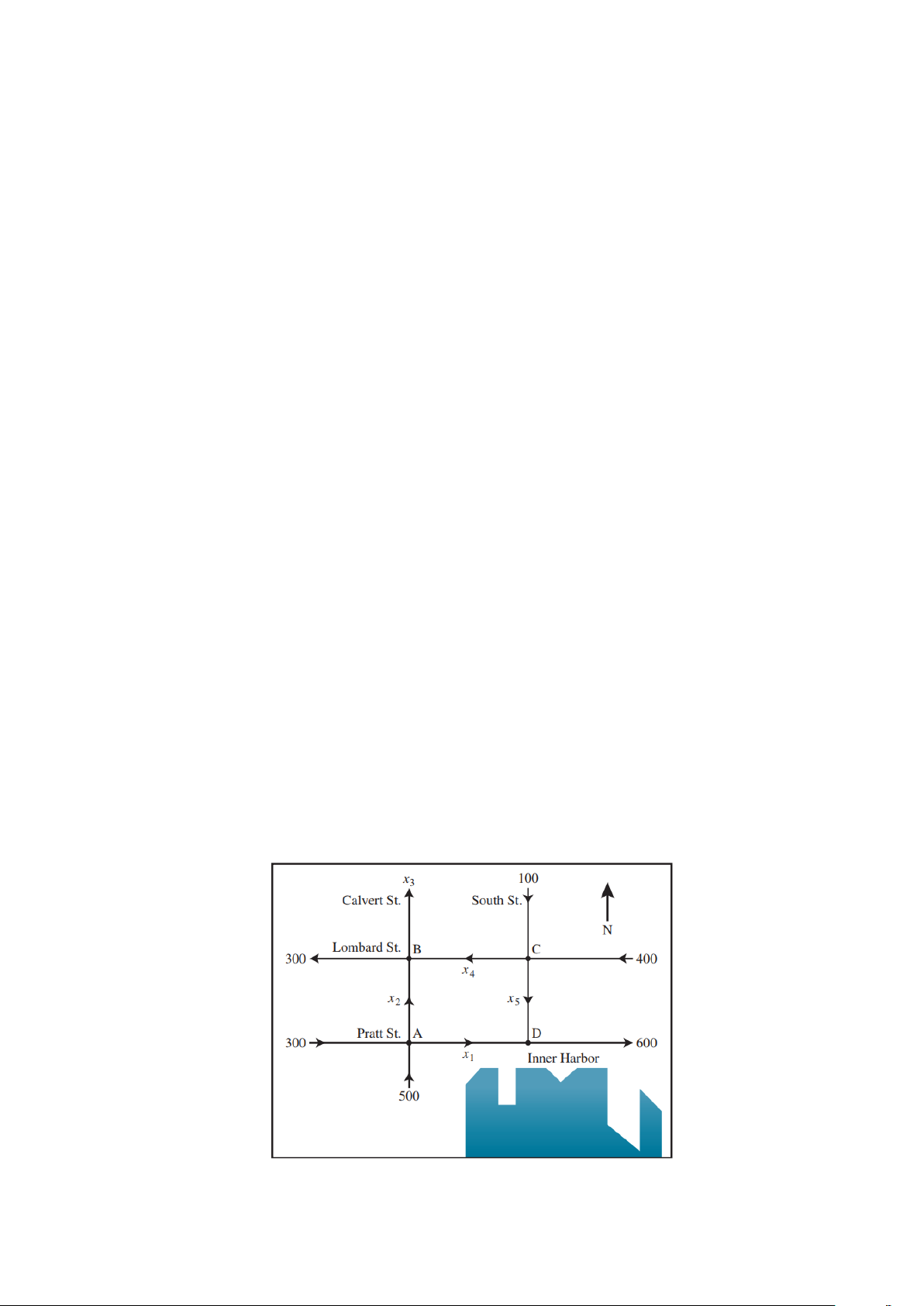
Bài 1.2 (Ứng Dụng Của Hệ Phương Trình Tuyến Tính) 1 II MA TRẬN – ĐỊNH THỨC
Bài 2.1 (Ma Trận – Định Thức) Với mỗi số thực a cho ma trận  a −1 2 3 −1 a 3 2 A =    2 3 a 1 3 2 1 a
(a) Chứng minh rằng với a = 10 thì ma trận A khả nghịch.
(b) Tìm a để ma trận A có hạng nhỏ nhất.
Bài 2.2 (Ma Trận – Định Thức) Cho Mm×n là tập các ma trận cỡ m × n.
(a) Với M ∈ M5×5, A ∈ M2×2, B ∈ M3×2, C ∈ M3×3 và 0 là ma trận 0 cỡ 2 × 3 thỏa A 0 M = B C .
Chứng minh rằng M khả nghịch khi và chỉ khi A, C khả nghịch. Tìm M −1. (b) Cho ma trận  m 1 0 0 0 −1 0 0 0 0   M =  1 −1 2 1 1    2 3 2 n 1 0 1 1 1 1
Tìm m, n để M khả nghịch. Áp dụng câu a để tìm M −1. III KHÔNG GIAN VECTOR
Bài 3.1 (Không Gian Véc Tơ) Trong không gian vectơ 4 R , cho
U = span{α1 = (1, 1, 0, 0), α2 = (1, 2, 1, 0), α3 = (1, 1, 1, 1)} và
V = {(x1, x2, x3, x4) | x1 + x2 + x3 = 0}.
(a) Tìm một cơ sở và số chiều của V .
(b) Tìm một cơ sở và số chiều của U ∩ V, U + V . (c) Tìm W sao cho 4 R = V ⊕ W. IV ÁNH XẠ TUYẾN TÍNH
Bài 3.1 (Ánh xạ tuyến tính) Ký hiệu P2 là tập các đa thức một biến x với hệ số thực,
có bậc nhỏ hơn hoặc bằng 2. Xét ánh xạ T : P 3 2 → R , xác định bởi T (p(x)) := (p(0), p(1), p(2))
với mọi đa thức p(x) = ax2 + bx + c ∈ P2. 2
(a) Chứng minh rằng T là một ánh xạ tuyến tính.
(b) Tìm ma trận của ánh xạ tuyến tính nói trên đối với cơ sở chính tắc B := {1, x, x2} của P 3
2 và cơ sở chính tắc của R .
(c) Tìm một cơ sở và số chiều của Ker(T ), một cơ sở và số chiều của Im(T ).
(d) T có là một đơn cấu, toàn cấu hay không? Vì sao?
Bài 3.2 (Ánh xạ tuyến tính) Cho P2 là không gian các đa thức theo biến x, với bậc nhỏ
hơn hay bằng 2. Xét ánh xạ tuyến tính T : P2 → R cho bởi Z 1 T (f ) = f (x) dx, với mọi f (x) ∈ P2. −1
(a) Tìm ma trận của T trong cặp cơ sở {1 + x, x + x2, x2 + 1} của P2 và {2} của R.
(b) Tìm một cơ sở và số chiều của KerT.
Bài 3.3 (Ánh xạ tuyến tính) Cho ánh xạ tuyến tính T : 3 3
R → R được xác định bởi
T (x, y, z) = (x + y + z + mxy, x − y + z + n, x + y − z).
(a) Tìm tất cả các giá trị của m, n để T là một ánh xạ tuyến tính.
(b) Tìm ma trận biểu diễn của T trong cơ sở
B = {(2, 1, 0), (1, 2, 0), (0, 0, 1)}. (c) Tìm [T (1, 2, 3)]B.
Bài 3.3 (Đổi tọa độ) Cho B′ = {(−1, 1, 1), (−1, −1, 1), (1, −1, 1)},
B = {(1, 0, 0), (0, 1, 0), (0, 0, 1)} là các cơ sở của 3 R và cho " 3 −2 −1# A = −1 4 1 1 2 5
là ma trận của ánh xạ tuyến tính T : 3 3 R → R trong cơ sở B.
(a) Tìm ma trận chuyển cơ sở P từ B′ sang B. 1 ! (b) Dùng A và P tìm [v] −
B và [T (v)]B , biết [v]B′ = 1 . 2
(c) Tìm P −1 và ma trận A′ của T trong cơ sở B′.
(d) Tìm [T (v)]B′ theo hai cách: A′[v]B′ và P −1[T (v)]B. V KHÔNG GIAN TÍCH TRONG
Bài 4.1 (Tích Trong) Xét không gian vectơ P3 gồm tất cả các đa thức hệ số thực, với
một biến x, có bậc nhỏ hơn hoặc bằng 3, cùng với tích trong (tích vô hướng) được xác định như sau:
⟨p, q⟩ = a0b0 + a1b1 + a2b2 + ka3b3, (1) 3
với k là tham số và mọi đa thức
p = p(x) = a0 + a1x + a2x2 + a3x3,
q = q(x) = b0 + b1x + b2x2 + b3x3.
Xét đa thức r = r(x) = 1 + 2x2 + x3, và tập S = { p1(x) = 1 + x, p2(x) = x + x3 }.
(a) Tìm tất cả các giá trị của k để (1) là một tích vô hướng. Trong trường hợp k = 1, thì
(b) Tìm một cơ sở trực chuẩn của không gian vectơ sinh bởi tập S.
(c) Tìm hình chiếu vuông góc của r lên không gian vectơ sinh bởi tập S.
(d) Tìm một cơ sở trực giao của phần bù trực giao của không gian vectơ sinh bởi tập S.
Bài 4.2 (Bài Toán Bình Phương Tối Thiểu) Cho {(−2, 1), (−1, 0), (0, 2), (1, 3), (2, 3)}
là các cặp biến - giá trị (xi, yi), i = 0, · · · , 4 của hàm số y = f (x). Tìm đa thức xấp
xỉ bình phương tối thiểu của f có dạng P (x) = a0 + a1x + a2x2 theo các bước sau
(a) Viết lại tổng bình phương sai số tại các mốc xi, i = 0, · · · , 4 dưới dạng
∥b − Ax∥2 , với A, b, x là các ma trận thích hợp.
(b1) Dùng phương trình chuẩn tắc để tìm một nghiệm bình phương tối thiểu.
(b2) Sử dụng phương pháp phân tích QR để tìm nghiệm bình phương tối thiểu. VI CHÉO HÓA
Bài 5.1 (Chéo hóa – Chéo hóa gtr phức) Cho ma trận "1 a −1# A = 3 5 −1 3 3 1
(a1) Tìm a để A có ba giá trị riêng phân biệt.
(a2) Tìm điều kiện của a để A chéo hóa được.
(b1) Với a = 1, tìm ma trận khả nghịch P để P −1AP có dạng đường chéo, và tính An.
(b2) Với a = 0, chéo hóa gtr phức ma trận A và tính An.
Bài 5.2 (Chéo hóa trực giao) Cho ma trận "3 a 1# A = a 4 a . 1 a 3
(a) Với a = 0, tìm một ma trận trực giao P sao cho P T AP là một ma trận đường
chéo. Viết ma trận đường chéo nhận được.
(b) Tìm công thức tính Ak, với k là một số nguyên dương. 4 VII DẠNG TOÀN PHƯƠNG
Bài 6.1 (Dạng Toàn Phương) Cho dạng toàn phương H = x2 + my2 + z2 + 2m2xz.
(a) Tìm điều kiện của m để H là dạng toàn phương xác định dương.
(b) Với m = 1, tìm phép biến đổi tọa độ để đưa dạng toàn phương trên về dạng
chính tắc và viết dạng chính tắc thu được.
Bài 6.2 (Phân Tích SVD) Tìm phân tích SVD của các ma trận sau " # 1 −1 4 11 14 A = −2 2 8 7 −2 B = 2 −2 5
Document Outline

• HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
• MA TRẬN – ĐỊNH THỨC
• KHÔNG GIAN VECTOR
• ÁNH XẠ TUYẾN TÍNH
• KHÔNG GIAN TÍCH TRONG
• CHÉO HÓA
• DẠNG TOÀN PHƯƠNG