




Preview text:
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
PHIẾU BÀI TẬP PHƯƠNG TRÌNH MẶT PHẲNG (NGÀY 6/1)
DẠNG 1: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG KHI BIẾT MỘT ĐIỂM VÀ VECTƠ PHÁP TUYẾN CỦA NÓ. Phương pháp
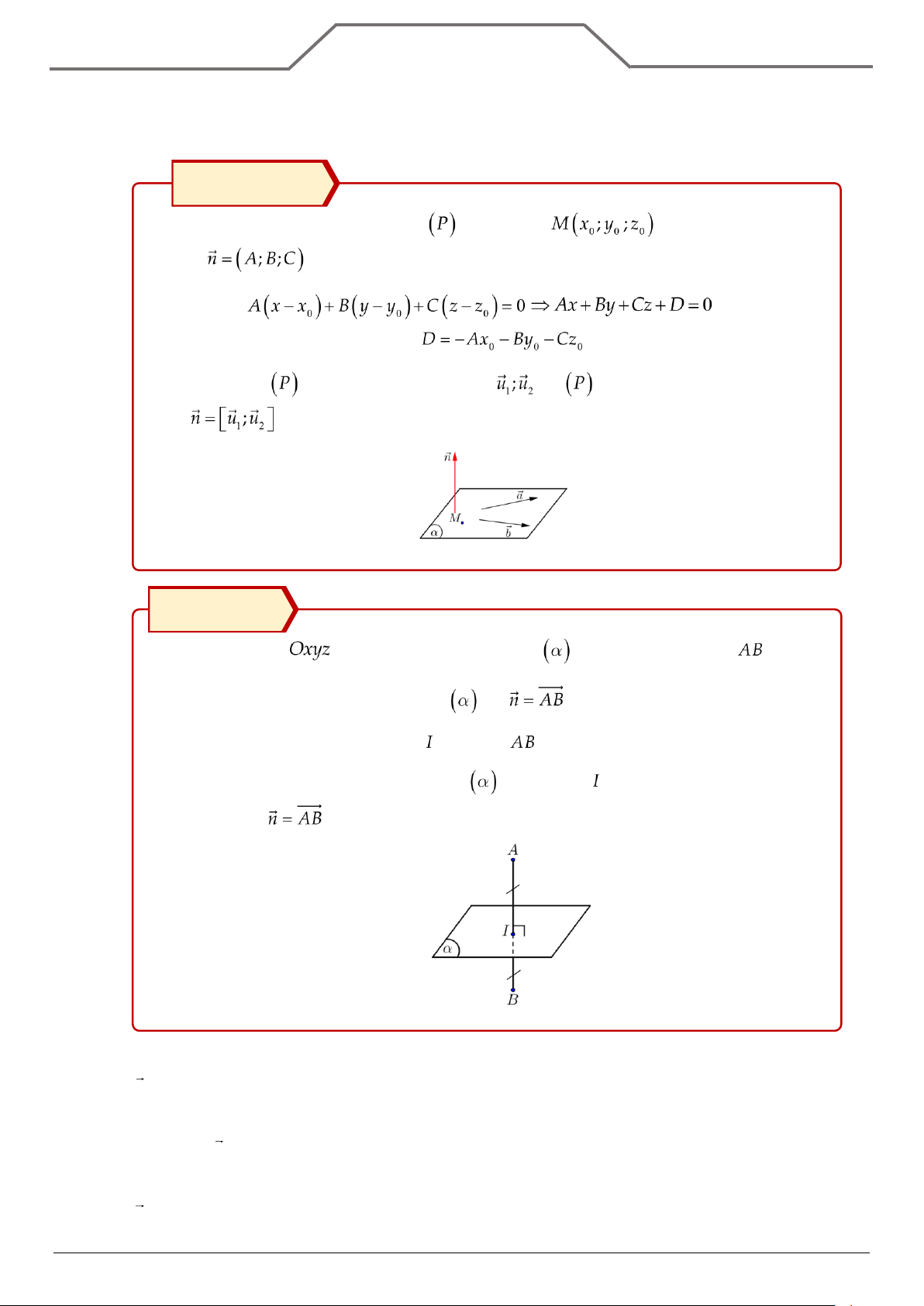
Phương trình tổng quát của mặt phẳng đi qua điểm
và có véctơ pháp tuyến là có dạng: (với ). Nếu mặt phẳng
có cặp véctơ chỉ phương là thì
có véctơ pháp tuyến là Phương pháp Trong không gian
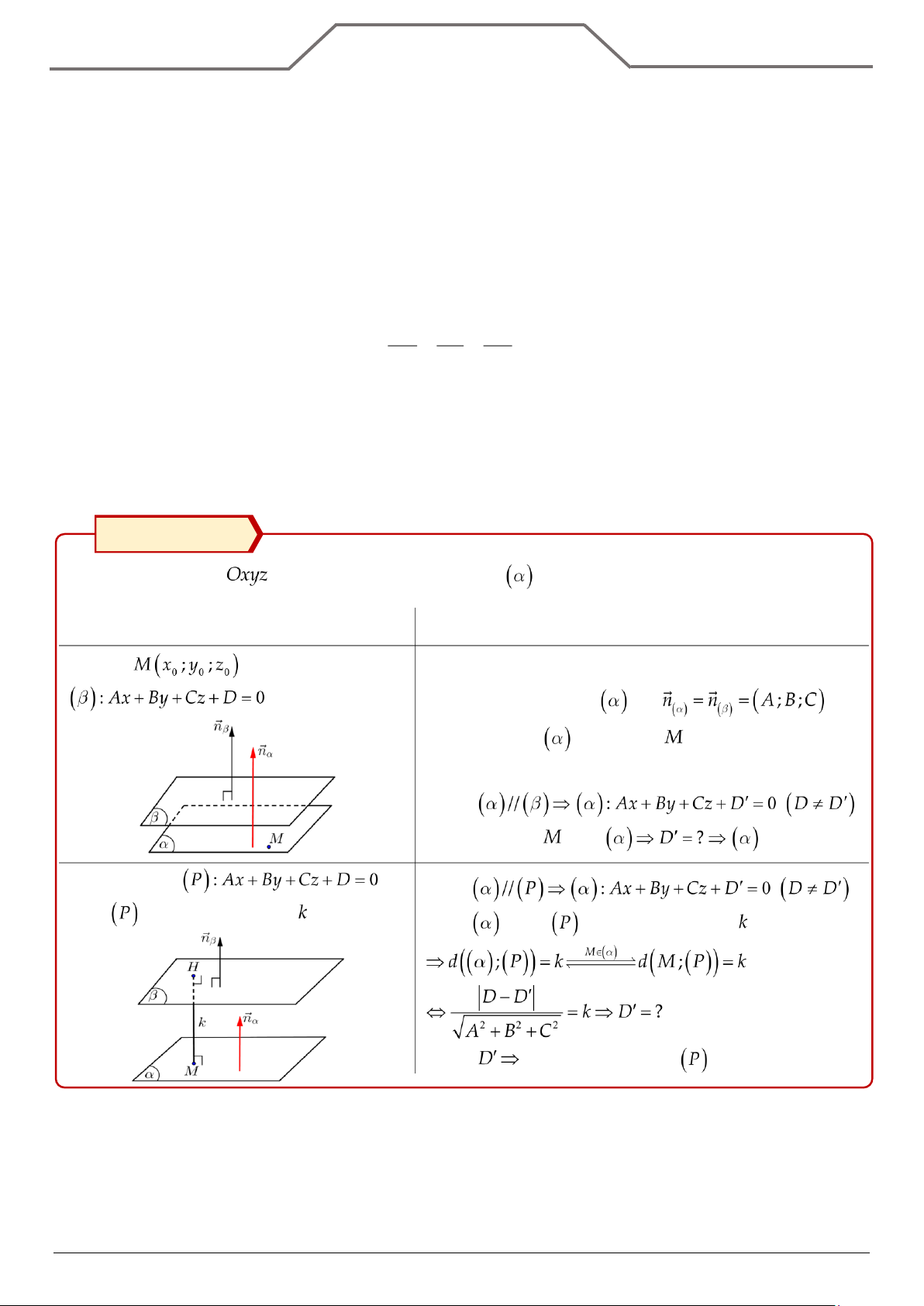
, viết phương trình mặt phẳng
trung trực đoạn thẳng
Bước 1: Véctơ pháp tuyến của mặt là: .
Bước 2: Tìm tọa độ trung điểm của đoạn .
Bước 3: Viết phương trình mặt phẳng
đi qua điểm và có vectơ pháp tuyến . Câu 1:
Trong không gian Oxyz , viết phương trình mặt phẳng (P) đi qua điểm ( A 1; 0; 2
− ) và có vectơ pháp tuyến (1 n ; −1; 2) . Câu 2:
Trong không gian với hệ trục tọa độ Oxyz , viết phương trình mặt phẳng đi qua điểm A(0;1; 2) và có vectơ pháp tuyến n = ( 2 − ;1;0). Câu 3:
Trong không gian Oxyz , viết phương trình mặt phẳng đi qua A( 1 − ;1; )
1 và có vectơ pháp tuyến n = ( 1 − ; 2 − ;2)
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 1
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014 Câu 4:
Trong không gian với hệ trục tọa độ Oxyz , cho các điểm A(0;1; 2) , B (2; − 2; ) 1 , C (−2;0; ) 1 . Phương
trình mặt phẳng đi qua A và vuông góc với BC là? Câu 5:
Trong không gian Oxyz , cho ba điểm A( 1 − ;1; )
1 , B (2;1;0) và C (1; 1
− ;2) . Mặt phẳng đi qua A và
vuông góc với đường thẳng BC có phương trình là? Câu 6:
Trong không gian Oxyz , cho A( 1 − ; 1 − ; ) 1 , B (3;1; )
1 . Phương trình mặt phẳng trung trực của đoạn AB là. Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;6; 7 − ) và B(3;2; )
1 . Phương trình mặt phẳng
trung trực đoạn AB là. Câu 8:
Trong không gian Oxyz , viết phương trình mặt phẳng (P) chứa điểm M (1;3; − 2), cắt các tia Ox , Oy OA OB OC
, Oz lần lượt tại A , B , C sao cho = = . 1 2 4 Câu 9:
Trong không gian Oxyz , cho hình hộp ABC . D A B C D
, biết rằng A( 3
− ;0;0) , B(0;2;0) , D(0;0; ) 1
, A(1; 2;3) . Viết phương trình mặt phẳng trung trực của C D .
DẠNG 2: Viết phương trình mặt phẳng ( ) đi qua 1 điểm M x ; y ; z và song song với 1 mặt phẳng 0 ( 0 0 0 )
( ): Ax+ By+Cz+ D = 0cho trước. Phương pháp Trong không gian
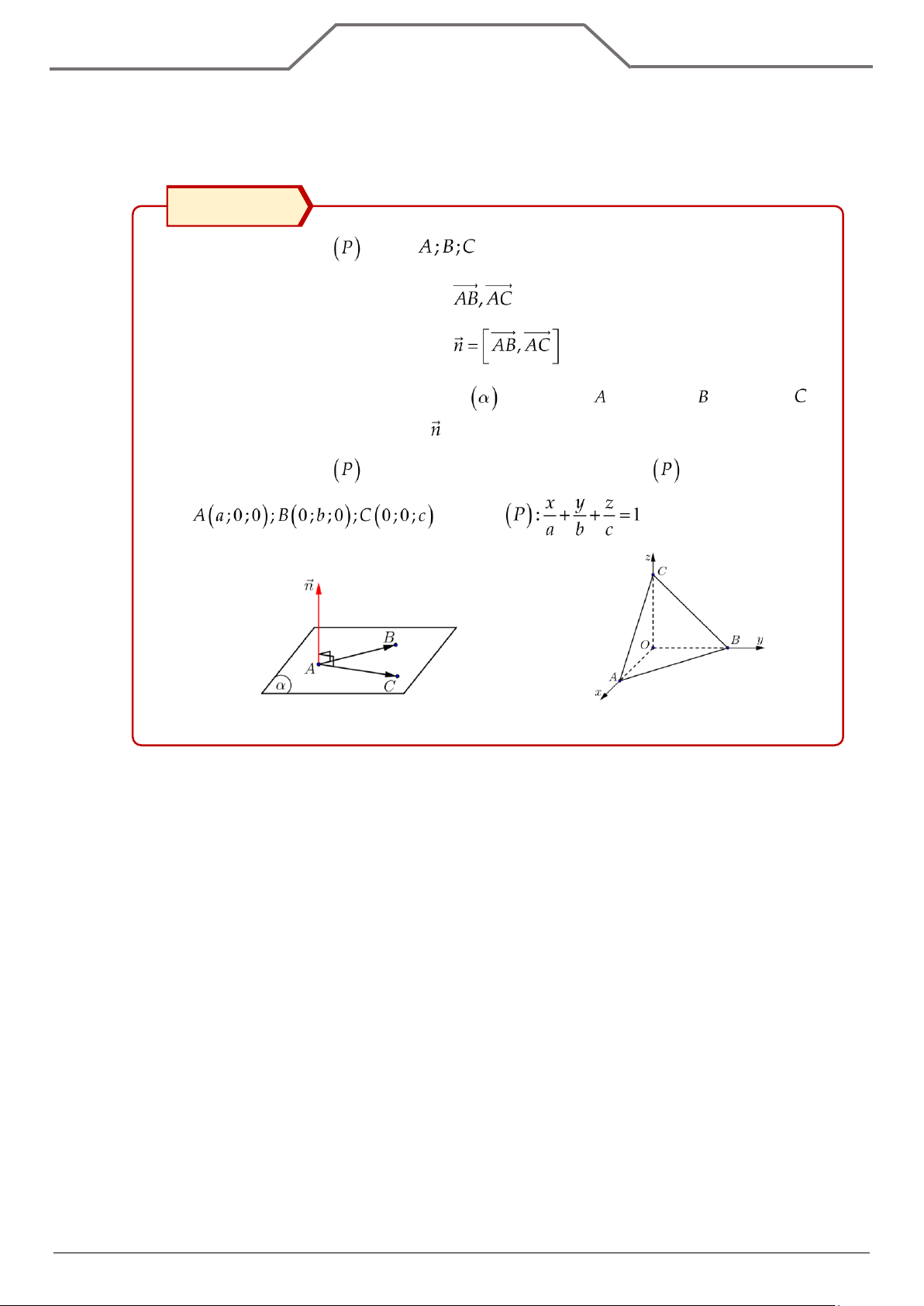
, viết phương trình mặt phẳng Loại Phương pháp ⑴ Qua và song song ⌘ Cách 1: . ≫ Véctơ pháp tuyến là: . ≫ Mặt phẳng qua điểm . ⌘ Cách 2: ≫ Do ≫ Thay điểm vào . ⑵ Song song và ≫ Vì . cách một khoảng bằng . ≫ Vì cách một khoảng bằng ≫ Có phương trình mặt hoàn chỉnh.
Câu 10: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(0;1; 3) và song song với mặt
phẳng (Q) : 2x − 3z + 1 = 0 .
Câu 11: Trong không gian Oxyz , viết phương trình mặt phẳng(P) đi qua điểm M(−2; 3;1) và song song với mặt phẳng ( )
Q : x + 3y − 2z + 2 = 0 .
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 2
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
Câu 12: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi điểm M (3;−1; −2) và song song
với mặt phẳng ( P) : 3x − y + 2z + 4 = 0 .
DẠNG 3: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG ( ) ĐI QUA 3 ĐIỂM A , B , C KHÔNG THẲNG HÀNG. Phương pháp Phương trình mặt phẳng di qua không thẳng hàng.
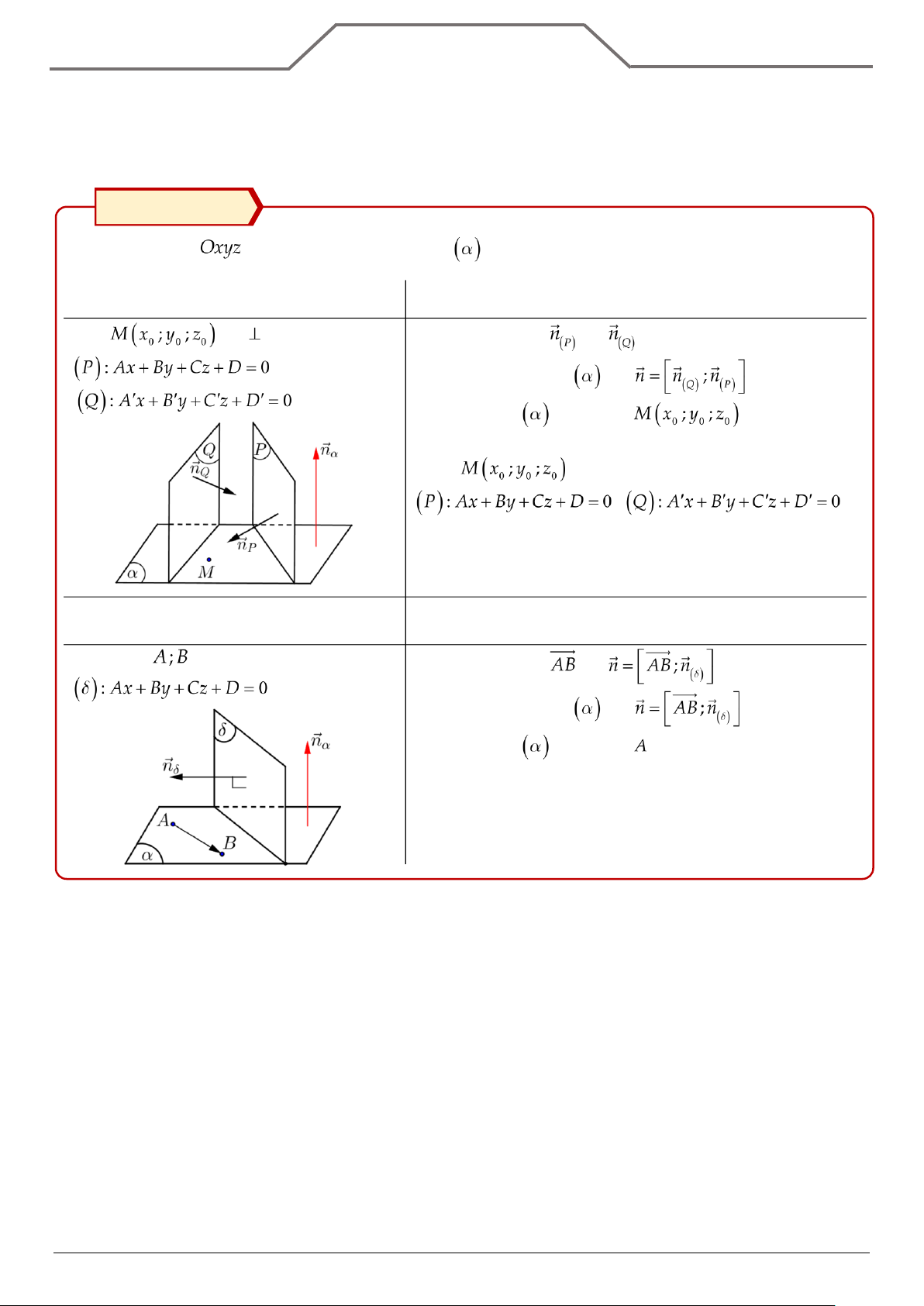
Bước 1: Tìm cặp vectơ chỉ phương .
Bước 2: Tìm một vectơ pháp tuyến .
Bước 3: Viết phương trình mặt phẳng đi qua điểm
(hoặc điểm hoặc điểm )
và có vectơ pháp tuyến . Phương trình mặt phẳng
là phương trình mặt chắn, tức mặt phẳng đi qua có dạng: .
Câu 13: Trong không gian Oxyz , viết phương trình mặt phẳng ( ABC)
a) Với ba điểm A( 1 − ;0;3), B(2; 1 − ; ) 1 , C (1; 1 − ;0) .
b) Với ba điểm A(1;0; 2) ,B( 2 − ;3; ) 1 ,C (3; 2; ) 1 .
Câu 14: Trong không gian Oxyz , viết phương trình mặt phẳng ( ABC)
a) Với ba điểm M (2;0;0) , N (0;−1;0) , P (0;0;2) .
b) Với ba điểm M (0; 2
− ;0), N (3;0;0), P(0;0; 3 − ) .
Câu 15: Trong không gian Oxyz , viết phương trình mặt phẳng đi qua ba điểm ( A 1; 0; 2) − , ( B 1;1;1), C(0; 1 − ; 2)
Câu 16: Trong không gian Oxyz , cho ba điểm A(1;0;0) , B (0; 1 − ;− ) 1 , C (5; 1 − ; )
1 . Viết phương trình mặt phẳng ( ABC).
Câu 17: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm A(2; 3; 5) ,
B (3; 2; 4) và C (4; 1; 2) .
Câu 18: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng đi qua ba điểm A(1;1; 4) , B (2;7;9) , C (0;9;13) .
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 3
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
DẠNG 4: VIẾT PHƯƠNG TRÌNH MẶT PHẲNG ( ) QUA HAI DIỂM A , B VÀ VUÔNG GÓC VỚI MẶT
PHẲNG ( ). VIẾT PHƯƠNG TRÌNH MẶT PHẲNG ( ) QUA DIỂM A VA VUÔNG GÓC VỚI
HAI MẶT PHẲNG ( ) ,( ). Phương pháp Trong không gian
, viết phương trình mặt phẳng Loại Phương pháp Qua và 2 mặt ≫ Tìm cặp véctơ và . , ≫ Véctơ pháp tuyến là: . . ≫ Mặt phẳng qua điểm .
Hoặc bài toán sẽ gặp: “Qua
và vuông góc với giao tuyến của ; ” Loại Phương pháp Qua điểm và vuông góc ≫ Tìm cặp véctơ và . . ≫ Véctơ pháp tuyến là: . ≫ Mặt phẳng qua điểm .
Câu 19: Trong không gian Oxyz , viết phương trình mặt phẳng () đi qua điểm ( A 1; 2; 2 − ), ( B 2; 1 − ; 4) và vuông
góc với ( ) : x − 2y − z +1 = 0.
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(2; 4; ) 1 , B( 1 − ;1;3) và mặt phẳng
(P): x −3y + 2z −5 = 0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng ( P) .
Câu 21: Trong không gian hệ tọa độ Oxyz, cho A(2;1; − ) 1 ; B (1;0; )
1 và mặt phẳng (P) :x + 2y − z +1 = 0. Viết
phương trình mặt phẳng (Q) qua ;
A B và vuông góc với ( P) .
Câu 22: Trong không gian Oxyz , viết phương trình mặt phẳng (P)đi qua điểm M( 1 − ; 2
− ; 5) và vuông góc với hai mặt phẳng ( )
Q : x + 2y − 3z + 1 = 0 và ( )
R : 2x − 3y + z + 1 = 0 .
Câu 23: Trong không gian Oxyz , cho hai mặt phẳng ( ) : 3x − 2y + 2z + 7 = 0 và ( ) : 5x − 4y + 3z +1 = 0.
Phương trình mặt phẳng qua O , đồng thời vuông góc với cả ( ) và ( ) có phương trình là
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 4
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
Câu 24: Cho hai mặt phẳng ( ) : 3x − 2y + 2z + 7 = 0,( ) : 5x − 4 y + 3z +1 = 0 . Phương trình mặt phẳng đi qua
gốc tọa độ O đồng thời vuông góc với cả ( ) và ( ) là:
Câu 25: Trong không gian Oxyz, cho hai mặt phẳng ( P) : x − 3y + 2z −1 = 0, (Q) : x − z + 2 = 0 . Mặt phẳng ( )
vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3. Phương trình của mp () là
Câu 26: Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng ( ) : 3x − 2 y + 2z + 7 = 0 và
( ) :5x − 4y + 3z +1= 0 . Phương trình mặt phẳng đi qua O đồng thời vuông góc với cả () và ( ) có phương trình là
Dạng 6: Viết phương trình mặt phẳng ( ) song song với mặt phẳng ( ) và cách
(): Ax+ By+Cz+ D = 0 một khoảng k cho trước.
Phương pháp :
1. Trên mặt phẳng ( ) chọn 1 điểm . M
2. Do ( ) //( ) nên ( ) có phương trình Ax + By +Cz + D = 0 ( D D ).
3. Sử dụng công thức khoảng cách d( ),( )) = d(M,( )) = k để tìm D.
Câu 27: Trong không gian Oxyz , viết phương trình mặt phẳng (P) song song với mặt phẳng ( )
Q : x + 2y − 2z + 1 = 0 và cách (Q) một khoảng bằng 3.
Câu 28: Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt phẳng ( P) song song và cách mặt phẳng
( ):3x − y + 2z −3 = 0 một khoảng bằng 14 .
Câu 29: Trong không gian Oxyz , cho mặt phẳng P: x 2y 2z 10
0 . Phương trình mặt phẳng Q với 7
Q song song với P và khoảng cách giữa hai mặt phẳng P và Q bằng là. 3
Câu 30: Trong không gian hệ toạ độ Oxyz , lập phương trình các mặt phẳng song song với mặt phẳng
( ): x + y − z +3 = 0 và cách ( ) một khoảng bằng 3 .
Câu 31: Trong không gian Oxyz , viết phương trình mặt phẳng (P) song song với mặt phẳng ( )
Q : x + 2y − 2z + 1 = 0 và (P) cách điểm M(1; 2
− ;1) một khoảng bằng 3.
Câu 32: Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng ( P) song song với mặt phẳng
(Q): x − 2y + 4z −1= 0 và cách điểm M (−1;3; )1 là một khoảng bằng 2.
Câu 33: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (Q) : 2x − y + 2z − 3 = 0 và điểm A(1; 2;3) . Viết
phương trình mặt phẳng ( P) song song với (Q) và cách A một khoảng bằng 4.
DẠNG 7. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 5
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014 Phương pháp
Tính khoảng cách từ điểm đến mặt phẳng như sau Bước 1: Tìm
; viết phương trình mặt phẳng .
Bước 2: Tính khoảng cách từ điểm đến mặt phẳng theo công thức
Câu 34: Cho hình lập phương ABC .
D EFGH cạnh 1. Điểm M được cho thỏa mãn hệ thức AM + AE = 3CD .
Tính khoảng cách từ điểm M đến mặt phẳng (EBD) .
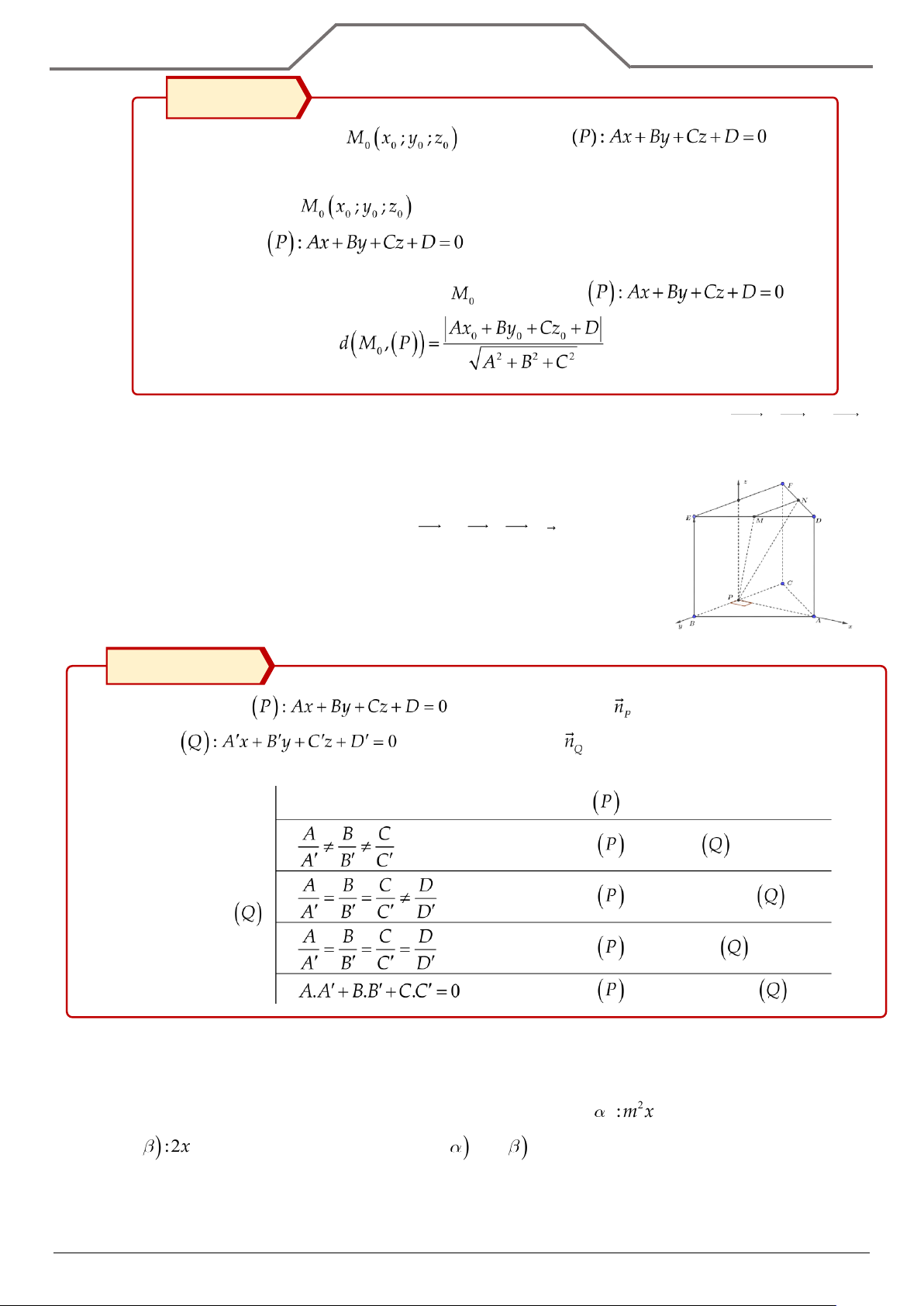
Câu 35: Cho hình lăng trụ tam giác đều AB .
C DEF , AB = 6 , AD = 2 . Gọi M , N
, P lần lượt là trung điểm DE , DF , BC . Lập hệ trục tọa độ Oxyz như
hình bên. Gọi điểm S thỏa mãn hệ thức SA + 2SB + SC = 0 . Tính khoảng
cách từ điểm S đến mặt phẳng (MNP) .
DẠNG 8. VỊ TRÍ TƯƠNG ĐỐI HAI MẶT PHẲNG Phương pháp Xét điểm mặt phẳng có vecto pháp tuyến , với: Mặt phẳng có vecto pháp tuyến ,
Ta có các vị trí tương đối sau: Mặt phẳng Mặt cắt mặt Mặt
song song mặt Mặt phẳng Mặt trùng mặt Mặt
vuông góc mặt
Câu 36: Cho ba mặt phẳng (P : 2x − y − 2z +1 = 0 , (P : 4x − 2y − 4z + 4 = 0 , (P : x + 4y − z +1 = 0 . Chứng 3 ) 2 ) 1 )
minh ( P // P và (P ⊥ P . 1 ) ( 3) 1 ) ( 2 )
Câu 37: Trong không gian
Oxyz , cho hai mặt phẳng ( ) 2 :m x − y + ( 2
m − 2) z + 2 = 0 và () 2
:2x + m y − 2z +1 = 0 . Hai mặt phẳng ( ) và ( ) vuông góc với nhau khi nào?
Câu 38: Trong không gian Oxyz cho A(2;0;0) ,B(0; 4;0) ,C (0;0;6),D(2; 4;6) . Gọi (P) là mặt phẳng song
song với mp(ABC) , (P) cách đều D và mặt phẳng ( ABC) . Phương trình của (P) là?
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 6
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
III HỆ THỐNG BÀI TẬP TRẮC NGHIỆM 4 LỰA CHỌN. == Câu 1:
(MĐ 103-2022) Trong không gian Oxyz , phương trình mặt phẳng (Oxy) là A. z = 0 . B. x = 0 . C. y = 0 .
D. x + y = 0 Câu 2:
Câu 25 (101-2023) Trong không gian Oxyz , mặt phẳng (Oxz) có phương trình là. A. x = 0 . B. z = 0 .
C. x + y + z = 0 . D. y = 0 . Câu 3:
(MĐ 102-2022) Trong không gian Oxyz , phương trình của mặt phẳng (Oyz) là: A. x = 0 .
B. x + y + z = 0 . C. z = 0 . D. y = 0 . Câu 4:
(MĐ 101 2020-2021 – ĐỢT 1) Trong không gian Oxyz , cho mặt phẳng (P) : 3x − y + 2z −1 = 0 . Vectơ
nào dưới đây là một vectơ pháp tuyến của (P) ? A. n = 3 − ;1;2 . B. n = 3;−1;2 . C. n = 3;1;2 . D. n = 3;1;− 2 . ( p) ( ) ( p) ( ) ( p) ( ) ( p) ( ) Câu 5:
(MĐ 102 2020-2021 – ĐỢT 1) Trong không gian Oxyz, cho mặt phẳng ( P) : 2
− x + 5y + z − 3 = 0 . Vectơ
nào dưới đây là một vectơ pháp tuyến của ( P) ? A. n = 2 − ;5;1 . B. n = 2;5;1 . C. n = 2;5; 1 − . D. n = 2; 5 − ;1 . 3 ( ) 4 ( ) 1 ( ) 2 ( ) Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : 3x − z + 2 = 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của ( P) ? A. n = 3;0; 1 − . B. n = 3; 1 − ;2 . C. n = 3; 1 − ;0 .
D. n = −1;0; −1 . 4 ( ) 3 ( ) 1 ( ) 2 ( ) Câu 7:
Trong không gian Oxyz, véctơ nào sau đây là một véctơ pháp tuyến của (P) , biết a = ( 1 − ; 2 − ; 2 − ), b = ( 1 − ;0; − )
1 là cặp véctơ chỉ phương của (P) ?
A. n = (2;1; 2) . B. n = (2; 1 − ; 2 − ) . C. n = (2;1; 2 − ) . D. n = ( 2 − ;1; 2 − ) . Câu 8:
Trong không gian Oxyz , cho ba điểm A(3; 2; ) 1 , B( 1 − ; 4; )
1 ,C (3; − 2;5) . Tọa độ nào sau đây là tọa độ
vectơ pháp tuyến của của mặt phẳng ( ABC) ? A. (1; 2; 2) . B. (8; −16;16). C. ( 1 − ; 2; − 2). D. (1; 4; 4) . Câu 9:
(MĐ 102 2020-2021 – ĐỢT 2) Trong không gian Oxyz , mặt phẳng đi qua O và nhận vectơ n = (2; 1 − ;4)
làm vectơ pháp tuyến có phương trình là
A. 2x + y − 4z +1 = 0 .
B. 2x + y − 4z = 0 .
C. 2x − y + 4z = 0 .
D. 2x − y + 4z +1 = 0 .
Câu 10: (MĐ 103 2020-2021 – ĐỢT 2) Trong không gian Oxyz, mặt phẳng đi qua O và nhận véctơ n = (1;2;− 3)
làm véctơ pháp tuyến có phương trình là
A. x + 2y − 3z +1 = 0 . B. x − 2y + 3z +1 = 0 . C. x − 2y + 3z = 0 .
D. x + 2y − 3z = 0 .
Câu 11: (Mã 104 2017) Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt
phẳng đi qua điểm M (1;2; −3) và có một vectơ pháp tuyến n = (1; 2 − ;3).
A. x − 2y + 3z +12 = 0 . B. x − 2y − 3z − 6 = 0 . C. x − 2y + 3z −12 = 0 . D. x − 2y − 3z + 6 = 0 .
Câu 12: Trong không gian Oxyz , phương trình mặt phẳng ( ) −
đi qua điểm A(2; 1; 3) và có vectơ pháp tuyến n = (2;3; − ) 1 là:
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 7
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
A. ( ) : 2x + 3y − z − 2 = 0 .
B. ( ) : 2x + 3y − z + 2 = 0 .
C. ( ) : 2x − y + 3z − 2 = 0 .
D. ( ) : 2x − y + 3z + 2 = 0 .
Câu 13: (Mã 101 - 2020 Lần 1) Trong không gian Oxyz , cho ba điểm A(3;0;0) , B (0;1;0) và C (0;0; 2 − ) . Mặt
phẳng ( ABC ) có phương trình là: x y z x y z x y z x y z A. + + = 1. B. + + = 1. C. + + = 1. D. + + = 1. 3 1 − 2 3 1 2 − 3 1 2 3 − 1 2
Câu 14: (Mã 102 - 2020 Lần 1) Trong không gian Oxyz , cho ba điểm A( 2
− ;0;0) , B(0;3;0) và C (0;0;4) . Mặt
phẳng ( ABC ) có phương trình là x y z x y z x y z x y z A. + + = 1. B. + + =1. C. + + = 1. D. + + = 1. 2 − 3 4 2 3 4 2 3 − 4 2 3 4 −
Câu 15: (Đề Tham Khảo 2018) Trong không gian Oxyz , cho ba điểm M (2;0;0) , N (0; −1;0) , P (0;0;2) . Mặt
phẳng (MNP) có phương trình là: x y z x y z x y z x y z A. + + = 1 − . B. + + =1. C. + + =1. D. + + = 0 . 2 1 − 2 2 1 2 2 1 − 2 2 1 − 2
Câu 16: Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua 3 điểm M (−2;0;0) , N (0;−1;0) , P (0;0;3) là
A. 3x + 6y − 2z − 6 = 0 . B. 2x + y − 3z −1 = 0 . C. 3x + 6y − 2z = 0 .
D. 3x + 6y − 2z + 6 = 0 .
Câu 17: Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua 3 điểm A(−1;1;3) , B (2; −1;3) , C (2;2;− ) 1 là.
A. 8x +12y + 9z − 31 = 0 .
B. 8x +12y + 9z + 31 = 0 .
C. 8x −12y + 9z − 31 = 0 .
D. 8x +12y − 9z + 31 = 0 .
Câu 18: (MĐ 103 2020-2021 – ĐỢT 1) Trong không gian Oxyz , cho hai điểm A(0;0; )
1 và B (1;2;3) . Mặt phẳng
đi qua A và vuông góc AB có phương trình là
A. x + 2y + 2z −11 = 0 . B. x + 2y + 2z − 2 = 0 . C. x + 2y + 4z − 4 = 0 . D. x + 2y + 4z −17 = 0 .
Câu 19: (MĐ 104 2020-2021 – ĐỢT 1) Trong không gian Oxyz , cho hai điểm A(1;0;0) và B(3;2; ) 1 . Mặt phẳng
đi qua A và vuông góc với AB có phương trình là
A. 2x + 2y + z − 2 = 0 .
B. 4x + 2 y + z −17 = 0 .
C. 4x + 2y + z − 4 = 0 .
D. 2x + 2y + z −11 = 0 .
Câu 20: (Mã 103 2018) Trong không gian Oxyz , cho ba điểm A( 1 − ;1; )
1 , B (2;1;0) C (1; 1 − ;2) . Mặt phẳng đi
qua A và vuông góc với đường thẳng BC có phương trình là
A. 3x + 2z +1 = 0 .
B. x + 2y − 2z +1 = 0 . C. x + 2y − 2z −1 = 0 . D. 3x + 2z −1 = 0 .
Câu 21: (MĐ 102 2020-2021 – ĐỢT 2) Trong không gian Oxyz , cho điểm A(1;2; − ) 1 và mặt phẳng
(P): 2x + y −3z +1= 0 . Mặt phẳng qua A và song song với (P) có phương trình là:
A. 2x + y − 3z − 7 = 0 . B. 2x + y − 3z + 7 = 0 . C. 2x + y − 3z −1 = 0 . D. 2x + y − 3z +1 = 0 .
Câu 22: (MĐ 103 2020-2021 – ĐỢT 2) Trong không gian Oxyz , cho điểm A(1; 1 − ;2) và mặt phẳng
(P): x + 2y −3z +1= 0 . Mặt phẳng đi qua Avà song song với (P) có phương trình là
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 8
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
A. x + 2y + 3z − 5 = 0. B. x + 2y + 3z + 5 = 0 . C. x + 2y − 3z − 7 = 0 . D. x + 2y − 3z + 7 = 0 .
Câu 23: (MĐ 104 BGD&ĐT NĂM 2020-2021 – ĐỢT 2) Trong không gian Oxyz , cho điểm A(1;2;− ) 1 và mặt
phẳng ( P) : x − 2y + 3z +1 = 0 . Mặt phẳng đi qua A và song song với mặt phẳng ( P) có phương trình là:
A. x + 2y + 3z + 2 = 0 . B. x − 2y + 3z − 6 = 0 . C. x − 2y + 3z + 6 = 0 . D. x + 2y + 3z − 2 = 0 .
Câu 24: (Mã 105 2017) Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( ) :x + y + z − 6 = 0 . Điểm nào
dưới đây không thuộc ( ) ?
A. Q (3;3;0) .
B. N (2;2;2) .
C. P (1; 2;3) . D. M (1;−1; ) 1 .
Câu 25: (Mã 123 2017) Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) : x − 2y + z − 5 = 0. Điểm nào
dưới đây thuộc ( P) ? A. P (0;0; 5 − ) .
B. M (1;1;6) . C. Q (2; 1 − ;5) .
D. N (−5;0;0) .
Câu 26: (Mã 104 - 2019) Trong không gian Oxyz, cho hai điểm A(4;0; )
1 và B (−2;2;3).Mặt phẳng trung trực
của đoạn thẳng AB có phương trình là
A. 3x − y − z = 0.
B. 3x + y + z − 6 = 0. C. x + y + 2z − 6 = 0. D. 6x − 2y − 2z −1 = 0.
Câu 27: (Mã 102 - 2019) Trong không gian Oxyz , cho hai điểm A( 1
− ;2;0) và B(3;0;2) . Mặt phẳng trung trực
của đoạn thẳng AB có phương trình là
A. x + y + z − 3 = 0 .
B. 2x − y + z + 2 = 0 . C. 2x + y + z − 4 = 0 . D. 2x − y + z − 2 = 0 .
Câu 28: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) có tâm I (3;2;− )
1 và đi qua điểm A(2;1;2) . Mặt
phẳng nào dưới đây tiếp xúc với (S ) tại A ?
A. x + y + 3z − 9 = 0 .
B. x + y − 3z + 3 = 0 . C. x + y − 3z − 8 = 0 . D. x − y − 3z + 3 = 0 .
Câu 29: Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua hai điểm A(2;−1;0) , B (1;1;2) và vuông
góc với mặt phẳng (Q) : x + y + 2z − 3 = 0 là.
A. 2x + 4y − 3z − 8 = 0 . B. 2x + 4y − 3z = 0 .
C. 2x + 4y − 3z + 8 = 0 . D. 2x − 4y − 3z = 0 .
Câu 30: Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua điểm M (2;1; − 2) và vuông góc với hai mặt
phẳng (Q) : x + y + 2z − 3 = 0 và ( R) : x − y − z + 4 = 0 là.
A. x + 3y − 2z + 9 = 0 . B. 2x + y − 2z − 9 = 0 . C. x + 3y − 2z − 9 = 0 . D. 2x + y − 2z + 9 = 0 .
Câu 31: Trong không gian Oxyz , cho hai điểm A(2;4 ) ;1 , B( 1
− ;1;3) và mặt phẳng (P):x −3y + 2z −5 = 0. Lập
phương trình mặt phẳng (Q) đi qua hai điểm A , B và vuông góc với mặt phẳng (P) .
A. 2y + 3z −11 = 0 .
B. 2x − 3y −11 = 0 .
C. x − 3y + 2z − 5 = 0 . D. 3y + 2z −11 = 0 .
Câu 32: Cho hai mặt phẳng ( )
: 3x − 2y + 2z + 7 = 0,( ) : 5x − 4y + 3z +1 = 0 . Phương trình mặt phẳng đi qua
gốc tọa độ O đồng thời vuông góc với cả ( ) và ( ) là:
A. 2x − y − 2z = 0.
B. 2x + y − 2z = 0.
C. 2x − y + 2z = 0.
D. 2x + y − 2z +1 = 0.
Câu 33: Trong không gian Oxyz , phương trình mặt phẳng ( P) đi qua điểm N (2;1;− 2) , song song với trục Oy
và vuông góc với mặt phẳng (Q) : x − 2y + z − 8 = 0 là
A. x − z − 4 = 0 .
B. x − z + 4 = 0 .
C. 2x + y − 2z − 4 = 0 . D. 2x + y − 2z + 4 = 0 .
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 9
Kỉ luật là sức mạnh! TOÁN HỌC CÔ LY
0979910014 - 0337590014
Câu 34: Trong không gian Oxyz , phương trình của mặt phẳng (P) đi qua điểm B (2;1;− 3) , đồng thời vuông góc
với hai mặt phẳng (Q) : x + y + 3z − 5 = 0 , ( R) : 2x − y + z −1 = 0 là
A. 4x + 5y − 3z + 22 = 0 .
B. 4x − 5y − 3z −12 = 0 .
C. 2x + y − 3z −14 = 0 .
D. 4x + 5y − 3z − 22 = 0 .
Câu 35: Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;−1; )
1 , N (2;1;2) và song song với trục Oz có phương trình là
A. x + 2y + z = 0 .
B. 2x − y − 3 = 0 .
C. x + 2y + z − 6 = 0 . D. 2x − y + 5 = 0 .
Câu 36: Trong không gian Oxyz , cho mặt phẳng ( P) :2x − y + 2z +11 = 0 và hai điểm A(1;0; 2 − ), B( 1; − −1;3)
. Mặt phẳng (Q) đi qua hai điểm ,
A B và vuông góc với mặt phẳng ( P) có phương trình là
A. 3x +14y + 4z + 5 = 0 .
B. 2x − y + 2z − 2 = 0 .
C. 2x − y + 2z + 2 = 0 .
D. 3x +14y + 4z − 5 = 0 .
Câu 37: Trong không gian Oxyz , cho mặt phẳng ( ) : 2x − y + 3 = 0 . Mặt phẳng nào sau đây vuông góc với mặt phẳng ( ) ? A. ( : 2
− x + y − 3z = 0 .
B. ( : x + 5y + z − 2 = 0 . 2 ) 1 )
C. ( : 4x − 2y + 7 = 0 .
D. ( : x + 2y − z +1 = 0 . 4 ) 3 )
Câu 38: Trong không gian Oxyz , cho mặt phẳng ( ) : 2x − y + 3 = 0 . Mặt phẳng nào sau đây song song với mặt phẳng ( ) ? A. ( : 2
− x + y − 3z = 0 .
B. ( : x + 5y + z − 2 = 0 . 2 ) 1 )
C. ( : 4x − 2y + 7 = 0 .
D. ( : x + 2y − z +1 = 0 . 4 ) 3 )
Câu 39: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P) có phương trình: 3x + 4y + 2z + 4 = 0 và điểm A(1; 2
− ;3) . Tính khoảng cách d từ A đến (P) . 5 5 5 5 A. d = . B. d = . C. d = . D. d = . 9 29 29 3
Câu 40: Trong không gian Oxyz , cho mặt phẳng (P) : 2x − y + 2z − 4 = 0 . Khoảng cách từ điểm M (3;1;− 2) đến
mặt phẳng ( P) bằng 1 A. 2 . B. . C. 1. D. 3 . 3
Câu 41: Trong không gian Oxyz , khoảng cách từ M (1; 2; 3
− ) đến (P) : x + 2y + 2z −10 = 0 là 2 4 11 A. 3 . B. . C. . D. . 3 3 3
Câu 42: Trong không gian Oxyz cho hai mặt phẳng song song ( P) và (Q) lần lượt có phương trình
2x − y + z = 0 và 2x − y + z − 7 = 0 . Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 7 A. 7 . B. 7 6 . C. 6 7 . D. . 6
Thà để giọt mồ hôi rơi trên trang sách, còn hơn là để giọt nước mắt rơi trên đề thi Trang 10



