







































































































































































Preview text:
CHỦ ĐỀ 1: TẬP HỢP
A/ KIẾN THỨC CƠ BẢN.
1. Tập hợp là một khái niệm cơ bản thường dùng trong toán học và trong cuộc sống, ta hiểu tập
hợp thông qua các ví dụ.
2. Tập hợp được đặt tên bằng chữ cái in hoa: VD: Tập hợp A, tập hợp B,…
3. Phần tử của tập hợp kí hiệu bằng chữ cái thường: VD: phần tử a, phần tử b,…. 4. Viết tập hợp:
- Liệt kê phần tử của tập hợp: A = {phần tử}
- Chỉ ra tính chất đặc trưng của các tập hợp: A = {x | tính chất đặc trưng}
5. Số phần tử của tập hợp: Một tập hợp có thể có một, có nhiều phần tử, có vô số phần tử,
cũng có thể không có phần tử nào.
6. Phần tử thuộc, không thuộc tập hợp:
- Nếu phần tử x thuộc tập hợp A, kí hiệu x ∈ A.
- Nếu phần tử a không thuộc tập hợp A, kí hiệu a ∉A.
7. Tập hợp rỗng: Là tập hợp không có phần tử nào, tập rỗng kí hiệu là: Ø.
8. Tập hợp con: Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập
hợp con của tập hợp B, kí hiệu là A ⊂ B hay B ⊃ A.
9. Hai tập hợp bằng nhau: Nếu A⊂B và B⊃ A, ta nói hai tập hợp bằng nhau, kí hiệu A = B.
10. Nếu tập hợp A có n phần tử thì số tập hợp con của A là 2n. B/ CÁC DẠNG TOÁN.
Dạng 1: Viết tập hợp, viết tập hợp con, sử dụng kí hiệu
* Với tập hợp ít phần tử thì viết tập hợp theo cách liệt kê phần tử.
* Với tập hợp có rất nhiều phần tử (vô số phần tử) thì viết tập hợp theo cách chỉ ra tính chất đặc
trưng của các phần tử trong tập hợp.
Bài 1: Cho tập hợp A là các chữ cái trong cụm từ “Thành phố Hồ Chí Minh”. (Không phân biệt chữ in
hoa và chữ in thường trong cụm từ đã cho).
a) Hãy liệt kê các phần tử của tập hợp A.
b) Điền kí hiệu thích hợp vào ô vuông b A c A h A
Bài 2: Cho tập hợp các chữ cái X = {A, C, O}
a/ Tìm cụm chữ tạo thành từ các chữ của tập hợp X.
b/ Viết tập hợp X bằng cách chỉ ra các tính chất đặc trưng cho các phần tử của X. Hướng dẫn
a/ Chẳng hạn cụm từ “CA CAO” hoặc “CÓ CÁ”
b/ X = {x: x-chữ cái trong cụm chữ “CA CAO”}
Bài 3: Cho các tập hợp: A = {1; 2; 3; 4; 5; 6;8;10} ; B = {1; 3; 5; 7; 9;11}
a/ Viết tập hợp C các phần tử thuộc A và không thuộc B.
b/ Viết tập hợp D các phần tử thuộc B và không thuộc A.
c/ Viết tập hợp E các phần tử vừa thuộc A vừa thuộc B.
d/ Viết tập hợp F các phần tử hoặc thuộc A hoặc thuộc B.
Bài 4: Cho tập hợp A = {1; 2;3;x; a; b}
a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.
b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.
c/ Tập hợp B = {a, b, c} có phải là tập hợp con của A không?
Bài 5: Cho tập hợp B = {a, b, c}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?
Bài 6: Cho A = {1; 3; a; b} ; B = {3; b} . Điền các kí hiệu , ∈ ,
∉ ⊂ thích hợp vào dấu (….) 1 ......A ; 3 ... A ; 3....... B ; B ...... A
Bài 7: Cho các tập hợp A = {x∈ N /9 < x < } 99 ; B = { *
x ∈ N / x < }
100 . Hãy điền dấu ⊂ hay ⊃ vào các ô dưới đây N .... N* ; A ......... B
Bài 8: Viết tập hợp sau bằng cách liệt kê các phần tử:
a) A = {x ∈ N* | 20 ≤ x < 30} b) B = {x ∈ N* | < 15}
Bài 9. Viết các tập hợp sau đây bằng cách liệt kê các phần tử của chúng :
Tập hợp A các số tự nhiên không lớn hơn 5.
Tập hợp B các số tự nhiên có hai chữ số không nhỏ hơn 90.
Tập hợp C các số chẵn lớn hơn 10 và nhỏ hơn hoặc bằng 20.
Bài 10. Chỉ ra tính chất đặc trưng cho các phần tử của các tập hợp sau đây : A = 10; 2; 4; 6; 8} ; B = (1; 3; 5; 7; 9; 11} ; C = {0; 5; 10; 15; 20; 25} ; D = (1; 4; 7;10; 13;16; 19}.
Bài 11: Viết tập hợp các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3. Các số 13 ; 25 ; 53 có
thuộc tập hợp ấy không ? Bài 12:
a) Một năm gồm bốn quý. Viết tập hợp A các tháng của quý một trong năm.
b) Viết tập hợp B các tháng (dương lịch) có ít hơn 30 ngày.
Dạng 2: Xác định số phần tử của một tập hợp.
* Với các tập hợp ít phần tử thì biểu diễn tập hợp rồi đếm số phần tử.
* Với tập hợp mà có phần tử tuân theo quy luật tăng đều với khoảng cách d thì số phần tử của
tập hợp này là: (Số đầu – Số cuối):d + 1
Bài 1: Gọi A là tập hợp các số tự nhiên có 3 chữ số. Hỏi tập hợp A có bao nhiêu phần tử? Hướng dẫn:
Tập hợp A có (999 – 100) + 1 = 900 phần tử.
Bài 2: Hãy tính số phần tử của các tập hợp sau:
a/ Tập hợp A các số tự nhiên lẻ có 3 chữ số.
b/ Tập hợp B các số 2, 5, 8, 11, …, 296, 299, 302
c/ Tập hợp C các số 7, 11, 15, 19, …, 275 , 279 Hướng dẫn
a/ Tập hợp A có (999 – 101):2 +1 = 450 phần tử.
b/ Tập hợp B có (302 – 2 ): 3 + 1 = 101 phần tử.
c/ Tập hợp C có (279 – 7 ):4 + 1 = 69 phần tử. TỔNG QUÁT:
+ Tập hợp các số chẵn từ số chẵn a đến số chẵn b có (b – a) : 2 + 1 phần tử.
+ Tập hợp các số lẻ từ số lẻ m đến số lẻ n có (n – m) : 2 + 1 phần tử.
+ Tập hợp các số từ số c đến số d là dãy số các đều, khoảng cách giữa hai số liên tiếp của dãy
là 3 có (d – c ): 3 + 1 phần tử.
Bài 3: Gọi A là tập hợp các số tự nhiên có 3 chữ số. Hỏi tập hợp A có bao nhiêu phần tử?
Bài 4: Hãy tính số phần tử của các tập hợp sau:
a/ Tập hợp A các số tự nhiên lẻ có 3 chữ số.
b/ Tập hợp B các số 2, 5, 8, 11, …, 296, 299, 302
c/ Tập hợp C các số 7, 11, 15, 19, …, 275 , 279
Bài 5: Cho biết mỗ tập hợp sau có bao nhiêu phần tử
a) Tập hợp A các số tự nhiên x sao cho x – 30 = 60
b) Tập hợp B các số tự nhiên y sao cho y . 0 = 0
c) Tập hợp C các số tự nhiên a sao cho 2.a < 20
d) Tập hợp D các số tự nhiên d sao cho (d – 5)2 ≠ 0
e) Tập hợp G các số tự nhiên z sao cho 2.z + 7 > 100
Bài 6: Dùng 4 chữ số 1, 2, 3, 4 để viết tất cả các số tự nhiên có bốn chữ số khác nhau. Hỏi tập này có bao nhiêu phần tử.
Bài 7: Cho hai tập hợp M = {0,2,4,…..,96,98,100;102;104;106};
Q = { x ∈ N* | x là số chẵn ,x<106};
a) Mỗi tập hợp có bao nhiêu phần tử?
b) Dùng kí hiệu ⊂ để thực hiên mối quan hệ giữa M và Q.
Bài 8. Cho hai tập hợp R={a ∈ N | 75 ≤ a ≤ 85}; S={b ∈ N | 75 ≤b ≤ 91};
a) Viết các tập hợp trên;
b) Mỗi tập hợp có bao nhiêu phần tử;
c) Dùng kí hiệu ⊂ để thực hiên mối quan hệ giữa hai tập hợp đó.
Bài 9. Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử:
a) Tập hợp A các số tự nhiên x mà 17 – x = 5 .
b) Tập hợp B các số tự nhiên y mà 15 – y = 18.
c) Tập hợp C các số tự nhiên z mà 13 : z > 6.
d) Tập hợp D các số tự nhiên x , x ∈ N* mà 2.x + 1 < 100. Dạng 3: Tập hợp con.
* Muốn chứng minh tập B là con của tập A, ta cần chỉ ra mỗi phần tử của B đều thuộc A.
* Để viết tập con của A, ta cần viết tập A dưới dạng liệt kê phần tử. Khi đó mỗi tập B gồm một
số phần tử của A sẽ là tập con của A. * Lưu ý:
- Nếu tập hợp A có n phần tử thì số tập hợp con của A là 2n
- Số phần tử của tập con của A không vượt quá số phần tử của A.
- Tập rỗng là tập con của mọi tập hợp.
Bài 1: Trong ba tập hợp con sau đây, tập hợp nào là tập hợp con của tập hợp còn lại. Dùng kí hiệu ⊂
để thể hiện quan hệ mỗi tập hợp trên với tập N.
A là tập hợp các số tự nhiên nhỏ hơn 20
B là tập hợp các số lẻ
C là tập hợp các số tự nhiên khác 20.
Bài 2: Trong các tập hợp sau, Tập hợp nào là tập con của tập còn lại?
a) A = {m ; n} và B = {m ; n ; p ; q}
b) C là tập hợp các số tự nhiên có ba chữ số giống nhau và D là tập hợp các số tự nhiên chia hết cho 3.
c) E = {a ∈N| 5 < a < 10} và F = {6 ; 7 ;8 ; 9}
Bài 3: Cho tập A = {1 ; 2; 3}
a) Tìm các tập hợp con của tập A.
b) Viết tập hợp B gồm các phần tử là các tập con của A
c) Khẳng định tập A là tập con của B đúng không?
Bài 4: Cho tập A = {nho, mận, hồng, cam, bưởi}
Hãy viết tất cả các tập hợp con của A sao cho mỗi tập hợp đó có: a) Một phần tử. b) Hai phần tử. c) Ba phần tử.
Dạng 3. Minh họa một tập hợp cho trước bằng hình vẽ
* Sử dụng biểu đồ Ven. Đó là một đường cong khép kín, không tự cắt, mỗi phần tử của tập hợp
được biểu diễn bởi một điểm ở bên trong đường cong đó.
VÍ DỤ. Gọi A là tập hợp các số tự nhiên chẵn m sao cho 4 < m < 11. Hãy minh họa tập hợp A bằng hình vẽ.
CHỦ ĐỀ 2: SỐ TỰ NHIÊN. CÁCH GHI SỐ TỰ NHIÊN
1/ Tập hợp các số tự nhiên kí hiệu là N, Tập hợp các số tự nhiên khác 0 kí hiệu là N* N = {0, 1, 2, 3, ….} N* = {1, 2, 3, ….}
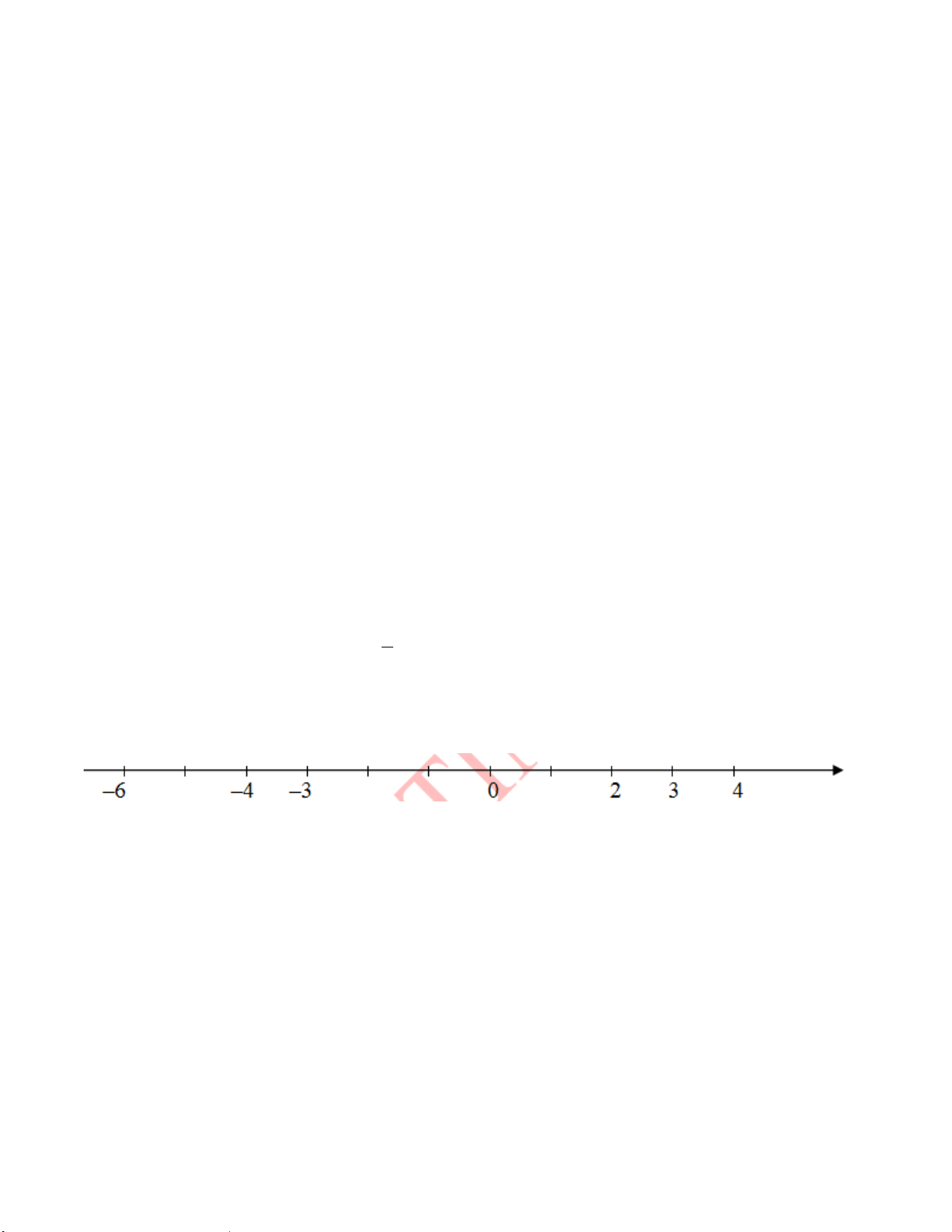
2/ Biểu diễn số tự nhiên trên tia số.
* Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số Ox
* Điểm biểu diễn số nhỏ ở bên trái điểm biểu diễn số lớn.
3/ Ghi số tự nhiên.
* Để ghi số tự nhiên trong hệ thập phân người ta dùng mười chữ số: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
* Trong hệ thập phân cứ 10 đợn vị ở một hàng thì làm thành 1 đơn vị ở hàng liền trước nó.
* Để biểu thị một số có nhiều chữ số, chẳng hạn có bốn chữ sô theo thứ tự từ trái sang phải là a,
b, c, d, ta thường viết abcd . Số này là "a nghìn, b trăm, c chục, d đơn vị.
Do đó abcd = a.1000 + b.100 + c.10 +d. 4. Chữ số La Mã.
* Trong hệ la mã, để ghi số tự nhiên người ta dùng bảy chữ số: I , V, X, L, C, D, M có giá trị
tương ứng là 1 , 5, 10, 50, 100, 500, 1000
* Mỗi số La Mã không được viết liền nhau quá 3 lần.
* Có 6 số La Mã đặc biệt: IV, IX, XL, XC, CD, CM có giá trị tương ứng 4, 9, 40, 90, 400, 900. B/ CÁC DẠNG BÀI TẬP.
DẠNG 1: CÁCH GHI SỐ TỰ NHIÊN.
* Cần phân biệt rõ:
số với chữ số ; số chục với chữ số hàng chục ; số trăm với chữ số hàng trăm, .. VD: Số 4315
+ các chữ số là 4, 3, 1, 5
+ Số chục là 431, chữ số hàng chục là 1
+ Số trăm là 43, chữ số hàng trăm là 3….
* Mỗi chữ số ở những vị trí khác nhau sẽ có giá trị khác nhau. Riêng chữ số 0 không thể đứng ở
vị trí đầu tiên.
* Số nhỏ nhất có n chữ số là 1000….000 (n - 1 chữ số 0 )
* Số lớn nhất có n chữ số là 999….99 (n chữ số 9 )
Bài 1. (Bài 11 trang 10 SGK)
a) Viết số tự nhiên có số chục là 135, chữ số hàng đơn vị là 7. b) Điền vào bảng :
Bài 2. (Bài 13 trang 10 SGK)
a) Viết số tự nhiên nhỏ nhất có bốn chữ số.
b) Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau. Giải
Để viết số tự nhiên nhỏ nhất có bốn chữ số, ta phải chọn các chữ số nhỏ nhất có thể được cho mỗi hàng. Ta có : a) 1000 ; b) 1023. Bài 3.
a) Viết số tự nhiên nhỏ nhất có tám chữ số.
b) Viết số tự nhiên lớn nhất có tám chữ số. Giải
Số có tám chữ số gồm tám hàng : nhỏ nhất là hàng đơn vị, lớn nhất là hàng chục triệu.
a) Số nhỏ nhất có tám chữ số, phải có chữ số có giá trị nhỏ nhất có thể được ở mỗi hàng. Vậy ở
tất cả các hàng là chữ số 0, riêng chữ số hàng chục triệu phải là chữ số 1 (chữ số nhỏ nhất có thể
được). Vậy số phải viết là 10 000 000.
b) Số lớn nhất có tám chữ số phải có chữ số có giá trị lớn nhất có thể được ở mỗi hàng. Chữ số
lớn nhất đó là 9 và số lớn nhất có tám chữ số là : 99 999 999. Bài 4.
a) Viết số tự nhiên nhỏ nhất có năm chữ số.
b) Viết số tự nhiên nhỏ nhất có năm chữ số khác nhau.
Bài 5. Viết tập hợp các chữ số của số 2010. Bài 6.
a) Viết số tự nhiên nhỏ nhất có sáu chữ số;
b) Viết số tự nhiên lớn nhất có sáu chữ số.
DẠNG 2: VIẾT SỐ TỰ NHIÊN CÓ m CHỮ SỐ TỪ n CHỮ SỐ CHO TRƯỚC.
* Chọn một chữ số trong các chữ số đã cho làm chữ số hàng cao nhất trong số tự nhiên cần viết.
* Lần lượt chọn các số còn lại xếp vào các hàng còn lại.
* Cứ làm như vậy cho đến khi lập được hết các số.
* Chú ý: Chữ số 0 không thể đứng đầu.
BÀI 1: (Bài 14 trang 10 SGK) Dùng ba chữ số 0, 1, 2, hãy viết tất cả các số tự nhiên có ba chữ số mà các chữ số khác nhau. Giải
Chữ số hàng trăm phải khác 0 để số phải viết là số có ba chữ số.
Do đó chữ số hàng trăm có thể là 1 hoặc 2.
Nếu chữ số hàng trăm là 1 ta có : 102 ; 120.
Nếu chữ số hàng trăm là 2 ta có : 201 ; 210.
Vậy với ba chữ số 0, 1, 2 ta có thể viết được tất cả bốn số tự nhiên có ba chữ số, các chữ số
khác nhau : 102 ; 120 ; 201; 210.
Bài 2. Viết số lớn nhất và số nhỏ nhất bằng cách dùng cả năm chữ số 0, 2, 5, 6, 9 (mỗi chữ số chỉ được viết một lần). Giải
Vì phải dùng cả 5 chữ số đã cho nên cả hai số đều có 5 chữ số.
* Số lớn nhất phải có chữ số lớn nhất có thể được ở hàng cao nhất là hàng vạn. Trong năm chữ
số đã cho, chữ số lớn nhất là 9.
Vậy chữ số hàng vạn là 9.
Hàng nghìn cũng phải có chữ số lớn nhất có thể được. Trong 4 chữ số còn lại 0, 2, 5, 6, chữ số
lớn nhất là 6. Vậy chữ số hàng nghìn là 6.
Lập luận tương tự ở các hàng tiếp theo (trăm, chục, đơn vị), ta có số lớn nhất phải viết là 96 520.
* Số nhỏ nhất phải có chữ số nhỏ nhất có thể được ở các hàng. Lập luận tương tự như trên đối
với các chữ số nhỏ nhất ở các hàng, ta viết được số nhỏ nhất là 20 569.
Chú ý : Chữ số hàng chục vạn phải khác 0 để số viết được là số có năm chữ số.
Bài 3. Dùng ba chữ số 2, 0, 7 viết tất cả các số tự nhiên có ba chữ số, các chữ số khác nhau.
Bài 4. Viết số lớn nhất và số nhỏ nhất bằng cách dùng cả sáu chữ số 0 ; 2; ; 5 ; 7 ; 9 (mỗi chữ số chỉ được viết một lần).
Bài 5. Viết số lớn nhất và số nhỏ nhất bằng cách dùng cả mười chữ số khác nhau (mỗi chữ số chỉ được viết một lần).
Bài 6. Viết tập hợp các số tự nhiên có hai chữ số, trong đó
a) Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị là 4
b) Chữ số hàng chục gấp ba lần chữ số hàng đơn vị
c) Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị, tổng hai chữ số bằng 12.
DẠNG 3: TÍNH SỐ CÁC SỐ TỰ NHIÊN.
* Tính số các số có n chữ số cho trước
+ Để tính số các chữ số có n chữ số, ta lấy số lớn nhất có n chữ số trừ đi số nhỏ nhất có n chữ
số rồi cộng với 1.
+ Số các số có n chữ số bằng:
999….99 (n chữ số 9 ) - 1000….000 (n - 1 chữ số 0) + 1
* Để đếm các số tự nhiên từ a đến b, hai số kế tiếp cách nhau d đơn vị, ta dùng công thức sau: Bài 1.
a) Có bao nhiêu số có năm chữ số?
b) Có bao nhiêu số có sáu chữ số ? Giải
a) Số lớn nhất có năm chữ số là: 99 999. Số nhỏ nhất có năm chữ số là :10 000. Số các số có
năm chữ số là : 99 999 – 10 000 + 1 = 90 000.
b) Làm tương tự câu a). Số các số có sáu chữ số là : 900 000 số.
Bài 2. Tính số các số tự nhiên chẵn có bốn chữ số. Giải
Các số tự nhiên chẵn có bốn chữ số là 1000 ; 1002 ; 1004 ; … ; 9998, trong đó số lớn nhất (số
cuối) là 9998, số nhỏ nhất (số đầu) là 1000, khoảng cách giữa hai số liên tiếp là : 1002 – 1000 = 1004 – 1002 = … = 2.
Theo công thức nêu trên, số các số tự nhiên chẵn có bốn chữ số là :
( 9998 – 1000 )/ 2 + 1 = 4500 (số)
Bài 3. Muốn viết tất cả các số tự nhiên từ 100 đến 999 phải dùng bao nhiêu chữ số 9 ? Giải
Ta lần lượt tính các chữ số 9 ở hàng đơn vị, ở hàng chục và ở hàng trăm.
Các số chứa chữ số9 ở hàng đơn vị : 109, 119, … , 999 gồm
( 999 – 109 )/10 + 1 = 90 (số).10
Các số chứa chữ số 9 ở hàng chục :
190, 191,… , 199 gồm 199 – 190 + 1 = 10 (số)
290, 291 ,… , 299 gồm 10 số … 990, 991,999 gồm 10 số.
Các số chứa chữ số 9 ở hàng chục có : 10.9 = 90 (số)
Các số chứa chữ số 9 ở hàng trăm : 900, 901,… , 999 gồm 999 – 900 + 1 = 100 (số)
Vậy tất cả có : 90 + 90 + 100 = 280 (chữ số 9).
Bài 4. Có bao nhiêu số có :
a) Hai chữ số; b) Ba chữ số; c) Chín chữ số ?
Bài 5. Có bao nhiêu số tự nhiên lẻ có ba chữ số ?
Bài 6. Viết 1000 số tự nhiên đầu tiên. Hỏi chữ số 3 có mặt bao nhiêu lần ?
DẠNG 4. ĐỌC VÀ VIẾT CÁC SỐ BẰNG CHỮ SỐ LA MÃ
* Dùng bảng số La Mã sau:
* Ta có: I , V, X, L, C, D, M có giá trị tương ứng là 1 , 5, 10, 50, 100, 500, 1000
* Ta có: IV, IX, XL, XC, CD, CM có giá trị tương ứng 4, 9, 40, 90, 400, 900. Bài 1:
a) Đọc các số La Mã sau: XIV ; XXVI
b) Viết các số sau bằng số La Mã: 17 ; 25
Bài 2: đọc các số la mã sau: XXXIX ; LXXXV ; CDXCV.
Bài 3: Viết các số tự nhiên bằng số La Mã: 25 ; 89 ; 2009 ; 1945
CHỦ ĐỀ 3: PHÉP CỘNG VÀ PHÉP NHÂN A/ KIẾN THỨC CẦN NHỚ.
1/ Phép cộng: a + b = c
(số hạng) + (số hạng) = (tổng) 2/ Phép nhân: a . b = d
(thừa số) . (thừa số) = (tích)
3/ Tính chất của phép cộng và phép nhân số tự nhiên: Phép tính Cộng Nhân Tính chất Giao hoán a + b = b + a a . b = b . a Kết hợp (a + b) + c = a + (b + c) (a . b) .c = a . (b . c) Cộng với số 0 a + 0 = 0 + a = a Nhân với số 1 a . 1 = 1 . a = a
Phân phối của phép nhân a. (b + c) = ab + ac đối với phép cộng 4/ Chú ý:
+ Tích của một số với 0 bằng 0
+ Nếu tích của hai thừa số bằng 0 thì ít nhất một thừa số bằng 0 B/ CÁC DẠNG BÀI TẬP.
DẠNG 1: CÁC BÀI TOÁN TÍNH NHANH
+ Nhóm các số có tổng tròn trục hoặc tạo ra phép nhân với số tròn trục.
+ Ta có thể thêm vào số hạng này đồng thời bớt đi số hạng kia với cùng một số.
+ Sử dụng tính chất phân phối của phép nhân đối với phép cộng. Chú ý:
+ Quy tắc đặt thừa số chung :
a. B + a.c = a. (b + c) hoặc a. b + a. c + a. d = a.(b + c + d)
+ Muốn nhân 1 số có 2 chữ số với 11 ta cộng 2 chữ số đó rồi ghi kết quả váo giữa 2 chữ
số đó. Nếu tổng lớn hơn 9 thì ghi hàng đơn vị váo giữa rồi cộng 1 vào chữ số hàng chục.
Ví dụ 1: có 34 .11 =374 ; 69.11 =759
Ví dụ 2: có 79.101 =79(100 +1) =7900 +79 =7979
+ Muốn nhân một số có 2 chữ số với 101 thì kết quả chính là 1 số có được bằng cách viết
chữ số đó 2 lần khít nhau
Ví dụ: 84 .101 =8484 ; 63 .101 =6363 ; 90.101 =9090
+ Muốn nhân một số có 3 chữ số với 1001 thì kết quả chính là 1 số có được bằng cách
viết chữ số đó 2 lần khít nhau
Ví dụ: 123.1001 = 123123
Bài 1: Tính tổng sau đây một cách hợp lý nhất. a/ 67 + 135 + 33 b/ 277 + 113 + 323 + 87 ĐS: a/ 235 b/ 800
Bài 2: Tính nhanh các phép tính sau: a/ 8 . 17 . 125 b/ 4 . 37 . 25 ĐS: a/ 17000 b/ 3700
Bài 3: Tính nhanh một cách hợp lí: a/ 997 + 86 b/ 37. 38 + 62. 37 c/ 43. 11; 67. 101; 423. 1001 d/ 67. 99 ; 998. 34 e) 135 + 360 + 65 + 40 Hướng dẫn
a/ Cách 1: Sử dụng tính chất kết hợp của phép cộng.
997 + (3 + 83) = (997 + 3) + 83 = 1000 + 80 = 1083
Cách 2: Thêm vào số hạng này đồng thời bớt đi số hạng kia với cùng một số.
997 + 86 = (997 + 3) + (86 -3) = 1000 + 83 = 1083
b/ Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
37. 38 + 62. 37 = 37.(38 + 62) = 37.100 = 3700.
c/ 43. 11 = 43.(10 + 1) = 43.10 + 43. 1 = 430 + 43 = 4373. 67. 101= 6767 423. 1001 = 423 423
d/ 67. 99 = 67.(100 – 1) = 67.100 – 67 = 6700 – 67 = 6633
998. 34 = 34. (100 – 2) = 34.100 – 34.2 = 3400 – 68 = 33 932
e) 135 + 360 + 65 + 40 = (135 + 65) + ( 360 + 40) = 200 + 400 = 600.
Bái 4: Tính nhanh các phép tính: a/ 37581 – 9999 b/ 7345 – 1998 c/ 485321 – 99999 d/ 7593 – 1997 Hướng dẫn:
a/ 37581 – 9999 = (37581 + 1 ) – (9999 + 1) = 37582 – 10000 = 89999
b/ 7345 – 1998 = (7345 + 2) – (1998 + 2) = 7347 – 2000 = 5347 c/ ĐS: 385322 d/ ĐS: 5596
Bài 5: Tính tổng sau đây một cách hợp lý nhất.
a) 67 + 135 + 33 b) 277 + 113 + 323 + 87
a) 28. 64 + 28. 36 = 28.(64 + 36 ) = 28. 100 = 2800
b) 3. 25. 8 + 4. 37. 6 + 2. 38. 12 = 24. 25 + 24. 37 + 24. 38 = 24.(25 + 37 + 38 ) = 24. 100 = 2400 Hướng dẫn
a) 67 + 135 + 33 =(67+33) + 135 = 100 + 135 = 235
b) 277 + 113 + 323 + 87 = (277+ 323) + (113+ 87) = 600 + 200 = 800
c) Quy tắc đặt thừa số chung :
28. 64 + 28. 36 = 28.(64 + 36 ) = 28. 100 = 2800
d) Quy tắc đặt thừa số chung :
3. 25. 8 + 4. 37. 6 + 2. 38. 12 = 24. 25 + 24. 37 + 24. 38 = 24.(25 + 37 + 38 )
Bài 6: Tính nhanh các phép tính sau: a) 8.17.125 b) 4.37.25 Hướng dẫn
a) 8.17.125 = (8 .25).17 =100.17=1700
b) 4.37.25 = ( 25.4).37 = 100.7=700
Bài 7: Tính nhanh: a) 25. 12 b) 34. 11 c) 47. 101 d) 15.302 e) 125.18 g) 123. 1001
Bài 8: Tính bằng cách hợp lí nhất:
a) 5. 125. 2. 41. 8 b) 25. 7. 10. 4 c) 8. 12. 125. 2 d) 4. 36. 25. 50
Bài 9: Tính bằng cách hợp lí nhất: a) 38. 63 + 37. 38 b) 12.53 + 53. 172– 53. 84
c) 35.34 +35.38 + 65.75 + 65.45 d) 39.8 + 60.2 + 21.8
e) 36.28 + 36.82 + 64.69 + 64.41 DẠNG 2: TOÁN TÌM x
+ Nếu f(x) . a = 0 => f(x) = 0 Với a ≠ 0
+ Nếu f(x) . a = a => f(x) = 1 Với a ≠ 0
Bài 1: Tìm x ∈N biết a) (x –15) .15 = 0 b) 32 (x –10 ) = 32 Đ/S: a) x = 15 b) x = 11
Bài 4: Tìm số tự nhiên x biết
a/ ( x – 5)(x – 7) = 0 b/ (x – 35).35 = 35 d/ 43(x – 19) = 86 Đ/S: a) x = 5 ; x = 7 b) x = 36 c) x = 21
Bài 3: Hãy điền số vào ô trống trong bảng sau sao cho tổng các số trong ba ô liền nhau bất kì bằng 100. 34 35 Đ/S: 31 34 35 31 34 35 31 34 35 31
Bài 4: Hãy điền số vào ô trống trong bảng sau sao cho tích các số trong ba ô liền nhau bất kì bằng 100. 4 4 Đ/S 4 5 5 4 5 5 4 5 5 4
Bài 5: Cho a là số tự nhiên khác 0. Tìm tập hợp các số tự nhiên x sao cho a) a + 2.x = a b) a + 2.x > a c) a + 2.x < a Đ/S: a) x = 0 b) x ∈ N* c) x ∈ ∅
Bài 6: Thay dấu * bằng những chữ số thích hợp trong phép tính sau: 5 ∗ ∗3×8 =12∗0∗ Đ/S: 1513 . 8 = 12104 hoặc 1563 . 8 = 12504. DẠNG 3: TÍNH TỔNG
Với các bài toán tính tổng theo quy luật ở mức độ cơ bản ta thường dùng kĩ thuật nhóm
số hạng sao cho mở mỗi nhóm tổng các số hạng đều bằng nhau.
Bài 1: Tính giá trị các biểu thức sau:
A = (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15).2
B = 17 + 19 + 21 + 23 + 25 + 27 + 29
Đ/S: A = 4. 16. 2 = 128 B = 46.3 + 23 = 161
Bài 2: Tính giá trị các biểu thức sau:
C = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18
D = (2 + 4 + 6 + 8 + 11 + 13 + 15 + 17 + 19).3
Đ/S: C = 4.20 + 10 = 90
D = (2.10 + 2.30 + 15).3 = 285
Bài 3: Tính giá trị các biểu thức sau:
C = 2.3 + 3.4 + 4.5 + 3.6 + 2.7 + 4.15
D = 3.(12 + 13 + 14 + 15) + 3(8 + 7 + 6 + 5)
CHỦ ĐỀ 4: PHÉP TRỪ VÀ PHÉP CHIA. A/ KIẾN THỨC CẦN NHỚ. 1/ Phép trừ:
Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao cho b + x = a thì ta có phép trừ a - b = x
(số bị trừ) - (số trừ) = (hiệu)
Chú ý: Điều kiện thực hiện phép trừ trong N là số bị trừ luôn lớn hơn hoặc bằng số trừ. 2/ Phép chia:
Cho hai số tự nhiên a và b, trong đó b ≠ 0, nếu có số tự nhiên x sao cho b.x = a thì ta nói a
chia hết cho b và ta có phép chia hết a : b = x
(số bị chia) : (số chia) = (thương)
Tổng quát: Cho hai số tự nhiên a và b, trong đó b ≠ 0, ta luôn tìm được hai số tự nhiên q
và r duy nhất sao cho: a = b . q + r trong đó 0 ≤ r < b
(số bị chia) = (số chia) . (thương) + (số dư)
Nếu r = 0 thì ta có phép chia hết.
Nếu r ≠ 0 thì ta có phép chia có dư.
Chú ý: Trong phép chia, số chia bao giờ cũng khác 0. 3/ Tính chất a.(b – c) = a.b – a.c (a + b): c = a : c + b : c
Với điều kiện a và b cùng chia hết cho c
(a – b): c = a : c – b : c
Với điều kiện a và b cùng chia hết cho c (a + b) – c = a + (b – c)
(a – b) – c = a – (b + c) a – (b – c) = a – b + c a + (b – c) = a + b - c B/ CÁC DẠNG BÀI TẬP.
DẠNG 1: TÍNH NHANH. THỰC HIỆN PHÉP TÍNH.
Để việc tính nhanh được thuận lời, chúng ta thường cộng trừ sao được các con số tròn
trục khi đó việc tính toán sẽ nhanh
Đôi khi chúng ta phải công thêm đơn vị vào số đã cho để được số tròn trục rồi mới thực hiện phép trừ.
Áp dụng tính chất của phép cộng và phép nhân một cách linh hoạt.
Nếu trong dãy có cả cộng, trừ, nhân, chia cần chú ý đến thứ tự phép tính.
Bài 1: Tính nhanh các phép tính: a/ 37581 – 9999 b/ 7345 – 1998 c/ 485321 – 99999 d/ 7593 – 1997 Hướng dẫn:
a/ 37581 – 9999 = (37581 + 1 ) – (9999 + 1) = 37582 – 10000 = 89999
(cộng cùng một số vào số bị trừ và số trừ)
b/ 7345 – 1998 = (7345 + 2) – (1998 + 2) = 7347 – 2000 = 5347 c/ ĐS: 385322 d/ ĐS: 5596 Bài 2: Tính a) 49.15 - 49.5 b) 13.52 + 52.36 – 52.19 b) 98.36 c) 999.202 Đ/S: a) 490 b) 1560 c) 3528 d) 201798 DẠNG 2: TOÁN TÌM X
Số bị chia (chưa biết) = số chia x Thương
Số chia (chưa biết) = Số bị chia : Thương
Số hạng (chưa biết) = Tổng – Số hạng đã biết
Số bị trừ (chưa biết) = Hiệu + Số trừ
Số trừ (chưa biết) = Số bị trừ - Hiệu
Thừa số (chưa biết) = Tích : Thừa số đã biết
Bài 1: Tìm x biết : a) x + 37 = 50 b) 2.x – 3 = 11 c) (2 + x ) : 5 = 6 d) 2 + x : 5 = 6 Đ/S: a) x = 13 b) x = 7 c) x = 28 d) x = 20
Bài 2:Tìm x ∈N biết : a) (x – 15 ) – 75 = 0 b) 575- (6x +70) =445 c) 315+(125-x)= 435
Đ/S: a) x = 90 b) x = 10 c) x = 5
Bài 3: Tìm x ∈N biết : a) x –105 : 21 =15 b) (x - 105) :21 = 15 Đ/S: a) x = 20 b) x = 420
Bài 3: Tìm số tự nhiên x biết a) ( x – 5)(x – 7) = 0 (ĐS: x = 5; x = 7) b) 541 + (218 – x) = 735 (ĐS: x = 24) c) 96 – 3(x + 1) = 42 (ĐS: x = 17) d) ( x – 47) – 115 = 0 (ĐS: x = 162) e) (x – 36):18 = 12 (ĐS: x = 252)
DẠNG 3: TỔNG CÁC SỐ NGUYÊN CÁCH ĐỀU.
Tổng của dãy số cách đều = (số đầu + số cuối) x (số số hạng : 2)
Số số hạng = (Số hạng cuối – số hạng đầu) : khoảng cách + 1
Số đầu của dãy = tổng . 2 : số số hạng – số hạng cuối.
Số cuối của dãy = tổng . 2 : số số hạng – số đầu.
Bài 1: Tính tổng của 19 số lẻ liên tiếp đầu tiên. Hướng dẫn
Tổng 19 số lẻ liên tiếp đầu tiên là:
S = 1 + 3 + 5 + …+ 33 + 35 + 37. (37 + )1.19 S = = 361
Cách 1: Tính tổng theo công thức trong phương pháp: 2
Cách 2: Nhóm số hạng tạo thành những cặp số có tổng bằng nhau:
Ta thấy: 1 + 37 = 38 5 + 33 = 38 1 + 35 = 38 7 + 31 = 38 ……
=> Nếu ta sắp xếp các cặp số từ hai đầu dãy số vào, ta được các cặp số đều có tổng số là 38.
Số cặp số là: 19 : 2 = 9 (cặp số) dư một số hạng ở chính giữa dãy số là số 19.
Vậy tổng của 19 số lẻ liên tiếp đầu tiên là: 38 x 9 + 19 = 361 Cách nhóm khác:
Ta bỏ lại số hạng đầu tiên là số 1 thì dãy số có: 19 – 1 = 18 (số hạng)
Ta thấy: 3 + 37 = 40 7 + 33 = 40 5 + 35 = 40 9 + 31 = 40 ………
=> Nếu ta sắp xếp các cặp số từ 2 đầu dãy số gồm 18 số hạng vào được các cặp số có tổng là 40.
Số cặp số là: 18 : 2 = 9 (cặp số)
Tổng của 19 số lẻ liên tiếp đầu tiên là: 1 + 40 x 9 = 361
Bài 2: Tính tổng của số tự nhiên từ 1 đến n. Hướng dẫn
Tổng S = 1 + 2 + 3 + ….+ n Số các số hạng = n Ta có: (n + )1.n S = 2
Bài 3: Tính tổng S = 1 + 2 + 3 + 4 + 5 + ….+ 100
Bài 4: Tính tổng S = 2 + 5 + 8 + 11 + …+ 47 + 50
Bài 5: Tính tổng: S = 5 + 10 + 15 + 20 + …+ 100
Bài 6. Tính bằng cách hợp lý. a) 44.66 34.41 A + = b) 1 2 3 ... 200 B + + + + = 3+ 7 +11+...+ 79 6 + 8 +10 +...+ 34 c)
1.5.6 + 2.10.12 + 4.20.24 + 9.45.54 C =
1.3.5 + 2.6.10 + 4.12.20 + 9.27.45
DẠNG 4: TOÁN VỀ PHÉP CHIA CÓ DƯ.
Số bị chia = số chia x Thương + Số dư
(0 ≤ Số dư < Số chia)
Số chia = (Số bị chia – số dư) : Thương
Thương số = (Số bị chia – Số dư) : Số chia
Số dư = Số bị chia – Số chia x Thương số
Bài 1: Tìm số dư trong các phép chia a) 571 chia cho 15 b) 763 chia cho 17
Hướng dẫn: Số dư bao giờ cũng nhỏ hơn số chia
a) 571 = 38.15 + 1 => 571 chia cho 15 được thương là 38 dư 1
b) 763 = 17.44 + 15 => 763 chia cho 17 được thương là 44 dư 15
Bài 2: Tìm số chia và thương số trong phép chia khi biết số bị chia bằng 49 và số dư là Hướng dẫn
Só chia . Thương số = Số bị chia – Số dư = 49 – 11 = 38
Số chia phải lớn hơn số dư => Số chia > 11
Ta có 38 = 38.1 = 19 . 2 nên có hai khả năng
+) Số chia là 38, thương số là 1
+) Số chia là 19, Thương số là 2
Bài 3.tìm số bị chia và số chia biết thương bằng 6 ,số dư bằng 49, tổngcủa số bị chia ,số chia và số dư bằng 595 Hướng dẫn
Gọi số b/c là a,số chia là b Ta có a = b . 6 + 49 (1) a+ b + 49 = 595 (2) thay 1 vào 2 ta được
6.b +49 +b+49 = 595 => 7b = 595 -49 .2
=> 7b = 497 => B = 497:7 => b = 71 thay vào 1 suy ra a = 495
Bài 4: Cho A= 1 + 11+ 111 + 1111 + . . + 111111111 +1111111111 ( có 10 số hạng ).
Hỏi A chia cho 9 dư bao nhiêu? Hướng dẫn:
Tổng các chữ số của tổng trên là: 1+2+3+4+5+6+7+8+9+10 = (1+10).10:2 = 55
Mà 55 chia cho 9 dư 1 nên tổng trên chia cho 9 cũng dư 1.
Bài 5: Một số chia 48 dư 39, nếu chia 24 thương 81 có dư. Tìm số đó? Hướng dẫn:
48 gấp 2 lần 24 nên số đó chia cho 24 dư: 39 - 24 = 15;
Số cần tìm là: 24 . 81 + 15 = 1959
Bài 6: Trong một phép chia 2 số tự nhiên, biết số bị chia bằng 324, thương bằng 12 và biết số
dư của phép chia là số dư lớn nhất có thể. Tìm số chia và số dư của phép chia đó? Hướng dẫn
Vì số dư là số dư lớn nhất có thể nên số dư chỉ kém số chia 1 đv.
Vậy nếu ta thêm vào số bị chia 1 đơn vị thì phép chia đó là phép chia hết và lúc này thương cũng tăng 1 đv.
Vậy số chia là : (324 + 1) : (12 + 1) = 25
Vậy số dư là : 25 - 1 = 24
Ta có phép chia : 324 : 25 = 12 dư 24
Bài 7: Một số chia 48 dư 39, nếu chia 24 thương 81 có dư. Tìm số đó Hướng dẫn
* Cách 1: Vì số A chia cho 48 thì dư 39 nên nếu bớt A đi 39 thì A chia hết cho 48 và
cũng chia hết cho 24 (vì 48 = 24 . 2) và khi đó thương khi chia cho 24 sẽ bớt đi 1 và còn 80. (vì 39 : 24 = 1 dư...)
Vậy số A là: 80 x 24 + 39 = 1959.
*Cách 2: Vì 48 gấp 2 lần 24 (48 : 24 = 2) nên thương của phép chia A cho 48 sẽ giảm đi
2 lần, ta thấy: 81 : 2 = 40 dư. . (Dư là do số dư 39 khi chia cho 24 được thêm thương là 1
Vậy số A là : 40 . 48 + 39 = 1959
CHỦ ĐỀ 5: LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN
A/ Kiến thức cơ bản:
1. Lũy thừa bậc n của số a là tích của n thừa số bằng nhau, mỗi thừa số bằng a n a = . a ...
a a ( n ≠ 0). a gọi là cơ số, no gọi là số mũ. n thừa số 2. Nhân hai
luỹ thừa cùng cơ số m. n m n a a a + =
3. Chia hai luỹ thừa cùng cơ số m : n m n a a a − = ( a ≠ 0, m ≥ n) Quy ước a0 = 1 ( a ≠ 0)
4. Luỹ thừa của luỹ thừa ( )n m m n a a ⋅ =
5. Luỹ thừa một tích ( . )m m = . m a b a b
6. Một số luỹ thừa của 10: - Một nghìn: 1 000 = 103 - Một vạn: 10 000 = 104
- Một triệu: 1 000 000 = 106
- Một tỉ: 1 000 000 000 = 109
Tổng quát: nếu n là số tự nhiên khác 0 thì: 10n = 1000…00 (có n chữ số 0)
7. Thứ tự thực hiện phép tính:
Trong một biểu thức có chứa nhiều dấu phép toán ta làm như sau:
- Nếu biểu thức không có dấu ngoặc chỉ có các phép cộng, trừ hoặc chỉ có các phép nhân
chia ta thực hiện phép tính theo thứ tự từ trái sang phải.
- Nếu biểu thức không có dấu ngoặc, có các phép cộng, trừ ,nhân ,chia, nâng lên lũy thừa,
ta thực hiện nâng lên lũy thừa trước rồi thực hiện nhân chia,cuối cùng đến cộng trừ.
- Nếu biểu thức có dấu ngoặc ( ), [ ],{ }ta thực hiện các phép tính trong ngoặc tròn trước,
rồi đến các phép tính trong ngoặc vuông, cuối cùng đến các phép tính trong ngoặc nhọn.
B/ CÁC DẠNG BÀI TẬP CƠ BẢN.
DẠNG 1: THỰC HIỆN TÍNH, VIẾT DƯỚI DẠNG LŨY THỪA.
Bài 1: viết các tích sau dưới dạng 1 luỹ thừa a) 5.5.5.5.5.5 b) 2.2.2.2.3.3.3.3 c) 100.10.2.5 Đáp số: a) 5.5.5.5.5.5 = 56 b) 2.2.2.2.3.3.3.3= 24. . 34
c)100.10.2.5 =10 .10.10.10 =104
Bài 2: Tính giá trị củ các biểu thức sau: a) 34: 32 b) 24.. 22 c) (24.)2 Đáp số: a) 34: 32 = 32 = 9 b) 24.. 22 = 16 .4 = 54 c) (24.)2 = 28 = 256
Bài 3: Viết các tích sau đây dưới dạng một luỹ thừa của một số: a) A = 82.324 b) B = 273.94.243 Hướng dẫn
a) A = 82.324 = 26.220 = 226. hoặc A = 413 b) B = 273.94.243 = 322
Bài 4: Tìm các số mũ n sao cho luỹ thừa 3n thảo mãn điều kiện: 25 < 3n < 250 Hướng dẫn
Ta có: 32 = 9, 33 = 27 > 25, 34 = 41, 35 = 243 < 250
nhưng 36 = 243. 3 = 729 > 250
Vậy với số mũ n = 3,4,5 ta có 25 < 3n < 250
Bài 5: Viết các số sau đây dưới dạng lũy thừa của một số.
a) A = 253.125 b) B = 643.2562
DẠNG 2: SO SÁNH CÁC LŨY THỪA.
Để so sánh hai lũy thừa ta thường biến đổi về hai lũy thừa có cùng cơ số hoặc có cùng số
mũ (có thể sử dụng các lũy thừa trung gian để so sánh)
Với a , b , m , n∈ N , ta có: a > b an > bn ∀ n∈ N*
m > n am > an (a > 1)
a = 0 hoặc a = 1 thì am = an ( m.n ≠ 0)
Với A , B là các biểu thức ta có :
An > Bn A > B > 0
Am > An => m > n và A > 1
m < n và 0 < A < 1
Bài 1 : So sánh : a) 33317 và 33323 b) 200710 và 200810
c) (2008-2007)2009 và (1998 - 1997)1999 Hướng dẫn
a) Vì 1 < 17 < 23 nên 33317 < 33323
b) Vì 2007 < 2008 nên 200710 < 200810
c) Ta có : (2008-2007)2009 = 12009 = 1
(1998 - 1997)1999 = 11999 = 1
Vậy (2008-2007)2009 = (1998 - 1997)1999 Bài 2: So sánh a, 2300 và 3200 e, 9920 và 999910 b, 3500 và 7300 f, 111979 và 371320 c, 85 và 3.47 g, 1010 và 48.505 d, 202303 và 303202 h, 199010 + 1990 9 và 199110 Hướng dẫn
a, Ta có : 2300 = 23)100 = 8100 3200 = (32)100 = 9100
Vì 8100 < 9100 => 2300 < 3200
b, Tương tự câu a, ta có : 3500 = (35)100 = 243100 7300 = (73)100 = 343100
Vì 243100 < 343100 nên 3500 < 7300
c, Ta có : 85 = 215 = 2.214 < 3.214 = 3.47 => 85 < 3.47
d, Ta có : 202303 = (2.101)3.101 = (23.1013)101 = (8.101.1012)101 = (808.101)101
303202 = (3.101)2.101 = (32.1012)101 = (9.1012)101
Vì 808.1012 > 9.1012 nên 202303 > 303202
e, Ta thấy : 992 < 99.101 = 9999 => (992)10 < 999910 hay 9920 < 999910
f, ta có : 111979 < 111980 = (113)660 = 1331660 (1) 371320 = 372)660 = 1369660 (2)
Từ (1) và (2) suy ra : 111979 < 371320
g, Ta có : 1010 = 210. 510 = 2. 29. 510 (*)
48. 505 = (3. 24). (25. 510) = 3. 29. 510 (**)
Từ (*) và (**) => 1010 < 48. 505
h, Có : 199010 + 19909 = 19909. (1990+1) = 1991. 19909 199110 = 1991. 19919
Vì 19909 < 19919 nên 199010 + 1990 9 < 199110
Bài 3 . Chứng tỏ rằng : 527 < 263 < 528 Hướng dẫn:
Hãy chứng tỏ 263 > 527 và 263 < 528 Ta có : 263 = (27)9 = 1289 527 =(53)9 = 1259 => 263 > 527 (1)
Lại có : 263 = (29)7 = 5127 528 = (54)7 = 6257 => 263 < 528 (2)
Từ (1) và (2) => 527 < 263 < 52 Bài 4 . So sánh : a, 10750 và 7375 b, 291 và 535 Hướng dẫn
a, Ta thấy : 10750 < 10850 = (4. 27)50 = 2100. 3150 (1)
7375 > 7275 = (8. 9)75 = 2225. 3150 (2)
Từ (1) và (2) => 10750 < 2100. 3150 < 2225. 3150 < 7375
b, 291 > 290 = (25)18 = 3218 và 535 < 536 = (52)18 = 2518 => 291 > 3218 > 2518 > 535 Vậy 291 > 535
Bài 5: So sách các cặp số sau: a) A = 275 và B = 2433 b) A = 2 300 và B = 3200 Hướng dẫn
a) Ta có A = 275 = (33)5 = 315 và B = (35)3 = 315 Vậy A = B
b) A = 2 300 = 33.100 = 8100 và B = 3200 = 32.100 = 9100
Vì 8 < 9 nên 8100 < 9100 và A < B.
Ghi chú: Trong hai luỹ thừa có cùng cơ số, luỹ thừa nào số mũ lớn hơn thì lớn hơn.
a2 gọi là bình phương của a hay a bình phương
a3 gọi là lập phương của a hay a lập phương
Bài 6: Tính và so sánh
a) A = (3 + 5)2 và B = 32 + 52
b) C = (3 + 5)3 và D = 33 + 53 Hướng dẫn a) A > B b) C > D
Lưu ý HS tránh sai lầm khi viết (a + b)2 = a2 + b2 hoặc (a + b)3 = a3 + b3
Bài 7: Tìm các giá trị của số mũ n sao cho. a) 5 < 2n < 100 b) 50 < 7n < 2500
Bài 8: So sánh các số. a) 1030 và 2100
b) 3450 và 5300 c) 333444 và 444333 Hướng dẫn
Biến đổi đưa về cùng số mũ hoặc cùng cơ số rồi so sánh
Bài 9: Tìm các số tự nhiên n sao cho : a, 3 < 3n ≤ 234 b, 8.16 ≥ 2n ≥ 4
Hướng dẫn: đưa các số về các lũy thừa có cùng cơ số .
Bài 10: Tìm số tự nhiên n biết rằng :
415 . 915 < 2n . 3n < 1816 . 216
Gợi ý: quan sát , nhận xét về số mũ của các lũy thừa trong một tích để đưa về cùng cơ số
Bài 11: So sánh các số sau?
a) 2711 và 818. b) 6255 và 1257 c) 536 và 1124 d) 32n và 23n (n ∈ N* ) Hướng dẫn:
a) Đưa về cùng cơ số 3. b) Đưa về cùng cơ số 5.
c) Đưa về cùng số mũ 12.
d) Đưa về cùng số mũ n
Bài 12: So sánh các số sau: a) 523 và 6.522 b) 7.213 và 216 c) 2115 và 275.498 Hướng dẫn:
a) Đưa hai số về dạng một tích trong đó có thừa số giống nhau 522.
b) Đưa hai số về dạng một tích trong đó có thừa số giống nhau là 213.
c) Đưa hai số về dạng một tích 2 luỹ thừa cơ số là 7 và 3.
Bài 13: So sánh các số sau: a) 19920 và 200315. b) 339 và 1121. Hướng dẫn :
a) 19920 < 20020 = (23 .52)20 = 260. 540.
200315 > 200015 = (2.103)15 = (24. 53)15 = 260.545
b) 339 <340 = (32)20 = 920<1121.
Bài 14: So sánh 2 hiệu,hiệu nào lớn hơn: 72 45-7244và 72 44-7243. Hướng dẫn:
7245 - 7244 = 7245(72 - 1) = 7245.71.
7244 - 7244 = 7244(72 - 1) = 7244.71.
Bài 15: So sánh các số sau: a) 95 và 273 b) 3200 và 2300 c) 3500 và 7300 d) 85 và 3 . 47 . 85 e) 202303 và 303202 Hướng dẫn:
a) Ta có: 95 = (32)5 = 310 273 = (33 )3 = 39
Vì 310 > 39 nên 95 > 273
b) Ta có: 3200 = (32)100 = 9100 2300 = (23) 100 = 8100
Vì 9100 > 8100 ; nên 3200 > 2300 c) 3500 và 7300
3500 = 35.100 = (35)100 = 243100
7300 = 73.100 . (73 )100 = (343)100
Vì 243100 < 343100 => 3500 < 7300
d) có 3 . 47 . 85 = (23)+5 = 215 <3.214 = 3.47 => 85 < 3 . 47 e) 202303 và 303202
202303 =(2023)201 ; 303202 = (3032)101 Ta so sánh 2023 và 3032
2023 = 23. 101 . 1013 và 3032 => 3032 < 2023 3032 = 33. 1012 = 9.1012 Vậy 303202 < 2002303
DẠNG 3: THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH - ƯỚC LƯỢNG CÁC PHÉP TÍNH
Bài 1: Tính giá trị của biểu thức: A = 2002.20012001 – 2001.20022002 Hướng dẫn
A = 2002.(20010000 + 2001) – 2001.(20020000 + 2002)
= 2002.(2001.104 + 2001) – 2001.(2002.104 + 2001)
= 2002.2001.104 + 2002.2001 – 2001.2002.104 – 2001.2002 = 0
Bài 2: Thực hiện phép tính
a) A = (456.11 + 912).37 : 13: 74
b) B = [(315 + 372).3 + (372 + 315).7] : (26.13 + 74.14) ĐS: A = 228 B = 5
Bài 3: Tính giá trị của biểu thức
a) 12:{390: [500 – (125 + 35.7)]}
b) 12000 –(1500.2 + 1800.3 + 1800.2:3) ĐS: a) 4 b) 2400
DẠNG 4: TÌM SỐ CHƯA BIẾT TRONG LŨY THỪA.
Khi giải bài toán tìm x có luỹ thừa phải biến đổi về các luỹ thừa cùng cơ số hoặc các luỹ
thừa cùng số mũ và các trường hợp đặc biệt
Bài 1: Tìm x, biết: a) 2x = 16 ĐS: x = 4 b) x50 = x =>x= 0;1 ĐS: x ∈{0; } 1
Bài 1: Tìm x biết rằng: a, x3 = -27 b, (2x – 1)3 = 8 c, (x – 2)2 = 16 d, (2x – 3)2 = 9
Bài 2. Tìm số hữu tỉ x biết : x2 = x5 2 x x =
2 = x5 => x5 – x2 = 0 => x2.(x3 - 1) = 0 => x = 0 0 x = 0 => => 3 x −1 = 0 3 x = 1 x = 1
Bài 3. Tìm số hữu tỉ y biết : (3y - 1)10 = (3y - 1)20 (*)
Hướng dẫn : Đặt 3y – 1 = x . Khi đó (*) trở thành : x10 = x20 x = 0 10
Giải tương tự bài 2 ở trên ta được : x = 0 x = 0 => => x = −1 10 x −1 = 0 10 x = 1 x =1
+) Với x = 0 ta có : 3y -1 = 0 => 3y = 1 => y = 1 3
+) Với x = 1 ta có : 3y -1 = 1 => 3y = 2 => y = 2 3
+) Với x = -1 ta có : 3y – 1 = -1 => 3y = 0 => y = 0 Vậy y = 1 ; 2 ; 0 3 3
Bài 4: Tìm x biết : (x - 5)2 = (1 – 3x)2
Bài 5: Tìm n ∈ N biết : a, 2008n = 1 c, 32-n. 16n = 1024 b, 5n + 5n+2 = 650 d, 3-1.3n + 5.3n-1 = 162
Bài 6: Tìm hai số tự nhiên m , n biết : 2m + 2n = 2m+n
Hướng dẫn: 2m+n – 2m – 2n = 0 => 2m.2n -2m -2n + 1 = 1
2m(2n - 1) – (2n - 1) = 1 => (2m - 1)( 2n - 1) = 1 (*)
Vì 2m ≥ 1 , 2n ≥ 1 ∀m,n ∈ N m m
Nên từ (*) =>2 −1 =1 2 = 2 m = 1 => => 2n −1 = 1 2n = 2 n = 1 Vậy : m = n = 1
Bài 7: Tìm x ∈ N biết
a) 13 + 23 + 33 + ...+ 103 = ( x +1)2
b) 1 + 3 + 5 + .. + 99 = (x -2)2 Hướng dẫn
a) 13 + 23 + 33 + ...+ 103 = (x +1)2
(1+ 2 + 3+.. + 10)2 = ( x +1)2
=> 552 = ( x +1) 2 => x = 54 2
b) 1 + 3 + 5 +.. + 99 = ( x -2)2 => 99 −1 +1
= ( x - 2)2 => 502 = ( x -2 )2 2 => x = 52
(Ta có: 1 + 3 + 5+ .. + ( 2n+1) = n2)
Bài 8: Tìm 1 cặp x ; y ∈ N thoả mãn 73 = x2 - y2 Hướng dẫn: Ta thấy: 73 = x2 - y2
(13 + 23 + 33 +...+73) - (13+ 23+ 33+...+ 63) = x2 - y2
(1+ 2 + 3 + .. + 7)2 - (1 + 2 + 3 +.. + 6)2 = x2 - y2 282 - 212 = x2 - y2
Vậy 1 cặp x; y thoả mãn là: x = 28; y = 21
DẠNG 4: MỘT SỐ BÀI TẬP BỔ SUNG.
Vận dụng linh hoạt các công thức, phép tính về lũy thừa để tính cho hợp lí và nhanh.
Biết kết hợp hài hòa một số phương pháp trong tính toán khi biến đổi. 30 7 13 27
Bài 1: Tính giá trị các biểu thức sau: A = 2 5. + 2 5. 27 7 10 27 2 5 . + 2 5 . Hướng dẫn: 30 7 13 27 13 7 17 20
A = 2 5. + 2 5. = 2 5. (2 + 5. ) = 23 = 8 27 7 10 27 2 5 . + 2 5 . 210 5 . 7 (217 + 520 )
Bài 2: Chứng tỏ rằng:
b) B = 52008 + 52007 + 52006 31 c) M = 88 + 220 17
d) H = 3135 . 299 – 3136 . 36 7 Hướng dẫn
Để chứng minh A (một biểu thức lũy thừa) chia hết cho số k ta cần biến đổi biểu thức
A về dạng A = P . k (với P là một số nào đó)
b, B = 52008 + 52007 + 52006 31
Ta không thể tính giá trị cụ thể của từng lũy thừa rồi thực hiện phép chia. Giáo viên có
thể gợi ý đặt thừa số chung. B = 52008 + 52007 + 52006 B = 52006 .( 52 + 51 + 1) B = 52006 . 31 31 c, M = 88 + 220 17
Cách làm tương tự như câu b, nhưng trước tiên phải đưa về hai lũy thừa có cùng cơ số:
M = 88 + 220 = (23)8 + 220 = 224 + 220
M = 220 (24 + 1) = 220 (16 + 1) = 220 . 17 17
d, H = 3135 . 299 – 3136 . 36 7
Với câu này, học sinh cũng phải nhận ra cần đặt thừa số chung, nhưng đặt thừa số
chung nào lại là một vấn đề. Nếu đặt 3135 làm thừa số chung thì buộc phải tính kết quả trong
ngoặc, và như vậy thì rất lâu và dễ nhầm. Khi đó, giáo viên có thể hướng dẫn. H = 3135 . 299 – 3136 . 36
H = 3135 . 299 – 3136 - 35. 3136
H = 3135 . (299 – 313) - 35. 3136 H = 3135 . 14 - 35. 3136
H = 7 . (3135 . 2 – 5. 3136 ) 7
Bài 3 . Cho A = 2+ 22 + 23 +……+ 260 . Chứng tỏ rằng : A3 , A7 , A5 Hướng dẫn: A = 2+ 22 + 23 +……+ 260
= (2+22)+(23+24)+(25+26)+…….+(257+258)+(259+260)
= 2.(1+2)+23.(1+2)+25.(1+2)+…….+257.(1+2)+259.(1+2)
= (1+2).(2+23+25+…..+257+259) = 3.( 2+23+25+…..+257+259) => A3 Tương tự ,ta có :
A = (2+ 22 + 23)+(24+25+26)+……+(258+259+ 260 )
= 2.(1+2+22)+24.(1+2+22)+…….+258.(1+2+22)
= (1+2+22).(2+24+27+…….+258)
= 7.(2+24+27+…….+258) => A 7
A = (2+ 23)+(22+24)+……+(257+259)+(258+ 260 )
A = 2(1+22)+22(1+22)+……+257(1+22)+258(1+22)
= (1+22).(2+22+25+26+…….+257+258)
= 5. (2+22+25+26+…….+257+258 => A5
Bài 4: Chứng tỏ rằng :
a, D = 3 + 32 + 33 + 34 +……..+ 32007 13
b, E = 71 + 72 + 73 + 74 +…. + 74n-1 + 74n 400 Hướng dẫn
a, Ta thấy : 13 = 1 + 3 + 32 nên ta sẽ nhóm 3 số hạng liên tiếp của tổng thành một nhóm như sau :
D = (3 + 32 + 33) + (34 +35 + 36) +…….+ (32005 + 32006.+ 32007)
=3.(1 + 3 + 32) +34.(1 + 3 + 32) +…….+ 32005.(1 + 3 + 32)
= 3. 13 + 34. 13 + ……..+ 32005. 13
= (3 + 34 + ……+ 32005). 13 => D 13
b, Tương tự câu a, có : 400 = 1 + 7 + 72 + 73 nên :
E = (71 + 72 + 73 + 74) + 74. (71 + 72 + 73 + 74) + …+ 74n-4. (71 + 72 + 73 + 74)
= (71 + 72 + 73 + 74). (1+74 + 78 + …+74n-4)
= 7.(1 + 71 + 72 + 73 ). (1+74 + 78 + …+74n-4)
= 7.(1 + 7 + 49 + 343 ). (1+74 + 78 + …+74n-4)
= 7.400 . (1+74 + 78 + …+74n-4) 400 => E 400
CHỦ ĐỀ 6: TÍNH TỔNG CÁC LŨY THỪA THEO QUY LUẬT.
DẠNG 1: TỔNG CÓ DẠNG: S = 1 + a + a2 + a3 + ….+ an (1) I/ PHƯƠNG PHÁP.
B1: Nhân vào hai vế của đẳng thức với số a ta được.
a.S = a + a2 + a3 + a4 + ….+ an + 1 (2)
B2: Lấy (2) trừ (1) vế theo vế được: n 1 +
a.S – S = an + 1 – 1 => a −1 S = a −1
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 1 + 2 + 22 + 23 + 24 +…..+ 2100
Bài 2: Tính tổng S = 6 + 62 + 63 + 64 + …..+ 699
Bài 3: Tính tổng S = 1 + 4 + 42 + 43 + …...+ 41000
Bài 4: Tính tổng S = 1 1 1 1 1 1 1+ + + + + ...+ + 2 3 4 99 100 2 2 2 2 2 2
Bài 5: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 2 3 4 99 100 3 3 3 3 3 3
DẠNG 2: TỔNG CÓ DẠNG: S = 1 + a2 + a4 + a6 + ….+ a2n (1) I/ PHƯƠNG PHÁP.
B1: Nhân vào hai vế của đẳng thức với số a2 ta được.
a2.S = a2 + a4 + a6 + a8 + ….+ a2n + 2 (2)
B2: Lấy (2) trừ (1) vế theo vế được: 2n+2
a2.S – S = a2n + 2 – 1 => a −1 S = 2 a −1
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 1 + 22 + 24 + 26 + …..+ 298 + 2100
Bài 2: Tính tổng S = 62 + 64 + 66 + …..+ 698 + 6100
Bài 3: Tính tổng S = 1 + 32 + 34 + 36 + …...+ 3100 + 3102
Bài 4: Tính tổng S = 1 1 1 1 1 1 1+ + + + + ...+ + 2 4 6 98 100 2 2 2 2 2 2
Bài 5: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 2 4 6 98 100 3 3 3 3 3 3 1
DẠNG 3: TỔNG CÓ DẠNG: S = a + a3 + a5 + a7 + ….+ a2n + 1 (1) I/ PHƯƠNG PHÁP.
B1: Nhân vào hai vế của đẳng thức với số a2 ta được.
a2.S = a3 + a5 + a7 + a9 + ….+ a2n + 3 (2)
B2: Lấy (2) trừ (1) vế theo vế được: 2n+2
a2.S – S = a2n + 3 – a => a − a S = 2 a −1
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 1 + 2 + 23 + 25 + …..+ 299 + 2101
Bài 2: Tính tổng S = 63 + 65 + 67 + …..+ 699 + 6101
Bài 3: Tính tổng S = 1 + 33 + 35 + 37 + …...+ 3101 + 3103
Bài 4: Tính tổng S = 1 1 1 1 1 1 1+ + + + + ...+ + 3 5 7 99 101 2 2 2 2 2 2
Bài 5: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 3 5 7 99 101 3 3 3 3 3 3
DẠNG 4: TỔNG CÓ DẠNG: S = 1.2 + 2.3 + 3.4 + 4.5 + ….+ (n – 1). n (1) I/ PHƯƠNG PHÁP.
Vì khoảng cách giữa 2 thừa số trong mỗi số hạng bằng 1 => Nhân vào hai vế của đẳng
thức với 3 lần khoảng cách (nhân với 3) ta được.
3.S = 1.2.3 + 2.3.3 + 3.4.3 + 4.5.3+ ….+ (n – 2).(n – 1) .3+ (n - 1).n.3
= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ….+ (n – 2).(n – 1).[n – (n – 3)]
+ (n -1).n.[(n + 1) – (n – 2)] = (n – 1).n.(n + 1) n – 1 .n. n + 1 ( ) ( ) S = 3
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 1.2 + 2.3 + 3.4 + 4.5 + …..+ 99.100
Bài 2: Tính tổng S = 1.3 + 3.5 + 5.7 + …..+ 99.101
Bài 3: Tính tổng S = 1.4 + 4.7 + 7.10 + …37.40 + 40.43
DẠNG 5: TỔNG CÓ DẠNG: P = 12 + 22 + 32 + 42 + … + n2 I/ PHƯƠNG PHÁP. 2
Áp dụng tổng của DẠNG 5 là: S = 1.2 + 2.3 + 3.4 + 4.5 + ….+ n(n+1)
S = 1.(1 + 1) +2 (2 +1 ) + 3(3 + 1) + 4(4 + 1) +…+ n(n + 1)
= (12 + 22 + 32 + 42 + … + n2) + (1 + 2 + 3 + …. + n) = P + (1 + 2 + 3 + …. + n)
P = S - (1 + 2 + 3 + …. + n)
Trong đó theo DẠNG 5 thì S = n.(n + ) 1 (n + 2) 3
Theo DẠNG 1 thì (1 + 2 + 3 + …. + n) = n(n +1) 2 n(n +1) 2n +1 P = ( ) 6
II/ BÀI TẬP VẬN DỤNG.
Bài 4: Tính tổng P = 12 + 22 + 32 + …+ 502
Bài 5: Tính tổng Q = 12 + 22 + 32 + …+ 512
DẠNG 6: TỔNG CÓ DẠNG: S = 12 + 32 + 52 + …+ (2n+1)2 I/ PHƯƠNG PHÁP.
Áp dụng tổng A = 1.2 + 2.3 + 3.4 + 4.5 + ….+ (k - 2)(k - 1) + (k – 1). k Với k = 2n + 2
= 0.1 + 1.2 + 2.3 + 3.4 + 4.5 + ….+ (k - 2)(k - 1) + (k – 1). k
= 1(0 + 2) + 3(2 + 4) + 5(4 + 6) + …+ (k – 1). [(k– 2) + k]
= 1.2 + 3. 6 + 5.10 +…+ (k - 1).(2k – 2)
= 1.1.2 + 3.3.2 + 5.5.2 +…+ (k – 1).(k – 1).2
= 2.[12 + 32 + 52 + ….+ (k – 1)2]
= 2.[12 + 32 + 52 + ….+ (2n + 1)2] = 2.S k – 1 .k. k + 1 2n + 1 . 2n + 2 . 2n + 3
S = A mà theo DẠNG 5 thì tổng ( ) ( ) ( ) ( ) ( ) A = = 2 3 3 2n + 1 . 2n + 2 . 2n + 3 S = ( ) ( ) ( ) 6
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 12 + 32 + 52 + …+ 992
Bài 2: Tính tổng S = 52 + 72 + 92 +…+ 1012 3
Bài 3: Tính tổng S = 112 + 132 + ….+ 20092
DẠNG 7: TỔNG CÓ DẠNG: S = 22 + 42 + 62 + …+ (2n)2 I/ PHƯƠNG PHÁP.
Áp dụng tổng A = 1.2 + 2.3 + 3.4 + 4.5 + ….+ (k - 2)(k - 1) + (k – 1). k Với k = 2n + 1
= 1.2 + 2.3 + 3.4 + 4.5 + ….+ (k - 2)(k - 1) + (k – 1). k
= 2(1 + 3) + 4(3 + 5) + 6(5 + 7) + …+ (k – 1). [(k– 2) + k]
= 2.4 + 4.8 + 6.12 +…+ (k - 1).(2k – 2)
= 2.2.2 + 4.4.2 + 6.6.2 +…+ (k – 1).(k – 1).2
= 2.[12 + 32 + 52 + ….+ (k – 1)2]
= 2.[22 + 42 + 62 + ….+ (2n)2] = 2.S k – 1 .k. k + 1 2n. 2n +1 . 2n + 2
S = A mà theo DẠNG 5 thì tổng ( ) ( ) ( ) ( ) A = = 2 3 3 2n. 2n +1 . 2n + 2 S = ( ) ( ) 6
Áp dụng tính: P = 12 + 22 + 32 + ….+ n2
Xét: S = 22 + 42 + 62 + …+ (2n)2 => S S
= = 12 + 22 + 32 + ….+ n2 => P = S 2 2 4 4
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng M = 22 + 42 + 62 + …+ 1002
Bài 2: Tính tổng N = 62 + 82 + 102 +…+ 1022
Bài 3: Tính tổng H = 122 + 142 + ….+ 20102
Bài 4: Tính tổng P = 12 + 22 + 32 + …+ 1002
Bài 5: Tính tổng Q = 12 + 22 + 32 + …+ 1012
Bài 6: Tính tổng A = 1 + 4 + 9 + 16 + 25 + …+ 10000.
Bài 7: Tính tổng K = - 12 + 22 – 32 + 42 – 52 +….- 192 + 202
Bài 8: Biết rằng 12 + 22 + 32 +…+ 102 = 385, Tính tổng S = 22 + 42 + 62 + … + 202
DẠNG 8: TỔNG CÓ DẠNG: S = a1.a2 + a2.a3 + a3.a4 + a4.a5 + ….+ an-1. an (1) I/ PHƯƠNG PHÁP.
* Với a2 – a1 = a3 – a2 = ….= an - an-1 = 2 4
S = a1.(a1 + 2) + a2. (a2 + 2) + a3. (a3 + 2) + a4. (a4 + 2) + ….+ an-1. (an - 1 + 2) = ( 2 2 2 2 a + a + a +...+ a + + + + + − 2 a a a ... a 1 2 3 n 1 ) ( 1 2 3 n 1 − ) = S1 + k. S2 Trong đó tổng S1 = 2 2 2 2
a + a + a +...+ a được tính theo DẠNG 6 và DẠNG 7. 1 2 3 n 1 −
S2 = a + a + a +...+ a được tính theo DẠNG 1. 1 2 3 n 1 −
* Với a2 – a1 = a3 – a2 = ….= an - an-1 = k > 2
Nhân cả hai vế với 3k , rồi tách 3k ở mỗi số hạng để tạo thành các số hạng mới tự triệt tiêu.
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng M = 1.3 + 3.5 + 5.7 + ….+ 49.51
Bài 2: Tính tổng N = 2.4 + 4.6 + 6.8 + …..+ 100.102
Bài 3: Tính tổng P = 1.4 + 4.7 + 7.10 + ….+ 49.52 Hướng dẫn
Vì khoảng cách giữa hai thừa số trong mỗi số hạng bằng 3
Nhân cả hai vế với 9 ta có:
9P = 1.4.9 + 4.7.9 + 7.10.9 + ….+ 46.49.9 + 49.52.9
= 1.4.(7 + 2) + 4.7.(10 – 1) + 7.10.(13 – 4) + …+ 46.49.(52 – 43) + 49.52.(55 – 46) = 1.4.2 + 49.52.55 = 140148 P = 15572
Bài 4: Tính tổng S = 2.6 + 6.10 + 10.14 + 14.18 + ….+42.46 + 50.54
DẠNG 9: TỔNG CÓ DẠNG: S = 1.a2.a3 + a2.a3 .a4 + a3.a4 .a5 + a4.a5.a6 + ….+ an-2 .an-1. an
Với a2 – 1 = a3 – a2 = a4 – a3 =….= an - an-1 = k I/ PHƯƠNG PHÁP.
Nhân hai vế với 4k, rồi tách 4k ở mỗi số hạng trong tổng để số hạng trước và số hạng sau
tạo thành những số tự triệt tiêu nhau.
4k.S = 1.a2.a3.4k + a2.a3 .a4.4k + a3.a4 .a5.4k + a4.a5.a6.4k + ….+ an-2 .an-1. an.4k = an-2 .an-1. an.(an + k)
II/ BÀI TẬP VẬN DỤNG. 5
Bài 1: Tính tổng S = 1.2.3 + 2.3.4 + 3.4.5 + …..+ 16.17.18 + 17.18.19 Hướng dẫn
Khoảng cách giữa các thừa số bằng 1 => Nhân hai vế với 4 ta được.
4S = 1.2.3.4 + 2.3.4.4 + 3.4.5.4 + …. + 16.17.18.4 + 17.18.19.4
= 1.2.3.4 + 2.3.4.(5 – 1) + 3.4.5.(6 – 2) + …+ 16.17.18.(19 – 15) + 17.18.19.(20 – 16) = 17.18.19.20 = 116280
Bài 2: Tính tổng S = 1.3.5 + 3.5.7 + 5.7.9 + …+ 95.97.99
Gợi ý: Nhân hai vế với 8
Bài 3: Tính tổng A = 1.2.3.4 + 2.3.4.5 + … + 18.19.20.21 + 19.20.21.22
Gợi ý: Nhân hai vế với 5
DẠNG 10: TỔNG CÓ DẠNG: S = 1 + 23 + 33 + 43 + …+ n3 I/ PHƯƠNG PHÁP.
Áp dụng tổng: B = 1.2.3 + 2.3.4 + … + (n - 1)n(n + 1)
Trong mỗi số hạng, tách thừa số đầu và thừa số sau theo tổng và hiệu của thừa số giữa với 1. Ta có:
B = (2 - 1).2.(2 + 1) + (3 - 1).3.(3 + 1) + … + (n - 1)n(n + 1)
= (23 - 2) + (33 - 3) + … + (n3 - n)
= (23 + 33 + …+ n3) - (2 + 3 + …+ n)
= (1 + 23 + 33 + …+ n3) - (1 + 2 + 3 + …+ n)
=> S = B + (1 + 2 + 3 + …+ n)
Trong đó: Theo DẠNG 10 thì: B = (n − ) 1 n (n + ) 1 (n + 2) 4
Theo DẠNG 1 thì: 1 + 2 + 3 + …+ n = (n + ) 1 .n 2 Vậy S = (n − ) 1 n (n + ) 1 (n + 2) + ( + ) 2 n 1 .n n(n +1) = 4 2 2 2
Hay S = 1 + 23 + 33 + 43 + …+ n3 = (1 + 2 + 3 + …+ n)2 = n(n +1) 2
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng S = 13 + 23 + 33 + … + 1003
Bài 2: Tính tổng S = 13 + 23 + 33 + … + 513 6
CHỦ ĐỀ 7: TÍNH CHẤT CHIA MỘT TỔNG
DẤU HIỆU CHIA HẾT CHO 2; 3; 5; 9 A/ KIẾN THỨC CẦN NHỚ. 1. Phép chia hết.
a,b là số TN b khác 0 . tanói a chia hết b nếu tồn tại số TN qsao cho a = b.q 2. Tính chất chung
a ⋮ b và b ⋮ c thìa a ⋮ c a ⋮ a với mọi a khác 0 0 ⋮ b với mọi b khác 0
Bất cứ số nào cũng chia hết cho 1
3. Tính chất chia hết của tổng , hiệu
* Nếu a, b cùng chia hết cho m thì a + b chia hết cho m và a - b chia hết cho m
* Tổng của 2 số chia hết cho m và 1 trong 2 số ấy chia hết cho m thì số còn lại cũng chia hết cho m
* Nếu 1 trong 2 số a, b chia hết cho m số kia không chia hết cho m thì tổng , hiệu của chúng không chia hết cho m
4. Tính chất chia hết của 1 tích
* Nếu một thừa số của tích chia hết cho m thì tích chia hết cho m
* Nếu a chia hết cho m, b chia hết cho n thì a.b chia hết cho m.n
* Nếu a chia hết cho b thì an ⋮ bn
5. DẤU HIỆU CHIA HẾT.
a. Dấu hiệu chia hết cho 2:
Một số chia hết cho 2 khi và chỉ khi chữ số tận cùng của số đó là số chẵn.
b. Dấu hiệu chia hết cho 3 (hoặc 9):
Một số chia hết cho 3 (hoặc 9) khi và chỉ khi tổng các chữ số của số đó chia hết cho 3(hoặc 9).
Chú ý: Một số chia hết cho 3 (hoặc 9) dư bao nhiêu thì tổng các chữ số của nó chia cho 3 (hoặc
9) cũng dư bấy nhiêu và ngược lại.
c. Dấu hiệu chia hết cho 5:
Một số chia hết cho 5 ⇔ chữ số của số đó có tận cùng bằng 0 hoặc bằng 5.
d. Dấu hiệu chia hết cho 4 (hoặc 25):
Một số chia hết cho 4 (hoặc 25) khi và chỉ khi hai chữ số tận cùng của số đó chia hết cho 4(hoặc 25).
e. Dấu hiệu chia hết cho 8 (hoặc 125):
Một số chia hết cho 8(hoặc 125) khi và chỉ khi ba chữ số tận cùng của số đó chia hết cho 8(hoặc 125).
f. Dấu hiệu chia hết cho 11:
Một số chia hết cho 11 khi và chỉ khi hiệu giữa tổng các chữ số hàng lẻ và tổng các chữ số hàng
chẵn(từ trái sang phải) chia hết cho 11.
II/ CÁC DẠNG BÀI TẬP.
DẠNG 1: XÉT TÍNH CHIA HẾT HAY KHÔNG CHIA HẾT.
Vận dụng tính chất chia hết của một tổng (hiệu) và các dấu hiệu chia hết cho 2; 3; 5; 9 để xét.
Bài 1: Không làm tính , xét xem tổng sau có chia hết cho 12 không ? Vì sao ? a) 120 + 36
b) 120a + 36b ( với a ; b ∈N ) Hướng dẫn:
a) 120 và 36 cùng chia hết cho 12 nên tổng 120 + 36 chia hết cho 12
b) 120 ⋮ 12 và 36 ⋮ 12 => 120a ⋮ 12 và 36a ⋮ 12 => tổng 120a + 36a chia hết cho 12
Bài 2: Cho A = 2.4.6.8.10.12 − 40 . Hỏi A có chia hết cho 6 ; cho 8 ; cho 20 không ? Vì sao? Hướng dẫn:
+ Ta có tích 2.4.6.8.10.12 ⋮ 6 nhưng 40 không chia hết cho 6 => A không chia hết cho 6
+ Ta có tích 2.4.6.8.10.12 ⋮ 6 và 40 ⋮ 8 => số A chia hết cho 8
+ Ta có tích 2.4.6.8.10.12 ⋮ 2 và 10 => Tích 2.4.6.8.10.12 ⋮ 20 và 40 ⋮ 20 => số A chia hết cho 20
Bài 3: Khi chia số tự nhiên a cho 36 ta được số dư 12 . Hỏi a có chia hết cho 4 ; cho 9 không vì sao ? Hướng dẫn:
a : 36 được thương là k và dư 12 => a = 36.k + 12
+ Ta có 36.k ⋮ 4 và 12⋮ 4 => Số a chia hết cho 4
+ Ta có 36.k ⋮ 4 và 12 không chia hết cho 4 => Số a không chia hết cho 4
Bài 4: Điền dấu X và ô thích hợp : Câu Đ S
Nếu a 4 và b 2 thì a + b 4
Nếu a 4 và b 2 thì a + b 2
Nếu tổng của hai số chia hết cho 9 và một trong hai số chia hết cho 3 thì số còn lại chia hết cho 3
Nếu hiệu của hai số chia hết cho 6 và số thứ nhất chia hết cho 6 thì số thứ hai chia hết cho 3
Nếu a 5 ; b 5 ; c không chia hết cho 5 thì abc không chia hết cho 5
Nếu a 18 ; b 9 ; c không chia hết cho 6 thì a + b + c không chia hết cho 3
125.7 – 50 chia hết cho 25
1001a + 28b – 22 không chia hết cho 7
Nếu cả hai số hạng của một tổng không chia hết cho 5 thì tổng không chia hết cho 5
Để tổng n + 12 6 thì n 3
Bài 4: Khi chia một số cho 255 ta được số dư là 170. Hỏi số đó có chia hết cho 85 không? Vì sao? Hướng dẫn:
Gọi số đó là a (a là số tự nhiên).
Vì a chia cho 255 có số dư là 170 nên a = 255.k + 170 (k là số tự nhiên).
Ta có: 255 chia hết cho 85 nên 255.k chia hết cho 85; 170 chia hết cho 85.
⇒ (255.k + 170) chia hết cho 85 (Tính chất chia hết của một tổng). Do vậy a chia hết cho 85.
DẠNG 2: CHỨNG MINH CHIA HẾT CHO MỘT SỐ.
Để chứng minh số A chia hết cho một số
+ Nếu số A là một số cụ thể ta vận dụng dấu hiệu chia hết 2 ; 3; 4; 8; 9; 11; ... để chứng minh.
+ Nếu số A có tổng hoặc hiệu các số, ta cần phân tích số A để đưa số A về hoặc hiệu hoặc tích
của các số có dấu hiệu chia hết rồi áp dụng tính chất chia hết của tổng (hiệu) haowcj tích để chứng minh.
+ Để chứng minh A chia hết cho p, ta xét mọi trường hợp về số dư khi chia A cho p.
+ Ngoài ra ta cũng có thể dùng cách tìm chữ số tận cùng của A để chứng minh A chia hết cho một số.
Bài 1: Chứng minh rằng tổng của ba số tự nhiên liên tiếp luôn chia hết cho 3. Hướng dẫn:
Gọi ba số tự nhiên liên tiếp là: a, a + 1, a + 2.
Tổng của ba số tự nhiên liên tiếp là
a + a + 1 + a + 2 = (a + a + a) + (1 + 2)
= (3a + 3) chia hết cho 3 (Tính chất chia hết của một tổng).
Vậy Có phải tổng của n số tự nhiên liên tiếp luôn luôn chia hết cho n hay không?
Bài 2: Tổng của 4 số tự nhiên liên tiếp có chia hết cho 4 hay không ?
Giải: Gọi 4 số tự nhiên liên tiếp là a, a + 1, a + 2, a + 3.
Tổng của 4 số tự nhiên liên tiếp là:
a + a + 1 + a + 2 + a + 3 = (a + a + a + a) + (1 + 2 + 3) = (4a + 6).
Do 4 chia hết cho 4 nên 4a chia hết cho 4 mà 6 không chia hết cho 4 nên
(4a + 6) không chia hết cho 4.
⇒ Tổng của 4 số tự nhiên liên tiếp không chia hết cho 4.
Kết luận: Vậy không phải lúc nào tổng n số tự nhiên liên tiếp cũng chia hết cho n
Bài 3: Chứng minh (495a + 1035b) chia hết cho 45 với mọi a , b là số tự nhiên. Hướng dẫn:
Vì 495 chia hết cho 9 nên 1980.a chia hết cho 9 với mọi a.
Vì 1035 chia hết cho 9 nên 1035.b chia hết cho 9 với mọi b.
Nên: (495a + 1035b) chia hết cho 9.
Chứng minh tương tự ta có: (1980a + 1995b) chia hết cho 5 với mọi a, b. Mà (9, 5) = 1.
⇒ (495a + 1035b) chia hết cho 45.
Bài 4: Chứng minh rằng tích của hai số chẵn liên tiếp luôn chia hết cho 8. Hướng dẫn:
Gọi hai số chẵn liên tiếp là 2n, 2n + 2.
Tích của hai số chẵn liên tiếp là: 2n.(2n + 2) = 4n.(n + 1).
Vì n, n + 1 không cùng tính chẵn lẻ nên n.(n + 1) chia hết cho 2.
Mà 4 chia hết cho 4 nên 4n.(n + 1) chia hết cho (4.2)
⇒ 4n.(n + 1) chia hết cho 8.
⇒ 2n.(2n + 2) chia hết cho 8.
Bài 5: Chứng minh rằng:
a. Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3.
b. Tích của bốn số tự nhiên liên tiếp luôn chia hết cho 4. Hướng dẫn:
a. Gọi ba số tự nhiên liên tiếp là n, n +1, n + 2.
Tích của ba số tự nhiên liên tiếp là: n.(n + 1).(n + 2).
Một số tự nhiên khi chia cho 3 có thể nhận một trong các số dư 0; 1; 2.
- Nếu r = 0 thì n chia hết cho 3 ⇒ n.(n +1).(n +2) chia hết cho 3.
- Nếu r = 1 thì n = 3k + 1 (k là số tự nhiên).
⇒ n + 2 = 3k + 1 + 2 = (3k + 3) chia hết cho 3.
⇒ n.(n + 1).(n + 2) chia hết cho 3.
- Nếu r = 2 thì n = 3k + 2 (k là số tự nhiên).
⇒ n + 1 = 3k + 2 + 1 = (3k +3) chia hết cho 3.
⇒ n.(n +1).(n +2) chia hết cho 3.
Tóm lại: n.(n +1).(n +2) chia hết cho 3 với mọi n là số tự nhiên.
b. Chứng minh tương tự ta có n.(n +1).(n +2).(n +3) chia hết cho 4 với mọi n là số tự nhiên.
Kết luận: Tích của n số tự nhiên liên tiếp luôn chia hết cho n.
Bài 6: Chứng minh rằng
a) ab + ba chia hết cho 11
b) ab − ba chia hết cho 9 với a > b Hướng dẫn:
a) ab + ba = (10a + b) + (10b + a) =11a +11b ,chia hết cho 11.
b) ab − ba =(10a + b) − (10b − a) = 9a − 9b , chia hết cho 9.
Bài 7: Chứng minh nếu ab + cd 1 1thì abcd 11 Hướng dẫn:
abcd =100.ab + cd = 99.ab + (ab + cd) 11
Bài 8: abc27 chứng minh bca27 Hướng dẫn: abc27
=> abc027 => 1000a + bc027
=> 999a + a + bc027 => 27.37a + bca27
Vì 27.37a27 nên bca27
Bài 9: Cho các chữ số 0, a, b. Hãy viết tất cả các số có ba chữ số tạo bởi ba số trên. Chứng minh rằng
tổng tất cả các số đó chia hết cho 211. Hướng dẫn:
Tất cả các số có ba chữ số tạo bởi ba chữ 0, a, b là: a b
0 ; ab0 ; ba0 ; b0a .
Tổng của các số đó là: a b
0 + ab0 + ba0 + b0a = 100a + b + 100a + 10b + 100b + 10a + 100b + a
= 211a + 211b = 211(a + b) chia hết cho 211.
Bài 10: Tìm số tự nhiên n để (3n + 14) chia hết cho (n + 2). Hướng dẫn:
Ta có 5n + 14 = 5.(n + 2) + 4.
Mà 5.(n +2) chia hết cho (n +2).
Do đó (5n + 14) chia hết cho (n +2) ⇔ 4 chia hết cho (n + 2) ⇔ (n + 2) là ước của 4. ⇔ (n +2) ∈{1; 2 ; } 4 ⇒ n ∈{0 ; } 2 .
Vậy với n ∈{0; 2} thì (5n + 14) chia hết cho (n +2).
Bài 11: Chứng minh 21132000 – 20112000 chia hết cho cả 2 và 5 Hướng dẫn:
Để số vừa chia hết cho cả 2 và 5 thì số phải có chữ số tận cùng là 0
=> Cần chứng minh số bị trừ và số trừ đều có chữ số tận cùng là 1
Chú ý: Số tự nhiên a có chữ số tận cùng là 1 thì an cũng có chữ số tận cùng là 1
21132000 = (21134)500 = ....1500 => 21132000 có chữ số tận cùng là 1
20112000 luôn có chữ số tận cùng là 1
=> 21132000 – 20112000 có chữ số tận cùng là 0 => 21132000 – 20112000 chia hết cho cả 2 và 5 Bài 12.
a) Chứng minh rằng nếu viết thêm vào đằng sau một số TN có 2 chữ số gồm chính 2 chữ số ấy
viết theo thứ tự ngược lại thì được 1 số chia hết cho 11
b) cũng chứng minh như trên đối với số TN có 3 chữ số Hướng dẫn
a) Gọi số TN có 3 chữ số là abc khi viết thêm ta được số abccba
Ta có abccba =100000a+10000b+1000c+100c+10b+a
=100001.a+10010.b+1100c chia hết cho 11
(Phần b chữ số làm tương tự )
Bài 13: Chứng minh nếu ab = 2cd thì abcd67 Hướng dẫn
abcd =100ab + cd =100.(2cd) + cd = 201.cd
Vì 201 ⋮ 67 => abcd67
Bài 14: Chứng minh rằng
a) abccba chia hết cho 7, 11, và 13
b) abcdeg chia hết cho 23 và 29, biết rằng abc = 2.deg
Bài 15: Chứng minh rằng ab + cd + eg chia hết cho 11 thì abcdeg chia hết cho
Bài 16: Chứng minh rằng tổng của ba số tự nhiên liên tiếp chia hết cho 3, tổng của 5 số tự nhiên liên
tiếp không chia hết cho 5.
Bài 17: Chứng minh rằng :
a) Tổng của ba số chẵn liên tiếp thì chia hết cho 6,
b) Tổng ba số lẻ liên tiếp không chia hết cho 6
c) Nếu a chia hết cho b và b chia hết cho c thì a chia hết cho c d) 2 3 2 = + + +.... n P a a a
+ a a +1;a,n∈ N
e) Nếu a và b chia cho 7 có cùng số dư thì hiệu a – b chia hết cho 7
Bài 18: Cho hai số tự nhiên abc và deg đều chia 11 dư 5. Chứng minh rằng số abcdeg 11
Bài 19: Cho biết số abc7.Chứng minh rằng: 2a + 3b + c7
Bài 20: Cho abc − deg 13
. Chứng minh rằng: abcdeg 13
Bài 21: Cho số abc4 trong đó a, b là các chữ số chẵn. Chứng minh rằng:
a) c4 b) bac4
Bài 22: Biết a + b7. Chứng minh rằng: aba7
DẠNG 3: TÌM ĐIỀU KIỆN ĐỂ CHIA HẾT.
Vận dụng tính chất chia hết của một tổng (hiệu) và các dấu hiệu chia hết cho 2; 3; 5; 9 để xét.
* Với bài toán điền chữ số vào * để thỏa mãn chia hết:
+ Thì ta phân tích số đó theo tổng các chữ số để lập luận chia hết cho 3 và 9
+ Dùng chữ số tận cùng để lập luận chia hết cho 2 và 5
Bài 1: Cho 1số có 4 chữ số: *26* . Điền các chữ số thích hợp vào dấu (*) để được số có 4 chữ số
khác nhau chia hết cho tất cả 4 số : 2; 3 ; 5 ; 9. Hướng dẫn:
Số đó đảm bảo chia hết cho 2 nên số đó là số chẳn.
Số đó chia hết cho 5 nên số đó phải có chữ số tận cùng là số 0 hoặc 5.
Số đó vừa chia hết cho 3 và 9 nên số đó phải có tổng các chữ số chia hết cho 9.
Vậy: Chữ số tận cùng của số đó là 0 ⇒ *260 . Chữ số đầu là số 1
Do đó số đã cho là 1260
Bài 2: Thay (*) bằng các số thích hợp để:
a) 510* ; 61*16 chia hết cho 3. ;
b) 261* chia hết cho 2 và chia 3 dư 1 Hướng dẫn
a) Để 510* ; 61*16 chia hết cho 3 thì:
5 + 1 + 0 + * chia hết cho 3; từ đó tìm được * = 0; 3; 6; 9
b) Để 261* chia hết cho 2 và chia 3 dư 1 thì:
* chẵn và 2 + 6 + 1 + * chia 3 dư 1; từ đó tìm được * = 4
Bài 3: Tìm các chữ số a,b, sao cho a) a – b = 4 và7a5 1 b 3
b) a – b = 6 và 4a7 +1 5 b 9 Hướng dẫn: a) số 7a5 1
b 3 nên 7+a+5+b 3
13+a+b 3 nên a+b chia cho 3 dư 2 (1) 4 ≤ a ≤ 9 Ta có a-b =4 nên 0 ≤ b ≤ 5
Suy ra 4 ≤ a + b ≤14 (2)
Mặt khác a-b là số chẵn nên a+b là số chẵn (3)
Từ 1,2,3 suy ra a+b = 8 hoặc 14
Với a+b=8, a-b=4 ta được a=6,b=2
Với a+b=14,a-b=4 tađược a=9,b=5 b) 4a7 +1 5
b 9 nên 512 +10(a+b) 9
504 +8+9(a+b)+a+b 9 nên a+b chia 9 dư 1
a + b ≥ a − b=6 nên a+b=10
Từ đó ta tìm được a = 8, b = 2
Bài 4: Tìm tất cả các số x, y để có số 34x5y chia hết cho 36. Hướng dẫn
Vì (4, 9) = 1 nên 34x5y chia hết cho 36 ⇔ 34x5y chia hết cho 9 và 34x5y chia hết cho 4.
Ta có: 34x5y chia hết cho 4 ⇔ 5y chia hết cho 4 ⇔ y ∈ {2 ; } 6 .
34x5y chia hết cho 9 ⇔ (3 + 4 + x + 5 + y) chia hết cho 9.
⇔ (9 + 13 + x + y) chia hết cho 9. ⇔ (3 + x + y) chia hết cho 9
Vì x, y ∈ N và 0 ≤ x; y ≤ 9 Nên x + y thuộc {6 ; } 15
Nếu y = 2 thì x = 4 hoặc x = 13 ( > 9 - Loại ).
Nếu y = 6 thì x = 0 hoặc x = 9.
Vậy các số phải tìm là: 34452; 34056; 34956.
Bài 5: Tìm số tự nhiên n để (3n + 14) chia hết cho (n + 2). Hướng dẫn
Ta có 5n + 14 = 5.(n + 2) + 4.
Mà 5.(n +2) chia hết cho (n +2).
Do đó (5n + 14) chia hết cho (n +2) ⇔ 4 chia hết cho (n + 2) ⇔ (n + 2) là ước của 4. ⇔ (n +2) ∈{1; 2 ; } 4 ⇒ n ∈{0 ; } 2 .
Vậy với n ∈{0; 2} thì (5n + 14) chia hết cho (n +2).
Bài 6: Tìm số tự nhiên n để n + 15 là số tự nhiên . n + 3 Hướng dẫn
Để n +15 là số tự nhiên thì (n + 15) chia hết cho (n + 3). n + 3
⇒ [(n + 15) - (n + 3)] chia hết cho (n + 3).
⇔ 12 chia hết cho (n +3) .
⇔ (n + 3) là Ư(12) = {1; 2; 3; 4; 6; 12}. ⇔ n ∈ {0; 1; 3; 9}.
Vậy với n ∈ {0; 1; 3; 9}thì n + 15 là số tự nhiên. n + 3
Bài 7: Phải viết thêm vào bên phải số 579 ba chữ số nào để được số chia hết cho 5; 7; 9. Hướng dẫn
Giả sử ba số viết thêm là abc .
Ta có: 579abc 5 ; 7 ; 9 ⇒ 579abc chia hết cho 5.7.9 = 315.
Mặt khác: 579abc = 579000 + abc = (315.1838 + 30 + abc ) chia hết cho 315.
Mà 315.1838 chia hết cho 315 ⇒(30 + abc ) chia hết cho 315 ⇒ 30 + abc ∈ (315).
Do 100 ≤ abc ≤ 999 ⇒ 130 ≤ 30 + abc ≤ 1029
⇒ 30 + abc ∈ {315; 630; 945}. ⇒ abc ∈{285 ; 600 ; } 915 .
Vậy ba số có thể viết thêm vào là 285; 600; 915. LUYỆN TẬP.
1) Tìm tất cả các số B = 62xy427, biết rằng số B chia hết cho 99
2) Tìm các chữ số x ,y sao cho: C = x1995y chia hết cho 55
3) Cho số 2539x với x là chữ số hàng đơn vị. Tìm x để 2539x chia hết cho cả 2 và 3.
4) Tìm các cặp số (a,b) sao cho : 4a5b45
5) Tìm số tự nhiên sao cho 4n - 5 chia hết cho 2n - 1 HƯỚNG DẪN 1)
* B chia hết cho 9 => ( 6+2+4+2+7+x+y) chia hết cho 9
=> (x+y+3) chia hết cho 9=> x+y=6 hoặc x+y =15
* B chia hết cho 11=> (7+4+x+6-2-2-y) chia hết cho11=> (13+x-y)chia hết cho 11
x – y = 9 (loại) hoặc y – x = 2
+ Với y – x = 2 và x+y=6 => y=4; x=2
+ Với y – x = 2 và x+y=15 (loại) vậy B=6224427 2)
Ta có 55 =5.11 mà (5 ;1) = 1 Do đó C =
x1995y 55 <=> C 5 (1) C 11 (2) (1) => y = 0 hoặc y = 5
+) y = 0 => x+ 9+5 – ( 1+9 +0) 11 => x = 7
+) y = 5 = > x+9 +5 – (1+9+5 ) 11 => x = 1 3)
Ta có: x =0; 1; 2; 3; 4; 5; 6; 7; 8; 9
- Vì 2539x chia hết cho 2 nên x = 0 ; 2 ; 4; 6 ; 8. .
- Vì 2539x chia hết cho 3 nên (2 + 5 + 3 + 9 + x) : 3 . Hay (19 + x) : 3 Suy ra: x = 2 ; 5 ; 8
Do đó để 2539x chia hết cho cả 2 và 3 thì x = 2 hoặc x = 8 4)
b = 0 => 9+a 9 => a = 0 hoặc a = 9
b = 5 => 14+a 9 => a = 4 5) Ta có 4n-5 = 2( 2n-1) - 3
Để 4n-5 chia hết cho 2n-1 thì 3 chia hết cho2n-1 Với 2n-1=1 => n=1 Với 2n-1=3 => n=2 vậy n=1;2
CHỦ ĐỀ 8: ƯỚC VÀ BỘI
A/ KIẾN THỨC CẦN NHỚ
1. Nhắc lại về quan hệ chia hết:
Nếu a = b.q ( b ≠ 0 ) thì ta nói a b
2. Định nghĩa Ước và Bội :
Nếu có số tự nhiên a chia hết cho b thì :
a là bội của b và b là ước của a
Tức là : a b ⇒ a là bội của b ⇒b là ước của a
3. Cách tìm ước và bội:
* Tập hợp ước của a – kí hiệu là Ư(a) . Tập hợp bội của b – Kí hiệu là B(b).
* Qui tắc tìm bội của b: Muốn tìm bội của b ta nhân b lần lượt với các số 0 ; 1 ; 2 ;
3 ; 4 …..Tích tìm được là bội của b.
Ví dụ : Tìm các bội của 6 mà nhỏ hơn 40
Ta nhân 6 lần lượt với các số 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ta được các bội nhỏ hơn 40 của
6 là : 0 ; 6 ;12 ; 18 ; 24 ; 30 ; 36.
* Qui tắc tìm ước của a: Ta có thể tìm ước của a bằng cách chia lần lượt a cho các
số từ 1 đến a . Khi a chia hết cho số nào thì số đó là ước của a .
Ví dụ: Viết tập hợp Ư(28)
Ư(28) = {1 ; 2 ; 4 ; 7 ; 14; 28}
B/ CÁC DẠNG BÀI TẬP
DẠNG 1: DẠNG TÌM ƯỚC VÀ BỘI CỦA MỘT SỐ TỰ NHIÊN.
Bài 1: Tìm tất cả các số có hai chữ số là: a) Bội của 32 b) Bội của 41
Bài 2: Tìm tất cả các số có hai chữ số là ước của : a) 50 b) 45
Bài 3: Viết các tập hợp sau.
a) Ư(6); Ư(9); Ư(12) d) B(23); B(10); B(8)
b) Ư(7); Ư(18); Ư(10) e) B(3); B(12); B(9)
c) Ư(15); Ư(16); Ư(250) g) B(18); B(20); B(14)
DẠNG 2: TÌM TỰ NHIÊN THỎA MÃN ĐIỀU KIỆN VỀ QUAN HỆ CHIA HẾT.
Bài 1: Tìm tất cả các số tự nhiên x sao cho
a) x 15 và 45 < x < 136 b) 18 x và x > 7
Bài 2: Tìm tất cả các số tự nhiên x sao cho a) 6(x −1) b) 14(2x + 3)
Bài 3: Tìm các số tự nhiên a biết : a) (a + 11) ( a + 3 )
b) ( a – 3 ) ( a – 14) b) ( 2a + 27 ) ( 2a + 1)
d) ( 5a + 28) ( a + 2) e) ( 3a + 15 ) ( 3a – 1)
Bài 4: Tìm các cặp số tự nhiên x ; y biết :
a) (3x − 2).(2y − 3) =1
b) (2x +1) ( y – 3 ) = 10 b) 2xy − x + 2y =13
c) 6xy − 9x − 4y + 5 = 0
d) 2xy − 6x + y =13
e) 2xy − 5x + 2y =148
Bài 5: Năm nay Bình học lớp 6. Tuổi của mẹ Bình là bội số tuổi của Bình và là số chia hết cho
4. Mẹ hơn Bình 24 tuổi. Tìm tuổi của Bình và mẹ Bình. Bài 6:
a) Tìm số chia và thương của một phép chia biết số bị chia bằng 145 , số dư bằng 12 và thương khác 1.
b) Tìm số chia và thương của một phép chia biết số bị chia bằng 155 , số dư bằng 12.
c) Tìm số chia của một phép chia biết số bị chia bằng 236 , số dư bằng 15 và số chia là số có hai chữ số .
Bài 7: Tìm hai số tự nhiên đều là bội của 9 biết :
a) Tổng hai số bằng *657 và hiệu hai số bằng 5*91
b) Tổng hai số bằng 513* và số lướn gấp đôi số nhỏ.
Bài 8: Tìm các số tự nhiên có ba chữ số chia hết cho cả 5 và 9 , biết rằng chữ số hàng chục bẳng
trung bình cộng của hai chữ số còn lại.
Bài 9: Tìm các số tự nhiên có ba chữ số chia hết cho cả 5 và 9 biết rằng hiệu số đó với số viết
theo thứ tự ngược lại bằng 297.
Bài 10: Tìm số tự nhiên n để 3n + 6 là số tự nhiên. n +1
DẠNG 3: CHỨNG MINH QUAN HỆ CHIA HẾT:
Bài 1: Cho n là số tự nhiên . Chứng tỏ :
a) (n + 10 ) ( n + 15) là bội của 2.
b) n ( n + 1) (n + 2) là bội của 2 và 3
c) n( n+1 )( 2n + 1) là bội của 2 là 3
Bài 2: Chứng tỏ rằng một số có ba chữ số mà chữ số hàng chục , hàng đơn vị bằng nhau và tổng
ba chữ số của số đó chia hết cho 7 thì số đó chia hết cho 7.
Bài 3: Cho hai số tự nhiên a và b . Chứng tỏ rằng :
a) Nếu a + 4b chia hết cho 13 thì 10a + b cũng chia hết cho 13 và ngược lại.
b) Nếu 3a + 2b chia hết cho 17 thì 10a + b cũng chia hết cho 17 và ngược lại. Bài 4:
a) Cho hai số abc và e
d f , giả sử abc < e
d f và mỗi số đều không chia hết cho 37 nhưng
tổng hai số đó chia hết cho 37. Chứng tỏ rằng abcdef chia hết cho 37.
b) Cho hai số abc và e
d f chia cho 7 có cùng số dư. Chứng tỏ rằng abcdef chia hết cho 7.
CHỦ ĐỀ 9: SỐ NGUYÊN TỐ - HỢP SỐ.
A/ KIẾN THỨC CẦN NHỚ. 1. Dịnh nghĩa:
* Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
* Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước. 2. Tính chất:
* Nếu số nguyên tố p chia hết cho số nguyên tố q thì p = q.
* Nếu tích abc chia hết cho số nguyên tố p thì ít nhất một thừa số của tích abc chia hết cho số nguyên tố p.
* Nếu a và b không chia hết cho số nguyên tố p thì tích ab không chia hết cho số nguyên tố p .
3. Cách nhận biết một số nguyên tố:
a) Chia số đó lần lượt cho các số nguyên tố đã biết từ nhỏ đến lớn.
- Nếu có một phép chia hết thì số đó không phải là số nguyên tố.
- Nếu chia cho đến lúc số thương nhỏ hơn số chia mà các phép chia vẫn còn số dư thì
số đó là số nguyên tố.
b) Một số có 2 ước số lớn hơn 1 thì số đó không phải là số nguyên tố.
4. Phân tích một số ra thừa số nguyên tố:
* Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một
tích các thừa số nguyên tố.
- Dạng phân tích ra thừa số nguyên tố của mỗi số nguyên tố là chính số đó.
- Mọi hợp số đều phân tích được ra thừa số nguyên tố.
A aα.bβ.....cγ = Víi , a ,
b c lµ nh÷ng sè nguyªn tè. , α , ..., β γ ∈ N vµ , α , ..., β γ ≥ 1
5. Số các ước số và tổng các ước số của một số:
Gi¶ sö A = aα.bβ.....cγ Víi , a ,
b c lµ nh÷ng sè nguyªn tè. , α , ..., β γ ∈ N vµ , α , ..., β γ ≥ 1
1. Sè c¸c íc sè cña A lµ: (α+1)( + β 1)...(γ+1). α+1 1 β+ γ 1 a
−1 b −1 c + −1
2. Tæng c¸c íc sè cña A lµ: . ... a −1 b −1 c −1 B/ CÁC DẠNG TOÁN.
DẠNG 1. NHẬN BIẾT SỐ NGUYÊN TỐ, HỢP SỐ
- Căn cứ vào định nghĩa số nguyên tố và hợp số.
- Căn cứ vào các dấu hiệu chia hết.
- Có thể dùng bảng nguyên tố ở cuối SGK để xác định một số (nhỏ hơn 1000) là số nguyên tố hay không.
Bài 1. Các số sau là số nguyên tố hay hợp số ?
312 ; 213 ; 435 ; 417 ; 3311 ; 67. Giải
Các số 312, 213, 435 và 417 là hợp số vì chúng lớn hơn 3 và chia hết cho 3.
Số 3311 là hợp số vì số này lớn hơn 11 và chia hết cho 11.
Số 67 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Bài 2. Gọi p là tập các số nguyên tố. Điền kí hiệu ∈ , ∉ hoặc ⊂ vào chỗ trống cho đúng :
83 … P, 91 … P, 15 … n, P … n Đáp số
83 ∈ P, 91 ∉ P, 15 ∈ n, P ⊂ n
Bài 3. Dùng bảng số nguyên tố ở cuối SGK, tìm các số nguyên tố trong các số sau : 117 ; 131 ; 313 ; 469 ; 647. Đáp số
Các số nguyên tố là : 131 ; 313 ; 647.
Bài 4. Tổng (hiệu) sau là số nguyên tố hay hợp số ? a) 3.4.5 + 6.7 ; b) 7.9.11.13 – 2 3.4.7; c) 5.7 + 11.13.17 ; d) 16354 + 67541. Giải
a) Mỗi số hạng của tổng đều chia hết cho 3. Tổng chia hết cho 3 và lớn hơn 3 nên là hợp số.
b) Mỗi số hạng của hiệu đều chia hết cho 7. Hiệu chia hết cho 7 và lớn hơn 7 nên là hợp số.
c) Mỗi số hạng của tổng đều là số lẻ nên tổng là số chẵn. Tổng chia hết cho 2 và lớn hơn 2 nên là hợp số.
d) Tổng tận cùng bằng 5 nên chia hết cho 5. Tổng này lại lớn hơn 5 nên là hợp số.
Bài 5. Điền dấu “x ” vào ô thích hợp : Câu Đúng Sai
a) Có hai số tự nhiên liên tiếp đều là số nguyên tố … …
b) Có ba số lẻ liên tiếp đều là số nguyên tố … …
c) Mọi số nguyên tố đều là số lẻ … …
d) Mọi số nguyên tố đều có chữ số tận cùng là một
trong các chữ số 1, 3, 7, 9. … Trả lời a) Đúng, ví dụ 2 và 3.
b) Đúng, ví dụ 3, 5 và 7.
c) Sai, ví dụ 2 là số nguyên tố chẵn.
Bổ sung thêm điều kiện để câu sau trở thành câu đúng :
Mọi số nguyên tố lớn hơn 2 đều là số lẻ.
d) Sai, ví dụ 5 là số nguyên tố tận cùng là 5.
Bổ sung : Mọi số nguyên tố lớn hơn 5 đều tận cùng bởi một trong các chữ số 1, 3, 7, 9.
DẠNG 2. VIẾT SỐ NGUYÊN TỐ HOẶC HỢP SỐ TỪ NHỮNG SỐ CHO TRƯỚC
- Dùng các dấu hiệu chia hết.
- Dùng bảng số nguyên tố nhỏ hơn 1000.
Bài 7. Thay chữ số vào dấu * để được hợp số : ; . Giải
Trong bảng số nguyên tố có 11, 13, 17, 19 là các số nguyên tố. Vậy các hợp số có
dạng là số 10, 12, 14, 15, 16, 18.
Trong bảng có 31, 37 là số nguyên tố.
Vậy các hợp số có dạng là 30, 32, 33, 34, 35, 36, 38, 39.
Cách khác: Với số có thể chọn * là 0, 2, 4, 6, 8 (để chia hết cho 2) có thể chọn
* = 5 (để chia hết cho 5).
Với số có thể chọn * là 0, 2, 4, 6, 8 (để chia hết cho 2), hoặc chọn * là 3, 9
(để chia hết cho 3), hoặc * = 5 (để chia hết cho 5).
Bài 8. Thay chữ số vào dấu * để được số nguyên tố : ;
Đáp số : 53 ; 59 ; 97. Bài 9.
a) Tìm số tự nhiên k để 3. k là số nguyên tố.
b) Tìm số tự nhiên k để 7. k là số nguyên tố. Giải
a) Với k = 0 thì 3. k = 0, không là số nguyên tố, không là hợp số.
Với k = 1 thì 3. k = 3, là số nguyên tố.
Với k ≥ 2 thì 3. k là hợp số (vì có 3 là ước khác 1 và khác chính nó).
Vậy với k = 1 thì 3. k là số nguyên tố. b) Đáp số : k = 1.
DẠNG 3: TÌM SỐ NGUYÊN TỐ, HỢP SỐ THỎA MÃN ĐIỀU KIỆN.
Bài 1: Ta biết rằng có 25 số nguyên tố nhỏ hơn 100. Tổng của 25 số nguyên tố là số chẵn hay số lẻ. HD:
Trong 25 số nguyên tố nhỏ hơn 100 có chứa một số nguyên tố chẵn duy nhất là 2, còn
24 số nguyên tố còn lại là số lẻ. Do đó tổng của 25 số nguyên tố là số chẵn.
Bài 2: Tổng của 3 số nguyên tố bằng 1012. Tìm số nguyên tố nhỏ nhất trong ba số nguyên tố đó. HD:
Vì tổng của 3 số nguyên tố bằng 1012, nên trong 3 số nguyên tố đó tồn tại ít nhất một
số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2 và là số nguyên tố nhỏ nhất. Vậy số
nguyên tố nhỏ nhất trong 3 số nguyên tố đó là 2.
Bài 3: Tổng của 2 số nguyên tố có thể bằng 2003 hay không? Vì sao? HD:
Vì tổng của 2 số nguyên tố bằng 2003, nên trong 2 số nguyên tố đó tồn tại 1 số nguyên
tố chẵn. Mà số nguyên tố chẵn duy nhất là 2. Do đó số nguyên tố còn lại là 2001. Do 2001
chia hết cho 3 và 2001 > 3.
Suy ra 2001 không phải là số nguyên tố.
Bài 4: Tìm số nguyên tố p, sao cho p + 2 và p + 4 cũng là các số nguyên tố. HD:
Giả sử p là số nguyên tố.
- Nếu p = 2 thì p + 2 = 4 và p + 4 = 6 đều không phải là số nguyên tố.
- Nếu p ≥ 3 thì số nguyên tố p có 1 trong 3 dạng: 3k, 3k + 1, 3k + 2 với k ∈N*.
+) Nếu p = 3k ⇒ p = 3 ⇒ p + 2 = 5 và p + 4 = 7 đều là các số nguyên tố.
+) Nếu p = 3k +1 thì p + 2 = 3k + 3 = 3(k + 1) ⇒ p + 2 3 và p + 2 > 3. Do đó p + 2 là hợp số.
+) Nếu p = 3k + 2 thì p + 4 = 3k + 6 = 3(k + 2) ⇒ p + 4 3 và p + 4 > 3. Do đó p + 4 là hợp số.
Vậy với p = 3 thì p + 2 và p + 4 cũng là các số nguyên tố.
Bài 5: Tìm số nguyên tố, biết rằng số đó bằng tổng của hai số nguyên tố và bằng hiệu của hai số nguyên tố. HD:
Gi¶ sö a, b, c, d, e lµ c¸c sè nguyªn tè vµ d > e.
Theo bµi ra: a = b + c = d - e (*).
Tõ (*) ⇒ a > 2 ⇒ a lµ sè nguyªn tè lÎ.
⇒ b + c vµ d - e lµ sè lÎ.
Do b, d lµ c¸c sè nguyªn tè ⇒ b, d lµ sè lÎ ⇒ c, e lµ sè ch½n.
⇒ c = e = 2 (do c, e lµ c¸c sè nguyªn tè).
⇒ a = b + 2 = d - 2 ⇒ d = b + 4.
VËy ta cÇn t×m sè nguyªn tè b sao cho b + 2 vµ b + 4 còng lµ c¸c sè nguyªn tè.
Bài 6: Tìm tất cả các số nguyên tố x, y sao cho: x2 – 6y2 = 1. HD: 2 2 2 2 2 Ta ã
c : x − 6y = 1 ⇒ x −1 = 6y ⇒ (x −1)(x +1) = 6y 2
Do 6y 2 ⇒ (x −1)(x +1)2
Mµ x - 1 + x + 1 = 2x ⇒ x - 1 vµ x + 1 cã cïng tÝnh ch½n lÎ.
⇒ x - 1 vµ x + 1 lµ hai sè ch½n liªn tiÕp 2 2
⇒ (x −1)(x +1)8 ⇒6y 8 ⇒3y 4 2
⇒ y 2 ⇒ y2 ⇒ y = 2 ⇒ x = 5
Bài 7: Tìm số nguyên tố p sao cho các số sau cũng là số nguyên tố: a) p + 2 và p + 10. b) p + 10 và p + 20. c) p + 10 và p + 14. d) p + 14 và p + 20. e) p + 2và p + 8. f) p + 2 và p + 14. g) p + 4 và p + 10. h) p + 8 và p + 10.
DẠNG 4. CHỨNG MINH MỘT SỐ LÀ SỐ NGUYÊN TỐ HAY HỢP SỐ
- Để chứng minh một số là số nguyên tố, ta chứng minh số đó không có ước nào khác
1 và khác chính nó.
- Để chứng minh một số là hợp số, ta chỉ ra rằng tồn tại một ước của nó khác 1 và
khác chính nó. Nói cách khác, ta chứng minh số đó có nhiều hơn hai ước.
Bài 1. Hãy chứng minh rằng tích của hai số nguyên tố là một hợp số. Giải
Tích của hai số nguyên tố giống nhau p.p có ba ước là 1, p và p2. Tích của hai số
nguyên tố khác nhau p1.p2 có bốn ước là 1, p1, p2 và p1.p2.
Vậy tích của hai số nguyên tố là một hợp số.
Bài 2: Cho p và p + 4 là các số nguyên tố (p > 3). Chứng minh rằng p + 8 là hợp số. HD:
Vì p là số nguyên tố và p > 3, nên số nguyên tố p có 1 trong 2 dạng: 3k + 1, 3k + 2 với k ∈N*.
- Nếu p = 3k + 2 thì p + 4 = 3k + 6 = 3(k + 2) ⇒ p + 4 3 và p + 4 > 3.
Do đó p + 4 là hợp số (Trái với đề bài p + 4 là số nguyên tố).
- Nếu p = 3k + 1 thì p + 8 = 3k + 9 = 3(k + 3) ⇒ p + 8 3 và p + 8 > 3. Do đó p + 8 là hợp số.
Vậy số nguyên tố p có dạng: p = 3k + 1 thì p + 8 là hợp số.
Bài 3: Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng 4n + 1 hoặc 4n – 1. HD:
Mỗi số tự nhiên n khi chia cho 4 có thể có 1 trong các số dư: 0; 1; 2; 3. Do đó mọi số
tự nhiên n đều có thể viết được dưới 1 trong 4 dạng: 4k, 4k + 1, 4k + 2, 4k + 3 với k ∈N*.
- Nếu n = 4k ⇒n4 ⇒n là hợp số.
- Nếu n = 4k + 2 ⇒n2 ⇒n là hợp số.
Vậy mọi số nguyên tố lớn hơn 2 đều có dạng 4k + 1 hoặc 4k – 1. Hay mọi số nguyên
tố lớn hơn 2 đều có dạng 4n + 1 hoặc 4n – 1 với n ∈N*.
Bài 4: Cho p và p + 2 là các số nguyên tố (p > 3). Chứng minh rằng p + 16. HD:
Vì p là số nguyên tố và p > 3, nên số nguyên tố p có 1 trong 2 dạng: 3k + 1, 3k + 2 với k ∈N*.
- Nếu p = 3k + 1 thì p + 2 = 3k + 3 = 3(k + 1) ⇒ p + 2 3 và p + 2 > 3.
=> p + 2 là hợp số ( Trái với đề bài p + 2 là số nguyên tố).
- Nếu p = 3k + 2 thì p + 1 = 3k + 3 = 3(k + 1) (1).
Do p là số nguyên tố và p > 3 ⇒p lẻ ⇒k lẻ ⇒k + 1 chẵn ⇒k + 12 (2)
Từ (1) và (2) ⇒p + 16. Bài 5:
a) Cho p và p + 4 là các số nguyên tố (p > 3). Chứng minh rằng: p + 8 là hợp số.
b) Cho p và 2p + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 4p + 1 là hợp số.
c) Cho p và 10p + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 5p + 1 là hợp số.
d) Cho p và p + 8 là các số nguyên tố (p > 3). Chứng minh rằng: p + 4 là hợp số.
e) Cho p và 4p + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 2p + 1 là hợp số.
f) Cho p và 5p + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 10p + 1 là hợp số.
g) Cho p và 8p + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 8p - 1 là hợp số.
h) Cho p và 8p - 1 là các số nguyên tố (p > 3). Chứng minh rằng: 8p + 1 là hợp số.
i) Cho p và 8p2 - 1 là các số nguyên tố (p > 3). Chứng minh rằng: 8p2 + 1 là hợp số.
j) Cho p và 8p2 + 1 là các số nguyên tố (p > 3). Chứng minh rằng: 8p2 - 1 là hợp số.
Bài 6: Chứng minh rằng:
a) Nếu p và q là hai số nguyên tố lớn hơn 3 thì p2 – q2 24.
b) Nếu a, a + k, a + 2k (a, k ∈N*) là các số nguyên tố lớn hơn 3 thì k 6.
CHỦ ĐỀ 10: PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ.
A. TÓM TẮT LÍ THUYẾT.
– Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một
tích các thừa số nguyên tố. Mọi số tự nhiên lớn hơn 1 đều phân tích được ra thừa số nguyên tố.
– Muốn phân tích một số ra thừa số nguyên tố ta dùng dấu hiệu chia hết cho các số
nguyên tố 2, 3, 5,… Phép chia dừng lại khi có thương bằng 1.
– Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả. B. CÁC DẠNG TOÁN.
Dạng 1. PHÂN TÍCH CÁC SỐ CHO TRƯỚC RA THỪA SỐ NGUYÊN TỐ
Thương có hai cách phân tích một số tự nhiên n (n > 1) ra thừa số nguyên tố.
Cách 1 (Phân tích theo cột dọc) : Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn),
rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy
cho đến khi thương bằng 1.
Cách 2 (Phân tích theo hàng ngang hoặc theo “sơ đồ cây”):
Viết n dưới dạng một tích các thừa số, mỗi thừa số lại viết thành tích cho đến khi các
thừa số đều là số nguyên tố.
Bài 1. Điền các số tự nhiên lớn hơn 1 vào ô vuông ở sơ đồ Giải
Bài 2. Phân tích các số sau ra thừa số nguyên tố : a) 60 ; b) 84 ; c) 285 ; d) 1035 ; e) 400 ; g) 1000 000. Đáp số
a) 60 = 22.3.5 ; b) 84 = 22.3.7; c) 285 = 3.5.19 ;
d) 1035 = 32.5.23 ; e) 400 – 24.52 ; g) 1 000 000 = 26.56.
Dạng 2. ỨNG DỤNG PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ ĐỂ TÌM CÁC ƯỚC CỦA SỐ ĐÓ
Phân tích số cho trước ra thừa số nguyên tố.
Chú ý rằng nếu c = a.b thì a và b là hai ước của c. Nhớ lại rằng:
a = b.q a ⋮ b a ∈ B(b) b ∈ Ư(a) (a, b, q ∈ N và b ≠ 0)
Bài 1. Phân tích các số sau ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho các số nguyên tố nào ? a) 225 ; b) 1800 ; c) 1050 ; d) 3060. Trả lời
225 = 32.52 ; 225 chia hết cho các số nguyên tố 3 và 5.
1800 = 23.32.52 ; 1800 chia hết cho các số nguyên tố 2, 3, 5.
1050 = 2.3.52.7 ; 1050 chia hết cho các số nguyên tố 2, 3, 5, 7.
3060 = 22.32.5.17 ; 3060 chia hết cho các số nguyên tố 2, 3, 5,17.
Bài 2. Cho a = 23.52.ll. Mỗi số 4, 8, 16, 11, 20 có là ước của a hay không ? Giải
4 = 22, 8 = 23,11, 20 = 22.5 là các số có mặt trong phân tích ra thừa số nguyên tố của a
nên chúng là các ước của a.
Sô 16 = 24 không có mặt trong phân tích trên nên 16 không là ước của a. Bài 3.
a) Cho số a = 5.13. Hãy viết tất cả các ước của a.
b) Cho số b = 25. Hãy viết tất cả các ước của b.
c) Cho số c = 32.7. Hãy viết tất cả các ước của c. Giải
a) a = 5.13 = 65 = 1.65 nên Ư(a) = {1; 5; 13; 65}.
b) b = 25 = 32 = 1.32 = 2.16 = 4.8 nên Ư(b) = {1 ; 2 ; 4 ; 8 ; 16 ; 32}
c) c = 32.7 = 63 = 1.63 = 3.21 = 7.9 nên Ư(c) = {1; 3 ; 7 ; 9 ; 21 ; 63).
Bài 4. Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số : 51; 75; 42; 30. Trả lời
51 = 3.17 => Ư(51) = {1; 3; 17 ; 51}.
75 = 3.52. => Ư(75) = {1 ; 3 ; 5 ; 15 ; 25 ; 75}.
42 = 2.3.7 => Ư(42) = {1 ; 2 ; 3 ; 6 ; 7 ; 14 ; 21 ; 42}.
30 = 2.3.5 => Ư(30) = { 1; 2 ; 3 ; 5 ; 6 ; 10 ; 15 ; 30}.
Dạng 3. BÀI TOÁN ĐƯA VỀ VIỆC PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ
Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố. Bài 1.
a) Tích của hai số tự nhiên bằng 42. Tìm mỗi số.
b) Tích của hai số tự nhiên a và b bằng 30. Tìm a và b biết rằng a < b. Giải
Mỗi số là một ước của 42. Ư(42) = {1 ; 2 ; 3 ; 6 ; 7 ; 14 ; 21 ; 42}.
Vậy các số phải tìm là 1 và 42, 2 và 21, 3 và 14, 6 và 7.
b) a và b là ước của 30 (a < b). Ư(30) = (1; 2 ; 3 ; 5 ; 6 ; 10 ; 15 ; 30). Ta có bảng sau : a 1 2 3 5 B 30 15 10 6
Bài 2. Tâm có 28 viên bi. Tâm muốn xếp số bi đó vào túi sao cho số bi ở các túi đều bằng
nhau. Hỏi Tâm có thể xếp 28 viên bi đó vào mấy túi ? (Kể cả trường hợp xếp vào một túi), Hướng dẫn
Số túi là ước của 28. Đáp số: 1, 2 , 4 , 7 , 14 , 28 túi. Bài 3.
a) Phân tích số 111 ra thừa số nguyên tố rồi tìm tập hợp các ước của 111.
b) Thay dấu * bởi chữ số thích hợp : **.* = 111. Hướng dẫn
a) 111 = 3.37. Ư(11) = {1 ; 3 ; 37 ; 111}.
b) ** là ước của 111 và có hai chữ số, ta tìm được ** = 37. Vậy ta có 27.3 = 111
CHỦ ĐỀ 11: ƯỚC CHUNG VÀ BỘI CHUNG
ƯỚC CHUNG LỚN NHẤT - BỘI CUNG NHỎ NHẤT A/ KIẾN THỨC CẦN NHỚ. I/ Ước chung, Bội chung.
1. Ước chung của hai hay nhiều số là ước của tất cả các số đó.
Ước chung của các số a, b, c được kí hiệu là ƯC(a, b, c).
2. Bội chung của hai hay nhiều số là bội của tất cả các số đó.
Bội chung của các số a, b, c được kí hiệu là: BC(a, b, c).
3. Giao của hai tập hợp là một tập hợp gồm các phần tử chung của hai tập hợp đó.
Ta kí hiệu giao của hai tập hợp A và B là A ∩ B.
II/ Ước chung lớn nhất. Bội chung nhỏ nhất 1. Định nghĩa:
* Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
* Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác không trong tập hợp các
bội chung của các số đó. 2. Cách tìm
a) Muốn tìm UCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước:
+) Bước 1: Phân tích mỗi số ra thừa số nguyên tố
+) Bước 2: Chọn ra các thừa số nguyên tố chung.
+) Bước 3: lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là UCLN phải tìm. Chú ý: +) UCLN(a,b,1)=1 +) a ; m b ;
m cm ⇒UCLN(a, ,
b c,m) = m
+) Để tìm UC ta tìm ước của UCLN các số đó.
b) Muốn tìm BCNN của hai hay nhiều số lớn hơn 1 ta thực hiện ba bước
+) Bước 1: Phân tích mỗi số ra thừa số nguyên tố
+) Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
+) Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với sô mũ lớn nhất. Tích đó chính là BCNN cần tìm. Chú ý:
+) Nếu các số đã cho đôi một nguyên tố cùng nhau thì BCNN là tích của các số đó. +) c ;
a cb ⇒UCLN(a, , b c) = c
+) Để tìm BC ta tìm bội của BCNN các số đó. 3/ Kiến thức bổ sung
+ Nếu abc và UCLN(a,c)=1 thì bc + Nếu a ;
m an ⇒ aBCNN( ; m n)
Đặc biệt nếu am ; an ; UCLN( ;
m n) =1 thì a . m n
a = d.m + Nếu UCLN( ; a b) d b = ⇒ = d.n UC LN( ; m n) = 1 q = . a m + Nếu BCNN( ; a b) q = ⇒ q = . b n UC LN( ; m n) = 1 + UCLN(a;b).BCNN(a,b)=a.b B/ CÁC DẠNG BÀI TẬP.
DẠNG 1: Tìm ƯC, BC, ƯCLN, BCNN.
Bài 1: Viết các tập hợp
a/ Ư(6), Ư(12), Ư(42) và ƯC(6, 12, 42);
b/ B(6), B(12), B(42) và BC(6, 12, 42) ĐS: a/ Ư(6) = {1;2;3; } 6 ; Ư(12) = {1;2;3;4;6;1 }
2 ; Ư(42) = {1;2;3;6;7;14;21;4 } 2 ƯC(6, 12, 42) = {1;2;3; } 6
b/ B(6) = {0;6;12;18;24;...;84;90;...;168; }
... ; B(12) = {0;12;24;36;...;84;90;...;168; } ... B(42) = {0;42;84;126;168; } ... ; BC = {84;168;252; } ...
Bài 2: Tìm ƯCLL của a/ 12, 80 và 56 b/ 144, 120 và 135 c/ 150 và 50 d/ 1800 và 90 Hướng dẫn
a/ 12 = 22.3 80 = 24. 5 56 = 33.7
Vậy ƯCLN(12, 80, 56) = 22 = 4. b/ 144 = 24. 32 120 = 23. 3. 5; 135 = 33. 5
Vậy ƯCLN (144, 120, 135) = 3.
c/ ƯCLN(150,50) = 50 vì 150 chia hết cho 50.
d/ ƯCLN(1800,90) = 90 vì 1800 chia hết cho 90. Bài 3: Tìm a/ BCNN (24, 10) b/ BCNN( 8, 12, 15) Hướng dẫn
a/ 24 = 23. 3 ; 10 = 2. 5 => BCNN (24, 10) = 23. 3. 5 = 120
b/ 8 = 23; 12 = 22. 3 ; 15 = 3.5 => BCNN( 8, 12, 15) = 23. 3. 5 = 120
DẠNG 2: Dùng thuật toán Ơclit để tìm ƯCLL (không cần phân tích chúng ra thừa số nguyên tố)
Giới thiệu thuật toán Ơclit: Để tìm ƯCLN(a, b) ta thực hiện như sau:
- Chia a cho b có số dư là r
+ Nếu r = 0 thì ƯCLN(a, b) = b. Việc tìm ƯCLN dừng lại.
+ Nếu r > 0, ta chia tiếp b cho r, được số dư r1
- Nếu r1 = 0 thì r1 = ƯCLN(a, b). Dừng lại việc tìm ƯCLN
- Nếu r1 > 0 thì ta thực hiện phép chia r cho r1 và lập lại quá trình như trên.
ƯCLN(a, b) là số dư khác 0 nhỏ nhất trong dãy phép chia nói trên.
Bài 1: Hãy tìm ƯCLN (1575, 343) Hướng dẫn:
Ta có: 1575 = 343. 4 + 203 343 = 203. 1 + 140 203 = 140. 1 + 63 140 = 63. 2 + 14 63 = 14.4 + 7 14 = 7.2 + 0 (chia hết)
Vậy: Hãy tìm ƯCLN (1575, 343) = 7
Trong thực hành người ta đặt phép chia đó như sau: 1575 343 343 203 4 203 140 1 140 63 1 63 14 2 14 7 4 0 2 Suy ra ƯCLN (1575, 343) = 7
Bài 2: Tìm ƯCLN(702, 306) bằng cách phân tích ra thừa số nguyên tố và bằng thuật toán Ơclit. ĐS: 18
Bài 2: Dùng thuật toán Ơclit để tìm a/ ƯCLN(318, 214) b/ ƯCLN(6756, 2463) ĐS: a/ 2
b/ 1 (nghĩa là 6756 và 2463 là hai số nguyên tố cùng nhau).
DẠNG 3: Tìm số chưa biết thỏa mãn điều kiện về ƯC, BC, ƯCLN, BCNN
* Nếu biết số x thỏa mãn m ⋮ x và n ⋮ x => x là ƯC(m, n)
* Nếu biết số x lớn nhất thỏa mãn m ⋮ x và n ⋮ x => x là ƯCLN(m, n)
* Nếu biết số x thỏa mãn x ⋮ m và x ⋮ n => x là BC(m, n)
* Nếu biết số x nhỏ nhất thỏa mãn x ⋮ m và x ⋮ n => x là BCNN(m, n)
* Nếu số a chia cho x dư k => số a – k ⋮ x hay x là Ư(a – k)
Bài 1/ Tìm số tự nhiên a là lớn nhất biết rằng 480 a 600 a Hướng dẫn :
vì 480 a 600 a và a là lớn nhất Nên a ∈ ƯC LN (480,600)
Ta có 480= 25.3.5 ; 600 = 23.3.52 => ƯCLN của (480,600) =23.3.5= 120 Vậy a =120
Bài 2/ Tìm số tự nhiên x biết rằng 126 x 210 x và 15 < x < 30 Hướng dẫn:
Vì 126 x ; 210 x và 15 < x < 30 nên x ∈ Ư C (126, 210) và 15 < x < 30
Ta có 126= 2.32..7 ; 210 = 2.3.5.7
=> ƯCLN(126, 210) = 2.3.7 = 42
Do đó Ư C (126,210) = { ,1 ,3 , 2 , 6 , 14 ,. 7 , 21 } 42
Vì 15 < x < 30 nên x =21
Bài 3/ Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a 15 a 18 Hướng dẫn
Vì a 15 ; a 18 và a nhỏ nhất khác 0 nên a ∈ BCNN(15,18)
Ta có 15 =3.5 ; 18 = 2.32 => BCNN(15,18) = 2.32.5 = 90 Vậy a = 90
Bài 4/ Tìm các bội chung của 15 và 25 mà nhỏ hơn 400 Hướng dẫn:
Ta có : 15=3.5 ; 25= 52 => BCNN(15,25) = 3.52 =75 Nên BC(15,25) = { , 150 , 75 , 0 , 375 , 300 , 225 ,......... 450 }.
Các bội chung của 15 và 25 mà nhỏ hơn 400 là 0, 75, 150, 225,300, 375
Bài 5. Tìm số tự nhiên a biết rằng khi chia 39 cho a thì dư 4, còn khi chia 48 cho a thì dư 6. Hướng dẫn
Chia 39 cho a thì dư 4 , nên a là ước của 39 – 4 = 35 và a > 4
Chia 48 cho a thì dư 6 nên a là ước của 48 – 6 = 42 và a > 6 .
=> a là ước chung của 35 và 42 đồng thời a > 6.
Ư(35) = { 1, 5, 7, 35} ; Ư(42) = {1,2,3,6,7,14,21,42}.
ƯC(35,42) = { 1,7}. Vậy a = 7 .
Bài 6. Tìm số tự nhiên a, biết rằng khi chia 264 cho a thì dư 24 ; khi chia 363 cho a thì dư 43. Hướng dẫn:
Số 264 chia cho a dư 24 nên a là ước của 264 − 24 = 240, a > 24
Số 363 chia cho a dư 43 nên a là ức của 363− 43 = 320, a > 43
Do a là ước chung của 240 và 320, đồng thời a > 43 .
Ư CLN (240,320) = 80 ước chung lớn hơn 43 là 80. Vậy a = 80
Bài 7. Xác định số chia và thương của một phép chia số tự nhiên biết
rằng số bị chia và các số dư được viết như sau Hướng dẫn:
Tính các tích của từng chữ số của thương với số chia, ta được:
452 − 46 = 406; 466 − 2 = 464; 210 − 36 = 174 Phép chia có dạng: 452610 Số chia 406 Thương 466 464 210 174 36
Số chia là ước chung của 406,464, 174 và lớn hơn 46 => Số chia là 58 và thương là 7803
Bài 8. Tìm số tự nhiên a nhỏ nhất sao cho a chia cho 3, cho 5 , cho 7 được số dư theo thứ tự là 2, 3, 4 Hướng dẫn
a = 3m + 2 (m ∈ N) ⇒ 2a = 6m+ 4, chia cho 3 dư 1
a = 5n + 3 (n ∈ N) ⇒ 2a = 10n + 6 chia cho 5 dư 1
a = 7 p + 4 (p ∈ N) ⇒ 2a = 14 p + 8, chia cho 7 dư 1
Do đó: 2a −1∈ BC(3,5,7) . Để a nhỏ nhất thì 2a −1 là BCNN(3,5, 7)
BCNN(3,5, 7) =105 => 2a−1 =105 => 2a =106 => a = 53
DẠNG 4: Các bài toán thực tế
Bài 1: Một lớp học có 24 HS nam và 18 HS nữ. Có bao nhiêu cách chia tổ sao cho số nam và số
nữ được chia đều vào các tổ? Hướng dẫn
Số tổ là ước chung của 24 và 18
Tập hợp các ước của 18 là A = {1;2;3;6;9;1 } 8
Tập hợp các ước của 24 là B = {1;2;3;4;6;8;12;2 } 4
Tập hợp các ước chung của 18 và 24 là C = A ∩ B = {1;2;3; } 6
Vậy có 3 cách chia tổ là 2 tổ hoặc 3 tổ hoặc 6 tổ.
Bài 2: Một đơn vị bộ đội khi xếp hàng, mỗi hàng có 20 người, hoặc 25 người, hoặc 30 người
đều thừa 15 người. Nếu xếp mỗi hàng 41 người thì vừa đủ (không có hàng nào thiếu, không có
ai ở ngoài hàng). Hỏi đơn vị có bao nhiêu người, biết rằng số người của đơn vị chưa đến 1000? Hướng dẫn
Gọi số người của đơn vị bộ đội là x (x∈N)
x : 20 dư 15 ⇒ x – 15 20
x : 25 dư 15 ⇒ x – 15 25
x : 30 dư 15 ⇒ x – 15 30
Suy ra x – 15 là BC(20, 25, 35)
Ta có 20 = 22. 5; 25 = 52 ; 30 = 2. 3. 5 => BCNN(20, 25, 30) = 22. 52. 3 = 300 BC(20, 25, 35) = 300k (k∈N)
x – 15 = 300k ⇔ x = 300k + 15 mà x < 1000 nên
300k + 15 < 1000 ⇔ 300k < 985 ⇔ k < 17 3 (k∈N) => k = 1; 2; 3 60
Chỉ có k = 2 thì x = 300k + 15 = 615 41
Vậy đơn vị bộ đội có 615 người
Bài 3.Tìm số tự nhiên bé nhất khi chia cho 2; 5; 11 và 26 đều dư 1.
Bài 4. Tìm các số tự nhiên a, b biết ƯCLN(a,b) = 5 và BCNN(ab) = 105
Bài 5. Tìm số tự nhiên nhỏ nhất khi chia cho 8 dư 6, chia cho 12 dư 10, chia cho 15 dư 13 và cxhia hết co 23.
Bài 6. Tìm hai số có 3 chữ số biết tổng của chúng là bội của 504 và thương của số lớn chia cho số nhỏ là bội của 6.
Bài 7. Cho BCN(a,b) = 60 và a = 12. Tìm b?
Bài 8. Cho một số A chia hết cho 7 và khi chia A ho 4 hoặc hoặc 6 đều dư 1. Tìm A biết A < 400.
Bài 9. Tổng số học sinh khối 6 cua một trường có khoảng từ 235 đến 250 em, khi chia cho 3 dư
2, chia cho 4 thì dư 3, chia cho 5 dư 4, chia cho 6 dư 5, chia 10 dư 9. tìm số học sinh của khối 6
DẠNG 5: Tìm hai số tự nhiên khi biết một số yếu tố trong đó có các dữ kiện về ƯCLN và BCNN.
* Dựa vào định nghĩa ƯCLN để biểu diễn hai số phải tìm, liên hệ với các yếu tố đã cho để tìm hai số.
* Quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số tự nhiên a, b đó là:
ab = (a, b).[a, b] (**)
Trong đó (a, b) là ƯCLN và [a, b] là BCNN của a và b.
* Chứng minh hệ thức (**):
Theo định nghĩa ƯCLN, gọi d = (a, b)
=> a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1 (*)
Từ (*) => ab = mnd2 ; [a, b] = mnd
=> (a, b).[a, b] = d.(mnd) = mnd2 = ab
=> ab = (a, b).[a, b] . (**)
Bài 1 : Tìm hai số tự nhiên a, b biết [a, b] = 240 và (a, b) = 16. Hướng dẫn:
Do vai trò của a, b là như nhau, không mất tính tổng quát, giả sử a ≤ b.
Từ (*), do (a, b) = 16 => a = 16m ; b = 16n (m ≤ n do a ≤ b) với m, n thuộc Z+ ;(m, n) = 1 Theo định nghĩa BCNN :
[a, b] = m.n.d = m.n.16 = 240 => m.n = 15
=> m = 1 , n = 15 hoặc m = 3, n = 5 => a = 16, b = 240 hoặc a = 48, b = 80.
Chú ý: Ta có thể áp dụng công thức (**) để giải bài toán này :
ab = (a, b).[a, b] => m.n.162 = 240.16 => m.n = 15.
Bài 2: Tìm hai số nguyên dương a, b biết ab = 216 và (a, b) = 6. Hướng dẫn :
Lập luận như bài 1, giả sử a ≤ b.
Do (a, b) = 6 => a = 6m ; b = 6n với m, n thuộc Z+ ; (m, n) = 1 ; m ≤ n.
Vì vậy : ab = 6m.6n = 36mn => ab = 216 mn = 6 => m = 1, n = 6 hoặc m = 2, n = 3
=> a = 6, b = 36 hoặc là a = 12, b = 18.
Bài 3: Tìm hai số nguyên dương a, b biết ab = 180, [a, b] = 60. Hướng dẫn:
Từ (**) => (a, b) = ab/[a, b] = 180/60 = 3.
Tìm được (a, b) = 3, bài toán được đưa về dạng bài toán 2.
Kết quả : a = 3, b = 60 hoặc a = 12, b = 15.
Chú ý: Ta có thể tính (a, b) một cách trực tiếp từ định nghĩa ƯCLN, BCNN :
Theo (*) ta có ab = m.n.d2 = 180 ; [a, b] = m.n.d = 60 => d = (a, b) = 3.
Bài 4: Tìm hai số nguyên dương a, b biết a/b = 2,6 và (a, b) = 5. Hướng dẫn:
Theo (*), (a, b) = 5 => a = 5m ; b = 5n với m, n thuộc Z+ ; (m, n) = 1.
Vì vậy : a/b = m/n = 2,6 => m/n = 13/5
=> m = 13 và n = 5 hay a = 65 và b = 25.
Chú ý : phân số tương ứng với 2,6 phải chọn là phân số tối giản do (m, n) = 1.
Bài 5: Tìm a, b biết a/b = 4/5 và [a, b] = 140. Hướng dẫn:
Đặt (a, b) = d. Vì , a/b = 4/5 , mặt khác (4, 5) = 1 nên a = 4d, b = 5d.
Lưu ý [a, b] = 4.5.d = 20d = 140 => d = 7 => a = 28 ; b = 35.
Bài 6: Tìm hai số nguyên dương a, b biết a + b = 128 và (a, b) = 16. Hướng dẫn:
Lập luận như bài 1, giả sử a ≤ b.
Ta có : a = 16m ; b = 16n với m, n thuộc Z+ ; (m, n) = 1 ; m ≤ n.
Vì vậy : a + b = 128 => 16(m + n) = 128 => m + n = 8
=> m = 1, n = 7 hoặc m = 3, n = 5 hay a = 16, b = 112 hoặc a = 48, b = 80
Bài 7: Tìm a, b biết a + b = 42 và [a, b] = 72. Hướng dẫn:
Gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1.
Không mất tính tổng quát, giả sử a ≤ b => m ≤ n.
Do đó : a + b = d(m + n) = 42 (1) [a, b] = mnd = 72 (2)
=> d là ước chung của 42 và 72 => d thuộc {1 ; 2 ; 3 ; 6}.
Lần lượt thay các giá trị của d vào (1) và (2) để tính m, n ta thấy chỉ có trường hợp d = 6
=> m + n = 7 và mn = 12 => m = 3 và n = 4 . (thỏa mãn các điều kiện của m, n).
Vậy d = 6 và a = 3.6 = 18 , b = 4.6 = 24
Bài 8: Tìm a, b biết a - b = 7, [a, b] = 140. Hướng dẫn:
Gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1.
Do đó : a - b = d(m - n) = 7 (1’) [a, b] = mnd = 140 (2’)
=> d là ước chung của 7 và 140 => d thuộc {1 ; 7}.
Thay lần lượt các giá trị của d vào (1’) và (2’) để tính m, n ta được kết quả duy nhất :
d = 7 => m - n = 1 và mn = 20 => m = 5, n = 4
Vậy d = 7 và a = 5.7 = 35 ; b = 4.7 = 28 .
Bài 9: Tìm hai số a, b biết 7a = 11b và (a, b) = 45.
Bài 10: Tìm hai số biết tổng của chúng bằng 448, ƯCLN của chúng bằng 16 và chúng có các
chữ số hàng đơn vị giống nhau.
Bài 11: Cho hai số tự nhiên a và b. Tìm tất cả các số tự nhiên c sao cho trong ba số, tích của hai
số luôn chia hết cho số còn lại.
BÀI TẬP TỔNG ÔN VỀ
ƯỚC CHUNG, ƯỚC CHUNG LỚN NHẤT
BỘI CHUNG, BỘI CHUNG NHỎ NHẤT
A/ Bài tập về ước chung I/ VÍ DỤ Ví dụ 1.
1) Số 12 có là ước chung của 24 và 40 không? Vì sao?
2) Số 13 có là ước chung của 65; 117; 195 không? Vì sao? Lời giải
1) Do 40 không chia hết cho 12 nên 12 không là ước chung của 24 và 40
2) Do 65 = 13.5; 117 = 13.9; 195 = 13.15 nên 13 là ước chung của 65; 117; 195
Ví dụ 2. Xác định các tập hợp
1) Ư(15); Ư(27); ƯC(15; 27)
2) Ư(16); Ư(20); Ư(30); ƯC(16; 20; 30) Lời giải
Trước hết phân tích các số ra thừa số nguyên tố, rồi dung nhận xét về ước số.
1) Do 15 = 3.5 nên Ư(15) = {1; 3; 5; 15}
Do 27 = 33 nên Ư(27) = {1; 3; 9; 27}. Từ đó suy ra ƯC(15; 27) = {1; 3}
2) Do 16 = 24; 20 = 22.5; 30 = 2.3.5
=> Ư(16) = {1; 2; 4; 8; 16}; Ư(20) = {1; 2; 4; 5; 10; 20};
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.
Từ đó suy ra ƯC(16; 20; 30) = {1; 2}
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Xác định các tập hợp
a) Ư(25); Ư(39); Ư(25; 39).
b) Ư(100);Ư(120);Ư(140);Ư(100; 120; 140).
Bài 2. Một khu đất hình chữ nhật dài 60m, rộng 24m. Người ta cần chia thành những khu đất
hình vuông bằng nhau (độ dài cạnh là một tự nhiên mét) để trồng hoa. Hỏi có bao nhiêu cách
chia? Cách chia nào thì diện tích hình vuông lớn nhất?
Bài 3. Bạn Lan có 48 viên bi đỏ, 30 viên bi xanh, 66 viên bi vàng. Lan muốn chia đều số bi vào
các túi sao cho mỗi túi đều có cả ba loại bi. Hỏi Lan có thể chia bằng mấy cách chia? Với cách
chia bi vào nhiều túi nhất thì mỗi túi có bao nhiêu bi mỗi loại?
Bài 4. Linh và Loan mua một số hộp bút chì màu, số bút đựng trong mỗi hộp bằng nhau và lớn
hơn 1. Kết quả Linh có 15 bút chì màu, Loan có 18 bút chì màu. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?
Bài 5. Hai lớp 6A và 6B tham gia phong trào “Tết trồng cây”. Mỗi em trồng được số cây như
nhau. Kết quả lớp 6A trồng được 132 cây, lớp 6B trồng được 135 cây. Hỏi mỗi lớp có bao nhiêu học sinh?
Bài 6. Tìm số tự nhiên a biết rằng khi chia số 111 cho a thì dư 15, còn khi chia 180 cho a thì dư 20
B/ Bài tập về tìm ước chung lớn nhất I/ VÍ DỤ
Ví dụ 1. Tìm ƯCLN của: 1) 32 và 80 2) 16; 32 và 128 3) 2009 và 3000 Lời giải
1) ƯCLN(32; 80) = ƯCLN(32; 16) = ƯCLN(16; 0) = 16
2) ƯCLN(16; 32; 128) = ƯCLN(16; 0; 0) = 16
3) ƯCLN(2009; 3000) = ƯCLN(2009; 991) = ƯCLN(991; 27) = ƯCLN(27; 19) = 1
Ví dụ 2. Một mảnh đất hình chữ nhật có chiều dài 120m, chiều rộng 36m. Người ta muốn trồng
cây xung quanh vườn sao cho mỗi góc vườn có một cây và khoảng cách giữa hai cây liên tiếp
bằng nhau. Hỏi số cây phải trồng ít nhất là bao nhiêu? Lời giải
Muốn số cây phải trồng ít nhất thì khoảng cách giữa hai cây trồng liên tiếp phải lớn nhất,
ta gọi khoảng cách này là a mét (a ∈ ) thì a phải là số lớn nhất sao cho 120a và 36a.
Vậy a = ƯCLN(120; 36)
Ta có 36 = 22.32; 120 = 23.3.5 nên a = 22.3 = 12
Vậy khoảng cách lớn nhất giữa hai cây trồng liên tiếp là 12m
Chu vi của vườn là: (120 + 36).2 = 312 (m)
Tổng số cây ít nhất phải trồng là: 312 : 12 = 26 (cây)
Ví dụ 3. Tìm ƯCLN rồi tìm ước chung của các số sau 1) 60 và 88 2) 150; 168; 210 Lời giải 1) 60 = 22.3.5; 88 = 23.11
Nên ƯCLN(60; 88) = 22 = 4 ⇒ƯC(60; 88) = {1; 2; 4}
2) 150 = 2.3.52; 168 = 23.3.7; 210 = 2.3.5.7
Nên ƯCLN(150; 168; 210) = 2.3 = 6 ⇒ƯC(150; 168; 210) = {1; 2; 3; 6}
II/ BÀI TẬP VẬN DỤNG
Bài 7. Tìm số tự nhiên a lớn hơn 25, biết rằng các số 525; 875; 280 đều chia hết cho a
Bài 8. Tìm ƯCLN và tập hợp ước chung của các số sau: a) 10; 20; 70 b) 5661; 5291; 4292
Bài 9. Tìm ƯCLN của hai số tự nhiên a và a + 2
Bài 10. Cho ƯCLN(a; b) = 1. Hãy tìm ƯCLN(11a + 2b; 18a + 5b)
Bài 11. Trong cuộc thi học sinh giỏi cấp Tỉnh cho ba môn Văn, Toán, Ngoại Ngữ có số học sinh
tham dự như sau: môn Văn có 96 học sinh dự thi, môn Toán có 120 học sinh dự thi, môn Ngoại
Ngữ có 72 học sinh dự thi. Trong buổi tổng kết giải các bạn được phân công đứng thành hàng
dọc, sao cho mỗi hàng có số bạn thi mỗi môn bằng nhau. Hỏi có thể phân công học sinh đứng
thành ít nhất bao nhiêu hàng?
C/ Bài tập về tập hợp I/ VÍ DỤ Ví dụ 1.
1) Viết tập hợp A các số tự nhiên là ước số của 50
2) Viết tập hợp B các số tự nhiên là bội số của 5
3) Viết tập hợp C = A∩B. Dùng kí hiệu ⊂ để thể hiện quan hệ giữa các tập hợp A, B, C. Lời giải
1) Do 50 = 2.52 nên A = Ư(50) = {1; 2; 5; 10; 25; 50}
2) B = B(5) = {5k| k ∈ }
3) C = A∩B = {5; 10; 25; 50}
Mối quan hệ C ⊂ B; C ⊂ A.
Ví dụ 2. Tìm giao của hai tập hợp A và B, biết rằng:
1) A là tập hợp các học sinh giỏi Ngoại Ngữ, B là tập hợp các học sinh giỏi Toán.
2) A là tập hợp các số chia hết cho 5, B là tập hợp các số không chia hết cho 10 Lời giải
1) A∩B là tập hợp các học sinh giỏi cả Toán và Ngoại Ngữ
2) A là tập hợp các số có tận cùng là 0 hoặc 5, B là tập hợp các số có tận cùng khác 0
Suy ra A∩B là tập hợp các số tự nhiên có tận cùng là 5
Ví dụ 3. Trong một lớp 6 có 8 học sinh giỏi Văn, 10 học sinh giỏi Toán và 5 học sinh giỏi cả
Toán và Văn. Hỏi lớp này có bao nhiêu học sinh giỏi? Lời giải
Nhận thấy 5 học sinh giỏi cả Toán và Văn vừa được tính trong số học sinh giỏi Toán, vừa
được tính trong số học sinh giỏi Văn, tức là được tính hai lần. Vì vậy số học sinh giỏi trong lớp
là: 8 + 10 – 5 = 13 (bạn)
II/ BÀI TẬP VẬN DỤNG
Bài 12. Tìm giao của hai tập hợp A và B, biết rằng
a) A là tập hợp các học sinh hát hay, B là tập hợp các học sinh múa dẻo.
b) A là tập hợp các số chia hết cho 4, B là tập hợp các số chia hết cho 10.
c) A là tập hợp các bội số của 15, B là tập hợp các bội số của 46.
d) A là tập hợp các số chẵn, B là tập hợp các số lẻ.
Bài 13. Cho hai tập hợp A = {n∈ | n là ước số của 15}, B = {n∈ | n là ước số của 25}. Tìm A∩B và A∪B.
Bài 14. Lớp 6A có 35 học sinh. Sau khi điều tra ý thích của các em về bơi, bóng đá, cầu lông,
giáo viên Thể dục biết:
a) Có 5 em thích cả bơi, bóng đá, cầu lông.
b) Có 7 em thích bơi và cầu lông.
c) Có 6 em thích bơi và bóng đá.
d) Có 9 em thích bóng đá và cầu lông.
e) Có 17 em thích bóng đá. g) Có 11 em thích bơi.
Hỏi có bao nhiêu em thích cầu lông?
D/ Bài tập về bội chung, bội chung nhỏ nhất I/ VÍ DỤ Ví dụ 1.
1) Số 88 có là bội chung của 22 và 40 không? Vì sao?
2) Số 124 có là bội chung của 31; 62 và 4 không? Vì sao? Lời giải
1) Do 88 không chia hết cho 40 nên 88 không là bội chung của 22 và 40.
2) Do 124 = 4.31 = 2.62 nên 124 chia hết cho 4; 31; 62.
Vậy 124 có là bội chung của 31; 62 và 4.
Ví dụ 2. Số đội viên của một liên đội là số có ba chữ số nhỏ hơn 300. Mỗi lần xếp thành 3 hàng,
7 hàng, 10 hàng đều vừa đủ. Tính số đội viên của liên đội đó. Lời giải
Gọi số đội viên của liên đội là a (100 ≤ a < 300 )
Do mỗi lần xếp thành 3 hàng, 7 hàng, 10 hàng đều vừa đủ nên a chia hết cho 3; 7; 10.
Tức là a ∈BC(3; 7; 10). Ta có BCNN(3; 7; 10) = 210 nên a là bội của 210 mà a< 300 nên a = 210
Vậy số đội viên của liên đội đó là 210 đội viên
Ví dụ 3. Tìm số có ba chữ số, biết rằng khi đem số đó chia cho 20; 25; 30 đều được cùng số dư là 15. Lời giải
Gọi số cần tìm là a (100 ≤ a ≤ 999)
a chia cho 20; 25; 30 cùng có số dư là 15 nên a – 15 ∈ BC(20; 25; 30)
Mà BCNN(20; 25; 30) = 300 nên a – 15 là bội của 30 ⇒a – 15 ∈ {300; 600; 900}
Vì vậy a ∈{315; 615; 915}.
Ví dụ 4. Số học sinh của lớp 6A có không quá 50 em. Khi xếp 2 hàng thì thừa 1 em, xếp 3 hàng
thì thừa 2 em, xếp 7 hàng thì thừa 6 em. Tính số học sinh của lớp 6A. Lời giải
Gọi số học sinh của lớp 6A là a(a ≤ 50)
Theo bài ra ta có a chia cho 2; 3; 7 có các số dư lần lượt là 1; 2; 6 nên a + 1 ∈ BC(2; 3; 7)
Mà BCNN(2; 3; 7) = 42 nên a + 1 là bội số của 42 và a +1≤ 51 nên a + 1 = 42 ⇒a = 41
Vậy số học sinh của lớp 6A là 41 học sinh.
Nhận xét:
- Số tự nhiên a chia cho m; n; p có cùng số dư là r thì a – r∈ BC(m; n; p)
- Số tự nhiên a chia cho m; n; p có số dư lần lượt là r; t; u sao cho m – r = n – t = p – u =
c thì a + c∈ BC(m; n; p).
II/ BÀI TẬP VẬN DỤNG.
Bài 15. Xác định các tập hợp a) B(25); B(39); B(25; 39) b) BC(100; 120; 140)
Bài 16. Một số tự nhiên khi chia cho 4 dư 3, chia cho 5 dư 4; chia cho 6 dư 5. Biết rằng số đó
nằm trong khoảng từ 200 đến 400. Hãy tìm số tự nhiên đó.
Bài 17. Số học sinh của một trường THCS là một số có ba chữ số lớn hơn 800. Mỗi lần xếp
hàng 5; hàng 6; hàng 7; hàng 8 đều vừa đủ không thừa học sinh nào. Hỏi trường đó có bao nhiêu học sinh?
Bài 19. Hai bạn An và Bình thường đến thư viện đọc sách. An cứ 7 ngày đến thư viện một lần.
Bình cứ 10 ngày đến thư viện một lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi
sau ít nhất bao nhiêu ngày thì hai bạn lại cùng đến thư viện?
Bài 19. Ba đội công nhân cùng trồng một số cây như nhau. Tính ra mỗi công nhân đội I trồng 7
cây, mỗi công nhân đội II trồng 8 cây, mỗi công nhân đội III trồng 6 cây. Tính số công nhân
mỗi đội, biết rằng số cây mỗi đội phải trồng trong khoảng từ 100 đến 200.
Bài 20. Một rổ trứng khi đếm theo chục hoặc tá đều thừa 6 quả, khi đếm theo 9 quả một thì vừa
hết. Hỏi rổ trứng đó có bao nhiêu quả? Biết rằng số trứng trong khoảng từ 100 đến 200 quả.
Bài 21. Một bến xe cứ 15 phút lại có một chuyến xa buýt rời bến, 20 phút lại có một chuyến xe
khách rời bến, 5 phút lại có mốt chiếc xe taxi rời bến. Lúc 5 giờ, một xe taxi, một xe khách, một
xe buýt rời bến cùng một lúc. Hỏi lúc mấy giờ lại có ba xe cùng rời bến một lần tiếp theo?
E/ Bài tập về quan hệ giữa ước chung, bội chung, ước chung lớn nhất, bội chung nhỏ nhất
I. PHƯƠNG PHÁP GIẢI
Kí hiệu d∈ ƯC(a; b); d* = ƯCLN(a; b), m∈ BC(a; b); m* = BCNN(a; b) thì d ≤ d* ≤ * m ≤ m
mm*; m*d *; d *d
m*.d* = ƯCLN(a; b). BCNN(a; b) = a.b (1)
Đặc biệt nếu ƯCLN(a; b) = 1 thì BCNN(a; b) = a.b II. VÍ DỤ
Ví dụ 1. Dựa vào công thức (1), hãy tìm 1) BCNN(15; 18) 2) BCNN(16; 25) Lời giải
1) ƯCLN(15;18) = 3 nên BCNN(15; 18) = (15.18):3 = 90
2. ƯCLN (6; 25) = 1 nên BCNN(6; 25) = 6.25 = 150
Ví dụ 2. Tìm hai số tự nhiên a và b, biết rằng: ƯCLN(a; b) = 3 và BCNN(a; b) = 90. Lời giải
Từ ƯCLN(a; b) = 3 suy ra ƯCLN( a ; b ) = 1 và áp dụng công thức (1) ta có: 3 3
a.b = ƯCLN(a; b) . BCNN(a; b) = 3.90 = 270 suy ra a ; b = 30 3 3
Viết 30 thành tích hai số nguyên tố cùng nhau:
30 = 1.30 = 2.15 = 3.10 = 5.6. Ta có bảng (a ≤ b ): a b a b 3 3 1 30 3 90 2 15 6 45 3 10 9 30 5 6 15 18
Ví dụ 3. Tìm hai số tự nhiên a và b biết a + b = 20 và BCNN(a; b) = 15 Lời giải
Gọi d = ƯCLN(a; b) thì d ∈ƯC(20; 15). Mà ƯCLN(20; 15) = 5 nên d = 1 hoặc d = 5
Nếu d = 1 thì a.b = 1.15 = 15 = 1.15 = 3.5, khi đó a + b = 3 + 5 = 8 hoặc a + b = 1 + 15 =
16 (Mâu thuẫn với giả thiết a + b = 20)
Nếu d = 5 thì a.b = 5.15 = 75, a + b = 20. Tìm được a = 5; b = 15
Vậy hai số tự nhiên cần tìm là: 5 và 15 III. BÀI TẬP
Bài 22. Vận dụng công thức (1) để tính nhanh 1) BCNN(325; 189) 2) BCNN(428; 564)
Bài 23. Tìm hai số tự nhiên lớn hơn 1, nguyên tố cùng nhau và có bội chung nhỏ nhất bằng 18.
Bài 24. Tìm hai số tự nhiên a, b. Biết ƯCLN(a; b) = 5 và BCNN(a; b) = 60
Bài 25. Tìm hai số tự nhiên a, b. Biết a – b = 6 và BCNN(a; b) = 180
Bài 26. Tìm hai số tự nhiên a, b. Biết a.b = 891 và ƯCLN(a; b) = 3 HƯỚNG DẪN Bài 1.
a) Ư(25) = {1; 5; 25}; Ư(39) = {1; 3; 13; 39}; ƯC(25; 39) = {1}.
b) Ư(100) = {1; 2; 4; 5; 10; 20; 25; 50; 100}
Ư(120) = {1; 2; 3; 4; 5; 6; 8; 10; 12; 15; 20; 24; 30; 40; 60; 120}
Ư(140) = {1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140}
ƯC(100; 120; 140) = {1; 2; 4; 5; 10; 20}
Bài 2. Chiều dài cạnh hình vuông là ƯC(24; 60) = {1; 2; 3; 4; 6; 12}. Có 6 cách chia, trong đó
cách chia cạnh hình vuông bằng 12m thì hình vuông có diện tích lớn nhất.
Bài 3. Số túi bi là ƯC(48; 30; 66) = {1; 2; 3; 6} nên Lan có 4 cách chia bi. Trong đó số túi
nhiều nhất là 6, lúc đó mỗi túi có 8 bi đỏ, 5 bi xanh và 11 bi vàng
Bài 4. Mỗi hộp bút chì có 3 bút chì màu
Bài 5. Mỗi em trồng 3 cây. Lớp 6A có 44 học sinh, lớp 6B có 45 học sinh.
Bài 6. Do 111 chia cho a dư 5 nên 111 – 15 = 96 a và a> 15.
180 chia cho a dư 20 nên 180 – 20 = 160 a và a> 20.
Vậy a là ƯC(96; 160) lớn hớn 20. Tìm được a = 32.
Bài 7. ƯCLN(525; 875; 280) = 35, a là Ư(35) và a > 25 nên a = 35
Bài 8. a) ƯCLN(10; 20; 70) = 10
ƯC(10; 20; 70) ={1; 2; 5; 10}
b) ƯCLN(5661; 5291; 4292) = 1 ƯC(5661; 5291; 4292) = {1}
Bài 9. Gọi d là ƯC(a; a + 2); ta có a d và a + 2d
Do đó 2 d, tức là d = 1 hoặc 2
- Với a lẻ thì ƯCLN(a; a + 2) = 1.
- Với a chẵn thì ƯCLN(a; a + 2) = 2 Bài 10:
Gọi d là ƯCLN của 11a +2b và 18a +5b
=> 11a +2b chia hết cho d và 18a +5b chia hết cho d
=> 18.(11a + 2b) chia hết cho d và 11(18a + 5b) chia hết cho d
=> 11(18a + 5b) - 18.(11a + 2b) chia hết cho d => 19b chia hết cho d
=> 19 chia hết cho d hoặc b chia hết cho d
=> d là ước của 19 hoặc d là ước của b (1)
Tương tự ta cũng có 5.(11a + 2b) chia hết cho d và 2(18a + 5b) chia hết cho d
=> 5.(11a + 2b) - 2(18a + 5b) chia hết cho d => 19a chia hết cho d
=> 19 chia hết cho d hoặc a chia hết cho d
=> d là ước của 19 hoặc d là ước của a (2)
Từ (1) và (2) suy ra d là ước của 19 hoặc d là ước chung của a và b => d = 19 hoặc d = 1
Vậy ƯCLN của 11a + 2b và 18a + 5b là 19 hoặc 1 Bài 11:
Số hàng ít nhất khi số học sinh trong một hàng nhiều nhất.
Vì số học sinh mỗi môn trong một hàng là bằng nhau nên số học sinh mỗi hàng phải là ƯCLN(96; 120; 72) = 24
=> Số hàng ít nhất là: (96 + 120 + 72) : 24 = 12 hàng
Bài 16: a : 4 dư 3 ; a : 5 dư 4 ; a : 6 dư 5 => a + 1 là BC(4, 5, 6)
Mà 200 ≤ a ≤ 400 => a ∈ {239; 299; 359}
Bài 17. Tương tự Ví dụ 3: Trường đó có 840 học sinh.
Bài 18. Số ngày ít nhất để An và Bình lại cùng đến thư viện là BCNN(7; 10) = 70.
Bài 19. Số cây mỗi đội trồng là BC(6; 7; 8) và nằm trong khoảng từ 100 đến 200.Tìm được số
cây mỗi đội trồng là 168. Đội I có 24 công nhân, đội II có 21 công nhân, đội III có 28 công nhân.
Bài 20. Tương tựVí dụ 3: Trong rổ có 126 quả trứng.
Bài 21. Số thời gian ba loại xe lại cùng rời bến là BCNN(15; 20; 5) = 60 (phút).
Bài 22. Vận dụng công thức (1) để tính nhanh
1) Do ƯCLN(325; 189) = 1 nên BCNN(325;189) = 325.189 = 61425
2) Do ƯCLN(428; 564) = 4 nên BCNN(428; 564) = 428.564 : 4 = 965568
Bài 23. Gọi hai số cần tìm là a, b. Ta có ƯCLN(a; b) = 1 và BCNN(a; b) = 18
Theo công thức (1) có a.b = 18 = 1.18 = 2.9. Vậy hai số cần tìm là 1 và 18 hoặc 2 và 9.
Bài 24. Tương tự Ví dụ 2: Ta tìm được a = 5; b = 60 hoặc a = 15; b = 20
Bài 25. Gọi d = ƯCLN(a; b) thì d∈ƯC(180; 6)
Mà ƯCLN(180; 6) = 6 nên d∈{1; 2; 3; 6}
Nếu d = 1 thì a.b = 180, a – b = 6 nên không tồn tại.
Nếu d = 2, khi đó a.b = 180.2 = 360 và a – b = 6 nên không tồn tại.
Nếu d = 3, khi đó a.b = 180.3 = 530 và a – b = 6 nên không tồn tại.
Nếu d = 6, khi đó a.b = 180.6 = 1080 và a – b = 6. Tìm được a = 36; b = 30
Bài 26. BCNN(a; b) = 891 : 3 = 297
Tương tự Ví dụ 2: tìm được a = 27; b = 33
CHỦ ĐỀ 13: TẬP HỢP SỐ NGUYÊN. A/ KIẾN THỨC CẦN NHỚ.
B/ CÁC DẠNG BÀI TẬP CƠ BẢN.
DẠNG 1: Xác định số nguyên, biểu diễn số nguyên trên trục số. So sánh hai số nguyên.
I. PHƯƠNG PHÁP GIẢI
1. Cách biểu diễn số nguyên trên trục số
- Số nguyên dương a nằm bên phải điểm 0 và cách 0 là a đơn vị
- Số nguyên âm b nằm bên trái điểm 0 và cách 0 là b = b đơn vị
2. Cách nhận biết một số nguyên: Trong các số đã biết thì số thập phân và phân số thực sự không phải số nguyên
3. Để so sánh hai số nguyên
- Nếu a, b đều nguyên dương thì so sánh như đã biết về số tự nhiên
- Nếu a, b đều nguyên âm và a < b thì a > b
- Nếu a nguyên âm, b nguyên dương thì a < b II. BÀI TẬP MẪU.
Bài 1. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? 1) –3 ∈ 2) 7 ∈ 3) 4,5 ∈ 4) 0 ∈ 5) ∈ 6) ⊂ Lời giải
Số 7 và 0 là số nguyên nên 2) và 4) Đúng
Số –3 không là số tự nhiên; 4,5 không là số nguyên nên 1) và 3) Sai
Tập là tập con của nên 6) Đúng 5) Sai
Bài 2. Vẽ một trục số
1) Biểu diễn các số 2; –3; 4; –6; 0; 3; 4 trên trục số
2) Cho biết những điểm cách điểm 0 bốn đơn vị biểu diễn những số nào? Nhận xét về những
điểm cách đều 0 biểu diễn những số nào?
3) Khẳng định, trên trục số điểm nào ở gần điểm 0 hơn thì biểu diễn số nhỏ hơn có đúng không? Hãy phát biểu cho đúng. Lời giải 1)
− 5 − 4 − 3 − 2 − 1 0 1 2 3 4 5
2) Những điểm cách 0 bốn đơn vị biểu diễn số 4 và –4 (hai số đối nhau). Những điểm cách đều
0 biểu diễn hai số đối nhau.
3) Khẳng định Sai. Cần phát biểu lại như sau: Trên trục số (nằm ngang), đối với những điểm
nằm bên phải điểm 0, điểm nào ở gần điểm 0 hơn thì biểu diễn số nhỏ hơn. Đối với những điểm nằm
bên trái điểm 0, điểm nào gần điểm 0 hơn thì biêu diễn số lớn hơn. Bài 3.
1) Sắp xếp các số nguyên sau theo thứ tự tăng dần: –12; 3; 15; 12; –7; –6; 0
2) Tìm số nguyên x sao cho 3 − < x < 9 Lời giải
1) Sắp xếp các số nguyên sau theo thứ tự tăng dần: –12; –7; –6; 0; 3; 12; 15.
2) Những số nguyên x cần tìm là: –2; –1; 0; 1; 2; 3; 4; 5; 6; 7; 8 Bài 4.
1) Tìm số đối của mỗi số nguyên sau: –15; 0; 3; 7.
2) Tìm số liền sau của mỗi số nguyên sau: –13; 0; 1; 7 Lời giải
1) Số đối của –15 là 15; số đối của 0 là 0; số đối của 3 là –3; số đối của 7 là –7.
2) Số liền sau của một số hơn số đó 1 đơn vị, do đó: Số liền sau của mỗi số nguyên –13; 0; 1; 7
lần lượt là –12; 1; 2; 8.
Bài 5. Vẽ một trục số và cho biết:
a) Những điểm nằm cách điểm 3 bốn đơn vị.
b) Những điểm nằm giữa các điểm 4 − và 2 . Lời giải
a) Những điểm nằm cách điểm 3 bốn đơn vị: 7 và 1 −
b) Những điểm nằm giữa các điểm 4 − và 2 : 3 − ; 2 − ; 1 − ;0;1.
III. BÀI TẬP VẬN DỤNG.
Bài 1. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? a) 6∈ b) 6 − ∈ c) 4,5∈ d) 0∈ e) 6 − ∈ g) 6∈
Bài 2. Điền kí hiệu thích hợp vào dấu …. 7 − .... 3 .... 0 .... 12 − .... 4,5 .... 1 .... 100 − .... 10 .... 3
Bài 3. Vẽ một trục số
a) Biểu diễn các số 2; –3; 4; –6; 0; 3; –4 trên trục số.
b) Cho biết những điểm cách điểm 0 bốn đơn vị biểu diễn những số nào? Nhận xét về những
điểm cách đều 0 biểu diễn những số nào?
c) Khẳng định “trên trục số điểm nào ở gần điểm 0 hơn thì biểu diễn số nhỏ hơn” có đúng
không? Nếu không đúng hãy phát biểu lại cho đúng.
Bài 4. Tìm số nguyên x sao cho: a) 8 − < x < 4 b) 2 − ≤ x ≤10 c) 7 − < x ≤1 d) 5 − ≤ x <1
Bài 5. Sắp xếp các số nguyên sau theo thứ tự giảm dần: 20 − ;10; 0; − 3; − 5; 17. Bài 6.
a) Tìm số đối của mỗi số nguyên sau: –298; 25; 0; –53; 71.
b) Tìm số liền sau của mỗi số nguyên sau: –63; 0; 11; –27
c) Tìm số liền trước của mỗi số nguyên sau: –110; 99; –999; 1000; 0. HƯỚNG DẪN
Bài 1. Các khẳng định đúng là a), d), e), g). Các khẳng định sai là b), c).
Bài 2. Cách điền như sau:
– 7∉N; 3∈Z; 0∈N; –12∈Z; 4,5∉Z; 1 ∉N; –100∈Z; 10∈Z 3 Bài 3.
a) Biểu diễn các số 2, –3, 4, –6, 0, 3, –4 trên trục số như sau:
b) Những điểm cách đều điểm 0 bốn đơn vị biểu diễn là số 4 và –4.
Những điểm cách đều 0 biểu diễn hai số đối nhau.
c) Khẳng định sai. Chẳng hạn, trên trục số điểm –3 gần điểm 0 hơn điểm –6, nhưng –3 > –6. Phát biểu đúng như sau:
Trên trục số, những điểm nằm bên trái điểm 0, điểm nào gần 0 hơn thì lớn hơn, những điểm nằm
bên phải điểm 0, điểm nào gần 0 hơn thì nhỏ hơn. Bài 4. a) x ∈{ 7 − ; 6 − ; 5 − ; 4 − ; 3 − ; 2 − ; 1 − ;0;1;2; } 3 ; b) x ∈{ 2; − 1 − ;0;1;2;3;4;5;6;7;8;9;1 } 0 ; c) x ∈{ 6 − ; 5 − ; 4 − ; 3 − ; 2 − ;− } 1 ; d) x ∈{ 5 − ; 4 − ; 3 − ; 2 − ; 1 − ; } 0 ;
Bài 5. Sắp xếp các số nguyên sau theo thứ tự giảm dần: 17, 10, 0, –3, –5, –20. Bài 6.
a) Số đối của mỗi số nguyên –289, 25, 0, –53, 71 thứ tự là: 289, –25, 0, 53, –71.
b) Số liền sau của mỗi số nguyên –63, 0, 11, –27 thứ tự là: –62, 1, 12, –26.
c) Số liền trước của mỗi số nguyên –110, 99, –999, 1000, 0 thứ tự là: –1111, 98, –1000, 999, –1.
DẠNG 2: Giá trị tuyệt đối của số nguyên
I. PHƯƠNG PHÁP GIẢI
* Với a nguyên thì a là số tự nhiên
* Tìm số nguyên x sao cho x = a
- Nếu a là số nguyên dương thì x = a hoặc a = –a. - Nếu a = 0 thì x = 0.
- Nếu a là số nguyên âm thì không có số x nào thỏa mãn.
* Tìm số nguyên x sao cho x
x ∈{0; 1; 2; … ; a – 1}. Tức là x ∈{0; ±1; ± 2;....; ± (a−1)}.
* Tìm số nguyên x sao cho x >a (a là số nguyên dương) thì cần tìm x sao cho
x ∈{a+1; a + 2; … }. Tức là x ∈{ ± (a +1); ± (a + 2);....}. II. BÀI TẬP MẪU
Bài 1. Tính giá trị của các biểu thức sau 1) 7 − − 4 − 2) 8 − − 3 − 3) 32 : 4 − 4) 0 + 16 − − 15 − Lời giải 1) 7 − − 4 − = 7 – 4 = 3 2) 8 − − 3 − = 8 – 3 = 5 3) 32 : 4 − = 32 : 4 = 8 4) 0 + 16 − − 15 − = 0 + 16 – 15 = 1
Bài 2. Tìm số nguyên x biết rằng 1) x = 5 2) x = 0 3) x = 5 − 4) x =10 và x > 0 5) x = 7 và x < 0 Lời giải
1) x = 5 ⇔ x = 5 hoặc x = 5 −
2) x = 0 ⇔ x = 0 3) x = 5
− ; do x > 0 nên không tồn tại số x nào
4) x =10 ⇔ x =10 hoặc x = 10
− vì x> 0 nên x = 10
5) x = 7 ⇔ x = 7 hoặc x = 7
− vì x < 0 nên x = 7 −
Bài 3. Tìm số nguyên x và biểu diễn chúng trên trục số: 1) x < 5 2) x ≥10 Lời giải
1) Cách 1: x < 5 nên x = 0; 1; 2; 3; 4.
- Với x = 0 thì x = 0
- Với x =1 thì x = 1 ±
- Với x = 2 thì x = 2 ±
- Với x = 3 thì x = 3 ±
- Với x = 4 thì x = 4 ±
Biểu diễn trên trục số
− 4 − 3 − 2 − 1 0 1 2 3 4 Cách 2: x < 5 ⇔ 5
− < x < 5và x là số nguyên nên: x ∈{0; ±1; ± 2; ± 3; ± 4}
2) x ≥10 nên x ≥10 hoặc x ≤ 10
− và x là số nguyên nên
x ∈{....;−13;−12;−11; 11; 12; 13;....}
Biểu diễn trên trục số:
… −14 −13 −12 −11 0 11 12 13 14 …
Bài 4: Tìm x∈ biết: 2000 − < | x | ≤ 2. Lời giải
x ∈ thì | x |∈
Ta có: | x | = 0; 1; 2 => x = 0; 1; 1; − 2; − 2
III. BÀI TẬP VẬN DỤNG
Bài 1. Tìm giá trị của các biểu thức sau a) 5 − + 3 + 15 + 1 − b) 9 − + 7 − + 5 − + 3 − + 1 − Bài 2.
a) Tìm số nguyên âm a sao cho a = 50.
b) Tìm số nguyên dương b sao cho b =15 .
Bài 3. Tìm các số nguyên x và biểu diễn chúng trên trục số a) 2 < x <10 b) x ≤ 7 c) x ≥ 5
Bài 4. So sánh các cặp số sau a) 12 − và 12 b) 11 − và 13 − c) 15 − và 14
Bài 5. Tìm x∈ để | x | 1963 +
đạt giá trị nhỏ nhất.
Bài 6. Tìm x, y∈ biết: | x | + | y |= 2 HƯỚNG DẪN Bài 1. a) 5 − + 3 + 15 − + 1 − = 5 + 3 +15 +1 = 24; b) 9 − + 7 − + 5 − + 3 − + 1 − = 9 + 7 + 5 + 3 +1 = 25. Bài 2. a) a = 5 − 0; b) b =15; c) c =10 hoặc c = 10. − Bài 3. a) x ∈{ 3
± ; ± 4; ± 5; ± 6; ± 7; ± 8; ± } 9 b) x ∈{0; ±1; ± 2; 3 ± ; ± 4; ± 5; ± 6; ± } 7 c) x ∈{ ± 5; ± 6; ± 7; 8; ± . }. Bài 4. a) 12 − = 12 ; b) 11 − < 13 − ; c) 15 − > 14 .
Bài 5: x∈ thì | x |∈ Ta có | x | 1963 +
≥1963. Dấu “=” xảy ra ⇔ x = 0.
Vậy giá trị nhỏ nhất của | x | 1963 + là 1963.
Bài 6: Ta có: | x |∈ ; | y |∈ | x | 0 2 1 | y | 2 0 1 x 0 2 ± 1 ± y 2 ± 0 1 ±
CHỦ ĐỀ 14: PHÉP CỘNG SỐ NGUYÊN.
TÍNH CHẤT CỦA PHÉP CỘNG SỐ NGUYÊN A. KIẾN THỨC CẦN NHỚ
1. Phép cộng hai số nguyên
- Để cộng hai số nguyên cùng dấu ta cộng hai giá trị tuyệt đối của chúng rồi đặt trước kết
quả tìm được dấu chung của chúng
- Hai số nguyên đối nhau có tổng bằng 0
- Để cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt đối của
chúng (số lớn trừ số nhỏ) rồi đặt kết quả tìm được dấu của số có giá trị tuyệt đối lớn hơn
2. Tính chất của phép cộng. Với mọi ; a ; b c ∈ ta có:
- Tính chất giao hoán: a + b = b + a
- Tính chất kết hợp: (a + b) + c = a + (b + c)
- Cộng với 0: a + 0 = 0 + a = a
- Cộng với số đối: a + (−a ) = −a + a = 0
- Nếu a + b = 0 thì a=− b và b = −a
B. CÁC DẠNG BÀI TẬP CƠ BẢN
DẠNG 1: Thực hiện phép cộng I. Phương pháp giải.
- Để thực hiện phép cộng các số nguyên, ta cần áp dụng quy tắc cộng hai số nguyên
- Tổng của một số với một số dương thì lớn hơn chính nó
- Tổng của một số với một số âm thì nhỏ hơn chính nó
- Tổng của một số với 0 thì bằng chính nó
- Tổng của hai số đối nhau bằng 0 II. Bài tập mẫu. Bài 1. Tính 1) 2316 + 115 2) ( 315 − ) + ( 1 − 5) 3) ( 215 − ) +125 4) ( 200) − + 200 Lời giải 1) 2316 + 115 = 2431 2) ( 315 − ) + ( 1 − 5) = −( 315 − + 15 − ) = −(315 +15) = 330 − 3) ( 215 − ) +125 = −( 215 − −125) = −(215 −125) = 90 − 4) ( 200) −
+ 200 = 0 (do 200 và –200 là hai số đối nhau) Bài 2. So sánh 1) 125 và 125 + ( 2 − ) 2) –13 và (–13) + 7 3) –15 và (–15) + (–3) Lời giải
1) Do –2 < 0 nên 125 > 125 + ( 2 − )
2) Do 7 > 0 nên –13 < (–13) + 7
3) Do –3 < 0 nên –15 > (–15) + (–3)
Bài 3. Tính và nhận xét kết quả tìm được 1) 52 + ( 23 − ) và ( 53 − ) + 23 2) 15 + ( 15 − ) và ( 27 − ) + 27 Lời giải 1) 52 + ( 23 − ) = 30 và ( 53 − ) + 23 = 30
− ; 30 và –30 là hai số đối nhau
Nhận xét: Khi đổi dấu các số hạng của tổng thì tổng đổi dấu. 2) 15 + ( 15 − ) = 0 và ( 27 − ) + 27 = 0
Nhận xét: Tổng của hai số đối nhau bất kì luôn bằng nhau và bằng 0.
III. Bài tập vận dụng.
Bài 1. Điền số thích hợp vào bảng sau a 13 –5 –12 –10 –10 12 b 21 3 –17 25 10 –12 a + b –8 8
Bài 2. Tính giá trị của các biểu thức
a) x + 123 với x = –23
b) (–203) + y với y = 16
c) z + (–115) với z = –20 Bài 3. Hãy so sánh a) 801 + (–65) và 801 b) (–125) + 15 và (–125)
c) (–123) + (–20) và (–123) d) 116 + (–20) và 116
Bài 4.Tính tổng của các số nguyên x thỏa mãn: 2009 − < x ≤ 2008 Bài 5.
a) Viết mỗi số dưới đây dưới dạng tổng của hai số nguyên bằng nhau:86;− 42;− 2286;2008
b)Viết mỗi số dưới đây dưới dạng tổng của ba số nguyên bằng nhau:33;−60;+3000;−369
Bài 6.Cho tập hợp A ={−51;47}; B ={23; 8 − }.
Viết tập hợp các giá trị của biểu thức x + y với x∈ ; A y ∈ B
Bài 7. Cho a, b là các số nguyên có bốn chữ số. Tìm giá trị lớn nhất, giá trị nhỏ nhất của tổng a + . b
Bài 8. Cho A ={ 14 − ;21; 23 − ;34;19; }
0 . Tìm x, y thuộc A , x và y khác nhau sao cho
a) Tổng x + y đạt giá trị lớn nhất.
b) Tổng x + y đạt giá trị nhỏ nhất.
Bài 9. Tính tổng của tất cả các số nguyên có giá trị tuyệt đối nhỏ hơn 43. HƯỚNG DẪN
Bài 1. Điền số thích hợp vào ô trống như sau: a 13 -5 -12 -10 -10 -2 12 b 21 3 -17 25 2 10 -12 a+b 34 -2 -29 15 -8 8 0 Bài 2.
a) Với x = -23, ta có x +123 = 23 − +123 =100; b) Với y = 16 thì ( 203 − ) + y = ( 203 − ) +16 = 187 − ; c) Với z = 20 − thì z + ( 115 − ) = 20 − + ( 115 − ) = 135. − Bài 3. a) 801+ ( 65 − ) < 801; b) ( 125 − ) +15 > ( 125 − ) c) ( 123 − ) + ( 20 − ) < ( 123 − ) d) 116 + ( 20 − ) <116 Bài 4: 2009 −
< x ≤ 2008; x ∈ Suy ra: x = 2008 − ; − 2007; ... ;2007; 2008.
Tổng các số nguyên x cần tìm là: ( 2008 − + 2008) + ( 2007 − + 2007) +...+ ( 1
− +1) + 0 = 0 + 0 +...+ 0 + 0 = 0 Bài 5: a) 86 = 43+ 43 42 − = ( 21 − ) + ( 21 − ) 2286 − = ( 1143 − ) + ( 1143 − ) 2008 =1004+1004 b) 33 =11+11+11 60 − = ( 20) − + ( 20) − + ( 20) − 3000 + =1000 +1000 +1000 369 − = ( 123 − ) + ( 123 − ) + ( 123 − )
Bài 6: M ={− 28; 59 − ; 70; 39} Bài 7.
Giá trị lớn nhất của a +b là: 9999+9999 =19998
Giá trị nhỏ nhất của a +b là: ( 9999 − )+( 9999 − ) = 19998 − Bài 8. 23 − < 14
− < 0 <19 < 21< 34
a) Tổng x + y đạt giá trị lớn nhất là: 21+34 = 55
b) Tổng x + y đạt giá trị nhỏ nhất là: −(23) +( 14 − ) = 37 − Bài 9.
Ta có x∈ thì x ∈ . Mà x < 43=> x = 0;1;2;...;42 x = 0; 1 ± ; 2 ± ; 3 ± ;...; 42 ± Tổng cần tìm là: 0+( 1 − + ) 1 + ( 2 − + 2) +...+ ( 42
− + 42) = 0 + 0 + 0 +...+ 0 = 0
DẠNG 2: Vận dụng tính chất của phép cộng các số nguyên tính tổng đại số
I/ Phương pháp giải.
Muốn tính nhanh kết quả của tổng đại số, cần vận dụng các tính chất của phép cộng các
số nguyên để thực hiện phép tính một cách hợp lí. Có thể cộng các số nguyên âm với nhau, các
số nguyên dương với nhau, rồi tính tổng chung. Nếu trong tổng có hai số nguyên đối nhau thì
nhóm cộng chúng với nhau. II/ Bài tập mẫu. Bài 1. Tính nhanh
1) 215 + 43 + (–215) + (–25)
2) (–312) + (–327) + (–28) + 27 Lời giải
1) 215 + 43 + (–215) + (–25) = [(215 + (–215)] + (–25) + 43 = 43 – 25 = 18
2) (–312) + (–327) + (–28) + 27 = [(–312) + (–28)] + [(–327) + 27]
= (–340) + (–300) = –640
Bài 2. Tính tổng của tất cả các số nguyên có giá trị tuyệt đối nhỏ hơn 20 Lời giải
Các số nguyên có giá trị tuyệt đối nhỏ hơn 20 là các số nguyên lớn hơn –20 và nhỏ hơn
20, tức là các số –19; –18; –17; …; 17; 18; 19.
Tổng của các số nguyên đó là ( 19) − + ( 18 − ) + ( 17 − ) + ....+17 +18 +19 = [( 19) − +19]+[( 18 − ) +18]+[( 17 − ) +17] + ....+[( 1 − ) +1] + 0 = 0
III/ Bài tập vận dụng. Bài 1. Hãy tính a) ( 457 − ) + ( 123 − ) + 23 + 237 b) ( 135 − ) + 48 +140 + ( 5 − )
Bài 2. Tìm tổng của tất cả các số nguyên x thỏa mãn a) 5 − < x < 8 b) 12 − < x <12 c) x ≤ 88
Bài 3. Tính tổng sau đây một cách hợp lí a) 329 + 64 + ( 329) − + 36 b) ( 464) − + ( 371 − ) + 564 + 71
Bài 4. Điền số nguyên vào ô trống sao cho ba số liền nhau trong bảng có tổng bằng 0 5 –15
Bài 5. Điền số nguyên vào ô trống sao cho bốn số liền nhau trong bảng có tổng bằng 0 –4 0 7
Bài 6. Vào một buổi sáng nhiệt độ ở Trung Quốc là –5oC. Nhiệt độ đếm hôm đó là bao nhiêu,
biết nhiệt độ giảm đi 6oC? Bài 7. Tính nhanh: a) 287 − + 499 + ( 499) − + 285 b) 3+ ( 5 − ) + 7 + ( 9) − +11+ ( 13 − ) +15 + ( 17 − )
Bài 8. Thực hiện phép tính M =1+ ( 2 − ) + 3+ ( 4 − ) +...+ 2001+ ( 2002 − )+ 2003 HƯỚNG DẪN Bài 1. a) ( 457 − ) + ( 123 − ) + 23+ 237 = ( 457 − ) + ( 123 − ) + (23+ 237) = 580 − + 260 = 320. − b) ( 135 − ) + 48+140 + ( 5 − ) = ( 135 − ) + ( 5 − ) + (48 +140) = 140 − +188 = 48. Bài 2.
a) Các số nguyên x sao cho 5 − < x < 8 là: 4; − 3 − ; 2; − 1
− ;0;1;2;3;4;5;6;7 và có tổng bằng 18. b) 0 c) 0. Bài 3. a) 329 + 64 + ( 329 − ) + 36 = 329 + ( 329 − ) + (64 + 36) = 100; b) ( 464 − ) + (− ) 371 + 564 + 71 = ( 464 − + 564) + ( 371 − + ) 71 = 200. −
Bài 4. Cách điền số nguyên vào ô trống sao cho ba số liền nhau trong bảng có tổng bằng 0 như sau: 10 5 -15 10 5 -15 10 5 -15
Bài 5. Cách điền số nguyên vào ô trống sao cho bốn số liền nhau trong bảng có tổng bằng 0 như sau: -4 -3 0 7 -4 -3 0 7 -4 -3 0 7 -4
Bài 6. Nhiệt độ đêm hôm đó là o 11 − C Bài 7: a) 287 − + 499 + ( 499) − + 285 = ( 287 − )+285 +499+ ( 499 − ) = ( 2 − ) + 0 = 2 − b) 3+ ( 5 − ) + 7 + ( 9) − +11+ ( 13 − ) +15 + ( 17 − ) = [3+ ( 5 − )]+[7 + ( 9) − ]+[11+ ( 13 − )]+[15 + ( 17 − )] = ( 2) − + ( 2) − + ( 2) − + ( 2) − = − 8 Bài 8: M =1+ ( 2 − ) + 3+ ( 4 − ) +...+ 2001+ ( 2002 − )+ 2003 =1+( 2 − + 3) + ( 4 − + 5) +...+ ( 2002 − + 2003) =1+1+1+...+1=1002 1002sohang
CHỦ ĐỀ 15: PHÉP TRỪ HAI SỐ NGUYÊN.
QUY TẮC DẤU NGOẶC. QUY TẮC CHUYỂN VẾ
A. KIẾN THỨC CẦN NHỚ
1. Phép trừ hai số nguyên
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b. a – b = a + (–b)
Phép trừ trong luôn thực hiện được
2. Quy tắc dấu ngoặc
- Khi bỏ dấu ngoặc có dấu “–“ đứng trước, ta phải đổi dấu các số hạng trong ngoặc: dấu
“+” thành dấu “–“; dấu “–“ thành dấu “+”.
- Khi bỏ dấu ngoặc có dấu “+” đứng trước, thì dấu các số hạng trong ngoặc vẫn giữ nguyên
a + (b − c + d) = a + b − c + d
a − (b − c + d) = a − b + c − d
3. Quy tắc chuyển vế
Khi chuyển về một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu các
số hạng đó: dấu “+” thành dấu “–“; dấu “–“ thành dấu “+”.
Nếu a + b − c = d thì a + b = c + d ; a = b
− + c + d; a − d = b − + c ; ….
4. Một số tính chất thường dùng khi biến đổi các đẳng thức
Nếu a = b thì a + c = b + c
Nếu a + c = b + c thì a = b
5. Một dãy các phép tính cộng trừ các số nguyên gọi là tổng đại số.
Trong một tổng đại số, ta có thể:
- Thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.
- Đặt dấu ngoặc để nhóm các số hạng một cách tùy ý với chú ý rằng nếu trước dấu ngoặc
là dấu “–“ thì ta phải đổi dấu tất cả các số hạng trong ngoặc.
a + b − c − d = a − c + b − d = a + b − (c + d)
B. CÁC DẠNG TOÁN CƠ BẢN
DẠNG 1: Quy tắc phép trừ hai số nguyên
I/ Phương pháp giải.
- Để thực hiện phép trừ hai số nguyên, ta biến đổi phép trừ thành phép cộng với số đối rồi
thực hiện quy tắc cộng hai số nguyên đã biết
a − b = a + ( b − ) a − ( b − ) = a + b
- Hai số a và –a là hai số đối của nhau, ta có: a = −(−a)
a + (−a) = a − a = 0 II/ Bài tập mẫu.
Bài 1. Biểu diễn các hiệu sau thành tổng rồi tính: 1) ( 23 − ) −12 2) 43− ( 53 − ) 3) ( 15 − ) − ( 17 − ) 4) 14 – 20 Lời giải 1) ( 23 − ) −12 = ( 23 − ) + ( 12) − = 35 − 2) 43− ( 53 − ) = 43 + 53 = 96 3) ( 15 − ) − ( 17 − ) = ( 15 − ) +17 = 2 4) 14 – 20 = 14 + ( 20) − = 6 −
Bài 2. Tìm khoảng cách giữa hai điểm a và b trên trục số, biết rằng: 1) a = 5; b =10 2) a = 6; − b = 1 − 1 3) a = 3 − ; b = 6 4) a = 6; b = 7 − Lời giải
Khoảng cách giữa hai điểm a và b trên trục số bằng hiệu của số lớn trừ đi số nhỏ và bằng
a – b (nếu a > b) hoặc bằng b – a (nếu a < b). Trong mỗi trường hợp ta có kết quả sau
1) b − a =10 − 5 = 5
2) a − b = ( 6) − − ( 11 − ) = 6 − +11 = 5
3) b − a = 6 − ( 3) − = 6 + 3 = 9
4) a − b = 6 − ( 7 − ) = 6 + 7 =13
Bài 3. Tìm số nguyên x, biết rằng 1) 4 + x = 7 2) x + ( 5 − ) = 1 − 8 3) ( 14) − + x − 7 = 10 − 4) ( 12) − − x − ( 19) − = 0 Lời giải
1) 4 + x = 7 ⇔ x = 7 − 4 ⇔ x = 3 2) x + ( 5 − ) = 1 − 8 ⇔ x = ( 1 − 8) − ( 5) − ⇔ x = 1 − 3 3) ( 14) − + x − 7 = 10 − ⇔ x + ( 14) − + ( 7 − ) = 10 − ⇔ x = 10 − − ( 21 − ) =11 4) ( 12) − − x − ( 19) − = 0 ⇔ ( 12) −
+19 − x = 0 ⇔ x =19 −12 ⇔ x = 7
III. Bài tập vận dụng.
Bài 1. Bạn Nam có 10 nghìn đồng, bạn mua quyển sách giá 15 nghìn đồng. Hỏi bạn Nam còn bao nhiêu đồng?
Bài 2. Biểu diễn các hiệu sau thành tổng rồi tính 1) ( 100) − −12 2) 143− ( 123 − ) 3) ( 116) − − ( 16) − 4) ( 123 − ) − 20
Bài 3. Điền số thích hợp vào bảng sau: a 1 − 4 − 8 0 b 5 10 − 18 13 − a − b −a b −
Bài 4. Tìm khoảng cách giữa hai điểm a và b trên trục số, biết rằng 1) a = 12 − ; b =12 2) a = 7; − b = 1 − 4 3) a = 2; − b = 8 4) a =13; b = 14 −
Bài 5. Tìm số nguyên x, biết rằng 1) ( 5 − ) + x = 7 2) 12 + x + ( 5 − ) = 18 − 3) ( 14) − − x + ( 15 − ) = 10 − 4) x − ( 19) − − ( 11 − ) = 0
Bài 6. Ba bạn An, Bình, Cam tranh luận về kí hiệu –a như sau:
An nói: “ –a luôn là số nguyên âm vì nó có dấu “–“ đằng trước”
Bình nói khác: “ –a là số đối của a, nên a là số nguyên dương”.
Cam tranh luận lại: “ –a có thể là bất kì số nguyên nào, vì –a là số đối của a nên nếu a là
số nguyên dương thì –a là số nguyên âm, nếu –a =0 thì a = 0”
Bạn đồng ý với ý kiến nào?
Bài 7. Ba bạn Quyết, Thắng, Trung tranh luận về các số hạng của phép trừ như sau:
Quyết nói: “Trong một phép trừ thì số bị trừ luôn không nhỏ hơn số trừ và hiệu số”
Thắng tranh luận: “Chưa đúng, tớ có thể tìm được một phép trừ trong đó số bị trừ nhỏ
hơn số trừ và hiệu số”
Trung nói thêm: “Theo tớ, phép trừ hai số nguyên luôn thực hiện được và số bị trừ có thể
lớn hơn, bằng hoặc nhỏ hơn số trừ và hiệu”
Bạn đồng ý với ý kiến của ai? Vì sao? Cho ví dụ? HƯỚNG DẪN
Bài 1. Nam còn -5 nghìn đồng, tức là Nam phải nợ 5 nghìn đồng. Bài 2. a) ( 100 − ) −12 = ( 100 − ) + ( 12 − ) = 112 − ; b) 143− ( 123 − ) =143+123 = 266; c) ( 116 − ) −( 16 − ) = ( 116 − ) +16 = 100 − ; d) ( 123 − ) − 20 = 123 − + ( 20 − ) = 143. − Bài 3. a -1 -4 8 0 b 5 -10 18 -13 a – b -6 6 -10 13 -a 1 4 -8 0 -b -5 10 -18 13
Bài 4. Khoảng cách giữa hai điểm a và b trên trục số là a − b nên ta có kết quả: a) 24 b) 7 c) 10 d) 27 Bài 5. a) ( 5
− ) + x = 7 ⇔ x = 7 − ( 5 − ) ⇔ x =12 b) 12 + x + ( 5 − ) = 18 − ⇔ x = 18 − −12 + 5 ⇔ x = 25 − c) ( 14 − ) − x + ( 15 − ) = 10 − ⇔ x = ( 14 − ) + ( 15 − ) +10 ⇔ x = 19. − d) x − ( 19 − ) − (− )
11 = 0 ⇔ x +19 +11 = 0 ⇔ x = 30. −
Bài 6. Bạn Cam nói đúng.
Bài 7. Bạn Trung nói đúng. Có thể xảy ra các khả năng. Ví dụ:
6 − 5 =1 thì 6 > 5 và 6 > 1; ( 7 − ) − ( 3 − ) = 4 − thì ( 7 − ) > 3 − và 7 − < 4; − ( 8 − ) − ( 10 − ) = 2 thì ( 8 − ) < 2 và 8 − > 1 − 0; 8 −10 = 2
− thì 8 <10 và 8 > 2. −
DẠNG 2: Quy tắc dấu ngoặc
I/ Phương pháp giải.
Để tính nhanh các tổng, ta áp dụng quy tắc dấu ngoặc để bỏ dấu ngoặc, trước ngoặc có
dấu “–“ khi bỏ dấu ngoặc phải đổi dấu các số hạng trong ngoặc, trước ngoặc có dấu “+” khi
bỏ ngoặc giữ nguyên dấu các số hạng bên trong ngoặc. Sau đó áp dụng các tính chất giao
hoán, kết hợp trong tổng đại số. Chú ý gộp các cặp số hạng đối nhau hoặc các cặp số hạng có
kết quả chẵn chục, chẵn trăm,….
Hoặc ta cần nhóm các số hạng vào trong ngoặc: Nếu đặt dấu “–“ đằng trước dấu ngoặc
thì phải đổi dấu các số hạng đó, còn nếu đặt dấu “+” đằng trước dấu ngoặc thì vẫn giữ nguyên dấu các số hạng đó. II/ Bài tập mẫu. Bài 1. Tính nhanh 1) (2354 − 45) − 2354 2) ( 2009) − − (234 − 2009)
3) (16 + 23) + (153−16 − 23)
4) (134 −167 + 45) − (134 + 45) Lời giải
Vận dụng quy tắc dấu ngoặc và tính chất giao hoán, kết hợp ta có:
1) (2354 − 45) − 2354 = 2354 − 45 − 2354 = 2354 − 2354 − 45 = 45 − 2) ( 2009) − − (234 − 2009) = ( 2009) − − 234 + 2009 = ( 2009) − + 2009 − 234 = 234 −
3) (16 + 23) + (153−16 − 23) =16 + 23+153−16 − 23 = (16 −16) + (23− 23) +153 =153
4) (134 −167 + 45) − (134 + 45) =134 −167 + 45 −134 − 45 = (134 −134) + (45 − 45) −167 = 167 −
Bài 2. Thu gọn các tổng sau:
1) (a + b + c) − (a − b + c)
2) (a + b − c) + (a − b) − (a − b − c)
3) −(a − b − c) − (−a + b + c) − (a − b + c) Lời giải
Vận dụng quy tắc dấu ngoặc ta có:
1) (a + b + c) − (a − b + c) = a + b + c − a + b − c = 2b
2) (a + b − c) + (a − b) − (a − b − c) = a + b − c + a − b − a + b + c = a + b
3) −(a − b − c) − (−a + b + c) − (a − b + c) = −a + b + c + a − b − c − a + b − c = −a + b − c
Bài 3. Cho x = 53
− , y = 45, z = 15
− . Tính giá trị của biểu thức sau 1) x + 8 − y
2) x + y + z − y
3) 16 + x − (y + z) − x Lời giải
1) x + 8 − y = ( 53 − ) + 8 − 45 = 45 − − 45 = 90 −
2) x + y + z − y = x + z = ( 53 − ) + ( 15 − ) = 68 −
3) 16 + x − (y + z) − x =16 −[45 + ( 15 − )] =16 − 30 = 14 −
Nhận xét: Trước khi thay số vào tính ta nên thu gọn phép tính
III/ Bài tập vận dụng. Bài 1. Tính nhanh a) (1456 + 23) −1456 b) ( 1999) − − ( 234 − −1999)
c) (116 +124) + (215 −116 −124)
d) (435 −167 −89) − (435 −89)
Bài 2. Thu gọn các tổng sau:
a) (a − b + c − d) − (a + b + c + d)
b) (−a + b − c) + (a − b) − (a − b + c)
c) −(a − b − c) + (b − c + d) − (−a + b + d)
Bài 3. Cho a = 13
− ; b = 25; c = 30
− . Tính giá trị biểu thức
a) a + a +12 − b
b) a + b − (c + b)
c) 25 + a − (b + c) − a
Bài 4. Tính tổng đại số sau một cách hợp lí a) 382 + 531− 282 − 331
b) 7 −8 + 9 −10 +11−12 +...+ 2009 − 2010 c) 1
− − 2 − 3 − 4 −...− 2009 − 2010
d) 1− 3− 5 + 7 − 9 −11+....+1000 −1002 −1004 HƯỚNG DẪN Bài 1.
a) (1456 + 23) −1456 = (1456 −1456) + 23 = 23. b) ( 1999 − ) −( 234 − −1999) = ( 1999 − ) + 234 +1999 = ( 1999 − +1999) + 234 = 234;
c) (116 +124) + (215 −116 −124) = (116 −116) + (124 −124) + 215 = 215;
d) (435 −167 −89) − (435 −89) = (435 − 435) + ( 89 − + 89) −167 = 167. − Bài 2.
a) (a − b + c − d) − (a + b + c + d) = a − b + c − d − a − b − c − d = 2 − b − 2d = 2 − (b + d)
b) (−a + b − c) + (a − b) − (a − b + c) = −a + b − c + a − b − a + b − c = −a + b − 2c;
c) −(a − b − c) + (b − c + d) − (−a + b + d) = −a + b + c + b − c + d + a − b − d = b.
Bài 3. Cho a = -13, b = 25, c = -30. Ta có
a) a + a +12 − b = 2a − b +12 = 2.( 13 − ) − 25 +12 = 39 −
b) a + b − (c + b) = a − c = 13 − + 30 =17.
c) 25 + a − (b + c) − a = 25 − b − c = 25 − 25 + 30 = 30. Bài 4.
a) 382 + 531− 282 − 331 = (382 − 282) + (531− ) 331 =100 + 200 = 300;
b)7 −8 + 9 −10 +11−12 +...+ 2009 − 2010
= (7 −8) + (9 −10) + (11−12) +...+ (2009 − 2010) = (− ) 1 + (− ) 1 + ...+ (− ) 1 = 1002 − ; gom1002so hang 1 − c) 1
− − 2 − 3 − 4 −...− 2008 − 2009 − 2010 = −( + + + + + + ) (1+ 2010).2010 1 2 3 ... 2008 2009 2010 = = 2021055 − 2
d) 1− 3− 5 + 7 − 9 −11+...+1000 −1002 − 2004
= (1− 3 − 5) + (7 − 9 − )
11 + ...+ (1000 −1002 −1004) ( = 7 − ) + ( 7 − ) +...+ ( 7
− ) = −7 + 7 +...+ 7 = 7 − .334 = 2338. − gom334sohang gom334so hang
DẠNG 3: Toán vận dụng quy tắc chuyển vế (toán tìm x)
I/ Phương pháp giải.
Đối với dạng toán tìm x trong một đẳng thức, ta cần vận dụng quy tắc bỏ dấu ngoặc và
quy tắc chuyển vế để rút gọn mỗi vế của đẳng thức. Cuối cùng vận dụng quan hệ giữa các số có
phép tính (nếu có) để tìm x. II/ Bài tập mẫu.
Bài 1. Tìm số nguyên x, biết: 15 − (13+ x) = x − (23−17) Lời giải
Áp dụng quy tắc bỏ dấu ngoặc, ta có: 15 −13− x = x − 6 ⇔ 2 − x = x − 6
Áp dụng quy tắc chuyển vế, ta có: 2 + 6 = x + x ⇔ 8 = 2x Vậy x = 8 : 2 = 4
Bài 2. Tìm số nguyên x, biết: 1) x − 5 =12
2) 3x −12 = x + 2 Lời giải
Vận dụng định nghĩa về giá trị tuyệt đối của số nguyên và quy tắc chuyển vế
1) x − 5 =12 ⇔ x − 5 =12 hoặc –12
Với x − 5 =12 ⇔ x =12 + 5 ⇔ x =17 Với x − 5 = 12 − ⇔ x = 12 − + 5 ⇔ x = 7 −
Vậy x =17 hoặc x = 7 −
2) Theo định nghĩa về giá trị tuyệt đối, ta cần có điều kiện: x + 2 ≥ 0 ⇔ x ≥ 2 −
Khi đó 3x −12 = x + 2 ⇔ 3x −12 = x + 2 hoặc 3x −12 = −(x + 2)
Với 3x −12 = x + 2 ⇔ 2x =14 ⇔ x = 7 Với 5
3x −12 = −(x + 2) ⇔ 3x −12 = −x − 2 ⇔ 4x =10 ⇔ x = (không phải là số nguyên) 2 Vậy x = 7
Bài 3. Đối với bất đẳng thức ta cũng cố quy tắc chuyển vế tương tự như đối với đẳng thức, tức
là:a + b − c > d ⇔ a > b
− + c + d . Hãy tìm số nguyên x, biết: 1) x + ( 3) − > 15
2) 12 − (x −13) < 5 Lời giải 1) x + ( 3
− ) >15 ⇔ x >15 + 3 ⇔ x >18 2) Cách 1:
12 − (x −13) < 5 ⇔ 5
− < 12 − (x −13) < 5 ⇔ 5
− < 25 − x < 5 ⇔ 25 − 5 < x < 25 + 5 ⇔ 20 < x < 30
Vậy x∈{21; 22; 23; 24; 25; 26; 27; 28; 29}
Cách 2: Từ 12 − (x −13) < 5 ⇒ 25 − x = 0; 1; 2; 3; 4
- Với 25 − x = 0 ⇔ 25 − x = 0 ⇔ x = 25
- Với 25 − x =1 ⇔ 25 − x = 1
± ⇔ x = 24; x = 26
- Với 25 − x = 2 ⇔ 25 − x = 2
± ⇔ x = 23; x = 27
- Với 25 − x = 3 ⇔ 25 − x = 3
± ⇔ x = 22; x = 28
- Với 25 − x = 4 ⇔ 25 − x = 4
± ⇔ x = 21; x = 29
III/ Bài tập vận dụng
Bài 1. Tìm số nguyên x, biết: a) 3− x =15 − ( 5) − b) −x −14 + 32 = 26 − c) x + ( 31 − ) − ( 42) − = 45 − d) ( 12) − − (13 − x) = 15 − − ( 17 − )
Bài 2. Tìm số nguyên x, biết:
a) x − 43 = (35 − x) − 48
b) 305 − x +14 = 48 + (x − 23)
c) −(x − 6 + 85) = (x + 51) − 54
d) −(35 − x) − (37 − x) = 33− x
Bài 3. Tìm số nguyên x, biết: a) 13− x = 4 − ; b) x − 3+ 6 =16; c) 35 − 2x −1 =14; d) 3x − 2 + 5 = 9 − x .
Bài 4. Tìm số nguyên x sao cho: a) x = −( 25
− + 7) >12 − (15 −14); b) 17 + (x −15) < 4. HƯỚNG DẪN Bài 1. a) 3− x =15 − ( 5
− ) ⇔ 3 − x =15 + 5 ⇔ x = 3 − 20 = 17 − ; b) −x −14 + 32 = 26
− ⇔ x = 26 −14 + 32 ⇔ x = 44. c) x + (− ) 31 − ( 42 − ) = 45 −
⇔ x = 31− 45 − 42 ⇔ x = 56 − ; d) ( 12 − ) − (13 − x) = 15 − − ( 17 − ) ⇔ 12 − −13 + x = 15 − +17 ⇔ x = 27. Bài 2.
a) x − 43 = (35 − x) − 48 ⇔ 2x = 43+ 35 − 48 ⇔ x =15.
b) 305 − x +14 = 48 + (x − 23) ⇔ 2x = 305 +14 − 48 + 23 ⇔ x =147. c) −(x − 6 + 85) = (x + ) 51 − 54 ⇔ 2x = 79 − + 3 ⇔ x = 38. −
d) −(35 − x) − (37 − x) = 33− x ⇔ 3x = 33+ 35 + 37 ⇔ x = 35. Bài 3. a) 13− x = 4
− ⇔ x = 9 ⇔ x = 9 hoặc x = 9. −
b) x − 3+ 6 =16 ⇔ x =13 ⇔ x =13 hoặc x = 1 − 3;
c) 35 − 2x −1 =14 ⇔ 2x −1 = 21.
⇔ 2x −1 = 21 hoặc 2x −1 = 21 − ⇔ x =11 hoặc x = 10. −
d) 3x − 2 + 5 = 9 − x ⇔ 3x − 2 = 4 − x suy ra x ≤ 4 và xảy ra hai khả năng:
3x − 2 = 4 − x ⇔ 4x = 6 không tìm được x nguyên nào. 3x − 2 = x − 4 ⇔ 2x = 2 − ⇔ x = 1
− (thỏa mãn x ≤ 4). Vậy x = 1. − Bài 4. a) x − ( 25
− + 7) >12 − (15 −14) ⇔ x +18 >11 ⇔ x > 7. − Vậy x ∈{ 6; − 5 − ; 4; − . }..
b) 17 + (x −15) < 4 ⇔ 2 + x < 4 ⇔ 4 − < 2 + x < 4 ⇔ 6 − < x < 2. Vậy x ∈{ 5 − ; 4 − ; 3 − ; 2 − ; 1 − ;0; } 1 .
CHỦ ĐỀ 16: NHÂN HAI SỐ NGUYÊN.
CÁC TÍNH CHẤT CỦA PHÉP NHÂN A. KIẾN THỨC CẦN NHỚ
1. Quy tắc nhân hai số nguyên
• a . 0 = 0 . a = 0 ;
• Nếu a, b cùng dấu thì a.b = a . b ;
• Nếu a, b trái dấu thì a.b=− ( a . b ).
2.Tính chất của phép nhân
– Tính chất giao hoán: a.b=b.a, với mọi a,b∈Z;
– Tính chất kết hợp: (a.b).c = a.(b.c), với mọi a,b,c∈Z;
– Nhân với 1: a.1=1.a =a, với mọi a ∈Z;
– Tính chất phân phối của phép nhân và phép cộng
a.(b+c) = a.b+a.c, với mọi a,b,c∈Z;
a.(b − c)=a.b−a.c với mọi a,b,c ∈Z 3. Nhận xét
• Nếu a.b=0 thì hoặc a = 0 hoặc b = 0.
• Nếu tích là số nguyên dương thì tích chứa một số chẵn các thừa số âm. Tích là số nguyên
âm thì tích chứa một số lẻ các thừa số âm.
• Khi đổi dấu một thừa số thì tích đổi dấu. Khi đổi dấu hai thừa số thì tích không thay đổi.
B/ CÁC DẠNG TOÁN CƠ BẢN
DẠNG 1. Thực hiện phép nhân
I/ Phương pháp giải.
Vận dụng quy tắc nhân hai số nguyên để tính và so sánh II/ Bài tập mẫu.
Bài 1. Hãy điền vào dấu * các dấu “+” hoặc “–” để được kết quả đúng: 1) (*4).(*5) = 20 2) (*4).(*5) = 2 − 0. Lời giải
Ta biết tích của hai số nguyên là một số nguyên dương khi hai số cùng dấu, là hai số
nguyên âm khi hai số trái dấu. Vì vậy, ta có kết quả sau: 1) ( 4 + ).( 5 + ) = 20 hoặc ( 4 − ).( 5 − ) = 20. 2) ( 4 − ).( 5 + ) = 20 − hoặc ( 4 + ).( 5 − ) = 20. −
Bài 2. Không tính kết quả, hãy so sánh: 1) ( 23 − ).5 và 0; 2) ( 6 − ).20 và 6 − ; 3) 14.( 16 − ) và 14.16; 4) (− ) 31 .12 và 31.( 12 − ). Lời giải 1) ( 23 − ).5 < 0 ; 2) ( 6 − ).20 = −(6.20) < 6 − ; 3) 14.( 16 − ) < 0 và 0 < ( 14 − ).( 16 − ) nên 14.( 16 − ) < ( 14 − ).( 16 − ); 4) (− ) 31 .12 = −(31.12) = 31.( 12 − ). Nhận xét:
Với a, b nguyên ta luôn có: ab = (−a).(−b); (−a).b = a.(−b) = −a.b
Bài 3. Dự đoán giá trị của x thỏa mãn đẳng thức dưới đây và kiểm tra lại. 1) ( 7 − ).x = 77; 2) 8.x = 80 − ; 3)( 5 − ).x = ( 6 − ).( 1 − 0); 4) 9.x = ( 12 − ).( 60 − ). Lời giải
1) Ta thấy 7.11=77 nên dự đoán x = 11. − Thử lại: ( 7 − ).(− ) 11 = 77;
2) Ta thấy 8.10=80 nên dự đoán x = 10. − Thử lại: 8.( 10 − ) = 80 − ; 3) Ta có ( 5
− ).x = 60. Nhận thấy 5.12=60 nên dự đoán x = 12. − Thử lại: ( 5 − ).( 12 − ) = ( 6 − ).( 10 − );
4) Ta có 9 . x = 720. Nhận thấy 9 . 80 = 720 nên dự đoán x = 80. Thử lại: 9.80 = ( 12 − ).( 60 − ). III/ Bài tập mẫu. Bài 1. Tính: a) ( 16 − ).10; b) 23.( 5 − ); c) ( 24 − ).( 25 − ); d) (− )2 12 .
Bài 2. Điền số thích hợp vào ô trống trong bảng: a 3 15 – 4 –7 –5 0 b –6 –13 12 3 –1000 a . b – 45 21 36 –27 0 Bài 3.
a) Biểu diễn các số 81, 100, 169 dưới dạng tích của hai số nguyên bằng nhau (các số như
vậy gọi là số chính phương).
b) Biểu diễn các số –4, –9, –16, –25 dưới dạng tích của hai số nguyên đối nhau.
Bài 4. Tính 1999 . 23, từ đó suy ra các kết quả: a) ( 1999 − ).23; b) 1999.( 23 − ) c) ( 1999 − ).( 23 − ).
Bài 5. Tính giá trị của biểu thức (x − 5)(y + 40) trong mỗi trường hợp sau: a) x = 5, y =1000; b) x = 10 − , y =15; c) x =16, y = 50 − ; d) x = 15 − , y = 60. −
Bài 6. Dự đoán giá trị của x thỏa mãn đẳng thức dưới đây và kiểm tra lại: a) ( 8 − ).x = 88; b) 10.x = 180 − ; c) ( 6 − ).x = ( 3 − ).( 1 − 8); d) 16.x = ( 12 − ).( 36 − ).
Bài 7. Không tính kết quả, hãy so sánh: a) ( 22 − ).( 5 − ) và 0; b) ( 7 − ).20 và 7; − c) 13.( 16 − ) và ( 13 − ).( 16 − ); d) ( 39 − ).12 và 39.( 12 − ).
Bài 8. Một xí nghiệp mỗi ngày may 250 bộ quần áo. Khi may theo mốt mới với cùng khổ vải,
số vải dùng để may một bộ quần áo tăng x (cm) và mỗi ngày may tăng y bộ quần áo. Hỏi mỗi
ngày số vải tăng bao nhiêu xen – ti – mét, biết để may bộ ban đầu hết 3m cùng khổ vải trên? a) x =10; y = 1; − b) x = 1 − 0; y = 5; c) x = 5; y = 6; d) x = 10 − ; y = 7. − HƯỚNG DẪN Bài 1. a) -160 b) -115 c) 600 d) 144.
Bài 2. Điền số thích hợp vào ô trống trong bảng như sau: a 3 15 -4 -7 3 -9 -5 0 b -6 -3 -13 -3 12 3 0 -1000 a . b -18 -45 52 21 36 -27 0 0 Bài 3. a) 81= 9.9 = ( 9 − ).( 9 − ); 100 =10.10 = ( 10 − ).( 10 − ) 169 =13.13 = ( 13 − ).( 13 − ). b) 4 − = 2.( 2 − ); 9 − = 3.( 3 − ); 16 − = 4.( 4 − ) 25 − = 5.( 5 − ).
Bài 4. Tính 1999.23 = (2000 − ) 1 .23 =15977. Suy ra: a) ( 1999 − ).23 = 45977 − ; b) 1999.( 23 − ) = 45977 − ; c) ( 1999 − ).( 23 − ) = 45977. Bài 5. a) 0; b) 110 − ; c) 110 − ; d) 400. Bài 6. a) x = 1 − 1, vì ( 8 − ).(− ) 11 = 88; b) x = 1 − 8, vì 10.( 18 − ) = 180 − ; c) x = 9, − vì ( 6 − ).( 9 − ) = ( 3 − ).( 1 − 8); d) x = 27, vì 16 . 27 = ( 12 − ).( 36 − ) Bài 7. a) ( 2 − 2).( 5 − ) > 0; b) ( 7 − ).20 < 7 − ; c) 13.( 16 − ) < 0 và ( 13 − ).( 16 − ) > 0 nên 13.( 16 − ) < ( 13 − ).( 16 − ); d) ( 39 − ).12 = 39.( 12 − ).
Bài 8. Mỗi ngày số vải tăng: S = (250 + y).x + 300.y (cm). a) Với x =10;y = 1 − thì S = 2190; b) x = 1 − 0;y = 5 thì S = 1050 − ;
c) x = 5;y = 6 thì S = 3080; d) x = 1 − 0;y = 7 − thì S = 4530. −
DẠNG 2. Vận dụng tính chất của phép nhân
I/ Phương pháp giải.
Để tìm kết quả của phép tính có dấu ngoặc ta có thể thực hiện trong ngoặc trước, rồi
thực hiện theo thứ tự nhân chia trước, cộng trừ sau. Cũng có thể áp dụng tính chất phân phối
của phép nhân với phép cộng rồi mới thực hiện các phép tính theo thứ tự. Tùy theo từng trường
hợp ta có thể thực hiện tính chất giao hoán và kết hợp của phép nhân sao cho việc tính toán
được thuận tiện nhất. II/ Bài tập mẫu. Bài 1. Tính: 1) (35 −15).( 4 − ) + 24( 13 − −17); 2) ( 13
− ).(57 − 34) + 57.(13− 45). Lời giải 1) (35 −15).( 4 − ) + 24.( 13 − −17) = 20.( 4 − ) + 24.( 30 − ) = 80 − − 720 = 800. − 2) Cách 1: ( 13
− ).(57 − 34) + 57.(13− 45) = ( 13 − ).23+ 57.( 32 − ) = 299 − −1824 = 2123. − Cách 2: ( 13 − ).57 − ( 13 − ).34 + 57.13 − 57.45 = ( 13
− ).57 +13.57 +13.34 − 57.45 = 442 − 2565 = 2123. −
Bài 2. Thực hiện phép tính một cách hợp lí nhất: 1) ( 8 − ).( 12 − ).( 125 − ); 2) ( 134 − ) + 51.134 + ( 134 − ).48; 3) 45.( 24 − ) + ( 10 − ).( 12 − ). Lời giải
Vận dụng tính chất giao hoán, kết hợp và phân phối giữa phép nhân và phép cộng để tính
(chú ý nếu số thừa số âm của tích là số chẵn thì tích mang dấu “+”, nếu số thừa số âm của tích
là số lẻ thì tích mang dấu “–”. 1) ( 8 − ).( 12 − ).( 125 − ) = ( 8 − ).( 125 − ).( 12 − ) =1000.( 12 − ) = 12000 − ; 2) ( 134 − ) + 51.134 + ( 134 − ).48 =134( 1 − + 51− 48) =134.2 = 268; 3) 45.( 24 − ) + ( 10 − ).( 12 − ) = 45.24 − + 5.24 = 24.( 45 − + 5) = 24.( 40 − ) = 960. − Bài 3. Tính nhanh: 1) ( 49 − ).99; 2) ( 52 − ).(− ) 101 . Lời giải
Để tính nhanh một tích, trước hết ta xác định dấu của tích và nhận xét: 99 =100 −1; 101 =100 +1. 1) ( 49 − ).99 = 49.99 − = 49. −
(100 − )1 = −(49.100 − 49) = 4851 − ; 2) ( 52 − ).(− ) 101 = 52.101 = 52.(100 + ) 1 = 5200 + 52 = 5252.
III/ Bài tập vận dụng.
Bài 1. Thực hiện phép tính một cách hợp lí nhất: a) 2.( 25 − ).( 4 − ).50; b) ( 125 − ).5.( 16 − ).( 8 − ); c) (− )2 (− )3 3 5 . 3 .2 ; d) −( 2 − ) 2 4 .3 .( 5 − )3 . Bài 2. Tính nhanh: a) ( 48 − ).98; b) ( 520 − ).( 102 − ); c) 124 + ( 52 − ).124 + ( 124 − ).( 47 − ); d) 55.78 − +13.( 78 − ) − 78.( 65 − ). Bài 3. So sánh: a) ( 3 − ).( 5 − ).( 7 − ).( 9 − ).( 1 − ) 1 với ( 9 − ).(− ) 11 ; b) 18 − ( 13 − ).( 15 − ).( 17 − ) với 0. Bài 4. Cho a = 5, − b = 6
− . Tính giá trị của biểu thức: a) 2 2 a − 2ab + b và ( − )2 a b ; b) (a + b).(a − b) và 2 2 a − b ; c) 2 2 a + 2ab + b và ( + )2 a b .
Từ kết quả nhận được, hãy nêu nhận xét.
Bài 5. Viết các tích sau dưới dạng lũy thừa của một số nguyên: a) ( 27 − ).8.( 125 − ).( 64 − ); b) ( 7 − ).8.( 49 − ).( 64 − ).( 1000 − ). HƯỚNG DẪN Bài 1. a) 2.( 25 − ).( 4 − ).50 = (2.50).( 25 − ).( 4 − ) =10000; b) ( 125 − ).5.( 16 − ).( 8 − ) = ( 125 − ).( 8 − ).5.( 16 − ) =1000.( 80 − ) = 80000 − ; c) (− )2 (− )3 3 5 . 3 .2 = 25.8.( 27 − ) = 200.( 27 − ) = 5400 − ; d) −( 2 − ) 2 4 .3 .( 5
− )3 =16.9.125 =16.125.9 =18000. Bài 2. a) ( 48
− ).98 = −(100 − 2).48 = −(4800 − 96) = 4704 − ; b) ( 52 − ).( 102 −
) = 52.(100 + 2) = 5200 +104 = 5304; c) 124 + ( 52 − ).124 + ( 124 − ).( 47
− ) =124.(1− 52 + 47) = 496 − ; d) 55.78 − +13.( 78 − ) − 78.( 65 − ) = 78.( 55 − −13 + 65) = 234. − Bài 3. a) ( 3 − ).( 5 − )( 7 − ).( 9 − ).( 1 − )
1 < 0 (do tích có một số lẻ thừa số âm) và ( 9 − ).(− ) 11 > 0 => ( 3 − ).( 5 − ).( 7 − ).( 9 − ).( 1 − ) 1 < ( 9 − ).( 1 − ) 1 Bài 4. Với a = 5, − b = 6 − , ta có: a) 2 2 a − 2ab + b =1 và ( − )2 a b =1. b) (a + b).(a − b) = 11 − và 2 2 a − b = 11. − c) 2 2 a + 2ab + b =121 và ( + )2 a b =121.
Từ kết quả nhận được, ta thấy: 2 2 a − 2ab + b = (a − b)2 ; ( + )( − ) 2 2 a b a b = a − b ; 2 2 a + 2ab + b = (a + b)2 . Bài 5. a) (− ) (− ) (− ) 3 3 3 3 3 27 .8. 125 . 64 = 3 − .2 .5 .4 = 120 − = ( 120 − )3 b) (− ) (− ) (− ) (− ) 3 3 3 3
7 .8. 49 . 64 . 1000 = 7.49.8.64.1000 = 7 .8 .10 = 560 DẠNG 3. Toán tìm x
I/ Phương pháp giải
- Một tích số bằng 0 thì ít nhất một thừa số trong tích bằng 0. Nếu ab = 0 thì a = 0 hoặc b = 0.
- Để tìm x sao cho đẳng thức đúng thì cần vận dụng định nghĩa và tính chất của phép
nhân, kết hợp với quy tắc bỏ dấu ngoặc, quy tắc chuyển vế. II/ Bài tập mẫu.
Bài 1. Tìm số nguyên x, biết: 1) 5.(x − 2) = 0; 2) (5 − x).(x + 7) = 0; 3) ( 4 − ).x = 20. Lời giải
1) 5.(x − 2) = 0 ⇔ x − 2 = 0 ⇔ x = 0;
2) (5 − x).(x + 7) = 0 ⇔ 5 − x = 0 hoặc x + 7 = 0 ⇔ x = 5 hoặc x = 7; − 3) ( 4
− ).x = 20. Nhận thấy 20 = ( 4 − ).( 5 − ) nên x = 5. −
Bài 2. Tìm số nguyên x, biết: 1) x + x + x + 91 = 2 − ; 2) 152 − − (3x + ) 1 = ( 2 − ).( 27 − ); 3) 5x +1 =11. Lời giải 1) x + x + x + 91 = 2 − ⇔ 3.x + 91 = 2 − ⇔ 3x = 2 − − 91 ⇔ 3x = 93. − Do 93 − = 3.(− ) 31 nên x = 31. − 2) 152 − − (3x + ) 1 = ( 2 − ).( 27 − ) ⇔ 152 − − 3x −1 = 54 ⇔ 3x = 153 − − 54 ⇔ 3x = 207. − Do 207 = 3.69, suy ra x = 69. −
3) 5x +1 =11 ⇔ 5x +1 =11 hoặc 5x +1 = 11. −
Với 5x +1 =11 ⇔ 5x =11−1 =10 ⇔ x = 2. Với 5x +1 = 11 − ⇔ 5x = 12
− nên không có x nguyên nào thỏa mãn. Vậy x = 2.
III/ Bài tập vận dụng.
Bài 1. Tìm số nguyên x, biết: a) ( 1005 − ).(x + 2) = 0; b) (8 + x).(6 − x) = 0; c) 8x.(5 − x) = 0; d) 2 x − 5x = 0.
Bài 2. Tìm số nguyên x, biết: a) x + x + x + 82 = 2 − − x; b) 5.( 4 − ).x = 100 − ; c) (− ) 1 .( 3 − ).( 6 − ).x = 36; d) 152 − − (3x + ) 1 = ( 2 − ).( 77 − ).
Bài 3. Tìm số nguyên x, biết: a) x − 9 .( 8 − ) = 1 − 6;
b) 4 − 5x = 24 với x ≤ 0; c) 1− 4x = 7;
d) 2x + x −12 = 60 với x >12.
Bài 4. Tìm số nguyên x,biết: a) x.(x − 2) = 0; b) x.(x − 2) > 0; c) x.(x − 2) < 0.
Bài 5. Tính giá trị của biểu thức: a) 2 x + x −8 với x = 2; − b) 3 5.
− x . x −1 +15 với x = 2; − c) −(x − ) 1 .(x + 2) với x = 3;
d) (4x − 5).(x − 7) với (x − 2).(x + 3) = 0. HƯỚNG DẪN Bài 1. a) ( 1005 −
).(x + 2) = 0 ⇔ x + 2 = 0 ⇔ x = 2. −
b) (8 + x).(6 − x) = 0 ⇔ 8 + x = 0 hoặc 6 − x = 0 ⇔ x = 8 − hoặc x = 6.
c) 8x.(5 − x) = 0 ⇔ x = 0 hoặc x = 5. d) 2
x − 5x = 0 ⇔ x.(x − 5) = 0 ⇔ x = 0 hoặc x = 5. Bài 2. a) x + x + x + 82 = 2 − − x ⇔ 4x = 84 − ⇔ x = 21 − ; b) 5.( 4 − ).x = 100 − ⇔ 20. − x = 100 − ⇔ x = 5; c) (− ) 1 .( 3 − ).( 6 − ).x = 36 ⇔ 18. − x = 36 ⇔ x = 2 − ; d) 152 − − (3x + ) 1 = ( 2 − ).( 77 − ) ⇔ 3x = 153 − −144 ⇔ x = 99. − Bài 3. a) x − 9 .( 8 − ) = 16 − ⇔ x − 9 = 2.
⇔ x − 9 = 2 hoặc x − 9 = 2 − ⇔ x =11 hoặc x = 7;
b) Do x ≤ 0 nên 4 − 5x > 0.
Từ đó suy ra 4 − 5x = 24 ⇔ x = 4 − (thỏa mãn x ≤ 0).
c) 1− 4x = 7 ⇔ 1− 4x = 7 hoặc 1− 4x = 7. − Tìm được x = 2. −
d) Do x >12 nên 2x = 2x; x −12 = x −12.
Từ 2x + x −12 = 60, suy ra 3x −12 = 60 ⇔ x = 24.
Bài 4. a) x = 0 hoặc x = 2; b) x ∈{...; 2 − ; 1 − ;3;4;5; } ... ; c) x =1. Bài 5. a) Với x = 2 − thì 2 x + x −8 = ( 2 − )2 − 2 −8 = 6; − b) Với x = 2 − thì 3 5. − x . x −1 +15 = 5. − ( 2 − )3. 2 − −1 +15 = 105 −
c) Với x = 3 ⇔ x = 3 hoặc x = 3 − ; + Khi x = 3 thì −(x − ) 1 .(x + 2) = 1 − 0; + Khi x = 3 − thì −(x − ) 1 .(x + 2) = 4. −
d) Với (x − 2).(x + 3) = 0 thì x = 2 hoặc x = 3 − ;
+ Khi x = 2 thì (4x − 5).(x − 7) = 1 − 5; + Khi x = 3
− thì (4x − 5).(x − 7) =170.
CHỦ ĐỀ 17: BỘI VÀ ƯỚC CỦA MỘT SỐ NGUYÊN A. KIẾN THỨC CẦN NHỚ
1. Định nghĩa
Với a,b∈Z và b ≠ 0. Nếu có số nguyên q sao cho a = b.q thì ta nói a chia hết cho b. Ta
còn nói a là bội của b và b là ướccủa a. 2. Nhận xét
- Nếu a = b.q thì ta nói a chia cho b được q và viết a : b = q.
- Số 0 là bội của mọi số nguyên khác 0. Số 0 không phải là ước của bất kì số nguyên nào.
- Các số 1 và -1 là ước của mọi số nguyên. 3. Tính chất
Có tất cả các tính chất như trong tập N.
- Nếu a chia hết cho b và b chia hết cho c thì a cũng chia hết cho c. ab và bc ⇒ ac
- Nếu a chia hết cho b thì bội của a cũng chia hết cho b.
ab ⇒ kab ( k ∈Z)
- Nếu a, b chia hết cho c thì tổng và hiệu của chúng cũng chia hết cho c.
ac, bc ⇒ a + b c; a − b c.
- Nếu a, b chia cho c cùng số dư thì a – b chia hết cho c. Nhận xét:
- Nếu a chia hết cho b, b chia hết cho a thì a = ±b.
- Nếu a chia hết cho hai số m, n nguyên tố cùng nhau thì a chia hết cho m.n. - Nếu n
a chia hết cho số nguyên tố p thì a chia hết cho p.
- Nếu ab chia hết cho m và b, m nguyên tố chung nhau thì a chia hết cho m.
- Trong n số nguyên liên tiếp có đúng một số chia hết cho n.
B. CÁC DẠNG TOÁN CƠ BẢN
DẠNG 1. Tìm bội và ước của số nguyên
I. PHƯƠNG PHÁP GIẢI
- Tập hợp các bội của số nguyên a có vô số phần tử và bằng {k.a | k ∈ } Z .
- Tập hợp các ước số của số nguyên a (a ≠ 0) luôn là hữu hạn. Cách tìm:
Trước hết ta tìm các ước số nguyên dương của a (làm như trong tập số tự nhiên),
chẳng hạn là p, q, r. Khi đó −p, − q, − r cũng là ước số của a. Do đó các ước của a là p, q, r, – p, –q, –r.
Như vậy số các ước nguyên của a gấp đôi số các ước tự nhiên của nó. II. VÍ DỤ Ví dụ 1.
1) Tìm năm bội của: – 5; 5;
2) Tìm các bội của – 12, biết rằng chúng nằm trong khoảng từ – 100 đến 24. Lời giải
1) Các bội số của 5; –5 đều có dạng 5.k (k ∈Z).
Chẳng hạn chọn năm bội số của 5; –5 là: –15, –10, –5, 0, 5.
2) Các bội số của –12 có dạng 12.k (k ∈Z). Cần tìm k sao cho: –100 < 12k < 24.
Tức là: –9 < k < 2, chọn k ∈{ 8 − ; 7 − ; 6 − ; 5 − ; 4 − ; 3 − ; 2 − ; 1 − ;0; } 1 .
Vậy các bội của –12 nằm trong khoảng từ –100 đến 24 là 96 − , 84 − , 72 − , 60 − , 48 − , 36 − , 24 − , 12 − ,0,12.
Ví dụ 2. Tìm tất cả các ước của: 1) –3; 2) –25; 3) 12. Lời giải
1) Các ước tự nhiên của 3 là 1, 3.
Do đó các ước của –3 là 3 − , 1, − 1, 3.
2) Các ước tự nhiên của 25 là 1, 5, 25.
Do đó các ước của 25 là 2 − 5, 5, − 1 − , 1, 5, 25.
3) Các ước tự nhiên của 12 là 1, 2, 3, 4, 6, 12.
Do đó các ước của 12 là 1 − 2, 6, − 4, − 3 − , 2, − 1 − , 0, 1, 2, 3, 4, 6, 12. Nhận xét:
Số tự nhiên a phân tích ra thừa số nguyên tố có dạng n m k
p .q .r (p, q, r là số nguyên tố) thì
số ước tự nhiên của a là (n + ) 1 (m + ) 1 (k + )
1 . Khi đó mỗi số nguyên a, –a đều có 2(n + ) 1 (m + ) 1 (k + ) 1 ước nguyên.
Số nguyên tố p có 4 ước nguyên là −p, 1, − 1, p.
Ví dụ 3. Tìm số nguyên n để: 1) 5 . n chia hết cho –2; 2) 8 chia hết cho n; 3) 9 chia hết cho n + 1;
4) n – 18 chia hết cho 17. Lời giải
1) 5 . n chia hết cho –2, nên n là bội của 2.
Vậy n = 2k (k là số nguyên tùy ý).
2) 8 chia hết cho n, nên n là ước của 8. Vậy n ∈{ 8 − ; 4; − 2; − 1 − ; 1; 2; 4; } 8 .
3) 9 chia hết cho n + 1, nên n + 1 là ước của 9. Suy ra n +1∈{ 9 − ; 3 − ; 1; − 1; 3; } 9 . Với n +1 = 9 − ⇔ n = 9 − −1 ⇔ n = 1 − 0; Với n +1 = 3 − ⇔ n = 3 − −1 ⇔ n = 4 − ; Với n +1 = 1 − ⇔ n = 1 − −1 ⇔ n = 2 − ;
Với n +1 =1 ⇔ n =1−1 ⇔ n = 0;
Với n +1 = 3 ⇔ n = 3−1 ⇔ n = 2;
Với n +1 = 9 ⇔ n = 9 −1 ⇔ n = 8; − Vậy n ∈{ 1 − 0; 4; − 2; − 0; 2; } 8 .
4) n – 18 chia hết cho 17, nên n – 18 là bội của 17. Do đó n – 18 = 17k (k ∈Z).
Vậy n = 18 + 17k (k ∈Z). III. BÀI TẬP Bài 1.
1) Tìm bốn bội của –9; 9.
2) Tìm các bội của –24, biết rằng chúng nằm trong khoảng từ 100 đến 200.
Bài 2. Tìm tất cả các ước của: 1) –17; 2) 49; 3) –100. Bài 3.
1) Tìm tập hợp ƯC(–12; 16);
2) Tìm tập hợp ƯC(15;–18;–20).
Bài 4. Tìm số nguyên n để: 1) 7 . n chia hết cho 3; 2) –22 chia hết cho n;
3) –16 chia hết cho n – 1; 4) n + 19 chia hết cho 18.
Bài 5. Tìm tập hợp BC (15;–12;–30).
Bài 6. Cho hai tập hợp A = {1; 2; 3; 4; } 5 và B = { 2; − 4; − − } 6 .
a) Viết tập hợp gồm các phần tử có dạng a . b với a ∈A, b∈B.
b) Trong các tích trên có bao nhiêu tích chia hết cho 5? HƯỚNG DẪN Bài 1.
a) Chẳng hạn là: –18; –9; 0; 9 b) 120; 144; 168; 192 Bài 2.
a) Ư(–17) = {–17; –1; 1; 17}
b) Ư(49) = {–49; –7; –1; 1; 7; 49}
c) Ư(100) = {–100; –50; –25; –20; –10; –5; –4; –2; –1; 1; 2; 4; 5; 10; 20; 25; 50; 100} Bài 3.
a) ƯCLN(12; 16) = 4 suy ra ƯC(–12; 16) = {–4; –2; –1; 2; 4}
b) ƯCLN(15; 18; 20) = 1 suy raƯC(15; –18; –20) = {–1; 1} Bài 4.
a) 7n 3 mà (7; 3) = 1 nên n 3 do đó n = 3k (k ∈) b) 22
− n nên n∈{− 22; −11; − 2; −1; 1; 2; 11; 22} c) 1
− 6 (n −1) nên (n −1)∈{−16; −8; − 4; − 2; −1; 1; 2; 4; 8; 16}
Vậy n∈{−15; − 7; − 3; −1; 0; 2; 3; 5; 9; 17}
d) (n +19) 18 nên (n +1) 18 suy ra n =18k −1 (k ∈)
Bài 5. BCNN(15; 20; 30) = 60
Suy ra BC(15; –20; –30) = B(60) = 60k(k ∈)
Bài 6. Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {–2; –4; –6}
a) C = {ab | a ∈A; b∈B} = {− 2; − 4; − 6; −8; −10; −12; −16; −18; − 20; − 24; − 30}
( Chú ý: Các phần tử trong tập hợp phải khác nhau đôi một)
b) Trong các tích trên có 3 tích chia hết cho 5 ứng với a = 5 và b∈B
DẠNG 2. Vận dụng tính chất chia hết của số nguyên
I. PHƯƠNG PHÁP GIẢI
Để chứng minh một biểu thức A chia hết cho số nguyên a;
- Nếu A có dạng tích m.n.p thì cần chỉ ra m (hoặc n, hoặc p) chia hết cho a. Hoặc m
chia hết cho a , n chia hết cho a , p chia hết cho a trong đó a = a a a 1 2 3 1 2 3.
- Nếu A có dạng tổng m + n + p thì cần chỉ ra m, n, p cùng chia hết cho a, hoặc tổng các
số dư khi chia m, n, p cho a phải chia hết cho a.
- Nếu A có dạng hiệu m – n thì cần chỉ ra m, n chia cho a có cùng số dư. Vận dụng tính
chất chia hết để làm bài toán về tìm điều kiện để một biểu thức thỏa mãn điều kiện cho hết. II. VÍ DỤ
Ví dụ 1. Chứng minh rằng: 2 3 4 5 6 7 8
S = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 chia hết cho (–6). Lời giải
Nhóm tổng S thành tổng của các bội số của (–6) bằng cách: S = ( 2 2 + 2 ) + ( 3 4 2 + 2 ) + ( 5 6 2 + 2 ) + ( 7 8 2 + 2 ) 2 4 6 = 6 + 2 .6 + 2 .6 + 2 .6
Mỗi số hạng của tổng S đều chia hết cho (–6), nên S chia hết cho (–6). Ví dụ 2. Cho số 8 3 a = 10 −
+ 2 . Hỏi số a có chia hết cho (–9) không? Lời giải 8 3 8 a = 10 − + 2 = 10 − +1+ 7 = 99...9 − + 7 . gom8chu so9
Số hạng đầu của a chia hết cho 9, còn 7 không chia hết cho 9 nên a không chia hết cho 9.
Do đó a cũng không chia hết cho –9.
Ví dụ 3. Cho a, b là các số nguyên. Chứng minh rằng nếu 6a +11b chia hết cho 31 thì a + 7b
cũng chia hết cho 31. Điều ngược lại có đúng không? Lời giải
Ta có: 6a +11b = 6.(a + 7b) − 31b. (*)
Do đó 31b31, và 6a +11b31, từ (*) suy ra 6(a + 7b)31,
Mà 6 và 31 nguyên tố cùng nhau, nên suy ra a + 7b31.
Ngược lại, nếu a + 7b31, mà 31b31, từ (*) suy ra 6a + 7b31.
Vậy điều ngược lại cũng đúng.
Ta có thể phát biểu bài toán lại như sau:
“Cho a, b là các số nguyên. Chứng minh rằng 6a +11b chia hết cho 31 khi và chỉ khi a + 7bchia hết cho 31”.
Ví dụ 4. Tìm số nguyên x sao cho:
1) 3x + 4 chia hết cho x − 3;
2) x +1 là ước số của 2 x + 7. Lời giải
1) Nhận thấy 3x + 4 = 3(x − 3) + 5.
Do 3(x − 3)(x − 3), nên (3x + 4)(x −3) khi và chỉ khi 5(x − 3). Suy ra x − 3∈{ 5 − ; 1; − 1; } 5 . Vậy x ∈{ 2; − 2; 4; } 8 . 2) Nhận thấy 2 x + 7 = x(x + ) 1 − (x + ) 1 + 8. Do x(x + ) 1 (x + ) 1 , nên 2 x + 7(x + ) 1 khi và chỉ khi 8(x + ) 1 . Suy ra x +1∈{ 8 − ; 4; − 2; − 1 − ; 1; 2; 4; } 8 . Vậy x ∈{ 9;
− − 5; − 3; − 2; 0; 1; 3; } 7 . III. BÀI TẬP
Bài 1. Chứng minh rằng: 2 3 4 5 6 7 8 9
S = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 chia hết cho ( 39 − ).
Bài 2. Cho số a =11...11 (gồm 20 chữ số 1). Hỏi số a có chia hết cho 111 không?
Bài 3. Cho a, b là các số nguyên. Chứng minh rằng 5a + 2b chia hết cho 17 khi và chỉ khi 9a + 7b chia hết cho 17.
Bài 4. Tìm số nguyên x sao cho:
a) 2x – 5 chia hết cho x – 1;
b) x + 2 là ước số của 2 x + 8.
Bài 5. Tìm cặp số nguyên x, y sao cho: a) (x − ) 1 .(y + ) 1 = 5; b) x.(y + 2) = 8; − c) xy − 2x − 2y = 0.
Bài 6. Tìm tất cả các cặp số nguyên x, y sao cho 20x + 10y = 2010.
Bài 7. Tìm số nguyên x sao cho x – 1 là bội của 15 và x + 1 là ước số của 1001. HƯỚNG DẪN Bài 1. 2 3 4 5 6 7 8 9
S = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 2 3 4 5 6 7 8 9
(3 + 3 + 3 ) + (3 + 3 + 3 ) + (3 + 3 + 3 )
= 39 + 33.39 + 36.39 = 39.(1 + 33 + 36) 39
Suy ra S 39 nên S ( 39) − Bài 2. Nhận thấy: 17 14 11 8 5 2
a =111.10 +111.10 +111.10 +111.10 +111.10 +111.10 +11 = 17 14 11 8 5 2
111.(10 +10 +10 +10 +10 +10 ) +11
=> a là tổng của hai số hạng trong đó có 1 số chia hết cho 111, 1 số không chia hết cho
111 nên a không chia hết cho 111
Vậy a không chia hết cho 111
Bài 3. Xét hiệu 5.(9a + 7b) − 9.(5a + 2b) =17b
Nhận thấy 17b 17 nên:
Nếu 9a + 7b 17 thì 9.(5a + 2b) 17, mà (9; 17) = 1 nên 5a + 2b 17
Nếu 5a + 2b 17thì 5.(9a + 7b) 17, mà (5; 17) = 1 nên (9a + 7b) 17 Bài 4.
a) 2x − 5 = 2(x −1) − 3 nên (2x − 5)(x −1) ⇔ 3(x −1) do đó (x −1) { ∈ − 3;−1; 1; 3} Vậy x −1 { ∈ − 2; 0; 2; 4} b) Do 2
x + 8 = x(x + 2) − 2(x + 2) +12 nên 2
(x + 8) (x + 2) ⇔ 12 (x + 2)
Do đó (x + 2)∈{−12;− 6;− 4;− 3;− 2;−1; 1; 2; 3; 4; 6; 12}
Vậy x∈{−14;−8;− 6;− 5;− 4;− 3; −1; 0; 1; 2; 4; 10} Bài 5. a) Vì 5 = 5.1 = ( 1 − ).( 5
− ) nên ta có các trường hợp sau:
1) x −1 =1 và y +1 = 5 ⇔ x = 2 và y = 4
2) x −1 = 5 và y +1 =1 ⇔ x = 6 và y = 0 3) x −1 = 1 − và y +1 = 5
− ⇔ x = 0 và y = 6 − 4) x −1 = 5 − và y +1 = 1 − ⇔ x = 4 − và y = 2 − b) ( ;x y) = ( 8 − ; 1 − ); (1; 1 − 0); (8; 3 − );( 1 − ; 6); ( 4 − ; 0); (2; 6 − ); (4; 4 − ); ( 2; − 6 − )
c) xy − 2x − 2y = 0 ⇔ (x − 2).(y − 2) = 4
Do đó tìm được ( ;x y) = (3; 6);(6; 3);(1; 2 − );( 2; − 1);(4; 4);(0; 0) .
Bài 6. Từ điều kiện đề bài suy ra 2x + y = 201
201 là số lẻ và 2x là số chẵn, suy ra y là số lẻ. Khi đó y có dạng:
y = 2k +1 (k∈ ) ⇒ x =100 − k
Chẳng hạn, bốn cặp số nguyên (x; y) thỏa mãn: ( ;
x y) = (100; 1); (99; 3); (101;−1); (98; 5)
Bài 7. Ư(1001) = {1001; –1001; 143; –143; 91; –91; 77; –77; 13; –13; 11; –11; 7; –7; 1; –1}
Ta có: x – 1 là bội của 15 nên x – 1 = 15k ( k ∈ )⇔ x + 1 = 15k + 2 (k ∈ )
Mà x + 1 là ước của 1001 nên kiểm tra thấy x + 1 = 77 ⇔ x =76 Vậy x = 76
CHỦ ĐỀ 18. KHÁI NIỆM PHÂN SỐ - PHÂN SỐ BẰNG NHAU
A/ KIẾN THỨC CẦN NHỚ.
1/ Với a, b ∈ N, b ≠ 0 thì ta có a gọi là phân số. b
Trong đó a là tử số, b là mẫu số của phân số.
2/ Phân số Ai cập là phân số có dạng 1/n (có tử bằng 1)
3/ Mọi số tự nhiên đều có thể viết dưới dạng phân số:
* Muốn viết 1 số tự nhiên dưới dạng phân số có mẫu số là 1 ta viết tử số bằng số tự nhiên đó, còn mẫu số là 1. VD: 9 = 9/
* Muốn viết 1 số tự nhiên dưới dạng 1 phân số có mẫu số là số cho trước ta viết mẫu số
bằng số cho trước, còn tử số bằng tích của số tự nhiên với mẫu số cho trước.
VD: 4 = x/3, ta có phân số: 4.3/3 = 12/3 TQ: A = x A.B = => x = A.B B B
4/ Phân số thập phân là phân số có mẫu là 10, 100, 1000,……. B/ CÁC DẠNG BÀI TẬP
DẠNG 1: CÁCH VIẾT PHÂN SỐ, ĐIỀU KIỆN ĐỂ CÓ PHÂN SỐ.
* Phân số có dạng a Với a, b ∈ N, b ≠ 0 b
Bài 1: Dùng 2 trong 3 số sau 2, 3, 5 để viết thành phân số (tử số và mẫu số khác nhau) Hướng dẫn
Có các phân số: 2 2 3 3 5 5 ; ; ; ; 3 5 5 2 2 3
Bài 2: Số nguyên a phải có điều kiện gì để ta có phân số? a/ 32 b/ a a −1 5a + 30 Hướng dẫn
a) a – 1 ≠ 0 a ≠ 1
b) 5a + 30 ≠ 0 a ≠ 6 −
Bài 3: Trong các cách viết sau, cách nào cho ta phân số: 3 9,1 0 45 2,3 ; ; ; ; 1 − 1 3 3 0 4, − 5 Hướng dẫn
Tử và mẫu của phân số phải là số nguyên nên trong các cách viết trên thì chỉ có 3 0 ; 11 − 3 là phân số.
Bài 4. Phần tô màu trong các hình 1,2,3,4 biểu diễn các phân số nào? Giải Hình 1) 1 Hình 2) 2 Hình 3) 3 Hình 4) 1 6 5 4 4
Bài 5. Viết các phép chia sau dưới dạng phân số: a) ( 2 − ) :11 b) ( 9 − ) :(− ) 31 c) 11:( 2 − ) d) ( 5 − ) :147 Giải a) 2 − − − b) 9 c) 11 d) 5 11 31 − 2 − 147
Bài 6. Dùng cả hai số m và n để viết thành phân số, mỗi số chỉ được viết một lần ( , m n∈ ; , m n ≠ 0) Giải
Phân số viết được là: m ; n n m Bài 7.
a) Dùng cả hai số 6và 7 để viết thành phân số (mỗi số chỉ được viết 1 lần). b) Dùng cả hai số 5
− và 9để viết thành phân số (mỗi số chỉ được viết 1 lần). Bài 8.
a) Cho tập hợp A = { 2 − ;1; }
3 . Viết tập hợp B các phân số có tử và mẫu khác nhau thuộc tập hợp A. b) Cho ba số nguyên 7;
− 2và 5. Viết tất cả các phân số có tử và mẫu là các số nguyên đã cho. Bài 9.
a) Cho tập hợpG = { 1; − 0; }
5 . Viết tập hợp V các phân số a trong đó a,b∈G . b
a) Cho tập hợp L = {2;0;− }
3 . Viết tập hợp T các phân số a trong đó a,b∈ L . b
Bài 10. Cho tập hợp M = {1;2;3; }
...20 .Có thể lập được bao nhiêu phân số có tử và mẫu khác
nhau thuộc tập hợp M .
Bài 11. Cho tập hợp N = {0;1;2;3; }
...19 .Có thể lập được bao nhiêu phân số có tử và mẫu khác
nhau thuộc tập hợp M .
Dạng 2. Biểu thị các số đo (độ dài, diện tích,...) dưới dạng phân số với đơn vị cho trước
Để biểu thị các số đo (độ dài, diện tích,...) dưới dạng phân số với đơn vị cho trước ta chú
ý quy tắc đối với đơn vị, chẳng hạn
Bài 1. Biểu thị các số sau đây dưới dạng phân số với đơn vị là:
a) Mét: 3dm ; 11cm ; 213mm ; b) Mét vuông: 2 7dm ; 2 129cm ; c) Mét khối: 3 521dm . Hướng dẫn a) 3dm = 0,3m = 3 m 11cm = 0,11m = 11 m 10 100 213mm = 0,213m = 213 m 100 b 7dm2 = 0,07m2 = 7 2 m 129cm2 = 0,0129m2 = 129 2 m 100 10000 c) 521dm3 = 0,521m3 = 521 3 m 1000
Bài 2. Biểu thị các số sau đây dưới dạng phân số với đơn vị là:
a) Mét: 9dm ; 27cm ; 109mm ; b) Mét vuông: 2 3dm ; 2 421cm ; c) Mét khối: 3 417dm .
Dạng 3. Tìm điều kiện để biểu thức A là một phân số B
Để tìm điều kiện để biểu thức A là một phân số ta làm theo các bước sau: B Bước 1: Chỉ ra ,
A B∈;
Bước 2: Tìm điều kiện để B ≠ 0 .
Bài 1. Cho biểu thức 3 M − =
với n là số nguyên: n
a) Số nguyên n phải có điều kiện gì để M là phân số?
b) Tìm phân số M , biết n = 2; n = 5; n = 4. − Hướng dẫn:
a) Mẫu phải là số nguyên khác 0 nên điều kiện: n ∈ Z*
b) Phân số có được là: 3 − 3 − 3 ; ; − 3 5 4 −
Bài 2. Cho biểu thức 5
M = với n là số nguyên: n
a) Số nguyên n phải có điều kiện gì để M là phân số?
b) Tìm phân số M , biết n = 6; n = 7; n = 3. −
Bài 3. Cho biểu thức 3 M − =
với n là số nguyên: n −1
a) Số nguyên n phải có điều kiện gì để M là phân số?
b) Tìm phân số M , biết n = 3; n = 5; n = 4. −
Bài 4. Cho biểu thức 5 M =
với n là số nguyên: n +1
a) Số nguyên n phải có điều kiện gì để M là phân số?
b) Tìm phân số M , biết n = 6; n = 7; n = 3. −
Dạng 4. Tìm điều kiện để một biểu thức phân số có giá trị là một số nguyên
Để phân số a có giá trị là một số nguyên thì a chia hết cho . b b
Bài 1: Số nguyên a phải có điều kiện gì để các phân số sau là số nguyên:
a/ a +1 b/ a − 2 3 5 Hướng dẫn:
a/ a +1 ∈ Z khi và chỉ khi a + 1 = 3k (k ∈ Z). Vậy a = 3k – 1 (k ∈ Z) 3
b/ a − 2 ∈ Z khi và chỉ khi a - 2 = 5k (k ∈ Z). Vậy a = 5k +2 (k ∈ Z) 5
Bài 2: Tìm số nguyên x để các phân số sau là số nguyên: a/ 13 b/ x +3 x −1 x − 2 Hướng dẫn
a) 13 ∈ Z khi và chỉ khi x – 1 là ước của 13. x −1
Các ước của 13 là 1; -1; 13; -13 Suy ra: x - 1 -1 1 -13 13 x 0 2 -12 14
b/ x +3 = x − 2+5 x − 2 5 5 = + = 1+
∈ Z khi và chỉ khi x – 2 là ước của 5. x − 2 x − 2 x − 2 x − 2 x − 2 x - 2 -1 1 -5 5 x 1 3 -3 7
Bài 3. Tìm các số nguyên n sao cho các phân số sau có giá trị là số nguyên: a) 3 b) 3 − c) 4 n − 3 n −1 3n +1
Bài 4. Tìm các số nguyên n sao cho các phân số sau có giá trị là số nguyên: a) 2 b) 2 − c) 3 − n −1 −n + 2 2n −1
DẠNG 5: PHÂN SỐ BẰNG NHAU.
Để xác định hai phân số a và c có bằng nhau không ta làm như sau: b d
- Tính hai tích a.d và b.c
+ Nếu a.d = b.c => hai phân số bằng nhau.
+ Nếu a.d ≠ b.c => hai phân số không bằng nhau.
- Ngược lại nếu đã có a.d = b.c thì ta viết được các cặp phân số bằng nhau là:
a = c ; a = b ; d = b ; d = c b d c d c a b a
Bài 1. Giải thích tại sao các phân số bằng nhau: 12 − 2 − = 30 5 Hướng dẫn 12.5 − = 60 − 30.( 2 − ) = 60 − Do đó ( ) 12 − 2 12.5 30. 2 − − = − ⇒ = 30 5
Bài 2: Các cặp phân số sau có bằng nhau không? Vì sao? 6 − và 2 b) 6 và 6 − c) 5 và 7 15 3 − 7 7 − 7 5 Hướng dẫn
a) Vì (-6).(-3) ≠ 15.2 => 6 − ≠ 2 15 3 −
b) Vì 6.(-7) = 7.(-6) => 6 = 6 − 7 7 −
c) Vì 5.5 ≠ 7.7 => 5 ≠ 7 7 5
Bài 3: Tìm các số nguyên x và y để các cặp phân số sau đây bằng nhau a) x và 12 − b) 5 − và 10 c) x và y d) −x và x +1 5 10 2 −y 5 6 − y −y +1 Hướng dẫn a) x = 12 −
x.10 = (-12).5 x = - 6 5 10 b) 5
− = 10 (-5).(-y) =10.2 y = 4 2 −y
c) x = y (-6).x = 5.y x = 5k ; y = - 6k, với k là số nguyên tùy ý. 5 6 −
d) −x = x +1 (-x).(-y + 1) = y .(x + 1) - x = y y −y +1
Vậy x = k; y = - k với k là số nguyên khác 0 và 1
Bài 4: Từ năm số nguyên 2, -6, 3, -9, 27 hãy lập các cặp phân số bằng nhau với tử và mẫu là các số trên. Hướng dẫn
Ta lập được đẳng thức (-6).3 = 2.(-9)
Lập được bốn cặp phân số bằng nhau như sau: 6 − và 9 − b) 6 − và 2 c) 3 và 2 c) 3 và 9 − 2 3 9 − 3 9 − 6 − 2 6
Bài 5. Tìm số nguyên x, biết a, x 2 x − − = ; b, 1 = ; c, 1 3 = ; d, 8 12 = ; 3 6 4 2 − 3 x 5 x e, x 3 − = ; f, x 4 = . 3 x 4 − x
Bài 6. Tìm số nguyên x, biết a, 5 x − = ; b, x 1 = ; c, 3 x = ; d, 3 9 = ; 8 14 6 3 − 5 − 10 5 x e, x 2 − = ; f, x 5 = . 2 x 5 − x
Bài 7. Tìm số nguyên x, biết a, x +1 2 − − = ; b, x −1 1 = ; c, 1 3 = ; d, 4 12 = ; 3 6 4 2 − 6 2x 5 9 − x e, x +1 3 − − = ; f, x 1 4 = . 3 x +1 4 − x −1
Bài 8. Tìm số nguyên x, biết a, 3 x + 5 − = ; b, x − 4 1 = ; c, 3 9 = ; d, 5 2x = ; 5 − 10 6 3 − 5 3x 7 14 e, 5 − x 2 − − = ; f, 4 x 5 = . 2 5 − x 5 − 4 − x
Bài 9. Tìm số nguyên x, biết a, 5 x −1 + − = ; b, 1 x 1 = ; c, 3 5 = ; d, 5 4 = ; 6 x 2 3x x + 2 2x +1 8x − 2 7 − x
Bài 10. Tìm số nguyên x, biết a, 4 2x −1 − + − = ; b, 2x 1 3x 1 = c, 4 7 = ; d, 3 4 = ; 3 x 3 4 x + 2 3x +1 x +1 2 − 2x
Bài 11. Liệt kê các cặp số nguyên x, y thỏa mãn: a, x 4 = ; b, 2 − y = ; c, x 2 = d, x y = . 2 y x 4 y 5 10 12 −
Bài 12. Liệt kê các cặp số nguyên x, y thỏa mãn: a, x 2 = ; b, 3 − y = ; c, x 3 = ; d, x y = . 3 y x 2 y 4 6 8 −
Bài 13. Tìm các số nguyên x, y biết: a, x y −
= và x + y =14; b, x 3 3
= và x − y = 4; 4 3 y − 2 2 c, x y =
và 2x + 3y =13. 8 12
Bài 14. Tìm các số nguyên x, y biết:
a, 3x = 2y và x + y =10 b, x − 2 4
= và y − x = 4 − y + 3 6 c, x y =
và x + 2y =12. 4 10 −
CHỦ ĐỀ 19: TÍNH CHẤT CƠ BẢN CỦA PHÂN SỐ A/ KIẾN THỨC CẦN NHỚ
1/ Tính chất cơ bản của phân số:
Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được
một phân số bằng phân số đã cho. a . a m =
với m∈,m ≠ 0 b . b m
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được
một phân số bằng phân số đã cho. a a : n =
với n∈ƯC( ;ab) b b : n 2/ Chú ý:
- Ta có thể viết một phân số bất kì có mẫu âm thành phân số bằng nó và có mẫu dương
bằng cách nhân cả tử và mẫu của phân số đó với 1 − .
- Mỗi phân số có vô số phân số bằng nó. Các phân số bằng nhau là cách viết khác nhau
của cùng một số gọi là số hữu tỉ.
B/ BÀI TẬP VẬN DỤNG.
DẠNG 1: LIÊN HỆ TÍNH CHẤT CƠ BẢN CỦA PHÂN SỐ VỚI PHÂN SỐ BẰNG NHAU. I/ PHƯƠNG PHÁP.
* Để giải thích phân số bằng a phân số c ta giải thích như sau: b d
+ Nếu tích a.d = b.c thì hai phân số bằng nhau.
+ Từ phân số a ta nhân (chia) cả tử và mẫu của phân số này cho cùng một số m mà b
được phân số c thì hai phân số bằng nhau. d
* Với phân số tối giản a thì phân số .ak là dạng chung của tất cả các phân số bằng b . b k phân số a b
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Giải thích tại sao các phân số bằng nhau: 12 − 2 − = 30 5 Giải 12.5 − = 60 − 30.( 2 − ) = 60 − Do đó ( ) 12 − 2 12.5 30. 2 − − = − ⇒ = 30 5
Bài 2. Giải thích tại sao các phân số sau bằng nhau: a) 51 − và 5151 − b) 313131 và 31 73 7373 474747 47 Giải a) 51 − 51.101 − 5151 − = = b) 313131 313131:10101 31 = = 73 73.101 7373 474747 474747 :10101 47
Bài 3. Tìm ba phân số bằng phân số 5 − 13 Giải 10 − 15 − 20 ; ; − 26 39 52 Bài 4. a) Tìm x − x ∈ , biết 48 = . 24 72
b) Viết dạng chung của tất cả các phân số bằng 48 − . 72 Giải a) x 48 − 48 − :3 16 − = = = . Vậy x = 16 − . 24 72 72 :3 24 b) 48 − 48 − : 24 2 − = = . 72 72 : 24 3
Dạng chung của tất cả các phân số bằng 48 − là 2
− k (k∈ ;k ≠ 0). 72 3k
Bài 5. Đúng ghi Đ, sai ghi S a) 37 − 37 − + 24 − = c) 5111 5111 131 = 191 191+ 24 9333 9333−131 b) 387 − 387.69 − 43 43. 9978 − = d) ( ) = 2911 2911.69 71 71.( 9978 − ) Giải S Đ S Đ a) b) c) d)
Bài 6. Giải thích tại sao các phân số sau bằng nhau: a) 24 − 14 − = b) 90 22 = 36 21 225 55 Giải a) 24 − 24 − :12 2 − 2.7 − 14 − = = = = . b) 90 90 : 45 2 22 = = = . 36 36 :12 3 3.7 21 225 225: 45 5 55
Bài 7. Giải thích tại sao các phân số sau bằng nhau: 3131 − 313131 − = 9797 979797 Giải 3131 − 3131 − :101 31 − 31.10101 − 313131 − = = = = 9797 9797 :101 97 97.10101 979797
Bài 8. Tìm bốn phân số bằng phân số 24 có mẫu là số tự nhiên nhỏ hơn 14. 36 Giải 24 24 :12 2 =
= => Bốn phân số cần tìm là 2 4 6 8 ; ; ; 36 36 :12 3 3 6 9 12 Bài 9.
a) Tìm tất cả các phân số bằng phân số 63
− và có mẫu là số tự nhiên nhỏ hơn 20. 84
b) Tìm tất cả các phân số bằng phân số 121212 −
có mẫu là số tự nhiên nhỏ hơn 50. 131313 Giải a) 3 − 6 − 9 − 1 − 2 ; ; ; b) 12 − 24 − 36 ; ; − 4 8 12 16 13 26 39
Bài 10. Cho biểu thức 3x − 4 M = x − 3
a) Tìm các số nguyên x để M là phân số.
b) Tìm các số nguyên x để M là một số nguyên. Giải a) x ≠ 3
b) M là số nguyên khi (3x – 4) ⋮ (x – 3) [3(x – 3) + 5] ⋮ (x – 3)
Nên x −3 là ước của 5. x − 3 =1; 1; − 5; 5 − hay x = 4;2;8; 2 −
Bài 11. Tìm phân số có giá trị bằng phân số 102 biết tổng của tử và mẫu của phân số đó là 80. 170 Giải 102 102 :34 3 = = . 170 170 :34 5
Phân số bằng phân số 102 có dạng 3n (n∈,n ≠ 0). 170 5n
Theo đầu bài, ta có 3n +5n = 80 ⇔ 8n = 80 ⇔ n =10 .
Phân số cần tìm là 30 . 50
DẠNG 2: RÚT GỌN PHÂN SỐ. I/ PHƯƠNG PHÁP.
Muốn rút gọn một phân số, ta chia cả tử và mẫu của một phân số cho một ước chung (khác 1 và 1 − ) của chúng.
Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà tử và mẫu chỉ có
ước chung là 1 và 1 − . Chú ý:
- Nếu chia cả tử và mẫu của phân số cho ƯCLN của chúng, ta sẽ được một phân số tối giản.
- Phân số a là tối giản nếu a và b là hai số nguyên tố cùng nhau. b
- Khi rút gọn phân số, ta thường rút gọn phân số đến tối giản.
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Rút gọn các phân số sau thành phân số tối giản: a) 300 b) 38 − c) 68 − 540 95 85 − Giải a) 300 300:60 5 − − − 68 − 68 − : 17 − 4 = = b) 38 38:19 2 = = c) ( ) = = 540 540 : 60 9 95 95:19 5 85 − 85 − :( 17 − ) 5 Bài 2. Rút gọn a) 12.13 b) 25.17 + 25.12 5.24 29.13+ 29.14 Giải a) 12.13 1.13 13 25.17 + 25.12 25. 17 +12 25.29 25 = = b) ( ) = = = 5.24 5.2 10
29.13+ 29.14 29.(13+14) 29.27 27
Bài 3. Tìm tất cả các phân số bằng phân số 32
− và có mẫu là số tự nhiên nhỏ hơn 15. 48 Giải 32 − 32 − :16 2 − − − − − = =
=> Các phân số cần tìm là 2 4 6 8 ; ; ; 48 48:16 3 3 6 9 12
Bài 4. Viết các phân số 5 2 − 1 ; ;
− dưới dạng phân số có mẫu là 48. 6 3 24 − Giải 5 40 2 − 32 − 1 − 2 = ; = ; = 6 48 3 48 24 − 48
Bài 5. Rút gọn: 1.2.5+3.4.15+ 4.8.20+ 7.14.350
2.5.11+ 6.10.33+ 8.20.44 +14.35.770 Giải
1.2.5 + 3.4.15 + 4.8.20 + 7.14.350
1.2.5.(1.1.1+ 3.2.3+ 4.4.4 + 7.7.70) 1 = =
2.5.11+ 6.10.33+ 8.20.44 +14.35.770 2.5.11.(1.1.1+ 3.2.3+ 4.4.4 + 7.7.70) 11 Bài 6.
a) Chứng tỏ rằng: 14n +3 là phân số tối giản với mọi n∈. 21n + 5
b) Chứng minh rằng: 25m + 7 là phân số tối giản với mọi m∈ . 15m + 4 Giải
Để chứng minh một phân số đã cho là phân số tối giản ta chứng minh TỬ SỐ và MẪU
SỐ có ƯCLN bằng 1
a) Gọi d là ƯCLN của 14n +3 và 21n +5 ( *
d ∈ ) . Ta có 14n + 3d và 21n + 5d .
Do đó 2(21n +5) −3(14n +3) =1d . Vậy d =1.
b) 3(25m + 7) −5(15m + 4) =1
Bài 7. Cộng cả tử và mẫu của phân số 12 với cùng một số tự nhiên x rồi rút gọn ta được 4 . 17 5 Tìm x Giải 12 + x 4
= ⇔ 5(12 + x) = 4(17 + x) ⇔ 60 + 5x = 68 + 4x ⇔ x = 8 17 + x 5 Bài 8. Cho 1 2 ... 8 9 A + + + + =
. Hãy xóa một số hạng ở tử và xóa một số hạng ở mẫu của A 11+12 +...+18 +19
để được một phân số có giá trị vẫn bằng A. Giải 1
A = nên có các cách Giải sau: 3
• Xóa số hạng 4 ở tử và xóa số hạng 12 ở mẫu, ta có: 1+ 2 + 3+ 5 + 6 + 7 + 8 + 9 41 1 = =
11+13+14 +15 +16 +17 +18 +19 123 3
• Xóa số hạng 5 ở tử và xóa số hạng 15 ở mẫu, ta có: 1+ 2 + 3+ 4 + 6 + 7 + 8 + 9 40 1 = =
11+12 +13+14 +16 +17 +18 +19 120 3
• Xóa số hạng 6 ở tử và xóa số hạng 18 ở mẫu, ta có: 1+ 2 + 3+ 4 + 5 + 7 + 8 + 9 39 1 = =
11+12 +13+14 +15 +16 +17 +19 117 3
Bài 9. Tìm phân số a bằng phân số 36 biết rằng ƯCLN(a;b) = 31. b 45 Giải 36 36 :9 4 = = 45 45:9 5
Phân số tối giản a có ƯCLN( ;ab) = 31 => phân số a đã rút gọn cho 31 để được 4 . b b 5 Vậy a 4.31 124 = = . b 5.31 155
Bài 10. Cho các phân số sau: 6 7 8 64 65 ; ; ;...; ;
. Tìm số tự nhiên n nhỏ nhất để
n + 8 n + 9 n +10 n + 66 n + 67
các phân số trên tối giản. Giải
Các phân số đã cho có dạng a
và tối giản nếu các số a và n + 2 nguyên tố cùng a + (n + 2) nhau vì: a +
(n + 2) − a = n + 2
, với a = 6;7;8;...;64;65.
Do đó n + 2 nguyên tố cùng nhau với các số 6;7;...;64;65.
Số tự nhiên n + 2 nhỏ nhất thỏa mãn tính chất này là 67 .
Ta có n + 2 = 67 nên n = 67 − 2 = 65.
Vậy số tự nhiên n nhỏ nhất cần tìm là 65.
Bài 11. Tìm phân số có mẫu bằng 13, biết rằng khi cộng tử với 14, nhân mẫu với 3 thì giá trị
phân số đó không thay đổi. Giải
Phân số cần tìm có dạng x x +14 = (x∈) 13 13.3 Do đó 3x x + 4 =
⇔ 3x = x +14 ⇔ 2x =14 ⇔ x = 7 . 39 39 Thử lại: 7 7 +14 21 = = (Thích hợp) 13 13.3 39
DẠNG 3: QUY ĐỒNG MẪU SỐ NHIỀU PHÂN SỐ. I/ PHƯƠNG PHÁP
Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:
- Bước 1: Tìm một bội chung các mẫu (thường là BCNN) để làm mẫu chung.
- Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
- Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Quy đồng mẫu các phân số: a) 5 và 4 − b) 7 − và 5 c) 1 2 ; − và 7 12 9 15 12 5 3 10 Giải a) 5 5.3 15 4 − 4.4 − 16 ; − = = = = 12 12.3 36 9 9.4 36 b) 7 − 7.4 − 28 − 5 5.5 25 = = ; = = 15 15.4 60 12 12.5 60 c) 1 1.6 6 2 − 2.10 − 20 − 7 7.3 21 = = ; = = ; = = 5 5.6 30 3 3.10 30 10 10.3 30
Bài 2: Quy đồng mẫu các phân số sau: a) 15 − 9 ; và 26 b) 7 5 ; − và 3 c) 4 − 3 ; − và 8 50 10 30 − 10 15 − 17 75 − 5 25 Lời giải
Đối với phân số chưa tối giản ta nên rút gọn trước rồi mới quy đồng mẫu dương a) 15 − 3.5 − 3 − 3.3 − 9 − − = = = = ; 9 9.3 27 = = ; 26 26 = . 50 10.5 10 10.3 30 10 10.3 30 30 − 30 b) Ta có 5 − 1
= . Chọn MSC = BCNN(10; 3; 17) = 510 15 − 3 7 − 7.51 − 375 − − = = ; 7 1 170 = = ; 3 3.30 90 = = 10 10.51 510 15 − 3 510 17 17.30 510 c) 4 − 4 3 − 3.15 − 45 − 8 8.3 24 = ; = = ; = = 75 − 75 5 5.15 75 25 25.3 75
Bài 3: Quy đồng mẫu các phân số sau: 2 4 a) 7 và 9 b) 5 + 7 và 3 −8 3 2 .3.5 2 2 2 .3 .10 7 − + 9.5 2 4 − + 3 Lời giải a) Rút gọn phân số 9 3 = nên MSC = 3 2 .3.5 2 2 3 2 .3 .10 2 .3.5 2 4 b) 5 + 7 32 16 16.5 80 − = = = = và 3 8 73 73.19 1387 = = = 7 − + 9.5 38 19 19.5 95 2 4 − + 3 5 5.19 95 MSC = 19.5 = 95
Nhận xét: Đối với phân số ở tử và mẫu mới rút gọn được ngay, còn dưới dạng tổng hoặc
hiệu thì phải tính đến kết quả rồi mới rút gọn được trước khi quy đồng mẫu.
Bài 4. Quy đồng mẫu các phân số sau: 2 4 a) 8 và 10 b) 6 −8 và 15 − 3 3 2 .25 2 2 2 .5 .7 2 12 − + 4 2 27 − + 3
DẠNG 4: SO SÁNH PHÂN SỐ. I/ PHƯƠNG PHÁP
1/ Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
2/ Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một
mẫu dương rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì lớn hơn. 3/ Nhận xét:
• Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0. Phân số lớn hơn không
gọi là phân số dương.
• Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0. Phân số nhỏ hơn 0 gọi là phân số âm.
• Hai phân số có mẫu dương, cùng tử dương, phân số nào có mẫu nhỏ hơn thì phân số đó lớn hơn.
II/ BÀI TẬP VẬN DỤNG
Bài 1. Trong các phân số sau: 54 − 33 − 151 47 ; ; ;
phân số nào dương, phân số nào âm? 1145 71 − 284 − 2008 Giải 54 − 33 − 151 47 < 0; > 0; < 0; > 0 1145 71 − 284 − 2008
Bài 2. So sánh các phân số sau: a) 13 và 11 b) 21 − và 19 − 15 15 37 37 c) 14 và 14 d) 13 − và 13 − 27 31 59 51 Giải a) 13 11 − − > b) 21 19 < 15 15 37 37 c) 14 14 − − > d) 13 13 13 13 < ⇒ > 27 31 59 51 59 51
Bài 3. So sánh các phân số sau: a) 42 và 60 b) 34 − và 93 − 63 72 119 248 Giải a) 42 2 60 5 2 4 5 = ; = ; = < . Vậy 42 60 < . 63 3 72 6 3 6 6 63 72 b) 34 − 2 − 93 − 3 − 2 − 16 − 21 − 3 ; ; − = = = > = . 119 7 248 8 7 56 56 8
Bài 4. So sánh các phân số sau: a) 49 − và 13 b) 51 và 1424 − 211 1999 511 1629 Giải a) 49 − 13 − < 0; 0 < nên 49 13 < . 211 1999 211 1999 b) 51 1424 0; − − > < 0 nên 51 1424 > . 511 1629 511 1629
Bài 5. Sắp xếp các phân số sau theo thứ tự tăng dần: 1 − 5 7 5 − 1 − 1 ; ; ; ; ; . 2 12 18 9 3 3 Giải 1 − 18 − 5 10 7 14 5 − 20 − 1 − 12 − 1 12 = ; = ; = ; = ; = ; = 2 36 12 36 18 36 9 36 3 36 3 36 Ta có 20 − 18 − 12 − 10 12 14 < < < < < 36 36 36 36 36 36 Nên 5 − 1 − 1 − 5 1 7 < < < < < . 9 2 3 12 3 18
Bài 6. Điền số thích hợp vào chỗ chấm a) 31 − ... ... ... 27 − < < < < b) 5 5 5 5 1 > > > > 59 59 59 59 59 31 ... ... ... 7 Giải a) 31 − 30 − 29 − 28 − 27 − < < < < 59 59 59 59 59 b) 5 5 5 5 1 > > > > 31 32 33 34 7
Bài 7. Tìm năm phân số có dạng a mà 5 a 5 < < . b 11 b 9 Giải Ta có 5 15 5 15 = ; = => 5 a 5 < < hay 15 a 15 < < 11 33 9 27 11 b 9 33 b 27 Suy ra a 15 15 15 15 15 = ; ; ; ; . b 32 31 30 29 28
Bài 8. Cho a∈{5; 7; } 13 ; b∈{12; 0; 29; }
18 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của a . b Giải ; a b > 0 . Do đó
a lớn nhất khi a lớn nhất và b nhỏ nhất (b ≠ 0). Suy ra a =13 và b =12. b
a nhỏ nhất khi a nhỏ nhất và b nhỏ nhất. Suy ra a =5 và b = 29. b Bài 9. a) Cho a c > (a,b,c,d ∈ ;
b,d > 0). Chứng minh rằng: ad > bc . b d
b) Cho ad> bc (a, b, c, d∈ ;
b,d > 0) . Chứng minh rằng: a c > . b d Giải a) a ad = ; c bc = . Do đó a c ad bc > ⇔ >
⇔ ad > bc . b bd d bd b d bd bd b) ad bc a c ad > bc ⇔ > ⇔ > . bd bd b d
Bài 10. Cho a, b, c N∗ ∈
. Chứng minh rằng: Nếu a + < 1 thì a a c < . b b b + c Giải
Cách 1: a <1⇒ a < b ⇒ ac < bc ⇒ ab + ac < ab +bc b ⇒ ( + ) < ( + ) a a + c a b c b a c ⇒ < (vận dụng bài 48) b b + c
Cách 2: a a(b + c) ab + ac a + c b(a + c) = = ; ab + bc = =
b b(b + c) b(b + c) b + c b(b + c) b(b + c)
Do đó, nếu a <1⇒ a < b ⇒ ac < bc b
ab + ac ab + bc a a + c ⇒ < ⇒ < .
b(b + c) b(b + c) b b + c
Bài 11. Tìm giá trị nguyên của x để a) 2008 A = có giá trị lớn nhất. x −1000 b) 148 C = có giá trị nhỏ nhất. x −11 Giải
a) Điều kiện x ≠100 .
• Xét x <100. Ta có x −100 < 0 . Do đó A < 0.
• Xét x >100 . Ta có x −100 > 0 . Mà x∈
Nên x −100 ≥1. Ta có 2008 A = ≤ 2008 x −100
A = 2008 khi x −100 =1 hay x =101.
Vậy A có giá trị lớn nhất là 2008.
b) Điều kiện x ≠11.
• Xét x >11. Ta có x −11> 0 . Do đó C > 0 .
• Xét x <11. Ta có 11− x > 0 . Mà x ∈ Nên 148 −
≤ 148. Vậy C ≥ 148 − . x −11 C = 148 −
khi 11− x =1 hay x =10 .
Vậy C có giá trị nhỏ nhất là 148 − . Bài 12.
a) Cho a c (a,c ; , b d N∗ + < ∈ ∈
) . Chứng minh rằng: a a c c < < . b d b b + c d b) So sánh 2008 2007 58 57 2009 +1 và 2009 +1 7 + 2 và 7 +2009 2009 2009 +1 2008 2009 +1 57 7 + 2 56 7 + 2009 Giải a) Ta có: • a c +
< ⇒ ad < bc ⇒ ab + ad < ab + bc ⇒ ( + ) < ( + ) a a c a b d b a c ⇒ < b d b b + d • a c +
< ⇒ ad < bc ⇒ ad + cd < bc + cd ⇒ ( + ) < ( + ) a c c d b c c b d ⇒ < . b d b + d d Vậy a a + c c < < . b b + d d b) 2008 2008 2008 • 2009 +1 2009 +1 2009 +1+ 2008 <1⇒ < 2009 2009 2009 2009 +1 2009 +1 2009 +1+ 2008 2008 2007 2007
Mà 2009 +1+ 2008 2009(2009 +1) 2009 +1 = = 2009 2008 2008 2009 +1+ 2008 2009(2009 +1) 2009 +1 58 58 58 57 57 • 7 + 2 7 + 2 7 + 2 + 5 7(7 +1) 7 +1 > 1⇒ > = = 57 57 57 56 56 7 + 2 7 + 2 7 + 2 + 5 7(7 +1) 7 +1 57 57 57 57 Mặt khác: 7 +1 7 +1 7 +1+ 2008 7 + 2009 >1⇒ > = . 58 58 56 56 7 +1 7 +1 7 +1+ 2008 7 + 2009
Bài 13. So sánh hai phân số: 1919.161616 và 25 323232.3838 102 Giải 1919.161616 1.1 1 25 25 = = = > . 323232.3838 2.2 4 100 102 Bài 14.
a) Tìm x, y∈ sao cho 1 x y 1 < < < . 18 12 9 4 8 8 b) Cho 10 2 A + = và 10 B = . So sánh A và B. 8 10 −1 8 10 − 3 Giải a) 1 x y 1 < < < hay 4 6x 8y 18 < < < 18 12 9 4 72 72 72 72
4 < 6x < 8y <18 • x =1; y =1 • x =1; y = 2
• x = 2; y = 2 8 8 8 8 b) 10 B = >1 => 10 10 + 2 10 + 2 B = > = = A 8 10 − 3 8 8 8
10 − 3 (10 − 3) + 2 10 −1
C/ BÀI TẬP TỰ LUYỆN.
Bài 1: Hãy viết một phân số sau thành hai phân số bằng nó và có mẫu số dương: a) 3 ; b) 5 ; c) 4 − ; 5 − 10 − 9 − d) 6 − ; e) 0 ; f) 0 ; 8 − 10 − 6 −
Bài 2: Hãy viết một phân số sau thành hai phân số bằng nó và có mẫu số dương: a) 2 ; b) 4 ; c) 3 − ; 5 − 6 − 8 − d) 10 − ; e) 0 ; f) 0 . 8 − 3 − 5 −
Bài 3: Trong các cặp phân số sau, cặp phân số nào bằng nhau? A. 2 và 4 − ; B. 4 và 8 − C. 1 − và 1 − ; D. 5 và 5 − . 5 10 3 − 6 5 5 − 11 11 −
Bài 4. Trong các cặp phân số sau, cặp phân số nào băng nhau? A. 2 và 10 − ; B. 14 − và 7 C. 3 − và 1 ; D. 4 − và 1 − . 7 35 10 5 9 3 − 8 − 2
Bài 5. Tìm các cặp phân số bằng nhau trong các phân số sau đây: 8 35 − 88 12 − 11 5 ; ; ; ; ; − . 18 14 56 27 − 7 2
Bài 6. Tìm các cặp phân số bằng nhau trong các phân số sau đây: 6 3 18 24 − 36 4 ; ; ; ; ; − . 8 − 4 24 − 30 48 5
Bài 7. Trong các phân số nào sau đây, chỉ ra phân số không bằng phân số bất kì nào của dãy: 15 6 − 21 21 − 14 24 − 6 ; ; ; ; ; ; . 35 33 49 91 77 − 104 22
Bài 8. Trong các phân số nào sau đây, chỉ ra phân số không bằng phân số bất kì nào của dãy: 12 − 20 12 24 − 36 − 4 ; ; ; ; ; − . 15 25 − 15 − 30 48 5
Bài 9: Viết số thích hợp vào ô trống: a) 1 1.6 3 − 3 − .5 3 3. 4 − = = b) ( ) = = c) 5 5. = = d) ( ) = = . 3 3.6 7 7.5 2 2.( 4 − ) 2 2.
Bài 10. Viết số thích hợp vào ô trống: a) 2 2.3 6 − 6 − .4 9 9. 2 − = = b) ( ) = = c) 4 4. = = d) ( ) = = . 7 7.3 7 7.4 11 11.( 3 − ) 8 8.
Bài 11. Viết số thích hợp vào ô trống: a) 9 9:3 − 16 − 16 − : 12 12 : 3 − = = b) 12 12: 3 = = c) ( ) 4 = = d) ( ) ( ) = = 6 6 :3 8 − 8: − 2 12 12 : 15 15:
Bài 12. Viết số thích hợp vào ô trống: a)12 12: 2 24 − 24 − : 25 25: 5 − = = b) ( ) 4 − = = c) 30 30 : 3 = = d) ( ) = = 14 14 : 2 18 18: 3 − 20 − ( 20 − ) : 35 35:
Bài 13. Viết số thích hợp vào ô trống: a) 1 − 3 − = b) 4 12 == c) 5 = d) 2 8 20 = = = . 3 5 − 7 28 − 3 18
Bài 14. Viết số thích hợp vào ô trống: a) 3 − − = b) 7 14 == c) 12 = d) 36 12 − = = . 5 − 20 − 16 8 16 − 27 3 Bài 15:
a) Viết tất cả các phân số bằng với phân số 6
− và mẫu số là các số có hai chữ số đều 13 dương.
b) Viết tất cả các phân số bằng với phân số 5 và tử số là các số có hai chữ số chẵn, 8 − dương. Bài 16.
a) Viết tất cả các phân số bằng với phân số 7
− và mẫu số là các số có hai chữ số đều 10 dương.
b) Viết tất cả các phân số bằng với phân số 5 và tử số là các số có hai chữ số lẻ, dương. 8 −
Bài 17. Giải thích tai sao các phân số sau đây bằng nhau: a) 28 − 52 − − = ; b) 4040 2 = ; c) 120120 1 = ; d) 18180 2 = . 21 39 − 6060 3 240240 2 27270 − 3 −
Bài 18. Giải thích tai sao các phân số sau đây bằng nhau: a) 54 1 − − − − = ; b) 1111 1 = ; c) 1414 2 = ; d) 131313 13 = . 270 5 2222 2 2121 − 3 171717 − 17
Bài 19. Giải thích tai sao các phân số sau đây bằng nhau: 2 a) a −a abab ababab abab xy − x x = ; b) = ; c) 101 = ; d) = . b b − cdcd cdcdcd cdcd 10101 2 y − xy y
Bài 20. Giải thích tai sao các phân số sau đây bằng nhau: a) −a a ab ab ab ab − = ; b) 0 = ; c) 1 = ; d) 7x 21 1 = . b b − cd cd0cd abab 10 14x − 42 2
CHỦ ĐỀ 20: PHÉP CỘNG (TRỪ) HAI PHÂN SỐ
A/ KIẾN THỨC CẦN NHỚ.
1/ Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu. a b a + b + = m m m
2/ Muốn cộng hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một
mẫu rồi cộng các tử và giữ nguyên mẫu chung. 3/ Các tính chất.
a) Tính chất giao hoán: a c c a + = + b d d b
b) Tính chất kết hợp: a c p a c p + + = + + b d q
b d q
c) Cộng với số 0 : a + 0 = 0 a a + = b b b 4/ Chú ý:
Khi cộng nhiều phân số, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào
sao cho việc tính toán được thuận tiện.
5/ Hai phân số đối nhau nếu tổng của chúng bằng 0. a a − + − = 0 a a a − = = b b b b − b
6/ Muốn trừ một phân số cho một phân số, ta cộng số bị trừ với số đối của số trừ a c a c − = + − b d b d B/ CÁC DẠNG TOÁN.
DẠNG 1: THỰC HIỆN CỘNG – TRỪ HAI (NHIỀU) PHÂN SỐ. I/ PHƯƠNG PHÁP.
Vận dụng quy tắc cộng (trừ) hai phân số cùng mẫu số, khác mẫu số…
Vận dụng thực hiện phép tính một cách hợp lý với phép tính cộng (trừ) nhiều phân số
Vận dụng tính chất giao hoán, tính chết kết hợp một cách linh hoạt.
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Cộng các phân số sau: a) 7 12 − − + b) 5 4 + 19 19 13 13 Hướng dẫn a) 7 12 19 − − − + = = 1 b) 5 4 9 + = 19 19 19 13 13 13
Bài 2. Tính các tổng dưới đây sau khi đã rút gọn phân số: 48 − 37 − + 96 148 Hướng dẫn 48 − 37 − 1 − 1 − 2 − 1 − 3 − + = + = + = 96 148 2 4 4 4 4
Bài 3. Tính tổng các phân số lớn hơn 1 − , nhỏ hơn 1 − và có tử là 3 − 12 13 Hướng dẫn 1 − 3 − 1 − 3 ; − − − − = = ; 3 3 225 + = 12 36 13 39 37 38 1406 Bài 4. Tính a) 3 − 1 3 − − − + + b) 1 9 7 + + 5 4 10 5 10 25 Hướng dẫn a) 3 − 1 3 − 12 − 5 6 − 13 − + + = + + = . 5 4 10 20 20 20 20 b) 1 9 − 7 − 10 45 − 14 − 49 − + + = + + = . 5 10 25 50 50 50 50 Bài 5: Tính a) 3 1 − − − − − b) 5 1 − c) 2 3 − d) 1 5 − − 5 2 7 3 5 4 6 Hướng dẫn a) 3 1 − 3 1 − 3 1 6 5 6 + 5 11 − = + − = + = + = = 5 2 5 2 5 2 10 10 10 10 b) 5 − 1 5 − 1 − 15 − 7 − 15 − + ( 7 − ) 22 − − = + = + = = 7 3 7 3 21 21 21 21 c) 2 − 3 − 2 − −( 3 − ) 2 − 3 8 − 15 8 − +15 7 − = + = + = + = = 5 4 5 4 5 4 20 20 20 20 d) 1 5 1 30 − + ( 1 − ) 31 5 − − − = − + − = = 6 1 6 6 6
Bài 6. Tính bằng phương pháp hợp lý nhất : a) 31 7 8 − + b) 38 8 17 3 − − −
c) 1 12 13 79 28 + + − − 23 32 23 45 45 51 11 3 67 41 67 41 Hướng dẫn a) 31 7 8 − + = 31 8 7 7 25 − − = 1− = 23 32 23 23 23 32 32 32 b) 38 8 17 3 − − − = 38 8 1 3 − + + = 2 1 3 3 14 + + = 1+ = 45 45 51 11 45 45 3 11 3 3 11 11 11
c) 1 12 13 79 28 + + − − = 1 12 79 13 28 + − + + = 1 1 −1+1 = 3 67 41 67 41 3 67 67 41 41 3 3
Bài 7. Tính nhanh: 1 1 − 1 1 − 1 1 1 − 1 1 − + + + + + + + + . 5 6 7 8 9 8 7 6 5 Hướng dẫn 1 1 − 1 1 − 1 1 1 − 1 1 − − − − − + + + + + + + + 1 1 1 1 1 1 1 1 1 = + + + + + + + + 5 6 7 8 9 8 7 6 5
5 5 6 6 7 7 8 8 9 1 1 = 0 + 0 + 0 + 0 + = . 9 9 Bài 8. a) Tính: 1 1 1 1 1 1 1 1 1 1 1
1− ; − ; − ; − ; − ; − . 2 2 3 3 4 4 5 5 6 6 7 b) Tính nhanh: 1 1 1 1 1 1 + + + + + . 2 6 12 20 30 42 Hướng dẫn a) 1 2 1 1 1− = − = 1 1 3 2 1 − = − = 1 1 4 3 1 − = − = 1 1 5 4 1 − = − = 2 2 2 2 2 3 6 6 6 3 4 12 12 12 4 5 20 20 20 1 1 6 5 1 − = − = 5 6 30 30 30 b) 1 1 1 1 1 1 + + + + + 1 1 1 1 1 1 1 1 1 1 1 1 6
= 1− + − + − + − + − + − =1− = 2 6 12 20 30 42 2 2 3 3 4 4 5 5 6 6 7 7 7
Bài 9: Tính nhanh giá trị các biểu thức sau: -7 1 A = − − + (1+ ) 2 5 6 B = + ( + ) -1 3 3 B= ( + ) + 21 3 15 9 9 5 12 4 Hướng dẫn -7 1 A = ( − − + ) +1 = 0 +1 =1 2 6 5 24 25 1 B = ( + ) + = + = 21 3 15 9 9 45 45 15 3 3 − 1 − 1 − 1 − 5 − 2 − 7 C= ( ) − + + = + = + = 12 4 5 2 5 10 10 10
Bài 10: Tính theo cách hợp lí: a/ 4 16 6 3 − 2 10 − 3 − − + + + + + + b/ 42 250 2121 125125 + + + 20 42 15 5 21 21 20 46 186 2323 143143 Hướng dẫn a/ 4 16 6 3 − 2 10 − 3 − − + + + + + + 1 8 2 3 2 10 3 = + + + + + + 20 42 15 5 21 21 10 5 21 5 5 21 21 20 1 2 3 − 8 2 10 − 3 3 = ( + + ) + ( + + ) + = 5 5 5 21 21 21 20 20 b/ 42 250 2121 − 125125 − − − − − + + + 21 125 21 125 21 21 125 125 = + + + = ( + ) + ( + ) = 0 + 0 = 0 46 186 2323 143143 23 143 23 143 23 23 143 143 Bài 11: Tính: a/ 7 1 3 − + − b/ 5 3 3 − + 3 2 70 12 16 − 4 ĐS: a/ 34 b/ 65 35 48
Bài 12: Cộng các phân số sau: a/ 65 33 − − + b/ 36 100 + c/ 650 588 + d/ 2004 8 + 91 55 84 − 450 1430 686 2010 670 − ĐS: a/ 4 b/ 13 − c/ 31 d/ 66 35 63 77 77
Bài 13: Có 9 quả cam chia cho 12 người. Làm cách nào mà không phải cắt bất kỳ quả nào thành 12 phần bằng nhau? Hướng dẫn
- Lấu 6 quả cam cắt mỗi quả thành 2 phần bằng nhau, mỗi người được 1 quả. Còn lại 3 2
quả cắt làm 4 phần bằng nhau, mỗi người được 1 quả. Như vạy 9 quả cam chia đều cho 12 4
người, mỗi người được 1 1 3 + = (quả). 2 4 4
- Chú ý: 9 quả cam chia đều cho 12 người thì mỗi người được 9 3 = quả nên ta có cách 12 4 chia như trên.
Bài 14: Nêu mọi cách viết các phân số sau thành tổng của 2 phân số có tử = 1, mẫu khác nhau. a/ 1/8 b/ 1/10 Hướng dẫn
a) Gọi 2 phân số cần tìm 1 , 1 (x, y ∈ N*). Ta có: 1 + 1 = 1 (1) x y x y 8
Do x và y có vai trò như nhau nên ta có thể giả sử rằng: x < y. Từ (1) => 1 1 < hay x > 8 (2) x 8
Do x < y nên 1 > 1 => 1 + 1 > 1 + 1 hay 2 > 1 x y x x y x x 8
Do đó 2 > 2 hay x < 16 (3) x 16
Từ (2), (3) ta có: 8 < x < 16
Thay x = 9, 10, 11, 12, 13, 14, 15 vào (1)
=> x = 9, y = 72; x = 10, y = 40 ; x = 12, y = 24
Vậy có tất cả 3 cách viết. 1 1 1 = + 1 1 1 = + 1 1 1 = + 8 9 72 8 10 40 8 12 24
b/ Tương tự câu a) ta viết được: 1 1 1 1 1 1 1 1 1 = + = + = + = + 10 11 110 12 60 14 35 15 30
Bài 15: Viết 3/11 thành tổng của 2 phân số có tử số là 1 và mẫu khác nhau?
Bài 16: Viết 5/21 thành tổng của 3 phân số có tử số là 1 và mẫu khác nhau?
Bài 17: Có 5 quả cam chia đều cho 6 người. Làm cách nào để chia được mà không phải cắt bất
kỳ quả nào thành 6 phần bằng nhau?
Bài 18: Hai vòi nước cùng chảy vào 1 bể. Vòi 1 chảy trong 8h, vòi 2 chảy trong 6h đầy bể. Vòi
3 tháo trong 4h thì bể cạn. Bể đang cạn nếu mở cả 3 vòi thì sau 1h chảy được bao nhiêu phần bể? ĐS: 1/24 bể
DẠNG 2: TÌM SỐ x BIẾT THỎA MÃN ĐIỀU KIỆN BÀI CHO.
* Nếu biết A < x < B mà A và B là các biểu thức tổng các phân số thì ta thực hiện tính biểu
thức A dược số a, tính biểu thức B được số b => a < x < b => Tìm được số x.
* Áp dụng phép tính: Số hạng + Số hạng = Tổng ; Số bị trừ - Số trừ = Hiệu để tìm x
* Với bài toán tìm x nguyên để biểu thức A = f(x) là số nguyên g(x)
+ Bước 1: Thực hiện đưa biểu thức A = b.g(x)+a a = b +
với a ; b là số nguyên g(x) g(x)
+ Bước 2: Lập luận A ∈ Z g(x) là ước của số a => tìm được x.
II/ BÀI TẬP VẬN DỤNG.
Bài 1. Tìm x , biết: a) 4 3 x − + = b) 2 5 x − − = 15 15 11 11 Hướng dẫn a) 4 3 x − + = => 3 4 x − = − => 7 x − = 15 15 15 15 15 b) 2 5 x − − = => 5 2 x − = + => 3 x − = 11 11 11 11 11
Bài 2. Tìm x , biết a) 1 1 5 x − − = + b) 5 1 5 x − − = − c) 1 1 5 x − − = + 24 8 6 8 9 4 24 8 6 Hướng dẫn a) 1 17 x − = => 17 1 x = + => 3 x = 24 24 24 24 4 b) 5 1 5 x − − = − => 5 49 − x = => 5 49 x = − => 53 x − = 8 9 4 8 36 8 36 72 Bài 3: Tìm x biết: a/ 7 1 x − − = + b/ 5 4 x = + c/ 5 x 1 + = 25 5 11 9 − 9 1 − 3 Hướng dẫn a/ 2 x = b/ 1 x = c/ 8 x = 25 99 9
Bài 4: Tìm x, biết: a/ 3 − x =1 b/ 1 x + 4 = c/ 1 x − = 2 d/ 5 1 x + = 4 5 5 3 81 ĐS: a/ 1 x = b/ 19 x = − c/ 11 x = d/ 134 x = − 4 5 5 81 Bài 5. Tìm x x ∈ , biết 4 5 1 3 − ≤ ≤ − 5 6 30 3 10 Hướng dẫn 4 5 x 1 3 1 − x 1 − ≤ ≤ − ⇔ ≤ ≤ ⇔ 1 − ≤ x ≤1. 5 6 30 3 10 30 30 30 ⇒ 1; x = − 0; 1.
Bài 6. Viết tập hợp − −
A các số nguyên x , biết 3 5 31 1 1 1 + + ≤ x ≤ + + . 2 7 14 2 3 6 Hướng dẫn 3 − 5 31 − 1 1 1 21 − 10 31 − 3 2 1 + + ≤ x < + + => + + ≤ x < + + => 3 − ≤ x <1 2 7 14 2 3 6 14 14 14 6 6 6 x = 3
− ; − 2; −1; 0 hay A = ( 3 − ; − 2; −1; 0)
Bài 7. Tìm các số nguyên x để: x + 4 2x −5 + là một số nguyên. x − 2 x − 2 Hướng dẫn
x + 4 2x − 5 x + 4 + 2x − 5 3x −1 3(x − 2) + 5 + = = = 5 = 3+
là số ngyên khi x − 2 là ước của 5. x − 2 x − 2 x − 2 x − 2 x − 2 x − 2
⇒ x − 2∈(1; −1; 5; − 5) => x ∈(3; 1; 7; − 3) Bài 8. Tìm a, b −
∈ biết rằng: a 1 1 + = . 7 14 b Hướng dẫn a 1 1 − 2a +1 1 − + = ⇔ =
⇔ (2a +1).b = 1 − 4 7 14 b 14 b
2a +1 là ước của 14 − và 2a +1/ 2 Ta có: 2a +1 1 − 1 7 7 b 14 14 − 2 − 2 2a 2 − 0 6 8 − b 14 14 − 2 − 2 a 1 − 0 3 4 − b 14 14 − 2 − 2
Bài 9. Tìm các số nguyên t sao cho 5t + 2 là một số nguyên. 17 Hướng dẫn
5t + 2 5(t − 3) +17 5(t − 3) = =
+1 là một số nguyên ⇒ 5(t − 3) 1 7 . Mà ƯCLN (5; 17) =1. 17 17 17
Do đó t −3 17 . Đặt t −3 =17k (k∈). Vậy t =17k +3(k ∈).
Bài 10. Tìm các số nguyên n để: 2n −1 n −14 − là số nguyên. n + 8 n + 8 Hướng dẫn
2n −1 n −14 (2n −1) − (n −14) − = n + 8 n + 8 n + 8 2n −1− 14 + n +13 n + 8 5 5 = = = + = 1+
là số nguyên khi n +8 là ước của 5. n + 8 n + 8 n + 8 n + 8 n + 8
n + 8∈{1; −1; 5; − } 5 => n = 7 − ; − 9; − 3; −13
Bài 11. Tìm các số nguyên x, y biết: 1 y 2 − − = . x 11 11 Hướng dẫn 1 y 2 − 1 2 − y 1 y − 2 − = ⇔ = + ⇔ =
⇔ x(y − 2) =11 x 11 11 x 11 11 x 11 x 1 1 − 11 11 − y − 2 11 11 − 1 1 − x 1 1 − 11 11 − y 13 9 − 3 1
DẠNG 3: TÍNH TỔNG THEO QUY LUẬT. I/ PHƯƠNG PHÁP.
1/ TỔNG CÓ DẠNG: S = 1 + a + a2 + a3 + ….+ an (1)
B1: Nhân vào hai vế của đẳng thức với số a ta được.
a.S = a + a2 + a3 + a4 + ….+ an + 1 (2)
B2: Lấy (2) trừ (1) vế theo vế được: n 1 +
a.S – S = an + 1 – 1 => a −1 S = a −1
2/ TỔNG CÓ DẠNG: S = 1 + a2 + a4 + a6 + ….+ a2n (1)
B1: Nhân vào hai vế của đẳng thức với số a2 ta được.
a2.S = a2 + a4 + a6 + a8 + ….+ a2n + 2 (2)
B2: Lấy (2) trừ (1) vế theo vế được: 2n+2
a2.S – S = a2n + 2 – 1 => a −1 S = 2 a −1
3/ TỔNG CÓ DẠNG: S = a + a3 + a5 + a7 + ….+ a2n + 1 (1)
B1: Nhân vào hai vế của đẳng thức với số a2 ta được.
a2.S = a3 + a5 + a7 + a9 + ….+ a2n + 3 (2)
B2: Lấy (2) trừ (1) vế theo vế được: 2n+2
a2.S – S = a2n + 3 – a => a − a S = 2 a −1
4/ TỔNG CÓ DẠNG: S = 1 1 1 1 + + +...+ a a a a a a a − a 1 2 2 3 3 4 n 1 n
* Với a2 – a1 = a3 – a2 = a4 – a3 = … = an – an-1 = 1 thì: S = 1 1 1 1 1 1 1 1 1 1 − + − + − + ...+ − = − a a a a a a a − a a a 1 2 2 3 3 4 n 1 n 1 n
* Với a2 – a1 = a3 – a2 = a4 – a3 = … = an – an-1 = k > 1 thì: S = 1 1 1 1 1 1 1 1 1 1 1 1 − + − + − +...+ − = − k a a a a a a a − a k a a 1 2 2 3 3 4 n 1 n 1 n
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Tính tổng các phân số sau đây 1 cách nhanh chóng nhất. a/ 1 1 1 1 + + + ...+ b/ 2 2 2 2 + + + ...+ 5.6 6.7 7.8 24.25 1.3 3.5 5.7 99.101 c/ 3 3 3 3 + + + ...+ d/ 1 1 1 1 1 1 + + + + + 1.3 3.5 5.7 49.51 7 91 247 475 775 1147 Đáp số
a/ 4/25 b/ 100/101 c/ 1.8/17 d/ 6/37 Bài 2. Tính nhanh: 1 1 1 1 A = + + +...+ . 1.2 2.3 3.4 99.100 Hướng dẫn 1 1 1 1 A − − − − = + + + ...+ 2 1 3 2 4 3 100 99 = + + + ...+ 1.2 2.3 3.4 99.100 1.2 2.3 3.4 99.100 1 1 1 1 1 1 1 1 1 1 99 = − + − + − + ...+ − = − = 1 2 2 3 3 4 99 100 1 100 100
Bài 3. Chứng minh rằng: 1 1 1 1 + + + ...+ < 1. 2 2 2 2 2 3 4 2009 Hướng dẫn 1 1 1 1 1 1 + + ...+ < + + ...+ 1 1 1 1 1 1 1 = − + − + ...+ − = 1− < 1 2 2 2 2 3 2009 1.2 2.3 2008.2009 1 2 2 3 2008 2009 2009 Bài 4. Tính: 3 11 12 70 99 + + + + . 5.8 8.19 19.31 31.101 101.200 Hướng dẫn 3 11 12 70 99 + + + + 5.8 8.19 19.31 31.101 101.200
8 − 5 19 −8 31−19 101− 31 200 −101 = + + + + 5.8 8.19 19.31 31.101 101.200 1 1 1 1 1 1 1 1 1 1 1 1 39 = − + − + − + − + − = − = .
5 8 8 19 19 31 31 101 101 200 5 200 200
Bài 5. Cho n N∗ ∈ . Chứng tỏ rằng: 1 1 1 1 + + + ...+
không phải là một số tự nhiên. 2 2 2 2 1 2 3 n Hướng dẫn 1 1 1 1 1 1 1 1<1+ + + +...+ <1+ + +...+ 2 2 2 2 1 2 3 n 1.2 2.3 n(n −1) 1 1 1 1 1 1 1 =1+ − + − +...+ − = 2 − < 2. 1 2 2 3 n −1 n n
Bài 6: Tìm số tự nhiên x biết rằng: 1 1 1 2 1999 + + + ...+ = 3 6 10 x.(x +1) 2001 Hướng dẫn
Viết vế trái dưới dạng: 2 2 2 2 1999 + + + ...+ = => x = 2000 2.3 3.4 4.5 x.(x +1) 2001
Bài 7: Tính tổng S = 1 1 1 1 1 1 1+ + + + + ...+ + 2 3 4 99 100 2 2 2 2 2 2
Bài 8: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 2 3 4 99 100 3 3 3 3 3 3
Bài 9: Tính tổng S = 1 1 1 1 1 1 1+ + + + +...+ + 2 4 6 98 100 2 2 2 2 2 2
Bài 10: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 2 4 6 98 100 3 3 3 3 3 3
Bài 11: Tính tổng S = 1 1 1 1 1 1 1+ + + + + ...+ + 3 5 7 99 101 2 2 2 2 2 2
Bài 12: Tính tổng S = 1 1 1 1 1 1 + + + + ...+ + 3 5 7 99 101 3 3 3 3 3 3 Bài 13: Tính tổng
A = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 2 6 12 20 30 42 56 72 89
Bài 14: Tính tổng B = 1 1 1 1 1 1 + + + + + 7 91 247 475 777 1147
Bài 15: Tính tổng C = 1 1 1 1 1 + + + + ...+ 3 6 10 15 45
Gợi ý: Nhân cả tử và mẫu với 2 thì mẫu sẽ xuất hiện quy luật.
Bài 16: Tính tổng D = 1 1 1 1 + + + ...+ 1.2.3 2.3.4 3.4.5 18.19.20
Gợi ý: Mỗi số hạng đặt thừa số 1 , còn lại tách thành hiệu hai phân số. 2
CHỦ ĐỀ 21: PHÉP NHÂN VÀ PHÉP CHIA PHÂN SỐ A/ KIẾN THỨC CẦN NHỚ.
1. Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau
2. Tính chất giao hoán: a . c c = . a b d d b
Tính chất kết hợp: a . c . p a = . c . p b d q b d q
Nhân với 1: a .1=1.a a = b b b
Tính chất phân phối của phép nhân với phép cộng: a . c p a + = . c a + . p
b d q b d b q
Chú ý:Khi nhân nhiều phân số, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ
cách nào sao cho việc tính toán được thuận tiên.
3. Hai số gọi là nghịch đảo của nhau nếu tích của chúng bằng 1.
4. Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia. a c a d . : = . a d = b d b c . b c c d . : = . a d a a = (c ≠ 0) d c c B/ CÁC DẠNG BÀI TẬP.
DẠNG 1: THỰC HIỆN NHÂN CHIA HAI HOẶC NHIỀU PHÂN SỐ.
Vận dụng quy tắc nhân, chia phân số, các tính chất giao hoán, tính chất kết hợp , tính chất
phân phối của phép nhân với phép cộng.
Bài 1: Thực hiện phép nhân sau: a/ 3 14 ⋅ b/ 35 81 ⋅ c/ 28 68 ⋅ d/ 35 23 ⋅ 7 5 9 7 17 14 46 205 Hướng dẫn a/ 6 b/ 45 c/ 8 d/ 1 5 6 Bài 2. Tính: a) 5 − 15 : b) 4 − 5 : − 7 31 13 39
Hướng dẫn a) 5 − 15 5 − 31 31 : . − = = 7 31 7 15 21 b) 4 − 5 − 4 − 39 12 : = . = 13 39 13 5 − 5
Bài 3. Làm tính nhân: a) 3 − 2 . b) 49 − 27 . 7 5 81 77 −
Hướng dẫn a) 3 − 2 3.2 − 6 . − = = 7 5 7.5 35 b) 49 − 27 ( 49) − .27 ( 7 − ).1 7 − 7 . = = = = 81 77 − 81.( 77 − ) 3.( 11 − ) 33 − 33
Bài 4: Tính giá trị của cắc biểu thức sau bằng cach tính nhanh nhất: a/ 21 11 5 . . b/ 5 17 5 9 . + . c/ 3 1 29 − ⋅ 25 9 7 23 26 23 26 29 5 3 Hướng dẫn a/ 21 11 5 21 5 11 11 . . = ( . ). = b/ 5 17 5 9 5 17 9 5 . + . = ( + ) = 25 9 7 25 7 9 15 23 26 23 26 23 26 26 23 c/ 3 1 29 29 3 29 29 16 − ⋅ = . − =1− = 29 15 3 3 29 45 45 45
Bài 5: Tìm các tích sau: a/ 16 5 − 54 56 . . . b/ 7 5 − 15 4 . . . 15 14 24 21 3 2 21 5 − Hướng dẫn a/ 16 5 − 54 56 16 . . . − = 15 14 24 21 7 b/ 7 5 − 15 4 10 . . . = 3 2 21 5 − 3 Bài 6: Tính nhẩm a/ 7 5. b. 3 7 1 7 . + . c/ 1 5 5 1 5 3 . + . + . d/ 3 9 4.11. . 5 4 9 4 9 7 9 9 7 9 7 4 121 Bài 7. Tính: 2 2 a) 2 − 1 3 3 4 3 − . + − b) 1 1 1 − .5 − c) d) 5 3 2 7 2 3 4 5 7
Hướng dẫn a) 2 − 1 3 3 1 − 15 1 + . − = . − = b) 1 1 1 1 19 19 − . 5 − = . = 5 3 2 7 15 14 14 2 3 4 6 4 24 2 2 c) 4 4 4 16 − − − = 3 3 3 9 . = d) = . = 5 5 5 25 7 7 7 49 Bài 8. Tính: 5 15 − 2 + . 17 34 5
Hướng dẫn 5 1 − 5 2 5 3 − 2 + . = + = 17 34 5 17 17 17
Bài 9. Tính nhanh: 11 4 − 57 7 . . . 57 5 7 11
Hướng dẫn 11 4 − 57 7 11.( 4) − .57.7 1.( 4) − .1.1 4 . . . − = = = 57 5 7 11 57.5.7.11 1.5.1.1 5
Bài 10. Tính giá trị của các biểu thức sau: 2 2 2 2 2 2 2 2 2 2 a) 1 2 3 4 5 A = . . . . b) 2 3 4 5 6 B = . . . . 1.2 2.3 3.4 4.5 5.6 1.3 2.4 3.5 4.6 5.7 c) 1 1 1 1 C 1 .1 .1 .1 = + + + + 2 3 4 5
Hướng dẫn 2 2 2 2 2 a) 1 2 3 4 5 1 2 3 4 5 1 A = . . . . = . . . . =
1.2 2.3 3.4 4.5 5.6 2 3 4 5 6 6 2 2 2 2 2 2 2 2 2 2 b) 2 3 4 5 6 B = . . . . 2 .3 .4 .5 .6 = (2.3.4.5.6).(2.3.4.5.6) 6.2 12 = = =
1.3 2.4 3.5 4.6 5.7 (1.3).(2.4).(3.5).(4.6).(5.7) (1.2.3.4.5).(3.4.5.6.7) 1.7 7 c) 1 1 1 1 3 4 5 6 C = 1+ . 1+ . 1+ . 1+ = . . . = 3. 2 3 4 5 2 3 4 5
Bài 11. Điền số thích hợp vào bảng sau: − − − − a 5 4 5 84 9 17 13 28 − 45 101 209 − − − − b 9 34 101 9 11 19 39 9 14 135 17 . a b 1 0
Hướng dẫn − − − − − a 5 4 5 17 84 9 17 13 28 − 45 101 9 209 − − − − b 9 34 101 9 11 19 39 9 14 135 17 0 − − . a b 5 8 11 19 15 − 18 1 3 1 0 Bài 12.
a) Viết phân số 10 dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương 21 có một chữ số.
b) Viết phân số 14 dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương 15 có một chữ số.
Hướng dẫn a) 10 2 7 2 3 5 7 5 3 = : = : = : = : b) 14 2 3 2 5 7 5 7 3 = : = : = : = : 21 3 5 7 5 3 2 7 2 15 5 7 3 7 3 2 5 2
Bài 13. Một hình chữ nhật có diện tích là 15 2
m , chiều dài là 5 .
m Tính chu vi hình chữ nhật đó. 8 2
Hướng dẫn
Chiều rộng của hình chữ nhật đó là: 15 5 3 : = (m). 8 2 4
Chu vi của hình chữ nhật đó là: 3 5 13 + .2 = (m). 4 2 2
Bài 14: Đồng hồ chỉ 6 giờ. Hỏi sau bao lâu kim phút và kim giờ lại gặp nhau? Hướng dẫn
Lúc 6 giờ hai kim giờ và phút cách nhau 1/ 2 vòng tròn.
Vận tốc của kim phút là: 1 (vòng/h) 12
Hiệu vận tốc giữa kim phút và kim giờ là: 1- 1 = 11 (vòng/h) 12 12
Vậy thời gian hai kim gặp nhau là: 1 11 : = 6 (giờ) 2 12 11
Bài 15: Một canô xuôi dòng từ A đến B mất 2 giờ và ngược dòng từ B về A mất 2 giờ 30 phút.
Hỏi một đám bèo trôi từ A đến B mất bao lâu? Hướng dẫn
Vận tốc xuôi dòng của canô là: AB (km/h) 2
Vân tốc ngược dòng của canô là: AB (km/h) 2,5
Vận tốc dòng nước là: AB AB − AB − AB AB : 2 = 5 4 : 2 = (km/h) 2 2,5 10 20
Vận tốc bèo trôi bằng vận tốc dòng nước, nên thời gian bèo trôi từ A đến B là:
AB: AB = AB . 20 = 20 (giờ) 20 AB
Bài 16: Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A đến B với vận tốc 15 km/h. Lúc 7 giờ 10
phút bạn Nam đi xe đạp từ B đến A với vận tốc 12 km/h/ Hai bạn gặp nhau ở C lúc 7 giờ 30
phút. Tính quãng đường AB. Hướng dẫn Thời gian Việt đi là:
7 giờ 30 phút – 6 giờ 50 phút = 40 phút = 2 giờ 3
Quãng đường Việt đi là: 2 15⋅ =10 (km) 3
Thời gian Nam đã đi là: 7 giờ 30 phút – 7 giờ 10 phút = 20 phút = 1 giờ 3
Quãng đường Nam đã đi là 1 12. = 4 (km) 3
Bài 17. Tính giá trị của biểu thức: 3 3 3 + − a) 5 7 11 − − − − A = b) 1 2 3 = c) 6 5 4 = 4 4 4 C − : : D − : : + − 2 3 4 5 4 3 5 7 11 Hướng dẫn 3 3 3 1 1 1 + − 3 + − a) 5 7 11 5 7 11 3 − − − A = b) 1 2 3 1 3 4 4 4 4 = = C − = : : = . . = 1 − 1 1 1 4 + − 4 + − 2 3 4 2 2 − 3 − 5 7 11 5 7 11 c) 6 5 − 4 − 6 − 4 3 18 D − : : . . − = = = . 5 4 3 5 5 − 4 − 25
Bài 18: Tính gí trị các biểu thức A, B, C rồi tìm số nghịch đảo của chúng. a/ A = 2002 1− b/ B = 179 59 3 − − c/ C = 46 1 − ⋅ 11 2003 30 30 5 5 11 Hướng dẫn a/ A = 2002 1 1− =
nên số nghịch đảo của A là 2003 2003 2003 b/ B = 179 59 3 23 − − =
nên số nghịch đảo cảu B là 5 30 30 5 5 23 c/ C = 46 1 501 − ⋅ 11 =
nên số nghịch đảo của C là 501 5 11 5 5
Bài 19. Tính giá trị của biểu thức sau: 1 1 1 1 A 1 . 1 . 1 . . 1 = + + + + 1 1 1 1 B = 1− . 1− 1− ... 1− 2 3 4 2009 2 3 4 1000 1 1 1 1 C 1 . 1 1 ... 1 = − − − − 2 3 4 1963 Hướng dẫn 1 1 1 1 3 4 5 2010 A = 1+ . 1+ . 1+ ... 1+ = . . ... = 1005 2 3 4 2009 2 3 4 2009 1 1 1 1 1 2 3 999 1 B = 1− . 1− 1− ... 1− = . . ... = 2 3
4 1000 2 3 4 1000 1000 1 1 1 1 C 1 . 1 1 ... 1 = − − − − 1 − 2 − 3 − 1962 − 1 2 − 3 1962 − 1 = . . ... = . . ... = 2 3 4 1963 2 3 4 1963 2 − 3 4 − 1963 1963 Bài 20. Tính nhanh: a) 4 4 4 C = + +...+ b) 18 18 18 D = + +...+ 3.5 5.7 97.99 2.5 5.8 203.206 Hướng dẫn a) 4 4 4 C = + +...+ 2 2 2 2. ... = + + + 3.5 5.7 97.99 3.5 5.7 97.99 1 1 1 1 1 1 2 ... = − + − + + − 3 5 5 7 97 99 1 1 64 = 2 − = 3 99 99 b) 18 18 18 D = + +...+ 3 3 3 6. ... = + + + 2.5 5.8 203.206 2.5 5.8 203.206 1 1 1 1 1 1 6 ... = − + − + + − 2 5 5 8 203 206 1 1 102 306 = 6 − = 6. = 2 206 206 103
Bài 21. Hãy nêu hai cách viết phân số 13 thành tích của năm phân số sao cho mõi phân số đó 18
có tử và mẫu là hai số nguyên liên tiếp. Hướng dẫn 13 13 14 15 16 17 = . . . . ; 18 14 15 16 17 18 13 13 − 14 − 15 − 16 − 17 . . . . − = 18 14 − 15 − 16 − 17 − 18 −
Bài 22: Tìm A biết: 7 7 7 A = + + + ... 2 3 10 10 10 Hướng dẫn
Ta có (A - 7 ).10 = A. VẬy 10A – 7 = A suy ra 9A = 7 hay A = 7 10 9
Bài 23: Tính giá trị của biểu thức: 5x 5y 5z A − − − = + + biết x + y = -z 21 21 21 Hướng dẫn 5 − x 5 − y 5 − z 5 − 5 A (x y z) − = + + = + + = (−z + z) = 0 21 21 21 21 21 DẠNG 2: TOÁN TÌM x Bài 1: Tìm x, biết: a/ x - 10 = 7 3 ⋅ b/ 3 27 11 x + = ⋅ c/ 8 46 1 ⋅ − x = d/ 49 5 1− x = ⋅ 3 15 5 22 121 9 23 24 3 65 7 Hướng dẫn a/ x - 10 = 7 3 ⋅ 7 3 14 15 29 => x = + => x = + => x = 3 15 5 25 10 50 50 50 b/ 3 27 11 x + = ⋅ 3 3 3 => x = − => x = 22 121 9 11 22 22 c/ 8 46 1 ⋅ − x = 8 46 1 2 1 1 => x = .
− => x = − => x = 23 24 3 23 24 3 3 3 3 d/ 49 5 1− x = ⋅ 49 5 7 6 => x =1− . => x =1− => x = 65 7 65 7 13 13 Bài 2: Tìm x biết: a/ 62 29 3 .x = : b/ 1 1 1 : x = + c/ 1 : x = 2 7 9 56 5 5 7 2 2a +1 Hướng dẫn a/ 62 29 3 5684 .x = : ⇒ x = 7 9 56 837 b/ 1 1 1 7 : x = + ⇒ x = 5 5 7 2 c/ 1 1 : x = 2 ⇒ x = 2 2 2a +1 2(2a +1)
Bài 3. Tìm x , biết: a) 2 3 1 : x − + = b) 5 2 4 − .x = c) 1 3 2 x x − + = d) 4 9 x x − − = 5 4 2 7 3 5 2 5 3 7 14
Hướng dẫn a) 2 3 1 : x − + = 3 1 − 2 3 9 : x : − − − => = − => x = 3 9 5 => x = : => x = 5 4 2 4 2 5 4 10 4 10 6 b) 5 2 4 − .x = 2 5 4 2 3 − − −
=> x = − => x = 3 2 9 => x = : => x = 7 3 5 3 7 5 3 35 35 3 70 c) 1 3 2 x x − + = => 5 6 2 x x − + = => 11 2 x − = 2 − 11 20 x : − => = => x = 2 5 3 10 10 3 10 3 3 10 33 − − − − d) 4 9 x x − − = => 4 7 9 x x − − = => 3 9 x = 9 3 3 => x = : => x = 7 14 7 7 14 7 14 14 7 2
Bài 4: Lớp 6A có 42 HS được chia làm 3 loại: Giỏi, khá, Tb. Biết rằng số HSG bằng 1/6 số HS
khá, số HS Tb bằng 1/5 tổng số HS giỏi và khá. Tìm số HS của mỗi loại. Hướng dẫn
Gọi số HS giỏi là x thì số HS khá là 6x,
số học sinh trung bình là (x + 6x). 1 x + 6x = 5 5
Mà lớp có 42 học sinh nên ta có: 7 + 6 x x x + = 42 5 Từ đó suy ra x = 5 (HS)
Vậy số HS giỏi là 5 học sinh.
Số học sinh khá là 5.6 = 30 (học sinh)
Số học sinh trung bình là (5 + 30):5 = 7 (HS)
Bài 5. Tìm x: biết: 1 1 1 2008 + + ...+ = 1.2 2.3 x(x +1) 2009 Hướng dẫn 1 1 1 2008 + + ...+ = 1.2 2.3 x(x +1) 2009 1 1 1 1 1 1 2008 ⇔ − + − + ...+ − = 1 2 2 3 x x +1 2009 1 2008 1 2008 ⇔ 1− = ⇔ =1− x +1 2009 x +1 2009 1 1 ⇔ = x +1 2009
⇔ x +1 = 2009 ⇔ x = 2008
Bài 6. Tìm x biết x +1 x + 2 x +3 x + 4 + + + = 4 − 99 98 97 96 Hướng dẫn
x +1 x + 2 x + 3 x + 4 + + + = 4 − 99 98 97 96 x +1 x + 2 x + 3 x + 4 1 1 1 1 + + + + + + + = 0 99 98 97 96 x +100 x +100 + + x +100 x +100 + = 0 99 98 97 96 1 1 1 1 (x 100) + + + + = 0 99 98 97 96
=> x+100 = 0(Vì 1 1 1 1 + + + ≠ 0 ) => x = 100 − 99 98 97 96
CHỦ ĐỀ 22: HỖN SỐ. SỐ THẬP PHÂN. PHẦN TRĂM A/ KIẾN THỨC CẦN NHỚ 1. Hỗn số
* Khi phân số có tử số lớn mẫu số ta viết phân số ra hỗn số
* Để viết phân số a dưới dạng hỗn số ta lấy tử số a chia cho mẫu số b để tìm thương là số b
k và số dư là m (k , m là các số tự nhiên)
=> Phân số a viết dưới dạng hỗn số là: m k b b 9 4
= 1 (đọc là một bốn phần năm) 5 5
Phần nguyên Phần phân số
Chú ý: Khi viết một phân số âm dưới dạng hỗn số, ta viết số đối của nó dưới dạng hỗn số
rồi đặt dấu “-” trước kết quả nhận được.
2. Phân số thập phân là phân số mà mẫu là lũy thừa của 10.
* Số thập phân gồm hai phần:
- Phần số nguyên viết bên trái dấu phẩy.
- Phần thập phân viết bên phải dấu phẩy.
3. Những phân số có mẫu là 100 còn được viết dưới dạng phần trăm với kí hiệu %. B/ BÀI TẬP
DẠNG 1: VIẾT PHÂN SỐ - HỖN SỐ - SỐ THẬP PHÂN - %. SO SÁNH HỖN SỐ.
* Để viết phân số a dưới dạng hỗn số ta lấy tử số a chia cho mẫu số b để tìm thương là số b
k và số dư là m (k , m là các số tự nhiên)
=> Phân số a viết dưới dạng hỗn số là: m k b b
* Để so sánh hai hỗn số ta viết các hỗn số về dạng phân số rồi so sánh. Bài 1:
1/ Viết các phân số sau đây dưới dạng hỗn số: 33 15 24 102 2003 ; ; ; ; 12 7 5 9 2002
2/ Viết các hỗn số sau đây dưới dạng phân số: 1 1 2000 2002 2010 5 ;9 ;5 ;7 ;2 5 7 2001 2006 2015
3/ So sánh các hỗn số sau: 3 3 và 1 4 ; 3 4 và 3 4 ; 3 9 và 6 8 2 2 7 8 5 7
Hướng dẫn: 1/ 3 1 4 1 1 2 ,2 ,4 ,11 ,1 4 7 5 3 2002 2/ 76 244 12005 16023 1208 , , , , 15 27 2001 2003 403
Bài 2. Viết các số đo thời gian sau đây dưới dạng hỗn số và phân số với đơn vị là giờ.
2 giờ 15phút; 4 giờ 10phút; 3giờ 24 phút; 8 giờ 20 phút. Hướng dẫn 2 giờ 15phút 1 = 2 giờ 9 = giờ. 4 4 4 giờ 10phút 1 = 4 giờ 25 = giờ. 6 6 3giờ 24 phút 2 = 3 giờ 17 = giờ. 5 5 8 giờ 20 phút. 1 = 8 giờ 25 = giờ. 3 3
Bài 3: Viết số thập phân sau dưới dạng phân số: 0,12 ; -3, 5 ; 12,45 Hướng dẫn 12 3 0,12 = = 35 7 3, − 5 = − = − 1245 249 12,45 = = 100 25 10 2 100 20
Bài 4: Viết phân số sau dưới dạng số thập phân: 2 17 − 15 77 ; ; ; − 5 1000 6 5 Hướng dẫn 2 4 17 − 15 5 77 − 154 0,4; 0,017; 2,5; − = = = − = = = = 1 − 5,4 5 10 1000 6 2 5 10
Bài 5. Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân): 3dm , 85cm , 52mm. Hướng dẫn
Vì 1dm = 1/10m ; 1cm = 1/100m ; 1mm = 1/1000m nên ta có :
3dm = 3/10 m = 0,3 m ; 85cm = 85m = 0,85m ; 52mm = 52/1000 m = 0,052m. Bài 6.
Dùng phần trăm với kí hiệu % để viết các số phần trăm trong các câu sau đây :
Đẻ đật tiêu chuẩn công nhận phổ cập giáo dục THCS, xã Bình Minh đề ra chỉ tiêu phấn đấu :
– Huy động số trẻ 6 tuổi đi học lớp 1 đặt chín mươi mốt phần trăm.
Có ít nhất tám mươi hai phần trăm số trẻ ở độ tuổi 11 – 14 tốt nghiệp Tiểu học.
– Huy động chín mươi sáu phần trăm số học sinh tốt nghiệp Tiểu học hàng năm vào học
lớp 6 THCS phổ thông và THCS bổ túc.
– Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ chín mươi tư phần trăm trở lên. Đáp số 91% 82% 96% 94%
Bài 7. Viết các phân số sau dưới dạng số thập phân và dùng kí hiệu % : 7 19 26 ; ; 25 4 65 Giải: 7 7.4 28 = = = 28% 25 25.4 100 19 19.25 475 = = = 475% 4 4.25 100 26 :13 2 2.20 40 = = = = 40% 65:13 5 5.20 100
Bài 8. Viết các phần trăm sau dưới dạng số thập phân : 7% ; 45% ; 216%. Đáp số :
7% = 0,07 ; 45% = 0,4 ; 216% = 2,16
Bài 9. Tìm số nghịch đảo của các số sau : 3 1 1 ; 6 ; − ; 0,31 7 3 12 Hướng dẫn Ta có 1 19 31 6 = ; 0,31 = 3 3 100
Các số nghịc đảo của 3 1 1
; 6 ; − ; 0,31 lần lượt là 7 3 100 ; ; −12; 7 3 12 3 19 31
DẠNG 2. CỘNG, TRỪ, NHÂN, CHIA HỖN SỐ
– Khi cộng hai hỗn số ta có thể viết chúng dưới dạng phân số rồi thực hiện phép cộng
phân số. Ta cũng có thể cộng phần nguyên với nhau, cộng phần phân số với nhau (khi hai hỗn số đều dương).
– Khi trừ hai hỗn số , ta có thể viết chúng dưới dạng phân số rồi thực hiện phép trừ phân
số. Ta cũng có thể lấy phần nguyên của số bị trừ trừ phần nguyên của số trừ, phần phân số của
số bị trừ trừ phần phân số của số trừ, rồi cộng hai kết quả với nhau (khi hai hỗn số đều dương,
số bị trừ lớn hơn hoặc bằng số trừ).
– Khi hai hỗn số đều dương, số bị trừ lớn hơn hoặc bằng số trừ nhưng phần phân số của
số bị trừ nhỏ hơn phần phân số của số trừ, ta phải rút một đơn vị ở phần nguyên của số bị trừ
để thêm vào phần phân số, sau đó tiếp tục trừ như trên.
– Khi nhân, chia hai hỗn số ta có thể viết chúng dưới dạng phân số rồi thực hiện phép
nhân, chia phân số. Bài 1. Tính: 2 1 7 +1 . 9 3 Hướng dẫn 2 1 65 4 65 12 77 7 +1 = + = + = 9 3 9 3 9 9 9 Bài 2. Tính: a) 1 1 1 1 1 1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1
b) 1 1 1 1 1 1 1 1 1 1 − ⋅ − ⋅ − ⋅ − ⋅ − . 5 6 7 8 9
13 14 15 16 17 Hướng dẫn a) 1 1 1 1 1 6 7 8 9 10
1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1 = ⋅ ⋅ ⋅ ⋅ = 2 5 6 7 8 9 5 6 7 8 9
b) 1 1 1 1 1 1 14 − 15 − 16 − 17 − 18 − 18 −
1 1 1 1 − ⋅ − ⋅ − ⋅ − ⋅ − = ⋅ ⋅ ⋅ ⋅ = 13 14 15 16 17 13 14 15 16 17 13 2 Bài 3. Tính: 3 2 . 5 Hướng dẫn 2 2 3 13 13 13 169 2 = = ⋅ = 5 5 5 5 25
Bài 4. Đúng ghi Đ, sai ghi S. a) 1 1 5 −3 = 2 b) 1 2 3 +3 =3 2 2 5 3 8 c) 1 2 2 2 − ⋅3 =6 d) 1 11 2 − :4= 5 7 35 5 20 Đáp án a) 1 1 5 −3 = 2 Đ b) 1 2 3 +3 =3 2 2 5 3 8 S c) 1 2 2 2 − ⋅3 =6 S d) 1 11 2 − :4= Đ 5 7 35 5 20
Bài 5. Tính giá trị biểu thức: a) ( − − , ) 15 4 23 3 2 . + 0,8 − 13 8 19 23 2 :1 b) 1 3.(0,5)2 .3+ − 1 :1 64 15 24 15 15 60 24 b) 16 − 1 158 1,75. − 4 + 2,25 : 21 3 60 Đ S: a) Bài 6: Tính a) 4 7 4 1 5 6 6 + 3 − 4 b)−1 − 2 . + 3: % 5 9 11 9 3 6 11 c) 2 2 2 2 + + + ....+ d) 5 5 5 2 5 14 + . − . 3.5 5.7 7.9 97.99 7 11 7 11 7 11 Đ S:
Bài 7. Thực hiện phép tính 2 3 a) 2 1 2 + 5 .(4,5 − 2) + b) 4 1 4 1 .19 − .39 5 2 ( 4) − 9 3 9 3 2 2 2 c) 1 1 1 − − 1 5 : − 2 − d)125%. 0 : 1 −1,5 + 2008 2 4 2 2 16 e)( )3 2 − ⋅ -1 + 4 5 5 −1 : 24 3 6 12 Bài 8. Tính nhanh: a) 1 1 1 1 1 1 ⋅ 1 ⋅ 1 ⋅⋅⋅
b) 1 1 1 1 1 1 1 1 − ⋅ − ⋅ − ⋅⋅⋅ − 2 3 4 2009 2 3 4 200 c) 1 1 1 1 1 ⋅ 1 ⋅ ⋅⋅⋅ (98thừa số) 3 8 15 Hướng dẫn a) 1 1 1 1 3 4 5 2010 1 1 ⋅ 1 ⋅ 1 ⋅⋅⋅ = ⋅ ⋅ ⋅⋅⋅ =1005 2 3 4 2009 2 3 4 2009
b) 1 1 1 1 3 − 4 − 5 − 201 − 201 1 − ⋅ 1 − ⋅ 1 − ⋅⋅⋅ 1 − − = ⋅ ⋅ ⋅⋅⋅ = . 2 3 4 200 2 3 4 200 2 c) 1 1 1 1 1 ⋅ 1 ⋅
⋅⋅⋅ (98thừa số) 4 9 16
= ⋅ ⋅ ⋅⋅⋅ (98thừa số) 3 8 15 3 8 15 2 2 2 2 2 2 2 2 2 3 4 99 2 .3 .4 ...99
(2.3.4...99)(2.3.4...99) 99.2 99 = ⋅ ⋅ ⋅⋅⋅ = = = =
1.3 2.4 3.5 98.100 (1.3)(2.4)(3.5)...(98.100) (1.2.3...98)(3.4.5...100) 1.100 50 DẠNG 3: TOÁN TÌM x
Bài 1: Tìm phần nguyên x của hỗn số x.3/4, biết a/ x.3/4 = 21989/7996 Đ/S: x = 2
b/ 2147/425 < x.3/4 < 2835/420 Đ/S: x = 5
Bài 2: Cho hỗn số 2.x/7. Tìm x biết: a/ 2.x/7 = 153/63 b/ 2.7/7 = (2x + 9)/7 Đ/S: a) x = 3 b) x = 5
Bài 5: Cho hỗn số 11.19/x. Tìm x biết: a/ 11.19/x = 1673/140 b/ 11.19/x = 273/x Đ/S: a) x= 20 b) x = 23
Bài 6: Cho hỗn số x.2/x. Tìm x biết: a/ x.2/x = 12597/1729 b/ x.2/x = 83/x Đ/S: x = 7 b) x = 9
Bài 7: Cho hỗn số x.12/13. Tìm x biết: 561/143 < x.12/13 < 1463/247 Bài 8. Tìm x biết a, 1 2 1 (3 + 2x).3 = 5 b) 3 - (17-x) = -12 2 3 3 c 1 1 1 1 x + x + x +....+ x =1 2 1 1 2.3 3.4 4.5 49.50 g, d) x + = 3 2 10 e) 3 2 − 2. 2x − = 2 f) 1 3 1 0 − ,6x − . − ( 1) − = 4 3 2 4 3 g) ( x − ) 1 3 1 − x + 5 = 0 k) 60%.x + 2 x = 1 1 ⋅ 6 2 3 3 3
Bài 9. Tìm x : a) 1 2 56 1 x x − + = b) 1 15 x 2 x − − = 5 3 125 4 8 Hướng dẫn a) 1 2 56 1 x x − + = => 6 2 56 x x − + = => 28 56 x − = 56 − 28 6 x : − => = => x = . 5 3 125 5 3 125 15 125 125 15 25 b) 1 15 x 2 x − − − − = => 9 15 x x − − = => 5 15 x = 15 − 5 − 3 => x = : => x = 4 8 4 8 4 8 8 4 2
Bài 10. Tìm x nếu biết: 60%x+0,4x+ x :3=2 Hướng dẫn
60%x + 0,4x + x :3= 2 => 3 2 1
x + x + x = 2 => 4 x =2 => 4 x = 2: => 3 x = 5 5 3 3 3 2
DẠNG 4:TOÁN LỜI VĂN VỀ PHÂN SỐ, HỖN SỐ, SỐ THẬP PHÂN VÀ %
Bài 1: Hai ô tô cùng xuất phát từ Hà Nội đi Vinh. Ô tô thứ nhất đo từ 4 giờ 10 phút, ô tô thứ
hai đia từ lúc 5 giờ 15 phút. a/ Lúc 1
11 giờ cùng ngày hai ôtô cách nhau bao nhiêu km? Biết rằng vận tốc của ôtô thứ 2
nhất là 35 km/h. Vận tốc của ôtô thứ hai là 1 34 km/h. 2
b/ Khi ôtô thứ nhất đến Vinh thì ôtô thứ hai cách Vinh bao nhiêu Km? Biết rằng Hà Nội cách Vinh 319 km.
Hướng dẫn:
a/ Thời gian ô tô thứ nhất đã đi: 1 1 1 1 1 1
11 − 4 = 7 + − = 7 + = 7 (giờ) 2 6 2 6 3 3
Quãng đường ô tô thứ nhất đã đi được: 1 2 35.7 = 256 (km) 2 3
Thời gian ô tô thứ hai đã đi: 1 1 1 11 − 5 = 6 (giờ) 2 4 4
Quãng đường ô tô thứ hai đã đi: 1 1 5 34 − 6 = 215 (km) 2 4 8
Lúc 11 giờ 30 phút cùng ngày hai ô tô cách nhau: 2 5 1 256 − 215 = 41 (km) 3 8 24
b/ Thời gian ô tô thứ nhất đến Vinh là: 4 319 :35 = 9 (giờ) 35
Ôtô đến Vinh vào lúc: 1 4 59 4 + 9 = 13 (giờ) 6 35 210
Khi ôtô thứ nhất đến Vinh thì thời gian ôtô thứ hai đã đi: 59 1 269 1 538 105 433 13 − 5 = 7 + − = 7 + − = 7 (giờ) 210 4 210 4 420 420 420
Quãng đường mà ôtô thứ hai đi được: 433 1 7 .34 ≈ 277 (km) 420 2
Vậy ôtô thứ nhất đến Vinh thì ôtô thứ hai cách Vinh là: 319 – 277 = 42 (km)
Bài 2: Tổng tiền lương của bác công nhân A, B, C là 2.500.000 đ. Biết 40% tiền lương của bác
A bằng 50% tiền lương của bác B và bằng 4/7 tiền lương của bác C. Hỏi tiền lương của mỗi bác là bao nhiêu? Hướng dẫn 40% = 40 2 = , 50% = 1 100 5 2
Quy đồng tử các phân số 1 2 4 , , được: 1 4 2 4 4 = , = , 2 5 7 2 8 5 10 7
Như vậy: 4 lương của bác A bằng 4 lương của bác B và bằng 4 lương của bác C. 10 8 7
Suy ra, 1 lương của bác A bằng 1 lương của bác B và bằng 1 lương của bác C. 10 8 7 Ta có sơ đồ như sau:
+ Lương của bác A : 2500000 : (10+8+7) x 10 = 1000000 (đ)
+ Lương của bác B : 2500000 : (10+8+7) x 8 = 800000 (đ)
+ Lương của bác C : 2500000 : (10+8+7) x 7 = 700000 (đ)
Bài 3. Khi nhân một số với 48 , bạn Minh đã đặt các tích riêng thẳng cột với nhau nên tìm được
kết quả là 98,04. Hãy tìm tích đúng. Hướng dẫn
Bạn Minh đã thực hiện phép nhân một số với một tổng4+8=12 được kết quả là 98,04.
Số đó là: 98,04:12=8,17 .
Vậy tích đúng là:8,17.48 = 392,16
Bài 4. Một phân số có mẫu lớn hơn tử là 55. Tìm phân số ấy biết mẫu bằng 3 3 tử. 4 Hướng dẫn
Gọi tử của phân số đó là x(x∈)
Mẫu của phân số đó là x +55
Phân số đó có mẫu bằng 3 3 tử, do đó 4 3 15 15 11 11
x +55=3 x⇒ x +55= x⇒
x − x =55⇒ x =55⇒ x =55: ⇒ x = 20 4 4 4 4 4 Phân số đó là 20 20 = . 20 + 55 75
CHỦ ĐỀ 23: TÌM GIÁ TRỊ PHÂN SỐ CỦA MỘT SỐ CHO TRƯỚC.
TÌM MỘT SỐ BIẾT GIÁ TRỊ MỘT PHÂN SỐ CỦA NÓ.
A/ KIẾN THỨC VÀ KỸ NĂNG CẦN NHỚ
1. Muốn tìm m của số b cho trước, ta tính .m b ( ,
m n∈ Ν,n ≠ 0). n n
2. Muốn tìm một số biết m cuả nó bằng m
a , ta tính a : ( , m n∈ Ν *). n n
B/ BÀI TẬP VẬN DỤNG. Bài 1: Tìm x, biết: a/ 50x 25x 1 x − + = 11 100 200 4 b/ ( ) 30 200 5 . x x − = + 5 100 100 Hướng dẫn a/ 50x 25x 1 x − + = x x x − x − x 11 ⇔ 100 25 1 x + − = 11 ⇔ 200 100 25 1 = 11 100 200 4 200 4 200 4
⇔ 75x = 45 .200 = 2250 ⇔ x = 2250: 75 = 30. 4 b/ ( ) 30 200 5 . x x − = + 5 100 100
Áp dụng tính chất phân phối của phép nhân đối với phép trừ ta có: 30x 150 20x − = + 5 100 100 100
Áp dụng mối quan hệ giữa số bị trừ, số trừ và hiệu ta có: 30x 20x 150 = + 5 + 100 100 100
Áp dụng quan hệ giữa các số hạng của tổng và tổng ta có: 10x 650 650 x .100 = ⇒ = :10 ⇒ x = 65 100 100 100
Bài 2: Trong một trường học số học sinh gái bằng 6/5 số học sinh trai.
a/ Tính xem số HS gái bằng mấy phần số HS toàn trường.
b/ Nếu số HS toàn trường là 1210 em thì trường đó có bao nhiêu HS trai, HS gái? Hướng dẫn
a/ Theo đề bài, trong trường đó cứ 5 phần học sinh nam thì có 6 phần học sinh nữ. Như
vậy, nếu học sinh trong toàn trường là 11 phần thì số học sinh nữ chiếm 6 phần, nên số học sinh
nữ bằng 6 số học sinh toàn trường. 11
Số học sinh nam bằng 5 số học sinh toàn trường. 11
b/ Nếu toàn tường có 1210 học sinh thì: Số học sinh nữ là: 6 1210× = 660 (học sinh) 11 Số học sinh nam là: 5 1210× = 550 (học sinh) 11
Bài 3: Một miếng đất hình chữ nhật dài 220m, chiều rộng bằng ¾ chiều lài. Người ta trông cây
xung quanh miếng đất, biết rằng cây nọ cách cây kia 5m và 4 góc có 4 cây. Hỏi cần tất cả bao nhiêu cây?
Hướng dẫn:
Chiều rộng hình chữ nhật: 3 220. =165 (m) 4
Chu vi hình chữ nhật: (220+165).2 = 770 (m)
Số cây cần thiết là: 770: 5 = 154 (cây)
Bài 4: Ba lớp 6 có 102 học sinh. Số HS lớp A bằng 8/9 số HS lớp B. Số HS lớp C bằng 17/16
số HS lớp A. Hỏi mỗi lớp có bao nhiêu học sinh? Hướng dẫn
Số học sinh lớp 6B bằng 9 học sinh lớp 6A (hay bằng 18 ) 8 16
Số học sinh lớp 6C bằng 17 học sinh lớp 6A 16
Tổng số phần của 3 lớp: 18+16+17 = 51 (phần)
Số học sinh lớp 6A là: (102 : 51) . 16 = 32 (học sinh)
Số học sinh lớp 6B là: (102 : 51) . 18 = 36 (học sinh)
Số học sinh lớp 6C là: (102 : 51) . 17 = 34 (học sinh)
Bài 5: Giữ nguyên tử số, hãy thay đổi mẫu số của phân số 275 soa cho giá trị của nó giảm đi 289
7 giá trị của nó. Mẫu số mới là bao nhiêu? 24 Hướng dẫn
Gọi mẫu số phải tìm là x, theo đề bài ta có: 275 275 7 275 275 7 275 17 275 = − . = 1− = . = x 289 24 289 289 24 289 24 408 Vậy x = 275 408
Bài 6: Ba tổ công nhân trồng được tất cả 286 cây ở công viên. Số cây tổ 1 trồng được bằng 9 10
số cây tổ 2 và số cây tổ 3 trồng được bằng 24 số cây tổ 2. Hỏi mỗi tổ trồng được bao nhiêu cây? 25 Hướng dẫn
90 cây; 100 cây; 96 cây.
Bài 7. Một đội văn nghệ có 24 người, trong đó 5 là số người nữ. Tính số người nam trong đội 8 văn nghệ đó.
Hướng dẫn
Số nữ trong đội văn nghệ là: 5 24. =15 (người). 8
Số nam trong đội văn nghệ là: 24−15 = 9 (người).
Bài 8. Tìm một số, biết: a) 3 của nó bằng 126. b) 4 % của nó bằng 16 − . 7 5
Hướng dẫn a) 3 126 : = 294 b) 4 16 : % − = 2000 − 7 5
Bài 9. Một tấm vải bớt đi 9m thì còn lại 5 tấm vải. Hỏi tấm vải dài bao nhiêu mét? 8
Hướng dẫn
Phân số chỉ 9 mét vải bằng: 5 3
1− = (chiều dài tấm vải) 8 8
Chiều dài tấm vải đó là: 3 9 : = 24 (m) 8
Bài 10. Tìm một số, biết rằng 5 của số đó bằng 4 của 1260 − . 9 7
Hướng dẫn 4 của 1260 − bằng: 4 1260. − = 720 − . 7 7 Số đó bằng: 5 720 − : = 1296 − . 9
Bài 11. Ba phường 1,2,3 có 18 000 dân, biết rằng 2 số dân phường 3 bằng 1 số dân phường 2 3 2
và bằng 40% số dân phường 1. Tính số dân mỗi phường.
Hướng dẫn Đổi: 2 40% = 5
Phân số chỉ số dân phường 2 bằng: 2 1 4 : = (Số dân phường 1) 5 2 5
Phân số chỉ số dân phường 3 bằng 2 2 3 : = (Số dân phường 2) 5 3 5
Phân số chỉ 18 000 dân là: 4 3 12 + +1 = (Số dân phường 1) 5 5 5
Số dân phường 1 có là: 12 18 000 : = 7 500 (dân) 5
Số dân phường 3 có là: 3 7 500. = 4 500 (dân) 5
Số dân phường 2 có là: 4 7 500. = 6 000 (dân) 5
CHỦ ĐỀ 24: TÌM TỈ SỐ CỦA HAI SỐ. BIỂU ĐỒ PHẦN TRĂM
A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ
1. Thương trong phép chia số a cho số b(b ≠ 0) gọi là tỉ số của a và b .
2. Muốn tìm tỉ số phần trăm của hai số a vàb , ta nhân a với 100 rồi chia cho b và viết kí hiệu a % vào kết quả: .100 %. b
3. Tỉ lệ xích T của một bản vẽ (hoặc một bản đồ)) là tỉ số khoảng cách giữa hai điểm trên bản
vẽ (hoặc bản đồ) và khoảng cách b giữa điểm tương ứng trên thực tế. a
T = ( a,b có cùng đơn vị đo) b
4. Để nêu bật và so sánh một cách trực quan các giá trị phần trăm của cùng một đại lượng, ta
dùng biểu đồ phần trăm. Biểu đồ phần trăm thường được dựng dưới dạng cột, ô vuông và hình quạt.
B/ BÀI TẬP VẬN DỤNG
Bài 1. Tỉ số của hai số a và b là 5 , tỉ số của hai số b và c là 2 . Tìm tỉ số của hai số c va b . 7 3
Hướng dẫn a a b 5 2 10 = . = . = . c b c 7 3 21
Bài 2. Tỉ số của hai số là 4 . Tổng của hai số đó là 65. Tìm hai số đó. 9
Hướng dẫn
Phân số chỉ 65 đơn vị bằng: 4 13 1+ = (số lớn). 9 9 Số lớn bằng: 13 65: = 45. 9
Số nhỏ bằng: 65− 45 = 20. Bài 3:
1/ Một ô tô đi từ A về phía B, một xe máy đi từ B về phía A. Hai xe khởi hành cùng một
lúc cho đến khi gặp nhau thì quãng đường ôtô đi được lớn hơn quãng đường của xe máy đi là
50km. Biết 30% quãng đường ô tô đi được bằng 45% quãng đường xe máy đi được. Hỏi quãng
đường mỗi xe đi được bằng mấy phần trăm quãng đường AB.
2/ Một ô tô khách chạy với tốc độ 45 km/h từ Hà Nội về Thái Sơn. Sau một thời gian một
ôtô du lịch cũng xuất phát từ Hà Nội đuổi theo ô tô khách với vận tốc 60 km/h. Dự định chúng
gặp nhau tại thị xã Thái Bình cách Thái Sơn 10 km. Hỏi quãng đường Hà Nội – Thái Sơn? Hướng dẫn 1/ 30% = 3 9 = ; 45% = 9 10 30 20
9 quãng đường ôtô đi được bằng 9 quãng đường xe máy đi được. 30 20
Suy ra, 1 quãng đường ôtô đi được bằng 1 quãng đường xe máy đi được. 30 20
Quãng đường ôtô đi được: 50: (30 – 20) x 30 = 150 (km)
Quãng đường xe máy đi được: 50: (30 – 20) x 20 = 100 (km)
2/ Quãng đường đi từ N đến Thái Bình dài là: 40 – 10 = 30 (km)
Thời gian ôtô du lịch đi quãng đường N đến Thái Bình là: 30 : 60 = 1 (h) 2
Trong thời gian đó ôtô khách chạy quãng đường NC là: 40. 1 = 20 (km) 2
Tỉ số vận tốc của xe khách trước và sau khi thay đổi là: 40 9 = 45 8
Tỉ số này chính lầ tỉ số quãng đường M đến Thái Bình và M đến C nên: M → TB 9 = MC 8
M→TB – MC = 9 MC – MC = 1 MC 8 8
Vậy quãng đường MC là: 10 : 1 = 80 (km) 8
Vì M→TS = 1 - 3 = 10 (H→TS) 13 13
Vậy khoảng cách Hà Nội đến Thái Sơn (HN→TS) dài là: 100 : 10 = 100.13 = 130 (km) 13 10
Bài 4: Nhà em có 60 kg gạo đựng trong hai thùng. Nếu lấy 25% số gạo của thùng thứ nhất
chuyển sang thùng thứ hai thì số gạo của hai thùng bằng nhau. Hỏi số gạo của mỗi thùng là bao nhiêu kg?
Hướng dẫn:
Nếu lấy số gạo thùng thứ nhất làm đơn vị thì số gạo của thùng thứ hai bằng 1 (đơn vị) (do 2
25% = 1 ) và 3 số gạo của thùng thứ nhất bằng số gạo của thùng thứ hai + 1 số gạo của thùng 4 4 4 thứ nhất.
Vậy số gạo của hai thùng là: 1 3 1+ = (đơn vị) 2 2
3 đơn vị bằng 60 kg. Vậy số gạo của thùng thứ nhất là: 3 2 60 : = 60. = 40 (kg) 2 2 3
Số gạo của thùng thứ hai là: 60 – 40 = 20 (kg) Bài 5:
1/ Một đội máy cày ngày thứ nhất cày được 50% ánh đồng và thêm 3 ha nữa. Ngày thứ hai
cày được 25% phần còn lại của cánh đồng và 9 ha cuối cùng. Hỏi diện tích cánh đồng đó là bao nhiêu ha?
2/ Nước biển chưa 6% muối (về khối lượng). Hỏi phải thêm bao nhiêu kg nước thường vào
50 kg nước biển để cho hỗn hợp có 3% muối? Hướng dẫn
1/ Ngày thứ hai cày được: 3 9 : =12 (ha). 4
Diện tích cánh đồng đó là: ( + ) 50 12 3 : = 30 (ha) 100
2/ Lượng muối chứa trong 50kg nước biển: 50×6 = 3(kg) 100
Lượng nước thường cần phải pha vào 50kg nước biển để được hỗn hợp cho 3% muối: 100 – 50 = 50 (kg)
Bài 6: Trên một bản đồ có tỉ lệ xích là 1: 500000. Hãy tìm:
a/ Khoảng cách trên thực tế của hai điểm trên bản đồ cách nhau 125 milimet.
b/ Khoảng cách trên bản đồ của hai thành phố cách nhau 350 km (trên thực tế). Hướng dẫn
a/ Khảng cách trên thực tế của hai điểm là:
125.500000 (mm) = 125500 (m) = 62.5 (km).
b/ Khảng cách giữa hai thành phố trên bản đồ là:
350 km: 500000 = 350000:500000 (m) = 0.7 m
Bài 7. Tỉ số của hai số bằng 4:9. Nếu thêm 20 vào số thứ nhất thì tỉ số của chúng sẽ bằng 2:3. Tìm hai số đó.
Hướng dẫn
Cách 1:Gọi hai số đó là a a + b
a và b . Theo đề bài ta có: 4 2 = , = . b 9 b 3 Ta có: a 20 2 4 20 2 20 2 4 + = ⇔ + = ⇔ = − 20 2 20.9 ⇔ = ⇔ b = ⇔ b = 90. b b 3 9 b 3 b 3 9 b 9 2 Suy ra: 4 a = .90 = 40. 9
Cách 2: Phân số chỉ 20 đơn vị bằng: 2 4 2 − = (số lớn). 3 9 9 Số lớn bằng 2 20 : = 90 . Số bé bằng: 4 90. = 40 . 9 9 Bài 8.
a) Tìm hai số, biết tỉ số của chúng bằng 1:5 và tích của chúng bằng 720.
b) Tìm hai số, biết tỉ số của chúng bằng 3:7 và tích của chúng bằng 189.
Hướng dẫn
a) Gọi hai số cần tìm là a và b .
Theo đề bài ta có: a 1 = ,ab = 720. b 5 Suy ra b = 5a . Do đó .5 a a = 720 2 2
⇔ a = 720 :5 ⇔ a =144 ⇔ a =12hoÆc a = 12. −
• a =12 thì b = 5a = 60. • a = 12
− thì b = 5a = 60. − b) a 3 3
= ; ab =189⇔ a = b b 7 7 3 3 2 ab =189 ⇔ .
b b =189 ⇔ .b =189 7 7 2 3
⇔ b =189 : = 441 ⇔ b = 21 hoặc b = 21 − 7 •b = 21 thì 3 a = .b = 9. 7 •b = 21 − thì 3 a = b = 9. − 7
Bài 9. Tháng 9 giá một loại rau thấp hơn tháng 7 là 20% nhưng tháng 11 lại cao hơn tháng 9 là
20% . Như vậy giá rau tháng 11 giảm hay tăng so với tháng 7 ?
Hướng dẫn
Giả sử giá rau đó tháng 7 là 100% .
Giá rau tháng 9 là: 100% − 20% = 80% .
Giá rau tháng 11 là: 80%.120% = 96% .
Vậy giá rau tháng 11 thấp hơn tháng 7 là: 100% −96% = 4%.
Bài 10. Giá vé xem ca nhạc là 50 000 đồng/vé. Sau khi giảm giá vé, số khán giả tăng thêm 25% ,
do đó doanh thu tăng thêm 12,5%. Hỏi giá vé sau khi giảm là bao nhiêu?
Hướng dẫn
Giả sử giá vé lúc đầu là 100% , số khán giả 100% , doanh thu 100% .
Sau khi giảm giá, số khán giả là 125% , doanh thu là 112,5%.
Do đó giá vé mới so với lúc đầu là: 112,5%:125% = 90% .
Giá vé sau khi giảm là: 50 000.90% = 45 000 (đồng).
Document Outline




