Bài tập Thống kê xác suất tổng hợp - Kỹ thuật công trình môn Xác suất thống kê | Trường Đại học Thủy Lợi

lOMoAR cPSD| 58478860
Bài tập môn thống kê trong kỹ thuật
1. Sử dụng bảng tra của hàm phân phối chuẩn, tìm a) P(z≤ -1.5) b) P(z≥2.4) c) P(0 ≤ z ≤ 1) d) P(-1.5≤ z ≤ 1.5)
2. Cho chuỗi số sau: 20, 19, 44, 45, 44, 51, 56, 12, 86, 105, 97. Yêu cầu tìm giá trị Trung vị, trung bình,
số đông, độ lệch chuẩn, hệ số biến thiên và hệ số thiên lệch, sai số chuẩn giá trị trung bình và độ lệch chuẩn.
3. Từ dữ liệu quan trắc thời kỳ dài về mưa xuất hiện trong tháng 12 tại vùng A cho thấy xác suất có
mưa vào một ngày bất kỳ trong tháng 12 là 0.15. Chính quyền địa phương vùng A có kế hoạch nâng
cấp hệ thống cấp nước của vùng trong tháng này và công việc nâng cấp dự kiến kéo dài 30 ngày. Hỏi
xác suất để mưa không xuất hiện trong suốt 30 ngày dự kiến nâng cấp hệ thống cấp nước?
4. Giả sử một con đường bị ngập với xác suất bị ngập trong năm là p = 0,25. Tìm xác suất mà con
đường đó sẽ bị ngập ít nhất một lần trong khoảng thời gian 10 năm?
5. Tìm xác suất có ít hơn 3 lần xuất hiện một trận bão số 1 trong khoảng thời gian 75 năm? Biết trận
bão số 1 có xác suất xuất hiện trong bất cứ năm nào là p = 0.15.
6. Tất cả các máy bơm nước của một nhà máy xử lý nước đều có cùng một thông số kỹ thuật và đều
được sản xuất từ cùng một nhà sản xuất. Từ kết quả kiểm tra hiệu năng của các máy bơm trong
khoảng thời gian 3 tháng, cho thấy trung bình có 4 sự cố xuất hiện trong thời kỳ trên. Giám đốc nhà
máy cho rằng vấn đề không nghiêm trọng nếu có không quá 3 sự cố trong khoảng thời gian 3 tháng.
Xác suất xuất hiện không quá ba sự cố trong khoảng thời gian 3 tháng là bao nhiêu?
7. Một hồ chứa có tuổi thọ công trình là 75 năm. Thông số thiết kế của hồ chứa đã được xác định dựa
trên trận lũ thiết kế với xác suất xuất hiện trận lũ đó trong bất cứ năm nào là p = 0.1. Hỏi xác suất để trận lũ thiết kế:
a) Xuất hiện 1 lần trong 75 năm sử dụng phân phối nhị thức
b) Xuất hiện 3 lần trong 75 năm sử dụng phân phối nhị thức
c) Sử dụng phân phối Poisson cho cả (a) và (b)
8. Cho chuỗi lượng mưa tháng, với độ dài chuỗi là 30 năm. Biết giá trị trung bình và độ lệch chuẩn của
chuỗi đó lần lượt là 75mm và 25 mm. Giả thiết rằng chuỗi số liệu mưa tháng này tuân theo luật phân
phối chuẩn, các tham số của hàm phân phối chuẩn có thể xác định theo phương pháp MOM. Tìm xác
suất để lượng mưa trong năm tới (X):
a) Rơi trong khoảng 80 mm và 100 mm b) Tối thiểu 110 mm.
9. Giả sử dòng chảy trung bình hàng năm Q của một nhánh sông tuân theo luật phân chuẩn với giá trị
trung bình 5000 m3/s và độ lệch chuẩn 700 m3/s. Xác định xác suất để dòng chảy trung bình trong
năm tới sẽ nhỏ hơn 4500 m3/s.
10. Giả sử chuỗi dòng chảy ngày lớn nhất hàng năm thu thập tại 1 trạm thủy văn tuân theo phân phối
Gumbel. Biết giá trị trung bình của chuỗi này là 5000 m3/s và độ lệch chuẩn là 800 m3/s. Tìm xác
suất để lưu lượng ngày lớn nhất hàng năm trong năm tới vượt quá 5600 m3/s?
11. Tiến hành phân tích thống kê các trận lũ lớn nhất hàng năm của một con sông trong 70 năm. Biết trận
lũ lớn thứ 5 trong chuỗi 70 năm đó có giá trị là 20.000 m3/s. Xác định:
c) Khoảng thời gian trận lũ 20.000 m3/s có thể lặp lại một lần sử dụng công thứcWeibull
d) Xác suất để trận lũ này có thể xảy ra trong một năm bất kỳ
e) Xác suất để trận lũ này có thể không xảy ra trong 30 năm tới sử dụng phân phối nhị thức.
f) Xác suất để trận lũ này có thể xảy ra nhiều hơn một lần trong 30 năm tới sử dụng phân phối nhị thức.
g) Xác suất để trận lũ với khoảng thời gian lặp lại 50 năm có thể xảy ra (a) một lần trong 50
năm, (b) nhiều hơn 1 lần trong 50 năm, sử dụng phân phối nhị thức. lOMoAR cPSD| 58478860
12. Xác định xác suất trận mưa bão thiết kế với chu kỳ lặp lại 20 năm sẽ xảy ra 2 lần trong 5 năm sử
dụng phân phối nhị thức và Poisson?
13. Nếu một con đập có thời gian tồn tại là 75 năm, hỏi xác suất xảy ra trận lũ có chu kỳ lặp lại 150 năm
sẽ xảy ra hai lần trong thời gian tồn tại của đập là bao nhiêu?
a) Sử dụng phân phối nhị thức
b) Sử dụng phân phối Poisson.
14. Một cây cầu có thời gian tồn tại là 50 năm và thiết kế với trận lũ có khoảng thời gian lặp lại là T = 100 năm.
a) Xác định rủi ro của thiết kế của cây cầu trên.
b) Nếu chấp nhận rủi ro thiết kế cây cầu trên là 5%, khoảng thời gian lặp lại của trận lũ lựa chọn để
thiết kế cây cầu trên nên điều chỉnh là bao nhiêu?
15. Một dự án bảo về đường bao liên quan đến việc trồng rừng và kỹ thuật sinh học đất. Tuy nhiên, việc
trồng rừng theo đề xuất sẽ không đảm bảo chịu được trận mưa bão lớn cho đến khi rừng đã phát triển
vững chắc. Nhà thiết kế yêu cầu đưa vào một lớp phủ gia cố sao cho 95% cơ hội dự án thành công
trong thời gian 10 năm tới. Xác định tần suất thiết kế của trận mưa bão cho dự án trên.
16. Một dự án tiêu thoát nước đô thị cần xác định lượng mưa lớn nhất trong khoảng thời gian 180 phút
với các khoảng thời gian lặp lại khác nhau. Biết chuỗi giá trị lớn nhất hàng năm của lượng mưa trong
thời gian 180 phút tại trạm mưa lân cận khu vực dự án (trạm Tân Sơn Hòa) từ năm 1982 đến năm
2017. Từ chuỗi đó tính được giá trị trung bình của chuỗi (x) là 89.53 mm, độ lệch chuẩn (Sx) là
25.58 mm và hệ số thiên lệch (Csx) là 0.88 .
Xác định lượng mưa lớn nhất xuất hiện trong khoảng thời gian 120 phút có khỏang thời gian lặp lại
là 20 và 200 năm. Giả sử giá trị lớn nhất hàng năm của lượng mưa trong khoảng thời gian 120 phút
tại trạmTân Sơn Hòa tuân theo luật: a) Phân phối chuẩn b) Phân phối Gumbel c) Phân phối PIII
17. Phân tích các đợt lũ hàng năm của một con sông cho kết quả trung bình mẫu là 5000 m3/s, độ lệch
chuẩn là 700 m3/s và hệ số thiên lệch là 0.37. Ước tính lũ thiết kế của một công trình trên sông đó để
đảm bảo 95% rằng công trình sẽ không bị hỏng trong vòng 75 năm tới.
a) Sử dụng phân phối chuẩn
b) Sử dụng phân phối Gumbel
c) Sử dụng phân phối P-III
18. Lượng mưa năm thu thập tại một trạm khí tượng có dung lượng mẫu n = 70 năm, biết giá trị trung
bình của mẫu là = 1700mm. Kiểm định giả thuyết liệu giá trị trung bình của chuỗi lượng mưa năm đã
thu thập khác biệt đáng kể với giá trị lượng mưa trung bình năm 1500mm đã biết đến trước đây (tổng
thể) tại mức ý nghĩa α = 0.01. Giả sử độ lệch chuẩn của lượng mưa năm tại trạm là 170 mm (tổng thể).
19. Biết giá trị trung bình và độ lệch chuẩn xác định từ một mẫu lưu lượng dòng chảy năm tại một trạm
thủy văn có dung lượng n = 32 lần lượt là 7602 m3/s và 150 m3/s. Kiểm định giả thuyết về độ lệch
chuẩn của mẫu đã thu thập liệu có khác biệt với giá trị 210 m3/s đã biết đến trước đây (tổng thể) tại mức ý nghĩa 0.05.
20. Xác suất vỡ đập do cát chảy và xói ngầm là 10%. Một nghiên cứu thực hiện trên các đập được xây
dựng trong các điều kiện tương tự và thông số thiết kế giống nhau cho thấy 5 trong số 70 đập bị
hỏng. Trên cơ sở nghiên cứu này, hãy kiểm tra tuyên bố rằng xác suất không vỡ đập do điều kiện cát
chảy và xói ngầm lớn hơn 90% tại mức ý nghĩa 0,05.
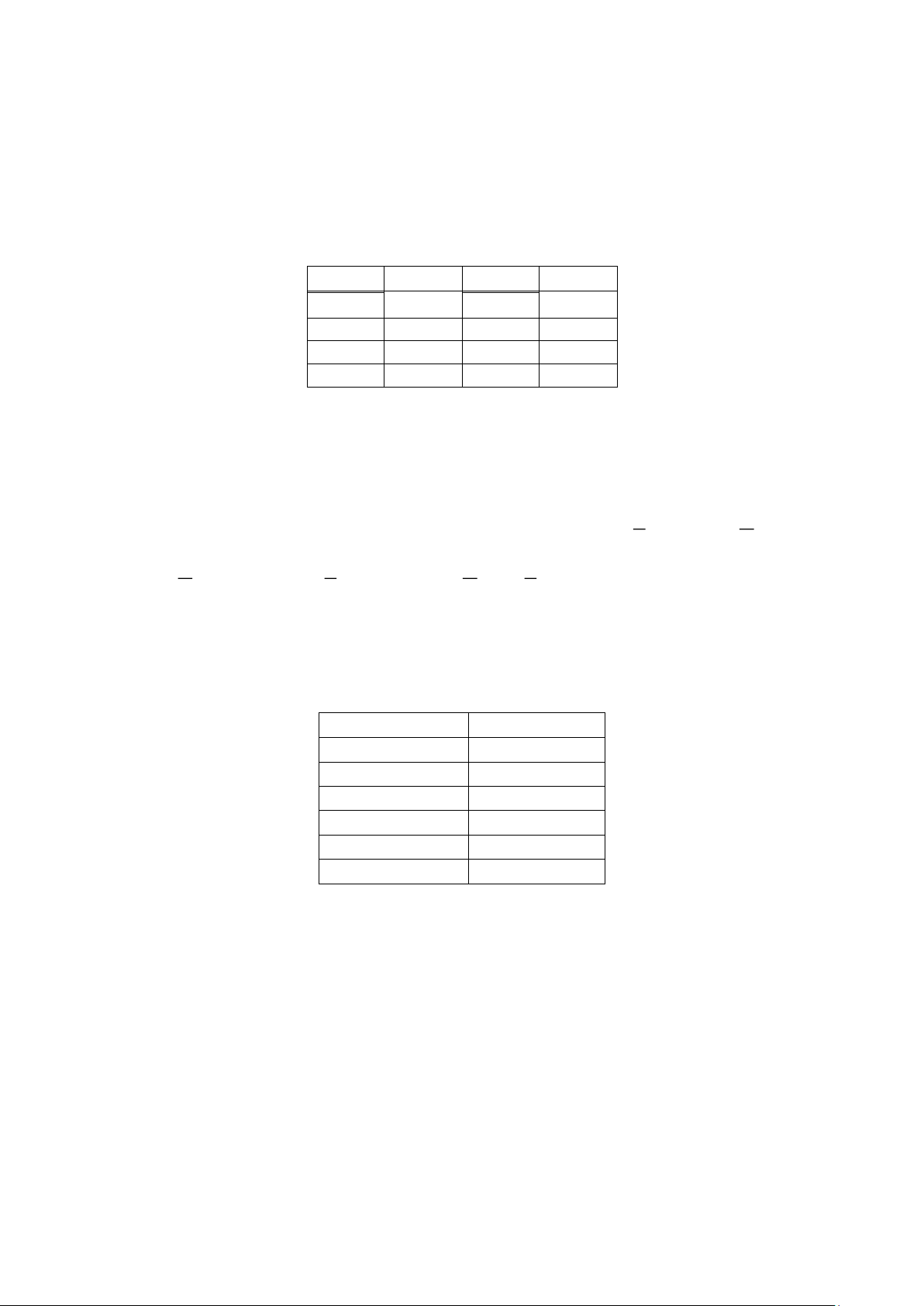
21. Cho số liệu mưa và dòng chảy của một lưu vực nhỏ. Các biến được giả định là có liên quan tuyến tính. X (mm) 25 27 14 11 35 15 Y (mm) 8 12 7 3 21 9 lOMoAR cPSD| 58478860
a) Xây dựng phương trình hồi quy tuyến tính của Y theo X
b) Tìm ra mối quan hệ giữa lượng mưa và dòng chảy cho lưu vực và sử dụng mối quan hệ để
ước tính lượng dòng chảy từ lượng mưa 27 mm.
c) Xác định khoảng tin cậy 95% của hệ số hồi quy
d) Kiểm định giả thuyết bo = 0.5
e) Kiểm định giả thuyết b1 = 0.7
f) Kiểm định giả thuyết ý nghĩa của phương trình hồi quy cho mô hình hồi quy
22. Lượng mưa năm thu thập tại một trạm khí tượng có dung lượng mẫu N = 60 năm. Chia chuỗi lượng
mưa năm trên làm 2 mẫu có độ dài mẫu như nhau, tham số thống kê của 2 chuỗi cho trong bảng. N1 30 N2 30 X1 1573 X2 1748 S1 229.00 S2 273.00 Cv1 0.17 Cv2 0.19 Cs1 -0.35 Cs2 -0.46
g) Xác định giá trị của tiêu chuẩn thống kê T trong kiểm định giả thuyết về sự khác biệt giá trị
trung bình của hai mẫu, với Ho: Giá trị trung bình của hai mẫu không chênh lệch nhau 40 mm
tại mức ý nghĩa α = 0.01.
h) Kiểm định giả thuyết trống H0: giá trị trung bình của mẫu 1 nhỏ hơn giá trị trung bình của
mẫu 2 tại mức ý nghĩa α = 0.05.
23. Phân tích số liệu đo đồng thời lưu lượng dòng chảy Q (m3/s) và mực nước H (m) tại một trạm đo
thủy văn để xây đường quan hệ Q ~ H. Biết độ dài chuỗi n = 30 năm; Q=2.1m3/s; H=3.8m; n n n
∑ ( Hi−H )2=11.2;∑ (Qi−Q )2=3.4;∑ (Hi−H )(Qi−Q)=4.5. Xác định phương trình hồi quy của i=1 i=1 i=1 Q theo H.
24. Tiến hành phân tích chuỗi lượng mưa năm với độ dài của chuỗi là 68 năm cho bảng phân bố sau.
Tầnsuất để có lượng mưa vượt quá 55 cm trong bất kỳ một năm nào là bao nhiêu?
Giá trị khoảng mưa Số năm xuất hiện ≤15 cm 4 15 - 24 cm 8 25 - 34 cm 13 35 - 44 cm 21 45-54 cm 10 ≥55 cm 12
25. Phân tích các đợt lũ hàng năm của một con sông cho kết quả trung bình mẫu là 16000 m3/s, độ lệch
chuẩn là 4500 m3/s và hệ số thiên lệch là 0.650. Sử dụng phân phối Pearson loại III ước tính lũ thiết
kế của một công trình trên sông đó để đảm bảo 90% rằng công trình sẽ không bị hỏng trong vòng 30 năm tới.
26. Tiến hành phân tích chuỗi lưu lượng đỉnh lũ lớn nhất hàng năm tại một trạm thủy văn A trong thời kỳ
35 năm cho giá trị trung bình và độ lệch chuẩn là 1300 và 750 m3/s. Xác định lưu lượng lũ thiết kế
cho 1 công trình xây dựng gần trạm thủy văn A để đảm bảo rằng 90% công trình không bị phá hủy
do lũ trong 60 năm tới sử dụng phân phối Gumbel.