Bài giảng môn Xác suất thống kê | Trường Đại học Thủy Lợi

BÀI GIẢNG
Lý thuyết Xác suất thống kê Hà Nội - 2014
MỞ ĐẦU
Lý thuyết Xác suất Thống kê là một bộ phân của Toán học nghiên cứu các hiện tượng ngẫu
nhiên và ứng dụng chúng vào thực tế. Ta có thể hiểu hiện tượng ngẫu nhiên là hiện tương không
thể nói trước được nó có thể xảy ra hay không khi thực hiện một lần quan sát. Tuy nhiên, nếu tiến
hành quan sát khá nhiều lần một hiệ tượng ngẫu nhiên trong các phép thử như nhau, ta có thể rút
ra những kết luận khoa học về hiện tượng này.
Lý thuyết Xác suất cũng là cơ sở để nghiên cứu Thống kê – môn học nghiên cứu các phương
pháp thu thập thông tin, chọn mẫu, xử lý thông tin nhằm rút ra các kết luận hoặc quyết định cần
thiết.
Lý thuyết Xác suất Thống kê ngày phát triển theo tiến trình phát triển của xã hội, nó đóng
vai trò rất quan trọng trong hầu hết mọi lĩnh vực của thế giới hiện đại, từ khoa học, công nghệ, đến
kinh tế, chính trị, đến sức khỏe, môi trường,…
Ngày nay, máy tính đã giúp cho việc tính toán các vấn đề xác suất thống kê ngày càng trở
nên dễ dàng, một khi đã có số liệu đúng đắn và mô hình hợp lý. Thế nhưng, bản thân máy tính
không biết mô hình nào là hợp lý. Đấy là vấn đề của người sử dụng: cần phải hiểu được bản chất
của các khái niệm và mô hình xác suất thống kê, thì mới có thể dùng chúng được. Chính vì vậy, mặc
dù đã được giới thiệu ở bậc học Phổ thông, Lý thuyết Xác suất Thống kê được giảng dạy cho hầu
hết các nhóm ngành ở bậc Đại học.
Chương trình học Môn Lý thuyết Xác suất Thống kế (tại
Trường Đại học Thủy Lợi)
1. Định nghĩa về xác suât
2. Đại lượng ngẫu nhiên và phân phối xác suât
3. Kỳ vọng và phương sai
4. Một số phân phối xác suất thường gặp
5. Mẫu ngẫu nhiên đơn giản và các hàm phân phối mẫu của các thống kê thường gặp
6. Bài toán ước lượng
7. Kiểm định giả thuyết
8. Đường hồi quy tuyến tính Giáo trình chính:
Giáo trình Lý thuyết Xác suất Thống kê, Bản dịch (đã chỉnh lý lần thứ nhất) - Tài liệu lưu hành nội
bộ của Trường Đại học Thủy Lợi – (Bản dich từ "Probability and statisics for Engineers and
Scientists" của Walpole. H. Myers, L. Myers) Bài số 1
NHỮNG KHÁI NIỆM CƠ BẢN VỀ XÁC SUẤT
I. NHẮC LẠI VÀ BỔ XUNG VỀ GIẢI TÍCH TỔ HỢP
Những kiến thức phần này liên quan tới việc đếm các điểm mẫu.
1.Quy tắc cộng. Giải sử một công việc nào có k trường hợp để thực hiện:
Trường hợp 1 có n1 cách thực hiện
Trường hợp 2 có n2 cách thực hiện …..
Trường hợp k có nk cách thực hiện
Khi đó ta có: n = + + +n1n2 ... nk cách thực hiện công việc đã cho.
2.Quy tắc nhân.Giải sử một công việc nào đó được chia thành k giai đoạn:
Có n1 cách thực hiện giai đoạn thứ nhất
Có n2 cách thực hiện giai đoạn thứ hai…..
Có nk cách thực hiện giai đoạn thứ k
Khi đó ta có: n = n n1. ...2 nk cách thực hiện công việc đã cho.
Ví dụ 1. Có bao nhiêu cách lựa chọn bữa ăn gồm có xúp, sandwich, món tráng miệng, và một đồ uống
từ 4 món xúp, 3 kiểu sandwich, 5 món tráng miệng, và 4 đồ uống?
Giải: Do n1 = 4, n2 = 3, n3 = 5 và n4 = 4, có n1×n2×n3×n4 = 4 × 3 × 5 × 4 = 240 cách khác nhau để chọn bữa ăn. 3. Hoán vị.
a. Định nghĩa: Hoán vị của n phần tử là một bộ có thứ tự gồm k phần tử khác nhau chọn từ n
phần tử đã cho hoặc gồm đúng n phần tử đã cho.
b. Công thức 1: Số các hoán vị của n phần tử phân biệt là Pn = n!.
c. Công thức 2: Số những hoán vị của n phần tử phân biệt được lấy k lần liên tiếp là n! A k n =
(còn gọi là chỉnh hợp chập k của n phần tử). (n k− )!
Ví dụ 2. Một đề tài nhánh của Hội Hóa học Mỹ có bao nhiêu cách bố trí 3 báo cáo viên cho 3 cuộc
họp khác nhau nếu họ đều có thể thu xếp được bất kỳ một trong 5 ngày? Giải: Tổng số cách bố trí bằng A53 = = 60 .
Những hoán vị xuất hiện khi sắp xếp các phần tử theo một vòng tròn được gọi là những hoán
vị vòng quanh.
d. Công thức 3: Số những hoán vị của n phần tử phân biệt được sắp xếp theo một vòng tròn là : (n − 1)!.
Cho đến bây giờ ta đã xét hoán vị của những phần tử phân biệt. Trường hợp có các phần tử gióng nhau thì sẽ thế nào.
e. Công thức 4: Số những hoán vị phân biệt của n phần tử mà trong đó n1 phần tử thuộc kiểu thứ nhất,
n2 phần tử thuộc kiểu thứ hai, ... , nk phần tử thuộc kiểu thứ k là: n! . n n1 ! 2 !⋯nk !
Ví dụ 3. Có bao nhiêu cách sắp khác nhau để tạo thành một xâu đèn của cây thông Noel có 3 bóng đèn
đỏ, 4 bóng đèn vàng, và 2 bóng đèn xanh với 9 ổ cắm? Giải: Tổng số sắp xếp phân biệt là 9! = 1260. 3!4!2!
4. Phân hoạch. Tổ hợp.
Ta thường quan tâm đến số cách phân hoạch một tập gồm n phần tử thành r tập con được gọi
là các ngăn. Một phân hoạch được hoàn thành khi giao của mọi cặp trong r tập con là tập rỗng ∅ và
hợp của tất cả những tập con là tập ban đầu. Thứ tự của các phần tử bên trong một ngăn là không quan trọng.
a. Công thức 1: Ta phân hoạch một tập gồm n phần tử thành k ngăn sao cho:
có n1 phần tử trong ngăn thứ nhất, có n2 phần tử trong ngăn thứ hai,...
có nk phân tử trong ngăn thứ k Khi
đó số cách phân hoạch là: nr = n n1 ! 2n!⋯! nk ! n n1, ,...,2 n trong đó n1 + + + =n2... nk n .
Ví dụ 4. Có bao nhiêu cách phân cho 7 nhà khoa học vào một buồng ba và hai buồng đôi của một khách sạn?
Giải: Tổng số phân hoạch có thể có là 3, 2,7 2 = 3!2! 2!7! = 210 .
Trong nhiều bài toán ta quan tâm đến số cách chọn r phần tử từ n phần tử mà không quan tâm đến thứ
tự. Những phép chọn này được gọi là các tổ hợp. Một tổ hợp thực chất là một phân hoạch có hai ngăn,
một ngăn chứa r đối tượng được chọn còn ngăn kia chứa (n − r) đối tượng còn lại.
b. Công thức 2: Số các tổ hợp của n phần tử phân biệt được tạo ra khi lấy r phần tử cùng một lúc là n =Cnk = r n!( n−! r)! r
Ví dụ 5. Hãy tìm số ủy ban gồm 2 nhà Hóa học và 1 nhà Vật lí mà có thể tạo được từ 4 nhà Hóa học và 3 nhà Vật lý. Giả:
Số cách chọn 2 trong 4 nhà hóa học là 24 = 2! 2!4! = 6.
Số cách chọn 1 trong 3 nhà vật lí là 13 = 1! 2! 3! = 3.
Sử dụng quy tắc nhân với n1 = 6 và n2 = 3 , ta có thể tạo được: n = n n1. 2 =(6).(3)=18 ủy ban với 2 nhà
Hóa học và 1 nhà Vật lí.
c. Chú ý: Ta có
i) Quy ước: 0! =1 ii) Cnk =Cnn k−
iii) Cnk =Cnk−−11 +Cnk−1 . n
5. Nhị thức Newton. (a +b)n = ∑C a k n k k− n b . k=0
II. BIẾN CỐ VÀ QUAN HỆ GIỮA CÁC BIẾN CỐ
1.Phép thử ngẫu nhiên và không gian mẫu.
Ví dụ mở đầu: Khi cho cuộn dây quay đều trong từ trường của một thanh nam châm, kết quả là chắc
chắn xuất hiện dòng điện trong cuộn dây
Đây là một phép thử không ngẫu nhiên.
Khi gieo một con xúc xắc cân đối và đồng chất, ta không đoán chắc chắn được kết quả. Chỉ biết được
kết quả là xuất hiện số chấm trong {1,2,3,4,5,6}.
Đây là một phép thử ngẫu nhiên.
Như vậy: Một phép thử ngẫu nhiên luôn thỏa hai đặc tính:
1. Không biết chắc kết quả nào sẽ xảy ra
2. Nhưng biết được các kết quả sẽ xảy ra
Việc dựa trên một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó được gọi là
một phép thử ngẫu nhiên, ở đây các kết quả của nó không dự đoán trước được. Do bài giảng này chỉ
xét các phép thử ngẫu nhiên, nên ta gọi tắt chúng là phép thử.
a. Định nghĩa. Tập hợp tất cả những kết quả có thể của một phép thử thống kê được gọi là không gian
mẫu và được ký hiệu bởi S ( hoặc Ω).
Mỗi kết quả trong không gian mẫu được gọi là một phần tử của không gian mẫu, hoặc đơn giản là một
điểm mẫu.
b. Cách mô tả không gian mẫu:
+ Khi không gian mẫu có hữu hạn phần tử, ta có thể liệt kê những phần tử .
+ Khi không gian mẫu có vô hạn phần tử, hoặc các phần tử có thuộc tính chung: ta có thể mô tả bằng
mệnh đề hoặc quy tắc
+ Ta cũng có thể dùng sơ đồ hình cây.
Ví dụ 6. Khi tung một đồng xu không gian mẫu Ω có thể viết là: Ω = {H T, }, trong đó H và T tương ứng
với “heads” và “tails”, nghĩa là "ngửa" và "sấp".
Ví dụ 7. Khi gieo một con xúc sắc:
+ Nếu ta quan tâm đến số chấm xuất hiện trên mỗi mặt thi không gian mẫu là: Ω = {1,2,3,4,5,6}
+ Nếu ta quan tâm đến mặt chẵn hay lẻ (số chấm xuất hiện trên mặt là chẵn hay lẻ) thì không gian mẫu là: Ω={chan le, }
Ví dụ 8. Khi tung hai đồng xu, với ký hiệu S: sấp còn N: ngửa khi đó không gian mẫu là: Ω= {SS SN NN NS, , , }
Ví dụ 9. Lấy ngẫu nhiên một điểm nằm trong miền hình chữ nhật trên mặt phẳng tọa độ Oxy với kích
thước [0;3]×[0;2], khi đó không gian mẫu là: S =Ω={(x y, ) 0 ≤ ≤x 3; 0 ≤ ≤y 2}
Ví dụ 10. Xét phép thử là tung một đồng xu.
+ Nếu xuất hiện mặt sấp xuất thì ta tung đồng xu đó lần thứ hai.
+ Nếu xuất hiện mặt ngửa thì ta tiếp tục tung một con xúc xắc được tung một lần.
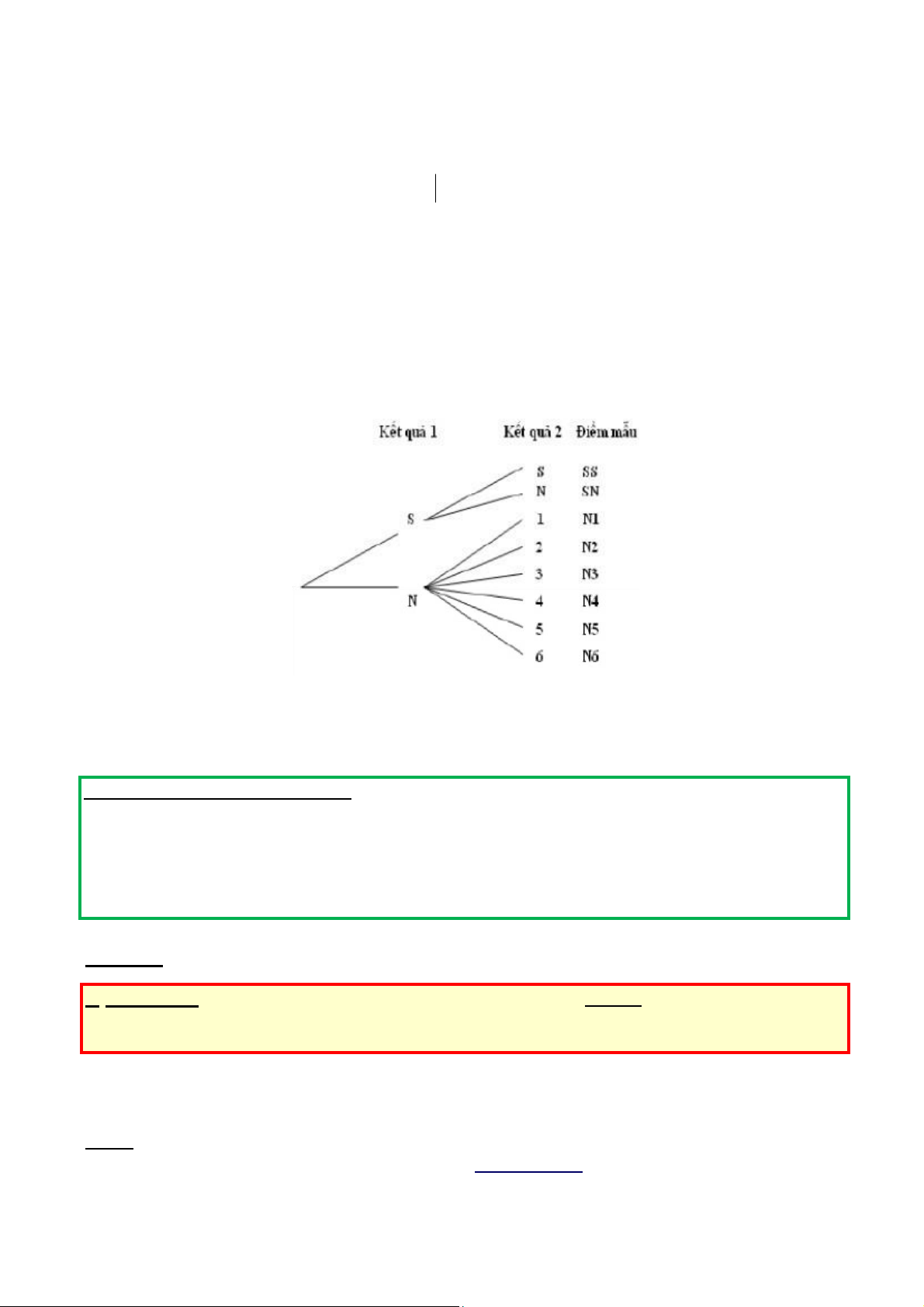
Trong trường hợp này ta đi xây dựng sơ đồ cây như hình vẽ để xác định không gian mẫu. Bây giờ,
những con đường khác nhau dọc theo các cành cây đi tới những điểm mẫu khác biệt.
Từ đó ta xác định được không gian mẫu là : Ω =
{SS NN N N;; 1; 2; 3; 4; 5; 6N N N N }.
c. Cách xây dựng không gian mẫu :
+ Đặt tên cho các phần tử có mặt hoặc các bước hình thành phép thử
+Mô tả điểm mẫu theo các kết quả xảy ra trong phép thử.
2. Biến cố
a. Định nghĩa. Các kết quả có thể xảy ra của phép thử được gọi là biến cố. Như vậy biến cố của một
phép thử chính là mỗi tập con của không gian mẫu.
Ký hiệu biến cố : Dùng các chữ in hoa như A B C, , ,... Chú ý
• Mỗi điểm mẫu là một biến cố và được gọ là biến cố sơ cấp.
• Biến cố không thể là biến cố không bao giờ xảy ra khi thực hiện phép thử, ký hiệu là ∅.
• Biến cố chắc chắn là biến cố luôn luôn xảy ra khi thực hiện phép thử, nó tương ứng với chính
không gian mẫu Ω nên ký hiệu là Ω.
b. Quan hệ giữa các biến cố. Cho A và B là hai biến cố của một phép thử với không gian mẫu Ω. Khi đó :
• Biến cố A được gọi là kéo theo biến cố B , ký hiệu A B⊂ , nếu A xảy ra thì B cũng xảy ra.
• Biến cố A được gọi là tương đương với biến cố B , ký hiệu A = B , nếu A xảy ra thì B xảy ra và ngược lại.
• Biến cố đối của biến cố A, ký hiệu A, là biến cố xảy ra khi và chỉ khi A không xảy ra.
• Hợp (tổng) của hai biến cố A và B , ký hiệu là A∪B (hoặc A B+ ) là biến cố xảy ra nếu có ít nhất một
biến cố nào đó trong các biến cố A hoặc B xảy ra. Nói cách khác : A∪B là biến cố gồm các điểm mẫu
hoặc thuộc A hoặc thuộc B .
Định nghĩa hợp của n biến cố cũng được định nghĩa tương tự : A1 ∪ ∪ ∪A2 ... A n
• Giao (tích) của hai biến cố A và B , kí hiệu A∩B (hoặc AB ) là biến cố xảy ra nếu cả A và
B cùng xảy ra. Nói cách khác A∩B là biến cố gồm các điểm mẫu thuộc cả A và B .
Nếu A1, A2, …, An là các biến cố liên quan đến cùng một phép thử, thì giao (hay tích) của chúng, ký hiệu là A A ... An .
• Hai biến cố A và B được gọi là xung khắc nếu A∩ =∅B .
Ví dụ 11. A là biến cố “ra số chấm chẵn” khi gieo một con xúc xắc , thì A = “ra số chấm lẻ”
Ví dụ 12. Xét biến cố A = {2,4,6}, biến cố B = {4,5,6} và biến cố C = {1,2,4,6} là những tập con của
cùng không gian mẫu Ω = {1,2,3,4,5,6}. Khi đó:
+ Ta có A kéo theo C , tức là A C⊂
+ A = {1,3,5}, B = {1,2,3}, A ∩ B = {4,6}, A ∪ B = {2,4,5,6}.
Ví dụ 13. Xét phép thử : T = gieo một con xúc xắc cân đối và các biến cố :
Ai : "Xuất hiện i chấm",
A:"Xuất hiện chấm chẵn",
B : "Xuất hiện chấm chia hết cho 3". Khi đó
+ A = A2 ∪ A4 ∪ A B6, = A3 ∪ A6. + A∩ =B AB = A6.
+ Các biến cố : A A1, 2,...,A6 đôi một xung khắc.
Ví dụ 14. Có ba xạ thủ A, B, C cùng bắn vào một mực tiêu. Gọi :
A là biến cố "xạ thủ A bắn trúng"
B là biến cố "xạ thủ B bắn trúng"
C là biến cố "xạ thủ C bắn trúng"
Khi đó: M = ABC là biến cố "cả ba xạ thủ bắn trúng"
N = ABC là biến cố "cả ba xạ thủ bắn trượt" P = A∪ ∪B
C là biến cố "có ít nhất một xạ thủ bắn trúng" Q =
AB ∪ BC ∪CA là biến cố "có ít nhất hai xạ thủ bắn trúng"
R = ABC ∪ ABC ∪ ABC là biến cố "có đúng một xạ thủ bắn trúng" U = AB
∪ BC ∪CA là biến cố "có nhiều nhất một xạ thủ bắn trúng" V = ABC là
biến cố "chỉ có xạ thủ A bắn trúng".
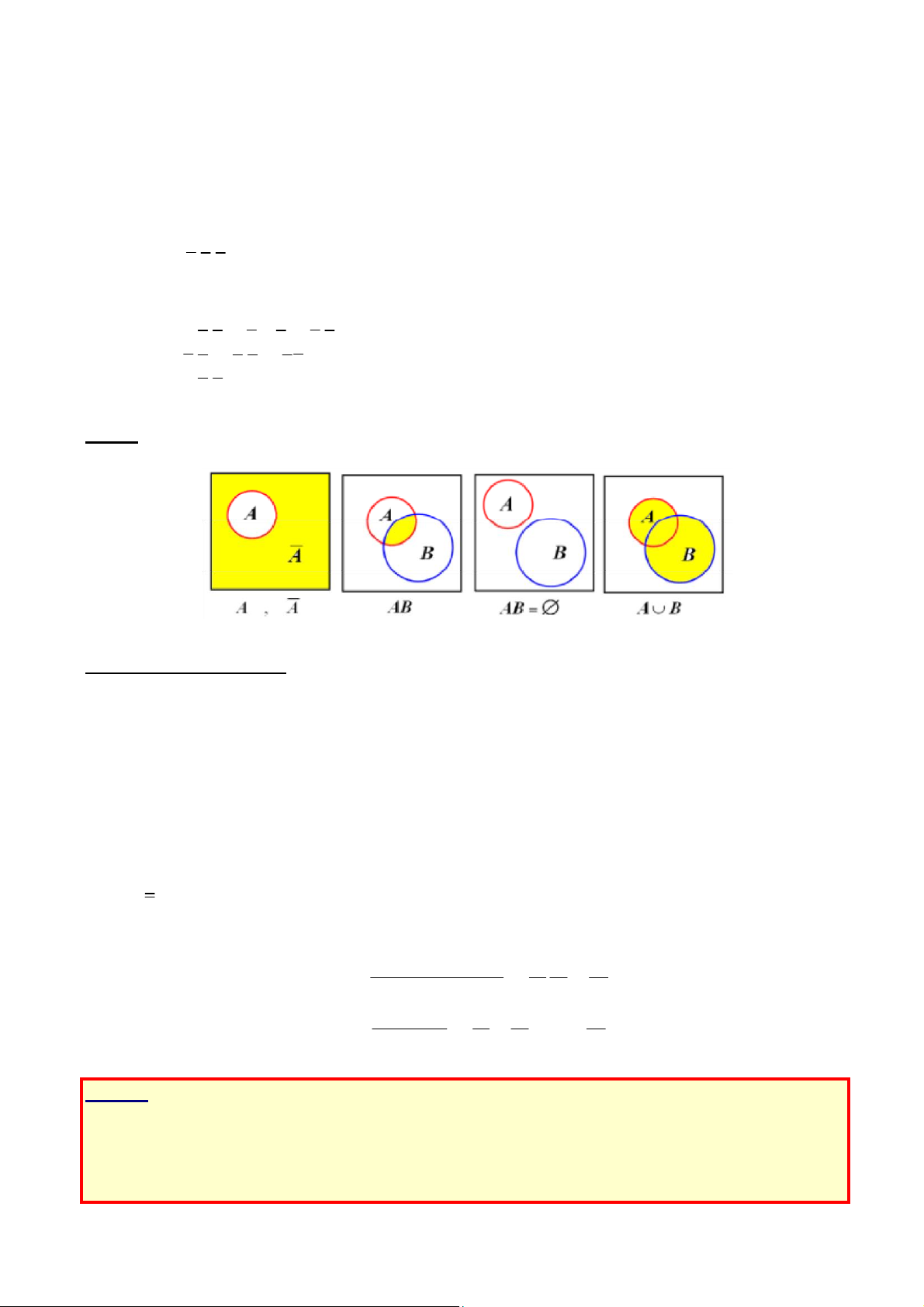
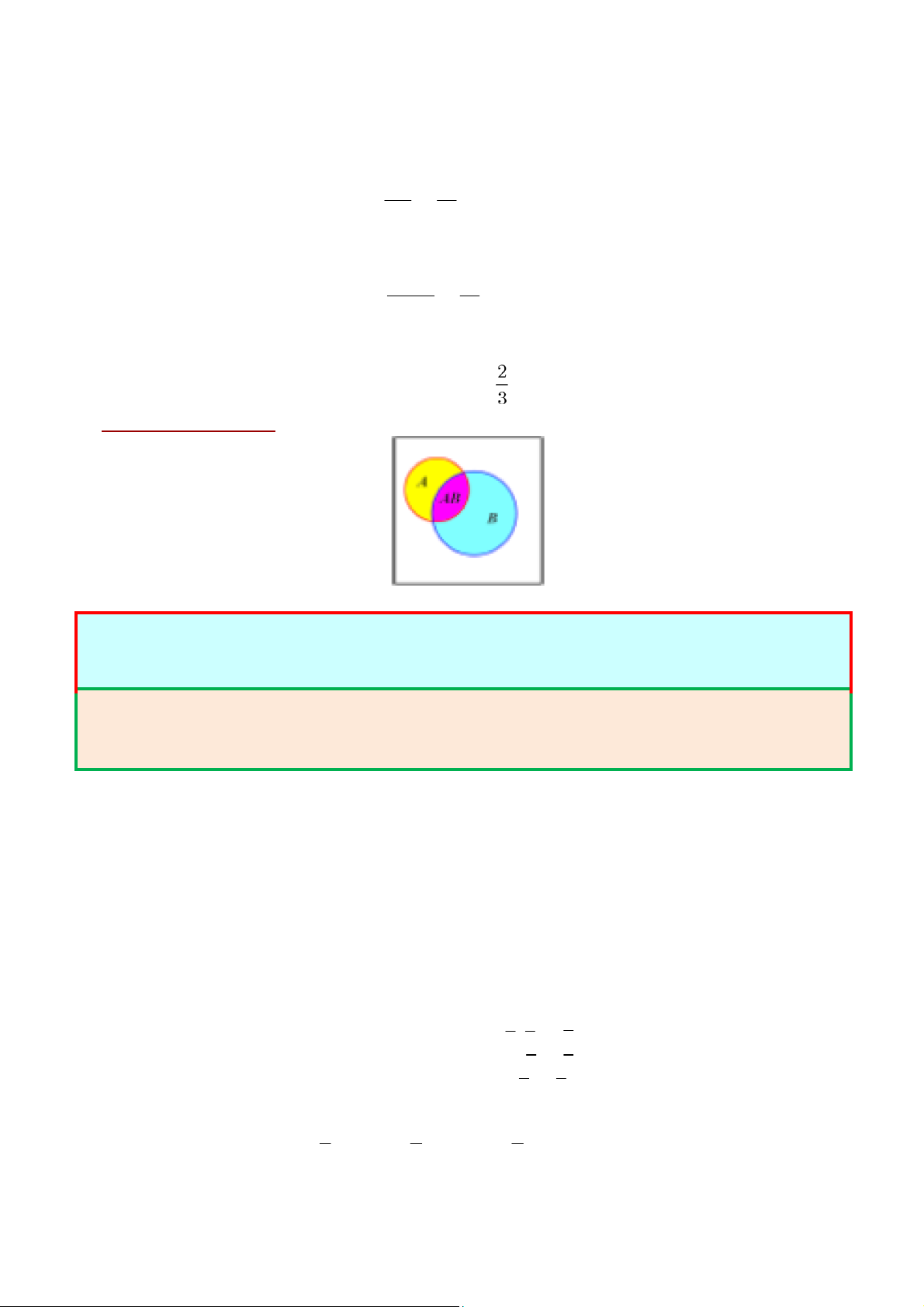
Chú ý: Ta cũng có thể sử dụng sơ đồ Ven để biểu diễn quan hệ giữa các biến cố
c. Một số hằng đẳng thức. • Tính giao hoán: A∪ = ∪B B A AB, = BA •
Tính kết hợp: A ∪ B ∪C = (A ∪ B) ∪C = A ∪ (B ∪C); ABC = (AB C) = A BC( ) •
Tính phân phối: (A∪B C) =(AC)∪(BC), (AB)∪ =C (A∪C B)( ∪C) • A∪ =A A AA, = A. •
A∪Ω=Ω Ω=, A A A, ∪∅= A A, ∅=∅. • A=A. • Luật De Morgan:
A A1 ∪ ∪ ∪ =2 ⋯ An A A1 2 ⋯An
AA1 2 ⋯An = A1 ∪ A2 ∪ ⋯ ∪ An Về nhà:
Tự đọc Chương 1
Bài tập: Mục 2.1+2.2: Tr. 27; Mục 2.3: tr. 37
Đọc trước các Mục 2.4 đến 2.8 chuẩn bị cho Bài số 2: Xác suất. Quy tắc tính xác suất. Bài số 2
XÁC SUẤT . QUY TẮC TÍNH XÁC SUẤT
I. XÁC SUẤT CỦA MỘT BIẾN CỐ
1. Mở đầu về xác suất.
Việc biến cố ngẫu nhiên xảy ra hay không trong kết quả của một phép thử là điều không thể biết
hoặc đoán trước được. Tuy nhiên bằng những cách khác nhau ta có thể định lượng khả năng xuất hiện
của biến cố, đó là xác suất xuất hiện của biến cố. Xác suất của biến cố là con số đặc trưng khả năng
khách quan xuất hiện biến cố đó khi thực hiện phép thử.
Dựa vào bản chất của phép thử (đồng khả năng) ta có thể suy luận về khả năng xuất hiện của
biến cố, với cách tieps cận này ta có định nghĩa xác suất theo phương pháp cổ điển.
Khi thực hiện nhiều lần lặp lại độc lập một phép thử ta có thể tính được tần suất xuất hiện (số
lần xuất hiện) của một biến cố nào đó. Tần suất thể hiện khả năng xuất hiện của biến cố, với cách tiếp
cận này ta có định nghĩa xác suất theo thống kê.
Trường hợp ta biểu diễn không gian mẫu và các biến cố bởi các miền hình học có độ đo ta sẽ
có định nghĩa xác suất theo quan điểm hình học.
2. Xác xuất của của một biến cố
Ta chỉ xét những phép thử mà không gian mẫu có hữu hạn phần tử: chằng hạn xét phép thử với không gian mẫu
Ω = {s s1, ,...2 sk }.
Khi đó, với mỗi điểm mẫu (biến cố sơ cấp) si được gán tương ứng với một số thực pi thỏa mãn p ∈ 0;1 ki
, số thực pi được gọi là xác suất của điểm mẫu (biến cố sơ cấp) si . Nếu ta có lý do để
∑i=1 pi = 1 tin rằng một điểm mẫu nào đó rất có khả năng xảy ra khi phép thử được tiến hành, xác
suất được gán sẽ gần 1. Mặt khác, một xác suất gần 0 được gán cho một điểm mẫu mà dường như
không xuất hiện. Trong nhiều phép thử, như tung một đồng xu hay một xúc xắc, tất cả những điểm
mẫu có cùng khả năng xuất hiện cũng được gán các xác suất bằng nhau. Đối với những điểm bên ngoài
không gian mẫu, tức là đối với các biến cố mà không thể xuất hiện, ta gán cho xác suất bằng 0 .
Ta chú ý rằng, mỗi biến cố là tập con của không gian mẫu Ω, nên một biến cố A của phép thử là một
tập gồm các điểm mẫu (biến cố sơ cấp), mỗi biến số sơ cấp trong A còn gọi là một khả năng thuận lợi cho A.
a. Định nghĩa. Xét phép thử với không gian mẫu Ω và A biến cố trong phép thử đó. Khi đó xác suất
của biến cố A là tổng xác xuất của tất cả các diểm mẫu trong A, ký hiệu là P A( ). Từ định nghĩa ta có:
1. 0 ≤ P A( ) ≤ 1 2. P S( ) = P( )Ω = 1 3. P( )∅ = 0.
Ví dụ 1. Một đồng xu được tung 2 lần. Xác suất để ít nhất một mặt ngửa xuất hiện là bao nhiêu? Giải:
+ Không gian mẫu đối với phép thử này là Ω = {SS SN NS NN, , , }.
+ Nếu đồng xu cân đối, mỗi kết cục như vậy có thể đồng khả năng xuất hiện. Do đó, ta gán một xác
suất w cho mỗi điểm mẫu. Khi ấy 4w = 1 → w = .
+ Nếu A biểu thị biến cố ít nhất một mặt ngửa xuất hiện, thì A = {SN NS NN, , } 1 1 1 3 + Và P A( ) = + + = . 4 4 4 4
Ví dụ 2. Một con súc sắc được đổ chì sao cho khả năng xuất hiện một chấm chẵn gấp 2 lần khả năng
xuất hiện một chấm lẻ. Gọi E là biến cố số chấm nhỏ hơn 4 xuất hiện trong một lần tung xúc xắc, hãy tìm P E( ) = ? Giải:
+ Không gian mẫu là Ω = {1,2,3,4,5,6}.
+ Ta gán một xác suất w cho mỗi số chấm lẻ và một xác suất 2w cho mỗi số chấm chẵn.
+ Do tổng của các xác suất phải bằng 1 nên ta có 9w = 1 → w = .
+ Từ đó, các xác suất 1/9 và 2/9 được gán cho mỗi số chấm chẵn và lẻ tương ứng. + Do đó: E {1,2,3) P E( ) .
Ví dụ 3. Trong Ví dụ 16 gọi A là biến cố xuất hiện số chấm chẵn và cho B là biến cố xuất hiện số chấm
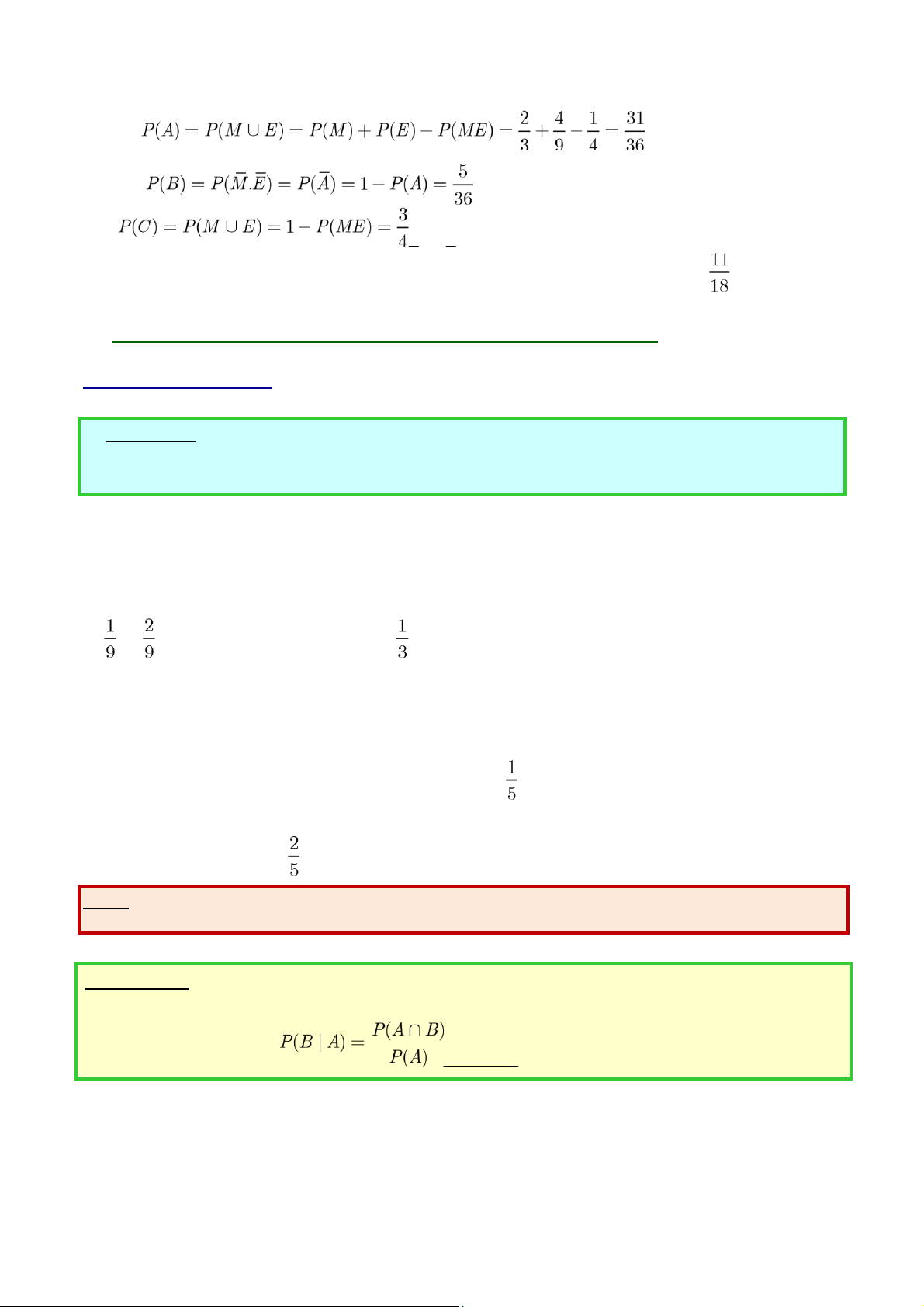
chia hết cho 3. Hãy tìm P A( ∪ B) và P A( ∩ B). Giải:
+ Ta có A = {2,4,6}, B = {3,6}, từ đó A∪ =B {2,3,4,6}, A∩ =B {6} .
+ Do xác suất cho mỗi số chấm lẻ là và mỗi số chấm chẵn , nên ta có P A B và P A( B) .
Trường hợp không gian mẫu có hữu hạn phần tử và các biến cố sơ cấp đồng khả năng.
b. Định nghĩa xác suất theo lối cổ điển
Giải sử phép thử có N biến cố sơ cấp đồng khả năng, trong đó biến cố Acó chứa n biến cố sơ cấp n
đồng khả năng. Khi đó xác suất của biến cố A được xác định bởi: P A( ) = . N
Các bước tìm xác suất của một biến cố A:
1.Đếm số biến số sơ cấp đồng khả năng trong không gian mẫu: N
2. Đếm số biến số sơ cấp đồng khả năng trong biến cố A: n n
3. Từ đó P A( ) = . N
Ví dụ 4. Một đống kẹo trộn lẫn 6 chiếc bạc hà, 4 chiếc kẹo bơ và 3 chiếc chocolate. Nếu một người
chọn ngẫu nhiên một trong những chiếc kẹo này, hãy tìm xác suất để được a. Một chiếc bạc hà;
b. Một chiếc kẹo bơ hoặc một chocolate.
Giải: Gọi M T, và C là các biến cố mà người chọn được, tương ứngmột chiếc bạc hà, kẹo bơ, hoặc
chocolate. Tổng số kẹo bằng 13 và tất cả đều đồng khả năng để chọn.
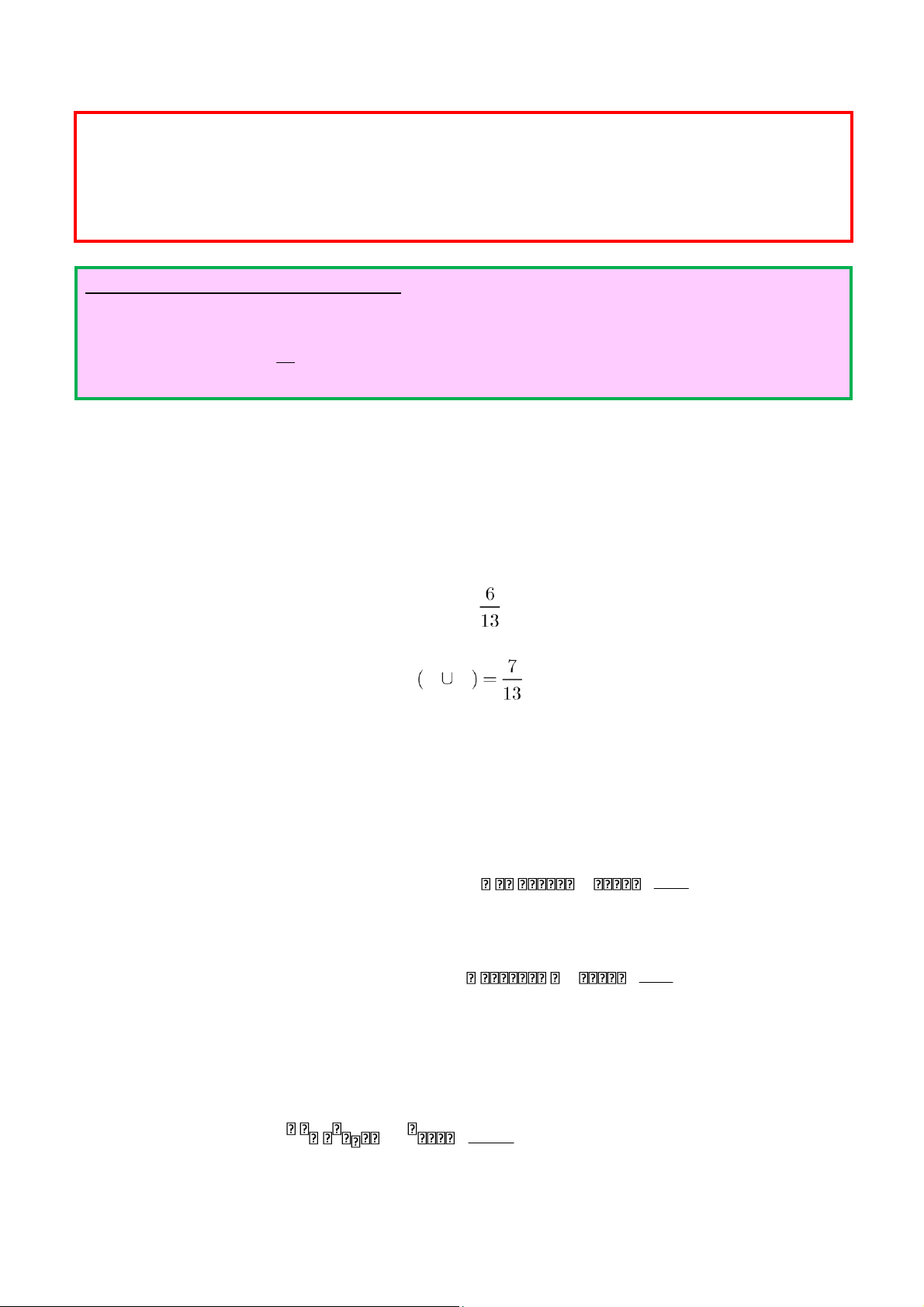
a. Do 6 trong 13 chiếc là bạc hà, xác suất của biến cố M chọn được ngẫu nhiên một bạc hà là P M( ) = .
b. Do 7 trong 13 chiếc kẹo là bơ hoặc chocolate, suy ra P T C .
Ví dụ 5. Lấy ngẫu nhiêu 5 cây Tú Lơ Khơ trong bộ 52 cây. Hãy tìm xác suất để trong đó có 2 cây Át và 3 cây J .
Giải: Gọi C là biến cố “Trong 5 cây có 2 cây Át và 3 cây J ”
+ Số cách chia riêng 2 cây từ 4 cây Át bằng: 24 = 2!2!4! = 6
+ Số cách chia riêng 3 cây từ 4 cây J bằng : 43 = 3!1!4! = 4.
+ Theo quy tắc nhân ta có n = =6.4 24 trường hợp rút ra có 2 Át và 3 cây J .
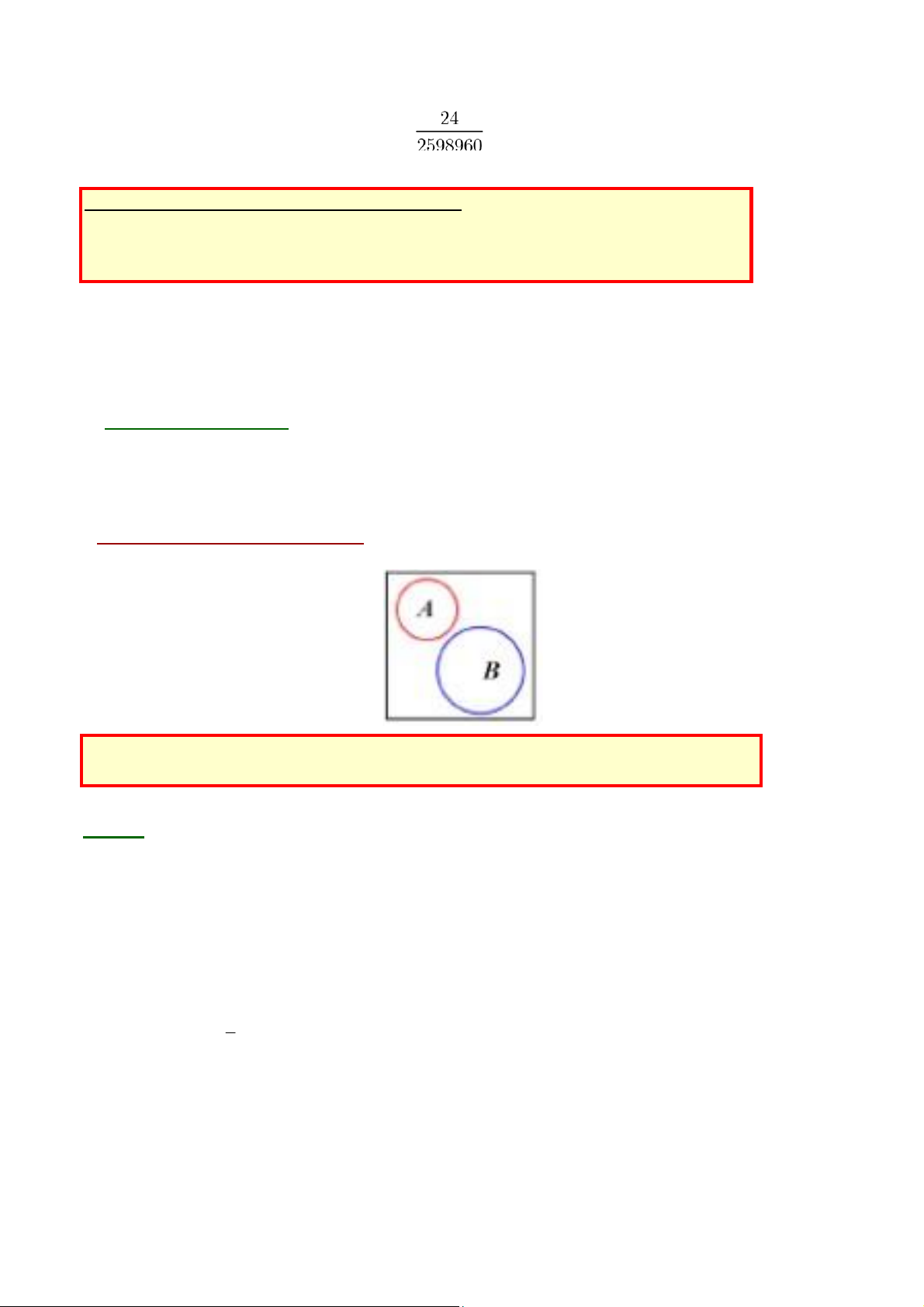
+ Mà tổng số trường hợp lấy ngẫu nhiên 5 cây bài (tất cả đều đồng khả năng) là N = 525 = 5!47!52! = 2598960.
+ Do đó xác suất của biến cố C là: P C( ) == 0,9.10 .−5
Hạn chế của định nghĩa xác suất theo lối cổ điển
1.Nó chỉ xét cho trường hợp không gian mẫu có hữu hạn các biến cố 2. Các
biến cố sơ cấp trong không gian mẫu “đồng khả năng” Tuy nhiên không phải lúc nào
không gian mẫu cũng thỏa mãn điều đó.
Trong thực tế, chúng ta thường phải tìm xác suất của những biến cố phức tạp, khi đó ta sẽ cố gắng biểu
diễn biến cố đó theo những biến cố đơn giản và xác suất của một biến cố ban đầu sẽ dễ dàng hơn nếu
ta dựa vào xác suất đã biết của các biến cố đơn giản hơn..
II. CÔNG THỨC CỘNG.
Mục đích: Trong một phép thử, đã biết xác xuất của một số biến cố nào đó ta có thể tính xác xuất của
biến cố hợp của chúng.
1.Trường hợp các biến cố xung khắc.
Nếu Avà B là 2 biến cố xung khắc (tức là A B∩ =∅) trong một phép thử thì ta có: P A( ∪ B) = P A( ) + P B( ).
Hệ quả:
i. Nếu A A1, 2,...,An là các biến cố đôi một xung khắc nhau trong cùng một phép thử thì ta có: P A( 1 ∪ ∪ ∪A2 ... An )= P A( )1 +P A( )2 + +... P A( n )
ii. Nếu A A1, 2,...,An là một phân hoạch của không gian mẫu Ω, thì: P(P A( 1 ∪ ∪ ∪A2 ....
An )= P A( )1 + +...P A( n )= Ω =P( ) 1.
iii. P A( ) = −1 P A( ).
Ví dụ 6. Có một lô hành gồm 10 sản phẩm, trong đó có 2 phế phẩm. Lấy ngẫu nhiên không hoàn lại từ
lô hàng ra 6 sản phẩm. Tìm xác suất để không có quá 1 phế phẩm trong 6 sản phẩm được lấy ra. Giải: Gọi
A là biến cố “không có phế phẩm trong 6 sản phẩm lấy ra”
B là biến cố “có đúng 1 phế phẩm trong 6 sản phẩm lấy ra”
C là biến cố “không có quá 1 phế phẩm trong 6 sản phẩm lấy ra”
+ Khi đó A và B là hai biến cố xung khắc
+ Xác suất của biến cố A là: P A( ) = CC10686= 152
+ Xác suất của biến cố B là: P B( ) = C C21.6 85 = 158 C10
+ Nhận thấy: C = A∪B do đó: P C( ) = P A( ) + P B( ) = .
2. Trường hợp tổng quát.
Nếu A và B là hai biến cố tùy ý trong một phép thử thì ta có
P A( ∪ B) = P A( ) + P B( ) − P AB( ).
Với 3 biến cố A B C, , ta có:
P A( ∪ B ∪C) = P A( ) + P B( ) + P C( ) − P A( ∩ B)– P B( ∩C)– P C( ∩ A) + P ABC( ).
Tương tự ta có thể nhận được công thức cộng xác suất trong trường hợp số biến cố tùy ý.
Ví dụ 7. Xác suất để Hồng thi đỗ môn toán là 2/3 và xác suất để cô ta thi đỗ môn tiếng Anh là 4/9.
Giả thiết rằng xác xuất để thi đỗ cả 2 môn là 1/4. Tìm xác suất để a) Hồng thi đỗ ít nhất một môn.
b) Hồng không đỗ môn nào
c) Hồng thi trượt ít nhật một môn
d) Hồng thi đỗ đúng một môn Giải: Gọi:
M là biến cố “thi đỗ môn Toán”,
E là biến cố “thi đỗ môn Tiếng Anh” , khi đó ME là biến cố “thi đỗ cả hai môn” A là
biến cố “thi đỗ ít nhất một môn”, khi đó A = M ∪E
B là biến cố “không đỗ môn nào”, khi đó B = M E. = A
C là biến cố “trượt ít nhất một môn”, khi đó C = M ∪E D là biến cố “đỗ đúng
một môn”, khi đó D = M E. ∪M E. 2 4 1
Theo giả thiết ta có: P M( ) = , ( )P E = , (P ME) = 3 9 4 Do đó: .
Để ý rằng:A = D ∪ME hơn nữa D ∩ (ME) = ∅ nên P D( ) = P A( ) − P ME( ) =
III. XÁC SUẤT CÓ ĐIỀU KIỆN VÀ CÔNG THỨC NHÂN XÁC SUẤT.
1. Xác suất có điều kiện.
a. Định nghĩa: Xác suất của biến cố B được tính khi biết biến cố A nào đó đã xảy ra được gọi là xác
suất có điều kiện và được ký hiệu là P B A( | ). Ký hiệu P B A( | ) thường được đọc là “ xác suất để B
xảy ra với điều kiện A đã xảy ra” hoặc đơn giản là “xác suất của B với điều kiện A”.
Ví dụ 8. Một con xúc xắc được chế tạo sao cho khả năng xuất hiện một chấm chẵn gấp hai lần khả
năng xuất hiện một chấm lẻ. Xét biến cố B nhận được số chính phương khi gieo một con xúc xắc đó.
Từ không gian mẫu Ω = {1,2,3,4,5,6}, với xác suất xuất hiện mỗi số chấm chẵn và lẻ tương ứng
là và , do đó xác suất để B xảy ra là .
Bây giờ ta chỉ xét biến cố B trong phép tung con xúc sắc với số chấm xuất hiện lớn hơn 3. Lúc
này ta xét không gian mẫu thu gọn A = {4,5,6} là tập con của Ω. Ta cần tính xác suất của biến cố B liên
quan đến không gian mẫu A.
+ Trước hết ta phải tính xác suất mới cho các phần tử của A. Khi gán xác suất w cho chấm lẻ trong A
và xác suất 2w cho hai chấm chẵn, ta có 5w = 1 → w = .
+ Trong không gian A, ta thấy B chỉ chứa phần tử 4. Ký hiệu biến cố này bởi B A| , khi đó B A| = {4} → P B A( | ) = .
Chú ý: Như vậy các biến cố có thể có xác suất khác nhau khi được xét trong các không gian mẫu khác nhau.
b. Công thức.
Xác suất có điều kiện của B với điều kiện A, ký hiệu P B A( | ), được xác định như sau: nếu P A( ) > 0 .
Ví dụ 9. (xét lại Ví dụ 8) Một con xúc xắc được chế tạo sao cho khả năng xuất hiện một chấm chẵn
gấp hai lần khả năng xuất hiện một chấm lẻ. Với biến cố A = {4,5,6}, xét biến cố B nhận được số
chính phương khi gieo một con xúc sắc.
Ta có không gian mẫu Ω = {1,2,3,4,5,6}, với xác suất xuất hiện mỗi số chấm chẵn và lẻ tương ứng là và . 2 1 2 5 {4} suy ra P A B . Dễ thấy : P A( ) = + + = , hơn nữa A ∩ B = 9 9 9 9
Khi đó theo công thức trên ta có: 2 P A( ∩ B) 9 = 2. P B A() = = P A( ) 5 5 9
Ví dụ 10. Xác suất để một chuyến bay khởi hành đúng giờ là P D( ) = 0,83, xác suất để nó đến đúng
giờ là P A( ) = 0,82, xác suất để nó khởi hành và đến đều đúng giờ là P D( ∩ A) = 0,78. Tính xác suất để một chiếc máy bay:
a) Đến đúng giờ biết rằng nó đã khởi hành đúng giờ;
b) Khởi hành đúng giờ biết rằng nó sẽ đến đúng giờ.
c) Đến đúng giờ biết rằng nó khởi hành không đúng giờ Giải:
a) Xác suất để một máy bay đến đúng giờ biết rằng nó đã khởi hành đúng giờ là: P D A( ∩ ) 0,78 P A D( | ) = = = 0,94 P D( ) 0,83
b) Xác suất để một máy bay khởi hành đúng giờ biết rằng nó đã đến đúng giờ là: P D A( ∩ ) 0,78 P D A( | ) = = = 0,95 P A( ) 0,82
c) Xác suất để máy bay đến đúng giờ khi nóp khởi hành không đúng giờ là: P A D( ∩ ) 0,82−0,78 P A D( | ) = = = 0,24 P D( ) 0,17
c. Sự độc lập và phụ thuộc của các biến cố. Hai biến cố Avà B được gọi là độc lập với nhau nếu sự
xuất hiện của B không có tác động gì đến khả năng xuất hiện của A. Ở đây sự xuất hiện của A là độc
lập với sự xuất hiện của B .
Định nghĩa: Hai biến cố A và B trong một phép thử được gọi là độc lập với nhau khi và chỉ khi P B
A( | ) = P B( ) hoặc P A B( | ) = P A( ).
Trong trường hợp ngược lại ta nói A và B phụ thuộc nhau.
Điều kiện P B A( | ) = P B( ) kéo theo P A B( | ) = P A( )và ngược lại.
Đối với phép thử là rút con bài ở trên , chúng ta đã chỉ ra rằng P A B( | ) = P A( ) = 1/4 . Chúng
ta cũng có thể thấy rằng P A B( | ) = P A( ) = 1/13 .
2.Công thức nhân xác suất.
Từ công thức xác suất có điều kiện ta nhận được quy tắc nhân quan trọng sau, nó cho phép ta tính
xác suất để hai biến cố cùng xảy ra.
Nếu trong một phép thử, các biến cố Avà B có thể cùng xảy ra thì
P A( ∩ B) = P A P B A( ) () = P B P A B( ) ()
Hai biến cố Avà B là độc lập với nhau khi và chỉ khi
P A( ∩ B) = P A P B( ). ( ).
Tổng quát:
Nếu trong một phép thử, các biến cố A1,...,An có thể xảy ra thì: P A( 1 ∩ ∩ ∩A2
... An )= P A P A( ). (1 2 |A1)... (P Ak |AA1 2...Ak−1).
Nếu các biến cố A1,...,An độc lập thì: P A( 1 ∩ ∩ ∩A2 ... An )= P A P A( ). ( )... (1 2 P An ).
Ví dụ 11. Giả sử ta có một hộp chứa 20 chiếc cầu chì, trong đó có 5 chiếc bị hỏng. Nếu lấy ngẫu nhiên
lần lượt 2 chiếc theo phương thức không hoàn lại, thì xác suất để cả hai chiếc đều bị hỏng bằng bao nhiêu? Giải: Gọi
A là biến cố “chiếc cầu chì thứ nhất bị hỏng”
B là biến cố “chiếc cầu chì thứ hai bị hỏng”
Khi đó A B∩ là biến cố A xảy ra và sau đó B cũng xảy ra, B A|
là biến cố chiếc cầu chì thứ hai lấy
ra là hỏng khi đã lấy được chiếc thứ nhất là hỏng.
Xác suất để lần lấy thứ nhất được chiếc cầu chì hỏng là P A( ) = .
Tiếp theo, xác suất để lấy được một cầu chì hỏng thứ hai từ bốn chiếc còn lại là: P B A( | ) = .
Do đó xác suất để lấy được (theo thứ tự) cả hai chiếc cầu chì hỏng là: P AB() = P A P B A( ) ( | ) = 1 4 = 191 . 4 19
Ví dụ 12. Một thị trấn nhỏ có một chiếc xe cứu hỏa và một chiếc xe cấp cứu sẵn sàng dùng cho những
trường hợp khẩn cấp. Xác suất để chiếc xe cứu hỏa sẵn có để dùng cho những trường hợp khẩn cấp là
0,98 và xác suất để chiếc xe cấp cứu khi được gọi là 0,92. Có một người bị thương do một tòa nhà
đang cháy, tìm xác suất để cả chiếc xe cấp cứu và cứu hỏa đều sẵn sàng có thể dùng.
Giải: Gọi A và B lần lượt là biến cố chiếc máy cứu hỏa và chiếc xe cấp cứu sẵn có để dùng, khi đó
A B∩ la biến cố cả hai xe đều sẵn sàng làm nhiệm vụ.
Nhận thấy: A và B là hai biến cố độc lập do đó ta có:
P AB( ) = P A P B( ). ( ) = 0,98.0,92 = 0,9016.
Ví dụ 13. Lấy liên tiếp 3 con bài từ một bộ bài theo phương thức không hoàn lại. Tìm xác suất để biến cố A
A A xảy ra , trong đó A1 là biến cố con bài thứ nhất là Át đỏ, A2 là biến cố con bài thứ
hai là 10 hoặc J , còn A3 là biến cố con bài thứ ba có số lớn hơn 3 nhưng bé hơn 7.
Giải: Ta có các biến cố
A1 : biến cố con bài thứ nhất là át đỏ,
A2 : biến cố con bài thứ hai là 10 hoặc J,
A3 : biến cố con bài thứ ba có số lớn hơn 3 nhưng bé hơn 7. Khi đó: 2 8 12 P A( )1 = , P A( 2 |A1) = , P A( 3 |AA1 2) = , 52 51 50 và ta có: P A A A P A P A A P A AA .
Ví dụ 14. Hộp thứ nhất có 2 bi trắng và 10 bi đen. Hộp thứ hai có 8 bi trắng và 4 bi đen. Từ mỗi
hộp lấy ra một viên bi. Tìm xác suất để: a) Cả 2 viên bi lấy ra đều trắng
b) Một viên lấy ra là trắng, còn một viên là đen. Giải: Gọi
T là biến cố “cả 2 viên bi lấy ra là trắng”
Ti là biến cố lấy được bi trắng từ hộp thứ i i, = 1,2 Di
là biến cố lấy được bi đen từ hộp thứ i i, =1,2.
A là biến cố một viên bi lấy ra là trắng còn một viên là đen Khi đó: T T , , ,
1 2 ,D D1 2 là các biến cố đôi một độc lập; TD T D1 2 2 1 cũng là hai biến cố độc lập. Ta có T =T1 ∩T2 , A =TD1 2 ∪T D2 1 1 2 P T( )1 = 6, ( )P T2 = 3, 5 1
P D( 1) = 1 − P T( )1 = 6, (P D2) = 1 − P T( )2 = 3
a) Xác suất để cả 2 bi lấy ra đều trắng là:
P T( ) = P TT( 1 2) = P T P T( ) ( )1 2 = .
b) Xác suất để một viên lấy ra là trắng còn một viên là đen
P A( ) = P TD( 1 2) + P T D( 2 1 = P T P D( ) (1 2) + P T P D( ) (2 1) = .
IV.CÔNG THỨC XÁC SUẤT ĐẦY ĐỦ VÀ CÔNG THỨC BAYES.
1. Công thức xác suất đầy đủ.
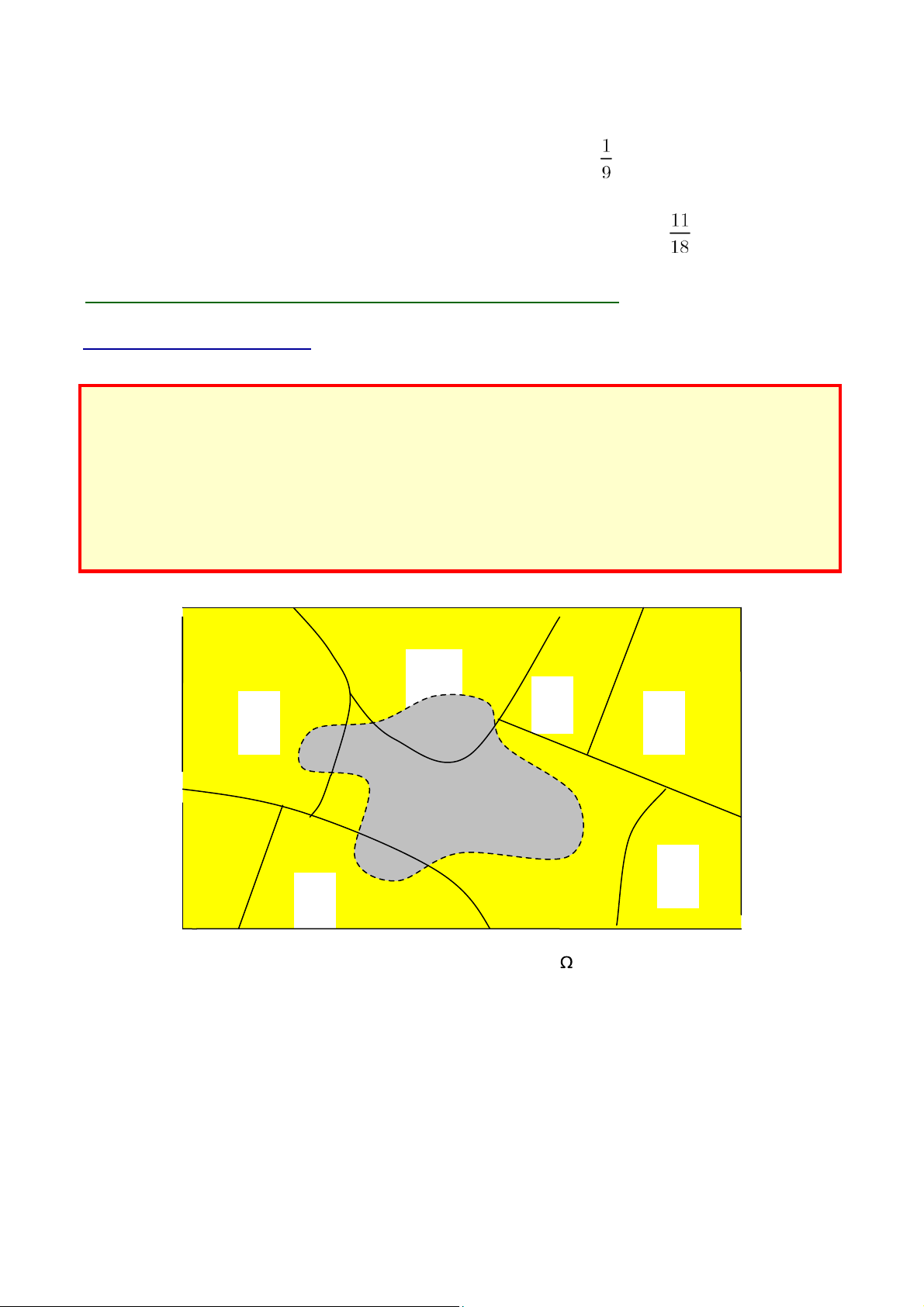
Nếu các biến cố B B1, 2,...,Bk là một phân hoạch của không gian mẫu Ω (tức B B1, 2,...,Bk là nhóm các
biến cố đầy đủ đôi một xung khắc), trong đó P B( )i ≠ 0 với mọi i = 1,2,...,k thì với biến cố A bất kì của Ω ta có: k k
P(A) = P A( )= ∑P B( i ∩A)= ∑P B P A B( ) (i | i). i=1 i=1 B 2 B 3 B 1 B 4 A B n B k
Phân ho ạ ch không gian m ẫ u
Ví dụ 15. Trong một dây chuyền sản xuất, ba máy B1, B2, và B3 tạo ra 30%, 45%, và 25% sản phẩm
tương ứng. Theo phép thử trước đây biết tỷ lệ phế phẩm được tạo bởi mỗi máy tương ứng là 2%, 3%
và 2%. Chọn ngẫu nhiên 1 sản phẩm. Tính xác suất để nó là phế phẩm.
Giải: Xét các biến cố sau:
A: sản phẩm được chọn là phế phẩm
B1 : sản phẩm được làm bởi máy B1: P B( )1 = 0,3
B2 : sản phẩm được làm bởi máy B2: P B( 2)= 0,45
B3 : sản phẩm được làm bởi máy B3: P B( 3)= 0,25
+ Khi đó: B B B1, 2, 3 là họ các biến cố đầy đủ đôi một xung khắc
+ Áp dụng công thức xác suất đầy đủ ta có:
P A( ) = P B P A B( 1) ( | 1) + P B P A B( 2 ) ( | 2) + P B P A B( 3 ) ( | 3) + Ta lại có: P B P A B( ) ( ) 1 | 1 = 0,3. 0,02 = 0,006 P B P A B( ) ( ) 2 | 2 = 0,45.0,03 = 0,0135 P B P A B( ) ( ) 3 | 3 = 0,25.0,02 = 0,005. + Do đó
P A( ) = 0,006 + 0,0135 + 0,005 = 0,0245.
2. Công thức Bayes.
Công thức Bayes, mang tên của linh mục và nhà Toán học người Anh Thomas Bayes (1702 – 1761),
là công thức ngược, cho phép tính xác suất có điều kiện P B A( | ) khi biết xác suất có điều kiện P A B(
| )và một số thông tin khác.
a) Dạng đơn giản nhất của công thức này là: Với A và B là hai biến cố bất kỳ với xác suất khác không, khi đó ta luôn có: P A B P B( | ) ( ) P B A( | ) = . P A( )
Công thức trên là hệ quả trực tiếp từ công thức nhân xác suất:
P A( ∩ B) = P B A P A( | ). ( ) = P A B P B( | ). ( ).
Công thức Bayes rất đơn giản nhưng nó có ý nghĩa rất sâu xa. Một trong những lỗi mà rất nhiều người
mắc phải là lẫn lộn giữa P A B( | ) và P B A( | ), coi hai con số đó như là bằng nhau. Nhưng Công thức
Bayes cho thấy hai con số đó có thể chênh lệch nhau rất nhiều nếu như P A( ) và P B( ) chênh nhau rất nhiều.