Bài tập Toán 6 học kì 2 – Nguyễn Ngọc Dũng

Tài liệu gồm 47 trang, được biên soạn bởi thầy giáo Nguyễn Ngọc Dũng, tóm tắt lý thuyết và tuyển chọn các bài tập Toán 6 giai đoạn học kì 2 (HK2). Mời mọi người đón xem.

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 6

Môn: Toán 6

Thông tin:

47 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
MỤC LỤC
Phần I Số học - Trang 3
Chương 2 Số nguyên Trang 5
Bài 1 Tập hợp các số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bài 2 Phép cộng số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Bài 3 Phép trừ số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Bài 4 Quy tắc dấu ngoặc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Bài 5 Quy tắc chuyển vế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Bài 6 Phép nhân và chia hai số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Bài 7 Tính chất của phép nhân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Chương 3 Phân số Trang 21
Bài 1 Khái niệm phân số. Phân số bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Bài 2 Tính chất cơ bản của phân số. Rút gọn phân số . . . . . . . . . . . . . . . . . . . . . . . . 22
Bài 3 Quy đồng mẫu số nhiều phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Bài 4 So sánh phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Bài 5 Phép cộng và trừ phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Bài 6 Luyện tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Bài 7 Phép nhân phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Bài 8 Phép chia phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Bài 9 Hỗn số. Số thập phân. Phần trăm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Bài 10 Tìm giá trị phân số của một số cho trước . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Bài 11 Tìm một số biết giá trị một phân số của nó . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Bài 12 Tìm tỉ số của hai số ........................................................ 34
Page 1 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Bài 13 Biểu đồ phần trăm ........................................................ 34
Phần II Hình học - Trang 37
Chương 2 Góc Trang 39
Bài 1 Nửa mặt phẳng. Góc, số đo góc ........................................ 39
Bài 2 Khi nào thì
’
xOy +
‘
yOz =
‘
xOz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Bài 3 Tia phân giác của góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
Page 2 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
PHẦN
I
SỐ HỌC
3
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
2
Chương
Số nguyên
Học sinh quét mã QR để tham gia nhóm học tập:
Nhóm TOÁN QUẬN 7
Trọng tâm chương:
• Biết được tập hợp các số nguyên, so sánh được hai số nguyên.
• Tính được giá trị tuyệt đối của một số nguyên.
• Cộng, trừ, nhân, chia số nguyên.
• Tìm x.
• Biết sử dụng quy tắc dấu ngoặc và quy tắc chuyển vế.
| Bài 1. Tập hợp các số nguyên
A KIẾN THỨC CẦN NHỚ
• Các số nguyên dương là: 1; 2; 3; 4; . . .
• Các số nguyên âm là: −1; −2; −3; −4; . . .
• Tập hợp các số nguyên gồm các số nguyên âm, số 0 và các số nguyên dương.
• Kí hiệu Z = {. . . − 3; −2; −1; 0; 1; 2; 3; . . .}.
• Số 0 không phải số nguyên âm cũng không phải số nguyên dương.
• Các số 1 và −1; 2 và −2; 3 và −3; . . . là các số đối nhau.
• Số đối của 0 là 0;
• Giá trị tuyệt đối của mọi số nguyên khác 0 đều là số nguyên dương (giá trị tuyệt
đối của 0 là 0).
5
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Điền chữ Đ (đúng) hoặc chữ S (sai) thích hợp vào ô trống:
7 ∈ N ;a 0 ∈ Z ;b 15, 3 ∈ Z ;c −2 ∈ N ;d
0 ∈ N ;e −10 ∈ N ;f 5 ∈ N ;g −4, 03 ∈ Z ;h
100200 ∈ Z ;i 1250000 ∈ N ;j 27 ∈ N ;k 72 ∈ Z .l
d Bài 2. Tìm các số đối của
−1;a 8;b
0;c 10;d
−2;e
+5;f −25;g −9;h 18;i −20.j
d Bài 3. Tìm giá trị tuyệt đối của mỗi số sau:
−2000;a −13;b −15;c 2311;d −9.e
d Bài 4. Điền vào chỗ trống các dấu ≥, ≤, >, <, =:
| − 99| |99|;a | − 30| 0;b 0 | − 1|;c |1| | − 105|;d
−|12| −|−11|;e |5| | − 5|;f |6| | − 7|;g | − 15| |20|.h
d Bài 5. Điền vào chỗ trống các dấu ≥, ≤, >, <, =:
−2 − 5;a −6 − 1;b 0 − 3;c −99 − 100;d
−542 − 263;e 100 − 100;f | − 50| 0;g 0 | − 9|;h
|6| | − 101|;i −|16| − | −16|.j
d Bài 6. Tính giá trị của biểu thức
| − 34| + |13|;a 513 + | − 742|;b | − 16| · |5|;c 100 − | − 25 | + | −
35|;
d
|9 − 8|;e |4 − 4|;f | − 5| + | − 9|;g | − 7| − | − 4|;h
|
| − 5|
|
;i |−2|+|−3|+|−4 |;j |5|+|−10|+|−15|;k | − 8| · |2|;l
| − 4| · | − 5|;m |18| : | − 2|;n | − 20| : |4|;o
| + 2018| + | − 2016| : | − 3|.p
d Bài 7. Sắp xếp các số sau theo thứ tự tăng dần (nhớ tăng dần là từ nhỏ đến lớn nhé):
Page 6 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
5; −15; 8; 3; −1; 0a −102; 16; 0; 8; −9; 2012b
2017; −2018; 0; −100; −7; 1c 123; −47; 0; −91; 14; −8d
0; −5; 7; −10; 15; −50e 28; −127; 0; −15; 20; −1f
2017; 0; −9; −2018; 6g −2; 14; −9; 0; 1; | − 3|h
d Bài 8. Sắp xếp các số sau theo thứ tự giảm dần (nhớ giảm dần là từ lớn đến nhỏ nhé):
−3; −1; 0; −2; 5; −13; 17; −99; 100a −97; 10; 0; 4; −9; 2000b
−129; 0; 35; −98; 27; −3c | − 5|; 0; 15; −1; −2018d
d Bài 9. Tìm x ∈ Z, biết
−10 < x ≤ 1;a −2 ≤ x ≤ 2;b −2 < x < 5;c −6 ≤ x ≤ −1;d
0 < x ≤ 7;e −1 < x < 6;f −6 < x < −2;g −2 < x < 2.h
d Bài 10. Tìm x ∈ Z, biết
|x| = 0;a |x| = −8;b 156 − x = | − 27|.c
| Bài 2. Phép cộng số nguyên
A KIẾN THỨC CẦN NHỚ
• Cộng hai số nguyên dương chính là cộng hai số tự nhiên.
• Cộng hai số nguyên âm ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu "−" trước
kết quả.
• Hai số nguyên đối nhau có tổng bằng 0.
• Muốn cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt
đối của chúng (số lớn trừ số nhỏ) rồi đặt trước kết quả tìm được dấu của số có giá
trị tuyệt đối lớn hơn.
• Tính chất giao hoán: a + b = b + a.
• Tính chất kết hợp: (a + b) + c = a + (b + c ).
• Cộng với số 0: a + 0 = a.
• Cộng với số đối: a + (−a) = 0.
Page 7 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Tính:
(+2) + (+5);a (+3) + (+17);b (+12) + (+7);c (−3) + (−7);d
(−16) + (−13);e (−25) + (−4);f (−30) + (−14);g (−6) + (−54).h
d Bài 2. Tính:
(−7) + (−14);a (−35) + (−9);b (−30) + (−5);c (−7) + (−13);d
(−37) + (−112);e (−5) + (−248);f 17 + | − 33|;g | − 37| + | + 15|.h
d Bài 3. Tính:
| − 35| + 18;a 15 + | − 55|;b 215 + 1025;c (−56) + (−15);d
(−12) + (−58);e | − 30| + 12;f 25 + | − 56|;g 234 + 4567;h
(−3) + (−9);i (−42) + (−54);j 12 + | − 25|.k
d Bài 4. Tính:
(−15) + (−|5|) + (−| − 23|) + (−9);a 11 + | − 11| + 0 + |10| + | − 10|;b
| − 3| + (−23) + (−10) + | − 51| + | − 49|.c
d Bài 5. Tính:
(−9) + | − 11|;a 42 + (−22);b (−25) + 25;c
262 + (−138);d 105 + (−150);e 22 + (−42);f
(−99) + 99;g (−85) + 40;h (−34) + 24 + (−7) + 27;i
99 + (−100) + 101;j 15 + 5 + (−8) + (−12);k (−2009) + 0;l
15 + (−14);m (−42) + 22;n 35 + (−135);o
−12 + | − 25|;p | − 22| + (−44);q | − 2| + (−| − 9|);r
(−9) + 10 + (−10) + (−45) + 55.s
d Bài 6. Tính:
Page 8 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
(−101) + (−399);a (−315) + (−1477);b
(−404) + 1002;c 21 + (−26) + 31 + (−36);d
17 + 100 + (−7);e (−74) + 124 + 131;f
(−99) + 114 + (−1);g 247 + (−30) + (−217);h
328 + [54 + (−44)];i (−125) + 125 + (−32);j
(−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4.k
d Bài 7. Tính tổng tất cả các số nguyên x thỏa mãn
−6 < x < 6;a −5 < x < 0;b −1 < x ≤ 4;c −10 < x < 5;d
−10 ≤ x ≤ 10;e −2009 < x < 2010;f −5 < x < 5;g −6 < x < 0 .h
d Bài 8. Tính tổng tất cả các số nguyên x thỏa mãn
−8 < x < 0 ;a −4 ≤ x ≤ 4;b −100 < x < 99;c −3 < x < 3;d
−5 < x ≤ 4;e −5 ≤ x ≤ 5;f −4 ≤ x < 3;g −6 < x < 6;h
−5 < x < 0;i −2 ≤ x < 5;j −10 < x < 5;k −10 ≤ x ≤ 10.l
d Bài 9. Tính hợp lý
328 + [54 + (−328) + (−44)];a (−125) + [432 + 125 + (−32)];b
647 + [88 + (−647) + 912] + (−1000);c (−540) + 2010 + (−460) + 1000;d
(−132) + [(−868) + (−234) + 1234] + 200;e (−101) + (−500) + (−399);f
(−200)+(−185)+1777+(−315)+(−1477);g (−404) + 1002 + (−2000) + 1998 + (−596);h
(−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 +
2 + 3 + 4;
i
1 + (−6) + 11 + (−16) + 21 + (−26) + 31 +
(−36).
j
d Bài 10. Tính hợp lý
(−135) + [128 + (−28) + (−47)];a (−75) + [232 + 75 + (−32)];b
526 + [88 + (−526) + 12];c 38 + [(−140) + 62 + (−860)] + 1000;d
(−199) + (−200) + (−201);e 217 + [43 + (−217) + (−23)];f
1 + (−3) + 5 + (−7) + 9 + (−11);g 248 + (−12) + 2064 + (−236);h
(−150) + [235 + 150 + (−35)].i
Page 9 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 11. Tìm x ∈ Z, biết
13 + |x| = | − 6| + 17;a |x| − 7 = −12;b x − | − 58| = 136 + 27;c
12 + x = | − 24| + | − 36|;d |x| + 25 = 56 + | − 8|;e |x| − 13 = −49.f
d Bài 12. Tính tổng:
a C = (−1) + 5 + (−9) + 13 + . . . + (−81) + 85;
b D = (−1) + 2 + (−3) + 4 + (−5) + 6 . . . + (−2013) + 2014.
d Bài 13. Một con chim đang ở vị trí 22 m so với mặt đất, nó bay cao lên 19 m nữa. Tính
độ cao của con chim so với mặt đất sau khi bay lên.
d Bài 14. Một con cá chuồn đang ở vị trí −2 m so với mực nước biển, nó bay cao lên 5 m
nữa. Tính độ cao của con cá chuồn sau khi bay lên.
d Bài 15. Một tòa nhà có 12 tầng và 3 tầng hầm (tầng trệt được đánh số là tầng 0), hãy
dùng phép cộng các số nguyên để diễn tả tình huống sau: Một thang máy đang ở tầng số 3,
nó đi lên 7 tầng và sau đó đi xuống 12 tầng. Hỏi cuối cùng thang máy dừng lại ở tầng mấy?
d Bài 16. Một chiếc tàu ngầm đang ở vị trí −200 m so với mực nước biển, tàu tiếp tục bơi
lên phía trên thêm 35 m nữa. Hỏi lúc này tàu ngầm sẽ ở vị trí nào?
| Bài 3. Phép trừ số nguyên
A KIẾN THỨC CẦN NHỚ
• Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b:
a − b = a + (−b)
• Hai dấu trừ liền nhau đổi thành một dấu cộng:
a − (−b) = a + b
• Số hạng bằng tổng trừ số hạng kia.
• Số bị trừ bằng hiệu cộng số trừ.
• Số trừ bằng số bị trừ trừ hiệu.
Page 10 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Tính:
−7 − 9;a −15 − 8;b −28 − 32;c −43 − 26;d
−5 − 9 − 11;e −6 − 8 − 13;f −3 − 7 − 25;g −7 − 4 − 15.h
d Bài 2. Tính:
1 − (−2);a (−3) − 4;b (−3) − (−4);c 5 − (7 − 9);d (−3)−(4−6).e
d Bài 3. Tính
(−9) − (−8);a 0 − (−9);b (−8) − 0;c
(−7) − (−7);d 10 − (−3);e 12 − (−14);f
(−21) − (−19);g (−18) − 28;h 13 − 30;i
9 − (−9);j 8 − (3 − 7).k
d Bài 4. Tính
126 + (−20) + 2004 + (−106);a (−199) + (−200) + (−201);b
1 + (−3) + 5 + (−7) + 9 + (−11);c (−2) + 4 + (−6) + 8 + (−10) + 12;d
483 + (−56) + 263 + (−64);e −87 + (−12) − (−487) + 512.f
d Bài 5. Tính
(−30) + (−23);a −52 + 102;b (−89) − 9;c 10 − | − 15| + |0|;d
3 − | − 14|;e −| − 8| − (−3);f 0 − | − 18| + |0|;g −| − 2| − | − 7|;h
28 + 42;i (−56) + | − 32|;j 40 − | − 14|;k | − 4| + | + 15|;l
88 + (−23);m 13 + | − 13|;n −43 − 26;o |30| − | − 17|;p
13 − 117 + 45 − (−|155|) − (−| − 171|).q
d Bài 6. Tìm x ∈ Z, biết
x + 9 = 2;a x + 10 = −14 ;b x + 5 = 0;c x + 9 = 2;d
2 − x = 17 − (−5);e x−12 = (−9)−15;f 37+x = 48+(−23);g 18−x = 11−(−24).h
d Bài 7. Tìm x, biết
Page 11 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
|x + 3| = 7;a |3x + 9| = 42;b |2x + 6| = 12;c
|x − 4| = | − 10|;d |3x + 9| − 15 = 27;e |x| + 1 = 3;f
−10 − |5 − x| = −12;g 13 · |x| = | − 13|;h 5 · |x + 4| = 20.i
d Bài 8. Tìm x ∈ Z, biết
x + 5 = 0;a (−4) − x = −9;b x − 18 = −18;c
x + 9 = 3;d x − (−4) = −6;e −18 + (12 − x) = −2;f
15 − (2 − x) = 5;g |x| = 11;h |x + 7| = 13;i
|x − 6| + 4 = 8;j 7 + (−x) = (−5) − (−14);k 7 − x = 5 − (−14);l
−18 + x = −8 + 13.m
d Bài 9. Tìm x, biết
−(−30) − (−x) = 13;a −(−x) + 14 = 12;b x + 20 = −(−23);c
15 − x + 17 = −(−6) + | −
12|;
d −| − 5| − (−x) + 4 = 3 −
(−25);
e |x| = 5;f
|x − 3| = 1;g |x + 2| = 4;h 3 − |2x + 1| = (−5).i
d Bài 10. Tính hợp lý
371 + 731 − 271 − 531;a 57+58+59+60+61−17−18−19−20−21.b
d Bài 11. Tính (hợp lý nếu có thể)
|(−9) + (−3)| · 5 + (−65);a | − 13| − (−7) + (−16);b
2018 + 2 ·
400 − (25 − 10)
2
;c
2
10
:
2
5
· 7 − 2
5
· 5

− (−2017)
0
.d
d Bài 12. Tính tuổi thọ của nhà bác học Ác-si-mét, biết rằng ông sinh năm −287 và mất
năm −212.
d Bài 13. Chiếc diều của bạn Minh bay cao 15 m (so với mặt đất). Sau một lúc, độ cao của
chiếc diều tăng 2 m, rồi sau đó lại giảm 3 m. Hỏi chiếc diều ở độ cao bao nhiêu (so với mặt
đất) sau hai lần thay đổi?
| Bài 4. Quy tắc dấu ngoặc
A KIẾN THỨC CẦN NHỚ
Page 12 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Khi bỏ dấu ngoặc
• Có dấu “−” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “−”
thành dấu “+” và dấu “+” thành dấu “−”.
34 − (12 + 20 − 7) = 34 − 12 − 20 + 7 = 22 − 20 + 7 = 2 + 7 = 9.
• Có dấu “+” đằng trước thì tất cả các số hạng vẫn giữ nguyên.
7 + (13 + 2 − 7) = 7 + 13 + 2 − 7 = 20 + 2 − 7 = 22 − 7 = 15.
B BÀI TẬP
d Bài 1. Phá ngoặc theo quy tắc
−(−8);a −(+5);b −(−7);c +(−25);d
+(+30);e −(+20);f −(−14);g −(−5) + (−12);h
−(−13) − (−10);i −(+15) − (−12);j −15 − (+9);k (−11) − (−13);l
−(−3 + 7 − 6);m +(−4 − 3 + 5);n −(5 − 9 + 8 − 3);o −(−9+15−4+7).p
d Bài 2. Tính
−(−5) + (−12);a −(−13) − (−10);b −(+15) − (−12);c −15 − (+9);d
4 − (−7);e (−11) − (−13);f (+4) + (−7);g −| − 13| + | − 15|;h
−| + 12| + (−14);i −(−17) − | + 15|.j
d Bài 3. Tính tổng:
−(−5) − (+7) + (+3) + (−8);a −| − 10| − (−12) + (−18) − (+3);b
−12 − (−9) − (+15) + (+14);c −(+15) + (−14) + | − 12| − (−8);d
−| − 3| − | + 7| + | − 2| − (−14);e −(−15) − | − 10| + | − 9| − | − 5|;f
14 − (−13) − (+17) + (−12);g (−12) − (−7) − (−21) + (−32);h
−| − 14| + | − 10| − (−12) + (−8);i −(−11) + (−5) + (+13) − 21.j
d Bài 4. Bỏ ngoặc rồi tính
Page 13 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
(27 + 65) + (346 − 27 − 65);a (42 − 69 + 17) − (42 + 17);b
(4 + 32 + 6) + (10 − 36 − 6);c (77 + 22 − 65) − (67 + 12 − 75);d
−(−21 + 43 + 7) − (11 − 53 − 17);e (−2014) − (148 − 2014);f
(18 + 29) + (158 − 18 − 29);g (13 − 135 + 49) − (13 + 49).h
d Bài 5. Tính hợp lý:
(2736 − 75) − 2736;a (−2002) − (57 − 2002);b
(5674 − 97) − 5674;c (−1075) − (29 − 1075).d
d Bài 6. Tính hợp lý:
(83 + 234) − (34 − 17);a (401 − 98765) + (98764 − 408);b
(91 − 99 + 98) − (−99 + 98);c (99 − 98 + 97) − (99 + 97 + 98);d
645 + [64 + (−645) + 36];e [24 + (−67)] − [−67 − (−24)].f
d Bài 7. Tính hợp lý
(−283 + 4568) − 4568;a (−46785) − (1500 − 46785);b
12345 − (−314 + 12345);c (38 + 76) + (456 − 38 − 76);d
(31 − 59 + 28) − (31 + 28);e (−9) + (9 − 2009) + 2009.f
d Bài 8. Tính
5 + [−(−12) + (−9)] − [ 7 − (−10) + 3];a [5 − (−4) + (−7)] − [−(−8) + (−9) + 1];b
13 − [5 − (4 − 5) + 6] − [3 − (2 − 7)];c (14 − 12 − 7) − [−(−3 + 2) + (5 − 9)].d
| Bài 5. Quy tắc chuyển vế
A KIẾN THỨC CẦN NHỚ
• Khi chuyển một số hạng từ vế này sang vế kia của đẳng thức, ta phải đổi dấu số
hạng đó: dấu “+” thành dấu “−” và dấu “−” thành dấu “+”.
A + B + C = D Ñ A + B = D − C
• Phương pháp giải toán tìm x: Phá ngoặc, sau đó chuyển x sang vế trái và số sang
vế phải.
Page 14 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Tìm x, biết
x + (−5) = −(−7);a x − 8 = −10;b x − (−12) = 14;c
−(−30) − (−x) = −(+13);d −(+12) − (+x) = 20;e (−34) − x = −(−45);f
−15 − x = −(−7);g x − (−10) = −14;h −x + (−15) = −13;i
16 + x = −(−15);j 7 − x = 8 − (−7);k x − 8 = (−3) − 8;l
2 − x = 17 − (−5);m x − 12 = (−9) − 15.n
d Bài 2. Tìm x, biết:
5x + 17 = x − 47;a −2x − 15 = x − 6;b
11 − (27 − 3) = x − (13 − 4);c 4 − (27 − 3) = x − (13 − 4);d
2 − x = 17 − (−5);e x − 12 = (−9) − 15;f
9 − 25 = (7 − x) − (25 + 7).g
d Bài 3. Tìm x, biết
−(+8) + (11 − x) = 10;a x + | − 5| + | + 7| = −(−9);b 15 − x = |13| − (−4);c
x − | − 3| = −9 + | − 8|;d −| − 2| − x = 8 − | − 9|;e | − 5| − x + (−11) = −3.f
d Bài 4. Tìm số nguyên x, biết:
9 − 25 = (7 − x) − (25 + 7);a 11 − (15 + 11) = x − (25 − 9);b
4 − (27 − 3) = x − (13 − 4);c (−10 + 5) − (4 − x) = 12 − (5 − 6).d
d Bài 5 (?). Tìm số nguyên x, biết:
x − (17 − x) = x − 7.
d Bài 6. Tìm x, biết:
|x| = 2;a |x + 2| = 0;b
|x + 3| = 7;c |x − 5| = (−5) + 8 ;d
|x + 3| − 9 = −5;e |x − 2| − 6 = 9;f
|x − 1| − 7 = 12;g |x + 7| = | − 7| + 13 − (−4);h
3 + |x + 5| = 11 − 2;i |x + 3| − (−5) = 13 − (+4).j
d Bài 7. Tìm x, biết:
(|x| + 73) − 26 = 70;a |x − 7| − (−15)
0
= | − 6|;b
3 · 2
3
− |x| = 4
2
.c
Page 15 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 6. Phép nhân và chia hai số nguyên
A KIẾN THỨC CẦN NHỚ
Quy tắc nhân và chia hai số nguyên:
• Cùng dấu Ñ Dương.
• Khác dấu Ñ Âm.
B BÀI TẬP
d Bài 1. Tính
(−225) · 8;a (−7) · 8;b 6 · (−4);c
(−12) · 12;d 450 · (−2);e (−260) : (−20);f
(−100) : (−5);g (+5) · (+11);h (−6) · 9;i
23 · (−7);j (+4) · (−3);k (−250) · (−8);l
(−2500) : (−100);m (−11)
2
;n (−5)
2
;o
(−2)
3
;p (−4)
3
;q (−42) : 2;r
10 : (−10);s (−51) : 17.t
d Bài 2. Tìm x, biết
(−8) · x = −72;a 6 · x = −54;b (−4) · x = −40;c
(−6) · x = −66;d 12 · x = −36;e (15 − 22) · x = 49;f
(3 + 6 − 10) · x = 200.g
d Bài 3. Tính hợp lý (nếu có thể)
(−15) + 13 + 15 ·
6
2
− 35
;a (−6)
2
· 5 + (−4)
2
: 16 ;b
7 · (−8)
2
+ (−3)
3
+ | − 2016|
0
;c
(−2)
2
· 2
3
− 3
5
+ 3
5
+ 2009
0
− (−1)
101
;d
(−5)
2
· 4 + 108 : (−3)
3
;e (−6 − 3) · (−6 + 3);f
(−5 + 8) · (−7);g (−4 − 14) : (−3);h
(−8)
2
· 3
3
;i 9
2
· (−5)
4
;j
| − 20| : (−5) − 2 · |3 − 5|.k
Page 16 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 4. Tìm x, biết:
26 − 3x = 5;a −3x + 19 = 10;b
x + 87 = −13;c 4 − x = −10;d
5 − x = −17;e 2x + 36 = 6;f
128 − 3(x + 4) = 23;g 75 − 5(x − 7) = 105 ;h
2(x + 5) + 8 = −| − 3| − 13;i 2016
0
− 5x = −49;j
2 · x + (−73) = −29;k
14 + 3 · (7 − x) = 20;l
2 · x − 18 = 10;m 3x + 26 = 5;n
35 − 5 · (x + 3) = | − 15|;o | − 140| : (x − 8) = |7|;p
2x + (−49) = (−5) · 3
2
.q
d Bài 5.
Trong trò chơi bắn bi vào các hình trong hình vẽ trên mặt đất (như
hình bên), bạn Hải bắn được hai viên điểm 5, một viên điểm 10, ba
viên điểm −3 và một điểm −5. Bạn Dũng bắn được ba viên điểm 5,
một viên điểm −5 và ba viên điểm 0 . Hỏi bạn nào điểm cao hơn.
−5
10
5
0
−3
d Bài 6. Một xí nghiệp may gia công có chế độ thưởng và phạt như sau: Một sản phẩm tốt
được thưởng 50 000 đồng. Một sản phẩm có lỗi bị phạt 40 000 đồng. Tháng vừa qua chị Mai
làm được 40 sản phẩm tốt và 8 sản phẩm có lỗi. Hỏi lương chị Mai trong tháng vừa qua là
bao nhiêu tiền.
d Bài 7. Một bạn học sinh làm bài kiểm tra Anh văn đầu vào để xếp lớp ở trung tâm anh
ngữ. Bạn buộc phải làm hết 50 câu hỏi, với cách tính điểm như sau: Mỗi câu đúng bạn được
2 điểm, mỗi câu sai bạn bị trừ 1 điểm. Với 40 câu đúng và 10 câu sai, các em hãy tính số
điểm bạn đạt được cho bài kiểm tra Anh văn này.
d Bài 8. Mỗi ngày Mai được mẹ cho 20 000 đồng, Mai ăn sáng hết 10 000 đồng, Mai mua
nước ngọt hết 5 000 đồng, phần tiền còn lại Mai để vào tủ tiết kiệm. Hỏi sau 15 ngày, Mai có
bao nhiêu tiền tiết kiệm.
d Bài 9. Hai ô tô cùng xuất phát từ thành phố A. Ô tô thứ nhất đi đến thành phố B với vận
tốc 45 km/h, còn ô tô thứ hai đi đến thành phố C với vận tốc 50 km/h. Biết rằng ba thành
phố cùng năm trên một đường thẳng và thành phố A nằm giữa hai thành phố B và C. Hỏi
sau khi cả hai ô tô đi được 2 giờ thì hai ô tô cách nhau bao nhiêu km?
Page 17 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 7. Tính chất của phép nhân
A KIẾN THỨC CẦN NHỚ
a Tính chất giao hoán
a · b = b · a
b Tính chất kết hợp
(a · b) · c = a · (b · c)
c Nhân với số 1
a · 1 = 1 · a = a
d Tính chất phân phối của phép nhân đối với phép cộng
a · (b + c) = a · b + a · c
e Tính chất phân phối của phép nhân đối với phép trừ
a · (b − c) = a · b − a · c
B BÀI TẬP
d Bài 1. Dùng tính chất phân phối của phép nhân với phép cộng để tính
5 · (−3 + 2) − 7 · (5 − 4);a −3 · (4 − 7) + 5 · (−3 + 2);b
4 · (5 − 3) + 2 · (−4 + 6);c −8 · (4 − 5) + 7 · (8 − 4).d
d Bài 2. Tính nhanh
26 · (−125) − 125 · (−36);a 20 · 17 − 4 · 5 · 7;b
100 · 23 − 25 · 23 · 4;c 48 − 6 · (12 + 8);d
54 − 6 · (17 + 9).e
d Bài 3. Tính
(26 − 6) · (−4) + 31 · (−7 − 13);a (−18) · (55 − 24) − 28 · (44 − 68).b
d Bài 4. Tính nhanh
(−4) · (+3) · (−125) · (+25) · (−8);a (−67) · (1 − 301) − 301 · 67.b
Page 18 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 5. Thực hiện phép tính (tính nhanh nếu có thể)
33 · (17 − 5) − 17 · (33 − 5);a (−39) · 217 + 217 · (−61);b
(−79) · 79 + 79 · (−21);c 3 · (−5)
2
+ 2 · (−6)
0
− 56 : 7;d
(−98) · (1 − 246) − 246 · 98.e
Page 19 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Page 20 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
3
Chương
Phân số
Học sinh quét mã QR để tham gia nhóm học tập:
Nhóm TOÁN QUẬN 7
| Bài 1. Khái niệm phân số. Phân số bằng nhau
A KIẾN THỨC CẦN NHỚ
• Phân số có dạng
a
b
với a, b ∈ Z, b 6= 0 , a là tử số, b là mẫu số của phân số.
• Nếu
a
b
=
c
d
thì a · d = b · c (tích chéo bằng nhau).
B BÀI TẬP
d Bài 1. Viết các phân số sau:
Bốn phần mười một;a Âm chín phần tám;b
Mười hai phần năm;c Âm bảy phần ba;d
Hai phần bảy;e Âm năm phần chín;f
Mười một phần mười ba;g Mười bốn phần năm;h
Một phần hai;i Mười chín phần bảy.j
d Bài 2. Viết các phép chia sau dưới dạng phân số:
3 : 2;a 3 : 11;b (−4) : 7;c 5 : (−13);d 9 : (−13);e
(−6) : (−11);f 1 : 3;g 2 : 5;h (−3) : 7;i (−7) : 9;j
4 : (−9);k 2 : (−7);l (−3) : (−8);m (−2) : (−11);n
x chia cho 3 (x ∈ Z);o 5 chia cho a (a ∈ Z, a 6= 0).p
d Bài 3. Tìm các số nguyên x, y, z biết rằng
21
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
x
5
=
16
40
;a
y
25
=
−2
5
;b
x
7
=
6
21
;c
−5
y
=
20
28
;d
4
−x
=
8
6
;e
−10
y
=
30
33
.f
d Bài 4. Tìm các số nguyên x, y, z biết rằng
x
45
=
−8
15
;a
x
3
=
−14
21
;b
x
7
=
−14
49
;c
4
x
=
2
25
;d
−7
3
=
x
15
;e
−6
y
=
3
−7
;f
80
−96
=
−x
6
;g
−7
14
=
5
x
;h
x
10
=
−7
5
.i
d Bài 5. Tìm các số nguyên x, y, z biết rằng
x
3
=
20
y
= 4 ;a
9
−x
=
y
5
= −3 ;b
−4
x
=
3
y
=
−1
2
;c
x
2
=
−y
3
=
z
−4
=
−18
9
;d
15
x
=
y
4
=
z
16
=
6
−8
;e
−6
12
=
x
8
=
−7
y
=
z
−18
.f
d Bài 6. Tìm x, y biết
x − 2
12
=
−4
3
;a
63
x − 7
=
3
147
;b
2x − 2
3
=
−10
15
;c
x − 1
7
=
15
21
;d
3x − 1
12
=
5
3
;e
x + 3
15
=
1
3
.f
d Bài 7. Tìm x, y biết
6
x
=
4
x + 27
;a
x
7
=
x + 16
35
;b
x − 2
4
=
5 + x
3
;c
6
x
=
24
x − 27
.d
| Bài 2. Tính chất cơ bản của phân số. Rút gọn phân số
A KIẾN THỨC CẦN NHỚ
• Nhân cả tử và mẫu cho một số khác 0:
a
b
=
a · m
b · m
(m 6= 0).
• Chia cả tử và mẫu cho một số khác 0:
a
b
=
a : n
b : n
(n 6= 0).
Page 22 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Điền số thích hợp vào ô trống:
2
3
=
60
;
a
3
4
=
60
;
b
4
5
=
60
;c
5
6
=
42
;d
1
4
=
20
;e
−3
4
=
15
;f 1 =
2
=
−4
=
6
=
−8
=
10
.g
d Bài 2. Ta có thể biết được 25 phút chiếm bao nhiêu phần của một giờ bằng cách đổi
25 phút =
25
60
giờ =
5
12
giờ.
Các số phút sau đây chiếm bao nhiêu phần của một giờ:
15 phút;a 30 phút;b 45 phút;c 20 phút;d
40 phút;e 10 phút;f 5 phút;g 2 phút.h
d Bài 3. Rút gọn các phân số sau:
30
−84
;a
−3
21
;b
−9
24
;c
−6
−9
;d
−8
10
;e
45
25
;f
36
24
;g
40
55
;h
−28
40
;i
15
−45
;j
56
70
;k
−18
90
.l
d Bài 4. Rút gọn các phân số sau:
2 · 14
7 · 8
;a
3 · 5
8 · 24
;b
12 · 5
3 · 12
;c
3 · 7 · 11
22 · 9
.d
d Bài 5. Bộ răng đầy đủ của một người trưởng thành có 32 chiếc trong đó có 8 răng cửa, 4
răng nanh, 8 răng cối nhỏ và 12 răng hàm. Hỏi mỗi loại chiếm mấy phần của tổng số răng?
(Viết dưới dạng phân số tối giản)
| Bài 3. Quy đồng mẫu số nhiều phân số
A KIẾN THỨC CẦN NHỚ
Các bước quy đồng mẫu nhiều phân số với mẫu số dương:
• Tìm mẫu số chung (số chia hết cho tất cả các mẫu).
• Tìm thừa số phụ (lấy mẫu chung chia cho từng mẫu).
• Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
# Ví dụ 1. Quy đồng mẫu các phân số sau:
5
12
và
7
−30
.
Page 23 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Quy đồng mẫu số các phân số sau:
1
5
và
3
10
;a
1
7
và
5
14
;b
3
4
và
5
−6
;c
1
6
và
−1
4
;d
7
20
và
−3
5
;e
2
5
và
−3
25
;f
3
−8
và
5
12
;g
7
24
và
−2
3
;h
−1
5
và −6;i
−1
−2
và
−3
4
.j
d Bài 2. Thực hiện quy đồng mẫu các phân số sau:
7
30
;
13
60
và
−9
40
;a
17
60
;
−5
18
và
−64
90
;b
−4
7
;
8
9
và
−10
21
;c
−6
−35
;
27
−180
và
−3
−28
.d
d Bài 3. Thực hiện quy đồng mẫu các phân số sau:
2
9
;
5
18
và
1
3
;a
7
15
;
1
5
và
−5
6
;b
−7
40
;
5
60
và
−1
30
;c
−3
16
;
5
24
và
−21
56
;d
−4
7
;
8
9
và
−10
21
;e
3
−20
;
−11
−30
và
7
15
.f
d Bài 4. Quy đồng các phân số sau:
15
28
và
−17
30
;a
17
320
và
−9
80
;b
−7
−10
và
1
33
;c
−6
35
;
27
−180
và
−3
28
;d
3;
−3
5
và
−5
6
;e
−5
−14
;
3
20
và
9
70
;f
−2
5
;
3
25
và
−1
3
;g
5
12
;
−3
8
;
−2
3
và
7
24
.h
d Bài 5. Quy đồng các phân số sau:
−31
36
và
13
60
;a
1
2
;
−7
9
và
11
12
;b
2
−7
;
1
3
và
2
5
;c
−1
5
;
14
20
và
6
21
;d
−7
21
;
1
−3
và 1;e
−1
5
;
3
−12
và
3
−4
.f
| Bài 4. So sánh phân số
A KIẾN THỨC CẦN NHỚ
Hai phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Các bước so sánh:
• Quy đồng mẫu số.
• So sánh hai phân số cùng mẫu.
Page 24 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. So sánh các phân số sau:
7
36
và
24
36
;a
−3
10
và
7
−10
;b
14
21
và
60
72
;c
−4
7
;
8
9
và
−10
21
;d
7
30
;
13
60
và
−9
40
;e
5
21
;
−3
28
và
−45
108
.f
d Bài 2. a Thời gian nào dài hơn:
2
3
giờ hay
4
5
giờ?
b Đoạn nào ngắn hơn:
2
3
mét hay
3
5
mét?
c Khối lượng nào lớn hơn:
6
7
kg hay
7
8
kg?
d Bài 3. So sánh các phân số sau:
5
24
;
15
24
và
5
8
;a
4
9
;
15
54
và
2
3
;b
−2
−5
;
−5
8
và 4;c
11
−20
;
7
−30
và
4
15
.d
d Bài 4. Sắp xếp các phân số sau theo thứ tự tăng dần:
9
19
;
−25
19
;
20
19
;
42
19
;
30
19
;
14
19
và
−13
19
a
1
3
;
1
5
;
−2
15
;
1
6
;
−2
−5
;
−1
10
; và
4
15
b
d Bài 5. a Thời gian nào dài hơn:
1
2
giờ hay
2
3
giờ?
b Đoạn nào ngắn hơn:
3
4
mét hay
5
6
mét?
c Khối lượng nào lớn hơn:
9
5
kg hay
11
6
kg?
d Bài 6. Lớp 6A có
4
5
số học sinh thích bóng bàn,
7
10
số học sinh thích bóng chuyền và
23
25
số học sinh thích bóng đá. Hỏi môn bóng nào được ít bạn thích nhất?
| Bài 5. Phép cộng và trừ phân số
A KIẾN THỨC CẦN NHỚ
Quy tắc:
a
c
+
b
c
=
a + b
c
.a
a
c
−
b
c
=
a − b
c
.b
Các bước:
• Rút gọn, chuyển mẫu âm thành mẫu dương.
• Quy đồng mẫu số.
• Cộng (trừ) các phân số cùng mẫu.
Page 25 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể):
2
7
+
3
7
;a
1
7
+
−4
7
;b
2
3
+
5
7
;c
1
6
+
−3
4
;d
−3
4
+
3
5
;e
6
42
−
3
21
;f
−5
8
− 2;g
6
42
−
5
21
.h
d Bài 2. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể):
1
8
−
1
2
;a
−1
16
−
1
15
;b
3
5
−
5
6
;c
−11
12
+ 1;d
1
3
−
2
9
;
e
−5
7
−
1
3
;
f
2
7
+
1
4
;g
3
5
−
−1
2
;h
−2
5
−
−3
4
;i −5 −
1
6
;j
−5
9
+
5
12
;k
−2
7
−
7
2
.l
d Bài 3. Tìm x, biết
x
5
=
5
6
+
−19
30
;a x =
−1
2
+
3
4
;b x =
1
2
−
2
3
;c
x
30
=
3
5
+
7
30
.d
d Bài 4. Hai người cùng làm một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ,
người thứ hai mất 3 giờ. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần
công việc?
d Bài 5. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể):
−3
5
+
1
5
;a
2
9
−
7
9
;b
1
6
+
−5
6
;c
1
14
+
−4
7
;d
23
36
−
1
24
;e 3 −
8
11
;f
1
3
+
3
4
−
5
12
;g
3
14
+
5
8
+
−1
2
.h
d Bài 6. Tìm x, biết
x =
7
5
+
−1
5
;a
x
−1
+
5
9
=
−1
3
;b x =
5
11
+
4
−9
.c
d Bài 7. Hai vòi nước cùng chảy vào bể, riêng vòi thứ nhất chảy trong 10 giờ thì đầy bể,
riêng vòi thứ hai thì chảy trong 15 giờ đầy bể. Hỏi nếu cùng chảy thì trong một giờ cả hai
vòi chảy được bao nhiêu phần bể?
d Bài 8. Tìm x, biết
x +
3
4
=
1
2
;a x +
−5
7
= 0 ;b
−5
7
− x =
1
14
.c
Page 26 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 6. Luyện tập
d Bài 1. Thực hiện phép tính
−7
21
+
Å
1 +
1
3
ã
;a
2
15
+
Å
5
9
+
−6
9
ã
;b
Å
−1
5
+
3
12
ã
+
−3
4
;c
Å
3
4
+
5
12
ã
+
−5
−4
.d
d Bài 2. Thực hiện phép tính
−3
7
+
5
13
+
−4
7
;a
−8
17
+
7
8
+
−9
17
;b
−5
21
+
−2
21
+
8
24
;c
−5
11
+
Å
−6
11
+ 1
ã
.d
d Bài 3. Thực hiện phép tính
2
9
+
5
−12
−
−3
4
;a
3
5
−
−7
10
−
13
−20
;b
3
14
−
5
−8
+
−1
2
;c
3
4
+
−1
3
−
5
18
.d
d Bài 4. Tìm x, biết
2
15
− x =
3
10
;a
3
10
− x = 1;b
1
4
− x =
1
20
;c
−1
3
+ x =
2
5
.d
d Bài 5. Ba người cùng làm một công việc. Nếu làm riêng thì người thứ nhất phải mất 4
giờ, người thứ hai mất 3 giờ, người thứ ba mất 6 giờ. Hỏi nếu làm chung thì mỗi giờ cả ba
người làm được mấy phần công việc?
d Bài 6. Vòi nước A chảy vào một bể không có nước trong 4 giờ thì đầy. Vòi nước B chảy
đầy bể ấy trong 5 giờ. Hỏi:
a Trong 1 giờ, mỗi vòi chảy được lượng nước bằng mấy phần bể?
b Trong 1 giờ, cả hai vòi cùng chảy thì được lượng nước bằng mấy phần bể?
d Bài 7. Vòi nước A chảy đầy một bể không có nước mất 3 giờ, vòi nước B chảy đầy bể đó
mất 4 giờ. Hỏi trong 1 giờ, vòi nào chảy được nhiều nước hơn và nhiều hơn bao nhiêu?
d Bài 8. Một khu đất hình chữ nhật có chiều dài là
3
4
km, chiều rộng là
8
5
km.
a Tính nửa chu vi của khu đất (bằng km).
b Chiều dài hơn chiều rộng bao nhiêu km?
d Bài 9. Một khay đựng 4 quả chuối, 1 quả táo và 1 quả cam. Biết rằng quả táo nặng
1
8
kg,
quả cam nặng
1
3
kg, quả chuối nặng
1
10
kg. Hỏi khay nặng bao nhiêu kg nếu khối lượng
tổng cộng là
5
4
kg?
| Bài 7. Phép nhân phân số
A KIẾN THỨC CẦN NHỚ
Áp dụng công thức:
A
B
·
C
D
=
A · C
B · D
Page 27 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
B BÀI TẬP
d Bài 1. Thực hiện tính (rút gọn nếu có thể):
−1
3
·
5
7
;a
−7
4
·
−3
5
;b
6
25
·
−15
4
;c 3 ·
−5
6
;d 0 ·
−11
13
.e
d Bài 2. Thực hiện tính (rút gọn nếu có thể):
Å
−4
15
ã
·
Å
−25
8
ã
;a
5
−14
·
Å
−
7
10
ã
;b 15 ·
Å
−13
25
ã
;c
Å
−
15
14
ã
· 21;d
9
−11
·
5
18
;e
−1
3
·
5
7
;f
−15
16
·
8
−25
;g
−21
24
·
8
−14
;h
−5
13
· 26;i (−17) ·
−3
52
.j
d Bài 3. Thực hiện tính (rút gọn nếu có thể):
2
3
+
1
5
·
10
7
;a
7
12
−
27
7
·
1
18
;b
Å
4
5
+
1
2
ã
·
Å
3
13
−
8
13
ã
;c
Å
−2
7
ã
2
.d
d Bài 4. Tìm x, biết
x
8
=
−2
5
·
3
16
;a
−5
x
=
−2
3
·
4
15
;b x +
4
5
=
−1
7
·
14
15
;c x −
1
3
=
−4
5
·
3
4
.d
d Bài 5. Thực hiện tính (rút gọn nếu có thể):
(−2) ·
−3
7
;a
−5
4
·
12
25
;b
−1
4
·
1
3
;c
−2
5
·
5
−9
;d
−3
4
·
−
16
17
;e (−5) ·
8
15
;f
−9
11
·
5
18
;g
3
5
· (−15).h
d Bài 6. Tìm x, biết
x −
1
4
=
5
8
·
2
3
;a
x
126
=
−5
9
·
4
7
.b
d Bài 7. Thực hiện phép tính (tính nhanh nếu có thể)
1
7
·
1
5
+
1
7
·
2
5
+
1
7
·
4
5
;a
Å
1
2
+
1
3
+
1
4
+
1
5
ã
· 30;b
2
9
·
Å
−3
4
·
6
−5
+
7
6
·
3
5
ã
;c
7
12
·
3
10
·
12
7
· (−10)
1
−3
;d
5
12
·
11
17
+
5
12
·
4
17
+
5
12
·
3
17
.e
d Bài 8. Lúc 7 giờ bạn Lan đi xe đạp từ A đến B với vận tốc 12 km/h. Đến 7h30 phút bạn
nam đạp xe đạp từ B về A với vận tốc 15 km/h. Hai bạn gặp nhau tại C lúc 7h50 phút. Tính
quãng đường AB.
d Bài 9. Tính chu vi và diện tích của một mảnh đất hình chữ nhật biết chiều rộng là
3
4
km
và chiều dài là
9
4
km.
d Bài 10. Thực hiện phép tính (tính nhanh nếu có thể)
8
19
·
15
7
−
8
19
·
6
7
−
8
19
·
2
7
;a
6
7
+
1
7
·
2
7
+
1
7
·
5
7
;b
4
9
·
13
3
−
4
3
·
40
9
;c
5
7
·
5
11
+
5
7
·
2
11
−
5
7
·
14
11
.d
d Bài 11 (?). Tính nhanh
1
9
−
1
7
−
1
11
4
9
−
4
7
−
4
11
+
3
5
−
3
25
−
3
125
−
3
625
4
5
−
4
25
−
4
125
−
4
625
;a
1
1 · 2 · 3
+
1
2 · 3 · 4
+
1
3 · 4 · 5
+
1
4 · 5 · 6
+ . . . +
1
97 · 98 · 99
+
1
98 · 99 · 100
.b
Page 28 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 8. Phép chia phân số
A KIẾN THỨC CẦN NHỚ
Áp dụng công thức:
A
B
:
C
D
=
A
B
·
D
C
=
A · D
B · C
B BÀI TẬP
d Bài 1. Tìm số nghịch đảo của:
3
4
; −
1
2
; −21; 0, 6; 1, 5;a
4
5
;
−1
3
; −2; 10; −1, 2.b
d Bài 2. Thực hiện phép tính (rút gọn nếu có thể):
4
5
:
7
9
;a −
3
8
:
15
22
;b
2
7
:
−1
2
;c 15 :
−3
14
;d
19
21
: (−38);e
1
2
:
2
3
:
3
4
.f
d Bài 3. Tìm x, biết:
x ·
3
7
=
2
3
;a x :
8
11
=
11
3
;b
2
5
: x =
−1
4
;c
4
7
· x −
2
3
=
1
5
;d
2
9
−
7
8
· x =
1
3
;e
1
3
− 2x
=
4
3
;f
4
5
+
5
7
: x =
1
6
;g
1
5
x − 7
=
12
3
.h
d Bài 4. Thực hiện phép tính (rút gọn nếu có thể):
12
5
:
16
15
;a
9
8
:
6
5
;b
7
5
:
14
25
;c 5 :
−15
24
;d
−12
25
: (−15);e
3
14
:
−6
−7
.f
d Bài 5. Người ta đóng 120 lít nước khoáng vào loại chai
1
2
lít. Hỏi đóng được tất cả bao
nhiêu chai?
d Bài 6. Tính chu vi của một cái sân hình chữ nhật biết diện tích sân là 40 m
2
và chiều
rộng bằng
2
5
chiều dài.
d Bài 7. Tìm x, biết:
x ·
−3
4
=
2
5
+
4
3
;a
5
6
· x =
−7
8
−
5
16
;b x :
−3
7
=
1
14
+
3
7
;c
−6
7
−
9
10
· x =
24
35
;d
d Bài 8. Thực hiện phép tính (rút gọn nếu có thể):
3
2
:
9
4
;a
−48
55
:
12
−11
;b
7
10
:
−7
5
;c 20 :
−10
12
;d
−15
24
: (−8);e
6
−7
:
−8
−7
.f
d Bài 9. Thực hiện phép tính (rút gọn nếu có thể):
9
34
:
−3
17
;a 24 :
−6
11
;b
4
7
:
Å
2
5
·
4
7
ã
;c
6
7
+
5
7
: 5 −
8
9
;d 5 :
3
4
−
24
5
:
3
4
.e
d Bài 10. Tìm x, biết
Page 29 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
−2
3
−
5
12
· x =
4
5
;a
2
3
· x +
2
3
=
1
5
;b
3
7
x +
1
2
=
5
14
;c
1
2
x +
3
2
x +x = 16.d
d Bài 11 (?). Một công việc nếu giao cho người thứ nhất thì làm 10 giờ xong, nếu giao cho
người thứ hai thì làm 15 giờ xong, nếu giao cho người thứ ba làm thì 30 giờ xong. Hỏi nếu
cả ba người cùng làm công việc ấy thì mất bao nhiêu giờ?
d Bài 12 (?). Một ô tô đi quãng đường AB với vận tốc 40 km/h. Lúc về xe đi quãng đường
BA với vận tốc 50 km/h. Thời gian cả đi lẫn về không kể thời gian nghỉ là 4 giờ 30 phút. Hỏi
độ dài quãng đường AB là bao nhiêu km?
| Bài 9. Hỗn số. Số thập phân. Phần trăm
A KIẾN THỨC CẦN NHỚ
B BÀI TẬP
d Bài 1. Viết các hỗn số sau dưới dạng phân số:
2
4
5
; 5
1
7
; −1
12
13
a 2
3
8
; 6
3
4
; −2
5
7
b
d Bài 2. Viết các hỗn số sau dưới dạng phân số:
6
3
8
; 3
1
2
; −2
3
7
a 6
2
7
; 3
1
5
; −4
3
8
b
d Bài 3. Thực hiện phép tính
6
3
8
+ 5
1
2
;a 5
3
7
− 2
3
7
;b 5
1
2
· 3 ·
3
4
;c 8
2
7
−
Å
3
4
9
+ 4
2
7
ã
.d
d Bài 4. Tìm x, biết
0, 5x −
2
3
=
7
12
;a x : 4
1
3
= −2 , 5;b 5, 5x =
13
15
;c
Å
3x
7
+ 1
ã
: (−4) =
−1
28
.
d
d Bài 5. Viết phần trăm sau dưới dạng phân số:
7%;a 45%;b 216%;c 35%.d
d Bài 6. Thực hiện phép tính
3
5
6
− 1
9
10
;a 7
1
8
− 5
3
4
;b −5
1
7
+ 3
2
5
;c −2
1
3
− 1
2
7
;d
6
1
3
: 4
2
9
;e
Å
10
2
9
+ 2
3
5
ã
−6
2
9
;f 11
3
13
−
Å
2
4
7
+ 5
3
13
ã
;g
Å
6
4
9
+ 3
7
11
ã
−4
4
9
.h
d Bài 7. Thực hiện phép tính:
Page 30 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
25% − 1
1
2
+ 0, 5 ·
3
8
;a
Å
−1
6
ã
2
:
5
−24
+
Å
7
25
− 36%
ã
·
−8
1
3
;b
25% − 1
1
2
· (−2019)
0
+ 0, 5 ·
12
5
;c
3
5
−
8
5
:
(
5, 25 + 75%
)
.d
d Bài 8. Thực hiện phép tính:
Å
−2
3
ã
2
:
5
9
+ 0, 25 · 10%;a 65% + 2, 5 − 1
1
4
+ (−3)
2
;b
30% − 2
2
5
+ 0, 2 ·
1
2
;c
11
13
·
3
8
+
11
13
· 50% +
11
18
·
11
13
;d
1, 2 :
Å
75% −
2
5
ã
− 3
3
14
;e
3
4
+ 2
1
4
· 0, 5 · (−80) · 0, 01;f
−25
30
·
37
44
+
−25
30
·
13
44
+
−25
30
·
−6
44
;g 25% − 1
1
4
+ 0, 5 ·
12
5
;h
75% −
Å
1, 25 − 2
3
4
ã
:
3
2
2
.i
d Bài 9. Tìm x, biết
x − 1
1
5
x = 60%;a 2, 5x +
4
7
= −1, 5;b 60%x +
2
3
x = 1368;c
1
3
· (3x − 2) + 25% = −
9
6
;d 1, 5−
Å
3
5
x + 70%
ã
= −2
1
2
;e
1
4
−
7
10
x = 1, 75.f
| Bài 10. Tìm giá trị phân số của một số cho trước
A KIẾN THỨC CẦN NHỚ
Muốn tìm
m
n
của số b cho trước, ta tính
m
n
· b.
# Ví dụ 1.
2
3
của 8, 7 là
2
3
· 8, 7 = 5, 8.
B BÀI TẬP
d Bài 1. Tìm
2
3
của 15;a
1
2
của 8, 4;b
2
7
của
−11
6
;c 2
1
3
của 5, 1;d
2
7
11
của 6
3
5
;e 85% của 25;f 48% của 50;g 0, 25 của 10.h
d Bài 2. Đổi sang phút:
1
6
giờ;a
1
3
giờ;b
3
4
giờ.c
Page 31 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 3. Tuấn có 21 viên bi, Tuấn cho Dũng
3
7
số bi của mình. Hỏi:
a Dũng được Tuấn cho bao nhiêu viên bi?
b Tuấn còn lại bao nhiêu viên bi?
d Bài 4. Tìm:
3
4
của 32;a
2
5
của 1, 5;b
5
4
của
−20
3
;c 1
2
3
của 1, 2;d
3
5
7
của −5
2
8
;e 25% của 40;f 58% của 100;g 0, 2 của 58.h
d Bài 5. Có bao nhiêu phút trong
2
5
giờ;a
7
12
giờ;b
4
15
giờ;c
3
12
giờ.d
d Bài 6. Một quả cam nặng 300 g. Hỏi
3
4
quả cam nặng bao nhiêu?
d Bài 7. Đoạn đường sắt Hà Nội - Hải Phòng dài 102 km. Một xe lửa xuất phát từ Hà Nội
đã đi được
2
3
quãng đường. Hỏi xe lửa còn cách Hải Phòng bao nhiêu km?
d Bài 8. Trên đĩa có 24 quả táo. Hạnh ăn 25% số táo. Sau đó, Hoàng ăn
4
9
số táo còn lại.
Hỏi trên đĩa còn mấy quả táo?
d Bài 9. Bốn thửa ruộng thu hoạch được tất cả 1 tấn thóc. Số thóc thu hoạch ở 3 thửa
ruộng đầu lần lượt bằng
1
4
; 0, 4 và 15% tổng số thóc thu hoạch ở cả bốn thửa. Tính số thóc
thu hoạch được ở thửa thứ tư?
d Bài 10. Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng
hành, đường và muối theo thứ tự bằng 5%;
1
1000
và
3
40
khối lượng rau cải. Vậy nếu muối 25
kg rau cải thì cần bao nhiêu kg hành, đường và muối?
d Bài 11. Một lớp có 45 học sinh bao gồm ba loại: giỏi, khá và trung bình. Số học sinh
trung bình chiếm
7
15
số học sinh cả lớp. Số học sinh khá bằng
5
8
số học sinh còn lại. Tính
số học sinh giỏi của lớp?
d Bài 12. Bố bạn Lan gửi tiết kiệm 1 triệu đồng tại ngân hàng theo thể thức "có kỳ hạn 12
tháng" với lãi suất 0, 58% một tháng (số tiền lãi mỗi tháng bằng 0, 58% số tiền gửi ban đầu
và sau 12 tháng mới được lấy lãi). Hỏi hết thời hạn 12 tháng ấy, bố bạn Lan lấy ra cả vốn lẫn
lãi là bao nhiêu tiền?
| Bài 11. Tìm một số biết giá trị một phân số của nó
A KIẾN THỨC CẦN NHỚ
Muốn tìm một số biết
m
n
của nó bằng a, ta tính a :
m
n
.
Page 32 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
# Ví dụ 1. Tìm một số biết
2
3
của nó bằng 7, 2.
Lời giải.
Số cần tìm là 7 , 2 :
2
3
= 7 , 2 ·
3
2
= 10 , 8.
B BÀI TẬP
d Bài 1. Tìm một số biết:
3
4
của nó bằng 7, 2;a 1
3
7
của nó bằng −5.b
d Bài 2. 25% của một quả dưa lê là 1 kg. Hỏi khối lượng quả dưa lê là bao nhiêu kg?
d Bài 3.
5
8
kho hàng bằng 1250 kg. Hỏi
1
4
kho hàng bằng bao nhiêu kg?
d Bài 4. Tìm một số biết
2
5
% của nó bằng 1, 5;a 3
5
8
% của nó bằng −5 , 8.b
d Bài 5.
2
3
quả dưa hấu nặng 4
1
2
kg. Hỏi quả dưa hấu nặng bao nhiêu kg?
d Bài 6.
2
3
số tuổi của Mai cách đây 3 năm là 6 tuổi. Hỏi hiện nay Mai bao nhiêu tuổi?
d Bài 7. Trong đậu đen nấu chín, tỉ lệ chất đạm chiếm 24%. Tính số kg đậu đen nấu chín
để có 1, 2 kg chất đạm?
d Bài 8. Trong sữa có 4 , 5% bơ. Tính lượng sữa trong một chai, biết rằng lượng bơ trong
chai này là 18 g?
d Bài 9. Một công nhân ăn hết
1
2
tiền lương, trả tiền nhà hết
1
6
tiền lương, tiêu vặt hết
1
5
tiền lương, cuối tháng để dành được 120 000 đồng. Tính lương của người đó?
d Bài 10. Một người mang đi chợ một rổ trứng. Người đó bán
2
5
số trứng thì còn lại 54 quả
trứng. Tính số trứng người đó mang ra chợ bán.
d Bài 11. Một người bán cam, buổi sáng bán
3
5
số cam mang đi, buổi chiều bán 52 quả
cam. Lúc về còn lại số cam bằng
1
8
số cam đã bán. Hỏi người đó mang số cam đi bán là bao
nhiêu?
d Bài 12 (?). Một lớp học có số học sinh nữ bằng
5
3
số học sinh nam. Nếu 10 học sinh nam
chưa vào lớp thì số học sinh nữ gấp 5 lần số học sinh nam. Tìm số học sinh nam và nữ của
lớp đó?
Page 33 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 12. Tìm tỉ số của hai số
A KIẾN THỨC CẦN NHỚ
B BÀI TẬP
d Bài 1. Tìm tỉ số của
6
13
và
11
26
;a 9 và 6;b 15 và 0, 5;c
3
10
giờ và 20 phút;d
3
8
và 1
2
5
;e 0, 6 tạ và 36 kg.f
d Bài 2. Tìm tỉ số phần trăm của
5
1
3
và 4
2
9
;a 16 và 32;b 0, 3 tạ và 50 kg;c 2, 8 và 0, 7.d
d Bài 3. Tìm tỉ số phần trăm của
2
1
3
và 3
1
9
;a 25 và 50;b 0, 2 tạ và 40 kg;c 1, 2 và 0, 6.d
d Bài 4. Năm nay con 16 tuổi, bố 50 tuổi. Tính tỉ số giữa tuổi con và tuổi bố
Hiện nay;a Cách đây 5 năm;b Sau đây 8 năm.c
d Bài 5. Trong 40 kg nước biển có 2 kg muối. Tính tỉ số phần trăm muối trong nước biển?
d Bài 6. Biết tỉ số phần trăm nước trong dưa chuột là 97, 2%. Tính lượng nước trong 4 kg
dưa chuột?
d Bài 7. Biết tỉ lệ xích là tỉ số giữa khoảng cách trên bản đồ và khoảng cách thực tế.
a Tìm tỉ lệ xích của một bản đồ biết rằng quãng đường từ Hà Nội đến Thái Nguyên trên
bản đồ là 4 cm còn trong thực tế là 80 km?
b Sài Gòn cách Phan Thiết 200 km. Khoảng cách 2 địa điểm này trên bản đồ là 10 cm.
Tìm tỉ lệ xích của bản đồ?
c Một căn nhà có chiều dài 26 m. Hỏi khi vẽ trên bản vẽ có tỉ lệ xích là
1
100
thì chiều
dài căn nhà là bao nhiêu cm?
| Bài 13. Biểu đồ phần trăm
A KIẾN THỨC CẦN NHỚ
B BÀI TẬP
d Bài 1. Tính
Page 34 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
28% của 376;a 9% của 12 ;b 2, 6% của 12, 5;c 3, 5% của 42, 8.d
d Bài 2. Cuối học kì I, lớp 6C có 8 bạn xếp loại giỏi, 15 bạn xếp loại khá, còn lại là trung
bình.
a Tính tỉ số phần trăm số học sinh lớp 6C được xếp loại giỏi, khá và trung bình so với
tổng số học sinh cả lớp là 40 người.
b Dựng biểu đồ phần trăm dưới dạng ô vuông.
d Bài 3. Trong một khu vườn có trồng ba loại cây mít, hồng và táo. Số cây táo chiếm 30%
tổng số cây, số cây hồng chiếm 50% tổng số cây, số cây mít là 40 cây.
a Hỏi tổng số cây trong vườn là bao nhiêu?
b Dựng biểu đồ ô vuông biểu diễn tỉ số phần trăm số cây mít, hồng, táo so với tổng số
cây trong vườn.
d Bài 4. Muốn đổ bê tông, người ta trộn 1 tạ xi măng, 2 tạ cát và 6 tạ sỏi.
a Tính tỉ số phần trăm từng thành phần của bê tông?
b Dựng biểu đồ ô vuông biểu diễn các tỉ số phần trăm đó?
Page 35 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Page 36 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
PHẦN
II
HÌNH HỌC
37
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
2
Chương
Góc
Học sinh quét mã QR để tham gia nhóm học tập:
Nhóm TOÁN QUẬN 7
| Bài 1. Nửa mặt phẳng. Góc, số đo góc
A KIẾN THỨC CẦN NHỚ
Góc là hình gồm hai tia chung gốc.
• Hai tia Ox và Oy tạo với nhau góc O.
• Kí hiệu:
[
xOy.
• Ox, Oy được gọi là hai cạnh và O được gọi là đỉnh của
[
xOy.
O
x
y
Để đo số đo một góc, ta dùng thước đo độ như sau
Số đo góc
[
xOy ở hình bên nhìn
thước đo độ ta thấy
[
xOy = 50
◦
.
O
0
◦
10
◦
20
◦
30
◦
40
◦
50
◦
60
◦
70
◦
80
◦
90
◦
100
◦
110
◦
120
◦
130
◦
140
◦
150
◦
160
◦
170
◦
180
◦
180
◦
0
◦
y
x
B BÀI TẬP
d Bài 1. Gọi M là điểm nằm giữa hai điểm A, B. Lấy điểm O không nằm trên đường thẳng
AB. Vẽ ba tia OA, OB, OM. Hỏi tia nào nằm giữa hai tia còn lại?
d Bài 2.
39
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Cho hình vẽ bên:
a Hãy chỉ ra các điểm thuộc nửa mặt phẳng chứa điểm
A bờ m .
b Hãy chỉ ra các điểm không thuộc nửa mặt phẳng chứa
điểm A bờ m.
m M N
A
B
C
D
E
F
d Bài 3. Cho ba điểm A, B, C không thẳng hàng. Vẽ đường thẳng a cắt các đoạn thẳng AB,
AC và không đi qua A, B, C.
a Gọi tên hai nửa mặt phẳng đối nhau bờ a.
b Đoạn thẳng BC có cắt đường thẳng a không?
d Bài 4. Quan sát hình vẽ bên dưới rồi điền vào bảng sau:
C
y
z
a)
M
N
P
b)
P
x
y
z
S
c)
Hình Tên góc Tên đỉnh Tên cạnh Kí hiệu
a) góc yCz, góc zCy, góc C C Cy, Cz
‘
yCz,
‘
zCy,
“
C
b)
c)
d Bài 5. Dùng thước đo độ, đo và viết số đo các góc trong các hình vẽ sau:
C
y
z
a)
A
B C
b)
M N
P
c)
d Bài 6. Vẽ góc xOy sao cho
[
xOy = 30
◦
.
d Bài 7. Vẽ góc xBy có số đo bằng 45
◦
.
d Bài 8. Vẽ góc IKM có số đo bằng 130
◦
.
Page 40 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 9. Vẽ trên cùng một hình góc xOy và góc xOz sao cho
[
xOy = 45
◦
,
[
xOz = 60
◦
.
d Bài 10. Vẽ góc cho biết một cạnh và số đo trong các trường hợp sau:
AB
a)
C
x
b)
D
y
c)
F
E
d)
[
BAC = 115
◦
;a
‘
xCz = 100
◦
;b
[
yDx = 70
◦
;c
[
EFy = 145
◦
.d
| Bài 2. Khi nào thì
[
xOy +
‘
yOz =
[
xOz
A KIẾN THỨC CẦN NHỚ
• Nếu tia Oy nằm giữa hai tia Ox và Oz thì
[
xOy +
‘
yOz =
[
xOz.
• Hai góc kề bù thì có tổng bằng 180
◦
.
Vì
[
xOz và
‘
zOy là hai góc kề bù nên
[
xOz +
‘
zOy = 180
◦
.
O
x y
z
B BÀI TẬP
Dạng 1. Các bài toán tính số đo góc
d Bài 1. Vẽ tia OA nằm giữa hai tia OB và OC sao cho
[
AOB = 50
◦
và
\
BOC = 50
◦
. Tính số
đo
\
AOC.
d Bài 2. Trên mặt phẳng vẽ ba tia Ox, Oy, Oz sao cho tia Oy nằm giữa hai tia Ox và Oz
với
[
xOy = 70
◦
,
‘
yOz = 60
◦
. Tính số đo
[
xOz.
d Bài 3. Trên mặt phẳng vẽ ba tia OE, O F, OG sao cho tia OE nằm giữa hai tia OF và OG
với
[
EOF = 35
◦
,
\
EOG = 50
◦
. Tính số đo
\
FOG.
d Bài 4. Cho tia Ot nằm giữa hai tia Om và On. Biết
[
mOt = 70
◦
,
‘
tOn = 85
◦
. Tính số đo
của góc
\
mOn.
d Bài 5. Cho tia AM nằm giữa hai tia A B và AC. Biết
\
MA B = 110
◦
,
\
CAM = 20
◦
. Tính số
đo
[
BAC.
Page 41 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 6. Trên mặt phẳng vẽ
[
AOB = 60
◦
. Vẽ tia OC sao cho OB nằm giữa hai tia OA và OC
với
\
AOC = 100
◦
. Tính số đo
\
BOC.
d Bài 7. Vẽ
[
AOB = 120
◦
. Vẽ tia OC nằm giữa hai tia OA và OB sao cho
\
COB = 50
◦
. Tính
số đo
\
AOC.
d Bài 8. Vẽ
\
AOC = 150
◦
. Vẽ tia OB nằm giữa hai tia OA và OC sao cho
[
AOB = 50
◦
. Tính
số đo
\
BOC.
Quan sát các hình vẽ dưới đây để làm các bài tập bên dưới
O B
A
C
45
◦
32
◦
Hình 1
O
x y
z
120
◦
?
Hình 2
O B
I
A
60
◦
Hình 3
d Bài 9. Hình 1 cho biết tia OA nằm giữa hai tia OB và OC;
[
BOA = 45
◦
,
\
AOC = 32
◦
. Tính
số đo
\
BOC.
d Bài 10. Hình 2 cho biết hai góc kề bù xOz và zOy;
[
xOz = 120
◦
. Tính
‘
zOy.
d Bài 11. Hình 3 cho biết tia OI nằm giữa hai tia OA và OB. Biết
[
AOB = 60
◦
,
‘
BOI =
1
4
[
AOB.
Tính
‘
BOI và
‘
AOI.
d Bài 12.
Hình 4 cho biết
‘
zOy và
[
yOx là hai góc kề bù, biết
[
xOy =
45
◦
. Tính số đo
‘
yOz.
O
z x
y
45
◦
?
Hình 4
d Bài 13. Cho hai góc kề bù
[
xOy và
[
yOy
0
sao cho
[
xOy = 120
◦
. Tính
[
yOy
0
.
d Bài 14. Cho hai góc kề bù
[
AOB và
\
BOC, biết
[
AOB = 72
◦
. Tính số đo
\
BOC.
d Bài 15. Cho hai góc kề bù
[
mOt và
\
mOn, biết
[
mOt = 125
◦
. Tính số đo
\
mOn.
d Bài 16 (?).
Hình 5 cho biết hai tia AM và AN đối nhau,
\
MA P = 33
◦
,
[
NAQ = 58
◦
, tia AQ nằm giữa hai tia AN và AP. Hãy tính
số đo x của
[
PAQ.
AM N
Q
P
58
◦
33
◦
x
Hình 5
Dạng 2. Các bài toán chứng minh tia nằm giữa hai tia
Page 42 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 1. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy và
Oz sao cho
[
xOy = 60
◦
,
[
xOz = 100
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại?
b Tính số đo
‘
yOz.
d Bài 2. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy và
Oz sao cho
[
xOy = 40
◦
,
[
xOz = 110
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại?
b Tính số đo
‘
yOz.
d Bài 3. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia OA, vẽ hai tia OB
và OC sao cho
[
BOA = 145
◦
,
\
COA = 55
◦
.
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại?
b Tính số đo
\
BOC.
d Bài 4. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ot, vẽ hai tia Om
và On sao cho
[
tOm = 120
◦
,
‘
tOn = 90
◦
.
a Trong ba tia Ot, Om , On tia nào nằm giữa hai tia còn lại?
b Tính số đo
\
mOn.
d Bài 5. Vẽ
[
AOB = 90
◦
và
\
AOC = 50
◦
sao cho
[
AOB kề với
\
AOC.
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại?
b Tính số đo
\
BOC.
d Bài 6. Vẽ
[
AOB =
\
BOC = 80
◦
sao cho
[
AOB kề với
\
BOC.
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại?
b Tính số đo
\
AOC.
| Bài 3. Tia phân giác của góc
A KIẾN THỨC CẦN NHỚ
Page 43 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
Cách chứng minh tia phân giác
Oy là tia phân giác của
[
xOz vì
• Tia Oy nằm giữa hai tia Ox và Oz.
•
[
xOy =
‘
yOz.
Công thức (dùng để tính số đo)
Vì Oy là tia phân giác của
[
xOz nên
[
xOy =
‘
yOz =
[
xOz : 2.
O
x
y
z
B BÀI TẬP
Dạng 1. Chứng minh tia phân giác
d Bài 1. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ các tia Oy và Oz sao cho
[
xOy = 70
◦
,
[
xOz = 140
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOz.
c Tia Oy có là tia phân giác của
[
xOz không? Vì sao?
d Bài 2. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ các tia Oy và Ot sao cho
[
xOy = 60
◦
,
‘
xOt = 120
◦
.
a Trong ba tia Ox, Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOt.
c Tia Oy có là tia phân giác của
‘
xOt không? Vì sao?
d Bài 3. Cho hai tia Oz, Oy cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, biết góc
[
xOy =
50
◦
,
[
xOz = 130
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOz.
c Vẽ tia Oa là tia đối của tia Ox. Tính số đo góc
‘
zOz.
d Bài 4. Cho hai tia Oz, Oy cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, biết góc
[
xOy =
75
◦
,
[
xOz = 150
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOz.
Page 44 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
c Tia Oy có phải là tia phân giác của góc
[
xOz không? Vì sao?
d Vẽ tia Oy
0
là tia đối của tia Oy. Tính số đo góc
[
y
0
Oz.
d Bài 5. Cho hai tia On, Ot cùng nằm trên nửa mặt phẳng bờ chứa tia Om, biết góc
\
mOn = 50
◦
,
[
mOt = 100
◦
.
a Trong ba tia Om , On, Ot tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
nOt.
c Vẽ tia Oa là tia đối của tia Om. Tính số đo góc
‘
aOt.
d Bài 6. Cho hai tia Oy, Ot cùng nằm trên nửa mặt phẳng bờ chứa tia Om, biết góc
\
mOy = 60
◦
,
[
mOt = 120
◦
.
a Trong ba tia Om , Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOt.
c Tia Oy có là tia phân giác của
[
mOt không? Vì sao?
d Vẽ tia Ob là tia đối của tia Oy. Tính số đo góc
‘
bOt.
d Bài 7. Trên cùng một nửa mặt phẳng bờ là đường thẳng chứa tia Ox, vẽ hai tia OA, OB
sao cho
[
xOA = 52
◦
,
[
xOB = 104
◦
.
a Trong ba tia OA, OB, Ox tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
[
AOB.
c Tia OA có phải tia phân giác của góc
[
xOB không? Vì sao?
d Vẽ tia Oy là tia đối của tia Ox. Tính góc
[
yOB.
d Bài 8. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy,
Oz sao cho
[
xOy = 70
◦
,
[
xOz = 35
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo góc
‘
yOz.
c Tia Oz có phải là tia phân giác của góc
[
xOy không? Vì sao?
d Vẽ tia Om là tia đối của tia Oz. So sánh
\
xOm và
\
yOm.
d Bài 9. Trên cùng nửa mặt phẳng có bờ chứa tia Ax. Vẽ hai tia Ay, Az sao cho
‘
xAy = 70
◦
,
‘
xAz = 125
◦
.
Page 45 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
a Hỏi trong ba tia Ax, Ay, Az tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yAz.
c Vẽ tia Am là tia đối của tia Ax. Hỏi Az có phải là tia phân giác của
[
mAy không? Vì sao.
Dạng 2. Áp dụng tính chất tia phân giác
d Bài 1. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy và Ot sao cho
[
xOy = 35
◦
,
‘
xOt = 70
◦
.
a Trong ba tia Ox, Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính góc
‘
yOt.
c Tia Oy có phải tia phân giác của góc
‘
xOt không? Vì sao?
d Gọi Om là tia đối của tia Ox. Tính góc
[
mOt.
e Gọi Oa là phân giác của góc
[
mOt, tính số đo góc
[
aOy?
d Bài 2. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia OA và OB sao cho
[
xOA = 52
◦
,
[
xOB = 104
◦
.
a Trong ba tia OA, OB, Ox tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính góc
[
AOB.
c Tia OA có phải tia phân giác của góc
[
xOB không? Vì sao?
d Gọi Oy là tia đối của tia Ox. Tính góc
[
yOB.
e Kẻ tia phân giác Ot của góc
[
yOB, tính số đo góc
‘
yOt và
‘
BOt?
d Bài 3 (Đề HK2 Nhà Bè 2015 - 2016). Trên cùng nửa mặt phẳng bờ là đường thẳng chứa
tia Ox, vẽ hai tia Ot và Oy sao cho
‘
xOt = 60
◦
và
[
xOy = 140
◦
.
a Trong ba tia Ox, Ot, Oy tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
tOy.
c Vẽ tia Om là tia phân giác của
‘
tOy. Tính số đo
\
xOm.
d Bài 4 (Đề HK2 Nhà Bè 2016 - 2017). Cho hai tia Oy, Oz cùng nằm trên một nửa mặt
phẳng bờ chứa tia Ox. Biết
[
xOy = 30
◦
,
[
xOz = 120
◦
.
a Tia nào nằm giữa hai tia còn lại? Tính số đo
‘
yOz.
b Vẽ tia Om là tia phân giác của
‘
yOz. Tính số đo
\
xOm.
Page 46 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 5 (Đề HK2 Nhà Bè 2017 - 2018). Trên cùng nửa mặt phẳng bờ là đường thẳng chứa
tia Ox, vẽ hai tia Oz và Oy sao cho
[
xOz = 80
◦
và
[
xOy = 30
◦
.
a Trong ba tia Ox, Oz, Oy tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
zOy.
c Vẽ Ot là tia phân giác của
[
xOy và tia Om là tia đối của tia Ox. Tính số đo
[
tOm.
d Bài 6 (Đề HK2 Nhà Bè 2018 - 2019). Trên cùng nửa mặt phẳng bờ chứa tia Ox, vẽ hai
tia Oy và Oz sao cho
[
xOy = 40
◦
và
[
xOz = 110
◦
.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
b Tính số đo
‘
yOz.
c Vẽ tia Om là tia phân giác của góc
‘
yOz và tia On là tia đối của Ox. Tính
\
mOn.
Page 47 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
| 1/47
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU MỤC LỤC Phần I
Số học - Trang 3 Chương 2 Số nguyên Trang 5 BỬU Bài 1
Tập hợp các số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 G Bài 2
Phép cộng số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 AN Bài 3
Phép trừ số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 QU Bài 4
Quy tắc dấu ngoặc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 TẠ Bài 5
Quy tắc chuyển vế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 THPT Bài 6
Phép nhân và chia hai số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 - Bài 7
Tính chất của phép nhân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 G Chương 3 Phân số 0976071956 Trang 21 DŨN Bài 1
Khái niệm phân số.MATH.ND
Phân số bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Bài 2
Tính chất cơ bản của phân số. Rút gọn phân số . . . . . . . . . . . . . . . . . . . . . . . . 22 GỌC N Bài 3
Quy đồng mẫu số nhiều phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 ? Lớp TOÁN THẦY DŨNG ? Bài 4
So sánh phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 Bài 5
Phép cộng và trừ phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 GUYỄN N Bài 6
Luyện tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Bài 7
Phép nhân phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Thầy Bài 8
Phép chia phân số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 Bài 9
Hỗn số. Số thập phân. Phần trăm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Bài 10 Tìm giá trị phân số của một số cho trước . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Bài 11 Tìm một số biết giá trị một phân số của nó . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Bài 12 Tìm tỉ số của hai số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 1 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
Bài 13 Biểu đồ phần trăm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 Phần II
Hình học - Trang 37 Chương 2 Góc Trang 39 Thầy Bài 1
Nửa mặt phẳng. Góc, số đo góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 Bài 2 Khi nào thì ’ xOy + ‘ yOz = ‘
xOz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 N GUYỄN Bài 3
Tia phân giác của góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 2 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? BỬU G PHẦN AN QU I TẠ THPT - G SỐ HỌC 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 3 Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 2 Số nguyên Chương
Học sinh quét mã QR để tham gia nhóm học tập: Nhóm TOÁN QUẬN 7 BỬU G Trọng tâm chương: AN
• Biết được tập hợp các số nguyên, so sánh được hai số nguyên. QU
• Tính được giá trị tuyệt đối của một số nguyên. TẠ
• Cộng, trừ, nhân, chia số nguyên. • Tìm x. THPT -
• Biết sử dụng quy tắc dấu ngoặc và quy tắc chuyển vế. G 0976071956 | DŨN
Bài 1. Tập hợp các số nguyên MATH.ND A
KIẾN THỨC CẦN NHỚ GỌC N
• Các số nguyên dương là: 1; 2; 3; 4; . . . ? Lớp TOÁN THẦY DŨNG ?
• Các số nguyên âm là: −1; −2; −3; −4; . . .
• Tập hợp các số nguyên gồm các số nguyên âm, số 0 và các số nguyên dương. GUYỄN N
• Kí hiệu Z = {. . . − 3; −2; −1; 0; 1; 2; 3; . . .}.
• Số 0 không phải số nguyên âm cũng không phải số nguyên dương. Thầy
• Các số 1 và −1; 2 và −2; 3 và −3; . . . là các số đối nhau. • Số đối của 0 là 0;
• Giá trị tuyệt đối của mọi số nguyên khác 0 đều là số nguyên dương (giá trị tuyệt
đối của 0 là 0). 5 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP
d Bài 1. Điền chữ Đ (đúng) hoặc chữ S (sai) thích hợp vào ô trống: a 7 ∈ N ; b 0 ∈ Z ;
c 15, 3 ∈ Z ;
d −2 ∈ N ; e 0 ∈ N ;
f −10 ∈ N ; g 5 ∈ N ;
h −4, 03 ∈ Z ; Thầy i 100200 ∈ Z ; j 1250000 ∈ N ; k 27 ∈ N ; l 72 ∈ Z . d N
Bài 2. Tìm các số đối của GUYỄN a −1; b 8; c 0; d 10; e −2; f +5; g −25; h −9; i 18; j −20. N
d Bài 3. Tìm giá trị tuyệt đối của mỗi số sau: GỌC a −2000; b −13; c −15; d 2311; e −9.
d Bài 4. Điền vào chỗ trống các dấu ≥, ≤, >, <, =: DŨN
a | − 99| |99|;
b | − 30| 0; c 0 | − 1|; d |1| | − 105|; G e −|12| − | − 11|; f |5| 0976071956 | − 5|; g |6| | − 7|;
h | − 15| |20|. - THPT
d Bài 5. Điền vào chỗ trống các dấu ≥, ≤, >, <, =: MATH.ND a −2 − 5; b −6 − 1; c 0 − 3; d −99 − 100; TẠ e −542 − 263; f 100 − 100;
g | − 50| 0; h 0 | − 9|; QU ? Lớp TOÁN THẦY DŨNG ? i |6| | − 101|; j −|16| − | − 16|. AN
d Bài 6. Tính giá trị của biểu thức G BỬU
a | − 34| + |13|;
b 513 + | − 742|;
c | − 16| · |5|;
d 100 − | − 25| + | − 35|;
e |9 − 8|;
f |4 − 4|;
g | − 5| + | − 9|;
h | − 7| − | − 4|;
i || − 5||;
j |−2|+|−3|+|−4|;
k |5|+|−10|+|−15|;
l | − 8| · |2|;
m | − 4| · | − 5|;
n |18| : | − 2|;
o | − 20| : |4|;
p | + 2018| + | − 2016| : | − 3|.
d Bài 7. Sắp xếp các số sau theo thứ tự tăng dần (nhớ tăng dần là từ nhỏ đến lớn nhé): Page 6 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
a 5; −15; 8; 3; −1; 0
b −102; 16; 0; 8; −9; 2012
c 2017; −2018; 0; −100; −7; 1
d 123; −47; 0; −91; 14; −8
e 0; −5; 7; −10; 15; −50
f 28; −127; 0; −15; 20; −1
g 2017; 0; −9; −2018; 6
h −2; 14; −9; 0; 1; | − 3|
d Bài 8. Sắp xếp các số sau theo thứ tự giảm dần (nhớ giảm dần là từ lớn đến nhỏ nhé):
a −3; −1; 0; −2; 5; −13; 17; −99; 100
b −97; 10; 0; 4; −9; 2000 BỬU
c −129; 0; 35; −98; 27; −3
d | − 5|; 0; 15; −1; −2018 G
d Bài 9. Tìm x ∈ Z, biết AN
a −10 < x ≤ 1;
b −2 ≤ x ≤ 2;
c −2 < x < 5;
d −6 ≤ x ≤ −1; QU
e 0 < x ≤ 7;
f −1 < x < 6;
g −6 < x < −2;
h −2 < x < 2. TẠ
d Bài 10. Tìm x ∈ Z, biết THPT a |x| = 0;
b |x| = −8;
c 156 − x = | − 27|. - G | Bài0976071956
2. Phép cộng số nguyên DŨN A
KIẾN THỨC CẦN NHỚ MATH.ND
• Cộng hai số nguyên dương chính là cộng hai số tự nhiên. GỌC N • Cộng hai số ? Lớp nguyên âm TO ta ÁN cộng THẦ hai giá trị Y DŨNG tuyệt đối của ?
chúng rồi đặt dấu "−" trước kết quả.
• Hai số nguyên đối nhau có tổng bằng 0. GUYỄN N
• Muốn cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt
đối của chúng (số lớn trừ số nhỏ) rồi đặt trước kết quả tìm được dấu của số có giá
trị tuyệt đối lớn hơn. Thầy
• Tính chất giao hoán: a + b = b + a.
• Tính chất kết hợp: (a + b) + c = a + (b + c).
• Cộng với số 0: a + 0 = a.
• Cộng với số đối: a + (−a) = 0.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 7 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP d Bài 1. Tính: a (+2) + (+5); b (+3) + (+17); c (+12) + (+7);
d (−3) + (−7); Thầy
e (−16) + (−13);
f (−25) + (−4);
g (−30) + (−14);
h (−6) + (−54). d N Bài 2. Tính: GUYỄN
a (−7) + (−14);
b (−35) + (−9);
c (−30) + (−5);
d (−7) + (−13);
e (−37) + (−112);
f (−5) + (−248);
g 17 + | − 33|;
h | − 37| + | + 15|. N d Bài 3. Tính: GỌC
a | − 35| + 18;
b 15 + | − 55|; c 215 + 1025;
d (−56) + (−15);
e (−12) + (−58);
f | − 30| + 12;
g 25 + | − 56|; h 234 + 4567; DŨN
i (−3) + (−9);
j (−42) + (−54);
k 12 + | − 25|. G d Bài 4. Tính: 0976071956 - THPT
a (−15) + (−|5|) + (−| − 23|) + (− MA 9); TH.ND
b 11 + | − 11| + 0 + |10| + | − 10|; T
c | − 3| + (−23) + (−10) + | − 51| + | − 49|. Ạ QU d Bài 5. Tính: ? Lớp TOÁN THẦY DŨNG ? AN
a (−9) + | − 11|; b 42 + (−22); c (−25) + 25; G
d 262 + (−138);
e 105 + (−150); f 22 + (−42); BỬU g (−99) + 99; h (−85) + 40;
i (−34) + 24 + (−7) + 27;
j 99 + (−100) + 101;
k 15 + 5 + (−8) + (−12); l (−2009) + 0; m 15 + (−14); n (−42) + 22; o 35 + (−135);
p −12 + | − 25|;
q | − 22| + (−44);
r | − 2| + (−| − 9|);
s (−9) + 10 + (−10) + (−45) + 55. d Bài 6. Tính: Page 8 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
a (−101) + (−399);
b (−315) + (−1477);
c (−404) + 1002;
d 21 + (−26) + 31 + (−36);
e 17 + 100 + (−7);
f (−74) + 124 + 131;
g (−99) + 114 + (−1);
h 247 + (−30) + (−217);
i 328 + [54 + (−44)];
j (−125) + 125 + (−32);
k (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4. BỬU
d Bài 7. Tính tổng tất cả các số nguyên x thỏa mãn G
a −6 < x < 6;
b −5 < x < 0;
c −1 < x ≤ 4;
d −10 < x < 5; AN
e −10 ≤ x ≤ 10;
f −2009 < x < 2010; g −5 < x < 5;
h −6 < x < 0. QU d TẠ
Bài 8. Tính tổng tất cả các số nguyên x thỏa mãn
a −8 < x < 0;
b −4 ≤ x ≤ 4;
c −100 < x < 99;
d −3 < x < 3; THPT
e −5 < x ≤ 4;
f −5 ≤ x ≤ 5;
g −4 ≤ x < 3;
h −6 < x < 6; - G
i −5 < x < 0;
j −2 ≤ x < 5;
k −10 < x < 5;
l −10 ≤ x ≤ 10. 0976071956
d Bài 9. Tính hợp lý DŨN
a 328 + [54 + (−328) + (−44)] MA ;
TH.NDb (−125) + [432 + 125 + (−32)];
c 647 + [88 + (−647) + 912] + (−1000);
d (−540) + 2010 + (−460) + 1000; GỌC N
e (−132) + [(−868)?+ Lớp (−234) TO + ÁN 1234] + THẦ 200; fY( DŨNG −101) + (− ? 500) + (−399);
g (−200)+(−185)+1777+(−315)+(−1477);
h (−404) + 1002 + (−2000) + 1998 + (−596);
i (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 +
j 1 + (−6) + 11 + (−16) + 21 + (−26) + 31 + GUYỄN N 2 + 3 + 4; (−36).
d Bài 10. Tính hợp lý Thầy
a (−135) + [128 + (−28) + (−47)];
b (−75) + [232 + 75 + (−32)];
c 526 + [88 + (−526) + 12];
d 38 + [(−140) + 62 + (−860)] + 1000;
e (−199) + (−200) + (−201);
f 217 + [43 + (−217) + (−23)];
g 1 + (−3) + 5 + (−7) + 9 + (−11);
h 248 + (−12) + 2064 + (−236);
i (−150) + [235 + 150 + (−35)].
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 9 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 11. Tìm x ∈ Z, biết
a 13 + |x| = | − 6| + 17;
b |x| − 7 = −12;
c x − | − 58| = 136 + 27;
d 12 + x = | − 24| + | − 36|;
e |x| + 25 = 56 + | − 8|;
f |x| − 13 = −49. d Thầy Bài 12. Tính tổng:
a C = (−1) + 5 + (−9) + 13 + . . . + (−81) + 85; N GUYỄN
b D = (−1) + 2 + (−3) + 4 + (−5) + 6 . . . + (−2013) + 2014.
d Bài 13. Một con chim đang ở vị trí 22 m so với mặt đất, nó bay cao lên 19 m nữa. Tính
độ cao của con chim so với mặt đất sau khi bay lên. N d GỌC
Bài 14. Một con cá chuồn đang ở vị trí −2 m so với mực nước biển, nó bay cao lên 5 m
nữa. Tính độ cao của con cá chuồn sau khi bay lên.
d Bài 15. Một tòa nhà có 12 tầng và 3 tầng hầm (tầng trệt được đánh số là tầng 0), hãy DŨN
dùng phép cộng các số nguyên để diễn tả tình huống sau: Một thang máy đang ở tầng số 3,
nó đi lên 7 tầng và sau đó đi xuống 12 tầng. Hỏi cuối cùng thang máy dừng lại ở tầng mấy? G
d Bài 16. Một chiếc tàu ngầm 0976071956
đang ở vị trí −200 m so với mực nước biển, tàu tiếp tục bơi - THPT
lên phía trên thêm 35 m nữa. Hỏi lúc này tàu ngầm sẽ ở vị trí nào? MATH.ND T | Ạ
Bài 3. Phép trừ số nguyên QU ? Lớp TOÁN THẦY DŨNG ? A
KIẾN THỨC CẦN NHỚ AN
• Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: G BỬU
a − b = a + (−b)
• Hai dấu trừ liền nhau đổi thành một dấu cộng:
a − (−b) = a + b
• Số hạng bằng tổng trừ số hạng kia.
• Số bị trừ bằng hiệu cộng số trừ.
• Số trừ bằng số bị trừ trừ hiệu. Page 10 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU B BÀI TẬP d Bài 1. Tính:
a −7 − 9;
b −15 − 8;
c −28 − 32;
d −43 − 26;
e −5 − 9 − 11;
f −6 − 8 − 13;
g −3 − 7 − 25;
h −7 − 4 − 15. d Bài 2. Tính:
a 1 − (−2);
b (−3) − 4;
c (−3) − (−4);
d 5 − (7 − 9);
e (−3) − (4 − 6). BỬU G d Bài 3. Tính AN
a (−9) − (−8);
b 0 − (−9);
c (−8) − 0; QU
d (−7) − (−7);
e 10 − (−3);
f 12 − (−14); TẠ
g (−21) − (−19);
h (−18) − 28; i 13 − 30;
j 9 − (−9);
k 8 − (3 − 7). THPT - d Bài 4. Tính G
a 126 + (−20) + 2004 + (−106);
b (−199) + (−200) + (−201); 0976071956 DŨN
c 1 + (−3) + 5 + (−7) + 9 + (−11);
d (−2) + 4 + (−6) + 8 + (−10) + 12; MATH.ND
e 483 + (−56) + 263 + (−64);
f −87 + (−12) − (−487) + 512. GỌC d Bài 5. Tính N a ? Lớp
b − TOÁN THẦY c DŨNG ?
(−30) + (−23); 52 + 102; (−89) − 9;
d 10 − | − 15| + |0|;
e 3 − | − 14|;
f −| − 8| − (−3);
g 0 − | − 18| + |0|;
h −| − 2| − | − 7|; GUYỄN i 28 + 42;
j (−56) + | − 32|;
k 40 − | − 14|;
l | − 4| + | + 15|; N m 88 + (−23);
n 13 + | − 13|;
o −43 − 26;
p |30| − | − 17|; Thầy
q 13 − 117 + 45 − (−|155|) − (−| − 171|).
d Bài 6. Tìm x ∈ Z, biết a x + 9 = 2;
b x + 10 = −14; c x + 5 = 0; d x + 9 = 2;
e 2 − x = 17 − (−5);
f x −12 = (−9)−15;
g 37+x = 48+(−23);
h 18−x = 11−(−24).
d Bài 7. Tìm x, biết
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 11 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
a |x + 3| = 7;
b |3x + 9| = 42;
c |2x + 6| = 12;
d |x − 4| = | − 10|;
e |3x + 9| − 15 = 27; f |x| + 1 = 3;
g −10 − |5 − x| = −12;
h 13 · |x| = | − 13|;
i 5 · |x + 4| = 20.
d Bài 8. Tìm x ∈ Z, biết Thầy a x + 5 = 0;
b (−4) − x = −9;
c x − 18 = −18; d x + 9 = 3;
e x − (−4) = −6;
f −18 + (12 − x) = −2; N GUYỄN
g 15 − (2 − x) = 5; h |x| = 11;
i |x + 7| = 13;
j |x − 6| + 4 = 8;
k 7 + (−x) = (−5) − (−14);
l 7 − x = 5 − (−14);
m −18 + x = −8 + 13. N GỌC
d Bài 9. Tìm x, biết
a −(−30) − (−x) = 13;
b −(−x) + 14 = 12;
c x + 20 = −(−23); DŨN
d 15 − x + 17 = −(−6) + | −
e −| − 5| − (−x) + 4 = 3 − f |x| = 5; 12|; (−25); G
g |x − 3| = 1; 0976071956
h |x + 2| = 4;
i 3 − |2x + 1| = (−5). - THPT
d Bài 10. Tính hợp lý MATH.ND
a 371 + 731 − 271 − 531;
b 57+58+59+60+61−17−18−19−20−21. TẠ
d Bài 11. Tính (hợp lý nếu có thể) QU
a |(−9) + (−3)| · 5 + ( ? − Lớp 65); TOÁN THẦ b | Y − 13 DŨNG
| − (−7) + ( ? −16); AN
c 2018 + 2 · 400 − (25 − 10)2; d
210 : 25 · 7 − 25 · 5 − (−2017)0. G
d Bài 12. Tính tuổi thọ của nhà bác học Ác-si-mét, biết rằng ông sinh năm −287 và mất BỬU năm −212.
d Bài 13. Chiếc diều của bạn Minh bay cao 15 m (so với mặt đất). Sau một lúc, độ cao của
chiếc diều tăng 2 m, rồi sau đó lại giảm 3 m. Hỏi chiếc diều ở độ cao bao nhiêu (so với mặt
đất) sau hai lần thay đổi?
| Bài 4. Quy tắc dấu ngoặc A
KIẾN THỨC CẦN NHỚ Page 12 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU Khi bỏ dấu ngoặc
• Có dấu “−” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “−”
thành dấu “+” và dấu “+” thành dấu “−”.
34 − (12 + 20 − 7) = 34 − 12 − 20 + 7 = 22 − 20 + 7 = 2 + 7 = 9.
• Có dấu “+” đằng trước thì tất cả các số hạng vẫn giữ nguyên.
7 + (13 + 2 − 7) = 7 + 13 + 2 − 7 = 20 + 2 − 7 = 22 − 7 = 15. BỬU G B BÀI TẬP AN
d Bài 1. Phá ngoặc theo quy tắc QU TẠ
a −(−8); b −(+5);
c −(−7); d +(−25); e +(+30); f −(+20);
g −(−14);
h −(−5) + (−12); THPT -
i −(−13) − (−10);
j −(+15) − (−12);
k −15 − (+9);
l (−11) − (−13); G
m −(−3 + 7 − 6); n 0976071956
+(−4 − 3 + 5);
o −(5 − 9 + 8 − 3);
p −(−9 + 15 − 4 + 7). DŨN d Bài 2. Tính MATH.ND
a −(−5) + (−12);
b −(−13) − (−10);
c −(+15) − (−12);
d −15 − (+9); GỌC N
e 4 − (−7);
f (−11) − (−13); g (+4) + (−7);
h −| − 13| + | − 15|; ? Lớp TOÁN THẦY DŨNG ?
i −| + 12| + (−14);
j −(−17) − | + 15|. d Bài 3. Tính tổng: GUYỄN N
a −(−5) − (+7) + (+3) + (−8);
b −| − 10| − (−12) + (−18) − (+3);
c −12 − (−9) − (+15) + (+14);
d −(+15) + (−14) + | − 12| − (−8); Thầy
e −| − 3| − | + 7| + | − 2| − (−14);
f −(−15) − | − 10| + | − 9| − | − 5|;
g 14 − (−13) − (+17) + (−12);
h (−12) − (−7) − (−21) + (−32);
i −| − 14| + | − 10| − (−12) + (−8);
j −(−11) + (−5) + (+13) − 21.
d Bài 4. Bỏ ngoặc rồi tính
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 13 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
a (27 + 65) + (346 − 27 − 65);
b (42 − 69 + 17) − (42 + 17);
c (4 + 32 + 6) + (10 − 36 − 6);
d (77 + 22 − 65) − (67 + 12 − 75);
e −(−21 + 43 + 7) − (11 − 53 − 17);
f (−2014) − (148 − 2014);
g (18 + 29) + (158 − 18 − 29);
h (13 − 135 + 49) − (13 + 49). Thầy
d Bài 5. Tính hợp lý:
a (2736 − 75) − 2736;
b (−2002) − (57 − 2002); N GUYỄN
c (5674 − 97) − 5674;
d (−1075) − (29 − 1075).
d Bài 6. Tính hợp lý:
a (83 + 234) − (34 − 17);
b (401 − 98765) + (98764 − 408); N c (91 d (99 GỌC
− 99 + 98) − (−99 + 98);
− 98 + 97) − (99 + 97 + 98);
e 645 + [64 + (−645) + 36];
f [24 + (−67)] − [−67 − (−24)]. DŨN
d Bài 7. Tính hợp lý
a (−283 + 4568) − 4568;
b (−46785) − (1500 − 46785); G
c 12345 − (−314 + 12345); 0976071956
d (38 + 76) + (456 − 38 − 76); - THPT
e (31 − 59 + 28) − (31 + 28);
f (−9) + (9 − 2009) + 2009. MATH.ND d Bài 8. Tính TẠ
a 5 + [−(−12) + (−9)] − [7 − (−10) + 3];
b [5 − (−4) + (−7)] − [−(−8) + (−9) + 1]; QU ? Lớp TOÁN THẦY DŨNG ?
c 13 − [5 − (4 − 5) + 6] − [3 − (2 − 7)];
d (14 − 12 − 7) − [−(−3 + 2) + (5 − 9)]. AN G
| Bài 5. Quy tắc chuyển vế BỬU A
KIẾN THỨC CẦN NHỚ
• Khi chuyển một số hạng từ vế này sang vế kia của đẳng thức, ta phải đổi dấu số
hạng đó: dấu “+” thành dấu “−” và dấu “−” thành dấu “+”.
A + B + C = D Ñ A + B = D − C
• Phương pháp giải toán tìm x: Phá ngoặc, sau đó chuyển x sang vế trái và số sang vế phải. Page 14 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU B BÀI TẬP
d Bài 1. Tìm x, biết
a x + (−5) = −(−7);
b x − 8 = −10;
c x − (−12) = 14;
d −(−30) − (−x) = −(+13);
e −(+12) − (+x) = 20;
f (−34) − x = −(−45);
g −15 − x = −(−7);
h x − (−10) = −14;
i −x + (−15) = −13;
j 16 + x = −(−15);
k 7 − x = 8 − (−7);
l x − 8 = (−3) − 8; BỬU m n x − G
2 − x = 17 − (−5);
12 = (−9) − 15.
d Bài 2. Tìm x, biết: AN
a 5x + 17 = x − 47;
b −2x − 15 = x − 6; QU
c 11 − (27 − 3) = x − (13 − 4);
d 4 − (27 − 3) = x − (13 − 4); TẠ
e 2 − x = 17 − (−5);
f x − 12 = (−9) − 15;
g 9 − 25 = (7 − x) − (25 + 7). THPT -
d Bài 3. Tìm x, biết G
a −(+8) + (11 − x) = 10;
b x + | − 5| + | + 7| = −(−9);
c 15 − x = |13| − (−4);
d x − | − 3| = −9 + | − 8|; 0976071956
e −| − 2| − x = 8 − | − 9|;
f | − 5| − x + (−11) = −3. DŨN
d Bài 4. Tìm số nguyên x, biết:MATH.ND
a 9 − 25 = (7 − x) − (25 + 7);
b 11 − (15 + 11) = x − (25 − 9); GỌC
c 4 − (27 − 3) = x − (13 − 4);
d (−10 + 5) − (4 − x) = 12 − (5 − 6). N
d Bài 5 (?). Tìm số ? Lớp nguyên x, TO biết: ÁN THẦY DŨNG ?
x − (17 − x) = x − 7.
d Bài 6. Tìm x, biết: GUYỄN N a |x| = 2;
b |x + 2| = 0;
c |x + 3| = 7;
d |x − 5| = (−5) + 8; Thầy
e |x + 3| − 9 = −5;
f |x − 2| − 6 = 9;
g |x − 1| − 7 = 12;
h |x + 7| = | − 7| + 13 − (−4);
i 3 + |x + 5| = 11 − 2;
j |x + 3| − (−5) = 13 − (+4).
d Bài 7. Tìm x, biết:
a (|x| + 73) − 26 = 70;
b |x − 7| − (−15)0 = | − 6|;
c 3 · 23 − |x| = 42.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 15 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
| Bài 6. Phép nhân và chia hai số nguyên A
KIẾN THỨC CẦN NHỚ
Quy tắc nhân và chia hai số nguyên: Thầy
• Cùng dấu Ñ Dương. • Khác dấu Ñ Âm. N GUYỄN B BÀI TẬP d Bài 1. Tính N
a (−225) · 8;
b (−7) · 8;
c 6 · (−4); GỌC
d (−12) · 12;
e 450 · (−2);
f (−260) : (−20);
g (−100) : (−5); h (+5) · (+11);
i (−6) · 9; DŨN
j 23 · (−7);
k (+4) · (−3);
l (−250) · (−8); G
m (−2500) : (−100); n (−11)2; o (−5)2; 0976071956 - THPT p (−2)3; q (−4)3; r (−42) : 2; MATH.ND s 10 : (−10); t (−51) : 17. TẠ
d Bài 2. Tìm x, biết QU
a (−8) · x = −72; ? Lớpb TO 6 · xÁN = − THẦ 54; Y DŨNG c ( ?
−4) · x = −40; AN
d (−6) · x = −66;
e 12 · x = −36;
f (15 − 22) · x = 49; G
g (3 + 6 − 10) · x = 200. BỬU
d Bài 3. Tính hợp lý (nếu có thể)
a (−15) + 13 + 15 · 62 − 35;
b (−6)2 · 5 + (−4)2 : 16;
c 7 · (−8)2 + (−3)3 + | − 2016|0; d ( + 35 + 20090
−2)2 · 23 − 35 − (−1)101;
e (−5)2 · 4 + 108 : (−3)3;
f (−6 − 3) · (−6 + 3);
g (−5 + 8) · (−7);
h (−4 − 14) : (−3);
i (−8)2 · 33;
j 92 · (−5)4;
k | − 20| : (−5) − 2 · |3 − 5|. Page 16 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 4. Tìm x, biết:
a 26 − 3x = 5;
b −3x + 19 = 10;
c x + 87 = −13;
d 4 − x = −10;
e 5 − x = −17; f 2x + 36 = 6;
g 128 − 3(x + 4) = 23;
h 75 − 5(x − 7) = 105;
i 2(x + 5) + 8 = −| − 3| − 13;
j 20160 − 5x = −49; BỬU
k 2 · x + (−73) = −29;
l 14 + 3 · (7 − x) = 20; G
m 2 · x − 18 = 10; n 3x + 26 = 5; AN
o 35 − 5 · (x + 3) = | − 15|;
p | − 140| : (x − 8) = |7|; QU
q 2x + (−49) = (−5) · 32. TẠ d Bài 5.
Trong trò chơi bắn bi vào các hình trong hình vẽ trên mặt đất (như −5 −3 THPT
hình bên), bạn Hải bắn được hai viên điểm 5, một viên điểm 10, ba - 0
viên điểm −3 và một điểm −5. Bạn Dũng bắn được ba viên điểm 5, 5 G
một viên điểm −5 và ba viên điểm 0. Hỏi bạn nào điểm cao hơn. 10 0976071956 DŨN MATH.ND
d Bài 6. Một xí nghiệp may gia công có chế độ thưởng và phạt như sau: Một sản phẩm tốt GỌC
được thưởng 50 000 đồng. Một sản phẩm có lỗi bị phạt 40 000 đồng. Tháng vừa qua chị Mai N
làm được 40 sản phẩm tốt và 8 sản phẩm có lỗi. Hỏi lương chị Mai trong tháng vừa qua là ? Lớp TOÁN THẦY DŨNG ? bao nhiêu tiền.
d Bài 7. Một bạn học sinh làm bài kiểm tra Anh văn đầu vào để xếp lớp ở trung tâm anh GUYỄN
ngữ. Bạn buộc phải làm hết 50 câu hỏi, với cách tính điểm như sau: Mỗi câu đúng bạn được N
2 điểm, mỗi câu sai bạn bị trừ 1 điểm. Với 40 câu đúng và 10 câu sai, các em hãy tính số
điểm bạn đạt được cho bài kiểm tra Anh văn này. d Thầy
Bài 8. Mỗi ngày Mai được mẹ cho 20 000 đồng, Mai ăn sáng hết 10 000 đồng, Mai mua
nước ngọt hết 5 000 đồng, phần tiền còn lại Mai để vào tủ tiết kiệm. Hỏi sau 15 ngày, Mai có
bao nhiêu tiền tiết kiệm.
d Bài 9. Hai ô tô cùng xuất phát từ thành phố A. Ô tô thứ nhất đi đến thành phố B với vận
tốc 45 km/h, còn ô tô thứ hai đi đến thành phố C với vận tốc 50 km/h. Biết rằng ba thành
phố cùng năm trên một đường thẳng và thành phố A nằm giữa hai thành phố B và C. Hỏi
sau khi cả hai ô tô đi được 2 giờ thì hai ô tô cách nhau bao nhiêu km?
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 17 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
| Bài 7. Tính chất của phép nhân A
KIẾN THỨC CẦN NHỚ
a Tính chất giao hoán a · b = b · a Thầy
b Tính chất kết hợp
(a · b) · c = a · (b · c) N GUYỄN c Nhân với số 1
a · 1 = 1 · a = a
d Tính chất phân phối của phép nhân đối với phép cộng N GỌC
a · (b + c) = a · b + a · c
e Tính chất phân phối của phép nhân đối với phép trừ DŨN
a · (b − c) = a · b − a · c G 0976071956 - B BÀI TẬP THPT
d Bài 1. Dùng tính chất phân phối MA của TH.ND
phép nhân với phép cộng để tính TẠ
a 5 · (−3 + 2) − 7 · (5 − 4);
b −3 · (4 − 7) + 5 · (−3 + 2); QU
c 4 · (5 − 3) + 2 · (−4 ? + 6) Lớp ; TOÁN THẦ d − Y 8 · DŨNG
(4 − 5) + 7 · ? (8 − 4). AN d Bài 2. Tính nhanh G
a 26 · (−125) − 125 · (−36);
b 20 · 17 − 4 · 5 · 7; BỬU
c 100 · 23 − 25 · 23 · 4;
d 48 − 6 · (12 + 8);
e 54 − 6 · (17 + 9). d Bài 3. Tính
a (26 − 6) · (−4) + 31 · (−7 − 13);
b (−18) · (55 − 24) − 28 · (44 − 68). d Bài 4. Tính nhanh
a (−4) · (+3) · (−125) · (+25) · (−8);
b (−67) · (1 − 301) − 301 · 67. Page 18 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 5. Thực hiện phép tính (tính nhanh nếu có thể)
a 33 · (17 − 5) − 17 · (33 − 5);
b (−39) · 217 + 217 · (−61);
c (−79) · 79 + 79 · (−21);
d 3 · (−5)2 + 2 · (−6)0 − 56 : 7;
e (−98) · (1 − 246) − 246 · 98. BỬU G AN QU TẠ THPT - G 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 19 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 20 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? 3 Phân số Chương
Học sinh quét mã QR để tham gia nhóm học tập: Nhóm TOÁN QUẬN 7 BỬU G
| Bài 1. Khái niệm phân số. Phân số bằng nhau AN QU A
KIẾN THỨC CẦN NHỚ TẠ
• Phân số có dạng a với a, b ∈ Z, b 6= 0, a là tử số, b là mẫu số của phân số. b
• Nếu a = c thì a · d = b · c (tích chéo bằng nhau). b d THPT - G B BÀI TẬP d 0976071956
Bài 1. Viết các phân số sau: DŨN
a Bốn phần mười một;
MATH.NDb Âm chín phần tám;
c Mười hai phần năm; d Âm bảy phần ba; GỌC N e Hai phần bảy;
? Lớp TOÁN THẦfY DŨNG Âm năm ? phần chín;
g Mười một phần mười ba;
h Mười bốn phần năm; GUYỄN i Một phần hai;
j Mười chín phần bảy. N
d Bài 2. Viết các phép chia sau dưới dạng phân số: a b c d e Thầy 3 : 2; 3 : 11; (−4) : 7; 5 : (−13); 9 : (−13);
f (−6) : (−11); g 1 : 3; h 2 : 5; i (−3) : 7; j (−7) : 9; k 4 : (−9); l 2 : (−7);
m (−3) : (−8);
n (−2) : (−11);
o x chia cho 3 (x ∈ Z);
p 5 chia cho a (a ∈ Z, a 6= 0).
d Bài 3. Tìm các số nguyên x, y, z biết rằng 21 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng x 16 y x 6 a = ; b = −2; c = ; 5 40 25 5 7 21 −5 20 4 8 −10 30 d = ; e = ; f = . y 28 −x 6 y 33
d Bài 4. Tìm các số nguyên x, y, z biết rằng Thầy x x x a = −8; b = −14; c = −14; 45 15 3 21 7 49 4 2 −7 −6 3 d = ; e = x ; f = ; N x 25 3 15 y −7 GUYỄN 80 −7 5 x g = −x ; h = ; i = −7. −96 6 14 x 10 5
d Bài 5. Tìm các số nguyên x, y, z biết rằng N 20 9 3 GỌC x −4 a = = 4; b = y = c = = −1; 3 −3; y −x 5 x y 2 x 15 6 −6 d
= −y = z = −18; e = y = z = ; f
= x = −7 = z . DŨN 2 3 −4 9 x 4 16 −8 12 8 y −18
d Bài 6. Tìm x, y biết G x − 2 63 3 2x − 2 a = −4; 0976071956 b = ; c = −10; - 12 3 x − 7 147 3 15 THPT x − 1 15 MA 3x − TH.ND 1 5 x + 3 1 d = ; e = ; f = . 7 21 12 3 15 3 TẠ
d Bài 7. Tìm x, y biết QU 6 4 ? Lớp x TOÁN THẦ x Y − 2 DŨNG 5 + x ? 6 24 a = ; b = x + 16; c = ; d = . 7 35 4 3 AN x x + 27 x x − 27 G
| Bài 2. Tính chất cơ bản của phân số. Rút gọn phân số BỬU A
KIẾN THỨC CẦN NHỚ
• Nhân cả tử và mẫu cho một số khác 0:
a = a · m (m 6= 0). b b · m
• Chia cả tử và mẫu cho một số khác 0:
a = a : n (n 6= 0). b b : n Page 22 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU B BÀI TẬP
d Bài 1. Điền số thích hợp vào ô trống: 2 3 4 5 a = ; b = ; c = ; d = ; 3 60 4 60 5 60 6 42 1 −3 15 10 e = ; f = ; g 1 = = = = −8 = . 4 20 4 2 −4 6
d Bài 2. Ta có thể biết được 25 phút chiếm bao nhiêu phần của một giờ bằng cách đổi 25 5 25 phút = BỬU
60 giờ = 12 giờ.
Các số phút sau đây chiếm bao nhiêu phần của một giờ: G a 15 phút; b 30 phút; c 45 phút; d 20 phút; AN e 40 phút; f 10 phút; g 5 phút; h 2 phút. QU
d Bài 3. Rút gọn các phân số sau: TẠ 30 −3 −9 −6 −8 45 a ; b ; c ; d ; e ; f ; −84 21 24 −9 10 25 THPT 36 40 −28 15 56 −18 - g ; h ; i ; j ; k ; l . 24 55 40 −45 70 90 G
d Bài 4. Rút gọn các phân số sau: 0976071956 2 · 14 3 · 5 12 · 5 3 · 7 · 11 a ; b ; c ; d . DŨN 7 · 8 8 · 24 3 · 12 22 · 9 d MATH.ND
Bài 5. Bộ răng đầy đủ của một người trưởng thành có 32 chiếc trong đó có 8 răng cửa, 4
răng nanh, 8 răng cối nhỏ và 12 răng hàm. Hỏi mỗi loại chiếm mấy phần của tổng số răng? GỌC
(Viết dưới dạng phân số tối giản) N ? Lớp TOÁN THẦY DŨNG ?
| Bài 3. Quy đồng mẫu số nhiều phân số GUYỄN A
KIẾN THỨC CẦN NHỚ N
Các bước quy đồng mẫu nhiều phân số với mẫu số dương: Thầy
• Tìm mẫu số chung (số chia hết cho tất cả các mẫu).
• Tìm thừa số phụ (lấy mẫu chung chia cho từng mẫu).
• Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng. 5 7
# Ví dụ 1. Quy đồng mẫu các phân số sau: và . 12 −30
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 23 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP
d Bài 1. Quy đồng mẫu số các phân số sau: 1 3 1 5 3 5 1 7 a và ; b và ; c và ; d và −1; e và −3; 5 10 7 14 4 −6 6 4 20 5 2 3 5 7 −1 −1 Thầy f và −3; g và ; h và −2; i và j và −3. 5 25 −6; −8 12 24 3 5 −2 4
d Bài 2. Thực hiện quy đồng mẫu các phân số sau: N GUYỄN 7 13 17 −4 8 −6 27 a ; và −9; b
; −5 và −64; c ; và −10; d ; và −3 . 30 60 40 60 18 90 7 9 21 −35 −180 −28
d Bài 3. Thực hiện quy đồng mẫu các phân số sau: 2 5 1 7 1 −7 5 N a ; và ; b ; và −5; c ; và −1; 9 18 3 15 5 6 40 60 30 GỌC −3 5 −4 8 3 7 d ; và −21; e ; và −10; f ; −11 và . 16 24 56 7 9 21 −20 −30 15 DŨN
d Bài 4. Quy đồng các phân số sau: 15 17 −7 1 −6 27 G a và −17; b và −9; c và ; d ; và −3; 28 30 320 80 33 35 28 0976071956 −10 −180 - THPT −5 3 9 −2 3 5 7
e 3; −3 và −5 ; f ; và ; g ; và −1; h ; −3; −2 và . 5 6 −14 MA 20 TH.ND 70 5 25 3 12 8 3 24
d Bài 5. Quy đồng các phân số sau: TẠ −31 13 1 11 2 1 2 QU a và ; b ; −7 và ; c ; và ; 36 60 ? Lớp TO 2 ÁN 9 THẦ 12 Y DŨNG−? 7 3 5 AN −1 14 6 −7 1 −1 3 3 d ; và ; e ; và 1; f ; và . 5 20 21 21 −3 5 −12 −4 G BỬU
| Bài 4. So sánh phân số A
KIẾN THỨC CẦN NHỚ
Hai phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn. Các bước so sánh: • Quy đồng mẫu số.
• So sánh hai phân số cùng mẫu. Page 24 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU B BÀI TẬP
d Bài 1. So sánh các phân số sau: 7 24 −3 7 14 60 a và ; b và ; c và ; 36 36 10 −10 21 72 −4 8 7 13 5 d ; và −10; e ; và −9; f
; −3 và −45. 7 9 21 30 60 40 21 28 108 2 4 d Bài 2.
a Thời gian nào dài hơn: giờ hay giờ? 3 5 BỬU 2 3
b Đoạn nào ngắn hơn: mét hay mét? 3 5 G 6 7
c Khối lượng nào lớn hơn: kg hay kg? 7 8 AN
d Bài 3. So sánh các phân số sau: QU 5 15 5 4 15 2 −2 11 7 4 a ; và ; b ; và ; c ; −5 và 4; d ; và . 24 24 8 9 54 3 −5 8 −20 −30 15 TẠ
d Bài 4. Sắp xếp các phân số sau theo thứ tự tăng dần: 9 20 42 30 14 1 1 1 4 a ; −25; ; ; ; và −13 b
; ; −2; ; −2; −1; và THPT 19 19 19 19 19 19 19 3 5 15 6 −5 10 15 - 1 2 d Bài 5.
a Thời gian nào dài hơn: giờ hay giờ? G 2 3 3 09760719565
b Đoạn nào ngắn hơn: mét hay mét? 4 6 DŨN 9 11
c Khối lượng nào lớn hơn: MA kg TH.ND hay kg? 5 6 4 7 23 d GỌC
Bài 6. Lớp 6A có
số học sinh thích bóng bàn,
số học sinh thích bóng chuyền và 5 10 25 N
số học sinh thích bóng đá. Hỏi môn bóng nào được ít bạn thích nhất? ? Lớp TOÁN THẦY DŨNG ?
| Bài 5. Phép cộng và trừ phân số GUYỄN N A
KIẾN THỨC CẦN NHỚ Quy tắc: Thầy a a b a
+ b = a + b. b − = a − b. c c c c c c Các bước:
• Rút gọn, chuyển mẫu âm thành mẫu dương. • Quy đồng mẫu số.
• Cộng (trừ) các phân số cùng mẫu.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 25 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP
d Bài 1. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể): 2 3 1 2 5 1 a + ; b + −4; c + ; d + −3; 7 7 7 7 3 7 6 4 −3 3 6 3 −5 6 5 Thầy e + ; f ; h . 4 5 42 − 21 g 8 − 2; 42 − 21
d Bài 2. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể): N GUYỄN 1 1 −1 1 3 5 −11 a ; b ; c ; d + 1; 8 − 2 16 − 15 5 − 6 12 1 2 −5 1 2 1 3 −1 e ; f ; g + ; h ; 3 − 9 7 − 3 7 4 5 − 2 N GỌC −2 −3 1 −5 5 −2 7 i ; j ; k + ; l . 5 − 4 −5 − 6 9 12 7 − 2
d Bài 3. Tìm x, biết DŨN x 5 3 1 2 x 3 7 a = + −19; b + ; c ; d = + . 5 6 30 x = −1 2 4 x = 2 − 3 30 5 30 G
d Bài 4. Hai người cùng làm 0976071956
một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, - THPT
người thứ hai mất 3 giờ. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần công việc? MATH.ND T
d Bài 5. Thực hiện cộng (trừ) các phân số (rút gọn kết quả nếu có thể): Ạ QU −3 1 2 7 1 1 a + ; b ; c + −5; d + −4; 5 5 ? Lớp 9 − 9 TOÁN THẦ 6 Y DŨNG 6 ? 14 7 AN 23 1 8 1 3 5 3 5 e ; f 3 − ; g + ; h + + −1. G 36 − 24 11 3 4 − 12 14 8 2 BỬU
d Bài 6. Tìm x, biết 7 x 5 5 4 a x = + −1; b + = −1; c + . 5 5 x = −1 9 3 11 −9
d Bài 7. Hai vòi nước cùng chảy vào bể, riêng vòi thứ nhất chảy trong 10 giờ thì đầy bể,
riêng vòi thứ hai thì chảy trong 15 giờ đầy bể. Hỏi nếu cùng chảy thì trong một giờ cả hai
vòi chảy được bao nhiêu phần bể?
d Bài 8. Tìm x, biết 3 1 −5 1 a x + = ; b = 0; c . 4 2 x + −5 7 7 − x = 14 Page 26 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU | Bài 6. Luyện tập
d Bài 1. Thực hiện phép tính −7 Å 1ã 2 Å 5 ã Å −1 3 ã Å 3 5 ã a + 1 + ; b + + −6 ; c + + −3; d + + −5. 21 3 15 9 9 5 12 4 4 12 −4
d Bài 2. Thực hiện phép tính −3 5 −8 7 −5 8 −5 Å −6 ã a + + −4; b + + −9; c + −2 + ; d + + 1 . 7 13 7 17 8 17 21 21 24 11 11
d Bài 3. Thực hiện phép tính BỬU 2 5 3 −7 13 3 5 3 5 a + −3; b ; c + −1; d + −1 . G 9 −12 − 4
5 − 10 − −20 14 − −8 2 4 3 − 18
d Bài 4. Tìm x, biết AN 2 3 3 1 1 −1 2 a ; c ; d + . 15 − x = 10 b 10 − x = 1; 4 − x = 20 3 x = 5 QU
d Bài 5. Ba người cùng làm một công việc. Nếu làm riêng thì người thứ nhất phải mất 4 TẠ
giờ, người thứ hai mất 3 giờ, người thứ ba mất 6 giờ. Hỏi nếu làm chung thì mỗi giờ cả ba
người làm được mấy phần công việc? d THPT
Bài 6. Vòi nước A chảy vào một bể không có nước trong 4 giờ thì đầy. Vòi nước B chảy -
đầy bể ấy trong 5 giờ. Hỏi: G
a Trong 1 giờ, mỗi vòi chảy được lượng nước bằng mấy phần bể? 0976071956
b Trong 1 giờ, cả hai vòi cùng chảy thì được lượng nước bằng mấy phần bể? DŨN
d Bài 7. Vòi nước A chảy đầy MA một TH.ND
bể không có nước mất 3 giờ, vòi nước B chảy đầy bể đó
mất 4 giờ. Hỏi trong 1 giờ, vòi nào chảy được nhiều nước hơn và nhiều hơn bao nhiêu? GỌC 3 8
d Bài 8. Một khu đất hình chữ nhật có chiều dài là km, chiều rộng là km. N 4 5
a Tính nửa chu vi ? Lớp của khu TO đất ÁN (bằng THẦ km). Y DŨNG ?
b Chiều dài hơn chiều rộng bao nhiêu km? 1 d GUYỄN
Bài 9. Một khay đựng 4 quả chuối, 1 quả táo và 1 quả cam. Biết rằng quả táo nặng kg, 8 N 1 1 quả cam nặng kg, quả chuối nặng
kg. Hỏi khay nặng bao nhiêu kg nếu khối lượng 3 10 5 tổng cộng là kg? 4 Thầy
| Bài 7. Phép nhân phân số A
KIẾN THỨC CẦN NHỚ Áp dụng công thức: A C · = A · C B D B · D
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 27 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng B BÀI TẬP
d Bài 1. Thực hiện tính (rút gọn nếu có thể): −1 5 −7 −3 6 −15 −5 −11 a ; b ; c ; d 3 ; e 0 . 3 · 7 4 · 5 25 · 4 · 6 · 13
d Bài 2. Thực hiện tính (rút gọn nếu có thể):
Å −4ã Å−25ã 5 Å 7 ã Å −13ã Å 15ã 9 5 a ; b ; c 15 ; e ; Thầy 15 · 8 − · d − · 21; −14· 10 25 14 −11 · 18 −1 5 −15 8 −21 8 −5 −3 f ; g ; h ; j . 3 · 7 16 · i (−17) · −25 24 · −14 13 · 26; 52 N
d Bài 3. Thực hiện tính (rút gọn nếu có thể): GUYỄN 2 1 10 7 27 1 Å 4 1ã Å 3 8 ã Å−2ã2 a + ; b ; c + ;d . 3 5 · 7 12 − 7 · 18 5 2 · 13 − 13 7
d Bài 4. Tìm x, biết x 3 −5 4 4 14 1 3 a = −2 ; b = −2 ; c x + = −1 ; d x − = −4 . N 8 5 · 16 x 3 · 15 5 7 · 15 3 5 · 4 GỌC
d Bài 5. Thực hiện tính (rút gọn nếu có thể): −5 12 −1 1 −2 5 a ( −3 −2) · ; b ; c ; d ; 7 · 4 25 4 · 3 5 · −9 −3 16 8 −9 5 3 DŨN e ; f ( ; g ; 4 · − −5) · · h 17 15 11 18 5 · (−15).
d Bài 6. Tìm x, biết G 1 5 2 x 4 a x − = ; b = −5 . 4 8 · 3 0976071956 126 9 · 7 - THPT
d Bài 7. Thực hiện phép tính (tính nhanh nếu có thể) 1 1 1 2 1 4 Å 1 1 1 1ã 2 Å−3 6 7 3ã a + + ; b MA + TH.ND + + c + ; 7 · 5 7 · 5 7 · 5 2 3 4 5 · 30; 9 · 4 · −5 6 · 5 T 7 3 12 1 5 11 5 4 5 3 Ạ d ; e + + .
12 · 10 · 7 · (−10)−3
12 · 17 12 · 17 12 · 17 QU
d Bài 8. Lúc 7 giờ bạn ? LanLớp đi xe TO đạp ÁN từ A THẦ đến B Y với DŨNG vận tốc 12 ? km/h. Đến 7h30 phút bạn
nam đạp xe đạp từ B về A với vận tốc 15 km/h. Hai bạn gặp nhau tại C lúc 7h50 phút. Tính AN quãng đường AB. G 3
d Bài 9. Tính chu vi và diện tích của một mảnh đất hình chữ nhật biết chiều rộng là km 4 BỬU 9 và chiều dài là km. 4
d Bài 10. Thực hiện phép tính (tính nhanh nếu có thể) 8 15 8 6 8 2 6 1 2 1 5 a ; b + + ;
19 · 7 − 19 · 7 − 19 · 7 7 7 · 7 7 · 7 4 13 4 40 5 5 5 2 5 14 c ; d + .
9 · 3 − 3 · 9 7 · 11
7 · 11 − 7 · 11
d Bài 11 (?). Tính nhanh 1 3 9 − 17 − 1 11 a
+ 5 − 325 − 3 125 − 3 625 ; 4 4 9 − 47 − 4 11 5 − 4 25 − 4 125 − 4 625 1 1 1 1 1 1 b + + + + + . 1 . . . + · 2 · 3 2 · 3 · 4 3 · 4 · 5 4 · 5 · 6 97 · 98 · 99 98 · 99 · 100 Page 28 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
| Bài 8. Phép chia phân số A
KIẾN THỨC CẦN NHỚ Áp dụng công thức:
A : C = A D · = A · D B D B C B · C B BÀI TẬP BỬU
d Bài 1. Tìm số nghịch đảo của: G 3 1 4 a
; − ; −21; 0, 6; 1, 5; b
; −1; −2; 10; −1, 2. AN 4 2 5 3
d Bài 2. Thực hiện phép tính (rút gọn nếu có thể): QU 4 7 3 15 2 19 1 2 3 a b − c d e − f TẠ : ; : ; : −1; 15 : −3; : ( 38); : : . 5 9 8 22 7 2 14 21 2 3 4
d Bài 3. Tìm x, biết: THPT 3 2 8 11 2 4 2 1 a x · = ; b x : = ; c : x = −1; d = ; - 7 3 11 3 5 4 7 · x − 3 5 G 2 7 1 1 4 4 5 1 1 12 e ; f = ; g + : ; h = . 9 − 8 · x = 3 x = 0976071956 3 − 2x 3 5 7 6 5 x − 7 3 d DŨN
Bài 4. Thực hiện phép tính (rút gọn nếu có thể): 12 16 9 6 MA 7 TH.ND 14 −12 3 a : ; b : ; c : ; d 5 : −15 ; e : ( f : −6. 5 15 8 5 5 25 24 25 −15); 14 −7 GỌC 1
d Bài 5. Người ta đóng 120 lít nước khoáng vào loại chai
lít. Hỏi đóng được tất cả bao N 2 nhiêu chai? ? Lớp TOÁN THẦY DŨNG ?
d Bài 6. Tính chu vi của một cái sân hình chữ nhật biết diện tích sân là 40 m2 và chiều 2 rộng bằng chiều dài. 5 GUYỄN
d Bài 7. Tìm x, biết: N −3 2 4 5 5 1 3 −6 9 24 a x · = + ; b ; c = + ; d ; 4 5 3 6 · x = −7 8 − 16 x : −3 7 14 7
7 − 10 · x = 35 Thầy
d Bài 8. Thực hiện phép tính (rút gọn nếu có thể): 3 9 −48 12 7 −15 6 a : ; b : ; c : −7; d 20 : −10 ; e : ( f : −8. 2 4 55 −8); −11 10 5 12 24 −7 −7
d Bài 9. Thực hiện phép tính (rút gọn nếu có thể): 9 4 Å2 4ã 6 5 8 3 24 3 a : −3; b 24 : −6 ; c : ; d + : 5 ; e 5 : : . 34 17 11 7 5 · 7 7 7 − 9 4 − 5 4
d Bài 10. Tìm x, biết
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 29 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng −2 5 4 2 2 1 3 1 5 1 3 a ; b = ; c = ;
3 − 12 · x = 5 3 · x + 3 5 7x + 2 14
d 2x+ 2x+x = 16.
d Bài 11 (?). Một công việc nếu giao cho người thứ nhất thì làm 10 giờ xong, nếu giao cho
người thứ hai thì làm 15 giờ xong, nếu giao cho người thứ ba làm thì 30 giờ xong. Hỏi nếu
cả ba người cùng làm công việc ấy thì mất bao nhiêu giờ?
d Bài 12 (?). Một ô tô đi quãng đường AB với vận tốc 40 km/h. Lúc về xe đi quãng đường Thầy
BA với vận tốc 50 km/h. Thời gian cả đi lẫn về không kể thời gian nghỉ là 4 giờ 30 phút. Hỏi
độ dài quãng đường AB là bao nhiêu km? N GUYỄN
| Bài 9. Hỗn số. Số thập phân. Phần trăm A
KIẾN THỨC CẦN NHỚ N GỌC B BÀI TẬP
d Bài 1. Viết các hỗn số sau dưới dạng phân số: 4 1 12 3 3 5 DŨN a 2 ; 5 ; b 2 ; 6 ; 5 7 −113 8 4 −27
d Bài 2. Viết các hỗn số sau dưới dạng phân số: G 3 1 3 0976071956 2 1 3 - a 6 ; 3 ; b 6 ; 3 ; 8 2 −27 7 5 −48 THPT
d Bài 3. Thực hiện phép tính MATH.ND 3 1 3 3 1 3 2 Å 4 2ã T a 6 + 5 ; b 5 ; c 5 ; d 8 3 + 4 . Ạ 8 2 7 − 27 2 · 3 · 4 7 − 9 7 QU
d Bài 4. Tìm x, biết ? Lớp TOÁN THẦY DŨNG ? AN 2 7 1 13 Å 3x ã
a 0, 5x − = ; b = c 5 ; d + 1 : ( 3 12
x : 43 −2,5; , 5x = 15 7 −4) = G −1. 28 BỬU
d Bài 5. Viết phần trăm sau dưới dạng phân số: a 7%; b 45%; c 216%; d 35%.
d Bài 6. Thực hiện phép tính 5 9 1 3 1 2 1 2 a 3 ; b 7 ; c + 3 ; d ; 6 − 110 8 − 54 −57 5 −23 − 17 1 2 Å 2 3ã 2 3 Å 4 3 ã Å 4 7 ã 4 e 6 : 4 ; f 10 + 2 ; g 11 2 + 5 ; h 6 + 3 . 3 9 9 5 −69 13− 7 13 9 11 −49
d Bài 7. Thực hiện phép tính: Page 30 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU 1 3 Å −1ã2 5 Å 7 ã 1 a 25% − 1 + 0 ; b : + ; 2 , 5 · 8 6 · −8 −24 25 − 36% 3 1 12 3 8 c 25% − 1 ; d : (5
2 · (−2019)0 + 0, 5 · 5 5 − 5 , 25 + 75%).
d Bài 8. Thực hiện phép tính: Å −2ã2 5 1 a : + 0 b 65% + 2 + ( 3 9 , 25 · 10%;
, 5 − 14 −3)2; 2 1 11 3 11 11 11 c 30% − 2 + 0 ; d + ; 5 , 2 · 2 13 · 8
13 · 50% + 18 · 13 BỬU Å 2ã 3 3 1
e 1, 2 : 75% − − 3 ; f + 2 G 5 14 4
4 · 0, 5 · (−80) · 0, 01; −25 37 13 −6 1 12 AN g + −25 + −25 ; h 25% + 0 ; 30 · 44 30 · 44 30 · 44 − 14 , 5 · 5 Å ã QU 3 32
i 75% − 1, 25 − 2 : . 4 2 TẠ
d Bài 9. Tìm x, biết 1 4 2 a x − 1 b 2, 5x + = −1, 5; c 60%x + THPT 5x = 60%; 7 3x = 1368; - 1 9 Å 3 ã 1 1 7 d ; e 1, 5− = −2 ; f G
3 · (3x − 2) + 25% = −6 5x + 70% 2
4 − 10x = 1, 75. 0976071956 DŨN
| Bài 10. Tìm giá trị phân số của một số cho trước MATH.ND A
KIẾN THỨC CẦN NHỚ GỌC N
Muốn tìm m của số b cho trước, ta tính m · b. n ? Lớp TOÁN THẦ n Y DŨNG ? 2 2 # Ví dụ 1. của 8 3
, 7 là 3 · 8,7 = 5,8. GUYỄN N B BÀI TẬP d Thầy Bài 1. Tìm 2 1 2 1 a của 15; b của 8 c của −11; d 2 của 5 3 2 , 4; 7 6 3 , 1; 7 3 e 2 của 6 ; f 85% của 25; g 48% của 50; h 0 11 5 , 25 của 10.
d Bài 2. Đổi sang phút: 1 1 3 a giờ; b giờ; c giờ. 6 3 4
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 31 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng 3
d Bài 3. Tuấn có 21 viên bi, Tuấn cho Dũng số bi của mình. Hỏi: 7
a Dũng được Tuấn cho bao nhiêu viên bi?
b Tuấn còn lại bao nhiêu viên bi? d Bài 4. Tìm: Thầy 3 2 5 2 a của 32; b của 1 c của −20; d 1 của 1 4 5 , 5; 4 3 3 , 2; 5 2 e 3 của −5 ; f 25% của 40; g 58% của 100; h 0, 2 của 58. N 7 8 GUYỄN
d Bài 5. Có bao nhiêu phút trong 2 7 4 3 a giờ; b giờ; c giờ; d giờ. 5 12 15 12 3
d Bài 6. Một quả cam nặng 300 g. Hỏi quả cam nặng bao nhiêu? N 4 GỌC
d Bài 7. Đoạn đường sắt Hà Nội - Hải Phòng dài 102 km. Một xe lửa xuất phát từ Hà Nội 2 đã đi được
quãng đường. Hỏi xe lửa còn cách Hải Phòng bao nhiêu km? 3 4 d số táo còn lại. DŨN
Bài 8. Trên đĩa có 24 quả táo. Hạnh ăn 25% số táo. Sau đó, Hoàng ăn 9
Hỏi trên đĩa còn mấy quả táo? G
d Bài 9. Bốn thửa ruộng thu hoạch được tất cả 1 tấn thóc. Số thóc thu hoạch ở 3 thửa 1
ruộng đầu lần lượt bằng ; 0, 4 0976071956
và 15% tổng số thóc thu hoạch ở cả bốn thửa. Tính số thóc - 4 THPT
thu hoạch được ở thửa thứ tư? MATH.ND
d Bài 10. Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng 1 3 T
hành, đường và muối theo thứ tự bằng 5%; và
khối lượng rau cải. Vậy nếu muối 25 Ạ 1000 40
kg rau cải thì cần bao nhiêu kg hành, đường và muối? QU ? Lớp TOÁN THẦY DŨNG ?
d Bài 11. Một lớp có 45 học sinh bao gồm ba loại: giỏi, khá và trung bình. Số học sinh AN 7 5 trung bình chiếm
số học sinh cả lớp. Số học sinh khá bằng
số học sinh còn lại. Tính 15 8 G
số học sinh giỏi của lớp? BỬU
d Bài 12. Bố bạn Lan gửi tiết kiệm 1 triệu đồng tại ngân hàng theo thể thức "có kỳ hạn 12
tháng" với lãi suất 0, 58% một tháng (số tiền lãi mỗi tháng bằng 0, 58% số tiền gửi ban đầu
và sau 12 tháng mới được lấy lãi). Hỏi hết thời hạn 12 tháng ấy, bố bạn Lan lấy ra cả vốn lẫn lãi là bao nhiêu tiền?
| Bài 11. Tìm một số biết giá trị một phân số của nó A
KIẾN THỨC CẦN NHỚ
Muốn tìm một số biết m của nó bằng a, ta tính a : m. n n Page 32 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU 2
# Ví dụ 1. Tìm một số biết của nó bằng 7 3 , 2. Lời giải. 2 3
Số cần tìm là 7, 2 : = 7 = 10 3 , 2 · 2 , 8. B BÀI TẬP
d Bài 1. Tìm một số biết: BỬU 3 3 G a của nó bằng 7 b 1 của nó bằng 4 , 2; 7 −5. AN
d Bài 2. 25% của một quả dưa lê là 1 kg. Hỏi khối lượng quả dưa lê là bao nhiêu kg? QU 5 1 d Bài 3.
kho hàng bằng 1250 kg. Hỏi
kho hàng bằng bao nhiêu kg? 8 4 TẠ
d Bài 4. Tìm một số biết 2 5 a , b − , THPT % của nó bằng 1 5; 3 % của nó bằng 5 8. 5 8 - 2 1 G d Bài 5.
quả dưa hấu nặng 4 kg. Hỏi quả dưa hấu nặng bao nhiêu kg? 3 2 0976071956 2 d Bài 6.
số tuổi của Mai cách đây 3 năm là 6 tuổi. Hỏi hiện nay Mai bao nhiêu tuổi? DŨN 3
d Bài 7. Trong đậu đen nấu MA chín, tỉ TH.ND
lệ chất đạm chiếm 24%. Tính số kg đậu đen nấu chín
để có 1, 2 kg chất đạm? GỌC N
d Bài 8. Trong sữa có 4, 5% bơ. Tính lượng sữa trong một chai, biết rằng lượng bơ trong ? Lớp TOÁN THẦY DŨNG ? chai này là 18 g? 1 1 1
d Bài 9. Một công nhân ăn hết
tiền lương, trả tiền nhà hết
tiền lương, tiêu vặt hết 2 6 5
tiền lương, cuối tháng để dành được 120 000 đồng. Tính lương của người đó? GUYỄN N 2
d Bài 10. Một người mang đi chợ một rổ trứng. Người đó bán
số trứng thì còn lại 54 quả 5
trứng. Tính số trứng người đó mang ra chợ bán. Thầy 3
d Bài 11. Một người bán cam, buổi sáng bán
số cam mang đi, buổi chiều bán 52 quả 5 1
cam. Lúc về còn lại số cam bằng
số cam đã bán. Hỏi người đó mang số cam đi bán là bao 8 nhiêu? 5
d Bài 12 (?). Một lớp học có số học sinh nữ bằng
số học sinh nam. Nếu 10 học sinh nam 3
chưa vào lớp thì số học sinh nữ gấp 5 lần số học sinh nam. Tìm số học sinh nam và nữ của lớp đó?
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 33 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
| Bài 12. Tìm tỉ số của hai số A
KIẾN THỨC CẦN NHỚ B BÀI TẬP Thầy
d Bài 1. Tìm tỉ số của 6 11 a và ; b 9 và 6; c 15 và 0 13 26 , 5; N 3 3 2 GUYỄN d giờ và 20 phút; e và 1 ; f 0 10 8 5 , 6 tạ và 36 kg.
d Bài 2. Tìm tỉ số phần trăm của 1 2 a 5 và 4 ; b 16 và 32; c 0 d 2 3 9 , 3 tạ và 50 kg; , 8 và 0, 7. N
d Bài 3. Tìm tỉ số phần trăm của GỌC 1 1 a 2 và 3 ; b 25 và 50; c 0 d 1 3 9 , 2 tạ và 40 kg; , 2 và 0, 6.
d Bài 4. Năm nay con 16 tuổi, bố 50 tuổi. Tính tỉ số giữa tuổi con và tuổi bố DŨN a Hiện nay; b Cách đây 5 năm; c Sau đây 8 năm. G
d Bài 5. Trong 40 kg nước biển có 2 kg muối. Tính tỉ số phần trăm muối trong nước biển? 0976071956 - d THPT
Bài 6. Biết tỉ số phần trăm nước trong dưa chuột là 97, 2%. Tính lượng nước trong 4 kg dưa chuột? MATH.ND
d Bài 7. Biết tỉ lệ xích là tỉ số giữa khoảng cách trên bản đồ và khoảng cách thực tế. TẠ
a Tìm tỉ lệ xích của một bản đồ biết rằng quãng đường từ Hà Nội đến Thái Nguyên trên QU
bản đồ là 4 cm còn ? Lớp trong TO thực tế ÁN là 80 THẦ km? Y DŨNG ? AN
b Sài Gòn cách Phan Thiết 200 km. Khoảng cách 2 địa điểm này trên bản đồ là 10 cm. G
Tìm tỉ lệ xích của bản đồ? BỬU 1
c Một căn nhà có chiều dài 26 m. Hỏi khi vẽ trên bản vẽ có tỉ lệ xích là thì chiều 100
dài căn nhà là bao nhiêu cm?
| Bài 13. Biểu đồ phần trăm A
KIẾN THỨC CẦN NHỚ B BÀI TẬP d Bài 1. Tính Page 34 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU a 28% của 376; b 9% của 12;
c 2, 6% của 12, 5;
d 3, 5% của 42, 8.
d Bài 2. Cuối học kì I, lớp 6C có 8 bạn xếp loại giỏi, 15 bạn xếp loại khá, còn lại là trung bình.
a Tính tỉ số phần trăm số học sinh lớp 6C được xếp loại giỏi, khá và trung bình so với
tổng số học sinh cả lớp là 40 người.
b Dựng biểu đồ phần trăm dưới dạng ô vuông. BỬU
d Bài 3. Trong một khu vườn có trồng ba loại cây mít, hồng và táo. Số cây táo chiếm 30% G
tổng số cây, số cây hồng chiếm 50% tổng số cây, số cây mít là 40 cây. AN
a Hỏi tổng số cây trong vườn là bao nhiêu? QU
b Dựng biểu đồ ô vuông biểu diễn tỉ số phần trăm số cây mít, hồng, táo so với tổng số cây trong vườn. TẠ
d Bài 4. Muốn đổ bê tông, người ta trộn 1 tạ xi măng, 2 tạ cát và 6 tạ sỏi. THPT
a Tính tỉ số phần trăm từng thành phần của bê tông? - G
b Dựng biểu đồ ô vuông biểu diễn các tỉ số phần trăm đó? 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 35 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU Page 36 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? BỬU G PHẦN AN QU II TẠ THPT - G HÌNH HỌC 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 37 Thầy N GUYỄN N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 2 Góc Chương
Học sinh quét mã QR để tham gia nhóm học tập: BỬU Nhóm TOÁN QUẬN 7 G AN QU
| Bài 1. Nửa mặt phẳng. Góc, số đo góc TẠ A
KIẾN THỨC CẦN NHỚ THPT -
Góc là hình gồm hai tia chung gốc. x G
• Hai tia Ox và Oy tạo với nhau góc O. 0976071956 • Kí hiệu: [ xOy. O DŨN
• Ox, Oy được gọi là hai MA cạnh TH.ND
và O được gọi là đỉnh của [ xOy. y
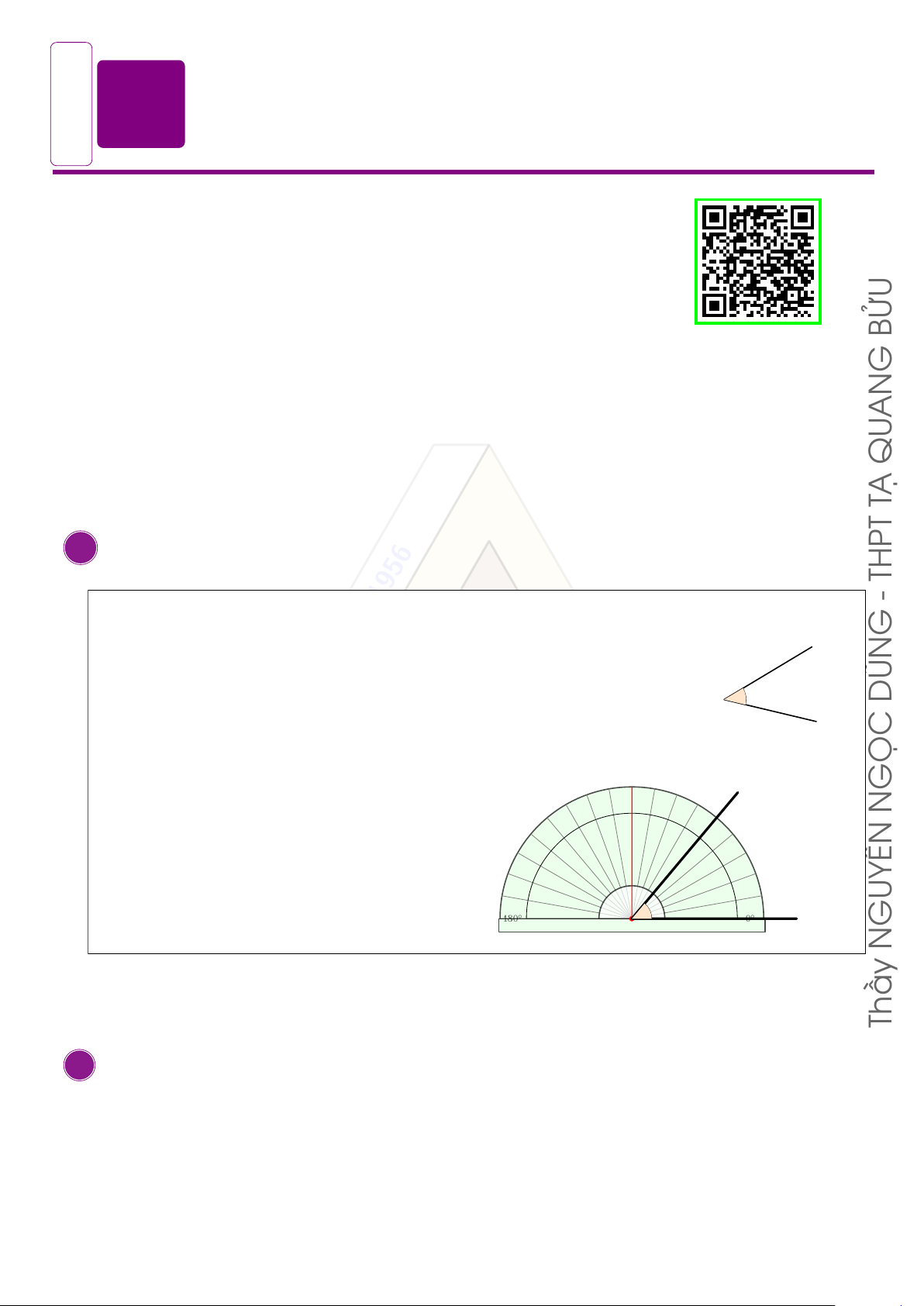
Để đo số đo một góc, ta dùng thước đo độ như sau y GỌC 80◦ 90◦ 100◦ 110◦ 70◦ N 120◦ 60◦ 130◦ 50◦ Số đo góc [ xOy ?ở Lớp hình TO bên ÁN nhìn THẦY DŨNG 140◦ ? 40◦ 150◦ 30◦ thước đo độ ta thấy [ xOy = 50◦. 160◦ 20◦ 170◦ 10◦ 180◦ 180 0◦ 0 GUYỄN O x N Thầy B BÀI TẬP
d Bài 1. Gọi M là điểm nằm giữa hai điểm A, B. Lấy điểm O không nằm trên đường thẳng
AB. Vẽ ba tia OA, OB, OM. Hỏi tia nào nằm giữa hai tia còn lại? d Bài 2. 39 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng Cho hình vẽ bên: B E
a Hãy chỉ ra các điểm thuộc nửa mặt phẳng chứa điểm A A bờ m. m M N
b Hãy chỉ ra các điểm không thuộc nửa mặt phẳng chứa
điểm A bờ m. C Thầy F D
d Bài 3. Cho ba điểm A, B, C không thẳng hàng. Vẽ đường thẳng a cắt các đoạn thẳng AB, N
AC và không đi qua A, B, C. GUYỄN
a Gọi tên hai nửa mặt phẳng đối nhau bờ a.
b Đoạn thẳng BC có cắt đường thẳng a không? N d GỌC
Bài 4. Quan sát hình vẽ bên dưới rồi điền vào bảng sau: N y z x y DŨN C z S G a) 0976071956 M P P - b) c) THPT MATH.ND Hình Tên góc Tên đỉnh Tên cạnh Kí hiệu TẠ a)
góc yCz, góc zCy, góc C C Cy, Cz ‘ yCz, ‘ zCy, “ C QU b) ? Lớp TOÁN THẦY DŨNG ? AN c) G
d Bài 5. Dùng thước đo độ, đo và viết số đo các góc trong các hình vẽ sau: BỬU A y P C z M N a) B C b) c)
d Bài 6. Vẽ góc xOy sao cho [ xOy = 30◦.
d Bài 7. Vẽ góc xBy có số đo bằng 45◦.
d Bài 8. Vẽ góc IKM có số đo bằng 130◦. Page 40 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 9. Vẽ trên cùng một hình góc xOy và góc xOz sao cho [ xOy = 45◦, [ xOz = 60◦.
d Bài 10. Vẽ góc cho biết một cạnh và số đo trong các trường hợp sau: x E y B A a) D C c) F b) d) a [ c [ d [ BỬU BAC = 115◦; b ‘ xCz = 100◦; yDx = 70◦; EF y = 145◦. G | AN Bài 2. Khi nào thì [ xOy + ‘ yOz = [ xOz QU A
KIẾN THỨC CẦN NHỚ TẠ
• Nếu tia Oy nằm giữa hai tia Ox và Oz thì [ xOy + ‘ yOz = [ xOz. THPT
• Hai góc kề bù thì có tổng bằng 180◦. - z G Vì [ xOz và ‘
zOy là hai góc kề bù nên 0976071956 [ xOz + ‘ zOy = 180◦. DŨN MATH.ND x O y GỌC N B BÀI TẬP ? Lớp TOÁN THẦY DŨNG ?
Dạng 1. Các bài toán tính số đo góc
d Bài 1. Vẽ tia OA nằm giữa hai tia OB và OC sao cho [
AOB = 50◦ và \
BOC = 50◦. Tính số GUYỄN đo \ AOC. N
d Bài 2. Trên mặt phẳng vẽ ba tia Ox, Oy, Oz sao cho tia Oy nằm giữa hai tia Ox và Oz với [ xOy = 70◦, ‘
yOz = 60◦. Tính số đo [ xOz. Thầy
d Bài 3. Trên mặt phẳng vẽ ba tia OE, OF, OG sao cho tia OE nằm giữa hai tia OF và OG với [ EOF = 35◦, \
EOG = 50◦. Tính số đo \ F OG.
d Bài 4. Cho tia Ot nằm giữa hai tia Om và On. Biết [ mOt = 70◦, ‘
tOn = 85◦. Tính số đo của góc \ mOn.
d Bài 5. Cho tia AM nằm giữa hai tia AB và AC. Biết \ MAB = 110◦, \
CAM = 20◦. Tính số đo [ BAC.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 41 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
d Bài 6. Trên mặt phẳng vẽ [
AOB = 60◦. Vẽ tia OC sao cho OB nằm giữa hai tia OA và OC với \
AOC = 100◦. Tính số đo \ BOC. d Bài 7. Vẽ [
AOB = 120◦. Vẽ tia OC nằm giữa hai tia OA và OB sao cho \
COB = 50◦. Tính số đo \ AOC. d Bài 8. Vẽ \
AOC = 150◦. Vẽ tia OB nằm giữa hai tia OA và OC sao cho [
AOB = 50◦. Tính Thầy số đo \ BOC.
Quan sát các hình vẽ dưới đây để làm các bài tập bên dưới C z N A A GUYỄN I 32◦ 120◦ 60◦ 45◦ ? x y O B O O B N Hình 1 Hình 2 Hình 3 GỌC
d Bài 9. Hình 1 cho biết tia OA nằm giữa hai tia OB và OC; [ BOA = 45◦, \
AOC = 32◦. Tính số đo \ BOC. d DŨN
Bài 10. Hình 2 cho biết hai góc kề bù xOz và zOy; [
xOz = 120◦. Tính ‘ zOy. 1
d Bài 11. Hình 3 cho biết tia OI nằm giữa hai tia OA và OB. Biết [ AOB = 60◦, ‘ BOI = [ 4AOB. G Tính ‘ BOI và ‘ AOI. 0976071956 - d Bài 12. THPT Hình 4 cho biết y ‘ zOy và [ yOx là hai MA góc TH.ND kề bù, biết [ xOy =
45◦. Tính số đo ‘ yOz. TẠ ? 45◦ QU ? Lớp TOÁN THẦY DŨNG z ? O x AN Hình 4
d Bài 13. Cho hai góc kề bù [ xOy và [ yOy0 sao cho [
xOy = 120◦. Tính [ yOy0. G
d Bài 14. Cho hai góc kề bù [ AOB và \ BOC, biết [
AOB = 72◦. Tính số đo \ BOC. BỬU
d Bài 15. Cho hai góc kề bù [ mOt và \ mOn, biết [
mOt = 125◦. Tính số đo \ mOn.
d Bài 16 (?).
Hình 5 cho biết hai tia AM và AN đối nhau, \ MAP = 33◦, Q P [
NAQ = 58◦, tia AQ nằm giữa hai tia AN và AP. Hãy tính số đo x của [ PAQ. x 58◦ 33◦ M A N Hình 5
Dạng 2. Các bài toán chứng minh tia nằm giữa hai tia Page 42 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 1. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy và Oz sao cho [ xOy = 60◦, [ xOz = 100◦.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? b Tính số đo ‘ yOz.
d Bài 2. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy và Oz sao cho [ xOy = 40◦, [ xOz = 110◦. BỬU
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? G b Tính số đo ‘ yOz. AN
d Bài 3. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia OA, vẽ hai tia OB và OC sao cho [ BOA = 145◦, \ COA = 55◦. QU TẠ
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại? b Tính số đo \ BOC. THPT d -
Bài 4. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ot, vẽ hai tia Om và On sao cho [
tOm = 120◦, ‘ tOn = 90◦. G
a Trong ba tia Ot, Om, 0976071956
On tia nào nằm giữa hai tia còn lại? DŨN b Tính số đo \ mOn. MATH.ND d Bài 5. Vẽ [
AOB = 90◦ và \
AOC = 50◦ sao cho [ AOB kề với \ AOC. GỌC N
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại? ? Lớp TOÁN THẦY DŨNG ? b Tính số đo \ BOC. d Bài 6. Vẽ [ AOB = \
BOC = 80◦ sao cho [ AOB kề với \ BOC. GUYỄN N
a Trong ba tia OA, OB, OC tia nào nằm giữa hai tia còn lại? b Tính số đo \ AOC. Thầy
| Bài 3. Tia phân giác của góc A
KIẾN THỨC CẦN NHỚ
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 43 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
Cách chứng minh tia phân giác
Oy là tia phân giác của [ xOz vì z y
• Tia Oy nằm giữa hai tia Ox và Oz. • [ xOy = ‘ yOz. O x Thầy
Công thức (dùng để tính số đo)
Vì Oy là tia phân giác của [ xOz nên [ xOy = ‘ yOz = [ xOz : 2. N GUYỄN B BÀI TẬP
Dạng 1. Chứng minh tia phân giác
d Bài 1. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ các tia Oy và Oz sao cho N [ xOy = 70◦, [ xOz = 140◦. GỌC
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao? DŨN b Tính số đo ‘ yOz.
c Tia Oy có là tia phân giác của [ xOz không? Vì sao? G
d Bài 2. Trên cùng một nửa 0976071956
mặt phẳng bờ chứa tia Ox, vẽ các tia Oy và Ot sao cho - THPT [ xOy = 60◦, ‘ xOt = 120◦. MATH.ND
a Trong ba tia Ox, Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao? TẠ b Tính số đo ‘ yOt. QU
c Tia Oy có là tia ? phân Lớp giác TO của ÁN ‘ xOt THẦ không? Vì Y sao? DŨNG ? AN
d Bài 3. Cho hai tia Oz, Oy cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, biết góc [ xOy = G 50◦, [ xOz = 130◦. BỬU
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ yOz.
c Vẽ tia Oa là tia đối của tia Ox. Tính số đo góc ‘ zOz.
d Bài 4. Cho hai tia Oz, Oy cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, biết góc [ xOy = 75◦, [ xOz = 150◦.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ yOz. Page 44 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
c Tia Oy có phải là tia phân giác của góc [ xOz không? Vì sao?
d Vẽ tia Oy0 là tia đối của tia Oy. Tính số đo góc [ y0Oz.
d Bài 5. Cho hai tia On, Ot cùng nằm trên nửa mặt phẳng bờ chứa tia Om, biết góc \ mOn = 50◦, [ mOt = 100◦.
a Trong ba tia Om, On, Ot tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ nOt. BỬU
c Vẽ tia Oa là tia đối của tia Om. Tính số đo góc ‘ aOt. G
d Bài 6. Cho hai tia Oy, Ot cùng nằm trên nửa mặt phẳng bờ chứa tia Om, biết góc AN \ mOy = 60◦, [ mOt = 120◦. QU
a Trong ba tia Om, Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao? TẠ b Tính số đo ‘ yOt.
c Tia Oy có là tia phân giác của [ mOt không? Vì sao? THPT -
d Vẽ tia Ob là tia đối của tia Oy. Tính số đo góc ‘ bOt. G
d Bài 7. Trên cùng một nửa0976071956
mặt phẳng bờ là đường thẳng chứa tia Ox, vẽ hai tia OA, OB sao cho [ xOA = 52◦, [ xOB = 104◦. DŨN
a Trong ba tia OA, OB, Ox MA tia TH.ND
nào nằm giữa hai tia còn lại? Vì sao? b GỌC Tính số đo [ AOB. N
c Tia OA có phải ? tia Lớp phân TO giác ÁN của THẦ góc [ xOB Y DŨNG không? Vì sao? ?
d Vẽ tia Oy là tia đối của tia Ox. Tính góc [ yOB. GUYỄN
d Bài 8. Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ hai tia Oy, N Oz sao cho [ xOy = 70◦, [ xOz = 35◦.
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao? Thầy
b Tính số đo góc ‘ yOz.
c Tia Oz có phải là tia phân giác của góc [ xOy không? Vì sao?
d Vẽ tia Om là tia đối của tia Oz. So sánh \ xOm và \ yOm.
d Bài 9. Trên cùng nửa mặt phẳng có bờ chứa tia Ax. Vẽ hai tia Ay, Az sao cho ‘ xAy = 70◦, ‘ xAz = 125◦.
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 45 of 47 #
TRƯỜNG THPT TẠ QUANG BỬU
| Lớp Toán Thầy Dũng
a Hỏi trong ba tia Ax, Ay, Az tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ yAz.
c Vẽ tia Am là tia đối của tia Ax. Hỏi Az có phải là tia phân giác của [ mAy không? Vì sao.
Dạng 2. Áp dụng tính chất tia phân giác Thầy
d Bài 1. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy và Ot sao cho [ xOy = 35◦, ‘ xOt = 70◦. N
a Trong ba tia Ox, Oy, Ot tia nào nằm giữa hai tia còn lại? Vì sao? GUYỄN b Tính góc ‘ yOt.
c Tia Oy có phải tia phân giác của góc ‘ xOt không? Vì sao? N
d Gọi Om là tia đối của tia Ox. Tính góc [ mOt. GỌC
e Gọi Oa là phân giác của góc [
mOt, tính số đo góc [ aOy?
d Bài 2. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia OA và OB sao cho [ xOA = 52◦, DŨN [ xOB = 104◦. G
a Trong ba tia OA, OB, Ox tia nào nằm giữa hai tia còn lại? Vì sao? 0976071956 - b Tính góc [ AOB. THPT
c Tia OA có phải tia phân giác MA của TH.ND góc [ xOB không? Vì sao? TẠ
d Gọi Oy là tia đối của tia Ox. Tính góc [ yOB. QU
e Kẻ tia phân giác Ot ? Lớp của góc TO [ yOB, ÁN tính THẦ số đo Y góc DŨNG ‘ yOt và ‘ BOt ? ? AN
d Bài 3 (Đề HK2 Nhà Bè 2015 - 2016). Trên cùng nửa mặt phẳng bờ là đường thẳng chứa G
tia Ox, vẽ hai tia Ot và Oy sao cho ‘
xOt = 60◦ và [ xOy = 140◦. BỬU
a Trong ba tia Ox, Ot, Oy tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ tOy.
c Vẽ tia Om là tia phân giác của ‘ tOy. Tính số đo \ xOm.
d Bài 4 (Đề HK2 Nhà Bè 2016 - 2017). Cho hai tia Oy, Oz cùng nằm trên một nửa mặt
phẳng bờ chứa tia Ox. Biết [ xOy = 30◦, [ xOz = 120◦.
a Tia nào nằm giữa hai tia còn lại? Tính số đo ‘ yOz.
b Vẽ tia Om là tia phân giác của ‘ yOz. Tính số đo \ xOm. Page 46 of 47
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ?
# | Lớp Toán Thầy Dũng
TRƯỜNG THPT TẠ QUANG BỬU
d Bài 5 (Đề HK2 Nhà Bè 2017 - 2018). Trên cùng nửa mặt phẳng bờ là đường thẳng chứa
tia Ox, vẽ hai tia Oz và Oy sao cho [
xOz = 80◦ và [ xOy = 30◦.
a Trong ba tia Ox, Oz, Oy tia nào nằm giữa hai tia còn lại? Vì sao? b Tính số đo ‘ zOy.
c Vẽ Ot là tia phân giác của [
xOy và tia Om là tia đối của tia Ox. Tính số đo [ tOm.
d Bài 6 (Đề HK2 Nhà Bè 2018 - 2019). Trên cùng nửa mặt phẳng bờ chứa tia Ox, vẽ hai BỬU
tia Oy và Oz sao cho [
xOy = 40◦ và [ xOz = 110◦. G
a Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao? AN b Tính số đo ‘ yOz. QU
c Vẽ tia Om là tia phân giác của góc ‘
yOz và tia On là tia đối của Ox. Tính \ mOn. TẠ THPT - G 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy
? Thầy NGUYỄN NGỌC DŨNG - Ô 0976071956 ? Page 47 of 47
Document Outline

  • I Số học
    • Số nguyên
      • Tập hợp các số nguyên
      • Phép cộng số nguyên
      • Phép trừ số nguyên
      • Quy tắc dấu ngoặc
      • Quy tắc chuyển vế
      • Phép nhân và chia hai số nguyên
      • Tính chất của phép nhân
      • Phân số
        • Khái niệm phân số. Phân số bằng nhau
        • Tính chất cơ bản của phân số. Rút gọn phân số
        • Quy đồng mẫu số nhiều phân số
        • So sánh phân số
        • Phép cộng và trừ phân số
        • Luyện tập
        • Phép nhân phân số
        • Phép chia phân số
        • Hỗn số. Số thập phân. Phần trăm
        • Tìm giá trị phân số của một số cho trước
        • Tìm một số biết giá trị một phân số của nó
        • Tìm tỉ số của hai số
        • Biểu đồ phần trăm
      • II Hình học
        • Góc
          • Nửa mặt phẳng. Góc, số đo góc
          • Khi nào thì xOy"0362xOy+yOz"0362yOz = xOz"0362xOz
          • Tia phân giác của góc