Định nghĩa hình tam giác cân, tam giác vuông cân và bài tập

Định nghĩa hình tam giác cân, tam giác vuông cân và bài tập
1. Định nghĩa tam giác cân, tam giác vuông cân * Tam giác cân:
Tam giác cân là một loại hình tam giác mà có hai cạnh bằng nhau và hai góc tại hai đỉnh
này cũng bằng nhau. Điều này đồng nghĩa với việc đỉnh tam giác cân có một trục đối xứng, gọi
là trục đối xứng đối với hai cạnh bằng nhau. Trong tam giác cân, đỉnh nằm giữa hai cạnh bằng
nhau được gọi là đỉnh cân và hai cạnh bằng nhau được gọi là cạnh cân.
Tam giác cân không nhất thiết phải có ba góc bằng nhau (tam giác đều), mà chỉ yêu cầu
hai góc ở đỉnh cân là bằng nhau. Tam giác cân có thể có các đặc điểm và tính chất khác nhau
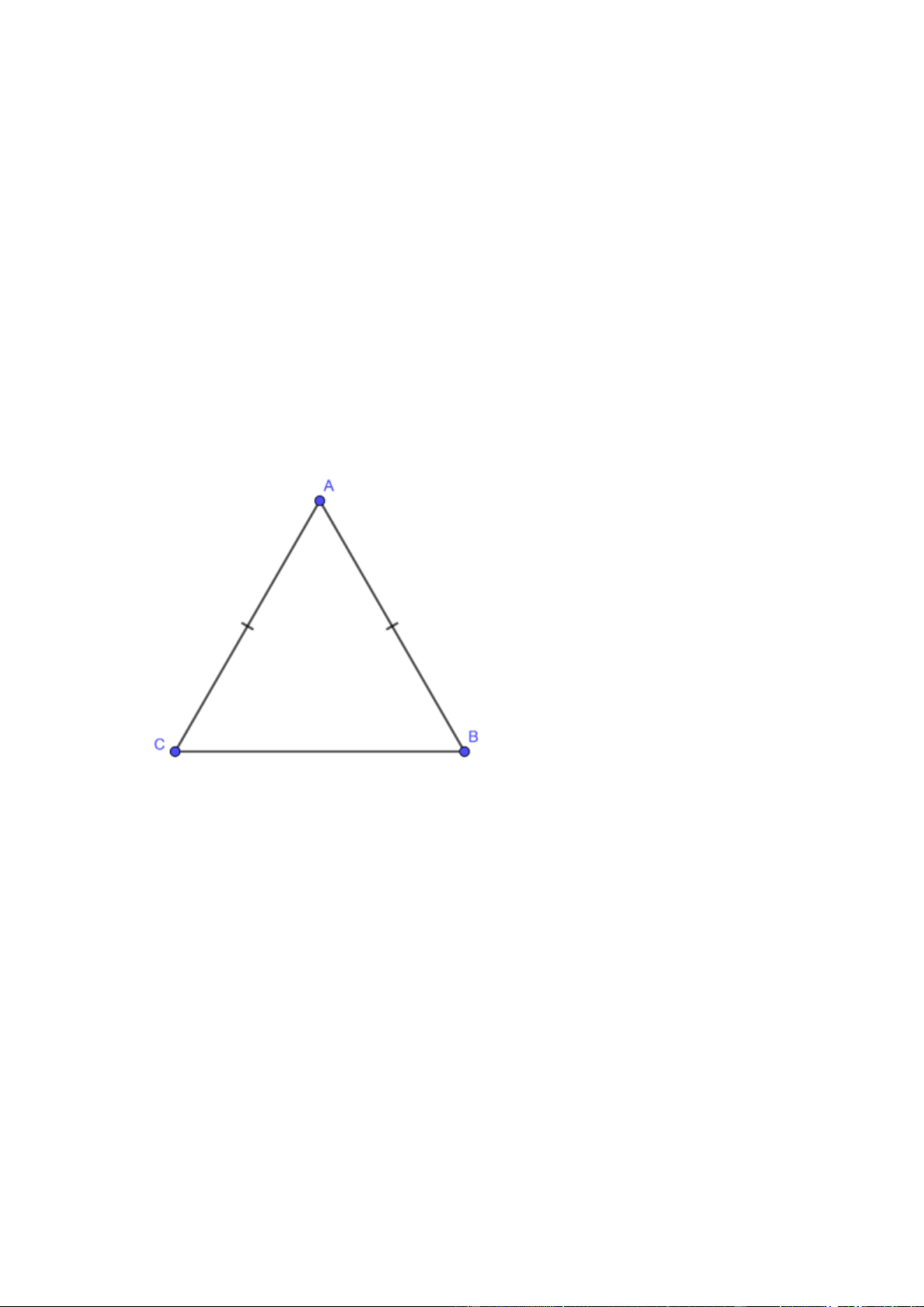
tùy thuộc vào các góc và cạnh còn lại của tam giác. Hình vẽ minh họa:
Nhận thấy trong tam giác ABC trên, có AB = AC, như vậy tam giác ABC cân tại A
* Tam giác vuông cân:
Tam giác vuông cân là một loại hình tam giác có ba cạnh và ba góc. Trong tam giác này,
một trong ba góc của tam giác là góc vuông, tức là góc có độ lớn chính xác bằng 90 độ (π/2
radian). Đồng thời, tam giác này cũng có hai cạnh bằng nhau, tức là hai cạnh gần góc vuông là độ dài bằng nhau.
Để làm rõ hơn, gọi hai cạnh bằng nhau là cạnh cân, và cạnh còn lại (khác với hai cạnh cân)
gọi là cạnh vuông. Trong tam giác vuông cân, cạnh vuông chia tam giác thành hai tam giác
vuông nhỏ hơn, mỗi tam giác vuông có một cạnh cân bằng với cạnh cân của tam giác vuông cân ban đầu.
Điểm giao nhau của các đường phân giác của tam giác vuông cân là trung điểm của cạnh
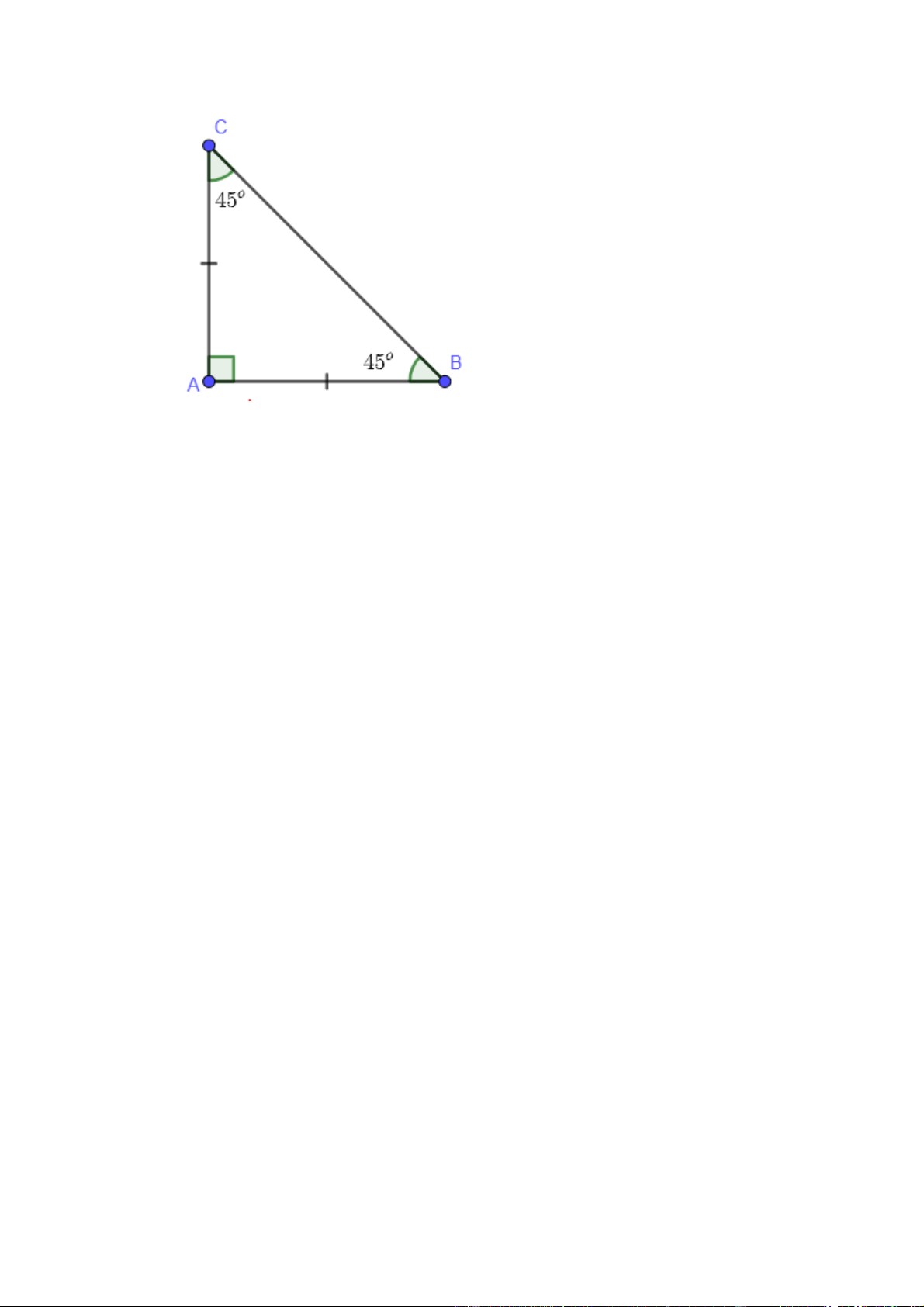
vuông, đồng thời cũng là tâm của đường tròn nội tiếp tam giác. Hình vẽ minh họa
2. Tính chất tam giác cân, tam giác vuông cân * Tam giác cân:
- Hai cạnh bằng nhau: Tam giác cân có hai cạnh có độ dài bằng nhau. Điểm giao nhau của
hai cạnh này là đỉnh cân của tam giác.
- Hai góc ở đỉnh cân bằng nhau: Tam giác cân có hai góc tại hai đỉnh cân có độ lớn bằng
nhau. Điều này có nghĩa là hai góc đó cùng có giá trị góc bằng nhau.
- Tính đối xứng: Tam giác cân có một trục đối xứng qua đỉnh cân. Điều này đồng nghĩa
với việc tam giác cân có tính chất đối xứng qua trục đi qua đỉnh cân và chia tam giác thành hai nửa đối xứng nhau.
- Điểm giao nhau của các đường phân giác là trung điểm của cạnh đối diện với đỉnh cân:
Điểm giao nhau của hai đường phân giác trong tam giác cân là trung điểm của cạnh đối diện
với đỉnh cân. Điểm này cùng lúc là tâm của đường tròn nội tiếp tam giác.
* Tam giác vuông cân:
- Tam giác vuông cân có hai góc đáy bằng nhau: Đó là hai góc nằm ở hai đỉnh chân của
tam giác vuông cân và có độ lớn bằng 45 độ (π/4 radian) mỗi góc.
- Đường cao và đường phân giác tính từ đỉnh góc vuông của tam giác vuông cân trùng với
nhau: Điểm giao nhau của đường cao từ đỉnh góc vuông và đường phân giác từ đỉnh góc vuông
tới giữa cạnh đối diện đỉnh góc vuông là cùng một điểm. Điểm này cũng là tâm của đường tròn nội tiếp tam giác.
- Đường trung tuyến từ đỉnh góc vuông của tam giác vuông cân trùng với đoạn thẳng nối
giữa trung điểm cạnh huyền và đỉnh góc vuông: Đoạn thẳng nối trung điểm cạnh huyền và đỉnh
góc vuông cắt nhau tại một điểm trên cạnh đối diện đỉnh góc vuông và cũng là điểm tâm của tam giác.
- Độ dài của đường cao và đường phân giác tính từ đỉnh góc vuông bằng một nửa chiều
dài cạnh huyền: Đường cao và đường phân giác tính từ đỉnh góc vuông có độ dài bằng một nửa chiều dài cạnh huyền.
3. Bài tập về tam giác cân, tam giác vuông cân Bài tập 1:
Đề bài: Trong các đáp án dưới đây đáp án nào sai
A. Tam giác đều có ba góc bằng nhau và mỗi góc bằng 60°
B. Tam giác đều là tam giác có ba cạnh bằng nhau
C. Tam giác cân là tam giác đều
D. Tam giác đều là tam giác cân đặc biệt.
Đáp án đúng: C. Tam giác cân là tam giác đều- đây là một khẳng định sai Giải thích:
- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc đều bằng nhau, mỗi góc có độ
lớn 60° (π/3 radian). Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc tại hai đỉnh
cân có độ lớn bằng nhau.
- Tam giác đều có thể coi là một trường hợp đặc biệt của tam giác cân, vì tam giác đều
không chỉ có hai cạnh bằng nhau mà còn có ba cạnh bằng nhau. Nhưng tam giác cân không
nhất thiết phải có ba cạnh bằng nhau, nó chỉ cần có hai cạnh bằng nhau.
Vậy, đáp án C là sai. Tam giác cân không phải là tam giác đều, mà chỉ là một loại tam giác có hai cạnh bằng nhau. Bài tập 2:
Đề bài: Dựa vào đặc điểm của tam giác cân, hãy chọn đáp án đúng
Tam giác cân là một tam giác mang đặc điểm là:
A. có hai đường cao trong tam giác bằng nhau
B. hai đường trung tuyến có độ dài bằng nhau
C. có hai cạnh bên bằng độ dài với nhau
D. có hai tia phân giác trong cùng số đo
Đáp án đúng: C. Tam giác cân là một tam giác có hai cạnh bên bằng độ dài với nhau Giải thích:
Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc ở đỉnh cân bằng nhau. Điều
này đồng nghĩa với việc tam giác cân có hai cạnh bên (hai cạnh có đỉnh chung) có độ dài bằng nhau.
Các đáp án khác không đúng với định nghĩa của tam giác cân:
A. Hai đường cao của tam giác cân không nhất thiết phải bằng nhau. Đường cao là đoạn
thẳng nối một đỉnh của tam giác với đối diện với cạnh đối diện đỉnh đó.
B. Hai đường trung tuyến của tam giác cân không nhất thiết phải bằng nhau. Đường trung
tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện đỉnh đó.
D. Hai tia phân giác trong của tam giác cân không nhất thiết phải bằng nhau. Tia phân giác
trong là tia xuất phát từ một đỉnh của tam giác và chia đôi góc tại đỉnh đó. Bài tập 3:
Đề bài: Chọn đáp án đúng trong các đáp án sau, biết Tam giác ABC cân tại A, biết rằng số
đo góc B là 50o , vậy số đo các góc còn lại của tam giác ABC đã cho là: A. Góc A = 50o, Góc C = 80o B. Góc A = 80o, Góc C = 50o C. Góc A = 40o, Góc C = 90o D. Góc A = 90o, Góc C = 40o
Đáp án đúng: B- Số đo các góc còn lại trong tam giá cân ABC là Góc A = 80o và Góc C = 50o Giải thích:
Tam giác ABC là tam giác cân tại A, tức là AB = AC và góc tại đỉnh A có độ lớn là 50o (theo
điều kiện trong câu hỏi).
Vì ABC là tam giác cân nên góc B và góc C (góc ở hai đỉnh chân) có độ lớn bằng nhau.
Vì tổng ba góc trong tam giác là 180o, ta có:
Góc B + Góc A + Góc C = 180o 50° + Góc A + Góc C = 180o
Do đó: Góc A + Góc C = 180o - 50o = 130o
Từ đó suy ra, số đo các góc sẽ là: góc B = góc C = 50o, góc A = 130o - góc C = 80o Bài tập 4:
Đề bài: Chọn đáp án đúng cho câu hỏi dưới đây
Tam giác ABC có hai góc B và góc C = 45o, Vậy tam giác ABC là tam giác gì? A. Tam giác cân B. Tam giác vuông C. Tam giác đều D. Tam giác vuông cân
Đáp án đúng: D- ABC là tam giác vuông cân Giải thích:
Tam giác có hai góc B và C bằng 45o, tức là góc B = góc C = 45o.
Vì tổng ba góc trong một tam giác là 180o, ta có: A + B + C = 180o.
Thay vào giá trị góc B = C = 45o, ta có: A + 45o + 45o = 180o.
Từ đó, ta tính được góc A là: A = 180o - 45o - 45o = 90o.
Vậy tam giác ABC có một góc bằng 90o (góc A = 90o) và hai góc bằng nhau (góc B = góc
C = 45o), nên đây là tam giác vuông cân.