



Preview text:
. CỘNG, TRỪ SỐ HỮU TỈ
I. KIẾN THỨC CƠ BẢN
1. Cộng, trừ hai số hữu tỉ.
• Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số
có cùng một mẫu dương rồi áp dụng quy tắc cộng, trừ phân số.
• Phép cộng số hữu tỉ có các tính chất của phép cộng phân số: Giao hoán, kết hợp,
cộng với số 0. Mỗi số hữu tỉ đều có một số đối.
2. Quy tắc “chuyển vế”.
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đối dấu số hạng đó. Với mọi ,
x y, z : x y z x z . y 3. Chú ý.
Trong , cũng có những tổng đại số, trong đó có thể đổi chỗ các số hạng, đặt dấu
ngoặc để nhóm các số hạng một cách tùy ý như các tổng đại số trong . II. BÀI TẬP
Bài 1: Tìm x biết: 1 1 a) x - = 15 10 - 2 - 3 b) - x = 15 10 1 2 æ 1ö - c) ç ÷ x + = - ç ÷ ç ÷ 3 5 çè 3 ÷ø 3 1 3 d) - x = - 7 4 5 4 e) x + - - 3, 75 = - - 2, 15 15 3 2 f) x - < 4 3 Trang 1
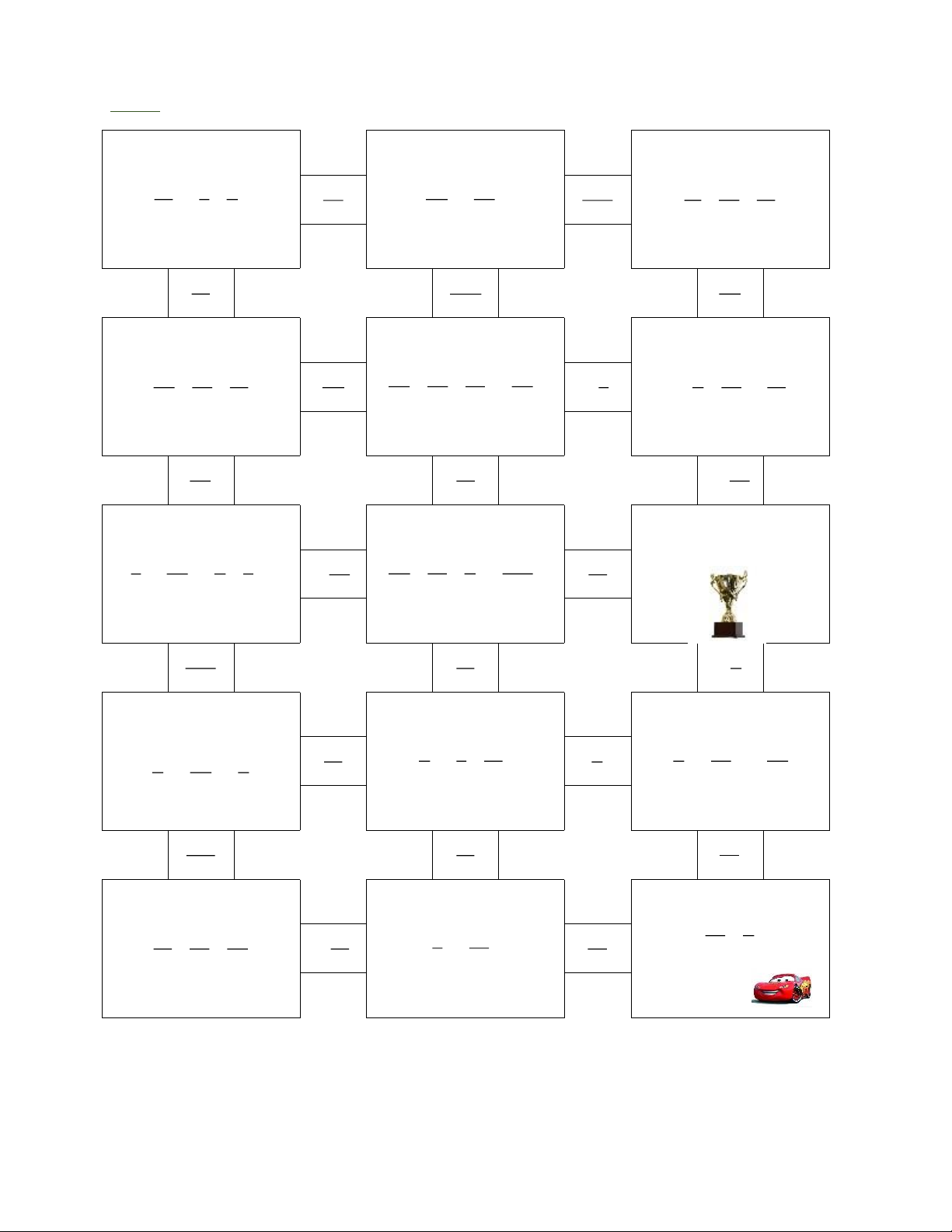
Bài 2: Hãy đi theo con đường đúng từ vạch khởi đầu tới điểm kết thúc. 1 1 1 1 7 5 23 5 23 16 12 3 4 2 8 9 72 11 29 11 7 17 6 15 132 29 5 32 9 7 5 7 4 5 1 2 15 6 2 13 1 18 45 10 15 11 22 33 44 3 5 23 10 53 11 15 15 24 12 23 END 1 5 1 3 53 6 8 4 15 3 3 4 4 8 24 7 21 3 12 12 43 1 6 30 15 5 1 1 1 1 2 6 1 4 2 4 1 2 15 2 3 10 5 5 5 5 5 3 2 11 4 11 15 15 21 1 2 12 1 4 4 11 3 1 7 3 15 5 3 15 5 3 21 START Trang 2 1 1 1 1 1 Bài 3: Tính: a) - - - - - 10 100 1000 10000 100000
…………………………………………………………………………………...………….
……………………………………………………………………………….………………… 1 3 5 7 9 11 13 11 9 7 5 3 b) - + - + - + + - + - + 3 5 7 9 11 13 15 13 11 9 7 5
………………………………………………………………………….…….……..………
……………………………………………………………………………….………………… 1 1 1 1 1 1 c) - - - - .... - - 99 99.98 98.97 97.96 3.2 2.1
………………………………………………………………………….…….….…………
……………………………………………………………………………….………………… x 1 1
Bài 4: Tìm các số nguyên x, y biết = = 6 y 2
………………………………………………………………………….…….…………… 1 1 1 1 Bài 6: M = + + + ... + 11 12 13 19 1 1 1 2 2 2 N = + + + + + 3 4 5 7 9 11
Chứng minh rằng M và N không
………………………………………………………………………….…….…….………… phải số nguyên. Bài 5: Tính nhanh: 1 1 1 1 A = + + + ... + ; 2.3 3.4 4.5 19.20 1 1 1 1 1 1 B = + + + + + 7 91 247 475 775 1147
………………………………………………………………………….…….……………
………………………………………………………………………….…….…….………… Trang 3
………………………………………………………………………….…….…….…………
………………………………………………………………………….…….……………
………………………………………………………………………….…….…….…………
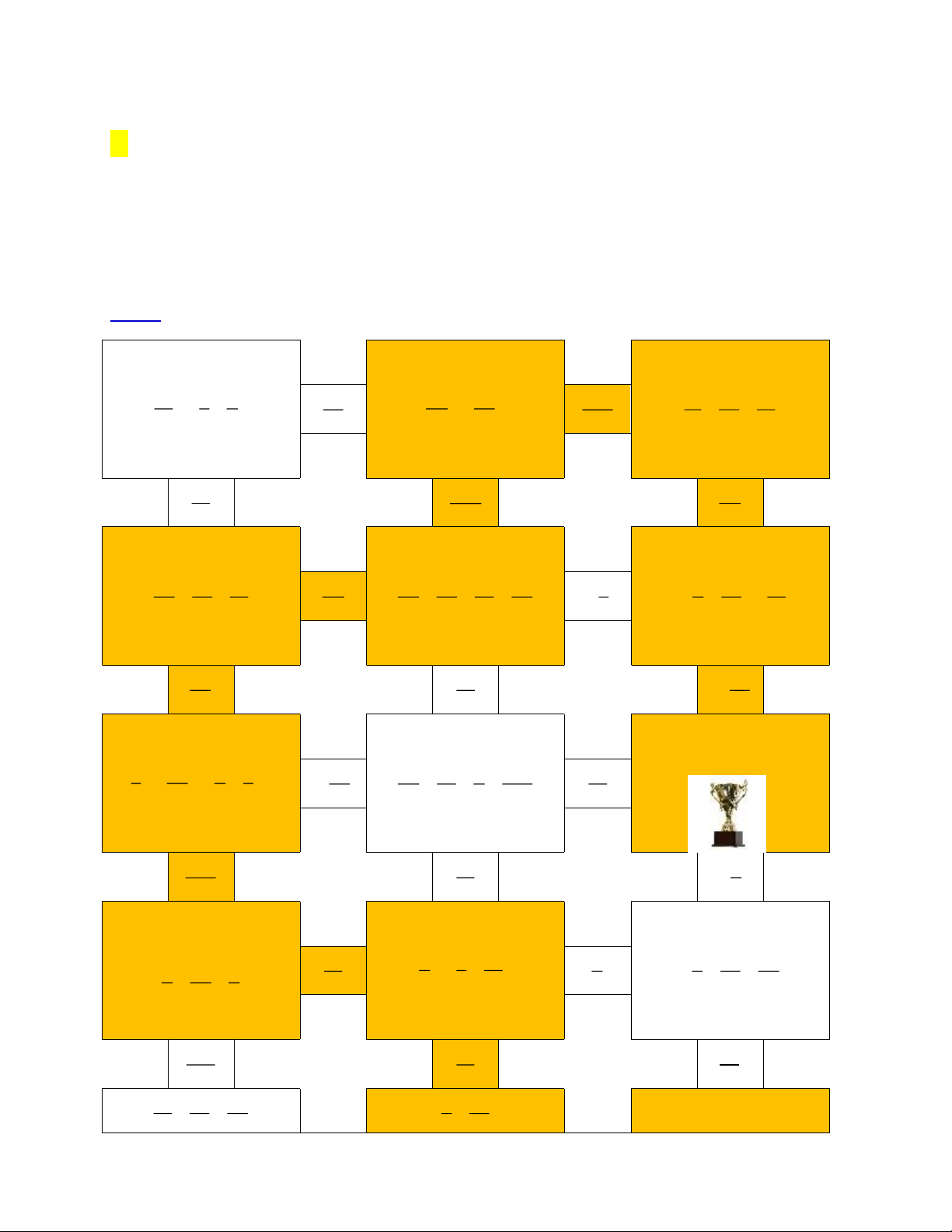
………………………………………………………………………….…….…….………… HƯỚNG DẪN GIẢI Bài 2: 1 1 1 1 7 5 23 5 23 16 12 3 4 2 8 9 72 11 29 11 7 17 6 15 132 29 5 32 9 7 5 7 4 5 1 2 15 6 2 13 1 18 45 10 15 11 22 33 44 3 5 23 10 53 11 15 15 24 12 23 END 1 5 1 3 53 6 8 4 1 5 3 3 4 4 8 24 7 21 3 12 12 43 1 6 30 15 5 1 1 1 1 2 6 1 4 2 4 1 2 15 2 3 10 5 5 5 5 5 3 2 11 4 11 15 15 21 12 1 4 3 1 15 5 3 5 3 Trang 4 4 11 1 2 15 21 7 3 START Bài 1: 1 1 1 - 2 3 1 a) x = + = b) x = + = 10 15 6 15 10 6 2 æ 1ö - ç ÷ 1 2 3 1 3 109 c) x = - ç ÷- = ç ÷ d) x = - + = 5 çè 3 ÷ø 3 5 7 4 5 140 é 4 ê 4 4 24 x = ê e) 3 x + = 3, 75 - 2,15 Û x + = Û ê 15 15 15 ê - 28 x = ê ë 15 3 2 3 2 17 f)* x - < Û x < + Û x < 4 3 4 3 12 Bài 3: a) 1 1 1 1 1 - - - - -
= - (0,1 + 0, 01 + 0, 001 + 0, 0001 + 0, 0000 ) 1 = - 0, 11111 10 100 1000 10000 100000 1 3 5 7 9 11 13 11 9 7 5 3 1 13 18 b) - + - + - + + - + - + = + = 3 5 7 9 11 13 15 13 11 9 7 5 3 15 15 1 1 1 1 1 1 æ 1 1 1 1 1 ö c) ç ÷ - - - .... - - = - ç + + + .... + + ÷ ç ÷ 99 99.98 98.97 3.2 2.1 99 çè99.98 98.97 97.96 3.2 2.1÷ ø 1 æ1 1 1 1 1 1 1 1 1 1ö ç ÷ = - ç - + - + - + .... + - + - ÷ ç ÷ 99 çè98 99 97 98 96 97 2 3 1 2÷ ø 1 æ 1 1ö ç ÷ 1 98 97 = - - ç + ÷= - = - ç ÷ 99 çè 99 1÷ø 99 99 99 x 1 1 x 1 6.1 1 1 Bài 4: = = . = Þ x = = 3 = Þ y = 1 6 y 2 6 2 2 y 2 Trang 5 Bài 5: 1 1 9
A 1 1 1 1 1 1 ... A . 2 3 3 4 19 20 2 20 20 1 1 1 1 1 æ 1 1 1 1 1 ö 1 æ 1 ö ç ÷ ç ÷ 6 B = + + + ... + = 1 ç - + - + ... + - ÷= . 1 ç - ÷= ç ÷ ç ÷ ç ÷ 1.7 7.13 13.19 31.37 6 è 7 7 13 31 37 ø 6 çè 37 ÷ ø 37 Bài 6: 1 1 1 1 1 1 1 1 9 M = + + + ... + < + + + ... + = < 1 11 12 13 19 10 10 10 10 10 Dễ thấy M > 0 Suy ra 0 M 1
Vậy M không thể là số nguyên 1 1 1 2 2 2 2 2 2 2 2 2 N = + + + + + = + + + + + 3 4 5 7 9 11 6 8 10 7 9 11 1 æ 1 1 1 1 1 ö 1 æ 1 1 1 1 1ö ç ÷ ç ÷ = 2ç + + + + + ÷< 2ç + + + + + ÷= 2 ç ÷ ç ÷ ç ÷ è6 7 8 9 10 11ø çè6 6 6 6 6 6÷ø Ta lại có 1 æ 1 1 1 1 1 ö æ1 1 1 1 1 1 ö ç ÷ ç ÷ 2ç + + + + + ÷> 2ç + + + + + ÷= 1 ç ÷ ç ÷ ç ÷ è6 7 8 9 10 11ø 12 çè 12 12 12 12 12÷ ø
Suy ra 1 N 2. Vậy N không là số nguyên. Trang 6




