











Preview text:
Chương 1
Ứng dụng đạo hàm để khảo sát hàm số
Câu 79. Hàm số y = x3 − 3x − 2024 đồng biến trên khoảng nào? a) R. b) (−∞; −1). c) (−1; 1). d) (1; +∞). Lời giải.
X Hàm số đã cho có tập xác định là D = R. T E A L
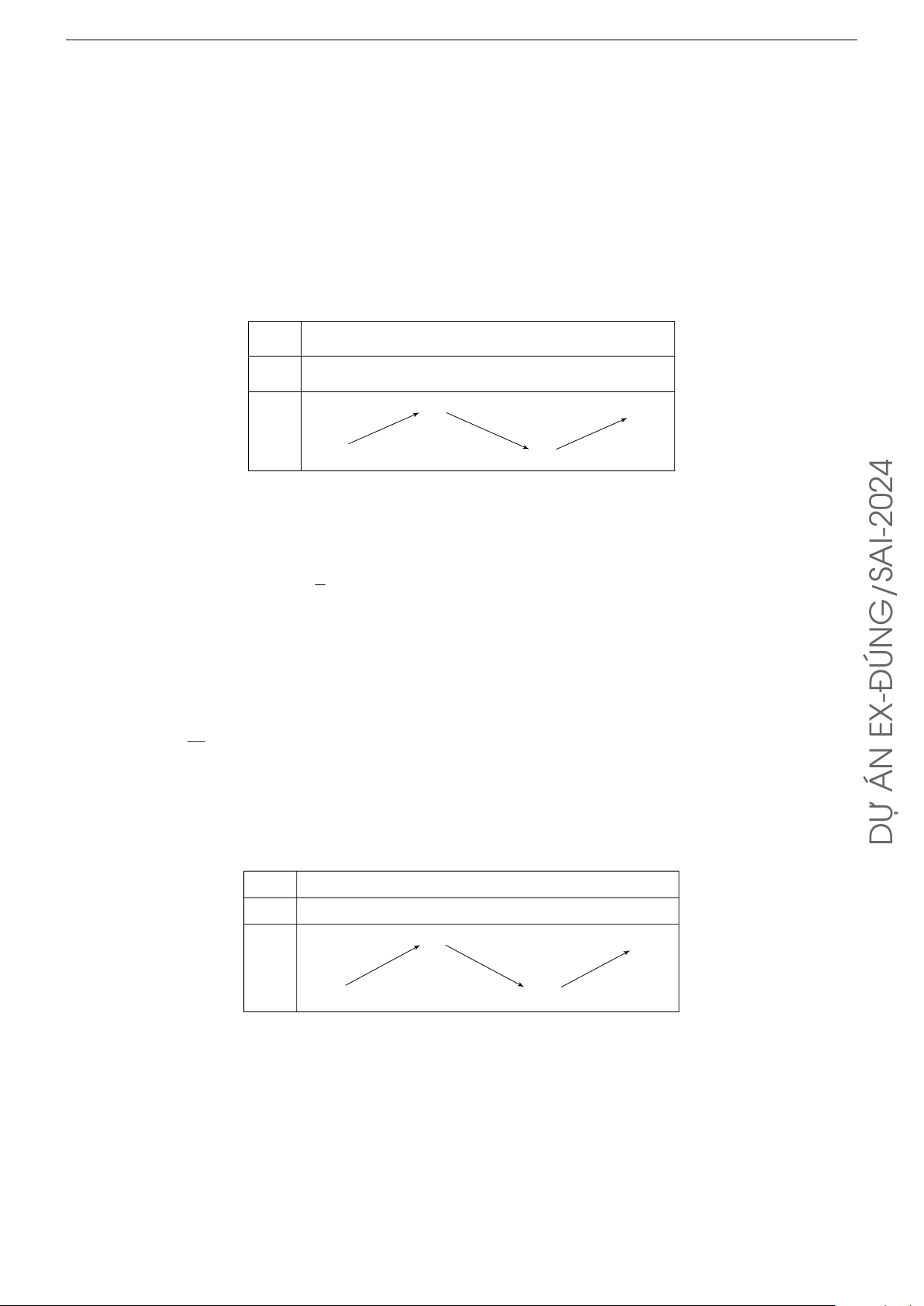
Ta có y0 = 3x2 − 3, y0 = 0 ⇔ x = ±1. À Bảng xét dấu V N x −∞ −1 1 +∞ Á y0 + 0 − 0 + TO
M Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên khoảng (−∞; −1) và (1; +∞).
Ó Đáp án: a sai b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H
N Câu 80. Hàm số y = x4 − 2x2 + 1 nghịch biến trên khoảng nào sau đây? a) (−∞; 1). b) (−1; 0). c) (−1; 1). d) (−∞; −1). Lời giải.
Hàm số xác định trên tập R. x = 0
Ta có y0 = 4x3 − 4x = 4x (x2 − 1) , y0 = 0 ⇔ x = ±1.
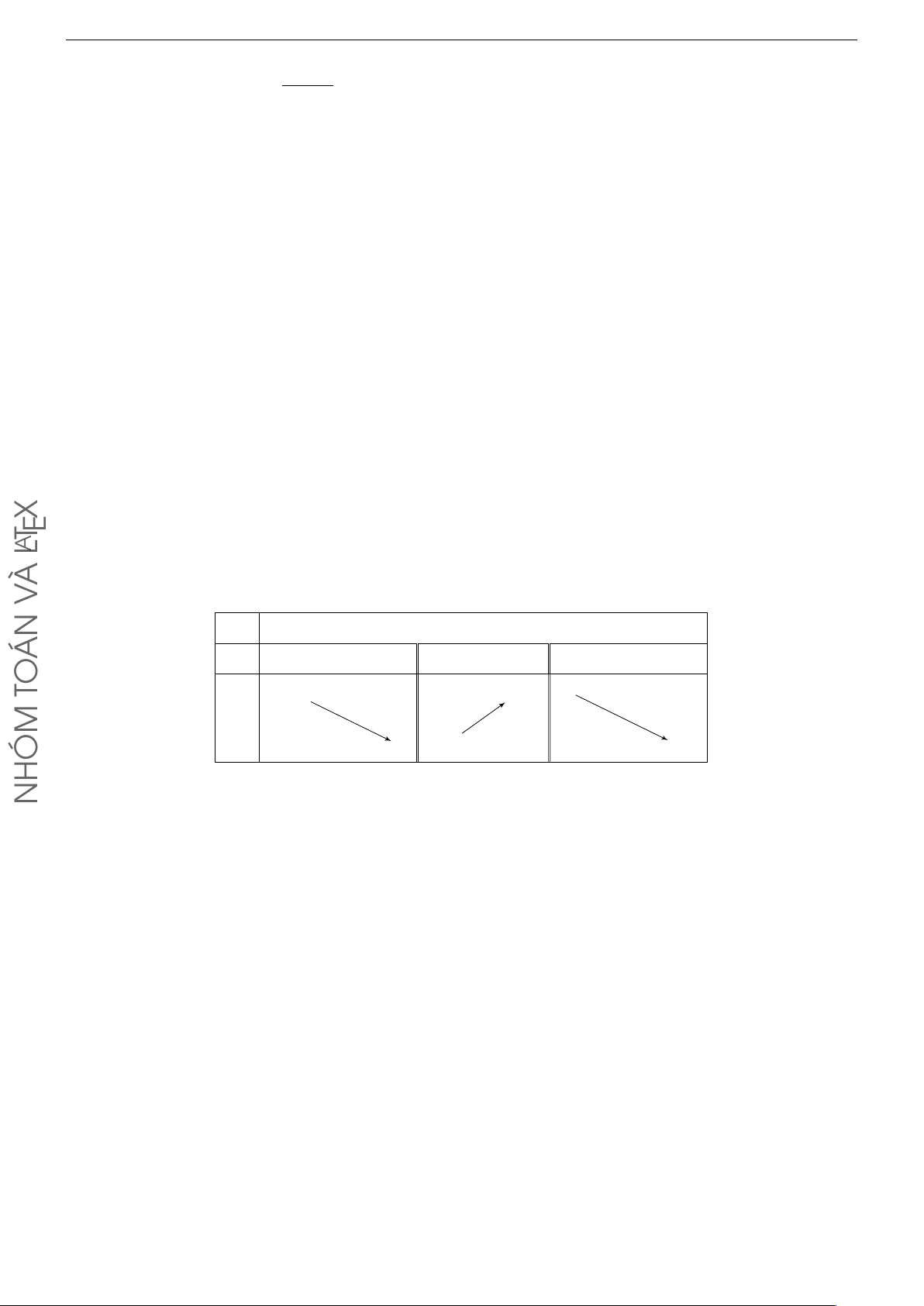
Ta có bảng xét dấu y0 như sau x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 +
Hàm số nghịch biến trên các khoảng (−∞; −1) và (0; 1).
Đáp án: a sai b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 81. Cho hàm số y = f (x) có đạo hàm liên tục trên R và có bảng biến thiên như hình bên dưới.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 254
Facebook “Nhóm Toán và LaTeX” 12-C1-B1.tex x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + +∞ + −3 +∞ + y −4 − −4 a) (−1; 0). b) (−4; −3). c) (1; +∞). d) (0; 1). Lời giải.
Dựa vào bảng biến thiên suy ra hàm số y = f (x) đồng biến trên các khoảng (−1; 0) và (1; +∞).
Đáp án: a đúng b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 82.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x) đồng biến trên y khoảng nào sau đây? 2 4 a) (−∞; 2). b) (0; 2). c) (2; +∞). d) (−∞; 0). x O 2 − 0 2 I-2 Lời giải. A
Dựa vào đồ thị suy ra hàm số y = f (x) đồng biến trên các khoảng (−1; 0) và (2; +∞). S /
Đáp án: a sai b sai c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . G 1
Câu 83. Cho hàm số f (x) = − x3 −mx2 +(2m−3)x+2109m−2020, m là tham số thực. N 3 Ú a) f 0(x) = −x2 − 2mx. -Đ
b) f 0(x) = −x2 − 2mx + 2m − 3. X E
c) Hàm số f (x) nghịch biến trên R ⇔ −3 ≤ m ≤ 1. N
d) Hàm số f (x) nghịch biến trên R ⇔ −3 < m < 1. Á Lời giải. Ự
Hàm số có tập xác định D = R. D
Ta có f 0(x) = −x2 − 2mx + 2m − 3.
Hàm số đã cho nghịch biến trên R
⇔ f 0(x) = −x2 − 2mx + 2m − 3 ≤ 0, ∀x ∈ R − 1 < 0 ⇔
(−m)2 − (−1)(2m − 3) ≤ 0 ⇔ m2 + 2m − 3 ≤ 0 ⇔ −3 ≤ m ≤ 1.
Đáp án: a sai b đúng c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x − 1 Câu 84. Cho hàm số y = . x − m
a) Tập xác định D = R \ {m}. 255
Facebook “Nhóm Toán và LaTeX” "T-F Giap Thin 2024".tex m − 1 b) y0 = , ∀x 6= m. (x − m)2
c) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi m < 1.
d) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi 0 ≤ m < 1. Lời giải.
Tập xác định D = R \ {m}. −m + 1 Ta có y0 = , ∀x 6= m. (x − m)2
Hàm số đã cho đồng biến trên (−∞; 0) khi và chỉ khi m / ∈ (−∞; 0) m ≥ 0 ⇔ ⇔ 0 ≤ m < 1. − m + 1 > 0 m < 1
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X T E A L À V N Á TO M Ó H N 256
Facebook “Nhóm Toán và LaTeX” 12-C1-B2.tex
Câu 85. Cho hàm số y = x3 + 3x2 + 2
a) Hàm số đạt cực đại tại x = 0. b) y0 = 3x2 + 6x.
c) Hàm số đạt cực tiểu tại x = −2.
d) Hàm số đạt cực đại tại x = −2. Lời giải. Tập xác định: D = R. x = 0 ⇒ y = 2
Ta có y0 = 3x2 + 6x, y0 = 0 ⇔ x = −2 ⇒ y = 6. Bảng biến thiên x −∞ −2 0 +∞ f 0(x) + 0 − 0 + 6 +∞ + f (x) −∞ − 2 4 2 0
Vậy hàm số đạt cực đại tại x = −2.
Đáp án: a sai b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . I-2 A 1 S
Câu 86. Cho hàm số y = x − . x /
a) Hàm số có tập xác định R \ {0}.
b) Hàm số nghịch biến trên R. G
c) Hàm số đạt cực đại tại x = 0.
d) Hàm số không có cực trị. N Ú Lời giải. -Đ
Hàm số có tập xác định R \ {0}. X 1 E Ta có y0 = 1 +
, y0 > 0 với mọi x 6= 0. x2 N
Vậy hàm số đã cho không có cực trị. Á
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ự
Câu 87. Cho hàm số y = f (x) có bảng biến thiên như sau D x −∞ 2 4 +∞ y0 + 0 − 0 + 3 +∞ y −∞ − −2 −
a) Hàm số đạt cực đại tại x = −2.
b) Hàm số đạt cực đại tại x = 2.
c) Hàm số đạt cực đại tại x = 4.
d) Hàm số đạt cực tiểu tại x = 3. Lời giải.
Dễ thấy hàm số đạt cực đại tại x = 2.
Đáp án: a sai b đúng c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 88. 257
Facebook “Nhóm Toán và LaTeX” 12-C1-B2.tex
Cho hàm số y = f (x) có đồ thị như hình bên. y
a) Giá trị cực tiểu của hàm số đã cho bằng −1. 3
b) Giá trị cực đại của hàm số đã cho bằng 3.
c) x = 0 là điểm cực tiểu của hàm số. 2 O x
d) x = 2 là điểm cực đại của hàm số. −1 Lời giải.
Dựa vào đồ thị suy ra hàm số đạt cực đại tại x = 0, yCĐ = 3.
Dựa vào đồ thị suy ra hàm số đạt cực tiểu tại x = 2, yCT = −1.
Đáp án: a đúng b đúng c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Câu 89. Cho hàm số y =
x3 − mx2 + (m2 − 4)x + 3, m là tham số thực. 3
a) Hàm số đạt cực đại tại x = 3 khi và chỉ khi m = 2.
b) Hàm số đạt cực đại tại x = 3 khi và chỉ khi m = 1.
c) Hàm số đạt cực đại tại x = 3 khi và chỉ khi m = 5. X d) y0 = x2 − 2mx + m2 − 4. T E Lời giải. A L
À Ta có y0 = x2 − 2mx + m2 − 4, ∀x ∈ R.
V Do hàm số đạt cực đại tại x = 3 nên y0(3) = 0 ⇔ m2 − 6m + 5 = 0 ⇔ m = 1 hoặc m = 5.
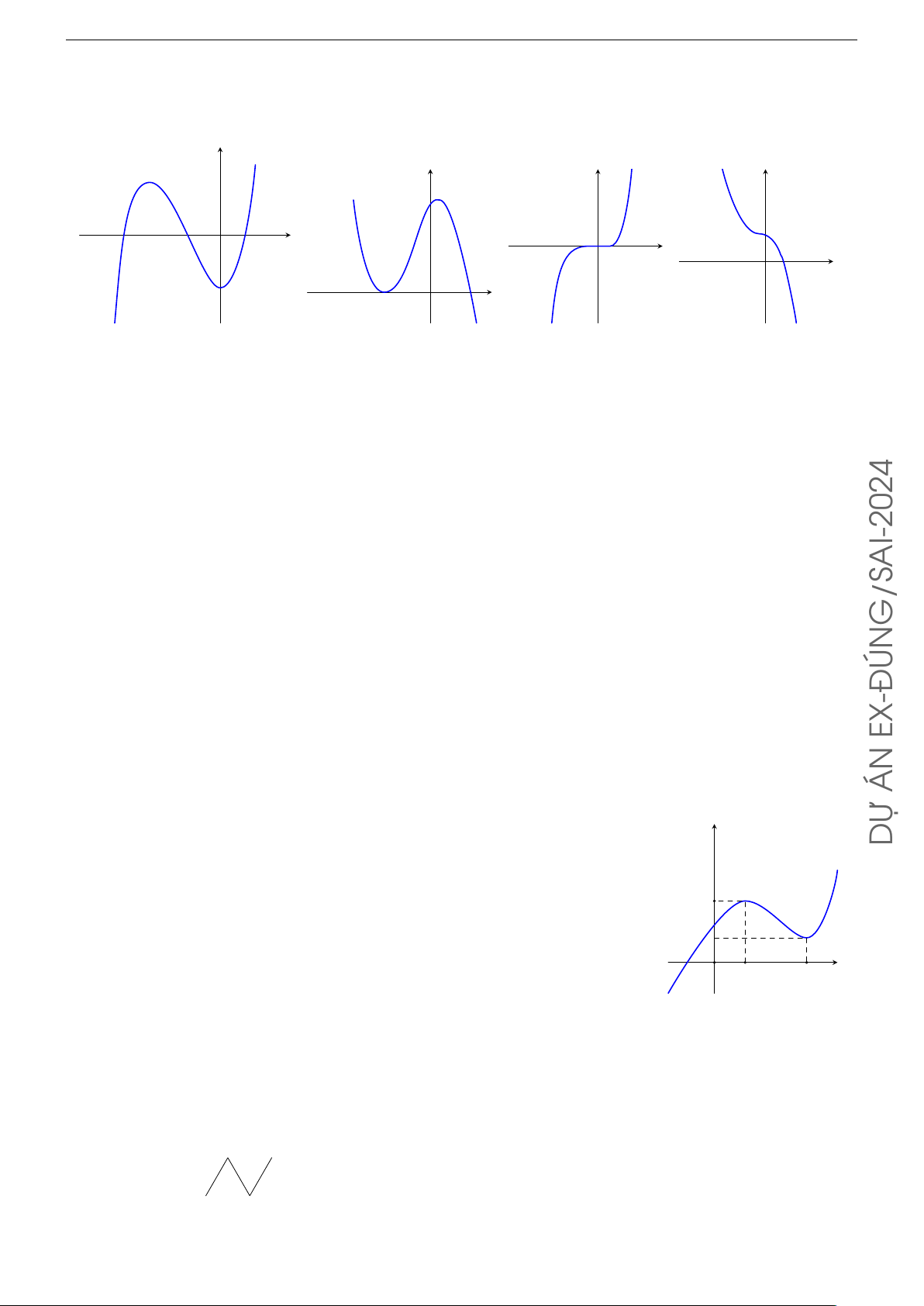
N Với m = 1, y0 = x2 − 2x − 3, y0 = 0 ⇔ x = −1 hoặc x = 3. Á x −∞ −1 3 +∞
Bảng xét dấu y0 như hình bên. y0 + 0 − 0 +
TO Từ bảng xét dấu, ta có hàm số đạt cực tiểu tại x = 3.
M Với m = 5, y0 = x2 − 10x + 21, y0 = 0 ⇔ x = 3 hoặc x = 7. x −∞ 3 7 +∞
Ó Bảng xét dấu của y0 như hình bên. H y0 + 0 − 0 +
N Từ bảng xét dấu, ta có hàm số đạt cực đại tại x = 3.
Vậy hàm số đã cho đạt cực đại tại x = 3 khi và chỉ khi m = 5.
Đáp án: a sai b sai c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 90. Cho hàm số y = x4 + mx2, m là tham số thực.
a) Hàm số đạt cực tiểu tại x = 0 khi và chỉ khi m ≥ 0. b) y0 = 4x3 + 2x.
c) Hàm số đạt cực tiểu tại x = 0 khi và chỉ khi m < 0. d) y0 = 4x3 khi m = 0. Lời giải. x = 0
Ta có y0 = 4x3 + 2mx = 2x(2x2 + m); y0 = 0 ⇔ m x2 = − . 2
• Nếu m = 0 thì x = 0 là nghiệm bội ba của phương trình y0 = 0 và khi đó x = 0 là điểm cực tiểu của hàm số. • m Nếu m > 0 thì x2 = −
< 0 (vô lí), khi đó x = 0 là điểm cực tiểu của hàm số. 2 258
Facebook “Nhóm Toán và LaTeX” 12-C1-B2.tex r • m m Nếu m < 0 thì x2 = − > 0 ⇒ x = ± −
và khi đó x = 0 là điểm cực đại của hàm số 2 2 (loại).
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 91. Cho hàm số y = x3 − 3(m + 1)x2 + 3(7m − 3)x. Gọi S là tập hợp tất cả các giá trị nguyên
của tham số m để hàm số không có cực trị. a) 2 ∈ S.
b) Số phần tử của S là 4. c) 0 ∈ S.
d) Số phần tử của S là 2. Lời giải.
• Hàm số có tập xác định D = R, y0 = 3x2 − 6(m + 1)x + 3(7m − 3) có ∆0 = 9m2 − 45m + 36.
• Hàm số không có cực trị ⇔ y0 = 0 vô nghiệm ⇔ ∆0 ≤ 0 ⇔ 1 ≤ m ≤ 4.
• Vậy có 4 giá trị nguyên của m thỏa mãn. 4 2 0
Đáp án: a đúng b đúng c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . I-2 x3
Câu 92. Tập hợp các giá trị m để hàm số y =
− mx2 + (10m − 25)x + 1 có hai điểm cực trị A 3 S là / G a) R. b) R \ {−5}. c) R \ {5}. d) (5; +∞). N Lời giải. Ú
Tập xác định của hàm số là D = R. -Đ
Ta có y0 = x2 − 2mx + 10m − 25. X E
Hàm số có hai cực trị khi và chỉ khi phương trình y0 = 0 có hai nghiệm phân biệt. N Á
⇔ ∆0 = m2 − 10m + 25 > 0 ⇔ m 6= 5. Ự D
Đáp án: a sai b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 93. Cho hàm số y = mx4 + (m − 1)x2 + 1, m là tham số thực.
a) Hàm số có ba điểm cực trị khi và chỉ 0 < m < 1.
b) Hàm số có hai điểm cực trị khi m = 0.
c) Hàm số có ba điểm cực trị khi và chỉ 0 ≤ m ≤ 1.
d) Hàm số có một điểm cực trị khi m = 0. Lời giải.
Nếu m = 0 thì hàm số đã cho trở thành y = −x2 + 1. Đây là hàm số đa thức bậc hai nên có 1 điểm cực trị.
Nếu m 6= 0 thì hàm số đã cho là hàm số trùng phương có y0 = 4mx3 +2(m−1)x = 2x (2mx2 + m − 1). x = 0 Ta có y0 = 0 ⇔ 2mx2 + m − 1 = 0. (∗) 259
Facebook “Nhóm Toán và LaTeX” "T-F Giap Thin 2024".tex
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình (∗) có hai nghiệm phân biệt khác 0.
Điều kiện tương đương là m 6= 0 m 6= 0 m(m − 1) < 0 ⇔
0 < m < 1 ⇔ 0 < m < 1. 2m · 02 + m − 1 6= 0 m 6= 1
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 94. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số y = x4 − (m2 − 4)x2 + 3 có 1 cực trị. a) y0 = 4x3 − 2(m2 − 4)x. b) 1 ∈ S. c) 4.
d) Số phần tử của tập S là 5. Lời giải.
Ta có y0 = 4x3 − 2(m2 − 4)x = 2x · [2x2 − (m2 − 4)]. X x = 0 T E Suy ra y0 = 0 ⇔ m2 − 4 A L x2 = . 2 À m2 − 4
V Hàm số có 1 cực trị khi và chỉ khi ≤ 0 ⇔ m ∈ [−2; 2]. 2
N Vì m ∈ Z nên m ∈ S = {−2; −1; 0; 1; 2}.
Á Số phần tử của S là 5.
TO Đáp án: a đúng b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . M Ó H N 260
Facebook “Nhóm Toán và LaTeX” 12-C1-B3.tex Câu 95.
Cho hàm số f (x) liên tục trên đoạn [−1; 3] và có đồ thị như hình vẽ y
bên. Xét tính đúng sai của các khẳng sau 3 2
a) Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
b) Giá trị lớn nhất của hàm số là 3. 1 2
c) Hàm số đạt giá trị nhỏ nhất tại x = 2. x −1 O 1 3
d) Hàm số đạt giá trị nhỏ nhất tại x = −1. −1 −2 Lời giải.
a) Hàm số liên tục trên đoạn [−1; 3] nên tồn tại giá trị lớn nhất và giá trị nhỏ nhất.
b) Giá trị lớn nhất của hàm số là 3. 4
c) Giá trị nhỏ nhất của hàm số là −2 tại x = 2. 2 0
d) Giá trị nhỏ nhất của hàm số là −2 tại x = 2. I-2 A
Đáp án: a sai b đúng c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S √ √ / Câu 96. Cho hàm số y = x + 1 +
3 − x. Xét tính đúng sai của các khẳng định sau G
a) Hàm số tồn tại giá trị lớn nhất và giá trị nhỏ nhất. N Ú
b) Giá trị nhỏ nhất của hàm số là 2. -Đ
c) Giá trị lớn nhất của hàm số là 3. X √
d) Tập giá trị của hàm số là T = 2; 2 2. E Lời giải. N Á
Tập xác định của hàm số là D = [−1; 3]. Ự 1 1 D y0 = √ − √ . 2 x + 1 2 3 − x 1 1 √ √ y0 = 0 ⇔ √ − √ = 0 ⇔ x + 1 =
3 − x ⇔ x + 1 = 3 − x ⇔ x = 1. 2 x + 1 2 3 − x √
Ta có y(−1) = 2, y(1) = 2 2, y(3) = 2.
a) Hàm số liên tục và xác định trên [−1; 3] nên tồn tại giá trị lớn nhất và giá trị nhỏ nhất.
b) Giá trị nhỏ nhất của hàm số là 2. √
c) Giá trị lớn nhất của hàm số là 2 2. √
d) Tập giá trị của hàm số là T = 2; 2 2.
Đáp án: a đúng b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 97. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên sau 261
Facebook “Nhóm Toán và LaTeX” 12-C1-B3.tex x −∞ 0 1 +∞ y0 + 0 − 0 + 0 +∞ + y −2 − −1 −
Xét tính đúng sai của các khẳng định sau
a) Hàm số y = f (x) không có giá trị lớn nhất.
b) Hàm số y = f (x) không có giá trị nhỏ nhất .
c) Giá trị nhỏ nhất của hàm số là −2.
d) Giá trị lớn nhất của hàm số là 0. Lời giải.
a) Ta có lim f (x) = +∞ nên hàm số không có giá trị lớn nhất. x→+∞
X b) Ta có −2 < f(x), ∀x nhưng không tồn tại giá trị của x để f(x) = −2 nên hàm số không có giá T E trị nhỏ nhất. A L À
c) Hàm số không có giá trị nhỏ nhất. V
N d) Hàm số không có giá trị lớn nhất. Á Đáp án: a đúng TO b đúng c sai
d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x2 + x + 1 M Câu 98. Cho hàm số y =
. Xét tính đúng sai của các khẳng định sau x2 − x + 1 Ó
a) Giá trị lớn nhất của hàm số là 3.
b) Giá trị nhỏ nhất của hàm số là 1. H
c) Giá trị nhỏ nhất trên (1; +∞) là 1.
d) Giá trị lớn nhất trên (−1; 1) là 3. N Lời giải.
Điều kiện x2 − x + 1 > 0 (luôn đúng). Tập xác định là D = R.
(2x + 1)(x2 − x + 1) − (2x − 1)(x2 + x + 1) −2x2 + 2 Ta có y0 = = . (x2 − x + 1)2 (x2 − x + 1)2 Khi đó y0 = 0 ⇔ x = ±1. Bảng biến thiên x −∞ −1 1 +∞ y0 − 0 + 0 − 1 3 y 1 3 1
a) Giá trị lớn nhất của hàm số là 3. 262
Facebook “Nhóm Toán và LaTeX” "T-F Giap Thin 2024".tex 1
b) Giá trị nhỏ nhất của hàm số là . 3
c) Trên (1; +∞) hàm số không có giá trị nhỏ nhất.
d) Trên (−1; 1) hàm số không có giá trị lớn nhất.
Đáp án: a đúng b sai c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2 0 I-2 A S / G N Ú -Đ X E N Á Ự D 263
Facebook “Nhóm Toán và LaTeX” 12-C1-B4.tex 2x − 3 Câu 99. Cho hàm số y =
. Xét tính đúng sai các khẳng định dưới đây x − 1
a) Đường tiệm cận đứng của đồ thị hàm số là x = 1.
b) Đường tiệm cận đứng của đồ thị hàm số là y = 2.
c) Đường tiệm cận ngang của đồ thị hàm số là x = 1.
d) Đường tiệm cận ngang của đồ thj hàm số là y = 2. Lời giải.
Ta có lim y = lim y = 2 nên đồ thị hàm số đã cho có tiệm cận ngang là y = 2. x→−∞ x→+∞
Ta có lim y = −∞ nên đồ thị hàm số đã cho có tiệm cận ngang là x = 1. x→1+
a) Đường tiệm cận đứng của đồ thị hàm số là x = 1.
b) Đường tiệm cận đứng của đồ thị hàm số là x = 1.
c) Đường tiệm cận ngang của đồ thj hàm số là y = 2.
X d) Đường tiệm cận ngang của đồ thj hàm số là y = 2. T E A L
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . À
V Câu 100. Cho hàm số y = f(x) có bảng biến thiên như sau N x −∞ −2 0 +∞ Á y0 − + − TO +∞ + +∞ 1 M y Ó 1 −∞ 0 H
N Xét tính đúng sai của các khẳng định sau
a) x = 0 là tiệm cận đứng của đồ thị hàm số y = f (x).
b) x = −2 là tiệm cận đứng của đồ thị hàm số y = f (x).
c) x = 1 là tiệm cận đứng của đồ thị hàm số y = f (x).
d) y = 0 là tiệm cận ngang của đồ thị hàm số y = f (x). Lời giải.
a) lim f (x) = +∞ ⇒ x = 0 là đường tiệm cận đứng của đồ thị hàm số f (x). x→0− b) lim
f (x) = −∞ ⇒ x = −2 là đường tiệm cận đứng của đồ thị hàm số f (x). x→(−2)+
c) Đồ thị hàm số chỉ có hai tiệm cận đứng là x = 0 và x = −2. d)
lim f (x) = 0 ⇒ y = 0 là đường tiệm cận ngang của đồ thị hàm số f (x). x→+∞
Đáp án: a đúng b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
Facebook “Nhóm Toán và LaTeX” 12-C1-B4.tex m2x + 1 Câu 101. Cho hàm số y =
. Xét tính đúng sai của các khẳng định sau x − 1
a) Đồ thị hàm số luôn có tiệm cận ngang.
b) Đồ thị hàm số luôn có tiệm cận đứng.
c) Khi m = 1 đồ thị hàm số có 2 đường tiệm cận.
d) Khi m = 0 đồ thị hàm số có 1 đường tiệm cận. Lời giải. a)
lim y = lim y = m2 suy ra hàm số luôn có tiệm cận ngang. x→−∞ x→+∞
b) lim y = +∞ nên đồ thị hàm số đã cho có tiệm cận ngang là x = 1. x→1+ x + 1
c) Khi m = 1 ta được hàm số y =
suy ra đồ thì hàm số có x = 1 là tiệm cận đứng và y = 1 x − 1
là tiệm cận ngang nên đồ thị hàm số có 2 tiệm cận. 1 4
d) Khi m = 0 ta được hàm số y =
suy ra đồ thì hàm số có x = 1 là tiệm cận đứng và y = 0 x − 1 2
là tiệm cận ngang nên đồ thị hàm số có 2 tiệm cận. 0 I-2
Đáp án: a đúng b đúng c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A S mx2 + 6x − 2 / Câu 102. Cho hàm số y =
. Xét tính đúng sai của các khẳng định sau x + 2 G
a) Đồ thị hàm số luôn có tiệm cận đứng với mọi m. N Ú
b) Đồ thị hàm số không có tiệm cận ngang với mọi m.
c) Khi m = 1 đồ thị hàm số có một tiệm cận xiên là y = x + 4 . -Đ X
d) Đồ thị hàm số luôn có tiệm cận xiên. E Lời giải. N Á 7 7 x2 + 6x − 2 2 7 2 Ự a) Khi m = hàm số trở thành y = = x −
suy ra đồ thị hàm số không có 2 x + 2 2 7 D tiệm cận đứng. 6x − 2
b) Khi m = 0 hàm số trở thành y =
từ đó suy ra đồ thị hàm số có y = 6 là tiệm cận ngang. x + 2 x2 + 6x − 2 10
c) Khi m = 1 hàm số trở thành y = = x + 4 −
từ đó suy ra y = x + 4 là một x + 2 x + 2 tiệm cận ngang. 6x − 2
d) Khi m = 0 hàm số trở thành y =
từ đó suy ra đồ thị hàm số có y = 6 là tiệm cận ngang, x + 2
x = −2 là tiệm cận đứng và không có tiệm cận xiên.
Đáp án: a sai b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 103. 265
Facebook “Nhóm Toán và LaTeX” "T-F Giap Thin 2024".tex
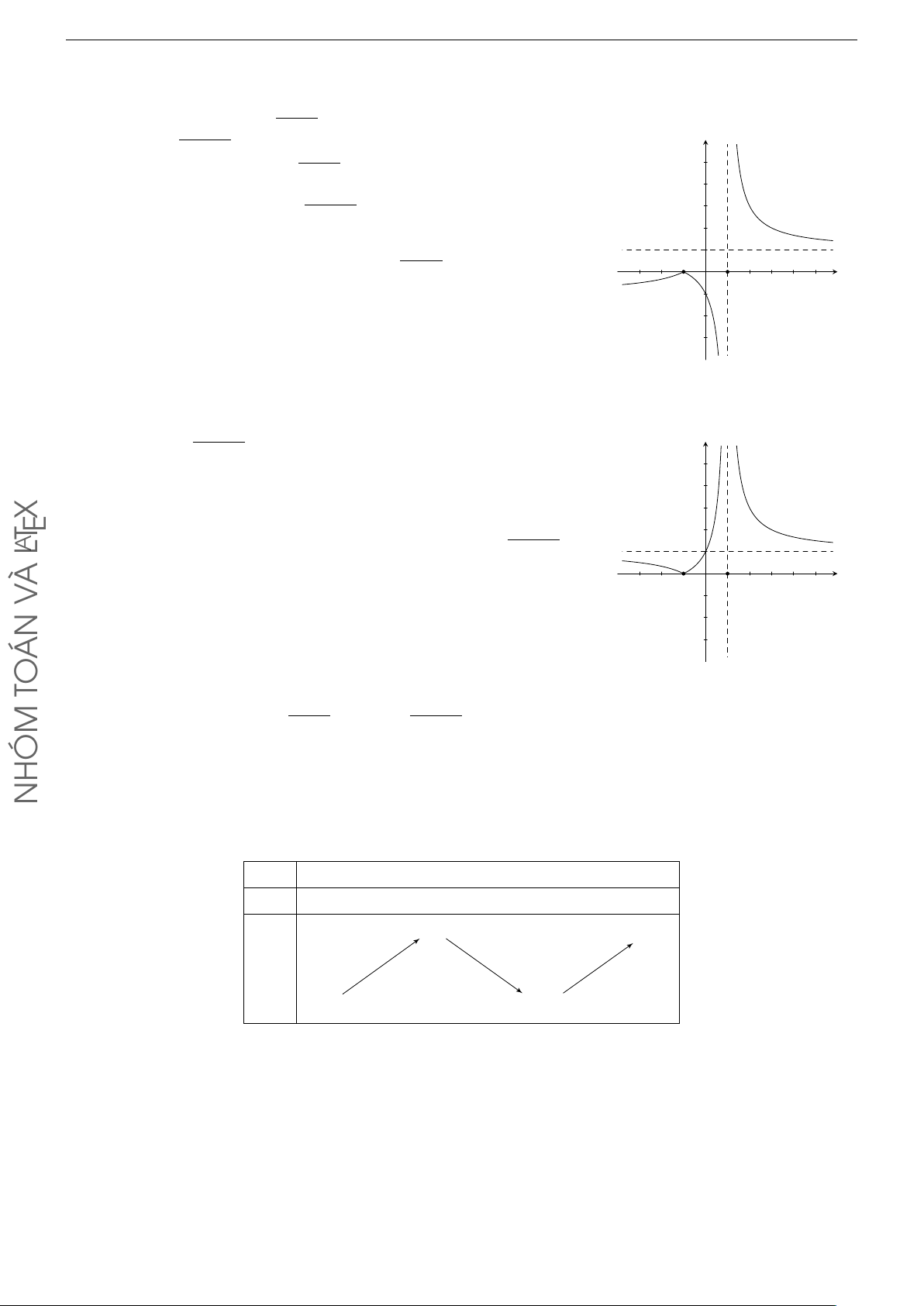
Cho hàm số y = f (x) có đồ thị như hình bên. Xét tính đúng sai y của các khẳng định sau
a) x = 2 là đường tiệm cận ngang của đồ thị hàm số. 2
b) x = −1 là đường tiệm cận đứng của đồ thị hàm số. O
c) Đồ thị hàm số có hai đường tiệm cận. −1 x
d) Đồ thị hàm số không có tiệm cận xiên. Lời giải.
a) y = 2 là đường tiệm cận ngang của đồ thị hàm số.
b) x = −1 là đường tiệm cận đứng của đồ thị hàm số.
c) x = −1 là đường tiệm cận đứng và y = 2 là đường tiệm cận ngang của đồ thị hàm số suy ra đồ
thị hàm số có hai đường tiệm cận.
X d) Đồ thị hàm số không có tiệm cận xiên. T E A L
Đáp án: a sai b đúng c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . À V Câu 104.
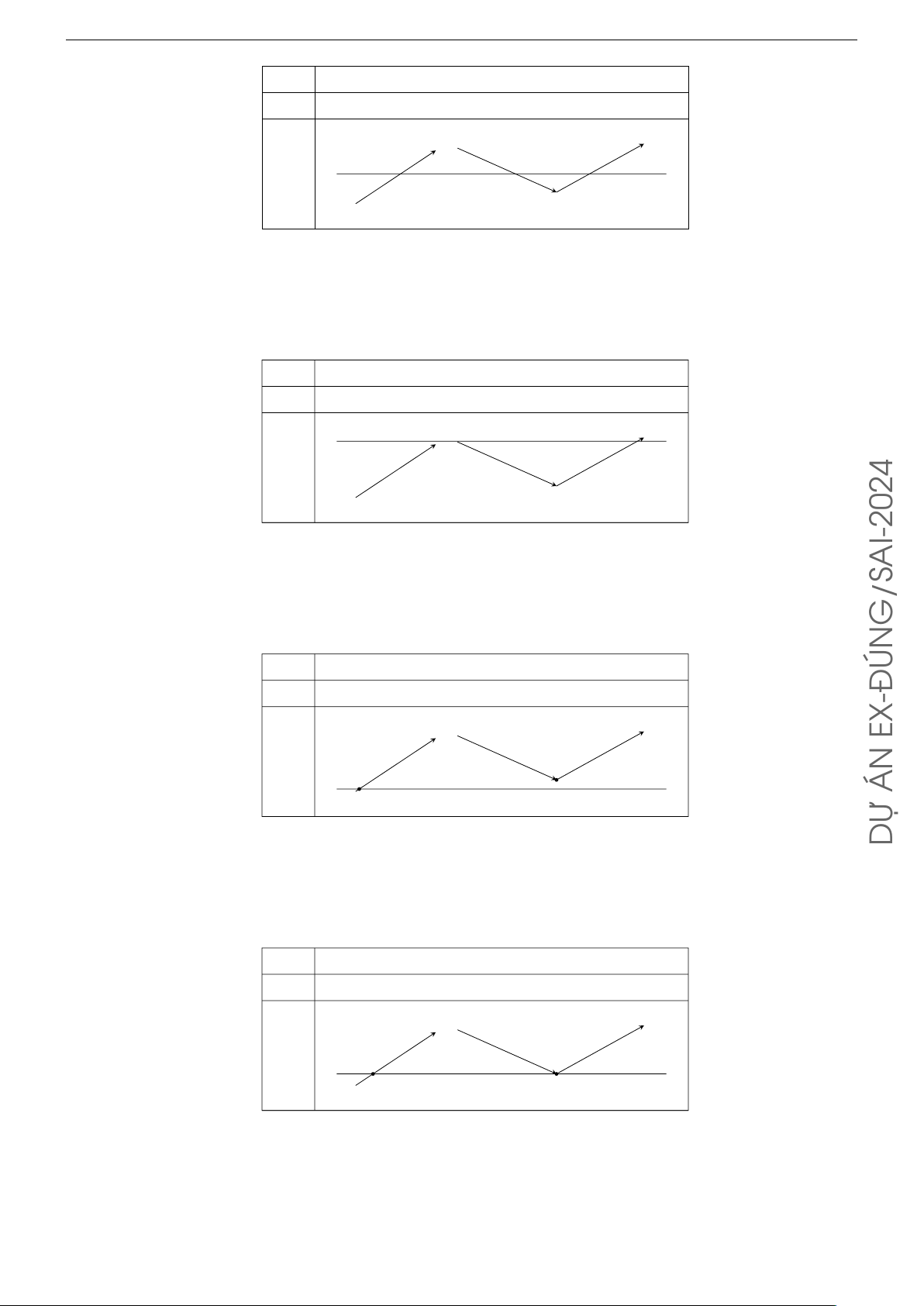
N Cho hàm số y = f(x) có đồ thị như hình bên. Xét tính đúng y
Á sai của các khẳng định sau TO
a) x = 0 là một đường tiệm cận đứng của đồ thị hàm số. M
b) y = −x là một đường tiệm cận xiên của đồ thị hàm số. Ó
c) y = x là một đường tiệm cận xiên của đồ thị hàm số. H O x N
d) Đồ thị hàm số có ba đường tiệm cận. Lời giải.
a) x = 0 là một đường tiệm cận đứng của đồ thị hàm số.
b) y = x là một đường tiệm cận xiên của đồ thị hàm số.
c) y = x là một đường tiệm cận xiên của đồ thị hàm số.
d) Đồ thị hàm số có x = 0 là tiệm cận đứng và y = x là tiệm cận xiên nên có hai tiệm cận.
Đáp án: a đúng b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 266
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex
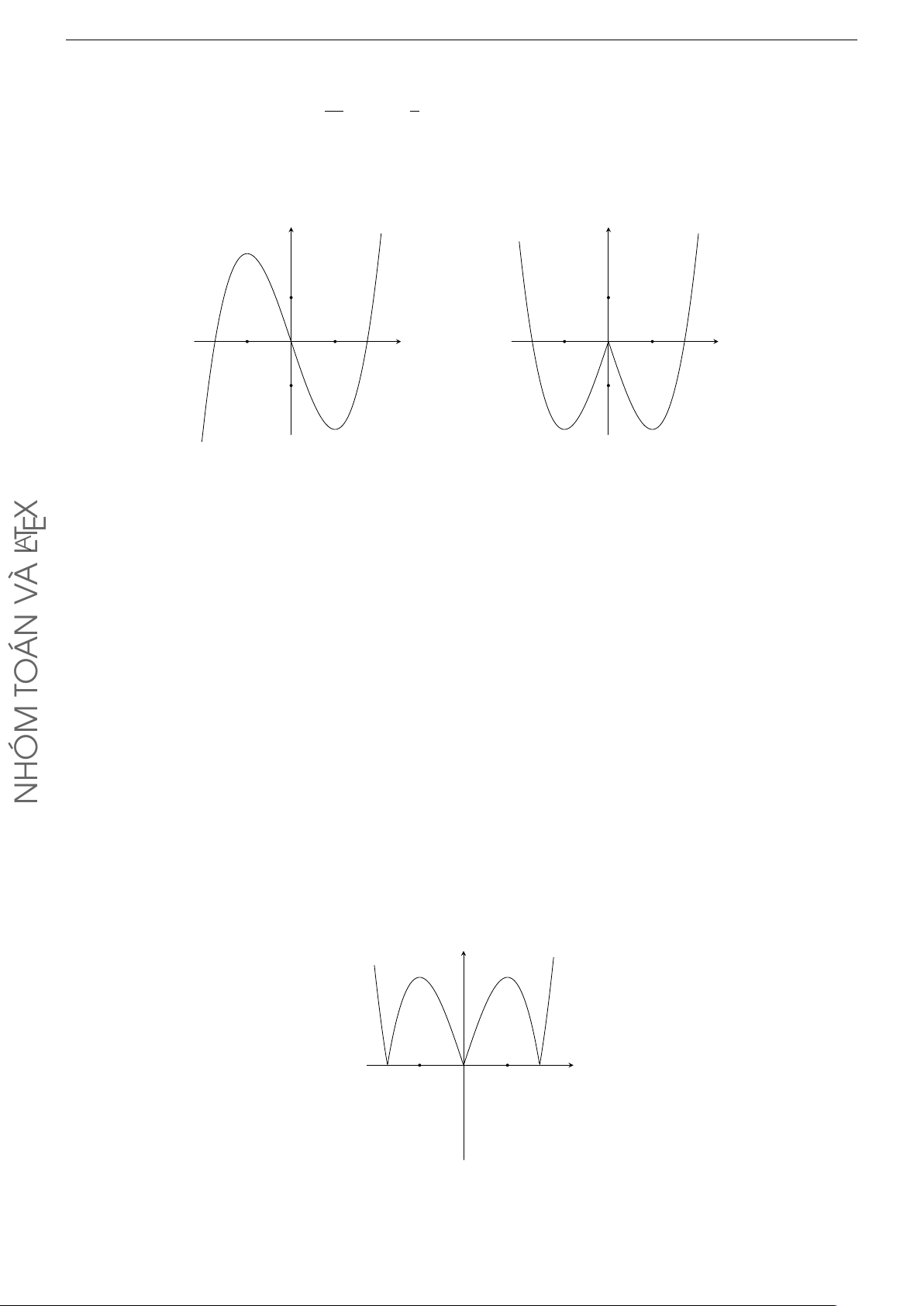
Câu 105. Cho hàm số y = ax3 + bx2 + cx + d có đồ thị các dạng sau. Các khẳng định sau đây đúng hay sai? y y y y x x x x (I) (II) (III) (IV )
a) Đồ thị (I) xảy ra khi a > 0 và f 0(x) = 0 có 2 nghiệm phân biệt.
b) Đồ thị (II) xảy ra khi a > 0 và f 0(x) = 0 có 2 nghiệm phân biệt.
c) Đồ thị (III) xảy ra khi a > 0 và f 0(x) = 0 vô nghiệm hoặc có nghiệm kép. 4
d) Đồ thị (IV ) xảy ra khi a > 0 và f 0(x) = 0 có nghiệm phân kép. 2 0 Lời giải. I-2
a) Dựa vào hình dạng đồ thị (I) ta có a > 0 và f 0(x) = 0 có 2 nghiệm phân biệt. A S /
b) Dựa vào hình dạng đồ thị (I) ta có a < 0 và f 0(x) = 0 có 2 nghiệm phân biệt. G N
c) Dựa vào hình dạng đồ thị (III) ta có a > 0 và f 0(x) = 0 vô nghiệm hoặc có nghiệm kép Ú -Đ
d) Dựa vào hình dạng đồ thị (IV ) ta có a < 0. X E
Đáp án: a đúng b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . N Câu 106. Á y Ự
Cho đồ thị hàm số y = ax3 + bx2 + cx + d. Mỗi mệnh đề sau đúng hay D sai?. a) y0 > 0, ∀x ∈ R. 2
b) a > 0, b < 0, c > 0, d > 0.
c) Đồ thị có a > 0 và f 0(x) = 0 có 2 nghiệm. x d) y0 > 0, ∀x < 1. O 1 3 Lời giải.
• Dựa vào đồ thị, dễ thấy 1 < x < 3 thì đồ thị đi xuống từ trái sang phải ⇒ y0 < 0. Do đó loại
đáp án y0 > 0, ∀x ∈ R và y0 > 0, ∀x > 1
• Dựa vào đồ thị, dễ thấy ∀x < 1 thì đồ thị đi lên từ trái sang phải ⇒ y0 > 0. • Hình dáng: ⇒ a > 0.
Hai cực trị nằm cùng một bên Oy ⇒ ac > 0 ⇒ c > 0 (vì a > 0). 267
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex
(C) ∩ Oy : x = 0 ⇒ y = d > 0. b b
Hoành độ điểm uốn x = − > 0 ⇒
< 0 ⇒ b < 0 (vì a > 0). 3a a
Đáp án: a sai b đúng c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 107. Cho hàm số y = x3 − 3x có đồ thị như hình 1. y y x O x O Hình 1 Hình 2
X Mỗi khẳng định sau đây đúng hay sai? T E
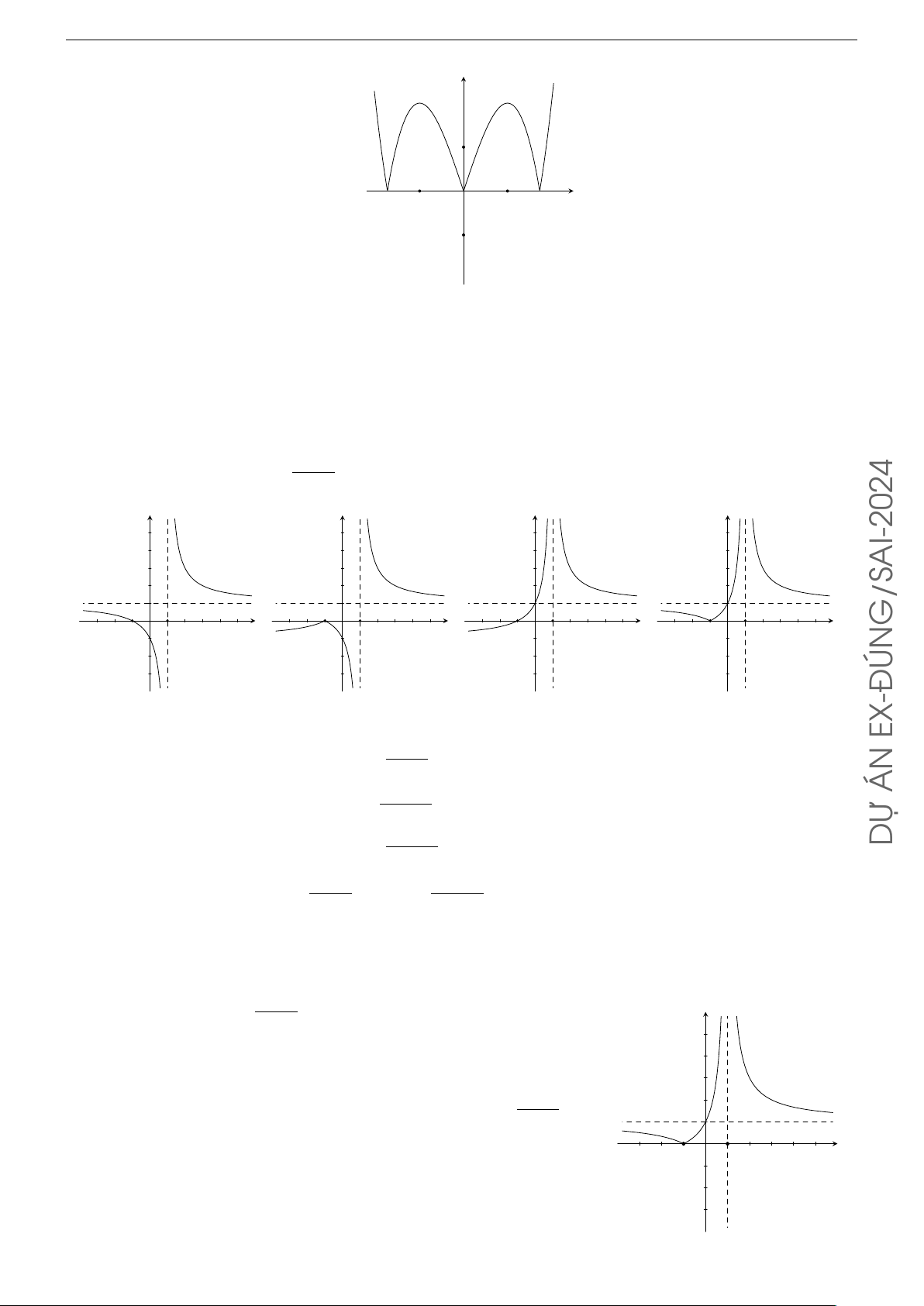
a) Đồ thị ở hình 2 là của hàm số y = |x|3 − 3 |x|. A L À
b) Đồ thị ở hình 1 và đồ thị y = |x3 − 3x| là giống nhau. V
c) Đồ thị y = |x3 − 3x| và y = |x|3 − 3 |x| là giống nhau. N
d) Đồ thị y = x3 − 3x và y = |x|3 − 3 |x| là giống nhau. Á Lời giải.
TO a) So với Hình 1, ta thấy Hình 2 là đồ thị của hàm số y = g(x) gồm 2 phần: M Ó
• Phần 1: Phần đồ thị của hàm số y = f(x) = x3 − 3x nằm phía bên phải trục tung. H N
• Phần 2: Đối xứng với phần 1 qua trục tung.
Suy ra g(x) = f (|x|) = |x|3 − 3 |x|.
b) Giữ nguyên phần đồ thị phía trên Ox của đồ thị y = |x3 − 3x|.
Bỏ phần đồ thị phía dưới Ox, lấy đối xứng phần đồ thị bị bỏ qua Ox. y x O
c) Đồ thị hàm y = |x|3 − 3 |x| 268
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex y x O Hình 2
d) Đồ thị y = x3 − 3x và y = |x|3 − 3 |x| là khác nhau.
Đáp án: a đúng b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x + 1 Câu 108. Cho hàm số y = có đồ thị như Hình 1. 4 x − 1 2 0 y y y y I-2 A S / G −1 1 x O −1 1 x O −1 1 x O −1 1 x O N Ú -Đ Hình 1 Hình 2 Hình 3 Hình 4 X E x + 1
a) Hình 4 là đồ thị của hàm số y = . N x − 1 |x + 1| Á
b) Hình 2 là đồ thị của hàm số y = . x − 1 Ự |x + 1|
c) Hình 3 là đồ thị của hàm số y = . D x − 1 x + 1 |x + 1|
d) Đồ thị của hàm số y = và y = khác nhau. x − 1 x − 1 Lời giải. a) x + 1 Đồ thị hàm số y = y . x − 1
• Phần 1: Giữ nguyên phần trên trục Ox. • x + 1
Phần 2: Đối xứng với phần bị bỏ của đồ thị y = qua x − 1 trục Ox. −1 1 x O 269
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex b) x + 1 khi x ≥ −1, x 6= 1 |x + 1| x − 1 Ta có y = = y x − 1 x + 1 − khi x < −1. x − 1 |x + 1|
Do đó, đồ thị hàm số y = gồm 2 phần: x − 1 • x + 1
Phần 1: Đồ thị hàm số y = f (x) = với x ≥ −1, x 6= 1. x − 1 −1 1 x O
• Phần 2: Đối xứng với phần còn lại của đồ thị y = f(x) với x < −1 qua trục Ox. c) |x + 1| Đồ thị y = y x − 1
• Phần 1: Giữ nguyên phần trên trục Ox. X T E |x + 1| A L
• Phần 2: Đối xứng với phần bị bỏ của đồ thị y = qua x − 1 À trục Ox. V −1 1 x O N Á TO x + 1 |x + 1|
M d) Đồ thị của hàm số y = và y = là giống nhau. x − 1 x − 1 Ó H
N Đáp án: a đúng b đúng c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 109. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. x −∞ −1 1 +∞ y0 + 0 − 0 + 2 +∞ + y −∞ − −3 −
a) Phương trình f (x) = 0 có 3 nghiệm.
b) Phương trình f (x) = 2 có 1 nghiệm.
c) Phương trình f (x) − 4 = 0 vô nghiệm.
d) Phương trình f (x) + 3 = 0 có 2 nghiệm. Lời giải. a) Ta có f (x) = 0. 270
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex x −∞ −1 1 +∞ y0 + 0 − 0 + +∞ 2 y y = 0 −3 −∞
Dựa vào bảng biến thiên, ta có phương trình f (x) = 0 có 3 nghiệm. b) Ta có f (x) = 2. x −∞ −1 1 +∞ y0 + 0 − 0 + +∞ 2 y 4 2 y = −3 −3 −∞ 0 I-2 A
Dựa vào bảng biến thiên, ta có phương trình f (x) = 2 có 1 nghiệm. S /
c) Ta có f (x) + 4 = 0 ⇔ f (x) = −4. G N x −∞ −1 1 +∞ Ú y0 + 0 − 0 + -Đ +∞ X 2 E y N −3 Á −∞ y = −4 Ự D
Dựa vào bảng biến thiên, ta có phương trình f (x) = −4 có 1 nghiệm.
d) Ta có f (x) + 3 = 0 ⇔ f (x) = −3. x −∞ −1 1 +∞ y0 + 0 − 0 + +∞ 2 y y = −3 −3 −∞
Dựa vào bảng biến thiên, ta có phương trình f (x) = −3 có 2 nghiệm.
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex Câu 110.
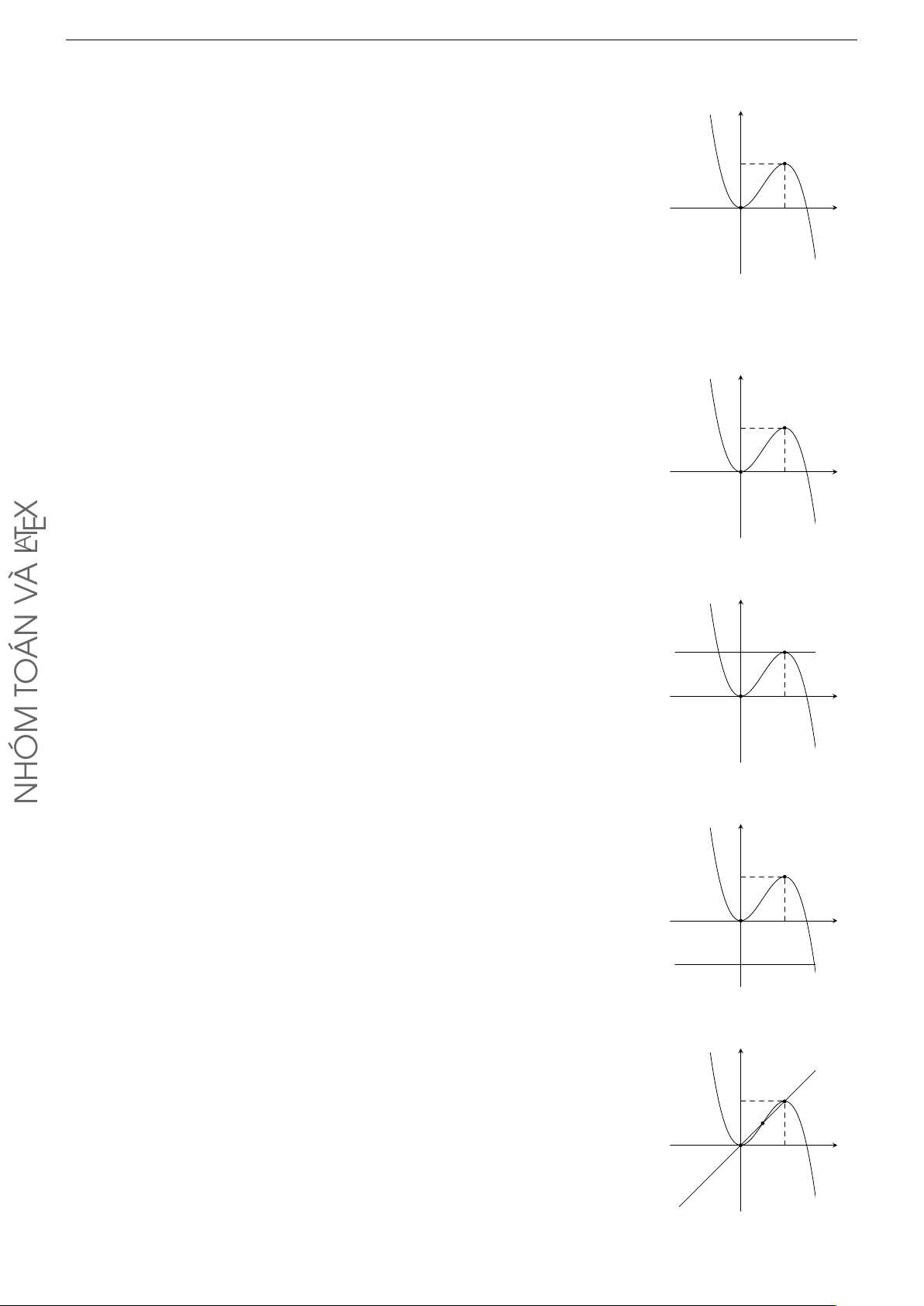
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Mỗi mệnh đề sau y đây đúng hay sai? 1
a) Phương trình f (x) = 0 có 2 nghiệm.
b) Phương trình f (x) = 1 vô nghiệm. x O 1
c) Phương trình f (x) + 1 = 0 có 2 nghiệm.
d) Phương trình f (x) = x có 3 nghiệm. Lời giải. a)
Đồ thị của hai hàm số y = f (x) và y = 0 như hình vẽ y
Dựa vào hình vẽ, ta có phương trình f (x) = 0 có 2 nghiệm phân biệt. 1 x O 1 X T E A L b) À V
Đồ thị của hai hàm số y = f (x) và y = 1 như hình vẽ y N
Dựa vào hình vẽ, ta có phương trình f (x) = 1 có 2 nghiệm phân biệt. Á 1 TO x O 1 M Ó H N c)
Đồ thị của hai hàm số y = f (x) và y = −1 như hình vẽ y
Dựa vào hình vẽ, ta có phương trình f (x) = −1 có 1 nghiệm phân biệt. 1 x O 1 d)
Đồ thị của hai hàm số y = f (x) và y = x như hình vẽ y
Dựa vào hình vẽ, ta có phương trình f (x) = x có 3 nghiệm phân biệt. 1 x O 1
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272
Facebook “Nhóm Toán và LaTeX” 12-C1-B5.tex 2x + 4
Câu 111. Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = . Mỗi khẳng x − 1
định sau đây đúng hay sai?
a) Tọa độ trung điểm I của đoạn thẳng M N là I(1; 2). # » b) M N = (2; 4). √ c) M N = 5. √ √ √ √ d) M (1 + 6, 2 + 6) và N (1 − 6; 2 − 6). Lời giải. 2x + 4
Tọa độ giao điểm của của đường y = x + 1 và đường cong y =
là nghiệm của hệ phương trình x − 1 √ x = 1 + 6 √ y = x + 1 y = 2 + 6 2x + 4 ⇔ √ y = x = 1 − 6 x − 1 √ y = 2 − 6. √ √ √ √ 4 Do đó M (1 + 6, 2 + 6) và N (1 − 6; 2 − 6). 2 0
Vậy tọa độ trung điểm của M N là I(1; 2). # » √ √ √
Vectơ M N = (−2 6; −2 6) và M N = 4 3. I-2 A
Đáp án: a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S /
Câu 112. Cho đồ thị của hàm số y = x3 + 2x2 − x + 1 và đồ thị của hàm số y = x2 − x + 3. Mỗi G
mệnh đề sau đây đúng hay sai? N Ú
a) Hai đồ thị đã cho không có điểm chung. -Đ
b) Hai đồ thị cắt nhau tại điểm (1; 3). X E
c) Tổng tung độ của các giao điểm là 3. N
d) Số giao điểm của hai đồ thị trên là số nghiệm phân biệt của phương trình hoành độ giao điểm. Á Lời giải. Ự
Số giao điểm của y = x3 + 2x2 − x + 1 và y = x2 − x + 3 là số nghiệm phân biệt của phương trình D
hoành độ giao điểm của y = x3 + 2x2 − x + 1 và y = x2 − x + 3
x3 + 2x2 − x + 1 = x2 − x + 3 ⇔ x3 + x2 − 2 = 0 ⇔ x = 1.
Vậy đồ thị của hàm số y = x3 + 2x2 − x + 1 và đồ thị của hàm số y = x2 − x + 3 cắt nhau tại điểm (1; 3).
Đáp án: a sai b đúng c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 113. 273




