Bài tập trắc nghiệm Góc giữa đường thẳng và mặt mặt phẳng môn Toán 11

Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Bài 1. Cho hình chóp S.ABCD đáy là hình chữ nhật, SA⊥(ABCD). Khi đó góc giữa SB và (SAD) là A. d BSA. B. d SBA. C. d BSD. D. d SBD.
Lời giải. Chọn đáp án A ( ( BA⊥AD SB ∩ (SAD) = S Ta có ⇒ BA⊥(SAD). Khi đó ⇒ (S \ B, (SAD)) = d BSA. BA⊥SA BA⊥(SAD) tại A
Bài 2. Cho hình chóp S.ABCD đáy là hình chữ nhật, SA⊥(ABCD). Khi đó góc giữa SC và (SAB) là A. d CSA. B. d CSB. C. d SCA. D. d SCB.
Lời giải. Chọn đáp án B ( ( CB⊥AB SC ∩ (SAB) = S Ta có ⇒ CB⊥(SAB). Khi đó ⇒ (S \ C, (SAB)) = d CSB. CB⊥SA CB⊥(SAB) tại B
Bài 3. Cho hình chóp S.ABCD đáy là hình thoi tâm O, SO⊥(ABCD). Khi đó góc giữa SA và (SBD) là A. d SAB. B. d ASB. C. d ASO. D. d ASD. thể
Lời giải. Chọn đáp án C ( ( có AO⊥BD SA ∩ (SBD) = S Ta có ⇒ AO⊥(SBD). Khi đó ⇒ (S \ A, (SBD)) = d ASO. AO⊥SO AO⊥(SBD) tại O còn
Bài 4. Cho hình chóp S.ABCD đáy là hình thoi tâm O, SA⊥(ABCD) (Cungnhauhoctoan.com). Khi đó góc khi giữa SD và (SAC) là A. d SDA. B. d DSA. C. d SDO. D. d DSO. gắng
Lời giải. Chọn đáp án D cố ( ( y DO⊥AC SD ∩ (SAC) = S Ta có ⇒ DO⊥(SAC). Khi đó ⇒ (S \ D, (SAC)) = d DSO. Hã DO⊥SA DO⊥(SAC) tại O
Bài 5. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA vuông góc với đáy. Góc giữa SC và đáy bằng
45o. Tính độ dài SA theo a. √ √ a 2 A. a 2. B. . C. a. D. 2a. 2
Lời giải. Chọn đáp án A ( SC ∩ (ABCD) = C Ta có ⇒ (SC \ , (ABCD)) = d SCA = 45o. SA⊥(ABCD) tại A √
⇒ ∆SAC vuông cân tại A ⇒ SA = AC = a 2.
Bài 6. Cho hình chóp S.ABCD đáy là hình vuông, SA vuông góc với đáy và SA = a. Góc giữa SB và đáy
bằng 45o. Tính diện tích đáy theo a. √ a2 A. a2 2. B. . C. 2a2. D. a2. 2
Lời giải. Chọn đáp án D ( SB ∩ (ABCD) = B Ta có ⇒ (SB \ , (ABCD)) = d SBA = 45o. SA⊥(ABCD) tại A
⇒ ∆SAB vuông cân tại A ⇒ AB = SA = a ⇒ SABCD = a2. Liên hệ: 0973 864 998 1 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
Bài 7. Trong các khẳng định sau, khẳng định nào ĐÚNG?
A. Góc giữa đường thẳng a và mp (P) bằng góc giữa a và mp (Q) thì (P) song song với (Q).
B. Góc giữa đường thẳng a và mp (P) bằng góc giữa đường thẳng b và mp (P) thì a song song với b.
C. Hai đường thẳng a và b song song thì góc giữa a và mp (P) bằng góc giữa b và mp (P).
D. Góc α là góc giữa đường thẳng và mặt phẳng thì 0o ≤ α ≤ 180o.
Lời giải. Chọn đáp án C Câu A, B sai.
Ví dụ: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA⊥(ABC). Khi đó   (B \ C, (SAB)) = (S \ B, (ABC)) =  d ABC  d SBA        (B \ C, (SAC)) = (S \ d ACB  C, (ABC)) = d SCA ⇒ A sai; ⇒ B sai  d ABC = d ACB  d SBA = d SCA        (SAB) ∦ (SAC)  SB ∦ SC Câu D sai. 0 ≤ α ≤ 90o.
Bài 8. Cho tứ diện ABCD có AB, BC và BD đôi một vuông góc với nhau (cungnhauhoctoan.com). Trong thể
các khẳng định sau khẳng định nào SAI? có
A. Góc giữa AC và (ABD) là góc d CAB.
B. Góc giữa AC và (BCD) là góc d BAC.
C. Góc giữa AD và (ABC) là góc còn d ADB.
D. Góc giữa CD và (ABD) là góc d CDB.
Lời giải. Chọn đáp án C khi
Ta có AD ∩ (ABC) = A và DB⊥(ABC) nên góc giữa AD và (ABC) là góc d DAB → C sai. gắng
Bài 9. Cho tứ diện ABCD có AB, BD và DC đôi một bằng nhau và vuông góc với nhau. Trong các khẳng cố
định sau khẳng định nào ĐÚNG? y
A. Góc giữa BC và (ABD) bằng 90o.
B. Góc giữa CD và (ABD) bằng 90o. Hã
C. Góc giữa AC và (BCD) bằng 45o.
D. Góc giữa AC và (ABD) bằng 45o.
Lời giải. Chọn đáp án B
Ta có CD⊥AB và CD⊥BD nên CD⊥(ABD) ⇒ góc giữa CD và (ABD) bằng 90o.
Bài 10. Cho hình vuông ABCD có độ dài cạnh là 2 cm và tâm O, trên đường thẳng qua O vuông góc với √
(ABCD) lấy điểm S sao cho SO =
2. Tính góc giữa SA và (ABCD) A. 30o. B. 45o. C. 60o. D. 90o.
Lời giải. Chọn đáp án B
Ta có SA ∩ (ABCD) = A và SO⊥(ABCD) nên góc giữa SA và (ABCD) là góc d SAO. AC √ Mà AO = =
2 = SO, nên ∆ASO vuông cân tại O ⇒ d SAO = 45o 2
Bài 11. Cho hình chóp tam giác S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy và 1 SA =
BC. Tính góc giữa SA và (SBC). 2 A. 30o. B. 45o. C. 60o. D. 90o.
Lời giải. Chọn đáp án B
Gọi M là trung điểm BC ta có BC⊥AM và BC⊥SA nên BC⊥(SAM) ⇒ (SAM)⊥(SBC) theo giao tuyến
SM. Do đó hình chiếu của SA lên (SBC) là SM. Liên hệ: 0973 864 998 2 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
Góc giữa SA và (SBC) là góc giữa SA và SM hay là góc d ASM. 1 Mà SA = AM =
BC, SA⊥AM nên ∆SAM vuông cân tại A ⇒ d ASM = 45o 2
Bài 12. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a và d
ABC = 60o. SA vuông góc với đáy và √
SA = a 2. Tính góc giữa SB và (SAC) A. 30o. B. 35o. C. 45o. D. 55o.
Lời giải. Chọn đáp án A
Gọi O = AC ∩ BD. Trước hết ta thấy BO⊥SAC nên góc giữa SB và (SAC) là góc d BSO. 1 a 3a
Lại có ∆ABC đều nên AO = AC = ⇒ SO = 2 2 2 BO 1 ⇒ tan √ d BSO = = ⇒ d BSO = 30o. SO 3
Bài 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, góc giữa SC và đáy
bằng 45o. Tính góc giữa SC và (SAD). A. 60o. B. 53o. C. 30o. D. 28o.
Lời giải. Chọn đáp án C
Ta có SA⊥(ABCD) nên góc giữa SC và đáy là góc d
SCA = 45o nên ∆SCA vuông cân tại A. thể √ ⇒ SC = AC 2 = 2a. có
Lại có CD⊥(SAD) nên góc giữa SC và (SAD) bằng góc d CSD. CD a 1 còn Mà sin d CSD = = = ⇒ d CSD = 30o. SC 2a 2 khi
Bài 14. Cho hình chóp S.ABCD đáy là hình thoi cạnh a, d
BAC = 60o (cungnhauhoctoan.com). ∆SAB đều
và nằm trong mặt phẳng vuông góc với đáy. Tính SC và góc α giữa SC với đáy. √ gắng √ a 6 A. AC = 2, α = 45o. B. AC = , α = 45o. cố 2 √ √ y a 3 C. AC = a 2, α = 60o. D. AC = , α = 60o. Hã 2
Lời giải. Chọn đáp án B
Gọi H là trung điểm AB ⇒ SH⊥AB ⇒ AH⊥(ABCD) ⇒ góc giữa SC với đáy là góc d SCH. √ a 3 ∆SAB đều nên SH = . 2 √ a 3 Lại có d
BAC = 60o nên ∆ABC đều ⇒ CH = . √ 2 a 6
⇒ ∆AHC vuông cân tại H ⇒ SC = và d SCH = 45o. 2 √
Bài 15. Cho hình lăng trụ ABC.A0B0C0 đáy ABC là tam giác vuông và CA = CB = a 2. ∆A0AB đều và
nằm trong mặt phẳng vuông góc với đáy. Tính giá trị tan của góc giữa A0C và (A0B0C0). 1 √ A. √ . B. 3. C. 0. D. 1. 3
Lời giải. Chọn đáp án B
Gọi H là trung điểm AB ⇒ A0H⊥AB ⇒ A0H⊥(ABC). Lại có (ABC) // (A0B0C0) nên góc giữa A0C với
(A0B0C0) cũng là góc giữa A0C với (ABC) và bằng góc [ A0CH. 1 √ A0H √ Mà CH = AB = a, A0H = a 3 ⇒ tan [ A0CH = = 3. 2 CH Liên hệ: 0973 864 998 3 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/ √
Bài 16. Cho hình lăng trụ ABC.A0B0C0 đáy ABC là tam giác vuông và AB = AC = a 2. ∆B0BC cân tại B0
và nằm trong mặt phẳng vuông góc với đáy, góc giữa AB0 và (A0B0C0) bằng 45o. Tính AA0. √ a √ A. a 3. B. √ . C. 2a. D. a 2. 2
Lời giải. Chọn đáp án D
Gọi H là trung điểm BC ⇒ B0H⊥BC ⇒ B0H⊥(ABC). Lại có (ABC) // (A0B0C0) nên góc giữa AB0 với
(A0B0C0) cũng là góc giữa AB0 với (ABC) và bằng góc [ B0AH = 45o. 1
⇒ ∆B0HA vuông cân tại H ⇒ B0H = AH = BC = a. √ √ 2 ⇒ AA0 = BB0 = BH2 + B0H2 = a 2. √
Bài 17. Cho hình chóp S.ABCD có đáy là hình thoi, d
BAC = 60o. SA⊥(ABCD) và SA = a 3, góc giữa SA
và (SBD) bằng 30o. Tính diện tích hình thoi ABCD. √ √ a2 3 √ A. a2 3. B. . C. 2a2. D. 2a2 3. 2
Lời giải. Chọn đáp án D
Gọi O là giao điểm của AC và BD. Ta thấy BD⊥(SAC) nên (SAC)⊥(SBD) theo giao tuyến SO.
⇒ Hình chiếu của SA lên (SBD) chính là SO. thể
⇒ Góc giữa SA với (SBD) là góc giữa SA và SO hay chính là góc d ASO = 30o. có
⇒ AO = SA tan 30o = a ⇒ AC = 2a. Mà d BAC = 60o nên ∆ABC đều. √ ⇒ S 3. còn ABCD = BA.BC. sin 60o = 2a2
Bài 18. Cho hình chóp tam giác đều, các cạnh bên có độ dài là a và tạo với đáy một góc 60o. Tính chu vi khi đáy của hình chóp đó. √ 3a 3a 3 √ gắng A. 3a. B. . C. . D. 3a 3. 2 2 cố
Lời giải. Chọn đáp án C y
Gọi O là tâm của đáy ⇒ SO⊥(ABC). Hã a
Góc giữa SA đáy là góc d
SAO = 60o ⇒ AO = SA. cos 60o = . 2 3 3a
Gọi M là trung điểm BC ⇒ AM = AO = . 2 √ 4 √ AM a 3 3a 3 ∆ABC đều nên BC = AB = = ⇒ Chu vi đáy là . sin 60o 2 2
Bài 19. Cho hình chóp S.ABCD có đáy là hình thoi, BD = 2AC = 2a. Tính góc giữa SC và (SBD) biết
SA = SC, tam giác SBD vuông cân tại S. A. 26o. B. 30o. C. 36o. D. 60o.
Lời giải. Chọn đáp án A
Gọi O = AC ∩ BD, tam giác SAC và SBD cân tại S nên SO vuông góc với AC và BD, tức là SO⊥(ABCD).
⇒ CO⊥(SBD) ⇒ góc giữa SC và (SBD) là góc d CSO. 1 1 a OC 1 Ta có SO = BD = a, OC = AC = ⇒ tan d CSO = = ⇒ d CSO ≈ 26o. 2 2 2 SO 2
Bài 20. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng 1 cm. Tính góc giữa AC0 và (BDD0B0). A. 35o. B. 45o. C. 55o. D. 60o.
Lời giải. Chọn đáp án C
Gọi O, O0 là tâm của hình vuông ABCD và A0B0C0D0, I là giao điểm của OO0 với AC0. Liên hệ: 0973 864 998 4 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
⇒ I là giao điểm của AC0 với (BDD0B0). Ta có AO0⊥BD và AO0⊥BB0 nên AO0⊥(BDD0B0).
⇒ Góc giữa AC0 và (BDD0B0) là góc d AIO0. √ a 2 OO0 a AO0 √ Lại có AO0 = , O0I = = ⇒ tan d AIO0 = = 2 ⇒ d AIO0 ≈ 55o. 2 2 2 IO0
Bài 21. Cho hình chóp tứ giác đều có các mặt bên là các tam giác đều (Cungnhauhoctoan.com). Tính góc
giữa cạnh bên và đáy của hình chóp. A. 30o. B. 45o. C. 15o. D. 60o.
Lời giải. Chọn đáp án B
Gọi S.ABCD là hình chóp đều thỏa mãn đề bài. Ta có đáy ABCD là hình vuông, gọi O là tâm của đáy
⇒ SO⊥(ABCD) ⇒ góc giữa cạnh bên SA và đáy là góc d SAO. √ √ a 2 AO 2
Gọi cạnh đáy của hình chóp là a ⇒ AO = ⇒ cos d SAO = = ⇒ d SAO = 45o 2 SA 2
Bài 22. Cho hình chóp tứ giác đều S.ABCD. M, N là trung điểm của SA, BC. Biết AB = a, góc giữa MN
và đáy bằng 45o. Tính SO. √ √ √ √ a 10 a 5 a 10 a 5 A. . B. . C. . D. . 2 4 4 2
Lời giải. Chọn đáp án A thể
Kẻ MI // SO ⇒ I là trung điểm AO và MI⊥(ABCD) ⇒ góc giữa MN và đáy là góc [ MNA = 45o. √ có 5a2 a 10
Xét trong ∆CIN có IN2 = IC2 +CN2 − 2IC.CN. cos 45o = ⇒ IN = . √ √ 8 4 còn a 10 a 10 ⇒ IM = IN tan 45o = ⇒ SO = 2IM = . khi 4 2
Bài 23. Cho hình chóp SABC có SA⊥(ABC), ∆ABC có ba góc nhọn. Gọi H, K lần lượt là trực tâm ∆ABC và gắng
∆SBC. Tính số đo góc giữa SC và (BHK) A. 30o. B. 45o. C. 60o. D. 90o. cố y
Lời giải. Chọn đáp án D Hã
Ta có BH⊥AC, BH⊥SA nên BH⊥(SAC) ⇒ SC⊥BH.
Mà SC⊥BK nên SC⊥(BHK). Vậy góc giữa SC và (BHK) bằng 90o. √
Bài 24. Cho hình chóp S.ABCD có đáy là hình thoi, d
ABC = 60o. SA⊥(ABCD) và SA = a 2, góc giữa SD
và (SAC) bằng 30o. Tính diện tích hình thoi ABCD. √ √ √ a2 2 a2 3 2a2 3 A. a2. B. . C. . D. . 4 2 5
Lời giải. Chọn đáp án C
DO⊥(SAC) nên góc giữa SD và (SAC) là góc d DSO = 30o.
Đặt AO = x ⇒ SO2 = 2a2 + x2. √ Ta có \
ABC = 60o nên ∆ABC đều và ∆ADC cũng đều. Do đó DO = x 3. DO a ⇒ SO =
= 3x. Nên ta có phương trình 9x2 = 2a2 + x2 ⇔ x = . tan 30o √ 2 a2 3 Vậy SABCD = 2AO.DO = . 2 √
Bài 25. Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = a, AD = a 3. SA vuông góc với đáy,
SA = 2a. Kẻ SM, SN lần lượt vuông góc với SB, SD. Tính góc giữa AC và (AMN). A. 15o. B. 30o. C. 45o. D. 60o. Liên hệ: 0973 864 998 5 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
Lời giải. Chọn đáp án C
Ta có BC⊥(SAB) nên AM⊥BC do đó AM⊥(SBC) ⇒ SC⊥AM. Tương tự
cũng có SC⊥(AMN). Kẻ AH⊥SC ⇒ H ∈ (AMN).
Như vậy ta có H là hình chiếu vuông góc của C lên (AMN)
⇒ góc giữa AC và (AMN) là góc [
CAH. Lại có AC = 2a = SA nên ∆SAC vuông cân, do đó [ CAH = 45o.
Bài 26. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. ∆SAB và ∆SAD là các tam giác vuông cân
tại A. Gọi M là trung điểm SD, (α) là mặt phẳng qua A vuông góc với SC. Tính sin của góc giữa CM và (α). √ √ √ √ 2 3 2 2 3 2 A. . B. . C. . D. . 3 2 3 2
Lời giải. Chọn đáp án C
Ta có SA⊥AB và SA⊥AD nên SA⊥(ABCD). thể
Từ đó CD⊥(SAD) ⇒ AM⊥CD ⇒ AM⊥(SCD) ⇒ AM⊥SC ⇒ M ∈ (α). có
Kẻ AH⊥SC ⇒ (α) chính là mặt (AHM). Lại có CH⊥(AHM),
CM ∩ (AHM) = M. Nên góc giữa CM và (α) chính là góc [ CMH. còn √ a 6 2a
Lại có ∆CDM vuông tại D nên CM = , CH = √ khi 2 3 √ CH 2 2 ⇒ sin [ CMH = = . CM 3 gắng cố
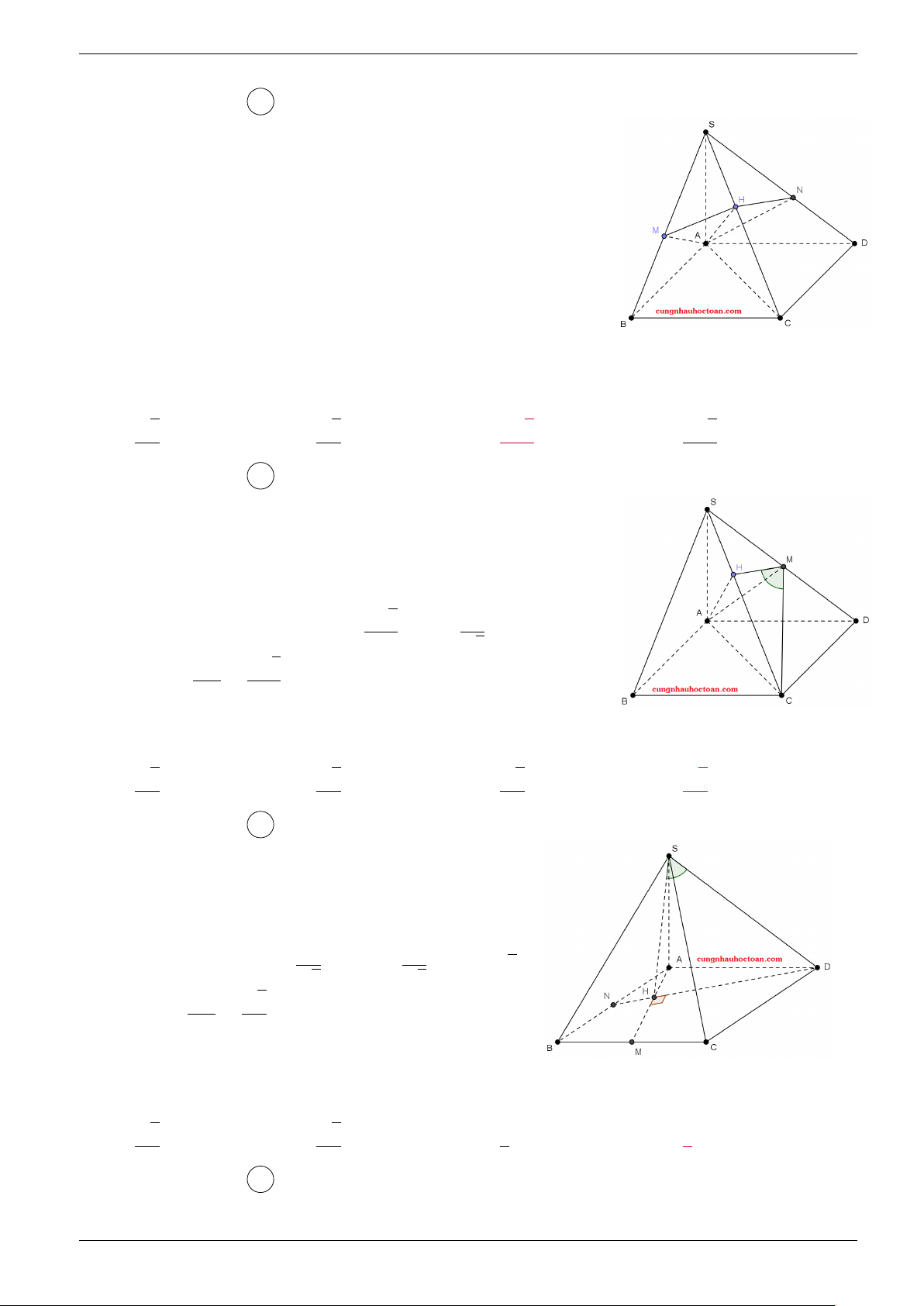
Bài 27. Cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA vuông góc với đáy, SA = a. M là trung y
điểm BD (Cungnhauhoctoan.com). Tính giá trị sin của góc giữa SD và (SAM). √ √ √ √ Hã 2 2 2 2 A. . B. . C. . D. . 2 3 4 5
Lời giải. Chọn đáp án D
Gọi N là trung điểm AB, H = DN ∩ AM. Ta có ∆ADN = ∆BAM
⇒ DN⊥AM ⇒ DN⊥(SAM) tại H ⇒ góc giữa SD và (SAM) là góc [ DSH. a 2a √
Mặt khác ta tính được AH = √ ⇒ HD = √ , SD = a 2 5 5 √ DH 2 ⇒ sin [ DSH = = . SD 5
Bài 28. Cho hình chóp S.ABCD đáy là hình vuông cạnh a. ∆SAB đều và nằm trong mặt phẳng vuông góc
với đáy. M, N lần lượt là trung điểm của AB, AD. Tính giá trị sin của góc giữa SN và (SCM). √ √ 3 3 3 3 A. . B. . C. . D. . 2 5 2 5
Lời giải. Chọn đáp án D Liên hệ: 0973 864 998 6 Xuân Trường - Nam Định Lê Minh An - Vũ Thị Duyên http://cungnhauhoctoan.com/
Ta có SM⊥AB, mà (SAB)⊥(ABCD) theo giao tuyến AB nên
SM⊥(ABCD). Gọi H = BN ∩ CM. Ta có ∆ABN = ∆BMC nên suy ra
được BM⊥CM tại H. Từ đó suy ra NH⊥(SCM) tại H nên góc giữa SN và (SCM) là góc [ NSH. √ a 3a 5
Mặt khác ta tính được BH = √ ⇒ NH = BN − BH = , 5 10 √ √ a 5 HN 3 SN = SM2 + MN2 = . ⇒ sin [ NSH = = . 2 SN 5
Bài 29. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, ∆SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. (Cungnhauhoctoan.com) Tính giá trị sin của góc giữa SD và (SBC). √ √ √ √ 3 6 3 6 A. . B. . C. . D. . 2 2 4 4
Lời giải. Chọn đáp án D
Kẻ đường thẳng d qua S và song song với AD, khi đó
d = (SBC) ∩ (SAC). Kẻ AF // SD (F ∈ d). Khi đó góc
giữa SD và (SBC) cũng là góc giữa AF và (SBC).
Mặt khác BC⊥AB mà (SAB)⊥(ABCD) theo giao tuyến thể
AB nên BC⊥(SAB). Kẻ AE⊥SB ⇒ AE⊥(SBC) ⇒ góc có
giữa AF với (SBC) chính là góc d AFE. √ √ còn a 3 Mà AE = , AF = SD = a 2. 2 √ khi AE 6 Vậy sin d AFE = = . AF 4 √ gắng
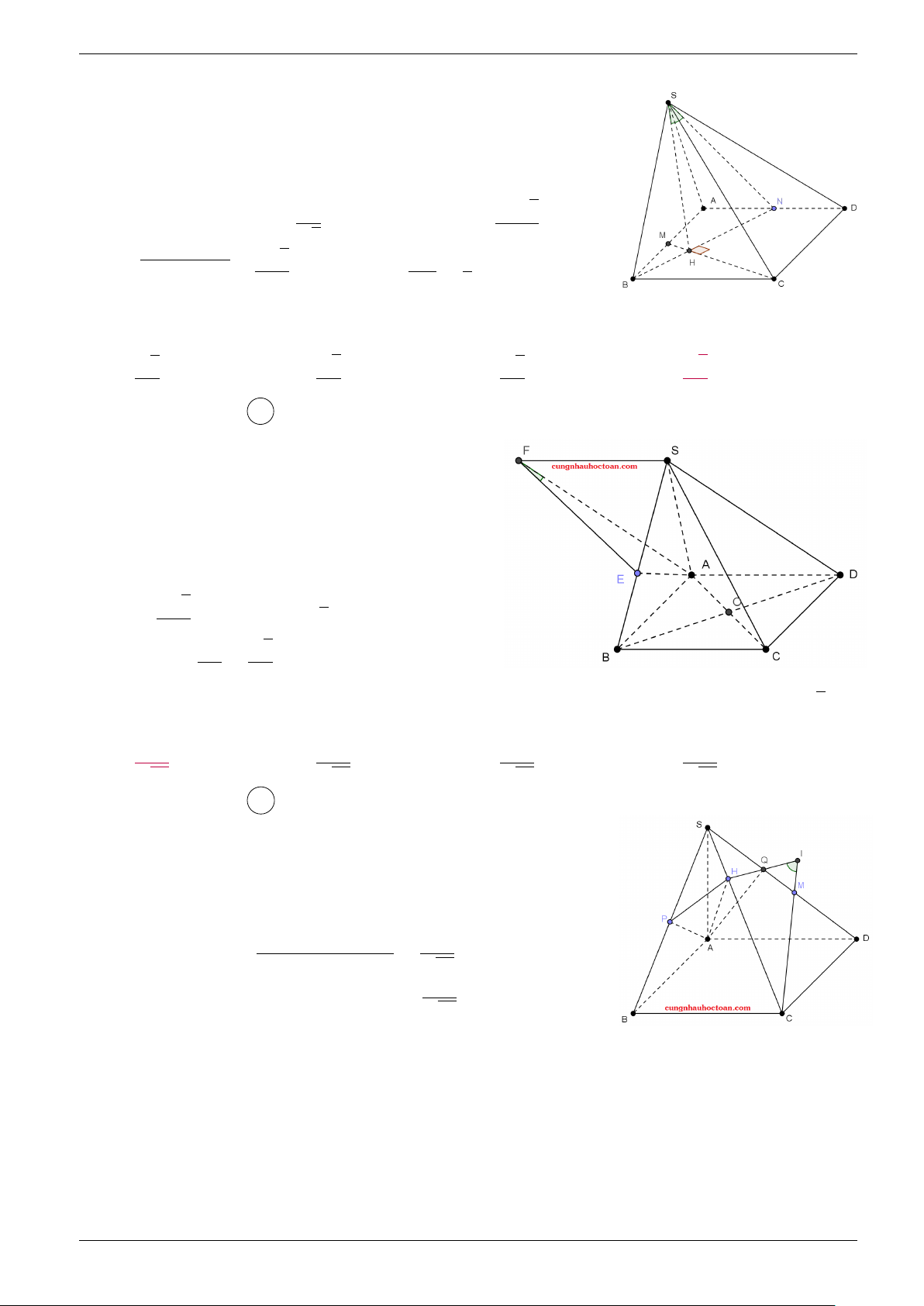
Bài 30. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = a 3. Kẻ cố
AP⊥SB, AQ⊥SD. Gọi M là trung điểm SD. Tính giá trị cosin của góc giữa CM và (APQ). y 1 3 7 9 A. √ . B. √ . C. √ . D. √ . Hã 10 10 10 10
Lời giải. Chọn đáp án A
Ta có BC⊥(SAB) nên AP⊥BC do đó AP⊥(SBC) ⇒ SC⊥AP. Tương tự
cũng có SC⊥AP nên SC⊥(APQ). Kẻ AH⊥SC ⇒ H ∈ (APQ).
⇒ SC⊥(AMN) tại H. Gọi I = CM ∩ HQ ⇒ I = CM ∩ (APQ)
⇒ góc giữa CM và (APQ) là góc d CIH. SC2 + CM2 − SM2 3 Xét ∆CSM, cos [ MCS = = √ . 2SC.CM 10 1 ∆CHI vuông tại H nên cos √ d CIH = sin [ MCS = . 10 ĐÁP ÁN 1 A 4 D 7 C 10 B 13 C 16 D 19 A 22 A 25 C 28 D 2 B 5 A 8 C 11 B 14 B 17 D 20 C 23 D 26 C 29 D 3 C 6 D 9 B 12 A 15 B 18 C 21 B 24 C 27 D 30 A Liên hệ: 0973 864 998 7 Xuân Trường - Nam Định