Bài tập trắc nghiệm phương pháp tọa độ trong mặt phẳng Oxy có lời giải chi tiết

Câu 1: [0H3-1-1] Phương trình đường thẳng đi qua

(1;2)N

và song song với đường thẳng

2 3 12 0xy  

là.

A.

2 3 8 0xy  

. B.

2 3 8 0xy  

. C.

4 6 1 0xy  

. D.

2 3 8 0xy  

.

Lời giải

Chọn A

Phương trình đường thẳng cần tìm là

2( 1) 3( 2) 0 2 3 8 0x y x y       

.

Câu 2: [0H3-1-1] Viết phương trình tổng quát của đường thẳng đi qua điểm

 

0 ; 0O

và song

song với đường thẳng có phương trình

6 4 1 0.xy  

A.

4 6 0xy

. B.

3 1 0xy  

. C.

3 2 0xy

. D.

6 4 1 0xy  

.

Lời giải

Chọn C

Đường thẳng đi qua

 

0

;

o

M x y

và song song với đường thẳng

:0d ax by c  

có dạng:

   

00

0 ( 0)

oo

a x x b y y ax by      

.

Nên đường thẳng đi qua điểm

 

0 ; 0O

và song song với đường thẳng có phương

trình

6 4 1 0xy  

là

3 2 0xy

.

Câu 3: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua

2

điểm

3 (); 2A 

và

 

1 ; 4B

A.

 

4 ; 2

. B.

 

1 ; 2

. C.

()1 ; 2

. D.

(2 ; .1)

Lời giải

Chọn C

Đường thẳng đi qua

2

điểm

3 (); 2A 

và

 

1 ; 4B

có vectơ chỉ phương là

 

4;2AB 

suy ra tọa độ vectơ pháp tuyến là

()1 ; 2

.

Câu 4: [0H3-1-1] Đường thẳng đi qua

 

1; 2A 

, nhận

(2; 4)n 

làm véctơ pháp tuyến có

phương trình là:

A.

– 2 – 4 0xy

. B.

40xy  

.

C.

– 2 – 4 0xy

. D.

– 2 5 0xy

.

Lời giải

Chọn D

Đường thẳng đi qua

 

1; 2A 

, nhận

(2; 4)n 

làm véctơ pháp tuyến có phương

trình là:

   

2 1 4 2 0 2 5 0x y x y       

.

Câu 5: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 1. B. 2. C. 3. D. Vô số.

Lời giải

Chọn D

Câu 6: [0H3-1-1] Đường thẳng

51 30 11 0xy  

đi qua điểm nào sau đây?

A.

3

1; .

4









B.

3

1; .

4









C.

3

1; .

4







D.

4

1; .

3









Lời giải

Chọn D

Thay tọa độ từng điểm vào phương trình đường thẳng: thỏa phương trình đường

thẳng thì điểm đó thuộc đường thẳng.

Tọa độ điểm của câu D thỏa phương trình.

Câu 7: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

( 3;2)A 

và

 

1;4B

.

A.

 

1;2

. B.

 

4;2

. C.

 

2;1

. D.

 

1;2

.

Chọn A

Đường thẳng

AB

có

 

vtcp 4;2AB 

,

   

vtpt 2; 4 2. 1;2n     

.

Câu 8: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

 

2;3A

và

 

4;1B

.

A.

 

2; 2

. B.

 

2; 1

. C.

 

1;1

. D.

 

1; 2

.

Chọn C

Đường thẳng

AB

có

 

vtcp 2; 2AB 

,

   

vtpt 2;2 2. 1;1n 

.

Câu 9: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

   

;0 và 0;A a B b

.

A.

 

;ba

. B.

 

;ba

. C.

 

;ba

. D.

 

;ab

.

Chọn B

Đường thẳng

AB

có

 

vtcp ;AB a b

,

 

vtpt ;n b a

.

Câu 10: [0H3-1-1] Cho đường thẳng

: 3 2 0xy   

. Tọa độ của vectơ nào không phải là

vectơ pháp tuyến của



.

A.

 

1;–3

. B.

 

–2;6

. C.

1

;1

3









. D.

 

3;1

.

Lời giải

Chọn D

Áp dụng lý thuyết: Đường thẳng có phương trình

0ax by c  

thì vectơ pháp

tuyến

 

;n k a b

và vectơ chỉ phương

 

;u k b a

với

0k 

.

Vectơ pháp tuyến của đường thẳng

 



là

 

1; 3nk

.

Với

 

1

1 1; 3kn   

;

 

2

2 2;6kn    

.

Câu 11: [0H3-1-1] Xét vị trí tương đối của hai đường thẳng sau:

1

: 2 1 0d x y  

và

2

: 3 6 10 0d x y   

.

A. Trùng nhau. B. Song song.

C. Cắt nhau nhưng không vuông góc nhau. D. Vuông góc với nhau.

Lời giải

Chọn B

Đường thẳng

1

: 2 1 0d x y  

có

 

1

1; 2vtpt n 

.

Đường thẳng

2

: 3 6 10 0d x y   

có

 

2

3;6vtpt n 

.

Ta có

21

3.nn

nên

1

n

,

2

n

cùng phương.

Chọn

 

1

1;0Ad

mà

 

2

1;0Ad

nên

1

d

,

2

d

song song với nhau.

HOẶC dùng dấu hiệu

1 1 1

2 2 2

a b c



kết luận ngay.

Câu 12: [0H3-1-1] Xét vị trí tương đối của hai đường thẳng sau:

1

:1

23

xy

d 

và

2

:6 4 8 0d x y  

.

A. song song. B. Trùng nhau.

C. Cắt nhau nhưng không vuông góc nhau. D. Vuông góc với nhau.

Lời giải

Chọn A

Đường thẳng

1

:1

23

xy

d 

có

 

1

3; 2vtpt n 

Đường thẳng

2

:6 4 8 0d x y  

có

 

2

6; 4vtpt n 

Ta có

21

2.nn

nên

1

n

,

2

n

cùng phương.

Chọn

 

1

2;0Ad

mà

 

2

2;0Ad

nên

1

d

,

2

d

song song với nhau.

HOẶC dùng dấu hiệu

1 1 1

2 2 2

a b c



kết luận ngay.

Câu 13: [0H3-1-1] Xét vị trí tương đối của hai đường thẳng sau:

1

:1

34

xy

d 

và

2

:3 4 10 0d x y  

.

A. Vuông góc với nhau. B. Trùng nhau.

C. Cắt nhau nhưng không vuông góc nhau. D. Song song.

Lời giải

Chọn A

Đường thẳng

1

:1

34

xy

d 

có

 

1

4; 3vtpt n 

Đường thẳng

2

:3 4 10 0d x y  

có

 

2

3;4vtpt n 

Ta có

12

.0nn 

nên

1

d

,

2

d

vuông góc nhau.

Câu 14: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

15 2 10 0xy  

và trục tung?

A.

2

;0

3







. B.

 

0; 5

. C.

 

0;5

. D.

 

5;0

.

Lời giải

Chọn B

Thay

0x 

vào phương trình đường thẳng ta có:

15.0 2 10 0 5     yy

.

Câu 15: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

5 2 10 0xy  

và trục hoành.

A.

 

2;0

. B.

 

0;5

. C.

 

2;0

. D.

 

0;2

.

Lời giải

Chọn A

Thay

0y 

vào phương trình đường thẳng ta có:

5 2.0 10 0 2xx    

.

Vậy đáp án đúng là

A

.

Câu 16: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

15 2 10 0xy  

và trục hoành.

A.

 

0; 5

. B.

2

;0

3







. C.

 

0;5

. D.

 

5;0

.

Lời giải

Chọn B

Thay

0y 

vào phương trình đường thẳng ta có:

2

15 2.0 10 0

3

xx    

.

Câu 17: [0H3-1-1] Tìm tọa độ giao điểm của 2 đường thẳng

7 3 16 0xy  

và

10 0x

.

A.

 

10; 18

. B.

 

10;18

. C.

 

10;18

. D.

 

10; 18

.

Lời giải

Chọn A

Ta có:

10 0x



10x 

.

Thay vào phương trình đường thẳng ta có:

 

7. 10 3 16 0 18yy      

.

Câu 18: [0H3-1-1] Tìm tọa độ giao điểm của 2 đường thẳng

5 2 29 0xy  

và

3 4 7 0xy  

.

A.

 

5; 2

. B.

 

2; 6

. C.

 

5;2

. D.

 

5;2

.

Lời giải

Chọn A

Xét hệ phương trình:

5 2 29 0 5 2 29 5

3 4 7 0 3 4 7 2

x y x y x

x y x y y

     

  



  

      

  

.

Câu 19: [0H3-1-1] Giao điểm của hai đường thẳng

1

: 2 – 8 0 d x y 

và

2

12

:

4

xt

d

yt











là:

A.

 

3; –2M

. B.

 

3;2M 

. C.

 

3;2M

. D.

 

3; –2M 

.

Lời giải.

Chọn B

Thay

x

,

y

từ phương trình

2

d

vào

1

d

ta được:

   

2 1 2 – 4 8 0    tt

3 6 2   tt

.

Vậy

1

d

và

2

d

cắt nhau tại

 

3;2M 

.

Câu 20: [0H3-1-1] Trong mặt phẳng

Oxy

, cặp đường thẳng nào sau đây song song với nhau?

A.

1

:

2

xt

d

yt











và

2

:

34

xt

d

yt

  









.

B.

1

10 5

:

12

xy

d







và

2

11

:

11

xy

d







.

C.

1

:1d y x

và

2

: 10 0d x y  

.

D.

1

:2 5 7 0d x y  

và

2

: 2 0d x y  

.

Lời giải

Chọn C

Đáp án

A

thì

1

d

,

2

d

lần lượt có VTCP

 

1

1;2u

,

 

2

1; 4u

không cùng phương.

Đáp án

B

thì

1

d

,

2

d

lần lượt có VTCP

 

1

1;2u

,

 

2

1;1u

không cùng

phương.

Đáp án

C

thì

1

d

,

2

d

lần lượt có tỉ số các hệ số

1 1 1

2 2 2

a b c



suy ra

1

d

,

2

d

song

song.

Đáp án

D

thì

1

d

,

2

d

lần lượt có tỉ số các hệ số

11

22

ab



suy ra

1

d

,

2

d

không song

song.

Câu 21: [0H3-1-1] Tìm tọa độ giao điểm của hai đường thẳng

 

1

12

:

75

xt

yt













và

 

2

14

:

63

xt

yt













  



.

A.

 

1;7

. B.

 

1; 3

. C.

 

3;1

. D.

 

3; 3

.

Lời giải:

Chọn D

Xét hệ:

1 2 1 4

7 5 6 4

tt



  







   



2

1

t

















giao điểm của

 

1



và

 

2



là

 

3; 3A 

.

Câu 22: [0H3-1-1] Xác định vị trí tương đối của hai đường thẳng

 

1

3

2

:

4

1

3

xt

yt













  





và

 

2

9

2

:

1

8

3

xt

yt























.

A. Song song nhau. B. Cắt nhau.

C. Vuông góc nhau. D. Trùng nhau.

Lời giải:

Chọn D

Xét hệ:

39

22

41

18

33

tt





  









   





6 ' 1

tt













: hệ có vô số nghiệm

12

   

.

Câu 23: [0H3-1.21-2] Đường thẳng

 

:5 3 15xy  

tạo với các trục tọa độ một tam giác

có diện tích bằng bao nhiêu?

A.

3

. B.

15

. C.

15

2

. D.

5

.

Lời giải:

Chọn C

Gọi

A

là giao điểm của



và

Ox

,

B

là giao điểm của



và

Oy

.

Ta có:

 

3;0A

,

 

0;5B

3OA

,

5OB 

15

2

OAB

S





.

Câu 24: [0H3-1-1] Tìm tọa độ giao điểm của hai đường thẳng

 

1

34

:

25

xt

yt

  











và

 

2

14

:

75

xt

yt

















.

A.

 

5;1A

. B.

 

1;7A

. C.

 

3;2A 

. D.

 

1; 3A 

.

Lời giải:

Chọn B

Xét hệ:

3 4 1 4

2 5 7 5

tt



   







  



1

'0

t















giao điểm

 

1;7A

.

Câu 25: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

:15 2 10 0xy   

và trục tung

Oy

.

A.

 

5;0

. B.

 

0;5

. C.

 

0; 5

. D.

2

;5

3







.

Lời giải

Chọn C

Giải hệ:

15 2 10 0 5

00

x y y

xx

    











.

Vậy tọa độ giao điểm của

:15 2 10 0xy   

và trục tung

Oy

là

 

0; 5

.

Câu 26: [0H3-1-1] Tìm tọa độ giao điểm của hai đường thẳng sau đây:

1

22 2

:

55 5

xt

yt













và

2

12 4

:

15 5

xt

yt













  



.

A.

 

6;5

. B.

 

0;0

. C.

 

5;4

. D.

 

2;5

.

Lời giải

Chọn B

Giải hệ:

22 2 12 4 11 0

55 5 15 5 3 0



     

  



  



      

  

t t t y

t t t x

.

Vậy tọa độ giao điểm của

1



và

2



là

 

0;0

.

Câu 27: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

:7 3 16 0xy   

và đường

thẳng

: 10 0dx

.

A.

 

10; 18

. B.

 

10;18

. C.

 

10;18

. D.

 

10; 18

.

Lời giải

Chọn D

Giải hệ:

7 3 16 0 10

10 0 18

x y x

xy

    







   



.

Vậy tọa độ giao điểm của



và

d

là

 

10; 18

.

Câu 28: [0H3-1-1] Xác định vị trí tương đối của hai đường thẳng:

1

32

:

13

xt

yt

















và

2

23

:

12

xt

yt





















.

A. Song song nhau. B. Cắt nhau nhưng không vuông

góc.

C. Trùng nhau. D. Vuông góc nhau.

Lời giải

Chọn D

Ta có

 

1

2; 3u 

là vectơ chỉ phương của đường thẳng

1



.

Và

 

2

3; 2u 

là vectơ chỉ phương của đường thẳng

2



.

Vì

12

.0uu 

nên

12

  

.

Câu 29: [0H3-1-1] Xác định vị trí tương đối của

2

đường thẳng:

 

1

2 3 2

:

2 3 2

xt

yt



  







   





và

 

2

3

:

3 5 2 6

xt

yt





  









   





.

A. Trùng nhau. B. Cắt nhau. C. Song song. D. Vuông

góc.

Lời giải

Chọn A

Giải hệ:

 

   

2 3 2 3

2 3 2 3 5 2 6

tt





    







      





. Ta được hệ vô số nghiệm.

Vậy

1



2



.

Câu 30: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng song song với trục

Oy

.

A.

 

0;1

. B.

 

1;1

C.

 

1; 1

. D.

 

1;0

.

Lời giải:

Chọn A

Hai đường thẳng song song có cùng vectơ chỉ phương hay hai vectơ chỉ phương cùng

phương.

Trục

Oy

có vectơ chỉ phương

 

0;1

nên chọn A.

Câu 31: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng song song với trục

Oy

.

A.

 

1;1

. B.

 

1;0

. C.

 

0;1

. D.

 

1;0

.

Lời giải:

Chọn B

VTPT của đường thẳng song song với

Oy

: vuông góc với VTCP của trục

Oy

là

 

0;1

.

Hai vectơ vuông góc khi tích vô hướng của chúng bằng

0

.

Chọn đáp án B (lật ngược đổi một dấu).

Câu 32: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

:5 2 12 0xy   

và đường

thẳng

: 1 0Dy

.

A.

 

1; 2

. B.

 

1;3

. C.

14

;1

5











. D.

14

1; .

5









Lời giải:

Chọn C

Dùng Casio bấm giải hệ phương trình từ hai phương trình của hai đường thẳng:

 Hệ vô nghiệm: hai đường thẳng song song.

 Hệ có nghiệm duy nhất: hai đường cắt nhau.

Nếu tích vô hướng của hai VTPT bằng

0

thì vuông góc.

 Hệ có vô số nghiệm: hai đường trùng nhau.

Câu 33: [0H3-1-1] Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 17 0xy   

là:

A.

2

5

B.

2

C.

18

5

D.

10

5

.

Lời giải

Chọn B

+

 

22

3.1 4.( 1) 17

,2

34

dM

  

  



.

Câu 34: [0H3-1-1] Khoảng cách từ điểm

 

1;3A

đến đường thẳng

3 4 0xy  

là:

A .

10

B.

1

C.

5

2

D.

2 10

Lời giải

Chọn A

+

 

22

3.1 3 4

A, 10

31

d



  



.

Câu 35: [0H3-1-1] Khoảng cách từ điểm

1(5; )B 

đến đường thẳng

:3 2 13 0d x y  

là:

A.

2 13.

B.

28

.

13

C.

2.

D.

13

.

2

Lời giải

Chọn A

 

3.5 2.1 13

, 2 13

13

d B d





.

Câu 36: [0H3-1-1] Khoảng cách từ điểm

O

đến đường thẳng

:1

68

xy

d 

là:

A.

4,8

B.

1

.

10

C.

1

.

14

D.

6.

Lời giải

Chọn A

 

48

:8 6 48 0 , 4,8

100

d x y d O d



     

.

Câu 37: [0H3-1-1] Khoảng cách từ điểm

 

0;1M

đến đường thẳng

:5 12 1 0d x y  

là:

A.

1.

B.

11

.

13

C.

13.

D.

13

.

17

Lời giải

Chọn A

 

5.0 12.1 1

,1

13

d M d





.

Câu 38: [0H3-1-1] Tìm khoảng cách từ

 

3;2M

đến đường thẳng

: 2 – 7 0xy  

A.

1

. B.

3

. C.

–1

. D.

0

.

Lời giải

Chọn D

Ta có:

 

   

22

3 2 2 – 7 0

;0

12

dM



  



Câu 39: [0H3-1-1] Khoảng cách từ điểm

1(5 ; )M 

đến đường thẳng

:

3 2 13 0xy  

là:

A.

13

2

. B.

2.

C.

28

.

13

D.

2 13

.

Lời giải

Chọn D

Khoảng cách từ điểm

1(5 ; )M 

đến đường thẳng

:

3 2 13 0xy  

là:

22

3.5 2.( 1) 13

( ; ) 2 13

32

dM

  

  



.

Câu 40: [0H3-1-1] Khoảng cách từ điểm

 

1; 1M 

đến đường thẳng

:3 4 17 0xy   

là:

A.

2

5

B.

10

5

. C.

2

D.

18

5



.

Lời giải

Chọn C

Khoảng cách từ điểm

1(1 ; )M 

đến đường thẳng

: 

3 4 17 0xy  

là:

 

2

3.1 4.( 1) 17

( ; ) 2.

34

dM

  

  



Câu 41: [0H3-1-1] Khoảng cách từ điểm

 

1;1M 

đến đường thẳng

: 

3 – 4 – 3 0xy 

bằng bao nhiêu?

A.

2

5

. B.

2

. C.

4

5

. D.

4

25

.

Lời giải

Chọn B

Khoảng cách từ điểm

 

1;1M 

đến đường thẳng

: 

3 – 4 – 3 0.xy

 

2

3. 1 4.1 3

( , ) 2.

34

dM

  

  



Câu 42: [0H3-1-1] Khoảng cách từ điểm

 

0;1M

đến đường thẳng

:5 12 1 0xy   

là

A.

11

13

. B.

13

17

. C.

1

. D.

13

.

Lời giải

Chọn C

Ta có:

 

12 1

,1

169

dM



  

.

Câu 43: [0H3-1-1] Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 0xy   

là:

A.

2 10

B.

3 10

5

. C.

5

2

D.

1

.

Lời giải

Chọn B

 

22

3.1 1 4

3 10

,

5

31

dM

  

  



.

Câu 44: [0H3-1-1] Tính góc giữa hai đường thẳng:

3 –1 0xy

và

4 – 2 – 4 0xy

.

A.

0

30

. B.

0

60

. C.

0

90

. D.

0

45

.

Lời giải

Chọn D

Đường thẳng:

3 –1 0xy

có

 

1

3;1 .vtpt n 

Đường thẳng:

4 – 2 – 4 0xy

có

 

2

4; 2 .vtpt n 

     

12

0

1 2 1 2 1 2

12

.

1

cos ; cos ; ; 45 .

.

2

nn

d d n n d d

nn

    

Câu 45: [0H3-1-1] Tìm côsin góc giữa

2

đường thẳng

1



:

2 2 0xy  

và

2



:

0xy

.

A.

10

. B.

2

. C.

2

3

. D.

3

.

Chọn A

Câu 46: [0H3-1-1] Tìm côsin giữa

2

đường thẳng

1



:

2 3 10 0xy  

và

2



:

2 3 4 0xy  

.

A.

7

13

. B.

6

13

. C.

13

. D.

5

13

.

Chọn D

Câu 47: [0H3-1-1] Tìm góc giữa

2

đường thẳng

1



:

2 2 3 5 0xy  

và

2



:

6 0.y

A.

60

. B.

125

. C.

145

. D.

30

.

Chọn D

Câu 48: [0H3-1-1] Tìm góc giữa hai đường thẳng

1



:

30xy

và

2



:

10 0.x

A.

45

. B.

125

. C.

30

. D.

60

.

Chọn D

Câu 49: [0H3-1-1] Tìm góc giữa

2

đường thẳng

1



:

2 10 0xy  

và

2



:

3 9 0.xy  

A.

60

. B.

0

. C.

90

. D.

45

.

Chọn D

Câu 50: [0H3-1-1] Tìm côsin góc giữa

2

đường thẳng

1

: 2 7 0xy   

và

2

:2 4 9 0.xy   

A.

3

5



. B.

2

5

. C.

1

5

. D.

3

5

.

Lời giải

Chọn A

Vectơ pháp tuyến của đường thẳng

1



là

1

(1;2).n 

Vectơ pháp tuyến của đường thẳng

2



là

2

(2; 4).n 

Gọi



là góc gữa

12

,

:

12

.

3

cos .

5

.

nn



  

Câu 51: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua

2

điểm

3 (); 2A 

và

 

1 ; 4B

A.

 

4 ; 2

B.

 

1 ; 2

C.

()1 ; 2

D.

(2 ; .1)

Lời giải

Chọn C

Đường thẳng đi qua

2

điểm

3 (); 2A 

và

 

1 ; 4B

có vectơ chỉ phương là

 

4;2AB 

suy ra tọa độ vectơ pháp tuyến là

()1 ; 2

Câu 52: [0H3-1-1] Đường thẳng đi qua

 

1; 2A 

, nhận

(2; 4)n 

làm véctơ pháp tuyến

có phương trình là:

A.

– 2 – 4 0xy

. B.

40xy  

.

C.

– 2 – 4 0xy

. D.

– 2 5 0xy

.

Lời giải

Chọn D

Đường thẳng đi qua

 

1; 2A 

, nhận

(2; 4)n 

làm véctơ pháp tuyến có phương

trình là:

   

2 1 4 2 0 2 5 0x y x y       

.

Câu 53: [0H3-1-1] Viết phương trình tổng quát của đường thẳng đi qua 2 điểm

 

0; 5A 

và

 

3;0B

A.

1

53

xy



B.

1

53

xy

  

C.

1

35

xy



D.

1

53

xy



Lời giải

Chọn C

Do

,A Oy B Ox

. Phương trình đường thẳng

AB

là:

1

35

xy



.

Câu 54: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ pháp tuyến ?

A. 1 B. 2 C. 3 D. Vô số.

Lời giải

Chọn D

Câu 55: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng

d

đi qua gốc tọa độ

O

và điểm

( ; )M a b

(với

,0ab

).

A.

(1;0).

B.

( ; )ab

. C.

( ; )ba

. D.

( ; )ab

.

Lời giải

Chọn C

Tìm tọa độ

( ; )OM a b

là VTCP của

d

. VTPT và VTCP của

d

vuông góc nhau.

Suy ra VTPT của

d

: câu C (lật ngược đổi 1 dấu)

Câu 56: [0H3-1-1] Đường thẳng

51 30 11 0xy  

đi qua điểm nào sau đây ?

A.

3

1; .

4









B.

3

1; .

4









C.

3

1; .

4







D.

4

1; .

3









Lời giải

Chọn D

Thay tọa độ từng điểm vào phương trình đường thẳng: thỏa phương trình đường

thẳng thì điểm đó thuộc đường thẳng.

Tọa độ điểm của câu D thỏa phương trình.

Câu 57: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng đi qua hai điểm phân biệt

 

;0Aa

và

 

0;Bb

với

 

ab

.

A.

 

;ba

. B.

 

;ba

. C.

 

;ba

. D.

 

;ab

.

Lời giải

Chọn C

Ta có

 

;AB a b

nên vtpt của của đường thẳng

AB

là

 

;ba

.

Câu 58: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

( 3;2)A 

và

 

1;4B

.

A.

 

1;2

. B.

 

4;2

. C.

 

2;1

. D.

 

1;2

.

Lời giải

Chọn A

Đường thẳng

AB

có

 

vtcp 4;2AB 

,

   

vtpt 2; 4 2. 1;2n     

.

Câu 59: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

 

2;3A

và

 

4;1B

.

A.

 

2; 2

. B.

 

2; 1

. C.

 

1;1

. D.

 

1; 2

.

Lời giải

Chọn C

Đường thẳng

AB

có

 

vtcp 2; 2AB 

,

   

vtpt 2;2 2. 1;1n 

.

Câu 60: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua 2 điểm

   

;0 và 0;A a B b

.

A.

 

;ba

. B.

 

;ba

. C.

 

;ba

. D.

 

;ab

.

Lời giải

Chọn B

Đường thẳng

AB

có

 

vtcp ;AB a b

,

 

vtpt ;n b a

.

Câu 61: [0H3-1-1] Tìm tọa độ vectơ pháp tuyến của đường thẳng đi qua gốc tọa độ và điểm

 

;A a b

?

A.

 

;ab

. B.

 

1;0

. C.

 

;ba

. D.

 

;ab

.

Lời giải

Chọn C

Đường thẳng

OA

có

 

vtcp ;OA a b

,

 

vtpt ;n b a

.

Câu 62: [0H3-1-1] Phương trình đoạn chắn của đường thẳng đi qua

 

()0; 5 , 3;0AB

là:

A.

1.

35

xy



B.

1.

35

xy



C.

1.

53

xy



D.

1.

53

xy

  

Lời giải

Chọn B

Đường thẳng



đi qua

5(0; )A 

và

 

3;0B

là phương trình đoạn chắn:

1.

35

xy



Câu 63: [0H3-1-1] Đường thẳng

51 30 11 0xy  

đi qua điểm nào sau đây?

A.

4

1; .

3









B.

4

1; .

3









C.

3

1; .

4







D.

3

1; .

4









Lời giải

Chọn A

Thay tọa độ các đáp án vào phương trình trên

Câu 64: [0H3-1-1] Đường thẳng

12 7 5 0xy  

không đi qua điểm nào sau đây ?

A.

 

1;1

. B.

 

1; 1

. C.

5

;0

12









. D.

17

1;

7







.

Lời giải

Chọn A

Thay tọa độ các điểm trên vào ta được đáp án là

A

.

Câu 65: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng song song với trục

Ox

.

A.

 

0;1

. B.

 

1;0

. C.

 

1;1

. D.

()1;0

.

Lời giải

Chọn A

Đường thẳng song song với trục

Ox

nhận vectơ cùng phương với

(0;1)j 

làm

VTPT của nó.

Câu 66: [0H3-1-1] Đường thẳng

12 7 5 0 xy  

không đi qua điểm nào sau đây?

A.

( 1; 1)

. B.

 

1;1

. C.

5

;0

12









. D.

17

1;

7







.

Lời giải

Chọn B

Thay tọa độ các điểm vào phương trình đường thẳng ta thấy điểm

(1;1)

không thỏa

mãn phương trình đường thẳng.

Câu 67: [0H3-1-1] Trong mặt phẳng

Oxy

, cho đường thẳng

24

:

53

xt

d

yt







  



. Trong các điểm

sau, điểm nào thuộc đường thẳng

d

?

A.

( 4;3)A 

. B.

(2;3)B

. C.

( 4; 5)C 

. D.

( 6;1)D 

.

Lời giải

Chọn D

Thay tọa độ

( 4;3)A 

vào hệ phương trình của

d

ta được

3

2

8

3

t

Ad

t



















.

Thay tọa độ

(2;3)B

vào hệ phương trình của

d

ta được

0

8

3

t

Bd

t

















.

Thay tọa độ

( 4; 5)C 

vào hệ phương trình của

d

ta được

3

2

0

t

Cd

t

















.

Thay tọa độ

( 6;1)D 

vào hệ phương trình của

d

ta được

2

t

Dd

t













.

Câu 68: [0H3-1-1] Cho đường thẳng

:3 5 15 0d x y  

. Phương trình nào sau đây không

phải là một phương trình khác của

?d

A.

1.

53

xy



B.

3

3.

5

yx  

C.

 

.

5

xt

t

y













D.

 

5

,.

3

xt

t

yt

















Lời giải

Chọn C

3

3 5.

5

x t y t    

Vậy

 

5

xt

t

y













không phải là phương trình tham số của

đường thẳng

d

.

Câu 69: [0H3-1-1] Cho đường thẳng

35

:

24

xt

yt

  











và các điểm

 

32; 50M

,

28;() 22N 

,

17;( 4)1P 

,

()3; 2Q 

. Các điểm nằm trên



là:

A. Chỉ

P

B.

N

và

P

C.

, , N P Q

D. Không có điểm nào

Lời giải

Chọn B

Lần lượt thế tọa độ

, , ,M N P Q

vào phương trình đường thẳng, thỏa mãn thì nhận.

Thế

17;( 4)1P 

:

17 3 5 4

4

14 2 4 4

tt

tP

tt

   



    



   



Thế

28;() 22N 

:

28 3 5 5

5

22 2 4 5

tt

tN

tt

     



     



   



Thế

()3; 2Q 

:

3 3 5 0

2 2 4 1

tt

Q

tt

    



  



   



Câu 70: [0H3-1-1] Cho đường thẳng  có phương trình chính tắc

12

32

xy





. Trong các hệ

phương trình được liệt kê ở mỗi phương án A, B, C, D dưới đây, hệ phương nào là

phương trình tham của đường thẳng



?

A.

31

.

14

xt

yt











B.

31

.

21

xt

yt

  









C.

31

.

22

xt

yt

  









D.

31

.

22

xt

yt

  









Lời giải

Chọn C

Từ phương trình

31

1 2 1 2

.

22

3 2 3 2

xt

x y x y

t

yt

  



   

    









Câu 71: [0H3-1-1] Phương trình tham số của đường thẳng

d

đi qua

6(3; )A 

và có vectơ chỉ

phương

4 )2( ;u 

là:

A.

32

6

xt

yt







  



B.

12

2

xt

yt







  



C.

64

32

xt

yt

  









D.

24

12

xt

yt

  









Lời giải

Chọn A

Đường thẳng

d

vtcp là

 

4; 2

suy ra có vtcp là

 

2; 1

. Đường thẳng cần viết

phương trình đi qua

6(3; )A 

và vtcp là

 

2; 1

nên có phương trình tham số

32

6

xt

yt







  



.

Câu 72: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng đi qua

 

3;2A 

và

 

1;4B

là

A.

 

1;2

. B.

 

2;1

. C.

 

2;6

. D.

 

1;1

.

Chọn B

Đường thẳng

AB

có VTCP

   

4; 2 2 2; 1AB 

.

Câu 73: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng song song trục

Ox

.

A.

 

1;0

. B.

(0; 1).

C.

( 1;0).

D.

 

1;1 .

Lời giải:

Chọn A

Đường thẳng song song với

Ox

nên vectơ chỉ phương là vectơ đơn vị của trục

Ox

:

 

1;0i 

.

Câu 74: [0H3-1-1] Cho phương trình:

 

01Ax By C  

với

22

0.AB

Mệnh đề nào sau

đây sai?

A.

 

1

là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là

 

; n A B

.

B.

0A

thì đường thẳng

 

1

song song hay trùng với

.xOx



C.

0B 

thì đường thẳng

 

1

song song hay trùng với

.y Oy



D. Điểm

 

0 0 0

; M x y

thuộc đường thẳng

 

1

khi và chỉ khi

00

0.Ax By C  

Lời giải

Chọn D

0 0 0

( ; )M x y

nằm trên đường thẳng khi và chỉ khi

00

0.Ax By C  

Câu 75: [0H3-1-1] Mệnh đề nào sau đây sai?

Đường thẳng

d

được xác định khi biết:

A. Một vectơ pháp tuyến hoặc một vectơ chỉ phương.

B. Hệ số góc và một điểm.

C. Một điểm thuộc

d

và biết

d

song song với một đường thẳng cho trước.

D. Hai điểm phân biệt của

d

.

Lời giải

Chọn A

Biết vectơ pháp tuyến hoặc vectơ chỉ phương thì đường thẳng chưa xác định (thiếu

một điểm mà đường thẳng đi qua).

Câu 76: [0H3-1-1] Cho tam giác

ABC

. Hỏi mệnh đề nào sau đây sai?

A.

BC

là một vectơ pháp tuyến của đường cao

.AH

B.

BC

là một vectơ chỉ phương của đường thẳng

.BC

C. Các đường thẳng

,,AB BC CA

đều có hệ số góc.

D. Đường trung trực của

AB

có

AB

là vectơ pháp tuyến.

Lời giải

Chọn C

Sai. Vì nếu có một trong ba đường thẳng

,,AB BC CA

song song hay trùng với

'y Oy

thì không có hệ số góc.

Câu 77: [0H3-1-1] Phương trình tổng quát của đường thẳng đi qua hai điểm

( 2; 4)A 

,

(1; 0)B

là

A.

4 3 4 0xy  

. B.

4 3 4 0xy  

. C.

4 3 4 0xy  

. D.

4 3 4 0xy  

.

Lời giải

Chọn B

Ta có

(3; 4)AB 

nên phương trình đường thẳng

AB

là

10

4 3 4 0

34

xy



    



Câu 78: [0H3-1-1]Phương trình đường thẳng



qua

( 3; 4)A 

và vuông góc với đường thẳng

:3 4 12 0d x y   

là

A.

3 4 24 0xy  

. B.

4 3 24 0xy  

. C.

3 4 24 0xy  

. D.

4 3 24 0xy  

.

Lời giải

Chọn A

Phương trình đường thẳng cần tìm là

34

3 4 24 0

34

xy



    

.

Câu 79: [0H3-1-1] Phương trình đường thẳng cắt hai trục toạ độ tại

( 2; 0)A 

và

(0; 3)B

là

A.

1

32

xy



. B.

3 2 6 0xy  

. C.

2 3 6 0xy  

. D.

3 2 6 0xy  

.

Lời giải

Chọn D

Phương trình đoạn chắn là

1 3 2 6 0

23

xy

xy     



.

Câu 80: [0H3-1-1] Cho hai đường thẳng

1

:1

34

  

xy

và

2

:3 4 10 0   xy

. Khi đó hai

đường thẳng này:

A. Cắt nhau nhưng không vuông góc. B. Vuông góc với nhau.

C. Song song với nhau. D. Trùng nhau.

Lời giải

Chọn B

Ta có

 

12

11

; , 3;4

34





  





nn

.

12

11

. .3 .4 0

34



  nn

nên hai đường thẳng

1



và

2



vuông góc với nhau.

Câu 81: [0H3-1-1] Xác định vị trí tương đối của

2

đường thẳng sau đây

1

: 2 1 0xy   

và

2

: 3 6 10 0xy    

.

A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt

nhau.

Lời giải.

Chọn A

Ta có:

1 2 1

3 6 10







12

  

.

Câu 82: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

:4 3 26 0xy   

và đường thẳng

:3 4 7 0d x y  

.

A.

 

5;2

. B. Không có giao điểm.

C.

 

2; 6

. D.

 

5; 2

.

Lời giải.

Chọn D

Tọa độ giao điểm của đường thẳng

:4 3 26 0xy   

và đường thẳng

:3 4 7 0d x y  

là nghiệm của hệ phương trình:

4 3 26 0 5

3 4 7 0 2

x y x

x y y

   







    



.

Câu 83: [0H3-1-1] Cho hai đường thẳng

1

:1

34

  

xy

và

2

:3 4 10 0   xy

. Khi đó hai

đường thẳng này:

A. Cắt nhau nhưng không vuông góc. B. Vuông góc với nhau.

C. Song song với nhau. D. Trùng nhau.

Lời giải

Chọn B

Ta có

 

12

11

; , 3;4

34





  





nn

.

12

11

. .3 .4 0

34



  nn

nên hai đường thẳng

1



và

2



vuông góc với nhau.

Câu 84: [0H3-1-1] Xác định vị trí tương đối của

2

đường thẳng sau đây

1

: 2 1 0xy   

và

2

: 3 6 10 0xy    

.

A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt

nhau.

Lời giải.

Chọn A

Ta có:

1 2 1

3 6 10







12

  

.

Câu 85: [0H3-1-1] Tìm tọa độ giao điểm của đường thẳng

:4 3 26 0xy   

và đường thẳng

:3 4 7 0d x y  

.

A.

 

5;2

. B. Không có giao điểm.

C.

 

2; 6

. D.

 

5; 2

.

Lời giải.

Chọn D

Tọa độ giao điểm của đường thẳng

:4 3 26 0xy   

và đường thẳng

:3 4 7 0d x y  

là nghiệm của hệ phương trình:

4 3 26 0 5

3 4 7 0 2

x y x

x y y

   







    



.

Câu 86: [0H3-1-1] Điểm nào nằm trên đường thẳng



:

 

12

3

xt

t

yt













.

A.

 

2; –1A

. B.

 

–7; 0B

. C.

 

3; 5C

. D.

 

3; 2D

.

Lời giải

Chọn D

Ta có:

 

1 2 3

12

2 7 0

3

xy

xt

xy

yt

ty

  









    









.

Thay lần lượt tọa độ của các điểm

,A

,B

,C

D

thấy chỉ có

 

3; 2D

thỏa mãn.

Câu 87: [0H3-1-1] Viết phương trình tham số của đường thẳng qua

 

2; 1A 

và

 

2; 5B

.

A.

2

16

x

yt







  



. B.

2

6

xt

yt











. C.

2

56

xt

yt











. D.

1

26

x

yt











.

Lời giải

Chọn A

 

0; 6AB 

Phương trình đường thẳng đi qua

 

2; 1A 

có véc tơ chỉ phương

 

0; 6AB 

là

2

16

x

yt







  



Câu 88: [0H3-1-1] Viết phương trình tham số của đường thẳng qua

 

3; 1A 

và

 

1; 5B

.

A.

3

13

xt

yt







  



. B.

3

13

xt

yt







  



. C.

3

13

xt

yt







  



. D.

1

53

xt

yt











.

Lời giải

Chọn C

 

2; 6AB 

Phương trình đường thẳng

AB

có véctơ chỉ phương

 

2; 6u 

chỉ có đáp án

C

.

Thay tọa điểm

,A

B

vào phương trình đường thẳng ở đáp án

C

thỏa.

Vậy đáp án đúng là

C

.

Cách khác:

 

2; 6AB 

.Chọn véctơ chỉ phương của đường thẳng đi qua hai điểm

,A

B

là

 

1; 3u 

Phương trình tham số của đường thẳng qua

 

3; 1A 

có véc tơ chỉ phương

 

1; 3u 

là:

3

13

xt

yt







  



.

Phương trình tham số của đường thẳng qua

 

1; 5B

có véc tơ chỉ phương

 

1; 3u 

là:

1

53

xt

yt











.

Câu 89: [0H3-1-1] Viết phương trình tham số của đường thẳng qua

 

3; 7A 

và

 

1; 7B 

.

A.

7

xt

y











. B.

7

xt

yt







  



. C.

3

17

xt

yt











. D.

7

xt

y











.

Lời giải

Chọn A

 

2; 0AB 

Phương trình đường thẳng có véc tơ chỉ phương

 

2; 0u 

chỉ có đáp án

A

và

D

.

Thay tọa điểm

,A

B

vào phương trình đường thẳng ở đáp án

A

và

D

ta thấy đáp

A

thỏa.

Vậy đáp án đúng là

A

.

Cách khác:

 

2;0AB 

, chọn véc tơ chỉ phương của đường thẳng đi qua hai điểm

,A

B

là

 

1; 0u 

Phương trình tham số của đường thẳng qua

 

3; 7A 

có véc tơ chỉ phương

 

1; 0u 

là:

7

xt

y











.

Phương trình tham số của đường thẳng qua

 

1; 7B 

có véc tơ chỉ phương

 

1; 0u 

là:

1

7

xt

y











.

Câu 90: [0H3-1-1] Phương trình nào dưới đây không là phương trình tham số của đường

thẳng đi qua

O

và

 

1; 3M 

?

A.

1

3

xt

yt











. B.

1

33

xt

yt







  



. C.

12

36

xt

yt







  



. D.

3

xt

yt











.

Lời giải

Chọn A

Trong 4 phương trình tham số trên ta dễ thấy đường thẳng ở đáp án

A

không đi

qua điểm

O

hoặc điểm

M

.

Câu 91: [0H3-1-1] Cho đường thẳng

12 5

:

36

xt

d

yt











. Điểm nào sau đây nằm trên đường

thẳng?

A.

 

13; 33

. B.

 

20; 9

. C.

 

7; 5

. D.

 

12; 0

.

Lời giải

Chọn A

Câu 92: [0H3-1-1] Cho đường thẳng

1

:

2

xt

d

yt











. Điểm nào sau đây nằm trên đường thẳng

?

A.

 

1; 2

. B.

 

1; 0

. C.

( 1; 4)

. D.

1

;1

2







.

Lời giải

Chọn B

Câu 93: [0H3-1-1] Viết phương trình tham số của đường thẳng đi qua

2

điểm

 

3; 7A 

và

 

1; 7B 

.

A.

7

xt

y











. B.

7

xt

yt







  



. C.

7

xt

y











. D.

37

17

xt

yt











.

Lời giải

Chọn C

   

2; 0 2 1; 0AB    

nên chọn

 

1; 0u 

là 1

vtcp

của

AB

và

AB

đi qua

 

1; 7B 

nên

AB

có phương trình tham số

1

7

xt

y











.

Cách 2:Vì

A

,

B

đều có tung độ bằng

7

nên chúng nằm trên đường thẳng

7y 

.

Câu 94: [0H3-1-1] Viết phương trình tham số của đường thẳng đi qua hai điểm

 

3; 1A 

và

 

1; 5B

.

A.

3

13

xt

yt







  



. B.

3

13

xt

yt







  



. C.

1

53

xt

yt











. D.

3

13

xt

yt







  



.

Lời giải

Chọn A

Có

   

2; 6 2 1; 3AB     

Phương trình tham số của

AB

đi qua

 

3; 1A 

và có

vtcp

 

1; 3u 

là

3

,

13

xt

t

yt









  



.

Câu 95: [0H3-1-1] Đường thẳng đi qua điểm

 

1; 2M

và vuông góc với vectơ

 

2; 3n 

có

phương trình chính tắc là:

A.

12

32

xy





. B.

12

23

xy



. C.

12

32

xy





. D.

12

23

xy



.

Lời giải

Chọn C

vtcp

 

2; 3n 



VTCP

 

3; 2u 

Phương trình chính tắc đi qua

 

1; 2M

và có

vtcp

 

3; 2u 

là

12

23

xy



.

Câu 96: [0H3-1-1] Cho đường thẳng

12 5

:

36

xt

yt













. Điểm nào sau đây nằm trên



?

A.

 

12; 0

. B.

 

7; 5

. C.

 

20; 9

. D.

 

13; 33

.

Lời giải

Chọn D

Từ phương trình ta rút được

12 3

56

xy



(*)

Thay tọa độ điểm vào phương trình (*), tọa độ nào thỏa thì nằm trên đường thẳng.

Câu 97: [0H3-1-1] Viết phương trình tham số của đường thẳng đi qua hai điểm

 

3; 1 ,A 

 

6; 2B 

.

A.

33

1

xt

yt







  



. B.

33

1

xt

yt







  



. C.

33

6

xt

yt







  



. D.

13

2

xt

yt

  









.

Lời giải

Chọn B

Đường thẳng đi qua

 

3; 1 ,A 

 

6; 2B 

có

vtcp

là

 

9; 3 ,uk

0k 

.

Câu 98: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng song song với trục

Oy

.

A.

 

0;1 .

B.

 

1;1 .

C.

(1; 1 .)

D.

 

1;0 .

Lời giải

Chọn A

Vectơ cơ sở của trục

Oy

là

 

0;1 .

Câu 99: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng song song với trục

Oy

.

A.

 

1;1 .

B.

 

1;0

. C.

 

0;1 .

D.

( 1;0 .)

Lời giải

Chọn B

VTCP của đường thẳng song song với trục

Oy

là

 

0;1

nên VTPT là

 

1;0

Câu 100: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng đi qua gốc tọa độ và điểm

 

; M a b

.

A.

 

0; .ab

B.

 

;.ab

C.

();.ab

D.

( .);ab

Lời giải

Chọn B

Vectơ chỉ phương của đường thẳng đi qua gốc tọa độ

(0;0)O

và điểm

 

; M a b

là:

( ; )OM a b

.

Câu 101: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ pháp tuyến?

A. 1. B. 2. C. 3. D. Vô số.

Lời giải

Chọn D

Đường thẳng có vô số vectơ pháp tuyến và vô số vectơ chỉ phương.

Câu 102: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ chỉ phương?

A. 1. B. 2. C. 3. D. Vô số.

Lời giải

Chọn D

Một đường thẳng có vô số VTCP

Câu 103: [0H3-1-1] Phương trình tham số của đường thẳng

:2 6 23 0xy   

là:

A.

53

11

2

xt

yt

  













. B.

53

11

2

xt

yt















. C.

53

11

2

xt

yt















. D.

0,5 3

4

xt

yt











.

Lời giải

Chọn D

VTCP của

 

: 3;1u

, điểm

1

;4

2

M









, vậy PTTS là:

1

3

2

4

x

yt















Câu 104: [0H3-1-1] Đường thẳng đi qua

 

1;2A 

, nhận

(2; 4)n 

làm véctơ pháp tuyến

có phương trình là:

A.

– 2 – 4 0xy

. B.

40xy  

. C.

– 2 – 4 0xy

. D.

– 2 5 0xy

.

Lời giải

Chọn D

PTTQ của đường tahwngr cần tìm là :

   

2 1 4 2 0 2 5 0x y x y       

Câu 105: [0H3-1-1] Tìm tọa độ vectơ chỉ phương của đường thẳng song song với trục

Ox

.

A.

(0; )1

. B.

 

1;1

. C.

 

0;1

. D.

 

1;0

.

Lời giải

Chọn D

Trục

Ox

có VTCP là

 

1;0i 

Câu 106: [0H3-1-1] Tìm vectơ pháp tuyến của đường thẳng song song với trục

Oy

.

A.

(1;1)

. B.

(1;0)

. C.

(0;1)

. D.

( 1;0)

.

Hướng dẫn giải:

Chọn B

VTPT của đường thẳng song song với

Oy

: vuông góc với VTCP của trục

Oy

là

(0;1).

Hai vectơ vuông góc khi tích vô hướng của chúng bằng 0

Chọn đáp án B (lật ngược đổi một dấu)

Câu 107: [0H3-1-1]Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 17 0xy   

là:

A.

2

5

B.

2

C.

18

5

D.

10

5

.

Hướng dẫn giải

Chọn B

+

 

22

3.1 4.( 1) 17

,2

34

dM

  

  



.

Câu 108: [0H3-1-1] Khoảng cách từ điểm

 

1;3A

đến đường thẳng

3 4 0xy  

là:

A .

10

B.

1

C.

5

2

D.

2 10

Hướng dẫn giải

Chọn A

+

 

22

3.1 3 4

A, 10

31

d



  



.

Câu 109: [0H3-1-1] Khoảng cách từ điểm

1(5; )B 

đến đường thẳng

:3 2 13 0d x y  

là:

A.

2 13.

B.

28

.

13

C.

2.

D.

13

.

2

Hướng dẫn giải

Chọn A

 

3.5 2.1 13

, 2 13

13

d B d





.

Câu 110: [0H3-1-1] Khoảng cách từ điểm

 

0;1M

đến đường thẳng

:5 12 1 0d x y  

là:

A.

1.

B.

11

.

13

C.

13.

D.

13

.

17

Lời giải

Chọn A.

 

5.0 12.1 1

,1

13

d M d





.

Câu 111: [0H3-1-1] Tìm khoảng cách từ

 

3;2M

đến đường thẳng

: 2 – 7 0xy  

A.

1

. B.

3

. C.

–1

. D.

0

.

Lời giải

Chọn D.

Ta có:

 

   

22

3 2 2 – 7 0

;0

12

dM



  



Câu 112: [0H3-1-1] Khoảng cách từ điểm

1(5 ; )M 

đến đường thẳng

:

3 2 13 0xy  

là:

A.

13

2

. B.

2.

C.

28

.

13

D.

2 13

.

Lời giải

Chọn D.

Khoảng cách từ điểm

1(5 ; )M 

đến đường thẳng

:

3 2 13 0xy  

là:

22

3.5 2.( 1) 13

( ; ) 2 13

32

dM

  

  



.

Câu 113: [0H3-1-1] Khoảng cách từ điểm

1(1 ; )M 

đến đường thẳng

:3 4 17 0xy   

là:

A.

2

.

5

B.

10

5

. C.

2.

D.

18

5



.

Lời giải.

Chọn C.

Khoảng cách từ điểm

1(1 ; )M 

đến đường thẳng

: 

3 4 17 0xy  

là:

 

2

3.1 4.( 1) 17

( ; ) 2.

34

dM

  

  



Câu 114: [0H3-1-1] Khoảng cách từ điểm

 

1;1M 

đến đường thẳng

: 

3 – 4 – 3 0xy 

bằng bao nhiêu?

A.

2

.

5

B.

2

. C.

4

5

D.

4

25

.

Lời giải

Chọn B.

Khoảng cách từ điểm

 

1;1M 

đến đường thẳng

: 

3 – 4 – 3 0xy

 

2

3. 1 4.1 3

( ; ) 2.

34

dM

  

  



Câu 115: [0H3-1-1] Khoảng cách từ điểm

 

0;1M

đến đường thẳng

:5 12 1 0xy   

là

A.

11

13

. B.

13

17

. C.

1

. D.

13

.

Lời giải

Chọn C.

Ta có:

 

12 1

,1

169

dM



  

.

Câu 116: [0H3-1-1] Khoảng cách từ điểm

1(1; )M 

đến đường thẳng

:3 4 0xy   

là:

A.

2 10

. B.

3 10

5

. C.

5

2

. D. 1.

Lời giải

Chọn B.

 

22

3.1 1 4

3 10

,

5

31

dM

  

  



.

Câu 117: [0H3-1-1] Khoảng cách từ điểm

 

0;0O

tới đường thẳng

:1

68

xy

  

là

A.

24

5

. B.

1

10

. C.

48

14

. D.

1

14

.

Lời giải

Chọn A

Ta có

: 1 4 3 24 0

68

xy

xy      

.

 

22

4.0 3.0 24

24

,

5

43

dO



  



.

Câu 118: [0H3-1.23-2] Tính diện tích

ABC

biết

     

3;2 , 0;1 , 1;5 .A B C

A.

11

17

. B.

17

.

C.

11

. D.

11

2

.

Lời giải

Chọn D

   

3; 1 10; 2;3 13AB AB AC AC        

   

. 6 3 3 11

cos , sin , .

| |.| |

10. 13 130 130

AB AC

AB AC AB AC

AB AC



    

 

1 11

. .sin , .

22

ABC

S AB AC AB AC





Câu 119: [0H3-1-1] Tính góc giữa hai đường thẳng:

3 –1 0xy

và

4 – 2 – 4 0xy

.

A.

0

30

. B.

0

60

. C.

0

90

. D.

0

45

.

Lời giải

Chọn D

Đường thẳng:

3 –1 0xy

có

 

1

3;1vtpt n 

Đường thẳng:

4 – 2 – 4 0xy

có

 

2

4; 2vtpt n 

     

12

0

1 2 1 2 1 2

12

.

1

cos ; cos ; ; 45

.

2

nn

d d n n d d

nn

    

Câu 120: [0H3-1-1] Tìm côsin góc giữa

2

đường thẳng

1



:

10 5 1 0xy  

và

2



:

2

1

xt

yt











.

A.

3

10

. B.

10

.

10

C.

3 10

.

10

D.

3

.

5

Lời giải

Chọn C

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(2;1), (1;1)nn

 

12

1 2 1 2

12

.

3

cos , cos ,

10

nn

    

Câu 121: [0H3-1-1] Tìm côsin góc giữa

2

đường thẳng

1



:

2 2 0xy  

và

2



:

0xy

.

A.

10

.

10

B.

2.

C.

2

.

3

D.

3

.

Lời giải

Chọn A

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(1;2), (1; 1)nn  

 

12

1 2 1 2

12

.

10

cos , cos , .

10

nn

    

Câu 122: [0H3-1-1] Tìm côsin giữa

2

đường thẳng

1



:

2 3 10 0xy  

và

2



:

2 3 4 0xy  

.

A.

7

13

. B.

6

13

. C.

13

. D.

5

13

.

Lời giải

Chọn D

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(2;3), (2; 3)nn  

 

12

1 2 1 2

12

.

5

cos , cos ,

13

nn

    

Câu 123: [0H3-1-1] Tìm góc giữa

2

đường thẳng

1



:

2 2 3 5 0xy  

và

2



:

60y 

A.

60

. B.

125

. C.

145

. D.

30

.

Lời giải

Chọn D

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(2;2 3), (0;1)nn

 

12

0

1 2 1 2 1 2

12

.

3

cos , cos , , 30

2

nn

        

Câu 124: [0H3-1-1] Tìm góc giữa hai đường thẳng

1



:

30xy

và

2



:

10 0x 

.

A.

45

. B.

125

. C.

30

. D.

60

.

Lời giải

Chọn D

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(1; 3), (1;0)nn

 

12

0

1 2 1 2 1 2

12

.

1

cos , cos , , 60

2

nn

        

Câu 125: [0H3-1-1] Tìm góc giữa

2

đường thẳng

1



:

2 10 0xy  

và

2



:

3 9 0xy  

A.

60

. B.

0

. C.

90

. D.

45

.

Lời giải

Chọn D

Vectơ pháp tuyến của

21

, 

lần lượt là

12

(2; 1), (1; 3)nn   

 

12

0

1 2 1 2 1 2

12

.

2

cos , cos , , 45

2

nn

        

Câu 126: [0H3-1-1] Tìm côsin góc giữa

2

đường thẳng

1

: 2 7 0xy   

và

2

:2 4 9 0xy   

.

A.

3

5

. B.

2

5

. C.

1

5

. D.

3

5

.

Lời giải

Chọn A

Vectơ pháp tuyến của đường thẳng

1



là

1

(1;2)n 

Vectơ pháp tuyến của đường thẳng

2



là

2

(2; 4)n 

Gọi



là góc gữa

12

,

:

12

.

3

cos

5

.

nn





Câu 127: [0H3-1-1] Tìm góc giữa hai đường thẳng

30xy

và

10 0x

?

A.

60

. B.

30

. C.

45

. D.

125

.

Lời giải

Chọn A

Vectơ pháp tuyến của đường thẳng

1



là

1

(1; 3)n 

Vectơ pháp tuyến của đường thẳng

2



là

2

(1;0)n 

Gọi



là góc gữa

12

,

:

12

.

1

cos

2

.

nn





60



  

Câu 128: [0H3-1-1] Tìm góc giữa hai đường thẳng

:2 2 3 5 0d x y  

và

: 6 0.y  

A.

60

B.

30

C.

45

D.

125

Lời giải

Chọn B

Đường thẳng d có một vectơ pháp tuyến:

 

1; 3 ;

d

n 

Đường thẳng



có một vectơ pháp tuyến:

 

0;1 ;n





   

.

3

cos , , 30 .

2

| |.| |

d

dd

d

nn

n n n n

nn







    



Góc giữa hai đường thẳng d và



là

30 .

Câu 129: [0H3-1-1] Tìm góc giữa hai đường thẳng

:2 10 0d x y  

và

: 3 9 0.xy   

A.

30

B.

60

C.

45 .

D.

125 .

Lời giải

Chọn C

Đường thẳng d có một vectơ pháp tuyến:

 

2; 1 ;

d

n 

Đường thẳng



có một vectơ pháp tuyến:

 

1; 3 ;n





 

   

 

22

2

.

2.1 1.3

2

cos , , 45 .

2

| |.| |

2 1 . 1 3

d

dd

d

nn

n n n n

nn









     

   



Góc giữa hai đường thẳng d và



là

45 .

Câu 130: [0H3-1-1] Tính cosin của góc giữa hai đường thẳng

1

: 2 2 0d x y  

và

2

:0d x y

.

A.

10

. B.

2

3

. C.

3

. D.

3

.

Lời giải

Chọn A

Có VTPT

1

(1;2)n 

và

2

d

có VTPT là

2

(1; 1)n 

. Ta có

12

.

10

cos( ; )

10

nn

dd

nn



.

Câu 131: [0H3-1-1] Tính cosin của góc giữa hai đường thẳng

1

:2 3 10 0d x y  

và

2

:2 3 4 0d x y  

?

A.

5

13

. B.

6

13

. C.

5

13

. D.

13

.

Lời giải

Chọn A

1

d

có VTPT

1

(2;3)n 

và

2

d

có VTPT là

2

(2; 3)n 

. Ta có

12

.

5

cos( ; )

13

nn

dd

nn



Câu 132: [0H3-1-1] Cho hai đường thẳng

7 – 3 6 0, 2 – 5 – 4 0.x y x y  

Góc giữa hai đường

thẳng trên là

A.

4



. B.

3

4



. C.

3



. D.

2

3



.

Lời giải

Chọn A

Ta có

 

7.2 3 5

2

cos , ,

24

58. 29

d d d d







   

.

Câu 133: [0H3-1-1] Đường thẳng

2 1 0xy  

có vectơ pháp tuyến là vectơ nào?

A.

 

2; 1n 

. B.

 

1; 1n 

. C.

 

2;1n 

. D.

 

1;2n 

.

Lời giải

Chọn C

Đường thẳng

2 1 0xy  

có vectơ pháp tuyến là vectơ

 

2;1n 

.

Câu 134: [0H3-1-1] Đường trung trực của đoạn thẳng

AB

với

 

3;2A 

,

 

3;3B 

có

vectơ pháp tuyến là vectơ nào?

A.

 

6;5n 

. B.

 

0;1n 

. C.

 

3;5n 

. D.

 

1;0n 

.

Lời giải

Chọn B

Đường trung trực của đoạn thẳng

AB

có vectơ pháp tuyến

 

0;1AB 

.

Câu 135: [0H3-1-1] Vectơ nào là vectơ pháp tuyến của đường thẳng có phương trình

12

3?

xt

yt

  









A.

 

2; 1n 

. B.

 

1;2n 

. C.

 

1; 2n 

. D.

 

1;2n 

.

Lời giải

Chọn D

2 5 0xy  

Ta có

 

2; 1 (1;2)un  

Câu 136: [0H3-1-1] Đường thẳng nào không cắt đường thẳng

2 3 1 0xy  

?

A.

2 3 1 0xy  

. B.

2 5 0xy  

. C.

2 3 3 0xy  

. D.

4 6 2 0xy  

.

Lời giải

Chọn A

Do 2 đường thẳng song song với nhau do cùng vectơ pháp tuyến .

Câu 137: [0H3-1-1] Đường thẳng nào song song với đường thẳng

3 4 0xy  

?

A.

1

2 3 .

xt

yt











. B.

1

2 3 .

xt

yt











. C.

13

2.

xt

yt











. D.

13

2.

xt

yt











.

Lời giải

Chọn C

Ta có

 

1; 3 ( 3; 1)nu    

Câu 138: [0H3-1-1] Khoảng cách từ điểm

 

0;0O

đến đường thẳng

4 3 5 0xy  

bằng bao

nhiêu?

A.

0

. B.

1

. C.

5

. D.

1

5

.

Lời giải

Chọn B

Câu 139: Ta có:

 

4.0 3.0 5

;1

16 9

dO



  



. [0H3-1-1] Trong các điểm sau đây, điểm nào

nằm trên đường thẳng



có phương trình tham số là

2

xt

yt











.

A.

 

1; 1

. B.

 

0; 2

. C.

 

1; 1

. D.

 

1; 1

.

Lời giải

Chọn A

Câu 140: [0H3-1-1] Cho đường thẳng

: 3 5 2006 0d x y  

. Trong các mệnh đề sau, mệnh

đề nào sai ?

A.

d

có vectơ pháp tuyến là

 

3; 5n 

. B.

d

có vectơ chỉ phương là

 

5; 3u 

.

C.

d

có hệ số góc

5

3

k 

. D.

d

song song với đường thẳng

3 5 0xy

Lời giải

Chọn C

Ta có

3 2006

3 5 2006 0

55

x y y x      

. Từ đó suy ra, hệ số góc của đường

thẳng

d

là

3

5

k 

. Vậy khẳng định C sai.

Câu 141: [0H3-1-1] Đường thẳng nào sau đây song với đường thẳng

32yx

?

A.

1

2

3

yx

. B.

2yx

. C.

32yx  

. D.

32yx

.

Lời giải

Chọn D

Vì hai đường thẳng

y ax b

và

y cx d

song song với nhau

ac

bd













.

Phân tích phương án nhiễu:

Chọn các phương án còn lại là do nhầm ln về điều kiện để hai đường thẳng song

song.

Câu 142: [0H3-1-1] Hai vectơ

u

và

v

được gọi là cùng phương khi nào ?

A. Giá của chúng trùng nhau. B. Tồn tại một số

k

sao cho

u kv

.

C. Hai vectơ vuông góc với nhau. D. Góc giữa hai vectơ là góc nhọn.

Lời giải

Chọn B

Theo đnh l: Điu kin đ hai vec tơ cng phương

Hai vectơ

u

và

v

được gọi là cùng phương khi và chỉ khi tồn tại một số

k

sao cho

u kv

.

Phân tích phương án nhiễu:

Hai véc tơ cùng phương thì hai véc tơ có giá song song nhau hoặc trùng nhau. Hơn

nữa góc giữa hai vectơ đó bằng

0

hoặc

180

nên các phương án còn lại SAI.

Câu 143: [0H3-1-1] Vectơ

u

được gọi là vectơ chỉ phương của đường thẳng



khi nào?

A. Giá của

u

song song hoặc trùng với



.

B. Vectơ

0u 

và giá của

u

song song với



.

C. Vectơ

0u 

và giá của

u

song song hoặc trùng với



.

D. Vectơ

u

vuông góc với



.

Lời giải

Chọn C

Theo định ngha VTCP của đường thẳng: Vectơ

u

được gọi là vectơ chỉ phương

của đường thẳng



nếu vectơ

0u 

và giá của

u

song song hoặc trùng với



.

Câu 144: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ chỉ phương ?

A.

1

. B.

2

. C.

3

. D. Vô số.

Lời giải

Chọn D

Một đường thẳng có vô số vectơ chỉ phương, các vectơ đó cùng phương với nhau.

Câu 145: [0H3-1-1] Cho đường thẳng

d

có phương trình

23

3

xt

yt







  



. Một vectơ chỉ phương

của

d

là ?

A.

 

2; –3

. B.

 

3; –1

. C.

 

3; 1

. D.

 

3; –3

.

Lời giải

Chọn B

PTTS của

d

là

23

3

xt

yt







  



suy ra

d

có 1 VTCP là

 

3; 1u 

và các vectơ dạng

ku

,

(

0k 

).

Câu 146: [0H3-1-1] Vectơ

n

được gọi là vectơ pháp tuyến của đường thẳng



khi nào ?

A.

0n 

.

B.

n

vuông góc với



.

C.

0n 

và

n

vuông góc với vectơ chỉ phương của



.

D.

n

song song với vectơ chỉ phương của



.

Lời giải

Chọn C

Vectơ

n

được gọi là vectơ pháp tuyến của đường thẳng



nếu

0n 

và

n

vuông

góc với vectơ chỉ phương của



.

Câu 147: [0H3-1-1] Đường thẳng

d

có VTPT là

n

và VTCP

u

. Khẳng định nào dưới đây

đúng ?

A.

n ku

, (

0k 

). B.

.0nu

. C.

nu

. D.

0nu

.

Lời giải

Chọn B

Theo định ngha VTPT và VTCP của một đường thẳng. Đường thẳng

d

có VTPT

là

n

và VTCP

u

thì

.0n u nu  

.

Câu 148: [0H3-1-1] Đường thẳng

3 5 0xy  

có vectơ chỉ phương là:

A.

 

2;2

. B.

 

2;3

. C.

 

3;2

. D.

 

3;1

.

Lời giải

Chọn D

Từ phương trình đường thẳng

3 5 0xy  

, ta có vtpt

(1;3)n 

.

Vtcp

( 3;1)u

.

Câu 149: [0H3-1-1] Đường thẳng

2 5 0xy  

song song với đường thẳng nào sau đây

A.

2yx  

. B.

25yx

. C.

25yx  

. D.

yx

.

Lời gii

Chọn C

Từ phương trình đường thẳng đã cho, ta có đường thẳng song song với nó s có

dạng :

20

5

x y c

c











.

Vậy, loại đáp án A,D,B.

Câu 150: [0H3-1-1] Cho đường thẳng

 

d

có phương trình tổng quát là

3 5 2017 0xy  

.

Tìm khẳng định sai trong các khẳng định sau :

A.

 

d

có véctơ pháp tuyến

(3;5)n 

.

B.

 

d

có véctơ chỉ phương

( 5;3)u

.

C.

 

d

có hệ số góc

5

3

k 

.

D.

 

d

song song với đường thẳng

3 5 0xy

.

Lời giải

Chọn C

Từ phương trình tổng quát

3 5 2017 0xy  

, ta có vtpt

(3;5)n 

suy ra vtcp

( 5;3)u

.

Ta cng viết lại được đường thẳng dưới dạng hệ số góc như sau :

3 2017

55

yx  

.

Hệ số góc

3

5

k 

.

Câu 151: [0H3-1-1] Tính khoảng cách

h

từ điểm

 

3;0A

tới đường thẳng

 

: 2 5 0d x y   

.

A.

5

h 

. B.

15

5

h 

. C.

10

5

h 

. D.

1

5

h 

.

Lời giải

Chọn A

Ta có :

 

  

  



22

3.( 2) 0.1 5

5

,

5

( 2) 1

h d A d

.

Câu 152: [0H3-1-1] Một vectơ chỉ phương của đường thẳng

 

: 2 3 5 0d x y   

là.

A.

 

2;1u 

. B.

 

3; 2u 

. C.

 

3;2u 

. D.

 

2;3u 

.

Lời giải

Chọn C

Từ phương trình tổng quát

 

: 2 3 5 0d x y   

, ta có vtpt

( 2;3)n 

nên vtcp

(3;2)u 

.

Câu 153: [0H3-1-1] Một đường thẳng có bao nhiêu vectơ chỉ phương?

A. Một vectơ. B. Hai vectơ.

C. Ba vectơ. D. Vô số vectơ.

Lời giải

Chọn D

Một đường thẳng nhận vectơ

u

làm vectơ chỉ phương thì cng nhận

ku

làm vectơ

chỉ phương nên có vô số vectơ chỉ phương của một đường thẳng.

Câu 154: [0H3-1-1] Cho đường thẳng có phương trình tham số

23

3

xt

yt







  



có tọa độ vectơ

chỉ phương là:

A.

 

2; – 3

. B.

 

3; –1

. C.

 

3;1

. D.

 

3; – 3

.

Lời giải

Chọn B

Đường thẳng có phương trình tham số

 

23

3; 1

3

xt

u

yt





  



  



.

Câu 155: [0H3-1-1] Cho đường thẳng có phương trình tham số

13

63

xt

yt











có hệ số góc là

A.

1k 

. B.

2k 

. C.

–1k 

. D.

–2k 

.

Lời giải

Chọn C

Đường thẳng có phương trình tham số

 

13

3

3; 3 1

63

3

xt

uk

yt







      







.

Câu 156: [0H3-1-1] Hai vectơ chỉ phương và vectơ pháp tuyến của một đường thẳng

A. Song song với nhau. B. Vuông góc với nhau.

C. Trùng nhau. D. Bằng nhau.

Lời giải

Chọn B

Theo định ngha SGK hình học 10.

Câu 157: [0H3-1-1] Khoảng cách từ điểm

 

2; –3M

đến đường thẳng

d

có phương trình

2 3 – 7 0xy

là:

A.

12

13



. B.

12

13

. C.

12

13



. D.

12

13

.

Lời giải

Chọn B

 

22

2.2 3. 3

12

,

13

23

–7

d M d 





nên chọn B.

Câu 158: [0H3-1-1] Hãy chọn phương án đúng. Đường thẳng đi qua hai điểm

 

1; 1A

,

 

3; 1B

có vectơ chỉ phương là:

A.

 

4; 2

. B.

 

2; 1

. C.

 

2; 0

. D.

(0; 2)

.

Lời giải

Chọn C

Đường thẳng đi qua hai điểm

 

1; 1A

,

 

3; 1B

có vectơ chỉ phương

 

2; 0AB 

.

Câu 159: [0H3-1-1] Các số sau đây, hệ số góc của đường thẳng đi qua hai điểm

 

2; –1A

,

 

–3; 4B

là:

A.

2

. B.

–2

. C.

1

. D.

–1

.

Lời giải

Chọn D

     

2

1

2;–1 –3;,54 ;1 5.

u

AB kAB

u

      

nên chọn D.

Câu 160: [0H3-1-1] Cho phương trình tham số của đường thẳng

5

:

92

xt

d

yt







  



. Trong các

phương trình sau, phương trình nào là phương trình tổng quát của

 

d

?

A.

2 –1 0xy

. B.

2 4 0xy  

.

C.

2 – 2 0xy

. D.

– 2 3 0xy

.

Lời giải

Chọn A

 

5

9

: 5 2 5 9 0 2 1 0

92

2

xt

y

d t x x y x y

yt







            



  





.

Câu 161: [0H3-1-1] Cho đường thẳng

d

có phương trình tổng quát:

3 5 2017 0xy  

. Tìm

mệnh đề sai trong các mệnh đề sau:

A.

 

d

có vectơ pháp tuyến

 

3; 5n 

.

B.

 

d

có véctơ chỉ phương

 

5; 3a 

.

C.

 

d

có hệ số góc

5

3

k 

.

D.

 

d

song song với đường thẳng

3 5 0xy

.

Lời giải

Chọn C

d

có phương trình tổng quát:

3 5 2017 0xy  

nên có hệ số góc

2

1

3

5

u

k

u

  

.

Vậy C là sai.

Câu 162: [0H3-1-1] Cho đường thẳng có vectơ pháp tuyến

 

2; 3n 

. Vectơ nào sau là vectơ

chỉ phương của đường thẳng đó?

A.

 

2; 3u 

. B.

– 3)( 2;u 

.

C.

 

3; 2u 

. D.

 

–3; 3u 

.

Lời giải

Chọn C

. 0 2. 3. 0 3; 2nu a b a b       

.

Câu 163: [0H3-1-1] Cho đường thẳng có vectơ pháp tuyến

 

2; 0n 

.Vectơ nào không là

vectơ chỉ phương của đường thẳng đó?

A.

 

0; 3u 

. B.

 

0; – 7u 

.

C.

 

8; 0u 

. D.

 

0; – 5u 

.

Lời giải

Chọn C

Ta có

. 0 2. 0. 0 0nu a b a      

. Vậy C sai.

Câu 164: [0H3-1-1] Cho đường thẳng



có phương trình tổng quát:

–2 3 –1 0xy

. Những

điểm sau, điểm nào thuộc



?

A.

 

3; 0

. B.

 

1; 1

. C.

 

–3; 0

. D.

 

0; – 3

.

Lời giải

Chọn B

Ta thay tọa độ điểm vào phương trình đường thẳng:

–2.3 3.0–1 7   

loại A;

–2.1 3.1–1 0  

B thỏa mãn.

Câu 165: [0H3-1-1] Cho đường thẳng



có phương trình tổng quát:

–2 3 –1 0xy

. Vectơ

nào sau đây không là vectơ chỉ phương của



?

A.

2

1;

3







. B.

 

3; 2

. C.

 

2; 3

. D.

 

–3; – 2

.

Lời giải

Chọn C

 

–2 3 –1 0 2; 3x y n    

mà

11

2

. 0 ,

3

nu u u u



  





. Vậy chỉ có C không

thỏa mãn.

Câu 166: [0H3-1-1] Cho đường thẳng



có phương trình tổng quát:

–2 3 –1 0xy

. Đường

thẳng song song với



là:

A.

2 – –1 0xy 

. B.

2 3 4 0xy  

.

C.

25xy

. D.

3

70

2

xy  

.

Lời giải

Chọn D

Đường thẳng



có vectơ pháp tuyến

 

2; 3n 

.

Ở đáp án D, đường thẳng

3

70

2

xy  

có vectơ pháp tuyến

3

1;

2









cùng phương

với

 

2; 3n 

. Nên đường thẳng

3

70

2

xy  

song song với



.

Cách 2: sử dụng mtct giải hệ pt: phương trình đường thẳng ở ý A cho nghiệm

 

1;1 .

phương trình đường thẳng ở ý B cho nghiệm

51

;.

43











phương trình đường thẳng

ở ý C cho nghiệm

73

;.

42







Nên chọn D (mất khoảng 2ph để tìm nghiệm của 3 hệ với

máy thôi).

Câu 167: [0H3-1-1] Trong các đường sau đây, đường thẳng nào song song với đường thẳng

: – 4 1 0xy  

?

A.

23yx

. B.

20xy

.

C.

2 8 0xy

. D.

– 4 – 2 0xy

.

Lời giải

Chọn D

Đường thẳng



có vectơ pháp tuyến

 

1; 4n 

.

Ở đáp án D, đường thẳng

– 4 – 2 0xy

có vectơ pháp tuyến

 

1; 4

cùng phương

với

 

1; 4n 

. Nên đường thẳng

– 4 – 2 0xy

song song với



.

Câu 168: [0H3-1-1] Đường nào sau đây cắt đường thẳng



có phương trình:

– 4 1 0xy

?

A.

23yx

. B.

–2 8 0xy

.

C.

2 – 8 0xy

. D.

– 4 – 2 0xy

.

Lời giải

Chọn A

Ta xét hệ phương trình:

11

4 1 0

7

.

2 3 0 1

7

x

xy

y







  









  











Do đó đường thẳng



và

đường thẳng

23yx

cắt nhau.

Cách 2 : nhẩm nhanh tỉ số

ab





hay không ? ví dụ :

28

/ / :

14

–2 8 0

B

d xy









Câu 169: [0H3-1-1] Góc giữa hai đường thẳng

1

: 2 4 0d x y  

;

2

: – 3 6 0d x y 

là:

A.

30

. B.

60

. C.

45

. D.

23 12'

.

Lời giải

Chọn C

Đặt góc giữa hai đường thẳng

 

1

d

và

 

2

d

là



. Khi đó



được tính bằng công

thức:

 

2

2 2 2

1.1 2. 3

2

cos 45

2

1 2 . 1 3





    

  

.

Câu 170: [0H3-1-1] Cho hai đường thẳng

 

1

: 2 4 0d x y  

và

 

2

:2 6 0d x y  

. Góc

giữa hai đường thẳng

 

1

d

và

 

2

d

là :

A.

30

. B.

60

. C.

90

. D.

45

.

Lời giải

Chọn C

Đặt góc giữa hai đường thẳng

 

1

d

và

 

2

d

là



. Khi đó



được tính bằng công

thức:

 

2 2 2 2

1.2 2. 1

cos 0 90

1 2 . 2 1





    



.

Cách 2: Nhận thấy

 

12

. . 1.2 2. 1 0 .a a bb d d



      

 

12

; 90dd

Câu 171: [0H3-1-1] Khoảng cách từ

 

1; 2C

đến đường thẳng

1:3 4 – 1 0xy 

là:

A.

3

. B.

2

. C.

1

. D.

0

.

Lời giải

Chọn D

Cách 1: Ta có

 

22

3.1 4.2 11

,0

34

dC



  



.

Cách 2: Ta có toạ độ điểm

C

thoả phương trình đường thẳng



vì

3.1 4.2 11 0  

.

Do đó

 

,0C d C   

.

Câu 172: [0H3-1-1] Tìm côsin góc giữa 2 đường thẳng

: 2 2 0

1

xy   

và

:0

2

xy  

.

A.

10

. B.

2

. C.

2

3

. D.

3

.

Lời giải

Chọn A

Có

(1;2) , (1; 1)

12

nn  



 

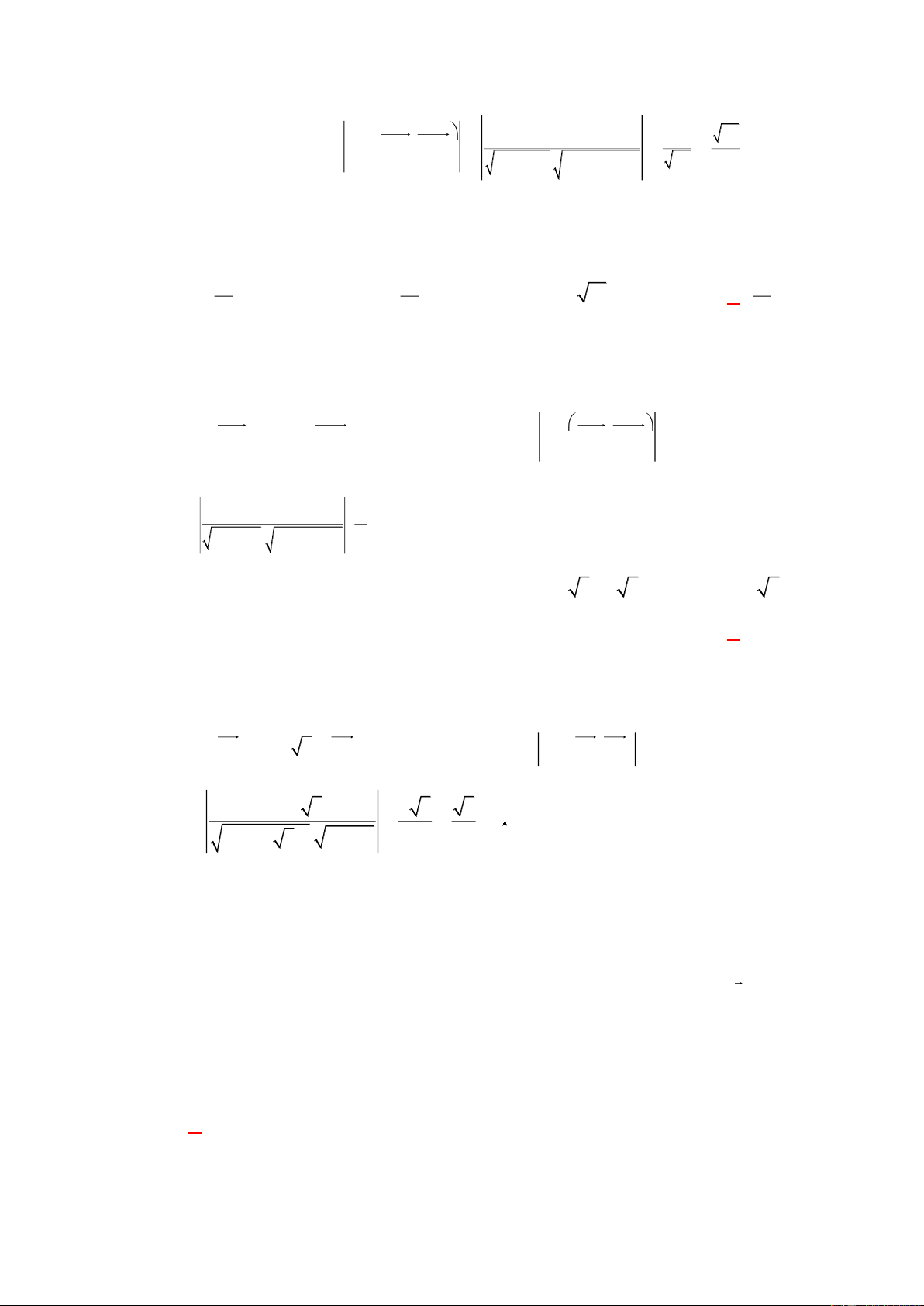
cos , cos ,

12

nn



   







1.1 2.( 1) 1 10

2 2 2 2

10

1 2 . 1 ( 1)



  

  

.

Câu 173: [0H3-1-1] Tìm côsin góc giữa 2 đường thẳng

1

:2 3 10 0xy   

và

2

:2 3 4 0xy   

.

A.

7

13

. B.

6

13

. C.

13

. D.

5

13

.

Lời giải

Chọn D

Có

 

(2;3) , (2;-3) cos , cos ,

12

1 2 1 2

n n Þ n n



    



   



5

13

2.2 3.(-3)

2 2 2 2

2 3 . 2 (-3)







Câu 174: [0H3-1-1] Tìm góc giữa 2 đường thẳng

1

:2 2 3 5 0xy   

và

2

: 6 0y  

A.

60

. B.

125

. C.

145

. D.

30

.

Lời giải

Chọn D

Có

 

1 2 1 2

12

(2;2 3) , (0;1) cos , cos ,n n n n

   

     

2 2 2 2

2.0 2 3.1 2 3 3

42

2 (2 3) . 0 1



   



.

Câu 175: [0H3-1-1] Cho phương trình:

 

01Ax By C  

với

22

0.AB

Mệnh đề nào

sau đây sai?

A.

 

1

là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là

 

;n A B

.

B.

0A 

thì đường thẳng

 

1

song song hay trùng với

x Ox



.

C.

0B 

thì đường thẳng

 

1

song song hay trùng với

y Oy



.

D. Điểm

 

0 0 0

;M x y

thuộc đường thẳng

 

1

khi và chỉ khi

00

0.Ax By C  

Lời giải

Chọn D

0 0 0

( ; )M x y

nằm trên đường thẳng khi và chỉ khi

00

0Ax By C  

.

Câu 176: [0H3-1-1] Mệnh đề nào sau đây sai?

Đường thẳng

d

được xác định khi biết:

A. Một vectơ pháp tuyến hoặc một vectơ chỉ phương.

B. Hệ số góc và một điểm.

C. Một điểm thuộc

d

và biết

d

song song với một đường thẳng cho trước.

D. Hai điểm phân biệt của

d

.

Lời giải

Chọn A

Biết vectơ pháp tuyến hoặc vectơ chỉ phương thì đường thẳng chưa xác định (thiếu

một điểm mà đường thẳng đi qua).

Câu 177: [0H3-1-1] Cho tam giác

ABC

. Hỏi mệnh đề nào sau đây sai?

A.

BC

là một vectơ pháp tuyến của đường cao

AH

.

B.

BC

là một vectơ chỉ phương của đường thẳng

BC

.

C. Các đường thẳng

,,AB BC CA

đều có hệ số góc.

D. Đường trung trực của

AB

có

AB

là vectơ pháp tuyến.

Lời giải

Chọn C

Sai. Vì nếu có một trong ba đường thẳng

,,AB BC CA

song song hay trùng với

'y Oy

thì không có hệ số góc.

Câu 178: [0H3-1-1] Cho đường thẳng

d

có vectơ pháp tuyến là

 

;n A B

.

Mệnh đề nào sau đây sai ?

A. Vectơ

 

1

;u B A

là vectơ chỉ phương của

d

.

B. Vectơ

 

2

;u B A

là vectơ chỉ phương của

d

.

C. Vectơ

 

;n kA kB





với

k

cng là vectơ pháp tuyến của

d

.

D.

d

có hệ số góc là

A

k

B



(nếu

0B 

).

Lời giải

Chọn C

( ; )n kA kB

không thể là vectơ pháp tuyến của

d

khi

0k 

.

Câu 179: [0H3-1-1] Cho đường thẳng

:2 3 4 0d x y  

. Vectơ nào sau đây là vectơ pháp

tuyến của

?d

A.

 

1

3;2n 

. B.

 

2

4; 6n   

. C.

 

3

2; 3n 

. D.

 

4

2;3 .n 

Lời giải

Chọn B

Một vectơ pháp tuyến của

d

là

(2;3)n 

nên vectơ

2 ( 4; 6)n   

là vectơ pháp

tuyến của

d

.

Câu 180: [0H3-1-1] Cho đường thẳng

:3 7 15 0d x y  

. Mệnh đề nào sau đây sai?

A.

 

7;3u 

là vectơ chỉ phương của

d

. B.

d

có hệ số góc

3

7

k 

.

C.

d

không qua gốc toạ độ. D.

d

đi qua

2

điểm

1

;2

3

M









và

 

5;0 .N

Lời giải

Chọn D

Cho

0 3 15 0 5y x x      

. Vậy

d

qua

 

5;0N 

.

Câu 181: [0H3-1-1] Cho đường thẳng

: 2 1 0d x y  

. Nếu đường thẳng



qua điểm

 

1; 1M 

và



song song với

d

thì



có phương trình:

A.

2 3 0xy  

. B.

2 5 0xy  

. C.

2 3 0xy  

. D.

2 1 0.xy  

Lời giải

Chọn A

D

có véc tơ pháp tuyến là

 

1; 2n 

.

d

qua

 

1; 1M 

và

//dD

nên

   

: 1 1 2 1 0 2 3 0d x y x y       

.

Câu 182: [0H3-1-1] Đường thẳng

:3 2 7 0xy   

cắt đường thẳng nào sau đây?

A.

1

:3 2 0.d x y

. B.

2

:3 2 0d x y

.

C.

3

: 3 2 7 0d x y   

. D.

4

:6 4 14 0.d x y  

Lời giải

Chọn A

:3 2 7 0xy   

và

1

:3 2 0d x y

có

32



  

cắt

1

.d

Câu 183: [0H3-1-1] Đường thẳng

:4 3 5 0d x y  

. Một đường thẳng



đi qua gốc toạ độ

và vuông góc với

d

có phương trình:

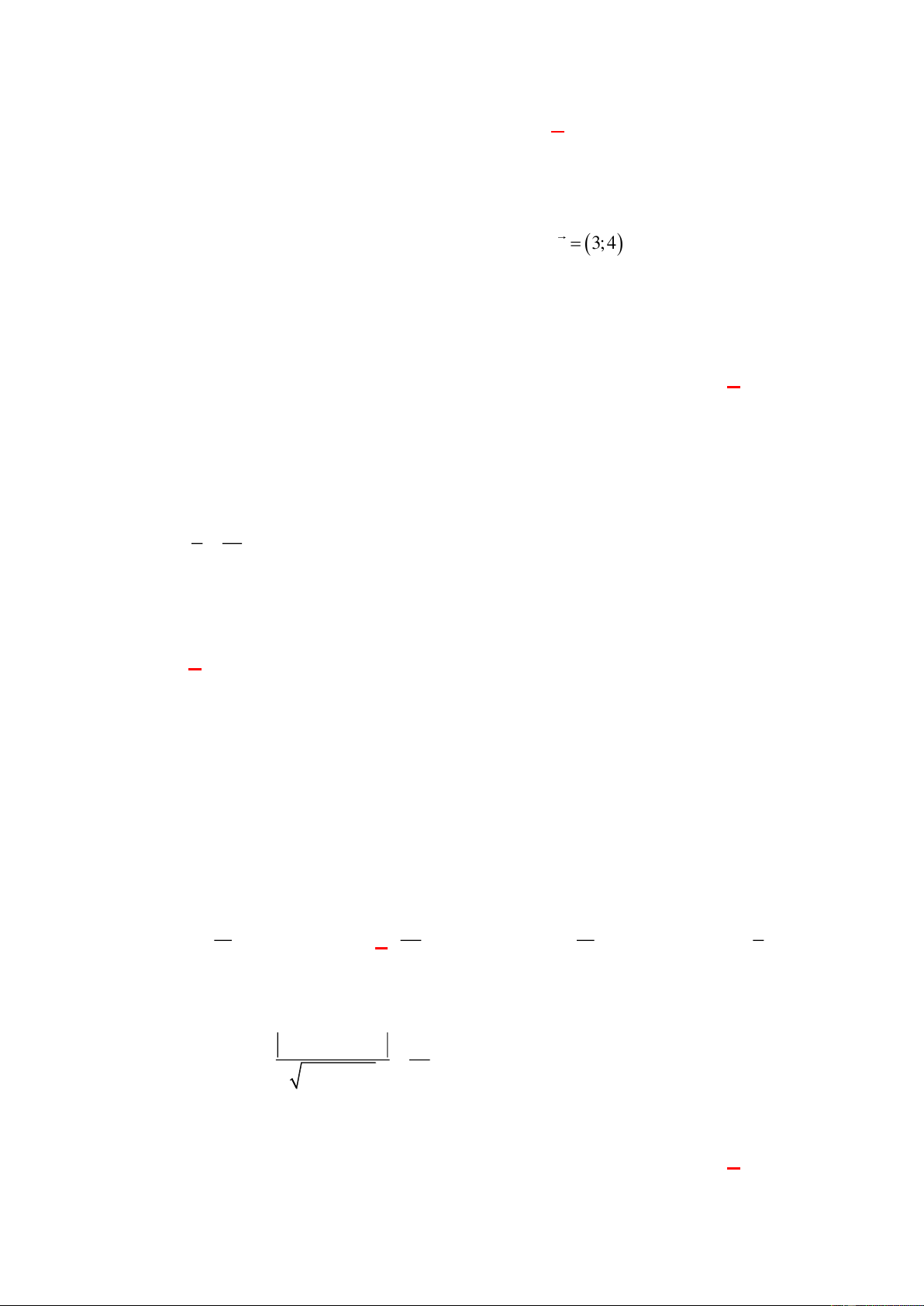
A.

4 3 0xy

. B.

3 4 0xy

. C.

3 4 0xy

. D.

4 3 0.xy

Lời giải

Chọn C



vuông góc với

d

nên



có vectơ pháp tuyến

 

3;4n 

và



qua

O

nên có

phương trình

3 4 0 ( 0)x y c  

.

Câu 184: [0H3-1-1] Phương trình nào sau đây biểu diễn đường thẳng không song song với

đường thẳng

: 2 1?d y x

A.

2 5 0xy  

. B.

2 5 0xy  

. C.

20xy  

. D.

2 5 0.xy  

Lời giải

Chọn D

 

: 2 1 2 1 0d y x x y     

và đường thẳng

2 5 0xy  

không song song vì

21





.

Câu 185: [0H3-1-1] Hai đường thẳng

12

:4 3 18 0; :3 5 19 0d x y d x y     

cắt nhau tại

điểm có toạ độ:

A.

 

3;2

. B.

 

3;2

. C.

 

3; 2

. D.

 

3; 2

.

Lời giải

Chọn A

Giải hệ phương trình

4 3 18 0

3 5 19 0

xy

  





  



ta được

3

2

x

y











.

Câu 186: [0H3-1-1] Khoảng cách từ điểm

 

3; 4M 

đến đường thẳng

:3 4 1 0xy   

bằng:

A.

12

5

. B.

24

5

. C.

12

5

. D.

8

.

5

Lời giải

Chọn B

 

22

3.3 4 4 1

24

,

5

3 ( 4)

dM

  

  



.

Câu 187: [0H3-1-1] Tính góc giữa hai đường thẳng:

2

:5 3 0; :5 7 0.d x y d x y     

A.

45

. B.

76 13





. C.

62 32





. D.

22 37.





Lời giải

Chọn D

 

5.5 1 1

12

cos , ' , ' 22 37

13

25 1. 25 1

D D D D





    



.

Câu 1: [0H3-1-3] Phương trình đường thẳng

d

qua

(1;4)M

và chắn trên hai trục toạ độ những

đoạn bằng nhau là

A.

30xy  

. B.

30xy  

. C.

50xy  

. D.

50xy  

.

Lời giải

Chọn C

Do

(1;4)M

thuộc góc phần tư thứ Nhất nên đường thẳng cần tìm song song với

đường thẳng

,

( ):

II IV

d y x  

, vậy đường thẳng cần tìm có phương trình

( 1) 4 5 0x y x y       

.

Câu 2: [0H3-1-3] Tam giác

ABC

có đỉnh

( 1; 3)A 

. Phương trình đường cao

:5 3 25 0BB x y



   

, phương trình đường cao

:3 8 12 0CC x y



   

. Toạ độ đỉnh

B

là

A.

(5;2)B

. B.

(2;5)B

. C.

(5; 2)B 

. D.

(2; 5)B 

.

Lời giải

Chọn B

Đường thẳng

AB

có phương trình

8( 1) 3( 3) 0 8 3 1 0x y x y       

nên tọa

độ điểm

( ; )B x y

là nghiệm của hệ phương trình

8 3 1 2

5 3 25 5

x y x

x y y

  







  



.

Câu 3: [0H3-1-3] Cho hai đường thẳng

1

: 1 0d x y  

,

2

: 3 3 0d x y  

. Phương trình

đường thẳng

d

đối xứng với

1

d

qua đường thẳng

2

d

là:

A.

7 1 0xy  

. B.

7 1 0xy  

. C.

7 1 0xy  

. D.

7 1 0xy  

.

Lời giải

Chọn D

Giao điểm của

1

d

và

2

d

là nghiệm của hệ

 

1 0 1 0

0;1

3 3 0 3 3 1

x y x y x

A

x y x y y

     

  

  

  

      

  

.

Lấy

 

1

1;0Md

. Tìm

'M

đối xứng

M

qua

2

d

.

Viết phương trình đường thẳng



đi qua

M

và vuông góc với

2

d

:

:3 3 0xy   

.

Gọi H là giao điểm của



và đường thẳng

2

d

. Tọa độ H là nghiệm của hệ

3

3 3 0 3 3

36

5

;

3 3 0 3 3 6

55

5

x

x y x y

H

x y x y

y







    







  

  



     













.

Ta có H là trung điểm của

'MM

. Từ đó suy ra tọa độ

1 12

';

55

M







.

Viết phương trình đường thẳng

d

đi qua 2 điểm

A

và

'M

: điểm đi qua

(0;1)A

,

vectơ chỉ phương

17

';

55

AM











vectơ pháp tuyến

71

;

55

n









.

   

71

: 0 1 0 7 1 0

55

d x y x y       

.

Câu 4: [0H3-1-3] Cho hai đường thẳng

:2 3 0d x y  

và

: 3 2 0xy   

. Phương trình

đường thẳng

'd

đối xứng với

d

qua



là:

A.

11 13 2 0xy  

. B.

11 2 13 0xy  

. C.

13 11 2 0xy  

. D.

11 2 13 0xy  

.

Lời giải

Chọn B

Giao điểm của

d

và



là nghiệm của hệ

 

2 3 0 2 3 1

1;1

3 2 0 3 2 1

x y x y x

A

x y x y y

       

  

   

  

     

  

.

Lấy

 

0;3Md

. Tìm

'M

đối xứng

M

qua



.

Viết phương trình đường thẳng

'

đi qua

M

và vuông góc với



:

':3 3 0xy   

.

Gọi

H

là giao điểm của

'

và đường thẳng



. Tọa độ

H

là nghiệm của hệ

7

3 2 0 3 2

79

10

;

3 3 0 3 3 9

10 10

10

x

x y x y

H

x y x y

y







    







   

  



     













.

Ta có

H

là trung điểm của

'MM

. Từ đó suy ra tọa độ

76

';

55

M









.

Viết phương trình đường thẳng

'd

đi qua 2 điểm

A

và

'M

: điểm đi qua

( 1;1)A 

,

vectơ chỉ phương

2 11

';

55

AM











vectơ pháp tuyến

11 2

;

55

n









.

   

11 2

': 1 1 0 11 2 13 0

55

d x y x y       

.

Câu 5: [0H3-1-3] Một điểm

M

di động có tọa độ:

2

4cos 3

cos2 1

xt

yt











. Tập hợp những điểm

M

là:

A. Đoạn thẳng có độ dài là

4

B. Đoạn thẳng có độ dài là

25

C. Đoạn thẳng có độ dài là

2

D. Hai nửa đường thẳng.

Lời giải

Chọn B

Gọi

 

00

;M x y

, ta có

22

0

00

0

00

0

5

2cos2 5

4cos 3 4cos 2 5 cos2

2

1 cos2

cos2 1 cos2 1

1 cos2

x

xt

x t x t t

yt

y t y t

yt









     



  

  

   



   













Vì

1 cos2 1t  

nên ta có:

0

5

1 1 3 7

2

x



     

0

x

chạy trên một đoạn có độ dài bằng

4

00

1 1 1 0 2yx      

0

y

chạy trên một đoạn có độ dài bằng

2

Khi đó

 

00

;M x y

chạy trên một đoạn có độ dài

22

2 4 2 5.

Câu 6: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng sau song song nhau:

 

2

2 1 3 0x m y   

và

100 0mx y  

.

A.

m

. B.

2m

.

C.

1m 

. D.

1m

hoặc

1m

.

Lời giải

Chọn C

2

3

2

12

21

20

1

2 1 3

200 200

// 1

1 100

33

0

00

m

mm

m

d d m m m

m

mm











  











  

      



  

  















.

Câu 7: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng sau song song nhau:

1

:3 2 6 0d mx y  

và

 

2

: 2 2 3 0d m x my   

.

A.

1m

hoặc

1m

. B.

m

. C.

2m

. D.

1m

.

Lời giải

Chọn A

2

12

32

44

22

3 2 6

1

21

// 2

2 2 3

1

22

0

m

mm

m

d d m

mm

m



























  

     



  







  















.

Câu 8: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng sau song song nhau:

 

1

81

:

10

   







x m t

d

yt

và

2

: 2 14 0d mx y  

.

A.

1m

hoặc

2m

. B.

1m 

. C.

2m 

. D.

m

.

Lời giải

Chọn A

12

// dd 

hệ phương trình

   

 

8 1 1

10 2

2 14 0 3

   









  



x m t

yt

mx y

vô nghiệm

Thay

   

1 , 2

vào

 

3

ta được

   

8 ( 1) 2 10 14 0m m t t     

 

2

2 8 6 4m m t m    

Phương trình

 

4

vô nghiệm khi và chỉ khi

2

1

20

2

8 6 0

m

mm

m





  

















.

Câu 9: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

22

:

1

xt

d

y mt











và

2

:4 3 0d x y m  

trùng nhau ?

A.

3m 

. B.

1m 

. C.

4

3

m 

. D.

m

.

Lời giải

Chọn D

12

dd



hệ phương trình

 

2 2 1

1 2

4 3 0 3

xt

y mt

x y m

  









  



có nghiệm tùy ý.

Thay

   

1 , 2

vào

 

3

ta được

   

4 2 2 3 1 0t mt m    

   

3 8 5 4m t m   

Phương trình

 

4

có nghiệm tùy ý khi và chỉ khi

3 8 0

50

m





 







.

Câu 10: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

 

1

: 2 1 10 0   d m x my

và

2

:3 2 6 0d x y  

vuông góc nhau ?

A.

3

2

m 

. B.

3

8

m 

. C.

3

8

m 

. D.

m

.

Lời giải

Chọn C

Đường thẳng

 

1

: 2 1 10 0   d m x my

có

 

1

2 1;vtpt n m m

.

Đường thẳng

2

:3 2 6 0d x y  

có

 

2

3;2vtpt n 

.

       

1 2 1 2

3

. 0 2 1 . 3 . 2 0

8

d d n n m m m        

.

Câu 11: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:2 3 10 0d x y  

và

2

23

:

14

xt

d

y mt











vuông góc nhau ?

A.

1

2

m 

. B.

9

8

m 

. C.

9

8

m 

. D.

m

.

Lời giải

Chọn C

Đường thẳng

1

:2 3 10 0d x y  

có

 

1

2; 3vtpt n 

Đường thẳng

2

23

:

14

xt

d

y mt











có

 

2

4 ; 3vtpt n m

       

1 2 1 2

9

. 0 2 . 4 3 . 3 0

8

d d n n m m          

.

Câu 12: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:3 4 10 0d x y  

và

 

2

: 2 1 10 0   d m x m y

trùng nhau ?

A.

m

. B.

1m

. C.

2m

. D.

m

.

Lời giải

Chọn C

2

12

22

21

3 8 4 0

2 1 10

34

3 4 10

10 4

4 10











  





     

















mm

dd

mm

2

3

2 2



  









   



mm

2m

.

Câu 13: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:4 3 3 0d x y m  

và

2

12

:

4

xt

d

y mt











trùng nhau ?

A.

8

3

m 

. B.

8

3

m 

. C.

4

3

m 

. D.

4

3

m 

.

Lời giải

Chọn B

12

dd

hệ phương trình

 

1 2 1

4 2

4 3 3 0 3

xt

y mt

x y m

  









  



có nghiệm tùy ý.

Thay

   

1 , 2

vào

 

3

ta được

   

4 1 2 3 4 3 0t mt m    

   

3 8 3 8 4m t m   

Phương trình

 

4

có nghiệm tùy ý khi và chỉ khi

8

3 8 0

3

mm   

.

Câu 14: [0H3-1-3] Cho hai điểm

 

–2;0A

,

 

1;4B

và đường thẳng

:

2

xt

d

yt











. Tìm giao

điểm của đường thẳng

và d AB

.

A.

 

2;0

. B.

 

–2;0

. C.

 

0;2

. D.

 

0; – 2

.

Lời giải

Chọn B

Đường thẳng

AB

đi qua điểm

 

–2;0A

và có

 

3;4vtcp AB 

,

 

4; 3vtpt n 

Vậy phương trình tổng quát của đường thẳng

:4 3 8 0AB x y  

.

Đường thẳng

d

. đi qua điểm

 

0;2M

và có

 

1; 1vtcp u   

,

 

1; 1vtpt p 

Vậy phương trình tổng quát của đường thẳng

: 2 0d x y

.

Gọi

K

là giao điểm của đường thẳng

và d AB

.

Tọa độ điểm

K

thỏa hệ phương trình

 

4 3 8 0 2

2;0

2 0 0

x y x

KA

x y y

    



   



   



.

Câu 15: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây trùng nhau?

 

1

2

:

11

x m t

y m t











  





và

2

1

:

x mt

y m t













A. Không có

m

. B.

4

3

m 

. C.

1m 

. D.

3m 

.

Lời giải

Chọn C

Chuyển về phương trình tổng quát, hai đường thẳng trùng nhau khi các hệ số tương

ứng tỷ lệ.

Giải ra được

1m 

. Chọn C

***Giải nhanh: lấy đáp án thế vào hai phương trình.

Câu 16: [0H3-1-3] Tìm tất cả giá trị

m

để hai đường thẳng sau đây song song.

1

:

8 ( 1)

10

x m t

yt

  









và

2

:

2 14 0mx y  

.

A. Không

m

nào. B.

2.m 

C.

1m 

hoặc

2.m 

D.

1.m 

Lời giải

Chọn C

Đường thẳng

1



có vtcp

 

1

1;1um  

nên vtpt

 

1

1; 1nm

.

Đường thẳng

2



có vtpt

 

2

;2nm

.

12

1

11

// .

2

m







    







Câu 17: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây trùng nhau ?

1

:

3 4 1 0xy  

và

2

:

2

(2 1) 1 0m x m y   

A.

2.m 

B. Mọi

m

C. Không có

m

D.

1.m 

Lời giải

Chọn C

Hai đường thẳng trùng nhau khi

2

2 1 1

3 4 1

mm





nên không có

m

.

Câu 18: [0H3-1-3] Tìm điểm

M

trên trục

Ox

sao cho nó cách đều hai đường thẳng:

1

:3 2 6 0d x y  

và

3

:3 2 6 0d x y  

?

A.

 

1;0 .

B.

 

0;0 .

C.

 

0; 2 .

D.

 

2;0 .

Lời giải

Chọn B

Gọi

   

;0 3 6 3 6 0 0;0M a a a a M      

Câu 19: [0H3-1-3] Cho hai điểm

1(3; )A 

và

 

0;3 .B

Tìm tọa độ điểm

M

trên trục

Ox

sao

cho khoảng cách từ

M

đến đường thẳng

AB

bằng

AB

?

A.

 

34

;0 ; 4;0 .

9









B.

 

2;0

và

 

1;0 .

C.

 

4;0 .

D.

( 13;0).

Lời giải

Chọn A

Ta gọi

 

;0Ma

, pt

:4 3 9 0, 5AB x y AB   

   

12

34

49

34

, 5 5 ;0 , 4;0

9

59

4

a

d M AB M M

a











      











Câu 20: [0H3-1-3] Cho hai điểm

 

1;2A

và

 

4;6 .B

Tìm tọa độ điểm

M

trên trục

Oy

sao

cho diện tích tam giác

MAB

bằng

1

?

A.

 

0;0

và

4

0; .

3







B.

 

1;0 .

C.

 

4;0 .

D.

 

0;2 .

Lời giải

Chọn A

5AB 

, Gọi

 

0;Mm

Vì diện tích tam giác

MAB

bằng

 

2

1 , ,

5

d M AB

0

32

2

:4 3 2 0

4

55

3

m

AB x y

m









     







Câu 21: [0H3-1-3] Cho hai điểm

1(2; )A 

và

 

0;100B

,

4(2; )C 

.Tính diện tích tam giác

ABC

?

A.

3.

B.

3

.

2

C.

3

.

2

D.

147.

Lời giải

Chọn A

Phương trình

   

1

: 2 0, 3, , 2 . , 3

2

ABC

AC x AC d B AC S AC d B AC



      

.

Câu 22: [0H3-1-3] Tìm tọa độ điểm

M

trên trục

Ox

và cách đều hai đường thẳng:

1

:3 2 6 0d x y  

và

2

:3 2 3 0d x y  

A.

1

;0

2







B.

(0; 2)

C.

 

2;0 .

D.

 

1;0 .

Lời giải

Chọn A

Gọi

( ;0)Mm

. Theo bài ra ta có

   

12

11

, , 3 6 3 3 ;0

22

d M d d M d m m m M



       





.

Câu 23: [0H3-1-3] Cho hai điểm

 

2;3A

và

 

1;4 .B

Đường thẳng nào sau đây cách đều hai

điểm

,AB

?

A.

20xy

. B.

100 0xy  

. C.

20xy

. D.

2 10 0xy  

.

Lời giải

Chọn A

Cách 1: Gọi

d

là đường thẳng cách đều hai điểm

,AB

, ta có:

         

2 2 2 2

22

; 2 3 1 4

2 2 4 0 2 0

M x y d MA MB x y x y

x y x y

          

       

Cách 2: Gọi

I

là trung điểm của đoạn

AB

37

;

22

I









Gọi

d

là đường thẳng cách đều hai điểm

,AB

d

là đường trung trực của đoạn

AB

.

d

đi qua

37

;

22

I







và nhận

 

1;1AB 

làm VTPT

37

: 0 : 2 0

22

d x y d x y

   

          

   

   

Câu 24: [0H3-1-3] Cho ba điểm

   

0;1 , 12;5AB

và

()3;0 .C 

Đường thẳng nào sau đây cách

đều ba điểm

,,A B C

A.

3 4 0xy  

. B.

10 0xy   

. C.

0xy

. D.

5 1 0xy  

.

Lời giải

Chọn A

Viết phương trình đường thẳng

d

qua ba điểm thẳng hàng

,,A B C

. Nếu đường

thẳng cách đều ba điểm

,,A B C

thì nó phải song song hoặc trùng với

d

Gọi

d

là đường thẳng qua hai điểm

,AC

: 1 3 3 0

31

xy

d x y      



Kiểm tra các phương án, ta thấy phương án A thỏa.

Câu 25: [0H3-1-3] Phương trình của đường thẳng qua

 

2;5P

và cách

 

5;1Q

một khoảng

bằng

3

là:

A.

7 24 –134 0xy

. B.

2 x 

C.

2, 7 24 –134 0x x y  

. D.

3 4 5 0xy  

Lời giải

Chọn C



qua

 

: ( 2) ( 5) 0 -2 -5; 025 a x b y ax by a bP         

 

22

5 2 5

, 3 3 3 4 3

a b a b

d Q a b a b

ab

  

       



2

0

24 7 0

24

7

b

ab b

ba







    







.

Với

0b 

, chọn

1 : 2ax   

Với

24

7

ba

, chọn

7 24 :7 24 134 0a b x y      

Câu 26: [0H3-1-3] Cho đường thẳng

:3 – 4 2 0.d x y 

Có đường thẳng

1

d

và

2

d

cùng song

song với

d

và cách

d

một khoảng bằng

1.

Hai đường thẳng đó có phương trình là:

A.

3 – 4 – 7 0; 3 – 4 3 0x y x y  

. B.

3 – 4 7 0; 3 – 4 – 3 0x y x y  

C.

3 – 4 4 0; 3 – 4 3 0x y x y   

. D.

3 – 4 – 7 0; 3 – 4 7 0x y x y  

.

Lời giải

Chọn B

Giả sử đường thẳng



song song với

:3 – 4 2 0d x y 

có phương trình là

:3 4 0x y C   

Lấy điểm

 

2; 1Md  

Do

 

2

7

3.( 2) 4( 1)

, 1 1 2 5

3

34

C

d d C

C



   



       









Câu 27: [0H3-1.26-3] Hai cạnh của hình chữ nhật nằm trên hai đường thẳng

12

: 4 – 3 5 0, :3 4 – 5 0d x y d x y   

, đỉnh

 

2; 1A

. Diện tích của hình chữ nhật là:

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn B

Do điểm

A

không thuộc hai đường thẳng trên.

Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ

 

2; 1A

đến hai đường

thẳng trên, do đó diện tích hình chữ nhật bằng

2 2 2 2

4.2 3.1 5 3.2 4.1 5

.2

4 3 4 3

S

   





.

Câu 28: [0H3-1-3] Khoảng cách giữa hai đường thẳng song song với đường thẳng



:

23

5

xt

yt











và cách

 

1;1A

một khoảng

35

là:

:0d x by c  

. Thế thì

bc

bằng

A.

14

hoặc

16

. B.

16

hoặc

14

. C.

10

hoặc

20

. D.

10

.

Lời giải

Chọn A

Gọi

:0d x by c  

Vì đường thẳng

23

:

5

xt

yt













d//

nên

2b 

Phương trình của

: 2 0d x y c  

.

Theo đề ra ta có:

 

14

; 3 5 1 15

16

c

d A d c

c





    







Câu 29: [0H3-1-3] Phương trình các đường thẳng qua

 

2;7M

và cách điểm

 

1; 2N

một

khoảng bằng

1

là

A.

12 – 5 –11 0; – 2 0.x y x

B.

12 5 –11 0; 2 0.x y x   

C.

12 – 5 11 0; – 2 0.x y x  

D.

12 5 11 0; 1 0.x y x    

Lời giải

Chọn C

Sử dụng phương pháp loại trừ:

Dễ thấy điểm

 

2;7M

không thuộc hai đường thẳng

2 0; 1 0xx   

nên loại B;

D.

Điểm

 

2;7M

không thuộc đường thẳng

12 5 11 0xy  

nên loại A.

Câu 30: [0H3-1-3] Cho đường thẳng

   

– 2 –1: 2 –1 0.m x m y m  

Với giá trị nào của

m

thì khoảng cách từ điểm

 

2;3

đến



lớn nhất ?

A.

11

.

5

m 

B.

11

.

5

m 

C.

11.m

D.

11.m 

Lời giải

Chọn A

Ta có

2

78

2 6 5

m

d

mm







. Bấm máy tính, chọn A.

Câu 31: [0H3-1-3] Cho đường thẳng

:3 – 4 2 0.d x y 

Có đường thẳng

1

d

và

2

d

cùng

song song với

d

và cách

d

một khoảng bằng

1

. Hai đường thẳng đó có phương

trình là

A.

3 – 4 – 7 0; 3 – 4 3 0.x y x y  

B.

3 – 4 +7 0; 3 – 4 3 0.x y x y  

C.

3 – 4 +4 0; 3 – 4 3 0.x y x y  

D.

3 – 4 +3 0; 3 – 4 13 0.x y x y  

Lời giải

Chọn B

Gọi

:3 4 0; 2x y C C    

Theo đề ra ta có:

3

( ; ) 1 2 5

7

C

d d C

C





     







Câu 32: [0H3-1-3] Cho tam giác

ABC

có

     

2;–2 , 1; –1 , 5;2 .A B C

Độ dài đường cao

AH

của tam giác

ABC

là

A.

3

5

B.

7

5

C.

9

5

D.

1

5

Lời giải

Chọn B

Phương trình đường thẳng

:3 4 7 0.BC x y  

Độ dài đường cao

 

7

;

5

AH d A BC

Câu 33: [0H3-1-3] Cho

   

2;2 , 5;1AB

và đường thẳng

: – 2 8 0.xy  

Điểm

C

.

C

có hoành độ dương sao cho diện tích tam giác

ABC

bằng

17

. Tọa độ của

C

là

A.

 

10;12 .

B.

 

12; 10 .

C.

 

8; 8 .

D.

 

10; 8 .

Lời giải

Chọn B

Phương trình đường thẳng

: 3 8 0AB x y  

. Điểm

 

2 8;C C t t  

Diện tích tam giác

ABC

:

   

10

5 16

11

. ; 17 10. 17 12;10

18

22

10

5

t

AB d C AB C

t









    







Câu 34: [0H3-1.26-3] Hai cạnh của hình chữ nhật nằm trên hai đường thẳng

4 – 3 5 0;3 4 – 5 0,x y x y   

đỉnh

 

2;1A

. Diện tích của hình chữ nhật là

A.

1

B.

2

C.

3

D.

4

Lời giải

Chọn B

Khoảng cách từ đỉnh

 

2;1A

đến đường thẳng

4 3 5 0xy  

là

2

Khoảng cách từ đỉnh

 

2;1A

đến đường thẳng

3 4 5 0xy  

là

1

Diện tích hình chữ nhật bằng

2.1 2

.

Câu 35: [0H3-1-3] Tìm tọa độ điểm

M

nằm trên trục

Ox

và cách đều

2

đường thẳng

1

:3 2 6 0xy   

và

2

:3 2 3 0.xy   

A.

 

0 ; 2

. B.

1

; 0

2







. C.

 

1; 0

. D.

 

2; 0

.

Lời giải

Chọn B

Ta có:

 

;0M Ox M x

.

12

3 6 3 3( )

3 6 3 3

( ; ) ( ; )

1

3 6 3 3

13 13

2

x x vn

xx

d M d M

x x x

  







     



     



.

Vậy

1

;0 .

2

M







Câu 36: [0H3-1-3] Tính diện tích

ABC

biết

     

2; 1 , 1; 2 , 2; 4A B C

:

A.

3

. B.

3

37

. C.

3

. D.

3

2

.

Lời giải

Chọn D

Đường thẳng đi qua

2

điểm

1(2; )A 

và

 

1 ; 2B

có vectơ chỉ phương là

 

1;3AB 

. Suy ra tọa độ vectơ pháp tuyến là

(3;1).

Suy ra

AB

:

   

3 2 1 1 0 3 5 0.x y x y       

22

3.2 4 5

3

( , )

10

31

d C AB







;

10.AB 

Diện tích

ABC

:

 

13

. , . .

22

S d C AB AB

Câu 37: [0H3-1-3] Cho đường thẳng đi qua

2

điểm

 

3; 1 , () 3 ,0;AB

tìm tọa độ điểm

M

thuộc

Ox

sao cho khoảng cách từ điểm

M

tới đường thẳng

AB

bằng

1.

A.

 

1; 0

và

 

3,5; 0

. B.

 

13; 0

C.

 

4; 0

D.

 

2; 0

Lời giải

Chọn A

Đường thẳng đi qua

2

điểm

1(3; )A 

và

 

0;3B

có vectơ chỉ phương là

 

3;4AB 

. Suy ra tọa độ vectơ pháp tuyến là

(4;3).

Suy ra:

AB

:

   

4 3 3 1 0 4 3 9 0.x y x y       

 

;0M Ox M x

.

 

22

77

;0

4 9 5

49

22

( , ) 1 1

4 9 5

43

1 1;0

xM

x

d M AB

x

xM

















   





  











.

Câu 38: [0H3-1-3] Cho

ABC

với

     

1;2 , 0;3 , 4;0A B C

. Chiều cao tam giác ứng với cạnh

BC

bằng:

A.

3

. B.

1

5

. C.

1

25

. D.

3

5

Lời giải

Chọn B

Đường thẳng

BC

có phương trình

1 3 4 12 0.

43

xy

xy     

Chiều cao cần tìm là

 

1

,.

5

d A BC 

Câu 39: [0H3-1-3] Tính diện tích

ABC

biết

     

3;2 , 0;1 , 1;5 .A B C

A.

11

17

. B.

17

.

C.

11

. D.

11

2

.

Lời giải

Chọn D

   

3; 1 10; 2;3 13.AB AB AC AC        

   

. 6 3 3 11

cos , sin , .

| |.| |

10. 13 130 130

AB AC

AB AC AB AC

AB AC



    

 

1 11

. .sin , .

22

ABC

S AB AC AB AC





Câu 40: [0H3-1-3] Cho đường thẳng đi qua 2 điểm

   

1;2 , 4;6 ,AB

tìm tọa độ điểm

M

thuộc

Oy

sao cho diện tích

MAB

bằng

1

.

A.

 

0;1

. B.

 

0;0

và

4

0;

3







. C.

 

0;2

. D.

 

1;0

.

Lời giải

Chọn B

     

3;4 5; 0; ; : 4 3 2 0.

M

AB AB M y AB x y     

 

22

0

| 4.0 3. 2|

1 2 2

. , 1 , .

4

2 5 5

43

3

M

MAB

M

y

S AB d M AB d M AB

y











      









Câu 41: [0H3-1-3] Tính diện tích

ABC

biết

   

3 ; 4 , 1 ; 5 , 3 ; ( 1)A B C

:

A.

10

. B.

5

. C.

26

. D.

25

.

Lời giải

Chọn B

Ta có

(0;5) (1;0)AC n  

là véctơ pháp tuyến của

.AC

Phương trình đường thẳng

1

: 3 0 ( , ) 5.

2

ABC

AC x S d B AC AC



    

Câu 42: [0H3-1-3] Tìm hình chiếu của

 

3; –4A

lên đường thẳng

2

:

2

1

xt

yt

d







  



. Sau đây

là bài giải:

Bước 1: Lấy điểm

 

2 2 ;–1–H t t

thuộc

d

. Ta có

 

2 –1; – 3tA tH 

.

Vectơ chỉ phương của

d

là

 

2;–1u 

.

Bước 2:

H

là hình chiếu của

A

trên

. 0.d AH d u AH   

   

2 2 –1 – – 3 0 1.t t t    

Bước 3: Với

1t 

ta có

 

.4; – 2H

Vậy hình chiếu của

A

trên

d

là

 

.4;–2H

Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ

bước 3

Lời giải

Chọn A

Bài giải trên đúng.

Câu 43: [0H3-1-3] Cho hai đường thẳng

: 2 1 0  d x y

,

: 2 1 0.d x y



  

Câu nào sau đây

đúng?

A.

d

và

d



đối xứng qua

.O

B.

d

và

d



đối xứng qua

Ox

.

C.

d

và

d



đối xứng qua

Oy

. D.

d

và

d



đối xứng qua đường

thẳng

.yx

Lời giải

Chọn B

Đường thẳng

 

1;0 .d Ox A d



  

Lấy điểm

1

0;

2

Md









 

ox

1

0; .

2

Đ M N d





  





Câu 44: [0H3-1-3] Cho đường thẳng

13

:

2

xt

yt













và điểm

 

3;3 .M

Tọa độ hình chiếu

vuông góc của

M

trên đường thẳng



là:

A.

 

4;–2

. B.

 

1;0

. C.

 

2;2

. D.

 

7; –4

.

Lời giải.

Chọn B

Gọi

H

là hình chiếu của

M

trên



. Ta có:

   

1 3 ; 2 , 2 3 ; 3 2 .H H t t MH t t        

Đường thẳng



có vectơ chỉ phương là

 

3; 2 .u 

   

. 0 3 2 3 2 3 2 0 13 0 0 (1;0).MH u MH u t t t t H              

Câu 45: [0H3-1-3] Cho đường thẳng

23

:

12

xt

yt













. Hoành độ hình chiếu của

 

4;5M

trên



gần nhất với số nào sau đây?

A.

1,1

. B.

1,2

. C.

1,3

. D.

1,5

.

Lời giải.

Chọn D

Gọi

H

là hình chiếu của

M

trên



. Ta có:

   

2 3 ;1 2 , 2 3 ; 4 2 .H H t t MH t t        

Đường thẳng



có vectơ chỉ phương là

 

3; 2u 

.

   

2 20 17

. 0 3 2 3 2 4 2 0 13 2 0 ; .

13 13 13

MH u MH u t t t t H



                





Câu 46: [0H3-1-3] Tìm hình chiếu của

 

3; –4A

lên đường thẳng

22

:

1

xt

d

yt







  



. Sau đây là

bài giải:

Bước 1: Lấy điểm

 

2 2 ;–1–H t t

thuộc

.d

Ta có:

 

2 –1; – 3 .AH t t

Vectơ chỉ phương của

d

là

 

2;–1 .u 

Bước 2:

H

là hình chiếu của

A

trên

d

   

. 0 2 2 –1 – – 3 0 1.AH d u AH t t t        

Bước 3: Với

1t 

ta có

 

4;–2 .H

Vậy hình chiếu của

A

trên

d

là

 

4;–2 .H

Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ

bước 3

Lời giải.

Chọn A

Đúng.

Câu 47: [0H3-1-3] Cho đường thẳng

: 2 – 3 3 0d x y 

và

 

8;2M

. Tọa độ của điểm

M



đối

xứng với

M

qua

d

là

A.

 

–4; 8

. B.

 

–4; –8

. C.

 

4;8

. D.

 

4; –8

.

Lời giải:

Chọn C

Gọi

d



qua

M

và vuông góc với

d

nên

:3 2 28 0.d x y



  

Gọi

 

6;5 .H d d H



  

Vì

M



đối xứng với

M

qua

d

nên

H

là trung điểm của

MM



suy ra

 

4;8 .M



Câu 48: [0H3-1-3] Cho hai đường thẳng

: 2 3 0, : 2 3 0.d x y d x y



     

Phương trình

các đường phân giác của các góc tạo bởi

d

và

d



là:

A.

0; – 2 0x y x y   

. B.

– 0; 2 0x y x y   

.

C.

2 0; – 0x y x y   

. D.

– 2 0; – –1 0x y x y  

.

Lời giải

Chọn C

Phương trình các đường phân giác của các góc tạo bởi

d

và

d



là:

 

2 2 2 2

2 3 2 3

0

2 3 2 3

20

1 2 1 2

x y x y

xy

x y x y

xy

    





   



  



     

  





.

Câu 49: [0H3-1-3] Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường

thẳng

1

:3 4 1 0xy   

và

2

: 2 4 0xy   

.

A.

(3 5) 2(2 5) 1 4 5 0xy     

và

(3 5) 2(2 5) 1 4 5 0xy     

.

B.

(3 5) 2(2 5) 1 4 5 0xy     

và

(3 5) 2(2 5) 1 4 5 0xy     

.

C.

(3 5) 2(2 5) 1 4 5 0xy     

và

(3 5) 2(2 5) 1 4 5 0xy     

.

D.

(3 5) 2(2 5) 1 4 5 0xy     

và

(3 5) 2(2 5) 1 4 5 0xy     

.

Lời giải

Chọn B

Cặp đường thẳng là phân giác của các góc tạo bởi

21

, 

là:

3 4 1 5( 2 4)

|3 4 1| | 2 4|

5

3 4 1 5( 2 4)

x y x y



    

   





     





3 4 1 5( 2 4)

x y x y



    





     





.

Câu 50: [0H3-1-3] Cho đường thẳng

d

:

2

13

xt

yt











và

2

điểm

 

(1 ; 2 , .)2 ;A B m

Định

m

để

A

và

B

nằm cùng phía đối với

.d

A.

13m 

. B.

13m

. C.

13m 

. D.

13m 

.

Lời giải

Chọn A

Phương trình tổng quát của đường thẳng

:3( 2) 1( 1) 0.d x y   

hay

:3x 7 0dy  

.

,AB

cùng phía với

(3 7)(3 7) 0 2( 13 ) 0 13.

A A B B

d x y x y m m            

Câu 51: [0H3-1-3] Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường

thẳng

:0xy  

và trục hoành

Ox

.

A.

(1 2) 0xy  

;

(1 2) 0xy  

. B.

(1 2) 0xy  

;

(1 2) 0xy  

.

C.

(1 2) 0xy  

;

(1 2) 0xy  

. D.

(1 2) 0xy  

;

(1 2) 0xy  

.

Lời giải

Chọn D

Gọi

( ; )M x y

là điểm thuộc đường phân giác

( , ) ( , ) (1 2) 0.

2

xy

d M d M Ox y x y



        

Câu 52: [0H3-1-3] Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi 2 đường

thẳng

1

: 2 3 0xy   

và

2

:2 3 0xy   

.

A.

30xy

và

30xy

. B.

30xy

và

3 6 0xy  

.

C.

30xy

và

3 6 0xy   

. D.

3 6 0xy  

và

3 6 0xy  

.

Lời giải

Chọn C

Gọi

( ; )M x y

là điểm thuộc đường phân giác

12

2 3 2 3

( , ) ( , ) .

55

3 6 0

2 3 (2 3) .

30

x y x y

d M d M

xy

x y x y

xy

   

     

   



       







Câu 53: [0H3-1-3] Cho đường thẳng

:3 4 5 0d x y  

và 2 điểm

   

.1;3 , 2;A B m

Định

m

để

A

và

B

nằm cùng phía đối với

.d

A.

0m 

. B.

1

4

m 

. C.

1m 

. D.

1

4

m 

.

Lời giải

Chọn B

,AB

nằm về hai phía của đường thẳng

1

(3 12 5)(6 4 5) 0 .

4

d m m        

Câu 54: [0H3-1-3] Cho

ABC

với

 

1;3 ,A

()2;4 ,B 

5()1;C 

và đường thẳng

:2 3 6 0.d x y  

Đường thẳng

d

cắt cạnh nào của

ABC

?

A. Cạnh

.AC

B. Không cạnh nào. C. Cạnh

.AB

D. Cạnh

.BC

Lời giải

Chọn B

Thay điểm

A

vào phương trình đường thẳng

d

ta được

2.

Thay điểm

B

vào phương trình đường thẳng

d

ta được

10.

Thay điểm

C

vào phương trình đường thẳng

d

ta được

11.

Câu 55: [0H3-1-3] Cho đường tròn

22

( ): 6 2 5 0C x y x y    

và đường thẳng

d

đi qua

điểm

( 4;2)A 

, cắt

()C

tại hai điểm

,MN

sao cho

A

là trung điểm của

MN

.

Phương trình của đường thẳng

d

là

A.

60xy  

. B.

7 3 34 0xy  

. C.

7 3 30 0xy  

. D.

7 35 0xy  

.

Hướng dẫn giải

Chọn A

 

C

có tâm

 

3;1 , 5IR

. Do đó,

2IA R A  

ở trong

 

C

.

A

là trung điểm của

 

1;1MN IA MN IA    

là vectơ pháp tuyến của

d

,

nên

d

có phương trình:

1( 4) 1( 2) 0 6 0x y x y        

.

Câu 56: [0H3-1-3] Cho tam giác

ABC

có

     

1;4 , 3;2 , 7;3 .A B C

Lập phương trình đường

trung tuyến

AM

của tam giác

ABC

.

A.

3 8 35 0.xy  

B.

3 8 35 0.xy  

C.

8 3 20 0.xy  

D.

8 3 4 0xy  

Lời giải

Chọn B

Vì

M

là trung điểm của

5

5;

2

BC M









Phương trình đường thẳng

14

: :3 8 35 0.

5

51

4

2

xy

AM AM x y



    



Câu 57: [0H3-1-3] Cho tam giác

ABC

có

   

1;1 , 0;()2 , 4;2 .A B C

Lập phương trình đường

trung tuyến của tam giác

ABC

kẻ từ

.B

A.

7 5 10 0xy   

B.

5 13 1 0.xy  

C.

7 7 14 0.xy  

D.

3 2 0.xy  

Lời giải

Chọn A

Gọi

M

là trung điểm của

53

;

22

AC M









Phương trình đường thẳng

02

: : 7 5 10 0

53

02

22

xy

BM BM x y



     



Câu 58: [0H3-1-3] Cho tam giác

ABC

có

   

1;1 , 0;()2 , 4;2 .A B C

Lập phương trình đường

trung tuyến của tam giác

ABC

kẻ từ

.A

A.

2 0.xy  

B.

2 3 0.xy  

C.

2 3 0.xy  

D.

0.xy

Lời giải

Chọn A

Gọi

M

là trung điểm của

 

2;0BC M

Phương trình đường thẳng

11

: : 2 0

1 2 1 0

xy

AM AM x y



    



Câu 59: [0H3-1-3] Cho tam giác

ABC

có

   

1;1 , 0;()2 , 4;2 .A B C

Lập phương trình đường

trung tuyến của tam giác

ABC

kẻ từ

.C

A.

5 7 6 0.xy  

B.

2 3 14 0.xy  

C.

3 7 26 0.xy  

D.

6 5 1 0.xy  

Lời giải

Chọn A

Gọi

M

là trung điểm của

11

;

22

AB M









Phương trình đường thẳng

42

: :5 7 6 0

11

42

22

xy

CM CM x y



    



Câu 60: [0H3-1-3] Viết phương trình đường thẳng qua

 

5; 1A 

và chắn trên hai nửa trục

dương

,Ox Oy

những đoạn bằng nhau.

A.

4xy

. B.

6xy

. C.

4xy

. D.

4xy  

.

Lời giải

Chọn C

Nhận thấy điểm

 

5; 1A 

thuộc 2 đường thẳng:

6xy

,

4xy

Với

6xy

: cho

0 6 6 0x y y       

(không thỏa đề bài)

Với

4xy

: cho

0 4 0xy   

; cho

0 4 0yx   

Cách khác:

Vì chắn hai nửa trục dương những đoạn bằng nhau nên đường thẳng đó song song

với đường thẳng

0y x x y    

, vậy có hai đáp án

,CD

.

Thay tọa độ

 

5; 1A 

vào thấy

C

thỏa mãn

Câu 61: [0H3-1-3] Tìm điểm

M

nằm trên

: 1 0xy   

và cách

 

1;3N 

một khoảng

bằng

5

.

A.

 

2; 1 .

B.

 

2; 1 .

C.

 

2;1 .

D.

 

2;1 .

Lời giải

Chọn A

 

2

22

( ;1 ): 5: 1 (2 ) 25 2 6 20 0M M t t MN t t t t            

 

2 2; 1

5 5;6

tM

  







   





Câu 62: [0H3-1-3] Tam giác

ABC

đều có

( 1; 3)A 

và đường cao

:5 3 15 0BB x y



  

. Tọa

độ đỉnh

C

là:

A.

128 36

;.

17 17

C







B.

128 36

;.

17 17

C









C.

128 36

;.

17 17

C









D.

128 36

;.

17 17

C









Lời giải

Chọn A

Vì tam giác

ABC

đều nên

A

và

C

đối xứng nhau qua

BB



Gọi

d

là đường thẳng qua

A

và

:3 5 12 0d BB d x y



    

H d BB



  

tọa độ điểm

H

là nghiệm của hệ:

5 3 15 0

128 15

;

3 5 12 0

34 34

xy

H

xy

  











  





Suy ra

128 36

;.

17 17

C







Câu 63: [0H3-1-3] Một điểm

M

di động có tọa độ:

2

4cos 3

cos2 1

xt

yt











. Tập hợp những điểm

M

là:

A. Đoạn thẳng có độ dài là

4

B. Đoạn thẳng có độ dài là

25

C. Đoạn thẳng có độ dài là

2

D. Hai nửa đường thẳng.

Lời giải.

Chọn B

Gọi

 

00

;M x y

, ta có

22

0

00

0

00

0

5

2cos2 5

4cos 3 4cos 2 5 cos2

2

1 cos2

cos2 1 cos2 1

1 cos2

x

xt

x t x t t

yt

y t y t

yt









     



  

  

   



   













Vì

1 cos2 1t  

nên ta có:

0

5

1 1 3 7

2

x



     

0

x

chạy trên một đoạn có độ dài bằng

4

00

1 1 1 0 2yx      

0

y

chạy trên một đoạn có độ dài bằng

2

Khi đó

 

00

;M x y

chạy trên một đoạn có độ dài

22

2 4 2 5.

Câu 64: [0H3-1-3] Gọi

H

là trực tâm tam giác

ABC

, phương trình của các cạnh và đường

cao tam giác là:

:7 4 0AB x y

;

:2 4 0BH x y  

;

: 2 0AH x y  

.

Phương trình đường cao

CH

của tam giác

ABC

là:

A.

7 2 0.xy  

B.

7 0.xy

C.

7 2 0.xy  

D.

7 2 0.xy  

Lời giải

Chọn D

CH AB

mà

:7 4 0AB x y

nên

CH

có phương trình

   

1 7 0

HH

x x y y   

trong đó

,

HH

xy

là nghiệm của hệ:

2 4 0 2

2 0 0

x y x

x y y

   







   



Từ đó

 

2; 0H

Vậy

   

1 2 7 0 0 7 2 0x y x y       

.

Ghi chú: Có thể đoán nhanh kết quả này như sau: Đường cao

CH AB

nên

CH

có

vectơ pháp tuyến

 

1; 7n 

Vậy chỉ chọn (D).

Câu 65: [0H3-1-3] Phương trình đường thẳng qua

 

5; 3M 

và cắt 2 trục

,x Ox y Oy



tại 2

điểm

A

và

B

sao cho

M

là trung điểm của

AB

là:

A.

3 5 30 0xy  

. B.

3 5 30 0xy  

. C.

5 3 34 0xy

. D.

3 5 30 0xy  

.

Lời giải

Chọn A

M

: trung điểm của

1

xy

AB

ab

  

. Đường thẳng này qua điểm

 

2; 3M 

nên

23

1

ab



. Ta có:

23

1 1 1 0

23

1 5 5 0

a b a x y

ab

a b a x y

ab



          







          





.

Ghi chú: Có thể giải nhanh như sau:

OAB

vuông cân nên cạnh

AB

song song

với phân giác góc phần tư thứ I, hoặc II. Do đó,

 

1; 1n 

, hay

 

1; 1

. Nhu thế

khả năng chọn là một trong hai câu

 

A

hoặc

 

B

. Thay tọa độ điểm

M

vào, loại

được

 

B

và chọn

 

A

.

Câu 66: [0H3-1-3] Viết phương trình đường thẳng qua

 

2; 3M 

và cắt hai trục

, Ox Oy

tại

A

và

B

sao cho tam giác

OAB

vuông cân.

A.

10

50

xy

  





  



. B.

10

50

xy

  





  



. C.

10xy  

. D.

50xy  

.

Lời giải

Chọn A

Phương trình đường thẳng

: 1

xy

AB

ab



. Đường thẳng này đi qua

 

2; 3M 

nên Ta có.

23

1

ab



:

23

1 1 1 0

23

1 5 5 0

a b a x y

ab

a b a x y

ab



          







           





.

Ghi chú có thể giải nhanh như sau:

OAB

vuông nên cạnh

AB

song song với phân

giác của góc phần tư thứ nhất hoặc thứ hai. Do đó

 

1; 1n 

hay

 

1; 1n 

. Như thế,

khả năng chọn một trong hai câu A hoặc B. Thay tọa độ

M

vào loại được đáp án B

và chọn đáp án A.

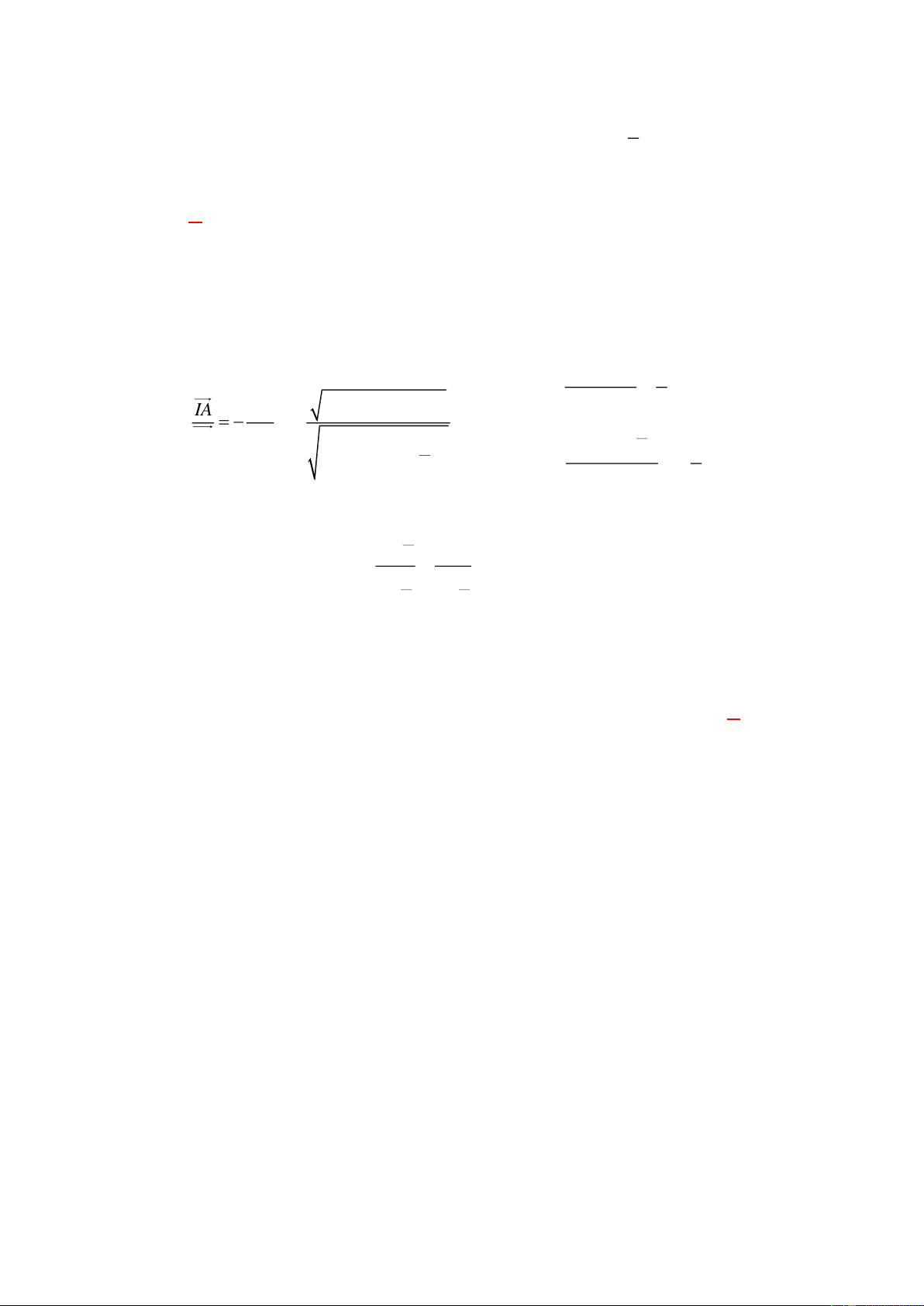
Câu 67: [0H3-1-3] Cho

ABC

với

 

4; 3A 

;

 

1; 1B

,

1

1;

2

C









. Phân giác trong của

góc

B

có phương trình:

A.

7 6 0xy  

. B.

7 6 0xy  

. C.

7 6 0xy  

. D.

7 6 0xy  

.

Lời giải

Chọn A

Gọi

I

là chân đường phân giác trong góc

B

, ta có:

   

 

22

2

4 2 1

2

1 2 3

1 4 1 3

2

1

32

1

4

2

1 1 1

2

33

x

IA BA

I

BC

IC

y











  



      





  









  





  





Phân giác trong là đường thẳng qua

,BI

nên có phương trình:

1

2

7 6 0

24

11

33

x

y

xy



    



.

Câu 68: [0H3-1-3] Cho hai đường thẳng

1

: 1 0d x y  

,

2

: 3 3 0d x y  

. Phương trình

đường thẳng

d

đối xứng với

1

d

qua đường thẳng

2

d

là:

A.

7 1 0xy  

. B.

7 1 0xy  

. C.

7 1 0xy  

. D.

7 1 0xy  

.

Lời giải

Chọn D

Giao điểm của

1

d

và

2

d

là nghiệm của hệ

 

1 0 1 0

0; 1

3 3 0 3 3 1

x y x y x

A

x y x y y

     

  

  

  

      

  

Lấy

 

1

1; 0Md

. Tìm

M



đối xứng

M

qua

2

d

Viết phương trình đường thẳng



đi qua

M

và vuông góc với

2

d

:

:3 3 0xy   

Gọi H là giao điểm của



và đường thẳng

2

d

. Tọa độ H là nghiệm của hệ

3

3 3 0 3 3

36

5

;

3 3 0 3 3 6

55

5

x

x y x y

H

x y x y

y







    







  

  



     













Ta có H là trung điểm của

MM



. Từ đó suy ra tọa độ

1 12

;

55

M









Viết phương trình đường thẳng

d

đi qua 2 điểm

A

và

M



: điểm đi qua

(0; 1)A

,

vectơ chỉ phương

17

' ;

55

AM











vectơ pháp tuyến

71

;

55

n









   

71

: 0 1 0 7 1 0

55

d x y x y       

Câu 69: [0H3-1-3] Cho hai đường thẳng

:2 3 0d x y  

và

: 3 2 0xy   

. Phương trình

đường thẳng

d



đối xứng với

d

qua



là:

A.

11 13 2 0xy  

. B.

11 2 13 0xy  

. C.

13 11 2 0xy  

. D.

11 2 13 0xy  

.

Lời giải

Chọn B

Giao điểm của

d

và



là nghiệm của hệ

 

2 3 0 2 3 1

1; 1

3 2 0 3 2 1

x y x y x

A

x y x y y

       

  

   

  

     

  

Lấy

 

0; 3Md

. Tìm

M



đối xứng

M

qua



Viết phương trình đường thẳng





đi qua

M

và vuông góc với



:

:3 3 0xy



   

Gọi

H

là giao điểm của





và đường thẳng



. Tọa độ

H

là nghiệm của hệ

7

3 2 0 3 2

79

10

;

3 3 0 3 3 9

10 10

10

x

x y x y

H

x y x y

y







    







   

  



     













Ta có

H

là trung điểm của

MM



. Từ đó suy ra tọa độ

76

;

55

M











Viết phương trình đường thẳng

d



đi qua 2 điểm

A

và

M



: điểm đi qua

( 1;1)A 

,

vectơ chỉ phương

2 11

;

55

AM













vectơ pháp tuyến

11 2

;

55

n









   

11 2

: 1 1 0 11 2 13 0

55

d x y x y



       

Câu 70: [0H3-1-3] Cho 4 điểm

 

1; 2A

,

 

1; 4B

,

 

2; 2C

,

 

3; 2D

. Tìm tọa độ giao điểm

của 2 đường thẳng

AB

và

CD

.

A.

 

1; 2

. B.

 

5; 5

. C.

 

3; 2

. D.

 

0; 1

.

Lời giải

Chọn A

Ta có

     

2; 2 2 1; 1 1; 1     

AB

AB n

. Đường thẳng

AB

đi qua

 

1; 2A

nhận

 

1; 1

AB

n

là véc tơ pháp tuyến có phương trình

: 1 2 0 30:     AB y A xyBx

.

Ta có

     

5; 0 5 1; 0 0; 1     

CD

CD n

. Đường thẳng

CD

đi qua

 

2; 2C

nhận

 

0; 1

CD

n

là véc tơ pháp tuyến có phương trình

 

: 0:0 22 2 0     xyCD y CD

. Tọa độ giao điểm của 2 đường thẳng

AB

và

CD

là nghiệm của hệ phương trình:

30

20

1

2

xy

y

x

y





















. Vậy độ giao điểm của

AB

và

CD

là

 

1; 2

.

Câu 71: [0H3-1-3] Cho điểm

 

1;2M

và đường thẳng

:2 5 0d x y  

. Toạ độ của điểm đối

xứng với điểm

M

qua

d

là:

A.

9 12

;

55







. B.

26

;

55









. C.

3

0;

5







. D.

3

;5

5









.

Lời giải.

Chọn A

+ Phương trình đường thẳng



qua

 

1;2M

và vuông góc với

d

là

: 2 3 0xy   

.

+ Tìm tọa độ giao điểm

I

của



và

d

là nghiệm của hệ phương trình:

7

2 5 0

7 11

5

;

2 3 0 11

55

5

x

xy

I

xy

y







  













  













.

+

 

;

MM

M x y





đối xứng với điểm

M

qua

d

I

là trung điểm

MM



.

79

2. 1

2

9 12

55

2

;

2 11 12

55

2. 2

55

2

MM

M

I

M I M

M M M I M

M

I

xx

x

x x x

M

y y y y y

y











  















   

  



  







  







.

Câu 72: [0H3-1-3] Cho

2

điểm

 

1; 4A 

,

 

3;2B

. Viết phương trình tổng quát đường trung

trực của đoạn thẳng

AB

.

A.

3 1 0xy  

. B.

3 1 0xy  

. C.

3 4 0xy

. D.

10xy  

.

Lời giải.

Chọn A

+ Giả sử



là đường trung trực của

AB



vuông góc với

AB

tại trung điểm

AB

.

+ Tọa độ trung điểm

M

của

AB

là :

 

2

2; 1

1

2

AB

M

AB

M

xx

x

M

yy

y

















  





.

+ Ta có

   

2;6 1;3AB 

 

1;3n AB



  

.



phương trình tổng quát đường trung trực



của đoạn thẳng

AB

là:

   

1 2 3 1 0 3 1 0x y x y       

.

Câu 73: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây vuông góc nhau?

1

: 19 0mx y   

và

   

2

: 1 1 20 0m x m y     

.

A. Mọi

m

. B.

2m

. C. Không có

m

. D.

1m

.

Lời giải.

Chọn C

Ta có

 

1

;1nm

,

 

2

1;m 1nm  

. Để

12

  

thì

12

.0nn

.

Ta có

 

2

12

. 1 1 1 0 n n m m m m m        



không có giá trị nào của

m

để

12

  

.

Câu 74: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây song song?

 

2

1

:2 1 3 0x m y    

và

2

: 100 0x my   

.

A.

2m

. B.

1m 

hoặc

2m

. C.

1m 

hoặc

0m 

. D.

1m 

.

Lời giải.

Chọn D

Ta có

 

2

1

2; 1nm

,

 

2

1;nm

và

12

3 100cc    

nên

 

1 2 1 2

0n kn k    

 

2

1

2

2 1 0

2; 1 1; 1

2

12

m

k

mm

m k m m

k tm

km m k







  



       

  



  







.

Câu 75: [0H3-1-3] Tìm

m

để

1

:3 2 6 0mx y   

và

 

2

: 2 2 6 0m x my    

song song

nhau:

A.

1m 

hoặc

1m 

. B.

1m 

. C.

1m 

và

1m 

. D. Không

có

m

.

Lời giải.

Chọn A

Ta có

 

1

3 ;2nm

,

 

2

2;2n m m

và

12

66cc   

nên

 

1 2 1 2

0n kn k    

 

22

2

1

3 2 2 2 0

2;2 3 ;2

1

22

1

m

k tm

m

km m m

m m k m

m

k m k m

m

k tm















  

   







      

































.

Câu 76: [0H3-1-3] Cho

4

điểm

 

3;1A 

,

 

9; 3B 

,

 

6;0C 

,

 

2;4D 

. Tìm tọa độ giao

điểm của

2

đường thẳng

AB

và

CD

.

A.

 

6; 1

. B.

 

9;3

. C.

 

9; 3

. D.

 

0;4

.

Lời giải.

Chọn C

Phương trình đương thẳng đi qua

 

3;1A 

,

 

9; 3B 

có dạng:

   

93

4 9 6 3 2 3 9 0

3 9 1 3

xy

x y x y



        

  

.

Phương trình đương thẳng đi qua

 

6;0C 

,

 

2;4D 

có dạng:

 

60

4 6 4 6 0

2 6 4 0

xy

x y x y



       

  

.

Tọa độ giao điểm của

2

đường thẳng

AB

và

CD

là nghiệm của hệ phương trình:

2 3 9 0 9

6 0 3

x y x

x y y

    







    



.

Câu 77: [0H3-1-3] Phần đường thẳng :

1

34

xy



nằm trong góc

xOy

có độ dài bằng bao

nhiêu?

A. 7. B.

5

. C. 12. D. 5.

Lời giải

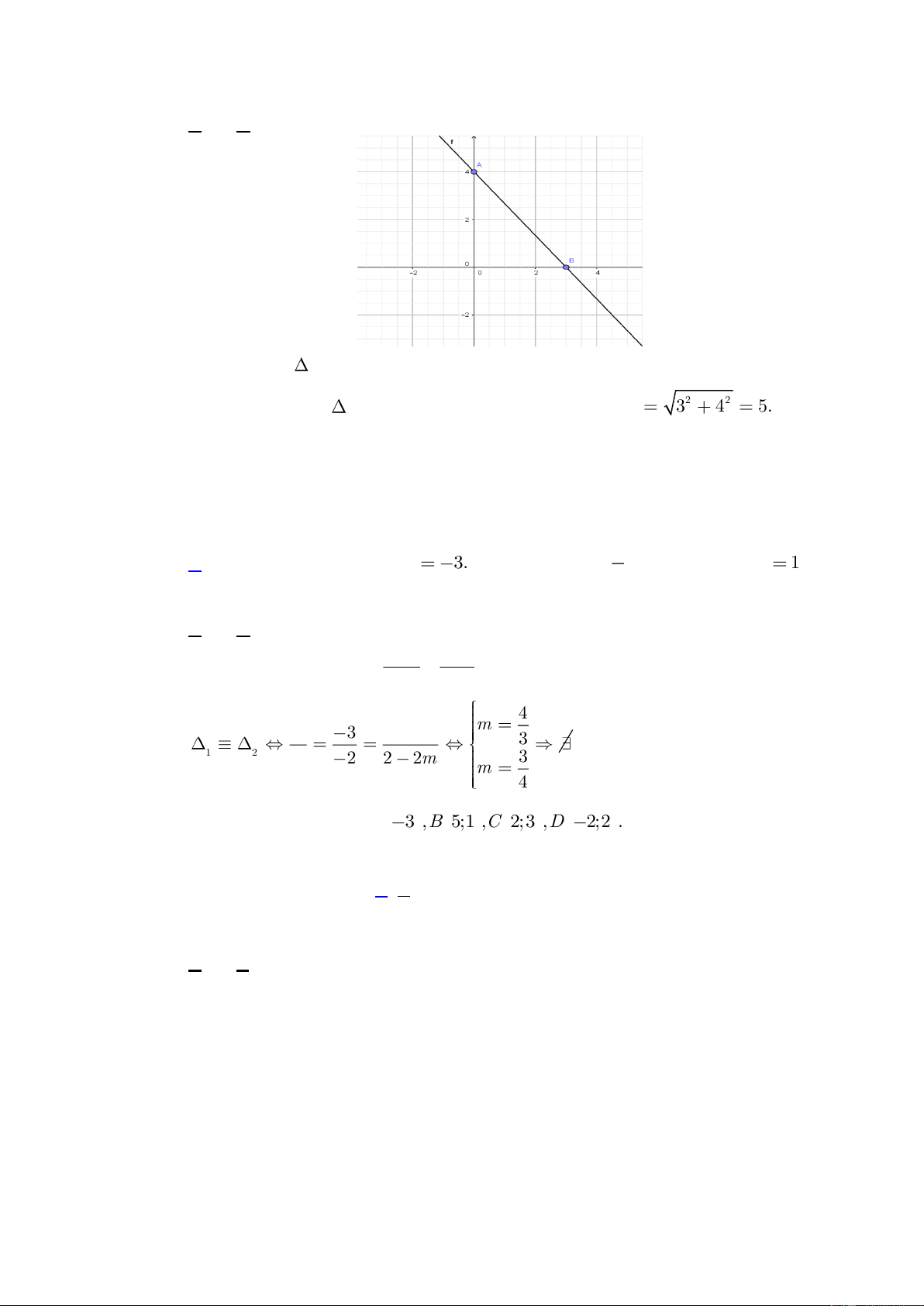
Chọn D

Đường thẳng cắt trục

,Ox Oy

lần lượt tại

3;0 , 0;4BA

(hình vẽ)

Phần đường thẳng nằm trong góc

xOy

là đoạn thẳng

22

3 4 5.AB

Câu 78: [0H3-1-3] Với giá trị nào của m hai đường thẳng sau đây trùng nhau?

1

:2 3 0x y m   

và

2

22

:

1

xt

y mt













A. Không có m. B.

3.m

C.

4

3

m 

. D.

1m

.

Lời giải

Chọn A

Ta có:

2

22

21

: 2 2 2 0.

1

2

xt

xy

mx y m

y mt

m







       







12

4

23

3

2 2 2

4

m

mm

m

.

Câu 79: [0H3-1-3] Cho 4 điểm

4; 3 , 5;1 , 2;3 , 2;2 .A B C D

Xác định vị trí tương đối

của hai đường thẳng AB và CD.

A. Trùng nhau. B. Cắt nhau. C. Song song. D. Vuông

góc nhau.

Lời giải

Chọn B

Phương trình tham số của đường thẳng

AB

là:

4

:.

34

xt

AB

yt







  



Phương trình tham số của đường thẳng

CD

là:

24

:.

3

xt

CD

yt















Giải hệ:

26 86

4 2 4 '

15 15

3 4 3 ' 14 14

15 15

tx

tt

ty







  







  

   







   





.

Câu 80: [0H3-1-3] Cho 4 điểm

 

1; 2A

,

 

1; 4B

,

 

2; 2C

,

 

3; 2D

. Tìm tọa độ giao

điểm của 2 đường thẳng

AB

và

CD

.

A.

 

1; 2

. B.

 

5; 5

. C.

 

3; 2

. D.

 

0; 1

.

Lời giải

Chọn A

Ta có

     

2; 2 2 1; 1 1; 1     

AB

AB n

. Đường thẳng

AB

đi qua

 

1; 2A

nhận

 

1; 1

AB

n

là véc tơ pháp tuyến có phương trình

: 1 2 0 30:     AB y A xyBx

.

Ta có

     

5; 0 5 1; 0 0; 1     

CD

CD n

. Đường thẳng

CD

đi qua

 

2; 2C

nhận

 

0; 1

CD

n

là véc tơ pháp tuyến có phương trình

 

: 0:0 22 2 0     xyCD y CD

. Tọa độ giao điểm của 2 đường thẳng

AB

và

CD

là nghiệm của hệ phương trình:

30

20

1

2

xy

y

x

y





















. Vậy độ giao điểm của

AB

và

CD

là

 

1; 2

.

Câu 81: [0H3-1-3] Cho điểm

 

1;2M

và đường thẳng

:2 5 0d x y  

. Toạ độ của điểm đối

xứng với điểm

M

qua

d

là:

A.

9 12

;

55







. B.

26

;

55









. C.

3

0;

5







. D.

3

;5

5









.

Lời giải.

Chọn A

+ Phương trình đường thẳng



qua

 

1;2M

và vuông góc với

d

là

: 2 3 0xy   

.

+ Tìm tọa độ giao điểm

I

của



và

d

là nghiệm của hệ phương trình:

7

2 5 0

7 11

5

;

2 3 0 11

55

5

x

xy

I

xy

y







  













  













.

+

 

;

MM

M x y





đối xứng với điểm

M

qua

d

I

là trung điểm

MM



.

79

2. 1

2

9 12

55

2

;

2 11 12

55

2. 2

55

2

MM

M

I

M I M

M M M I M

M

I

xx

x

x x x

M

y y y y y

y











  















   

  



  







  







.

Câu 82: [0H3-1-3] Cho

2

điểm

 

1; 4A 

,

 

3;2B

. Viết phương trình tổng quát đường trung

trực của đoạn thẳng

AB

.

A.

3 1 0xy  

. B.

3 1 0xy  

. C.

3 4 0xy

. D.

10xy  

.

Lời giải.

Chọn A

+ Giả sử



là đường trung trực của

AB



vuông góc với

AB

tại trung điểm

AB

.

+ Tọa độ trung điểm

M

của

AB

là :

 

2

2; 1

1

2

AB

M

AB

M

xx

x

M

yy

y

















  





.

+ Ta có

   

2;6 1;3AB 

 

1;3n AB



  

.



phương trình tổng quát đường trung trực



của đoạn thẳng

AB

là:

   

1 2 3 1 0 3 1 0x y x y       

.

Câu 83: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây vuông góc nhau?

1

: 19 0mx y   

và

   

2

: 1 1 20 0m x m y     

.

A. Mọi

m

. B.

2m 

. C. Không có

m

. D.

1m 

.

Lời giải.

Chọn C

Ta có

 

1

;1nm

,

 

2

1;m 1nm  

. Để

12

  

thì

12

.0nn 

.

Ta có

 

2

12

. 1 1 1 0 n n m m m m m        



không có giá trị nào của

m

để

12

  

.

Câu 84: [0H3-1-3] Với giá trị nào của

m

hai đường thẳng sau đây song song?

 

2

1

:2 1 3 0x m y    

và

2

: 100 0x my   

.

A.

2m 

. B.

1m 

hoặc

2m 

. C.

1m 

hoặc

0m 

. D.

1m 

.

Lời giải.

Chọn D

Ta có

 

2

1

2; 1nm

,

 

2

1;nm

và

12

3 100cc    

nên

 

1 2 1 2

0n kn k    

 

2

1

2

2 1 0

2; 1 1; 1

2

12

m

k

mm

m k m m

k tm

km m k







  



       

  



  







.

Câu 85: [0H3-1-3] Tìm

m

để

1

:3 2 6 0mx y   

và

 

2

: 2 2 6 0m x my    

song song

nhau:

A.

1m 

hoặc

1m 

. B.

1m 

. C.

1m 

và

1m 

. D. Không

có

m

.

Lời giải.

Chọn A

Ta có

 

1

3 ;2nm

,

 

2

2;2n m m

và

12

66cc   

nên

 

1 2 1 2

0n kn k    

 

22

2

1

3 2 2 2 0

2;2 3 ;2

1

22

1

m

k tm

m

km m m

m m k m

m

k m k m

m

k tm















  

   







      

































.

Câu 86: [0H3-1-3] Cho

4

điểm

 

3;1A 

,

 

9; 3B 

,

 

6;0C 

,

 

2;4D 

. Tìm tọa độ giao

điểm của

2

đường thẳng

AB

và

CD

.

A.

 

6; 1

. B.

 

9;3

. C.

 

9; 3

. D.

 

0;4

.

Lời giải.

Chọn C

Phương trình đương thẳng đi qua

 

3;1A 

,

 

9; 3B 

có dạng:

   

93

4 9 6 3 2 3 9 0

3 9 1 3

xy

x y x y



        

  

.

Phương trình đương thẳng đi qua

 

6;0C 

,

 

2;4D 

có dạng:

 

60

4 6 4 6 0

2 6 4 0

xy

x y x y



       

  

.

Tọa độ giao điểm của

2

đường thẳng

AB

và

CD

là nghiệm của hệ phương trình:

2 3 9 0 9

6 0 3

x y x

x y y

    







    



.

Câu 87: [0H3-1-3] Phần đường thẳng :

1

34

xy



nằm trong góc

xOy

có độ dài bằng bao

nhiêu?

A. 7. B.

5

. C. 12. D. 5.

Lời giải

Chọn D

Đường thẳng cắt trục

,Ox Oy

lần lượt tại

3;0 , 0;4BA

(hình vẽ)

Phần đường thẳng nằm trong góc

xOy

là đoạn thẳng

22

3 4 5.AB

Câu 88: [0H3-1-3] Với giá trị nào của m hai đường thẳng sau đây trùng nhau?

1

:2 3 0x y m   

và

2

22

:

1

xt

y mt













A. Không có m. B.

3.m

C.

4

3

m 

. D.

1m

.

Lời giải

Chọn A

Ta có:

2

22

21

: 2 2 2 0.

1

2

xt

xy

mx y m

y mt

m







       







12

4

23

3

2 2 2

4

m

mm

m

.

Câu 89: [0H3-1-3] Cho 4 điểm

4; 3 , 5;1 , 2;3 , 2;2 .A B C D

Xác định vị trí tương đối

của hai đường thẳng AB và CD.

A. Trùng nhau. B. Cắt nhau. C. Song song. D. Vuông

góc nhau.

Lời giải

Chọn B

Phương trình tham số của đường thẳng

AB

là:

4

:.

34

xt

AB

yt







  



Phương trình tham số của đường thẳng

CD

là:

24

:.

3

xt

CD

yt















Giải hệ:

26 86

4 2 4 '

15 15

3 4 3 ' 14 14

15 15

tx

tt

ty







  







  

   







   





.

Câu 90: [0H3-1-3] Cho điểm

(0;1)A

và đường thẳng

12

:

xt

d

yt











. Tìm một điểm

M

trên

d

và cách

A

một khoảng bằng

10

.

A.

 

2; 3

. B.

 

3; 2

. C.

 

3; 2

. D.

 

3; 2

.

Lời giải

Chọn B

(1 2 ; )M d M t t  

 

2

22

2 3; 2

10 1 2 ( 1) 10 5 6 8 0

4 13 4

;

5 5 5

tM

MA t t t t

tM

  





          





  









.

Câu 91: [0H3-1-3] Trong mặt phẳng tọa độ

Oxy

, cho đường thẳng



có phương trình

1

34

xy



. Gọi

,A

B

là các giao điểm của đường thẳng



với các trục tọa độ. Độ dài

của đoạn thẳng

AB

bằng:

A.

7

. B.

5

. C.

12

. D.

5

.

Lời giải

Chọn D

Đường thẳng đi qua

 

0; 4A

,

 

3; 0B

.

Phần đường thẳng nằm trong góc

xOy

có độ dài là

5AB 

.

Câu 92: [0H3-1-3] Cho hai đường thẳng

1

5

:

1

3

xt

y

d

t











,

2

: – 2 1 0d x y 

. Tìm mệnh đề

đúng:

A.

12

// dd

. B.

2

// d Ox

. C.

2

1

0;

2

d Oy A









D.

12

13

;

88

d d B









.

Lời giải

Chọn C

+

 

1

1; 3u 

,

 

2

1; 2n 

nên phương án

A

,

B

loại.

+

2

d Oy

:

1

0

2

xy  

. Phương án

C

đúng.

+ Kiểm tra phương án D: Thế tọa độ

B

vào PT

2

d

, không thỏa mãn.

Câu 93: [0H3-1-3] Xác định

a

để hai đường thẳng

1

: 3 – 4 0d ax y

và

2

1

:

33

xt

d

yt

  









cắt

nhau tại một điểm nằm trên trục hoành.

A.

1a 

. B.

–1a 

. C.

2a 

. D.

–2a 

.

Lời giải

Chọn D

+

3 3 0 1tt    

.

+

   

. 1 3 3 3 4 0 2 4 0 2a t t a a           

.

Câu 94: [0H3-1-3] Phần đường thẳng

10xy  

nằm trong góc

xOy

có độ dài bằng bao

nhiêu ?

A.

1

. B.

2

. C.

2

. D.

5

.

Lời giải

Chọn B

Do tam giác

ABC

vuông tại

O

.

Suy ra

21

1 1 2.AB   

Câu 95: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng sau song song nhau:

 

1

81

:

10

x m t

d

yt

   







và

2

: 2 14 0d mx y  

.

A.

1 và 2mm  

. B.

1m 

. C.

2m 

. D.

m

.

Lời giải

Chọn A

12

//dd

hệ phương trình:

 

8 ( 1) 1

10 2

2 14 0 3

x m t

yt

mx y

   









  



vô nghiệm

Thay

 

1,

 

2

vào

 

3

ta được:

   

8 ( 1) 2 10 14 0m m t t     

 

2

2 8 6 4m m t m    

Phương trình

 

4

vô nghiệm khi và chỉ khi:

2

1

20

2

8 6 0

m

mm

m





  

















.

Câu 96: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

22

:

1

xt

d

y mt











và

2

:4 3 0d x y m  

trùng nhau?

A.

3m 

. B.

1m 

. C.

4

3

m 

. D.

m

.

Lời giải

Chọn D

12

dd

hệ phương trình

 

2 2 1

1 2

4 3 0 3

xt

y mt

x y m

  









  



có nghiệm tùy ý.

Thay

 

1,

 

2

vào

 

3

ta được:

   

4 2 2 3 1 0t mt m    

   

3 8 5 4m t m   

Phương trình

 

4

có nghiệm tùy ý khi và chỉ khi:

3 8 0

50

m





 







.

Câu 97: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:(2 1) 10 0d m x my   

và

2

:3 2 6 0d x y  

vuông góc nhau?

A.

3

2

m 

. B.

3

8

m 

. C.

3

8

m 

. D.

m

.

Lời giải

Chọn C

Đường thẳng

1

:(2 1) 10 0d m x my   

có

 

1

2 1;vtpt n m m

.

Đường thẳng

2

:3 2 6 0d x y  

có

 

2

3;2vtpt n 

.

       

1 2 1 2

3

. 0 2 1 . 3 . 2 0

8

d d n n m m m        

.

Câu 98: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:2 3 10 0d x y  

và

2

23

:

14

xt

d

y mt











vuông góc nhau?

A.

1

2

m 

. B.

9

8

m 

. C.

9

8

m 

. D.

m

.

Lời giải

Chọn C

Đường thẳng

1

:2 3 10 0d x y  

có

 

1

2; 3vtpt n 

.

Đường thẳng

2

23

:

14

xt

d

y mt











có

 

2

4 ; 3vtpt n m

.

       

1 2 1 2

9

. 0 2 . 4 3 . 3 0

8

d d n n m m          

.

Câu 99: [0H3-1-3] Với giá trị nào của

m

thì hai đường thẳng

1

:4 3 3 0d x y m  

và

2

12

:

4

xt

d

y mt











trùng nhau?

A.

8

3

m 

. B.

8

3

m 

. C.

4

3

m 

. D.

4

3

m 

.

Lời giải

Chọn B

12

dd

hệ phương trình

 

1 2 1

4 2

4 3 3 0 3

xt

y mt

x y m

  









  



có nghiệm tùy ý.

Thay

 

1,

 

2

vào

 

3

ta được:

   

4 1 2 3 4 3 0t mt m    

   

3 8 3 8 4m t m   

Phương trình

 

4

có nghiệm tùy ý khi và chỉ khi:

8

3 8 0

3

mm   

.

Câu 100: [0H3-1-3] Nếu ba đường thẳng

1

: 2 – 4 0d x y

;

2

:5 – 2 3 0d x y 

;

3

: 3 – 2 0d mx y

đồng qui thì

m

có giá trị là:

A.

12

5

. B.

12

5



. C.

12

. D.

12

.

Lời giải

Chọn D

Tọa độ giao điểm của hai đường thẳng

1

d

và

2

d

là nghiệm của hệ phương trình:

5

2 – 4 0

9

5 – 2 3 0 26

9

x

xy

y





























.Suy ra

1

d

,

2

d

cắt nhau tại

5 26

( ; )

99

M

.

Vì

1

d

,

2

d

,

3

d

đồng quy nên

3

Md

ta có:

5 26

. 3. 2 0 12.

99

mm     

Câu 101: [0H3-1-3]Cho hai điểm

   

–2;0 , 1;4AB

và đường thẳng

:

2

xt

d

yt











. Tìm giao

điểm của đường thẳng

và d AB

.

A.

 

2;0

. B.

 

–2;0

. C.

 

0;2

. D.

 

0; – 2

.

Hướng dẫn giải

Chọn B

Đường thẳng

AB

đi qua điểm

 

–2;0A

và có

 

3;4vtcp AB 

,

 

4; 3vtpt n 

Vậy phương trình tổng quát của đường thẳng

:4 3 8 0AB x y  

.

Đường thẳng

d

. đi qua điểm

 

0;2M

và có

 

1; 1vtcp u   

,

 

1; 1vtpt p 

Vậy phương trình tổng quát của đường thẳng

: 2 0d x y

.

Gọi

K

là giao điểm của đường thẳng

và d AB

.

Tọa độ điểm

K

thỏa hệ phương trình

 

4 3 8 0 2

2;0

2 0 0

x y x

KA

x y y

    



   



   



Câu 102: [0H3-1-3]Hai đường thẳng

2 4 1 0 xy  

và

1

3 ( 1)

x at

y a t

  





  



vuông góc với nhau

thì giá trị của

a

là:

A.

–2a 

B.

2a 

C.

–1a 

D.

1a 

Hướng dẫn giải.

Chọn D

Ta có:

1

:2x 4y 1 0    

có vectơ chỉ pháp tuyến

 

1

2; 4n 

suy ra vectơ chỉ phương là

 

1

2;1u 

2

1

:

3 ( 1)

x at

y a t

  







  



có vectơ chỉ phương là

 

2

;1u a a  

.

Hai đường thẳng vuông góc với nhau

 

12

. 0 2 1 1 0 1.u u a a a        

Câu 103: [0H3-1-3]Xác định a để hai đường thẳng

1

: 3 – 4 0 d ax y

và

2

1

:

33

xt

d

yt

  









cắt

nhau tại một điểm nằm trên trục hoành.

A.

1a 

B.

–1a 

C.

2a 

D.

–2a 

Hướng dẫn giải.

Chọn D

Cách 1: Gọi

 

1 2 2

1 ;3 3 , 3 3 0 –1M d d M t t d M Ox t t            

Suy ra

 

2;0M 

.

1

Md

, thay tọa độ của M vào phương trình

1

d

ta được

 

2 3.0 – 4 0 –2aa    

. Vậy

2a 

là giá trị cần tìm.

Cách 2:Thay

, xy

từ phương trình

2

d

vào

1

d

ta được:

     

5

1 3 3 3 – 4 0 9 5

9

a

a t t a t a t

a



          



Gọi

12

14 6 12

;

99

a

M d d M

aa





  







. Theo đề

6 12 0 2M Ox a a      

.

Vậy

–2a 

là giá trị cần tìm.

Câu 104: [0H3-1-3]Định

m

sao chohai đường thẳng

 

1

:(2 1) 10 0m x my    

và

 

2

:3 2 6 0xy   

vuông góc với nhau.

A.

0m 

. B. Không

m

nào. C.

2m

. D.

3

8

m 

.

Hướng dẫn giải:

Chọn D

1



có vectơ pháp tuyến là

 

1

2 1;n m m

,

2



có vectơ pháp tuyến là

 

2

3;2n 

.

Ta có:

 

1 2 1 2

3

. 0 3 2 1 2 0

8

n n m m m          

.

Câu 105: [0H3-1-3]Đường thẳng

 

:5 3 15xy  

tạo với các trục tọa độ một tam giác có

diện tích bằng bao nhiêu?

A.

3

. B.

15

. C.

15

2

. D.

5

.

Hướng dẫn giải:

Chọn C

Gọi

A

là giao điểm của



và

Ox

,

B

là giao điểm của



và

Oy

.

Ta có:

 

3;0A

,

 

0;5B

3OA

,

5OB 

15

2

OAB

S





.

Câu 106: [0H3-1-3] Cho 4 điểm

 

4; 3A 

,

 

5;1B

,

 

2;3C

,

 

2; 2D 

. Xác định vị trí

tương đối của hai đường thẳng

AB

và

CD

.

A. Trùng nhau. B. Cắt nhau. C. Song song. D. Vuông

góc nhau.

Hướng dẫn giải

Chọn B

Phương trình tham số của đường thẳng

AB

là:

4

:.

34

xt

AB

yt







  



Phương trình tham số của đường thẳng

CD

là:

24

:.

3

xt

CD

yt















Giải hệ:

26 86

4 2 4 '

15 15

3 4 3 ' 14 14

15 15

tx

tt

ty







  







  

   







   





.

Câu 107: [0H3-1-3] Xác định vị trí tương đối của hai đường thẳng:

1

25

:

36

xt

yt













và

2

75

:

36

xt

yt













  



.

A. Trùng nhau. B. Vuông góc nhau.

C. Cắt nhau nhưng không vuông góc. D. Song song nhau.

Hướng dẫn giải

Chọn C

Ta có

 

1

5; 6u 

là vectơ chỉ phương của đường thẳng

1



.

Và

 

2

5;6u 

là vectơ chỉ phương của đường thẳng

2



.

Vì

12

. 11uu 

nên

1



không vuông góc với

2



.

Giải hệ

2 5 7 5 1

3 6 3 6 0

t t t



   









    



.

Vậy

1



và

2



cắt nhau tại điểm

 

7; 3I 

nhưng không vuông góc với nhau.

Câu 108: [0H3-1-3] Cho 4 điểm

(0;1)A

,

(2;1)B

,

(0;1)C

,

(3;1)D

. Xác định vị trí tương đối

của hai đường thẳng

AB

và

CD

.

A. Song song. B. Trùng nhau. C. Cắt nhau. D. Vuông

góc nhau.

Hướng dẫn giải:

Chọn B

Biểu diễn bốn điểm lên hệ trục tọa độ: cùng nằm trên một đường thẳng.

Hay nhìn nhanh: bốn điểm có cùng tung độ, vì vậy cùng nằm trên đường thẳng

1y 

.

Câu 109: [0H3-1-3] Cho 4 điểm

       

1;2 , 4;0 , 1; 3 , 7; 7A B C D

. Xác định vị trí tương

đối của hai đường thẳng

AB

và

CD

.

A. Trùng nhau. B. Song song.

C. Cắt nhau nhưng không vuông góc. D. Vuông góc nhau.

Hướng dẫn giải

Chọn B

   

3; 2 , 6; 4AB CD   

. Ta có:

32

64







. Suy ra

AB

và

CD

song song.

Câu 110: [0H3-1-3] Định

m

để 2 đường thẳng sau đây vuông góc:

1

:

2 3 4 0xy  

và

2

:

23

14

xt

y mt











A.

1

.

2

m 

B.

9

.

8

m 

C.

1

.

2

m 

D.

9

.

8

m 

Hướng dẫn giải

Chọn D

Đường thẳng

1



có vtpt

 

1

2; 3n 

,

2



có vtcp

   

22

3; 4 4 ;3u m vtpt n m     

.

Để

1 2 1 2

9

. 0 .

8

n n m       

Câu 111: [0H3-1-3] Cho 4 điểm

       

0;2 , 1;1 , 3;5 , 3; 1A B C D  

. Xác định vị trí tương

đối của hai đường thẳng

AB

và

CD

.

A. Song song. B. Vuông góc nhau. C. Cắt nhau. D. Trùng

nhau.

Hướng dẫn giải

Chọn D

Câu 112: [0H3-1-3] Cho

4

điểm

0 ; 2 , 1 ; 0 , 0 ; 4( ) ( ) ( ), ); ( 2 0A B C D   

. Tìm tọa độ

giao điểm của

2

đường thẳng

AB

và

CD

A.

(1 ; )4

. B.

31

;.

22









C.

()2 ; 2

. D. Không có giao điểm.

Hướng dẫn giải

Chọn D

AB

có vectơ chỉ phương là

 

1;2AB 

và

CD

có vectơ chỉ phương là

 

2;4CD 

.

Ta có:

 

1;2AB 

và

 

2;4CD 

cùng phương nên

AB

và

CD

không có giao

điểm.

Câu 113: [0H3-1-3] Tìm điểm M trên trục

Ox

sao cho nó cách đều hai đường thẳng:

1

:3 2 6 0d x y  

và

3

:3 2 6 0d x y  

?

A.

 

1;0 .

B.

 

0;0 .

C.

 

0; 2 .

D.

 

2;0 .

Lời giải

Chọn B.

Gọi

   

;0 3 6 3 6 2 0 0;0M a a a M      

Câu 114: [0H3-1-3] Cho hai điểm

1(3; )A 

và

 

0;3 .B

Tìm tọa độ điểm

M

trên trục

Ox

sao

cho khoảng cách từ

M

đến đường thẳng

AB

bằng

AB

?

A.

 

34

;0 ; 4;0 .

9









B.

 

2;0

và

 

1;0 .

C.

 

4;0 .

D.

( 13;0).

Lời giải

Chọn A.

Ta gọi

 

;0Ma

, pt

:4 3 9 0, 5AB x y AB   

   

12

34

49

34

, 5 5 ;0 , 4;0

9

59

4

a

d M AB M M

a











      











Câu 115: [0H3-1-3] Cho hai điểm

 

1;2A

và

 

4;6 .B

Tìm tọa độ điểm

M

trên trục

Oy

sao

cho diện tích tam giác

MAB

bằng

1

?

A.

13

0;

4







và

9

0; .

4







B.

 

1;0 .

C.

 

4;0 .

D.

 

0;2 .

Lời giải

Chọn A.

5AB 

, Gọi

 

0;Mm

Vì diện tích tam giác

MAB

bằng

 

2

1 , ,

5

d M AB

13

4 11

2

4

:3 4 11 0

9

55

4

m

AB x y

m









     









Câu 116: [0H3-1-3] Cho hai điểm

1(2; )A 

và

 

0;100B

,

4(2; )C 

.Tính diện tích tam giác

ABC

?

A.

3.

B.

3

.

2

C.

3

.

2

D.

147.

Lời giải

Chọn A.

Phương trình

   

1

: 2 0, 3, , 2 . , 3

2

ABC

AC x AC d B AC S AC d B AC



      

.

Câu 117: [0H3-1-3] Cho hai điểm

 

2;3A

và

 

1;4 .B

Đường thẳng nào sau đây cách đều hai

điểm

,AB

?

A.

20xy

. B.

100 0xy  

. C.

20xy

. D.

2 10 0xy  

.

Lời giải

Chọn A.

Cách 1: Gọi

d

là đường thẳng cách đều 2 điểm

,AB

, ta có:

         

2 2 2 2

22

; 2 3 1 4

2 2 4 0 2 0

M x y d MA MB x y x y

x y x y

          

       

Cách 2: Gọi I là trung điểm của đoạn AB

37

;

22

I









Gọi

d

là đường thẳng cách đều 2 điểm

,AB

d

là đường trung trực của đoạn AB

d

đi qua

37

;

22

I







và nhận

 

1;1AB 

làm VTPT

37

: 0 : 2 0

22

d x y d x y

   

          

   

   

Câu 118: [0H3-1-3] Cho ba điểm

   

0;1 , 12;5AB

và

()3;0 .C 

Đường thẳng nào sau đây cách

đều ba điểm

,,A B C

A.

3 4 0xy  

. B.

10 0xy   

. C.

0xy

. D.

5 1 0xy  

.

Lời giải

Chọn A.

Cách 1: Viết phương trình đường thẳng

d

qua 3 điểm thẳng hàng

,,A B C

. Nếu

đường thẳng cách đều 3 điểm

,,A B C

thì nó phải song song hoặc trùng với

d

Gọi

d

là đường thẳng qua 2 điểm

,AC

: 1 3 3 0

31

xy

d x y      



Kiểm tra các phương án, ta thấy phương án A thỏa.

Cách 2:

Tính khoảng cách từ 3 điểm đến lần lượt các đường trong các phương án A, B, C, D

.

Câu 119: [0H3-1-3] Khoảng cách giữa hai đường thẳng song song

1

:6 – 8 101 0dxy

và

2

:3 – 4 0d x y

là:

A.

10,1

. B.

1,01

. C.

101

. D.

101

.

Lời giải

Chọn A.

Kí hiệu

: 6 – 8 101 0xy  

và

:3 – 4 0d x y 

Lấy điểm

 

0;0 :3 4 0O d x y  

   

 

2

101

; ; 10,1

10

68

d d d O



     



Câu 120: [0H3-1-3] Khoảng cách giữa hai đường thẳng song song

7 3 0xy  

và

7 12 0 xy  

là:

A.

32

2

. B.

15

. C.

9

. D.

9

50

.

Lời giải

Chọn A.

Kí hiệu

:7 3 0d x y  

và

:7 12 0 xy   

Lấy điểm

 

70;3 30: xAdy  

   

22

3 12

15 3 2

;;

2

50

71

d d d A



     



Câu 121: [0H3-1-3] Phương trình của đường thẳng qua

 

2;5P

và cách

 

5;1Q

một khoảng

bằng

3

là:

A.

7 24 –134 0xy

. B.

2 x 

C.

2, 7 24 –134 0x x y  

. D.

3 4 5 0xy  

Lời giải

Chọn C.



qua

 

: ( 2) ( 5) 0 -2 -5; 025 a x b y ax by a bP         

 

22

5 2 5

, 3 3 3 4 3

a b a b

d Q a b a b

ab

  

       



2

0

24 7 0

24

7

b

ab b

ba







    







.

Với

0b 

, chọn

1 : 2ax   

Với

24

7

ba

, chọn

7 24 :7 24 134 0a b x y      

Câu 122: [0H3-1-3] Cho đường thẳng

:3 – 4 2 0.d x y 

Có đường thẳng

1

d

và

2

d

cùng song

song với

d

và cách

d

một khoảng bằng

1.

Hai đường thẳng đó có phương trình là:

A.

3 – 4 – 7 0; 3 – 4 3 0x y x y  

. B.

3 – 4 7 0; 3 – 4 – 3 0x y x y  

C.

3 – 4 4 0; 3 – 4 3 0x y x y   

. D.

3 – 4 – 7 0; 3 – 4 7 0x y x y  

.

Lời giải

Chọn B.

Giả sử đường thẳng



song song với

:3 – 4 2 0d x y 

có phương trình là

:3 4 0x y C   

Lấy điểm

 

2; 1Md  

Do

 

2

7

3.( 2) 4( 1)

, 1 1 2 5

3

34

C

d d C

C



   



       









Câu 123: [0H3-1.26-3] Hai cạnh của hình chữ nhật nằm trên hai đường thẳng

12

: 4 – 3 5 0, :3 4 – 5 0d x y d x y   

, đỉnh

 

2; 1A

. Diện tích của hình chữ nhật là:

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn B.

Do điểm

A

không thuộc hai đường thẳng trên.

Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ

 

2; 1A

đến hai đường

thẳng trên, do đó diện tích hình chữ nhật bằng

2 2 2 2

4.2 3.1 5 3.2 4.1 5

.2

4 3 4 3

S

   





.

Câu 124: [0H3-1-3] Khoảng cách giữa hai đường thẳng song song với đường thẳng



:

23

5

xt

yt











và cách

 

1;1A

một khoảng

35

là:

0x bx c  

. Thế thì

bc

bằng

A. 14 hoặc –16. B. 16 hoặc –14. C. 10 hoặc –20. D. 10.

Hướng dẫn:

Chọn A.

Gọi

:0d x by c  

Vì đường thẳng

23

// :

5













xt

d

yt

nên

2b 

Phương trình của

: 2 0d x y c  

.

Theo đề ra ta có:

 

14

; 3 5 1 15

16

c

d A d c

c





    







Câu 125: [0H3-1-3] Cho đường thẳng

2: – 2 0xyd 

. Phương trình các đường thẳng song

song với

d

và cách

d

một đoạn bằng

5

là

A.

– 2 – 3 0; – 2 7 0.x y x y  

B.

– 2 3 0; – 2 7 0.x y x y   

C.

– 2 – 3 0; – 2 7 0.x y x y  

D.

– 2 3 0; – 2 7 0.x y x y   

.

Hướng dẫn:

Chọn A.

Gọi



là đường thẳng song song với

2: – 2 0xyd 

: 2 0; 2x y c c     

Theo đề ra ta có

 

7

; 5 2 5

3

c

d d c

c





     







Câu 126: [0H3-1-3] Phương trình các đường thẳng qua

 

2;7M

và cách điểm

 

1; 2N

một

khoảng bằng 1 là

A.

12 – 5 –11 0; – 2 0.x y x

B.

12 5 –11 0; 2 0.x y x   

C.

12 – 5 11 0; – 2 0.x y x  

D.

12 5 11 0; 1 0.x y x    

Hướng dẫn:

Chọn C.

Sử dụng phương pháp loại trừ:

Dễ thấy điểm

 

2;7M

không thuộc hai đường thẳng

2 0; 1 0xx   

nên loại

,BD

.

Điểm

 

2;7M

không thuộc đường thẳng

12 5 11 0xy  

nên loại

A

.

Câu 127: [0H3-1-3] (trùng câu 3064) Cho đường thẳng

:3 – 4 2 0.d x y 

Có đường thẳng

1

d

và

2

d

cùng song song với

d

và cách

d

một khoảng bằng 1. Hai đường thẳng đó

có phương trình là

A.

3 – 4 – 7 0; 3 – 4 3 0.x y x y  

B.

3 – 4 +7 0; 3 – 4 3 0.x y x y  

C.

3 – 4 +4 0; 3 – 4 3 0.x y x y  

D.

3 – 4 +3 0; 3 – 4 13 0.x y x y  

Hướng dẫn:

Chọn B.

Gọi

:3 4 0; 2x y C C    

Theo đề ra ta có:

3

( ; ) 1 2 5

7

C

d d C

C





     







Câu 128: [0H3-1-3] Cho tam giác

ABC

có

     

2;–2 , 1; –1 , 5;2 .A B C

Độ dài đường cao

AH

của tam giác

ABC

là

A.

3

5

B.

7

5

C.

9

5

D.

1

5

Hướng dẫn:

Chọn B.

Phương trình đường thẳng

:3 4 7 0.BC x y  

Độ dài đường cao

 

7

;

5

AH d A BC

Câu 129: [0H3-1-3] Tìm tọa độ điểm

M

nằm trên trục

Ox

và cách đều

2

đường thẳng

1

:3 2 6 0xy   

và

2

:3 2 3 0xy   

A.

(0 ; 2)

. B.

1

; 0

2







. C.

 

1 ; 0

. D.

(2 ; 0).

Lời giải

Chọn B.

Ta có:

 

;0M Ox M x

12

3 6 3 3( )

3 6 3 3

( ; ) ( ; )

1

3 6 3 3

13 13

2

x x vn

xx

d M d M

x x x

  







     



     



.Vậy

1

;0

2

M







.

Câu 130: [0H3-1-3] Tính diện tích

ABC

biết

 

2; 1 , 1; 2 , ( ) (2; )4A B C

:

A.

3

. B.

3

.

37

C.

3

. D.

3

2

.

Lời giải

Chọn D.

Đường thẳng đi qua

2

điểm

1(2; )A 

và

 

1 ; 2B

có vectơ chỉ phương là

 

1;3AB 

suy ra tọa độ vectơ pháp tuyến là

(3;1)

.

Suy ra

AB

:

   

3 2 1 1 0 3 5 0x y x y       

22

3.2 4 5

3

( ; )

10

31

d C AB







;

10AB 

.

Diện tích

ABC

:

 

13

. ; .

22

S d C AB AB

.

Câu 131: [0H3-1-3] Cho đường thẳng đi qua

2

điểm

 

3; 1 , () 0; 3AB

, tìm tọa độ điểm

M

thuộc

Ox

sao cho khoảng cách từ

M

tới đường thẳng

AB

bằng

1

.

A.

 

1; 0

và

 

3,5; 0

. B.

( 13; 0).

C.

 

4; 0

D.

 

2; 0

.

Lời giải

Chọn A.

Đường thẳng đi qua

2

điểm

1(3; )A 

và

 

0;3B

có vectơ chỉ phương là

 

3;4AB 

suy ra tọa độ vectơ pháp tuyến là

(4;3)

.

Suy ra:

AB

:

   

4 3 3 1 0 4 3 9 0x y x y       

 

;0M Ox M x

 

22

77

;0

4 9 5

49

22

( ; ) 1 1

4 9 5

43

1 1;0

xM

x

d M AB

x

xM

















   





  











.

Câu 132: [0H3-1-3] Cho đường thẳng đi qua

2

điểm

 

(3;0 , 0; 4 ,)AB

tìm tọa độ điểm

M

thuộc

Oy

sao cho diện tích

MAB

bằng

6

.

A.

 

0;1

B.

 

0;0

và

(0; 8 .)

C.

 

1;0

. D.

 

0;8

.

Lời giải

Chọn B.

Ta có

 

3; 4 5ABAB  

,

Đường thẳng

AB

đi qua

 

3;0 , 4()0;AB

nên có phương trình

4 3 12 0xy  

.

M

thuộc

Oy

nên

   

3 12

0; ; ,

5

m

M m d M AB





0

6 3 12 12

8

MAB

m

Sm

m







    







.

Vậy tọa độ của

M

là

 

0;0

và

(0; 8 .)

Câu 133: [0H3-1-3] (trùng câu 3055) Cho

2

điểm

   

2;3 , 1;4 .AB

Đường thẳng nào sau

đây cách đều

2

điểm

,AB

?

A.

10xy  

B.

20xy

C.

2 2 10 0xy  

D.

100 0xy  

Lời giải

Chọn A.

Ta có đường thẳng cách đều hai điểm

,AB

là đường thẳng đi qua trung điểm

37

;

22

I







của

AB

hoặc là đường thẳng song song với

: 5 0.AB x y  

Ta chọn

A

.

Câu 134: [0H3-1-3] Khoảng cách giữa

2

đường thẳng

1

:7 3 0xy   

và

2

:7 12 0xy   

là

A.

9

50

. B. 9. C.

32

2

. D. 15.

Lời giải

Chọn C.

Ta có

 

1

0;3M 

và

12

//

nên:

   

1 2 2

32

,,

2

d d M    

.

Câu 135: [0H3-1-3] Cho đường thẳng đi qua 2 điểm

   

1;2 , 4;6 ,AB

tìm tọa độ điểm

M

thuộc

Oy

sao cho diện tích

MAB

bằng

1

.

A.

 

0;1

. B.

 

0;0

và

4

0;

3







.

C.

 

0;2

. D.

 

1;0

.

Lời giải

Chọn B

     

3;4 5; 0; ; :4 3 2 0

M

AB AB M y AB x y     

 

22

0

| 4.0 3. 2|

1 2 2

. , 1 , .

4

2 5 5

43

3

M

MAB

M

y

S AB d M AB d M AB

y











      









Câu 136: [0H3-1-3] Tính diện tích

ABC

biết

   

3 ; 4 , 1 ; 5 , 3 ; ( 1)A B C

:

A.

10

. B.

5

. C.

26

. D.

25

.

Lời giải

Chọn B

Ta có

(0;5) (1;0)AC n  

là véctơ pháp tuyến của

AC

Phương trình đường thẳng

1

: 3 0 ( , ) 5

2

ABC

AC x S d B AC AC



    

Câu 137: [0H3-1-3] Khoảng cách giữa

2

đường thẳng:

1

:3 4 0xy

và

2

0:6 8 1 1 0xy 

A.

1,01

. B.

101

. C.

10,1

. D.

101

.

Lời giải

Chọn C

1 1 2 1 2 2

(0;0) , // ( , ) ( , ) 10,1O d d O        

HÌNH CHIẾU – ĐỐI XỨNG

Câu 138: [0H3-1-3] Cho điểm

(1;2)M

và đường thẳng

:2 5 0d x y  

. Toạ độ của điểm đối

xứng với điểm

M

qua

d

là:

A.

9 12

;

55







. B.

26

;

55









. C.

3

0;

5







. D.

3

;5

5









.

Lời giải

Chọn A

Ta thấy

Md

.

Gọi

 

,H a b

là hình chiếu của điểm

M

lên đường thẳng

d

.

Ta có đường thẳng

:2x 5 0dy  

nên có vtpt:

 

2;1n 

Suy ra

 

1;2u 

là vectơ chỉ phương của đường thẳng

d

    

7

1 1 2 2 0

2 3 0

.0

5

2a 5 0 11

2 5 0

5

a

ab

MH u MH u

b

ab

H d H d

b









    



   





   

   

    

  



















Do đó

7 11

;

55

H







.

Gọi

 

,M x y



đỗi xứng với

M

qua đường thẳng

d

. Khi đó ta có:

H

là trung điểm

của

MM



Ta có:

7 1 9

5 2 5

11 2 12

5 2 5

x

y























Vậy tọa độ điểm đối xứng với

M

qua

d

là

9 12

;

55

M









.

Câu 139: [0H3-1-3] Cho đường thẳng

: 2 – 3 3 0 d x y 

và

 

8; 2M

. Tọa độ của điểm

M



đối xứng với

M

qua

d

là:

A.

( 4 );8

. B.

( 84; ) 

. C.

(4;8)

. D.

(4; )8

.

Lời giải

Chọn C

Ta thấy hoành độ và tung độ của điểm

M



chỉ nhận một trong 2 giá trị nên ta có thể

làm như sau:

Đường thẳng

d

có 1 VTPT

(2; 3)n 

, Gọi

'( ; )M x y

thì

'( 2; 3)MM x y

M



đối xứng với

M

qua

d

nên

'( 2; 3)MM x y

và

(2; 3)n 

cùng phương khi và

chỉ khi

2 3 28 2

2 3 3

x y y

x

  

  



Thay

8y 

vào ta được

4x 

Thay

8y 

vào thấy không ra đúng

4x 

.

Cách 2:

+ptdt



đi qua

M

và vuông góc với

d

là:

3( 8) 2( 2) 0 3 2 28 0x y x y       

.

+ Gọi

(6;5)H d H   

.

+ Khi đó H là trung điểm của đoạn

MM



Áp dụng công thức trung điểm ta suy ra

2 12 8 4

2 10 2 8

M H M

x x x

y y y



    





    



. Vậy

(4;8)M



.

Câu 140: [0H3-1-3] Toạ độ hình chiếu của

 

4;1M

trên đường thẳng

: – 2 4 0xy 

là:

A.

)14;( 19 

. B.

(2;3 )

. C.

14 17

;

55







. D.

14 17

;

55









.

Lời giải

Chọn C

Đường thẳng

()

có 1 VTPT

(1; 2)n 

, Gọi

(2 4; )H t t

là hình chiếu của

 

4;1M

trên đường thẳng

()

thì

(2 8; 1)MH t t

(2 4; )H t t

là hình chiếu của

 

4;1M

trên đường thẳng

()

nên

(2 8; 1)MH t t

và

(2; 3)n 

cùng phương khi và chỉ khi

2 8 1 17

1 2 5

tt

t



  



14 17

;

55

H









Câu 141: [0H3-1-3] Tìm hình chiếu của

 

3; –4A

lên đường thẳng

2

:

2

1

xt

yt

d







  



. Sau đây

là bài giải:

Bước 1: Lấy điểm

 

2 2 ;–1–H t t

thuộc

d

. Ta có

 

2 –1; – 3tA tH 

Vectơ chỉ phương của

d

là

 

2;–1u 

Bước 2:

H

là hình chiếu của

A

trên

.0d AH d u AH   

   

2 2 –1 – – 3 0 1t t t    

Bước 3: Với

1t 

ta có

 

4; – 2H

. Vậy hình chiếu của

A

trên

d

là

 

4; – 2H

.

Bài giải trên đúng hay sai ? Nếu sai thì sai từ bước nào ?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ

bước 3.

Lời giải

Chọn A

Bài giải trên đúng.

Câu 142: [0H3-1-3] Cho hai đường thẳng

: 2 1 0d x y  

,

: 2 1 0d x y



  

. Câu nào sau

đây đúng ?

A.

d

và

d



đối xứng qua

O

. B.

d

và

d



đối xứng qua

Ox

.

C.

d

và

d



đối xứng qua

Oy

. D.

d

,

d



đối xứng qua đường thẳng

yx

.

Lời giải

Chọn B

Đường thẳng

 

1;0d Ox A d



  

Lấy điểm

1

0;

2

Md









 

ox

1

0;

2

Đ M N d





  





Câu 143: [0H3-1-3] Cho đường thẳng

13

:

2

xt

yt













và điểm

 

3;3 .M

Tọa độ hình chiếu

vuông góc của

M

trên đường thẳng



là:

A.

 

4;–2

. B.

 

1;0

. C.

 

2;2

. D.

 

7; –4

.

Lời giải

Chọn B

Gọi

H

là hình chiếu của

M

trên



. Ta có:

   

1 3 ; 2 , 2 3 ; 3 2H H t t MH t t        

Đường thẳng



có vectơ chỉ phương là

 

3; 2u 

.

   

. 0 3 2 3 2 3 2 0 13 0 0 (1;0).MH u MH u t t t t H              

Câu 144: [0H3-1-3] Cho đường thẳng

23

:

12

xt

yt













. Hoành độ hình chiếu của

 

4;5M

trên



gần nhất với số nào sau đây ?

A.

1,1

. B.

1,2

. C.

1,3

. D.

1,5

.

Lời giải

Chọn D

Gọi

H

là hình chiếu của

M

trên



. Ta có:

   

2 3 ;1 2 , 2 3 ; 4 2H H t t MH t t        

Đường thẳng



có vectơ chỉ phương là

 

3; 2u 

.

   

2 20 17

. 0 3 2 3 2 4 2 0 13 2 0 ; .

13 13 13

MH u MH u t t t t H



                





Câu 145: [0H3-1-3] Cho điểm

 

–1;2A

và đường thẳng

2

:

3

xt

yt









  



. Tìm điểm

M

trên



sao cho

AM

ngắn nhất.

Bước 1: Điểm

 

– 2;– – 3M t t 

Bước 2: Có

     

2 2 2

–1 – – 5 2 8 26 4 13 2 9 9MA t t t t t t t           

Bước 3:

2

93MA MA  

.

Vậy

 

min 3MA 

khi

–2t 

. Khi đó

 

–4;–1M

.

Bài giải trên đúng hay sai ? Nếu sai thì sai ở đâu ?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai ở

bước 3.

Lời giải

Chọn C

Điểm

 

– 2;– – 3M t t 

Có

   

 

2 2 2

–1 – – 5 2 8 26 2 4 13 2 2 18 18MA t t t t t t t           

2

18 3 2MA MA  

. Vậy

 

min 3 2MA 

khi

–2t 

. Khi đó

 

–4; –1 .M

Sai từ bước 2.

Câu 146: [0H3-1-3] Tìm hình chiếu của

 

3; –4A

lên đường thẳng

22

:

1

xt

d

yt







  



. Sau đây là

bài giải:

Bước 1: Lấy điểm

 

2 2 ;–1–H t t

thuộc

d

. Ta có

 

2 –1; – 3AH t t

Vectơ chỉ phương của

d

là

 

2; –1u 

Bước 2:

H

là hình chiếu của

A

trên

d

   

. 0 2 2 –1 – – 3 0 1AH d u AH t t t        

Bước 3: Với

1t 

ta có

 

4;–2 .H

Vậy hình chiếu của

A

trên

d

là

 

4;–2 .H

Bài giải trên đúng hay sai ? Nếu sai thì sai từ bước nào ?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ

bước 3.

Lời giải

Chọn A

Đúng.

Câu 147: [0H3-1-3] Cho đường thẳng

: 2 – 3 3 0d x y 

và

 

8;2M

. Tọa độ của điểm

M



đối

xứng với

M

qua

d

là

A.

 

–4; 8 .

B.

 

–4;–8 .

C.

 

4;8 .

D.

 

4; –8 .

Lời giải

Chọn C

Gọi

d



qua

M

và vuông góc với

d

nên

:3 2 28 0d x y



  

Gọi

 

6;5H d d H



  

Vì

M



đối xứng với

M

qua

d

nên

H

là trung điểm của

MM



suy ra

 

4;8M



Câu 148: [0H3-1-3] Cho hai điểm

 

1;2A

và

4()3;B 

và đường thẳng

D: 4 7 0x y m  

.

Tìm điều kiện của

m

để đường thẳng

D

và đoạn thẳng

AB

có điểm chung.

A.

10 40m

. B.

10m

hoặc

40m 

.

C.

40m 

. D.

10m 

.

Lời giải

Chọn A

Để

D

và đoạn

AB

có điểm chung thì A và B phải nằm khác phía với

D

(4 14 )( 12 2 ) 10 4080mm m       

.

Câu 149: [0H3-1-3] Cho đường thẳng

:3 – 4 –12 0.d x y 

Phương trình các đường thẳng qua

 

2;–1M

và tạo với

d

một góc

4



là

A.

7 – –15 0; 7 5 0x y x y   

. B.

7 –15 0; – 7 5 0x y x y   

.

C.

7 – 15 0; 7 – 5 0x y x y   

. D.

7 15 0; – 7 – 5 0x y x y   

.

Lời giải

Chọn B

Gọi

 

;n A B

và

22

0AB

là véctơ pháp tuyến của



Ta có:

22

2 2 2 2

34

cos 2 3 4 5

4

3 4 .

AB

A B A B

AB





    



22

7

7 48 7 0

7

BA

A AB B

AB





    







Với

7BA

chọn

1, 7 7 5A B x y    

Với

7AB

chọn

7, 1 7 15 0A B x y      

.

Câu 150: [0H3-1-3] Cho hai đường thẳng

: – 3 5 0d x y 

và

’: 3 – 15 0d x y 

. Phương

trình đường phân giác góc tù tạo bởi

d

và

’d

là

A.

– – 5 0xy 

. B.

5 0xy  

. C.

– 5 0xy

. D.

– 5 0xy

.

Lời giải

Chọn B

Ta có:

 

1

1; 3n 

và

 

2

3; 1n 

là véctơ pháp tuyến của

d

và

’d

và

12

. 3 4 0nn  

Nên phương trình đường phân giác của góc nhọn là:

3 5 3 15

50

10 10

x y x y

xy

   

    

.

Câu 151: [0H3-1-3] Lập phương trình đường thẳng



song song với đường thẳng

: 3 2 12 0d x y  

và cắt

,Ox Oy

lần lượt tại

,AB

sao cho

13AB 

, ta được một

kết quả là

A.

3 2 12 0xy  

. B.

3 2 12 0xy  

. C.

6 4 12 0xy  

. D.

3 4 6 0xy  

.

Lời giải

Chọn C

Do



song song với đường thẳng

d

nên

: 3 2 0x y c   

.

Từ đó suy ra,

; 0 , 0;

32

cc

AB

   



   

   

.

Theo giả thiết

22

6

13 13 13 36

6

94

c

cc

AB AB c

c





        







.

Vậy ta có hai đường thẳng thỏa mãn là

3 2 6 0xy  

và

3 2 6 0xy  

.

Câu 152: [0H3-1-3] Hình chiếu vuông góc của

 

1;4M

xuống đường thẳng

: 2 2 0xy   

có

tọa độ là

A.

 

3;0

. B.

 

0;3

. C.

 

2;2

. D.

 

2; 2

.

Lời giải

Chọn C

Gọi

 

;H x y

là hình chiếu của

M

lên



.

Ta có

   

2 2 0

2

2 1 1 4 0

2

xy

Hx

xy

HM y

  



 







  

   

  







.

Vậy

 

2;2H

.

Câu 153: [0H3-1-3] Phương trình đường thẳng qua

 

5; 3M 

và cắt 2 trục

,x Ox y Oy



tại 2

điểm

A

và

B

sao cho

M

là trung điểm của

AB

là:

A.

3 5 30 0xy  

. B.

3 5 30 0xy  

. C.

5 3 34 0xy

. D.

3 5 30 0.xy  

Lời giải

Chọn A

M

: trung điểm của

1

xy

AB

ab

  

. Đường thẳng này qua điểm

 

2; 3M 

nên

23

1

ab



. Ta có:

23

1 1 1 0

23

1 5 5 0

a b a x y

ab

a b a x y

ab



          







          





.

Ghi chú: Có thể giải nhanh như sau:

OAB

vuông cân nên cạnh

AB

song song

với phân giác góc phần tư thứ I, hoặc II. Do đó,

 

1;1n 

, hay

 

1; 1

. Nhu thế khả

năng chọn là một trong hai câu

 

A

hoặc

 

B

. Thay tọa độ điểm

M

vào, loại

được

 

B

và chọn

 

A

.

Câu 154: [0H3-1-3] Viết phương trình đường thẳng qua

 

2; 3M 

và cắt hai trục

,Ox Oy

tại

A

và

B

sao cho tam giác

OAB

vuông cân.

A.

10

50

xy

  





  



. B.

10

50

xy

  





  



. C.

10xy  

. D.

50xy  

.

Lời giải

Chọn A

Phương trình đường thẳng

: 1.

xy

AB

ab



Đường thẳng này đi qua

 

2; 3M 

nên

23

1.

ab



Ta có.:

23

1 1 1 0

23

1 5 5 0

a b a x y

aa

ab

a b a x y

aa



          







          





Ghi chú có thể giải nhanh như sau:

OAB

vuông nên cạnh

AB

song song với phân

giác của góc phần tư thứ nhất hoặc thứ hai. Do đó

 

1;1 ,n 

hay

 

1; 1 .n 

Như thế,

khả năng chọn một trong hai câu A hoặc BThay tọa độ

M

vào loại được đáp án B

và chọn đáp án A.

Câu 155: [0H3-1-3] Viết phương trình đường thẳng

d

đi qua

 

2;0A 

và tạo với đường

thẳng

: 3 3 0d x y  

một góc

45 .

A.

2 4 0xy

và

2 2 0xy  

.

B.

2 4 0xy  

và

2 2 0xy  

.

C.

   

6 5 3 3 2 6 5 3 0xy    

và

   

6 5 3 3 2 6 5 3 0xy    

.

D.

2 4 0xy

và

2 2 0.xy  

Lời giải

Chọn B

Phương trình đường thẳng

D

có dạng:

 

20A x By  

.

Theo giả thiết, ta có:

 

0

22

3

2

cos , cos45

2

. 10

AB

Dd

AB



  



, hay:

22

2 2, 1

2 3 2 0

1

1, 2

2

A

AB

B

A AB B

A

AB

B



   



   



     





.

Vậy:

:2 4 0D x y  

hoặc

: 2 2 0D x y  

.

Câu 1: [0H3-1-4] Cho đường thẳng

   

– 2 –1: 2 –1 0.m x m y m  

Với giá trị nào của

m

thì khoảng cách từ điểm

 

2;3

đến  lớn nhất?

A.

11

.

5

m 

B.

11

.

5

m 

C.

11.m 

D.

11.m 

Hướng dẫn:

Chọn A.

Ta có

2

78

2 6 5

m

d

mm







.

Tự luận :

Trắc nghiệm : Bấm máy tính, chọn

.A

Câu 2: [0H3-1-4] Cho

   

2;2 , 5;1AB

và đường thẳng

: – 2 8 0.xy  

Điểm

C

.

C

có

hoành độ dương sao cho diện tích tam giác

ABC

bằng 17. Tọa độ của

C

là

A.

 

10;12 .

B.

 

12; 10 .

C.

 

8; 8 .

D.

 

10; 8 .

Hướng dẫn:

Chọn B.

Phương trình đường thẳng

: 3 8 0AB x y  

. Điểm

 

2 8;C C t t  

Diện tích tam giác

ABC

:

   

10

5 16

11

. ; 17 10. 17 12;10

18

22

10

5

t

AB d C AB C

t









    







Câu 3: [0H3-1.26-3] (trùng câu 3065) Hai cạnh của hình chữ nhật nằm trên hai đường thẳng

4 – 3 5 0;3 4 – 5 0,x y x y   

đỉnh

 

2;1A

. Diện tích của hình chữ nhật là

A. 1 B. 2 C. 3 D. 4

Hướng dẫn:

Chọn D.

Khoảng cách từ đỉnh

 

2;1A

đến đường thẳng

4 3 5 0xy  

là 2

Khoảng cách từ đỉnh

 

2;1A

đến đường thẳng

3 4 5 0xy  

là 2

Diện tích hình chữ nhật bằng

2.2 4

.

Câu 4: [0H3-1-4] Cho 2 đường thẳng

: – 2 2 0; : 2 – – 4 0d x y d x y



  

. Hai đường thẳng

này chia mặt phẳng thành những miền đánh số 1, 2, 3, 4. Điểm

M

thuộc miền nào

để

 

; xy

nghiệm đúng

  

– 2 2 – – 4 0x y x y

A. Miền 1 và 3 B. Miền 2 và 4 C. Miền 1 và 4 D. Miền 2

và 3

Lời giải:

Chọn D.

Ta có:

  

20

2 4 0

– 2 2 – – 4 0

20

2 4 0

xy

x y x y

xy

   







  





  



  







  







Câu 5: [0H3-1-4] Cho hai đường thẳng

1

: 2 1 0d x y  

,

2

: 3 3 0d x y  

. Phương trình

đường thẳng

d

đối xứng với

1

d

qua

2

d

là:

A.

7 1 0xy  

. B.

7 1 0xy  

.

C.

7 1 0xy  

. D.

7 1 0xy  

.

Lời giải

Chọn B

Gọi

I

là giao điểm của hai đường thẳng

12

,dd

. Tọa độ điểm

I

là nghiệm của hệ:

2 1 0

34

;

3 3 0

55

xy

I

xy

  











  





Lấy điểm

 

1

1;0Md

. Đường thẳng



qua

M

và vuông góc với

2

d

có phương trình:

3 3 0.xy  

1

2

3

4

y

Gọi

2

Hd  

, suy ra tọa độ điểm

H

là nghiệm của hệ:

3 3 0

36

;

3 3 0

55

xy

H

xy

  











  





Phương trình đường thẳng

34

qua ;

55

:

62

;

55

d

I

d

u IH











  

















có dạng:

3 1 0.xy  

Câu 6: [0H3-1-4] Cho hai đường thẳng

: 3 – 6 0d x y

và

:3 3 0.d x y



  

Phương trình

đường phân giác của góc tạo bởi

d

và

d



nằm trong miền xác định bởi

, dd



và

chứa gốc

O

là

A.

2 – 2 9 0.xy

B.

4 4 3 0.xy  

C.

2 2 9 0.xy  

D.

4 4 3 0.xy  

Lời giải

Chọn B

Gọi

 

,M x y

thuộc đường phân giác của

, dd



khi

   

3 6 3 3

;;

10 10

x y x y

d M d d M d

   



  

2 2 9 0

3 6 3 3

4 4 3 0

xy

x y x y

xy

  



     



  



Câu 7: [0H3-1-4] Cho tam giác

ABC

có

: 2 – 4 0; : – 2 – 6 0AB x y AC x y  

. Hai đểm

B

và

C

thuộc

Ox

. Phương trình

phân giác góc ngoài của góc

BAC

là

A.

3 – 3 – 2 0xy 

.

B.

– 10 0xy

. C.

3 3 10 0xy  

.

D.

10 0xy  

.

Lời giải

Chọn A

Do

   

, 2;0 , 6;0B C Ox B C  

. Gọi

 

;M x y

thuộc đường phân giác của góc

BAC

Ta có:

   

2 4 2 6

, , 2 4 2 6

55

x y x y

d M AB d M AC x y x y

   

        

10 0

3 3 2 0

xy

  







  



Khi đó:

  

2 10 6 2 0    

nên

3 3 2 0xy  

là đường thẳng cần tìm.

Câu 8: [0H3-1-4] Cho đường thẳng đi qua

2

điểm

 

(3;0 , 0; 4 ,)AB

tìm tọa độ điểm

M

thuộc

Oy

sao cho diện tích

MAB

bằng

6.

A.

 

0;1

. B.

 

0;0

và

(0; )8

. C.

 

1;0

. D.

 

0;8

.

Lời giải

Chọn B

Ta có

 

3; 4 5.ABAB  

Đường thẳng

AB

đi qua

 

3;0 , 4()0;AB

nên có phương trình

4 3 12 0xy  

.

M

thuộc

Oy

nên

   

3 12

0; ; ,

5

m

M m d M AB





.

0

6 3 12 12

8

MAB

m

Sm

m







    







.

Vậy tọa độ của

M

là

 

0;0

và

 

0; 8

.

Câu 9: [0H3-1-4] Cho điểm

(1;2)M

và đường thẳng

:2 5 0.d x y  

Toạ độ của điểm đối

xứng với điểm

M

qua

d

là:

A.

9 12

;

55







. B.

26

;

55









. C.

3

0;

5







D.

3

;5

5









.

Lời giải

Chọn A

Ta thấy

.Md

Gọi

 

,H a b

là hình chiếu của điểm

M

lên đường thẳng

.d

Ta có đường thẳng

:2x 5 0dy  

nên có vtpt:

 

2;1 .n 

Suy ra:

 

1;2u 

là vectơ chỉ phương của đường thẳng

.d

    

7

1 1 2 2 0

2 3 0

.0

5

2a 5 0 11

2 5 0

5

a

ab

MH u MH u

b

ab

H d H d

b









    



   





   

   

    

  



















Do đó:

7 11

;.

55

H







Gọi

 

,M x y



đỗi xứng với

M

qua đường thẳng

d

. Khi đó ta có:

H

là trung điểm

của

MM



Ta có:

7 1 9

5 2 5

11 2 12

5 2 5

x

y























Vậy tọa độ điểm đối xứng với

M

qua

d

là

9 12

;

55

M









.

Câu 10: [0H3-1-4] Cho đường thẳng

: 2 – 3 3 0 d x y 

và

 

.8; 2M

Tọa độ của điểm

M



đối xứng với

M

qua

d

là:

A.

( 4 );8

. B.

( 84; ) 

. C.

(4;8)

. D.

(4; )8

.

Lời giải

Chọn C

Ta thấy hoành độ và tung độ của điểm

M



chỉ nhận một trong 2 giá trị nên ta có thể

làm như sau:

Đường thẳng

d

có 1 VTPT

(2; 3).n 

Gọi

'( ; )M x y

thì

( 2; 3).MM x y



  

M



đối xứng với

M

qua

d

nên

( 2; 3)MM x y



  

và

(2; 3)n 

cùng phương

khi và chỉ khi

2 3 28 2

.

2 3 3

x y y

x

  

  



Thay

8y 

vào ta được

4.x 

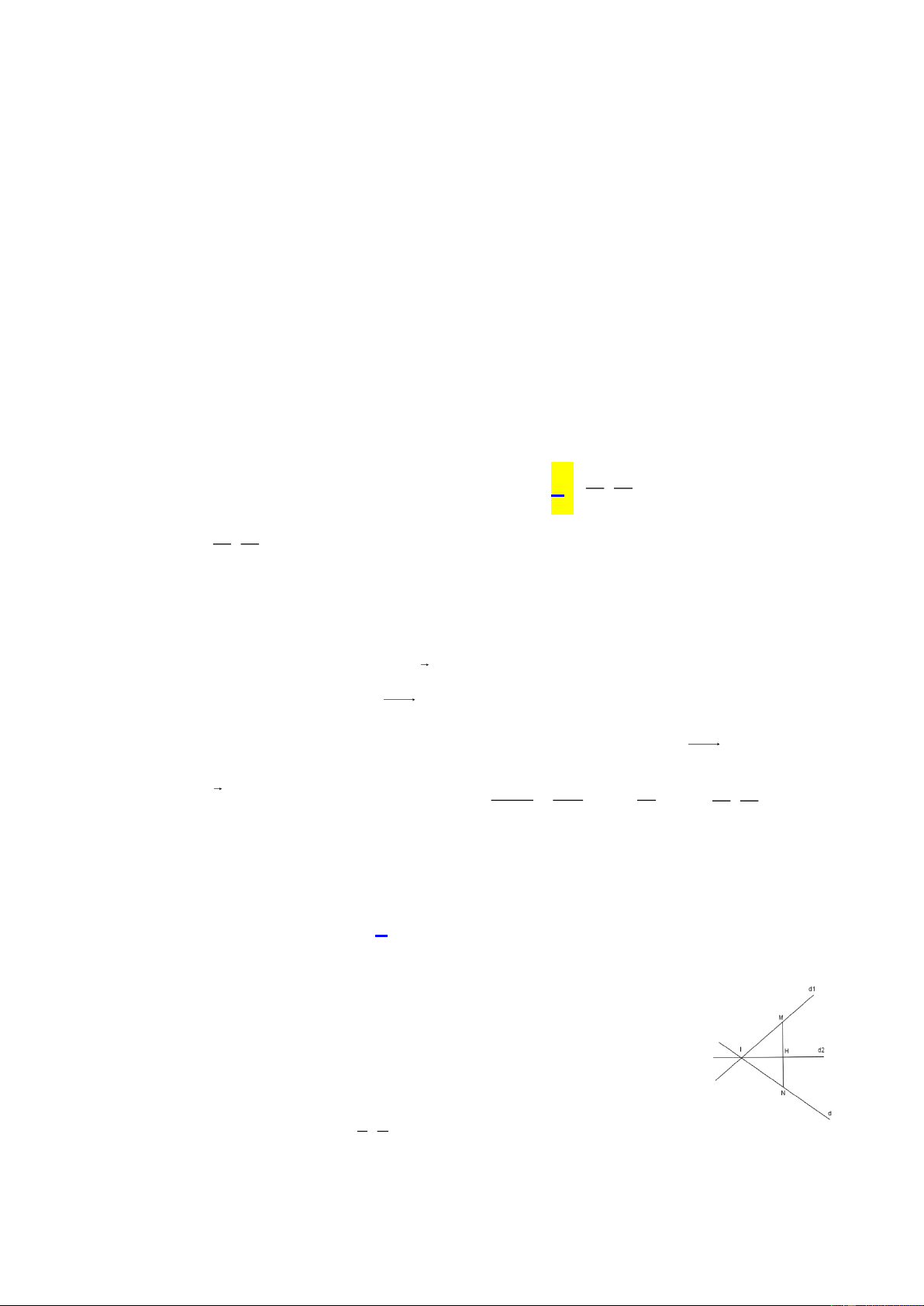
Thay

8y 

vào thấy không ra đúng

4x 

.

Cách 2:

+ Ptđt



đi qua

M

và vuông góc với

d

là:

   

3 8 2 2 0 3 2 28 0.x y x y       

+ Gọi

(6;5).H d H   

+ Khi đó H là trung điểm của đoạn

.MM



Áp dụng công thức trung điểm ta suy ra

2 12 8 4

2 10 2 8

M H M

x x x

y y y



    





    



. Vậy

(4;8)M



.

Câu 11: [0H3-1-4] Toạ độ hình chiếu của

 

4;1M

trên đường thẳng

: – 2 4 0xy 

là:

A.

 

14; 19

. B.

 

2;3

. C.

14 17

;

55







. D.

14 17

;

55









.

Lời giải

Chọn C

Đường thẳng

()

có 1 VTPT

(1; 2)n 

, Gọi

(2 4; )H t t

là hình chiếu của

 

4;1M

trên đường thẳng

()

thì

(2 8; 1)MH t t

.

(2 4; )H t t

là hình chiếu của

 

4;1M

trên đường thẳng

()

nên

(2 8; 1)MH t t

và

(2; 3)n 

cùng phương khi và chỉ khi

2 8 1 17

1 2 5

tt

t



  



14 17

;.

55

H









Câu 12: [0H3-1-4] Cho hai đường thẳng

1

: 2 1 0  d x y

,

2

: 3 3 0.d x y  

Phương trình

đường thẳng

d

đối xứng với

1

d

qua

2

d

là:

A.

7 1 0xy  

. B.

7 1 0xy  

. C.

7 1 0xy  

. D.

7 1 0xy  

.

Lời giải

Chọn B

Gọi

I

là giao điểm của hai đường thẳng

12

,dd

.

Tọa độ điểm

I

là nghiệm của hệ:

2 1 0

34

;

3 3 0

55

xy

I

xy

  











  





.

Lấy điểm

 

1

1;0 .Md

Đường thẳng



qua

M

và vuông góc với

2

d

có phương trình:

3 3 0.xy  

Gọi

2

Hd  

, suy ra tọa độ điểm

H

là nghiệm của hệ:

3 3 0

36

;.

3 3 0

55

xy

H

xy

  











  





Phương trình đường thẳng

34

qua ;

55

:

62

;

55

d

I

d

u IH











  

















có dạng:

3 1 0.xy  

Câu 13: [0H3-1-4] Cho điểm

 

–1;2A

và đường thẳng

2

:

3

xt

yt









  



. Tìm điểm

M

trên



sao cho

AM

ngắn nhất.

Bước 1: Điểm

 

– 2; – – 3 .M t t 

Bước 2: Có

     

2 2 2

–1 – – 5 2 8 26 4 13 2 9 9.MA t t t t t t t           

Bước 3:

2

93MA MA  

.

Vậy

 

min 3MA 

khi

–2t 

. Khi đó

 

–4; –1 .M

Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai ở

bước 3.

Lời giải.

Chọn C

Điểm

 

– 2;– – 3M t t 

.

Có

   

 

2 2 2

–1 – – 5 2 8 26 2 4 13 2 2 18 18.MA t t t t t t t           

2

18 3 2MA MA  

. Vậy

 

min 3 2MA 

khi

–2t 

. Khi đó

 

–4; –1 .M

Sai từ bước 2.

Câu 14: [0H3-1-4] Cho đoạn thẳng

AB

với

 

(;2 , ; )1 3 4AB

và đường thẳng

:4 7 0d x y m  

. Định

m

để

d

và đoạn thẳng

AB

có điểm chung.

A.

10 40m

B.

40m 

hoặc

10m

.

C.

40m 

. D.

10m

.

Lời giải

Chọn A

Đường thẳng

d

và đoạn thẳng

AB

có điểm chung

,AB

nằm về hai phía của đường thẳng

d

(4 14 )( 12 28 ) 0mm      

10 40m  

.

Câu 15: [0H3-1-4] Cho đoạn thẳng

AB

với

 

(;2 , ; )1 3 4AB

và đường thẳng

2

:

1

x m t

d

yt











. Định

m

để

d

cắt đoạn thẳng

.AB

A.

3m 

. B.

3m 

. C.

3m 

. D. Không

có

m

nào.

Lời giải

Chọn D

Dạng tổng quát của đường thẳng

: 2 2 0.d x y m   

Đường thẳng

d

và đoạn thẳng

AB

có điểm chung

,AB

nằm về hai phía của đường thẳng

d

(1 4 2)( 3 8 2) 0 (3 )(3 ) 0 (VN).m m m m            

Câu 1: [0H3-2-1] Đường tròn nào dưới đây đi qua điểm

4; 2A

A.

22

2 6 24 0x y x y

. B.

22

4 7 8 0x y x y

.

C.

22

6 2 9 0x y x y

. D.

22

2 20 0x y x

.

Lời giải

Chọn A

Thế tọa độ điểm

A

vào lần lượt các phương trình, ta được đáp án A

Câu 2: [0H3-2-1] Đường tròn

22

2 10 1 0x y x y

đi qua điểm nào trong các điểm dưới

đây?

A.

2;1 .

B.

3; 2

. C.

1;3 .

D.

4; 1 .

Lời giải

Chọn D

Thay tọa độ

4; 1

vào PT đường tròn ta có :

16 1 8 10 1 0.

Câu 3: [0H3-2.21-2] Xác định vị trí tương đối giữa 2 đường tròn (C

1

):

22

40x y x

và

(C

2

):

22

80x y y

.

A. Tiếp xúc trong. B. Không cắt nhau. C. Cắt nhau. D. Tiếp

xúc ngoài.

Lời giải

Chọn C

Đường tròn

1

C

có tâm

1

2;0I

và bán kính

1

2.R

Đường tròn

2

C

có tâm

2

0; 4I

và bán kính

2

4.R

Ta có :

1 2 1 2

6 2 5.R R I I

Vậy

1

C

cắt

2

.C

Câu 4: [0H3-2-1] Đường tròn nào dưới đây đi qua 2 điểm A(1; 0), B(3; 4)?

A.

22

8 2 9 0x y x y

. B.

22

3 16 0x y x

.

C.

22

0x y x y

. D.

22

4 4 3 0x y x y

.

Lời giải

Chọn D

Thay tọa độ A, B vào đáp án D thỏa mãn.

Câu 5: [0H3-2-1] Đường tròn

22

6 8 0x y x y

có bán kính bằng bao nhiêu?

A. 10. B. 25. C. 5. D.

10

.

Lời giải

Chọn C

22

9 16 0 5R a b c

Câu 6: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng :

70xy

và đường tròn (C):

22

25 0xy

.

A.

 

3;4

và

()4;3

. B.

 

4;3

. C.

 

3;4

. D.

 

3;4

và

 

4;3

.

Lời giải

Chọn D

Tọa độ giao điểm của  và (C) là nghiệm hệ phương trình :

22

70

25 0

xy

2

3

7

4

7

3

2 14 49 0

4

3

x

yx

y

yx

x

xx

x

y

.

Câu 7: [0H3-2-2] Đường thẳng :

70xy

cắt đường tròn (C):

22

25 0xy

theo

một dây cung có độ dài bằng bao nhiêu ?

A. 5. B.

2

. C. 2. D.

52

.

Lời giải

Chọn B

Tọa độ giao điểm của  và (C) là

3;4 , 4;3 .AB

Độ dài dây cung là

2.AB

Câu 8: [0H3-2-1] Phương trình nào sau đây là phương trình đường tròn?

A.

22

90x y x y

. B.

22

0x y x

.

C.

22

2 1 0x y xy

. D.

22

2 3 1 0x y x y

.

Lời giải

Chọn B

22

: 2a 2 0PT x y x by c

là phương trình đường tròn

22

0.a b c

Câu 9: [0H3-2-1] Phương trình nào sau đây không phải là phương trình đường tròn?

A.

22

40x y x y

. B.

22

0x y y

.

C.

22

20xy

. D.

22

100 1 0x y y

.

Lời giải

Chọn A

22

: 2a 2 0PT x y x by c

là phương trình đường tròn

22

0.a b c

Xét đáp án A.

Ta có

11

, , 4.

22

a b c

22

7

0.

2

a b c

Câu 10: [0H3-2-1] Phương trình nào sau đây là phương trình đường tròn?

A.

22

2 8 20 0x y x y

. B.

22

4 10 6 2 0x y x y

C.

22

4 6 12 0.x y x y

D.

22

2 4 8 1 0.x y x y

Lời giải

Chọn C

22

: 2a 2 0PT x y x by c

là phương trình đường tròn

22

0.a b c

Xét đáp án C.

Ta có

2, 3, 12.a b c

22

25 0.a b c

§.5 ELIP.

Câu 11: [0H3-2-1] Đường tròn

 

22

: 1 0C x y x y    

có tâm

I

và bán kính

R

là:

A.

 

1;1 , 1IR

. B.

1 1 6

; ,

2 2 2

IR









.

C.

1 1 6

; ,

2 2 2

IR









. D.

 

1; 1 , 6IR

.

Lời giải

Chọn B

 

22

: 1 0C x y x y    

có

1

2

1

2

1

a

b

c



















Tọa độ tâm

11

;

22

I









, bán kính

22

6

2

R a b c   

.

Câu 12: [0H3-2-1] Phương trình nào là phương trình của đường tròn có tâm

 

3;4I 

và bán

kính

2R 

?

A.

   

22

3 4 4 0xy    

. B.

   

22

3 4 4xy   

.

C.

   

22

3 4 4xy   

. D.

   

22

3 4 2xy   

.

Lời giải

Chọn A

Phương trình của đường tròn có tâm

 

3;4I 

và bán kính

2R 

có dạng :

       

2 2 2 2

3 4 4 3 4 4 0x y x y         

.

Câu 13: [0H3-2-1] Phương trình

22

2 4 1 0x y x y    

là phương trình của đường tròn

nào?

A. Đường tròn có tâm

 

1;2

, bán kính

1R 

.

B. Đường tròn có tâm

 

1; 2

, bán kính

2R 

.

C. Đường tròn có tâm

 

2; 4

, bán kính

2R 

.

D. Đường tròn có tâm

 

1; 2

, bán kính

1R 

.

Lời giải

Chọn B

Phương trình

22

2 4 1 0x y x y    

   

22

1 2 4xy    

. Vậy đường tròn có

tâm

 

1; 2

, bán kính

2R 

.

Câu 14: [0H3-2-1] Điểm nào là tiêu điểm của parabol

2

5yx

?

A.

 

5; 0F

. B.

5

;0

2

F







. C.

5

;0

4

F









. D.

5

;0

4

F







.

Lời giải

Chọn D

Phương trình chính tắc của parabol là

2

2y px

. Theo giả thiết, ta có

5

25

2

pp  

.

Vậy tiêu điểm của parabol là

5

; 0 ; 0

24

p

FF

   



   

   

.

Câu 15: [0H3-2-1] Đường thẳng

d

có phương trình tham số

13

63

xt

yt











có hệ số góc

k

là ?

A.

1k 

. B.

2k 

. C.

–1k 

. D.

–2k 

.

Lời giải

Chọn C

Đường thẳng

d

có vectơ chỉ phương là

 

3

13; –3

3

uk



   

.

Câu 16: [0H3-2-1] Tâm của đường tròn

 

C

có phương trình

   

22

3 4 12xy   

là:

A.

 

3; 4

. B.

 

4; 3

. C.

 

3; 4

. D.

 

3; 4

.

Lời giải

Chọn C

Phương trình tổng quát của đường tròn:

   

22

2

x a y b R   

với

 

,I a b

là tâm

của đường tròn.

Từ phương trình tổng quát của

     

22

: 3 4 12C x y   

ta suy ra

3a 

,

4b 

. Vậy tâm của đường tròn

 

C

là

 

3; 4

.

Câu 17: [0H3-2-1] Cho đường tròn có phương trình

22

5 4 4 0x y x y    

. Tâm của đường

tròn có tọa độ là:

A.

 

5; 4

. B.

 

4; 5

. C.

5

;2

2









. D.

5

;2

2









.

Lời giải

Chọn C

Phương trình tổng quát của đường tròn có dạng:

22

2 2 0x y ax by c    

với

 

;I a b

là tâm và bán kính được tính bằng công thức

22

R a b c  

.

Từ phương trình tổng quát của

 

22

: 5 4 4 0C x y x y    

ta suy ra

5

2

a 

,

2b 

. Vậy tâm của đường tròn

 

C

là

5

;2

2









.

Câu 18: [0H3-2-1] Cho đường tròn có phương trình

22

5 4 4 0x y x y    

. Bán kính của

đường tròn là:

A.

3

2

. B.

4

2

. C.

5

.

2

D.

6

2

.

Lời giải

Chọn C

Phương trình tổng quát của đường tròn có dạng:

22

2 2 0x y ax by c    

với

 

;I a b

là tâm và bán kính được tính bằng công thức

22

R a b c  

.

Từ phương trình tổng quát của

 

22

: 5 4 4 0C x y x y    

ta suy ra

2

55

24

22

R



    





.

Câu 19: [0H3-2-1] Cho đường tròn

 

22

: 2 4 20 0C x y x y    

. Tìm mệnh đề sai trong

các mệnh đề sau:

A.

 

C

có tâm

 

1; 2I

. B.

 

C

có bán kính

5R 

.

C.

 

C

đi qua điểm

 

2; 2M

. D.

 

C

không đi qua điểm

 

1; 1A

.

Lời giải

Chọn A

Phương trình tổng quát của đường tròn có dạng:

22

2 2 0x y ax by c    

với

 

;I a b

là tâm.

Từ phương trình tổng quát của

 

22

: 2 4 20 0C x y x y    

ta suy ra

1a 

,

2b 

. Nên tâm của đường tròn

 

C

là

 

1; 2

. Vậy A sai.

Câu 20: [0H3-2-1] Tọa độ tâm và bán kính

R

đường tròn có phương trình

   

22

2 3 25   xy

.

A.

 

2; 3I

và

5R

. B.

 

2;3I

và

5R

.

C.

 

2; 3I

và

25R

. D.

 

2;3I

và

5R

.

Lời giải

Chọn A

Phương trình đường tròn có dạng:

   

22

2

x a y b R   

.

Do đó :

22

33

aa

bb

   







   





tâm

 

2; 3I 

và

2

25 5RR  

.

Câu 21: [0H3-2-1] Tọa độ tâm và bán kính

R

đường tròn

 

C

có phương trình

22

2 2 2 0    x y x y

.

A.

 

2; 3I

và

3R

. B.

 

2; 3I

và

4R

.

C.

 

1;1I

và

2R

. D.

 

1; 1I

và

2R

.

Lời giải

Chọn C

Phương trình đường tròn dạng khai triển có dạng:

22

2 2 0x y ax by c    

Do đó,

2 2 1

22

aa

bb

cc

   





    





   





tâm

 

1;1I

Bán kính

22

1 1 2 2R a b c      

.

Câu 22: [0H3-2-1] Đường tròn

22

– 5 0x y y

có bán kính bằng bao nhiêu?

A.

5

. B.

25

. C.

25

2

. D.

2,5

.

Chọn D

Câu 23: [0H3-2-1] Đường tròn

22

3 3 – 6 9 9 0x y x y   

có bán kính bằng bao nhiêu?

A.

7,5

. B.

2,5

. C.

25

. D.

5

.

Chọn B

Câu 24: [0H3-2-1] Một đường tròn có tâm

 

3; 2I 

tiếp xúc với đường thẳng

: 5 1 0xy   

.

Hỏi bán kính đường tròn bằng bao nhiêu?

A.

6

. B.

26

. C.

14

26

. D.

7

13

.

Lời giải

Chọn C

Bán kính bằng khoảng cách từ tâm đến đường thẳng 

 

14

,

26

R d I  

Câu 25: [0H3-2-1] Một đường tròn có tâm là điểm

 

0;0

và tiếp xúc với đường thẳng

: 4 2 0xy   

. Hỏi bán kính đường tròn đó bằng bao nhiêu?

A.

2

. B.

1

. C.

4

. D.

42

.

Lời giải

Chọn C

Bán kính bằng khoảng cách từ tâm đến đường thẳng 

 

42

,4

2

R d I   

Câu 26: [0H3-2.21-2] Xác định vị trí tương đối giữa 2 đường tròn

 

22

1

:4C x y

và

 

22

2

:( 10) ( 16) 1C x y   

.

A.Cắt nhau. B.Không cắt nhau. C.Tiếp xúc ngoài. D.Tiếp xúc

trong.

Lời giải

Chọn B

 

1

C

có tâm và bán kính:

 

1

0;0I 

,

1

2R 

;

 

2

C

có tâm và bán kính:

 

2

10;16I 

,

2

1R 

; khoảng cách giữa hai tâm

22

1 2 1 2

10 16 2 89I I R R    

.

Vậy

 

1

C

và

 

2

C

không có điểm chung

Câu 27: [0H3-2-2] Với những giá trị nào của

m

thì đường thẳng

:4 3 0x y m   

tiếp xúc với

đường tròn

 

22

: 9 0C x y  

.

A.

3m 

. B.

3m 

và

3m 

.

C.

3m 

. D.

15m 

và

15m 

.

Lời giải

Chọn D

Đường tròn

 

C

có tâm và bán kính là

 

0;0I 

,

3R 

.



tiếp xúc

 

C



 

,d I R



3

5

m





15

m











Câu 28: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Ox

?

A.

22

2 10 0x y x y   

. B.

22

6 5 9 0x y x y    

.

C.

22

10 1 0x y y   

. D.

22

50xy  

.

Lời giải

Chọn B

Ta có: Đường tròn:

 

22

2

22

55

6 5 9 0 3

22

x y x y x y

   

         

   

   

có tâm và bán

kính lần lượt là

55

3; ;

22

IR



  





.Mà

 

,

5

2

I Ox

dR

Câu 29: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Oy

?

A.

22

10 1 0x y y   

. B.

22

6 5 1 0x y x y    

.

C.

22

20x y x  

. D.

22

50xy  

.

Lời giải

Chọn C

Ta có: đường tròn:

 

2

2 2 2

2 0 1 1x y x x y      

có tâm và bán kính lần lượt là

 

1;0 , 1IR

.Mà

 

,

1

I Oy

dR

Câu 30: [0H3-2-1] Tâm đường tròn

22

10 1 0x y x   

cách trục

Oy

một khoảng bằng

A.

5

. B.

0

. C.

10

. D.

5

.

Lời giải

Chọn D

Ta có đường tròn:

 

2

2 2 2

10 1 0 5 24x y x x y       

có tâm

 

5;0I

.

Khoảng cách từ

I

đến

Oy

là

 

,

5

I Oy

d 

Câu 31: [0H3-2-1] Đường tròn nào dưới đây đi qua điểm

2(4; )A 

A.

22

2 6 0x y x y   

. B.

22

4 7 8 0x y x y    

.

C.

22

6 2 9 0x y x y    

. D.

22

2 20 0x y x   

.

Lời giải

Chọn A

Thế tọa độ của điểm

2(4; )A 

vào phương trình đường tròn

22

2 6 0x y x y   

ta có:

   

2

4 2 2.4 6 2 16 4 8 12 0         

nên

2(4; )A 

thuộc đường tròn.

Câu 32: [0H3-2-1] Một đường tròn có tâm

(1;3)I

tiếp xúc với đường thẳng

:3 4 0xy  

. Hỏi

bán kính đường tròn bằng bao nhiêu ?

A.

3

5

. B.

1

. C.

3

. D.

15

.

Lời giải

Chọn C

22

3.1 3.4

( ; ) 3

34

ycbt R d I



    



.

Câu 33: [0H3-2-3] Đường tròn

2 2 2

( ) ( )x a y b R   

cắt đường thẳng

0x y a b   

theo một

dây cung có độ dài bằng bao nhiêu ?

A.

2R

. B.

2R

. C.

2

R

. D.

R

.

Lời giải

Chọn A

Vì đường tròn có tâm

( ; )I a b

, bán kính

R

và tâm

( ; )I a b

thuộc đường thẳng

0x y a b   

.

Nên độ dài của dây cung bằng độ dài đường kính bằng

2R

.

Câu 34: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng

: 2 3 0xy   

và đường tròn

22

( ): 2 4 0C x y x y   

A.

 

3;3

và

 

1;1

. B.

 

1;1

và

 

3; 3

. C.

 

3;3

và

 

1;1

. D.

 

2;1

và

 

2; 1

.

Lời giải

Chọn A

Tọa độ giao điểm là nghiệm của hệ phương trình sau

   

2

22

2

23

2 3 0

2 4 0

2 3 2 2 3 4 0

xy

x y x y

y y y y





  









   

     





2

1

4 3 0

1

23

y

yy

x

xy





  











hoặc

3

y

x











Vậy tọa độ giao điểm là

 

3;3

và

 

1;1

.

Câu 35: [0H3-2-1] Đường tròn

22

2 10 1 0x y x y    

đi qua điểm nào trong các điểm dưới đây

?

A.

 

2;1

. B.

 

3; 2

. C.

 

1;3

. D.

 

4; 1

.

Lời giải

Chọn D

Cách 1

Thay lần lượt các điểm vào đường tròn điểm nào thỏa mãn phương trình đường tròn

thì điểm đó thuộc đường tròn

22

2 1 2.2 10.1 1 12

3 2 2.3 10.2 1 12

1 3 2.1 10.3 1 43

4 1 2.4 10.1 1 0



    



     





    



    



.

Cách 2

Đường tròn

22

2 10 1 0x y x y    

có tâm

(1; 5)I 

và bán kính

5R 

.

Ta tính độ dài lần lượt các phương án

37 ; 13 ; 2 17 ; 5IA R IB R IC R ID R       

Câu 36: [0H3-2.21-2] Xác định vị trí tương đối giữa 2 đường tròn

22

1

( ): 4 0C x y x  

và

22

2

( ): 8 0C x y y  

.

A.Tiếp xúc trong. B.Không cắt nhau. C.Cắt nhau. D.Tiếp xúc

ngoài.

Lời giải

Chọn C

Đường tròn

22

1

( ): 4 0C x y x  

có tâm

1

(2;0)I

, bán kính

1

2R 

.

Đường tròn

22

2

( ): 8 0C x y y  

có tâm

2

(0; 4)I 

, bán kính

2

4R 

.

Ta có

2 1 1 2 2 1

25R R I I R R    

nên hai đường tròn cắt nhau.

Câu 37: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng

: 7 0xy   

và đường tròn

 

22

: 25 0C x y  

.

A.

 

3;4

và

 

4;3

. B.

 

4;3

. C.

 

3;4

. D.

 

3;4

và

 

4;3

.

Lời giải

Chọn D

Giải hệ PT

22

25 0

70

xy



  



  





2

2 14 24 0

7

xx

yx



  









43

34

xx

hay

yy











Câu 38: [0H3-2-2] Đường tròn

22

2 2 23 0x y x y    

cắt đường thẳng

20xy

theo một

dây cung có độ dài bằng bao nhiêu?

A.

5

. B.

2 23

. C.

10

. D.

52

.

Lời giải

Chọn B

Giải hệ PT

22

2 2 23 0

20

x y x y

xy



    









2

2 23 0

2

x

yx













46 46

22

4 46 4 46

22

xx

hay

yy



  















. Vậy hai giao điểm là

46 4 46

;

22

A









,

46 4 46

;

22

B









. Độ dài dây cung

2 23AB 

Câu 39: [0H3-2-2] Đường tròn

22

2 2 23 0x y x y    

cắt đường thẳng

20xy  

theo một

dây cung có độ dài bằng bao nhiêu?

A.

10

. B.

8

. C.

6

. D.

32

.

Lời giải

Chọn A

Giải hệ PT

22

2 2 23 0

20

x y x y

xy



    



  





2

2 4 23 0

2

xx

yx













2 5 2 2 5 2

22

2 5 2 2 5 2

22

xx

hay

yy





















Độ dài dây cung

10AB 

Câu 40: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Oy

?

A.

22

10 2 1 0x y x y    

. B.

22

4 5 0x y y   

.

C.

22

10xy  

. D.

22

30x y x y    

.

Lời giải

Chọn A

PT

:0Oy x 

– Tâm và bán kính của

22

10 2 1 0x y x y    

là

 

1

5; 1I 

,

1

5R 

.

Khoảng cách

 

11

;5d I Oy R

 đường tròn này tiếp xúc

Oy

– Tâm và bán kính của

22

4 5 0x y y   

là

 

2

0;2I

,

2

3R 

Khoảng cách

 

22

;0d I Oy R

 đường tròn này không tiếp xúc

Oy

– Tâm và bán kính của

22

10xy  

là

 

3

0;0IO

,

3

1R 

Khoảng cách

 

33

;0d I Oy R

 đường tròn này không tiếp xúc

Oy

– Tâm và bán kính của

22

30x y x y    

là

4

11

;

22

I









,

4

14

2

R 

Khoảng cách

 

44

1

;

2

d I Oy R

đường tròn này không tiếp xúc

Oy

CÁCH 2: PT

:0Oy x 

. Giải hệ PT

Oy

và PT đường tròn bằng phương pháp thế

0x 

vào PT đường tròn; nếu PT nào được nghiệm kép theo

y

thì khi đó

Oy

tiếp xúc đường

tròn.

Hệ

22

0

10 2 1 0

x

x y x y







    



có nghiệm kép

1y 

nên đường tròn này tiếp xúc

Oy

Câu 41: [0H3-2.21-2] Tìm giao điểm 2 đường tròn

 

22

1

: 2 0C x y  

và

 

22

2

: 2 0C x y x  

A.

 

2;0

và

 

0;2

. B.

 

2;1

và

 

1; 2

.

C.

 

1; 1

và

 

1;1

. D.

 

1;0

và

 

0; 1

.

Lời giải

Chọn C

Giải hệ PT

22

20

xy

x y x



  





  







22

20

2 2 0

xy

x



  









11

xx

hay

yy







  



.

Vậy hai giao điểm

 

1;1A

,

 

1; 1B 

Câu 42: [0H3-2-2] Đường tròn

22

4 2 1 0x y x y    

tiếp xúc đường thẳng nào trong các đường

thẳng dưới đây?

A.Trục tung. B.

4 2 1 0xy  

. C.Trục hoành. D.

2 4 0xy  

.

Lời giải

Chọn A

Đường tròn có tâm và bán kính:

 

2;1I

,

2R 

. Tính khoảng cách từ tâm

I

đến từng

đường thẳng và so sánh

R

.

* Xét trục tung

:0Oy x 

có

 

,2d I Oy R

 đường tròn tiếp xúc trục tung

Oy

* Xét đường thẳng

:4 2 1 0xy   

có

 

9

,

20

d I R  

 đường tròn không tiếp

xúc



* Xét trục hoành

:0Ox y 

có

 

,1d I Ox R

 đường tròn tiếp xúc trục tung

Ox

* Xét đường thẳng

:2 4 0D x y  

có

 

1

,

5

d I D R

 đường tròn không tiếp

xúc

D

Câu 43: [0H3-2-1] Cho đường tròn

22

5 7 3 0x y x y    

. Tìm khoảng cách từ tâm đường tròn

tới trục

Ox

A.

5

. B.

7

. C.

3,5

. D.

2,5

.

Lời giải

Chọn C

Đường tròn có tâm :

57

;

22

I









. Khoảng cách

 

7

,

2

d I Ox 

=

3,5

Câu 44: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng  :

yx

và đường tròn (C) :

22

20x y x  

.

A.

 

0;0

. B.

 

0;0

và

 

1;1

. C.

 

2;0

. D.

 

1;1

.

Lời giải

Chọn B

Ta có:

2 2 2

0

1

2 0 2 2 0

y x y x

xy

x y x x x















    





Câu 45: [0H3-2-3] Với những giá trị nào của

m

thì đường thẳng

:3 4 3 0xy   

tiếp xúc với

đường tròn

 

22

:( ) 9C x m y  

A.

0m 

và

1m 

. B.

4m 

và

6m 

C.

2m 

D.

6m 

Lời giải

Chọn B

Ta có

 

C

có tâm

 

;0Im

và bán kính

3R 

nên theo đề bài ta được:

 

22

3 4.0 3

; 3 3 3 3 15 4 6

34

m

d I m m m



           



Câu 46: [0H3-2-2] Tọa độ giao điểm của đường tròn

 

22

: 2 2 1 0x y x yC     

và đường thẳng

1

:

22

xt

yt













A.

 

1; 2

và

 

2; 1

. B.

 

1; 2

và

12

;

55







.

C.

 

2; 5

. D.

 

1; 0

và

 

0; 1

.

Lời giải

Chọn B

Thế

1

22

xt

yt











vào

 

C

ta có:

           

 

2 2 2

1;2

11

1 2 2 2 1 2 2 2 1 0 5 1 6 1 1 0

1

12

1

;

5

55

t

t t t t t t

t









                

















Câu 47: [0H3-2.21-2] Xác định vị trí tương đối giữa 2 đường tròn

 

22

1

:4C x y

và

 

22

2

:( 3) ( 4) 25C x y   

.

A.Không cắt nhau. B.Cắt nhau. C.Tiếp xúc ngoài. D.Tiếp xúc

trong.

Lời giải

Chọn B

Ta có: tâm

   

12

0;0 , 3;4II

, bán kính

12

2, 5RR

nên

2 1 1 2 2 1

3 5 7R R I I R R      

nên 2 đường tròn trên cắt nhau, do đó

Câu 48: [0H3-2-2] Đường tròn (C):

22

60x y x  

không tiếp xúc đường thẳng nào trong các

đường thẳng dưới đây?

A.

20y 

. B.

60x

. C.Trục tung. D.

30y

.

Lời giải

Chọn A

Ta có: tâm

 

3;0I

và bán kính

3R 

.

Với

 

: 2 0y  

thì

 

;2d I R  

nên (C) cắt

 



do đó chọn B.

Câu 49: [0H3-2-2] Đường tròn

22

2 2 23 0x y x y    

cắt đường thẳng

20xy  

theo một

dây cung có độ dài bằng bao nhiêu ?

A.

6

. B.

10

. C.

5

. D.

52

.

Lời giải

Chọn B

Đường tròn

22

2 2 23 0x y x y    

có tâm

 

1;1I

và bán kính

5R 

.

Vì

I

thuộc đường thẳng

: 2 0xy   

nên



cắt đường tròn theo đường kính có độ

dài

2 10R 

.

Câu 50: [0H3-2-2] Đường tròn.

22

2 2 23 0x y x y    

cắt đường thẳng

3 4 8 0xy  

theo

một dây cung có độ dài bằng bao nhiêu ?

A.

8

. B.

6

. C.

4

. D.

32

.

Lời giải

Chọn A

Đường tròn

22

2 2 23 0x y x y    

có tâm

 

1;1I

và bán kính

5R 

.

Vì khoảng cách từ

I

đến đường thẳng

:3 4 8 0xy   

là

 

,3d d I  

nên



cắt

đường tròn theo đường kính có độ dài

22

28l R d  

.

Câu 51: [0H3-2-2] Đường tròn

22

–1 0xy

tiếp xúc với đường thẳng nào sau đây ?

A.

3 4 5 0xy  

. B.

10xy  

. C.

0xy

. D.

3 4 1 0xy  

.

Lời giải

Chọn A

Đường tròn

22

–1 0xy

có tâm là gốc tọa độ

O

và bán kính

1R 

.

Để đường thẳng tiếp xúc với đường tròn thì khoảng cách từ

O

đến đường thẳng bằng 1.

Câu 52: [0H3-2-2] Đường tròn

22

– 4 2 1 0x y x y   

tiếp xúc với đường thẳng nào sau đây ?

A. Trục tung. B.

4 2 1 0xy  

. C.

2 4 0xy  

. D. Trục hoành.

Lời giải

Chọn A

Đường tròn

22

– 4 2 1 0x y x y   

có tâm

 

2;1I

và bán kính

2R 

.

Để đường thẳng tiếp xúc với đường tròn thì khoảng cách từ

I

đến đường thẳng bằng 2.

Câu 53: [0H3-2-2] Đường tròn

22

– 4 2 4 0x y x y   

tiếp xúc với đường thẳng nào sau đây ?

A. Trục tung. B.

4 2 1 0xy  

. C.

3 4 13 0xy  

. D. Trục hoành.

Lời giải

Chọn C

Đường tròn

22

– 4 2 4 0x y x y   

có tâm

 

2;1I

và bán kính

3R 

.

Để đường thẳng tiếp xúc với đường tròn thì khoảng cách từ

I

đến đường thẳng bằng 3.

Câu 54: [0H3-2-2] Đường tròn

22

– 6 0x y x

không tiếp xúc với đường thẳng nào sau đây ?

A.

20y 

. B. Trục tung. C.

60x

. D.

30y 

.

Lời giải

Chọn A

Đường tròn

22

– 6 0x y x

có tâm

 

3;0I

và bán kính

3R 

.

Để đường thẳng không tiếp xúc với đường tròn thì khoảng cách từ

I

đến đường thẳng

khác 3.

Câu 55: [0H3-2-2] Đường tròn

22

60x y x  

không tiếp xúc với đường thẳng nào sau đây ?

A.

20y 

. B. Trục tung. C.

60x 

. D.

30y 

.

Lời giải

Chọn A

Đường tròn

22

60x y x  

có tâm

 

3;0I 

và bán kính

3R 

.

Để đường thẳng không tiếp xúc với đường tròn thì khoảng cách từ

I

đến đường thẳng

khác 3.

Câu 56: [0H3-2-2] Đường tròn

22

40x y y  

không tiếp xúc với đường thẳng nào sau đây ?

A.

30xy  

. B. Trục hoành. C.

20x

. D.

20x 

.

Lời giải

Chọn A

Đường tròn

22

40x y y  

có tâm

 

0; 2I 

và bán kính

2R 

.

Để đường thẳng không tiếp xúc với đường tròn thì khoảng cách từ

I

đến đường thẳng

khác 2.

Câu 57: [0H3-2-2] Trong các đường tròn sau đây, đường tròn nào tiếp xúc với trục

Ox

?

A.

22

– 5 0xy

. B.

22

– 2 10 0x y x y  

.

C.

22

–10 1 0x y x  

. D.

22

6 5 9 0x y x y    

.

Lời giải

Chọn D

Đường tròn tiếp xúc với trục

Ox

thì khoảng cách từ tâm của đường tròn đến trục

Ox

bằng bán kính. Tức là đường tròn có tâm

 

,I a b

và bán kính

Rb

.

Trắc nghiệm: cho

0y 

được phương trình bậc hai theo ẩn

x

có nghiệm kép.

Câu 58: [0H3-2-2] Trong các đường tròn sau đây, đường tròn nào tiếp xúc với trục

Ox

?

A.

22

– 5 0xy

. B.

22

4 2 4 0x y x y    

.

C.

22

–10 1 0x y x  

. D.

22

– 2 10 0x y x  

.

Lời giải

Chọn B

Đường tròn tiếp xúc với trục

Ox

thì khoảng cách từ tâm của đường tròn đến trục

Ox

bằng bán kính. Tức là đường tròn có tâm

 

,I a b

và bán kính

Rb

.

Trắc nghiệm: cho

0y 

được phương trình bậc hai theo ẩn

x

có nghiệm kép.

Câu 59: [0H3-2-2] Trong các đường tròn sau đây đường tròn nào tiếp xúc với trục

Oy

?

A.

22

+y 5=0x 

. B.

22

– 2 0yxx 

.

C.

22

–10 1 0x y x 

. D.

22

6 5 1 0x y x y    

.

Lời giải

Chọn B

-Trục

Oy

có phương trình trục

0x 

Đường tròn

2 2 2 2

– 2 0 ( 1) 1yx x x y   

có tâm

 

1,0I

và bán kính

1R 

.

Khoảng cách từ tâm

 

1,0I

đến đường thẳng

 

Oy

là

|1|

( , ) 1

1

d I Oy R  

.Chọn B

Đường tròn

22

+y 5=0x 

có tâm

 

0,0O

và bán kính

5R 

,

Khoảng cách từ tâm

 

0,0O

đến đường thẳng

 

Oy

là

| 0 |

(O, ) 0

1

d Oy R  

loại A.

Đường tròn

22

–10 1 0x y x 

có tâm

 

5,0I

và bán kính

2

5 1 24R   

,

Khoảng cách từ tâm

 

5,0I

đến đường thẳng

 

Oy

là

|5|

(I, ) 5

1

d Oy R  

loại C.

Đường tròn

22

6 5 1 0x y x y    

có tâm

5

3,

2

I













và bán kính

22

5 65

( 3) ( ) 1

24

R      

Khoảng cách từ tâm

5

3,

2

I













đến đường thẳng

 

Oy

là

| 3|

(I, ) 3

1

d Oy R



  

loại

D.

Câu 60: [0H3-2-2] Trong các đường tròn sau đây đường tròn nào tiếp xúc với trục

Oy

?

A.

22

–1 0xy

. B.

22

–10 2 1 0x y x y   

.

C.

22

30x y x y

. D.

22

+ 4 5 0x y y 

.

Lời giải

Chọn B

-Trục

Oy

có phương trình trục

0x 

Đường tròn

22

–10 2 1 0x y x y   

có tâm

 

5, 1I 

và bán kính

21

5 1 1 5R    

.

Khoảng cách từ tâm

 

5, 1I 

đến đường thẳng

 

Oy

là

|5|

( , ) 5

1

d I Oy R  

. Chọn B

Đường tròn

22

+y =01x 

có tâm

 

0,0O

và bán kính

1R 

,

Khoảng cách từ tâm

 

0,0O

đến đường thẳng

 

Oy

là

| 0 |

(O, ) 0

1

d Oy R  

loại A.

Đường tròn

22

30x y x y

có tâm

11

,

22

I













và bán kính

22

1 1 7

( ) ( ) 3

2 2 2

R



    

,

Khoảng cách từ tâm

11

,

22

I













đến đường thẳng

 

Oy

là

1

||

1

2

(I, )

12

d Oy R



  

loại C.

Đường tròn

22

+ 4 5 0x y y 

có tâm

 

0,2I

và bán kính

22

5 65

( 3) ( ) 1

24

R      

,

Khoảng cách từ tâm

 

0,2I

đến đường thẳng

 

Oy

là

| 0 |

(I, ) 0

1

d Oy R  

loại D.

Câu 61: [0H3-2-3] Với giá trị nào của

m

thì đường thẳng

4 3 0x y m  

tiếp xúc với đường

tròn

22

90xy  

?

A.

15m 

. B.

3m  

. C.

3m 

. D.

3m 

.

Lời giải

Chọn A

Đường tròn

22

90xy  

có tâm

 

0,0I

và bán kính

3R 

. Gọi

 

3 4: 0d x y m  

Khoảng cách từ tâm

 

0,0I

đến đường thẳng

 

d

là

| m |

( ,d) 3 15

5

h I m    

.

Câu 62: [0H3-2-3] Với giá trị nào của

m

thì đường thẳng

:3 4 3 0d x y  

tiếp xúc với đường

tròn

 

22

:( ) 9mC xy  

?

A.

4 6m và m  

. B.

= 2m

. C.

6m 

. D.

0 1m và m

.

Lời giải

Chọn A

Đường tròn

22

9()x m y  

có tâm

 

;0Im

và bán kính

3R 

. Gọi

3 4: 30xyd   

Khoảng cách từ tâm

 

,0Im

đến đường thẳng

 

d

là

6

|3m 3|

( ,d) 3

4

5

m

dI

m







  







.

Câu 1: [0H3-2-2] Cho đường cong

 

22

: –8 10 0

m

C x y x y m   

. Với giá trị nào của

m

thì

 

m

C

là đường tròn có bán kính bằng

7

?

A.

4m

. B.

8m 

. C.

–8m 

. D.

= – 4m

.

Hướng dẫn giải

Chọn C

Ta có

22

4 5 7 8R m m      

.

Dạng 2. Viết phương trình đường tròn

Câu 2: [0H3-2-2] Đường tròn tâm

(3; 1)I 

và bán kính

2R 

có phương trình là

A.

22

( 3) ( 1) 4xy   

. B.

22

( 3) ( 1) 4xy   

.

C.

22

( 3) ( 1) 4xy   

. D.

22

( 3) ( 1) 4xy   

.

Hướng dẫn giải

Chọn C

Phương trình đường tròn có tâm

 

3; 1I 

, bán kính

2R 

là:

   

22

3 1 4xy   

Câu 3: [0H3-2-2] Đường tròn tâm

( 1;2)I 

và đi qua điểm

(2;1)M

có phương trình là

A.

22

2 4 5 0x y x y    

. B.

22

2 4 3 0.x y x y    

C.

22

2 4 5 0x y x y    

. D.

22

2 4 5 0.x y x y    

Hướng dẫn giải

Chọn A

Đường tròn có tâm

 

1;2I 

và đi qua

 

2;1M

thì có bán kính là:

 

2

3 1 10R IM    

Khi đó có phương trình là:

   

22

1 2 10 2 4 5 0x y x y x y         

Câu 4: [0H3-2-2] Đường tròn tâm

(1; 4)I

và đi qua điểm

(2; 6)B

có phương trình là

A.

   

22

1 4 5xy   

. B.

   

22

1 4 5xy   

C.

   

22

1 4 5xy   

. D.

   

22

1 4 5xy   

Hướng dẫn giải

Chọn D

Đường tròn có tâm

(1; 4)I

và đi qua

(2; 6)B

thì có bán kính là:

   

22

2 1 6 4 5R IB     

Khi đó có phương trình là:

   

22

1 4 5xy   

Câu 5: [0H3-2-2] Đường tròn

()C

tâm

( 4;3)I 

và tiếp xúc với trục tung có phương trình là

A.

22

304 9x y x y

. B.

22

( 4) ( 3) 16xy   

.

C.

22

( 4) ( 3) 16xy   

. D.

22

8 6 12 0.x y x y    

Hướng dẫn giải

Chọn B

 

C

tiếp xúc với

'y Oy

và có tâm

 

4; 3I 

nên:

4, 3, 4a b R a    

.

Do đó,

 

C

có phương trình

   

22

4 3 16xy   

.

Câu 6: [0H3-2-2] Đường tròn

()C

tâm

(4; 3)I

và tiếp xúc với đườngthẳng

:3 4 5 0xy   

có phương trình là

A.

22

( 4) ( 3) 1xy   

. B.

22

( 4) ( 3) 1xy   

.

C.

22

( 4) ( 3) 1xy   

. D.

22

( 4) ( 3) 1xy   

Hướng dẫn giải

Chọn B

 

C

có bán kính

 

2

3.4 4.3 5

,1

34

R d I



   



.

Do đó,

 

C

có phương trình

22

( 4) ( 3) 1xy   

.

Câu 7: [0H3-2-2] Đường tròn

 

C

đi qua điểm

 

2;4A

và tiếp xúc với các trục tọa độ có

phương trình là

A.

22

( 2) ( 2) 4xy   

hoặc

22

( 10) ( 10) 100xy   

B.

22

( 2) ( 2) 4xy   

hoặc

22

( 10) ( 10) 100xy   

C.

22

( 2) ( 2) 4xy   

hoặc

22

( 10) ( 10) 100xy   

D.

22

( 2) ( 2) 4xy   

hoặc

22

( 10) ( 10) 100xy   

Hướng dẫn giải

Chọn A

     

22

2

:C x a y b R   

tiếp xúc với các trục tọa độ nên

a b R

và điểm

   

2; 4AC

nằm trong góc phần tư thứ nhất nên

 

;I a b

cũng ở góc phần tư thứ

nhất. Suy ra

a b R

. Vậy

     

22

2

x a y a a C   

.

     

22

2 4 12 20 0A C a a a a a         

   

22

2 2 4

2

10

10 10 100

xy

a

xy



   

















   



Câu 8: [0H3-2-2] Đường tròn

()C

có tâm

( 1;3)I 

và tiếp xúc với đường thẳng

:3 4 5 0d x y  

có phương trình là

A.

22

( 1) ( 3) 4xy   

. B.

22

( 1) ( 3) 2xy   

.

C.

22

( 1) ( 3) 10xy   

. D.

22

( 1) ( 3) 2xy   

.

Hướng dẫn giải

Chọn A

Đường tròn có bán kính

 

22

3.( 1) 4(3) 5

,2

3 ( 4)

R d I d

  

  



.

Vậy phương đường tròn là:

   

22

1 3 4xy   

Câu 9: [0H3-2-2] Có một đường tròn đi qua hai điểm

(1;3)A

,

( 2;5)B 

và tiếp xúc với đường

thẳng

:2 4 0d x y

. Khi đó

A. phương trình đường tròn là

22

3 2 8 0x y x y    

.

B. phương trình đường tròn là

22

3 4 6 0x y x y    

.

C. phương trình đường tròn là

22

5 7 9 0x y x y    

.

D. Không có đường tròn nào thỏa mãn bài toán.

Hướng dẫn giải

Chọn D

Đặt

 

; 2 4f x y x y  

. Ta có:

   

1;3 3 0, 2;5 4 5 4 0ff       

ở ngoài

 

C

.



A

,

B

ở hai bên đường thẳng

d

; do đó không có đường tròn nào thỏa điều kiện

đề bài.

Câu 10: [0H3-2-2] Đường tròn

()C

đi qua hai điểm

(1;3)A

,

(3;1)B

và có tâm nằm trên đường

thẳng

:2 7 0d x y

có phương trình là

A.

22

( 7) ( 7) 102xy   

. B.

22

( 7) ( 7) 164xy   

.

C.

22

( 3) ( 5) 25xy   

. C.

22

( 3) ( 5) 25xy   

.

Hướng dẫn giải

Chọn B

 

;I a b

là tâm của đường tròn

 

C

, do đó:

       

2 2 2 2

22

1 3 3 1AI BI a b a b        

Hay:

(1)ab

. Mà

 

; :2 7 0 nên 2 7 0 (2)I a b d x y a b      

.

Thay (1) vào (2) ta có:

22

7 7 164a b R AI       

.

Vậy

     

22

: 7 7 164C x y   

.

Câu 11: [0H3-2-2] Đường tròn

()C

tiếp xúc với trục tung tại điểm

(0; 2)A 

và đi qua điểm

(4; 2)B 

có phương trình là

A.

22

( 2) ( 2) 4xy   

. B.

22

( 2) ( 2) 4xy   

C.

22

( 3) ( 2) 4xy   

D.

22

( 3) ( 2) 4xy   

Hướng dẫn giải

Chọn A

Vì

2 nên '

AB

y y AB y Oy   

và

AB

là đường kính của

 

C

. Suy ra

 

2; 2I 

và bán kính

2R IA

. Vậy

     

22

: 2 2 4C x y   

.

Câu 12: [0H3-2-2] Tâm của đường tròn qua ba điểm

 

2; 1A

,

 

2; 5B

,

 

2; 1C 

thuộc đường

thẳng có phương trình

A.

30xy  

. B.

30xy  

C.

30xy  

D.

30xy  

Hướng dẫn giải

Chọn A

Phương trình

 

C

có dạng:

2 2 2 2

2 2 0 ( 0)x y ax by c a b c       

. Tâm

 

;I a b

.

   

 

2; 1

4 1 4 2 0 0

2; 5 4 25 4 10 0 3 0; 3

4 1 4 2 0 1

2; 1

AC

a b c a

B C a b c b I

a b c c

CC





     







         

  

  

     







Lần lượt thế tọa độ

I

vào các phương trình để kiểm tra.

Câu 13: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua 3 điểm

 

0;4A

,

 

2;4B

,

 

4;0C

.

A.

 

0;0

. B.

 

1;0

. C.

 

3;2

. D.

 

1;1

.

Hướng dẫn giải

Chọn D

Gọi

 

22

: 2 2 0C x y ax by c    

.

 

,,A B C C

nên

16 8 0

20 4 8 0

16 8 0

bc

a b c

ac

  





   





  





1

8

a

b

c

















.

Vậy tâm

 

1;1I

Câu 14: [0H3-2-2] Tìm bán kính đường tròn đi qua 3 điểm

 

0;4A

,

 

3;4B

,

 

3;0C

.

A.

5

. B.

3

. C.

10

. D.

5

2

.

Hướng dẫn giải

Chọn C

Gọi

 

22

: 2 2 0C x y ax by c    

.

 

,,A B C C

nên

16 8 0

25 6 8 0

9 6 0

bc

a b c

ac

  





   





  





3

2

0

a

b

c

















.

Vậy bán kính

22

R a b c  

=

10

Câu 15: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua 3 điểm

 

0;5A

,

 

3;4B

,

 

4;3C 

.

A.

 

6; 2

. B.

 

1; 1

. C.

 

3;1

. D.

 

0;0

.

Hướng dẫn giải

Chọn D

Gọi

 

22

: 2 2 0C x y ax by c    

.

 

,,A B C C

nên

25 10 0

25 6 8 0

25 8 6 0

bc

a b c

  





   





   





0

25

a

b

c

















.

Vậy tâm

 

0;0IO

Câu 16: [0H3-2-2] Tìm bán kính đường tròn đi qua 3 điểm

 

0;0A

,

 

0;6B

,

 

8;0C

.

A.

6

. B.

5

. C.

10

. D.

5

.

Hướng dẫn giải

Chọn B

Gọi

 

22

: 2 2 0C x y ax by c    

.

 

,,A B C C

nên

00

36 12 0

64 16 0

c

bc

ac







  





  





4

3

0

a

b

c

















.

Vậy bán kính

22

R a b c  

=

5

Câu 17: [0H3-2-2] Đường tròn nào dưới đây đi qua 3 điểm

 

2;0A

,

 

0;6B

,

 

0;0O

?

A.

22

3 8 0x y y   

B.

22

2 6 1 0x y x y    

.

C.

22

2 3 0x y x y   

D.

22

2 6 0x y x y   

.

Hướng dẫn giải

Chọn D

Thay toạ độ ba điểm

,,A B C

vào từng phương trình; nếu cùng thoả một phương trình

nào thì đường tròn đó qua ba điểm

,,A B C

Câu 18: [0H3-2-2] Đường tròn đi qua 3 điểm

     

0;0 , ;0 , 0;O A a B b

có phương trình là

A.

22

20x y ax by   

. B.

22

0x y ax by xy    

.

C.

22

0.   x y ax by

D.

22

0x y ay by   

.

Hướng dẫn giải

Chọn C

Ta có tam giác

OAB

vuông tại

O

nên tâm

I

của đường tròn đi qua 3 điểm

     

0;0 , ;0 , 0;O A a B b

là trung điểm

;

22

ab

AB I









và bán kính

22

1

2

R a b

.

Phương trình đường tròn đi qua 3 điểm

     

0;0 , ;0 , 0;O A a B b

là

22

0

2 2 4

a b a b

x y x y ax by



   

        

   

   

Câu 19: [0H3-2-2] Đường tròn đi qua 3 điểm

   

0;2 , 2;2 , 1; 2()1A B C 

có phương trình

là

A.

22

2 2 2 0x y x y    

. B.

22

2 2 0x y x y   

.

C.

22

2 2 2 0x y x y    

. D.

22

2 2 2 0x y x y    

.

Hướng dẫn giải

Chọn B

Gọi phương trình đường tròn cần tìm có dạng:

 

2 2 2 2

2 2 0 0x y ax by c a b c       

.

Đường tròn đi qua 3 điểm

   

0;2 , 2;2 , 1; 2()1A B C 

nên ta có:

 

4 4 0 1

8 4 4 0 1

0

4 2 2 2 2 1 2 0

b c a

a b c b

c

a b c



   







     









     





Vậy phương trình đường tròn đi qua 3 điểm

   

0;2 , 2;2 , 1; 2()1A B C 

là

22

2 2 0x y x y   

Câu 20: [0H3-2-2] Đường tròn đi qua 3 điểm

     

11;8 , 13;8 , 14;7A B C

có bán kính

R

bằng

A.

2

. B.

1

. C.

5

. D.

2

.

Hướng dẫn giải

Chọn C

Gọi phương trình đường tròn cần tìm có dạng:

 

2 2 2 2

2 2 0 0x y ax by c a b c       

.

Đường tròn đi qua 3 điểm

     

11;8 , 13;8 , 14;7A B C

nên ta có:

121 64 22 16 0 12

169 64 26 16 0 6

196 49 28 14 0 175

a b c a

a b c b

a b c c

     





      





     



Ta có

22

5R a b c   

Vậy phương trình đường tròn đi qua 3 điểm

     

11;8 , 13;8 , 14;7A B C

có bán kính

là

5R 

.

Câu 21: [0H3-2-2] Đường tròn đi qua 3 điểm

   

1;2 , 2();3 , 4;1A B C

có tâm

I

có tọa độ là

A.

(0; )1

.

B.

 

0;0

.

C. Không có đường tròn đi qua 3 điểm đã cho.

D.

1

3;

2







.

Hướng dẫn giải

Chọn C

Ta có:

   

3;1 , 6; 2AB BC

2BC AB  

nên 3 điểm

,,A B C

thẳng hàng.

Vậy không có đường tròn qua 3 điểm

   

1;2 , 2();3 , 4;1A B C

.

Câu 22: [0H3-2-2] Viết phương trình đường tròn đi qua 3 điểm

( 1;1), (3;1), (1;3)A B C

.

A.

22

2 2 2 0x y x y    

. B.

22

2 2 0x y x y   

.

C.

22

2 2 2 0x y x y    

. D.

22

2 2 2 0x y x y    

.

Hướng dẫn giải

Chọn A

Gọi phương trình đường tròn có dạng

22

( ): 2 2 0C x y ax by c    

trong đó

22

0a b c  

.

Vì

()C

đi qua 3 điểm

( 1;1), (3;1), (1;3)A B C

nên ta có hệ phương trình

1 1 2 2 0 2 2 2 1

9 1 6 2 0 6 2 10 1

1 9 2 6 0 2 6 10 2

a b c a b c a

a b c a b c b

a b c a b c c

           

  

  

            

  

  

          

  

.

Vậy phương trình đường tròn là

22

2 2 2 0x y x y    

.

Câu 23: [0H3-2-2] Đường tròn nào dưới đây đi qua 2 điểm

(1;0), (3;4)AB

?

A.

22

8 2 9 0x y x y    

. B.

22

3 16 0x y x   

.

C.

22

0x y x y   

. D.

22

4 4 3 0x y x y    

.

Hướng dẫn giải

Chọn D

Thử phương án

Điểm

(3;4)B

không thuộc đường trònA.

Điểm

(1;0)A

không thuộc đường tròn B.

Điểm

(3;4)B

không thuộc đường tròn C.

Điểm

(1;0), (3;4)AB

thuộc đường tròn D.

Câu 24: [0H3-2-2] Đường tròn nào sau đây đi qua ba điểm

     

2;0 , 0;6 , 0;0A B O

?

A.

22

2 6 1 0.x y x y    

B.

22

2 6 0.x y x y   

C.

22

2 3 0.x y x y   

D.

22

3 8 0.x y x   

Hướng dẫn giải

Chọn B

Câu 25: [0H3-2-2] Đường tròn nào sau đây đi qua ba điểm

   

, ;0 , 0;O A a B b

?

A.

22

0x y ax by   

B.

22

2 2 0.x y ax by   

C.

22

0x y ax by xy    

D.

22

0.x y ax by   

Hướng dẫn giải

Chọn D

Câu 26: [0H3-2-2] Đường tròn nào sau đây đi qua ba điểm

1()1;A 

,

 

3;1B

,

 

1;3C

?

A.

22

2 2 2 0x y x y    

. B.

22

2 2 2 0x y x y    

C.

22

2 2 0x y x y   

. D.

22

2 2 2 0x y x y    

.

Hướng dẫn giải

Chọn A

Câu 27: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua ba điểm có tọa độ

 

0;5

,

 

3;4

,

()4;3

?

A.

 

0;0

. B.

 

3;1

. C.

( 6; 2)

. D.

( 1; 1)

.

Hướng dẫn giải

Chọn A

Câu 28: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua ba điểm có tọa độ

 

0;4

,

 

2;4

,

 

4;0

?

A.

 

3;2

. B.

 

1;1

. C.

 

0;0

. D.

 

1;0

.

Hướng dẫn giải

Chọn B

Câu 29: [0H3-2-2] Tìm bán kính đường tròn đi qua ba điểm

 

0;4

,

 

3;4

,

 

3;0

?

A.

3

. B.

5

. C.

2,5

. D.

10

.

Hướng dẫn giải

Chọn C

Câu 30: [0H3-2-2] Tìm bán kính đường tròn đi qua ba điểm (0;0), (0;6), (8;0)?

A.

10

. B.

6

. C.

5

. D.

5

.

Hướng dẫn giải

Chọn D

Câu 31: [0H3-2-2] Phương trình nào sau đây là phương trình đường tròn đi qua 3 điểm

 

1;0A

,

 

0;2B

,

 

3;1C

?

A.

22

3 3 2 0x y x y    

. B.

22

3 3 2 0x y x y    

C.

22

3 3 2 0x y x y    

D.

22

3 3 0x y x y   

Hướng dẫn giải

Chọn B

Gọi

 

22

: 2 2 0C x y ax by c    

là đường tròn đi qua ba điểm

 

1;0A

,

 

0;2B

,

 

3;1C

Ta có hệ

2 0 1

3

0 4 2 4

2

6 2 10

a b c

ab

c

a b c

   











    







   



Vậy phương trình đường tròn

 

22

: 3 3 2 0C x y x y    

.

Câu 32: [0H3-2-2] Cho đường tròn

22

( ):( 3) ( 1) 10C x y   

. Phương trình tiếp tuyến của

()C

tại điểm

(4;4)A

là

A.

3 5 0xy  

. B.

3 4 0xy  

. C.

3 16 0xy  

. D.

3 16 0xy  

.

Hướng dẫn giải

Chọn D

 

C

có tâm

   

3;1 1; 3I IA

là vectơ pháp tuyến của tiếp tuyến

.D

Suy ra

   

:1 4 3 4 0 3 16 0D x y x y       

.

Câu 33: [0H3-2-2] Cho đường tròn

22

( ):( 2) ( 2) 9C x y   

. Phương trình tiếp tuyến của

()C

đi qua điểm

( 5;1)A 

là

A.

40xy  

và

20xy  

. B.

5x 

và

1y 

.

C.

2 3 0xy  

và

3 2 2 0xy  

. D.

3 2 2 0xy  

và

2 3 5 0xy  

.

Hướng dẫn giải

Chọn B

 

C

có tâm

 

2; 2I

và bán kính

3R 

.

 

;n A B

là vectơ pháp tuyến nên

   

: 5 1 0D A x B y   

.

D

là tiếp tuyến của

 

C

khi và chỉ khi :

 

   

22

2 5 2 1

, 3 . 0

AB

d I R A B

AB

  

     



0 chon 0 1

0 chon 0 5

A B y

B A x

    







   



.

Câu 34: [0H3-2-2] Cho đường tròn

22

( ): 2 2 0C x y ax by c    

22

( 0)a b c  

. Hỏi mệnh đề

nào sau đây sai?

A.

()C

có bán kính

22

R a b c  

.

B.

()C

tiếp xúc với trục hoành khi và chỉ khi

22

bR

.

C.

()C

tiếp xúc với trục tung khi và chỉ khi

aR

.

D.

()C

tiếp xúc với trục tung khi và chỉ khi

2

bc

.

Lời giải

Chọn C

 

C

tiếp xúc với

'y Oy

khi

 

,'d I y Oy R a R  

.

Do đó đáp án

 

C

sai vì nếu

9 9 0aR     

(vô lý)

Câu 35: [0H3-2-2] Mệnh đề nào sau đây đúng?

(I) Đường tròn

22

( 2) ( 3) 9xy   

tiếp xúc với trục tung.

(II) Đường tròn

22

( 3) ( 3) 9xy   

tiếp xúc với các trục tọa độ.

A. Chỉ (I). B. Chỉ (II). C. Cả (I) và (II). D. Không có.

Lời giải

Chọn B

     

22

: 2 3 9I x y   

. Vì

3bR

nên đường tròn tiếp xúc với

 

'x Ox I

sai.

     

22

: 3 3 9II x y   

. Vì

3a b R  

nên đường tròn tiếp xúc với các trục tọa

độ nên

 

II

đúng.

Câu 36: [0H3-2-2]Đường tròn có tâm

O

và tiếp xúc với đường thẳng

: 4 2 0d x y  

. Hỏi

bán kính của đường tròn bằng bao nhiêu?

A.

42

. B.

4

. C.

15

. D.

1

.

Lời giải

Chọn B

Tâm

 

0,0O

bán kính

R

. Gọi

4: 2 0xyd   

Khoảng cách từ tâm

 

0,0O

đến đường thẳng

 

d

là

| 4 2 |

(O,d) 4 4

2

dR   

.

Câu 37: [0H3-2-3]Đường tròn

 

22

: – 2 2 1 0C x y x y   

cắt đường thẳng

: 2 0d x y  

theo một dây cung có độ dài bằng bao nhiêu?

A.

1

. B.

2

. C.

2

. D.

2

.

Lời giải

Chọn B

Tâm

 

1,1I

bán kính

1R 

. Gọi

2: 0xyd   

,

Khoảng cách từ tâm

(1 );1I

đến đường thẳng

 

d

là

(I,d) 0d 

nên dây cung đi qua

tâm

I

có độ dài bằng đường kính.

Câu 38: [0H3-2-2]Đường tròn có tâm

2(3; )I 

và tiếp xúc với đường thẳng

: 5 1 0.d x y  

Hỏi bán kính của đường tròn bằng bao nhiêu?

A.

26

. B.

14

26

. C.

7

13

. D.

6

.

Lời giải

Chọn B

Tâm

2(3; )I 

bán kính

R

. Gọi

5: 10  xyd

Khoảng cách từ tâm

2(3; )I 

đến đường thẳng

d

là

|3 10 1| 14 14

( , )

1 25 26 26

d I d R



   



.

Câu 39: [0H3-2-2]Đường tròn có tâm

 

1;3 I

và tiếp xúc với đường thẳng

:3 4 0d x y

.

Hỏi bán kính của đường tròn bằng bao nhiêu?

A.

3

5

. B.

3

. C.

1

. D.

2

.

Lời giải

Chọn B

Tâm

 

1;3 I

bán kính

R

. Gọi

0:34xd y

Khoảng cách từ tâm

 

1;3 I

đến đường thẳng

d

là

22

|3 3.4|

( , ) 3 3

34

d I d R



   



.

Câu 40: [0H3-2-2]Tìm toạ độ giao điểm của đường tròn

 

22

: + 25 0C x y 

và đường thẳng

: 7 0xy   

?

A.

 

3;4

. B.

 

4;3

. C.

 

3;4

và

 

4;3

. D.

 

3;4

và

( )4;3

.

Lời giải

Chọn C

Tọa độ giao điểm là nghiệm của hệ

 

22

– 25 0 1

7 02

xy



 











Từ

 

2

ta được

 

73yx  

Thay

 

3

vào

 

1

ta được phương trình

2

34

2 14 24

4

0

3

xy

xx

xy

  







 







Câu 41: [0H3-2-2]Tìm toạ độ giao điểm của đường tròn

 

22

: – 2 4 0C x y x y  

và đường

thẳng

: 2 3 0d x y  

A.

 

3;3

và

 

1;1

. B.

()1;1

và

(3; )3

. C.

 

2;1

và

(2; )1

. D.

 

3;3

và

()1;1

.

Lời giải

Chọn D

Tọa độ giao điểm là nghiệm của hệ

 

22

–2

02

4 0 1

23

x y x y

xy



















Từ

 

2

ta được

 

2 3 3xy

Thay

 

3

vào

 

1

ta được phương trình

2

33

5 20 15

1

0

1

yx

yy

yx

  



  



   





Câu 42: [0H3-2-2]Tìm toạ độ giao điểm của đường tròn

 

22

: – 2 0C x y x

và đường thẳng

:0d x y

?

A.

 

0;0

. B.

 

1;1

. C.

 

2;0

. D.

 

0;0

và

(1;1)

.

Lời giải

Chọn D

Toạ độ giao điểm của

d

và

 

C

là nghiệm của hệ

2 2 2 2 2 2

0

1

2 0 2 0 2 0

0





  

     





  



   





  

   









x y x x y x x x x

x y y

x

x y x

yx

x

0

x

y













hoặc

1

x

y











.

Câu 43: [0H3-2-2]Toạ độ giao điểm của đường tròn

 

22

: – 2 2 1 0C x y x y   

và đường

thẳng

1

:

22

xt

yt













A.

 

1;0

và

 

0;1

. B.

 

1;2

và

 

2;1

. C.

 

1;2

và

12

;

55







. D.

 

2;5

.

Lời giải

Chọn D

Tọa độ giao điểm của

 

C

và



là nghiệm của hệ

 

22

1

– 2 2

2

22

01

3

1x y x y

xt

yt























Thay

 

2

,

 

3

vào

 

1

ta được phương trình

2 2 2

(2 2 ) – 2(1 ) 2(2 2 ) 1 0( 501 4) 0t t t tt tt          

hoặc

4

5

t





Câu 44: [0H3-2.21-2]Tìm toạ độ giao điểm của hai đường tròn

 

22

1

: 2 0C x y  

và

 

22

2

: – 2 0C x y x

?

A.

 

2;0

và

()2;0

. B.

(1; )1

và

 

1;1

.

C.

( 2;1)

và

(1; 2)

. D.

( 2; 2)

và

(2; 2)

.

Lời giải

Chọn B

Tọa độ giao điểm của

 

1

C

và

 

2

C

là nghiệm của hệ

 

22

+

– 2 0 1

2 0 2

x y x

xy

















Lấy

 

1

trừ

 

2

ta được

 

2 0 1 32xx  

Thay

 

3

vào

 

2

ta được phương trình

2

1

0

y















Câu 45: [0H3-2.21-3]Tìm toạ độ giao điểm của hai đường tròn

 

22

1

: 4 0C x y  

và

 

22

2

: – 4 4 4 0C x y x y   

A.

 

2;0

và

()2;0

. B.

 

2;0

và

(0;2)

.

C.

( 2;1)

và

(1; 2)

. D.

( 2; 2)

và

(2; 2)

.

Lời giải

Chọn B

Tọa độ giao điểm của

 

1

C

và

 

2

C

là nghiệm của hệ

 

22

– 4 4

+4 0

41

2

0x y x y

xy











  







Lấy

 

1

trừ

 

2

ta được

 

4 4 +4 4 0 2 3x y x y     

Thay

 

3

vào

 

2

ta được phương trình

2

02

24

20

0

yx

yy

yx

  





  

 





Câu 46: [0H3-2.21-3]Tìm toạ độ giao điểm của hai đường tròn

 

22

1

: 5 0C x y  

và

 

22

2

: 4 8 +15 0C x y x y

A.

 

1;2

và

 

2;1

. B.

 

1;2

. C.

 

1;2

và

( 2; 3)

. D.

 

1;2

và

 

0;1

.

Lời giải

Chọn B

Tọa độ giao điểm của

 

1

C

và

 

2

C

là nghiệm của hệ

 

22

4 8 +15 0 1

+2 50

x y x y

xy





















Lấy

 

1

trừ

 

2

ta được

 

4 8 +15 5 0 2 5 3x y x y    

Thay

 

3

vào

 

2

ta được phương trình

2

5 20 0 2 102y y y x     

Câu 47: [0H3-2.21-3]Xác định vị trí tương đối của hai đường tròn

 

22

1

: 4 0C x y  

và

 

2

3 4 2() 5: ( )xyC    

A. Không cắt nhau. B. Cắt nhau. C. Tiếp xúc nhau. D. Tiếp

xúc ngoài.

Lời giải

Chọn B

 

22

1

: 4 0C x y  

có tâm

 

0,0O

bán kính

2R 

;

 

2

3 4 2() 5: ( )xyC    

có tâm

 

3;4 I

bán kính

5R 

Mà

5 2 5 5 2OI    

nên chúng cắt nhau.

Câu 48: [0H3-2.21-3]Xác định vị trí tương đối của hai đường tròn

 

22

1

: 4 0C x y  

và

   

2

:(10 1 )61xyC    

A. Không cắt nhau. B. Cắt nhau. C. Tiếp xúc nhau. D. Tiếp

xúc ngoài.

Lời giải

Chọn A

Đường tròn

 

22

1

: 4 0C x y  

có tâm

 

0,0O

bán kính

2R 

;

   

2

:(10 1 )61xyC    

có tâm

 

10;16 I 

bán kính

1R 

. Mà

356 1 2OI   

. Nên chúng không cắt nhau.

Câu 49: [0H3-2.21-3]Xác định vị trí tương đối của hai đường tròn

 

22

: 4 0C x y x  

và

 

22

: 8 0C x y y



  

?

A. Không cắt nhau. B. Cắt nhau. C. Tiếp xúc nhau. D. Tiếp

xúc ngoài.

Lời giải

Chọn B

 

22

: 4 0C x y x  

có tâm

 

2,0I

bán kính

2R 

;

 

22

: 8 0C x y y



  

có tâm

 

0; 4 J 

bán kính

4R 

mà

4 2 20 4 2OI    

. Nên chúng cắt nhau.

Câu 50: [0H3-2-2]Cho đường tròn

 

22

: 3 0C x y x y   

. Phương trình tiếp tuyến của

 

C

tại

 

1; 1M 

là:

A.

3 2 0xy  

. B.

3 2 0xy  

. C.

3 2 0xy  

. D.

3 2 0xy  

.

Lời giải

Chọn D

Áp dụng công thức phân đôi tọa độ ta được phương trình tiếp tuyến

 

00

11

3 0 1. 1 . 3 0

2 2 2 2

x x y y

xy

x x y y x y



  

          

3 2 0xy   

Cách khác :

Dễ thấy điểm

 

1; 1M 

không thuộc các đường thẳng

3 2 0xy  

,

3 2 0xy  

,

3 2 0xy  

, và thuộc đường thẳng

3 2 0xy  

.

Cách khác :

Đường tròn

 

22

: 3 0C x y x y   

có tâm

31

;

22

I







.

Điểm

 

1; 1M 

thuộc đường tròn

 

C

.

Phương trình tiếp tuyến của đường tròn

 

C

tại điểm

 

1; 1M 

là đường thẳng đi

qua

M

và nhận vec tơ

 

1 3 1

; 1;3

2 2 2

IM



    





nên có phương trình

3 2 0xy  

.

Câu 51: [0H3-2.21-3]Xác định vị trí tương đối của hai đường tròn

 

22

1

: 4 0C x y x  

và

 

22

2

: 2 0C x y y  

.

A. Không cắt nhau. B. Cắt nhau tại 2 điểm.

C. Tiếp xúc trong. D. Tiếp xúc ngoài.

Lời giải

Chọn B

Đường tròn

 

22

1

: 4 0C x y x  

có tâm

 

1

2;0I

và bán kính

1

2R 

.

Đường tròn

 

22

2

: 2 0C x y y  

có tâm

 

2

0;1I

và bán kính

2

1R 

.

 

1 2 1 2 1 2 1

5R R I I R R C     



 

1

C

và

 

2

C

cắt nhau.

Câu 52: [0H3-2.21-3]Cho 2 đường tròn

 

22

1

: 8 2 7 0C x y x y    

,

 

22

2

: 3 7 12 0C x y x y    

. Mệnh đề nào sau đây đúng ?

A.

 

1

C

và

 

2

C

không có điểm chung. B.

 

1

C

và

 

2

C

tiếp xúc ngoài.

C.

 

1

C

và

 

2

C

tiếp xúc trong. D.

 

1

C

và

 

2

C

cắt nhau.

Lời giải

Chọn D

 

1

C

có tâm

 

1

4;1I

bán kính

1

10R 

;

 

2

C

có tâm

2

37

;

22

I







, bán kính

2

10

2

R 

1 2 1 2 1 2

25

2

R R I I R R    



 

1

C

và

 

2

C

cắt nhau.

§.5 ELIP

Câu 53: [0H3-2-2] Một đường tròn có tâm là điểm

0; 0O

và tiếp xúc với đường thẳng

:

4 2 0xy

. Hỏi bán kính đường tròn đó bằng bao nhiêu?

A.

2

. B.

1

. C.

4

. D.

42

.

Lời giải

Chọn C

;4R d I

Câu 54: [0H3-2.21-2] Vị trí tương đối giữa

2

đường tròn

1

:C

22

4xy

và

2

:C

22

( 10) ( 16) 1xy

là

A. Cắt nhau. B. Không cắt nhau. C. Tiếp xúc ngoài. D. Tiếp

xúc trong.

Lời giải

Chọn B

Ta có đường tròn

1

:C

có tâm

1

0;0I

và bán kính

1

2R

Đường tròn

2

:C

có tâm

2

10;16I

và bán kính

2

1R

1 2 1 2

356 3I I R R

Câu 55: [0H3-2-2] Với những giá trị nào của

m

thì đường thẳng

43: 0x y m

tiếp

xúc với đường tròn

22

: 90xyC

.

A.

3m

. B.

3m

và

3m

.

C.

3m

. D.

1 5m

và

1 5m

.

Lời giải

Chọn D

Đường thẳng tiếp xúc với đường tròn khi

;d I R

15

3 15

15

5

m

Câu 56: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Ox

?

A.

22

2 10 0x y x y

. B.

22

6 5 9 0x y x y

.

C.

22

10 0x y y

. D.

22

50xy

.

Lời giải

Chọn C

0;5I

,

5R

;5d I Ox R

Câu 57: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Oy

?

A.

22

10 1 0x y y

. B.

22

6 5 1 0x y x y

.

C.

22

20x y x

. D.

22

50xy

.

Lời giải

Chọn C

1;0I

,

1R

;1d I Oy R

Câu 58: [0H3-2-2] Tâm đường tròn

22

10 1 0x y x

cách trục

Oy

bao nhiêu?

A.

1 5

. B.

0

. C.

10

. D.

5

.

Lời giải

Chọn D

5;0I

;5d I Oy

Câu 59: [0H3-2-2] Một đường tròn có tâm

1;3I

tiếp xúc với đường thẳng

4:30xy

. Hỏi bán kính đường tròn bằng bao nhiêu?

A.

3

5

. B.

1

. C.

3

. D.

15

.

Lời giải

Chọn C

3 12

;3

5

R d I

Câu 60: [0H3-2-2] Đường tròn

2 2 2

( ) ( )x a y b R

cắt đường thẳng

0x y a b

theo một dây cung có độ dài bằng bao nhiêu?

A.

2R

. B.

2R

. C.

2

R

. D.

.R

Lời giải

Chọn A

Đường thẳng đi qua tâm đường tròn nên độ dài dây cung bằng đường kính bằng

2R

Câu 61: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng :

2 3 0xy

và đường tròn

(C) :

22

2 4 0x y x y

.

A. ( 3; 3) và (1; 1). B. (1; 1) và (3; 3). C. ( 3; 3) và (1; 1). D. ( 2; 1)

và (2; 1).

Lời giải

Chọn A

Tọa độ giao điểm của  và (C) là nghiệm hệ phương trình :

22

2 3 0

2 4 0

xy

x y x y

2

3

23

3

23

3

5 20 15 0

1

x

xy

y

xy

y

yy

x

y

.

Câu 62: [0H3-2-2] Tìm

m

để

22

: 4 2 2 3 0

m

C x y mx my m

là phương trình

đường tròn ?

A.

5

3

m

hoặc

1.m

B.

5

3

m

.

C.

1.m

D.

3

1.

5

m

Lời giải

Chọn A

m

C

là phương trình đường tròn

2

2 2 2

0 2 2 3 0a b c m m m

2

5

5 2 3 0 1.

3

m m m m

Câu 63: [0H3-2-2] Đường tròn nào sau đây tiếp xúc với trục

Oy

?

A.

22

10 2 1 0x y x y

. B.

22

4 5 0x y y

.

C.

22

10xy

. D.

22

30x y x y

.

Lời giải

Chọn A

Đường thẳng d tiếp xúc với đường tròn (C) khi và chỉ khi

;.d I d R

Xét đáp án A. Đường tròn có tâm

5; 1 ,I

bán kính

5.R

Ta có

; 5 .d I Oy R

Câu 64: [0H3-2.21-2] Tìm giao điểm 2 đường tròn (C

1

):

22

20xy

và (C

2

):

22

2 0.x y x

A.

2;0 , 0;2 .

B.

2;1 , 1; 2 .

C.

1; 1 , 1;1 .

D.

1;0 , 0; 1 .

Lời giải

Chọn C

Tọa độ giao điểm của

12

,CC

là nghiệm hệ phương trình:

22

2 0 1

.

1

20

x y x

y

x y x

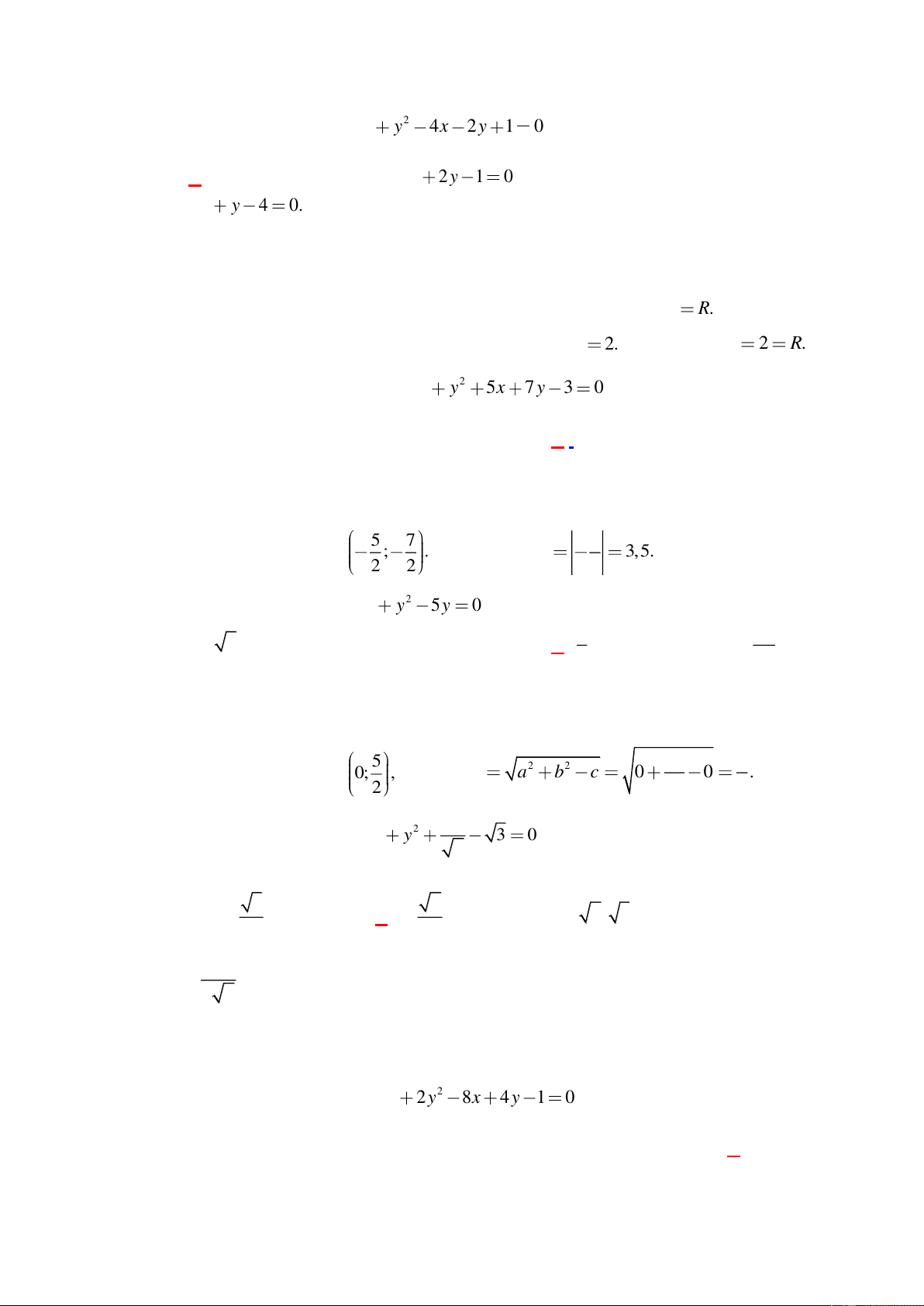
Câu 65: [0H3-2-2] Đường tròn

22

4 2 1 0x y x y

tiếp xúc đường thẳng nào trong các

đường thẳng dưới đây?

A. Trục tung. B.

4 2 1 0xy

. C. Trục hoành. D.

2 4 0.xy

Lời giải

Chọn A

Đường thẳng d tiếp xúc với đường tròn (C) khi và chỉ khi

;.d I d R

Xét đáp án A. Đường tròn có tâm

2;1 ,I

bán kính

2.R

Ta có

; 2 .d I Oy R

Câu 66: [0H3-2-1] Cho đường tròn

22

5 7 3 0x y x y

. Tìm khoảng cách từ tâm

đường tròn tới trục

.Ox

A. 5. B. 7. C.

3,5

. D.

2,5

.

Lời giải

Chọn C

Đường tròn có tâm

57

;.

22

I

Ta có

7

; 3,5.

2

d I Ox

Câu 67: [0H3-2-2] Đường tròn

22

50x y y

có bán kính bằng bao nhiêu?

A.

5

. B. 25. C.

5

2

. D.

25

2

.

Lời giải

Chọn C

Đường tròn có tâm

5

0; ,

2

I

bán kính

22

25 5

0 0 .

42

R a b c

Câu 68: [0H3-2-2] Đường tròn

22

30

2

x

xy

có tâm là điểm nào trong các điểm

sau đây?

A.

3

0;

2







. B.

2

;0

4









. C.

 

2; 3

. D.

1

;0

22







.

Lời giải

Chọn B

Câu 69: [0H3-2-2] Đường tròn

22

2 2 8 4 1 0x y x y

có tâm là điểm nào trong các

điểm sau đây?

A.

()2;1

. B.

(8; )4

. C.

()8;4

. D.

(2; )1

Lời giải

Chọn D

2 2 2 2

1

2 2 8 4 1 0 4 2 0.

2

x y x y x y x y

Đường tròn có tâm

2; 1 .I

Câu 70: [0H3-2-2] Tìm tọa độ giao điểm của đường thẳng :

yx

và đường tròn (C):

22

20x y x

.

A.

 

0;0

B.

 

0;0

và

 

1;1

. C.

 

2;0

D.

 

1;1

.

Lời giải

Chọn D

Tọa độ giao điểm của  và

 

C

là nghiệm hệ phương trình :

22

20

yx

x y x

2

0

1

2 2 0

1

yx

xy

x

xy

xx

x

.

Câu 71: [0H3-2-2] Với những giá trị nào của m thì đường thẳng :

3 4 3 0xy

tiếp xúc

với đường tròn (C):

22

( ) 9x m y

A.

0m 

và

1m 

. B.

4m 

và

6m 

. C.

2m 

. D.

6m 

.

Lời giải

Chọn B

Đường thẳng  tiếp xúc với đường tròn (C) khi và chỉ khi

;.d I R

Đường tròn có tâm

;0 ,Im

bán kính

3.R

Ta có :

4

3 4.0 3

; 3 3 3 15 .

6

9 16

m

d I m

m

Câu 72: [0H3-2-2] Tìm tọa độ giao điểm của đường tròn (C):

22

2 2 1 0x y x y

và

đường thẳng :

1

22

xt

yt

A.

 

1;2

và

 

2;1

. B.

 

1;2

và

12

;

55

.

C.

 

2;5

. D.

 

1;0

và

 

0;1

.

Lời giải

Chọn B

Tọa độ giao điểm của  và (C) là nghiệm hệ phương trình:

2 2 2

1, 2

11

12

,

2 2 2 2 .

55

4

2 2 1 0 5 4 0

0,

5

xy

x t x t

xy

y t y t

x y x y t t

tt

Câu 73: [0H3-2.21-2] Xác định vị trí tương đối giữa 2 đường tròn (C

1

):

22

4xy

và (C

2

):

22

( 3) ( 4) 25xy

.

A. Không cắt nhau. B. Cắt nhau. C. Tiếp xúc ngoài. D. Tiếp

xúc trong.

Lời giải

Chọn B

Đường tròn

1

C

có tâm

1

0;0I

và bán kính

1

2.R

Đường tròn

2

C

có tâm

2

3;4I

và bán kính

2

5.R

Ta có :

1 2 1 2

7 5.R R I I

Vậy

1

C

cắt

2

.C

Câu 74: [0H3-2-2] Đường tròn

22

60x y x

không tiếp xúc đường thẳng nào trong các

đường thẳng dưới đây?

A.

2 0.y

B.

6 0.x

C. Trục tung. D.

3 0.y

Lời giải

Chọn A

Đường thẳng  không tiếp xúc với đường tròn (C) khi và chỉ khi

;.d I R

Đường tròn có tâm

3;0 ,I

bán kính

3.R

Xét đáp án A, ta có :

02

; 2 0.

1

dI

Câu 75: [0H3-2-2] Đường tròn

22

3 3 6 9 9 0x y x y

có bán kính bằng bao nhiêu?

A.

5

2

. B.

5

. C.

25

2

. D.

25

4

.

Lời giải

Chọn D

2 2 2 2

3 3 6 9 9 0 2 3 3 0.x y x y x y x y

Đường tròn có tâm

3

1; ,

2

I

bán kính

95

1 3 .

42

R

Câu 76: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua

3

điểm

     

0;4 , 2;4 , 4;0 .ABC

A.

 

0; 0

. B.

 

1; 0

. C.

 

3; 2

. D.

 

1;1

.

Lời giải

Chọn D

Gọi phương trình đường tròn là

 

22

: 2 2 0C x y ax by c    

Ta có:

   

0;4 8 16

2;4 4 8 20

4;0 8 16

A C b c

B C a b c

C C a c

     

      

     

Giải hệ trên ta được

1

8

a

b

c

















Vậy tâm

 

1;1I

Câu 77: [0H3-2-2] Tìm bán kính đường tròn đi qua

3

điểm

     

0; 4 , 3; 4 , 3; 0A B C

.

A.

5

. B.

3

. C.

10

2

. D.

5

2

.

Lời giải

Chọn C

Gọi phương trình đường tròn là

 

22

: 2 2 0C x y ax by c    

Ta có:

   

0;4 8 16

3;4 6 8 25

3;0 6 9

A C b c

B C a b c

C C a c

     

      

     

Giải hệ trên ta được

3

2

0

a

b

c



















Vậy bán kính

22

95

4

42

R a b c     

Câu 78: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua

3

điểm

     

0; 5 , 3; 4 , 4; 3 .A B C

A.

 

6; 2

. B.

 

1;1

. C.

 

3;1

. D.

 

0; 0

.

Lời giải

Chọn D

Gọi phương trình đường tròn là

 

22

: 2 2 0C x y ax by c    

Ta có:

   

0;5 10 25

3;4 6 8 25

4;3 8 6 25

A C b c

B C a b c

C C a b c

     

      

Giải hệ trên ta được

0

25

a

b

c

















Vậy tâm

 

0;0I

Câu 79: [0H3-2-2] Đường tròn

22

40x y y  

không tiếp xúc đường thẳng nào trong các

đường thẳng dưới đây?

A.

2 0x

. B.

3 0xy  

. C.

2 0x

. D. Trục

hoành.

Lời giải

Chọn B

Ta có đường tròn

 

22

: 4 0C x y y  

có tâm

 

0; 2I 

, bán kính

2R 

Đường thẳng

: 3 0xy   

Xét khoảng cách

 

5

;2

2

d I R   

Vậy đường tròn không tiếp xúc



Câu 80: [0H3-2-2] Đường tròn

22

10xy  

tiếp xúc đường thẳng nào trong các đường

thẳng dưới đây?

A.

0xy

. B.

3 4 1 0xy  

. C.

3 4 5 0xy  

. D.

1 0xy  

.

Lời giải

Chọn C

Ta có đường tròn

 

22

: 1 0C x y  

có tâm

 

0;0I

, bán kính

1R 

Đường thẳng

:3 4 5 0xy   

Xét khoảng cách

 

;1d I R  

Vậy đường tròn tiếp xúc



Câu 81: [0H3-2-2] Tìm bán kính đường tròn đi qua

3

điểm

   

0; 0 , 0; 6 , (8; 0A B C

).

A.

6

. B.

5

. C.

10

. D.

5

.

Lời giải

Chọn B

Gọi phương trình đường tròn là

 

22

: 2 2 0C x y ax by c    

Ta có:

   

0;0 0

0;6 12 36

8;0 16 64

A C c

B C b c

C C a c

  

     

Giải hệ trên ta được

4

3

0

a

b

c

















Vậy bán kính

22

5R a b c   

Câu 82: [0H3-2-2] Tìm giao điểm

2

đường tròn

 

1

:C

22

40xy  

và

 

2

:C

22

4 4 4 0x y x y    

A.

 

2;2

và

 

2; 2

. B.

   

0; 2 ; 0; 2 .

C.

   

2; 0 ; 0; 2

. D.

   

2; 0 ; 2; 0

.

Lời giải

Chọn C

Tọa độ giao điểm là nghiệm của hệ

22

40

4 4 4 0

xy

x y x y



  





    





22

4 4 8 0

4

xy

  









 

2

02

24

20

yx

xy

xx

xy







  





   





  





Câu 83: [0H3-2.21-2] Tìm giao điểm

2

đường tròn

 

1

:C

22

5xy

và

 

2

:C

22

4 8 15 0.x y x y    

A.

 

1; 2

và

 

2; 3

. B.

 

1; 2

. C.

 

1; 2

và

 

3; 2

. D.

 

1; 2

và

 

2;1 .

Lời giải

Chọn B

Tọa độ giao điểm là nghiệm của hệ

22

5

4 8 15 0

xy

x y x y









    





22

4 8 20

5

xy











 

2

52

5 2 5 2 1

xy

y y y x









      





Câu 84: [0H3-2-2] Đường tròn

 

:C

22

( 2) ( 1) 25xy   

không cắt đường thẳng nào

trong các đường thẳng sau đây?

A. Đường thẳng đi qua điểm

 

2; 6

và điểm

 

45; 50 .

B. Đường thẳng có phương trình

– 4 0y 

.

C. Đường thẳng đi qua điểm

 

3; 2

và điểm

 

19; 33 .

D. Đường thẳng có phương trình

8 0.x

Lời giải

Chọn D

Ta có đường tròn

 

:C

22

( 2) ( 1) 25xy   

có tâm

 

2;1 , 5IR

Đường thẳng

: 8 0x  

Xét khoảng cách

 

; 6 5d I R   

Nên đường tròn không cắt



Câu 85: [0H3-2-2] Đường tròn

22

10 11 0x y x   

có bán kính bằng bao nhiêu?

A.

6

. B.

2

. C.

36

. D.

6

.

Lời giải

Chọn A

Ta có

 

5;0I

22

5 0 11 6R    

Câu 86: [0H3-2-2] Đường tròn nào dưới đây đi qua

3

điểm

     

2; 0 , 0; 6 , 0; 0A B O

?

A.

22

3 8 0x y y   

. B.

22

2 6 1 0x y x y    

.

C.

22

2 3 0x y x y   

. D.

22

2 6 0x y x y   

.

Lời giải

Chọn D

Gọi phương trình đường tròn là

 

22

: 2 2 0C x y ax by c    

Ta có:

   

2;0 4 4

0;6 12 36

0;0 0

A C a c

B C b c

C C c

     

  

Giải hệ trên ta được

1

3

0

a

b

c

















Câu 87: [0H3-2-2] Một đường tròn có tâm

 

3; 2I

tiếp xúc với đường thẳng

:

5 1 0xy  

. Hỏi bán kính đường tròn bằng bao nhiêu?

A.

6

. B.

26

. C.

14

26

. D.

7

13

.

Lời giải

Chọn C

 

14

;

26

R d I  

Câu 88: [0H3-2-2] Bán kính của đường tròn tâm

 

0; 2I 

tiếp xúc với đường thẳng

:3 4 23 0xy   

là:

A. 15. B. 5. C.

3

5

. D. 3.

Lời giải

Chọn D

 

2

3.0 4. 2 23

,3

34

R d I

  

   



.

Câu 89: [0H3-2-2] Phương trình nào sau đây là phương trình đường tròn?

A.

22

2 4 8 1 0x y x y    

. B.

22

4 10 6 2 0x y x y    

.

C.

22

2 8 20 0x y x y    

. D.

22

4 6 12 0x y x y    

.

Lời giải

Chọn D

Phương trình đường tròn có dạng

22

2 2 0x y ax by c    

.

A, B không có dạng phương trình đường tròn



Loại.

Xét

22

2 8 20 0x y x y    

có

1

4

20

a

b

c

















;

2 2 2 2

1 4 20 3 0a b c       



không phải là phương trình đường tròn.



Loại C.

Xét

22

4 6 12 0x y x y    

có

2

3

12

a

b

c

















;

 

2

2 2 2

2 3 12 25 0a b c       



là phương trình đường tròn



Chọn D

Câu 90: [0H3-2-2] Cho đường tròn

 

22

: 2 4 20 0C x y x y    

. Tìm mệnh đề sai trong

các mệnh đề sau:

A.

 

C

có tâm

 

1;2I

. B.

 

C

có bán kính

5R 

.

C.

 

C

đi qua điểm

 

2;2M

. D.

 

C

không đi qua điểm

 

1;1A

.

Lời giải

Chọn A

 

22

: 2 4 20 0C x y x y    

có

1

2

20

a

b

c

















Tọa độ tâm

 

1; 2I 

.

Bán kính

22

5R a b c   

.

Thay

 

2;2M

vào

 

C

22

2 2 2.2 4.2 20 0     

 

MC

.

Thay

 

1;1A

vào

 

C

22

1 1 2.1 4.1 20 12 0       

 

AC

.

Vậy chọn A.

Câu 91: [0H3-2-2]Phương trình tiếp tuyến tại điểm

 

3;4M

với đường tròn

 

22

: 2 4 3 0C x y x y    

là:

A.

70xy  

. B.

70xy  

. C.

70xy  

. D.

30xy  

.

Lời giải

Chọn A

Đường tròn

 

C

có tọa độ tâm

 

1;2I

.

Tiếp tuyến tại

 

3;4M

đi qua

 

3;4M

và nhận

 

2;2IM 

làm vec tơ pháp tuyến

có phương trình

2 2 14 0 7 0x y x y      

.

Câu 92: [0H3-2-3] Cho đường tròn

 

22

: 4 2 0C x y x y   

và đường thẳng

: 2 1 0xy   

. Tìm mệnh đề đúng trong các mệnh đề sau:

A.



đi qua tâm của

 

C

. B.



cắt

 

C

tại hai điểm.

C.



tiếp xúc với

 

C

. D.



không có điểm chung với

 

C

.

Lời giải

Chọn C

Đường tròn

 

C

có tọa độ tâm

 

2;1I

.

Thay

 

2;1I

vào



2 2.1 1 5 0    

I 

.

Tọa độ giao điểm là nghiệm của hệ phương trình

   

22

2

4 2 0

2 1 0

12

1 2 4 1 2 2 0

12

1

5 10 5 0

x y x y

xy

y y y y

xy

y

x

yy



   



  



  









       





  











  



Vậy



tiếp xúc

 

C

tại điểm

 

1; 1

.

Câu 93: [0H3-2-2] Với giá trị nào của

m

thì phương trình sau đây là phương trình sau đây

là phương trình của đường tròn

 

22

2 2 4 19 6 0x y m x my m      

?

A.

12m

. B.

21m  

.

C.

1m 

hoặc

2m

. D.

2m 

hoặc

1m 

.

Lời Giải

Chọn C

Xét phương trình

 

22

2 2 4 19 6 0x y m x my m      

 



. Để

 



là phương

trình đường tròn thì

Ta có

     

22

2 2 2

2 2 19 6 5 15 10 0a b c m m m m m            

1m 

hoặc

2m

.

Câu 94: [0H3-2-2] Cho hai điểm

 

1;1A

và

 

7;5B

. Phương trình đường tròn đường kính

AB

là:

A.

22

8 6 12 0x y x y    

. B.

22

8 6 12 0x y x y    

.

C.

22

8 6 12 0x y x y    

. D.

22

8 6 12 0x y x y    

.

Lời Giải

Chọn C

Gọi

I

là trung điểm của

AB

suy ra

 

4;3I

   

22

4 1 3 1 13AI     

Đường tròn cần tìm có đường kính

AB

suy ra nó nhận

 

4;3I

làm tâm và bán kính

13R AI

có dạng

   

22

4 3 13 8 6 12 0x y x y x y         

Câu 95: [0H3-2-2] Cho điểm

 

0;4M

và đường tròn

 

C

có phương trình

22

8 6 21 0x y x y    

. Tìm phát biểu đúng trong các phát biểu sau:

A.

M

nằm ngoài

 

C

. B.

M

nằm trên

 

C

.

C.

M

nằm trong

 

C

. D.

M

trùng với tâm của

 

C

.

Lời Giải

Chọn A

Đường tròn

 

C

có tâm

 

4;3I

, bán kính

4R 

Ta có

16 1 17IM R   

nên điểm

M

nằm ngoài

 

C

.

Câu 96: [0H3-2-2] Đường tròn

 

C

có tâm là gốc

 

0;0O

và tiếp xúc với đường thẳng

:8 6 100 0xy   

. Bán kính của đường tròn

 

C

là:

A. 4. B. 6. C. 8. D. 10.

Lời giải

Chọn D

Bán kính của đường tròn

 

C

là:

 

100

; 10

36 64

R d O d  



.

Câu 97: [0H3-2-2] Phương trình nào trong các phương trình sau đây không là phương trình đường

tròn?

A.

22

40xy  

. B.

22

20x y x y    

.

C.

22

0x y x y   

. D.

22

2 2 1 0x y x y    

.

Lời giải

Chọn B

Câu 98: [0H3-2-2] Tiếp tuyến với đường tròn

 

22

:2C x y

tại điểm

 

1;1M

có phương trình là:

A.

20xy  

. B.

10xy  

. C.

2 3 0xy  

. D.

0xy

.

Lời giải

Chọn A

Tiếp tuyến cần tìm đi qua

 

1;1M

và có vtpt

 

1;1OM

có pt là:

20xy  

.

Câu 99: [0H3-2-3] Số đường thẳng đi qua điểm

 

5;6M

và tiếp xúc với đường tròn

 

22

:( 1) ( 2) 1C x y   

là

A. 0. B. 1. C. 2. D. 3.

Lời giải

Chọn C

Đường tròn

 

C

có tâm

 

1;2I

và bán kính

1R 

.

Đường thẳng



đi qua

 

5;6M

có phương trình là:

   

5 6 0a x b y   

.



là tiếp tuyến của đường tròn

 

C

 

22

44

, 1 15 32 15 0

ab

d I R a ab b

ab



        



.

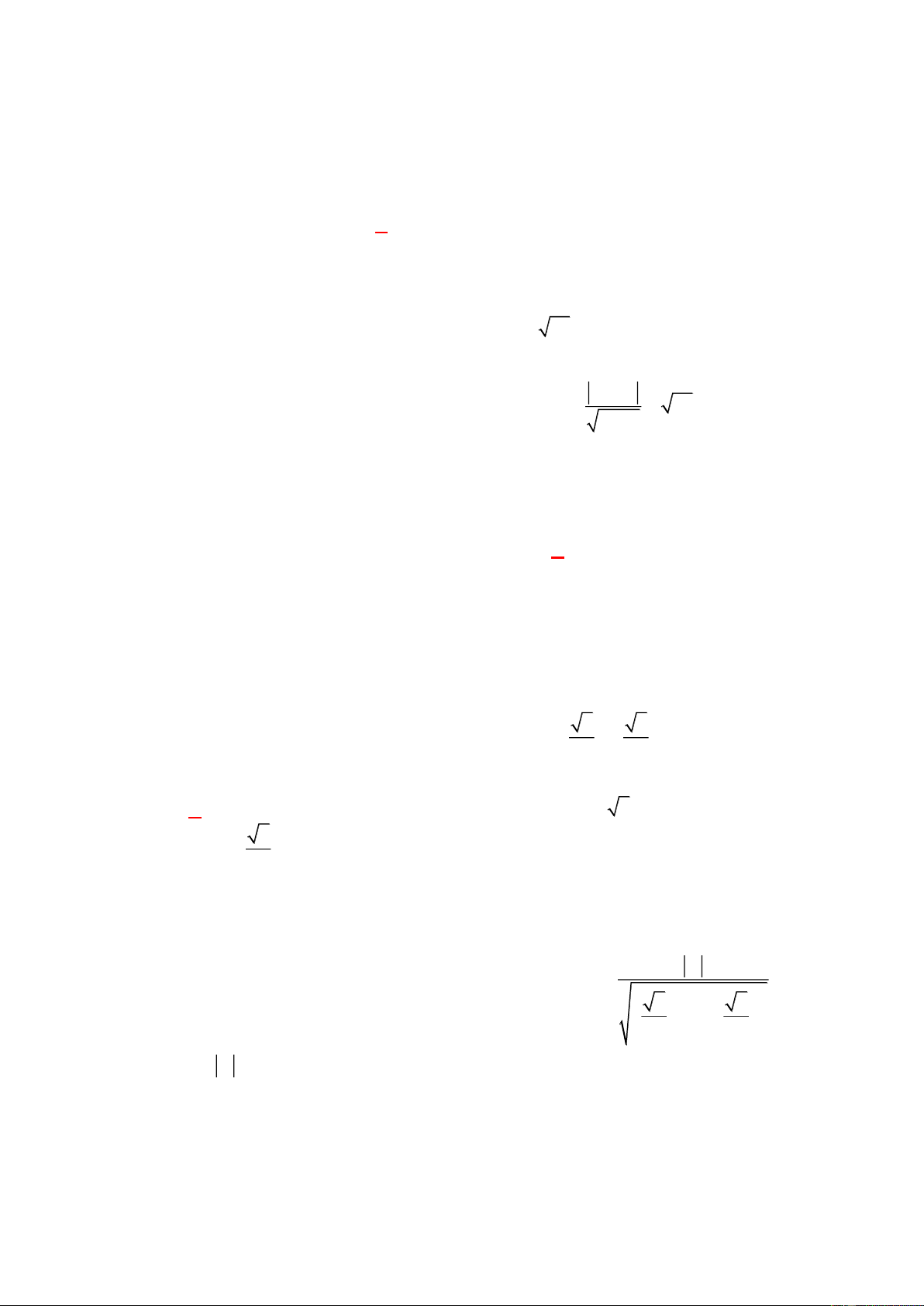
Phương trình có hai nghiệm nên có

2

tiếp tuyến đi qua

 

5;6M

.

Câu 100: [0H3-2-3] Có bao nhiêu tiếp tuyến với đường tròn

 

22

: 8 4 0C x y x y   

đi qua gốc

tọa độ?

A. 0. B. 1. C. 2. D. 3.

Lời giải

Chọn B

Đường tròn

 

C

có tâm

 

4;2I

và bán kính

20R 

.

Đường thẳng



đi qua gốc tọa độ có phương trình là:

y kx

.



là tiếp tuyến của đường tròn

 

C

 

2

42

, 20 2

1

k

d I R k

k



       



.

Vậy có duy nhất một tiếp tuyến đi qua gốc tọa độ.

Câu 101: [0H3-2-2] Đường tròn đi qua ba điểm

     

0;3 , 3;0 , 3;0A B C

có phương trình là

A.

22

3xy

. B.

22

6 6 9 0x y x y    

.

C.

22

6 6 0x y x y   

. D.

22

90xy  

.

Lời giải

Chọn D

Cách 1: Dể dàng ta thay lần lượt 3 điểm

     

0;3 , 3;0 , 3;0A B C

vào

 

22

: 9 0C x y  

thấy thỏa mản.

Cách 2: giải hệ 3 phương trình.

Câu 102: [0H3-2-3] Với giá trị nào của

m

thì đường thẳng

22

:0

22

x y m   

tiếp xúc với

đường tròn

22

1xy

?

A.

1m 

. B.

0m 

. C.

2m 

. D.

2

m 

.

Lời giải

Chọn A

 

22

:1C x y

 

0;0 , 1IR

Để



tiếp xúc với đường tròn khi và chỉ khi

 

,1dI

22

1

22

m



   



   

   

1m

.

Câu 103: [0H3-2-2] Cho hai đường thẳng

1

: 4 – 3 5 0d x y 

và

2

: 2 – 4 0d x y

. Tính

 

12

cos ,dd

.

A.

2

55

. B.

2

5



. C.

2

5

. D.

2

55



.

Lời giải

Chọn A

Ta có:

 

2

1

2

4.1 3 .2

cos ,

2

55

4 3 . 1 2

dd





  

.

Câu 104: [0H3-2-2] Khoảng cách từ điểm

 

2; –3M

đến đường thẳng

2 3 –: 70xy 

bằng ?

A.

12

13

. B.

12

13

. C.

12

13



. D.

12

13



.

Lời giải

Chọn B

Ta có:

 

22

2.2 3. 3

,

7

12

13

23

d M

  

  



.

Câu 105: [0H3-2-2] Đường thẳng đi qua hai điểm

 

2; –1A

,

 

–3; 4B

có hệ số góc

k

bằng ?

A.

2

. B.

–2

. C.

1

. D.

–1

.

Lời giải

Chọn D

Đường thẳng có vectơ chỉ phương là

 

5;5

5

1

5

AB k    



.

Câu 106: [0H3-2-2] Cho đường thẳng

–2 3 –: 10xy 

. Đường thẳng nào sau đây vuông

góc với



?

A.

3 – 2 –1 0xy

. B.

3 2 4 0xy  

. C.

3 2 1xy  

. D.

4 6 3 0xy  

.

Lời giải

Chọn B

Đường thẳng



có 1 VTPT là

 

1

2;3n 

. Đường thẳng

3 2 4 0xy  

có 1 VTPT

là

 

2

3;2n 

. Ta có

1 2 1 2

. 2.3 3.2 0n n n n     

. Dó đó hai đường thẳng đó

vuông góc nhau.

Câu 107: [0H3-2-2] Đường thẳng nào sau đây song song với đường thẳng

: – 4 1 0xy  

?

A.

8 2 2yx  

. B.

1 4 0xy  

. C.

2 8 0xy

. D.

24xy

.

Lời giải

Chọn D

Giải hệ phương trình

– 4 1

42

xy



  







(vô nghiệm). Nên đường thẳng song song với



là

24xy

.

Cách khác: Đưa đường thẳng

24xy

về dạng

4 2 0xy  

. Có tỉ số giữa



và

đường thẳng

4 2 0xy  

là:

1 4 1

1 4 2







.

Câu 108: [0H3-2-2] Đường nào sau đây cắt đường thẳng

1: – 4 0xy

.

A.

2 – 8 2 0xy

. B.

–2 8 0.xy

C.

2 8 0xy

. D.

– 4 – 2 0xy

.

Lời giải

Chọn C

Giải hệ phương trình

– 4 1

2 8 0

xy











(có 1 nghiệm). Nên đường thẳng cắt



là

2 8 0xy

.

Cách khác: Đường thẳng

1: – 4 0xy

cắt đường thẳng

2 8 0xy

vì có tỉ số

2 8 0

1 4 1





.

Câu 109: [0H3-2-2] Góc giữa hai đường thẳng

1

: 2 4 0d x y  

và

2

– 3 0: 6d x y 

là

A.

30

. B.

60

. C.

45

. D.

135

.

Lời giải

Chọn C

Đường thẳng

1

d

,

2

d

có VTPT tương ứng là

 

1

1;2n 

và

 

2

1; 3n 

.

Ta có:

 

1 2 1 2

2

2 2 2

1.1 2. 3 5 1

cos , , 45

50 2

1 2 . 1 3

d d d d

  

     

  

.

Câu 110: [0H3-2-2] Tính tích khoảng cách từ điểm

 

–2;1M

và gốc tọa độ

 

0;0O

đến

đường thẳng

:5 –12 +9 0xy

.

A.

0

. B.

9

13

. C.

1

. D.

9

13



.

Lời giải

Chọn B

Ta có:

 

2

5. 2 12.1 9 13

,1

13

5 12

dM

   

   



và

 

2

5.0 12.0 9 9

,

13

5 12

dO



  



.

Khi đó

   

9

, . ,

13

d M d O  

.

Câu 111: [0H3-2-2] Tìm

x

sao cho

uv

trong đó

 

2;3u

,

 

2;vx

.

A.

1x 

. B.

–1x 

. C.

3

4

x 

. D.

4

3

x 

.

Lời giải

Chọn D

Ta có

 

4

. 0 2. 2 3. 0

3

u v u v x x        

.

Câu 112: [0H3-2-2] Cho

 

12; 4u 

,

 

1;0v 

. Mệnh đề nào dưới đây là mệnh đề SAI ?

A.

 

13; 4uv  

. B.

 

11; 4uv  

. C.

. 12uv

. D.

12uv

.

Lời giải

Chọn D

Ta có

 

12; 4u 

,

 

1;0 12 12;0vv  

. Do vậy MĐ SAI là

12uv

. Hơn thế

nữa:

 

12 1; 4 0 13; 4uv      

,

 

12 1; 4 0 11; 4uv      

,

 

. 12.1 4 .0 12uv   

.

Câu 113: [0H3-2-2] Cho

 

4;0A

,

 

2; – 3B

,

 

9;6C

. Tìm tọa độ trọng tâm

G

của tam giác

ABC

.

A.

 

3;5

. B. (5;1). C.

 

15;3

. D.

 

3;3

.

Lời giải

Chọn B

Tọa độ trọng tâm của tam giác

ABC

là

 

4 2 9 0 3 6

; 5;1

33

GG

   









.

Câu 114: [0H3-2-2] Bán kính đường tròn tâm

 

–2; –2C

tiếp xúc với đường thẳng

:5 12 –10 0xy  

là?

A.

44

13

. B.

43

13

. C.

42

13

. D.

41

13

.

Lời giải

Chọn A

Ta có bán kính

R

của đường tròn tâm

C

tiếp xúc với đường thẳng



là:

 

   

22

5. 2 12. 2 10 44 44

,

13 13

5 12

R d C

    

    



.

Câu 115: [0H3-2-2] Khoảng cách từ

 

1;2A

đến đường thẳng

1:3 4 – 1 0xy 

là :

A.

1

5

. B.

1

. C.

5

. D.

0

.

Lời giải

Chọn D

Ta có:

 

22

3.1 4.2 11 0

,0

5

34

da



   



.

Câu 116: [0H3-2-2] Viết phương trình đường tròn

 

C

có đường kính

AB

với

   

1;1 , 7;5AB

A.

 

22

:( 4) ( 2) 13C x y   

. B.

 

22

:( 4) ( 3) 13C x y   

.

C.

 

22

:( 4) ( 3) 13C x y   

. D.

 

22

:( 4) ( 3) 13C x y   

.

Lời giải

Chọn B

Gọi

I

là trung điểm của

AB

thì

 

4;3I

là tâm đường tròn

 

C

có đường kính

AB

.

 

6;4 2 13AB AB  

.

Phương trình đường tròn

 

22

:( 4) ( 3) 13C x y   

.

Câu 117: [0H3-2-2] Tìm phương trình đường tròn

 

C

đi qua ba điểm

     

1;1 , 3;1 , 1;3A B C

.

A.

 

22

: 2 2 2 0C x y x y    

. B.

 

22

: 2 2 2 0C x y x y    

.

C.

 

22

: 2 2 0C x y x y   

. D.

 

22

: 2 2 2 0C x y x y    

.

Lời giải

Chọn D

Cch 1 :

Gọi phương trình đường tròn đi qua ba điểm

,,A B C

là

 

C

với tâm

 

;I a b

.

Khi đó

IA IB IC R  

.

Từ đó, ta có hệ phương trình sau :

2 2 2 2

( 1 ) (1 ) (3 ) (1 )

( 1 ) (1 ) (1 ) (3 )

IA IB a b a b

IB IC

a b a b



        









       





8 8 1

4 4 8 1

aa

a b b









  



.

      

22

( 1 1) (1 1) 2R IA

.

22

( ):( 1) ( 1) 4C x y   



 

22

: 2 2 2 0C x y x y    

.

Cch 2:

Gọi phương trình đường tròn đi qua ba điểm

,,A B C

là

 

C

với tâm

 

;I a b

.

 

C

có dạng :

22

2 2 0x y ax by c    

.

Thế tọa độ

,,A B C

vào phương trình

 

C

ta có hệ sau :

22

( 1) 1 2 2 0

1

3 1 6 2 0 1

2

1 3 2 6 0

a b c

a

a b c b

c

a b c



     







      







    



.

Khi đó

 

22

: 2 2 2 0C x y x y    

.

Câu 118: [0H3-2-2] Tìm tọa độ tâm đường tròn đi qua 3 điểm

     

1;2 , 2;3 , 4;1A B C

.

A.

 

0; 1

. B.

1

3;

2







. C.

 

0;0

. D. Không

có.

Lời giải

Chọn D

Gọi phương trình đường tròn đi qua ba điểm

,,A B C

là

 

C

với tâm

 

;I a b

.

Khi đó

IA IB IC R  

.

Từ đó, ta có hệ phương trình sau :

2 2 2 2

(1 ) (2 ) ( 2 ) (3 )

(1 ) (2 ) (4 ) (1 )

IA IB a b a b

IB IC

a b a b



        









      







      





    



6 2 8 2 6 8

6 2 12 6 6 8 12

a b b a

a b a a

Hệ phương trình vô nghiệm nên không tn tại đường tròn đi qua ba điểm nêu trên.

Câu 119: [0H3-2.21-2] Xác định vị trí tương đối giữa hai đường tròn

 

22

1

:4C x y

và

     

22

2

: 10 16 1C x y   

.

A. Không cắt nhau. B. Cắt nhau.

C. Tiếp xúc trong. D. Tiếp xúc ngoài.

Lời giải

Chọn A

Đường tròn

 

22

1

:4C x y

có tâm

 

1

0; 0I

,

1

2R 

.

Đường tròn

     

22

2

: 10 16 1C x y   

có tâm

 

2

10; 16I 

,

2

1R 

nên khoảng

cách giữa 2 tâm

 

2

1 2 1 2

10 16 2 89 18,86 3I I R R       

nên hai đường

tròn không cắt nhau.

Câu 120: [0H3-2-2] Đường thẳng

:4 3 0x y m   

tiếp xúc với đường tròn

 

22

:1C x y

khi:

A.

3m 

. B.

5m 

. C.

1m 

. D.

0m 

.

Lời giải

Chọn B

Đường tròn

 

22

:1C x y

có tâm

 

0; 0I

,

1R 

. Đường thẳng

:4 3 0x y m   

tiếp xúc với đường tròn

 

22

:1C x y

khi:

 

22

4.0 3.0

, 1 1 5

5

43

mm

d I C R m



       



. Vậy chọn B.

Câu 121: [0H3-2-2] Phương trình nào sau đây là phương trình đường tròn:

A.

22

2 4 8 1 0x y x y    

. B.

22

4 10 6 2 0x y x y    

.

C.

22

2 8 20 0x y x y    

. D.

22

4 6 12 0x y x y    

.

Lời giải

Chọn D

Phương trình

22

2 2 0x y ax by c    

là phương trình của đường tròn khi và chỉ

khi

22

0a b c  

.

Ở đáp án D, vì

 

2

2 2 2

2 3 12 25 0a b c       

nên

22

4 6 12 0x y x y    

là phương trình đường tròn.

Loại đáp án A và B vì không có dạng

22

2 2 0x y ax by c    

.

Loại đáp án C vì

2 2 2 2

1 4 20 3 0a b c       

.

Câu 122: [0H3-2-2] Phương trình đường tròn

 

C

có tâm

 

1; 3I

và đi qua

 

3; 1M

là:

A.

   

22

1 3 8xy   

. B.

   

22

1 3 10.xy   

C.

   

22

3 1 10xy   

. D.

   

22

3 1 8xy   

.

Lời giải

Chọn A

Điểm

 

3; 1M

thuộc đường tròn

 

C

nên

   

22

3 1 1 3 2 2R IM     

.

Đường tròn

 

C

có tâm

 

1; 3I

và bán kính

22R 

có phương trình tổng quát là:

     

22

: 1 3 8C x y   

.

Cách 2: thay tọa độ điểm

M

vào cc phương trình đường tròn.

   

22

3 1 1 3 8 10.    

nên loại B;

   

22

3 3 1 1 0 10; 8.     

nên loại C; D.

Do đó chọn A.

Câu 123: [0H3-2-2] Phương trình đường tròn

 

C

có tâm

 

2; 0I 

và tiếp xúc với đường

thẳng

:2 1 0d x y  

là:

A.

 

2

25xy  

. B.

 

2

25xy  

. C.

 

2

25xy  

. D.

 

2

25xy  

.

Lời giải

Chọn B

Vì đường tròn

 

C

tiếp xúc với đường thẳng

d

nên

 

22

2. 2 1

,5

21

R d I d



  



.

Đường tròn

 

C

có tâm

 

2; 0I 

và bán kính

5R 

có phương trình tổng quát là:

   

2

: 2 5C x y  

.

Câu 124: [0H3-2-2] Phương trình đường tròn

 

C

đi qua ba điểm

 

1; 1A 

,

 

3; 1B

,

 

1; 3C

là:

A.

 

22

: 2 2 2 0C x y x y    

. B.

 

22

: 2 2 2 0C x y x y    

.

C.

 

22

: 2 2 0C x y x y   

. D.

 

22

: 2 2 2 0C x y x y    

.

Lời giải

Chọn D

Giả sử phương trình tổng quát của đường tròn

 

C

có dạng

22

2 2 0x y ax by c    

.

Vì ba điểm

 

1; 1A 

,

 

3; 1B

,

 

1; 3C

thuộc đường tròn

 

C

nên ta có hệ phương

trình:

 

1 1 2 1 2 0 1

9 1 2.3 2 0 1

1 9 2 2.3 0 2

a b c a

a b c b

a b c c

       





      





      



.

Khi đó ta có phương trình tổng quát của đường tròn

 

22

: 2 2 2 0C x y x y    

.

Câu 125: [0H3-2-2] Tọa độ tâm đường tròn đi qua 3 điểm

 

1; 2A

,

 

2; 3B 

,

 

4; 1C

là:

A.

 

0; 1

. B.

1

3;

2







. C.

 

0; 0

. D. Không

có.

Lời giải

Chọn D

Cách 1: Ta có

24

1

22

31

2

22

BC

A

BC

A

xx

x

yy

y







  









  





nên

A

là trung điểm

BC

. Suy ra

A

,

B

,

C

thẳng hàng nên không tn tại đường tròn đi qua 3 điểm

A

,

B

,

C

.

Cách 2: Giả sử phương trình tổng quát của đường tròn

 

C

có dạng

22

2 2 0x y ax by c    

.

Vì ba điểm

 

1; 2A

,

 

2; 3B 

,

 

4; 1C

thuộc đường tròn

 

C

nên ta có hệ phương

trình:

 

1 4 2 2.2. 0 2 4 5 1

4 9 2 2 2.3. 0 4 6 13 2

16 1 2.4. 2 0 8 2 17 3

a b c a b c

        





          





         



.

Lấy phương trình

 

1

nhân

2

ri cộng vào phương trình

 

2

và

 

3

ta được

0 20

(Vô lí).

Do đó không tn tại đường tròn đi qua 3 điểm

A

,

B

,

C

.

Câu 126: [0H3-2.21-2] Vị trí tương đối giữa hai đường tròn

 

22

1

:4C x y

và

     

22

2

: 10 16 1C x y   

là:

A. Không cắt nhau. B. Cắt nhau. C. Tiếp xúc trong. D. Tiếp

xúc ngoài.

Lời giải

Chọn A

Đường tròn

 

22

1

:4C x y

có tâm

 

0; 0O

và bán kính

1

2R 

.

Đường tròn

     

22

2

: 10 16 1C x y   

có tâm

 

10; 16I 

và bán kính

2

1R 

.

Ta có

 

2

10 16 2 89OI    

,

12

2 1 3RR   

.

Vì

12

OI R R

nên hai đường tròn không cắt nhau.

Câu 127: [0H3-2-2] Đường thẳng

:4 3 0x y m   

tiếp xúc với đường tròn

 

22

:1C x y

khi:

A.

3m 

. B.

5m 

. C.

1m 

. D.

0m 

.

Lời giải

Chọn B

Đường tròn

 

22

:1C x y

có tâm

 

0; 0O

và bán kính

1R 

.

Đường thẳng



tiếp xúc với đường tròn

 

C

 

22

, 1 5 5

34

m

d O d R m m        



.

Câu 128: [0H3-2-2] Phương trình tiếp tuyến của đường tròn

 

C

có phương trình :

22

4 8 5 0    x y x y

. Đi qua điểm

 

1;0A

.

A.

3 – 4 3 0xy

. B.

3 4 3 0  xy

. C.

3 4 3 0   xy

. D.

3 4 3 0  xy

.

Lời giải

Chọn B

Đường tròn

 

C

có tâm

 

2;4I

, bán kính

22

2 ( 4) 5 5R     

.

Nhận xét :

 

1;0 ( )AC

(tọa độ của

A

thỏa phương trình

 

C

).

Do đó, tiếp tuyến của (C) đi qua

 

1;0A

có VTPT

   

3; 4 3; 4    IA

Phương trình tiếp tuyến có dạng :

 

3 1 4 0 3 4 3 0      x y x y

.

Câu 129: [0H3-2-2] Đường thẳng

:4 3 0  d x y m

tiếp xúc với đường tròn

 

22

:4C x y

khi :

A.

3m

. B.

10m

. C.

1m

. D.

4m

.

Lời giải

Chọn B

Đường tròn

 

C

có tâm

 

0;0O

, bán kính

2R 

Ta có,

d

tiếp xúc với

 

C

 

,d O d R

22

2

43

m





10 10mm    

.

Câu 130: [0H3-2-2] Phương trình tiếp tuyến tại điểm

 

3;4M

với đường tròn

 

22

: 2 4 3 0    C x y x y

là:

A.

70  xy

. B.

70  xy

. C.

70  xy

. D.

30  xy

.

Lời giải

Chọn A

Đường tròn

 

C

có tâm

 

1;2I

, bán kính

22

1 2 3 2 2R    

Tiếp tuyến của (C) tại

 

3;4M

có VTPT

   

2;2 2 1; 1IM

Phương trình tiếp tuyến có dạng :

3 4 0 7 0       x y x y

.

Câu 131: [0H3-2-2] Cho đường tròn

 

22

: 4 2 0   C x y x y

và đường thẳng

: 2 1 0   xy

.Tìm mệnh đề đúng trong các mệnh đề sau :

A.



đi qua tâm

 

C

. B.



cắt

 

C

và không đi qua tâm

 

C

.

C.



tiếp xúc với

 

C

. D.



không có điểm chung với

 

C

.

Lời giải

Chọn C

Đường tròn

 

C

có tâm

 

2;1I

, bán kính

22

2 1 0 5R    

Thay tọa độ của

I

vào phương trình đường thẳng



, ta được :

2 2.1 1 0  

(sai)

nên

I 

( loại đáp án A)

Ta có,

 

22

2 2.1 1

,5

12

dI



  



 

,d I R  

. Do đó,



tiếp xúc với

 

C

.

Câu 132: [0H3-2-2] Cho hai điểm

   

1;1 , 7;5AB

. Phương trình đường tròn đường kính

AB

là:

A.

22

8 6 12 0    x y x y

. B.

22

8 6 12 0    x y x y

.

C.

22

8 6 12 0    x y x y

. D.

22

8 6 12 0    x y x y

.

Lời giải

Chọn D

Gọi

I

là trung điểm

AB

 

17

4

2

4;3

15

3

2

I

x

I

y























 

22

6;4 6 4 2 13AB AB    

Đường tròn

 

C

có đường kính

AB 

 

C

có tâm

I

và bán kính

13

2

AB

R 

Nên phương trình đường tròn là:

   

22

4 3 13xy   

22

8 6 12 0x y x y     

.

Câu 133: [0H3-2-2] Viết phương trình đường tròn

 

C

có đường kính

AB

với

   

1; 1 , 7;5AB

.

A.

 

22

:( 3) ( 2) 25C x y   

. B.

 

22

:( 3) ( 2) 25C x y   

.

C.

 

22

:( 3) ( 2) 25C x y   

. D.

 

22

:( 3) ( 2) 5C x y   

.

Lời giải

Chọn B

Gọi

I

là trung điểm

AB

 

17

3

2

3;2

15

2

I

x

I

y























 

22

8;6 8 6 10AB AB    

Đường tròn

 

C

có đường kính

AB 

 

C

có tâm

I

và bán kính

5

2

AB

R 

Nên phương trình đường tròn là:

   

22

3 2 25xy   

.

Câu 134: [0H3-2-2] Cho điểm

 

0;4M

và đường tròn

 

22

: 8 6 21 0    C x y x y

. Tìm

phát biểu đúng trong các phát biểu sau:

A.

M

nằm ngoài

 

C

. B.

M

nằm trên

 

C

.

C.

M

nằm trong

 

C

. D.

M

trùng với tâm

 

C

.

Lời giải

Chọn A

Đường tròn

 

C

có tâm

 

4;3I

, bán kinh

22

4 3 21 2R    

Ta có:

   

22

4 0 3 4 17IM R     

. Do đó,

M

nằm ngoài

 

C

.

Câu 135: [0H3-2-2] Các đường thẳng

 

51yx  

;

3y x a

;

3y ax

đng quy với giá

trị của

a

là

A.

10

. B.

11

. C.

12

. D.

13

.

Lời giải

Chọn D

Phương trình hoành độ giao điểm giữa hai đường thẳng

 

51yx  

,

3y x a

là:

5 5 3 8 5x x a x a       

(1)

Phương trình hoành độ giao điểm giữa hai đường thẳng

3y x a

,

3y ax

là:

   

3 3 3 3 1 3ax x a a x a x a         

.

Thế

1x 

vào (1) ta được:

8 5 13 ( )a a n     

. Vậy

13a 

.

Câu 1: [0H3-2-3] Viết phương trình đường tròn đi qua

3

điểm

0; 0 , ; 0 , 0; .O A a B b

A.

22

20x y ax by

. B.

22

0x y ax by xy

.

C.

22

0x y ax by

. D.

22

0x y ay by

.

Lời giải

Chọn C

Nhận xét: tam giác

OAB

vuông tại

O

, nên đường tròn đi qua ba điểm

OAB

có tâm

;

22

ab

I

là trung điểm

AB

và

22

44

ab

R OI

Phương trình đường tròn cần tìm là :

22

2 2 4 4

a b a b

xy

22

0x y ax by

Câu 2: [0H3-2-3] Viết phương trình đường tròn đi qua

3

điểm

0; 2 , 2; 2 , 1;1 2ABC

.

A.

22

2 2 2 0x y x y

. B.

22

2 2 0x y x y

.

C.

22

2 2 2 0x y x y

. D.

22

2 2 2 0x y x y

.

Lời giải

Chọn B

Gọi phương trình đường tròn là

22

: 2 2 0C x y ax by c

Ta có:

2

0;2 4 4

2;2 4 4 8

1;1 2 2 2 1 2 1 1 2

A C b c

B C a b c

C C a b c

Giải hệ trên ta được

1

0

a

b

c

Câu 3: [0H3-2-3] Tìm bán kính đường tròn đi qua

3

điểm

11; 8 , 13; 8 , 14; 7A B C

.

A.

2

. B.

1

. C.

5

. D.

2

.

Lời giải

Chọn C

Gọi phương trình đường tròn là

22

: 2 2 0C x y ax by c

Ta có:

11;8 22 16 185

13;8 26 16 233

14;7 28 14 245

A C a b c

B C a b c

C C a b c

Giải hệ trên ta được

12

6

175

a

b

c

22

5R a b c

Câu 4: [0H3-2-3] Tìm tọa độ tâm đường tròn đi qua

3

điểm

1; 2 , 2; 3 , 4;1A B C

.

A.

(0; 1 .)

B.

0;0

. C.

53

;

22

. D.

3;0,5 .

Lời giải

Chọn C

Gọi phương trình đường tròn là

22

: 2 2 0C x y ax by c

Ta có:

1;2 2 4 5

2;3 4 6 13

4;1 8 2 17

A C a b c

B C a b c

C C a b c

Giải hệ trên ta được

5

2

3

2

6

a

b

c

Câu 5: [0H3-2-3] Viết phương trình đường tròn đi qua 3 điểm

1;1 , 3;1 , 1;3 .A B C

A.

22

2 2 2 0x y x y

. B.

22

2 2 0x y x y

.

C.

22

2 2 2 0x y x y

. D.

22

2 2 2 0x y x y

.

Lời giải

Chọn A

Gọi phương trình đường tròn cần tìm có

dạng

2 2 2 2

: 2a 2 0, (a 0).C x y x by c b c

Vì (C) đi qua ba điểm A, B, C nên ta có hệ phương trình:

1 1 2a 2 0 2a 2 2 1

9 1 6a 2 0 6a 2 10 1 ( ).

1 9 2a 6 0 2a 6 10 2

b c b c a

b c b c b tm

b c b c c

Vậy PT đường tròn cần tìm:

22

: 2 2 2 0.C x y x y

Câu 6: [0H3-2-3] Đường thẳng

:4 3 0x y m   

tiếp xúc với đường tròn

 

22

:1C x y

khi:

A.

3m 

. B.

5m 

. C.

1m 

. D.

0m 

.

Lời Giải

Chọn B

Đường tròn

 

22

:1C x y

có tâm

 

0;0I

bán kính

1R 

Để

 



tiếp xúc với

 

C

thì

 

4.0 3.0

, 1 5 5

16 9

m

d I R m m



        



.

Câu 7: [0H3-2-3] Đường tròn đi qua ba điểm

 

0;2A

,

 

2;0B 

và

 

2;0C

có phương trình

là:

A.

22

8xy

. B.

22

2 4 0x y x   

.

C.

22

2 8 0x y x   

. D.

22

40xy  

.

Lời Giải

Chọn D

Gọi phương trình đường tròn

 

C

có dạng:

22

2 2 0x y ax by c    

Vì

 

C

đi qua ba điểm

,,A B C

nên ta có hệ

4 4 0 4 4 0

4 4 0 4 4 4

b c b c a

a c a c b

a c a c c

     

  

  

        

  

  

      

  

Vậy phương trình đường tròn cần tìm là:

22

40xy  

Câu 8: [0H3-2-3] Cho ba điểm

     

1; 4 , 3; 2 , 5; 4A B C

. Tọa độ tâm đường tròn ngoại tiếp

tam giác

ABC

là

A.

 

2; 5

. B.

3

;2

2







. C.

 

9; 10

. D.

 

3; 4

.

Lời giải

Chọn D

Ta có

   

22

2 2 2

22

3 1 2 4 8

5 1 4 4 16

5 3 4 2 8

AB

AC AB BC AC

BC

    

       

    

.

Vậy tam giác

ABC

vuông tại

B

. Từ đó suy ra, tâm đường tròn ngoại tiếp tam giác

ABC

là trung điểm của đoạn

AC

, điểm này có tọa độ

 

3; 4

.

Câu 9: [0H3-2-3] Cho 3 điểm

 

2;0A 

,

 

2; 2B

,

 

2;0C

. Đường tròn ngoại tiếp tam giác

ABC

có phương trình là:

A.

22

40xy  

. B.

22

4 4 0x y x   

.

C.

22

4 4 4 0x y x y    

. D.

22

2xy

.

Lời giải

Chọn B

Gọi

 

;I x y

là tâm đường tròn ngoại tiếp tam giác

ABC

.

Ta có:

 

   

 

22

2

22

2 2 2

2 2 2 0

0

22

x y x y

xy

IA IB x

IA IC y

x

x y x y



     

  







  

   









    



Bán kính

2R IA

.

Vậy phương trình đường tròn là:

22

40xy  

Câu 10: [0H3-2-3] Cho hai điểm

 

3;0A

,

 

0;4B

. Đường tròn nội tiếp tam giác

OAB

có phương

trình là

A.

22

1xy

. B.

22

2xy

.

C.

22

2 2 1 0x y x y    

. D.

22

6 8 25 0x y x y    

.

Lời giải

Chọn C

Phương trình đường thẳng

AB

:

1 4 3 12 0

34

xy

xy     

.

Gọi

 

;I x y

là tâm đường tròn nội tiếp tam giác

OAB

.

Nhận xét:

0x 

,

0y 

.

Ta có:

   

,,

1

7 12

3 4 12

1

,,

5

xy

d I OA d I OB

x

xy

y

d I OA d I BA

x















  

  



   













Bán kính

 

,1R d I OA

.

Vậy phương trình đường tròn là:

22

2 2 1 0x y x y    

Câu 11: [0H3-2.21-2] Cho hai đường tròn:

 

22

1

: 2 6 6 0C x y x y    

,

 

22

2

: 4 2 4 0C x y x y    

. Tìm mệnh đề đúng trong các mệnh đề sau:

A.

 

1

C

cắt

 

2

C

. B.

 

1

C

không có điểm chung với

 

2

C

.

C.

 

1

C

tiếp xúc trong với

 

2

C

. D.

1

()C

tiếp xúc ngoài với

 

2

C

.

Lời giải

Chọn B

Đường tròn

 

1

C

có tâm

 

1;3I 

và bán kính

1

2R 

.

Đường tròn

 

2

C

có tâm

 

2; 1I 

và bán kính

2

3R 

.

Vì

1 2 1 2

5I I R R  

nên

1

()C

tiếp xúc ngoài với

 

2

C

.

Câu 12: [0H3-2-3] Trong mặt phẳng toạ độ cho ba điểm

( 2;0), (8;0), (0;4)A B C

. Tính bán

kính đường tròn ngoại tiếp tam giác.

A.

26

. B.

26

. C.

6

. D.

5

.

Lời giải

Chọn D

Gọi

( ; )I a b

là tâm đường tròn ngoại tiếp tam giác

Ta có

   

22

28

24

x y x y

IA IB

IA IC

x y x y



    















    





 

20 60 3

(3;0) 5;0 5

4 8 12 0

xx

I IA R IA

x y y





       



  



.

Câu 13: [0H3-2-3] Trong mặt phẳng toạ độ cho ba điểm

(100;0), (0;75), (72;96)A B C

. Tính bán

kính đường tròn ngoại tiếp tam giác.

A.

6

. B.

62,5

. C.

7,15

. D.

7,5

.

Lời giải

Chọn B

Gọi

( ; )I a b

là tâm đường tròn ngoại tiếp tam giác

Ta có

   

     

22

2 2 2

2

100 75

100 72 96

x y x y

IA IB

IA IC

x y x y



    















     





50

8 6 175

75 75 125

50; 50;

75

7 24 550

2 2 2

2

x

xy

I IA R IA

xy

y













   

      



   

  



   







.

Câu 14: [0H3-2-3] Trong mặt phẳng toạ độ cho ba điểm

(4;0), (0;2),C(1,6;3,2)AB

. Tính bán

kính đường tròn ngoại tiếp tam giác.

A.

5

. B.

4,75

. C.

25

. D.

4,5

.

Lời giải

Chọn A

Gọi

( ; )I a b

là tâm đường tròn ngoại tiếp tam giác

Ta có

   

     

22

2 2 2

2

42

4 1,6 3,2

x y x y

IA IB

IA IC

x y x y



    















     





 

2 3 2

(2;1) 2; 1 5

0,3 0,4 0,2 1

x y x

I IA R IA

x y y

  



       



  



.

Câu 15: [0H3-2-3] Trong mặt phẳng toạ độ cho ba điểm

(0;3), (0; 12), (6;0)A B C

. Tìm toạ độ

tâm đường tròn ngoại tiếp.

A.

( 4,5;0,5)

. B.

(0; 4,5)

. C.

( 4;0)

. D.

(5; 1)

.

Lời giải

Chọn B

Gọi

( ; )I a b

là tâm đường tròn ngoại tiếp tam giác

Ta có

   

22

0

3 12

30 135

9

0;

9

4 2 9

2

36

2

x

x y x y

IA IB y

I

IA IC x y

y

x y x y





    

  







    

   



  







    





.

Câu 16: [0H3-2-3] Cho điểm

( ; )M x y

có

1 2cos

()

2 2sin

xt

t

yt

  











. Tập hợp điểm

M

là

A. Đường tròn tâm

(1; 2)I 

, bán kính

2R 

. B. Đường tròn tâm

( 1;2)I 

, bán

kính

2R 

.

C. Đường tròn tâm

( 1;2)I 

, bán kính

4R 

. D. Đường tròn tâm

(1; 2)I 

, bán

kính

4R 

.

Hướng dẫn giải

Chọn B

Ta có:

 

2

1 4cos

1 2cos 1 2cos

2 2sin 2 2sin

2 4sin

xt

x t x t

M

y t y t

yt





    







  

    









       

 

   

2 2 2 2

22

1 2 4cos 4sin 1 2 4 sin cos

1 2 4

x y t t x y t t

xy

           

    

Vậy tập hợp điểm

M

là phương trình đường tròn có tâm

 

1;2I 

, bán kính

2R 

Câu 17: [0H3-2-3] Phương trình

2 4sin

()

3 4cos

xt

t

yt









  



là phương trình đường tròn có

A. Tâm

( 2;3)I 

, bán kính

4R 

. B. Tâm

(2; 3)I 

, bán kính

4R 

.

C. Tâm

( 2;3)I 

, bán kính

16R 

. D. Tâm

(2; 3)I 

, bán kính

16R 

.

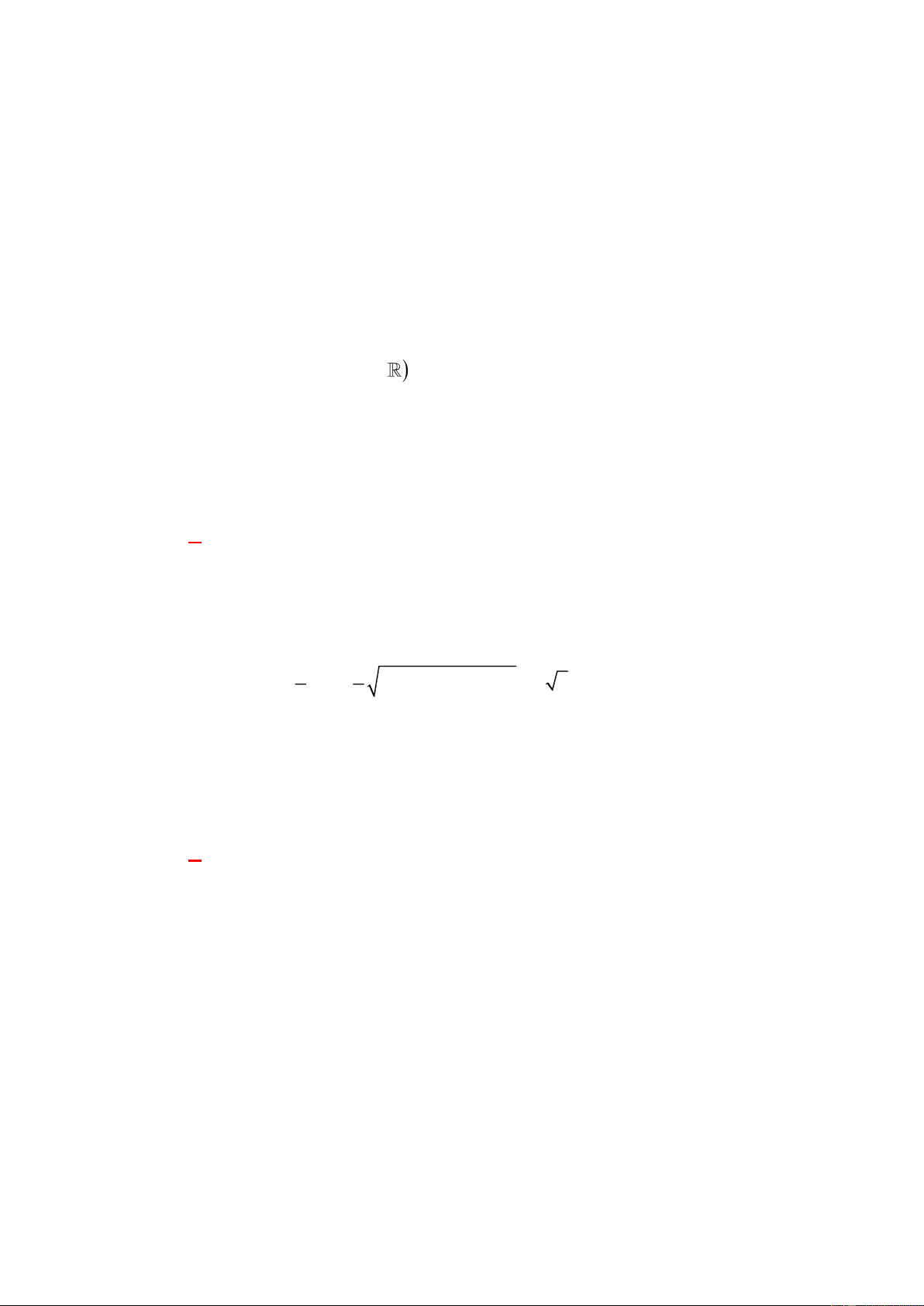
Hướng dẫn giải

Chọn B

Ta có:

 

2

2 16sin

2 4sin 2 4sin

3 4cos 3 4cos

3 16cos

xt

x t x t

y t y t

yt





   







  

    









       

 

   

2 2 2 2

22

2 3 16sin 16cos 2 3 16 sin cos

2 3 16

x y t t x y t t

xy

           

    

Vậy

 

2 4sin

34

xt

t

y cost









  



là phương trình đường tròn có tâm

 

2; 3I 

, bán

kính

4R 

.

Câu 18: [0H3-2-3] Cho hai điểm

(5; 1)A 

,

( 3;7)B 

. Đường tròn có đường kính

AB

có

phương trình là

A.

22

2 6 22 0x y x y    

. B.

22

2 6 22 0.x y x y   

C.

22

2 1 0x y x y    

. D.

22

6 5 1 0.x y x y    

Hướng dẫn giải

Chọn C

Tâm

I

của đường tròn là trung điểm

AB

nên

 

1;3I

.

Bán kính

   

22

11

3 5 7 1 4 2

22

R AB      

Vậy phương trình đường tròn là:

   

22

1 3 32 2 6 22 0x y x y x y         

Câu 19: [0H3-2-3] Cho hai điểm

( 4;2)A 

và

(2; 3)B 

. Tập hợp điểm

( ; )M x y

thỏa mãn

22

31MA MB

có phương trình là

A.

22

2 6 1 0x y x y    

. B.

22

6 5 1 0.x y x y   

C.

22

2 6 22 0x y x y    

. D.

22

2 6 22 0.x y x y    

Hướng dẫn giải

Chọn A

Ta có:

22

31MA MB

       

2 2 2 2

22

4 2 2 3 31 2 1 0x y x y x y x y              

Câu 20: [0H3-2-3] Phương trình đường tròn

 

C

có tâm

 

6; 2I

và tiếp xúc ngoài với đường

tròn

 

22

: 4 2 1 0C x y x y



    

là

A.

22

12 4 9 0x y x y    

. B.

22

6 12 31 0x y x y    

.

C.

22

12 4 31 0x y x y    

. D.

22

12 4 31 0x y x y    

.

Hướng dẫn:

Chọn D

Đường tròn

 

22

: 4 2 1 0C x y x y



    

có tâm

 

2; 1I





bán kính

2R





.

Đường tròn

 

C

tâm

 

6; 2I

tiếp xúc ngoài với

 

C



khi

3II R R R II R

   

     

3II R R II R

  

    

.

Phương trình đường tròn cần tìm

   

22

6 2 9xx   

hay

22

12 4 31 0x y x y    

.

Câu 21: [0H3-2-3] Phương trình đường tròn đường kính

AB

với

   

1;1 ,B 7;5 A

là:

A.

22

– 8 – 6 12 0x y x y  

. B.

22

8 – 6 –12 0x y x y  

.

C.

22

8 6 12 0x y x y    

. D.

22

– 8 – 6 –12 0x y x y

.

Hướng dẫn giải

Chọn A

Có trung điểm của

AB

là

(4,3), 13I IA

nên phương trình đường tròn đường

kính

AB

là

2 2 2 2

( 4) ( 3) – 8 – 13 6 12 0x y x y x y     

Dạng 3. Vị trí tường đối. Phương trình tiếp tuyến của đường tròn

Câu 22: [0H3-2-3] Cho đường tròn

22

( ): 2 6 5 0C x y x y    

. Phương trình tiếp tuyến

của

()C

song song với đường thẳng

: 2 15 0D x y  

là

A.

20xy

và

2 10 0xy  

. B.

20xy

và

2 10 0xy  

.

C.

2 1 0xy  

và

2 3 0xy  

. D.

2 1 0xy  

và

2 3 0xy  

.

Hướng dẫn giải

Chọn A

 

C

có tâm

 

1; 3I 

và bán kính

1 9 5 5, : 2 0R d x y m      

.

d

là tiếp tuyến của

 

C

khi và chỉ khi:

 

16

, 5 5 5

14

m

d I d R m

  

     



5 5 0 : 2 0

5 5 10 : 2 10 0

m m d x y

      







      



.

Câu 23: [0H3-2-3] Cho đường tròn

22

( ): 6 2 5 0C x y x y    

và đường thẳng

:2 ( 2) 7 0d x m y m    

. Với giá trị nào của

m

thì

d

là tiếp tuyến của

()C

?

A.

3m 

. B.

15m 

. C.

13m 

. D.

3m 

hoặc

13m 

.

Hướng dẫn giải

Chọn D

 

C

có tâm

 

3; 1I 

và bán kính

5R 

.

d

là tiếp tuyến của

 

C

khi va chỉ khi:

 

2

3

6 2 7

, 5 16 39 0 .

13

4 ( 2)

m

mm

d I d R m m

m



   



       









Câu 24: [0H3-2-3] Cho hai điểm

( 2;1)A 

,

(3;5)B

và điểm

M

thỏa mãn

90

o

AMB 

. Khi đó

điểm

M

nằm trên đường tròn nào sau đây?

A.

22

6 1 0x y x y    

. B.

22

6 1 0x y x y    

.

C.

22

5 4 11 0x y x y    

. D.

22

5 4 11 0x y x y    

.

Hướng dẫn giải

Chọn A

M

nằm trên đường tròn đường kính

AB

, có tâm

1

;3

2

I







là trung điểm của

AB

và bán kính

1 1 1

25 16 41

2 2 2

R AB   

nên có phương trình

 

2

22

1 41

3 6 1 0

24

x y x y x y



         





.

Câu 25: [0H3-2-3] Đường tròn

()C

có tâm

( 1;3)I 

và tiếp xúc với đường thẳng

:3 4 5 0d x y  

tại điểm

H

có tọa độ là

A.

17

;

55









. B.

17

;

55







. C.

17

;

55









. D.

17

;

55









.

Hướng dẫn giải

Chọn B

:4 3 0IH IH x y cd    

. Đường thẳng

IH

qua

 

1; 3I 

nên

4( 1) 3.3 0 5cc      

. Vậy

:4 3 5 0IH x y  

.

Giải hệ:

1

4 3 5 0

17

5

;

3 4 5 0 7

55

5

x

xy

H

xy

y







  













  













.

Câu 26: [0H3-2-2] Cho đường tròn

22

( ): 4 6 3 0C x y x y    

. Mệnh đề nào sau đây đúng?

(I) Điểm

(1;1)A

nằm ngoài

()C

.

(II) Điểm

(0;0)O

nằm trong

()C

.

(III)

()C

cắt trục tung tại hai điểm phân biệt.

A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Cả (I),

(II) và (III).

Hướng dẫn giải

Chọn D

Đặt

 

22

; 4 6 3f x y x y x y    

 

1;1 1 1 4 6 3 1 0fA       

ở ngoài

 

C

.

   

0;0 3 0 0; 0fO   

ở trong

 

C

.

2

0 6 3 0x y y    

. Phương trình này có hai nghiệm, suy ra

 

C

cắt

'y Oy

tại

2 điểm.

Câu 27: [0H3-2-3] Cho phương trình

2 2 2

4 2 0(1)x y x my m    

. Mệnh đề nào sau đây sai?

A. Phương trình

(1)

là phương trình đường tròn, với mọi giá trị của

m

.

B. Đường tròn

(1)

luôn tiếp xúc với trục tung.

C. Đường tròn

(1)

tiếp xúc với các trục tọa độ khi và chỉ khi

2m 

.

D. Đường tròn

(1)

có bán kính

2R 

.

Lời giải

Chọn C

Ta có:

2 2 2 2

4 4 0a b c m m      

nên

A

,

D

đúng.

Vì

2aR

nên

B

đúng.

Từ đó suy ra

C

sai, vì đường tròn tiếp xúc với

'x Ox

khi và chỉ khi

22b m m    

.

Câu 28: [0H3-2-3] Cho đường tròn

22

( ): 2 6 6 0C x y x y    

và đường thẳng

:4 3 5 0d x y  

. Đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một

dây cung có độ dại bằng

23

có phương trình là

A.

4 3 8 0xy  

. B.

4 3 8 0xy  

hoặc

4 3 18xy

.

C.

4 3 8 0xy  

. D.

4 3 8 0xy  

.

Lời giải

 

C

có tâm

 

1; 3 , 2IR

//d d d





có phương trình

 

4 3 0 5x y m m   

.

Vẽ

2 2 2

3 4 3 1IH MN HM IH R HM        

.

 

8

4.1 3.( 3)

, 1 13 5

18.

16 9

m

d I d IH m

m



  





      









Vậy:

:4 3 8 0

:4 3 18 0

d x y



  







  



.

Câu 29: [0H3-2-3] Đường thẳng

: cos sin 2sin 3 4 0d x y cos

   

    

(



là tham số) luôn

tiếp xúc với đường tròn nào sau đây?

A. Đường tròn tâm

(3; 2)I 

và bán kính

4R 

.

B. Đường tròn tâm

( 3;2)I 

và bán kính

4R 

.

C. Đường tròn tâm

(0;0)O

và bán kính

1R 

.

D. Đường tròn tâm

( 3; 2)I 

và bán kính

4R 

.

Lời giải

Chọn A

Khoảng cách từ điểm

 

;

oo

M x y

đến

d

là:

   

22

3 os 2 sin 4

sin os

oo

x c y

d x c y

c



   

     



Chọn

3, 2

oo

xy  

thì

4d 

: không lệ thuộc vào



.

Suy ra

d

luôn tiếp xúc với đường tròn tâm

 

3; 2I 

, bán kính

4R 

Câu 30: [0H3-2-3] Đường thẳng

: cos2 sin 2 2sin (cos sin ) 3 0xy

    

     

(



là tham

số) luôn tiếp xúc với đường tròn nào sau đây?

A. Đường tròn tâm

(2;3)I

và bán kính

1R 

.

B. Đường tròn tâm

( 1;1)I 

và bán kính

1R 

.

C. Đường tròn tâm

( 1;1)I 

và bán kính

2R 

.

D. Đường tròn tâm

( 2; 3)I 

và bán kính

1R 

.

Lời giải

Chọn C

Cho

 

;

oo

M x y

, ta có:

 

2

22

cos2 sin2 2sin .cos 3 2sin

,

sin 2 cos 2

oo

xy

dM

    





   





H

I

M

N

   

1 cos2 1 sin2 2 2

oo

xy



     

(khi chọn

1; 1

oo

xy  

).

Vậy đường thẳng



luôn tiếp xúc với đường tròn tâm

 

1;1 , 2IR

.

Câu 31: [0H3-2-2] Đường tròn

22

40x y y  

không tiếp xúc đường thẳng nào trong các đường

thẳng dưới đây?

A.

20x

. B.

30xy  

. C.

20x

. D.Trục hoành.

Lời giải

Chọn B

Đường tròn có tâm

 

0; 2I 

, bán kính

2R 

.

– Khoảng cách từ tâm

I

đến đường thẳng

 

1

: 2 0x  

:

 

1

02

,2

1

d I R



   



 

C

tiếp xúc

 

1



– Tương tự:

 

C

tiếp xúc

 

2

: 2 0x  

;

 

C

tiếp xúc trục hoành

 

:0Ox y 

– Khoảng cách từ tâm

I

đến đường thẳng

 

3

: 3 0xy   

:

 

1

2 3 5

,

1 1 2

d I R



   





 

C

không tiếp xúc

 

3



Câu 32: [0H3-2-2] Đường tròn

22

10xy  

tiếp xúc đường thẳng nào trong các đường thẳng dưới

đây ?

A.

0xy

. B.

3 4 1 0xy  

. C.

3 4 5 0xy  

. D.

10xy  

.

Lời giải

Chọn C

Đường tròn

 

22

: 1 0C x y  

có tâm

 

0;0IO

, bán kính

1R 

.

– Khoảng cách từ tâm

I

đến đường thẳng

 

1

:0xy  

:

 

1

0

,0

2

d I R   



 

C

không tiếp xúc

 

1



– Tương tự,

 

C

không tiếp xúc

 

2

:3 4 1 0xy   

;

 

3

10xy   

– Khoảng cách từ tâm

I

đến đường thẳng

 

4

:3 4 5 0xy   

:

 

4

22

5

,1

34

d I R   





 

C

tiếp xúc

 

4



Câu 33: [0H3-2.21-2] Tìm giao điểm 2 đường tròn

 

22

1

: 4 0C x y  

và

 

22

2

: 4 4 4 0C x y x y    

A.

 

2; 2

và (

 

2; 2

. B.

 

0;2

và

 

0; 2

.

C.

 

2;0

và

 

0;2

. D.

 

2;0

và

 

2;0

.

Lời giải

Chọn C

Giải hệ PT

22

40

4 4 4 0

xy

x y x y



  





    







22

40

4 4 4 4 0

xy



  



   





22

40

2

xy



  









 

2

2 4 0

2

xx

yx



   













 

2

2 4 0

2

xx

yx



   













02

20

xx

hay

yy











.

Vậy giao điểm

 

0;2A

,

 

2;0B

Câu 34: [0H3-2.21-2] Tìm toạ độ giao điểm hai đường tròn

 

22

1

:5C x y

và

 

22

2

: 4 8 15 0C x y x y    

A.

 

1;2

và

 

2; 3

. B.

 

1;2

.

C.

 

1;2

và

 

3; 2

. D.

 

1;2

và

 

2;1

.

Lời giải

Chọn B

Giải hệ PT

22

5

4 8 15 0

xy

x y x y









    







22

5

4 8 20 0

xy







   





2

5 20 20 0

52

yy

xy



  









1

2

x

y











. Vậy toạ độ giao điểm là

 

1;2

.

Câu 35: [0H3-2-3] Đường tròn

 

22

:( 2) ( 1) 25C x y   

không cắt đường thẳng nào trong các

đường thẳng sau đây?

A.Đường thẳng đi qua điểm

 

2;6

và điểm

 

45;50

.

B.Đường thẳng có phương trình

40y 

.

C.Đường thẳng đi qua điểm

 

3; 2

và điểm

 

19;33

.

D.Đường thẳng có phương trình

80x

.

Lời giải

Chọn D

Đường tròn có tâm và bán kính là:

 

2;1I

,

5R 

Xét khoảng cách

d

từ tâm

I

đến từng đường thẳng và so sánh với

R

; nếu

dR

thì

đường tròn không cắt đường thẳng

* Đường thẳng đi qua điểm

 

2;6

và điểm

 

45;50

:

1

:44 43 170 0xy   

 khoảng

cách

 

1

215

,

3785

d I R  



 

C

cắt

1



*

2

: 4 0y  

 khoảng cách

 

2

,3d I R  



 

C

cắt

1



* Đường thẳng đi qua điểm

 

3; 2

và điểm

 

19;33

:

3

:35 16 137 0xy   

 khoảng cách

 

3

116

,

1481

d I R  



 

C

cắt

3



*

4

: 8 0x  

 khoảng cách

 

4

,6d I R  



 

C

không cắt

1



Câu 36: [0H3-2-3]Cho đường tròn

     

22

: 3 1 5C x y   

. Phương trình tiếp tuyến của

 

C

song song với đường thẳng

:2 7 0d x y  

là

A.

2 0; 2 10 0x y x y    

. B.

2 1 0; 2 1 0x y x y     

.

C.

2 10 0; 2 10 0x y x y     

. D.

2 0; 2 10 0x y x y    

.

Lời giải

Chọn A

Phương trình tiếp tuyến có dạng

:2 0x y m   

với

7m

.

Đường tròn

     

22

: 3 1 5C x y   

có tâm

 

3; 1I 

và bán kính

5R 

Đường thẳng



tiếp xúc với đường tròn

 

C

khi

 

0

2.3 1

;5

10

5

m

d I R

m







    







Vậy

12

:2 0; :2 10 0x y x y      

.

Câu 37: [0H3-2-3]Nếu đường tròn

     

22

2

: 1 3C x y R   

tiếp xúc với đường thẳng

:5 12 60 0d x y  

thì giá trị của

R

là:

A.

22R 

. B.

19

13

R 

. C.

5R 

. D.

2R 

.

Lời giải

Chọn B

Đường tròn

     

22

2

: 1 3C x y R   

có tâm

 

1;3I

bán kính

R

.

Đường thẳng

:5 12 60 0d x y  

tiếp xúc với đường tròn

 

C

khi

 

33

5.1 12.3 60

19

,

13

5 12

d d I d



  



.

Câu 38: [0H3-2-3]Cho đường tròn

 

22

: 2 8 23 9C x y x y    

và điểm

 

8; 3M 

. Độ dài

đoạn tiếp tuyến của

 

C

xuất phát từ

M

là :

A.

10

. B.

2 10

. C.

10

2

. D.

10

.

Lời giải

Chọn D

Đường tròn

 

22

: 2 8 23 9C x y x y    

có tâm

 

1; 4I 

bán kính

40R 

.

Độ dài tiếp tuyến là

22

10IM R

.

Câu 1: [0H3-2-4] Cho đường tròn

22

( ):( 1) ( 3) 4C x y   

và đường thẳng

:3 4 5 0d x y  

. Phương trình của đường thẳng

d



song song với đường thẳng

d

và chắn trên

()C

một dây cung có độ dài lớn nhất là

A.

4 3 13 0xy  

. B.

3 4 25 0xy  

. C.

3 4 15 0xy  

. D.

4 3 20 0xy  

.

Hướng dẫn giải

Chọn C

 

C

có tâm

 

1;3I 

và

2. // :3 4 0R d d d x y c



    

.

Yêu cầu bài toán có nghĩa là

d



qua tâm

 

1; 3I 

của

 

C

, tức là :

3 12 0 1cc     

Vậy

:3 4 15 0d x y



  

.

Câu 2: [0H3-2-4] Cho đường tròn

22

( ): 4 6 5 0C x y x y    

. Đường thẳng

d

đi qua

(3;2)A

và cắt

()C

theo một dây cung dài nhất có phương trình là

A.

50xy  

. B.

50xy  

. C.

2 5 0xy  

. D.

2 5 0xy  

.

Hướng dẫn giải

Chọn A

Dây cung dài nhất khi dây cung đó là đường kính của

 

C

. Vậy

d

qua

 

2; 3I

và

 

3;2A

.

Do đó:

32

: 5 0

3 2 2 3

xy

d x y



    



Câu 3: [0H3-2-4] Cho đường tròn

22

( ): 4 6 5 0C x y x y    

. Đường thẳng

d

đi qua

(3;2)A

và cắt

()C

theo một dây cung ngắn nhất có phương trình là

A.

2 2 0xy

. B.

10xy  

.

C.

10xy  

. D.

10xy  

.

Hướng dẫn giải

H

I

M

N

A

.

Chọn C

 

22

; 4 6 5.

(3;2) 9 4 12 12 5 6 0.

f x y x y x y

f

    

       

Vậy

 

3; 2A

ở trong

 

C

.

Dây cung

MN

ngắn nhất

IH

lớn nhất

HA

MN

có vectơ pháp tuyến

là

 

1; 1IA 

. Vậy

d

có phương trình:

1( 3) 1( 2) 0 1 0x y x y       

.

Câu 1: [0H3-3-1] Đường Elip

 

22

:1

96

xy

E 

có một tiêu điểm là:

A.

 

0;3

. B.

(0 ; 3)

. C.

( 3;0)

. D.

 

3;0

.

Lời giải

Chọn C

 

22

:1

96

xy

E 

2

9

6

a

b

















Mặt khác

2 2 2

9 6 3 3c a b c      

.

Vậy

 

E

có một tiêu điểm

 

3;0

.

Câu 2: [0H3-3-1] Đường Elip

 

22

:1

16 7

xy

E 

có tiêu cự bằng:

A.

18

. B.

6

. C.

9

. D.

3

.

Lời giải

Chọn B

 

22

:1

16 7

xy

E 

2

16

7

a

b

















Mặt khác

2 2 2

16 7 9 3c a b c      

.

Vậy

 

E

có tiêu cự bằng

6

.

Câu 3: [0H3-3-1] Đường Elip

 

22

:1

54

xy

E 

có tiêu cự bằng:

A.

2

. B.

4

. C.

9

. D.

1

.

Lời giải

Chọn A

 

22

:1

54

xy

E 

2

5

4

a

b

















Mặt khác

2 2 2

5 4 1 1c a b c      

Vậy

 

E

có tiêu cự bằng

22c 

.

Câu 4: [0H3-3-1] Đường Elip

22

1

16 7

xy



có tiêu cự bằng:

A.

3

. B.

6

. C.

9

16

. D.

6

7

.

Lời giải

Chọn B

Ta có

22

16; 7ab

mà

2 2 2 2 2 2

93b a c c a b c       

Vậy tiêu cự là

12

26F F c

Câu 5: [0H3-3-1] Elip (E):

22

1

25 9

xy



có tâm sai bằng bao nhiêu?

A.

4

5

. B.

5

4

. C.

5

3

. D.

3

5

.

Lời giải

Chọn A

Ta có

22

25 5; 9a a b   

mà

 

2 2 2 2 2 2

16 4 0b a c c a b c Do c        

Vậy tâm sai là

4

5

c

e

a



.

Câu 6: [0H3-3-1] Cặp điểm nào là các tiêu điểm của elip

 

22

:1

54

xy

E 

?

A.

 

1;2

1;0F 

. B.

 

1;2

3;0F 

. C.

 

1;2

0; 1F 

. D.

 

1;2

1; 2F 

.

Lời giải

Chọn A

Ta có

 

22

2 2 2 2 2

: 1 5, 4, 1

54

       

xy

E a b c a b

Câu 7: [0H3-3-1] Elip

 

22

:1

94

xy

E 

có tâm sai bằng bao nhiêu?

A.

3

2

e 

. B.

5

3

e 

. C.

2

3

e 

. D.

5

3

e 

.

Lời giải

Chọn D

Ta có

 

22

222

: 1 9, 4, 5

94

xy

E a b c     

Tâm sai của elip là:

5

3

c

e

a



.

Câu 8: [0H3-3-1] Cho elip

 

22

:1

xy

E

pq



với

0pq

, khi đó tiêu cự của elip

 

E

bằng

A.

pq

. B.

22

pq

. C.

pq

. D.

22

2 pq

.

Lời giải

Chọn D

Tiêu cự của elip

 

E

được tính bởi

22

22c p q

.

Câu 9: [0H3-3-1] Phương trình

22

1

xy

ab



, với

0, 0ab

, là phương trình chính tắc của

đường nào?

A. Elip với trục lớn bằng

2a

, trục bé bằng

2b

.

B. Hypebol với trục lớn bằng

2a

, trục bé bằng

2b

.

C. Hypebol với trục hoành bằng

2a

, trục tung bằng

2b

.

D. Hypebol với trục thực bằng

2a

, trục ảo bằng

2b

.

Lời giải

Chọn D

Câu 10: [0H3-3-1] Cặp điểm nào là các tiêu điểm của hypebol

22

1

95

xy



?

A.

 

4; 0

và

 

4; 0

. B.

 

14; 0

và

 

14; 0

.

C.

 

2; 0

và

 

2; 0

. D.

 

0; 14

và

 

0; 14

.

Lời giải

Chọn B

Ta có

22

9 5 14c a b    

. Vậy cặp điểm

   

14; 0 , 14; 0

là các tiêu

điểm của hypebol.

Câu 11: [0H3-3-1] Cặp đường thẳng nào là các đường tiệm cận của hypebol

22

1

16 25

xy



?

A.

5

4

yx

. B.

4

5

yx

. C.

25

16

yx

. D.

16

25

yx

.

Lời giải

Chọn A

Ta có

22

16 4, 25 5a a b b     

. Vậy phương trình các đường tiệm cận của

hypebol là

5

4

b

y x x

a

   

.

Câu 12: [0H3-3-1] Cặp đường thẳng nào dưới đây là các đường chuẩn của hypebol

22

1

xy

qp



?

A.

p

x

q



. B.

q

x

p



. C.

2

22

q

x

pq





. D.

2

22

p

x

pq





.

Lời giải

Chọn C

Ta có

22

c p q

.

Tâm sai của hypebol là

22

pq

c

e

aq





.

Vậy phương trình các đường chuẩn là

2

2 2 2 2

a q q

x

e

p q q p

q

     



.

Câu 13: [0H3-3-1] Đường tròn ngoại tiếp hình chữ nhật cơ sở của hypebol

22

1

16 9

xy



?

A.

22

25xy

. B.

22

7xy

. C.

22

7xy

. D.

22

7xy

.

Lời giải

Chọn A

Ta có

22

16 4, 9 3a a b b     

.

Vậy hình chữ nhật cơ sở có độ dài hai cạnh là

28a 

và

26b 

. Từ đó, suy ra bán

kính đường tròn ngoại tiếp hình chữ nhật cơ sở được tính bởi

22

86

5

2

R





.

Đường tròn ngoại tiếp hình chữ nhật cơ sở có tâm tại gốc tọa độ nên phương trình

của đường tròn này là

22

25xy

.

Câu 14: [0H3-3-1] Đường thẳng nào dưới đây là đường chuẩn của parabol

2

4yx

?

A.

4x 

. B.

2x 

. C.

1x 

. D.

1x 

.

Lời giải

Chọn D

Ta có

2 4 2pp  

.

Phương trình đường chuẩn là

0 1 0 1

2

p

x x x       

.

Câu 15: [0H3-3-1] Cho elip

 

E

có hai tiêu điểm

1

F

,

2

F

và có độ dài trục lớn bằng

2a

. Trong các

mệnh đề sau, mệnh đề nào đúng ?

A.

12

2a F F

. B.

12

2a F F

. C.

12

2a F F

. D.

12

4a F F

.

Lời giải

Chọn B

Câu 16: [0H3-3-1] Cho một elip

 

E

có phương trình chính tắc

22

1

xy

ab



. Gọi

2c

là tiêu cự của

 

E

. Trong các mệnh đề sau, mệnh đề nào đúng ?

A.

2 2 2

c a b

. B.

2 2 2

b a c

. C.

2 2 2

a b c

. D.

c a b

.

Lời giải

Chọn C

Câu 17: [0H3-3-1] Cho điểm

 

2;3M

nằm trên đường elip

 

E

có phương trình chính tắc:

22

1

xy

ab



. Trong các điểm sau đây điểm nào không nằm trên

 

E

:

A.

1

( 2;3)M 

. B.

2

(2; 3)M 

. C.

3

( 2; 3)M 

. D.

4

(3;2)M

.

Lời giải

Chọn D

Câu 18: [0H3-3-1] Cho elip

 

E

có phương trình chính tắc

22

1

100 36

xy



. Trong các điểm có tọa độ

sau đây điểm nào là tiêu điểm của elip

 

E

?

A.

 

10;0

. B.

 

6;0

. C.

 

4;0

. D.

 

8;0

.

Lời giải

Chọn D

Ta có:

100 36 8c     

Vậy ta có hai tiêu điểm

 

1

8;0F 

và

 

2

8;0F

Câu 19: [0H3-3-1] Cho phương trình chính tắc của đường tròn

 

   

22

2

:C x a y b R   

.

Khẳng định nào đúng?

A. tâm

 

– ; –I a b

bán kính

R

. B. tâm

 

;I a b

bán kính

2

R

.

C. tâm

 

;I a b

bán kính

R

. D. tâm

 

;–I a b

bán kính

R

.

Lời giải

Chọn C

Đường tròn có PTCT

   

22

2

x a y b R   

cho biết

 

C

có tâm

 

;I a b

và bán

kính

R

.

Câu 20: [0H3-3-1] Tâm của đường tròn

 

C

có phương trình

   

22

3 4 12xy   

là

A.

 

3;4

. B.

 

4;3

. C.

 

3; 4

. D.

 

3;4

.

Lời giải

Chọn C

Đường tròn

 

C

có phương trình

   

22

3 4 12xy   

thì có tọa độ tâm là

 

3; 4

.

Câu 21: [0H3-3-1] Phương trình đường tròn

 

C

có tâm

 

–2;3I

và đi qua

 

2;–3M

là:

A.

   

22

3 4 12xy   

. B.

   

22

3 4 5xy   

.

C.

   

22

2 3 52xy   

. D.

   

22

2 3 52xy   

.

Lời giải

Chọn C

 

22

4; 6 52IM R IM    

nên phương trình đường tròn

 

C

là

   

22

2 3 52xy   

.

Câu 22: [0H3-3-1] Phương trình đường tròn

 

C

có tâm

 

1;3I

và đi qua

 

3;1M

là

A.

   

22

1 3 8xy   

. B.

   

22

1 3 10.xy   

C.

   

22

3 1 10xy   

. D.

   

22

3 1 8xy   

.

Lời giải

Chọn A

 

22

2; 2 8IM R IM    

nên phương trình đường tròn

 

C

là

   

22

1 3 8xy   

.

Câu 23: [0H3-3-1] Phương trình chính tắc của

 

E

có độ dài trục lớn

2 10a 

và tiêu cự

26c 

là:

A.

22

1

53

xy



. B.

22

1

53

xy



.

C.

22

1

25 16

xy



. D.

22

1

25 16

xy



.

Lời giải

Chọn D

22

2 10 5

4

2 6 3

aa

b a c

cc





    







.

Câu 24: [0H3-3-1] Viết phương trình chính tắc của elip

 

E

biết trục lớn

28a 

, trục bé

26b 

.

A.

 

22

:1

16 9

xy

E 

. B.

 

22

:1

25 9

xy

E 

.

C.

 

22

:1

25 16

xy

E 

. D.

 

22

:1

9 16

xy

E 

.

Lời giải

Chọn A

Từ đề bài, ta có :













2 8 4

2 6 3

aa

bb

.

Phương trình chính tắc

   

2 2 2 2

22

: 1 : 1.

16 9

x y x y

EE

ab

    

Câu 25: [0H3-3-1] Viết phương trình chính tắc của elip

 

E

biết trục lớn

2 10a 

, trục bé

28b 

.

A.

 

22

:1

16 9

xy

E 

. B.

 

22

:1

25 9

xy

E 

.

C.

 

22

:1

25 16

xy

E 

. D.

 

22

:1

9 16

xy

E 

.

Lời giải

Chọn C

Từ đề bài, ta có :













2 10 5

2 8 4

aa

bb

.

Phương trình chính tắc

   

2 2 2 2

22

: 1 : 1.

25 16

x y x y

EE

ab

    

Câu 26: [0H3-3-1] Viết phương trình chính tắc của

 

E

có độ dài trục lớn

28a 

và tiêu cự

26c 

.

A.

 

22

:1

16 7

xy

E 

. B.

 

22

:1

25 7

xy

E 

.

C.

 

22

:1

25 16

xy

E 

. D.

 

22

:1

7 16

xy

E 

.

Lời giải

Chọn A

Từ đề bài, ta có :













2 8 4

2 6 3

aa

cc

.

Mà

2 2 2 2 2

4 3 7b a c    

.

   

2 2 2 2

22

: 1 : 1.

16 7

x y x y

EE

ab

    

Câu 27: [0H3-3-1] Hãy chọn đáp án đúng điền vào chỗ trống

 

1

.

Cho hai điểm cố định

12

,FF

và một độ dài không đổi

2a

lớn hơn

12

FF

. Elip là tập

hợp các điểm

M

trong mặt phẳng sao cho..

 

1

... Các điểm

1

F

và

2

F

gọi là các tiêu

điểm của elip. Độ dài

12

2F F c

gọi là tiêu cự của elip.

A.

12

2FM F M a

. B.

12

2FM F M a

. C.

12

2FM F M a

. D.

12

2F M F M c

Lời giải

Chọn C

Theo định nghĩa Elip của SGK.

Câu 28: [0H3-3-1] Cho Elip có trục lớn nằm trên trục hoành. Tọa độ các tiêu điểm của Elip

là

A.

 

1

;0Fc

và

 

2

;0Fc

. B.

 

1

;0Fc

và

 

2

;0Fc

.

C.

 

1

;0Fc

và

 

2

0;Fc

. D.

 

1

;0Fc

và

 

2

0;Fc

.

Lời giải

Chọn A

Theo công thức tiêu điểm của Elip:

 

1

;0Fc

và

 

2

;0Fc

.

Cách khác: Vì 2 tiêu điểm không thể trùng nhau nên loại đáp án B .

Vì tiêu điểm nằm trên trục hoành nên loại các đáp án C, D .

Câu 29: [0H3-3-1] Phương trình chính tắc của elip là :

A.

22

1

xy

ab

. B.

22

1,( 0)   

xy

ab

.

C.

22

1  

xy

ab

. D.

22

1  

xy

ab

.

Lời giải

Chọn B

Theo công thức phương trình chính tắc trong SGK.

Câu 30: [0H3-3-1] Tìm các tiêu điểm của

 

22

: 1.

91



xy

E

A.

 

1

3;0F

và

 

2

0; 3F

. B.

 

1

3;0F

và

 

2

0; 3F

.

C.

 

1

8;0F

và

 

2

8;0F

. D.

 

1

8;0F

và

 

2

0; 8F

.

Lời giải

Chọn C

Ta có:

2

9

1















a

b

. Mà

2 2 2 2

88a b c c c     

Công thức tiêu điểm :

 

1

;0Fc

và

 

2

;0Fc



 

1

8;0F

và

 

2

8;0F

.

Câu 31: [0H3-3-1] Đường elip

 

22

:1

62



xy

E

có tiêu cự bằng?

A.

2 3.

B.

22

. C.

4

. D.

2

.

Lời giải

Chọn C

Ta có:

2

6

2















a

b

. Mà

2 2 2 2

42a b c c c     

Công thức tiêu cự :

12

24F F c

.

Câu 32: [0H3-3-1] Viết phương trình chính tắc của

 

E

có độ dài trục lớn bằng 8 và tiêu cự

bằng 6.

A.

 

22

: 1.

16 7



xy

E

B.

 

22

: 1.

25 7



xy

E

C.

 

22

: 1.

25 16



xy

E

D.

 

22

: 1.

7 16



xy

E

Lời giải

Chọn A

Phương trình Elip có dạng :

22

1

xy

ab



Ta có, độ dài trục lớn

2 8 4aa  

và tiêu cự

2 6 3cc  

Mà

2 2 2 2

7a b c b   

Vậy:

 

22

: 1.

16 7

xy

E 

Câu 33: [0H3-3-1]Đường Elip

22

1

16 7

xy



có tiêu cự bằng

A. 18. B. 6. C. 9. D. 3.

Lời giải

Chọn B

Ta có

2 2 2

93c a b c    

suy ra tiêu cự:

26c 

.

Câu 34: [0H3-3-1]Đường Elip

22

1

54

xy



có tiêu cự bằng

A.

2

. B.

4

. C.

9

. D.

1

.

Lời giải

Chọn A

Ta có

22

5, 4ab

suy ra

22

1c a b  

.Tiêu cự bằng

22c 

. Chọn A

Câu 35: [NC] Cho Elip

22

9 36 144 0xy  

. Câu nào sau đây sai?

A. Trục lớn bằng 8. B. Tiêu cự bằng

43

.

C. Tâm sai bằng

3

7

. D. Phương trình đường chuẩn

83

3

x 

.

Lời giải

Chọn C

Ta có

22

4

3

9 36 144 0 1 2 3,

2

16 4 2

a

x y c

x y x e

b

a





          







Nên: Trục lớn

28a 

, trục nhỏ

24b 

,

Tiêu cự

2 4 3c 

Tâm sai

3

2

e 

,

Phương trình đường chuẩn

8 8 3

3

x    

8 8 3

3

x    

Câu 36: [0H3-3-1]Đường thẳng nào dưới đây là 1 đường chuẩn của Elip

22

1

20 15

xy



?

A.

1

0.

2

x 

B.

4 0.x

C.

2 0.x 

D.

4 0.x 

Lời giải

Chọn A

Ta có

2 2 2 2

20, 15 5a b c a b     

do đó

51

2

25

c

e

a

  

.

Vậy phương trình đường chuẩn là

1

2

x 

.

Câu 37: [0H3-3-1]Cho hai phương trình

22

1

95

xy



(1) ,

22

1

59

xy



(2). Phương trình nào là

phương trình chính tắc của elip có độ dài trục lớn bằng 6, tiêu cự bằng 4?

A. Phương trình (1). B. Phương trình (2).

C. Cả (1) và (2). D. Không phỉa hai phương trình

đã cho.

Lời giải

Chọn A

 

2

22

2

3

9

1 : 1 5 5

95

2

4

a

xy

bb

c









     









,

 

2

22

2

5

2 : 1 9 3

59

2

4

a

xy

bb

c







     









Cả hai phương trình (1) và (2) đều là phương trình của elip có độ dài trục lớn bằng

6, tiêu cự bằng 4. Nhưng (1) là phương trình chính tắc thỏa yêu cầu bài toán.

Câu 38: [0H3-3-1] Lập phương trình chính tắc của elip có tâm

O

, hai trục đối xứng là hai

trục toạ độ và qua hai điểm

3

2 3;

2

M









,

33

2;

2

N







.

A.

22

1.

12 9

xy



B.

22

1.

12 6

xy



C.

22

1.

16 9

xy



D.

22

1.

9 16

xy



Lời giải

Chọn C

Gọi phương trình chính tắc elip cần tìm là

 

22

: 1 0

xy

E a b

ab

   

. Do elip đi

qua

3

2 3;

2

M









,

33

2;

2

N







nên ta có hệ

2

22

2

22

12 9

1

16

4

4 27

9

1

4

a

ab

b

ab































Vậy elip cần tìm là

22

1

16 9

xy



.

Câu 39: [0H3-3-1] Elip

22

+1

96

xy



có một tiêu điểm là

A.

 

3;0

. B.

 

0; 6

. C.

 

3;0

. D.

 

0;3

.

Lời giải

Chọn C

Từ dạng của elip

22

1

xy

ab



ta có

3

6

a

b















.

Từ công thức

   

2 2 2

12

3 3;0 , 0; 3b a c c F F     

Câu 40: [0H3-3-1] Elip

22

+1

95

xy



có một tiêu điểm là

A.

 

0; 3

. B.

 

2;0

. C.

 

3;0

. D.

 

0;3

.

Lời giải

Chọn B

Từ dạng của elip

22

1

xy

ab



ta có

3

5

a

b















.

Từ công thức

   

2 2 2

12

2 2;0 , 0;2b a c c F F     

Câu 41: [0H3-3-1] Elip

22

+1

54

xy



có tiêu cự bằng

A.

2

. B.

1

. C.

4

. D.

9

.

Lời giải

Chọn A

Từ dạng của elip

22

1

xy

ab



ta có

5

2

a

b















.

Từ công thức

2 2 2

12

1 2 2b a c c F F c      

.

Câu 42: [0H3-3-1] Elip

22

+1

16 7

xy



có tiêu cự bằng

A.

18

. B.

3

. C.

9

. D.

6

.

Lời giải

Chọn D

Từ dạng của elip

22

1

xy

ab



ta có

4

7

a

b















.

Từ công thức

2 2 2

12

3 2 6b a c c F F c      

.

Câu 43: [0H3-3-1] Elip

22

+1

16 7

xy



có tâm sai bằng

A.

3

. B.

1

2

. C.

3

4

. D.

1

8

.

Lời giải

Chọn C

Từ dạng của elip

22

1

xy

ab



ta có

4

7

a

b















.

Từ công thức

2 2 2

3b a c c   

.

Tâm sai của elip

3

4

c

ee

a

  

.

Câu 44: [0H3-3-1] Tâm sai của elip

22

+1

54

xy



bằng

A.

0,4

. B.

0,2

. C.

5

. D.

4

.

Lời giải

Chọn C

Từ dạng của elip

22

1

xy

ab



ta có

5

2

a

b















.

Từ công thức

2 2 2

1b a c c   

.

Tâm sai của elip

15

5

c

ee

a

   

.

Câu 45: [0H3-3-1] Tâm sai của elip

22

+1

16 7

xy



bằng

A.

2

. B.

4

. C.

7

4

. D.

3

.

Lời giải

Chọn A

Từ dạng của elip

22

1

xy

ab



ta có

4

7

a

b















.

Từ công thức

2 2 2

3b a c c   

.

Tâm sai của elip

2 2 2

42

c

ee

a

   

.

Câu 1: [0H3-3-2]Cho Elip

22

1

54

xy



. Tính tỉ số của tiêu cự với độ dài trục lớn của Elip.

A.

5

.

4

B.

5

.

5

C.

35

.

5

D.

25

.

5

Lời giải

Chọn B

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Elip

22

1

54

xy



có

2 2 2 2 2

5, 4 1 1a b c a b c       

Độ dài trục lớn:

2 2 5a 

. Tiêu cự:

22c 

Tỉ số

21

.

2

5

c

e

a



Câu 2: [0H3-3-2]Cho Elip có phương trình :

22

9 25 225xy

. Lúc đó hình chữ nhật cơ sở

có diện tích bằng

A.

15

. B.

40

. C.

60

. D.

30

.

Lời giải

Chọn C

Ta có

2

22

2

25 5

9 25 225 1

3

25 9

9

aa

xy

b









      









Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở )

2 10a 

.

Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở)

26b 

.

Diện tích hình chữ nhật cơ sở là

2 .2 60ab

Câu 3: [0H3-3-2]Đường thẳng nào dưới đây là 1 đường chuẩn của Elip

22

1

16 12

xy



A.

4

0.

3

x 

B.

2 0.x 

C.

3

0.

4

x 

D.

80x

.

Lời giải

Chọn D

Ta có

2

16 12 4 2cc    

đường chuẩn

2

: 0 0 8 0

aa

x x x

ec

        

.

Câu 4: [0H3-3-2]Đường Elip

22

1

96

xy



có 1 tiêu điểm là

A.

 

0;3 .

B.

(0; 6).

C.

 

3;0 .

D.

 

3;0 .

Lời giải

Chọn C

Ta có:

2 2 2

33c a b c    

suy ra tiêu điểm

 

3;0F 

.

Câu 5: [0H3-3-2]Một elip có trục lớn bằng 26, tâm sai e =

12

13

. Trục nhỏ của elip có độ dài

bằng bao nhiêu?

A. 10. B. 12. C. 24. D. 5.

Lời giải

Chọn A

Ta có

13a 

, mà

12

13

c

ec

a

   

. Suy ra

22

5b a c  

.

Câu 6: [0H3-3-2]Phương trình chính tắc của Elip có một tiêu điểm

 

1

3;0F 

và đi qua

3

1;

2

M







là

A.

22

1.

42

xy



B.

22

1.

94

xy



C.

22

1.

41

xy



D.

22

1.

14

xy



Lời giải

Chọn C

Phương trình chính tắc của elip có dạng

 

22

2 2 2 2

22

: 1, 0 3 3

xy

E a b c a b a b

ab

          

(1)

 

2 2 2 2

22

3 1 1

1; 1 4 3 4

24

M E b a a b

ab



      





(2)

Giải hệ (1) và (2)

   

22

2 2 2 2 2

2 2 2 2

2 2 2 2 4 2 2

3

3 3 4

4 3 3 4 3

4 3 4 4 5 9 0 1

ab

a b a b a

b b b b

b a a b b b b





  

    

   

  

   

   

     

  

  





Vậy phương trình elip là:

 

22

:1

41

xy

E 

.

Câu 7: [0H3-3-2] Lập phương trình chính tắc của Elip có tâm sai

2

e 

, khoảng cách giữa

hai đường chuẩn là

82

.

A.

22

1.

16 8

xy



B.

22

1.

16 9

xy



C.

22

1.

16 12

xy



D.

22

1.

16 4

xy



Lời giải

Chọn D

Ta có

2

e 

, khoảng cách giữa hai đường chuẩn là

2

2. 2 2 8 2 4

2

     

aa

d a a

e

2 2 2

2 2 8c b a c     

. Suy ra phương trình elip là:

22

1

16 8

xy



.

Câu 8: [0H3-3-2] Cho Elip

22

4 9 36 0xy  

. Khẳng định nào sau đây sai?

A. Trục nhỏ bằng

4

. B. Tiêu điểm

   

12

5;0 , 5;0FF

.

C. Tâm sai

5

3

e 

. D. Phương trình đường chuẩn

5

3

x

.

Lời giải

Chọn D

Ta đưa elip về dạng chính tắc

22

1

94

xy



Từ dạng của elip

22

1

xy

ab



ta có

3

2

a

b











. Trục bé

12

24B B b

(A đúng)

Từ công thức

   

2 2 2

12

5 5;0 , 5;0b a c c F F      

(B đúng.

Tâm sai của elip

5

3

c

ee

a

  

(C đúng).

Phương trình đường chuẩn

95

:

5

a

xx

e

     

(D sai)

Câu 9: [0H3-3-2] Cho Elip

22

9 36 144 0xy  

. Khẳng định nào sau đây đúng?

A. Trục lớn bằng

8

. B. Tiêu cự bằng

27

.

C. Tâm sai bằng

7

3

. D. Phương trình đường chuẩn

16 7

7

x 

.

Lời giải

Chọn A

Ta đưa elip về dạng chính tắc

22

1

16 4

xy



Từ dạng của elip

22

1

xy

ab



ta có

4

2

a

b











. Trục lớn

12

28A A a

(A đúng).

Từ công thức

2 2 2

12

2 3 2 4 3b a c c F F c      

(B sai)

Tâm sai của elip

3

2

c

ee

a

  

(C sai)

Phương trình đường chuẩn

83

:

3

a

xx

e

     

(D sai)

Câu 10: [0H3-3-2] Cho elip

 

22

: + 1

16 12

xy

E 

và điểm

M

nằm trên

 

E

. Nếu

M

có hoành

độ bằng

1

thì khoảng cách từ

M

đến hai tiêu điểm bằng

A.

3,5

và

4,5

. B.

3

và

5

. C.

42

. D.

2

4

2



.

Lời giải

Chọn A

Từ dạng của elip

22

1

xy

ab



ta có

4

23

a

b















.

Từ công thức

2 2 2

2b a c c   

.

Tâm sai của elip

1

2

c

ee

a

  

.

1

4,5

M

MF a ex  

;

2

3,5

M

MF a ex  

Câu 11: [0H3-3-2] Cho elip

 

22

: + 1

169 144

xy

E 

và điểm

M

nằm trên (E). Nếu

M

có hoành

độ bằng

13

thì khỏang cách từ

M

đến hai tiêu điểm bằng

A. 10 và 6. B. 8 và 18. C. 13

5

. D. 13

10

.

Lời giải

Chọn B

Từ dạng của elip

22

1

xy

ab



ta có

13

12

a

b











.

Từ công thức

2 2 2

5b a c c   

.

Tâm sai của elip

5

13

c

ee

a

  

.

1

8

M

MF a ex  

;

2

18

M

MF a ex  

.

Câu 12: [0H3-3-2] Cho elip

 

22

: + 1

16 7

xy

E 

. Khoảng cách giữa hai đường chuẩn của elip

là

A.

32

3

. B.

16

3

. C.

16

. D.

16

3



.

Lời giải

Chọn A

Từ dạng của elip

22

1

xy

ab



ta có

4

7

a

b















.

Từ công thức

2 2 2

3b a c c   

.

Tâm sai của elip

3

4

c

ee

a

  

.

Phương trình đường chuẩn

16

:

3

a

xx

e

     

.

Khoảng cách giữa hai đường chuẩn của elip là:

32

3

.

Câu 13: [0H3-3-2] Cho elip (E) :

22

xy

+

25 9

= 1. Khoảng cách giữa hai đường chuẩn của elip

là

A.9. B.

25

4

. C.



25

4

. D.

25

2

.

Lời giải

Chọn D

Từ dạng của elip

22

1

xy

ab



ta có

5

3

a

b











.

Từ công thức

2 2 2

4b a c c   

.

Tâm sai của elip

4

5

c

ee

a

  

.

Phương trình đường chuẩn

25

:

4

a

xx

e

     

.

Khoảng cách giữa hai đường chuẩn của elip là:

25

2

.

Câu 14: [0H3-3-2] Cho elip

 

22

: + 1

25 16

xy

E 

. Khoảng cách giữa hai đường chuẩn của elip

là

A.

25

3

. B.

50

3

. C.

25

3



. D.

16

.

Lời giải

Chọn B

Từ dạng của elip

22

1

xy

ab



ta có

5

4

a

b











.

Từ công thức

2 2 2

3b a c c   

.

Tâm sai của elip

3

5

c

ee

a

  

.

Phương trình đường chuẩn

25

:

3

a

xx

e

     

.

Khoảng cách giữa hai đường chuẩn của elip là:

50

3

.

Câu 15: [0H3-3-2] Đường nào dưới đây là phương trình đường chuẩn của elip

22

+1

16 12

xy



?

A.

20x 

. B.

80x

. C.

4

0

3

x 

. D.

4

0

3

x 

.

Lời giải

Chọn B

Từ dạng của elip

22

1

xy

ab



ta có

4

23

a

b















.

Từ công thức

2 2 2

2b a c c   

.

Tâm sai của elip

1

2

c

ee

a

  

.

Phương trình đường chuẩn

:8

a

xx

e

     

.

Câu 16: [0H3-3-2] Đường nào dưới đây là phương trình đường chuẩn của elip

22

+1

20 15

xy



?

A.

20x 

. B.

40x 

. C.

40x

. D.

4 5 0x 

.

Lời giải

Chọn D

Từ dạng của elip

22

1

xy

ab



ta có

20

15

a

b















.

Từ công thức

2 2 2

5b a c c   

.

Tâm sai của elip

1

2

c

ee

a

  

.

Phương trình đường chuẩn

: 4 5

a

xx

e

     

.

Câu 17: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó có tiêu cự bằng 6 và trục lớn

bằng 10?

A.

22

+1

25 9

xy



. B.

22

1

25 16

xy



. C.

22

+1

25 16

xy



. D.

22

+1

100 81

xy



.

Lời giải

Chọn C

Từ đề ta có:

12

26

3

2 10 5

F F c

c

A A a a











  



Từ công thức

2 2 2

4b a c b   

.

Phương trình elip

22

+1

25 16

xy



.

Câu 18: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó có tiêu cự bằng 2 và trục lớn

bằng 10?

A.

22

+1

25 24

xy



. B.

22

1

25 16

xy



. C.

22

+1

25 9

xy



. D.

22

xy

+

100 81

= 1 .

Lời giải

Chọn A

Từ đề ta có:

12

22

1

2 10 5

F F c

c

A A a a











  



Từ công thức

2 2 2

24b a c b   

.

Phương trình đường chuẩn

22

+1

25 24

xy



.

Câu 19: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó có tiêu cự bằng

6

và đi qua

 

5;0A

?

A..

22

1

25 16

xy



. B.

22

+1

25 16

xy



. C.

22

+1

25 9

xy



. D.

22

+1

100 81

xy



.

Lời giải

Chọn B

Gọi phương trình chính tắc của elip

22

1

xy

ab



.

Từ đề ta có:

12

2 6 3F F c c   

.

Mà

   

5;0AE

nên ta có:

5a 

.

Từ công thức

2 2 2

4b a c b   

.

Phương trình đường chuẩn

22

+1

25 16

xy



.

Câu 20: [0H3-3-2] Tìm phương trình chính tắc của elip nếu một đỉnh của hình chữ nhật cơ

sở của elip đó là

 

4;3 ?M

A.

22

+1

43

xy



. B.

22

1

16 9

xy



. C.

22

+1

16 9

xy



. D.

22

+1

16 4

xy



.

Lời giải

Chọn C

Vì hình chữ nhật cơ sở của elip đó là

 

4;3M

nên elip có

4; 3.ab

 

2 2 2 2

22

: 1 1

16 9

x y x y

E

ab

    

.

Câu 21: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó đi qua điểm

 

2;1A

và có

tiêu cự bằng

23

?

A.

22

+1

94

xy



. B.

22

1

82

xy



. C.

22

1

85

xy



. D.

22

+1

63

xy



.

Lời giải

Chọn D

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

đi qua điểm

 

2;1A

và có tiêu cự bằng

23

nên ta có

 

2

22

2 2 2 2

2

2 2 4 2

2 2 2

41

4 1 4 1

1

11

6

:1

63

3

3 2 3 0

33

a

xy

ab

E

a b a b

b

a b b b

a b c









   





  

     

   







  

    

   





Câu 22: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó đi qua điểm

 

6;0A

và có

tâm sai bằng

1

?

2

A.

22

1

63

xy



. B.

22

+1

36 27

xy



. C.

22

+1

36 18

xy



. D.

22

+1

62

xy



.

Lời giải

Chọn B

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

đi qua điểm

 

6;0A

và có tâm sai bằng

1

2

nên ta có:

 

22

2

22

2

22

2

36

1

36 36

36

:1

11

1

36 27

9

27

24

2

aa

a

xy

a

E

c

c a c a

b

e

a















   

     

   

  







  









.

Câu 23: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó có tâm sai bằng

1

3

và độ dài

trục lớn bằng 6?

A.

22

1

65

xy



. B.

22

1

95

xy



. C.

22

+1

98

xy



. D.

22

+1

93

xy



.

Lời giải

Chọn C

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có tâm sai bằng

1

3

và độ dài trục lớn bằng 6 nên ta có:

 

22

1

3

:1

3

1

98

22

26

c

a

e

xy

E

a

c

b

a















    

  













Câu 24: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó có một đường chuẩn

40x

và một tiêu điểm là

()1;0 ?A 

A.

22

+1

43

xy



. B.

22

1

16 9

xy



. C.

22

1

16 15

xy



. D.

22

+1

98

xy



.

Lời giải

Chọn A

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có một đường chuẩn

40x

và một tiêu điểm là

0()1;A 

nên ta có:

 

2

22

2

4

:1

43

3

1





  

    

  













a

xy

E

e

c

b

c

Câu 25: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó đi qua điểm là

2(0; )A 

và

có một đường chuẩn

5 0?x

A.

22

+1

16 10

xy



. B.

22

1

16 12

xy



. C.

22

1

20 16

xy



. D.

22

+1

29 4

xy



.

Lời giải

Chọn D

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

đi qua điểm là

2(0; )A 

và có một đường chuẩn

50x

nên ta có

2

4

1

4

5

b

a

ac

c































Câu 26: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó trục lớn gấp đôi trục bé và có

tiêu cự bằng

4 3?

A.

22

1

36 9

xy



. B.

22

+1

16 4

xy



. C.

22

1

36 24

xy



. D.

22

+1

24 16

xy



.

Lời giải

Chọn B

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có trục lớn gấp đôi trục bé và có tiêu cự bằng

43

nên

 

2

22

2

22

2

16

:1

16 4

3 12

23

4

23

ab

a

xy

E

b

c

b

ab













  

     

   









Câu 27: [0H3-3-2] Tìm phương trình chính tắc của elip nếu nó trục lớn gấp đôi trục bé và đi

qua

()2; ?2M 

A.

22

1

24 6

xy



. B.

22

1

36 9

xy



. C.

22

+1

20 5

xy



. D.

22

+1

16 4

xy



.

Lời giải

Chọn C

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có trục lớn gấp đôi trục bé và đi qua

2(2; )M 

nên ta có

 

2

22

2

2 2 2

22

5

:1

4 4 5

20 5

11

20

a b a b

b

xy

E

a

a b b









  

    

  

  











Câu 28: [0H3-3-2] Phương trình chính tắc của elip có một tiêu điểm

 

1

3;0F 

và đi qua

3

1;

2

M







là:

A.

22

1

42

xy



. B.

22

1

94

xy



. C.

22

1

41

xy



. D.

22

1

14

xy



.

Lời giải

Chọn C

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có một tiêu điểm

 

1

3;0F 

và đi qua

3

1;

2

M







nên

 

22

2 2 2

22

4 2 2

22

3

34

:1

13

41

1

4 5 9 0 1

1

4

ab

c

a b a

xy

E

b b b

ab









  

   

     

   



   











Câu 29: [0H3-3-2] Phương trình chính tắc của elip có độ dài trục lớn bằng

26,

tâm sai

12

13

e 

là :

A.

22

1

25 169

xy



. B.

22

1

169 25

xy



. C.

22

1

36 25

xy



. D.

22

1

25 36

xy



.

Lời giải

Chọn B

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có độ dài trục lớn bằng

26,

tâm sai

12

13

e 

nên

 

22

2

13

:1

12

169 25

25

13

a

xy

E

c

e

b

a











    

  













.

Câu 30: [0H3-3-2] Lập phương trình chính tắc của elip có tâm sai

2

e 

và khoảng cách

giữa hai đường chuẩn là

82

.

A.

22

1

16 8

xy



. B.

22

1

16 9

xy



. C.

22

1

16 12

xy



. D.

22

1

16 4

xy



.

Lời giải

Chọn B

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có tâm sai

2

e 

và khoảng cách giữa hai đường chuẩn là

82

nên

 

22

2

4

2

:1

2

16 8

8

2 2 2

4

82

c

e

a

xy

e

a

E

a

b

ac

a

e















     

   

















.

Câu 31: [0H3-3-2] Cho elip

22

3 4 48 0xy  

và đường thẳng

: 2 4 0.d x y  

Giao

điểm của

d

và Elip là :

A.

   

0; –4 , –2;–3 .

B.

   

4;0 , 3;2 .

C.

   

0;4 , –2;3 .

D.

   

–4;0 , 2;3 .

Lời giải

Chọn D

Xét hệ phương trình:

 

22 2

4

0

2 4 0 2 4

16 48 0

2

3 4 48 0

3

x

d

y

x y x y

E

yy

x

xy

y

  









    









  

  



























  

Câu 32: [0H3-3-2] Lập phương trình chính tắc của elip có tiêu cự bằng

8

và đi qua

 

15; 1M 

A.

22

1

20 4

xy



. B.

22

1

12 4

xy



. C.

22

1

94

xy



. D.

22

1

20 16

xy



.

Lời giải

Chọn A

Giả sử elip có phương trình tổng quát là

 

22

:1

xy

E

ab



.

Do

 

E

có tiêu cự bằng

8

và đi qua

 

15; 1M 

nên

 

2 2 2 2

2 2 2

22

42

22

2 2 2 2

4

16 16

16 4

:1

15 1

15 1 15 1

20 4

1

11

16 20

c

a b a b

a b b

xy

E

ba

ab

a b a b





   





  

    

      

    



   







  





.

Câu 33: [0H3-3-2] Cho Elip

 

E

:

22

1

25 9

xy



. Đường thẳng

 

:4d x 

cắt

 

E

tại hai điểm

, MN

. Khi đó:

A.

9

25

MN 

. B.

18

25

MN 

. C.

18

5

MN 

. D.

9

5

MN 

.

Lời giải

Chọn C

Ta có tọa độ M, N lần lượt là

99

4; ; 4;

55

MN

   

  

   

   

vậy

18

5

MN 

Câu 34: [0H3-3-2] Tìm phương trình chính tắc của Elip có tâm sai bằng

1

3

và trục lớn bằng

6

A.

22

1

93

xy

. B.

22

1

98

xy

. C.

22

1

95

xy

. D.

22

1

65

xy

.

Lời giải:

Chọn B

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có tâm sai bằng

1

3

và trục lớn bằng

6

3

1

3

a

c

a

Mặt khác

2 2 2

9 1 8b a c

Vậy

22

:1

98

xy

E

.

Câu 35: [0H3-3-2] Tâm sai của Elip

22

:1

54

xy

E

bằng:

A.

5

4

. B.

0,4

. C.

1

5

. D.

0,2

.

Lời giải:

Chọn C

22

:1

54

xy

E

2

5

2

4

a

b

Mặt khác

2 2 2

5 4 1c a b

Suy ra:

1c

Vậy

1

5

c

e

a

.

Câu 36: [0H3-3-2] Phương trình của Elip có độ dài trục lớn bằng

8,

độ dài trục nhỏ bằng

6

là:

A.

22

9 16 144xy

. B.

22

1

9 16

xy

. C.

22

9 16 1xy

. D.

22

1

64 36

xy

.

Lời giải:

Chọn A

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có độ dài trục lớn bằng

8,

độ dài trục nhỏ bằng

6

2 8 4

2 6 3

aa

bb

Vậy

22

:1

16 9

xy

E

.

Câu 37: [0H3-3-2] Tìm phương trình chính tắc của Elip đi qua điểm

 

6;0

và có tâm sai bằng

1

2

A.

22

1

36 27

xy



. B.

22

1

63

xy



. C.

22

1

62

xy



. D.

22

1

36 18

xy



.

Lời giải

Chọn A

Giả sử phương trình chính tắc của

   

22

: 1 0

xy

E a b

ab

   

Elip đi qua điểm

 

6;0

và có tâm sai bằng

1

6

2

36

1

36

1

9

2

a

c

a





























Mặt khác

2 2 2

36 9 27b a c    

.

Vậy

 

22

:1

36 27

xy

E 

.

Câu 38: [0H3-3-2] Trong các phương trình sau, phương trình nào biểu diễn một elíp có khoảng

cách giữa các đường chuẩn là

50

3

và tiêu cự

6

?

A.

22

1

64 25

xy



. B.

22

1

89 64

xy



. C.

22

1

25 16

xy



. D.

22

1

16 7

xy



.

Lời giải

Chọn C

Giả sử phương trình chính tắc của

   

22

: 1 0

xy

E a b

ab

   

Vì

 

E

có tiêu cự bằng

6

nên

 

2 6 3 1cc  

Hai đường chuẩn của

 

E

có phương trình là:

1

2

:0

a

x

e

a

x

e



  







  





Do đó khoảng cách giữa

2

đường chuẩn là:

2

22

aa

ec



 

2

50

22

3

a

c



Từ

 

1

và

 

2

25a

Mặt khác

2 2 2

25 9 16b a c    

.

Vậy

 

22

:1

25 16

xy

E 

.

Câu 39: [0H3-3-2] Tìm phương trình chính tắc của Elip có tiêu cự bằng

6

và trục lớn bằng

10

A.

22

1

25 9

xy



. B.

22

1

100 81

xy



. C.

22

1

25 16

xy



. D.

22

1

25 16

xy



.

Lời giải

Chọn D

Giả sử phương trình chính tắc của

   

22

: 1 0

xy

E a b

ab

   

Elip có tiêu cự bằng

6

và trục lớn bằng

10

2 10 5

2 6 3

aa

cc













Mặt khác

2 2 2

25 9 16b a c    

.

Vậy

 

22

:1

25 16

xy

E 

.

Câu 40: [0H3-3-2] Cho Elip

 

22

:1

16 12

xy

E 

và điểm

M

nằm trên

 

.E

Nếu điểm

M

có

hoành độ bằng

1

thì các khoảng cách từ

M

tới

2

tiêu điểm của

 

E

bằng:

A.

42

. B.

3

và

5

. C.

3,5

và

4,5

. D.

2

4

2



.

Lời giải

Chọn C

 

22

:1

16 12

xy

E 

2

4

16

23

12

a

b



















Mặt khác

2 2 2

16 12 4 2c a b c      

.

Ta có:

1

2

29

. 4 .1

42

27

. 4 .1

42

M

c

MF a x

a

c

MF a x

a

    

    

.

Câu 41:

[0H3-3-2] Đường thẳng nào dưới đây là một đường chuẩn của Elip

 

22

:1

16 12

xy

E 

A.

4

3

x 

. B.

20x 

. C.

3

0

4

x 

. D.

80x 

.

Lời giải

Chọn D

 

22

:1

16 12

xy

E 

2

4

16

23

12

a

b



















Mặt

khác

2 2 2

16 12 4 2c a b c      

.

Một phương trình đường chuẩn của

 

E

là:

2

0 8 0

a

xx

c

    

.

Câu 42: [0H3-3-2] Một Elip có trục lớn bằng

26,

tâm sai

12

13

e 

Trục nhỏ của elip có độ dài

bằng bao nhiêu?

A.

10

. B.

12

. C.

24

. D.

5

.

Lời giải

Chọn A

Giả sử phương trình chính tắc của

   

22

: 1 0

xy

E a b

ab

   

Elip có trục lớn bằng

26,

tâm sai

e 

12

13

2 26

13

12

13

a

c

a























Mặt

khác

2 2 2

169 144 25 5b a c b      

Vậy độ dài trục nhỏ bằng 10.

Câu 43: [0H3-3-2] Đường thẳng nào dưới đây là 1 đường chuẩn của Elip

22

1

20 15

xy



A.

4 5 0x 

. B.

40x 

. C.

20x 

. D.

40x 

Lời giải

Chọn A

Elíp (E):

22

1

xy

ab



với

0ab

có 2 đường chuẩn

a

x

e



Với Elip (E):

22

1

20 15

xy



có

2 2 2 2 2

20 2 5 , 15 15;a a b b b a c       

2 2 2

55c a b c     

. nên

51

2

25

c

e

a

  

Vậy đường chuẩn của Elíp trên là :

25

4 5 4 5 0

1

2

a

xx

e

        

.

Cách gắn id câu 27- Đã sửa

Câu 44: [0H3-3-2] Phương trình chính tắc của Elip có tâm sai

4

5

e 

, độ dài trục nhỏ bằng

12

là:

A.

22

1

36 25

xy



. B.

22

1

100 36

xy



. C.

22

1

25 36

xy



. D.

22

1

64 36

xy



.

Lời giải

Chọn B

Gọi phương trình chính tắc của Elíp (E) là:

22

1

xy

ab



với

0ab

Đô dài trục nhỏ là:

2 12 6bb  

Mà

 

2 2 2 2 2

36 1b a c a c    

Tâm sai

 

44

2

55

c

e c a

a

   

.

Thay (2) vào (1):

 

2 2 2

16 9

36 36 10 0

25 25

a a a a do a      

.

Vậy phương trình chính tắc của Elíp (E) là:

22

1

100 36

xy



.

Câu 45: [0H3-3-2] Cho elip

 

22

:1

25 9

xy

E 

và cho các mệnh đề:

(I)

 

E

có các tiêu điểm

 

1

4;0F 

và

 

2

4;0F

;

(II)

 

E

có tỉ số

4

5

c

a



;

(III)

 

E

có đỉnh

 

1

5;0A 

;

(IV)

 

E

có độ dài trục nhỏ bằng 3.

Tìm mệnh đề sai trong các mệnh đề sau:

A. (I) và (II). B. (II) và (III). C. (I) và (III). D. (II) và

(IV).

Lời Giải

Đã sửa đáp án D(II) và (IV).

Chọn D

Ta có

2 2 2 2 2

25, 9 25 9 16a b c a b       

Độ dài trục nhỏ

12

26B B b

Suy ra mệnh đề

   

,I III

đúng

Mệnh đề

   

,II IV

sai.

Câu 46: [0H3-3-2] Phương trình chính tắc của elip có hai đỉnh là

   

3;0 , 3;0

và hai tiêu

điểm là

   

1;0 , 1;0

là:

A.

22

1

91

xy



. B.

22

1

89

xy



C.

22

1

98

xy



. D.

22

1

19

xy



.

Lời Giải

Chọn C

Từ giả thiết suy ra

2 2 2 2 2

9, 1 8a c b a c     

Vậy Phương trình chính tắc của elip là:

22

1

98

xy



Câu 47: [0H3-3-2] Cho elip

 

22

: 4 1E x y

và cho các mệnh đề:

(I)

 

E

có trục lớn bằng 1 ; (II)

 

E

có trục nhỏ bằng 4 ;

(III)

 

E

có tiêu điểm

1

3

0;

2

F







; (IV)

 

E

có tiêu cự bằng

3

.

Tìm mệnh đề đúng trong các mệnh đề sau:

A. (I) B. (II) và (IV) C. (I) và (III) D. (IV)

Lời Giải

Chọn D

 

22

: 4 1 1

1

4

xy

E x y    

2 2 2 2 2

13

1,

44

a b c a b      

Trục lớn

12

22A A a

, trục nhỏ

12

1

2 2. 1

2

B B b  

 

E

có tiêu điểm

1

3

;0

2

F









, Tiêu cự

12

3

2 2. 3

2

F F c  

Vậy mệnh đề

 

IV

đúng.

Câu 48: [0H3-3-2] Một elip có trục lớn bằng

26

, tỉ số

12

13

c

a



. Trục nhỏ của elip bằng bao

nhiêu?

A.

5

. B.

10

. C.

12

. D.

24

.

Lời Giải

Chọn B

Trục lớn

12

2 26 13A A a a   

12

13

c

a

  

. Ta có

2 2 2 2 2

13 12 25b a c    

Suy ra trục nhỏ

12

2 5.2 10B B b  

.

Câu 49: [0H3-3-2] Cho elip

 

22

:4 9 36E x y

. Tìm mệnh đề sai trong các mệnh đề sau:

A.

 

E

có trục lớn bằng 6. B.

 

E

có trục nhỏ bằng 4.

C.

 

E

có tiêu cự bằng

5

. D.

 

E

có tỉ số

5

3

c

a



.

Lời Giải

Chọn C

 

22

:4 9 36 1

94

xy

E x y    

2 2 2 2 2

9, 4, 5a b c a b     

Trục lớn

12

2 2.3 6A A a  

, trục nhỏ

12

2 2.2 4B B b  

Tiêu cự

12

2 2. 5F F c

,

5

3

c

a



Vậy mệnh đề C sai.

Câu 50: [0H3-3-2] Cho elip

 

22

:1

16 9

xy

E 

và đường thẳng

: 3 0y  

. Tích các khoảng

cách từ hai tiêu điểm của

 

E

đến đường thẳng



bằng giá trị nào sau đây:

A.

16

. B.

9

. C.

81

. D.

7

.

Lời Giải

Chọn B

Ta có

2 2 2

16 9 7c a b    

 

1

7;0F 

,

 

2

7;0F

.

nên

   

11

0 3 0 3

; . ; . 9

11

d F d F



   

.

Câu 51: [0H3-3-2] Cho elip có các tiêu điểm

   

12

3;0 , 3;0FF

và đi qua

 

5;0A 

. Điểm

 

;M x y

thuộc elip đã cho có các bán kính qua tiêu là bao nhiêu?

A.

12

33

5 , 5

55

MF x MF x   

. B.

12

44

5 , 5

55

MF x MF x   

.

C.

12

3 5 , 3 5MF x MF x    

. D.

12

5 4 , 5 4MF x MF x   

Lời giải

Chọn A

Phương trình chính tắc của elip có dạng

 

22

:1

xy

E

ab



.

Elip có các tiêu điểm

   

12

3;0 , 3;0FF

suy ra

3c 

hay

22

9ab

 

1

Elip đi qua

 

5;0A 

nên

2

25

1 25 5aa

a

    

 

2

Từ

   

1 , 2

suy ra

2

16 4bb  

.

Bán kính qua tiêu là

12

,

cc

MF a x MF a x

aa

   

Câu 52: [0H3-3-2] Cônic có tâm sai

1

2

e 

là đường nào ?

A. Hypebol. B. Parabol. C. Elip. D. Đường

tròn.

Lời giải

Chọn C

Ta có

1

2

e   

đây là tâm sai của đường Elip.

Câu 53: [0H3-3-2] Tìm tâm của đường tròn

 

C

có phương trình

22

5 4 4 0x y x y    

.

A.

 

5;4

. B.

 

4; 5

. C.

5

;2

2









. D.

5

;2

2









.

Lời giải

Chọn C

Đường tròn

 

C

có phương trình

22

5 4 4 0x y x y    

thì có tọa độ tâm là

5

;2

2









.

Câu 54: [0H3-3-2] Cho đường cong có phương trình

22

5 4 4 0x y x y    

. Bán kính của

đường tròn là:

A.

3

2

. B.

4

2

. C.

5

.

2

D.

6

2

.

Lời giải

Chọn C

Ta có

22

5 4 4 0x y x y    

có

5

; 2; 4

2

a b c



  

nên

22

5

2

R a b c   

.

Câu 55: [0H3-3-2] Phương trình nào sau đây là phương trình đường tròn.

A.

22

2 4 8 1 0x y x y    

. B.

22

4 10 6 2 0x y x y    

.

C.

22

2 8 20 0x y x y    

. D.

22

4 6 12 0x y x y    

.

Lời giải

Chọn D

Hệ số của

22

,xy

không giống nhau nên loại A,B.

22

2 8 20 0x y x y    

có

1; 4; 20a b c  

nên

22

15 0a b c    

nên

không phải là phương trình đường tròn. Loại C.

22

4 6 12 0x y x y    

có

2; 3; 12a b c    

nên

22

0a b c  

.

Câu 56: [0H3-3-2] Cho đường tròn

 

22

: 2 4 20 0C x y x y    

. Tìm mệnh đề sai trong

các mệnh đề sau

A.

 

C

có tâm

 

1;2 .I

B.

 

C

có bán kính

5R 

.

C.

 

C

đi qua điểm

 

2;2M

. D.

 

C

không đi qua điểm

 

1;1 .A

Lời giải

Chọn A

 

22

: 2 4 20 0C x y x y    

có

1; 2; 20a b c     

nên

22

25 0a b c   

nên

 

C

là

phương trình đường tròn và có tâm

 

1; 2I 

và bán kính

5R 

.

Thế tọa độ điểm

 

2;2M

vào

 

C

thỏa nên

 

C

đi qua điểm

 

2;2M

.

Thế tọa độ điểm

 

1;1A

vào

 

C

không thỏa nên

 

C

không đi qua điểm

 

2;2M

.

Câu 57: [0H3-3-2] Phương trình đường tròn

 

C

có tâm

 

2;0I 

và tiếp xúc với đường thẳng

:2 1 0d x y  

.

A.

 

2

25xy  

. B.

 

2

25xy  

. C.

 

2

25xy  

. D.

 

2

25xy  

.

Lời giải

Chọn B

 

21

,5

5

II

xy

R d I d



  

nên phương trình đường tròn

 

C

là

 

2

25xy  

.

Câu 58: [0H3-3-2] Tọa độ tâm và bán kính

R

đường tròn có phương trình

   

22

2 3 25xy   

.

A.

 

2; 3I 

và

5R 

. B.

 

2;3I 

và

5R 

.

C.

 

2; 3I 

và

25R 

. D.

 

2;3I 

và

5R 

.

Lời giải

Chọn A

   

22

2 3 25xy   

có tâm và bán kính

 

2; 3I 

và

5R 

.

Câu 59: [0H3-3-2] Tọa độ tâm và bán kính

R

đường tròn

 

C

có phương trình

22

2 2 2 0x y x y    

.

A.

 

2; 3I 

và

3R 

. B.

 

2; 3I 

và

4R 

.

C.

 

1;1I

và

2R 

. D.

 

1; 1I 

và

2R 

.

Lời giải

Chọn C

22

2 2 2 0x y x y    

có

1; 1; 2abc   

nên

22

40a b c   

Khi đó tâm và bán kính

R

đường tròn

 

C

là

 

1;1I

và

2R 

.

Câu 60: [0H3-3-2] Phương trình tiếp tuyến của đường tròn

 

C

có phương trình :

22

4 8 5 0x y x y    

đi qua điểm

 

1;0A 

.

A.

3 – 4 3 0xy

. B.

3 4 3 0xy  

. C.

3 4 3 0xy   

. D.

3 4 3 0xy  

.

Lời giải

Chọn B

Trắc nghiệm.

Thế tọa độ điểm

 

1;0A 

vào phương trình các đường thẳng ở các đáp án, ta loại

đáp án C,D.

 

C

có tâm

 

2;4 ; 5IR

.

Đường thẳng

1

:3 – 4 3 0d x y 

có

 

1

7

,

5

d I d R

.

Đường thẳng

2

:3 4 3 0d x y  

có

 

2

,d I d R

. Chọn B

Tự luận.

I

A

Phương trình đường thẳng

d

qua

 

1;0A 

có vectơ pháp tuyến

 

;n A B

(học

sinh s nhầm ln

với điểm A ) có dạng

0Ax By A  

(hơi tắt).

Sửa lại : Phương trình đường thẳng

d

qua

 

1;0A 

có vectơ pháp tuyến

 

;n a b

có dạng

( 1) 0 0      a x by ax by a

 

22

34

3

,5

4



   



ab

d I d a b

ab

.

Chọn

43  ba

nên PTĐT là

:3 4 3 0d x y  

.

Câu 61: [0H3-3-2] Đường thẳng

:4 3 0d x y m  

tiếp xúc với đường tròn

 

22

:1C x y

khi :

A.

3m 

. B.

5m 

. C.

1m 

. D.

4m

.

Lời giải

Chọn B

 

22

:1C x y

có tâm và bán kính

 

0;0 ; 1OR

.

Đường thẳng

:4 3 0d x y m  

tiếp xúc với đường tròn

 

22

:1C x y

 

, 5 5d O d R m m      

.

Câu 62: [0H3-3-2] Phương trình tiếp tuyến tại điểm

 

3;4M

với đường tròn

 

22

: 2 4 3 0C x y x y    

là:

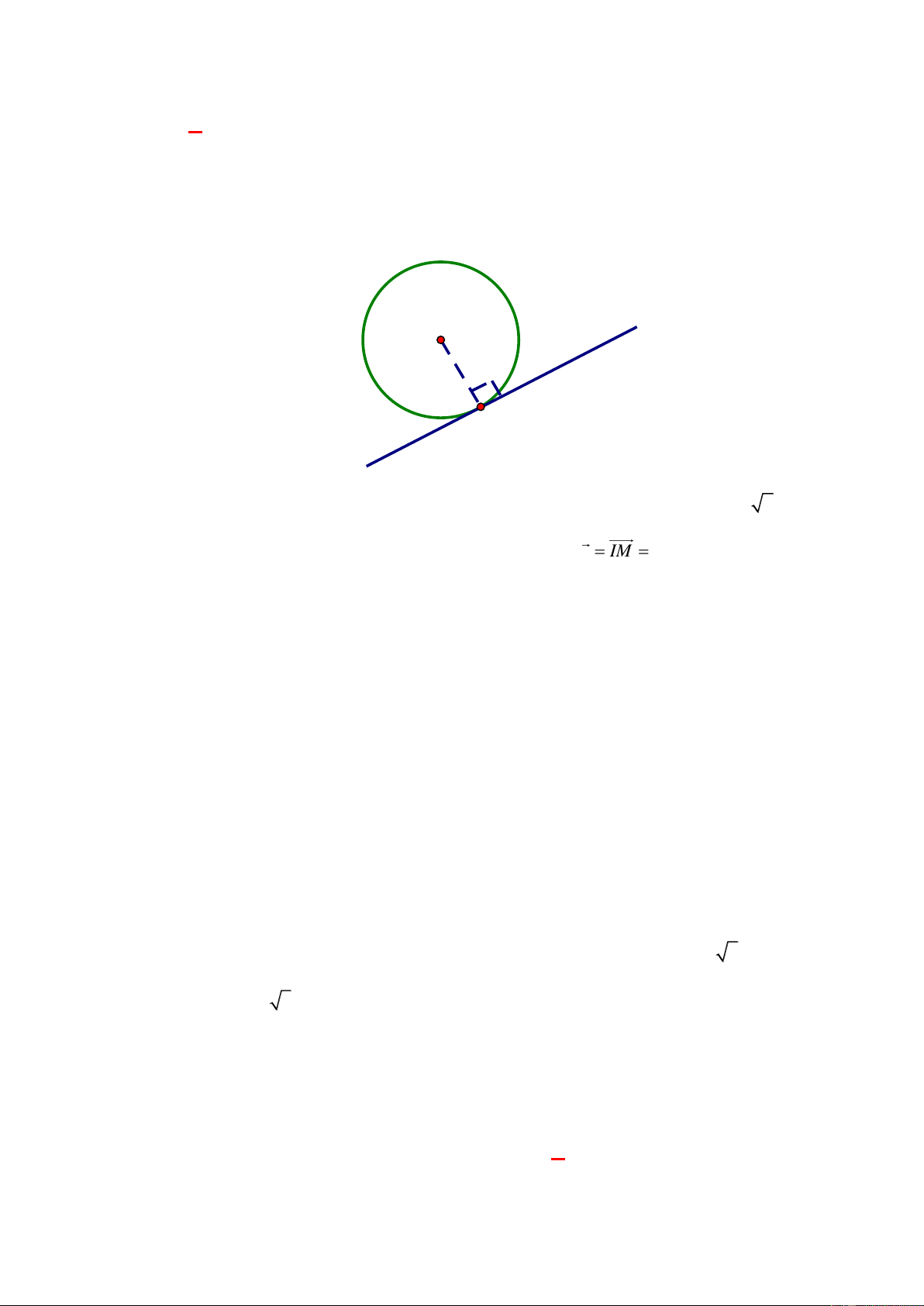
A.

70xy  

. B.

70xy  

. C.

70xy  

. D.

30xy  

.

Lời giải

Chọn A

I

M

Đường tròn

 

22

: 2 4 3 0C x y x y    

có tâm

 

1;2I

và bán kinh

22R 

.

Phương trình tiếp tuyến tại điểm

 

3;4M

có VTPT

 

2; 2n IM   

có dạng :

70xy  

.

Câu 63: [0H3-3-2] Cho đường tròn

 

22

: 4 2 0C x y x y   

và đường thẳng

: 2 1 0xy   

. Tìm mệnh đề đúng trong các mệnh đề sau :

A.



đi qua tâm

 

C

. B.



cắt

 

C

và không đi qua tâm

 

C

.

C.



tiếp xúc với

 

C

. D.



không có điểm chung với

 

C

.

Lời giải

Chọn C

Đường tròn

 

22

: 4 2 0C x y x y   

có tâm

 

2;1I

và bán kính

5R 

.

 

;5d I R  

nên



tiếp xúc với

 

C

Câu 64: [0H3-3-2] Cho hai điểm

   

1;1 , 7;5AB

. Phương trình đường tròn đường kính

AB

là:

A.

22

8 6 12 0x y x y    

. B.

22

8 6 12 0x y x y    

.

C.

22

8 6 12 0x y x y    

. D.

22

8 6 12 0x y x y    

.

Lời giải

Chọn D

 

6;4 52 2 13AB AB   

.

Gọi

I

là trung điểm của

AB

thì

 

4;3I

là tâm đường tròn đường kính

AB

Phương trình

   

22

4 3 13 8 6 12 0x y x y x y         

Câu 65: [0H3-3-2] Cho điểm

 

0;4M

và đường tròn

 

22

: 8 6 21 0C x y x y    

.Tìm phát

biểu đúng trong các phát biểu sau:

A.

M

nằm ngoài

 

C

. B.

M

nằm trên

 

C

.

C.

M

nằm trong

 

C

. D.

M

trùng với tâm

 

C

.

Lời giải

Chọn A

Đường tròn

 

22

: 8 6 21 0C x y x y    

có tâm

 

4;3I

và bán kính

2R 

.

 

4; 1 17 2IM IM R     

nên

M

nằm ngoài

 

C

.

Câu 66: [0H3-3-2] Tìm các tiêu điểm của

 

22

:1

91

xy

E 

.

A.

 

1

3;0F 

và

 

2

0; 3F 

. B.

 

1

3;0F

và

 

2

0; 3F 

.

C.

 

1

8;0F 

và

 

2

8;0F

. D.

 

1

8;0F

và

 

2

0; 8F 

.

Lời giải

Chọn C

 

22

:1

91

xy

E 

có

3; 1ab

nên

22c 

.

Tiêu điểm của

 

E

là

 

1

8;0F 

và

 

2

8;0F

.

Câu 67: [0H3-3-2] Đường elip

 

22

:1

62

xy

E 

có tiêu cự bằng?

A.

23

. B.

22

. C.

4

. D.

–2

.

Lời giải

Chọn C

 

22

:1

62

xy

E 

có

6; 2ab

.

Mà

   

2 2 2

2c a b c

12

24F F c  

.

Câu 68: [0H3-3-2] Đường

 

22

:1

42

xy

E 

có tiêu cự bằng?

A.

22

. B.

22

. C.

3

. D.

23

.

Lời giải

Chọn A

Từ đề bài, ta có :

2

4

2

a

b















.

Vậy, ta có:

    

2 2 2

4 2 2c a b

   2 2 2 2cc

.

Câu 69: [0H3-3-2] Một elip có trục lớn bằng

26

, tỉ số

12

13

c

a



. Trục nhỏ của elip bằng bao

nhiêu ?

A.

5

. B.

10

. C.

12

. D.

24

.

Lời giải

Chọn B

Từ đề bài, ta có :























2 26

13

12

13

a

c

a

.

Mà

2 2 2 2 2

13 12 25b a c    

.

   5 2 10bb

.

Câu 70: [0H3-3-2] Phương trình chính tắc của elip

 

E

có hai đỉnh

   

3;0 ; 3;0

và hai tiêu

điểm

   

1;0 ; 1;0

là.

A.

 

22

:1

91

xy

E 

. B.

 

22

:1

89

xy

E 

.

C.

 

22

:1

98

xy

E 

. D.

 

22

:1

19

xy

E 

.

Lời giải

Chọn C

Từ đề bài, ta có :

3

1

a

c











.

Mà

2 2 2 2 2

3 1 8b a c    

.

   

2 2 2 2

22

: 1 : 1

98

x y x y

EE

ab

    

.

Câu 71: [0H3-3-2] Viết phương trình chính tắc của elip

 

E

biết tiêu cự

26c 

và trục bé

28b 

là:

A.

 

22

:1

16 25

xy

E 

. B.

 

22

:1

16 9

xy

E 

.

C.

 

22

:1

16 9

xy

E   

. D.

 

22

:1

25 16

xy

E 

.

Lời giải

Chọn D

Từ













2 6 3

2 8 4

cc

bb

.

Ta có

      

2 2 2

16 9 25 5a b c a

.

Phương trình elip cần tìm

   

2 2 2 2

22

: 1 : 1

25 16

    

x y x y

EE

ab

.

Câu 72: [0H3-3-2] Cho elíp có phương trình

 

22

:1

16 9

xy

E 

và đường thẳng

 

: 3 0dy

Tính tích các khoảng cách

h

từ hai tiêu điểm của elip

 

E

tới đường thẳng

 

d

.

A.

81h 

. B.

16h 

. C.

9h 

. D.

7h 

.

Lời giải

Chọn C

Từ phương trình

 

22

:1

16 9

xy

E 

, ta có :













      



2 2 2

4

3

16 9 7 7

a

b

c a b c

.

 

E

có hai tiêu cự là

 



1

7;0F

và

 

2

7;0F

.

   

    

  

12

7.0 0.1 3 7.0 0.1 3

, . , . 9

11

h d F d d F d

.

Câu 73: [0H3-3-2] Cho phương trình elip

 

22

:4 9 36E x y

. Tìm khẳng định sai trong các

khẳng định sau?

A.

 

E

có trục lớn bằng

6

. B.

 

E

có trục nhỏ bằng

4

.

C.

 

E

có tiêu cự bằng

5

. D.

 

E

có tỉ số

5

3

c

a



.

Lời giải

Chọn C

Từ phương trình

 

22

:4 9 36E x y

, ta đưa về dạng chính tắc:

22

( ): 1

94

xy

E 

.

Khi đó



  



  





        



2 2 2

3 2 6

2 2 4

9 4 5 5 2 2 5

aa

bb

c a b c c

.

Câu 74: [0H3-3-2] Cho elip

 

22

:1

25 9

xy

E 

và các mệnh đề sau

 

:I

Elip

 

E

có các tiêu điểm

 

1

4;0F 

và

 

2

4;0F

.

 

:II

Elip

 

E

có tỉ số

4

5

c

a



.

 

:III

Elip

 

E

có đỉnh

 

1

5;0A 

.

 

:IV

Elip

 

E

có độ dài trục nhỏ bằng 3.

Tìm khẳng định sai trong các khẳng định sau:

A.

 

I

và

 

II

. B.

 

II

và

 

III

. C. I và

 

III

D.

 

IV

.

Lời giải

Chọn D

Từ phương trình chính tắc

 

22

:1

25 9

xy

E 

, ta có :



  



  





        



2 2 2

5 2 10

3 2 6

25 9 16 4 2 8

aa

bb

c a b c c

.

Câu 75: [0H3-3-2] Cho elip

 

22

: 4 1E x y

và cho các mệnh đề:

 

I

:

 

E

có trục lớn bằng

1

.

 

II

:

 

E

có trục nhỏ bằng

4

.

 

III

:

 

E

có tiêu điểm

1

3

0;

2

F







.

 

IV

:

 

E

có tiêu cự bằng

3

.

Tìm khẳng định đúng trong các khẳng định sau:

A.

 

I

. B.

 

II

và

 

IV

. C.

 

I

và

 

III

. D.

 

IV

.

Lời giải

Chọn D

Từ phương trình

 

22

: 4 1E x y

, ta đưa về dạng chính tắc :

22

2

( ): 1

1

2

xy

E 







.





  



  





        





2 2 2

1 2 2

1

21

2

1 3 3

1 2 3

4 4 2

aa

bb

c a b c c

Câu 76: [0H3-3-2] Phương trình chính tắc của elip

 

E

có trục lớn gấp đôi trục bé và đi qua

điểm

 

2; 2

là:

A.

 

22

:1

16 4

xy

E 

. B.

 

22

:1

20 5

xy

E 

.

C.

 

22

:1

36 9

xy

E 

. D.

 

22

:1

24 6

xy

E 

.

Lời giải

Chọn B

Giả sử phương trình chính tắc của elip

 

E

có dạng

22

1

xy

ab



. Elip

 

E

có trục

lớn gấp đôi trục bé suy ra

2ab

, đi qua điểm

 

2; 2

nên ta có

 

2

2 2 2

2

2 1 4

1 1 5 2 5

2

ba

b b b

b



        

.

Vậy phương trình chính tắc của elip cần tìm là

 

22

:1

20 5

xy

E 

.

Câu 77: [0H3-3-2] Phương trình chính tắc của

 

E

có độ dài trục lớn

2 10a

và tiêu cự

26c

là:

A.

22

1.

53



xy

B.

22

1.

53



xy

C.

22

1.

25 16



xy

D.

22

1.

25 16



xy

Lời giải

Chọn D

Phương trình Elip có dạng :

22

1

xy

ab



Ta có độ dài trục lớn

2 10 5aa  

và tiêu cự

2 6 3cc  

Mà

2 2 2 2

16a b c b   

Vậy,

 

22

: 1.

25 16

xy

E 

Câu 78: [0H3-3-2] Đường

 

22

:1

42



xy

E

có tiêu cự bằng?

A.

2 2.

B.

2 2.

C.

3.

D.

2 3.

Lời giải

Chọn A

Ta có:

2

4

2















a

b

. Mà

2 2 2 2

22a b c c c     

Tiêu cự :

12

2 2 2FF c

Câu 79: [0H3-3-2] Viết phương trình chính tắc của elip

 

E

biết trục lớn

2 10a

, trục bé

28b

.

A.

 

22

: 1.

16 9



xy

E

B.

 

22

: 1.

25 9



xy

E

C.

 

22

: 1.

25 16



xy

E

D.

 

22

: 1.

9 16



xy

E

Lời giải

Chọn C

Phương trình Elip có dạng :

22

1

xy

ab



Ta có, độ dài trục lớn

2 10 5aa  

và trục bé

2 8 4bb  

Vậy,

 

22

: 1.

25 16

xy

E 

Câu 80: [0H3-3-2] Một elip có trục lớn bằng

26

, tỉ số

12

13



c

a

. Trục nhỏ của elip bằng bao

nhiêu ?

A.

5

. B.

10

. C.

12

. D.

24

.

Lời giải

Chọn B

Ta có, độ dài trục lớn

2 26 13aa  

và

12 12

12

13 13

c

c a c

a

    

Mà

2 2 2 2

25 5a b c b b     

Độ dài trục nhỏ :

2 10b 

.

Câu 81: [0H3-3-2] Phương trình chính tắc của elip

 

E

có hai đỉnh

   

3;0 ; 3;0

và hai tiêu

điểm

   

1;0 ; 1;0

là

A.

 

22

:1

91



xy

E

. B.

 

22

:1

89



xy

E

. C.

 

22

: 1.

98

xy

E 

D.

 

22

: 1.

19

xy

E 

Lời giải

Chọn C

Phương trình Elip có dạng :

22

1

xy

ab



Vì elip có hai tiêu điểm

   

1;0 ; 1;0

nên suy ra

1c 

và tiêu điểm nằm trên trục

hoành.

Vì elip có hai đỉnh

   

3;0 ; 3;0

nên suy ra

3a 

Mà

2 2 2 2

8   a b c b

Vậy

 

22

: 1.

98

xy

E 

Câu 82: [0H3-3-2] Viết phương trình chính tắc của elip

 

E

biết tiêu cự bằng

6

và trục bé

bằng

8

là:

A

22

1.

16 25

xy



B.

22

1.

9 16

xy



C.

22

1.

25 16

xy



D.

22

1.

25 16

xy



Lời giải

Chọn D

Ta có, tiêu cự

2 6 3cc  

và trục bé

2 8 4bb  

Mà

2 2 2 2

25   a b c a

Phương trình Elip có dạng :

22

1

xy

ab



22

1.

25 16

xy

  

Câu 83: [0H3-3-2] Cho elíp có phương trình

 

22

:1

16 9

xy

E 

và đường thẳng

 

: 3 0dy

. Tính tích các khoảng cách

h

từ hai tiêu điểm của elip

 

E

tới đường thẳng

 

d

.

A.

81h 

. B.

16h 

. C.

9h 

. D.

7h 

.

Lời giải

Chọn C

Ta có:

2

16 4

3

9

aa

b



















Mà

2 2 2 2

77a b c c c     

Tiêu điểm :

 

1

7;0F 

và

 

2

7;0F

.

Ta có :

 

12

33

, . , . 9

11

h d F d d F d  

.

Câu 84: [0H3-3-2] Cho phương trình elip

 

22

:4 9 36E x y

.Tìm khẳng định sai trong các

khẳng định sau?

A.

E

có trục lớn bằng

6

. B.

E

có trục nhỏ bằng

4

.

C.

E

có tiêu cự bằng

5

. D.

E

có tỉ số

5

3

c

a



.

Lời giải

Chọn C

Phương trình elip

 

22

:4 9 36E x y

22

1

94

xy

  

Ta có:

2

93

2

4

aa

b



















Mà

2 2 2 2

55a b c c c     

Vậy trục lớn bằng

26a 

Trục nhỏ bằng

24b 

Tiêu cự bằng

2 2 5c 

. Do đó, ta chọn đáp án là C

Câu 85: [0H3-3-2] Cho elip

 

22

:1

25 9

xy

E 

và các mệnh đề sau

I

Elip có các tiêu điểm

   

12

4;0 , 4;0FF

.

II

Elip

E

có tỉ số

4

5

c

a



.

III

Elip

 

E

có đỉnh

 

1

5;0A 

.

IV

Elip

 

E

có độ dài trục nhỏ bằng

3

.

Tìm khẳng định sai trong các khẳng định sau:

A.

I

và

II

. B.

II

và

III

. C.

I

và

III

. D.

IV

.

Lời giải

Chọn D

Ta có:

2

25 5

3

9

aa

b



















Mà

2 2 2 2

16 4a b c c c     

Vậy

Tiêu điểm là :

   

12

4;0 , 4;0FF

( mệnh đề

 

I

đúng)

Tỷ số

4

5

c

a



( mệnh đề

 

II

đúng)

Đỉnh

   

12

5;0 , 5;0AA

( mệnh đề

 

III

đúng)

Trục nhỏ bằng

26b 

( mệnh đề

 

IV

sai)

Câu 86: [0H3-3-2] Cho elip

22

41xy

và cho các mệnh đề:

 

I

:

 

E

có trục lớn bằng

1

.

 

II

:

 

E

có trục nhỏ bằng

4

.

 

III

:

 

E

có tiêu điểm

1

3

0;

2

F









.

 

IV

:

 

E

có tiêu cự bằng

3

.

Tìm khẳng định đúng trong các khẳng định sau:

A.

 

I

. B.

 

II

và

 

IV

. C.

 

I

và

 

III

. D.

 

IV

.

Lời giải

Chọn D

Phương trình elip:

22

4 1 1

1

4

xy

xy    

Ta có:

2

1

2

4

a

b





















Mà

2 2 2 2

33

42

a b c c c     

Khi đó:

 

E

có trục lớn bằng

22a 

( mệnh đề

 

I

sai)

 

E

có trục nhỏ bằng

21b 

( mệnh đề

 

II

sai)

 

E

có tiêu điểm

1

3

;0

2

F









( mệnh đề

 

III

sai)

 

E

có tiêu cự bằng

23c 

( mệnh đề

 

IV

đúng).

Câu 87: [0H3-3-2] (THPT Chuyên Lê Quý Đôn - Q Trị - HKII - 2016 - 2017 - BTN) Ta

xem quả bóng bầu dục là một khối tròn xoay tạo bởi khi quay một elip quanh trục

lớn của nó. Biết chiều dài quả bóng

30cm

và đo được (bằng thước kẹp) đoạn lớn

nhất có đường kính là

20cm

. Giả thiết độ dày của vỏ bóng không đáng kể. Tính thể

tích khí bên trong quả bóng.

A.

 

3

0,6 dm



. B.

 

3

dm



. C.

 

3

0,15 dm



. D.

 

3

2 dm



.

Lời giải

Chọn D

Phương trình elip có dạng:

 

22

:1

xy

E

ab



.

Theo đề bài ta có:

2 3dm 1,5dmaa  

,

2 2dm 1dmbb  

.

Suy ra

 

22

2

:1

1

1,5

xy

E 

2

1

2,25

x

y



  





.

Thể tích khí bên trong quả bóng là:

1,5 1,5

2

00

2 d 2 1 d

2,25

x

y x x













1,5

3

0

22

6,75

x





  





.

Câu 1: [0H3-3-3]Cho Elip

 

E

:

22

1

25 9

xy



. Đường thẳng

 

:4d x 

cắt

 

E

tại hai điểm

, MN

. Khi đó:

A.

9

.

25

MN 

B.

18

.

25

MN 

C.

18

.

5

MN 

D.

9

.

5

MN 

Lời giải

Chọn C

Dể thấy

 

:4d x 

là đường thẳng đi qua tiêu điểm

 

1

4;0F 

của

 

E

.

Do đó

1

18

22

5

M

c

MN MF a x

a



   





.

Câu 2: [0H3-3-3]Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu

cự bằng

43

A.

22

1.

36 9

xy



B.

22

1.

36 24

xy



C.

22

1.

24 6

xy



D.

22

1.

16 4

xy



Lời giải

Chọn D

Gọi phương trình chính tắc của Elip

 

22

1, 0

xy

ab

   

.

Ta có

2 2 2

2 2.2

4 16

2 4 3

12 4

ab

a b a

c

a b b









  



  



  









.

Câu 3: [0H3-3-3]Tìm phương trình chính tắc của Elip có trục lớn bằng 6 và tỉ số của tiêu cự

với độ dài trục lớn bằng

1

3

.

A.

22

1.

93

xy



B.

22

1.

98

xy



C.

22

1.

95

xy



D.

22

1.

65

xy



Lời giải

Chọn B

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Tỉ số

21

3.

23

c

ac

a

  

Lại có

2 2 2

2 6 3 1 8.a a c b a c        

Câu 4: [NC] Tìm phương trình chính tắc của Elip có một đường chuẩn là

40x 

và một

tiêu điểm là điểm

 

1;0

.

A.

22

1

43

xy



B.

22

1

16 15

xy



. C.

22

1

16 9

xy



. D.

22

1

98

xy



.

Lời giải

Chọn A

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Ta có

2

22

2

4 16. 4

ac

a a c

ea

    

   

2 2 2 2

;0 1;0 1 4 3F c F c a b a c          

.

Câu 5: [0H3-3-3]Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và đi qua điểm

 

0;5A

( Không có đáp án đúng)

A.

22

1.

100 81

xy



B.

22

1.

15 16

xy



C.

22

1.

25 9

xy



D.

22

1.

25 16

xy



Lời giải

Chọn C

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Ta có

22

2 6 9c a b   

   

22

0;5 25 34A E b a    

 

22

:1

34 25

xy

E  

.

Câu 6: [0H3-3-3]Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua

điểm

(2; )2

A.

22

1.

24 6

xy



B.

22

1.

36 9

xy



C.

22

1.

16 4

xy



D.

22

1.

20 5

xy



Lời giải

Chọn D

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Theo đề ra: Trục lớn gấp đôi trục bé

22

24a b a b   

Điểm

(2; )2

thuộc Elip

 

2

2 2 2

2 2 2 2

2

11

xy

a b a b



    

Ta được hệ:

22

2

22

4

5

44

1

20

4

ab

b

a

bb



























.

Câu 7: [0H3-3-3]Cho Elip (E):

22

1

16 9

xy



.

M

là điểm nằm trên

 

E

. Lúc đó đoạn thẳng

OM

thoả:

A.

4 5.OM

B.

5.OM 

C.

3.OM 

D.

3 4.OM

Lời giải

Chọn D

Gọi

   

4cos ;3sinM t t E

.Khi đó

2 2 2

16cos 9sin 9 7cosOM t t t   

.Vì

2

0 cos 1t

nên

3 4.OM

Câu 8: [0H3-3-3]Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là

 

4;3M

A.

22

1.

16 9

xy



B.

22

1.

16 9

xy



C.

22

1.

16 4

xy



D.

22

1.

43

xy



Lời giải

Chọn A

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Các đỉnh của hình chữ nhật cơ sở có tọa độ:

       

; , ; , ; , ;a b a b a b a b   

Ta có

 

4;3M

là một đỉnh của hình chữ nhật cơ sở nên chọn

4

3

a

b











.

Câu 9: [0H3-3-3]Phương trình của Elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:

A.

22

9 16 144.xy

B.

22

1.

9 16

xy



C.

22

9 16 1.xy

D.

22

1.

64 36

xy



Lời giải

Chọn A

Gọi phương trình chính tắc của Elip có dạng

 

22

1, 0

xy

ab

   

.

Ta có

2 8 4

2 6 3

aa

bb













.

Câu 10: [0H3-3-3]Đường thẳng

y kx

cắt Elip

 

22

1, 0

xy

ab

   

tại hai điểm

A. đối xứng nhau qua trục

Oy

. B. đối xứng nhau qua trục

Ox

.

C. đối xứng nhau qua gốc toạ độ

O

. D. Các khẳng định trên đều sai.

Lời giải

Chọn C

Vì

 

E

có tâm đối xứng là gốc tọa độ

 

0;0O

, hàm số

y kx

là hàm số lẻ nên đồ

thị của nó cũng có tâm đối xứng là

 

0;0O

nên chọn C.

Cách khác:

Tọa độ giao điểm của đường thẳng

y kx

với Elip

 

22

1, 0

xy

ab

   

là

nghiệm của hệ:

22

0

22

1

y kx

ab

x

xy

b ka

ab







  











Suy ra hai giao điểm là:

   

22

0 0 0 0

22

; ; ; ;

o

ab

A x kx B x kx x

b kb

  



.

Câu 11: [0H3-3-3]Tìm phương trình chính tắc của Elip đi qua điểm

 

6;0

và có tâm sai

bằng

1

.

2

A.

22

1.

36 27

xy



B.

22

1.

63

xy



C.

22

1.

62

xy



D.

22

1.

36 18

xy



Lời giải

Chọn A

Ta có có

1

22

ca

ec

a

   

mà Elip qua điểm

 

6;0

nên

6a 

từ đó

2

3 27cb  

. Vậy

 

22

:1

36 27

xy

E 

.

Câu 12: [0H3-3-3]Trong các phương trình sau, phương trình nào biểu diễn một elíp có

khoảng cách giữa các đường chuẩn là

50

3

và tiêu cự 6?

A.

22

1

64 25

xy



.

B.

22

1.

89 64

xy



C.

22

1.

25 16

xy



D.

22

1.

16 7

xy



Lời giải

Chọn C

Ta có: Tiêu cự

2 6 3cc  

, khoảng cách giữa 2 đường chuẩn

2 2 2

2 50

6 50 25 16

3

a

a c a b

e

      

.

Câu 13: [0H3-3-3]Biết Elip (E) có các tiêu điểm

   

12

7;0 , 7;0FF

và đi qua

9

7;

4

M









. Gọi

N

là điểm đối xứng với

M

qua gốc toạ độ. Khi đó

A.

22

1.

16 12

xy



. B.

 

2;3M

. C.

   

12

2;0 ,F 2;0F 

. D.

11

8NF MF

.

Lời giải

Chọn D

Ta có:

9

7;

4

N









. Suy ra:

 

2

11

9 23 9

2 7 ;

4 4 4

NF MF



     





Từ đó:

11

8NF MF

.

Câu 14: [0H3-3-3]Cho elíp có phương trình

22

16 25 100xy

.Tính tổng khoảng cách từ

điểm thuộc elíp có hoành độ

2x 

đến hai tiêu điểm.

A.

3.

B.

2 2.

C.

5

. D.

4 3.

Lời giải

Chọn C

Ta có:

22

5

16 25 100 1

25

42

4

xy

x y a      

Tổng khoảng cách từ 1 điểm

thuộc

Elip đến 2 tiêu điểm bẳng

25a 

.

Câu 15: [0H3-3-3]Tìm phương trình chính tắc của Elip có tiêu cự bằng 6 và trục lớn bằng

10

A.

22

1

25 9

xy



. B.

22

1

100 81

xy



. C.

22

1

25 16

xy



. D.

22

1

25 16

xy



.

Lời giải

Chọn D

Ta có:

2 2 2

2 6 3

16

2 10 5

cc

b a c

aa

  



   



  



.

Câu 16: [0H3-3-3]Cho Elip

 

E

:

22

1

16 12

xy



và điểm

M

nằm trên

 

E

. Nếu điểm

M

có

hoành độ bằng 1 thì các khoảng cách từ

M

tới 2 tiêu điểm của

 

E

bằng

A.

4 2.

B. 3 và 5. C.

3,5

và

4,5

. D.

2

4.

2



Lời giải

Chọn C

Ta có

   

2

12

16 12 4 2 2;0 , 2;0c c F F      

Điểm

M

thuộc

 

E

và

35

1

2

MM

xy   

Từ đó

12

97

;

22

MF MF

.

Câu 17: [0H3-3-3]Đường thẳng qua

 

1;1M

và cắt elíp

 

E

:

22

4 9 36xy

tại hai điểm

12

;MM

sao cho

12

MM MM

có phương trình là

A.

2 4 5 0.xy  

B.

4 9 13 0.xy  

C.

5 0.xy  

D.

16 15 100 0.xy

Lời giải

Chọn B

Cách 1: Thử điểm

 

1;1M

vào các đáp án, thỏa phương án B.

Cách 2: Gọi

   

1 0 0

;M x y E

. Vì

12

MM MM

nên

M

là trung điểm của

12

MM

 

2 0 0

2 ;2M x y  

. Hai điểm

12

;MM

cùng thuộc

 

E

nên ta có hệ phương

trình

   

22

00

22

00

4 9 36

4 2 9 2 36

xy









   





. Giải hệ ta tìm được tọa độ hai điểm

12

;MM

,

suy ra phương trình đường thẳng.

Câu 18: [0H3-3-3]Phương trình chính tắc của elip có hai tiêu điểm

   

12

2;0 ,F 2;0F 

và đi

qua điểm

 

2;3M

là

A.

22

1.

16 12

xy



B.

22

1.

16 9

xy



C.

22

1.

16 4

xy



D.

22

1.

16 8

xy



Lời giải

Chọn A

Ta có

2 2 2

24c c a b    

nên chỉ có A thỏa.

Câu 19: [0H3-3-3]Phương trình chính tắc của Elip có độ dài trục lớn bằng 26, tâm sai

12

13

e 

là

A.

22

1.

25 169

xy



B.

22

1.

169 25

xy



C.

22

1.

36 25

xy



D.

22

1.

25 36

xy



Lời giải

Chọn B

Ta có

2 2 2 2

12

13 169, 12 25

13

c

a a e c b a c

a

          

Phương trình chính tắc của elip là:

 

22

:1

25 16

xy

E 

.

Câu 20: [0H3-3-3] Tìm phương trình chính tắc của elip nếu phương trình đường chuẩn của

nó là

3

5

x 

và độ dài trục lớn là 10?

A.

22

+1

25 9

xy



. B.

22

1

25 9

xy



. C.

22

+1

25 16

xy



. D.

22

+1

81 64

xy



.

Lời giải

Chọn A

Gọi phương trình chính tắc của elip

22

1

xy

ab



Phương trình đường chuẩn của elip là

3

5

x 

nên

2

25 25

44

aa

ec

  

.

Độ dài trục lớn

12

2 10 5A A a a   

Thay vào công thức

2

25

4

a

c

  

Từ công thức

2 2 2

3b a c b   

.

Phương trình đường chuẩn

22

+1

25 9

xy



.

Câu 21: [0H3-3-3] Cho Elip

22

:1

25 9

xy

E

. Đường thẳng

:4dx

cắt

E

tại hai

điểm

,.MN

Khi đó:

A.

9

25

MN

. B.

18

25

MN

. C.

18

5

MN

. D.

9

5

MN

.

Lời giải:

Chọn C

Phương trình tung độ giao điểm của

E

và

2

4

:1

25 9

y

d

9

5

y

Khi đó,

99

; 4 ; ; 4

55

MN

Vậy

18

5

MN

.

Câu 22: [0H3-3-3] Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu

cự bằng

43

A.

22

1

36 9

xy

. B.

22

1

36 24

xy

. C.

22

1

24 6

xy

. D.

22

1

16 4

xy

.

Lời giải:

Chọn D

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng

43

2

23

ab

c

Mặt khác:

2 2 2 2 2 2 2

4 12 4 16a b c b b b a

Vậy

22

:1

16 4

xy

E

.

Câu 23: [0H3-3-3] Tìm phương trình chính tắc của Elip có một đường chuẩn là

40x

và

một tiêu điểm là điểm

1;0

A.

22

1

43

xy

. B.

22

1

16 15

xy

. C.

22

0

16 9

xy

. D.

22

1

98

xy

.

Lời giải:

Chọn A

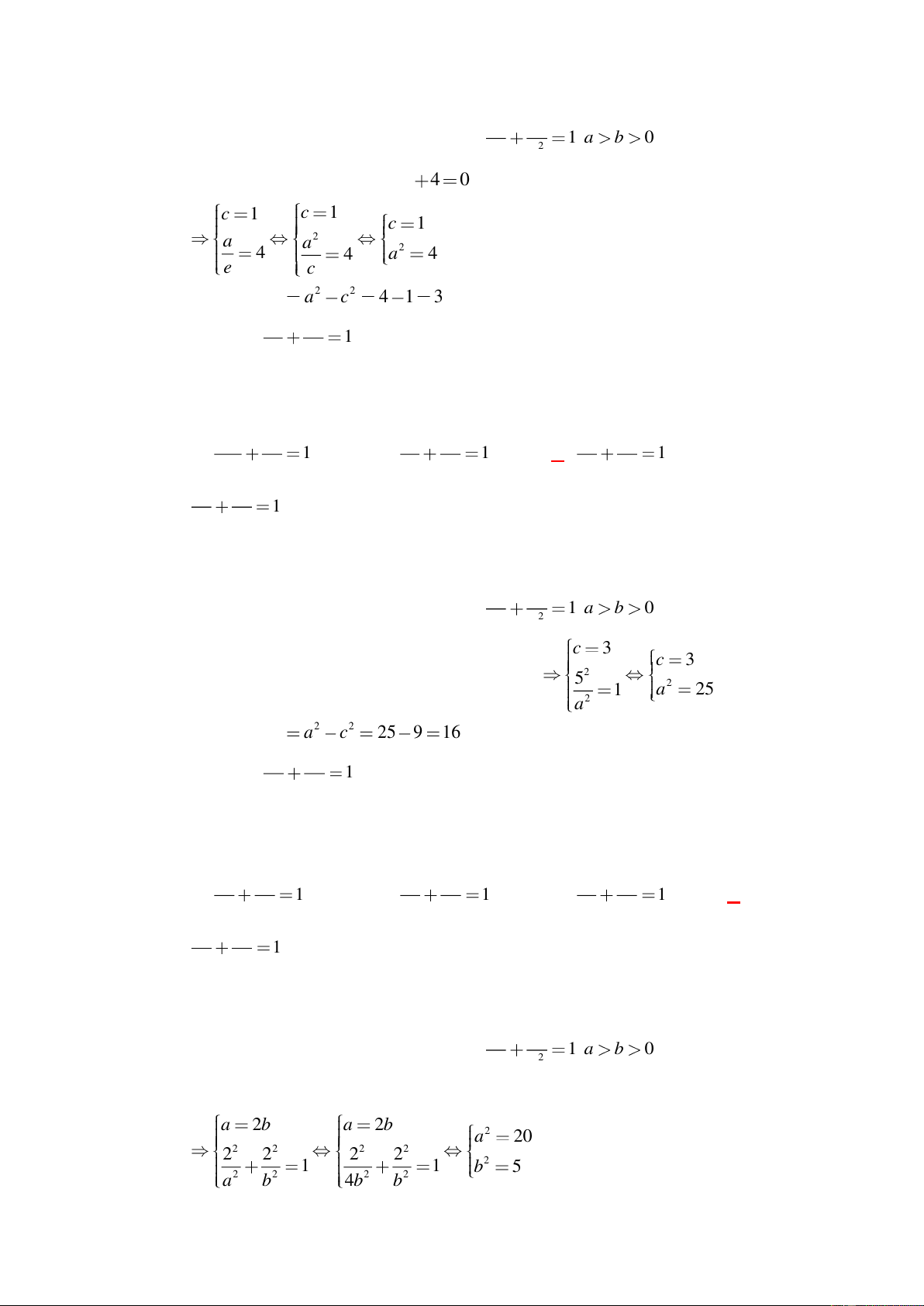
Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có một đường chuẩn là

40x

và một tiêu điểm là điểm

1;0

2

1

4

c

a

e

c

Mặt khác

2 2 2

4 1 3b a c

Vậy

22

:1

43

xy

E

.

Câu 24: [0H3-3-3] Tìm phương trình chính tắc của Elip có tiêu cự bằng

6

và đi qua điểm

()5;0A

A.

22

1

100 81

xy

. B.

22

1

15 16

xy

. C.

22

1

25 9

xy

. D.

22

1

25 16

xy

.

Lời giải:

Chọn C

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có tiêu cự bằng

6

và đi qua điểm

0;5A

2

3

5

25

1

c

a

Mặt khác

2 2 2

25 9 16b a c

Vậy

22

:1

25 16

xy

E

.

Câu 25: [0H3-3-3] Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua

điểm

2;2

A.

22

1

24 6

xy

. B.

22

1

36 9

xy

. C.

22

1

16 4

xy

. D.

22

1

20 5

xy

.

Lời giải:

Chọn D

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có trục lớn gấp đôi trục bé và đi qua điểm

2;2

2

2 2 2 2

2

2 2 2 2

22

20

2 2 2 2

11

5

4

a b a b

a

b

a b b b

Vậy

22

:1

20 5

xy

E

.

Câu 26: [0H3-3-3] Cho Elip có phương trình:

22

:9 25 225E x y

. Lúc đó hình chữ nhật

cơ sở có diện tích bằng:

A.

15

. B.

40

. C.

60

. D.

30

.

Lời giải:

Chọn C

22

:9 25 225 1

25 9

xy

E x y

2

25 5

3

9

aa

b

Diện tích hình chữ nhật cơ sở bằng:

1 2 1 2

. 2 .2 60A A B B a b

.

Câu 27: [0H3-3-3] Cho Elip

22

:1

16 9

xy

E

.

M

là điểm nằm trên

.E

Lúc đó đoạn thẳng

OM

thoả:

A.

45OM

. B.

5OM

. C.

3OM

. D.

34OM

.

Lời giải:

Chọn D

22

:1

16 9

xy

E

2

16 4

3

9

aa

b

Ta có:

b OM a

Vậy

34OM

.

Câu 28: [0H3-3-3] Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở

là

4;3M

A.

22

1

16 9

xy

. B.

22

1

16 9

xy

. C.

22

1

16 4

xy

. D.

22

1

43

xy

.

Lời giải:

Chọn A

Giả sử phương trình chính tắc của

22

: 1 0

xy

E a b

ab

Elip có một đỉnh của hình chữ nhật cơ sở là

4;3M

4

3

a

b

Vậy

22

:1

16 9

xy

E

.

Câu 29: [0H3-3-3] Đường thẳng

:d y kx

cắt Elip

22

:1

xy

E

ab

tại hai điểm

A. đối xứng nhau qua trục

Oy

. B. đối xứng nhau qua trục

Ox

.

C. đối xứng nhau qua gốc toạ độ

O

. D. Các khẳng định trên đều sai.

Lời giải:

Chọn C

Phương trình hoành độ giao điểm của

d

và

:E

2 2 2 2

2

2 2 2 2

2 2 2 2 2 2

1.

11

x k x k a b abk

x x y

a b a b

b a k b a k

Vậy đường thẳng

d

cắt

E

tại hai điểm đối xứng nhau qua gốc tọa độ

O

.

Câu 30: [0H3-3-3] Biết Elip

 

E

có các tiêu điểm

12

( 7;0), ( 7;0)FF

và đi qua

9

7;

4

M









. Gọi

N

là điểm đối xứng với

M

qua gốc toạ độ. Khi đó:

A.

12

NF MF

9

2

. B.

21

NF MF

23

2

. C.

21

NF NF 

7

2

. D.

11

8NF MF

.

Lời giải

Chọn D

12

( 7;0), ( 7;0),FF

9

7;

4

M









.

N

là điểm đối xứng với

M

qua gốc toạ độ. Suy ra

9

7;

4

N









.

Vậy

11

8NF MF

.

Câu 31: [0H3-3-3] Cho Elíp có phương trình

22

16 25 100.xy

Tính tổng khoảng cách từ

điểm thuộc Elíp có hoành độ

2x 

đến hai tiêu điểm.

A.

3

. B.

22

. C.

5

. D.

43

.

Lời giải

Chọn C

 

22

:16 25 100 1

25

4

xy

E x y    

2

25

5

4

2

4

a

b

















Ta có:

12

5

2 2. 5

2

MF MF a   

.

Vậy tổng khoảng cách từ điểm thuộc Elíp có hoành độ

2x 

đến hai tiêu điểm bằng

5

.

Câu 32: [0H3-3-3] Cho Elip

 

22

:1

169 144

xy

E 

và điểm

M

nằm trên

 

.E

Nếu điểm

M

có

hoành độ bằng

13

thì các khoảng cách từ

M

tới

2

tiêu điểm của

 

E

bằng:

A.

8

và

18

. B.

13 5

. C.

10

và

16

. D.

13 10

.

Lời giải

Chọn A

Ta có:

 

22

:1

169 144

xy

E 

2

169 13

12

144

aa

b



















Mặt khác

2 2 2

169 144 25 5c a b c      

Ta có:

1

2

5

. 13 .13 18.

13

5

. 13 .13 8.

13

M

c

MF a x

a

c

MF a x

a

    

    

Câu 33: [0H3-3-3] Tìm phương trình chính tắc của Elip có một đường chuẩn là

50x 

và

đi qua điểm

(0; 2)

A.

22

1

16 12

xy



. B.

22

1

20 4

xy



. C.

22

1

16 10

xy



. D.

22

1

20 16

xy



.

Lời giải

Chọn B

Gọi phương trình chính tắc của Elíp (E) là:

22

1

xy

ab



với

0ab

Đường chuẩn

a

x

e



nên ta chọn

2

5 5 5

aa

ac

c

e

a

     

.

Elíp đi qua

 

2

22

2

0

(0; 2) 1 4 2bb

ab



       

.

Mà

2 2 2 2 2 2 2

1

54

4

c

b a c c a b c c

c





        







.

Với

2

4 20ca  

.

Vậy phương trình chính tắc của Elíp (E) là

22

1

20 4

xy



.

Câu 34: [0H3-3-3] Tìm phương trình chính tắc của Elip đi qua điểm

 

2;1

và có tiêu cự bằng

23

.

A.

22

1

85

xy



. B.

22

1

82

xy



. C.

22

1

94

xy



. D. .

Lời giải

Chọn D

Gọi phương trình chính tắc của Elíp (E) là: với

Elíp đi qua (1)

Tiêu cự

Mà (2)

Thay (2) vào (1) ta được :

Chọn suy ra

Vậy phương trình chính tắc của Elíp (E) là

Câu 35: [0H3-3-3] Cho Elip (E) có các tiêu điểm và một điểm M nằm trên (E) biết rằng chu

vi của tam giác MF

1

F

2

bằng 18. Lúc đó tâm sai của (E) là:

A. e = - . B. e = . C. e =. D. e =

Lời giải

Chọn D

Vì tiêu điểm suy ra

Chu vi của tam giác MF

1

F

2

bằng

Theo định nghĩa Elíp thì

Tâm sai của (E) là :

Câu 36: [0H3-3-3] Dây cung của elip

 

22

:1

xy

E

ab



 

0 ba

vuông góc với trục lớn tại

tiêu điểm có độ dài là:

A.

2

2c

a

. B.

2

2b

a

. C.

2

2a

c

. D.

2

a

c

.

Lời Giải

Chọn B

Xét tiêu điểm trái

 

1

;0Fc

. Phương trình đường thẳng qua

1

F

và vuông góc với

trục

Ox

là

xc

Giao điểm

,AB

của

 

E

và đường thẳng

xc

có tọa độ

22

; , ;

bb

A c B c

aa

   

  

   

   

Suy ra độ dài của dây cung

2

22

22bb

AB

aa









.

Câu 37: [0H3-3-3] Cho đường tròn

 

C

tâm

1

F

bán kính

2a

và một điểm

2

F

ở bên trong của

 

C

. Tập hợp tâm

M

của các đường tròn

 

'C

thay đổi nhưng luôn đi qua

2

F

và

tiếp xúc

 

C

là đường nào sau đây?

A. Đường thẳng. B. Đường tròn. C. Elip. D. Parabol.

Lời Giải

Chọn C

Gọi bán kính của đường tròn

 

C



là

r

.

Ta có:

 

C



tiếp xúc trong với đường tròn

 

C

nên

1

2–F M a r

.

 

2

’FC

nên

2

F M r

.

Ta có:

12

2 – 2F M F M a r r a   

.

Suy ra: Tập hợp tâm

M

của đường tròn

 

C



là một elip.

Câu 38: [0H3-3-3] Khi cho

t

thay đổi, điểm

 

5cos ;4sinM t t

đi dộng trên đường nào sau

đây?

A. Elip. B. Đường thẳng. C. Parabol. D. Đường

tròn.

Lời Giải

Chọn A

Ta có

22

25cos 16sin

1

25 16 25 16

MM

xy

tt

   

.

Nên khi cho

t

thay đổi, điểm

 

5cos ;4sinM t t

đi dộng trên đường Elip :

22

1

25 16

xy



.

Câu 39: [0H3-3-3] Cho elip

 

22

:1

xy

E

ab



 

0 ba

. Gọi

12

, FF

là hai tiêu điểm và cho

điểm

 

0;Mb

. Giá trị nào sau đây bằng giá trị biểu thức

2

12

.MF MF OM

?

A.

2

c

. B.

2

2a

. C.

2

2b

. D.

22

ab

.

Lời Giải

Chọn D

Ta có

 

1

;0Fc

,

 

2

;0Fc

nên

2 2 2

1

MF c b a a   

( do

2 2 2

b a c

), tương

tự

2

MF a

.

OM b

nên

2 2 2 2

12

..MF MF OM a a b a b    

.

Câu 40: [0H3-3-3] Cho elip

 

E

có tiêu điểm

1

(4;0)F

và có một đỉnh là

 

5;0A

. Phương trình

chính tắc của

 

E

là

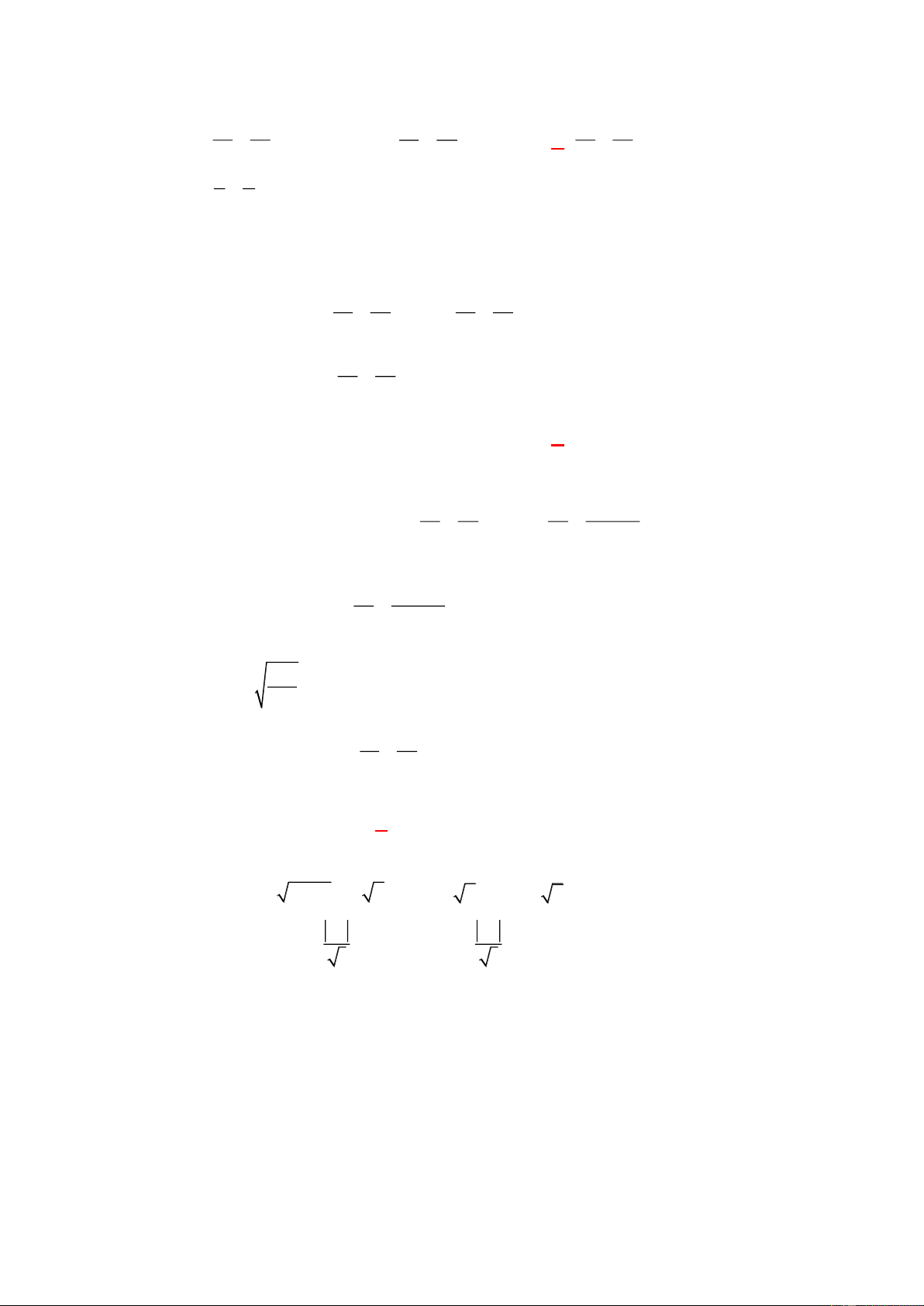
A.

22

1

25 16

xy



. B.

22

1

54

xy



. C.

22

1

25 9

xy



. D.

1

54

xy



.

Lời giải

Chọn C

Ta có:

2 2 2

c a b

2 2 2

b a c  

22

5 4 9  

Mặt khác ta có

 

22

:1

xy

E

ab



hay

22

1

25 9

xy



.

Câu 41: [0H3-3-3] Elip

 

22

:1

25 16

xy

E 

và đường tròn

 

22

: 25C x y

có bao nhiêu điểm

chung?

A. 0. B. 1. C. 2. D. 4.

Lời giải

Chọn C

Ta có phương hệ phương trình:

 

2 2 2 2

25

1 1 1

25 16 25 16

25 25

x y x x

x y y x





   









   



Giải phương trình

 

1

:

22

25

1

25 16

xx



 

22

16 25 25 25.16 0xx    

2

9 225 0x   

225

5

9

x    

. Vậy có hai điểm chung.

Câu 42: [0H3-3-3] Cho elip

 

22

:1

16 9

xy

E 

và đường thẳng

:3y

. Tích các khoảng cách từ

hai tiêu điểm của

 

E

đến



bằng giá trị nào sau đây?

A. 16. B. 9. C. 81. D. 7.

Lời giải

Chọn B

Ta có:

16 9 7c     

 

1

7;0F

,

 

2

7;0F

Do đó:

 

1

3

,3

1

dF



  

,

 

2

3

,3

1

dF



  

Vậy tích

   

12

, . , 9d F d F  

.

Câu 43: [0H3-3-3] Tìm phương trình chính tắc của elip

 

E

có trục lớn gấp đôi trục bé và đi

qua điểm

 

2; 2

.

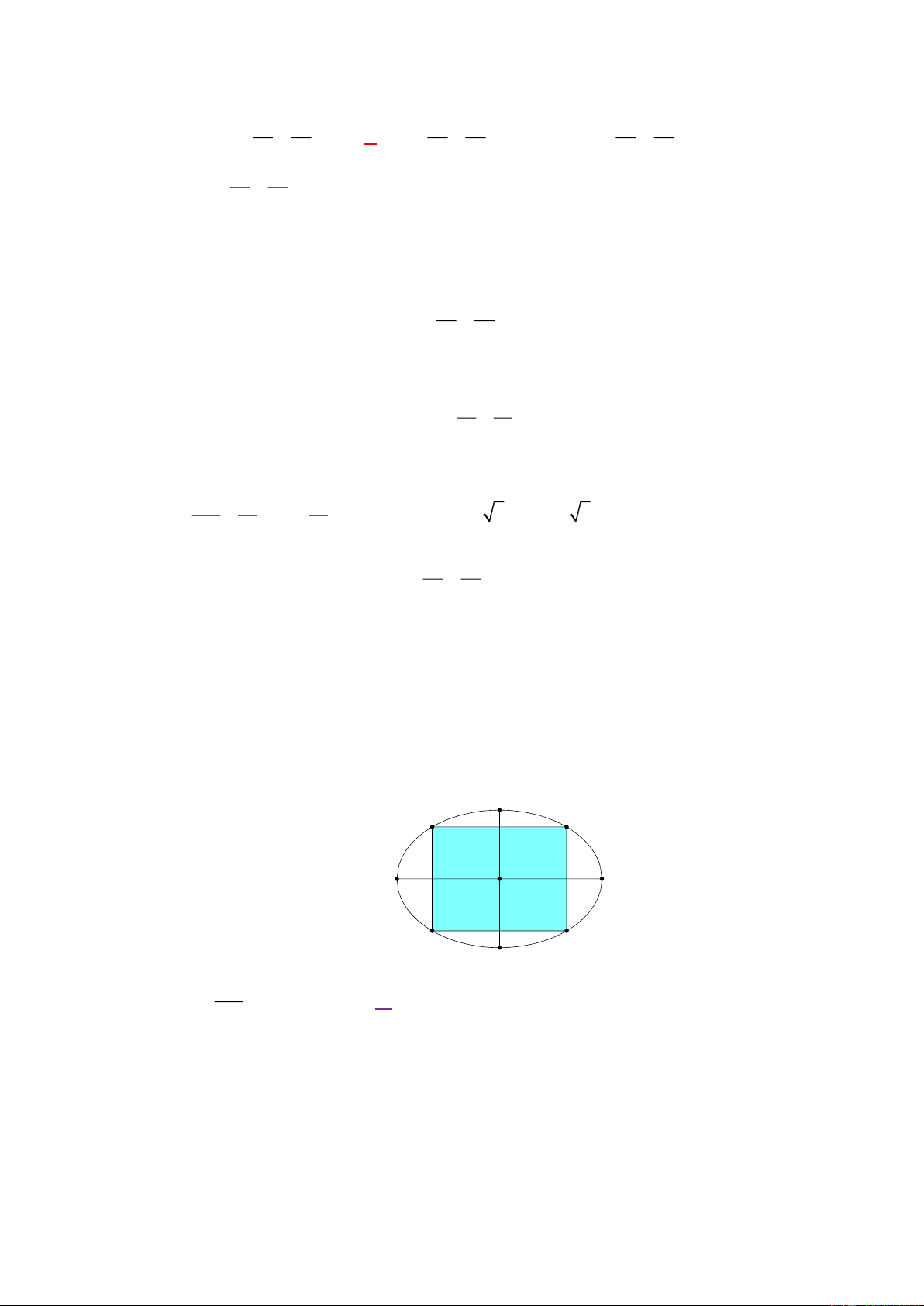
A.

 

22

:1

16 4

xy

E 

. B.

 

22

:1

20 5

xy

E 

. C.

 

22

:1

36 9

xy

E 

. D.

 

22

:1

24 6

xy

E 

.

Lời giải

Chọn B

Phương trình Elip có dạng

 

22

:1

xy

E

ab



Trục lớn gấp đôi trục bé nên

2 2.2 2a b a b  

(1)

Vì elip đi qua điểm

 

2; 2M 

nên

22

44

1

ab



(2)

Thay (1) vào (2), ta có:

2 2 2

4 4 5

11

4b b b

   

2

5 5 2 5b b a     

Vậy phương trình elip là:

 

22

:1

20 5

xy

E 

.

§3. GÓC GIỮA HAI ĐƯỜNG THẲNG.

Câu 44: [0H3-3-3] [THPT Chuyên Bình Long - 2017] Một mảnh vườn hình elip có độ dài

trục lớn bằng

12m

, độ dài trục bé bằng

8m

. Người ta dự định trồng hoa trong một

hình chữ nhật nội tiếp của elip như hình vẽ. Hỏi diện tích trồng hoa lớn nhất có thể

là ?

AA'=12

BB'=8

B'

B

A'

A

.

A.

2

576

m

13

. B.

2

48m

. C.

2

62m

. D.

2

46m

.

Lời giải

Chọn B

AA'=12

BB'=8

B'

B

A'

A

.

Đặt phương trình chính tắc của

 

22

:1

xy

E

ab



.

Ta có

2 12 6aa  

,

2 8 4bb  

. Suy ra

 

22

:1

36 16

xy

E 

.

Chọn

 

;

AA

A x y

là đỉnh hình chữ nhật và

0

A

x 

,

0

A

y 

.

22

1

36 16

AA

xy

  

;

Diện tích hình chữ nhật là

22

4 48.2. . 48 48

6 4 36 16

A A A A

AA

x y x y

S x y



    





.

Câu 1: [0H3-3-4] Đường thẳng qua

 

1;1M

và cắt Elíp

 

:E

22

4 9 36xy

tại hai điểm

12

,MM

sao cho

12

MM MM

có phương trình là

A.

2 4 5 0xy

. B.

4 9 13 0xy

.

C.

50xy  

. D.

16 15 100 0xy

.

Lời giải

Chọn B

Thay tọa độ điểm

M

và biểu thức ta có:

22

4.1 9.1 36

M

nằm trong

 

E

.

Mà

12

MM MM

M

là trung điểm

12

MM

12

22

M

x x x   

.

Đường thẳng qua

 

1;1M

có dạng:

 

11y k x  

.

Hoành độ

12

,MM

thỏa mãn phương trình:

 

2

4 9 1 1 36x k x



   



.

 

   

2

22

4 9 18 1 9 1 36 0k x k k x k       

.

Ta có

 

12

2

18 1

4

2

9

49

kk

x x k

k



     



.

Suy ra phương trình đường thẳng cần tìm là

 

4

1 1 4 9 13 0

9

y x x y       

.

Bài tập trắc nghiệm phương pháp tọa độ trong mặt phẳng Oxy có lời giải chi tiết

Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT) 78 tài liệu

Toán 10 2.8 K tài liệu

Bình luận

Bài tập trắc nghiệm phương pháp tọa độ trong mặt phẳng Oxy có lời giải chi tiết