












Preview text:
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
TỔ HỢP – XÁC SUẤT
Xin gửi lời cảm ơn chân thành đến tập thể các tác giả!
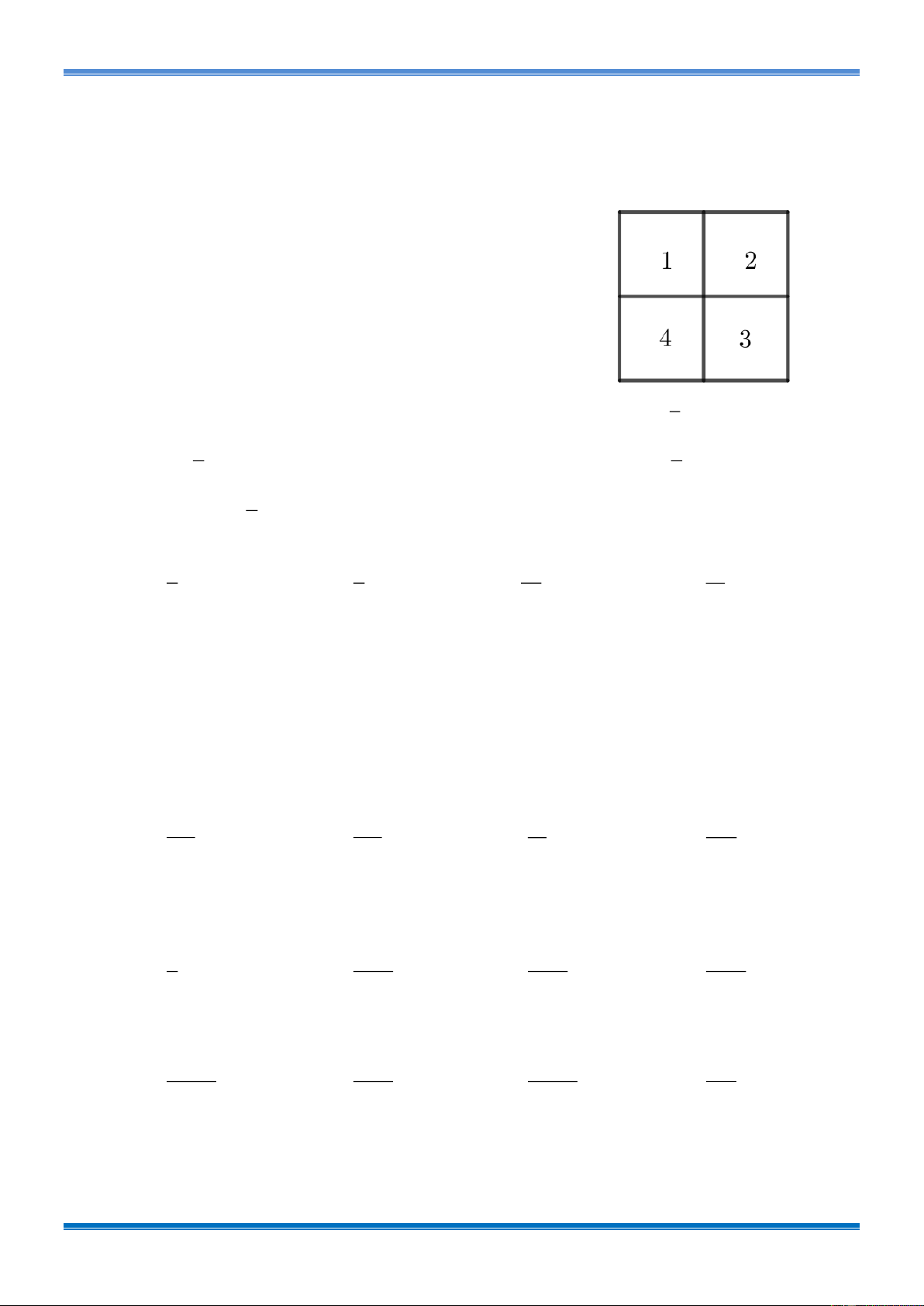
Câu 1: [1D2-2-4] Một quán cafe nhạc cần trang trí một bức
tường vuông được chia thành 4 ô như hình vẽ. Có bao
nhiêu cách để người thợ sơn có thể dùng 4 màu khác
nhau để sơn tấm tường này sao cho những ô vuông cạnh
nhau không có màu trùng nhau? A. 48 . B. 24 . C. 84 . D. 78 . 3
Câu 2: [1D2-4-3] Một bao hạt giống gồm đậu xanh và đậu đỏ trong đó có là hạt giống đậu 5 2 2
xanh, là hạt giống đậu đỏ. Do bao hạt giống này bị lỗi nên chỉ có hạt giống đậu xanh 5 3 3
nảy mầm và hạt giống đậu đỏ nảy mần. Lấy ngẫu nhiên trong bao 1 hạt giống và gieo 4
thì thấy nó nảy mầm thành 1 cây đậu. Tính xác suất để cây đậu đó là cây đậu xanh. 2 1 6 7 A. . B. . C. . D. . 5 2 25 10
Câu 3: [1D2-4-4] Cho đa giác đều (H) có 12 đỉnh nội tiếp đường tròn tâm O . Có bao nhiêu hình
thang cân có 4 đỉnh là đỉnh của (H) . A. 135 . B. 150 . C. 120 . D. 180 .
Câu 4: [1D2-4-4] Cho đa giác đều (H) có 18 đỉnh nội tiếp trong một đường tròn tâm O . Gọi X
là tập hợp các tam giác có các đỉnh là đỉnh của (H) . Tính xác suất để chọn được một tam
giác từ tập X là tam giác cân nhưng không phải là tam giác đều. 23 21 3 7 A. . B. . C. . D. . 136 136 17 816
Câu 5: [1D2-4-4] Bạn A chọn ngẫu nhiên một số từ nhiên từ 1 đến 2018, bạn B chọn ngẫu
nhiên một số tự nhiên từ 1 đến 4016 . Tính xác suất để số bạn A chọn luôn bé hơn số bạn B chọn. 1 6053 6035 2017 A. . B. . C. . D. . 2 8072 8072 4015
Câu 6: [1D2-4-3] Gieo 1 con súc sắc đồng chất, cân đối 6 lần. Tính xác suất để được một số lớn
hơn bằng 5 xuất hiện ít nhất 5 lần là 31 17 17 1 A. . B. . C. . D. . 23328 7776 23328 648
Câu 7: [1D2-2-4] Xếp 2 viên bi xanh khác nhau, 3 viên bi đỏ giống hết nhau và một viên bi vàng
thành một hàng ngang. Có bao nhiêu cách xếp 6 viên bi trên sao cho không có 2 viên bi
cùng màu nào đứng cạnh nhau. A. 4 . B. 6 . C. 12 . D. 20 .
Chịu trách nhiệm: Quý Bắc Ninh Trang 1
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Câu 8: [1D2-4-4] Một hộp chứa 5 viên bi đỏ, 6 viên bi xanh và 7 viên bi trắng. Chọn ngẫu nhiên
6 viên bi từ hộp, tính xác suất để được 6 viên bi có cả ba màu đồng thời hiệu của số bi
xanh và bi đỏ, hiệu của số bi trắng và số bi xanh, hiệu của số bi đỏ và số bi trắng theo thứ
tự là ba số hạng liên tiếp của một cấp số cộng. 75 5 40 35 A. . B. . C. . D. . 442 442 221 442
Câu 9: [1D2-2-3] Có 16 học sinh gồm 3 học sinh giỏi, 5 khá, 8 trung bình. Có bao nhiêu cách
chia số học sinh thành 2 tổ , mỗi tổ có 8 người, đều có học sinh giỏi và ít nhất 2 học sinh A. 3780 . B. 7560 . C. 1680 . D. 2100.
Câu 10: [1D2-2-4] Có bao nhiêu số tự nhiên có 7 chữ số mà tích của các chữ số bằng 1800 . A. 3780 . B. 4410 . C. 210 . D. 3150 .
Câu 11: [1D2-4-4] Cho đa giác 20 đỉnh nội tiếp đường tròn, gọi (S ) là tập hợp các đường thẳng đi
qua 2 trong số 20 đỉnh đã cho. Chọn hai đường thẳng bất kì thuộc tập (S ) . Tính xác suất
để được chọn được hai đường thẳng mà giao điểm của chúng nằm bên trong đường tròn. 5 1 20 17 A. . B. . C. . D. . 126 5 189 63
Câu 12: [1D2-4-4] Chọn ngẫu nhiên một số nguyên thuộc 1;500 . Tính xác suất để chọn được một số là ước của 10800 ? 16 49 23 18 A. . B. . C. . D. . 125 500 250 125
Câu 13: [1D2-2-3] Đội sinh viên tình nguyện gồm 12 bạn nam, 4 bạn nữ. Chia ngẫu nhiên thành
4 tổ, mỗi tổ 4 bạn sao cho có ít nhất hai tổ có nữ. Hỏi có bao nhiêu cách chia? A. 63028350 . B. 2621850 . C. 32432400 . D. 5775 .
Câu 14: [1D2-4-4] Từ các tập con của tập A = 1, 2, 3, ..., 201
8 , người ta chọn ngẫu nhiên ra hai
tập. Tính xác suất của biến cố cả hai tập được chọn đều khác rỗng đồng thời có số phần tử
là một số chẵn nhỏ hơn 1009 . 2 C 2 C 2 C 2 C A. 2018 2 1 P − = . B. 1008 P = . C. 2016 2 1 P − = . D. 2016 2 P = . 2 C 2 C 2 C 2 C 2018 2 2018 2018 2 2018 2
Câu 15: [1D2-2-4] Trong kỳ thi KSCL các môn thi THPT QUỐC GIA dành cho khối 12 của trường
THPT Triệu Sơn 4 có tất cả 10 phòng thi. Có 7 em học sinh lớp 11 cũng đăng kí dự thi.
Hỏi có bao nhiêu cách xếp 7 em học sinh này vào phòng thi nếu một phòng thi có 3 em và
hai phòng thi mỗi phòng có 2 em. A. 151200 . B. 75600 . C. 37800 . D. 302400 .
Câu 16: [1D2-4-3] Trên mặt phẳng Oxy, ta xét đa giác ABCD với các điểm A (1;4), B (5;4), C (1;0), D ( 3
− ;0) . Gọi S là tập hợp tất cả các điểm M (x; y) với x, y nằm bên trong
(kể cả trên cạnh) của đa giác ABCD . Lấy ngẫu nhiên một điểm M (x; y)S . Tính xác suất
để 3x + y 3 . 11 14 9 16 A. . B. . C. . D. . 25 25 25 25
Chịu trách nhiệm: Quý Bắc Ninh Trang 2
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Câu 17: [1D2-4-3] Trên mặt phẳng tọa độ Oxy , gọi S là tập hợp tất cả các điểm M (x; y) với
x, y và x 6, y 6 . Lấy ngẫu nhiên một điểm M S . Tính xác suất để điểm M
thỏa mãn hệ thức: ME + MF 10 với E (−4;0), F (4;0). 44 43 124 45 A. . B. . C. . D. . 169 169 169 169
Câu 18: [1D2-4-4] Từ ba chữ cái V, D, C ta xếp chúng thành 1 dãy có 2019 chữ cái. Hỏi xác suất
để xếp được dãy mà các chữ cái V, D, C đều xuất hiện số lẻ lần là bao nhiêu. 1 1 1 1 1 1 1 1 A. 1− . B. 1− . C. 1− . D. 1− . 2018 8 3 2018 4 3 2019 8 3 2019 4 3
Câu 19: [1D2-2-4] Có bao nhiêu số tự nhiên có 7 chữ số thỏa mãn đồng thời các điều kiện sau:
Hai chữ số đứng cạnh nhau thì khác nhau, các chữ số đứng giữa thì khác chữ số đứng đầu và đứng cuối. A. 1677888 . B. 1887624 . C. 1555848 . D. 331776 .
Câu 20: [1D2-4-4] Cho một tập hợp X có 10 phần tử. Một người chọn ngẫu nhiên ba tập con
khác nhau của tập X . Tính xác suất (chính xác đến hàng phần nghìn) để giao của mỗi hai
trong ba tập con được chọn đều có 2 phần tử và giao của ba tập con được chọn có 1 phần tử. A. 0,017 . B. 0,018 . C. 0,019 . D. 0,020 .
Câu 21: [1D2-4-4] Một chiếc hộp đựng 8 viên bi màu xanh được đánh số từ 1 đến 8 , 9 viên bi
màu đỏ được đánh số từ 1 đến 9 và 10 viên bi màu vàng được đánh số từ 1 đến 10 . Một
người chọn ngẫu nhiên 3 viên bi trong hộp. Tính xác suất để 3 viên bi được chọn có số đôi một khác nhau. 772 209 512 2319 A. . B. . C. . D. . 975 225 2925 2915
Câu 22: [1D2-4-4] Cho A là tập hợp các số tự nhiên có 2 chữ số khác nhau được lập thành từ tập
hợp X = 1; 2; 3; 4; 5;
8 . Chọn ngẫu nhiên 2 số từ tập A . Tính xác suất để hai số được
chọn có các chữ số khác nhau và có tổng bằng 19 ? 22 12 132 11 A. . B. . C. . D. . 145 435 435 435
Câu 23: [1D2-4-4] Cho tập X = 4; 5; 6; 7;
8 . Viết ngẫu nhiên lên bảng 2 số tự nhiên , mỗi số có
3 chữ số đôi một khác nhau lập từ X . Tính xác suất để hai số đó có đúng một số có chữ số 4 . 13 9 12 4 A. . B. . C. . D. . 25 25 25 25
Câu 24: [1D2-4-4] Một hộp đựng 6 bi xanh đánh số từ 1 đến 6 , 7 bi vàng đánh số từ 1 đến 7 và
8 bi đỏ đánh số từ 1 đến 8 . Lấy ngẫu nhiên 3 bi từ hộp. Xác suất để ba bi lấy được có 3 số khác nhau là: A. 73,76% . B. 67,45% . C. 81,23% . D. 56,92% .
Câu 25: [1D2-4-4] Một hộp đựng 6 bi xanh đánh số từ 1 đến 6 , 7 bi vàng đánh số từ 1 đến 7 và
8 bi đỏ đánh số từ 1 đến 8 . Lấy ngẫu nhiên 3 bi từ hộp. Tính xác suất để ba bi lấy được
có 3 số khác nhau và khác màu.
Chịu trách nhiệm: Quý Bắc Ninh Trang 3
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm 108 108 116 109 A. . B. . C. . D. . 775 665 565 785
Câu 26: Có bao nhiêu số tự nhiên có bốn chữ số mà tổng của các chữ số đó chia hết cho 5? A. 18120 . B. 18150 . C. 18000 . D. 18140 .
Câu 27: [1D2-4-4] Cho tập A = 0;1;2;3;4;5;
6 . Gọi S là tập hợp gồm 5 chữ số khác nhau chọn từ
các phần tử của tập A . Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số được chọn chia hết cho 15 . 97 43 31 37 A. . B. . C. . D. . 360 360 360 360
Câu 28: [1D2-2-3] Một tổ có 17 bạn gồm 8 nam và 9 nữ. Chọn từ tổ ra 5 bạn và xếp vào 1 bàn
học ngang có thứ tự 5 vị trí. Có bao nhiêu cách xếp sao cho 5 bạn được chọn có 2 nữ và 3 nam. A. 241920 . B. 282240 . C. 28224 . D. 24192 .
Câu 29: [1D2-4-3] Cho đa giác đều 12 cạnh. Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất
để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho. 24 27 28 31 A. . B. . C. . D. . 55 55 55 55
Câu 30: [1D2-4-4] Có 2 hộp đựng bi, trong mỗi hộp chỉ có bi màu đỏ và màu đen. Tổng số bi của
hai hộp là 20 . Chọn ngẫu nhiên từ mỗi hộp ra 1 viên bi. Biết xác suất để chọn được hai bi 55 màu đỏ là
. Xác suất để chọn được 2 bi màu đen là 84 1 29 5 13 A. . B. . C. . D. . 28 84 84 42
Câu 31: [1D2-2-4] Cho đa giác đều có 100 . Số tam giác tù tạo thành từ 3 trong 100 đỉnh của đa giác là A. 44100 . B. 58800 . C. 78400 . D. 117600 .
Câu 32: [1D2-4-4] Cho tập A = 1; 2; 3; 4; 5; 6; 7; 8
; 9 . Gọi S là tập các số tự nhiên có 4 chữ số
lập từ A . Chọn ngẫu nhiên một số từ S , xác suất để số được chọn chia hết cho 6 bằng 1 4 4 9 A. . B. . C. . D. . 9 9 27 28
Câu 33: [1D2-4-4] Cho K là tập hợp các số tự nhiên có bốn chữ số. Chọn ngẫu nhiên một số từ
K . Tính xác suất để số được chọn có tổng các chữ số là bội của 4 . 2249 2243 11 49 A. . B. . C. . D. . 9000 9000 45 9000
Câu 34: [1D2-2-4] Có bao nhiêu số tự nhiên có 2018 chữ số, trong mỗi số đó các chữ số đều lớn
hơn 1 và không có hai chữ số khác nhau cùng nhỏ hơn 7 đứng liền nhau? 1 A. ( 2018 2018 5.6 − 2 ). B. ( 2018 2018 5.6 + 2 ). 4 1 1 C. ( 2018 2018 5.6 − 2 ). D. ( 2018 2018 5.6 + 2 ). 4 4
Chịu trách nhiệm: Quý Bắc Ninh Trang 4
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
TỔ HỢP – XÁC SUẤT
Câu 1: [1D2-2-4] Một quán cafe nhạc cần trang trí một bức
tường vuông được chia thành 4 ô như hình vẽ. Có bao
nhiêu cách để người thợ sơn có thể dùng 4 màu khác
nhau để sơn tấm tường này sao cho những ô vuông cạnh
nhau không có màu trùng nhau? A. 48 . B. 24 . C. 84 . D. 78 . Lời giải Chọn C.
Trường hợp 1: (1) và (3) cùng màu.
(1) có 4 cách chọn; (3) có 1 cách chọn; (2) có 3 cách chọn; (4) có 3 cách chọn. 4.1.3.3 = 36 cách chọn
Trường hợp 2 : (1) và (3) khác màu.
(1) có 4 cách chọn; (3) có 3 cách chọn; (2) có 2 cách chọn; (4) có 2 cách chọn 4.3.2.2 = 48 cách chọn
Vậy có: 36 + 48 = 84 cách chọn. 3
Câu 2: [1D2-4-3] Một bao hạt giống gồm đậu xanh và đậu đỏ trong đó có là hạt giống đậu 5 2 2
xanh, là hạt giống đậu đỏ. Do bao hạt giống này bị lỗi nên chỉ có hạt giống đậu xanh 5 3 3
nảy mầm và hạt giống đậu đỏ nảy mần. Lấy ngẫu nhiên trong bao 1 hạt giống và gieo 4
thì thấy nó nảy mầm thành 1 cây đậu. Tính xác suất để cây đậu đó là cây đậu xanh. 2 1 6 7 A. . B. . C. . D. . 5 2 25 10 Lời giải Chọn A.
Gọi số hạt giống trong bao là 10n số hạt giống đậu xanh là 6n , số hạt giống đậu đỏ là
4n . Số hạt giống đậu xanh nảy mần là 4n , số hạt giống đậu đỏ nảy mần là 3n .
Số phần tử không gian mẫu là n () = 10n .
Gọi A là biến cố thỏa đề bài n ( A) = 4n .
Chịu trách nhiệm: Quý Bắc Ninh Trang 5
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm n A 2
Xác suất cần tìm là P (A) ( ) = = . n () 5
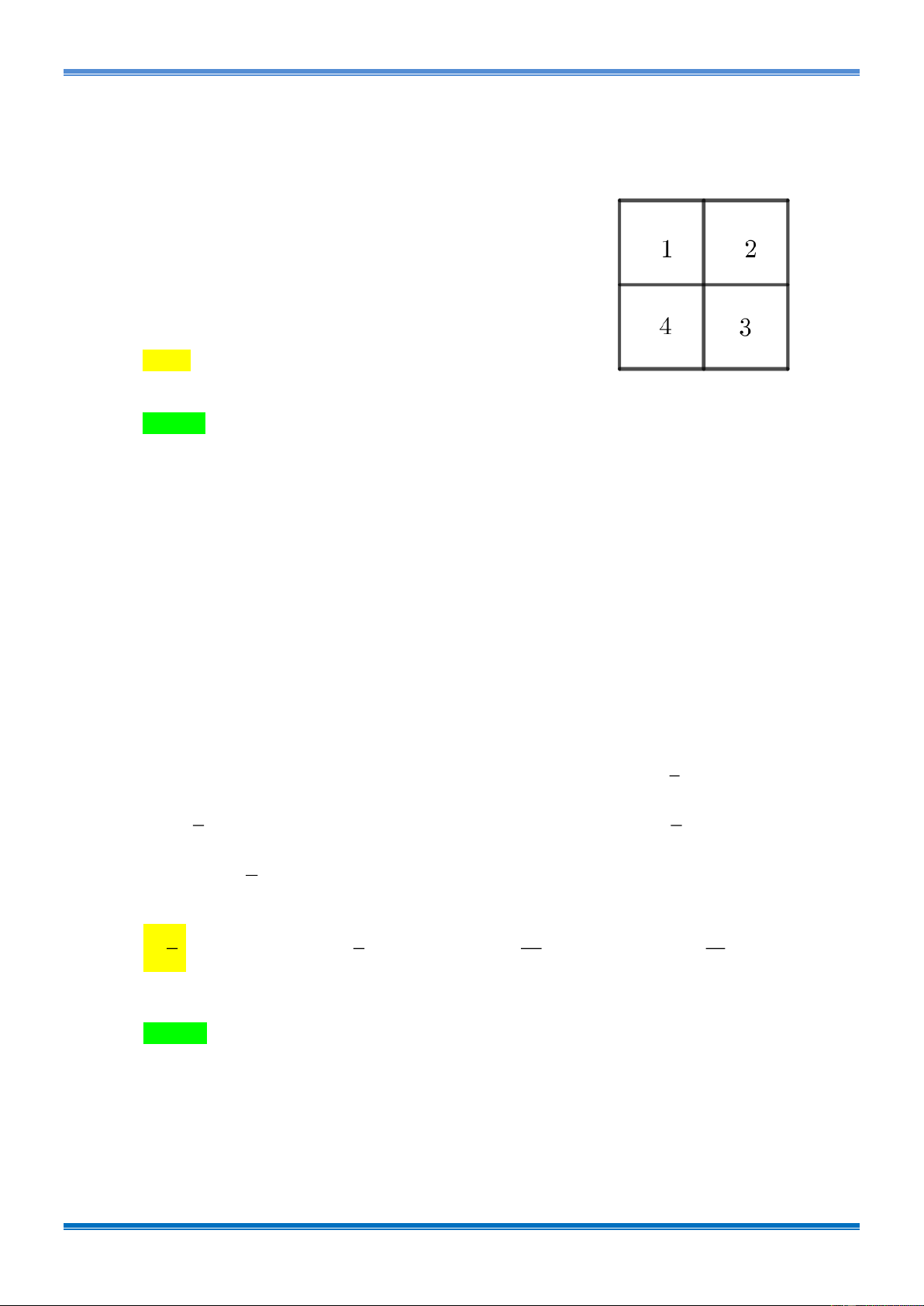
Câu 3: [1D2-4-4] Cho đa giác đều (H) có 12 đỉnh nội tiếp đường tròn tâm O . Có bao nhiêu hình
thang cân có 4 đỉnh là đỉnh của (H) . A. 135 . B. 150 . C. 120 . D. 180 . Lời giải Chọn A.
Gọi d là trục đối xứng của hình thang cân có 4 đỉnh là đỉnh của (H) .
Trường hợp 1: d đi qua hai đỉnh của (H) . Có 6 trục đối xứng.
Ứng với mỗi trục đối xứng có 2
C hình thang (lấy 2 trong 5 đỉnh một bên rồi đối xứng 5 qua d ).
Trường hợp 2: d đi qua hai cạnh của (H) . Có 6 trục đối xứng.
Chịu trách nhiệm: Quý Bắc Ninh Trang 6
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Ứng với mỗi trục đối xứng có 2
C hình thang (Lấy 2 trong 6 đỉnh một bên rồi đối xứng 6 qua d ).
Trong các hình thang trên có 2
C hình chữ nhật được đếm hai lần. 6
Vậy đáp số của bài toán là: 6( 2 2 C +C ) 2
−C = 135 hình thang. 5 6 6 Tổng quát:
Nếu đa giác (H) có 2k đỉnh (k 3) thì có k ( 2 2 C +C
−C hình thang cân có 4 đỉnh k k − ) 2 1 k là đỉnh của (H) .
Nếu đa giác (H) có 2k +1 đỉnh (k 2) thì có ( k + ) 2 2
1 C hình thang cân có 4 đỉnh k là đỉnh của (H) .
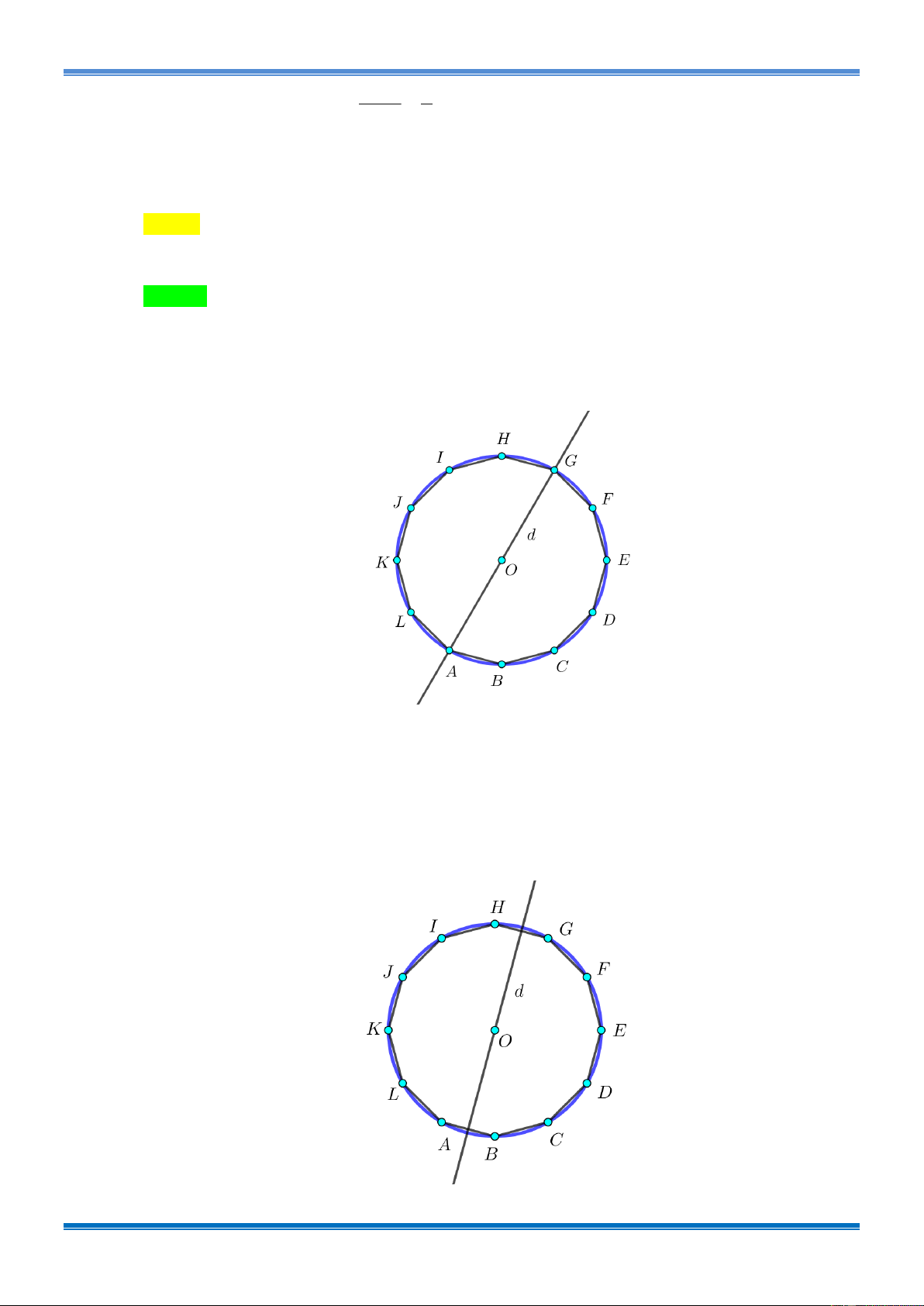
Câu 4: [1D2-4-4] Cho đa giác đều (H) có 18 đỉnh nội tiếp trong một đường tròn tâm O . Gọi X
là tập hợp các tam giác có các đỉnh là đỉnh của (H) . Tính xác suất để chọn được một tam
giác từ tập X là tam giác cân nhưng không phải là tam giác đều. 23 21 3 7 A. . B. . C. . D. . 136 136 17 816 Lời giải Chọn B.
Không gian mẫu là số cách chọn 3 đỉnh trong 18 đỉnh của (H) , do đó: 3 = C = 816 . 18
Gọi A là biến cố cần tính xác suất.
Gọi d là trục đối xứng của tam giác cân có 3 đỉnh là đỉnh của (H) . Có 18 trục đối xứng.
Ứng với mỗi trục đối xứng có 8 tam giác cân, trong đó có 1 tam giác đều.
Do đó A = 18.7 = 126 .
Chịu trách nhiệm: Quý Bắc Ninh Trang 7
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm A 21 Vậy P(A) = = . 136
Câu 5: [1D2-4-4] Bạn A chọn ngẫu nhiên một số từ nhiên từ 1 đến 2018, bạn B chọn ngẫu
nhiên một số tự nhiên từ 1 đến 4016 . Tính xác suất để số bạn A chọn luôn bé hơn số bạn B chọn. 1 6053 6035 2017 A. . B. . C. . D. . 2 8072 8072 4015 Lời giải Chọn B.
Số phần tử của không gian mẫu = 2018.4016 .
Giả sử bạn A chọn được số tự nhiên x , thì số tự nhiên bạn B chọn có 4016 − x cách. 2018
Khi đó số cách chọn số của bạn A luôn bé hơn số của bạn B có (4016 − x) = 6107477 x 1 = 6053
Khi đó xác suất để số của A chọn nhỏ hơn số của B chọn là : P = .. 8072
Câu 6: [1D2-4-3] Gieo 1 con súc sắc đồng chất, cân đối 6 lần. Tính xác suất để được một số lớn
hơn bằng 5 xuất hiện ít nhất 5 lần là 31 17 17 1 A. . B. . C. . D. . 23328 7776 23328 648 Lời giải Chọn A.
Số phần tử của không gian mẫu 6 = 6 .
TH1: có đúng 5 số 5 có 5 5.C cách. 6
TH2: có đúng 5 số 6 có 5 5.C cách. 6
TH3 : có 6 số 5 hoặc 6 số 6 có 2 cách. Nên = 62 . A 31 Do đó P = . 23328
Câu 7: [1D2-2-4] Xếp 2 viên bi xanh khác nhau, 3 viên bi đỏ giống hết nhau và một viên bi vàng
thành một hàng ngang. Có bao nhiêu cách xếp 6 viên bi trên sao cho không có 2 viên bi
cùng màu nào đứng cạnh nhau. A. 4 . B. 6 . C. 12 . D. 20 . Lời giải Chọn D.
Chịu trách nhiệm: Quý Bắc Ninh Trang 8
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Cách 1: Xếp 2 xanh và 1 vàng có 6 cách trong đó có 2 cách vàng ở giữa và 4 cách 2 xanh cạnh nhau.
TH1: Nếu vàng ở giữa có 2 cách ^X ^V ^ X ^
Chọn 3 vị trí trong 4 khoảng trống xếp đỏ có 3 C = 4 cách. 4 TH này có 8 cách.
TH2: Nếu 2 xanh cạnh nhau có 4 cách.
^X ^ X ^V ^
Xếp 1 đỏ vào giữa 2 xanh, còn các khoảng trống 1, 3, 4 .
có 3 cách xếp 2 đỏ TH này có 12 cách. Có 20 cách.
Cách 2: Do có 4 viên bi đỏ mà 2 viên cùng màu khác nhau cạnh nhau thì bắt buộc phải có
ít nhất 1 viên đỏ đứng đầu hoặc cuối hàng.
TH1: Viên bi đỏ đứng đầu hàng.
Đ^Đ^Đ^: Xếp 1 vàng 2 xanh có 3! cách.
Đ^Đ^^Đ: Xếp 1 vàng, 2 xanh sao cho 2 xanh khác nhau gồm có 4 cách.
Đ^^Đ^Đ: Tương tự có 4 cách.
TH2: Viên bi đỏ đứng cuối. ^Đ^Đ^Đ có 3! Cách.
Đ^Đ^^Đ Trùng với TH1 3 − .
Đ^^Đ^Đ Trùng với TH1 2 − .
có 3!.2 + 4 + 4 = 20 cách.
Câu 8: [1D2-4-4] Một hộp chứa 5 viên bi đỏ, 6 viên bi xanh và 7 viên bi trắng. Chọn ngẫu nhiên
6 viên bi từ hộp, tính xác suất để được 6 viên bi có cả ba màu đồng thời hiệu của số bi
xanh và bi đỏ, hiệu của số bi trắng và số bi xanh, hiệu của số bi đỏ và số bi trắng theo thứ
tự là ba số hạng liên tiếp của một cấp số cộng. 75 5 40 35 A. . B. . C. . D. . 442 442 221 442 Lời giải Chọn A
Không gian mẫu là số cách chọn ngẫu nhiên 6 viên bi từ hộp chứa 18 viên bi.
Suy ra số phần tử của không gian mẫu là 6 = C = 18564 . 18
Gọi A là biến cố "6 viên bi được chọn có cả ba màu đồng thời hiệu của số bi xanh và bi
đỏ, hiệu của số bi trắng và số bi xanh, hiệu của số bi đỏ và số bi trắng theo thứ tự là ba số
hạng liên tiếp của một cấp số cộng" .
Chịu trách nhiệm: Quý Bắc Ninh Trang 9
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Gọi x, y, z lần lượt là số bi đỏ, bi xanh và bi trắng được lấy. Suy ra
Hiệu của số bi xanh và bi đỏ là y − x .
Hiệu của số bi trắng và bi xanh là z − y .
Hiệu của số bi đỏ và bi trắng là x − z .
Theo giả thiết, ta có ( y − z ) + (x − z ) = 2(z − y) y − z = 2( y − z ) y = z .
Do đó biến cố A được phát biểu lại như sau "6 viên bi được chọn có cả ba màu đồng thời
số bi xanh bằng số bi trắng" . Ta có các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Chọn 2 viên bi đỏ, 2 viên bi xanh và 2 viên bi trắng.
Do đó trường hợp này có 2 2 2
C .C .C cách. 5 6 7
● Trường hợp 2. Chọn 4 viên bi đỏ, 1 viên bi xanh và 1 viên bi trắng.
Do đó trường hợp này có 4 1 1
C .C .C cách. 5 6 7
Suy ra số phần tử của biến cố A là 2 2 2 4 1 1
= C .C .C +C .C .C = 3360 . A 5 6 7 5 6 7
Vậy xác suất cần tính P (A) A 3360 40 = = = . 18564 221
Câu 9: [1D2-2-3] Có 16 học sinh gồm 3 học sinh giỏi, 5 khá, 8 trung bình. Có bao nhiêu cách
chia số học sinh thành 2 tổ , mỗi tổ có 8 người, đều có học sinh giỏi và ít nhất 2 học sinh A. 3780 . B. 7560 . C. 1680 . D. 2100. Lời giải Chọn A.
Mỗi tổ có học sinh giỏi. suy ra số học sinh giỏi ở mỗi tổ hoặc là 1 hoặc là 2 .
Vì mỗi tổ đều có học sinh khá, suy ra số học sinh khá ở mỗi tổ là 2 hoặc 3 .
Khi đó ta có số học sinh giỏi, khá, trung bình ở mỗi tổ tương ứng như sau Tổ 1 1, 2, 5 1, 3, 4 2, 2, 4 2, 3, 3 Tổ 2 2, 3, 3 2, 2, 4 1, 3, 4 1, 2, 5
Như vậy có hai trường hợp bị trùng
Vậy chỉ còn hai trường hợp
Trường hợp 1: số cách chọn một tổ nào đó có 1 giỏi, 2 khá, 5 trung bình là 2 5 3.C .C . 5 8
Trường hợp 2 : số cách chọn một tổ nào đó có 1 giỏi, 3 khá, 4 trung bình là 3 4 3.C .C . 5 8 Vậy tất cả có 2 5 3 4
3.C .C + 3.C .C = 3780 . 5 8 5 8 Nhận xét:
Bài toán này chỉ là bài toán chia thành 2 tổ (không có thứ tự). Học sinh có thể hiểu
sai đề và nhân đôi kết quả
Một sai lầm nữa của bài toán là học sinh có thể chọn học sinh trong tổ 1 và ứng với
mỗi cách chọn học sinh của tổ 1 thì có 1 cách chọn số học sinh của tổ 2 từ đó dẫn đến sai lầm
Nếu kẻ bảng như trên và nhấn mạnh cái không có thứ thự chia tổ, học sinh sẽ hiểu bài toán một cách rõ ràng.
Chịu trách nhiệm: Quý Bắc Ninh Trang 10
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Câu 10: [1D2-2-4] Có bao nhiêu số tự nhiên có 7 chữ số mà tích của các chữ số bằng 1800 . A. 3780 . B. 4410 . C. 210 . D. 3150 . Lời giải Chọn B. Ta có: 3 2 2 2 2 2 2 2 2 3 2
1800 = 2 .3 .5 = 1.2.4.3 .5 = 1.1.8.3 .5 = 1.2 .6.3.5 = 1.2 .9.5 . 7!
Số số tự nhiên có 7 chữ số trong đó 3 chữ số 2 , 3 chữ số 3 , 2 chữ số 5 là . 2!.3!.2!
Số số tự nhiên có 7 chữ số trong đó chữ số 1, 2, 4 có mặt 1 lần, chữ số 3, 5 có mặt 2 7! lần là . 2!.2!
Số số tự nhiên có 7 chữ số trong đó chữ số 1, 3, 5 có mặt 2 lần, chữ số 8 có mặt 1 lần 7! là . 2!.2!
Số số tự nhiên có 7 chữ số trong đó chữ số 1, 6, 3 có mặt một lần và chữ số 2, 5 có 7! mặt 2 lần là . 2!.2!
Số số tự nhiên có 7 chữ số trong đó chữ số 1, 9 có mặt 1 lần và chữ số 5 có mặt 2 lần 7!
và chữ số 2 có mặt 3 lần là . 3!.2! 7! 7! 7! Vậy tất cả có + .3 + = 4410 . 2!.3!.2! 2!.2! 3!.2!
Câu 11: [1D2-4-4] Cho đa giác 20 đỉnh nội tiếp đường tròn, gọi (S ) là tập hợp các đường thẳng đi
qua 2 trong số 20 đỉnh đã cho. Chọn hai đường thẳng bất kì thuộc tập (S ) . Tính xác suất
để được chọn được hai đường thẳng mà giao điểm của chúng nằm bên trong đường tròn. 5 1 20 17 A. . B. . C. . D. . 126 5 189 63 Lời giải Chọn D.
Số phần tử thuộc tập (S ) bằng 2 C = 190 . 20
Chọn hai phần tử thuộc (S ) suy ra: 2 n( ) = C . 190
Nhận thấy: hai đường có giao điểm nằm bên trong đường tròn là hai đường chéo của tứ
giác. Chọn một tứ giác có 4 C cách. 20 4 C 17
Xác suất cần tính bằng 20 = . 2 C 63 190
Câu 12: [1D2-4-4] Chọn ngẫu nhiên một số nguyên thuộc 1;500 . Tính xác suất để chọn được một số là ước của 10800 ?
Chịu trách nhiệm: Quý Bắc Ninh Trang 11
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm 16 49 23 18 A. . B. . C. . D. . 125 500 250 125 Lời giải Chọn C.
Số phần tử không gian mẫu: n() = 500 . Ta có: 4 3 2 10800 = 2 .3 .5 .
Gọi x là một ước của 10800 suy ra 2 .3 m .5 n p x =
, với m 0;4; n 0;3; p 0;2 .
Có 5 cách chọn m , 4 cách chọn n , 3 cách chọn p ,
Suy ra số ước của 10800 là 5.4.3 = 60 . 10800
Số ước lớn hơn 500 bằng số nhỏ hơn hoặc bằng 20 (phần nguyên của ) 500
Các ước nhỏ hơn 20 là 1, 2, 4, 8, 16, 3, 9, 5, 6, 12, 18, 10, 15, 20 có 14 ước.
Vậy số ước nhỏ hơn 500 bằng 60 −14 = 46 . 46 23
Xác suất cần tính bằng = . 500 250
Câu 13: [1D2-2-3] Đội sinh viên tình nguyện gồm 12 bạn nam, 4 bạn nữ. Chia ngẫu nhiên thành
4 tổ, mỗi tổ 4 bạn sao cho có ít nhất hai tổ có nữ. Hỏi có bao nhiêu cách chia? A. 63028350 . B. 2621850 . C. 32432400 . D. 5775 . Lời giải Chọn B.
Xét trường hợp phủ định chỉ có đúng một tổ có nữ. khi đó tổ đó có đúng 4 bạn nữ, ba tổ 4 4 C C
còn lại mỗi tổ 4 bạn nam. Nên số cách chia là: 12 8 . Do đó đáp số 3! 4 4 4 4 4 C C C C C 16 12 8 12 8 − = 2621850 . 4! 3!
Câu 14: [1D2-4-4] Từ các tập con của tập A = 1, 2, 3, ..., 201
8 , người ta chọn ngẫu nhiên ra hai
tập. Tính xác suất của biến cố cả hai tập được chọn đều khác rỗng đồng thời có số phần tử
là một số chẵn nhỏ hơn 1009 . 2 C 2 C 2 C 2 C A. 2018 2 1 P − = . B. 1008 P = . C. 2016 2 1 P − = . D. 2016 2 P = . 2 C 2 C 2 C 2 C 2018 2 2018 2018 2 2018 2 Lời giải Chọn C.
Số tập con của tập A bằng 2018 2 .
Số tập con khác rỗng đồng thời có số phần tử là một số chẵn nhỏ hơn 1009 của tập A bằng: 2 4 6 1008 T = C +C +C +...+C . 2018 2018 2018 2018 Vậy 0 2 4 6 1008 1010 2018 2T + 2 = C +C +C +C +...+C +C +...+C . 2018 2018 2018 2018 2018 2018 2018 Ta lại có: 0 2 4 6 1008 1010 2018 C +C +C +C +...+C +C +...+C 2018 2018 2018 2018 2018 2018 2018
Chịu trách nhiệm: Quý Bắc Ninh Trang 12
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm 1 3 5 7 1009 1011 2017 = C +C +C +C +...+C +C +...+C . 2018 2018 2018 2018 2018 2018 2018 Do đó 2018 2016 4T + 4 = 2 T = 2 −1 . 2 C Vậy xác suất cần tìm: 2016 2 1 P − = . 2 C 2018 2
Câu 15: [1D2-2-4] Trong kỳ thi KSCL các môn thi THPT QUỐC GIA dành cho khối 12 của trường
THPT Triệu Sơn 4 có tất cả 10 phòng thi. Có 7 em học sinh lớp 11 cũng đăng kí dự thi.
Hỏi có bao nhiêu cách xếp 7 em học sinh này vào phòng thi nếu một phòng thi có 3 em và
hai phòng thi mỗi phòng có 2 em. A. 151200 . B. 75600 . C. 37800 . D. 302400 . Lời giải Chọn B.
Chọn một phòng thi rồi xếp 3 em có 1 3
C .C = 350 cách. 10 7
Chọn tiếp 2 phòng từ 9 phòng thi còn lại và xếp mỗi phòng 2 em có 2 2 C .C = 216 . 9 4
Vậy có tất cả 350.216 = 75600 cách xếp.
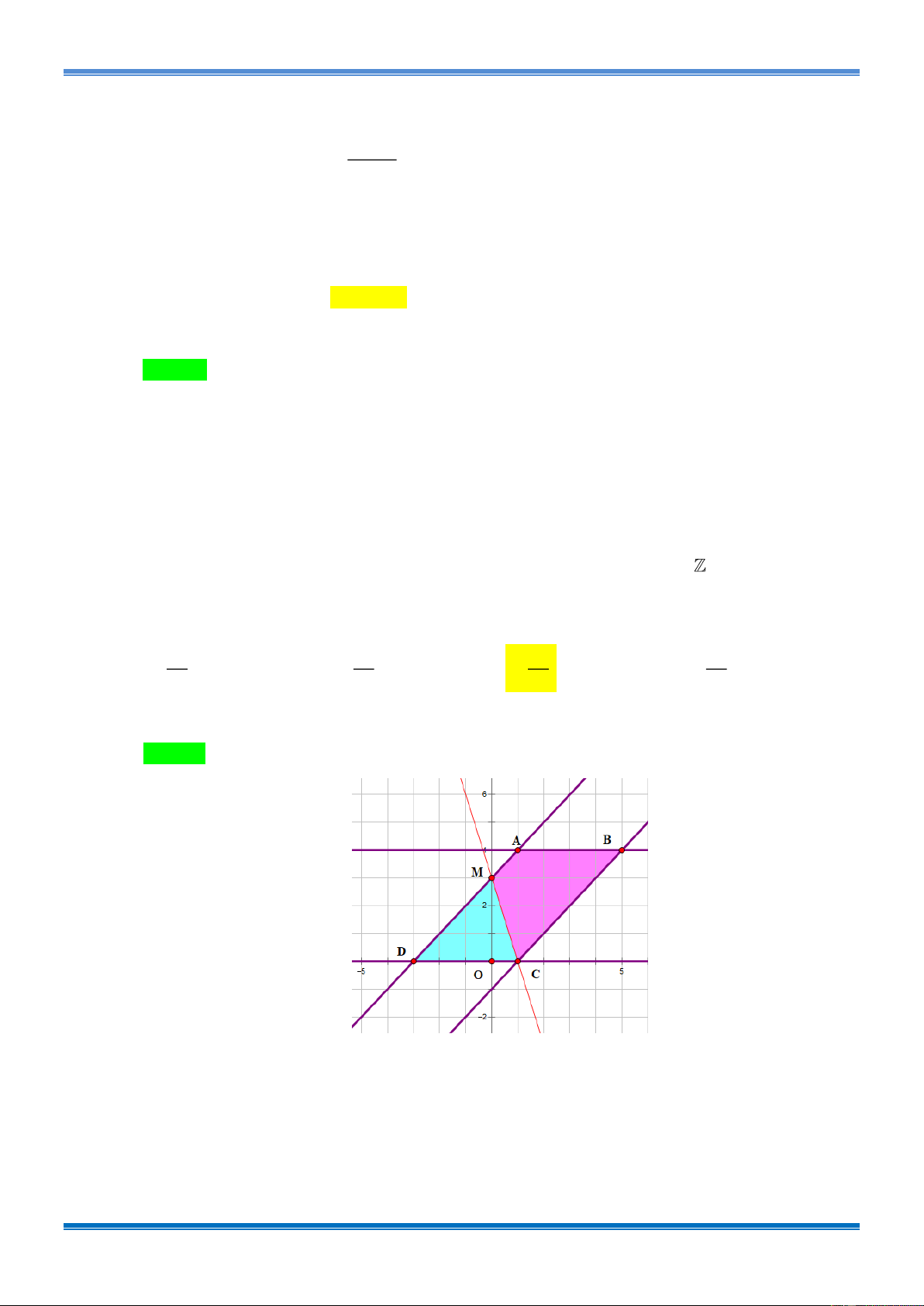
Câu 16: [1D2-4-3] Trên mặt phẳng Oxy, ta xét đa giác ABCD với các điểm A (1;4), B (5;4), C (1;0), D ( 3
− ;0) . Gọi S là tập hợp tất cả các điểm M (x; y) với x, y nằm bên trong
(kể cả trên cạnh) của đa giác ABCD . Lấy ngẫu nhiên một điểm M (x; y)S . Tính xác suất
để 3x + y 3 . 11 14 9 16 A. . B. . C. . D. . 25 25 25 25 Lời giải Chọn C.
Miền đa giác ABCD là hình bình hành như hình vẽ. Vẽ đường thẳng y = −3x + 3 .
Miền đa giác ABCD có 5.5 = 25 điểm có tọa độ nguyên. Vậy n (S ) = 25 . Điểm M (x; y)
thỏa mãn yêu cầu bài toán khi nó thuộc miền tam giác MDC ( không kể cạnh MC ). Miền
này có 9 điểm có tọa độ nguyên.
Chịu trách nhiệm: Quý Bắc Ninh Trang 13
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm 9
Vậy xác suất cần tìm là . 25
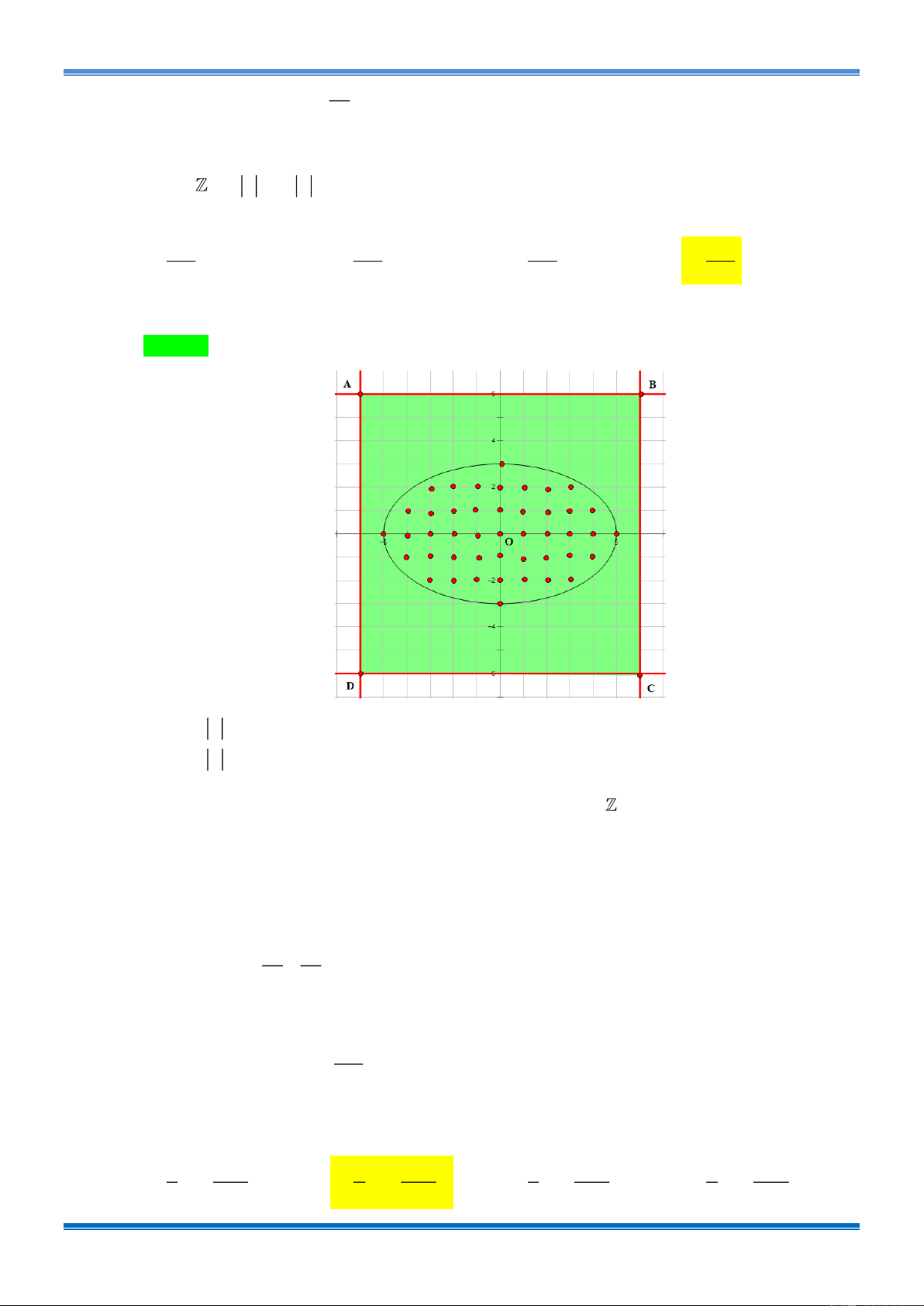
Câu 17: [1D2-4-3] Trên mặt phẳng tọa độ Oxy , gọi S là tập hợp tất cả các điểm M (x; y) với
x, y và x 6, y 6 . Lấy ngẫu nhiên một điểm M S . Tính xác suất để điểm M
thỏa mãn hệ thức: ME + MF 10 với E (−4;0), F (4;0). 44 43 124 45 A. . B. . C. . D. . 169 169 169 169 Lời giải Chọn D. x 6 −6 x 6 Ta có: . y 6 −6 y 6
Vậy S chính là tập hợp tất cả các điểm M (x; y) với x, y thuộc hình vuông ABCD ( kể cả các cạnh).
n (S ) = 13.13 = 169 .
Điểm M thỏa mãn hệ thức: ME + MF 10 với E ( 4
− ;0), F (4;0) suy ra M thuộc Elip có 2 2 x y phương trình: + = 1. 25 9
Miền này có: 1.2 + 3.2 + 5.3.2 +7 = 45 điểm thỏa mãn. 45
Vậy xác suất cần tìm là: . 169
Câu 18: [1D2-4-4] Từ ba chữ cái V, D, C ta xếp chúng thành 1 dãy có 2019 chữ cái. Hỏi xác suất
để xếp được dãy mà các chữ cái V, D, C đều xuất hiện số lẻ lần là bao nhiêu. 1 1 1 1 1 1 1 1 A. 1− . B. 1− . C. 1− . D. 1− . 2018 8 3 2018 4 3 2019 8 3 2019 4 3
Chịu trách nhiệm: Quý Bắc Ninh Trang 14
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm Bài giải Chọn B.
Nếu tổng quát gọi x là số dãy có n = 2m +1 chữ cái VDC ở trên (n 3) . n
Tổng số dãy tạo thành là 3n .
Do số các chữ cái là số lẻ nên ta có:
Nếu x thỏa mãn đề bài hay cả ba chữ cái VDC đều xuất hiện lẻ lần thì ta có 3 cách thêm 2 n
chữ cái giống nhau vào cuối để được dãy x n+2
Nếu x không thảo mãn đề bài và do số chữ cái là số lẻ nên sẽ có hai chữ cái xuất hiện n
chẵn lần và một chữ cái xuất hiện lẻ lần. Như vậy ta cũng có hai cách thêm hai chữ cái bất
kỳ từ các chữ cái VDC vào cuối để được dãy x n+2 Vậy x
= 3x + 2 3n − x = x + 2.3n . n+2 n ( n ) n 3n − 3
Ta có: x = 3! = 6 nên x = . n n 4 1 1
Vậy xác suất cần tìm là: 1− . 1 4 3n−
Câu 19: [1D2-2-4] Có bao nhiêu số tự nhiên có 7 chữ số thỏa mãn đồng thời các điều kiện sau:
Hai chữ số đứng cạnh nhau thì khác nhau, các chữ số đứng giữa thì khác chữ số đứng đầu và đứng cuối. A. 1677888 . B. 1887624 . C. 1555848 . D. 331776 . Lời giải Chọn B.
Giải: Gọi X = 0, 1, ...,
9 và số thỏa đề là: a a a a a a a , a 0 . 1 2 3 4 5 6 7 1
Có 2 trường hợp xảy ra:
TH1. a = a 1 7
Chọn a 0 có 9 cách 1
Chọn a a có 9 cách 2 1
Chọn a a và a a có 8 cách (tương tự với a ,a ,a cũng có 8 cách cho mỗi lần chọn) 3 1 3 2 4 5 6 Trường hợp này có 4 9.9.8 = 331776 số
TH2. a a 1 7
Chọn a 0 có 9 cách 1
Chọn a a có 9 cách 7 1
Chịu trách nhiệm: Quý Bắc Ninh Trang 15
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Chọn a a và a a có 8 cách 2 1 2 7
Chọn a X \ a ,a ,a có 7 cách 3 1 2 7
Các số còn lại cũng có 7 cách (chọn khác 2 số đầu cuối và khác số cạnh nó) Trường hợp này có 4 9.9.8.7 = 1555848 số.
Vậy tổng cộng có 331776 +1555848 =1887624 số.
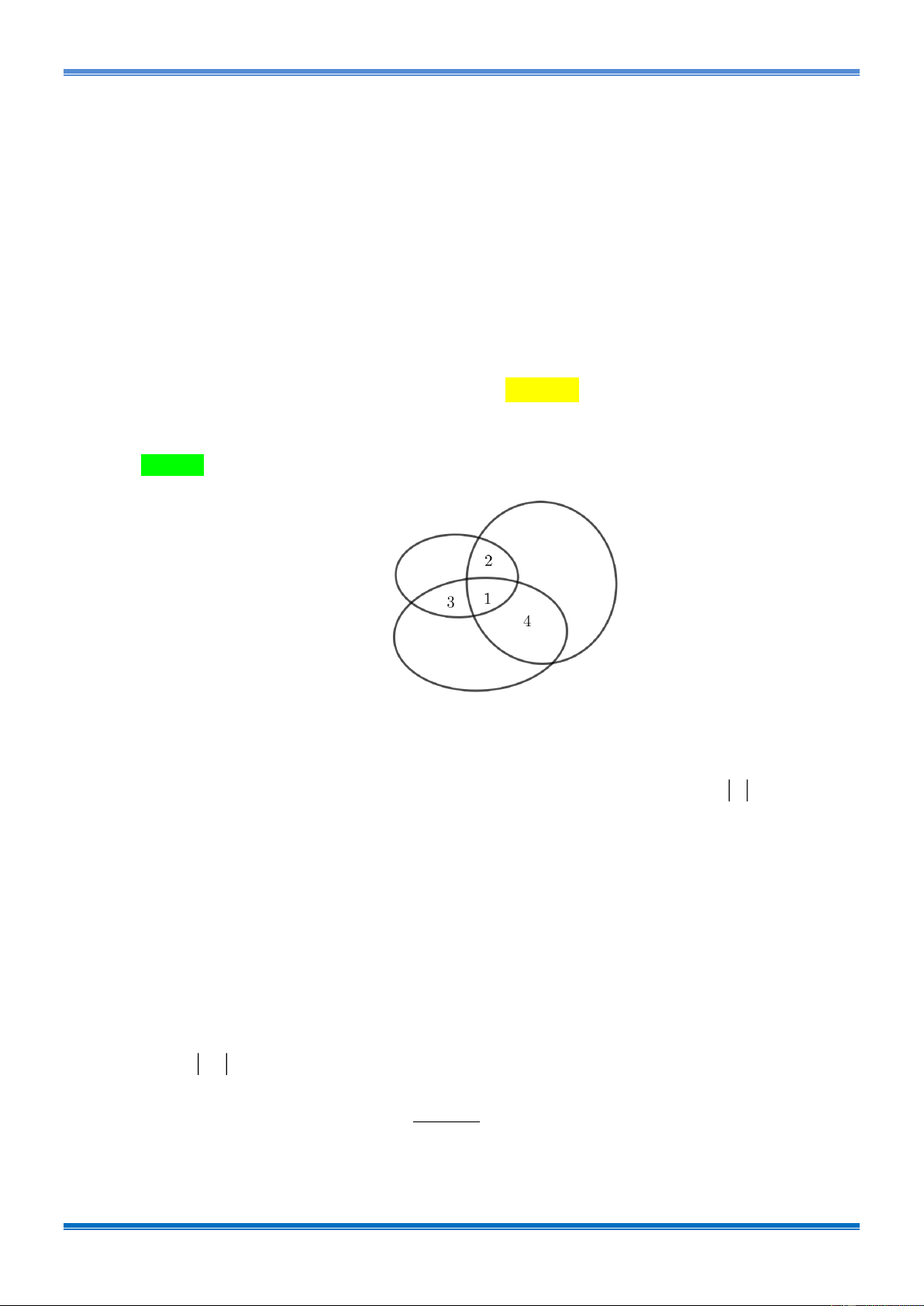
Câu 20: [1D2-4-4] Cho một tập hợp X có 10 phần tử. Một người chọn ngẫu nhiên ba tập con
khác nhau của tập X . Tính xác suất (chính xác đến hàng phần nghìn) để giao của mỗi hai
trong ba tập con được chọn đều có 2 phần tử và giao của ba tập con được chọn có 1 phần tử. A. 0,017 . B. 0,018 . C. 0,019 . D. 0,020 . Lời giải Chọn C.
Dùng biểu đồ Ven biểu diễn ba tập con. Các tập con nhỏ được đánh số 1, 2, 3, 4 có 1 phần
tử còn các tập con nhỏ không đánh số có thể rỗng.
Do số tập con của tập hợp X là 10
2 nên số phần tử của không gian mẫu là 3 = C . 1024
Ta sẽ đếm số phần tử của không gian thuận lợi cho biến cố A trong bài bằng cách lựa
phần tử cho các tập con được chọn.
Bước 1: chọn phần tử cho giao ba tập con (tập con đánh số 1). Bước này có 10 cách.
Bước 2: chọn 3 phần tử cho 3 giao của hai tập con (các tập con đánh số 2, 3, 4 ), mỗi giao
có 1 phần tử. Bước này có 3 C cách. 9
Bước 3: quyết định xem 6 phần tử còn lại thuộc tập con nào hoặc không thuộc cả ba (các
tập con không đánh số), mỗi phần tử có 4 cách lựa chọn. Bước này có 6 4 cách. Suy ra 3 6 = 10.C .4 . A 9 3 6 10.C .4
Vậy xác suất của biến cố A là 9 P = 0,019 . 3 C1024
Câu 21: [1D2-4-4] Một chiếc hộp đựng 8 viên bi màu xanh được đánh số từ 1 đến 8 , 9 viên bi
màu đỏ được đánh số từ 1 đến 9 và 10 viên bi màu vàng được đánh số từ 1 đến 10 . Một
Chịu trách nhiệm: Quý Bắc Ninh Trang 16
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
người chọn ngẫu nhiên 3 viên bi trong hộp. Tính xác suất để 3 viên bi được chọn có số đôi một khác nhau. 772 209 512 2319 A. . B. . C. . D. . 975 225 2925 2915 Lời giải Chọn A.
Cách 1. (Cô Nguyễn Thắm)
Số phần tử của không gian mẫu là 3 = C = 2925 . 27
Để đếm số phần tử của không gian thuận lợi cho biến cố A trong bài ta chia nhiều trường
hợp theo số màu của 3 viên bi được chọn. TH 1: một màu. Trường hợp này có 3 3 3
C +C +C = 260 phần tử (ứng với màu xanh, đỏ, vàng). 8 9 10 TH 2: hai màu. Trường hợp này có 1 2 2 1 1 2 2 1 1 2 2 1
C .C +C .C +C .C +C .C +C .C +C .C = 1544 phần tử (ứng với 8 8 8 7 8 9 8 8 9 9 9 8
các cặp màu xanh-đỏ, đỏ-vàng, xanh-vàng). TH 3: ba màu. Trường hợp này có 1 1 1
C .C .C = 512 phần tử (ứng với màu xanh, đỏ, vàng). 8 8 8 Như vậy = 2316 . A 2316 772
Vậy xác suất của biến cố A là P = = . 2925 975
Cách 2. (Thầy Nguyễn Thanh Hải)
Nhận thấy số viên bi mang cùng số thuộc tập hợp X = 1; 2; 3;...;
8 đều là 3 , trong chỉ có
2 viên bi mang số 9 và 1 viên bi mang số 10 . Vì vậy để đếm số phần tử của không gian
thuận lợi cho biến cố A trong bài ta chia nhiều trường hợp theo việc ba viên bi có viên
nào mang số 9 hoặc số 10 hay không.
TH 1: có đúng một viên bi mang số thuộc tập hợp X . Trường hợp này có 1
C .3.2 = 48 phần tử (chọn một số trong tập X , chọn một viên bi mang 8
số này, chọn một viên bi mang số 9 , viên bi còn lại là viên bi mang số 10 ).
TH 2: có đúng hai viên bi mang số thuộc tập hợp X . Trường hợp này có 2
C .3.3.3 = 756 phần tử (chọn hai số trong tập X , chọn một viên bi 8
mang số thứ nhất, chọn một viên bi mang số thứ hai, chọn một viên bi trong ba viên bi mang số 9 hoặc số 10 .
TH 3: cả ba viên bi mang số thuộc tập hợp X .
Chịu trách nhiệm: Quý Bắc Ninh Trang 17
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm Trường hợp này có 3
C .3.3.3 = 1512 phần tử (chọn ba số trong tập X , chọn lần lượt các 8
viên bi mang các số này). Như vậy = 2316 . A
Câu 22: [1D2-4-4] Cho A là tập hợp các số tự nhiên có 2 chữ số khác nhau được lập thành từ tập
hợp X = 1; 2; 3; 4; 5;
8 . Chọn ngẫu nhiên 2 số từ tập A . Tính xác suất để hai số được
chọn có các chữ số khác nhau và có tổng bằng 19 ? 22 12 132 11 A. . B. . C. . D. . 145 435 435 435 Lời giải Chọn B.
Gọi B: ''hai số được chọn có các chữ số khác nhau và có tổng bằng 19 ''
Từ tập hợp X = 1; 2; 3; 4; 7;
8 lập được 30 số tự nhiên có 2 chữ số khác nhau n () 2 = C = 435 (cách). 30
Ta có từ X chỉ có 1 bộ số (2, 4, 5, 8) thỏa: 2 + 4 +5+8 =19 . Có 2
A = 12 số tự nhiên có 2 4
chữ số khác nhau lập từ 2; 4; 5; 8 .
Chia 12 số đó thành 2 nhóm : nhóm chứa chữ số 2 và nhóm không chứa chữ số 2 . Mỗi nhóm có 6 số
Ứng với mỗi số ab nhóm thứ nhất, có 2 số cd ở nhóm thứ hai sao cho a + b + c + d =19
n (B) = 6.2 = 12 (cách). n B 12 Vậy P (B) ( ) = = . n () 435
Câu 23: [1D2-4-4] Cho tập X = 4; 5; 6; 7;
8 . Viết ngẫu nhiên lên bảng 2 số tự nhiên , mỗi số có
3 chữ số đôi một khác nhau lập từ X . Tính xác suất để hai số đó có đúng một số có chữ số 4 . 13 9 12 4 A. . B. . C. . D. . 25 25 25 25 Lời giải Chọn C.
Từ tập X lập được 5.4.3 = 60 số tự nhiên đôi một khác nhau
Số các số có mặt chữ số 4 là 3.4.3 = 36 số. Số các số không có mặt chữ số 4 là 24 số.
Gọi A là biến cố hai số viết lên bảng đều có mặt chữ số 4 .
B là biến cố hai số viết lên bảng không có mặt chữ số 4 .
C là biến cố hai số viết lên bảng có đúng một số có chữ số 4 . Ta có n () 1 1 = C .C 60 60
Chịu trách nhiệm: Quý Bắc Ninh Trang 18
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm 1 1 1 1 C .C C .C 13
Ta có P (A B) = P (A) + P (B) 36 36 24 24 = + = . 1 1 1 1 C .C C .C 25 60 60 60 60
Vậy P (C ) = − P (A B) 12 1 = . 25
Câu 24: [1D2-4-4] Một hộp đựng 6 bi xanh đánh số từ 1 đến 6 , 7 bi vàng đánh số từ 1 đến 7 và
8 bi đỏ đánh số từ 1 đến 8 . Lấy ngẫu nhiên 3 bi từ hộp. Xác suất để ba bi lấy được có 3 số khác nhau là: A. 73,76% . B. 67,45% . C. 81,23% . D. 56,92% . Lời giải Chọn A.
Số phần tử của không gian mẫu là: 3 = C . 21
Gọi A là biến cố 3 bi được chọn có số khác nhau.
Để tính số phần tử của biến cố A ta loại trừ các trường hợp sau:
Trường hợp 1. Cả ba bi lấy được ghi cùng 1 số: Có 6 trường hợp như vậy.
Trường hợp 2. Có đúng 2 bi ghi số giống nhau:
Khả năng 1. 2 bi ghi số giống nhau từ 1 đến 6 : Có 2
6.C cách chọn 2 trong ba bi ghi cùng 3
1 số nào đó. Bi còn lại có 18 cách chọn (khác số với hai bi kia). Khả năng này có 2 6.C .18 3 cách chọn
Khả năng 2. 2 bi ghi số giống nhau là số 7 : Có 1 cách chọn hai bi ghi số giống nhau là số
7 . Có 19 cách chọn bi còn lại. Khả năng này có 19 cách chọn.
Vậy số phần từ của biến cố A là: 2
A = − 6 − 6C .18 −19 = 981 . 3 A
Xác suất cần tìm là P (A) 981 = = 73,76% . 1330
Câu 25: [1D2-4-4] Một hộp đựng 6 bi xanh đánh số từ 1 đến 6 , 7 bi vàng đánh số từ 1 đến 7 và
8 bi đỏ đánh số từ 1 đến 8 . Lấy ngẫu nhiên 3 bi từ hộp. Tính xác suất để ba bi lấy được
có 3 số khác nhau và khác màu. 108 108 116 109 A. . B. . C. . D. . 775 665 565 785 Lời giải Chọn B.
Số phần tử không gian mẫu là: 3 = C . 21
Gọi A là biến cố ba bi lấy được có 3 số khác nhau và 3 màu khác nhau. Cách 1.
Ta có các trường hợp sau:
Trường hợp 1. Bi đỏ được chọn ghi số 8 . Khi đó có hai khả năng sau:
Khả năng 1. Bi vàng được chọn ghi số 7 . Khi đó có 6 cách chọn bi xanh.
Khả năng 2. Bi vàng được chọn ghi số bé hơn 7 . Khi đó bi vàng có 6 cách chọn, bi xanh có 5 cách chọn.
Trường hợp 1 có 6 + 6.5 = 36 cách chọn.
Chịu trách nhiệm: Quý Bắc Ninh Trang 19
Bài Tập VDC Chuyên Đề : TỔ HỢP – XÁC SUẤT. Tài liệu sưu tầm
Trường hợp 2. Bi đỏ được chọn ghi số 7 . Khi đó bi vàng có 6 cách chọn (từ 1 đến 6 ) và
bi xanh có 5 cách chọn (vì ghi số phải khác số bi vàng). Trường hợp này có 6.5 = 30 cách chọn.
Trường hợp 3. Bi đỏ được chọn ghi số bé hơn 7 . Bi đỏ có 6 cách chọn.
Khả năng 1. Bi vàng được chọn ghi số 7 . Khi đó bi xanh có 5 cách chọn (ghi số khác bi đỏ).
Khả năng 2. Bi vàng được chọn ghi số bé hơn 7 và khác số bi đỏ. Khi đó bi vàng có 5 cách
chọn và bi xanh có 4 cách chọn.
Trường hợp 3 này có 6 (5 + 5.4) = 150 cách chọn.
Vậy số phần tử của biến cố A là: A = 36 + 30 = 150 = 216 . 216 108
Vậy xác suất cần tìm là: P ( A) = = . 3 C 665 21 Cách 2.
Có 6 cách chọn bi xanh.
Với mỗi cách chọn bi xanh có 6 cách chọn bi vàng để bi vàng ghi số khác với bi xanh.
Với mỗi cách chọn bi xanh và bi vàng có 6 cách chọn bi đỏ ghi số khác với bi vàng, bi xanh.
Vậy số phần từ của biến cố A là: 3 A = 6 . 3 6 108
Xác suất cần tìm là: P (A) = = . 3 C 665 21
Câu 26: Có bao nhiêu số tự nhiên có bốn chữ số mà tổng của các chữ số đó chia hết cho 5? A. 18120 . B. 18150 . C. 18000 . D. 18140 . Lời giải Chọn C.
Với 10 số tự nhiên từ 0 đến 9 ta chia là 5 nhóm, mỗi nhóm gồm 2 chữ số đồng dư với nhau khi chia cho 5.
Gọi số cần lập là abcd .
Rõ ràng với mỗi cách chọn ba chữ số a, b, c có hai cách chọn chữ số d để tổng của chúng chia hết cho 5.
Do đó, số các số tự nhiên có tổng các chữ số chia hết cho 5 đúng bằng hai lần số cách chọn
số có ba chữ số abc .
Vậy nên số cách chọn là 2 9.10 .2 = 1800 số.
Câu 27: [1D2-4-4] Cho tập A = 0;1;2;3;4;5;
6 . Gọi S là tập hợp gồm 5 chữ số khác nhau chọn từ
các phần tử của tập A . Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số được chọn chia hết cho 15 . 97 43 31 37 A. . B. . C. . D. . 360 360 360 360 Lời giải Chọn D.
Số phần tử của tập S là 6.6.5.4.3 = 2160 .
Gọi là không gian mẫu. Khi đó n () = 2160 .
Chịu trách nhiệm: Quý Bắc Ninh Trang 20




