
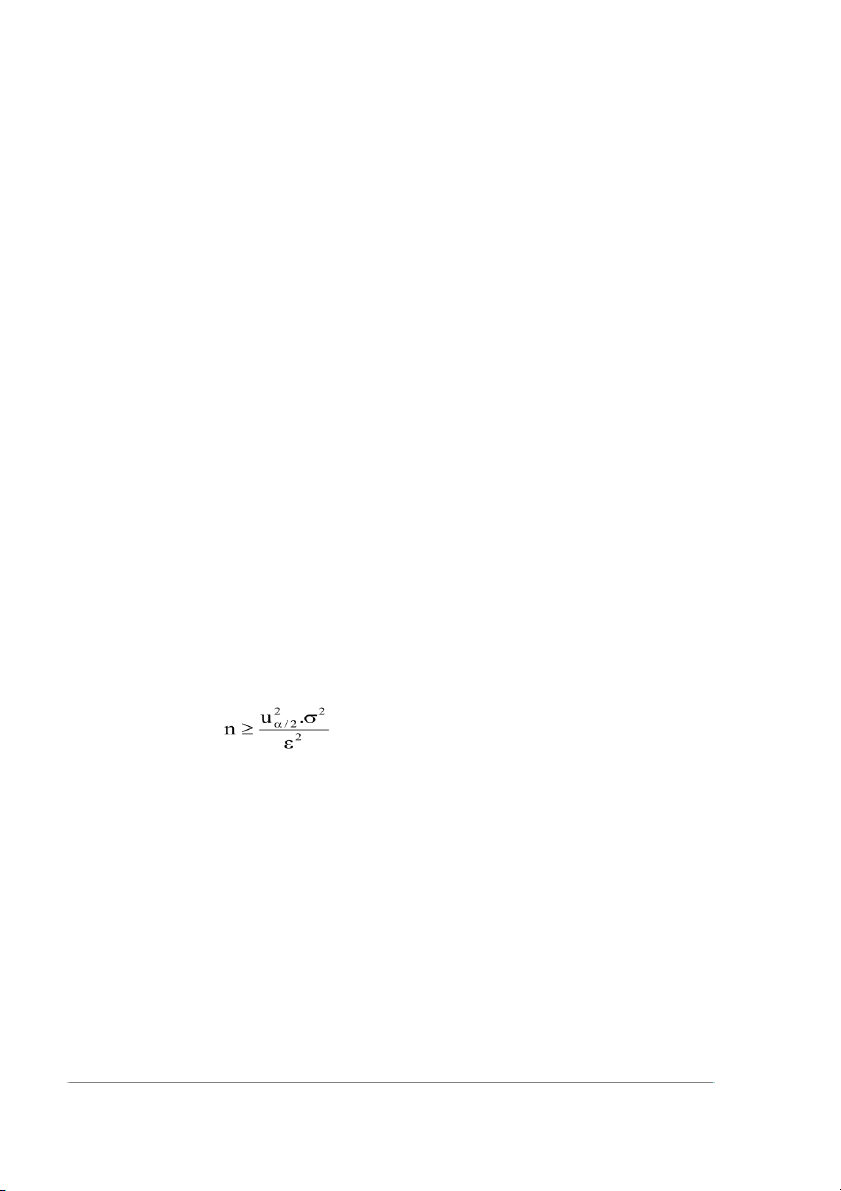









Preview text:
Chương V
ƯỚC LƯỢNG CÁC THAM SỐ CỦA BIẾN NGẪU NHIÊN Nội dung
● Bài toán ước lượng điểm
+ Ước lượng không chệch,
+ Ước lượng hiệu quả,
+ Ước lượng kỳ vọng.phương sai, tỷ lệ.
● Bài toán ước lượng khoảng
✔Ước lượng khoảng cho kỳ vọng toán của biến ngẫu nhiên phân phối chuẩn
✔Bài toán ước lượng khoảng cho tỷ lệ
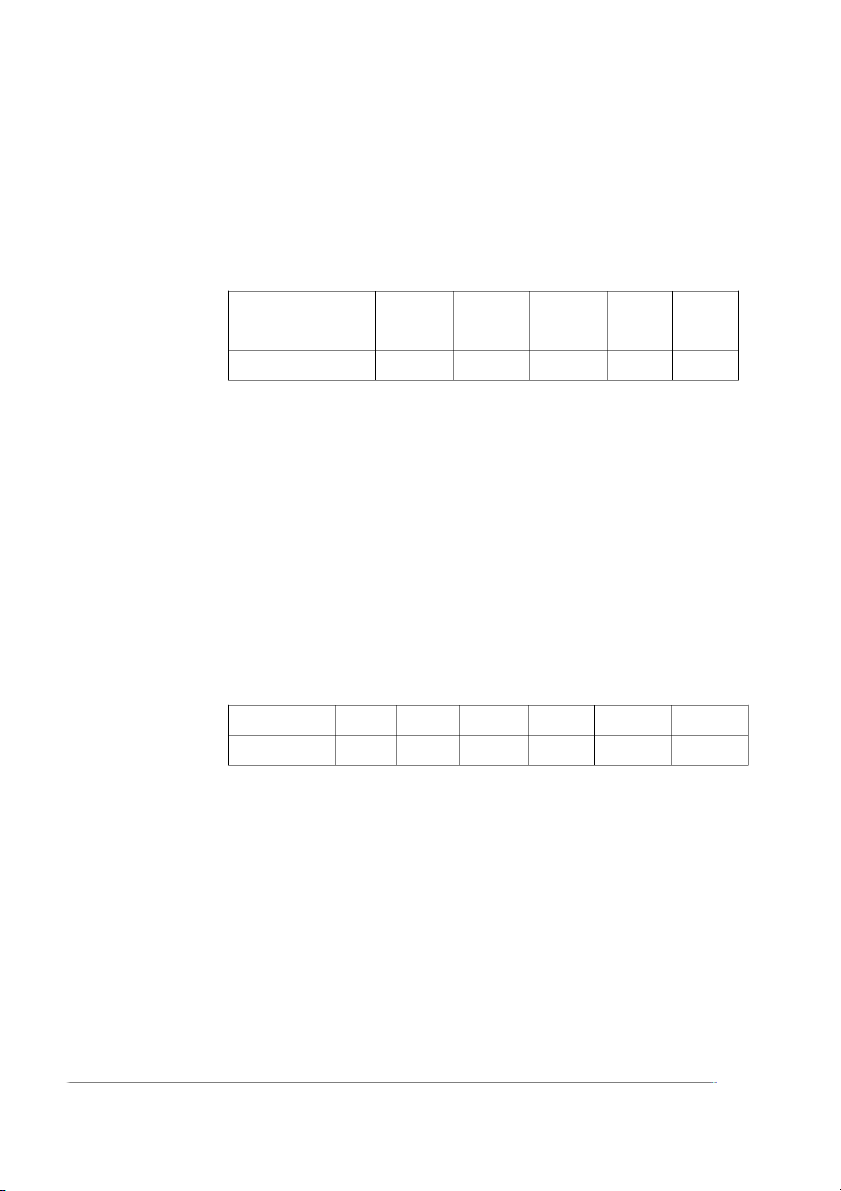
Câu 1. Cân thử 100 trái cây của một nông trường, ta có kết quả sau đây. Khối Số trái lượng(g) 35 – 55 3 55 – 75 10 75 – 95 25 95 – 115 35 115 – 135 20 135 – 155 6 155 – 175 1
a) Tìm ước lượng không chệch cho khối lượng trung bình của một trái cây trong nông trường.
b) Tìm ước lượng không chệch cho phương sai của khối lượng trái cây trong nông trường.
c) Xem các trái có khối lượng không quá 95gam là trái cây loại hai.
Tìm ước lượng không chệch cho tỉ lệ trái cây loại hai trong nông trường
Câu 2. Một phân xưởng cắt giấy muốn ước lượng thời gian trung bình để cắt
1 cuộn. Giả sử thời gian để cắt 1 cuốn giấy là biến ngẫu nhiên phân phối
chuẩn với độ lệch chuẩn là 0,3 phút. Người ta tính trên 36 cuộn được thời gian trung bình là 2 phút.
a. Tìm khoảng tin cậy 95% cho thời gian trung bình để cắt 1 cuộn giấy.
b. Nếu muốn độ chính xác tăng gấp đôi thì cần lấy mẫu kích thước bao nhiêu? Giải a. Độ chính xác = 0.098
Khoảng ước lượng (1.902 ; 2.098)
b. Độ chính xác tăng lên gấp đôi = sai số giảm đi 1 nửa => 0,098/2 = 0,049 n>= 144
Vậy cần lấy mẫu có kích thước = 144
Câu 3. Để ước lượng số lần gọi đến một tổng đài trong 1 ngày, người ta
thống kê trong 25 ngày thu được số lần gọi trung bình là 525. Hãy xác định
khoảng tin cậy 98% cho số lần gọi trung bình đã. Biết số lần gọi đến tổng đài
hàng ngày là biến ngẫu nhiên phân phối chuẩn với độ lệch chuẩn là 10. Nếu
muốn ước lượng với độ chính xác là 3 thì cần thống kê trong bao nhiêu ngày? Giải. Độ chính xác = 4,65 n>= 60,0625 n=61
Câu 4. Từ một lô túi đường người ta rút ra 16 túi để kiểm tra thấy trọng
lượng của mỗi túi (tính bằng kg) như sau: 0,8 0,9 1 0,9 0,8 1,1 1 0,9 1 1 0,9 0,9 1,1 1 0,8 0,9
Biết trọng lượng mỗi túi đường là biến ngẫu nhiên phân phối chuẩn.
A. Hãy ước lượng trọng lượng trung bình cho lô đường trên với độ tin cậy 95%.
B. Hãy ước lượng trọng lượng trung bình tối đa cho lô đường trên với độ tin cậy 95%
C. Hãy ước lượng trọng lượng trung bình tối thiểu cho lô đường
trên với độ tin cậy 95%. Giải Trung bình mẫu = 0.9375 Phương sai mẫu = 0.0092
Độ lệch chuẩn của mẫu = 0.0959 Độ chính xác = 0.051 a. (0.9886; 0.8864)
Câu 5. Nghiên cứu 1 mẫu 64 học sinh Trung học Cơ sở thấy số giờ chơi điện
tử trung bình là 15 giờ trong 1 tuần, độ lệch chuẩn là 2 giờ. Với độ tin cậy 99%, hãy ước lượng
A. Số giờ chơi điện tử trung bình trong 1 tuần của học sinh THCS.
B. Số giờ chơi điện tử trung bình tối thiểu trong 1 tuần của học sinh THCS.
C. Số giờ chơi điện tử trung bình tối đa trong 1 tuần của học sinh THCS.
Câu 6. Để ước lượng số xe ôtô tải qua 1 trạm thu phí, người ta theo dõi 20
ngày thấy trung bình có 250 xe qua 1 ngày với độ lệch tiêu chuẩn là 6 xe. Biết
lượng ôtô qua trạm mỗi ngày là biến ngẫu nhiên phân phối chuẩn .
A. Tìm khoảng tin cậy trung bình cho lượng ôtô trung bình qua trạm thu
phí hàng ngày với độ tin cậy 95%.
B. Tìm khoảng tin cậy trung bình cho lượng ôtô trung bình tối đa qua trạm
thu phí hàng ngày với độ tin cậy 95%.
C. Tìm khoảng tin cậy trung bình cho lượng ôtô trung bình tối thiểu qua
trạm thu phí hàng ngày với độ tin cậy 95%.
Câu 7. Để định mức thời gian gia công một loại chi tiết máy người ta theo dõi
ngẫu nhiên quá trình gia công 25 chi tiết và thu được số liệu sau:
Thời gian(phút) 15-17 17-19 19-21 21-23 23-25 25-27 Số chi tiết 1 3 4 12 2
Với độ tin cậy 95%, hãy ước lượng:
A. Thời gian gia công trung bình cho một chi tiết.
B. Thời gian gia công trung bình tối đa cho một chi tiết.
C. Thời gian gia công trung bình tối thiểu cho một chi tiết.
Câu 8. Cho chạy thử 25 lần trên cùng 1 quãng đường của một loại oto thu được số liệu
Lượng xăng hao 9,6-9,8 9,8-10 10-10,2 10,2-10,4 phí(lít) Số lần 3 5 10 7
Biết lượng xăng hao phí trong mỗi lần chạy là biến ngẫu nhiên phân phối chuẩn .
Với độ tin cậy 95% hãy tìm khoảng tin cậy
A. Trung bình cho mức xăng hao phí của một loại ôtô,
B. Trung bình tối thiểu cho mức xăng hao phí của một loại ôtô,
C. Trung bình tối đa cho mức xăng hao phí của một loại ôtô,
Câu 8. Điều tra ngẫu nhiên 324 sinh viên về chi phí cho sinh hoạt và tìm được nghìn đồng một tháng, nghìn đồng.
a) Với độ tin cậy 97% hãy ước lượng
● Chi phí trung bình cho sinh hoạt của sinh viên.
● Chi phí trung bình tối đa cho sinh hoạt của sinh viên.
● Chi phí trung bình tối thiểu cho sinh hoạt của sinh viên.
b) Nếu độ tin cậy 95% mà muốn độ chính xác là 20 nghìn đồng thì phải
điều tra bao nhiêu sinh viên?
Câu 9. Đo đường kính của 20 trục máy do một máy tiện tự động sản xuất ra,
ta được kết quả sau (tính bằng mm)
250; 249 251; 253; 248; 250; 250 ; 252 ; 257 ; 245 ;
248; 247; 249; 249; 250; 280; 250 ; 247 ; 253 ; 256.
Giả sử đường kính của các trục máy là biến ngẫu nhiên có phân phối chuẩn.
Với độ tin cậy 95% hãy ước lượng:
A. Đường kính trung bình của của trục máy do máy tiện sản xuất
B. Đường kính trung bình tối đa của của trục máy do máy tiện sản xuất
C. Đường kính trung bình tối thiểu của trục máy do máy tiện sản xuất
Câu 10. Ở một cửa hàng chế biến thủy sản, theo dõi lượng nước mắm bán ra
trong một số ngày, người ta ghi được bảng số liệu sau. Số lượng bán Số ngày ra (lít) 20 - 30 3 30 - 40 8 40 - 50 30 50 - 60 45 60 - 70 20 70 - 80 25 80 - 90 17 90 - 100 9 100-130 4 a)
Biết phương sai σ2 = 132,25 và với độ tin cậy 99%, hãy ước lượng
● số lít nước mắm bán ra trung bình mỗi ngày
● số lít nước mắm bán ra trung bình tối đa mỗi ngày
● số lít nước mắm bán ra trung bình tối thiểu mỗi ngày b)
Chưa biết phương sai và với độ tin cậy 99%, hãy ước lượng
● số lít nước mắm bán ra trung bình mỗi ngày
● số lít nước mắm bán ra trung bình tối đa mỗi ngày
● số lít nước mắm bán ra trung bình tối thiểu mỗi ngày
Câu 11. Để xác định định mức thời gian gia công một chi tiết máy,
người ta tiến hành thử nghiệm gia công 25 chi tiết. Kết quả trên tập mẫu thu được như sau.
Thời gian trung bình = 20 phút, độ lệch chuẩn S = 2,02 phút.
Giả sử thời gian gia công tuân theo quy luật phân phối chuẩn. Với độ
tin cậy 90%, hãy xác định:
A. Thời gian gia công trung bình đối với loại chi tiết máy trên.
B. Thời gian gia công trung bình tối đa đối với loại chi tiết máy trên.
C. Thời gian gia công trung bình tối thiểu đối với loại chi tiết máy trên.
Câu 12. Cân thử khối lượng của một số gia cầm ở một trại chăn nuôi, ta được
kết quả sau (tính bằng kilôgam).
3,25 ; 2,5 ; 4 ; 3,75 ; 3,8 ; 3,9 ; 4,02 ;
3,8 ; 3,2 ; 3,82 ; 3,4 ; 3,6 ; 3,75 ; 4 ; 3,5
Với độ tin cậy 99% và giả sử khối lượng gia cầm tuân theo quy luật
phân phối chuẩn với phương sai 0,01. Hãy ước lượng:
A. Khối lượng trung bình của một con gia cầm.
B. Khối lượng trung bình tối đa của một con gia cầm.
C. Khối lượng trung bình tối thiểu của một con gia cầm.
Câu 13. Nghiên cứu điểm trung bình môn Toỏn của 50 sinh viên ta có kết quả: = 6,1; S = 1,0.
a- Tìm khoảng ước lượng cho điểm trung bình với độ tin cậy 95%.
b- Nếu khoảng ước lượng có độ dài bằng 2 thì độ tin cậy đạt được là bao nhiêu ?
Câu 14. Quan sát năng suất của 100 công nhân trong một xí nghiệp, người ta
tính được năng suất trung bình của một công nhân là = 12 sản phẩm / ngày và S2 = 25.
a) Hãy ước lượng năng suất trung bình của một công nhân trong xí
nghiệp với độ tin cậy 99%.
b) Muốn ước lượng năng suất trung bình của một công nhân trong xí
nghiệp với độ tin cậy 98,36% thì độ chính xác đạt được bao nhiêu ?
c) Muốn ước lượng năng suất trung bình của một công nhân trong xí
nghiệp với độ tin cậy 99,73% và độ chính xác ε = 1 thì cần quan sát năng suất
của bao nhiêu công nhân nữa?
Câu 15. Chọn ngẫu nhiên 484 sinh viên trong trường có 121 em là người dân tộc thiểu số.
Với độ tin cậy 96% , hãy ước lượng:
A. Tỉ lệ sinh viên dân tộc thiểu số.
B. Tỉ lệ tối đa sinh viên dân tộc thiểu số.
C. Tỉ lệ tối thiểu sinh viên dân tộc thiểu số.
Câu 16. Điều tra thu nhập trong 1 khu dân cư. Người ta chọn ngẫu nhiên 100
hộ và thu được kết quả
Thu nhập(triệu) 2,5 3 3,5 4 4,5 Số hộ 10 25 30 20 15
Biết thu nhập của của hộ là biến ngẫu nhiên phân phối chuẩn. Với độ tin cậy 96%:
a- Hãy ước lượng thu nhập trung bình của của hộ.
b- Hãy ước lượng tỉ lệ hộ có thu nhập từ 3,5 triệu trở lên. Khu dân cư đã
có 3200 hộ, hãy ước lượng số hộ có thu nhập từ 3,5 triệu trở lên.
Câu 17. Kiểm tra ngẫu nhiên 400 sản phẩm của nhà máy thấy có 36 sản
phẩm loại 2. Với độ tin cậy 95%, hãy ước lượng
A. Tỉ lệ sản phẩm loại 2 của nhà máy
B. Tỉ lệ tối đa sản phẩm loại 2 của nhà máy
C. Tỉ lệ tối thiểu sản phẩm loại 2 của nhà máy
Câu 18. Tại một trung tâm thương mại người ta quan sát trong số 400 khách
hàng vào có 300 khách mua hàng.
a. Với độ tin cậy 95% hãy ước lượng:
● Tỉ lệ khách vào trung tâm thương mại mà không mua hàng.
● Tỉ lệ tối đa khách vào trung tâm thương mại mà không mua hàng.
● Tỉ lệ tối thiểu khách vào trung tâm thương mại mà không mua hàng.
b. Nếu muốn độ chính xác không vượt quá 0,02 thì phải quan sát bao nhiêu khách hàng?
Câu 19. Kiểm tra ngẫu nhiên 500 sản phẩm của một nhà máy thì thấy có 360
sản phẩm loại một. Với độ tin cậy 95%, hãy ước lượng
A. Tỉ lệ sản phẩm loại một tối thiểu của cả nhà máy.
B. Tỉ lệ tối đa sản phẩm loại một tối thiểu của cả nhà máy.
C. Tỉ lệ tối thiểu sản phẩm loại một tối thiểu của cả nhà máy.
Câu 20. Tại một khu rừng nguyên sinh, người ta đeo vòng vào chân của 1200
con chim. Sau một thời gian bắt lại 250 con thì thấy 40 con có đeo vòng. Hãy
ước lượng số chim trong khu rừng đã với độ tin cậy 99%.
Câu 21. Muốn biết số cỏ có trong một hồ lớn, người ta bắt lên 2000 con,
đánh dấu xong lại thả chúng xuống hồ . Sau đã người ta bắt lên 400 con thì
thấy có 55 con bị đánh dấu. Với độ tin cậy 0,95 hãy ước lượng số cá trong hồ.
Cho biết mỗi con cá có khối lượng trung bình 800 gam và mỗi kilôgam cá
bán được 22000đ. Tính doanh thu tối thiểu khi bán hết số cá trong hồ.
Câu 22. Biết tỉ lệ nảy mầm của một loại hạt giống là 0,9. Với độ tin cậy 0,99,
nếu muốn độ dài khoảng ước lượng của tỉ lệ nảy mầm không vượt quá 0,02
thì cần phải gieo bao nhiêu hạt?
Câu 23. Người ta đo chiều sâu của biển, sai lệch ngẫu nhiên được giả thiết
phân phối theo quy luật chuẩn với độ lệch là 30m. Cần đo bao nhiêu lần để
xác định chiều sâu của biển với sai lệch không quá 12m và độ tin cậy đạt được 99,73%.
Câu 24. Kiểm tra ngẫu nhiên 28 sản phẩm cùng loại do một máy sản xuất, ta thu được kết quả Khối lượng sản 3,94 3,97 4,00 4,03 4,06 phẩm (kg) Số sản phẩm 2 7 10 6 3
a) Với độ tin cậy 0,95, hãy Tìm khoảng ước lượng của khối lượng
trung bình của sản phẩm do máy đã sản xuất.
b) Với độ tin cậy 0,95, hãy Tìm khoảng ước lượng của khối lượng
trung bình tối đa của sản phẩm do máy đã sản xuất.
c) Với độ tin cậy 0,95, hãy Tìm khoảng ước lượng của khối lượng
trung bình tối thiểu của sản phẩm do máy đã sản xuất.
Câu 25. Đo áp lực X (tính bằng kg/cm2) của một số thùng chứa, ta được bảng kết quả sau. Áp lực 200 210 220 230 240 250 Số thùng 10 26 56 64 30 14
Biết rằng áp lực là một đại lượng có phân phối chuẩn. Với γ = 0,99, hãy tìm
A. Khoảng ước lượng của áp lực trung bình.
B. Khoảng ước lượng của áp lực trung bình tối đa
C. Khoảng ước lượng của áp lực trung bình tối thiểu
Câu 26.. Tại một trạm đăng kí xe môtô của thành phố người ta thấy nếu 576 xe đăng kí có 72 xe SH.
a- Hãy ước lượng tỉ lệ tối đa loại xe SH được đăng kí với độ tin cậy 95%.
b- Trên toàn thành phố 1 năm có 450 xe SH được đăng kí, hãy ước
lượng tổng số xe môtô tối đa được đăng kí toàn thành phố trong năm đã.
Câu 27. Đo đường kính của một số chi tiết do một máy sản xuất, ta có số liệu sau: Đường kính (mm) Số chi tiết 19,80 – 19,85 3 19,85 – 19,90 5 19,90 – 19,95 16 19,95 – 20,00 28 20,00 – 20,05 23 20,05 – 20,10 14 20,10 – 20,15 7 20,15 – 20,20 4
Quy định những chi tiết có đường kính từ 19,9 mm đến 20,1 mm là
những chi tiết đạt tiêu chuẩn.
a) Ước lượng đường kính trung bình của của chi tiết do máy đã sản
xuất với độ tin cậy 95%.
b) Ước lượng tỉ lệ chi tiết đạt tiêu chuẩn với độ tin cậy 95,45%.
c) Ước lượng đường kính trung bình của của chi tiết đạt tiêu chuẩn với độ tin cậy 96%.
d) Khi ước lượng đường kính trung bình của của chi tiết đạt tiêu chuẩn,
nếu muốn độ chính xác đạt được 0,02mm và độ tin cậy 99% thì cần đo thêm bao nhiêu chi tiết nữa?
e) Nếu muốn độ chính xác khi ước lượng tỉ lệ chi tiết đạt tiêu chuẩn là
5% với cùng độ tin cậy 99% thì cần đo bao nhiêu chi tiết ?
Câu 28. Qua kiểm tra số giờ tự học trong ngày của sinh viên trường Đại học
Lao động- Xã hội, người ta hỏi 100 sinh viên có kết quả Số giờ tự học
0,5-1,5 1,5-2,5 2,5-3,5 3,5-4,5 4,5-5,5 Số SV 10 30 30 20 10
a) Hãy ước lượng số giờ tự học trung bình tối đa cho sinh viên của
trường với độ tin cậy 95%. Biết số giờ tự học của mỗi sinh viên là biến ngẫu nhiên phân phối chuẩn.
b) Trường có 4000 sinh viên thì có khoảng bao nhiêu sinh viên có số
giờ tự học trên 3,5 giờ (Độ tin cậy của ước lượng là 95%)




