Bài tập xác suất thống kê có lời giải chi tiết nhất

Bài tập xác suất thống kê có lời giải chi tiết nhất
1. Giới thiệu về xác suất thống kê
Xác suất thống kê là một trong những lĩnh vực quan trọng trong toán học ứng
dụng, có vai trò then chốt trong việc phân tích dữ liệu và đưa ra những quyết
định chính xác trong nhiều lĩnh vực như khoa học, kinh tế, y học và kỹ thuật.
Việc hiểu rõ các khái niệm cơ bản và phương pháp giải bài tập xác suất
thống kê không chỉ giúp người học nâng cao kỹ năng tư duy logic mà còn tạo
nền tảng vững chắc để áp dụng trong thực tiễn.
Mục tiêu của bài viết
Mục tiêu của bài viết này là giúp người đọc hiểu sâu hơn về các khái niệm cốt
lõi trong xác suất thống kê và phát triển kỹ năng giải quyết các bài toán thống
kê từ cơ bản đến nâng cao. Các bài tập được trình bày sẽ đi kèm với lời giải
chi tiết, giúp người đọc dễ dàng nắm bắt phương pháp giải bài tập và vận
dụng vào các tình huống thực tế.
Đối tượng hướng đến
Bài viết này được thiết kế dành cho sinh viên, học sinh các cấp, những người
đang học hoặc nghiên cứu về xác suất thống kê. Ngoài ra, bài viết cũng có
thể hữu ích cho các nhà nghiên cứu, chuyên gia hoặc bất kỳ ai đang quan
tâm đến việc áp dụng các kỹ thuật thống kê trong công việc hay nghiên cứu khoa học.
Tổng quan về xác suất thống kê
Xác suất thống kê là sự kết hợp giữa lý thuyết xác suất và các phương pháp
thống kê, giúp chúng ta phân tích và dự đoán các hiện tượng ngẫu nhiên
trong đời sống. Xác suất là khái niệm đo lường khả năng xảy ra của một sự
kiện, trong khi thống kê cung cấp các công cụ để thu thập, phân tích và diễn
giải dữ liệu. Tầm quan trọng của xác suất thống kê ngày càng được thể hiện
rõ trong các ngành khoa học, nghiên cứu thị trường, y tế và các quyết định
chính sách, giúp con người đưa ra các dự báo và quyết định dựa trên dữ liệu
một cách chính xác và hiệu quả.
2. Các khái niệm cơ bản trong xác suất thống kê Không gian mẫu:
Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là
không gian mẫu, ký hiệu là Ω.
Ví dụ: Xúc xắc có 6 mặt đánh số chấm từ 1 chấm đến 6 chấm. Không gian
mẫu của 1 lần tung xúc xắc là Ω = {1; 2; 3; 4; 5; 6}. Biến cố:
Mỗi tập con của không gian mẫu được gọi là một biến cố, kí hiệu là A, B, C, …
Biến cố có thể phân loại thành: - Biến cố chắc chắn:
Là biến cố chắc chắn xảy ra trong một phép thử, và người ta kí hiệu là: W
Ví dụ: Tung một con xúc xắc. Gọi A là biến cố xúc xắc xuất hiện mặt có số
chấm nhỏ hơn hoặc bằng 6. Khi đó ta nói A là biến cố chắc chắn, A = W. - Biến cố không thể:
Là biến cố không thể xảy ra trong một phép thử, và người ta kí hiệu là: Ø
Ví dụ: Tung một con xúc xắc. Gọi B là biến cố xúc xắc xuất hiện mặt 7 chấm.
Khi đó ta nói A là biến cố không thể, A = Ø - Biến cố ngẫu nhiên:
Là biến cố có thể xảy ra cũng không thể xảy ra trong một phép thử. Ta
thường dùng các chữ cái A, B, C,.. để kí hiệu cho biến cố ngẫu nhiên.
Ví dụ: Một xạ thủ bắn vào một tấm bia, gọi A là biến cố xạ thủ bắn trúng bia,
A là biến cố ngẫu nhiên.
- Biến cố thuận lợi (Biến cố kéo theo)
Biến cố A được gọi là thuận lợi cho biến cố B nếu A xảy ra thì B cũng xảy ra. Kí hiệu: AB.
Ví dụ: Tung một con xúc xắc. Gọi A là biến cố xúc xắc xuất hiện mặt 2 chấm
và B là biến cố xuất hiện mặt chẵn. Khi đó ta nói A B.
Đặc biệt: Nếu A B và B A thì A và B là hai biến cố tương đương. Kí hiệu A = B.
Ví dụ: Mỗi số chấm trên mặt xúc xắc tương ứng 5 điểm. Gọi A là biến cố xúc
xắc xuất hiện mặt 6 chấm, B là biến cố được 30 điểm. Khi đó A = B. - Biến cố sơ cấp:
Biến cố A được gọi là biến cố sơ cấp nếu nó không có biến cố cố nào thuận
lợi cho nó (trừ chính nó), tức là không thể phân tích được nữa.
Ví dụ 7: Gọi Ai là biến cố xúc xắc xuất hiện mặt i chấm (i = 1,..,6) thì A1,
A2, .. , A6 là các biến cố sơ cấp.
Gọi B là biến cố thu được mặt có số chấm chẵn.
B = A2 + A4 + A6 thì B không phải là biến cố sơ cấp.
Tập hợp tất cả các biến cố sơ cấp của một phép thử được gọi là không gian
các biến cố sơ cấp và kí hiệu: W
Ví dụ: W = { A1, A2, A3, A4, A5, A6}. - … Xác suất:
Xác suất của một biến cố là một con số đặc trưng cho khả năng xảy ra khách quan của biến cố đó.
Xác suất của biến cố A, ký hiệu là P(A ), có thể được định nghĩa bằng nhiều cách.
Giá trị kỳ vọng và phương sai: Kỳ vọng
Cho X là biến ngẫu nhiên rời rạc có hàm mật độ xác định bởi bảng sau: X x1 x2 x3 . . x(n) fX(x) p1 p2 p3 . . p(n)
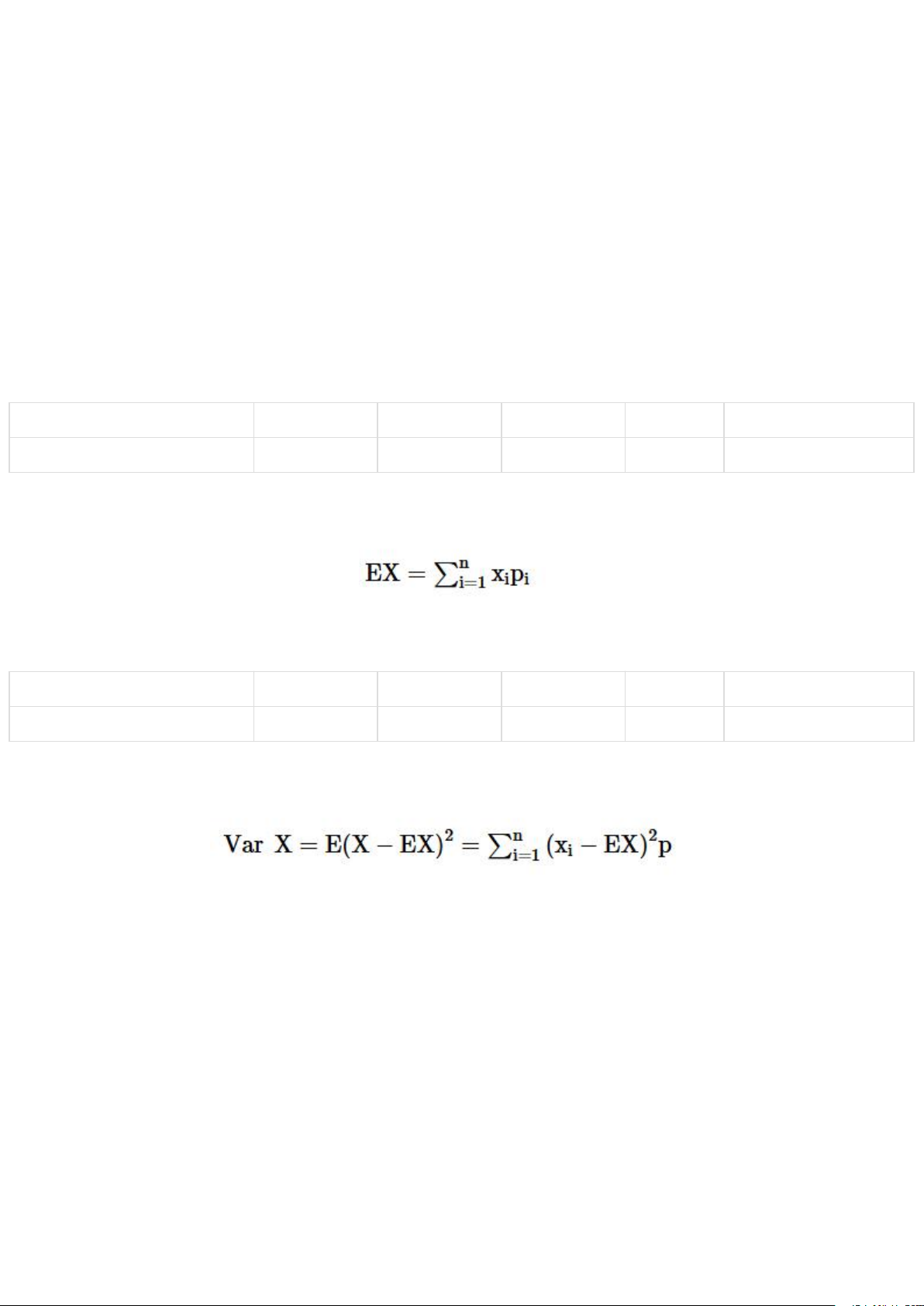
Kỳ vọng của X, kí hiệu EX, là đại lượng đặc trưng cho giá trị trung bình của X
(về xác suất) và được tính bởi công thức Phương sai
Cho X là biến ngẫu nhiên rời rạc có hàm mật độ xác định bởi bảng sau: X x1 x2 x3 . . x(n) fX(x) p1 p2 p3 . . p(n)
Phương sai của X, kí hiệu VarX, là đại lượng đặc trưng cho độ phân tán của
X và được xác định bởi công thức
3. Các bài tập xác suất thống kê thường gặp Bài tập về tổ hợp:
Từ các số 1; 2; 3; 4; 5; 6; 7. Có bao nhiêu số tự nhiên thỏa mãn
a) Số có 7 chữ số khác nhau
b) Số có 5 chữ số khác nhau
c) Số có 7 chữ số khác nhau và có chữ số 1 là hàng chục nghìn
d) Số có 7 chữ số khác nhau và chữ số 2 không ở hàng đơn vị Lời giải
a) Số các số có 7 chữ số khác nhau được lập từ 7 chữ số trên là 7! = 5040
b) Số các số có 5 chữ số khác nhau được lập từ 7 chữ số trên là 2520
c) Số có 7 chữ số khác nhau và có chữ số 1 là hàng chục nghìn
Chữ số hàng chục nghìn có 1 cách chọn (là chữ số 1)
Các hàng khác, số cách chọn là một hoán vị của 6 chữ số còn lại: 6!
Vậy có 1 x 6! = 720 số có 7 chữ số khác nhau và có chữ số 1 là hàng chục nghìn.
d) Số có 7 chữ số khác nhau và chữ số 2 không ở hàng đơn vị
Số các số có 7 chữ số khác nhau là 7!
Ta lập số có 7 chữ số khác nhau có chữ số 2 ở hàng đơn vị
Chữ số hàng đơn vị có 1 cách chọn (là chữ số 2)
Các hàng khác, số cách chọn là một hoán vị của 6 chữ số còn lại: 6!
Số các số có 7 chữ số và chữ số 2 ở hàng đơn vị là: 1 x 6!
Vậy có 7! – 6! = 4320 số có 7 chữ số khác nhau và chữ số 2 không ở hàng đơn vị.
Bài tập về biến cố:
Gieo một đồng xu cân đối và đồng chất 3 lần và quan sát sự xuất hiện mặt
sấp (S) và mặt ngửa (N).
a) Mô tả không gian mẫu. Tính số phần tử của không gian mẫu
b) Xác định và tính số phần tử của các biến cố
A: “Lần gieo đầu xuất hiện mặt sấp”.
B: “Ba lần xuất hiện các mặt như nhau”.
C: “Đúng 2 lần xuất hiện mặt ngửa”.
D: “Ít nhất 1 lần xuất hiện mặt sấp”. Lời giải a) Không gian mẫu
Ω ={SSS; SSN; SNS; SNN; NNN; NNS; NSN; NSS}
Do đó: Số phần tử của không gian mẫu: |Ω| = 8
(Cách khác: Số phần tử được tính bằng: 2 x 2 x 2 = 8)
b) A = {SSS; SSN; SNS; SNN}; |A| = 4 B = {SSS; NNN}; |A| = 2 C = {SNN; NNS; NSN}; |C| = 3
D = {SSS; SSN; SNS; SNN; NNS; NSN; NSS}; |D| = 7
Bài tập về phân phối xác suất:
Với Ví dụ 4, giả sử tất cả các bản fax chỉ gồm 1, 2, 3 hoặc 4 trang với xác
suất như nhau. Tìm bảng phân phối xác suất của biến ngẫu nhiên Y chỉ chi phí cho một bản fax.
Giải. Theo Ví dụ 4, Y là một biến ngẫu nhiên rời rạc với Y = {10, 19, 27, 34} và P(Y = 10) = P(X = 1) = 0,25 P(Y = 19) = P(X = 2) = 0,25 P(Y = 27) = P(X = 3) = 0,25 P(Y = 34) = P (X = 4) = 0,25
Do đó, bảng phân phối xác suất của Y là Y 10 19 27 34 P(Y = y) 0,25 0,25 0,25 0,25
4. Hướng dẫn giải chi tiết các bài tập
Để giải quyết một bài tập xác suất thống kê hiệu quả, chúng ta cần tuân thủ
một quy trình cụ thể. Quy trình này sẽ giúp bạn hiểu rõ hơn về từng bước cần
thực hiện để đạt được kết quả chính xác: - Phân tích đề bài
Đầu tiên, bạn cần đọc kỹ và phân tích đề bài để xác định các yếu tố cần thiết
và những thông tin quan trọng. Các yếu tố này có thể bao gồm:
+ Đối tượng xác suất: Xác định sự kiện ngẫu nhiên mà bạn cần tính xác suất,
chẳng hạn như khả năng xuất hiện của một kết quả cụ thể trong một thí
nghiệm ngẫu nhiên (ví dụ: tung đồng xu, quay vòng quay, v.v.).
+ Dữ liệu cho sẵn: Các thông tin trong đề bài như tần suất, số liệu thống kê,
đặc điểm phân phối xác suất, v.v.
+ Yêu cầu bài toán: Bạn cần làm rõ bài toán yêu cầu tính toán gì, có phải là
xác suất của một sự kiện, trung bình, phương sai hay là một yếu tố nào khác
liên quan đến phân phối xác suất. - Lựa chọn công thức
Sau khi phân tích đề bài, bước tiếp theo là lựa chọn các công thức phù hợp
để giải quyết bài toán. Tùy theo từng loại bài toán, bạn sẽ phải sử dụng các
công thức xác suất và thống kê khác nhau. - Thực hiện tính toán
Khi đã xác định được công thức phù hợp, bước tiếp theo là thực hiện tính
toán. Lúc này, bạn cần làm rõ từng bước và tính toán cẩn thận, tránh nhầm
lẫn. Việc trình bày rõ ràng từng bước giải quyết bài toán sẽ giúp bạn dễ dàng
kiểm tra lại và hạn chế sai sót.
+ Tính toán cẩn thận: Lưu ý đến các phép toán như cộng, trừ, nhân, chia khi áp dụng công thức.
+ Trình bày rõ ràng: Viết lại các bước tính toán theo trình tự hợp lý, đồng thời
chú thích các giá trị đã sử dụng để minh bạch hóa quá trình giải.
Ví dụ, nếu bài toán yêu cầu tính xác suất trong một phân phối nhị thức, bạn
cần thay các giá trị vào công thức của phân phối nhị thức và tính toán kết quả. - Kiểm tra kết quả
Sau khi hoàn tất các bước tính toán, bạn cần kiểm tra lại kết quả để đảm bảo
tính chính xác. Một số phương pháp kiểm tra bao gồm:
+ So sánh với đáp án: Nếu bài toán có đáp án có sẵn, bạn có thể so sánh kết
quả tính toán của mình với đáp án để kiểm tra tính chính xác.
+ Kiểm tra tính hợp lý: Đối với các bài toán xác suất, kết quả cuối cùng phải
nằm trong khoảng [0,1]. Nếu kết quả vượt quá khoảng này, đó là dấu hiệu
của sai sót trong quá trình tính toán.
+ Kiểm tra với thực tế: Nếu có thể, bạn có thể kiểm tra kết quả bằng cách so
sánh với các tình huống thực tế hoặc áp dụng phương pháp khác để kiểm chứng kết quả.
Document Outline

• Bài tập xác suất thống kê có lời giải chi tiết nhấ
  • 1. Giới thiệu về xác suất thống kê
  • 2. Các khái niệm cơ bản trong xác suất thống kê
  • 3. Các bài tập xác suất thống kê thường gặp
  • 4. Hướng dẫn giải chi tiết các bài tập