Bài Tập Xác Suất Thống Kê (XSTK) - Tổng Hợp Chương 1 và 2 (Btxstk-2023) | Đại học Điện lực

lOMoARcPSD| 59149108
BỘ CÔNG THƯƠNG - ĐẠI HỌC ĐIỆN LỰC
BÀI TẬP XÁC SUẤT THỐNG KÊ
Tên sinh viên: . . . . . . . . . . . . . . . . . . . .
Sư tầm từ đề thi XSTK các năm
Biên tập lại theo trình tự bài giảng lý thuyết
Tài liệu lưu hành nội bộ HÀ NỘI – 4 / 202 3 lOMoARcPSD| 59149108 Câu hỏi 1:
Có 50 đề thi trong đó có 15 đề khó, 35 đề trung bình. Một học sinh bốc ngẫu nhiên hai đề thi. Tính xác suất để
học sinh đó bốc được ít nhất một đề trung bình? Câu hỏi 2:
Một máy có ba bộ phận hoạt động độc lập với nhau. Xác suất để các bộ phận bị hỏng lần lượt là 0,15; 0,35 và
0,25. Tính xác suất của các biến cố sau:
Có đúng 2 bộ phận bị hỏng.
Có ít nhất 1 bộ phận bị hỏng. Câu hỏi 3:
Một hộp có 25 bóng đèn, trong đó có 7 bóng hỏng. Một người lấy ngẫu nhiên 3 bóng trong hộp để kiểm tra. Tính xác suất để:
có bóng hỏng; số bóng hỏng nhiều hơn số bóng không hỏng. Câu hỏi 4:
Một nhân viên bán hàng mỗi năm đến chào hàng ở công ty Phương Đông ba lần. Xác suất để lần đầu bán được
hàng là 0,7. Nếu lần trước bán được hàng thì xác suất để lần sau bán được hàng là 0,8, còn nếu lần trước không
bán được hàng thì xác suất để lần sau bán được hàng chỉ là 0,5. Tìm xác suất để:
Cả ba lần đều bán được hàng.
Có đúng hai lần bán được hàng. Câu hỏi 5:
Ba máy 1, 2 và 3 của một xí nghiệp sản xuất theo thứ tự 60%, 25% và 15% tổng số sản phẩm của một xí nghiệp.
Tỉ lệ sản xuất ra phế phẩm của các máy trên, theo thứ tự, là 5%, 3% và 4%. Lấy ngẫu nhiên một sản phẩm từ lô
hàng của xí nghiệp, trong đó để lẫn lộn các sản phẩm do ba máy sản xuất. Tính xác suất để sản phẩm lấy ra là sản phẩm tốt? Câu hỏi 6: lOMoARcPSD| 59149108
Một hộp có chứa 9 quả cầu trắng và 3 quả cầu đen cùng kích thước. Rút ngẫu nhiên cùng một lúc 4 quả cầu. Tính
xác suất để trong 4 quả cầu rút được có ít nhất 2 quả cầu đen. Câu hỏi 7:
Một công ty cần tuyển 4 nhân viên. Có 10 người, gồm 7 nam và 3 nữ nộp đơn xin dự tuyển, và mỗi người đều
có cơ hội được tuyển như nhau. Tính xác suất để trong 4 người được tuyển có ít nhất một nữ? Câu hỏi 8:
Có 10 chiếc túi như sau: 4 túi loại 1, trong mỗi túi loại 1 chứa 6 viên bi trắng và 4 viên bi đen; 6 túi loại 2, trong
mỗi túi loại 2 chứa 3 viên bi trắng và 7 viên bi đen. Chọn ngẫu nhiên 1 chiếc túi rồi lấy ngẫu nhiên 2 viên bi. Tính
xác suất để lấy được hai viên bi trắng. Câu hỏi 9:
Có hai lô sản phẩm: Lô I có 8 chính phẩm và 4 phế phẩm, lô II có 9 chính phẩm và 3 phế phẩm. Lấy ngẫu nhiên 1
sản phẩm từ lô I bỏ sang lô II rồi từ lô II lấy ngẫu nhiên một sản phẩm. Tính xác suất để sản phẩm lấy ra sau cùng là chính phẩm. Câu hỏi 10:
Một lô hàng gồm có 80 sản phẩn loại A và 20 sản phẩm loại B . Trong quá trình vận chuyển về kho bị mất một sản
phẩm. Lấy ngẫu nhiên trong các sản phẩm còn lại 1 sản phẩm. Tính xác suất để lấy được một sản phẩm loại A? Câu hỏi 11:
Hai máy tiện cùng sản xuất ra một loại trục xe đạp như nhau. Các trục xe được đóng chung vào một kiện. Năng
suất của máy tiện thứ hai gấp đôi năng suất của máy tiện thứ nhất. Máy tiện thứ nhất sản xuất trung bình được
85 % trục loại tốt, máy tiện thứ hai sản xuất trung bình được 90 % trục loại tốt. Lấy ngẫu nhiên từ kiện một trục.
Tìm xác suất để lấy được trục loại tốt? Câu hỏi 12:
Ba sinh viên A,B,C cùng làm bài thi. Xác suất làm được bài của sinh viên A là 0,7; của sinh viên B là 0,8; của sinh
viên C là 0,6. Tìm xác suất để: Có 1 sinh viên làm được bài; Có 2 sinh viên làm được bài. Câu hỏi 13:
Có 2 máy cùng sản xuất một loại sản phẩm. Tỉ lệ chính phẩm của máy thứ nhất là 0,9;
của máy thứ hailà 0,85. Từ một kho chứa 1 sản phẩm của máy thứ nhất (còn lại của máy thứ hai) lấy ngẫu nhiên một 3
sản phẩm để kiểm tra. lOMoARcPSD| 59149108
Tính xác suất lấy được phế phẩm.
Nếu sản phẩm lấy ra là chính phẩm. Tính xác suất sản phẩm đó do máy thứ hai sản xuất. Câu hỏi 14:
Có hai lô hàng. Lô thứ nhất có 8 chính phẩm và 4 phế phẩm, lô thứ hai có 9 chính phẩm và 3 phế phẩm. Chọn
ngẫu nhiên 1 lô và từ đó lấy ngẫu nhiên ra 2 sản phẩm:
Tìm xác suất để lấy được 2 chính phẩm;
Giả sử đã lấy được 2 chính phẩm. Tìm xác suất để đó là 2 sản phẩm của lô thứ nhất. Câu hỏi 15:
Một lô hàng có 70% sản phẩm của máy A và 30% sản phẩm của máy B. Tỷ lệ phế phẩm của các máy tương ứng là
3% và 4%. Lấy ngẫu nhiên 1 sản phẩm để kiểm tra:
Tìm xác suất để lấy được phế phẩm;
Giả sử đã lấy được phế phẩm thì phế phẩm đó có khả năng do máy nào sản xuất là nhiều hơn. Câu hỏi 16:
Một túi chứa 9 nhẫn bạc và 1 nhẫn vàng. Túi kia có 1 nhẫn bạc và 5 nhẫn vàng. Từ mỗi túi rút ra ngẫu nhiên một
nhẫn. Những chiếc nhẫn còn lại được dồn vào một túi thứ ba. Từ túi thứ ba này lại rút ngẫu nhiên một chiếc
nhẫn. Tính xác suất để ta rút ra được nhẫn vàng ở túi thứ ba. Câu hỏi 17:
Hộp thứ nhất có 7 sản phẩm loại A và 3 sản phẩm loại B ; hộp thứ hai có 5 sản phẩm loại A và 5 sản phẩm loại
B . Lấy ngẫu nhiên từ mỗi hộp ra 2 sản phẩm. Tính xác suất để được ba sản phẩm loại A? Câu hỏi 18:
Trước cổng trường đại học có 3 quán cơm chất lượng ngang nhau. Có 3 sinh viên, mỗi người độc lập chọn một
quán để ăn. Tính xác suất để
3 sinh viên vào cùng một quán;
2 sinh viên vào cùng một quán, còn người kia thì vào quán khác. Câu hỏi 19:
Một nhà máy có 3 phân xưởng. Phân xưởng I có tỷ lệ làm hỏng sản phẩm (hay còn gọi là tỷ lệ phế phẩm) là 3%;
phân xưởng II có tỷ lệ phế phẩm là 5%, và phân xưởng III có tỷ lệ phế phẩm 7%. Biết rằng năng suất chế tạo sản
phẩm của phân xưởng I và II là như nhau và năng suất của phân xưởng III bằng năng suất của phân xưởng I và II cộng lại.
Từ kho của nhà máy, lấy ra ngẫu nhiên 1 sản phẩm để kiểm tra. Tìm xác suất để lấy được phế phẩm.
Giả sử đã lấy được chính phẩm. Tìm xác suất để sản phẩm đó do phân xưởng II sản xuất. lOMoARcPSD| 59149108 Câu hỏi 20:
Một hộp đựng 10 phong bì bốc thăm trúng thưởng, trong đó có 3 phong bì đựng 500 nghìn và 7 phong bì đựng
100 nghìn. Bốc ngẫu nhiên liên tiếp hai phong bì. Nếu biết phong bì thứ hai có 500 nghìn, tìm xác suất để phong
bì đầu tiên cũng có 500 nghìn?
BÀI TẬP TỔNG HỢP CHƯƠNG 2
(BIẾN NGẪU NHIÊN VÀ QUI LUẬT PHÂN PHỐI XÁC SUẤT CỦA BIẾN NGẪU NHIÊN) X có hàm mt đ xác sut
( a.x (3 x ) x , 3] f ( x ) = 0
x / [0 , 3] .
a, E ( X ) , V ( X ) ? Câu hỏi 2:
Một lô hàng gồm 20 máy tính xách tay tương tự nhau, trong đó có 3 máy có khiếm khuyết. Một trường học mua
ngẫu nhiên 3 máy. Lập bảng phân phối xác suất cho số máy tính xác tay có khiếm khuyết X mà trường h c mua
ph i, tính ọ ả E(X),V (X). Câu hỏi 3:
Một lô hàng có 8 chính phẩm và 6 phế phẩm. Lấy ngẫu nhiên từ lô hàng 3 sản phẩm. Gọi X là số chính ph m l
y đẩ ấ ược. Hãy l p b ng phân ph i xác su t c a X; tính kì v ng ậ ả ố ấ ủ ọ E(X), phương sai V (X)? Câu hỏi 4:
Có 2 hộp, mỗi hộp đựng 10 sản phẩm. Số phế phẩm có trong mỗi hộp tương ứng là 3 và 6(còn lại là sản phẩm
tốt). Lấy ngẫu nhiên từ mỗi hộp ra một sản phẩm. Gọi X là số sản phẩm tốt có trong 2 sản phẩm lấy ra. Hãy lập
bảng phân phối xác suất của X; Tính E(X); V (X). Câu hỏi 5:
Một hộp có 3 bi xanh và 2 bi đỏ. Một người lấy lần lượt từng viên bi (không hoàn lại) cho đến khi lấy được 1
bi xanh. Gọi X là s bi l y ra. Hãy l p b ng phân ph i xác su t c a X; tính ố ấ ậ ả ố ấ ủ E(X),V (X). lOMoARcPSD| 59149108
X có qui lut phân phi xác sut nh sau: X x x p x , x p
E ( X ) = 1 , 8 và V ( X ) = 2 , 76 ( x < x Câu hỏi 7:
Trong 1 000 000 vé xổ số phát hành có 1 giải trị giá 100 triệu đồng, 20 giải trị giá 20 triệu đồng, 150 giải trị giá 5
triệu đồng, 1500 giải trị giá 1 triệu đồng. Một người mua ngẫu nhiên một vé xổ số. Lập bảng phân phối của số
tiền người đó nhận được, tìm kì vọng, phương sai.
X có hàm mt đ xác sut nh sa u (đn v: n gà n sn phm) :
( k (30 x ) vi x , 30)
f ( x ) = 0 vi x / (0 , 30) ( k x x , f x
x / , . k f x k
E X , V X ( kx x , f x
x / , . k f x X k E X Câu hỏi 11:
Một lô hàng có 600 sản phẩm loại I và 400 sản phẩm loại II. Lấy ngẫu nhiên ra 5 sản phẩm có hoàn lại. Gọi X là s
s n ph m lo i I l y đố ả ẩ ạ ấ ược. L pậ b ngả phân ph iố xác su tấ c aủ X; Tìm kỳ v ngọ và phương sai c aủ X. lOMoARcPSD| 59149108 X có hàm mt đ xác sut
( a.x (5 x ) x , 5]
f ( x ) = 0 x / [0 , 5] .
a, E ( X ) , V ( X ) ? X có hàm mt đ xác sut
( k. ( x x , f ( x ) = 4]
x / [0 , 4]
k, E ( X ) , V ( X ) ? .
X liên tc có hàm mt đ xác sut k f ( x ) = x x , 0 3]
x / [1 , 3] .
k, E ( X ) , V ( X ) ? X có hàm mt đ xác sut
( k. sin x , khi x , π ] f ( x ) = , khi 0
x / [0 , π ] . Tìm hằng số k ; Tìm kỳ vng, ph ng sai ca X . Câu hỏi 16:
Một hộp đựng 7 chai thuốc trong đó có 1 chai giả. Người ta kiểm tra lần lượt từng chai(không hoàn lại) cho
đến khi phát hiện được chai thuốc giả thì thôi. Gọi X là s chai ố được ki m tra.ể L pậ b ngả
phân ph iố xác su tấ c aủ X;
Tìm kỳ v ngọ và phương sai c aủ X. Câu hỏi 17:
Một thiết bị gồm 3 bộ phận hoạt động độc lập với nhau. Xác suất trong thời gian hoạt động các bộ phận bị hỏng
tương ứng là 0,3; 0,4 và 0,5. Gọi X là s b ph n b h ng trong th i ố ộ ậ ị ỏ ờ gian ho t đ ng.ạ ộ lOMoARcPSD| 59149108
Tìm b ngả phân ph iố xác su tấ c aủ X.
Tính xác su tấ để trong th iờ gian ho tạ đ ngộ có không quá 2 bộ ph nậ bị h ng.ỏ Câu hỏi 18:
Có hai hộp sản phẩm: hộp thứ nhất có 9 chính phẩm và 3 phế phẩm, hộp thứ hai có 10 chính phẩm và 2 phế
phẩm. Lấy ngẫu nhiên một hộp rồi từ đó lấy ngẫu nhiên ra 1 sản phẩm.
Lập bảng phân phối xác suất của số chính phẩm được lấy ra; Tính số chính phẩm
trung bình được lấy ra. ( ae− x x , 2] f ( x ) = 0
x / [0 , 2] .
a, E ( X ) , V ( X ) ? f x , 0) k (1 + 2 x ) ( x ) = vi x , 2] k (1 vi x / [ , 2] 0 x )
Xác đn h k đ f ( x ) là hàm mt đ xác sut ca bin ngu nhiên X . Tìm kỳ vng và ph ng sai ca X . lOMoARcPSD| 59149108 X i n i
Ước lượng mức thu nhập/tháng trung bình của nhân viên công ty A với độ 琀椀 n cậy 0,95. Biết thu
xỉ) chuẩn. Ước lượng nhu cầu trung bình về mặt hàng này của khu vực trong một năm với độ 琀椀 n cậy 95%. lOMoARcPSD| 59149108 Câu hỏi 5:
Kết quả quan sát về hàm lượng vitamin C của một loại trái cây cho ở bảng sau: Hàm lượng vitamin
3 - 7 8 - 10 11 - 13 14 -16 17 - 19 20 - 24 C(%) Số trái cây 5 10 20 35 25 5
Biết hàm lượng vitamin C ở trái cây này là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Với độ 琀椀 n cậy
95%, hãy 琀 m khoảng 琀椀 n cậy đối xứng của hàm lượng vitamin C trung bình trong mỗi trái; x i Câu hỏi 7:
Điều tra doanh số bán hàng X (đơn vị: triệu đồng/tháng) của các hộ kinh doanh một loại hàng năm nay cho số liệu:Doanh số(triệu 11 11,5 12 12,5 13 13,5 đồng/tháng) Số hộ 10 15 20 30 15 10
Năm trước doanh số bán hàng trung bình của các hộ này là 120 triệu/1 năm. Có thể cho rằng doanh số
bán hàng của các hộ này năm nay tăng lên không, với mức ý nghĩa 5%? Câu hỏi 8: Kích thước (cm) 11 13 15 17 19
Một loại sản phẩm A có kích thước trung bình là 14cm, nghi ngờ kích thước của sản phẩm A thay đổi nên
người ta kiểm tra một số sản phẩm và bảng số liệu sau:Số sản phẩm tương 5 10 16 12 3 ứng lOMoARcPSD| 59149108
Với mức ý nghĩa 0,05 hãy kết luận về điều trên, biết rằng kích thước của sản phẩm A là biến ngẫu nhiên
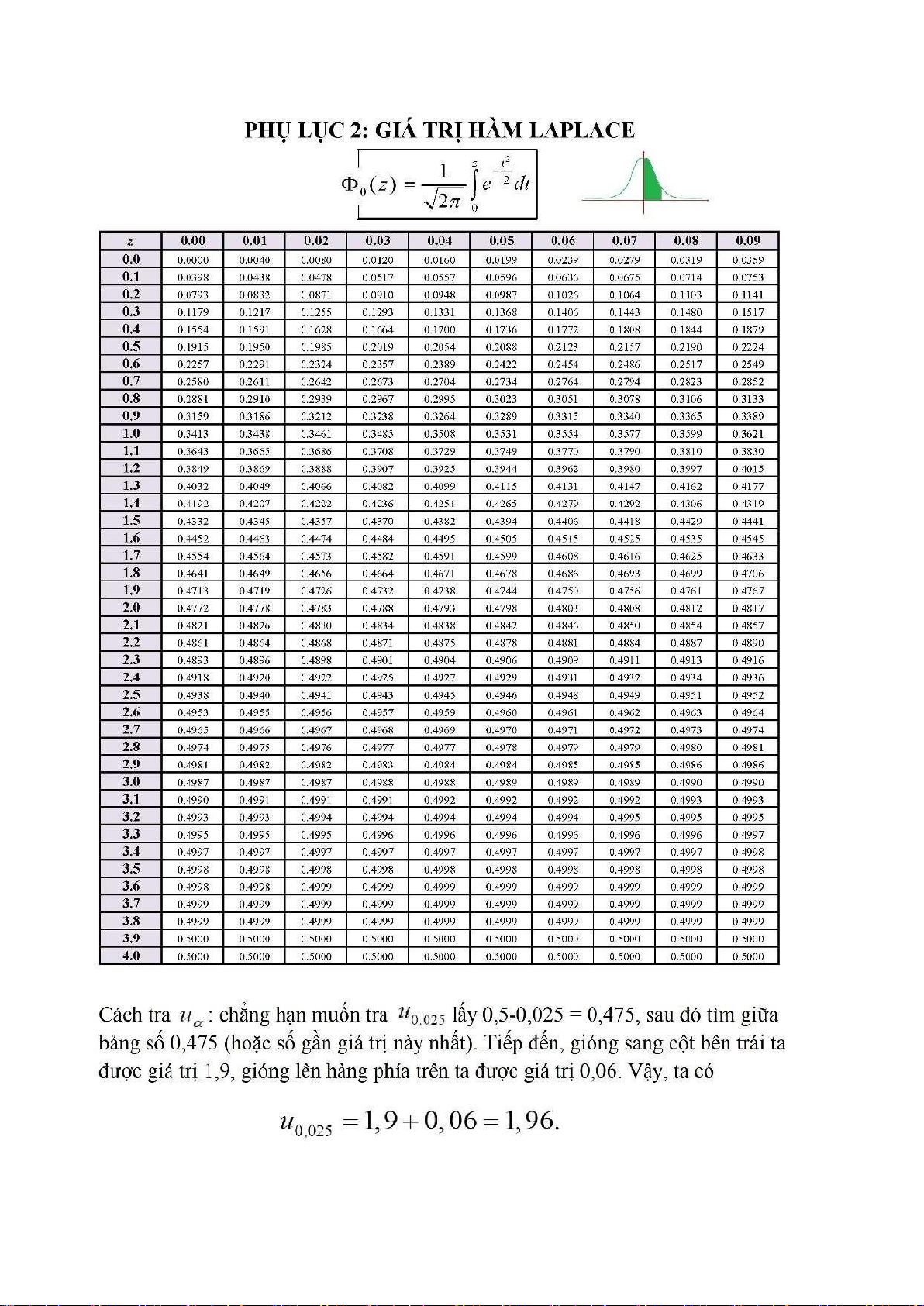
phân phối chuẩn, cho u0,025 = 1, 96; u0,05 = 1, 65. Câu hỏi 9:
Doanh số của một cửa hàng là biến ngẫu nhiên phân phối chuẩn. Điều tra doanh số của một số cửa hàng có quy
mô tương tự nhau, ta có bảng số liệu sau: Doanh số 14 16 18 20 22 (triệu/tháng) Số cửa hàng 7 15 32 24 8
Tìm khoảng 琀椀 n cậy đối xứng doanh số trung bình của các cửa hàng nói trên, với độ 琀椀 n cậy 95%.
Cho u0,025 = 1, 96; u0,05 = 1, 65. Câu hỏi 10:
Điều tra doanh số bán của một số hộ kinh doanh một ngành hàng, ta có Doanh số 11,5 11,6 11,7 11,8 11,9 12 bảng số liệu sau: (triệu/tháng) Số hộ 9 17 20 31 12 10
Tìm khoảng 琀椀 n cậy đối xứng doanh số trung bình của các hộ nói trên, với độ 琀椀 n cậy 95%. Biết
doanh số bán hàng của các hộ là đại lượng ngẫu nhiên phân phối chuẩn, cho u0,025 = 1, 96; u0,05 = 1, 65. Câu hỏi 11:
Khảo sát năng suất giống ngô của một vùng qua các điểm thu hoạch ta thu được Năng suất (tạ/ha) 7 9 11 13
17 bảng số liệu sau: Số điểm thu 3 6 11 3 1 hoạch
Với độ 琀椀 n cậy 95%, hãy 琀 nh năng suất giống ngô trung bình tối thiểu của vùng này, biết rằng năng , 064
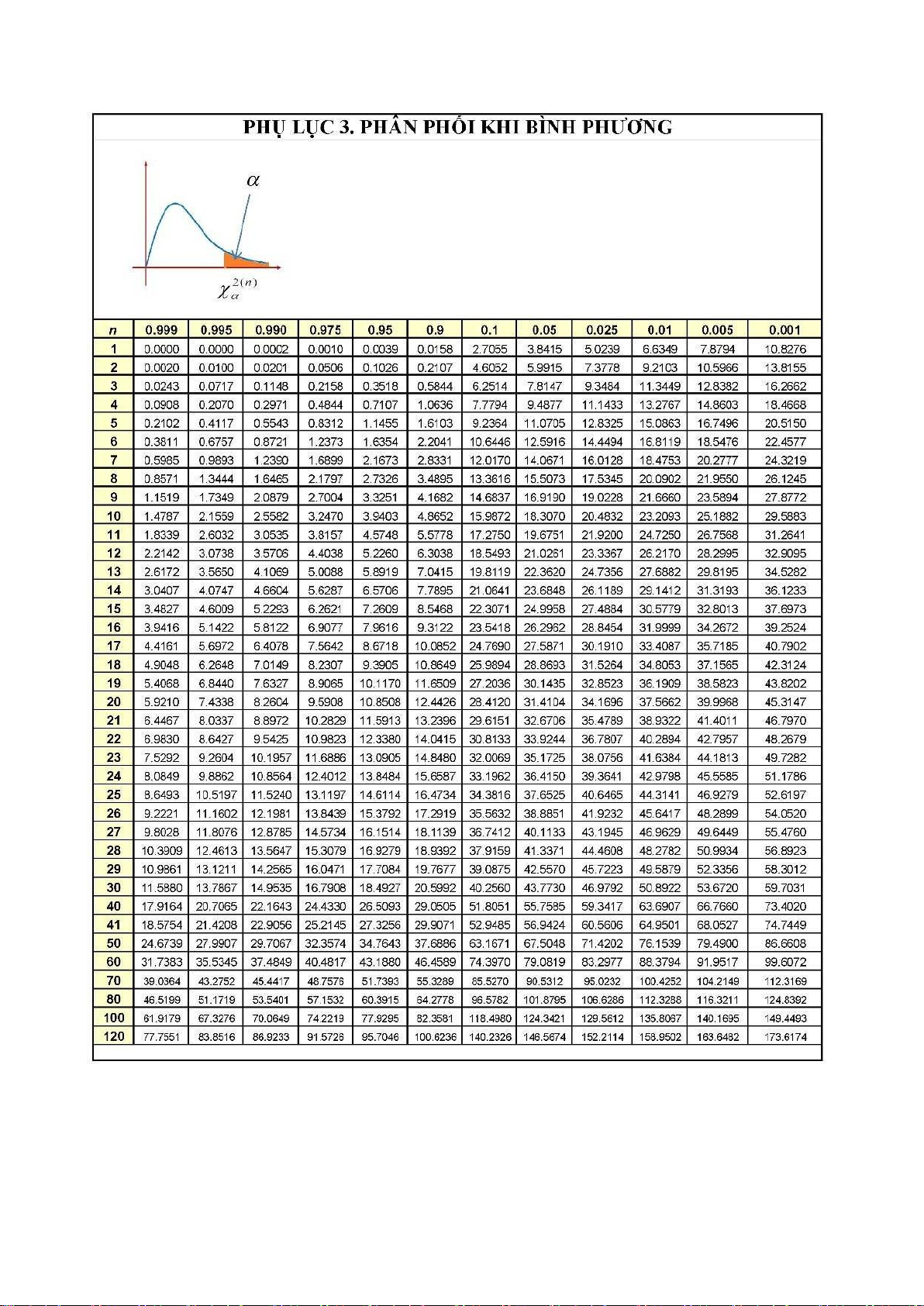
suất giống ngô của vùng này là biến ngẫu nhiên có phân phối chuẩn. Cho biết:t(23) = 20 ,
02 ; t(23) = 0,0
1, 711; u0,05 = 1, 65; u0,025 = 5 5 1,96. Câu hỏi 12:
Mức hao phí xăng trung bình cho một loại xe ôtô chạy trên đoạn đường AB là 50 lít. Do đường được tu sửa lại,
người ta cho rằng mức hao phí xăng trung bình đã giảm xuống. Điều tra một số chuyến xe chạy trên đoạn đường
AB ta thu được bảng số liệu:Mức hao phí xăng 48,5-49 49-49,5 49,5-50 50-50,5 50,5-51 lOMoARcPSD| 59149108 (lít) Số lần 5 8 10 4 2
Với mức ý nghĩa 5% hãy kết luận về ý kiến nêu trên, biết rằng mức hao phí xăng cho một loại xe ôtô chạy trên
đoạn đường AB là biến ngẫu nhiên có phân phối chuẩn. Cho biết: t(28) = 2 = 1
0,02 , 045; t(28)0 ,0
, 699; u0,05 =
1, 65; u0,025 = 1, 5 5 96. Câu hỏi 13:
Theo dõi một ôtô chạy trên đoạn đường AB ta thu được bảng số liệu về lượng xăng hao phí như sau: Mức
hao phí xăng 9,6-9,8 9,8-10 10-10,210,2-10,410,4-10,6 (lít) Số lần 6 15 27 8 3
Biết rằng lượng hao phí xăng là biến ngẫu nhiên có phân phối chuẩn, bằng khoảng 琀椀 n cậy đối xứng với
độ 琀椀 n cậy 95%, hãy ước lượng lượng hao phí xăng trung bình cho một ôtô chạy trên đoạn đường AB?
Cho biết: u0,05 = 1, 65; u0,025 = 1, 96. Câu hỏi 14:
Trọng lượng sản phẩm X do nhà máy sản suất là biến ngẫu nhiên có phân phối chuẩn với trọng lượng trung bình
là 20 (kg). Nghi ngờ máy hoạt động không bình thường làm thay
đổi trọng lượng trung bình của sản phẩm, người ta cân thử một số sản phẩm và thu được bảng số liệu sau:
Trọng lượng sản 19 20 21 22 23 phẩm Số sản phẩm 7 22 27 11 6
Với mức ý nghĩa 5%, hãy kết luận về điều nghi ngờ nói trên. Cho biết: u0,05 = 1, 65; u0,025 = 1, 96. Câu hỏi 15:
Điều tra mức thu nhập hàng tháng của một số công nhân ngành cơ khí, ta có Mức thu nhập 14 16 18 20 22 bảng số liệu sau: (triệu/tháng) Số công nhân 3 19 30 11 7
Tìm khoảng 琀椀 n cậy đối xứng mức thu nhập trung bình của công nhân ngành cơ khí nói trên, với độ 琀椀 n
cậy 95%. Biết mức thu nhập hàng tháng của công nhân ngành cơ khí là đại lượng ngẫu nhiên phân phối chuẩn,
cho u0,025 = 1, 96; u0,05 = 1, 65. lOMoARcPSD| 59149108 Câu hỏi 16:
Trọng lượng của các bao bột mỳ do một nhà máy sản xuất là 37kg. Người ta nghi ngờ Trọng lượng (kg) 34 35 36
37 38 39 trọng lượng của các bao bột mỳ đang giảm, theo dõi một số bao ta được kết quả sau:Số bao tương 2 15 21 10 5 7 ứng
Với mức ý nghĩa 0,05 hãy cho kết luận về nhận định trên, biết rằng trọng lượng của các bao bột mỳ là
biến ngẫu nhiên phân phối chuẩn, cho u0,05 = 1, 65; u0,025 = 1, 96. Câu hỏi 17:
Điều tra mức thu nhập hàng năm của một số công nhân nghành điện, ta thu được bảng: Thu nhập (triệu 8,5 8,8 9 9,2 9,5 đồng/năm) Số công nhân 5 21 26 10 5
Bằng khoảng 琀椀 n cậy đối xứng hãy ước lượng mức thu nhập trung bình hàng năm của công nhân nghành
điện, với độ 琀椀 n cậy 95%. Biết mức thu nhập hàng năm của công nhân nghành điện là đại lương ngẫu
nhiên phân phối chuẩn, cho u0,025 = 1, 96; u0,05 = 1, 65. Câu hỏi 18:
Một xí nghiệp đúc một số rất lớn các sản phẩm bằng thép với số khuyết tật trung bình ở mỗi sản phẩm là 3.
Người ta cải tiến cách sản xuất nhằm làm giảm số khuyết tật trung bình. Kiểm tra 36 sản phẩm, kếtquả thu được như sau:
Số khuyết tật trên sản 0 1 2 3 4 5 6 phẩm
Số sản phẩm tương ứngg 6 8 9 6 5 3 1
Giả sử số khuyết tật của các sản phẩm có phân phối chuẩn. Với mức ý nghĩa là 0,05 hãy cho kết luận về
hiểu quả của việc cải 琀椀 ến sản xuất đó. Cho biết: u0,05 = 1, 65; u0,025 = 1, 96. Câu hỏi 19:
Đo ion Na+ trên 14 người thu được kết quả như sau:
129; 132; 140; 141; 138; 143; 133; 138; 140; 143; 138; 140; 129; 135
Bằng khoảng tin cậy đối xứng, hãy ước lượng trung bình ion Na+ trên 14 người nêu trên ,
95%. Biết rằng lượng ion Na+ trên người là biến ngẫu nhiên có phân phối chuẩn. Cho với độ tin cậyt(13) = 1 796 0 ,0 ; lOMoARcPSD| 59149108
t)(130,02 = 2, 201. 5 5 Câu hỏi 20:
Đo lượng cholesterCholesterol150-160160-170170-180180-190190-200200-210 (đơn vị: mg%) cho
một số người, ta thu được bảng số liệu sau: Số người 2 4 5 6 4 3
Với độ 琀椀 n cậy 95%, hãy ước lượng cholesterol trung bình của nhóm người này, biết rằng lượng cholesterol
của nhóm người này là biến ngẫu nhiên có phân phối chuẩn. Cho:t(23) = 20,02 , 069; t(23) = 10,0 , 714. 5 5 lOMoARcPSD| 59149108 CÁC BẢNG PHỤ LỤC lOMoARcPSD| 59149108 lOMoARcPSD| 59149108 lOMoARcPSD| 59149108